Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jul;85(1):85–96. doi: 10.1016/S0006-3495(03)74457-9

Membrane Fission: Model for Intermediate Structures

Yonathan Kozlovsky 1, Michael M Kozlov 1
PMCID: PMC1303068  PMID: 12829467

Abstract

Membrane budding-fission is a fundamental process generating intracellular carriers of proteins. Earlier works were focused only on formation of coated buds connected to the initial membrane by narrow membrane necks. We present the theoretical analysis of the whole pathway of budding-fission, including the crucial stage where the membrane neck undergoes fission and the carrier separates from the donor membrane. We consider two successive intermediates of the reaction: 1), a constricted membrane neck coming out of aperture of the assembling protein coat, and 2), hemifission intermediate resulting from self-fusion of the inner monolayer of the neck, while its outer monolayer remains continuous. Transformation of the constricted neck into the hemifission intermediate is driven by the membrane stress produced in the neck by the protein coat. Although apparently similar to hemifusion, the fission is predicted to have an opposite dependence on the monolayer spontaneous curvature. Analysis of the further stages of the process demonstrates that in all practically important cases the hemifission intermediate decays spontaneously into two separate membranes, thereby completing the fission process. We formulate the “job description” for fission proteins by calculating the energy they have to deliver and the radii of the protein coat aperture which have to be reached to drive the fission process.

INTRODUCTION

Membrane fission—division of one membrane into two—is a crucial stage in formation of all kinds of small intracellular carriers from vesicles to tubular objects. Fission of plasma membrane generates endocytic vesicles, which transport proteins from the outside medium to the cytoplasm (Schmid, 1997). Fission of membranes of the endoplasmic reticulum and the Golgi complex produces carriers trafficking between different compartments of these organelles and mediating secretion (Griffiths, 2000; Lippincott-Schwartz, 2001; Mironov et al., 1997). While being of major biological importance, the molecular mechanism of membrane fission remains poorly understood. In particular, the actual stage of lipid bilayer division and the role of the fission proteins known to be involved in this reaction remain unknown. The present study is the first theoretical analysis of membrane fission based on the elastic model of lipid bilayers that provides a job description for the fission proteins.

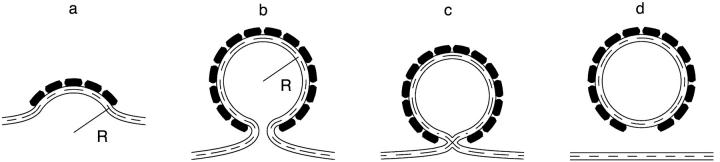
A lipid bilayer is a stable continuous structure characterized by a certain shape of the two membrane monolayers. The bilayer integrity is guaranteed by the powerful hydrophobic effect (Tanford, 1973) while the monolayer shapes are maintained by the membrane resistance to deformations. Analogous to membrane fusion (Chernomordik and Kozlov, 2003), evolution of the initial intact bilayer into two separate membranes must proceed via a pathway of intermediate structures (Fig. 1). This requires both deformations of the membrane monolayers and their transient disruptions. The deformations are necessary at the early stages of the process, where the membrane site committed to fission adopts a typical necklike shape (Fig. 1 b), and then at the later stages of formation of the nonbilayer intermediates (Fig. 1 c). The perturbations of the membrane integrity accompany, most probably, the transitions from one intermediate structure to another. The forces required to drive all these energy consuming structures and events have to be provided by the protein machine.

FIGURE 1.

FIGURE 1

Open in a new tab

The intermediates of membrane fission. (a) The coated bud at an initial stage of the coat protein self-assembly. (b) Constricted neck. (c) Hemifission intermediate. (d) Separated coated vesicle.

The three protein complexes involved in membrane fission are the clathrin-based complex, the COPI, and COPII complexes (reviewed in Kirchhausen, 2000). All of them are capable of deforming a lipid bilayer. They self-assemble on the membrane surfaces, form protein coats, and bend the bilayers into small buds of 50- to 100-nm diameter connected to the initial membrane by narrow necks (Matsuoka et al., 1998; Spang et al., 1998; Takei et al., 1998). Taking into account that the thickness of the protein coat is in the range of 10–20 nm (Matsuoka et al., 2001; Smith et al., 1998), the diameter of the lipid bilayer underneath the coat varies from 30 to 70 nm, what corresponds to the smallest vesicle radii reachable artificially by harsh ultrasound treatment of protein free lipid dispersions (Lichtenberg and Barenholz, 1988). The fission proteins differ in their ability to drive the stages of fission downstream of the neck formation, leading to the complete membrane separation. Clathrin needs assistance of other protein partners, which are capable of constricting the membrane into tubular shapes (Farsad et al., 2001; Ford et al., 2002; Hinshaw, 2000; Takei et al., 1999) and modifying the bilayer lipid composition (Schmidt et al., 1999). In contrast, the COPI and COPII complexes, at least in vitro, apparently do not need any additional protein factors to complete the fission reaction (Matsuoka et al., 1998; Spang et al., 1998).

What energy has to be delivered by a protein coat to guarantee the formation of the strongly curved membrane buds and their highly constricted membrane necks? What features of a protein coat determine its ability to finalize the bilayer fission and, hence, may be different for the clathrin and the COP coats? These fundamental questions require analysis of micromechanics of the fission intermediates.

Most previous models proposed for membrane fission address the best-characterized reaction mediated by clathrin partners, dynamin, and endophilin (Kozlov, 1999, 2001; Sever et al., 2000b). While different views exist on the mode of action of these proteins (Marks et al., 2001; Sever et al., 2000a), all these models relate to the earlier stage of the fission reaction, namely, formation of a constricted membrane neck. None of them analyzes the membrane division per se, i.e., scission of the neck.

In the present study, we suggest a model for the whole pathway of membrane fission beginning from the constricted membrane neck and proceeding via the hemifission intermediate to the complete membrane separation. We show that hemifission is driven by the elastic stress accumulated in the constricted neck provided that the constriction is sufficiently strong, and estimate the required energy, which has to be delivered by the fission proteins. We demonstrate that, once hemifission occurred, the membrane undergoes further transition to the complete fission spontaneously, because the energy of the hemifission intermediate is larger than that of the separated membranes in all practically important cases. We analyze the effects of the membrane lipid composition on fission for the case of symmetric bilayers. Our prediction is that the lipid molecules having the effective shapes of inverted cones, such as lysolipids, support division of the membrane necks. This is opposite to the well-investigated hemifusion, which is promoted by the conelike molecules (Chernomordik et al., 1995).

MODEL FOR FISSION PATHWAY

Our goal is to study the most basic features of the fission reaction. Therefore, we consider the simplest system consisting of an initially flat membrane and fission proteins, which self-assemble on the surface of the lipid bilayer into a spherical coat and bend the membrane underneath (Fig. 1). Since we are interested in the behavior of the lipid bilayer we do not specify the mechanism by which the protein coat deforms the membrane.

The bilayer portion covered by the coat and referred to below as the coated bud has a shape of a spherical segment with radius R (Fig. 1 a). Progressing self-assembly of the coat is accompanied by a decrease in the coat aperture. This results in deformation of the surrounding coat-free bilayer, which adopts a necklike shape relaxing back to the flat surface at increasing distances from the bud (Fig. 1 b). The closer the shape of the bud is to that of the complete sphere, the narrower is the membrane neck and, accordingly, the stronger the deformation of the neck membrane and the related bilayer stress.

At a certain stage of budding, the elastic stress results in decay of the membrane neck. Two scenarios of this events are possible, a priori. First, the neck may simply rupture and then reseal into a new configuration of two separate membranes. In this case, fission would be expected to be leaky. This prediction has been tested for membrane fission mediated by COPII proteins, which did not exhibit any significant transmembrane exchange of water-soluble dye (Matsuoka et al., 1998). Hence, formation of large and long living pores necessary to disrupt the neck has not been observed, meaning that, analogously to membrane fusion, the rupture-resealing mode of membrane fission is unlikely.

We focus on the second scenario where the membrane remains impermeable through the whole process of fission. We assume that the neck undergoes hemifission: its internal monolayer self-fuses, whereas the outer monolayer maintains its integrity. The resulting structure referred to as the hemifission intermediate is illustrated in (Fig. 1 c). This stage is followed by self-fusion of the outer monolayer that completes the fission reaction and results in separation of the coated vesicle from the donor membrane (Fig. 1 d).

To substantiate this model we have to calculate and compare the energies of the constricted neck, the hemifission intermediate and the separated membranes, and find the conditions where the hierarchy of these energies validates the suggested fission pathway.

PHYSICAL MODEL

The constricted neck and the hemifission intermediate are characterized by deformations of their monolayers. Therefore, the theoretical tool convenient for analyzing the energies of these structures is the elastic model of lipid membranes.

Elastic energy

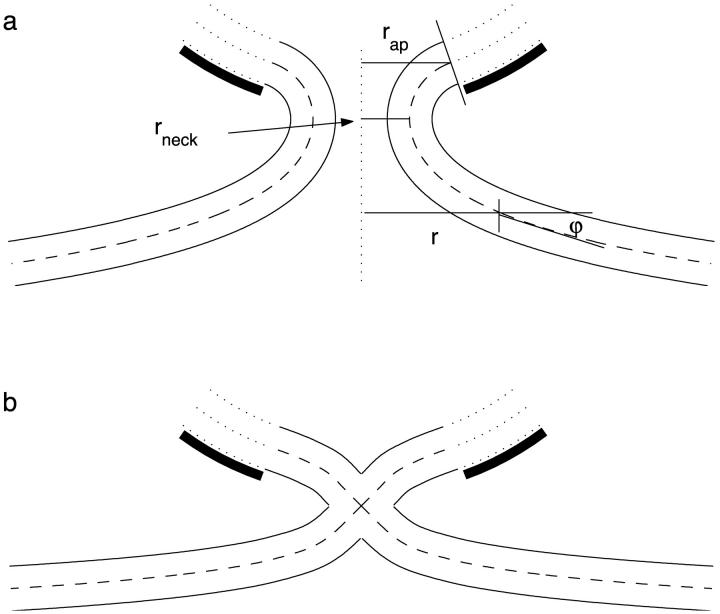
The membrane of the neck is bent as compared to its initial flat shape (Fig. 2 a). We account for the neck energy using the Helfrich bending model (Helfrich, 1973) reviewed in Helfrich (1990).

FIGURE 2.

FIGURE 2

Open in a new tab

Enlarged representation of (a) constricted neck and (b) hemifission intermediate.

We consider, separately, each monolayer of the lipid bilayer. The monolayer shape is described by the shape of its neutral surface lying at the interface between the polar heads and the hydrocarbon chains (Leikin et al., 1996) at a distance δ ≈ 1.2 nm (Rand and Parsegian, 1989) from the bilayer midsurface. Although δ corresponds to the thickness of the hydrocarbon chains layer and does not include the polar heads, we will use a loose terminology and refer to δ as the monolayer thickness.

Monolayer bending is quantified by the total curvature of its surface, J. The structure of the monolayer is characterized by its spontaneous curvature, Js, while the resistance of the monolayer to deformation is accounted by the monolayer bending modulus, κ ≈ 4 · 10−20 J (Niggemann et al., 1995). The bending energy per unit area of the membrane monolayer related to the energy of the flat shape is given by (Helfrich, 1973):

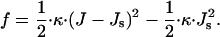graphic file with name M1.gif (1)

Deformation of the monolayers of the hemifission intermediate is more complex (Fig. 2 b). Analogously to the hemifusion structure considered in detail in Kozlovsky and Kozlov (2002), the monolayers undergo, in addition to bending, tilt, t, of the hydrocarbon chains with respect to the membrane surface (Hamm and Kozlov, 2000). The tilt deformation is generated by packing the hydrocarbon chains in the nonbilayer structural defect (Kozlovsky and Kozlov, 2002), which unavoidably emerges in the middle of the hemifission intermediate and is referred to as the hydrophobic interstice (Siegel, 1993). Change of the tilt along the monolayer surface generates an effective additional contribution to the bending deformation, J, so that the latter is considered in more general terms of splay of the hydrocarbon chains, J̃ (Hamm and Kozlov, 2000). The energy of the resulting combined deformation per monolayer unit area related to the initial state of vanishing tilt and splay is given by

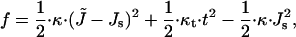graphic file with name M2.gif (2)

where κt ≈ 40 mN/m is the tilt modulus (Hamm and Kozlov, 1998). Equations 1 and 2 are valid for small deformations, satisfying

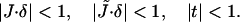graphic file with name M3.gif (3)

The total energy is obtained by integration of Eq. 1 for the constricted neck, or Eq. 2 for the hemifission intermediate, over the areas of the two monolayers,

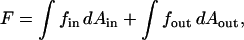graphic file with name M4.gif (4)

where the subscripts in and out refer to the inner and outer monolayers, respectively.

Strategy of calculations

The degree of constriction of the membrane neck is determined by the radius of the aperture in the coat, rap (Fig. 2 a), and the radius R of the bud membrane (Fig. 1 b). We compute the shape of the neck, which minimizes the elastic energy (Eq. 4) and is connected smoothly to the lipid bilayer of the bud. We do not assume any constrictions on the membrane shape far from the bud. The energy of the resulting membrane shape as a function of the bud and the bilayer parameters, Fneck (rap, R, Js), represents the constricted neck.

A similar although more complicated procedure using Eqs. 2 and 4 is performed for the hemifission intermediate. The configurations of the membrane monolayers including their shapes and distributions of tilt are optimized to minimize the elastic energy. The constraints on the membrane tilt and splay come in this case from the requirement of smooth monolayer connections to the bud and from the conditions of packing the hydrocarbon chains in the region of the monolayer junction in the middle of the structure. The latter constraints have been considered in the context of the hemifusion intermediate in Kozlovsky and Kozlov (2002). The resulting energy of the hemifission intermediate is also computed as a function of the spontaneous curvature and the bud parameters, Fhf (rap, R, Js).

Comparison among Fneck, Fhf, and the energy of two separated membranes provides us with the criteria of transitions between different stages of the fission process. The computations are performed numerically by the method of Finite Elements, which is equivalent to solution of the Euler-Lagrange equations.

RESULTS

To emphasize the major features of configurations and energies of the constricted neck and the hemifission intermediate, we first present the results for the case of vanishing spontaneous curvature of the membrane monolayers, 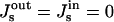Inline graphic, and then in a separate section we investigate the effects of nonzero spontaneous curvature.

Constricted neck

The shape

We describe the configuration of the constricted neck by the shape of its midsurface. Since we consider only the axisymmetric shapes, they will be described by the angle ϕ tangential to the surface profile as a function of the radial distance, r (Fig. 2 a). The neck membrane is connected smoothly to the membrane of the bud, meaning that sin ϕ = rap/R at the boundary between the bud and the neck.

The major characteristic of the neck shape is the radius of its narrowest cross-section, rneck (Fig. 2 a), measured at the midsurface and referred to below as the neck radius.

The character of the neck shape is determined by the relationship between the neck radius rneck and the monolayer thickness δ. The neck is wide, meaning that rneck ≫ δ, if the parameters of the coated bud satisfy 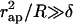Inline graphic. In this case, the neck adopts a shape of a catenoid—the axisymmetric surface of vanishing total curvature, J = 0 (see, for example, Nitsche, 1989). This result is expected, inasmuch as, in such conditions, the absolute values of the curvatures of the two monolayers are practically equal to that of the midsurface (Appendix A) |Jout| ≈ |Jin| ≈ |J|, so that the catenoidal shape corresponds to the vanishing curvatures, Jout ≈ Jin ≈ 0, and, hence, the vanishing bending energy (Eq. 1), fin ≈ fout ≈ 0, of each membrane monolayer. The catenoidal shape is determined by (Nitsche 1989),

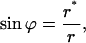graphic file with name M7.gif (5)

where r* is a parameter determining the minimal radius of the catenoid cross-section, and, hence, is equal to the neck radius, r* = rneck. Satisfying the constraint of smooth connection of the neck to the bud, we obtain 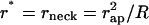Inline graphic.

If the constriction of the neck is strong enough so that the neck radius, rneck, becomes of the same order of magnitude as the monolayer thickness, δ, the difference between Jin and Jout is considerable and the catenoidal surface does not minimize the energy. In this case, the shape of the neck resulting from the energy minimization is illustrated in Fig. 2 a for the coat parameters R = 15 nm, rap = 5 nm. The neck radius in this case is rneck ≈ 2.7 nm, and the shape deviates considerably from the catenoid of the same rneck. The detailed distribution of curvature over the monolayer surfaces is presented in the Appendix A. Note that, although the neck is very narrow, rneck ≈ 2.2 δ, the maximal value of the monolayer curvature reached in the inner monolayer of the neck, constitutes |Jmax · δ| ≈ 0.6 due to partial mutual compensation of the two principal curvatures of opposite signs. This means that the relationships in Eq. 3 are satisfied, and that the elastic model (Eq. 1) we are using is applicable on a semiquantitative level.

The energy

The energy of the neck, Fneck, for 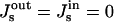Inline graphic is presented in Fig. 3 a as a function of the coat aperture radius, rap, for different values of the bud radius, R. As expected, the energy grows with increasing constriction resulting from decreasing rap. It is instructive to re-plot the energy Fneck as a function of the neck radius rneck, as presented in Fig. 3 b. The curves obtained for the different bud radii R practically converged, especially in the region of the small neck radii. This result implies that the major energy is contributed by a relatively limited region of the membrane around the narrowest neck cross-section, and that the shape of this region depending mostly on rneck is rather insensitive to the parameters of the coated bud.

FIGURE 3.

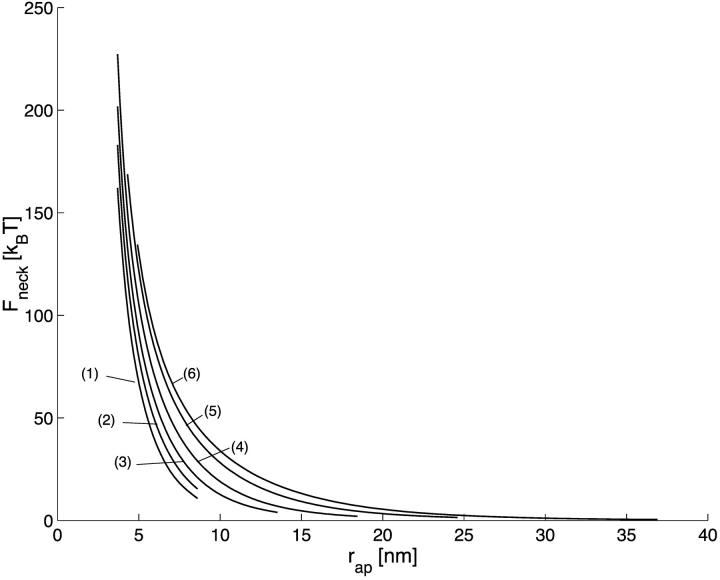
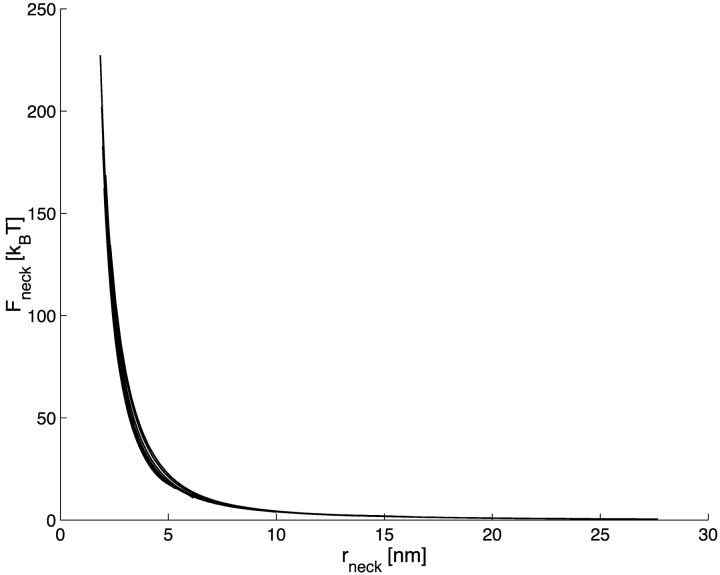
FIGURE 3

FIGURE 3

Open in a new tab

The neck energy, Fneck, as a function of (a) the coat aperture radius, rap, and (b) the neck radius rneck. The bud radius, R, is (1) 12 nm; (2) 15 nm; (3) 18 nm; (4) 25 nm; (5) 37 nm; and (6) 50 nm.

Hemifission intermediate

Membrane configuration

It is convenient to consider separately the lower part of the hemifission structure, which begins at the monolayer junction site and extends downwards, and the upper part connecting the junction site with the coated bud (Fig. 2 b).

The lower part is analogous to a half of the fusion stalk considered in detail in Kozlovsky et al. (2002). The tangential angle of the membrane profile, ϕ, and the tilt angle, φt, equal π/4 at the junction point and vanish at large distances from the hemifission site. At a distance of ∼6 nm measured from the junction point along the contour of the bilayer midsurface, the hydrocarbon chain tilt decays to zero and the membrane shape relaxes to that of a catenoid with r* ≈ 1.2 nm (the latter playing in this case a role of a parameter determining the catenoidal surface (Eq. 5) rather than having a meaning of a real neck radius).

The configuration of the upper part is constrained at one boundary by the junction point where ϕ = φt = −π/4, and at the other by the condition of smooth connection to the bilayer of the bud, sin ϕ = rap/R. The tilt relaxes along an ∼6-nm distance form the junction point, similar to the tilt behavior in the lower part. The shape of the membrane profile minimizing the energy of the upper part cannot be described analytically. The numerical result for the membrane shape of the hemifission site is illustrated in Fig. 2 b for the coat parameters rap = 5 nm and R = 15 nm.

The membrane region expanding to the ≈6-nm distance upwards and downwards from the junction point will be referred to as the core of the hemifission intermediate, where the major membrane deformations are concentrated. According to the results of our calculations, the structure of the core region is practically not influenced by the parameters of the coated bud.

The energy

The energy of the lower part of the hemifission intermediate is independent of the parameters of the coat and for Js = 0, constitutes 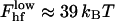Inline graphic (Kozlovsky and Kozlov, 2002), where kBT ≈ 4.1 × 10−14 erg is the product of the Boltzmann constant and the absolute temperature, T = 300 K. Almost the whole energy is contributed by the core region, while the energy of the catenoidal part of the membrane vanishes.

The energy of the upper part, 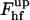Inline graphic, depends on the coat aperture radius, rap, and the bud radius, R. It has a minimum corresponding to ∼39 kBT at certain relationships between rap and R. One can easily understand this result by taking into account that 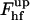Inline graphic consists of the contribution of the core region, ∼39 kBT, and the additional energy of membrane deformation induced by the constraints on the boundary with the coated bud. The latter contribution vanishes and 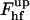Inline graphic becomes minimal if the membrane region connecting the core to the bud has a shape of a catenoidal segment. 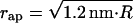This happens if the coated bud parameters are related by Inline graphic.

The total energy of the hemifission intermediate 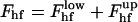Inline graphic, is presented in Fig. 4 as a function of rap for different R, its minimal value for Js = 0 constituting Fhf ∼ 78 kBT.

FIGURE 4.

FIGURE 4

Open in a new tab

The energy of the hemifission intermediate, Fhf, as a function of the coat aperture radius, rap. The curves (1–6) correspond to values of R as in Fig. 3 a.

Relative energies of fission intermediates: criterion for fission

Hemifission

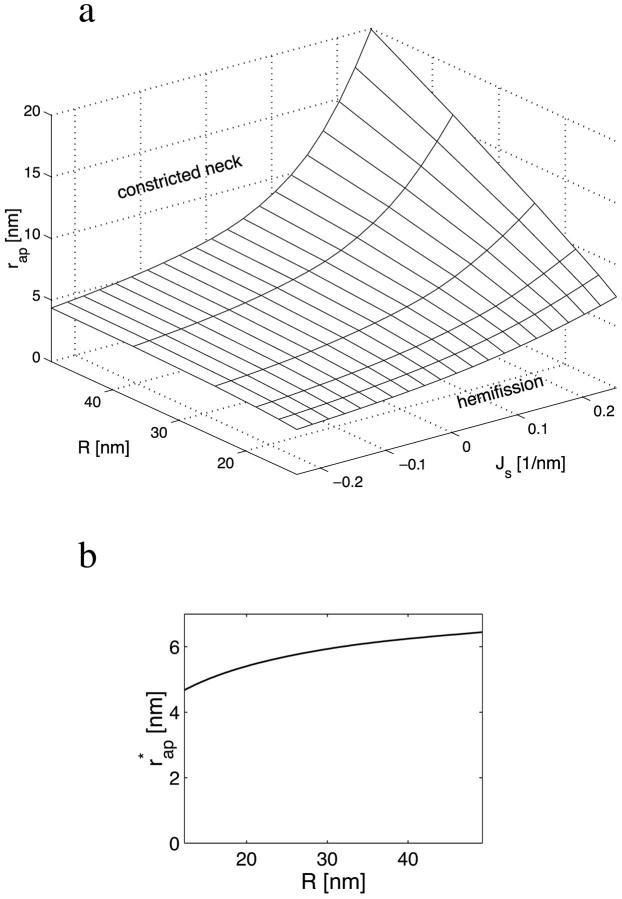
The energy of transition from the constricted neck to the hemifission intermediate, ΔFhf = Fhf − Fneck, as a function of the coated bud parameters, is presented in Fig. 5 a for Js = 0. As expected, decrease of the coat aperture radius, rap, results in decreasing energy ΔFhf, meaning that it promotes formation of the hemifission intermediate. At the aperture radius, rap, smaller than a certain value 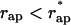Inline graphic, hemifission becomes energetically favorable, ΔFhf < 0, and, hence, is predicted to proceed spontaneously. The value 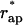Inline graphic referred to as the critical aperture radius is determined by ΔFhf = 0. The relationship between 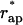Inline graphic and the coat radius R is presented in Fig. 8 b.

FIGURE 5.

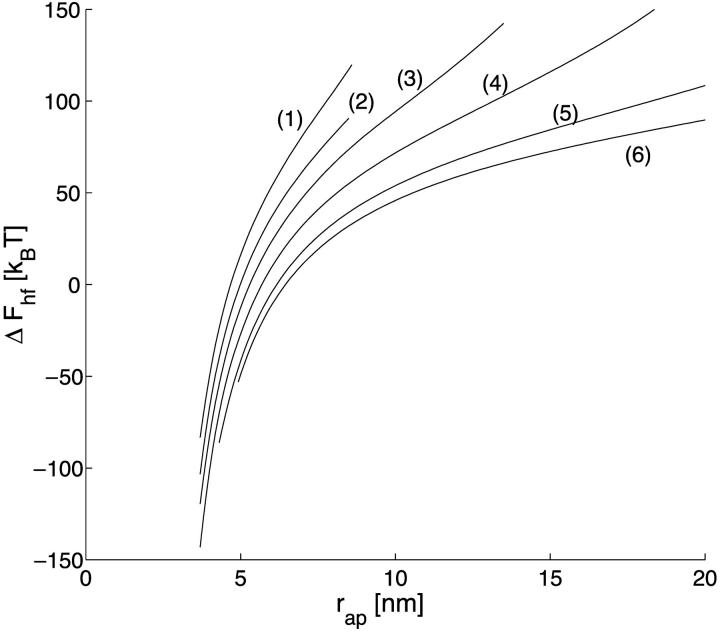
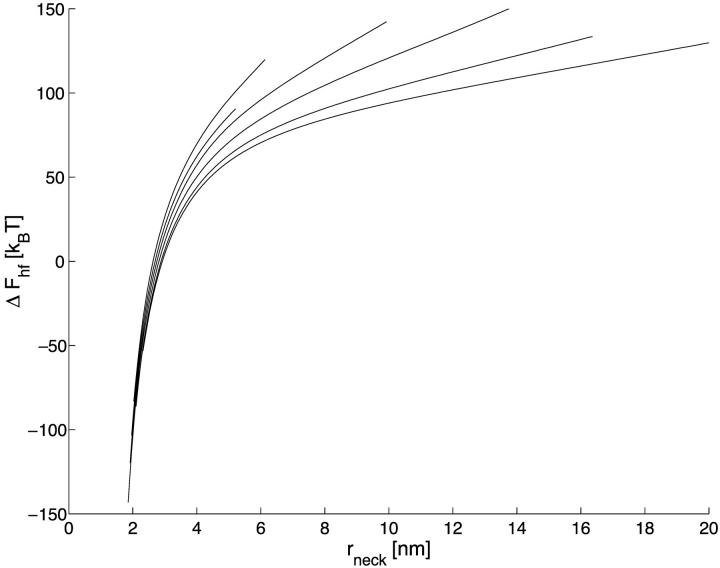
FIGURE 5

FIGURE 5

Open in a new tab

The energy of transition from the constricted neck to the hemifission intermediate, ΔFhf, as a function of (a) the coat aperture radius, rap, and (b) the neck radius rneck. Curves (1–6) correspond to the values of R as in Fig. 3 a.

FIGURE 8.

FIGURE 8

Open in a new tab

Parameter ranges determining the relative stability of the constricted neck and the hemifission intermediate. (a) Phase diagram. (b) The critical aperture radius as a function of the bud radius (the curve is the intersection of the surface in Fig. 8 a with the plane Js = 0).

Representation of the transition energy Fhf as a function of the neck radius, rneck, shows (Fig. 5 b) that the critical neck radius corresponding to spontaneous hemifission has the value of 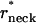Inline graphic ∼ 2.7–2.9 nm depending on the coat radius, R. Taking into account that the total monolayer thickness including the hydrophobic moiety and the polar heads is ∼1.8 nm (Rand and Parsegian, 1989), the diameter of the water lumen of the critical neck is ∼2 nm.

Completion of fission

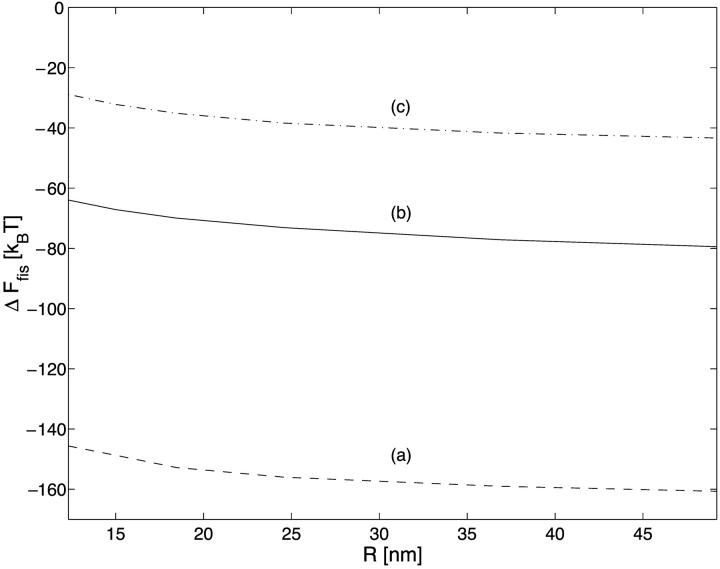
Decay of the hemifission intermediate into two separate membranes results in the flat membrane and the membrane of a closed vesicle of radius R (Fig. 1 d). The energy of the flat membrane vanishes, while the membrane of the closed vesicle possesses the bending energy, which can be easily calculated using Eqs. 1 and 4. The energy of transition from the hemifission state to two separate membranes, ΔFfis, is the difference between the bending energy of the membrane fragment, which completes the closure of the bud into the vesicle, Fves, and the energy of the hemifission intermediate, ΔFfis = Fves − Fhf. It is presented in Fig. 6 (curve b) as function of R for the critical aperture radii, 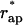Inline graphic (Fig. 8 b). The energy ΔFfis is negative, meaning that once the conditions for hemifission are satisfied, the transition to the complete fission has to proceed spontaneously.

FIGURE 6.

FIGURE 6

Open in a new tab

The energy of transition from the hemifission state to two separate membranes, ΔFfis, as a function of the bud radius, R, for different values of the spontaneous curvature: (a) Js = 0.26 nm−1, (b) Js = 0, and (c) Js = −0.11 nm−1. The values of the other parameter, the aperture radius, rap, are represented in Fig. 8 b.

Effects of spontaneous curvature

The spontaneous curvature of the membrane monolayers influences considerably the energies of all stages of the fission reaction. We consider the symmetric membranes where the two monolayers have the same spontaneous curvature, 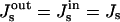Inline graphic, and show the results of calculation for the representative values of the coated bud parameters, R = 15 nm and rap = 5 nm. According to our analysis, the effect of the spontaneous curvature is similar, qualitatively, for different values of R and rap.

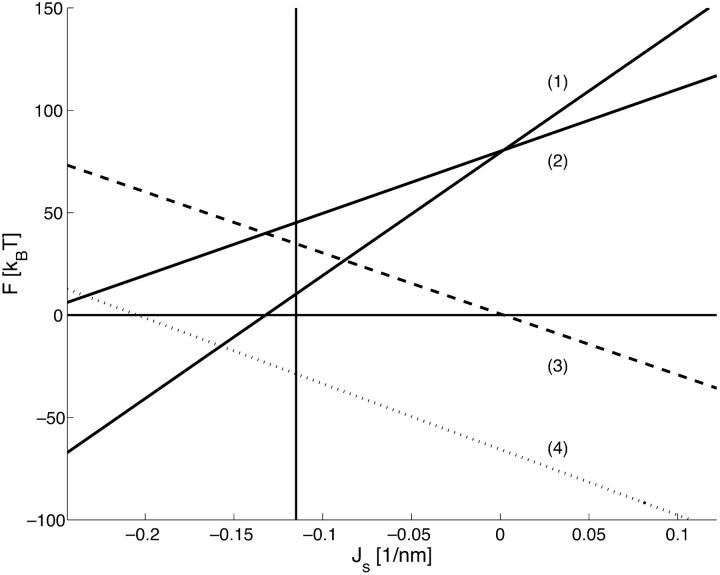
The energies of the constricted neck, Fneck, and the hemifission intermediate, Fhf, as functions of Js are presented in Fig. 7(1) and Fig. 7(2), respectively. The two energies grow with Js, but the slope of Fneck (Js ) is larger than that of Fhf (Js). This means that increase of the spontaneous curvature influences the constricted neck to a larger extent than the hemifission intermediate. As a result, the energy of transition to the hemifission intermediate, ΔFhf, decreases with Js as illustrated in Fig. 7(3). For the specific values of the coat parameters we are using in Fig. 7, ΔFhf vanishes at 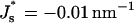Inline graphic, and becomes negative for more positive values of the spontaneous curvature, 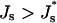Inline graphic. The value 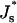Inline graphic determines the criterion of hemifission.

FIGURE 7.

FIGURE 7

Open in a new tab

The energies (1) Fneck, (2) Fhf, (3) ΔFhf, and (4) ΔFfis, as functions of Js. The coated bud parameters are R = 15 nm and rap = 5 nm. The vertical line corresponds to the spontaneous curvature of dioleoylphosphatidylcholine, Js = −0.11 nm−1.

Remarkably, the energies of the constricted neck, Fneck, and of the hemifission intermediate, ΔFhf, depend linearly on Js. A more detailed analysis (Appendix B) shows that the slopes of the curves Fig. 7(1–3), have a very weak dependence on the coated bud parameters, and that the contribution of the spontaneous curvature to the energy of hemifission, ΔFhf, can be presented as −7.7π · κ · δ · Js.

The energy of transition from hemifission to complete fission, ΔFfis, is presented as a function of Js in Fig. 7(4). The completion of fission is favorable energetically for all values of the spontaneous curvature, which allow for hemifission, and the energy of this stage decreases with increasing Js.

Summarizing phase diagram

The criteria of transition of the constricted neck to the hemifission intermediate can be summarized in the form of a phase diagram (Fig. 8 a), which is expressed in terms of three parameters: the coat aperture radius, rap, bud radius, R, and the monolayer spontaneous curvature, Js. The surface in the phase diagram Fig. 8 a plays a role of a phase boundary. The parameter ranges bellow the phase boundary correspond to the negative energy of transition from the constricted neck to the hemifission intermediate, ΔFhf < 0, and, hence, describes a spontaneous hemifission followed by completion of fission. The parameter values above the surface result in ΔFhf > 0, and, therefore, correspond to a stable membrane neck.

DISCUSSION

We have suggested a pathway of lipid bilayer fission. The assumed successive structures formed in the course of the fission process are: the constricted membrane neck, the hemifission intermediate, and the two separate membranes. We have shown that the elastic stresses generated in the constricted neck can induce spontaneous self-fusion of the neck into the hemifission intermediate and found the conditions of this event. According to our results, further decay of the hemifission structure that results in completion of fission proceeds spontaneously in all practically important cases.

The job description for fission proteins

The job of formation of the membrane neck and its constriction resulting, eventually, in fission has to be performed by proteins. How large is the energy, which has to be delivered by the proteins to drive the whole process of fission, and how does this energy depend on the properties of the lipid bilayer? The present model considers a specific protein machine, namely, a protein coat, which self-assembles on the membrane surface and bends the latter into a shape of spherical segment with radius R. This can be directly related to vesicle formation by the clathrin, COPI, and COPII coats in the in vitro experiments (Matsuoka et al., 1998; Spang et al., 1998; Takei et al., 1998) and, hopefully, accounts for the major features of the in vivo reactions despite various unclear issues (Nossal and Zimmerberg, 2002). In addition, the presented estimations should give a correct order of magnitude of the energy required to drive fission in other membrane configurations such as, for example, in the ER-Golgi system (Griffiths, 2000; Lippincott-Schwartz, 2001; Mironov et al., 1997) generating tubular carriers.

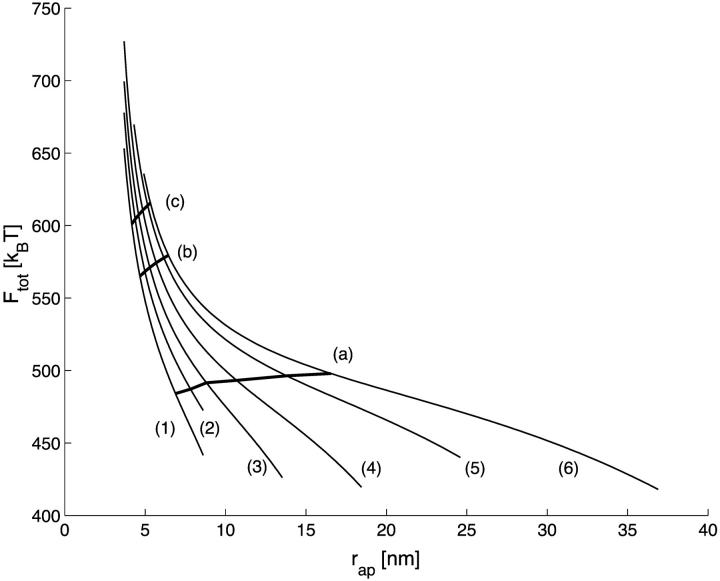
The protein coat-induced bending of the membrane into the spherical bud forms the membrane neck connecting the bud with the donor membrane. Hence, the proteins have to deliver the energy, Ftot, required for both the bud and the neck. This energy is presented in Fig. 9 as a function of the coat aperture radius, rap, for different radii of the membrane bud, R. In many cases the energy significantly exceeds the bending energy of a complete sphere, Fsp = 16π · κ ≈ 500 kBT. This means that the neck formation and tightening requires from the proteins an additional considerable energy. Hence, constriction of the neck, which is the critical stage of the fission process, might require involvement of an additional protein machine working locally on the neck membrane.

FIGURE 9.

FIGURE 9

Open in a new tab

The total energy of the bud and the neck, Ftot, as a function of the coat aperture radius, rap. The curves (1–6) correspond to values of R as in Fig. 3 a. The lines (a–c) represent the energies corresponding to spontaneous hemifission (ΔFhf = 0) for Js = 0.26 nm−1, Js = 0, and Js = −0.11 nm−1, respectively.

Are the protein complexes known to be involved in the fission process capable of constricting the neck to the extent required for hemifission? Based on the structures of the clathrin-coated vesicles (Pearse, 1975; Schmid, 1997) and the clathrin baskets (Smith et al., 1998), the internal and the aperture radii of a clathrin-coated bud can be estimated as R ≈ 16 nm and rap ≈ 10 nm. According to the predictions of our model for Js = 0, such aperture radius is not sufficiently small to promote hemifission. This may be a reason for necessity of involvement of dynamin and its partners at the stage of scission of a clathrin-coated vesicle (Schmid et al., 1998). The current structural data on the COPI and COPII coats do not allow for determination of their aperture radii, rap. However, based on the recent results (Matsuoka et al., 2001), this value may be expected to be considerably smaller than that for clathrin coats, what would explain the ability of COP complexes to drive both the membrane budding and the complete fission of the neck.

Effect of the monolayer spontaneous curvature: predictions for experimental verification

According to our model, increasing spontaneous curvature of the membrane monolayers favors the fission reaction, while decreasing Js makes it more energy-consuming. To illustrate this we indicate in Fig. 9 the energy Ftot required to induce hemifission for three characteristic values of Js. The line (a) corresponds to the positive spontaneous curvature, Js = 0.26 nm−1, of lysophosphatidylcholine (Fuller and Rand, 2001), the line (b) describes a vanishing spontaneous curvature, Js = 0, and the line (c) corresponds to a slightly negative spontaneous curvature, Js = −0.11 nm−1, of a common lipid dioleoylphosphatidylcholine (Chen and Rand, 1997). The energies in these three specific cases are close to 500 kBT, 570 kBT, and 610 kBT, respectively. Hence, the activation energy of fission depends considerably on the spontaneous curvature of membrane monolayers and may be considerably different for various lipid compositions.

To complete the fission process, the hemifission intermediate must decay to two separate membranes. The energy of this transition, ΔFfis, is given by the lines in Fig. 6, a–c, which correspond to the same Js as the lines Fig. 9, a–c. The energy ΔFfis is negative in all cases, meaning that the transition to the complete fission proceeds spontaneously. Therefore, the energy Ftot given by Fig. 9, a–c, is sufficient not only to drive hemifission but also to mediate complete fission.

The predicted dependence of the fission reaction on the monolayer spontaneous curvature is opposite to that found both theoretically and experimentally for membrane hemifusion (see, for example, Chernomordik et al., 1995; Kozlovsky and Kozlov, 2002) where the negative Js promotes merger of the contacting monolayers. This may appear counterintuitive because the essence of hemifission is self-fusion of the inner monolayer of the membrane neck, and, hence, its dependence on Js can be expected to be similar to that of the hemifusion per se. The origin of the difference between the fission and fusion reactions relates to the membrane shape, which precedes the monolayer merger and plays a role of a reference state. In the case of hemifusion, the energy of the early intermediate structure, the fusion stalk (Kozlov and Markin, 1983), is calculated with respect to the energy of two flat membranes. At the same time, the energy of the hemifission intermediate is compared to that of the constricted neck, which has a curved shape. Decreasing Js leads to reduction of the energy of the fusion stalk and the hemifission intermediate, Fhf, as compared to that of the flat membranes, but it also reduces the energy of the constricted neck, Fneck, the latter effect being stronger than the former (Fig. 7). As a result we predict that the decreasing monolayer spontaneous curvature stabilizes the constricted neck as compared to the hemifission intermediate and, hence, inhibits the fission reaction.

The dependence of the fission reaction on the spontaneous curvature requires experimental verification. At first glance, the interpretations of the existing experimental results (Schmidt et al., 1999; Weigert et al., 1999) do not support the predictions of our analysis. Formation of membrane carriers in the endocytic (Schmidt et al., 1999) and the trans-Golgi systems (Weigert et al., 1999), has been shown to correlate with transformation of lysophosphatidic acid, characterized by a positive spontaneous curvature, Js > 0, (Kooijman et al., 2003) into phosphatidic acid and, possibly diacylglycerol having a negative spontaneous curvature, Js < 0 (Kooijman et al., 2003; Szule et al., 2002). However, interpretation of such results has to make a clear difference between the two stages of the fission process: thinning of the membrane neck and its pinching off. The neck constriction to the radii of few nanometers may be interpreted as complete fission. Promotion of this stage by negative spontaneous curvature agrees with our model, which predicts that the neck constriction is favored and stabilized by the decreasing Js. We predict, however, that the next stage of neck severing requires an increasing Js. The experimental setup needed for verification of the model has to be able to discriminate between the two stages of the process.

Limitations of the model

Our model has several obvious limitations. First, the elastic model (Eqs. 1 and 2) is valid for small deformations of the monolayer splay |J̃ · δ| < 1; bending, |J · δ| < 1; and tilt of the hydrocarbon chains, |t| < 1. In the middle of the hemifission intermediate these deformations approach the value of ‘1’, what makes the quantitative predictions less accurate but does not influence the character of the qualitative predictions. A detailed discussion of this issue is given in Kozlovsky et al. (2002) and Kozlovsky and Kozlov (2002).

We have assumed that the membrane shape and the monolayer configurations are fixed at the boundary of the coated bud and in the hemifission site, while at the large distances from the bud the membrane is unconstrained. In reality, the initial membrane has a certain shape maintained by various factors such as cytoskeleton in the case of the plasma membrane, and the membrane neck has to match this shape. We have tested the effect of this additional constraint on the results of our analysis by assuming that the neck membrane must become flat at a certain distance from the coated bud. The resulting elastic energy increased negligibly and its dependence on Js did not change.

We did not include in our analysis the possible effects of the modulus of Gaussian curvature of the membrane monolayers, 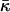Inline graphic (Helfrich, 1973, 1990). As previously discussed (Kozlovsky et al., 2002; Kozlovsky and Kozlov, 2002), the value of this modulus has not been directly measured, while the estimations show that it is considerably smaller than the bending rigidity, κ (Ben-Shaul, 1995), so that the related effects can be neglected. On the other hand, the contributions of 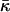Inline graphic to the energy of the fission reaction can be easily taken into account using the Gauss-Bonnett theorem and considering the sequential topological transformations of the membrane monolayers resulting from hemifission and completion of fission. The energy contribution to each stage is 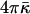Inline graphic. A reliable quantitative determination of 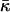Inline graphic is needed to understand its influence on the fission reaction.

The energies of the constricted neck and the hemifission intermediate have been attributed to the elasticity of the lipid monolayers only. On the other hand, the neck becomes as narrow as a couple of nanometers meaning that the intermonolayer interaction such as hydration repulsion (Leikin et al., 1993) may contribute to the energy of the neck constriction and, hence, facilitate hemifission. Accurate analysis of these effects is complicated. However, the qualitative estimations show that the energy contribution of the hydration forces is relatively small since the relevant values of the neck radius are still larger than the characteristic decay length of the hydration repulsion, the latter constituting several Ångstroms.

Finally, this study considers symmetric membranes consisting of monolayers characterized by the same spontaneous curvature. Preliminary consideration of the effects of asymmetric lipid composition, which can be produced by several proteins involved in the fission reaction (Burger et al., 2000; Huttner and Schmidt, 2000; Weigert et al., 1999) and result in different spontaneous curvatures of the monolayers, did not reveal any effects, which would be qualitatively different from those considered in this article (results not shown). Detailed analysis of this issue will be presented elsewhere.

CONCLUDING REMARKS

Previous models of membrane budding and fission have been mainly focused on the process of formation and constriction of a membrane neck connecting the forming bud with the initial membrane. At the same time, the crucial step of membrane division consists in fission of the neck. How does it happen? What requirements do the protein machine and the lipid composition of the membrane have to fulfill to be able to drive and facilitate the fission reaction? The present work suggests that a specific lipid structure, the hemifission intermediate, is formed at the stage of transition from the constricted neck to two separate membranes. Based on this assumption, we formulate the job description for fission proteins in terms of the stresses, which have to be induced in the neck to trigger its fission, and predict that, in contrast to membrane hemifusion, the fission reaction has to be promoted by lipids with positive spontaneous curvature, such as lysolipids. This model remains hypothetical and requires experimental verification. Moreover, the model does not consider the energy barriers related to probable transient disruption of the membrane monolayer at the stages of transition from the constricted neck to the hemifission intermediate and further to two separate membranes. Analysis of these barriers and their influence on the rate of the fission reaction is a matter for future work.

Acknowledgments

We are grateful to Leonid Chernomordik and Koert Burger for discussions and critical reading of the manuscript.

This work was supported by the Human Frontier Science Program Organization.

APPENDIX A

Structure of the constricted neck

Relationships between the curvatures

We describe the membrane by three parallel surfaces—the bilayer midsurface and the neutral surfaces of the two monolayers. A monolayer neutral surface lies close to the interface between the polar heads and the hydrocarbon tails at a distance δ from the midplane.

The total curvatures of each neutral surface of the outer, Jout, and inner, Jin, monolayers are related to the total curvature, J, and the Gaussian curvature, K, of the midsurface (see, e.g., Safran, 1994) by:

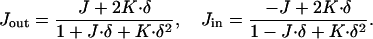graphic file with name M29.gif (A1)

In the case of small curvatures, |J · δ| ≪ 1 and |K · δ2| ≪ 1, and absolute values of the monolayer total curvatures approach that of the midsurface Jout ≈ −Jin ≈ J.

Catenoid

An axisymmetric surface is commonly described by the tangential angle of the surface profile, ϕ, and the distance from the axis of symmetry, r (see Helfrich, 1990) The principal curvatures of an axisymmetric surface are the parallel curvature, cp, and the meridian curvature, cm, expressed by

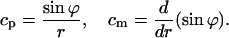graphic file with name M30.gif (A2)

A catenoid is described by

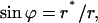graphic file with name M31.gif (A3)

where the parameter r* is the minimal radius of the surface cross-section. The corresponding principal curvatures are cp = r*/r2 and cm = −r*/r2, while the total and the Gaussian curvatures are given by

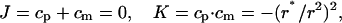graphic file with name M32.gif (A4)

The catenoid shape minimizes the elastic energy (Eqs. 1 and 4 of the main part) of an axisymmetric surface if its minimal radius, r*, is much larger than the monolayer thickness, r* ≫ δ. This is shown by the following calculation. The Gaussian curvature (Eq. A4) satisfies |K| ≤ 1/(r*)2 since r ≥ r*. Then the total curvatures (Eq. A1) satisfy Jout = Jin ≈ 2K · δ ≪ 1/δ. The elastic energy of the catenoid, F, can be estimated as the energy density at the neck, 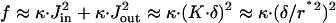Inline graphic multiplied by the characteristic area of the narrowest region of the catenoid ∼r*2. This results in vanishing energy, F/κ ≈ (δ/r*)2 ≪ 1.

Total curvatures of the strongly constricted neck

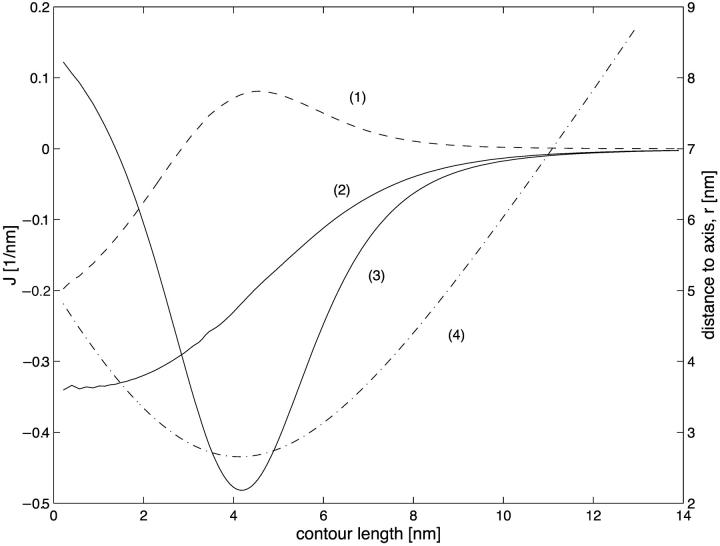
The shape of a strongly constricted neck characterized by a small neck radius is found by numeric calculations. The monolayer total curvatures are shown in Fig. 10 for the coated bud parameters R = 15 nm and rap = 5 nm. The curvatures are presented as a function of the contour length measured from the aperture of the coated bud. Fig. 10(4) gives the radial distance of the midsurface as a function of the contour length. The minimal membrane radius is rneck = 2.7 nm and it occurs at contour length of ∼4 nm.

FIGURE 10.

FIGURE 10

Open in a new tab

The total curvatures of the monolayers of a constricted neck as functions of the contour length along the midsurface: (1) J, (2) Jout, and (3) Jin. ( 4) Corresponding radial distance, r, of the midsurface. The coated bud parameters are R = 15 nm and rap = 5 nm.

We divide the constricted neck to three regions: 1), the region near the coat aperture, which corresponds to small contour lengths; 2), the neck region surrounding the cross-section of the minimal radius; and 3), the region corresponding to large contour length. The total curvature of the midsurface, J (Fig. 10(1)), is negative near the coat aperture. The maximum occurs at the neck region and is positive. The total curvature of the neutral surface of the outer monolayer, Jout (Fig. 10(2)), is negative at the coat aperture, whereas that of the inner monolayer, Jin (Fig. 10(3)), is positive in this region. At the neck region both Jin and Jout are negative. The minimum of Jin occurs at the minimal radius of the constricted neck, rneck. Away from the neck the total curvatures approach zero and the membrane tends to form the shape of a catenoid. Note that it is impossible to discern the sign of the total curvature of the neck region just by looking at the surface shape (Fig. 2 a of the main part). The total curvature of a saddlelike surface results from a delicate balance between the negative meridian curvature and the positive parallel curvature.

APPENDIX B

Energy dependence on the spontaneous curvature in symmetric bilayers

We analyze the energy contribution to the fission intermediates related to the spontaneous curvature by considering symmetric bilayers, which are composed of monolayers with the same spontaneous curvature. We first discuss the constricted neck where tilt is not involved. The part of the bending energy (Eqs. 1 and 4) depending on the spontaneous curvature, FJ, is:

graphic file with name M34.gif (B1)

By using the relations between the geometrical characteristics of parallel surfaces (see, for example, Safran, 1994), it can be shown that the sum of two integrals depends only on the Gaussian curvature, K, of the midsurface:

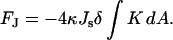graphic file with name M35.gif (B2)

The integral of the Gaussian curvature depends only on the boundary conditions and the topology of the surface as stated by the Gauss-Bonnet theorem. Therefore, for symmetric bilayers the monolayer spontaneous curvature does not affect the membrane shape unless the membrane topology changes.

The integral of the Gaussian curvature of an axial symmetric shape (Eq. A2) is expressed by the tangential angle at the two boundaries, ϕR and ϕ2:

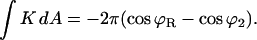graphic file with name M36.gif (B3)

The angle at the coated bud boundary is fixed by the bud, ϕR = arcsin(rap/R), while the angle at the free boundary is ϕ2 = π. The resulting dependence of the energy on the spontaneous curvature is linear:

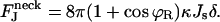graphic file with name M37.gif (B4)

This result determines the linear character and the slope of the graph; see Fig. 7(1). For coated buds with small ϕR, we obtain cos ϕR ≈ 1, and the slope of the curve does not practically depend on the coated bud parameters R and rap.

The hemifission intermediate includes tilt deformation, so its elastic energy is given by Eqs. 2 and 4. The energy dependence on the spontaneous curvature is:

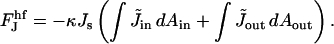graphic file with name M38.gif (B5)

We do not have analytical expressions for these integrals and we calculate them numerically. We calculated 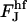Inline graphic for different coated bud parameters and obtained that it is given by

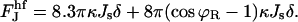graphic file with name M40.gif (B6)

This linear relation determines the slope of the graph Fig. 7(2). The second term of Eq. B6 arises from the connection of the core region of the hemifission intermediate to the coated bud. Because ϕR is small, it is much smaller than the first term. The first term arises from the splay at the hemifission core. Remarkably, it is linear in Js and insensitive to the values of the coated bud parameters, R and rap, provided that the latter are in an experimentally relevant range. The energy of the core region consists of approximately equal contributions of the splay of the inner and the outer monolayers.

The contribution from the spontaneous curvature to the energy difference, 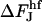Inline graphic, between the hemifission intermediate (Eq. B6) and constricted neck (Eq. B4) is:

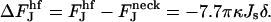graphic file with name M42.gif (B7)

The difference 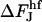Inline graphic does not depend on the coated bud parameters. This relation determines the linear character and the slope of the line; see Fig. 7(3).

The energy of the transition from the hemifission state to two separate membranes, 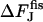Inline graphic, illustrated by Fig. 7(4) depends on the spontaneous curvature according to 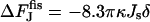Inline graphic. It is also independent of the coat parameters. In this case, the energy of the membrane fragment, which completes the closure of the bud into the vesicle, exactly compensates the second term of Eq. B6.

References

  1. Ben-Shaul, A. 1995. Molecular theory of chain packing, elasticity and lipid-protein interaction in lipid bilayers. In Structure and Dynamics of Membranes. R. Lipowsky, and E. Sackmann, editors. Elsevier, Amsterdam, the Netherlands. pp.359–401.
  2. Burger, K. N., R. A. Demel, S. L. Schmid, and B. de Kruijff. 2000. Dynamin is membrane-active: lipid insertion is induced by phosphoinositides and phosphatidic acid. Biochemistry. 39:12485–12493. [DOI] [PubMed] [Google Scholar]
  3. Chen, Z., and R. P. Rand. 1997. The influence of cholesterol on phospholipid membrane curvature and bending elasticity. Biophys. J. 73:267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chernomordik, L., M. Kozlov, and J. Zimmerberg. 1995. Lipids in biological membrane fusion. J. Membr. Biol. 146:1–14. [DOI] [PubMed] [Google Scholar]
  5. Chernomordik, L. V., and M. M. Kozlov. 2003. Protein-lipid interplay in fusion and fission of biological membranes. Annu. Rev. Biochem. 72:175–207. [DOI] [PubMed] [Google Scholar]
  6. Farsad, K., N. Ringstad, K. Takei, S. R. Floyd, K. Rose, and P. De Camilli. 2001. Generation of high curvature membranes mediated by direct endophilin bilayer interactions. J. Cell Biol. 155:193–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ford, M. G., I. G. Mills, B. J. Peter, Y. Vallis, G. J. Praefcke, P. R. Evans, and H. T. McMahon. 2002. Curvature of clathrin-coated pits driven by epsin. Nature. 419:361–366. [DOI] [PubMed] [Google Scholar]
  8. Fuller, N., and R. P. Rand. 2001. The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes. Biophys. J. 81:243–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Griffiths, G. 2000. Gut thoughts on the Golgi complex. Traffic. 1:738–745. [DOI] [PubMed] [Google Scholar]
  10. Hamm, M., and M. Kozlov. 1998. Tilt model of inverted amphiphilic mesophases. Euro. Phys. J. B. 6:519–528. [Google Scholar]
  11. Hamm, M., and M. Kozlov. 2000. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E. 3:323–335. [Google Scholar]
  12. Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28c:693–703. [DOI] [PubMed] [Google Scholar]
  13. Helfrich, W. 1990. Elasticity and thermal undulations of fluid films of amphiphiles. In Liquids and Interfaces. J. Charvolin, J.-F. Joanny, and J. Zinn-Justin, editors. Elsevier Science Publishers, Les Houches.
  14. Hinshaw, J. E. 2000. Dynamin and its role in membrane fission. Annu. Rev. Cell Dev. Biol. 16:483–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Huttner, W. B., and A. Schmidt. 2000. Lipids, lipid modification and lipid-protein interaction in membrane budding and fission-insights from the roles of endophilin A1 and synaptophysin in synaptic vesicle endocytosis. Curr. Opin. Neurobiol. 10:543–551. [DOI] [PubMed] [Google Scholar]
  16. Kirchhausen, T. 2000. Three ways to make a vesicle. Nat. Rev. Mol. Cell Biol. 1:187–198. [DOI] [PubMed] [Google Scholar]
  17. Kooijman, E. E., V. Chupin, B. de Kruijff, and K. N. J. Burger. 2003. Modulation of membrane curvature by phosphatidic acid and lysophosphatidic acid. Traffic. 4:162–174. [DOI] [PubMed] [Google Scholar]
  18. Kozlov, M. M. 1999. Dynamin: possible mechanism of “Pinchase” action. Biophys. J. 77:604–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kozlov, M. M. 2001. Fission of biological membranes: interplay between dynamin and lipids. Traffic. 2:51–65. [DOI] [PubMed] [Google Scholar]
  20. Kozlov, M. M., and V. S. Markin. 1983. Possible mechanism of membrane fusion. Biofizika. 28:255–261. [PubMed] [Google Scholar]
  21. Kozlovsky, Y., L. V. Chernomordik, and M. M. Kozlov. 2002. Lipid intermediates in membrane fusion: formation, structure, and decay of hemifusion diaphragm. Biophys. J. 83:2634–2651. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kozlovsky, Y., and M. Kozlov. 2002. Stalk model of membrane fusion: solution of energy crisis. Biophys. J. 88:882–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Leikin, S., M. M. Kozlov, N. L. Fuller, and R. P. Rand. 1996. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 71:2623–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Leikin, S., V. A. Parsegian, D. C. Rau, and R. P. Rand. 1993. Hydration forces. Annu. Rev. Phys. Chem. 44:369–395. [DOI] [PubMed] [Google Scholar]
  25. Lichtenberg, D., and Y. Barenholz. 1988. Liposomes: preparation, characterization, and preservation. Methods Biochem. Anal. 33:337–462. [DOI] [PubMed] [Google Scholar]
  26. Lippincott-Schwartz, J. 2001. The secretory membrane system studied in real-time. Robert Feulgen Prize Lecture for 2001. Histochem. Cell Biol. 116:97–107. [DOI] [PubMed] [Google Scholar]
  27. Marks, B., M. H. Stowell, Y. Vallis, I. G. Mills, A. Gibson, C. R. Hopkins, and H. T. McMahon. 2001. GTPase activity of dynamin and resulting conformation change are essential for endocytosis. Nature. 410:231–235. [DOI] [PubMed] [Google Scholar]
  28. Matsuoka, K., L. Orci, M. Amherdt, S. Y. Bednarek, S. Hamamoto, R. Schekman, and T. Yeung. 1998. COPII-coated vesicle formation reconstituted with purified coat proteins and chemically defined liposomes. Cell. 93:263–275. [DOI] [PubMed] [Google Scholar]
  29. Matsuoka, K., R. Schekman, L. Orci, and J. E. Heuser. 2001. Surface structure of the COPII-coated vesicle. Proc. Natl. Acad. Sci. USA. 98:13705–13709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mironov, A. A., P. Weidman, and A. Luini. 1997. Variations on the intracellular transport theme: maturing cisternae and trafficking tubules. J. Cell Biol. 138:481–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Niggemann, G., M. Kummrow, and W. Helfrich. 1995. The bending rigidity of phosphatidylcholine bilayers. Dependence on experimental methods, sample cell sealing and temperature. J. Phys. II. 5:413–425. [Google Scholar]
  32. Nitsche, J. C. C. 1989. Lectures on Minimal Surfaces. Cambridge University Press, Cambridge, UK.
  33. Nossal, R., and J. Zimmerberg. 2002. Endocytosis: curvature to the nth degree. Curr. Biol. 12:R770–R772. [DOI] [PubMed] [Google Scholar]
  34. Pearse, B. M. F. 1975. Coated vesicles from pig brain: purification and biochemical characterization. J. Mol. Biol. 97:93–98. [DOI] [PubMed] [Google Scholar]
  35. Rand, R. P., and V. A. Parsegian. 1989. Hydration forces between phospholipid bilayers. Biochim. Biophys. Acta. 988:351–376. [Google Scholar]
  36. Safran, S. A. 1994. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. D. Pines, editor. Addison-Wesley, Reading, NY.
  37. Schmid, S. L. 1997. Clathrin-coated vesicle formation and protein sorting: an integrated process. Annu. Rev. Biochem. 66:511–548. [DOI] [PubMed] [Google Scholar]
  38. Schmid, S. L., M. A. McNiven, and P. De Camilli. 1998. Dynamin and its partners: a progress report. Curr. Opin. Cell Biol. 10:504–512. [DOI] [PubMed] [Google Scholar]
  39. Schmidt, A., M. Wolde, C. Thiele, W. Fest, H. Kratzin, A. Podtelejnikov, W. Witke, W. Huttner, and H. Soling. 1999. Endophilin I mediates synaptic vesicle formation by transfer of arachidonate to lysophosphatidic acid. Nature. 401:133–141. [DOI] [PubMed] [Google Scholar]
  40. Sever, S., H. Damke, and S. L. Schmid. 2000a. Dynamin:GTP controls the formation of constricted coated pits, the rate limiting step in clathrin-mediated endocytosis. J. Cell Biol. 150:1137–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sever, S., H. Damke, and S. L. Schmid. 2000b. Garrotes, springs, ratchets, and whips: putting dynamin models to the test. Traffic. 1:385–392. [DOI] [PubMed] [Google Scholar]
  42. Siegel, D. P. 1993. Energetics of intermediates in membrane fusion: comparison of stalk and inverted micellar intermediate mechanisms. Biophys. J. 65:2124–2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Smith, C. J., N. Grigorieff, and B. M. Pearse. 1998. Clathrin coats at 21 Å resolution: a cellular assembly designed to recycle multiple membrane receptors. EMBO J. 17:4943–4953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Spang, A., K. Matsuoka, S. Hamamoto, R. Schekman, and L. Orci. 1998. Coatomer, Arf1p, and nucleotide are required to bud coat protein complex I-coated vesicles from large synthetic liposomes. Proc. Natl. Acad. Sci. USA. 95:11199–11204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Szule, J. A., N. L. Fuller, and R. P. Rand. 2002. The effects of acyl chain length and saturation of diacylglycerols and phosphatidylcholines on membrane monolayer curvature. Biophys. J. 83:977–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Takei, K., V. Haucke, V. Slepnev, K. Farsad, M. Salazar, H. Chen, and P. De Camilli. 1998. Generation of coated intermediates of clathrin-mediated endocytosis on protein-free liposomes. Cell. 94:131–141. [DOI] [PubMed] [Google Scholar]
  47. Takei, K., V. I. Slepnev, V. Haucke, and P. De Camilli. 1999. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat. Cell Biol. 1:33–39. [DOI] [PubMed] [Google Scholar]
  48. Tanford, C. 1973. The Hydrophobic Effect: Formation of Micelles and Biological Membranes. Wiley and Sons, New York.
  49. Weigert, R., M. G. Silletta, S. Spano, G. Turacchio, C. Cericola, A. Colanzi, S. Senatore, R. Mancini, E. V. Polishchuk, M. Salmona, F. Facchiano, K. N. Burger, A. Mironov, A. Luini, and D. Corda. 1999. CtBP/BARS induces fission of Golgi membranes by acylating lysophosphatidic acid. Nature. 402:429–433. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES