Abstract
We model the energy transfer and trapping kinetics in PSI. Rather than simply applying Förster theory, we develop a new approach to self-consistently describe energy transfer in a complex with heterogeneous couplings. Experimentally determined spectral densities are employed to calculate the energy transfer rates. The absorption spectrum and fluorescence decay time components of the complex at room temperature were reasonably reproduced. The roles of the special chlorophylls (red, linker, and reaction center, respectively) molecules are discussed. A formally exact expression for the trapping time is derived in terms of the intrinsic trapping time, mean first passage time to trap, and detrapping time. The energy transfer mechanism is discussed and the slowest steps of the arrival at the primary electron donor are found to contain two dominant steps: transfer-to-reaction-center, and transfer-to-trap-from-reaction-center. The intrinsic charge transfer time is estimated to be 0.8∼1.7 ps. The optimality with respect to the trapping time of the calculated transition energies and the orientation of Chls is discussed.
INTRODUCTION
Photosynthesis provides almost all the energy for life on Earth. At the core of photosynthesis in cyanobacteria, algae, and green plants are the two reaction centers (RCs) and their associated light harvesting complexes, i.e., Photosystem I (PSI) and Photosystem II (PSII). These complexes contain a large number of Chlorophyll (Chl) molecules that absorb visible light and efficiently transfer the excitation energy to the RCs where the energy is trapped and electron transfer takes place. The mechanism and path of the energy flow has been the subject of much research (van Grondelle et al., 1994; Fleming and van Grondelle, 1997; Karapetyan et al., 1999; Gobets and van Grondelle, 2001; Melkozernov, 2001). In this article we will focus on energy transfer and trapping dynamics in Photosystem I.
Unique to PSI are antenna Chls that absorb slightly to the red of the special pair (P700) in the RC (Gobets and van Grondelle, 2001). The origin of the red shift of these Chls has been proposed to be excitonic interaction (Gobets et al., 1994; Engelmann et al., 2001; Jordan et al., 2001; Zazubovich et al., 2002), as well as a combination of excitonic interactions and energetic shifts induced by the protein (Damjanovic et al., 2002). The role of these red Chls is unclear, although several have been suggested: to protect the complex in high light conditions (Karapetyan et al., 1999), to broaden the antenna absorption cross-section as an evolutionary advantage to adapt the system to spectrally filtered light (Trissl, 1993; Rivadossi et al., 1999), or to increase the efficiency of energy transfer to the RC (Holzwarth et al., 1993; Trissl, 1993; van Grondelle et al., 1994). The last is plausible only when the red Chls are located at a position guiding the excitations to the RC. In a trimer of a cyanobacteria Synechococcus elongatus, the location of the far red Chls absorbing at 719 nm is believed to be at the trimeric interface region since the monomeric unit is characterized by a reduced content of the spectral form (Palsson et al., 1998). Gobets and van Grondelle (2001) suggested that the red Chls may simply be a consequence of the relatively dense packing of Chls in PSI.
Time-resolved experiments have revealed several timescales of energy transfer in PSI. When the red Chls are selectively excited, rapid (380–1600 fs; see Melkozernov et al., 2000; Gobets et al., 2002a) energy transfer is observed from the red Chls to either the bulk or the RC Chls. When the peak of the Chl Qy band is excited directly, three timescales have been observed for Synechocystis sp. PCC 6803 monomers and trimers (Melkozernov et al., 2000, 2001; Gobets et al., 2002a) and Synechococcus elongatus (Kennis et al., 2001; Gobets et al., 2002a). The shortest timescale, between 300 and 500 fs, has been attributed to bulk Chl equilibration. The second timescale, between 1 and 5 ps, corresponds to equilibration between bulk antenna Chls and those Chls absorbing further to the red. In Synechococcus elongatus another timescale of 9.6 ps was found. This also has been attributed to energy transfer from the bulk to the red Chls. Finally, the longest timescale, largely insensitive to excitation wavelength, is the species-dependent trapping time ranging from 22–67 ps (Gobets and van Grondelle, 2001).
While these timescales provide invaluable information, many questions about the design principles of the PSI core antenna remain. Have the transition frequencies and orientations of the PSI antenna Chls been optimized to facilitate energy transfer to the electron transfer chain by creating specific pathways for energy flow? Does any kind of energy funnel exist? Does a parallel exist between PSI and the purple bacterial LHI/RC system, where the final energy transfer step to the primary electron donor is the slowest step in the overall trapping process? In this context, do the so-called linker Chls (Jordan et al., 2001) serve a key role in connecting the PSI antenna to the electron transfer chain? What is the influence of the red Chls on the trapping process? To answer these questions, calculations incorporating both the spatial and energetic structures of PSI are required. Early studies were made in the absence of any structural information, and most calculations were performed based on simple kinetic models (Somsen et al., 1996; Jennings et al., 1997; Melkozernov et al., 2001), or lattice models (Hemenger et al., 1972; Pearlstein, 1982; Owens et al., 1987; Jean et al., 1989; Beauregard et al., 1991; Jia et al., 1992; Werst et al., 1992; Gobets et al., 2002b).
Early discussions of the trapping dynamics were couched in terms of diffusion-limited (Owens et al., 1987) vs. trap-limited (Holzwarth et al., 1993) trapping. A more elaborate picture, the transfer-to-trap-limited model, was proposed by Timpmann et al. (1995) and Valkunas et al. (1995) and, in our view, all these viewpoints can be reconciled by introducing an inhomogeneous medium in the model of Owens et al. (1987) and by redefining the trap in the model of Holzwarth et al. (1993). In other words, the apparently contradictory pictures arise from the use of over-simplified models. Lattice models were also used to address the role of red pigments by Trinkunas and Holzwarth (1994, 1996) and Gobets et al. (2002b), but the uncertainty in the relationship of spectral and spatial positions of the individual Chls makes it difficult to assess the reliability of the conclusions.
Even without spectral assignments it is clearly an improvement to base models on the actual spatial structure of PSI. Beddard and co-workers (White et al., 1996; Beddard, 1998) carried out transient absorption experiments after excitation of mainly the primary electron donor and modeled the kinetics based on the 6-Å resolution x-ray structure (Krauss, 1993), Gobets et al (1998) calculated time resolved fluorescence for 89 Chls constituting three pools of Chls; bulk Chls absorbing light at 680 nm, P700 at 700 nm, and a few red Chls based on the 4-Å resolution x-ray structure (Krauss et al., 1996). The Förster overlap integral using absorption and emission data from solution spectra was used to calculate the pair wise transfer rate while all the other parameters including the orientation factor and the refractive index were contained in a single floating parameter. From the calculation they obtained four timescales which are comparable with their experimental data.
The recently determined 2.5-Å resolution crystal structure of PSI from Synechococcus elongatus (Jordan et al., 2001) raised the possibility of calculating energy transfer and trapping dynamics in PSI in a more realistic way. The structure is shown in Fig. 1. Byrdin et al. (2002) used exciton coupling theory to study the spectra and energy transfer rates of PSI based on the real structure. Förster theory was used to calculate energy transfer rates. Individual site energies were assigned by fitting spectra assuming excitonic interactions only. Over 1000 different assignments of Chl site energies were made and were used to follow excitations through the antenna using Monte Carlo simulations. Sener et al. (2002) also calculated energy transfer rates using full Coulomb coupling in the master equation where the couplings are calculated based on the 2.5-Å structure. Both homogeneous and heterogeneous site energies were modeled by comparing their calculation for exciton splitting with hole burning experiments. In the case of heterogeneous site energies, red Chls were assigned based on excitonic coupling only. The other Chls were randomly assigned based on a fixed value for the distribution of site energies and an ensemble of effective Hamiltonians was created. The full-width at half-maximum of the site energy distribution was set to be 424 cm−1, which is significantly smaller than the width of our calculated distribution (∼565 cm−1; Damjanovic et al., 2002). In our previous article (Damjanovic et al., 2002), we found that the presence of specific amino acids, especially charged ones, in addition to excitonic interactions spectrally shifted Chls significantly and hence should be included in the assignment of red Chls.
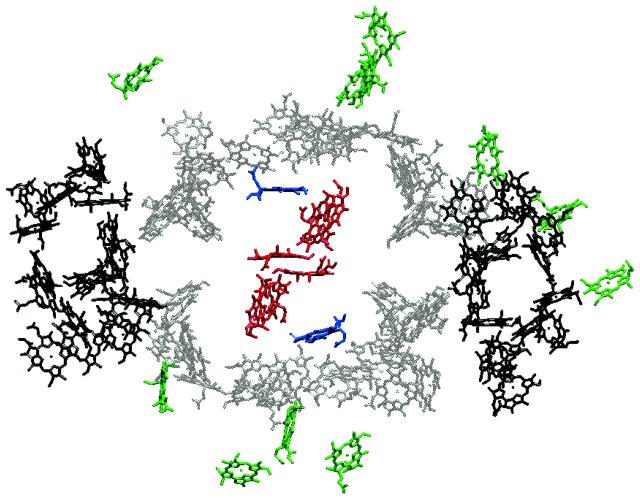
FIGURE 1.
Structure of a monomeric unit of PSI. Only the 96 chlorophyll molecules are drawn as Mg-chlorin rings, lacking the phytyl tail. The Chls in the RC are colored in red and the two linker Chls are in blue. The other antenna Chls are sectioned into three parts: central (gray) and peripheral (black) coordinated by protein units PsaA and PsaB (Jordan et al., 2001). The Chls in green are antenna Chls coordinated by other protein units. P700 was calculated to be a single Chl a located at the center of the RC in Article I.
In this work we take these calculations one step further by including the spectral heterogeneity of PSI using our previous calculations of the excitation energies of the Chls in PSI (Damjanovic et al., 2002). We will call this Article I. In that article, the Qy excitation energy of each of the 96 Chls in the complex was calculated by a semi-empirical method, and as a test, for a smaller number of Chls with an ab initio electronic structure method. In addition to the transition energies, inter-Chl electronic coupling energies were also determined by use of quantum chemistry calculations for pairs of molecules with a separation smaller than the size of a Chl and by use of the dipole-dipole interaction for pairs of molecules with a larger separation. This makes a calculation incorporating both spectral and spatial location of the dynamics occurring in PSI feasible. Our previous calculation of the low temperature absorption spectrum of PSI was in agreement with the experimental spectrum, leading us to believe our calculated spectral assignment of the Chls should lead us to a more incisive model of the energy transfer dynamics in PSI. An additional feature of the PSI system that makes calculation of the energy transfer dynamics challenging is the presence of groups of moderately or strongly interacting pigments, along with pigments spaced by distances such as to make a weak coupling picture appropriate. To handle such a system self-consistently a theoretical approach that is capable of interpolating correctly between the weak and strong coupling limits is necessary. We have recently shown that the modified form of Redfield theory developed by Mukamel and co-workers (Zhang et al., 1998) provides such an approach (Yang and Fleming, 2002), and this method is applied to PSI in the present article.
Spectral hole burning of PSI from Synechococcus elongatus (Zazubovich et al., 2002) determined three red Chl states at 708, 715 (both states assigned to dimers/trimers), and at 719 nm. The Chls absorbing at 719 nm were determined to have the strongest electron-phonon coupling and a large change in permanent dipole moment, although the location of these Chls is still unknown. Moreover, the electron-phonon coupling was shown to be very large for the primary electron donor (Gillie et al., 1989a). It was also proposed that antenna Chls in PSI and PSII absorbing longer wavelength light have larger electron-phonon coupling strengths (Zucchelli et al., 1996; Croce et al., 1998; Gobets et al., 1998). The difference in electron-phonon coupling observed by the hole-burning experiments is taken into account in our calculation. All the necessary static and dynamical quantities are well defined in our model from calculation or from experiments. The only freely adjustable parameter is the refractive index used to calculate the dipole-dipole interaction between two Chls. Since this scales the energy transfer rate as a fourth power, an accurate determination of its value is important for quantitatively accurate prediction of trapping kinetics.
Our goal is to calculate energy transfer dynamics as realistically and accurately as possible for the given spectroscopic and theoretical information. Within the model, we study the absorption spectrum and fluorescence kinetics at room temperature and compare the results with experimental data. The detailed energy transfer mechanism and the roles of some special Chls (the red and linker Chls) are discussed. We derive a formally exact expression for the mean trapping time. Based on this expression combined with a microscopic model calculation and the experimental trapping time, we estimate a timescale of electron transfer from the primary donor to a primary acceptor. We conclude with a discussion of the optimality of the energy configuration and orientation of the Chls with respect to the energy transfer process.
THEORY AND METHODS
Molecular aggregate Hamiltonian
To describe transition energies of a Chl aggregate in which the chromophores are coupled through Coulombic interactions, we use the Frenkel molecular Hamiltonian
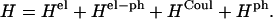 |
(1) |
Hph is a phonon Hamiltonian. Hel and Hel−ph are the Hamiltonians describing the static electronic excitations and the electron-phonon coupling, respectively,
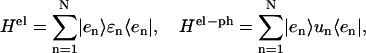 |
(2) |
where N = 96 is the number of Chls. Here, 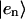 represents the excited electronic states of the nth monomer. Within the monomer n, ɛn is its excited state energy, and un the electron-phonon coupling which is assumed to be independent from one Chl to another. The excitation energies, ɛn, were determined through the semi-empirical intermediate neglect of differential overlap, parameterized for spectroscopy (INDO/S) calculations for the 96 Chls in PSI in Article I. The only change from Article I is that the transition energy of Chl B26 is blue-shifted by 273 cm−1 because of the inclusion of an arginine residue, initially excluded by the selection criterion of Article I.
represents the excited electronic states of the nth monomer. Within the monomer n, ɛn is its excited state energy, and un the electron-phonon coupling which is assumed to be independent from one Chl to another. The excitation energies, ɛn, were determined through the semi-empirical intermediate neglect of differential overlap, parameterized for spectroscopy (INDO/S) calculations for the 96 Chls in PSI in Article I. The only change from Article I is that the transition energy of Chl B26 is blue-shifted by 273 cm−1 because of the inclusion of an arginine residue, initially excluded by the selection criterion of Article I.
HCoul is the Hamiltonian describing the Coulombic interaction between the electronic states of different Chls, then
 |
(3) |
where Jnm is the Coulombic coupling between  and
and 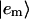 . For a small number of closely spaced Chls in PSI (which are thus, in most cases, strongly coupled), we determined the Coulombic couplings through the INDO/S method in Article I. For most of the Chl pairs in PSI, the Coulombic couplings can be approximated by dipole-dipole couplings:
. For a small number of closely spaced Chls in PSI (which are thus, in most cases, strongly coupled), we determined the Coulombic couplings through the INDO/S method in Article I. For most of the Chl pairs in PSI, the Coulombic couplings can be approximated by dipole-dipole couplings:
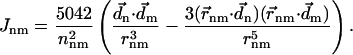 |
(4) |
Here, the vector 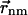 connects the centers of chlorophylls n and m, and is expressed in Å. The vector
connects the centers of chlorophylls n and m, and is expressed in Å. The vector 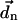 is the magnitude of the Qy transition dipole moment of Chl n. Using the absorption spectrum of Chl in peridinin-chlorophyll protein and a value of the extinction coefficient of 110 mM−1 cm−1 (Kleima et al., 2000) we calculate
is the magnitude of the Qy transition dipole moment of Chl n. Using the absorption spectrum of Chl in peridinin-chlorophyll protein and a value of the extinction coefficient of 110 mM−1 cm−1 (Kleima et al., 2000) we calculate 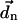 as 5.2384 Debye. (This value is different from the one used in Article I which corresponds to a Chl in vacuum. The main concern of that article was to estimate a reasonable absorption spectrum profile which is insensitive to the dipole strength. In this article, we need a more accurate value of the dipole strength in the protein environment and we obtained this value following the procedure mentioned in text.) nnm is the site-dependent refractive index, and we introduce a field model for this as follows. Chls in PSI are held in place by the protein scaffold. Fig. 2 shows the spatial distribution of the trans-membrane α-helices in PSI. Inspired by this distribution we have constructed a simple “field” model of the protein in which α-helices are represented with a cylinder, as shown in white in Fig. 2. We use this model to define the refractive index nnm: if the line connecting the Mg atom of Chl n and the Mg atom of Chl m intercepts one of these cylinders, nnm = 1.2; otherwise, nnm = 1. While this model neglects possible screening by the Chl phytyl tails, and treats the protein in a simple way, we prefer it to a homogeneous model, in which all Chl interactions are screened, and nnm is assigned a single value (usually ranging between 1.2 and 1.6). Within the field model, there is no screening between pairs of Chls that is not directly intercepted by the protein. Furthermore, Hsu et al. (2001) have observed that, for closely spaced Chls, a dielectric medium can both enhance or decrease the couplings, depending on the orientation and alignment between the two chromophores. As stressed above, for a small number of the most closely spaced Chls, the latter geometrical factors are accounted for by employing the couplings derived from quantum calculations in Article I.
as 5.2384 Debye. (This value is different from the one used in Article I which corresponds to a Chl in vacuum. The main concern of that article was to estimate a reasonable absorption spectrum profile which is insensitive to the dipole strength. In this article, we need a more accurate value of the dipole strength in the protein environment and we obtained this value following the procedure mentioned in text.) nnm is the site-dependent refractive index, and we introduce a field model for this as follows. Chls in PSI are held in place by the protein scaffold. Fig. 2 shows the spatial distribution of the trans-membrane α-helices in PSI. Inspired by this distribution we have constructed a simple “field” model of the protein in which α-helices are represented with a cylinder, as shown in white in Fig. 2. We use this model to define the refractive index nnm: if the line connecting the Mg atom of Chl n and the Mg atom of Chl m intercepts one of these cylinders, nnm = 1.2; otherwise, nnm = 1. While this model neglects possible screening by the Chl phytyl tails, and treats the protein in a simple way, we prefer it to a homogeneous model, in which all Chl interactions are screened, and nnm is assigned a single value (usually ranging between 1.2 and 1.6). Within the field model, there is no screening between pairs of Chls that is not directly intercepted by the protein. Furthermore, Hsu et al. (2001) have observed that, for closely spaced Chls, a dielectric medium can both enhance or decrease the couplings, depending on the orientation and alignment between the two chromophores. As stressed above, for a small number of the most closely spaced Chls, the latter geometrical factors are accounted for by employing the couplings derived from quantum calculations in Article I.
FIGURE 2.
Field model of the protein. Within this model, the protein medium (i.e., the medium with the refractive index of n = 1.2) is represented with a set of cylinders. The cross-section of these cylinders is shown with white circles. The real location of the trans-membrane part of α-helices in PSI is shown in turquoise, with the tube representation. Chlorophylls are presented in green as Mg-chlorin rings, lacking the phytyl tail. Chlorophyll Mg atoms are shown in van der Waals representation.
Energy transfer in a complex with heterogeneous Coulombic coupling
The theoretical description of energy transfer dynamics is usually based on perturbation theory. In a dimer system with weak Coulombic coupling between the two molecules, the well-known Förster theory can be successfully applied. However, when the Coulombic coupling is greater than the electron-phonon coupling strength, Redfield theory is more appropriate. Recently, we have shown how the Redfield and Förster theories can be combined to reasonably describe energy transfer dynamics over a wide range of parameters. The static Hamiltonian of the present system calculated in Article I shows that there are some Chl pairs with quite strong Coulombic coupling (see Table 3 of Article I), but many pairs have sufficiently weak Coulombic coupling for Förster theory to apply. Rather than simply applying the Förster or Redfield theories, we will apply a more reasonable model for such systems with a wide range of Coulombic couplings.
First, we split the Coulombic Hamiltonian into two groups of pairs: the strong Coulombic Hamiltonian HCoul,S and the weak Coulombic Hamiltonian HCoul,W,
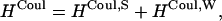 |
(5) |
if Jnm ≥ Jcutoff, 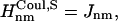 and
and 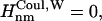 and if Jnm < Jcutoff,
and if Jnm < Jcutoff, 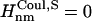 , and
, and 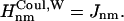 The value of Jcutoff is picked by comparison with the strength of the fluctuation amplitude of the dissipative phonon modes. For Chl a in PSI, a value of ∼90 cm−1 is found from hole-burning experiments (Gillie et al., 1989b). For practical reasons, we pick a value of Jcutoff = 120 cm−1. So the Hamiltonian (Eq. 1) is written as
The value of Jcutoff is picked by comparison with the strength of the fluctuation amplitude of the dissipative phonon modes. For Chl a in PSI, a value of ∼90 cm−1 is found from hole-burning experiments (Gillie et al., 1989b). For practical reasons, we pick a value of Jcutoff = 120 cm−1. So the Hamiltonian (Eq. 1) is written as
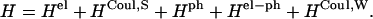 |
(6) |
Next, we will express the Hamiltonian (Eq. 6) in the basis set of exciton states. This basis set is obtained when the electronic Hamiltonian Hel + HCoul,S is numerically diagonalized to give an eigenvalue Eμ and an eigen exciton state
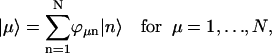 |
(7) |
where
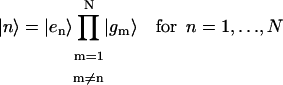 |
represents a state where only the nth molecule is in its excited electronic state and the others are in their ground electronic states. ϕμn is the amplitude of nth Chl molecule contributing to the μth exciton state. For example, if an exciton state μ is completely localized at a single Chl m, ϕμn = δnm and if it is equally delocalized over two Chls, k and m, ϕμn = (δnm + δnk)/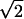 . The former situation is realized for all Chls which have vanishing contributions from the strong Coulombic Hamiltonian.
. The former situation is realized for all Chls which have vanishing contributions from the strong Coulombic Hamiltonian.
With the new electronic state representation, we have diagonal (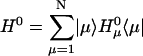 ) and off-diagonal (
) and off-diagonal (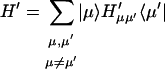 ) Hamiltonians:
) Hamiltonians:
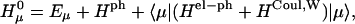 |
(8) |
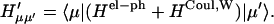 |
(9) |
In the diagonal part of Eq. 8, 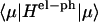 and
and 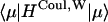 are responsible, respectively, for the energy fluctuation and energy shift of the state μ. These diagonal parts are treated in a nonperturbative way. Energy transfer between the exciton states is induced by the off-diagonal Hamiltonian. The magnitude of the off-diagonal Hamiltonian is controlled not only by the strength of the coupling un and Jnm, but also the overlap of the two exciton wavefunctions ϕμnϕμ′n. Thus a perturbative approach is justified even when the couplings un and Jnm are large, if the overlap of the exciton wavefunctions is small.
are responsible, respectively, for the energy fluctuation and energy shift of the state μ. These diagonal parts are treated in a nonperturbative way. Energy transfer between the exciton states is induced by the off-diagonal Hamiltonian. The magnitude of the off-diagonal Hamiltonian is controlled not only by the strength of the coupling un and Jnm, but also the overlap of the two exciton wavefunctions ϕμnϕμ′n. Thus a perturbative approach is justified even when the couplings un and Jnm are large, if the overlap of the exciton wavefunctions is small.
The energy transfer rate constant from a state μ′ to a state μ, kμ←μ′ is calculated by the Fermi golden rule (Schatz and Ratner, 1993):
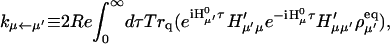 |
(10) |
where Trq denotes a trace over nuclear degrees of freedom and 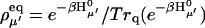 with the Boltzmann factor β. By use of the generating function method (Yang and Fleming, 2002), we can derive an expression for Eq. 10 in terms of the line broadening functions of the Chls. The expression is presented in Appendix A. It can be analytically proved that the forward and backward rate constants between two exciton states satisfy the detailed balance condition
with the Boltzmann factor β. By use of the generating function method (Yang and Fleming, 2002), we can derive an expression for Eq. 10 in terms of the line broadening functions of the Chls. The expression is presented in Appendix A. It can be analytically proved that the forward and backward rate constants between two exciton states satisfy the detailed balance condition
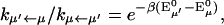 |
(11) |
where  corresponds to the 0-0 transition energy of the state μ. Here λμμ,μμ is the reorganization energy (see Eq. A6). In our calculations, a downhill energy transfer rate is evaluated from numerical integration of Eq. A1 obtained from Eq. 10 and the reverse, uphill, transfer rate for the same pair of Chls is obtained using Eq. 11.
corresponds to the 0-0 transition energy of the state μ. Here λμμ,μμ is the reorganization energy (see Eq. A6). In our calculations, a downhill energy transfer rate is evaluated from numerical integration of Eq. A1 obtained from Eq. 10 and the reverse, uphill, transfer rate for the same pair of Chls is obtained using Eq. 11.
When the exciton states are localized on individual Chls, Eq. 10 reduces to the well-known Förster formula (see Appendix A). In the case when Jcutoff → ∞, this is true for all of the transfer rates. For illustrative purpose, in Fig. 3 we show the pair-wise energy transfer rate between individual Chls, calculated from Eq. 10 with Jcutoff → ∞.
FIGURE 3.
(Top) Energy transfer rates (only rates >100 fs−1 are shown), and (bottom) square of the Coulombic couplings (only couplings >120 cm−1 are chosen) between Chl pairs in PSI. The thickness of the bond is proportional to the corresponding calculated physical quantity. Rates were determined with Förster formula, Eq. A8.
Heterogeneous spectral density
Charge transfer interactions arise in closely spaced Chl pairs. The latter usually exhibit strong Coulombic coupling. In addition to the heterogeneity of the Coulombic couplings, the magnitudes of the electron-phonon couplings have been shown to be heterogeneous. Small and co-workers have shown that there are, at least, two types of Chl a molecules in the PSI complex which are characterized by different spectral densities (with larger electron-phonon couplings) from the bulk of Chl a because of charge transfer (CT) character in their electronic excited states (Gillie et al., 1989a; Zazubovich et al., 2002). The mean frequencies and Huang-Rhys (HR) factors for the low frequency phonon modes that are associated with the Chl a molecules with CT character are presented in Table 1. To account for this type of heterogeneity, we will introduce three different spectral densities: one for P700, the primary electron donor, gP(t); one for molecules with CT character, gCT(t); and one for the majority of molecules without CT character, g(t). For convenience, we identify the pairs with CT characters as Chl pairs with a Coulombic coupling strength greater than our cutoff frequency of 120 cm−1 and assign them the line broadening function gCT(t). For all the other monomers except for P700, we assign an identical line broadening function, g(t).
TABLE 1.
Frequencies (ω in cm−1), HR factors (S), and reorganization energies (λ in cm−1) for the dissipative phonon modes
For P700, Gillie et al. (1989a).
For Chls with CT character, Zazubovich et al. (2002).
With a simplified model for nuclear motion, a line broadening function at room temperature can be obtained from the spectral density determined at very low temperature (Jia et al., 1992; Mukamel, 1995; Nagasawa et al., 1997). Gillie et al. (1989b) determined the frequencies and HR factors for 42 vibrational modes plus a low frequency phonon mode coupled to the optical transition of the Chl a molecules in PSI from a hole-burning spectroscopy at 1.6 K. The HR factors for these 43 modes are presented in the second column of Table 2. To test whether this spectral density could be applied effectively to room temperature dynamics, first we tried to simulate the absorption spectrum of the PSI complex at room temperature with the low temperature spectral density. The absorption spectrum is calculated by an expression based on the cumulant expansion technique (See Eq. 16 in Ohta et al., 2001).
TABLE 2.
Chlorophyll a vibrational frequencies (ω in cm−1) and HR factors (S)
| ω | S* | S† |
|---|---|---|
| 22 | 0.8 | |
| 25‡ | 0.6 | |
| 262 | 0.012 | 0.1775 |
| 283 | 0.004 | 0.00312 |
| 350 | 0.02 | 0.001562 |
| 390 | 0.015 | 0.0117 |
| 425 | 0.007 | 0.00711 |
| 469 | 0.019 | 0.02226 |
| 501 | 0.007 | 0.0082 |
| 521 | 0.017 | 0.00133 |
| 541 | 0.009 | 0.000791 |
| 574 | 0.025 | 0.0022 |
| 588 | 0.005 | 0.000439 |
| 607 | 0.012 | 0.00105 |
| 638 | 0.009 | 0.000791 |
| 692 | 0.015 | 0.00132 |
| 714 | 0.010 | 0.000879 |
| 746 | 0.044 | 0.00387 |
| 771 | 0.007 | 0.000615 |
| 791 | 0.014 | 0.00123 |
| 805 | 0.012 | 0.00105 |
| 819 | 0.005 | 0.000439 |
| 855 | 0.009 | 0.00703 |
| 864 | 0.007 | 0.00547 |
| 874 | 0.007 | 0.00547 |
| 896 | 0.013 | 0.01015 |
| 932 | 0.025 | 0.01952 |
| 994 | 0.028 | 0.02332 |
| 1009 | 0.005 | 0.00586 |
| 1075 | 0.012 | 0.01406 |
| 1114 | 0.009 | 0.01054 |
| 1178 | 0.018 | 0.01751 |
| 1203 | 0.012 | 0.00937 |
| 1259 | 0.041 | 0.03202 |
| 1285 | 0.011 | 0.00859 |
| 1340 | 0.011 | 0.00859 |
| 1364 | 0.032 | 0.02499 |
| 1390 | 0.018 | 0.01406 |
| 1411 | 0.005 | 0.0039 |
| 1433 | 0.009 | 0.00703 |
| 1455 | 0.006 | 0.00469 |
| 1465 | 0.006 | 0.00469 |
| 1504 | 0.010 | 0.00781 |
| 1524 | 0.032 | 0.02499 |
From Gillie et al. (1989b).
From Fig. 7 of Zuchelli et al. (2002). These values are used for a bulk Chl a in the present article.
For P700 and Chls with CT character, this mode is replaced by those given in Table 1.
Following this procedure we obtained an absorption spectrum with more intensity in the region of the vibronic band (700 cm−1) than the experimental data. A similar result was obtained by Zucchelli et al. (2002) in their calculation of the room temperature absorption bandshape for a single Chl a molecule. The authors concluded that a change of coordination number of the Chl molecule as the temperature changes from low to room temperature requires modification of the spectral density in the region of vibronic transitions. They fit the room temperature absorption spectrum by taking the HR factors of the 43 modes including the dissipative phonon mode as floating parameters. The resulting values are presented in the third column of Table 2. We used these values to construct a model spectral density for Chl a with no CT character at room temperature. A comparison of the absorption spectra calculated by the two spectral densities is shown in Fig. 4 a.
FIGURE 4.
(a) Absorption spectra calculated by the two spectral densities for a Chl a, data from Gillie et al. (1989b) (dashed) and Zucchelli et al. (2002) (solid). (b) Absorption spectra calculated from the three spectral densities for a bulk Chl a (solid), a Chl a with charge transfer character (dashed), and for P700 (dotted). For high frequency modes, the spectral density of Zucchelli et al. (2002) is used. The HR factors and the frequencies are given in Tables 1 and 2. Zero energy in a and b corresponds to the vertical transition energy associated with each spectral density. (c) Comparison of the calculated (solid line) and experimental (solid circles) absorption spectra of the PSI complex at room temperature.
To incorporate the heterogeneity in the electron-phonon coupling strength discussed above into the spectral density of Zucchelli et al. (2002), we simply replaced the frequencies and HR factors for the dissipative phonon modes with those in Table 1. A similar modification for gP(t) was also made by referring to Gillie et al. (1989a). The absorption spectra of a single Chl a calculated using the three spectral densities are shown in Fig. 4 b. Finally, a comparison of the simulated absorption spectrum for the PSI complex with the experimental data is given in Fig. 4 c. The energies of all Chls are blue-shifted by 1185 cm−1 to match the experimental absorption maximum. (In the present article, we employ realistic spectral densities including vibronic transitions. The vibronic transitions red-shift the absorption peak compared to its vertical transition energy as we can see in Fig. 4, a and b. Therefore, a larger energy shift than in Article I is necessary to match the calculated absorption spectrum to the experimental one.) Other than being a little bit wider than the experimental spectrum, the simulated spectrum matches the experimental one quite well.
Excitation transfer kinetics
In this article, we assume the intensity of external light perturbation to be sufficiently weak that any excitation annihilation processes can be ignored. In this case, the decay of the fluorescence intensity arises from two pathways. One is unimolecular dissipative decay due to internal conversion or fluorescence emission. The rate constant of this pathway is denoted by kS which is usually assumed to be uniform over all the Chls. As a result of the assumption, the effect of the unimolecular decay can be easily taken into account at the final step by adding 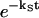 and thus we assume kS = 0 hereafter. The other process is decay of excitation energy population due to trapping of the energy at P700 and subsequent initiation of the electron transfer chain. Recombination of the electron to P700 is ignored and thus the excitation decay due to the charge separation at P700 is assumed to be an irreversible process. For the excitation energy absorbed by antenna Chls to be trapped at P700, a series of energy transfers from one Chl to another must occur before trapping. Such processes are described by the following master equations for the population of excitation energy,
and thus we assume kS = 0 hereafter. The other process is decay of excitation energy population due to trapping of the energy at P700 and subsequent initiation of the electron transfer chain. Recombination of the electron to P700 is ignored and thus the excitation decay due to the charge separation at P700 is assumed to be an irreversible process. For the excitation energy absorbed by antenna Chls to be trapped at P700, a series of energy transfers from one Chl to another must occur before trapping. Such processes are described by the following master equations for the population of excitation energy,
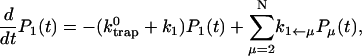 |
(12) |
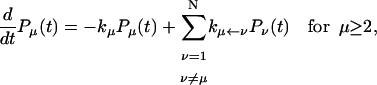 |
(13) |
where Pμ(t) is the population of excitation existing on state μ at time t. ktrap0 is the intrinsic trapping (in this case, the charge transfer) rate constant at P700 denoted by μ = 1 (hereafter, we will call this the trap). kμ←v is the excitation energy transfer rate constant from state ν to state μ which is calculated by Eq. A1.
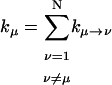 |
is the depopulation rate constant of the state μ due to energy transfer to other exciton states. In vector notation, Eqs. 12 and 13 are written as
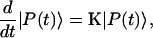 |
(14) |
where 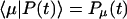 . The rate matrix K is
. The rate matrix K is
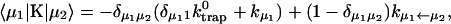 |
(15) |
which is assumed to be time-independent. The formal solution of Eq. 14 is given by 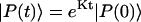 where
where 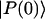 is a normalized initial distribution of excitation energies.
is a normalized initial distribution of excitation energies.
In Fig. 5 we show a few snapshots of the evolution of excitation initially created on a single Chl (PL01) in the peripheral region on the stromal side. The intrinsic trapping rate constant at P700 is set to be 1 ps−1 in this figure. The populations at each time are normalized with respect to total population at the time. The figure shows that 10∼50 ps elapses before an excitation on one side of the peripheral antenna reaches the other peripheral region. The stromal sides of the PsaA and PsaB peripheral regions are not directly connected to each other in terms of excitation transfer. An excitation created in the peripheral region of the stromal side in PsaA first diffuses to the central (PsaA) region and then extends to the lumenal side via the central (PsaA) region. The excitation then further diffuses to the lumenal side of the PsaA peripheral or of the PsaB central regions. When excitation reaches the PsaB lumenal side it finally diffuses to the stromal side of the PsaB peripheral region.
FIGURE 5.
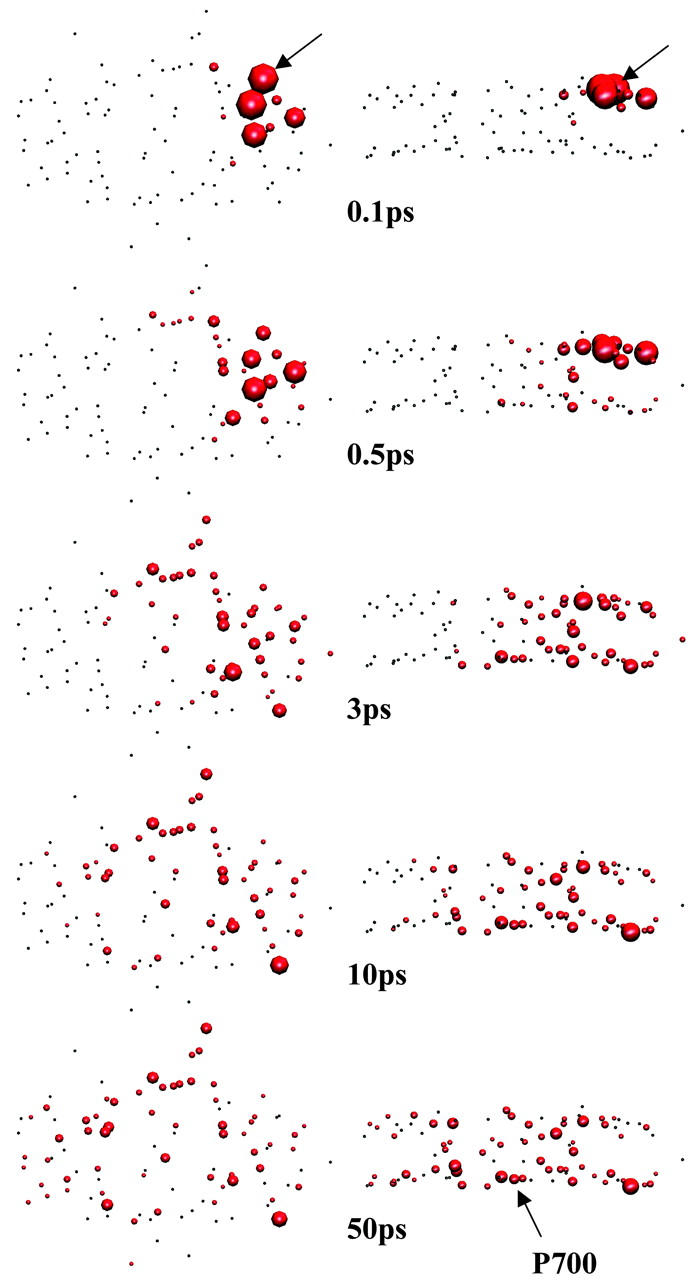
Snapshots of top (left) and side (right) views of the excitation at five times (0.1, 0.5, 3, 10, and 50 ps from top to bottom). Chl PL01 indicated by arrows drawn at 0.1 ps is excited at time zero. The surface area of a sphere is proportional to the population staying at that site normalized by the total population at that time. The arrow drawn on the side view at 50 ps shows the location of P700. The charge transfer time at P700 is 1 ps for these figures.
Usually the excitation kinetics is experimentally probed by measuring fluorescence intensity which can be written in terms of our equations as
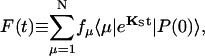 |
(16) |
where 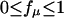 is a weighting factor of the μth state to experimentally measured fluorescence. Eq. 16 in terms of the eigenvalues and eigenvectors of the rate matrix K is rewritten as
is a weighting factor of the μth state to experimentally measured fluorescence. Eq. 16 in terms of the eigenvalues and eigenvectors of the rate matrix K is rewritten as
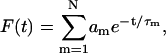 |
(17) |
where 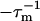 is the mth eigenvalue of K. The amplitude am is given by
is the mth eigenvalue of K. The amplitude am is given by
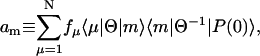 |
(18) |
where Θ is a similarity transformation matrix constructed by the eigenvectors of the rate matrix K; i.e., Θ−1KΘ is a diagonal matrix whose elements are the eigenvalues of K. The fluorescence amplitudes are determined by the various experimental conditions such as pulse shape and bandwidth as well as by the rate matrix.
The survival probability of the excitations, 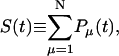 is also given by a multiexponential function, Eq. 17; now, however, the amplitudes are determined by the rate matrix only. The rate matrix constructed above yields amplitudes of nearly zero for all the time components except for the longest one. The kinetic equation for the survival probability can be simply written as
is also given by a multiexponential function, Eq. 17; now, however, the amplitudes are determined by the rate matrix only. The rate matrix constructed above yields amplitudes of nearly zero for all the time components except for the longest one. The kinetic equation for the survival probability can be simply written as
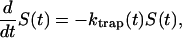 |
(19) |
where the time-dependent trapping coefficient is defined by
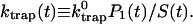 |
(20) |
Therefore, single exponential behavior obtained from our calculation implies that the trapping coefficient given in Eq. 20 becomes time-independent very rapidly to
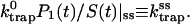 |
(21) |
RESULTS
We calculate the time components and the amplitudes for fluorescence decay after an excitation of a subset of Chls which are located on the blue side of the spectrum (640–660 nm). Fig. 6 a shows the amplitudes of the time components at four different detection windows when ktrap0 = 1 ps−1. Since the excitation and detection schemes in the present article are roughly defined, the calculated amplitudes may not match exactly with that from experiment. We note, however, that the 96 time components are determined within the model independently of the experimental conditions and we believe that, if the model reasonably represents the actual system, the experimental time components can be extracted even with the rough excitation and detection schemes.
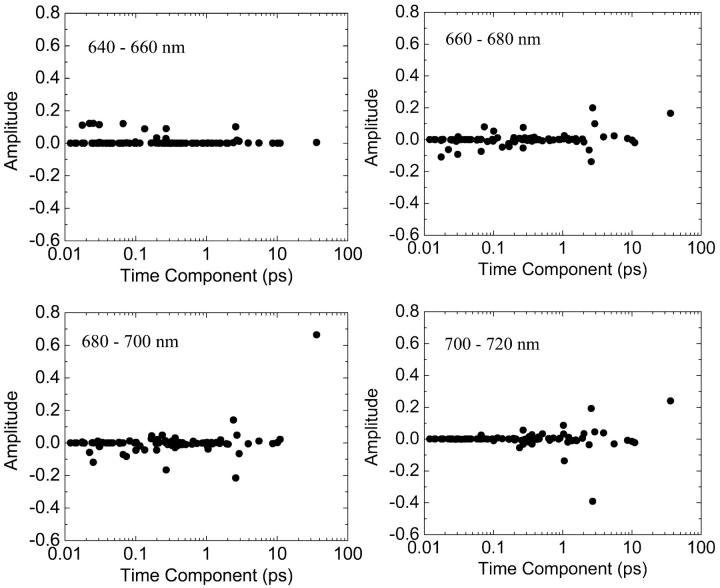
FIGURE 6.
Distribution of the calculated time components of fluorescence decay at four different detection windows after excitation at 660∼640 nm. The charge transfer time is 1 ps.
We see a few dominant time components which are categorized into four groups; sub-100 fs, 0.3 ps, 2∼3 ps, and 35∼40 ps. Interestingly, the experimentally observed time components (360 fs, 3.6 ps, 9.6 ps, and 38 ps; see Gobets et al., 2001; Kennis et al., 2001) are remarkably similar to those predicted by our calculation. In our calculation, the time component of 9.6 ps is not amplified. This component is similar to the 12-ps component measured in fluorescence and transient absorption experiments by Holzwarth et al. (1993). They assigned this component to an equilibration process between bulk Chls and far red Chls absorbing at 719 nm which are believed to be caused by interaction between two monomeric PSI complexes. The excitation dynamics involving the far red Chls might not be properly simulated in our model because our Hamiltonian was obtained for the monomeric complex in Article I. This may be the reason for the lack of 9.6-ps component in our calculation. Finally, the time resolution of the up-conversion experiment might not be adequate to capture the sub-100-fs component. Our prediction of such ultrafast dynamics may be tested by higher time resolution experiments.
In Fig. 7, we show the so-called decay-associated spectrum (DAS) with 10 nm resolution for six groups of time components: sub-100-fs, 0.1∼0.5 ps, 0.5∼1.5 ps, 1.5∼5 ps, 5∼10 ps, and 35∼40 ps. The 0.5∼1.5-ps time components are related to the intrinsic trapping constant (1 ps−1) we employed. When the experimental fluorescence decay is given by a multiexponential function, e.g.,
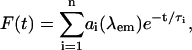 |
where λem is an emission wavelength and n is the number of measured time components, a DAS for the ith component is obtained as a plot of ai (λem) vs. λem. A positive (negative) amplitude of a DAS means decay (rise) behavior of the fluorescence. In our calculation, an amplitude for the DAS at a wavelength λ is calculated from Eq. 18, when Eμ corresponds to a small range of wavelength λ ± 5 nm and fμ = 0 otherwise. It is again noted that these spectra should not be exactly matched with experimental DAS since our excitation and detection schemes are not the same as those in a real experiment. The sub-100-fs component (solid squares) appears as a decay component in the 650–670-nm window and as a rise component in the 670–690-nm and even in the 690∼710-nm windows. This shows that extremely fast energy transfer on the sub-100-fs timescale which might not have been detected by experiments occurs from the blue Chls to a wide range of redder Chls. The 0.3-ps component (solid circles) also shows up as a decay component in the 650–670-nm windows and as a major rise component at 680–700 nm. The 2∼3-ps component appears as a decay component in the intermediate region (660∼690 nm) and a rise component in the 690–710-nm region for the case of a selective excitation (all the Chls are equally excited) in Fig. 7 a. For blue side excitation (Fig. 7 b), the 2∼3-ps component appears only as a rise term in the 690∼710-nm window. The disappearance of the 2∼3-ps component in the 660∼690-nm region of Fig. 7 b reflects a steady flow of excitation from the blue to red region via the 660∼690 nm region for this time period. The 5∼10-ps group does not appear for all wavelengths. Finally the longest timescale of 35∼40 ps is a minor component <670 nm but shows up as a major decay component in all other wavelengths. This reflects the fact that a steady state in the spectral distribution is attained before the longest timescale and, in this steady state, excitation energy has been depleted in the bluest region of the spectrum. We note that the spectra of the longest time component for the two different excitation conditions are different. This suggests that the steady state is not a thermodynamic equilibrium and that the kinetics are not purely trap-limited in which the trapping process takes place from a thermal equilibrium distribution of the excitations. The reasonable predictions of the absorption spectrum and fluorescence time components to be consistent with the experimental values suggests that our calculated system provides a good model for the real system. Thus encouraged, we use the model to speculate on the microscopic details of the energy transfer processes.
FIGURE 7.
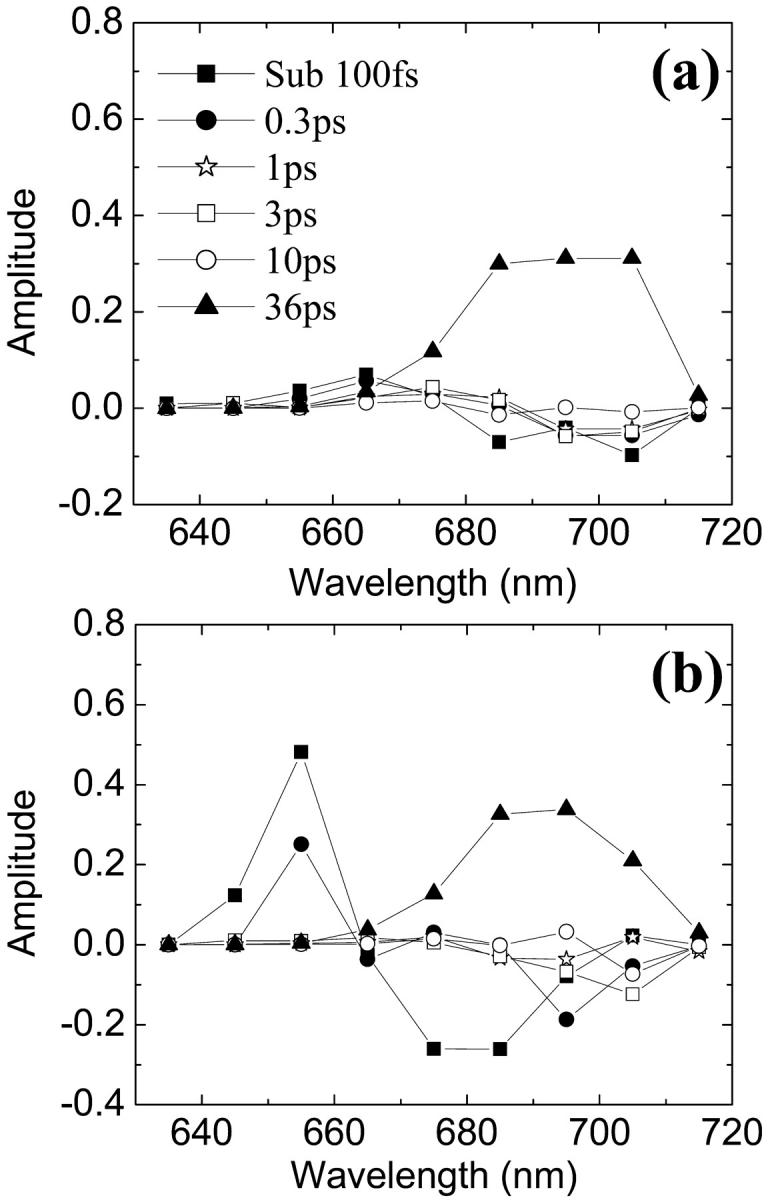
DAS with 10-nm resolution for six groups of time components. (a) All Chls equally excited initially. (b) Only Chls with energies in the range of 660∼640 nm excited initially.
DISCUSSION
Mechanism of energy transfer (rate-determining step)
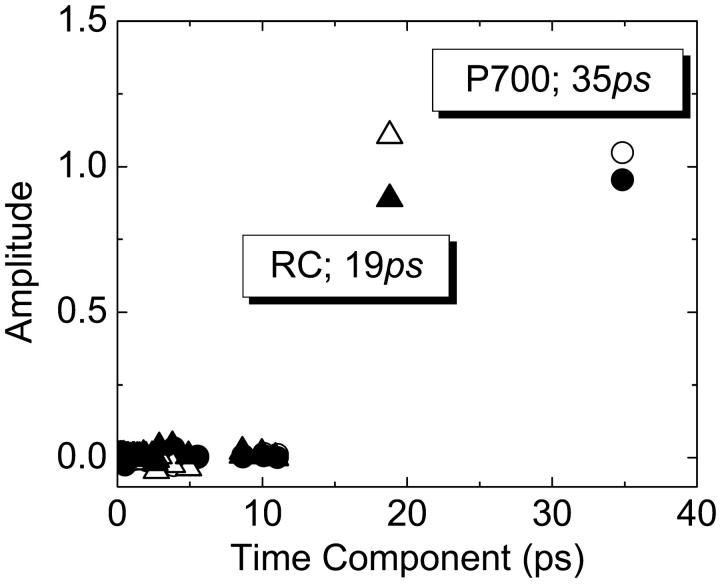
In Fig. 8, we plot the distribution of the decay time components for the survival probabilities after excitation of Chls, separately, in two different spatial regions corresponding to peripheral and central Chls as shown in Fig. 1. In these calculations, the excitations decay away instantaneously as soon as they arrive at a), any Chl of the RC including P700; or b), at P700. For the two different initial distributions of excitations, the majority of the total excitation decay is described by a single exponential of 19 ps for the case a), arrival at the RC; and of 35 ps for the case b), arrival at P700. We will refer to these timescales as the arrival time, respectively, at the RC and at P700. The single exponential decay found independently of the initial conditions implies that a steady-state spatial distribution of the excitations around the sink (RC or P700) is achieved before any major transfer of the excitation to the sink takes place. This steady-state distribution is not necessarily that of a thermodynamic equilibrium state and has been called a transfer-equilibrium state by Laible et al. (1994). Fig. 9 compares spatial distributions of excitations (normalized to total population) after 50 ps from their equal creation over all Chls when the charge transfer process is on (with a rate constant of 1 ps−1) or turned off. These two distributions (transfer equilibrium vs. Boltzmann distribution) near the trap are different but the distributions in the antenna regions are quite similar. Of course this conclusion depends on the value of the intrinsic trapping constant. When this is small, the two distributions should be the same. The timescale required to achieve the transfer-equilibrium state appears to be <5 ps, which is consistent with experimental observations (Hastings et al, 1994, 1995; Gobets et al., 2001; Kennis et al., 2001; Melkozernov et al., 2001; Gibasiewics et al., 2002).
FIGURE 8.
Distributions of arrival times at the RC (triangles) and at P700 (circles) from the two spatial domains (unfilled, from the peripheral domain; solid, from the central domain).
FIGURE 9.

Comparison between the normalized populations at 50 ps with the charge transfer ON (upper panel) and OFF (lower panel). The population at P700 in the thermal equilibrium (lower panel) is greater than that calculated in Article I because the reorganization energy of P700 in the present article is set larger than those of other Chls. In this case, the excited state of P700 is lower than in Article I, in which the same electron-phonon coupling was assumed for all Chls.
Primary rate-determining step (RDS)
Arriving at the RC (with a timescale of 19 ps) is a slower process than the spatial equilibration outside the RC (with a timescale <5 ps) and is called the primary RDS. This RDS may result from either the spatial separation between the two units, or the excitation trapping by the red Chls located in the antenna (A32-B07 and B24-B25 as suggested in Article I, and B37-B38 newly obtained by the ‘field’ model introduced in Theory and Methods). To test the second possibility, we removed the red Chls and the arrival times in this case were obtained as, respectively, 23 ps (RC) and 36 ps (P700). Other than these changes, the major feature of the kinetics, i.e., the single exponential dominated kinetics, does not change. Based on this result, the second possibility is excluded, and the spatial separation between the RC and the antenna does seem to be the origin of the primary RDS. From the small increases in the timescales resulting from the removal of the red Chls, we conclude that the red Chls act to gather excitation energy in the reaction center region. However, since the changes of timescales (at room temperature) are very small, these Chls do not seem to play a significant role in focusing excitation toward the RC.
Secondary RDS
Even though the spatial separation between the antenna and the RC causes the arrival time at the RC to be slow, another 16 ps is needed for the excitations to reach P700. We refer to the processes responsible for this additional time as the secondary RDS, and will discuss the physical origin below.
Comparison with transfer-to-trap-limited mechanism
Based on the observation that there are two distinct distance scales (inter-Chls distance in the antenna, ∼9 Å; and distance between the primary electron donor and the antenna Chls, 42.6 Å) in the light harvesting complex of purple bacteria (Hu and Schulten, 1998), the transfer-to-trap-limit mechanism was proposed (Timpmann et al., 1995; Valkunas et al., 1995). When this model was suggested, a well-resolved structure for PSI was not available and the authors assumed that the spatial and spectral isolation of the primary electron donor from the antenna Chls as is found in the purple bacteria would be a general feature of photosynthetic systems. In this mechanism, the effective transfer rate from the antenna to the primary electron donor is the slowest step in determining the global trapping time of the excitations.
However, the recent structural data of PSI shows that the analogy between the ring structure of the RC antenna complex of the purple bacteria and PSI may not be so strong. The antenna Chls are separated from the RC Chls by not less than 18 Å and distances between antenna Chls range between 7 and 16 Å, and, more importantly, there are the so-called linker Chls located between the RC and the antenna (linkers are 11∼13 Å from their closest RC Chls; Jordan et al., 2001). In addition, unlike the purple bacteria, the energies of the antenna Chls are similar to those of the RC Chls and thus energy transfer between the RC Chls and the antenna Chls can occur. Then we should not expect the distance between P700 and the antenna to be such a dominant component of the RDS in PSI as it is in purple bacteria. Due to the existence of the RC Chls as a mediator, the overall trapping time seems to be controlled by the two RDSs discussed above.
Linker Chls
It has been suggested that the linker Chls mediate the energy transfer between the RC and the antenna (Krauss et al., 1996; Schubert et al., 1997). To examine the role of these linker Chls, we compare the arrival times of the excitations at the RC and at P700 starting from the antenna Chls (central + peripheral domains) with and without the linkers. The calculated arrival times at the RC and at P700 become longer, respectively, changing from 19 ps to 29 ps and from 35 ps to 40 ps, when the linkers are removed. From this result, we see that the linkers do enhance, to a certain degree, energy transfer from the antenna to the RC (34% improvement in the arrival time) but their existence does not seem essential. A significant fraction of excitations directly transfer from the antenna to the RC Chls even without the linkers. Actually, if we remove the RC Chls other than P700 in the network, the arrival time at P700 greatly increases to 145 ps and pathways involving the other RC Chls seem essential to get such a short arrival time (35 ps) at P700.
The arrival time at the RC is more affected by the linker than is the arrival time at P700. In other words, the gap between the arrival times at the RC and at P700, which is the timescale for the secondary RDS, is reduced from 16 ps to 11 ps by removing the linker Chls. The linkers reduce the timescale of the primary RDS (from 29 ps to 19 ps) but increase the timescale of the secondary RDS (from 11 ps to 16 ps). Both of these effects are believed to be caused by the enhanced connectivity between the RC and the antenna via the linkers. The increase of the secondary RDS is because excitations having arrived at the RC have more chances to move back to the antenna in the presence of the linkers. If the downhill transfer to P700 occurring after the excitations arrive at the RC was the entire secondary RDS, the timescale of the secondary RDS should not be influenced by the linker Chls. From this, we conclude that the secondary RDS is very likely to be related to the back transfer process from the RC Chls to the antenna. Our calculation shows that the arrival kinetics of excitations at P700 is equally limited by the primary and the secondary RDSs. In addition to these two RDSs, of course, if the charge transfer time is very long, the intrinsic trapping at the trap can be one of the RDSs of the global trapping.
Intrinsic and global trapping times
A single quantity representing the excitation decay timescales is the trapping time defined by 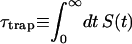 . In Appendix B, we derive the survival probability of the reversible kinetics in terms of the survival probabilities of irreversible kinetics. From the result, Eq. B11, of the derivation, we can obtain an exact expression of the trapping time in the presence of back-transfer from the trap:
. In Appendix B, we derive the survival probability of the reversible kinetics in terms of the survival probabilities of irreversible kinetics. From the result, Eq. B11, of the derivation, we can obtain an exact expression of the trapping time in the presence of back-transfer from the trap:
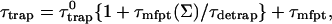 |
(22) |
where 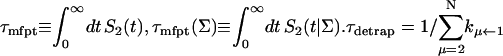 and
and 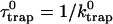 are, respectively, the detrapping time from the trap and the intrinsic trapping time. τmfpt describes the timescale for the excitation, initially created by an external perturbation, to arrive at the trap for the first time (mean first passage time of initial excitation), and τmfpt(Σ) is a similar mean first passage time but for the excitations created by back-energy transfer from the trap. Formal expressions for them in terms of the rate matrix can be obtained from Appendix B. Here, S2(t) and S2(t|Σ) are survival probabilities of an irreversible trapping problem for two different initial conditions defined in Appendix B. The second term in the curly bracket of Eq. 22 is responsible for processes following back-energy transfer from the trap. Since we define P700 as the trap, the sum of the two timescales for the primary and the secondary RDS is considered as τmfpt. If, instead, we define the RC Chls including P700 as a trap, the timescale of the primary RDS can be considered as τmfpt and the timescale of the secondary RDS can be considered as the first two terms of Eq. 22.
are, respectively, the detrapping time from the trap and the intrinsic trapping time. τmfpt describes the timescale for the excitation, initially created by an external perturbation, to arrive at the trap for the first time (mean first passage time of initial excitation), and τmfpt(Σ) is a similar mean first passage time but for the excitations created by back-energy transfer from the trap. Formal expressions for them in terms of the rate matrix can be obtained from Appendix B. Here, S2(t) and S2(t|Σ) are survival probabilities of an irreversible trapping problem for two different initial conditions defined in Appendix B. The second term in the curly bracket of Eq. 22 is responsible for processes following back-energy transfer from the trap. Since we define P700 as the trap, the sum of the two timescales for the primary and the secondary RDS is considered as τmfpt. If, instead, we define the RC Chls including P700 as a trap, the timescale of the primary RDS can be considered as τmfpt and the timescale of the secondary RDS can be considered as the first two terms of Eq. 22.
With P700 as the trap in our rate matrix, we obtained τmfpt = 34 ps for an initial distribution with all the Chls equally populated, τdetrap = 11 ps, and τmfpt(Σ) = 14 ps. Since the trap energy was calculated in Article I to be lower than any other Chls and, furthermore, the reorganization energy of P700 is set larger than other Chls (see Table 1), the excited state of P700 is stabilized so that the detrapping time is calculated to be fairly large. For this configuration, if τtrap0 < 2.7 ps, we have τtrap ≈ τmfpt in PSI and exclude the possibility of trap(P700)-limited kinetics.
Due to the difficulties in isolation of the RC and spectral congestion of the RC Chls with antenna Chls, the intrinsic trapping time has not been accurately determined yet. From the calculated three microscopic times, i.e., τmfpt, τdetrap, and τmfpt(Σ), and experimentally measured trapping time, we may estimate the intrinsic trapping time by use of Eq. 22 (in this case,  ). Considering that an experimental trapping time of ∼36∼38 ps has been reported (Gobets et al., 2001; Kennis et al., 2001), the intrinsic trapping time is estimated to be 0.87∼1.7 ps. This is in the same order of magnitude as the charge transfer time in the purple bacteria (Woodbury et al., 1985; Breton et al., 1986; Martin et al., 1986) and similar to the charge transfer time in PSI estimated by others (Owens et al., 1987; Hastings et al., 1994; Kumazaki et al., 1994; DiMagno et al., 1995). A shorter time (0.5∼0.8 ps) was also reported recently (Kumazaki et al., 2001). A similar charge transfer time (1.1 ps) was predicted by a simulation of Byrdin et al. (2002). Of course this kind of quantification from our calculation should be sensitive to the Hamiltonians and spectral densities adopted for the calculation and also on the experimental trapping time.
). Considering that an experimental trapping time of ∼36∼38 ps has been reported (Gobets et al., 2001; Kennis et al., 2001), the intrinsic trapping time is estimated to be 0.87∼1.7 ps. This is in the same order of magnitude as the charge transfer time in the purple bacteria (Woodbury et al., 1985; Breton et al., 1986; Martin et al., 1986) and similar to the charge transfer time in PSI estimated by others (Owens et al., 1987; Hastings et al., 1994; Kumazaki et al., 1994; DiMagno et al., 1995). A shorter time (0.5∼0.8 ps) was also reported recently (Kumazaki et al., 2001). A similar charge transfer time (1.1 ps) was predicted by a simulation of Byrdin et al. (2002). Of course this kind of quantification from our calculation should be sensitive to the Hamiltonians and spectral densities adopted for the calculation and also on the experimental trapping time.
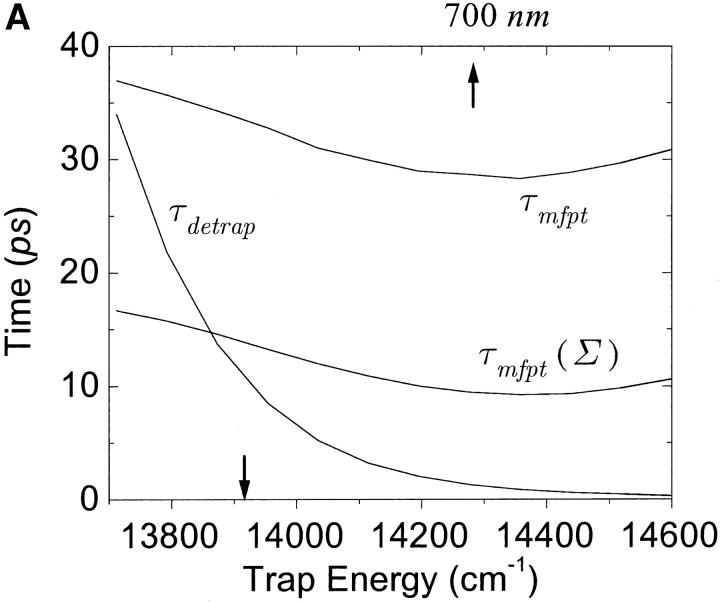
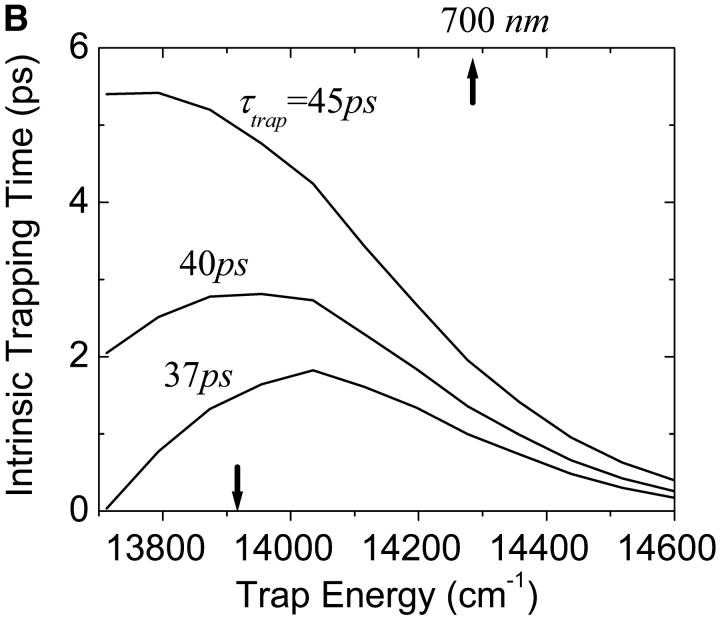
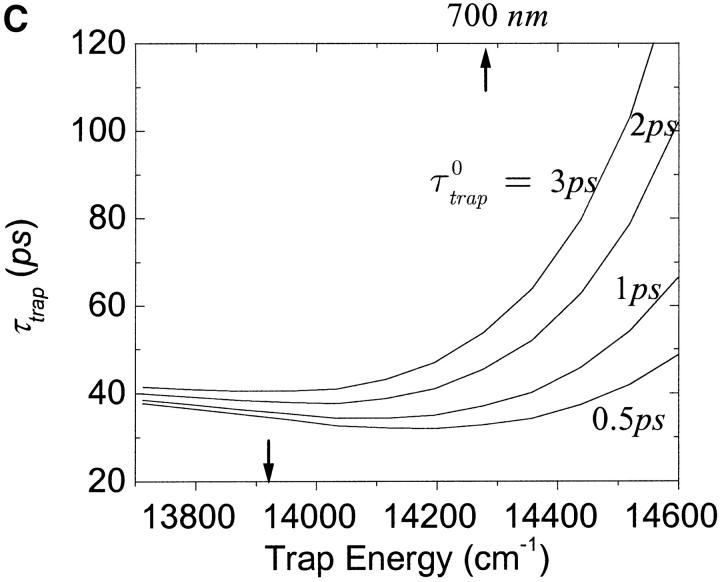
One of the most crucial factors influencing the calculated trapping timescales could be the energy of the trap. We plot the dependence of the microscopic timescales on the energy of the trap in Fig. 10 a. As we might expect, the back-transfer rate is strongly dependent on the trap energy, but the two mean first passage times are more or less insensitive to the trap energy, showing a minimum at ∼14,350 cm−1 (697 nm). This insensitivity reflects the fact that the major component of the RDS of the trapping kinetics is not the final step of the trapping process, i.e., the transfer from the RC Chls to P700. With these results and Eq. 22, we calculate intrinsic trapping times as a function of the trap energy for three arbitrary values of the global trapping time (37, 40, and 45 ps) in Fig. 10 b. The variation of the resulting intrinsic trapping time, τtrap0, for τtrap = 37 ps, is within the range of 0.2∼1.8 ps and if the energy of P700 is 700 nm, our calculation estimates the intrinsic charge transfer time of 1 ps. We now reverse the calculation and obtain the global trapping time as a function of the trap energy for four different intrinsic trapping times in Fig. 10 c. In the lower energy regime (<14,000 cm−1 (714 nm)), the back-energy transfer process (which may constitute another RDS for the trapping process, the tertiary RDS) does not contribute much and so the trapping time is almost independent of the intrinsic trapping time. It is interesting that the trapping time is insensitive to a change of trap energy from 719 nm (calculated in Article I) to 700 nm when τtrap0 = 1 ps. Fig. 10 a shows that this change of energy reduces the arrival times at P700 (τmfpt) and the detrapping time (τdetrap), respectively, by ∼6 and 9 ps. Cancellation between the reduced arrival time at P700 (secondary RDS), and the increase of timescale associated with the tertiary RDS, results in little change in the trapping time when τtrap0 = 1 ps.
FIGURE 10.
(a) Dependence of the three microscopic timescales on the trap energy for the calculated energies of the other Chls. (b) Variation of intrinsic trapping time calculated by Eq. 22 as a function of trap energy for the three trapping times written on the curves. (c) Dependence of the trapping time on the trap energy for four different intrinsic trapping times shown on the curves. In these figures, the arrow on the bottom axis of “trap energy” dictates the trap energy calculated in Article I. For reference we place another arrow on the top axis at 700 nm. The trap energy is defined as the energy corresponding to absorption peak of the trap.
Optimality of design
An overall trapping time of 30∼40 ps in a system with ∼100 Chl molecules represents an extremely high quantum yield of trapping (>97%). It is natural to ask if the locations, energies, and orientations of the individual antenna molecules have been selected by evolution to produce a highly optimal system. To investigate this question we have carried out two different types of simulations. In the first we vary the energies of specific sets of Chls (e.g., the entire system aside from P700) and calculate the trapping time for 1000 different sets of energies. In the second calculation we consider variation of the Coulombic couplings between the Chls via variation of the orientations of the transition moments of individual Chls, keeping each molecule at the geometry of the crystal structure.
Variation of excitation energies
In the first calculation, the energies of all the Chls except Chl EC-A1 (which is assumed to be P700) are randomly shuffled. The mean value of the trapping times averaged over the 1000 realizations is 59.4 ps with a standard deviation of 18.9 ps. The ratio of the standard deviation to the mean value is 0.32. Fig. 11 a shows the distribution of trapping times obtained for this ensemble. The trapping times are distributed in an asymmetric way with a tail extending to long trapping times. The arrow in the figure shows the location of the trapping time (35.9 ps) for the energy configuration obtained in Article I and, interestingly, it is near the lowest bound of the distribution. This calculation suggests to us that the assignment of static energies determined in Article I is highly optimized for P700 for the given distribution of static energies.
FIGURE 11.
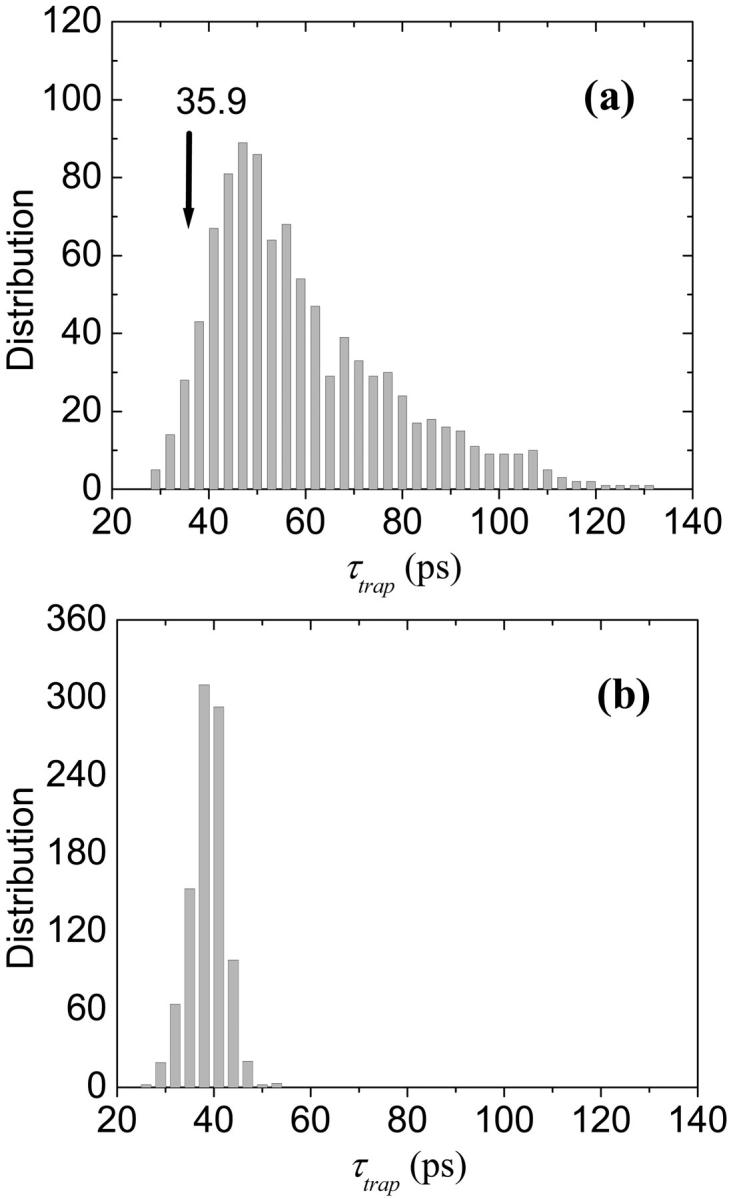
Histogram of trapping times (a) when the energies of all the Chls except P700 are randomly shuffled, and (b) when the energies of the RC and the linkers are fixed to the values calculated in Article I and the other energies are randomly shuffled (1000 samples).
Another 1000 different sets of energies are obtained by random shuffling of the energies of the antenna Chls while the energies of the RC Chls and the linker Chls are fixed at their calculated values in Article I. The distribution of trapping times for this case is shown in Fig. 11 b. In contrast with Fig. 11 a, the distribution is much more symmetric and significantly narrower. The mean and standard deviation are, respectively, 38.8 ps and 3.7 ps, and the ratio of the standard deviation to the mean value is only 0.095. Clearly the variation in the trapping times over the different samples is much reduced when we fix the energies of the RC and the linker Chls.
From these two results, we suggest that the calculated energy configuration of the RC and the linker Chls is highly optimized and that the energy configuration of the antenna Chls is less important in obtaining an optimal trapping time. The optimality associated with the RC and the linker Chls seems to result from a quasi-funnel structure around the RC. The energy of the Chl EC-A1 was calculated as 13,913 cm−1 (719 nm). The mean energy of the other RC and linker Chls is 14,664 cm−1 (682 nm) and the mean of the antenna Chls is 14,787 cm−1 (676 nm) with a standard deviation of 261 cm−1. We show the energy landscapes of the optimized (as calculated in Article I) configuration and one of the configurations which give a long trapping time (>100 ps) in Fig. 12. In the long-lifetime configuration, high energies are assigned to the RC Chls, EC-A2, and EC-A3, and the energy of the linker B39 is lowered. As a result, the P700 is spectrally isolated from the antenna Chls.
FIGURE 12.
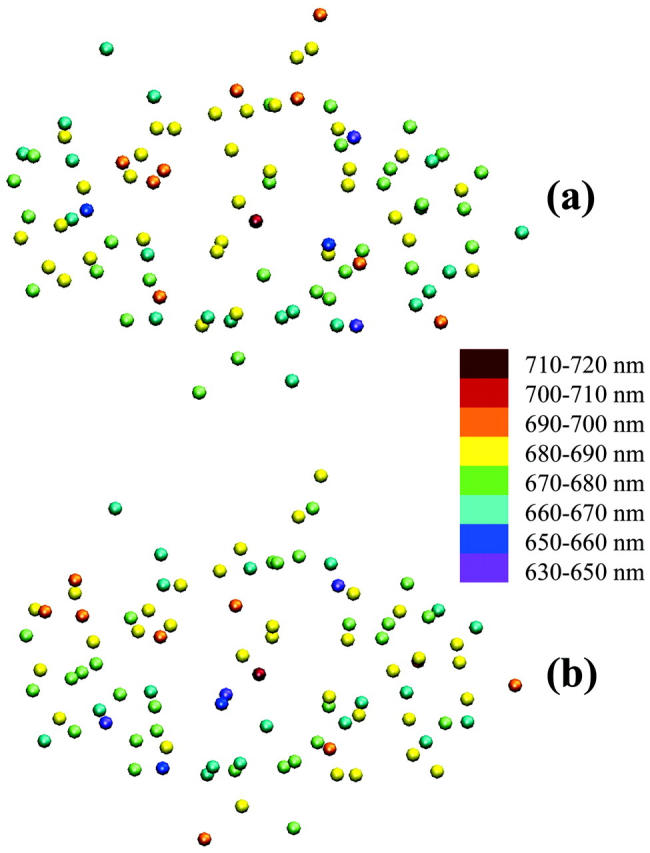
Energy distribution of the 96 Chls: (a) in the configuration suggested in Article I, and (b) in an arbitrary configuration yielding very long trapping time (104 ps).
Since in Fig. 11 b the ratio of the standard deviation to the mean value is very small and the mean value is quite close to 35.9 ps, it does not appear that any optimality in design is involved in the energy configuration of the antenna Chls for the given RC energies. Rather than a situation in which the static energies of the antenna Chls provide an optimal configuration for excitation flow, any given set of excitation energies seem to find optimal pathways by exploiting the higher connectivity of the structure. This conclusion is consistent with the observation of the robustness of the energy transfer network which has been ascribed to the multiple connections among the Chls by Byrdin et al. (2002). Sener et al (2002) also found that the trapping time is insensitive to removal of individual Chl molecules. In this aspect PSI differs significantly from the antenna systems of purple bacteria, i.e., LH1 and LH2, where the connectivity is pseudo-one-dimensional.
The introduction of disorder to the antenna Chls (rather than just change of the configuration of the disordered energies), however, does influence the energy transfer kinetics. For example, a trapping time of 25.4 ps is obtained when the energies of the antenna Chls are set homogeneous at their mean value (14,787 cm−1) and the quasi-funnel structure around the RC remains as calculated. This means that the amount of energetic disorder of the antenna Chls estimated in Article I reduces the efficiency of photosynthesis slightly as a result of the increases in trapping time from 25.4 ps to 35.9 ps. Against this cost, the system gains total absorption cross-section by extending the absorption region (Trissl, 1993). However the details of the disordered energetic configuration does not influence the trapping efficiency as discussed in connection with Fig. 11 b.
Variation of orientations of Chls
Now we examine optimality associated with the Coulombic couplings. For a full examination of this we need to calculate Coulombic couplings for various configurations of orientations of the Chls and inter-Chls distances which are, of course, coupled to their excitation energies. To reduce computational expense without loss of generality, we constructed Coulombic couplings including only the dipole-dipole couplings for the fixed positions of the Chls obtained from the x-ray structure and the refractive index values are determined by the field model discussed above. In this case only the directions of the transition dipoles of the Chls remain as random variables for the Coulombic coupling. The spectral density of each monomer is not altered from one sample to another. First we calculate the trapping time when the orientations of transition dipoles are determined based on the x-ray structure. In this case we obtained τtrap = 28 ps, which is a little bit (∼20%) shorter than the trapping time (36 ps) when quantum chemistry is used to obtain the Coulombic coupling.
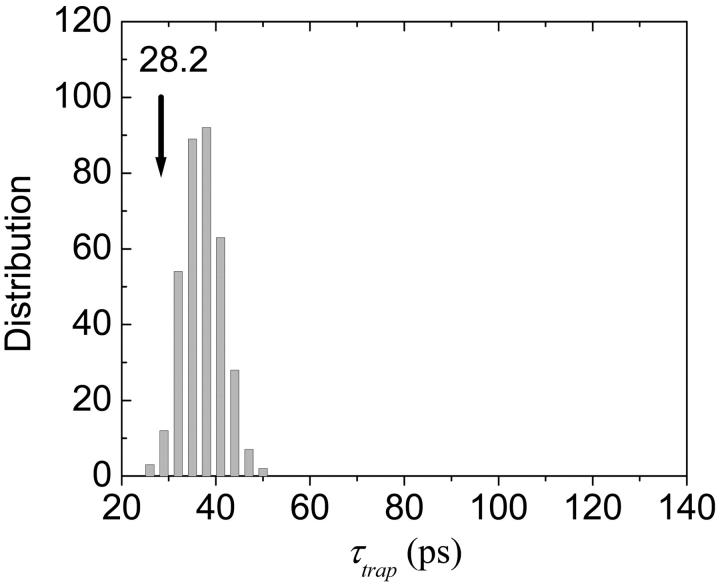
Next, the orientations of the RC and the linker Chls are fixed to those of the x-ray structure and the other Chls are randomly oriented. In this case we obtain the mean trapping time of 37 ps and a standard deviation of 4 ps. A histogram for this calculation is shown in Fig. 13. Interestingly, the trapping time for the x-ray structure (28 ps) lies on the lower bound of the distribution. This observation leads us to conclude that, in contrast with the diagonal energies, the actual orientations of the antenna Chls are in an optimized configuration for efficient trapping.
FIGURE 13.
Histogram of trapping times when the orientations of the RC and the linker Chls are fixed to the real structure and the others are randomly varied (400 samples). The Coulombic coupling is assumed to be dipole-dipole interaction only.
REMARKS ON TRAPPING TIME
When the first two terms of Eq. 22 are much greater than τmfpt, the kinetics is usually called trap-limited. The other case with τmfpt ≫ τtrap0 {1 + τmfpt (Σ)/τdetrap}, as in the present calculation, is called diffusion-limited in a homogeneous medium. In a disordered medium such as PSI, transfer dynamics in a specific subdomain (e.g., for our calculation, in the primary and the secondary RDS) may be much slower than the diffusion process in another domain (e.g., in the antenna Chls). In such a case, even if τmfpt ≫ τtrap0, the conventional concept of diffusion-limited kinetics may not be appropriate. For instance, as discussed above, in our calculation τmfpt consists of two main timescales for the primary and the secondary RDSs.
Since τmfpt (Σ), τdetrap, and τmfpt are independent of the intrinsic trapping time τtrap0, we can see that the global trapping time given by Eq. 22 is a linear function of the intrinsic trapping time. When the kinetics is dominated by a single exponential decay, the trapping time is the same as the inverse of the steady-state trapping rate constant defined in Eq. 21:
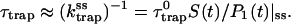 |
(23) |
In Eq. 23, the trapping time is an apparent linear function of the intrinsic trapping time with an intercept of zero. However, since the factor 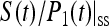 in Eq. 23 should implicitly depend on the intrinsic trapping time, one usually expects the trapping time will be a complicated function of the intrinsic trapping time (Laible et al., 1994). Interestingly, we re-obtained the linear dependence in Eq. 22 but with a nonzero intercept equal to τmfpt. Actually a similar linear dependence has been derived by Pearlstein (1982), based on a regular lattice model, and Eq. 22 is a generalization to energy-trapping systems arbitrary in their spatial and spectral structures.
in Eq. 23 should implicitly depend on the intrinsic trapping time, one usually expects the trapping time will be a complicated function of the intrinsic trapping time (Laible et al., 1994). Interestingly, we re-obtained the linear dependence in Eq. 22 but with a nonzero intercept equal to τmfpt. Actually a similar linear dependence has been derived by Pearlstein (1982), based on a regular lattice model, and Eq. 22 is a generalization to energy-trapping systems arbitrary in their spatial and spectral structures.
In trap-limited kinetic systems where the spatial distribution of excitations satisfy the Boltzmann distribution, Eq. 23 simplifies to (van Grondelle et al., 1994),
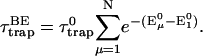 |
(24) |
In the absence of an exact expression such as Eq. 22, the trapping time for general cases has been approximated as a sum of two terms (Trinkunas and Holzwarth, 1996, 1997):
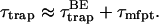 |
(25) |
The first term is for purely trap-limited thermal equilibrium kinetics and the second term is for purely diffusion-limited kinetics. However, the correct expression is not given by just the sum of the two extremes as in Eq. 25 but, in addition, the effects of the intrinsic trapping and diffusion rates should be convoluted as in the second term in the curly bracket of Eq. 22 to incorporate the transfer-equilibrium effect (Laible et al., 1994).
Another type of exact expression called the sojourn expansion for the trapping time was derived by Sener et al. (2002). In this expansion, the trapping time is given by an infinite series of timescales and the series is resumed to give a closed expression. As a result, the trapping time is separated into various orders of repeated detrapping and the linear dependence of τtrap on τtrap0 found in Eq. 22 is not obvious from the sojourn expansion.
CONCLUDING REMARKS
The transfer of excitation to, and the trapping at, P700 of Photosystem I is an exceedingly efficient process. Overall it differs substantially from the same process in purple bacteria, which is well studied, and in Photosystem II where atomic resolution structural data is not yet available. In looking at a two-dimensional projection of the PSI structure it is tempting to conclude that a similar isolation of the antenna from the electron transfer components exists in PSI as in purple bacteria (RC + LH1). Three important differences between these two systems are: 1), the quasi-three-dimensional structure of PSI vs. the quasi-one-dimensional structure of the RC/LH1 structure; 2), the fact that all six members of the RC Chls are energetically accessible from the antenna system in PSI, whereas only the primary electron donor is accessible in purple bacteria; and 3), the presence of the linker Chls in PSI.
In this article, we have developed a self-consistent approach to describe energy transfer dynamics in a complex system with both strong and weak Coulombic coupling such as PSI. A model of energy transfer in PSI has been constructed using microscopic Hamiltonian (excitation energies and Coulombic coupling) calculated in Article I and the spectral densities of the Chls determined by independent experiments. Using the model, we can reasonably reproduce experimental absorption and fluorescence timescales at room temperature and have arrived at the following conclusion about the mechanism of energy flow to P700, and the design principles at work in Photosystem I.
The overall trapping timescale (∼40 ps) in PSI has two main contributions when the charge transfer time is shorter than 2.7 ps: i) excitation energy diffusion in the antenna and transfer from the antenna to the RC Chls for the first time, which we refer to as the primary rate-determining step (RDS); this contributes ∼54% of the total timescale. ii) subsequent processes leading to the arrival of excitation at P700, occurring after the excitations have arrived at the RC, the secondary RDS. This includes back-transfer from the RC to antenna. This contributes ∼46% of the total timescale. Since the energy of P700 was calculated very low and furthermore, its excited electronic state is more stabilized by electron-phonon coupling than other Chls, the detrapping process is almost negligible (irreversible trapping at P700). If the energy of P700 is arbitrarily shifted up to 700 nm, the timescale of secondary RDS reduces, but the timescale of tertiary RDS (which is associated with the detrapping process) increases, to make the trapping time invariant if the charge transfer time is shorter than 1 ps.
Spectral equilibration occurs within the antenna in less than 5 ps and leads to a state characterized as a transfer equilibrium state rather than a thermodynamic equilibrium state. By this we mean that single exponential fluorescence kinetics is observed at all detection wavelengths on timescales longer than 5 ps.
The energy configuration of the six RC Chls and two linker Chls is highly optimized for efficient trapping at P700 by forming a quasi-funnel structure.
The energy configuration of the remaining 88 Chls of the antenna does not (at room temperature) influence the overall trapping time greatly. This arises from the high connectivity (dimensionality) of the PSI antenna which mitigates against trapping of excitation on energetically unfavorable antenna sites.
The orientation of the antenna pigments (via its influence on the Coulombic coupling) does influence the efficiency of trapping to a moderate extent.
Our model suggests an electron transfer timescale of 0.87∼1.7 ps from P700 to the primary electron acceptor and that this timescale does not have a strong influence on the overall trapping timescale.
Acknowledgments
We thank Dr. G. Zucchelli for providing us with the data in Table 2 and Dr. R. van Grondelle for valuable comments.
This work was supported by the Director of the Office of Science, Office of Basic Energy Sciences, Chemical Sciences Division of the United States Department of Energy, under Contract No. DE-AC03-76SF00098.
APPENDIX A
The functional form of the rate constant obtained by use of the generating function method (Yang and Fleming, 2002) is
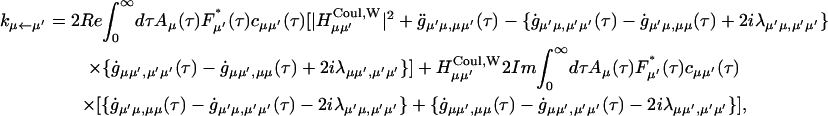 |
(A1) |
where
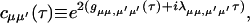 |
(A2) |
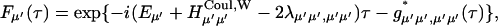 |
(A3) |
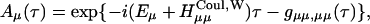 |
(A4) |
with
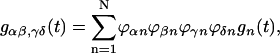 |
(A5) |
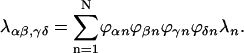 |
(A6) |
Here, gn(t) is a line broadening function of the nth Chl a molecule which characterizes the fluctuation dynamics of the molecule caused by the electron-phonon coupling:
 |
(A7) |
and λn is the reorganization energy of Chl n.  is a phonon Hamiltonian associated with Chl n. Fμ′(t) given by Eq. A3 is the kernel of fluorescence line shape function of the exciton state μ′ and Aμ(t) given by Eq. A4 is the kernel of absorption line shape function of the exciton state μ. gαβ,γδ(t) and λαβ,γδ are, respectively, the renormalized line broadening functions and reorganization energies associated with the exciton states dictated by the subscripts. The dot and double-dot on the various g(t) functions in Eq. A1 denote first and second time derivatives, respectively.
is a phonon Hamiltonian associated with Chl n. Fμ′(t) given by Eq. A3 is the kernel of fluorescence line shape function of the exciton state μ′ and Aμ(t) given by Eq. A4 is the kernel of absorption line shape function of the exciton state μ. gαβ,γδ(t) and λαβ,γδ are, respectively, the renormalized line broadening functions and reorganization energies associated with the exciton states dictated by the subscripts. The dot and double-dot on the various g(t) functions in Eq. A1 denote first and second time derivatives, respectively.
When Jcutoff → ∞, all the Coulombic coupling terms are treated as HCoul,W, and the excited electronic states of each Chl constitute the electronic eigenstates. In this case, Eq. A1 reduces to the well-known Förster overlap integral,
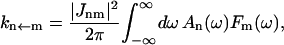 |
(A8) |
where the line shapes of fluorescence of energy donor and of absorption of energy acceptor are given, respectively, by
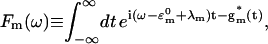 |
(A9) |
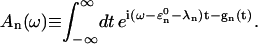 |
(A10) |
When Jcutoff → 0, all the Coulombic coupling terms are treated as HCoul,S and then HCoul,W = 0. In this case, Eq. A1 reduces to the expression for the rate constant derived from the modified Redfield theory (see Eq. 49 of Yang and Fleming, 2002).
APPENDIX B
We define a nontrapping probability as
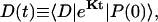 |
(B1) |
and a trapping probability as
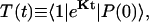 |
(B2) |
where 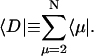 The sum of the two probabilities equals to the survival probability.We consider an integral expression of the propagator
The sum of the two probabilities equals to the survival probability.We consider an integral expression of the propagator
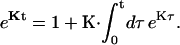 |
(B3) |
Using the property 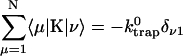 from Eq. B3 we obtain a relation between the survival probability and trapping probability
from Eq. B3 we obtain a relation between the survival probability and trapping probability
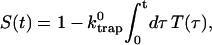 |
(B4) |
which describes the population conservation. Eq. B4 can be turned into a relation between the nontrapping and trapping probabilities in the Laplace transform domain
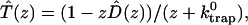 |
(B5) |
and so the survival probability is given in terms of the nontrapping probability
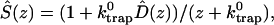 |
(B6) |
where  is the Laplace transform of a function f(t).
is the Laplace transform of a function f(t).
We introduce a submatrix of K defined by
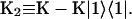 |
(B7) |
The rate matrix K2 describes the irreversible energy transfer dynamics in which 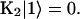 Then the Laplace transform of the propagator is expanded with respect to the rate matrix
Then the Laplace transform of the propagator is expanded with respect to the rate matrix 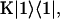
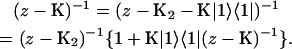 |
(B8) |
Now we introduce a vector 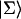 defined by
defined by 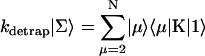 where
where 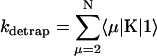 is the rate constant of back-energy transfer from the trap.
is the rate constant of back-energy transfer from the trap.  can be thought of as an acceptor vector receiving excitation energy by the back-energy transfer from the trap.
can be thought of as an acceptor vector receiving excitation energy by the back-energy transfer from the trap.
Operating  and
and  on Eq. B8, we have
on Eq. B8, we have
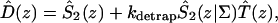 |
(B9) |
where 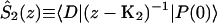 and
and  Eq. B9 separates the dynamics into two parts: irreversible trapping of an initial population (first term) and the irreversible trapping of the population newly created by the detrapping process (second term). Inserting
Eq. B9 separates the dynamics into two parts: irreversible trapping of an initial population (first term) and the irreversible trapping of the population newly created by the detrapping process (second term). Inserting 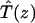 given by Eq. B5 into Eq. B9, we obtain the total nontrapping probability written as
given by Eq. B5 into Eq. B9, we obtain the total nontrapping probability written as
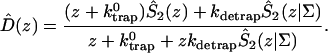 |
(B10) |
Inserting Eq. B10 into Eq. B6, we have the survival probability of the reversible trapping problem in terms of two survival probabilities in the irreversible trapping problem
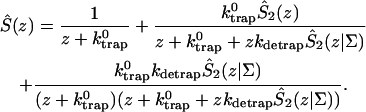 |
(B11) |
Mino Yang's present address is Dept. of Chemistry, Chungbuk National University, Cheongju, 361-763, South Korea.
Ana Damjanović's present address is Dept. of Physics, 012 Jenkins Hall, Johns Hopkins University, Baltimore, MD 21218.
References
- Beauregard, M., I. Martin, and A. R. Holzwarth. 1991. Kinetic modeling of exciton migration in photosynthetic systems 1. Effects of pigment heterogeneity and antenna topography on exciton kinetics and charge separation yields. Biochim. Biophys. Acta. 1060:271–283. [Google Scholar]
- Beddard, G. S. 1998. Excitations and excitons in Photosystem I. Phil. Trans. R. Soc. Lond. A. 356:421–448. [Google Scholar]
- Breton, J., J.-L. Martin, A. Migus, A. Antonetti, and A. Orszag. 1986. Femtosecond spectroscopy of excitation energy transfer and initial charge separation in the reaction center of the photosynthetic bacterium Rhodopseudomonas viridis. Proc. Natl. Acad. Sci. USA. 83:5121–5125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrdin, M., P. Jordan, N. Krauss, P. Fromme, D. Stehlik, and E. Schlodder. 2002. Light harvesting in Photosystem I: modeling based on the 2.5-A structure of Photosystem I from Synechococcus elongatus. Biophys. J. 83:433–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croce, R., G. Zucchelli, F. M. Garlaschi, and R. C. Jennings. 1998. A thermal broadening study of the antenna chlorophylls in PSI-200, LHCI, and PSI Core. Biochemistry. 37:17355–17360. [DOI] [PubMed] [Google Scholar]
- Damjanovic, A., H. M. Vaswani, P. Fromme, and G. R. Fleming. 2002. Chlorophyll excitations in PSI of Synechococcus elongatus. J. Phys. Chem. B. 106:10251–10262. [Google Scholar]
- DiMagno, L., C.-K. Chan, Y. Jia, M. J. Lang, J. R. Newman, L. Mets, G. R. Fleming, and R. Haselkorn. 1995. Energy transfer and trapping in Photosystem I reaction centers from cyanobacteria. Proc. Natl. Acad. Sci. USA. 92:2715–2719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelmann, E., T. Tagliabue, N. V. Karapetyan, F. M. Garlaschi, G. Zucchelli, and R. C. Jennings. 2001. CD spectroscopy provides evidence for excitonic interactions involving red-shifted chlorophyll forms in Photosystem I. FEBS Lett. 499:112–115. [DOI] [PubMed] [Google Scholar]
- Fleming, G. R., and R. van Grondelle. 1997. Femtosecond spectroscopy of photosynthetic light-harvesting systems. Curr. Opin. Struct. Biol. 7:738–748. [DOI] [PubMed] [Google Scholar]
- Gibasiewics, K., V. M. Ramesh, A. N. Melkozernov, S. Lin, N. W. Woodbury, R. E. Blankenship, and A. N. Webber. 2002. Excitation dynamics in the core antenna of PS I from Chlamydomonas reinhardtii CC 2696 at room temperature. J. Phys. Chem. B. 105:11498–11506. [Google Scholar]
- Gillie, J. K., P. A. Lyle, G. J. Small, and J. H. Golbeck. 1989a. Spectral hole burning of the primary electron donor state of Photosystem I. Photosynth. Res. 22:233–246. [DOI] [PubMed] [Google Scholar]
- Gillie, J. K., G. J. Small, and J. H. Golbeck. 1989b. Nonphotochemical hole burning of the native antenna complex of Photosystem I. J. Phys. Chem. 93:1620–1627. [Google Scholar]
- Gobets, B., H. van Amerongen, R. Monshouwer, J. Kruip, M. Rögner, R. van Grondelle, and J. P. Dekker. 1994. Polarized site-selected fluorescence spectroscopy of isolated Photosystem I particles. Biochim. Biophys. Acta. 1188:75–85. [Google Scholar]
- Gobets, B., and J. P. Dekker. and R. van Grondelle. 1998. Transfer-to-trap limited model of energy transfer in Photosystem I. In Photosynthesis: Mechanisms and Effects. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, the Netherlands. pp.503–508.
- Gobets, B., I. H. M. van Stokkum, M. Rogner, J. Kruip, E. Schlodder, N. V. Karapetyan, J. P. Dekker, and R. van Grondelle. 2001. Time-resolved fluorescence emission measurements of Photosystem I particles of various cyanobacteria: a unified compartmental model. Biophys. J. 81:407–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gobets, B., and R. van Grondelle. 2001. Energy transfer and trapping in Photosystem I. Biochim. Biophys. Acta. 1507:80–99. [DOI] [PubMed] [Google Scholar]
- Gobets, B., I. H. M. van Stokkum, F. van Mourik, M. Rögner, J. Kruip, E. Schlodder, J. P. Dekker, and R. van Grondelle. 2002a. Excitation wavelength dependence of the fluorescence kinetics in Photosystem I particles from Synechocystis PCC 6803 and Synechococcus elongatus. PhD thesis. Urije Universiteit, Amsterdam. 6:133–160. [DOI] [PMC free article] [PubMed]
- Gobets, B., L. Valkunas, and R. van Grondelle. 2002b. Bridging the gap between structural and lattice models: a parametrization of energy transfer and trapping in Photosystem I. PhD thesis. Urije Universiteit, Amsterdam. 5:113–132. [DOI] [PMC free article] [PubMed]
- Hastings, G., F. A. M. Kleinherenbrink, S. Lin, and R. E. Blankenship. 1994. Time-resolved fluorescence and absorption spectroscopy of Photosystem I. Biochemistry. 33:3185–3192. [DOI] [PubMed] [Google Scholar]
- Hastings, G., L. J. Leed, S. Lin, and R. E. Blankenship. 1995. Excited state dynamics in Photosystem I: effects of detergent and excitation wavelength. Biophys. J. 69:2044–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemenger, R. P., R. M. Pearlstein, and K. L. Lindenberg. 1972. Incoherent exciton quenching on lattices. J. Math. Phys. 13:1056–1063. [Google Scholar]
- Holzwarth, A. R., G. Schatz, H. Brock, and E. Bittersmann. 1993. Energy transfer and charge separation kinetics in Photosystem I. Part 1: picosecond transient absorption and fluorescence study of cyanobacterial Photosystem I particles. Biophys. J. 64:1813–1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu, C.-P., G. R. Fleming, M. Head-Gordon, and T. Head-Gordon. 2001. Excitation energy transfer in condensed media. J. Chem. Phys. 114:3065–3072. [Google Scholar]
- Hu, X., and K. Schulten. 1998. Model for the light-harvesting complex I (B875) of Rhodobacter sphaeroides. Biophys. J. 75:683–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jean, J. M., C.-K. Chan, G. R. Fleming, and T. G. Owens. 1989. Excitation transport and trapping on spectrally disordered lattice. Biophys. J. 56:1203–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennings, R. C., G. Zucchelli, R. Croce, L. Valkunas, L. Finzi, and F. M. Garlaschi. 1997. Model studies on the excited state equilibrium perturbation due to reaction center trapping in Photosystem I. Photosynth. Res. 52:245–253. [Google Scholar]
- Jia, Y., J. M. Jean, M. M. Werst, C.-K. Chan, and G. R. Fleming. 1992. Simulations of the temperature dependence of energy transfer in the PSI core antenna. Biophys. J. 63:259–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan, P., P. Fromme, H. T. Witt, O. Klukas, W. Saenger, and N. Krauss. 2001. Three-dimensional structure of cyanobacterial Photosystem I at 2.5 Å resolution. Nature. 411:909–917. [DOI] [PubMed] [Google Scholar]
- Karapetyan, N. V., A. R. Holzwarth, and M. Roegner. 1999. The Photosystem I trimer of cyanobacteria: molecular organization, excitation dynamics and physiological significance. FEBS Lett. 460:395–400. [DOI] [PubMed] [Google Scholar]
- Kennis, J. T. M., B. Gobets, I. H. M. V. Stokkum, J. Dekker, R. V. Grondelle, and G. R. Fleming. 2001. Light harvesting by chlorophylls and carotenoids in the Photosystem I core complex of Synechococcus elongatus: a fluorescence upconversion study. J. Phys. Chem. B. 105:4485–4494. [Google Scholar]
- Kleima, F. J., E. Hofmann, B. Gobets, I. H. M. van Stokkum, R. van Grondelle, K. Diederichs, and H. van Amerongen. 2000. Forster excitation energy transfer in peridinin-chlorophyll-a-protein. Biophys. J. 78:344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauss, N. 1993. Three-dimensional structure of system-I of photosynthesis at 6-Å resolution. Nature. 361:326–331. [Google Scholar]
- Krauss, N., W.-D. Schubert, O. Klukas, P. Fromme, H. T. Witt, and W. Saenger. 1996. Photosystem I at 4-Å resolution represents the first structural model of a joint photosynthetic reaction center and core antenna system. Nat. Struct. Biol. 3:965–973. [DOI] [PubMed] [Google Scholar]
- Kumazaki, S., H. Kandori, H. Petek, K. Yoshihara, and I. Ikegami. 1994. Primary photochemical processes in P700-enriched Photosystem I particles: trap-limited excitation decay and primary charge separation. J. Phys. Chem. 98:10335–10342. [Google Scholar]
- Kumazaki, S., I. Ikegami, H. Furusawa, S. Yasuda, and K. Yoshihara. 2001. Observation of the excited state of the primary electron donor chlorophyll (P700) and the ultrafast charge separation in the spinach Photosystem I reaction center. J. Phys. Chem. B. 105:1093–1099. [Google Scholar]
- Laible, P. D., W. Zipfel, and T. G. Owens. 1994. Excited state dynamics in chlorophyll-based antennae: the role of transfer equilibrium. Biophys. J. 66:844–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, J.-L., J. Breton, A. J. Hoff, A. Migus, and A. Antonetti. 1986. Femtosecond spectroscopy of electron-transfer in the reaction center of the photosynthetic bacterium Rhodopseudomonas sphaeroides R-26: direct electron-transfer from the dimeric bacteriochlorophyll primary donor to the bacteriopheophetin acceptor with a time constant 2.8 ± 0.2 psec. Proc. Natl. Acad. Sci. USA. 83:957–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melkozernov, A. N., S. Lin, and R. E. Blankenship. 2000. Excitation dynamics and heterogeneity of energy equilibration in the core antenna of Photosystem I from the cyanobacterium Synechocystis sp. PCC 6803. Biochemistry. 39:1489–1498. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N. 2001. Excitation energy transfer in Photosystem I from oxygenic organisms. Photosynth. Res. 70:129–153. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N., S. Lin, R. E. Blankenship, and L. Valkunas. 2001. Spectral inhomogeneity of Photosystem I and its influence on excitation equilibration and trapping in the cyanobacterium Synechocystis sp. PCC6803 at 77. Biophys. J. 81:1144–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel, S. 1995. Principles of Nonlinear Optical Spectroscopy. Oxford University Press, New York.
- Nagasawa, Y., S. A. Passino, T. Joo, and G. R. Fleming. 1997. Temperature dependence of optical dephasing in an organic polymer glass (PMMA) from 300K to 30K. J. Chem. Phys. 106:4840–4852. [Google Scholar]
- Ohta, K., M. Yang, and G. R. Fleming. 2001. Ultrafast exciton dynamics of J aggregates in room temperature solution: a third-order nonlinear spectroscopy and numerical modeling study. J. Chem. Phys. 115:7609–7621. [Google Scholar]
- Owens, T. G., S. P. Webb, L. Mets, R. S. Alberte, and G. R. Fleming. 1987. Antenna size dependence of fluorescence decay in the core antenna of Photosystem I: estimates of charge separation and energy transfer rates. Proc. Natl. Acad. Sci. USA. 84:1532–1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, L.-O., C. Flemming, B. Gobets, R. van Grondelle, J. P. Dekker, and E. Schlodder. 1998. Energy transfer and charge separation in Photosystem I: P700 oxidation upon selective excitation of the long-wavelength antenna chlorophylls of Synechococcus elongatus. Biophys. J. 74:2611–2622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearlstein, R. M. 1982. Exciton migration and trapping in photosynthesis. Photochem. Photobiol. 35:835–844. [Google Scholar]
- Rivadossi, A., G. Zucchelli, F. M. Garlaschi, and R. C. Jennings. 1999. The importance of PS I chlorophyll red forms in light-harvesting by leaves. Photosynth. Res. 60:209–215. [Google Scholar]
- Schatz, G. C., and M. A. Ratner. 1993. Quantum mechanics in chemistry. Prentice Hall, Englewood Cliffs, NJ.
- Schubert, W.-D., O. Klukas, N. Krauss, W. Saenger, P. Fromme, and H. T. Witt. 1997. Photosystem I of Synechococcus elongatus at 4 Å resolution: comprehensive structure analysis. J. Mol. Biol. 272:741–769. [DOI] [PubMed] [Google Scholar]
- Sener, M. K., D. Lu, T. Ritz, S. Park, P. Fromme, and K. Schulten. 2002. Robustness and optimality of light harvesting in cyanobacterial Photosystem I. J. Phys. Chem. B. 106:7948–7960. [Google Scholar]
- Somsen, O. J. G., L. Valkunas, and R. van Grondelle. 1996. A perturbed two-level model for exciton trapping in small photosynthetic systems. Biophys. J. 70:669–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timpmann, K., A. Freiberg, and V. Sundstrom. 1995. Energy trapping and detrapping in the photosynthetic bacterium Rhodopseudomonas viridis: transfer-to-trap-limited dynamics. Chem. Phys. 194:275–283. [Google Scholar]
- Trinkunas, G., and A. R. Holzwarth. 1994. Kinetic modeling of exciton migration in photosynthetic systems. 2. Simulations of excitation dynamics in two-dimensional Photosystem I core antenna/reaction center complexes. Biophys. J. 66:415–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trinkunas, G., and A. R. Holzwarth. 1996. Kinetic modeling of exciton migration in photosynthetic systems. 3. Application of genetic algorithms to simulations of excitation dynamics in three-dimensional Photosystem I core antenna/reaction center complexes. Biophys. J. 71:351–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trinkunas, G., and A. R. Holzwarth. 1997. On the rate-limiting process of energy transfer in the light harvesting antenna. J. Luminesc. 72–74:615–617. [Google Scholar]
- Trissl, H.-W. 1993. Long-wavelength absorbing antenna pigments and heterogeneous absorption bands concentrate excitons and increase absorption cross section. Photosynth. Res. 35:247–263. [DOI] [PubMed] [Google Scholar]
- Valkunas, L., V. Liouolia, J. P. Dekker, and R. van Grondelle. 1995. Description of energy migration and trapping in Photosystem I by a model with two distance scaling parameters. Photosynth. Res. 43:149–154. [DOI] [PubMed] [Google Scholar]
- van Grondelle, R., J. Dekker, T. Gillbro, and V. Sundstrom. 1994. Energy transfer and trapping in photosynthesis. Biochim. Biophys. Acta. 1187:1–65. [Google Scholar]
- Werst, M., Y. Jia, L. Mets, and G. R. Fleming. 1992. Energy transfer and trapping in the Photosystem I core antenna. Biophys. J. 61:868–878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White, N. T. H., G. S. Beddard, J. R. G. Thorne, T. M. Feehan, T. E. Keyes, and P. Heathcote. 1996. Primary charge separation and energy transfer in the Photosystem I reaction center of higher plants. J. Phys. Chem. 100:12086–12099. [Google Scholar]
- Woodbury, N. W., M. Becker, D. Middendorf, and W. W. Parson. 1985. Picosecond kinetics of the initial photochemical electron-transfer reaction in bacterial photosynthetic reaction centers. Biochemistry. 24:7516–7521. [DOI] [PubMed] [Google Scholar]
- Yang, M., and G. R. Fleming. 2002. Influence of phonons on exciton transfer dynamics: comparison of the Redfield, Förster, and modified Redfield equations. Chem. Phys. 282:163–180. [Google Scholar]
- Zazubovich, V., S. Matsuzaki, T. W. Johnson, J. M. Hayes, P. R. Chitnis, and G. J. Small. 2002. Red antenna states of Photosystem I from cyanobacterium Synechococcus elongatus: a spectral hole burning study. Chem. Phys. 275:47–59. [Google Scholar]
- Zhang, W. M., T. Meier, V. Chernyak, and S. Mukamel. 1998. Exciton-migration and three-pulse femtosecond optical spectroscopies of photosynthetic antenna complexes. J. Chem. Phys. 108:7763–7774. [Google Scholar]
- Zucchelli, G., F. M. Garlaschi, and R. C. Jennings. 1996. Thermal broadening analysis of the Light Harvesting Complex II absorption spectrum. Biochemistry. 35:16247–16254. [DOI] [PubMed] [Google Scholar]
- Zucchelli, G., R. C. Jennings, F. M. Garlaschi, G. Cinque, R. Bassi, and O. Cremonesi. 2002. The calculated in vitro and in vivo chlorophyll a absorption bandshape. Biophys. J. 82:378–390. [DOI] [PMC free article] [PubMed] [Google Scholar]