Protocol for MM/PBSA Molecular Dynamics Simulations of Proteins

Abstract

Continuum solvent models have been employed in past years for understanding processes such as protein folding or biomolecular association. In the last decade, several attempts have been made to merge atomic detail molecular dynamics simulations with solvent continuum models. Among continuum models, the Poisson-Boltzmann solvent accessible surface area model is one of the oldest and most fundamental. Notwithstanding its wide usage for simulation of biomolecular electrostatic potential, the Poisson-Boltzmann equation has been very seldom used to obtain solvation forces for molecular dynamics simulation. We propose here a fast and reliable methodology to implement continuum forces in standard molecular mechanics and dynamics algorithms. Results for a totally unrestrained 1 ns molecular dynamics simulation of a small protein are quantitatively similar to results obtained by explicit solvent molecular dynamics simulations.

INTRODUCTION

Our understanding of complex biomolecular processes like protein folding or molecular recognition has greatly benefited from concepts such as hydrophobicity or solvation of electrostatic charges. Much of our capability to predict biomolecular behavior depends on concepts where the solvent is taken into account through its average effects, rather than through an atomic detail representation (Tanford, 1978; Eisenberg and McLachlan, 1986; Perutz, 1978).

One of the most popular solvent models is based on the Poisson-Boltzmann (PB) equation, as far as electrostatic effects are considered, and on the definition of a surface tension energy proportional to the solvent accessible (SA) surface area to take into account the tendency of nonpolar parts of a molecule to collapse (Fogolari et al., 2002; Honig and Nicholls, 1995; Davis and McCammon, 1990; Nicholls et al., 1991; Sitkoff et al., 1994).

Although analyses of biomolecules based on the Poisson-Boltzmann solvent accessible surface area (PBSA) model are widespread in the literature, very seldom has the same model been used for generating molecular dynamics trajectories in conjunction with standard molecular dynamics protocols (Sharp, 1991; Niedermeier and Schulten, 1992; Gilson et al., 1995; Smart et al., 1997; Smart and McCammon, 1999; David et al., 2000; Luo et al., 2002; Lu et al., 2002; Im et al., 1998; Fogolari et al., 2001; Huber, 1998). Other models, using a molecular mechanics (MM) force field and a solvent model, often derived from the PBSA model by approximation, have been conceived and used, which are practical and attain good accuracy (e.g., Roux and Simonson, 1999; Simonson, 2001; Still et al., 1990; Qiu et al., 1997).

The advantage of performing molecular dynamics (MD) simulations using implicit versus explicit solvent models are manifold, including faster equilibration times, easily tunable solvent properties, and, depending on the model, shorter computation times. It is therefore of interest exploring implicit solvent MD simulations and in particular the MM/PBSA model, which constitutes a reference for many other simpler models. The limited number of applications of the MM/PBSA methodology to MD simulations poses a question on its reliability.

We wish to remark that the MM/PBSA model, like other implicit models (see, e.g., Lazaridis and Karplus, 1999), is based on the potential of mean force theory (Hill, 1956), and on the assumption that electrostatic and nonpolar contributions to the free energy and the mean force can be treated separately in a simple additive way. It is worth pointing out that both the latter assumption and the possibility of finding accurate functional forms for the potential of mean force are highly questionable. In the MM/PBSA approach, rather than looking for more physical (and complex) implicit solvent representations, much attention has been devoted to adjusting model parameters, such as atomic radii and solute dielectric constant, to reproduce experimental observations. When parameters are properly chosen, the PBSA approach affords an accuracy comparable or superior to explicit solvent simulation methods. With a limited number of parameters, Honig and coworkers were able to describe solvation energies for a large number of small organic compounds (Sitkoff et al., 1994). An even more impressive application of the methodology has been developed by Kollman and coworkers who analyzed explicit solvent MD trajectories using the MM/PBSA approach and used the free energy thus computed to discriminate between native- and nonnative-like conformations for two small peptides (Kollman et al., 2000; Lee et al., 2001). The approach, however, makes use of PBSA free energy, rather than PBSA forces, and conformations are generated with independent methods. Although results are impressive, strictly speaking, as far as the PBSA methodology is concerned, compensating errors may occur in computing the global free energy, and there is no guarantee that other conformations (not sampled because sampling is performed with different methods) could not have a lesser free energy. In this respect, the study of Gilson and coworkers (David et al., 2000), who simulated the dynamics of a loop of a protein with several implicit solvent models, is more sensitive to possible pitfalls of the methods. In that study, however, the rest of the protein was kept fixed. We presented recent MD simulations using the MM/PBSA approach for a small protein and a DNA hairpin (Fogolari et al., 2001).

In our previous work, we were able to obtain trajectories preserving native structure only by imposing a dielectric constant >1.0. Similar conclusions have been reached more recently by Lu et al. (2002), who determined an optimal dielectric constant of 17.0. The choice of dielectric constants higher than 1.0 poses theoretical and practical problems that are discussed at length in the Materials and Methods section.

Another problem particularly relevant for small systems is that fluctuations in standard or even Langevin MD are too small, due to overall energy conservation and to the paucity of degrees of freedom. Therefore conformational sampling must be enforced, e.g., by high temperature (see, e.g., Gilson et al., 1995) or Monte Carlo steps (see, e.g., Smart et al., 1997).

In this communication, i), we propose a simple way to treat the dielectric constant problem; ii), we test an updating scheme more consistent with the dielectric relaxation time of water (∼10 ps) (Harvey 1989), and iii), we apply the methodology to a small protein.

Our results indicate that even with standard parameters, the accuracy is comparable to that obtained by explicit solvent MD simulations. In view of recent advances in both MD simulation and Poisson-Boltzmann equation (PBE) solution methodologies, our results show that MM/PBSA methodology is likely to play a relevant role in long time MD simulations.

MATERIALS AND METHODS

MM/PBSA methodology

In the MM/PBSA methodology (Fogolari et al., 2002; Honig and Nicholls, 1995; Davis and McCammon, 1990; Baginski et al., 1997; Kollman et al., 2000), the potential of mean force W for a macromolecular system is written as the sum of an intermolecular energy term 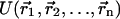and a solvation free energy term that can be further split in a polar (electrostatic) and a nonpolar (hydrophobic) term:

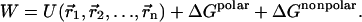(1)

Both ΔG^polar and ΔG^nonpolar depend only on solute coordinates. 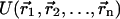is computed according to one of the available force fields, ΔG^polar is computed according to the Poisson-Boltzmann theoretical framework (Sharp and Honig, 1990; Marcus, 1955; Zhou, 1994; Fogolari and Briggs, 1997) as the difference in free energy for the hypothetical charging process of the solute in a homogeneous medium (ideally vacuum) and in ionic solvent.

ΔG^nonpolar is taken to be proportional to the solvent accessible surface area A, i.e., ΔG^nonpolar = γA.

Derivatives of W with respect to atomic coordinates give mean forces that include an intramolecular term and two solvation terms. Expressions for the derivative of ΔG^polar from the solution of the PB equation have been given by Gilson et al. (1993), Im et al. (1998), and Friedrichs et al. (1999) for different computational models. We have used the method of Gilson et al. (1993), as implemented in the software package University of Houston Brownian Dynamics (UHBD) (Madura et al., 1994, 1995). Solvation electrostatic forces include a classical electrostatic field term and additional dielectric and ionic boundary force terms. The ionic boundary force term, of smaller magnitude with respect to other terms, has been neglected, similarly to Gilson et al. (1993).

A fast algorithm for the computation of surface area derivatives with respect to atomic coordinates due to Sridharan et al. (1995) has been used as implemented in UHBD (version 6.x).

When a straightforward implementation was tested with the various protocols described hereafter, employing dielectric constant ɛ = 1.0, as adopted in most common force fields, the resulting molecular dynamics trajectories, which use Poisson-Boltzmann forces (with or without a solvent accessible surface area term), did not preserve native structures. This result is consistent with the results obtained, using different protocols and programs from the one employed here, by Fogolari et al. (2001) and Lu et al. (2002).

This is at odds with the many successful simulations that use other implicit solvent methods, which are in different ways derived from the more fundamental Poisson equation, like, e.g., the generalized Born/solvent accessible method (GB/SA) (Still et al., 1990; Qiu et al., 1997) or the methods developed in the group of Karplus (e.g., Lazaridis and Karplus, 1999). In these methods, however, solvation forces are computed analytically by means of smooth functions and parameters that are tailored to provide reasonable results. For instance, in the GB/SA method, there are no dielectric discontinuities and the five parameters used for calculating effective Born radii have been optimized (Qiu et al., 1997) to reproduce electrostatic energies computed by the finite difference Poisson-Boltzmann equation.

Failure of molecular dynamics trajectories (employing PB forces) to preserve native structures may be conceivably due to a number of reasons. Numerical inaccuracies of the Poisson-Boltzmann solver were ruled out by tests with a finer grid or a more stringent convergence criterion, which all led to similar results. Another explanation could be that the macroscopic treatment provided by the Poisson-Boltzmann equation is not suitable for merging with atomic detail simulations, which is at variance with the many successful applications of the Poisson-Boltzmann equation (see for reviews, e.g., Madura et al., 1994; Honig and Nicholls, 1995; Fogolari et al., 2002). In these applications, however, electrostatic forces acting on solute atoms are very seldom considered, and rather electrostatic potentials and fields (at the surface or outside the molecule) and free energies are used. Also in many studies static models are considered and a rather large range of dielectric constants (in the range 1.0–20.0) are used.

Another possible explanation is that the parameters employed for atomic radii and charges are not proper, but the values employed here are rather standard and work excellently for small molecules like the dialanine peptide (see, e.g., Fogolari et al., 2001). On the other hand, extensive optimization on such large systems as the one considered here was computationally not feasible.

Finally, the most striking feature of the simulation are the very high solvation electrostatic forces. Based on our previous work on the linearized version of the Poisson-Boltzmann equation (Fogolari et al., 1999), we can exclude that this is due to only to linearization (employed in the present work) because the system is not so much charged as to give large artifacts, like observed, e.g., for DNA.

To reduce solvation forces, we decided to raise the dielectric constant to 4.0, consistent with many studies in the literature. The proper dielectric constant for use in various kind of atomic detail simulations is a controversial issue in the literature (see, e.g., Schutz and Warshel, 2001). The choice of the dielectric constant strictly depends on “what is included explicitly in the given model” (Schutz and Warshel, 2001). In most popular force fields, like CHARMM, which is used in the present work, no polarizability (i.e., no induced dipole) is considered. Under such a model, the best dielectric constant should be 2.0, according to Schutz and Warshel (2001) (see also Debye, 1929). Although this holds in principle, it is possible that force field parameters may implicitly account for polarizability, like for instance for some of the many water models available. Force field parameters for proteins, however, are fitted to structural experimental data, in vacuo quantum mechanical calculations and vibrational frequencies rather than to dielectric constants. In a recent study, Simonson (1999) found that the simulated dielectric constant of a protein, applying the Frolich-Kirkwood theory on molecular dynamics trajectories without considering charged groups fluctuations (i.e., considering only dipoles), is very small (2–3) similar to that of alkanes and smaller than expected. For the sake of clarity, as an extreme case, we consider the dielectric constant of a solution of an alkane. When the alkane is simulated with a united atom force field (i.e., with no partial charges on apolar groups), the dielectric constant for the interaction of two solute charges far apart will be the one used by the force field, i.e., 1.0 (contrary to the experimental value of ∼2.0). It is likely that similar results are obtained in all atoms simulations where apolar molecules have very small partial charges. In the latter case, the simulation of the interactions of two separated charges would overestimate electrostatic interactions and forces by a factor ∼2.0. Motivated by the theoretical and practical limitations of most popular force fields, progress has been made in recent years in the development of polarizable force fields where permanent charges and inducible dipoles are clearly separated (Halgren and Damm, 2001).

The choice of using a higher dielectric constant faces the problem that the dielectric constant in 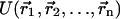cannot be changed at will because hydrogen bonds, of utmost importance for biomolecular structure, are reproduced in modern force fields through electrostatic and van der Waals terms. On the other hand, if a dielectric constant 1.0 is retained in the MM part of the potential of mean force W and a dielectric constant 4.0 is used for the PBSA part, two widely separated and solvated charges will interact with an approximate dielectric constant of 4/3 instead of ∼80, because the solvation term is depressed by a factor 4.0:

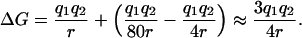In this work, we adopted the following procedure to have a dielectric constant ɛ = 4.0 while retaining short ranged hydrogen bond interactions and optimal local geometry: we implemented in CHARMM a switching function (the same used by CHARMM to implement cutoffs) to turn off the ɛ = 1 interactions and to turn on the ɛ = 4 interactions:

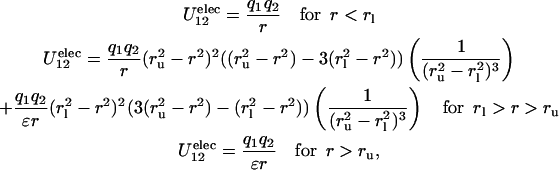(2)

where r_l and r_u are the lower and upper limits of the switching region and ɛ is the “long range” dielectric constant (4.0 in the present work). An unwanted consequence of this treatment is that Ramachandran plots obtained on a model system do not resemble very closely those found in explicit solvent molecular dynamics or with MM/PBSA using a dielectric constant of 1.0 (see, e.g., Fogolari et al., 2001).

We tested at first as switching distance 6–8 Å. Note that this is a rather rough implementation leading to nonmonotonic behavior of electrostatic forces and sometimes very strong electrostatic forces in the switching region. Even applying this scheme (and therefore an inner dielectric constant of 4.0 in the PB computation), solvation forces may be rather high (in the range 5–10 kcal mol⁻¹ Å⁻¹).

We chose at first to impose an upper limit on solvation electrostatic forces of 2 kcal mol⁻¹ Å⁻¹. After a first trial, the same scheme has been implemented using a switching function between 0 and 8 Å and imposing a 10 kcal mol⁻¹ Å⁻¹ upper limit on solvation electrostatic forces. This value has been chosen higher than all forces at the beginning of the simulation.

For the surface tension coefficient γ, several values have been used in the literature. According to Nicholls et al. (1991), a value of 0.05 kcal mol⁻¹ Å⁻² should be appropriate for the surface tension at the interface between proteins and water. When this term is considered in hybrid MM/PBSA protocols, however, it should also be considered that intramolecular van der Waals forces, in the absence of an explicit representation of solvent, will provide a strong tendency toward collapse because of missing solute-solvent van der Waals forces. We considered the energy minimized extended (with disulfide bridges reduced) and folded form of the protein. Upon folding, a solvent accessible area of ∼3200 Ų is buried corresponding to a free energy of ∼160 kcal mol⁻¹ using the surface tension coefficient 0.05 kcal mol⁻¹ Å⁻² proposed by Nicholls et al. (1991). Upon folding, the van der Waals energy of the protein decreases by ∼100 kcal mol⁻¹. Since the surface tension coefficient is already taking into account implicitly van der Waals interactions, to avoid double counting, we have to decrease the value of γ to a new value 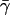in such a way that 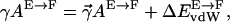where 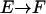indicates the transition from extended to folded conformation. In this way, we obtain approximately the value of 0.02 kcal mol⁻¹ Å⁻² for 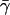, which has been used in the simulations. This surface tension coefficient value is comparable to the value of 0.01 kcal mol ⁻¹ Å⁻² suggested for the GB/SA methodology (Qiu et al., 1997). It must be noted that in many studies, the SA free energy term is neglected altogether, because for small fluctuations around an equilibrium structure, the overall change in solvent accessible surface area is rather small (see the Results section).

Compared to analytic computation of forces in explicit solvent MD simulations, computation of PBSA solvation forces, requiring accurate solution of the PB equation and proper treatment of molecular surface, is computationally demanding. Therefore, PBSA solvation forces are not computed at every minimization or MD time step, but they are updated as seldom as possible.

One issue that must be considered is that the orientational dielectric relaxation constant of water (∼10 ps) would allow a large update interval. Indeed, both electrostatic and hydrophobic solvation forces are due to bulk water molecules that do not reorient immediately. The measured orientational dielectric relaxation time of water is ∼10 ps (Harvey, 1989) consistent with the average lifetime of 4 ps for a hydrogen bond in bulk water (McCammon and Harvey, 1987) and with estimates based on simple macroscopic models (Debye, 1929). The rather long orientational dielectric relaxation time of water offers the possibility of updating solvation forces more seldom than usually done, as noted a decade ago by Niedermeier and Schulten (1992). However, update intervals longer than ∼50 fs imply large changes in computed forces.

With these issues in mind, we followed a protocol very similar to that used originally by Sharp (1991) where: i), a starting structure is minimized in vacuo; ii), solvation forces are computed; iii), N minimization or MD steps are performed using MM and PBSA solvation forces; and iv), steps ii and iii are iterated until the wanted total number of steps has been performed. A slight modification to this scheme has been used previously (Fogolari et al., 2001) where, to smooth fluctuations in solvation forces, newly computed forces are averaged with previous forces, thus introducing de facto a kind of relaxation time on solvation forces. In this work, we use this smoothing approach to lengthen substantially the time between two PBSA calculations while matching more closely the dielectric relaxation time of water. In particular, we test an updating scheme where solvation forces 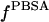are computed every 1 ps and multiplied by 0.1 and added to solvation forces at the previous step 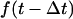multiplied by 0.9, except for the first step where no previous forces are available:

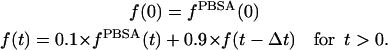(3)

This simple procedure implies an exponential decay or rise of solvation forces with a relaxation time constant of ∼10 ps.

For computation of PB forces, a large grid of 65 × 65 × 65 nodes spaced by 1 Å has been used that entails all the protein and roughly two Debye lengths, then for each amino acid a focusing step is performed employing a grid of 33 × 33 × 33 spaced by 0.45 Å and employing boundary conditions taken from the previous PBE solution on the coarse grid. Note that the focusing steps are parallelizable and the amount of computation is roughly proportional to the number of amino acids. The choice of these parameters has been previously determined (Fogolari et al., 2001). Solute and solvent dielectric constants were 4.0 and 80.0, respectively. Solvation energies and forces have been determined with respect to a homogeneous medium with a dielectric constant of 4.0. Ionic strength was 100 mM, ionic radius 2.0 Å, and solvent probe radius 1.4 Å. The linearized PB equation (see Fogolari et al., 1999, for applicability limits) was solved using the incomplete Choleski preconditioned conjugate gradients algorithm, as implemented in UHBD, using 100 surface points at each atom and a convergence criterion of 10⁻². Atomic charges were the same employed for molecular dynamics, i.e., those provided by the CHARMM package v.22 (MacKerell et al., 1998). We scaled forces exceeding 2 kcal mol⁻¹ Å⁻¹ or alternatively 10 kcal mol⁻¹ Å⁻¹ resulting in no scaling on a few sampled snapshots from the trajectories.

To enhance sampling, we used Langevin dynamics employing a time constant of 20 ps⁻¹ and the integration scheme of Verlet (1967).

No cutoff has been used for nonbonded interaction. Due to the nonanalytic procedure used for computation of solvation forces, we stopped overall translation and rotation every 10 time steps. Not all MD simulation programs offer this possibility, which is of fundamental importance to prevent all kinetic energy to be associated with center of mass motions and overall rotations.

We have used as a test system viscotoxin A3 (Protein Data Bank identification code: 1ed0, model 1) for which an ensemble of structures has been determined by Romagnoli et al. (2000). This protein belongs to the thionin protein family; it entails two helices and a two-strand β-sheet, and is stabilized by three disulfide bonds.

The protein has been first minimized in vacuo with 200 steepest descent steps and 500 conjugate gradient (50 cycles) steps. The system was further minimized adding PBSA forces for another 50 steps conjugate gradients steps (20 cycles). The system was then heated to 300 K in 1 ps. During this time electrostatic forces were not updated.

Explicit solvent simulations

Model 1 of the 10 NMR structures of the viscotoxin A3 (Romagnoli et al., 2000) was used as the initial structure (Protein Data Bank identification code: 1ed0). The ionization states of the protein residues were predicted following the methodology of Antosiewicz et al. (1994). Six chloride ions were added to neutralize the +6 charge of the protein. The Poisson-Boltzmann equation was solved using standard parameters and 100 mM ionic strength. The first ion was placed at the highest potential point at 0.56 nm from the van der Waals surface of the protein. The calculation was performed again and the ions were placed following the same procedure. This procedure was used to have hydrated counterions in the high potential regions and therefore to start from a rather stable system. A word of caution is due, because equilibration and configurational sampling for ions might take much longer times than the one simulated here.

The protein, whose largest dimension is ∼3.4 nm, and six counterions were solvated in a cubic box (with 5.6 nm edges) of preequilibrated waters using the CHARMM program version 27b2 (Brooks et al., 1983). Water molecules that were found to be within 0.28 nm of any atom in the solute were removed. The resulting system contained 673 solute atoms and 16,641 solvent atoms. The TIP3P (Jorgensen et al., 1983; Neria et al., 1996) water model was used to describe the solvent. A 1.0 nm short-range cutoff was used for all nonbonded interactions and long-range electrostatic interactions were treated by the particle mesh Ewald method (Essmann et al., 1995), with a grid size of 5.4 × 5.4 × 5.4 nm. The SHAKE algorithm (Ryckaert et al., 1977) with a tolerance of 10⁻⁴ nm was applied to constrain all bonds involving hydrogen atoms in all simulations.

The system was energy minimized and equilibrated as follows. The protein was energy minimized using 200 steps of steepest descent to eliminate bad atomic contacts and then it was surrounded by six chloride ions whose coordinates were determined as described above. The solvent cubic box alone was heated up to 300 K in 12 ps using 2 fs time step and then equilibrated at 300 K for 30 ps using a 2 fs time step. The entire box of water was overlayed onto the solute (protein and six ions) and those water molecules that overlapped with it were removed. The final system was treated as described below, in a stepwise fashion. The solute (protein and ions) was fixed and the solvent was energy minimized using 200 steps of steepest descent followed by further 200 steps of steepest descent for the whole system without solute constraints. A solvent equilibration (solute fixed) was carried out by performing molecular dynamics for 10 ps at 300 K using 2 fs time step to let the water molecules move to adjust to the conformation of the solute. The whole simulation system (solute and solvent) was heated up to 300 K over a period of 12 ps using a 2 fs time step. Finally, it was equilibrated for 20 ps at 300 K with velocity rescaling every 0.1 ps using a 2 fs time step and for further 20 ps at 300 K using a 2 fs time step. After the equilibration, data acquisition was carried out for 1.0 ns at 300 K using periodic boundary conditions in the NPT ensemble (constant pressure equal to 1 atm). A 2 fs time step was used and a snapshot of the trajectory was stored every ps (500 time steps) for later analysis. All energy/MD calculations were performed using CHARMM force field in the NPT ensemble using the CPT algorithm implemented in the CHARMM program.

We wish to point out that even after 1.5 ns explicit solvent simulations, ion distribution is not equilibrated. During the simulation, only one ion crosses the box boundary.

The simulation was performed on a single 500 MHz Pentium III processor personal computer and continued for ∼1500 h.

RESULTS

The results of five different simulations have been compared to assess the reliability of the MM/PBSA methodology for molecular dynamics simulations. It must be noted that such comparison does not provide an absolute validation of the methodology, but rather a validation relative to a generally accepted and much more validated methodology.

The five 1 ns totally unrestrained MD simulations will be referred to as S0, S1, … , S4 and have been performed using:

1. An explicit solvent and ions representation as described in the Methods section (S0).

2. PBSA solvation forces updated every 50 fs and averaged with previous step solvation forces, using a switching function between 6 and 8 Å for the MM electrostatic terms and imposing an upper limit to PBSA forces at 2 kcal mol⁻¹ Å⁻¹ (S1).

3. PBSA solvation forces updated every 1 ps and mixing newly computed solvation forces with forces at the previous step corresponding to a relaxation time of ∼10 ps, using a switching function between 6 and 8 Å for the MM electrostatic terms and imposing an upper limit to PBSA forces at 2 kcal mol⁻¹ Å⁻¹ (S2).

4. PBSA solvation forces updated every 1 ps and mixing newly computed solvation forces with forces at the previous step corresponding to a relaxation time of ∼10 ps, using a switching function between 0 and 8 Å for the MM electrostatic terms and imposing an upper limit to PBSA forces at 2 kcal mol⁻¹ Å⁻¹ (S3).

5. PBSA solvation forces updated every 1 ps and mixing newly computed solvation forces with forces at the previous step corresponding to a relaxation time of ∼10 ps, using a switching function between 0 and 8 Å for the MM electrostatic terms and without imposing any upper limit to PBSA forces (S4).

Analysis of viscotoxin simulated dynamical features

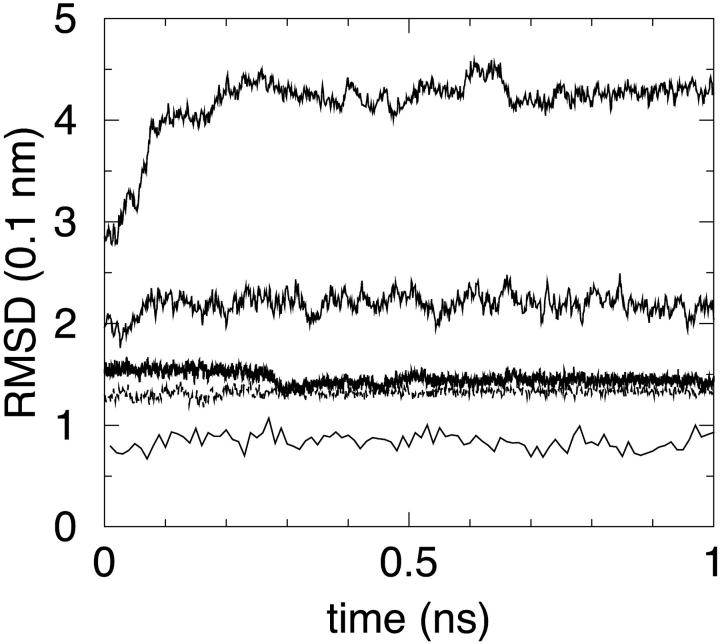
One of the key issues used to improve the MM/PBSA methodology presented in this work is the observation that for deliberately (and trial) misset switching functions or simulation parameters, the root mean-square deviation (RMSD) for backbone atoms from the starting deposited structure was largely increasing within the first ∼100 ps of the dynamics. We have therefore compared the RMSD with respect to the starting structure for all simulations. All schemes gave reasonable results except S3 that lead to an increasing RMSD approaching 4.5 Å after 1 ns simulation. This scheme was not therefore further examined.

As mentioned in the Introduction, there is no guarantee that for simulations longer than 1 ns RMSD will not be increasing, but in view of the results obtained with misset parameters, this seems unlikely. The same observation, however, holds for explicit solvent simulations.

In Fig. 1, the RMSD for all 1 ns MD trajectories (S0, S1, S2, S3, and S4) are reported. It is to be noted that the lowest curve is the one for the explicit solvent MD trajectory, as expected, but other trajectories (except S3) do not have very high values, mostly between 1.3 and 2.0 Å. Most important, for trajectories employing trimmed solvation forces, very similar curves are obtained with different updating schemes, thus supporting longer update intervals usage.

FIGURE 1.

RMSD for the five different MD simulations. The lower curve refers to reference explicit solvent simulation S0. Other curves, starting from the lower one, refer to MM/PBSA simulations S2, S1, S4, and S3, respectively.

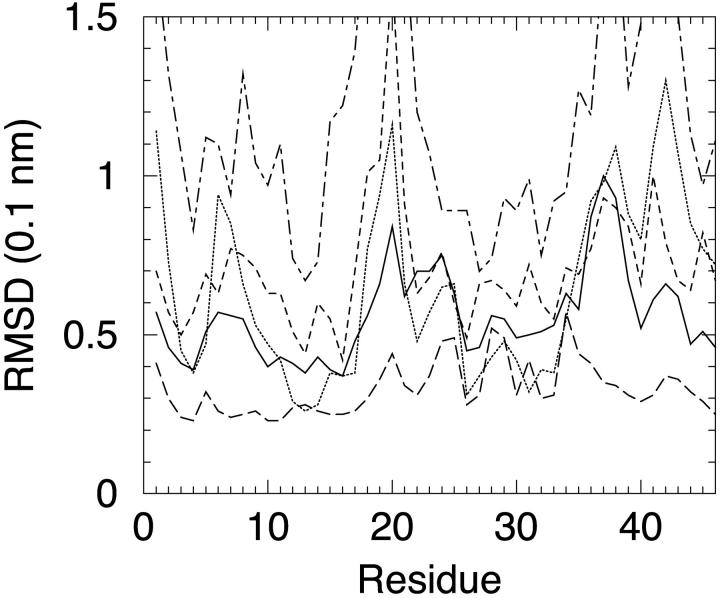
Perhaps more significant than the RMSD itself is the analysis of the average single residues contributions to the RMSD. This has been computed by pairwise superposition of the backbone for 100 snapshots of each trajectory, and averaging the results. The plot of local RMSDs that monitor the mobility at each residue compared to the global structure is reported in Fig. 2. It is apparent that the same features are present in explicit and implicit solvent simulations, although details vary, also due to the limited sampling performed.

FIGURE 2.

Average residue backbone RMSDs upon global backbone superposition obtained on 100 snapshots of a 1 ns MD trajectory: S0 (continuous line), S1 (dotted line), S2 (long dashed line), S3 (dot-dashed line), and S4 (dashed line).

In particular, local RMSD minima are observed at some, but not all, cysteine residues involved in disulfide bonds (namely Cys-3, Cys-4, Cys-26, and Cys-40). In general, as expected, regions most constrained by secondary structure and disulfide bonds are found with lower RMSD, with very similar patterns in explicit and implicit solvent simulations. For instance, the first β-strand, the center of the first helix, and the region encompassing the second helix and the second strand exhibit lower RMSD in all simulations. The same features appear also in simulation S3 in which deviation from the deposited structure was fairly high. The lowest RMSD is found for simulation S2, although this should be regarded as artifactual, probably because an overall rotation acquired during the simulation. The simulation was repeated and the same overall rotation was found. This could be a consequence of imposing an upper limit to solvation forces.

Ramachandran plots have been generated for all trajectories at 1 ps intervals. Overall features of the Ramachandran maps are similar in the five trajectories, although in explicit solvent simulations, regions corresponding to helices and extended structures seem more defined than in implicit solvent simulations. This could reflect poorer sampling or, as we believe, less accurate features of the PBSA methodology. In particular, the two simulations employing a switching function for electrostatic energy between 6 and 8 Å display rather irregular φ, ψ distributions. This may be a consequence of rather high forces in the switching region. This feature is lost with increasing the width of the switching region (simulation S4), although also here the distribution is not exactly matching what was expected. It is likely that much work should be devoted to refine parameters to recover typical Ramachandran map.

We tested also the presence of typical secondary structure elements using the DSSP emulator of WHATIF. Helical regions are reasonably well preserved during all simulations. When discontinuities in helical regions appear, a tendency to an interchange of α-helical and 3–10 helical conformation is found. β-sheet regions are somewhat less well preserved than helical regions.

Analysis of free energy components

For all continuum solvent simulations, we have analyzed the behavior of different free energy components during the trajectory. PBSA free energy components were computed according to an averaging scheme parallel to PBSA forces averaging scheme.

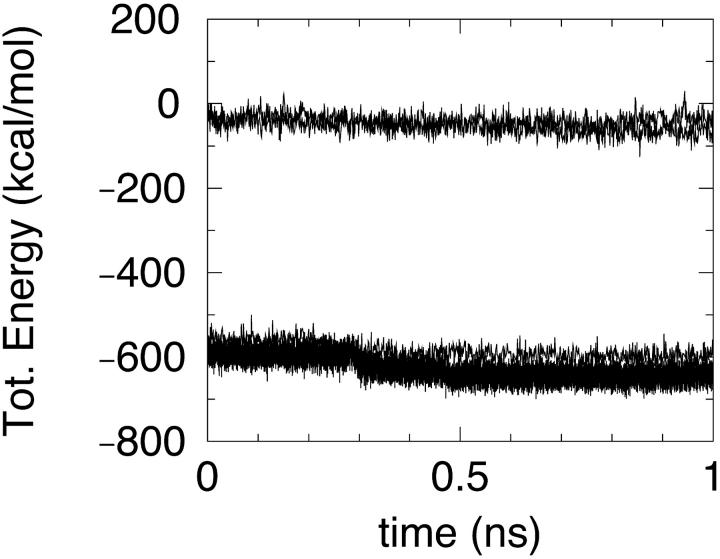
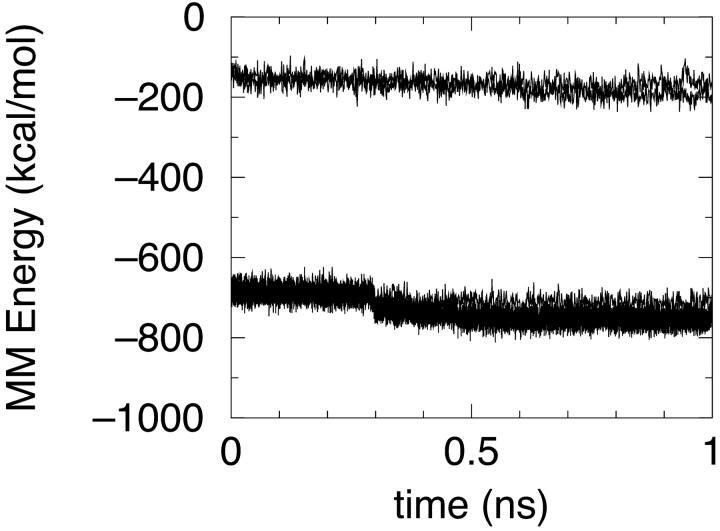
In all PBSA simulations, the larger energy variations were associated with force field energy terms (Figs. 3–6) with changes in the range of 100 kcal/mol. These changes thus dominate the total potential of mean force that is decreasing in the first equilibration 100 ps and later exhibits large fluctuations around an average value.

FIGURE 3.

MM/PBSA total energy in simulations S1 and S2 (lower curves), S3, and S4 (upper curves).

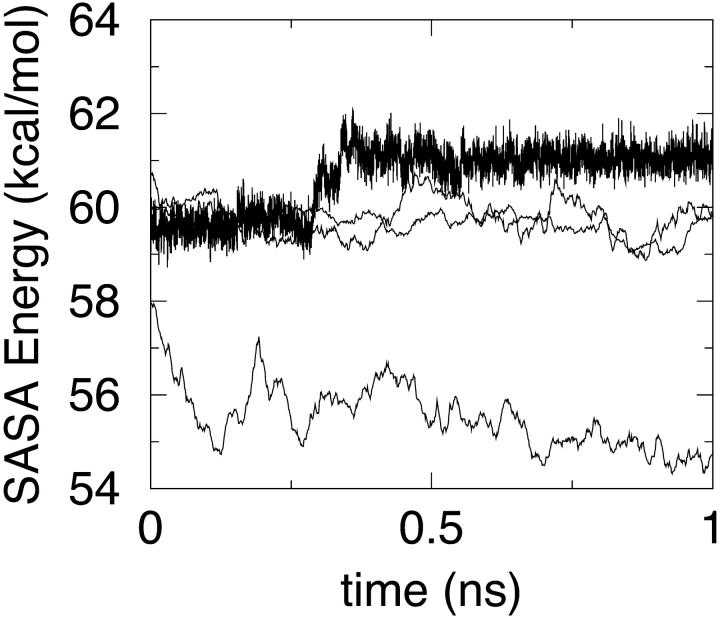
FIGURE 6.

MM/PBSA energy components: SASA free energy. The densest curve refers to simulation S1, the lowest energy curve to S3, and the other two curves to S2 and S4.

The absolute values of force field energy in simulations using different dielectric constant switching schemes are obviously not directly comparable.

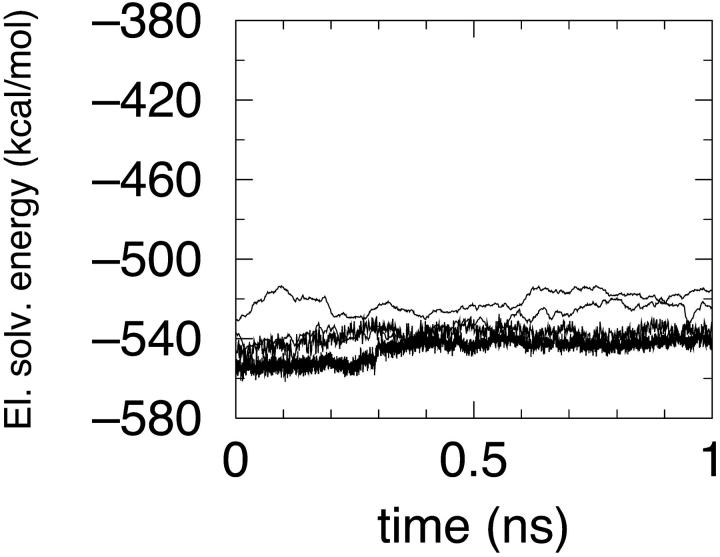
In the case of simulation S1, a sudden jump in the MM energy component is seen (Fig. 4) corresponding to a rearrangement in the region between the two helices. It is worth remarking that this rearrangement is rather limited in size, corresponding to an RMSD, with the conformation 1 ps earlier of just 0.64 Å. Actually this observation is pointing out once more the difficulties of continuum approaches where the stability of a folded protein (typically around 10 kcal/mol) should be obtained by addition and subtraction of very large energy components. The electrostatic free energy of solvation in all simulations is large and negative as expected (Fig. 5). The dependence on protein conformation is not very strong provided that a compact state is maintained.

FIGURE 4.

MM/PBSA energy components: force field energy in simulations S1 and S2 (lower curves), and S3 and S4 (upper curves).

FIGURE 5.

MM/PBSA energy components: electrostatic solvation free energy in simulations S1 (lowest curve), S2 (second curve from bottom), S3 (highest curve), and S4 (second curve from top).

Indeed, changing dielectric switching schemes for electrostatic interactions leads to differences <50 kcal/mol in electrostatic solvation energies. The same switching scheme and different upper limits to solvation forces resulted in overall similar electrostatic solvation energies and overall similar total energies. In simulation S3, the average RMSD with respect to the reference deposited structure is at the end of the 1 ns MD run around 4.5 Å. It is, however, reassuring the observation that the average potential of mean force is higher by a few tens kcal/mol than the potential of mean force computed, using the same parameters, on snapshots of S4 (not employing an upper bound on PBSA forces), which is much closer to the native conformation.

CONCLUSIONS

The main conclusion of this work is that MM/PBSA simulations are feasible on proteins (and possibly other biomolecules) provided that electronic polarizability is taken into account. In particular, the scheme employing a switching function for electrostatic interactions between 6 and 8 Å, with an upper bound on forces of 2 kcal mol⁻¹ Å⁻¹ and updating continuum forces every 1 ps, with the smoothing function proposed here, corresponding to a dielectric relaxation time of ∼10 ps, is able to provide a 1 ns trajectory, which preserves native structure for a small protein.

The scheme we developed produced good results in terms of RMSD with respect to the deposited structure and the overall preservation of structural elements, at least on a very stable system such as the one tested.

The analysis of free energy components points out the problems associated with this and other continuum-based approaches where solvation free energy is split in a polar and an apolar component.

Our results show that, even applying different molecular mechanics schemes, the electrostatic solvation free energy terms is very large and opposing intramolecular electrostatic energy. Small molecular changes have a rather large effect on both MM and PB terms, compared to the typical experimental free energy difference between the folded and unfolded state. Moreover, the Ramachandran plots obtained in all MM/PBSA simulations deviate somehow from typical Ramachandran plots.

It is thus of fundamental importance to refine the parameters and scheme employed in this work to make MM/PBSA simulations useful.

The computation time needed by MM/PBSA methodology (it should be stressed here, without any particular optimization on the molecular dynamics algorithm, but just employing an almost straightforward implementation) updating electrostatic forces every 1 ps is approximately one-tenth of the time employed by the reference explicit solvent simulation. The recent work of Luo et al. (2002) could speed up significantly computation because initial conditions for iterative PBE solution are set starting from the PBE solution at the previous step, thus reducing the number of iterations.

The price paid in accuracy is obviously high, as judged by the RMSD with respect to the deposited structure in all MM/PBSA simulations. Future work will be devoted to parameter optimization on small systems to make the approach useful for accurate simulations.