Mineralization of Type I Collagen

Abstract

It was previously found that the lateral spacing of the collagen molecules in wet mineralized tissues is exactly proportional to the inverse wet density. Several properties were investigated and the same type of relationship was observed each time. A possible explanation is offered. It is hypothesized that mineral is deposited initially in the extrafibrillar space so as to isolate the fibrils. Further deposition reduces the net free fibril volume thereby decreasing the spacing between collagen molecules. The linear relationship is derived from density considerations together with limitations on the collagen packing structure described as the generalized packing model. Three experimental situations were studied: lateral spacing wet tissue versus density; lateral spacing dry tissue versus density; and lateral spacing versus water content. The observed variations of the spacing can be attributed to a structure where the mass of the tissue remains constant but the volume decreases linearly with increasing mineral content.

INTRODUCTION

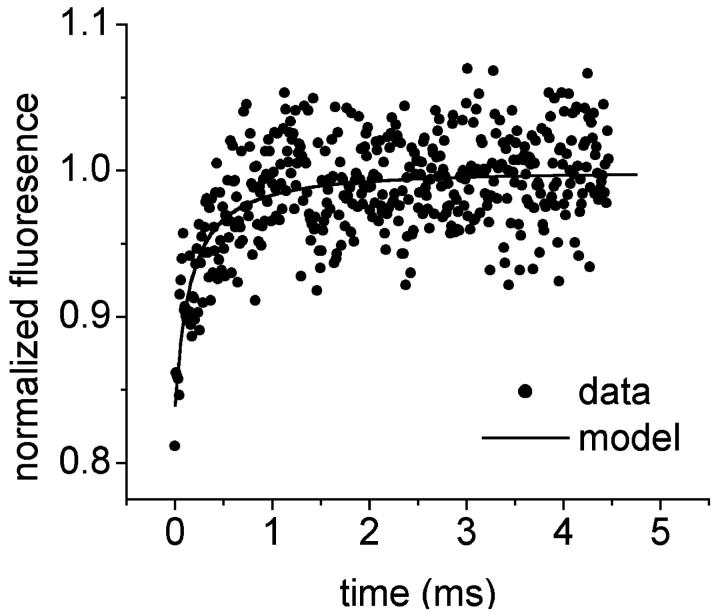
It has been reported that the equatorial diffraction spacing in wet fully mineralized tissues, as measured by neutron diffraction, decreases as the density increases (Lees et al., 1984a). The equatorial diffraction spacing has been identified as the lateral spacing between collagen molecules. This observation was confirmed by measurements using x-ray diffraction (Eanes et al., 1970; Lees and Hukins, 1992). More recently a linear relationship with positive slope was found between the lateral spacing in wet tissue and the reciprocal wet density of the tissue (Lees, 1989) as seen in Fig. 1. A different linear relationship with negative slope exists between the lateral spacing of collagen in dry tissue and the inverse wet tissue density as shown in the figure.

FIGURE 1.

The relationship between the wet density of a mineralized tissue and the equatorial diffraction spacing. The upper line refers to the wet tissue; the lower line to the same tissues when dried. The abscissa is the inverse density (Lees et al., 1984a; Lees, 1998). Parameters: d_w = 0.887 + 0.772/ρ (R² = 0.98); d_d = 1.364 − 0.437/ρ (R² = 0.92); d_w = lateral spacing of wet tissue; d_d of dry tissue; and ρ = wet tissue density.

A satisfactory explanation for these conditions and other similar ones must reside in the process of mineral deposition since it is strongly dependent on the inverse density of the wet tissue n a linear fashion. Fratzl et al. (1993) presented a packing model based on the liquid crystal model of Hukins and Woodhead-Galloway (1977). The independent variable is the packing factor for randomly deposited collagen molecules. They showed they could calculate the equatorial diffraction spacing for dry fully mineralized turkey leg tendon. They did not explain the linear relationships or why the dry tissue results show a negative slope whereas for wet tissues it is positive.

It is hypothesized that the mineral crystallites fill the extrafibrillar volume first. In particular, the mineral completely encases each fibril, enclosing the fibrillar volume. Any mineral deposited subsequently within the structure of the tissue can do so only by compressing the fibril, not by decreasing the collagen content.

The deposition of a particle of mineral creates an increment of volume within the mineral phase that must be compensated by an equal or greater decrease of the fibril volume. Since the length of the collagen molecules is essentially constant (Lees et al., 1984a) a change in the fibril volume is reflected only by a change in the cross-sectional area and, therefore, the lateral spacing between collagen molecules. An incremental increase of mineral presumably increases the mass of the material, while by the same process, decreasing the lateral spacing.

Landis and Song (1991) observed mineral depositing first in the extrafibrillar volume that was apt to deposit on the walls of the fibrils (Landis et al., 1996). Prostak and Lees (1996) showed the extrafibrillar region is much denser than the fibrillar regions of fully mineralized tissues.

An incremental decrease in the area per unit length of the fibril implies changes in two dimensions but they do not have to be equal. If one of these dimensions remains constant then the entire decrease of the fibril volume results in a one-dimensional compression of the fibril. The generalized packing model (Lees et al., 1984b; Lees, 1989) is an example of linear compression.

It is assumed that the density is the same at every scale from the macroscopic to the molecular and that the definition of density in Eq. 1 is equally applicable. An argument based on changes of the packing of collagen molecules may be applied to the whole tissue. This assumption relates the macroscopic determination of density to the molecular estimation employing the lateral spacing of the collagen.

Two hypotheses are considered. First, the consequences are presented when the volume is held constant and the mass varies. In the second, the mass is held constant and the volume varies.

The first hypothesis (V = constant)

The definition of density is

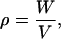(1)

where W is the mass of the sample, and V is its volume.

Bone is a complex material, a mixture of three major and many minor components. A change in the composition may be effected in such a way that the mass and the volume are independent quantities so that

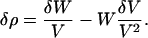(2)

Each term in Eq. 2 has the dimensions of mass divided by length cubed. It has just previously been demonstrated that for mineralized tissues, two dimensions are constant. The volume V is given as a multiple of the lateral spacing of collagen as the unit of length. When V is constant, only the first term is nonzero. When W is constant only the second term is nonzero. If the volume V is constant, then the change in density is due solely to the incremental increase in the mass of the unit of volume.

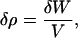(3)

which shows that only the addition of mineral can increase the tissue density for this hypothesis. The mass may be expressed as

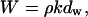(4)

where kd_w represents the volume of the sample expressed as a multiple of the lateral spacing, d_w, as the unit of length. The mass W is directly proportional to this factor. The term V is a constant according to the hypothesis. Consequently, from Eq. 3 the density in this model increases with d_w, not the inverse of d_w.

The second hypothesis (W = constant)

The description of mineral deposition is the same. The data presented in Table 1 supports the constant mass hypothesis. The entries were obtained in a study of aging in horse bone, specifically the third metacarpal. Equations 5 and 6 (see Table 1 for these equations) are the least-squares fit to the respective columns in the table. The mineral mass fraction increases slightly and the water mass fraction decreases while the mass fraction of the organic matter does not vary within experimental error. As a consequence, the sum of the mineral and water mass fractions is constant as shown by Eqs. 5d and 6d (see Table 1 for these equations) at a value of ∼0.75.

TABLE 1.

Composition of the third horse metacarpal as a function of age and sex

Age (Months)	Log (Age)	WF Water	WF Organic	WF Mineral
Male
0.10	−1.00	0.20	0.25	0.55
0.13	−0.89	0.17	0.26	0.57
0.33	−0.48	0.19	0.26	0.55
0.40	−0.40	0.18	0.28	0.54
7.00	0.85	0.12	0.26	0.62
12.00	1.08	0.11	0.27	0.62
12.00	1.08	0.12	0.26	0.62
17.00	1.23	0.13	0.26	0.61
19.00	1.28	0.13	0.25	0.62
Female
0.03	−1.48	0.23	0.23	0.54
0.23	−0.64	0.23	0.24	0.53
2.50	0.40	0.19	0.27	0.54
4.00	0.60	0.15	0.22	0.63
6.00	0.78	0.13	0.25	0.62
7.00	0.85	0.12	0.26	0.62
12.00	1.08	0.13	0.23	0.64
15.00	1.18	0.12	0.26	0.62
24.00	1.38	0.12	0.23	0.66
32.00	1.51	0.13	0.24	0.63

Male:

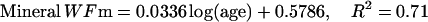(5a)

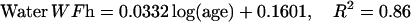(5b)

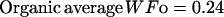(5c)

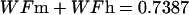(5d)

Female:

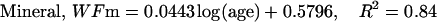(6a)

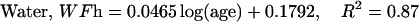(6b)

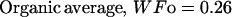(6c)

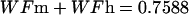(6d)

Again, since the amount of organic matter does not change, the amount of mineral plus water is also constant. The magnitude of the slope for the mineral line is identical to that for water; an increase in mineral content is exactly matched by an equal loss of water.

Referring to Eq. 1, the only way the density of mineralizing tissue can increase when the mass is constant is for the volume to decrease. Since the density of HAP is 3.0 g/cc, the volume of the mineral is one-third of the water it replaces. The total volume decreases by one-third the mineral mass, that in terms of its components, is

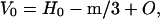(7a)

or

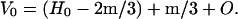(7b)

H₀ = volume of water in the tissue before mineralizing; m = mass of mineral component that replaces water in the fibril; and O = volume of organic matter.

Since the density of water is 1.0 g/cc, its volume is equal numerically to its mass but not the volume of the replacing mineral. A unit of water volume is replaced by only one-third of a unit. As the mineral content increases, the volume decreases; the density increases, the inverse density decreases, and so does the lateral spacing, d_w, between collagen molecules.

When tissue is dried, the water between layers is removed and there is shrinkage. The term, (H₀ − 2m/3), is ‘0’ and the dried volume is

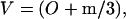(8)

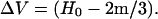(9)

Since mineral replaces water in mineralizing tissue, there is less water to be removed as the mineral content increases, and consequently less shrinkage, as indicated by Eq. 9. When there is little mineral, there is more shrinkage. The plot for dry tissue spacing in Fig. 1 is linear because the mineral deposition in wet tissue is linear.

Fig. 2 shows the spacing increases with water content when the amount of mineral is constant. In the expression for V, the term, m, is constant and H varies. When H₁ > H₀,

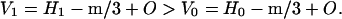(10)

The volume, V, increases with water content, and the spacing increases as observed.

FIGURE 2.

Lateral spacing of mineralized bovine tibia as a function of water content, h (from Lees and Mook, 1986). Parameters: d_w = 1.165 + 0.164 h (R² = 0.90).

DISCUSSION

It is implicitly assumed that the structure is that of a disordered crystal. The collagen molecules are parallel and located by the cross-links between them. In mineralized tissues the molecules are further tied by calcium and phosphate bridges to the mineral crystallites. Long stretches of collagen between cross-links are thermally driven into vibration (Lees, 1998).

The generalized packing model explained why four examples of unmineralized type I collagen had different packings. These were rat tail tendon, kangaroo tail tendon, turkey leg tendon, and rat bone matrix (Lees et al., 1984b). The list was expanded to include mineralized tissues (Lees et al., 1984a) (See Table 2). The modification of the packing when the water content changed while the mineral content was constant was determined for fully mineralized cow bone (Lees and Mook, 1986). The water content of mineralized tissue was calculated for a wide range of mineral content using the generalized packing model to calculate the volume. The results matched the measured values within 3%. (Lees, 1986). In all instances the lateral spacing was found by displacing the molecules in only one direction.

TABLE 2.

Lateral spacing data; MTLT = mineralized turkey leg tendon

	Density	dw	dd
Cod clythrum	1.44	1.38	1,07
MTLT	1.66	1.34	1.03
MTLT	1.58	1.33	1.08
Deer antler	1.80	1.29	1.11
Cow tibia	2.04	1.24	1.16

The lateral spacing varies significantly between rat-tail tendon collagen, bone matrix collagen, and turkey leg tendon collagen (Brodsky and Eikenberry, 1982). There must be a corresponding structural difference within the molecule. It would be surprising if a single packing model fitted all type I collagens.

The first finding was to see that the mineral replacing water has only one-third the volume of the water it replaced. It is the cause for the decrease in the lateral spacing of collagen but it is insufficient to account for the inverse relationship or the precise linearity of the relationship. It is inverse because the weight is constant as mineral is deposited, in an amount exactly equal to the amount of water removed. The linearity is a consequence of the fibril packing model. The generalized packing model confines changes of the molecular volume so as to be proportional to the collagen spacing, that is, to a one-dimensional factor. It is shown that other relations, depending on the composition, may also be understood in terms of this model. Where the relationship is linear as in the figures, the explanation invokes the generalized packing model.

This implies that after the collagen gap region is filled, additional mineral can only fill the space between bundles of collagen molecules. The figures of Prostak and Lees (1996) show most of the mineral is outside the fibrils.

Such a structure is compatible with what has been observed previously. The collagen molecules are free to move within the fibrils and yet the spacing between molecules will be reduced as the mineral volume fraction increases. Since the collagen molecules are packed together and their neighborhood is free of mineral, it is possible to calculate the water content as a function of the spacing. The calculated values compare closely with the measured water content (Lees, 1986). These are two instances (mineral content and water content) in which the generalized packing model has been employed successfully. No other explanation has been offered.

The characteristic length is essentially the difference between the collagen lateral spacing for unmineralized tissues when wet and when dry. The minimum spacing is 1.09 nm for most tissues, suggesting that the molecules are impinging on each other. The maximum spacing indicates the presence of other constraints like cross-linking. The Brodsky and Eikenberry (1982) data show wet rat tail tendon collagen spacing to be 1.33 nm compared with 1.53 nm for many other type I collagen tissues including bone matrix collagen. This suggests that the packing model for rat tail tendon collagen differs from that for bone collagen. A long-time effort has been underway to determine the packing model for rat tail collagen because it provided the best x-ray diffraction patterns (Wess et al., 1998) and because it has been assumed that all type I collagens are the same whatever the source. The examples in this report shows it is not so.

CONCLUSION

The calculated variation in the equatorial diffraction spacing with density, where the mass of the tissue is constant and the volume varies, matches the results observed experimentally. This model was demonstrated by invoking several conditions. It requires that the deposited mineral replace exactly the same amount of water as is removed. It also requires that changes in volume are restricted to the collagen in fibrils as mineral is deposited in the extrafibrillar region. The process that contributes to this condition is not known, but it is probably due to the chemical structure of the collagen fibril and the way the structure is packed.