Differential Effects of Voltage-Dependent Inactivation and Local Anesthetics on Kinetic Phases of Ca²⁺ Release in Frog Skeletal Muscle

Abstract

In voltage-clamped frog skeletal muscle fibers, Ca²⁺ release rises rapidly to a peak, then decays to a nearly steady state. The voltage dependence of the ratio of amplitudes of these two phases (p/s) shows a maximum at low voltages and declines with further depolarization. The peak phase has been attributed to a component of Ca²⁺ release induced by Ca²⁺, which is proportionally greater at low voltages. We compared the effects of two interventions that inhibit Ca²⁺ release: inactivation of voltage sensors, and local anesthetics reputed to block Ca²⁺ release induced by Ca²⁺. Holding the cells partially depolarized strongly reduced the peak and steady levels of Ca²⁺ release elicited by a test pulse and suppressed the maximum of the p/s ratio at low voltages. The p/s ratio increased monotonically with test voltage, eventually reaching a value similar to the maximum found in noninactivated fibers. This implies that the marked peak of Ca²⁺ release is a property of a cooperating collection of voltage sensors rather than individual ones. Local anesthetics reduced the peak of release flux at every test voltage, and the steady phase to a lesser degree. At variance with sustained depolarization, they made p/s low at all voltages. These observations were well-reproduced by the “couplon” model of dual control, which assumes that depolarization and anesthetics respectively, and selectively, disable its Ca²⁺-dependent or its voltage-operated channels. This duality of effects and their simulation under such hypotheses are consistent with the operation of a dual, two-stage control of Ca²⁺ release in muscle, whereby Ca²⁺ released through multiple directly voltage-activated channels builds up at junctions to secondarily open Ca²⁺-operated channels.

INTRODUCTION

From a phenomenological standpoint, the release of sarcoplasmic reticulum (SR) Ca²⁺ that triggers contraction in skeletal muscle is entirely controlled by the transmembrane potential in transverse (T) tubules. The time course of the SR Ca²⁺ permeability upon step depolarization shows an early peak, then inactivates to a steady level that may be maintained for hundreds of milliseconds. The mechanism of this fast inactivation is not established. It may be mediated by Ca²⁺ (Schneider and Simon, 1988; Jong et al., 1995), but not by voltage, as it is not accompanied by any change in intramembranous charge movement.

Amphibian and mammalian muscles differ strikingly in the voltage dependence of the ratio, p/s, between peak and steady release levels. In the frog, the ratio is generally greater, and exhibits a distinct maximum at ∼10–20 mV positive to the threshold of Ca²⁺ release detection. In mammals, however, the maximum is reached asymptotically at high voltages (Shirokova et al., 1996). The difference has been ascribed to a component of Ca²⁺ release induced by Ca²⁺ (CICR, Endo et al., 1970; Endo, 1985) that differs between the two taxonomic classes.

A reappraisal of the functional significance of CICR has taken place during the last 10 years. This was initially motivated by the structural findings of Block et al. (1988) of a precise arrangement that leaves every other release channel devoid of T-membrane voltage sensors. A dual control mechanism was proposed accordingly, where Ca²⁺-gated and voltage-gated channels respectively contribute peak and steady components of release flux (Ríos and Pizarro, 1988). Functional (Csernoch et al., 1993; Brum and Pizarro, 1998) and pharmacological data in frog twitch muscle (Pizarro et al., 1992) generally support the scheme, while studies of Ca²⁺ sparks have added to the evidence. Because the peak of Ca²⁺ release appears to reflect superposition of many synchronous sparks, the evidence that sparks are gated by Ca²⁺ (Klein et al., 1996) upholds the CICR hypothesis. However, it has also become clear that the steady component of Ca²⁺ release comprises sparks, making it necessary to admit a contribution of CICR to its activation as well.

The meaning of the phases of release is clarified by calculations with a model that gives explicit form to the hypothesis (Stern et al. 1997), assuming release generators—couplons—composed of equal numbers of voltage- and Ca²⁺-operated channels interacting through the local [Ca²⁺]. With this model the peak is largely due to the Ca²⁺-gated flux, while the steady phase is mixed, largely mediated by Ca²⁺ at low voltages, and increasingly carried through voltage-gated channels as voltage increases. Increasing the weight of CICR in the model (by assuming, for instance, greater unitary current through its channels) increases the p/s ratio.

Differences in CICR contribution might therefore explain the different voltage dependence of p/s in frogs and mammals (Shirokova et al., 1996; Stern et al., 1997). The presence of two isoforms of release channels in amphibia, only one of which may interact with the voltage sensor (Protasi et al., 2000), suggests that mechanistic differences between the two taxonomic classes correspond to differences in molecular endowment and arrangement. This plausible structural correlate heightens the relevance of the kinetic features, including the characteristic voltage dependence of p/s.

In the present study we compare the effects of two modifiers of this ratio: voltage-dependent inactivation, to affect direct control by the voltage sensors, and local anesthetics, because they are reputed to block CICR (Pizarro et al., 1992; Särközi et al., 1996; in the presence of caffeine, Klein et al., 1992). The experimental results are then interpreted through simulations with the couplon model.

METHODS

The experiments were carried out on cut fibers voltage-clamped in a two-Vaseline gap (Kovacs et al., 1983). Depending on the availability of frog species, semitendinosus muscles were removed from either Leptodactylus ocellatus or Rana catesbeiana. The frogs were euthanized by decapitation under deep ethanol anesthesia. A 2-cm-long piece of fiber was dissected from the muscle and mounted in a three-compartment Lucite chamber where the double-Vaseline gap was made. Fibers obtained from L. ocellatus were immobilized by stretching whereas fibers from R. catesbeiana were immobilized using high intracellular EGTA (see below). Several notches were made to the regions of the fiber in both end compartments to allow exchange of intracellular solution. The preparation was cooled to temperatures between 10 and 15°C by means of a Peltier device.

Solutions

The extracellular solution consisted of 130 mM Tetraethylammonium methylsulfonate (TEA-CH₃SO₃), 6 mM CaSO₄, and 10 mM Tris maleate. The pH value was titrated to 7 with TEAOH. The intracellular solution contained 120 mM Cs Glutamate, 10 mM Cs Tris maleate, and 5 mM Mg ATP. In experiments with stretched fibers, 1 mM ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid (EGTA), and 0.8 mM antipyrylazo III (APIII; Sigma, St. Louis, MO) were included. In experiments with slack fibers, 8 mM EGTA and 0.25–0.4 mM fluo-3 (pentapotassium or ammonium salt; Molecular Probes, Eugene, OR) were used instead. Free Ca²⁺ was set to 50 nM with CaCl₂, assuming a K_D = 0.37 μM for EGTA. Dissection and mounting of single fibers were carried out in a relaxing solution containing 130 mM K Glutamate, 2 mM MgCl₂, 5 mM Tris maleate buffer, and 0.1 mM EGTA. Despite the use of different techniques for fiber immobilization, no differences were observed among results with the different frog species.

Electronics and data acquisition

The voltage-clamp amplifier was built according to a design of Francini and Stefani (1989). Data acquisition was performed with a 16-bit resolution, 200-kHz board (HSDAS-16; Analogic Corporation, Wakefield, MA). Sampling rates ranged between 3 and 20 kHz per channel. Data were filtered before acquisition by a one–pole passive filter with 0.3-kHz cutoff frequency. Command pulses were generated with the D/A channels of the HSDAS board. Membrane currents, membrane voltage, and the change in transmitted or emitted light were measured simultaneously during fiber activation by clamp pulses.

Optical measurements and processing of the optical signals

Optical signals were recorded as described by De Armas et al. (1998). Briefly, in light absorption experiments (using APIII) a slit of light of λ > 600 nm was imaged on the fiber. The transmitted light, collected by a water immersion objective (numerical aperture 0.75, 40×; Zeiss Oberkochen, Germany), was split into two beams, of wavelengths ≥800 nm. These were further filtered and measured with photodiodes. The signal at 720 nm contained an APIII-related absorbance change together with a change in intrinsic fiber absorbance. The latter was measured in isolation at λ > 800 nm, then scaled and subtracted to yield the APIII-related signal. The latter was processed (Kovacs et al., 1983) to derive the change in myoplasmic Ca²⁺ concentration. In fluorescence experiments, fluo-3 was excited by epi-illumination at 490 nm, through an interference filter placed between a halogen light source and a 510-nm high-pass dichroic mirror. The emitted light was filtered at 530 nm by a second interference filter and recorded by a high sensitivity photodiode (HUV-200; EG&G, Quebec, Canada). The Ca²⁺ transient was derived as described by Shirokova et al. (1996), with k_off = 80 s⁻¹ and k_on = 90 s⁻¹ μM⁻¹ as rate constants of fluo-3 and extinction coefficients of fluo-3 measured in our optical apparatus (ɛ₄₉₀ = 5.44 × 10⁴ M⁻¹ cm⁻¹, ɛ₅₃₀ = 0.97 × 10⁴ M⁻¹ cm⁻¹). Concentrations of both dyes were determined from light path and absorbance measurements made at regular intervals during the experiment; at 550 nm for APIII (ɛ₅₅₀ = 2.44 × 10⁴ M⁻¹ cm⁻¹) and at 510 nm for fluo-3 (ɛ₅₁₀ = 6.95 × 10⁴ M⁻¹ cm⁻¹).

SR Ca²⁺ release flux was derived from the Ca²⁺ transient using the procedure of Melzer et al. (1984) modified by Brum et al. (1988). Briefly, release flux was calculated as the sum of the rate of increase of free [Ca²⁺] and the rate of extrusion by an explicit removal model, fitted to the decay of a set of Ca²⁺ transients elicited by pulses of various amplitudes and duration. The removal model included Ca²⁺ buffers in the myoplasm, plus those added to the internal solution (i.e., EGTA, APIII, fluo-3). Some of the parameters characterizing the Ca²⁺ binding sites were adjusted in the fit. Values of parameters for the significant buffers are given in the figure legends.

The waveform obtained this way, termed Ca²⁺ release flux, was corrected for SR Ca²⁺ depletion as described by Schneider et al. (1987). The correction procedure assumes that the SR Ca²⁺ permeability attains a steady level after 100–200 ms of depolarization, and thereafter the flux is simply proportional to the total [Ca] in the SR (CaSR), as stated in Eq. 1,

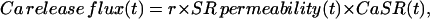(1)

with

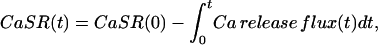(2)

where r is the surface-to-volume ratio of the SR; CaSR(0) is the initial [Ca ] in the SR (expressed as Ca content of the SR per unit volume of myoplasmic water); and the running integral of the flux is the change in SR [Ca], again per unit volume of myoplasm. The release flux was divided point-by-point by the difference in Eq. 2, yielding a record proportional to the time course of the SR Ca²⁺ permeability (with units of ms⁻¹). CaSR(0) was adjusted, if necessary, to achieve a steady late phase of release after every new intervention, but in most cases these adjustments were not significant. Pooled data for each intervention gave differences in SR content (before and after intervention) that were not significantly different.

Intramembranous charge movement

Charge movement currents were recorded as described previously (De Armas et al., 1998). Briefly, asymmetric currents were obtained as difference between the current during the test pulses and the voltage-scaled current measured during control pulses. Current transients were then obtained by subtraction of sloping baselines separately fitted to ON and OFF portions. When the fiber was normally polarized, control pulses were to −100 mV from a subtracting holding potential of −120 mV. Alternatively in depolarized fibers, the control pulses were positive from a holding potential (HP) of 0 mV. Charge displacements Q_ON and Q_OFF were obtained by integration of the corresponding transients. In the brief repriming experiments in which charge movement was studied, the controls obtained in the depolarized condition were used also to analyze the charge movement after polarization to a negative HP.

Plots of Ca²⁺ release or charge movement versus voltage were fitted to a two-state Boltzmann function (Eq. 3) by a least-squares routine,

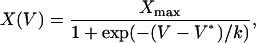(3)

where V^* is th1e central voltage of the distribution, k the slope at the inflexion point, and X_max the limiting value at high positive voltages.

Statistical significance was determined by the two-tailed Student's t-test at the level of p = 0.05.

Simulations

These were carried out using the couplon model (Stern et al., 1997) with parameter values listed therein. Macroscopic release waveforms were generated adding 1000 Monte Carlo realizations of the model. The synthesized waveforms were treated in the same way as the experimental ones, deriving a permeability time course by the depletion correction procedure described in the preceding paragraph.

RESULTS

Inactivating holding potentials changed the voltage dependence of p/s, but not its maximum

Skeletal muscle excitation-contraction coupling is known to undergo a voltage-dependent inactivation process (Hodgkin and Horowicz, 1960). Less polarized holding potentials progressively inhibit Ca²⁺ release, as they reduce the availability of charge movement (e.g., see Ríos and Pizarro, 1991).

The effect of such intervention on permeability waveforms in a fiber from R. catesbeiana is shown in Fig. 1. The experiment consisted in the determination of kinetics of Ca²⁺ release, as a function of voltage, in three conditions: 1), reference; 2), partial inactivation at a depolarized HP; and 3), partial recovery after inactivation.

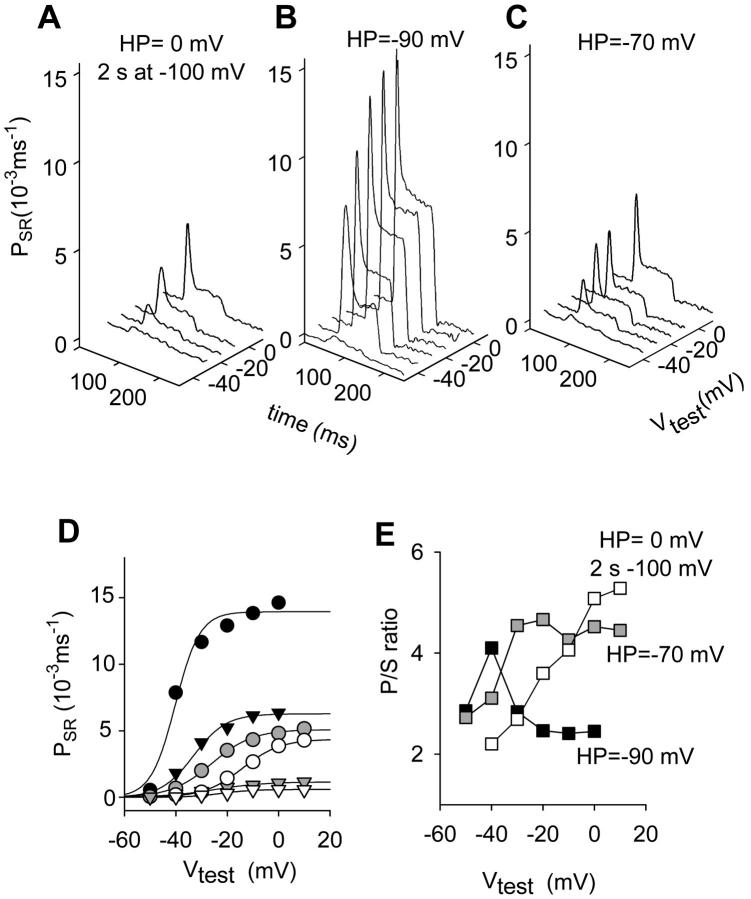
FIGURE 1.

Effect of depolarized HP on release flux permeability components and their ratio. (A) Corrected release records taken while the fiber was held at 0 mV and a prepulse to −100 mV for 2 s before the test pulse was applied. (B) Records taken after full repriming at −90 mV. (C) Effect of changing HP from −90 to −70 mV. Fiber 4088, from R. catesbeiana; [fluo-3] ranged from 121 to 290 μM. Time elapsed was 28 min. Initial Ca content of the SR was 800 μM in all cases. Parameters of removal, [EGTA] = 4.5 mM; k_offEGTA = 2.4 μM⁻¹ s⁻¹; and k_onEGTA = 3.2 s⁻¹. (D) Voltage dependence of peak and steady permeability. (E) The p/s ratio. In D and E, HP = −90 mV (black symbols). HP = −70 mV (gray symbols). Brief repriming protocol (unfilled symbols). In D, peak (circles); and steady values of permeability (triangles). Best-fit of a two-states Boltzmann function to the data points (continuous lines). Parameters of the Boltzmann fit, P_SRmax = 13.94 × 10⁻³ ms⁻¹, V^* = −40.18 mV, and k = 4.74 mV for the peak permeability; P_SRmax = 6.27 × 10⁻³ ms⁻¹, V^* = −33.07 mV, and k = 6.28 mV for the steady SR permeability at V_h = −90 mV; P_SRmax = 5.09 × 10⁻³ ms⁻¹, V^* = −26 mV, and k = 7.93 mV for the peak permeability; P_SRmax = 1.16 × 10⁻³ ms⁻¹, V^* = −24.99 mV, and k = 9.7 mV for the steady SR permeability at V_h = −70 mV; P_SRmax = 4.37 × 10⁻³ ms⁻¹, V^* = −14.06 mV, and k = 7.38 mV; and P_SRmax = 5.89 × 10⁻⁴ ms⁻¹, V^* = −22.21 mV, and k = 6.13 mV for the brief repriming protocol.

To explore condition 3, the fiber was first held at 0 mV. A partial recovery (“repriming”) interval of 2 s at −100 mV was applied, followed by test pulses to different potentials (Fig. 1 A). Next, to obtain the (reference) voltage dependence of release the fiber was polarized to −90 mV and allowed to recover fully (Fig. 1 B). Finally, for condition 2 the HP was set to −70 mV and the same test voltages were explored (Fig. 1 C). Upon partial inactivation, peak and steady permeability were markedly reduced (Fig. 1 D). The biggest reduction was found with the brief repriming protocol.

In reference condition, the p/s ratio had a maximum at ∼15 mV positive to the threshold for Ca²⁺ release. The partial inactivation or repriming protocols changed this voltage dependence, making it monotonically increasing (Fig. 1 E). Values for p/s were greater upon partial inactivation or repriming than in reference at intermediate and high test voltages. Similar results with depolarized HP (in the range between −70 and −60 mV) were obtained in seven fibers (averages in Fig. 5 A). To make different fibers comparable, the individual curves were shifted by V_max, the voltage corresponding to the maximum value of the ratio. The maximum p/s in partially depolarized fibers was not statistically different from that in the fully polarized fibers. However, it occurred at low to intermediate voltages in the polarized fiber, and in an extended, more positive range after partial inactivation. Fig. 5 B shows average results for the brief repriming protocol.

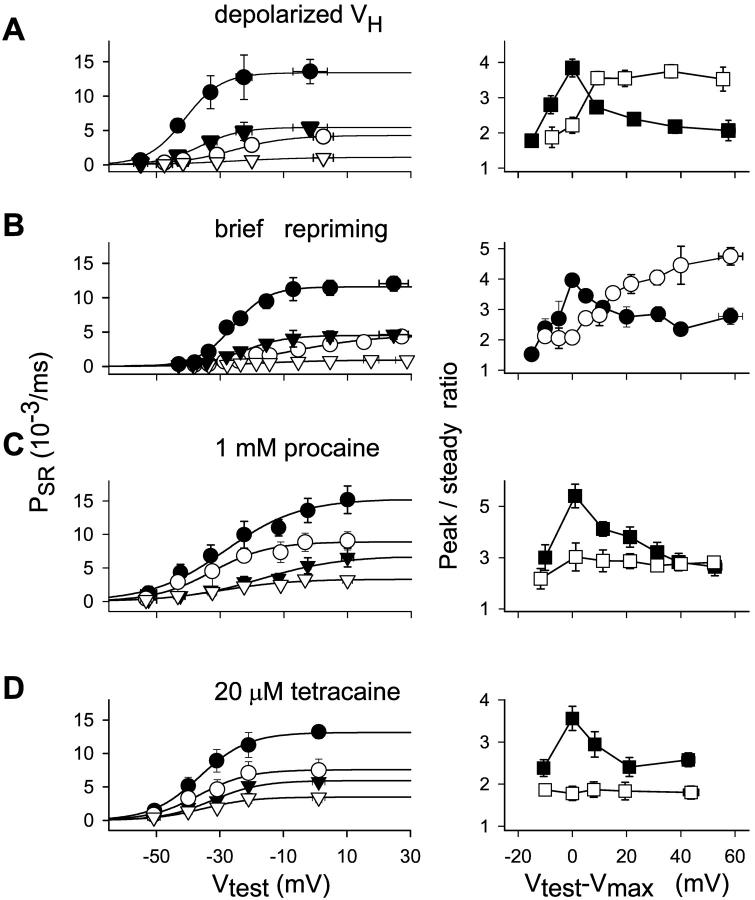
FIGURE 5.

Effect of three interventions on peak and steady components of Ca²⁺ release flux permeability and their ratio. (A) Depolarized holding potential. Left, Data points (mean ± SE) in seven slack fibers from R. catesbeiana. Peak permeability values (circles) in reference (solid) or at depolarized HP (unfilled). Corresponding steady values (triangles). Curves traced with Eq. 3 fitted to the averaged data. Fit parameters, P_SRmax = 13.17 × 10⁻³ ms⁻¹, V^* = 27.6 mV, and k = 7.89 mV for the peak permeability in reference; P_SRmax = 5.33 × 10⁻³ ms⁻¹, V^* = −25.35 mV, and k = 7.09 mV for the steady SR permeability in reference; P_SRmax = 4.8 × 10⁻³ ms⁻¹, V^* = −33.63 mV, and k = 7.25 mV; and P_SRmax = 1.54 × 10⁻³ ms⁻¹, V^* = −16.82 mV, and k = 11.63 mV for the depolarized HP. Right, Peak/steady ratio in reference (solid) or at depolarized HP (unfilled). Test voltages in the abscissa are shifted by the value at which the maximum was observed in each fiber (V_test − V_max). (B) Brief repriming. Left, Data points (mean ± SE) obtained in four slack fibers from R. catesbeiana. Peak permeability values (circles) in reference (filled) or at depolarized HP (unfilled). Corresponding steady values (triangles). Fit parameters, P_SRmax = 11.6 × 10⁻³ ms⁻¹, V^* = −26.1 mV, and k = 5.54 mV for the peak permeability in reference; P_SRmax = 4.50 × 10⁻³ ms⁻¹, V^* = −22.65 mV, and k = 6.63 mV for the steady SR permeability in reference; P_SRmax = 4.35 × 10⁻³ ms⁻¹, V^* = −8.18 mV, and k = 12.36 mV; and P_SRmax = 0.92 × 10⁻³ ms⁻¹, V^* = −17.47 mV, and k = 11.54 mV for the brief repriming protocol. Right, Peak/steady ratio in reference (solid) or after brief repriming (unfilled). (C) Procaine. (Left) Data points (mean ± SE) obtained in four stretched fibers from L. ocellatus. Peak permeability values (circles) in reference (filled) or 1 mM procaine (unfilled). Corresponding steady values (triangles). Fit parameters, P_SRmax = 15.3 × 10⁻³ ms⁻¹, V^* = −28.82 mV, and k = 12.72 mV for the peak permeability in reference; P_SRmax = 6.87 × 10⁻³ ms⁻¹, V^* = −16.47 mV, and k = 12.69 mV for the steady SR permeability in reference; P_SRmax = 9.03 × 10⁻³ ms⁻¹, V^* = −32.69 mV, and k = 10.26 mV; and P_SRmax = 3.23 × 10⁻³ ms⁻¹, V^* = −30.18 mV, and k = 10.48 mV in 1 mM procaine. Right, Peak/steady ratio in reference (solid) or procaine (unfilled). (D) Tetracaine. Left, Averages (mean ± SE) from six slack fibers from R. catesbeiana with same internal solution as in A. Peak permeability values (circles) in reference (solid) or 20 μM tetracaine (unfilled). Corresponding steady values (triangles). Fit parameters, P_SRmax = 13.07 × 10⁻³ ms⁻¹, V^* = −36.74 mV, and k = 6.51 mV for the peak permeability in reference; P_SRmax = 5.64 × 10⁻³ ms⁻¹, V^* = −33.52 mV, and k = 6.88 mV for the steady SR permeability in reference; P_SRmax = 7.56 × 10⁻³ ms⁻¹, V^* = −36.51 mV, and k = 7.7 mV; and P_SRmax = 3.49 × 10⁻³ ms⁻¹, V^* = −35.29 mV, and k = 7.8 mV for the same quantities in 20 μM tetracaine. Right, peak/steady ratio in reference (solid) or tetracaine (unfilled). In all graphs, points from proximate voltages (10-mV intervals) were averaged and ascribed to the mean voltage. Internal solutions had 5 mM EGTA in A, B, and D, and 1 mM in C. Nominal [Ca²⁺] was 50 nM.

The positive shift of the ratio as well as the loss of its local maximum were associated with a shift in the same direction of the voltage dependence of peak and steady release activation. Also a reduction in the slope of Boltzmann fits was found (with parameters given in the legend of Fig. 5). All these changes were greater for the brief repriming situation, even more noticeable than the reduction of the amplitude of SR permeability itself. In principle, this may have been due to inactivation of the voltage sensor, perhaps accompanied by changes in voltage dependence of its activation. The possibility was tested in the experiments illustrated in Fig. 2. The movement of intramembranous charge in fibers inactivated by depolarization, which occurs at potentials <−50 mV, is attributed to transitions between inactivated states of the voltage sensors (Brum and Ríos, 1987; Brum et al., 1988; Ríos and Pizarro 1991; Shirokov et al., 1998). To emphasize the difference with the polarized situation and the fact that its movement does not gate channels, the charge mobile in depolarized fibers is called “charge 2.” If the holding voltage is made more negative, some recovery, or “repriming” occurs, and the overall charge distribution is shifted to more positive voltages. This is interpreted as partial conversion of charge 2 to charge 1, which moves positive to −70 mV and gates Ca²⁺ release. The slight superposition of the distributions of charge 1 and charge 2 required a special procedure to quantify charge 1 in the substantially inactivated fibers, particularly after the brief repriming protocol. The distribution measured in the partially recovered condition was fitted with the sum of two Boltzmann functions, one of which had the voltage dependence of charge 2, first determined in the fully inactivated fiber held at 0 mV. The difference between total charge transfer and charge 2 (calculated from the fit) is plotted against test voltage in Fig. 2 A.

FIGURE 2.

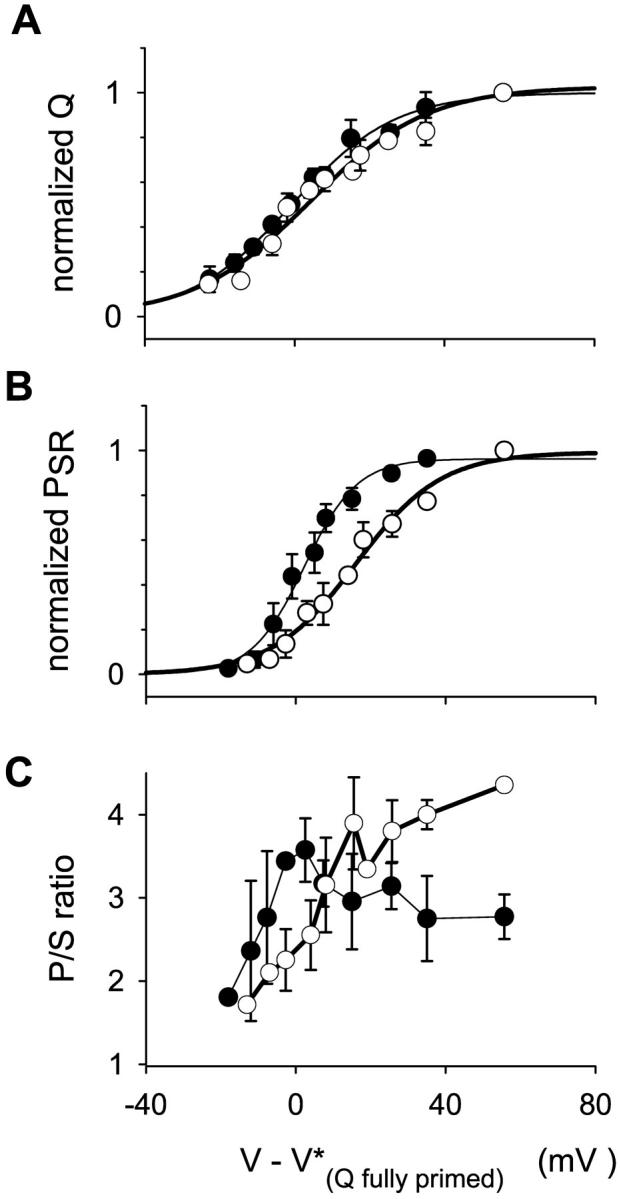
Effect of partial inactivation on the distribution of transmembrane mobile charge. The voltage dependence of charge movement and Ca²⁺ release flux was studied in fully reprimed condition at HP = −90 mV (solid circles) and after partial repriming produced by a conditioning pulse of 2 s to −100 mV from HP = 0 (unfilled circles) in three fibers of the four used in Fig. 5. To compare different fibers, data from each fiber were shifted by the value of V^* fitted to the charge distribution in the fully primed condition (Average V^* = −22.2 ± 5.8 mV). (A) Charge 1, estimated as explained in the text, and normalized to the maximum value measured in each condition, is plotted vs. test voltage. Q_max at HP = −90 mV was 33.6 ± 3.6 nC/μF. Brief repriming protocol, 14.0 ± 3.1 nC/μF. Parameters of the fit, HP = −90 mV, Q_max = 1.00, k = 13.75 mV, and V^* = −0.70 mV. Brief repriming protocol, Q_max = 1.02, k = 15.55 mV, and V^* = 4.14 mV. (B) Normalized peak release flux, P_SRmax at HP = −90 mV was 23.2 ± 3.8 μM/ms⁻¹. Brief repriming protocol, 8.0 ± 1.4 μM/ms⁻¹. Parameters of the fit, HP = −90 mV, P_SRmax = 0.96, k = 7.01 mV, and V^* = 2.26 mV. Brief repriming protocol, P_SRmax = 0.99, k = 11.33 mV, and V^* = 16.11 mV. [Ca]_SR used for correction varied from 1600 to 2500 μM. (C) Peak/steady permeability ratios.

The analysis is rather indirect and susceptible to errors, associated with changes in linear electrical properties upon prolonged changes in holding potentials. Even allowing for such errors, shifts in the voltage dependence of charge 1 were comparatively minor, and certainly insufficient to explain the consistent right shift of release activation shown in Fig. 2 B. The voltage dependence of the p/s ratio calculated for this set of fibers in the two conditions is plotted in Fig. 2 C.

Procaine and tetracaine changed the peak/steady release ratio

The local anesthetics procaine and tetracaine are known inhibitors of excitation-contraction coupling in frog skeletal muscle (Donaldson, 1989; Endo, 1985). Here the drugs were applied extracellularly to stretched and slack fibers, at concentrations that did not suppress charge movement. Application of either drug reversibly reduced the Ca²⁺ transients and the underlying Ca²⁺ release flux at every test voltage. Procaine required a higher extracellular concentration, consistent with its lower membrane permeability at physiological pH (Hille, 1977; Sánchez and Caputo, 1987) and its lower efficacy (Xu et al., 1993).

The effect of procaine (1 mM) at various test voltages in a stretched fiber of L. ocellatus is illustrated in Fig. 3. Whereas the permeability peak was reduced at every test voltage, the steady level was affected more at higher test voltages. Peak and steady permeabilities as well as their ratio are plotted at bottom (Fig. 3, C and D).

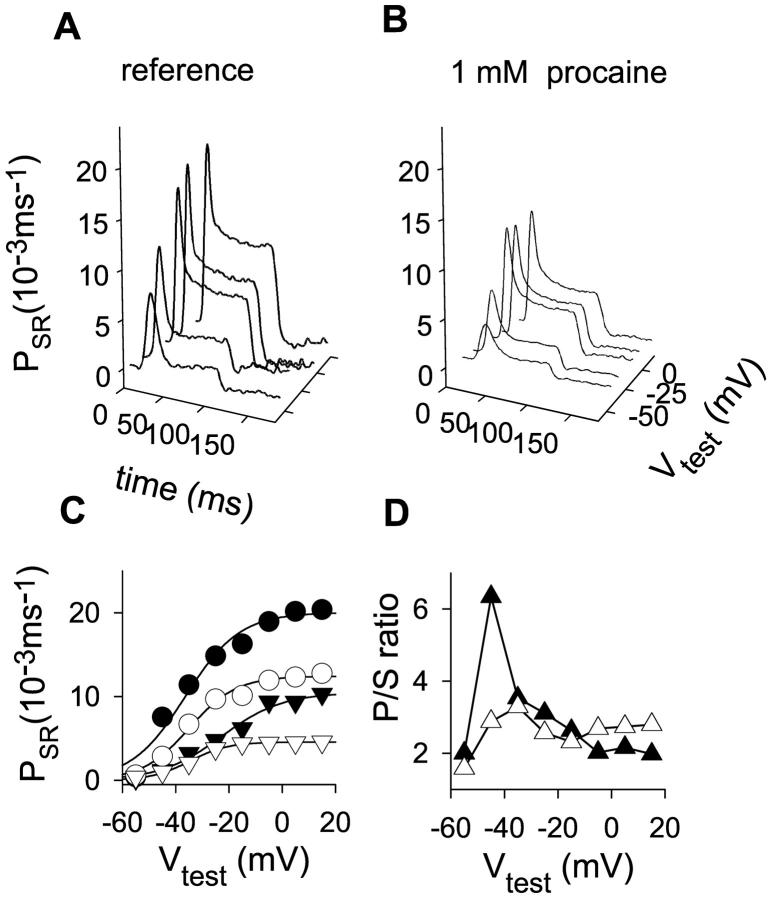
FIGURE 3.

Effect of 1 mM procaine on kinetic terms of Ca²⁺ release permeability and their ratio. (A) Corrected release records obtained in a stretched L. ocellatus with 1 mM EGTA in the internal solution. (B) Release records at the same voltages after 1 mM procaine. Fiber 412. [APIII] ranged from 0.75 to 1.11 mM; time elapsed was 21 min. Initial Ca content of the SR was 1600 μM both in reference and in procaine. Parameters of removal, [EGTA] = 1.08 mM, k_offEGTA = 3 μM⁻¹ s⁻¹, k_onEGTA = 2.46 s⁻¹, maximum pump rate = 0.46 mM⁻¹ s⁻¹, and [Parvalbumin] = 2.96 mM, 50 nM free Ca²⁺. (C) Voltage dependence of both kinetic components of corrected release waveforms. The black symbols correspond to the reference values (peak permeability, circles; steady permeability, triangles), and the unfilled symbols are in the presence of 1 mM procaine. One-Boltzmann function fits to the data points (continuous lines). Parameters of the Boltzmann fit to the averages, P_SRmax = 20.02 × 10⁻³ ms⁻¹, V^* = 36.36 mV, and k = 10.18 mV for the peak permeability in reference; P_SRmax = 10.47 × 10⁻³ ms⁻¹, V^* = −22.77 mV, and k = 11.45 mV for the steady SR permeability in reference; P_SRmax = 12.42 × 10⁻³ ms⁻¹, V^* = −34.95 mV, and k = 8.83 mV; and P_SRmax = 4.57 × 10⁻³ ms⁻¹, V^* = 34.7 mV, and k = 7.2 mV for the same quantities in 1 mM procaine. (D) Ratios of peak/steady permeability. Solid symbols are in reference; and unfilled symbols in 1 mM procaine.

The effects of procaine on peak and steady levels of SR permeability, which depend on test voltage, are summarized for four experiments in Fig. 5 C. As mentioned above, the effect on the steady level became significant only at the more depolarized voltages. The p/s ratio is also plotted in Fig. 5 C (right). As in Fig. 5, A and B, the abscissa was shifted by V_max (established in records obtained before the application of procaine). The drug abolished the maximum, making the ratio almost voltage-independent. Despite an almost 50% reduction in permeability, the ratio at positive test voltages was not significantly changed. The reversibility of the effect after washout of the drug was tested for large voltage pulses. The peak recovered to 97 ± 16% of its reference amplitude at 0 mV, whereas the steady component recovered to 105 ± 8%. The ratio obtained corresponded to 92 ± 11% (n = 4) of the value computed in reference.

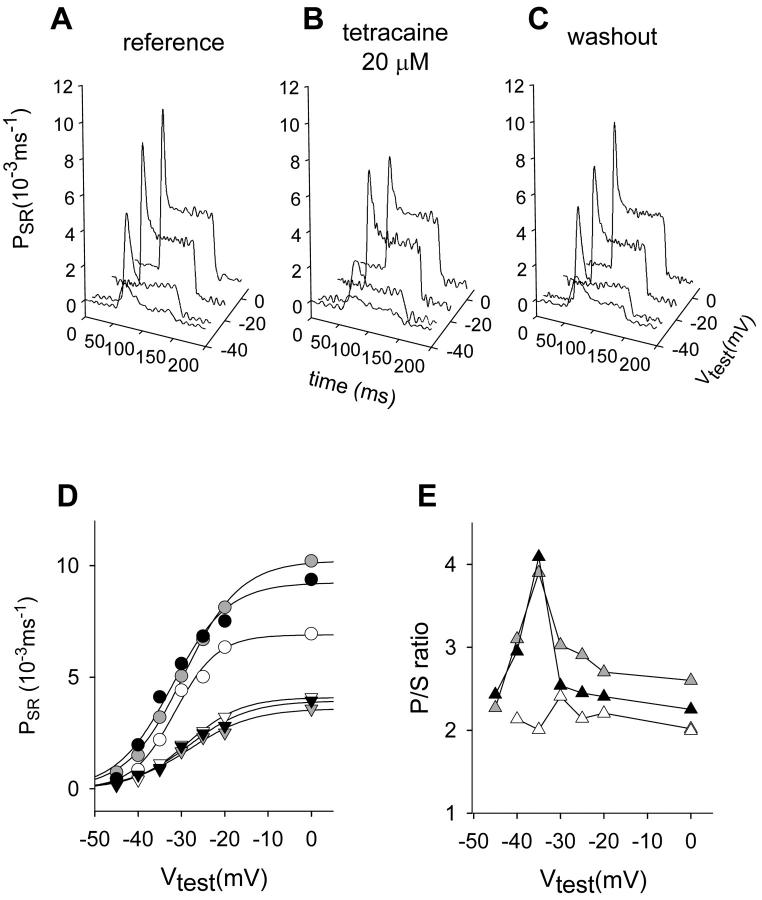
20 μM tetracaine had qualitatively similar effects, as shown in Fig. 4, where the reversibility of the effect is also documented. Average effects on seven fibers are represented in Fig. 5 D. While not seen in the experiment of Fig. 4 D, a reduction of the steady level at higher voltages became apparent in the averages. In this particular set of experiments we found a significant reduction of the p/s ratio at every test voltage. Despite this quantitative difference, both local anesthetics abolished the maximum and made the ratio essentially voltage-independent.

FIGURE 4.

Effect of 20 μM tetracaine on both kinetic components of Ca²⁺ release flux and their ratio. (A) Corrected release waveforms obtained in a fiber held at 90 mV with an internal solution containing 5 mM EGTA. (B) Records obtained after the application of 20 μM tetracaine to the center pool at the same test voltages. (C) Records obtained after washout of the drug. Note that all three sets of records are shown with the same scale. Fiber 4191, R. catesbeiana. [Fluo-3] ranged from 95 to 121 μM; time elapsed was 28 min. Initial Ca content of the SR was 2200 μM in all cases. Parameters of removal, [EGTA] = 5 mM, k_offEGTA = 2 μM⁻¹ s⁻¹, and k_onEGTA = 5 s⁻¹. (D) Voltage dependence of peak and steady permeability. Reference (black symbols), tetracaine (unfilled symbols), and washout (gray solid symbols). Peak (circles), steady values of permeability (down-triangles), and best-fit of a two-states Boltzmann function to the data points (continuous lines). Parameters of the Boltzmann fit, P_SRmax = 10.22 × 10⁻³ ms⁻¹, V^* = 29.41 mV, and k = 6.55 mV for the peak permeability; P_SRmax = 3.59 × 10⁻³ ms⁻¹, V^* = −28.01 mV, and k = 7.24 mV for the steady SR permeability in reference; P_SRmax = 9.24 × 10⁻³ ms⁻¹, V^* = 32.15 mV, and k = 6.41 mV for the peak permeability; P_SRmax = 3.94 × 10⁻³ ms⁻¹, V^* = −28.09 mV, and k = 6.86 mV for the steady SR permeability in washout; P_SRmax = 6.89 × 10⁻³ ms⁻¹, V^* = −31.49 mV, and k = 4.91 mV; and P_SRmax = 4.1 × 10⁻³ ms⁻¹, V^* = 28.66 mV, and k = 6.21 mV for the same quantities in 20 μM tetracaine. (E) Peak/steady ratio. Same color code as in D.

DISCUSSION

In amphibian muscle, two classes of Ca²⁺ release channels are present in similar densities, comprising four identical protomers of either of two ryanodine receptor isoforms. Even in mammalian muscle, where isoform 1 vastly predominates, two structurally different groups of channels can be distinguished, on the basis of their relationship with the T-membrane voltage sensors. Whether this structural duality has a functional correlate, i.e., multiplicity of release mechanisms, is controversial. One possibility is that all channels are controlled—via the DHPr—by membrane voltage. Alternatively, a second form of release could exist, dependent on an initial increase in [Ca²⁺] on the cytoplasmic side of all, or some, of the channels. This second form is customarily termed CICR.

Two interventions modified Ca²⁺ release differently

Two interventions were devised in the present work to interfere with each component specifically. Depolarization patterns were designed to partially inactivate voltage sensors, through steady partial depolarization or long lasting periods at 0 mV followed by brief recovery. Given their effect on transmembrane mobile charge, such patterns should reduce the availability of voltage sensors and interfere with release activation.

The second intervention, local anesthetics, is expected to selectively affect release beyond the voltage-sensing stage, based on the ability of the drugs to interact directly with release channels reconstituted in bilayers (Xu et al., 1993). Moreover, the anesthetics should interfere with Ca²⁺-mediated activation, based on their effects on the [Ca²⁺] dependence of channel opening in bilayer-reconstituted systems (Xu et al., 1993), skinned fibers (Donaldson, 1989; Endo, 1985) and vesicular fractions. While local anesthetics are known to also affect voltage sensor function in whole fibers (Sánchez and Caputo 1987, Hui and Chen, 1992; Csernoch et al., 1988), such effects appear at higher concentrations than used here.

While both anesthetics determined a sharp reduction in the p/s ratio (bringing the release waveform to a shape similar to that of mammalian muscle, compare to Shirokova et al., 1996), the effect of partial depolarization—leading to inactivation of voltage sensors—was very different. It suppressed the peak of release at lower activation voltages, but the waveform of release and its high p/s ratio fully recovered when greater activation pulses were applied.

The ability of these two kinds of interventions to modify release flux differently is consistent with the hypothesis of dual control. To quantitatively test these ideas, a specific formalization of dual control is applied in the next section.

A dual control model reproduces the experimental findings

The experimental results were confronted with simulations using the couplon model (Stern et al., 1997), in which release is produced by interacting channels, separately gated by voltage or Ca²⁺. The model is based on evidence (Block et al., 1988) that every other Ca²⁺ release channel in the junctional double row faces a voltage sensor (tetrad of DHP receptors) across the triadic gap. It assumes that such channels (named “V”), are voltage-gated, while the others (named “C”), are gated by Ca²⁺. In simulations with this model, the peak component of release at lower voltages flows largely through the Ca²⁺-operated channels.

In keeping with the interventions applied here, we explored whether the effects of depolarization and local anesthetics would be reproduced by selectively suppressing C- or V-channels in the model.

No attempt was made to fit the parameters of the model to our experimental data. The simulation of “whole cell” records involved averaging 1000 realizations of a Monte Carlo run in a couplon of fixed size, usually 14 C- and 14 V-channels. A fraction F of channels in either class was disabled as follows. In each realization and for every channel in the couplon, a random number between 0 and 1 was compared with F, and the channel was disabled every time the random number was less than F. This resulted in a variable fraction of disabled channels at random positions in each realization, which averaged to F. Channels made unavailable (representing block by local anesthetics or inactivation by voltage) remained so throughout the realization. This is justified for V-channels, as recovery from voltage-dependent inactivation takes seconds. In regard to C-channels, tetracaine induces long-lasting closed states of 200 ms in Ryr 1 in bilayers (Xu et al., 1993), and similar observations were made for procaine acting on Ryr 2 (Zahradnikova and Palade, 1993). This implementation of V-channel inactivation assumes that all four sensors associated with a given channel undergo concerted inactivation. This feature, chosen for computational convenience, may not be an actual property of the inactivation of the voltage sensors. The channels that remained available were assumed normal in every sense, including conductance. The assumption is based on the effects of tetracaine in bilayers, which at 500 μM reduced the single channel current by 20%, probably by fast open channel blockade. Assuming one-to-one stoichiometry of block, 20 μM tetracaine should reduce single channel current by 1%.

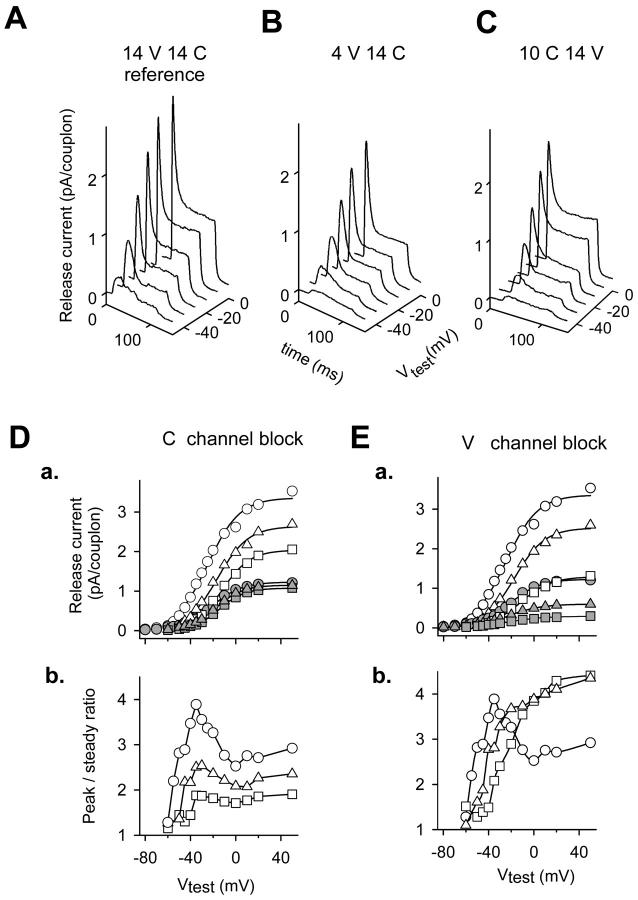
Fig. 6 illustrates the outcome of simulations carried out with varying fractions of C- or V-channels disabled to explore the effects on release and p/s ratio. Fig. 6, A–C, shows representative simulated release current records for the reference condition (Fig. 6 A), voltage-dependent inactivation (Fig. 6 B), and local anesthetic block (Fig. 6 C). The effect of suppressing C-channels on the release components or the p/s ratio is shown respectively in Fig. 6, Da and Db. Simulations with F = 0.3 (10 C-channels available out of 14) or 0.5 (seven C-channels available) are compared with reference simulations, F = 0, similar to previously published ones (Stern et al., 1997). This degree of block of C-channels reproduced well the effects of tetracaine or procaine. One exception was the steady component of release, experimentally reduced in most fibers, but not in the simulations. An unspecific block of release channels by local anesthetics, as discussed below, could explain the discrepancy.

FIGURE 6.

Simulations; selective blockade of V- and C-channels. Top, Simulated release currents corrected for depletion for three conditions. (A) Reference, 14 channel couplon, with all C- and V-channels available. (B) Block of V-channels; 4 V-channels and 14 C-channels available. (C) Block of C-channels; 10 C-channels and 14 V-channels available. (D) a, Peak and steady release currents for all (circles), 10 (triangles), or seven (squares) C-channels available. The larger plot in each pair corresponding to the three conditions represents peak currents (unfilled symbols), the smaller steady currents (solid symbols). Fit parameters for 14C and 14V: maximum release current (MRC) = 3.36 pA/couplon, V^* = −24.7 mV, and k = 14.05 mV for the peak current, MRC = 1.23 pA/couplon, V^* = −21.3 mV, and k = 13.4 mV for the steady current. Fit parameters for 10C and 14V: MRC = 2.64 pA/couplon, V^* = −16.2 mV, and k = 13.6 mV for the peak current; MRC = 1.15 pA/couplon, V^* = −17.6 mV, and k = 11.9 mV for the steady current. Fit parameters for 7C and 14V: MRC = 2.04 pA/couplon, V^* = −12.2 mV, k = 12.5 mV for the peak, and MRC = 1.08 pA/couplon, V^* = −14.7 mV, and k = 11.3 mV for the steady current. b, Simulated voltage dependence of peak/steady ratio, with the same symbol code. (E) a, Peak and steady release currents for all (circles), four (triangles), or one V-channel available (squares). Fit parameters for 14C and 14V: same as in D a. For fit parameters 14C and 4V: MRC = 2.56 pA/couplon, V^* = −17.2 mV, and k = 13.4 mV for the peak current; and MRC = 0.60 pA/couplon, V^* = −23.0 mV, and k = 14.7 mV for the steady current. Fit parameters for 14C and 1V: MRC = 1.30 pA/couplon, V^* = −11.8 mV, and k = 13.6 mV for the peak current; and MRC = 0.29 pA/couplon, V^* = −22.9 mV, and k = 15.7 mV for the steady current. b, Peak/steady voltage dependence calculated from the values in a (same symbol code). Simulations were carried out with parameter values of Stern et al. (1997).

In the simulations of Stern et al. (1997) the maximum of p/s achieved at low voltages depended on the length or number of channels of the couplon. The ascending limb of the voltage dependence at constant couplon length reflected the synchronization of triggering of C-channels that follows faster activation of the voltage-gated ones. Inhibition of C-channels in the model results in a condition similar to the short couplons of Stern et al. (1997). Thus the effect of local anesthetics, based on this interpretation, would be equivalent to splitting the couplons in operatively shorter units.

Curves in Fig. 6 E were generated after disabling V-channels. At F = 0.7 or 0.93, the voltage dependence of p/s became similar to that obtained experimentally in fibers inactivated by voltage (as shown in Figs. 1, 2, and 5). The extent of the assumed inactivation had an effect on the simulated p/s ratio similar to that of increasing inactivation experimentally. Namely, with greater inactivation the dependence shifted to more positive voltages and, somewhat surprisingly, the value of the ratio attained at the most positive test potentials increased above reference values, both experimentally and in the simulations.

Despite the success in reproducing the experimental p/s there are relevant differences between the outcome of the simulations and the experimental voltage dependence of the inactivated release. While the experiments show a right shift of the midvoltage and a less steep voltage dependence, only the first finding is reproduced by the model (see parameters of Boltzmann fits in legend of Fig. 6). Simulations also had to assume a more substantial difference in the degree of inactivation to reproduce the differences in p/s between briefly reprimed and partially inactivated (V_h = −70 mV) fibers.

We do not have definitive explanations for these differences. They might reflect the contribution of Q_γ to the voltage dependence of release activation in reference conditions, a feature not included in the model. The absence of Q_γ may also explain the broader voltage dependence of p/s in the simulations. Alternatively, the different slope might be due to the concerted inactivation mechanism assumed in the simulations. Finally, with regard to the larger inactivation required to reproduce the experimental observations in the briefly reprimed fibers, the small releases recorded in these conditions could induce an underestimation of the SR Ca content which may result in an overestimated SR permeability.

As stated in the Introduction, there is no direct correspondence in the simulation between phases of release flux and components going through C- or V-channels. To better understand the processes within the model, we looked at the relative contributions of each channel class separately (data not shown). The p/s of the C-component studied in isolation shows a monotonically increasing voltage dependence. At low voltage this component dominates the total release current, endowing it with a high p/s ratio. At higher voltages the V-component becomes significant, determining a reduction in the p/s ratio. When C- or V-channels are selectively blocked, the voltage dependence of the p/s ratio curve changes, largely depending on the resulting relative weight of the release components. Most importantly, when V-channels are suppressed, the monotonically increasing ratio of the C-current becomes a property of the total release current, thus explaining the large value of the p/s ratio attained at positive voltages.

It is also worth noting that the magnitude of C-release activation only depends on membrane voltage through its relationship with activation of V-channels.

The previous simulations assumed a specific block of a fraction of C-channels. We have considered other possibilities, including nonspecific block of both release channels, as well as reduction in the single channel current. Suppressing equal number of C- and V-channels eliminates the maximum at low voltages of the p/s ratio, producing an almost flat voltage dependence of this variable, qualitatively similar to that obtained after specific suppression of C-channels. Alternatively, a reduction of the single channel current to 50% of its reference value reproduced the p/s voltage dependence obtained with 50% block of both channel types. Thus, based on the present simulations, the observed experimental effects of the local anesthetics do not have a unique interpretation. On the other hand, the monotonically increasing p/s ratio observed experimentally upon voltage-dependent inactivation was reproduced in the model simulations only through V-channel suppression.

The reduction in p/s ratio by the anesthetics could alternatively be explained as a consequence of a diminished inactivation by Ca²⁺, secondary to the general reduction in release flux. As shown in Figs. 1 and 5, however, the reduction of release flux attained through voltage-dependent inactivation was significantly greater than that produced by any of the drugs. This excludes a reduction in Ca²⁺-dependent inactivation as explanation for the drug effects. Furthermore, this feature adds to the evidence that the fast inactivation process does not depend on bulk Ca²⁺ (Pizarro et al., 1997).

Comparisons with earlier work and implications for release control

The ability of voltage-dependent inactivation to alter the kinetics of Ca²⁺ release supports analysis of the latter into two separately gated components. It also weighs in favor of a specific picture of the functional Ca²⁺ release unit. This picture is more complex than one emerging from a study (Klein et al., 1997), in which partial inactivation of voltage sensors was used to decimate Ca²⁺ sparks and make them separable.

In that study the latencies of sparks occurring during an activating voltage pulse were determined as functions of pulse voltage, while sparks themselves were found to be similar at all voltages. A waveform, constructed by summation of the Ca²⁺ flux time course for each event at its time of occurrence (i.e., latency), was found to roughly reproduce main aspects of the macroscopic release record, specifically peak and decay to a steady phase. Taken at face value, this result implies that the properties of release in the partially inactivated system (time course and voltage dependence), are representative of the fully primed situation. Such “scaling” property implies that voltage sensors are in charge of a cohort of “slave” release channels, constituting a unit that has in itself all the time- and voltage-dependent properties of macroscopic release. In particular, such voltage sensors do not interact. Voltage-dependent inactivation would just reduce their number, without altering their properties, including the sparks that they generate with their cohorts, and the temporal pattern of activation.

By contrast, the present results highlight macroscopic properties of Ca²⁺ release that are radically altered by voltage-dependent inactivation, namely the magnitude of its peak (relative to its steady level) and its dependence on pulse voltage. It is impossible to explain these results without assuming some type of interaction among voltage sensors (or their release channel cohorts), an interaction reduced when their ranks are thinned by inactivation. Such an interaction of voltage sensors and their associated release channels was first proposed and simulated quantitatively by Shirokova et al. (1996).

The effect of the anesthetics used here on the p/s ratio is similar to that of high intracellular [Mg²⁺] (Kirsch et al., 1999) or BDM (De Armas et al., 1998), two interventions known to reduce the P_o by direct interaction with ryanodine receptors. At higher doses, i.e., 0.2 mM tetracaine (Pizarro et al., 1992, Särközi et al, 1996), the peak is totally suppressed. Although this intervention was not used here to avoid direct block of voltage sensors, it indicates that the anesthetics are capable of preferentially affecting one phase—the peak—in support of the dual gating model.

In the present experiments both drugs reduced release flux during its steady phase. This is in contrast with a study by Särközi et al. (1996), who found no effect of tetracaine on the steady phase <50 μM. Pizarro et al. (1992), who also reported no effect on this component using 20 μM tetracaine, limited their study of the steady phase to low test voltages (V_test < −30 mV). This is in consonance with the results obtained in the present work for the same voltage range (see Figs. 3–5). We believe that our observations are consistent with the notion that CICR contributes to the steady phase of release. It could also reflect an effect of the drugs on channels gated by voltage.

Tetracaine applied at 0.2 mM totally abolished sparks in the frog (Shirokova and Ríos, 1997). Assuming that sparks largely reflect CICR, the result is consistent with the drug effects reported here, and the interpretation that at lower concentrations the drugs partially inhibit the Ca²⁺-gated component. By contrast, treatment with D-600 deferred the occurrence of sparks and peak generation to more positive test potentials (Shirokova and Ríos, 1997). Because D-600 blocks voltage sensors by stabilizing their inactivated state, its effects are expected to be similar to those of partial voltage-dependent inactivation, and entirely consistent with the present results.

Taken together, the results of these studies are best interpreted as outcomes of selective anesthetic block of one release component, gated separately by Ca²⁺. The experiments and simulations, however, do not establish to what extent the drugs also block the putatively voltage-controlled component. A related issue is whether the Ca²⁺ gated component is solely responsible for fast, presumably Ca²⁺-dependent, inactivation (as proposed by Ríos and Pizarro, 1988). This hypothesis was contradicted by the demonstration (Jong et al., 1995) that fast inactivation affects both kinetic components of release flux. It seems therefore reasonable that both should be sensitive to the anesthetics.

In summary, the radical alteration observed here of macroscopic Ca²⁺ release kinetics by inactivation of voltage sensors, is inconsistent with release units separately gated by individual voltage sensors, requiring instead a degree of cooperation among sensors. The recovery of Ca²⁺ release kinetics at high test voltages suggests a secondarily gated contribution, not directly sensitive to voltage. When dominant, this contribution imbues the macroscopic release with its characteristic two-phase kinetics. While there are indications that this component is activated (and inactivated) by Ca²⁺, the attempt carried out here to specifically block it with drugs was inconclusive. Its assignment to a subset of junctional channels, namely those not in contact with voltage sensors, constitutes a seductive possibility, but is based solely on the general agreement between the results and simulations with the couplon model. Other possibilities, including the involvement of parajunctional channels recently described in muscles endowed with two ryanodine receptor isoforms (Felder and Franzini-Armstrong, 2001), must be considered as well.