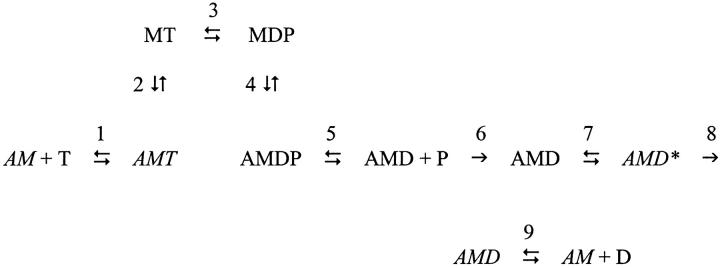Kinetic Effects of Fiber Type on the Two Subcomponents of the Huxley-Simmons Phase 2 in Muscle

Abstract

The Huxley-Simmons phase 2 controls the kinetics of the first stages of tension recovery after a step-change in fiber length and is considered intimately associated with tension generation. It had been shown that phase 2 is comprised of two distinct unrelated phases. This is confirmed here by showing that the properties of phase 2_fast are independent of fiber type, whereas those of phase 2_slow are fiber type dependent. Phase 2_fast has a rate of 1000–2000 s⁻¹ and is temperature insensitive (Q₁₀ ∼ 1.16) in fast, medium, and slow speed fibers. Regardless of fiber type and temperature, the amplitude of phase 2_fast is half (∼0.46) that of phase 1 (fiber instantaneous stiffness). Consequently, fiber compliance (cross-bridge and thick/thin filament) appears to be the common source of both phase 1 elasticity and phase 2_fast viscoelasticity. In fast fibers, stiffness increases in direct proportion to tension from an extrapolated positive origin at zero tension. The simplest explanation is that tension generation can be approximated by two-state transition from attached preforce generating (moderate stiffness) to attached force generating (high stiffness) states. Phase 2_slow is quite different, progressively slowing in concert with fiber type. An interesting interpretation of the amplitude and rate data is that reverse coupling of phase 2_slow back to P_i release and ATP hydrolysis appears absent in fast fibers, detectable in medium speed fibers, and marked in slow fibers contracting isometrically. Contracting slow and heart muscles stretched under load could employ this enhanced reversibility of the cross-bridge cycle as a mechanism to conserve energy.

INTRODUCTION

Application of a step change in length to an isometrically contracting fiber causes an immediate, synchronous change in tension (phase 1) followed by a kinetically controlled return to the initial isometric tension. These tension transients can be subdivided into a series of exponentials with rates and amplitudes called phases. Most of the return to isometric tension occurs rapidly during phase 2. Phase 3 is evident next as a slowing or reversal of the return to isometric tension while phase 4 governs the final asymptotic return to the prejump isometric tension. The high speed (primary transition) and large size (significant contribution) of tension recovery during phase 2 firmly establishes it as a prime candidate for tension generation. As such, it has been and is the subject of a number of mechanochemical and time-resolved x-ray and probe structural studies into the mechanism of tension generation. It is therefore critical to understand the source and function of phase 2 in fibers. To do this, it is necessary to 1), determine the number of exponential phases that constitute phase 2; 2), quantify each phase in terms of an amplitude and an apparent rate constant; 3), characterize the distinctive properties of the phase to determine its origin and role in the mechanochemistry of the cross-bridge cycle; and 4), establish the generality of these observations by studying these individual phases in different animals and fiber types. This paper is primarily concerned with the fourth goal.

Historically, the number of kinetic phases allocated to phase 2 has varied between four and one (Huxley and Simmons, 1971; Abbott and Steiger, 1977; Ford et al., 1977; Davis and Harrington, 1993b). Recent work has the advantage of the availability of computerized methods of analysis capable of subdividing the entire tension transient into exponential components, whereas earlier researchers were limited by the techniques available to analyze partial tension transients. Artifacts introduced by applying tangents as endpoints to truncated tension transients can now be avoided by using nonlinear least squares analysis to subdivide the entire tension transient into exponential components (see Davis, 2000 and references therein). Length-jump (L-jump) data, together with insights from laser temperature-jump experiments, the only other technique to elicit these fast responses, gave support to a biexponential phase 2 in the millisecond and longer time domains in both frog and rabbit fibers (Davis and Harrington, 1987, 1993b).

Extensive studies on the effect of temperature on the apparent rate constants of the L-jump phases 2_fast, 2_slow, 3, and 4 has revealed that each has a unique temperature dependence (Abbott and Steiger, 1977; Davis and Harrington, 1993b; Zhao and Kawai, 1994; Davis and Rodgers, 1995a,b; Davis, 1998). Apart from providing insights into the physical origin of the various phases, the form of the temperature dependencies of rate (Arrhenius plots) provides a unique signature that can be used to identify a particular phase in different fiber types. In the experiments described, the marked temperature insensitivity of the rate of phase 2_fast (Q₁₀ of 1.2) and the temperature sensitivity of the rate of phase 2_slow (Q₁₀ of 2.8) together with its particular dog's leg or break in the Arrhenius plot provide signatures to identify each phase (Davis and Harrington, 1993b).

On the basis of experiments on fast, type IIb rabbit psoas fibers, it was proposed that phase 2_slow results from a perturbation of the de novo tension generating step in the cross-bridge cycle, whereas perturbation of a slow-responding series elastic element gives rise to phase 2_fast (Davis and Harrington, 1993b). As a frame of reference for the changes in phase 2 kinetics arising from changes in fiber type, we describe the relationship between the Huxley-Simmons L-jump phases and the biochemical cross-bridge cycle. Details of the mechanochemical mechanism and how it compares to mechanisms devised by others is presented in the Discussion.

In the simplified cross-bridge cycle shown in Scheme 1, M is myosin, A is actin, T is ATP, D is ADP, and P is P_i. The central feature of the mechanism is that the tension generating state is created by an isomerization between strongly bound AMD states in step 7. Step 7 is isolated from P_i release in the back direction by irreversible step 6 and from ADP release in the forward direction by irreversible step 8 (Davis and Rodgers, 1995b). Indications are that phase 2_slow (with a rate constant that is insensitive to P_i) is linked to the creation of a primary force-generating state in step 7 (Davis and Harrington, 1993b; Davis and Rodgers, 1995b); phase 3 (with a rate constant that is sensitive to P_i) to the actin-catalyzed release of phosphate from myosin and step 5 (Davis and Rodgers, 1995b); phase 4 to the sequential functioning of the two heads of myosin where binding of the second head is prevented when the first head is strongly bound to actin, but has not yet passed through step 7 to generate force (Davis and Rodgers, 1995a; Davis, 1998).

Scheme 1.

This paper presents a comparative study of the kinetics of phase 2 in fast rabbit IIb and mouse IIa fibers and slow type I fibers. A prediction of our earlier work would be that phase 2_fast arising from the elasticity of the sarcomere would probably change little with fiber type. We explored this to find that the rate of phase 2_fast is fiber type independent (at 1000–2000 s⁻¹) with an amplitude that scales in direct proportion to instantaneous stiffness of the fiber (phase 1 amplitude)—very much a mechanical property of thick and thin filaments linked by myosin cross-bridges. Phase 2_slow, on the other hand, slows in rate when comparing fast, medium, and slow speed fibers. Earlier work on fast fibers is confirmed and shows that the amplitude of phase 2_slow scales in fixed ratio to isometric tension at 5°C and above. Interestingly, this proportionality is less pronounced in medium speed fibers and is absent in slow fibers, indicating a change in rates related to fiber type. We argue that this change in the kinetics of slow fibers is indicative of increased back-reversibility of the cross-bridge cycle from tension generation at step 7 to P_i release and ATP hydrolysis, steps that are largely irreversible in fast fibers. This reversibility could increase the efficiency of slow fibers, particularly under conditions where the muscle is cyclically stretched under load (eccentric contractures). Fiber stiffness (Huxley-Simmons T₁ and phase 1) is roughly halved when the contribution from phase 2_fast is included. Thus, of the two components, phase 2_slow alone correlates with tension generation. A preliminary account of these experiments has appeared in abstract form (Davis, 1999).

MATERIALS AND METHODS

Fiber preparation and solutions

Rabbits and mice were sacrificed under NHLBI Animal Care and Use Protocol 9CB-2 and 8CB-3R respectively. Psoas muscle was cut longitudinally in situ into ∼4 cm × 2 mm wide strips. The entire soleus muscle of the mouse was removed after cutting the proximal and distal tendons as close to the bone as possible. Both muscles were stretched a small amount beyond slack length and tied by their ends to wooden applicator sticks using silk thread. Each was then placed in a 15 ml plastic tube containing the following skinning solution and stored on ice at 0°C until used. Skinning solution contained 0.5% Brij 58, 3 mM Mg acetate, 5 mM EGTA, 3 mM vanadium free ATP, 50 mM creatine phosphate, 5 mM KH₂PO₄, 0.2 mM NaN₃, 3 mM DTT, 1 mg ml⁻¹ of creatine phosphokinase, and one EDTA-free protease inhibitor cocktail tablet (Roche Applied Science, Indianapolis, IN) per 30 ml of solution. The pH was adjusted to 7.0 at room temperature with 1N KOH. The principle behind the method is that the small volume of skinning solution serves to concentrate sarcomeric proteins thereby reducing further dissociation from the fibers and decreasing fiber damage. Fibers were used within five days of dissection. Dissections were performed in the standard relaxing solution held at 5°C and single fibers were drawn from the ends (Yu and Brenner, 1989) of ∼6 mm long segments of the psoas muscle and from the lateral edge of the pinnate soleus muscle. Aluminum T-clips fitted ∼3 mm apart were used to attach the fiber to Invar mounting hooks in the tension transducer cell. Fiber lengths and diameters (at 3 positions along the fiber length) were measured in the transducer cell containing relaxing solution after setting the sarcomere spacing using the diffraction pattern from a He/Ne laser. Fibers were first activated at 5°C by washing with preactivating solution and then rapidly flowing chilled activating solution into and through the cell (Davis and Harrington, 1993b; Davis et al., 2002). After activation, the fiber temperature was rapidly raised (<35 s) to the temperature of the experiment. The Brenner protocol was used to stabilize the sarcomere diffraction pattern (Brenner, 1983). Once fiber temperature and tension had stabilized, 10 tension transients were recorded for later averaging and analysis. On completion of the experiment, each fiber was typed by PAGE and checked to ensure that the myosin regulatory light chain/s were unphosphorylated (Davis et al., 2002).

The ionic strength of the solutions was 0.2 M and were the same as those used by Davis and Harrington (Davis and Harrington, 1993b). Glycerol 2-phosphate is used as a temperature-insensitive buffer. Relaxing solution: 7.52 mM MgCl₂, 5.48 mM vanadium free ATP, 20 mM EGTA, 20 mM creatine phosphate, 15 mM disodium glycerol 2-phosphate. Preactivating solution: 7.52 mM MgCl₂, 5.48 mM vanadium free ATP, 0.1 mM EGTA, 19.9 mM HDTA (1, 6-diaminohexane-N, N, N′,N′- tetraacetic acid), 19.9 mM creatine phosphate, 15 mM disodium glycerol 2-phosphate. Activating solution: 7.39 mM MgCl₂, 5.52 mM vanadium free ATP, 20 mM CaEGTA, 20 mM creatine phosphate, 15 mM disodium glycerol 2-phosphate. All solutions contained 2 mg ml⁻¹ of creatine phosphokinase, and were adjusted to pH 7.1 at room temperature with 1N KOH.

L-jump tension and sarcomere length measurements

The apparatus used to record the tension transients is described briefly, details are presented elsewhere (Davis and Harrington, 1993b; Davis and Rodgers, 1995a). A fast Model 407A (Cambridge Technology Inc., Cambridge, MA) capacitor-based force transducer with a resonant frequency of 12 KHz, 100 μs rise time, and low compliance of 0.1 μm g⁻¹ was used for all tension measurements. An ergometer (Model 300S, Cambridge Technology Inc., Cambridge, MA) was set to apply small L-jump stretches with a 100% rise time of 180 μs to the fiber. Sarcomere lengths were measured from the diffraction pattern produced by a 10 mW He/Ne laser set at the Bragg angle to the fiber. Changes in the diffraction pattern in experiments up to 16°C were followed with a SL15 super linear position sensor and Model 301DIV-30 position-sensing amplifier (UDT Sensors, Hawthorne, CA) (Davis and Harrington, 1993b). Ten tension transients were recorded at each temperature for later averaging and analysis. Tension transients from three to eight different fibers were recorded at each temperature.

Data collection, analysis, and presentation

Voltage output from the force transducer amplifier and the detector measuring the position of the first order of the sarcomere diffraction pattern was recorded on a dual time base, four channel digital oscilloscope (Integra 20, Nicolet Instrument Corporation, Madison, WI). Tension and sarcomere length changes were simultaneously recorded as 50,000 12-bit data points at fast rate of 20 μs per point, and slow rates of 200 μs for fast, and 400 μs per point for slow fibers. An in house program using National Instruments LabView software running on a Dell Dimension XPS 400 personal computer with a PCI-GPIB interface card (National Instruments, Austin, TX) was used to control and acquire data from the digital oscilloscope.

Methods used to optimize the nonlinear least squares fit (Johnson and Frasier, 1985) to the transients by reducing the large raw data sets to smaller sets with 1000 point log-spaced time-bases for fitting remain unchanged (Davis, 2000). An important technical point is that it is imperative to fit the entire tension transient when analyzing the data. Truncated data sets frequently cause phase 2_slow to split into two artifactual subcomponents as the nonlinear least-squares program forces a fit to the data (see Davis, 2000). Rabbit-fiber tension transients are fitted to four exponentials (phases 2_fast, 2_slow, 3, and 4), those from mouse fibers to three exponentials (phases 2_fast, 2_slow, and 4). The absence of a detectable phase 3 in mouse fibers is probably due to the fact that they are much thinner than rabbit fibers. Slow diffusion of P_i out of the larger diameter fibers leads to a buildup of endogenous P_i and an associated phase 3 response. It is well established that phase 3 is sensitive to phosphate (see Davis and Rodgers, 1995b). Phase 3 can be elicited in mouse fibers by adding P_i to the standard activating solution.

Time courses of the individual kinetic phases and the overall fit to these data were simulated in Kaleidagraph (Synergy Software; Reading, PA) using the constants obtained from the nonlinear least squares analysis of the raw data.

RESULTS

Biexponential phase 2 kinetics in different fiber types

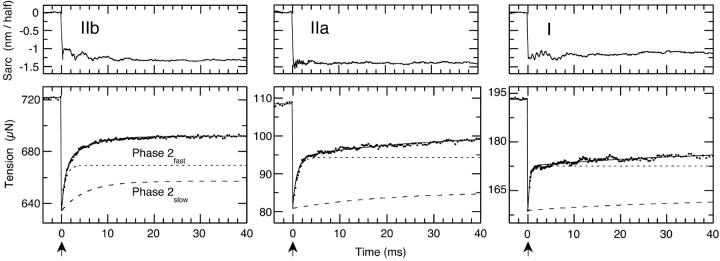
Typical L-jump tension transients of all three fiber types are illustrated in Fig. 1. Quantitative analysis requires subdivision of the entire tension transient into the classical Huxley-Simmons phases by nonlinear least squares analysis. The fit to the prejump isometric tension and phases 1, 2_fast, 2_slow, 3, and 4 are drawn as a solid lines though the data points of the tension transients. The quality of fit to these data from rabbit fast IIb, mouse medium speed type IIa and mouse slow type I fibers is excellent and shows that a small step-change in length in 180 μs induces a phase 2 response with two characteristic exponential sub phases. Relative contributions of phases 2_fast and 2_slow to the tension transient can be assessed from the time courses computed from the fitted rate constants and amplitudes and plotted in each panel of Fig. 1. As noted in the legend, averaged tensions, once normalized to cross-sectional area, are similar for all fiber types. The results are straightforward: The rate of phase 2_fast changes little with fiber type, and the rate of phase 2_slow declines with fiber type from fast, to medium, to slow. Changes in the rate of phase 2_slow are accentuated by the selection of the same 40 ms time-base for all three fiber types in Fig. 1.

FIGURE 1.

L-jump tension transients typical of fast, medium speed, and slow-fiber types. The Rabbit type IIb (fast) and mouse type IIa (medium speed) and I (slow fibers) fibers were subjected to small −1.5 nm/half-sarcomere step releases in ∼180 μs at a temperature of 6°C. Ten tension and sarcomere length transients were recorded and averaged. Contributions of the Huxley-Simmons phases 1, 2_fast, 2_slow, and 4 to the tension transient were determined by nonlinear least squares analysis and the resultant fit to these data drawn as a solid line through each data set. The simulated time-course of phase 2_fast shows its rate to be independent of fiber type. The rate of phase 2_slow, on the other hand, correlates with fiber type at low to moderate temperatures, slowing progressively from type IIb to IIa to I. Averaged tensions normalized to cross-sectional area presented as the mean ± SE were 117.4 ± 4.6 kN m⁻², n = 9 at 6°C for type IIb fibers; 91.3 ± 7.6 kN m⁻², n = 8 at 5°C for type IIa fibers and 97.6 ± 9.9 kN m⁻², n = 10 at 5°C for type I fibers. The arrow indicates the point at which the step-release is applied.

Temperature dependencies of the rate and amplitude of phases 2_fast in different fiber types

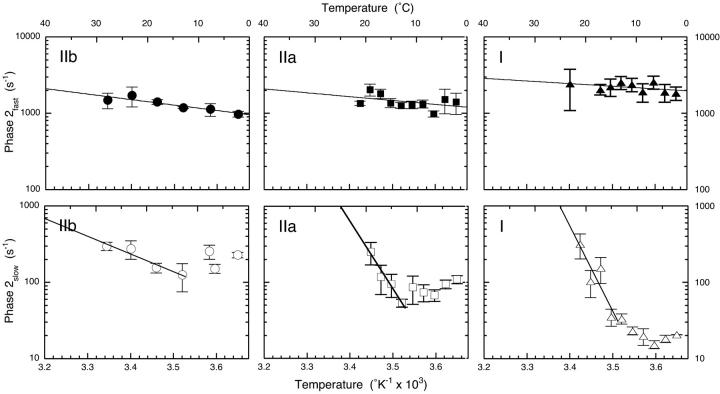
Fig. 1 shows that the rate of phase 2_fast changes little with fiber type in the tension transients obtained from L-jump experiments performed at 6°C. This confirms and extends our earlier work on fast fibers (Davis and Harrington, 1987, 1993b). Arrhenius plots of the apparent rate constants in the upper three panels of Fig. 2 bear out and extend this observation over a range of temperatures. Quantitative analysis of these data shows that the rates at 10°C and the Q₁₀ values vary little with fiber type for rabbit IIb and mouse IIa and I fibers, as listed in the legend of Fig. 2 and Table 1.

FIGURE 2.

Temperature dependencies of the rates of phases 2_fast and 2_slow in fast, medium speed and slow fibers. The distinctly different properties of phases 2_fast and 2_slow are apparent in these Arrhenius plots. Phase 2_fast shows a typical, minimal dependence of rate on temperature in all fiber types. Q₁₀ values of 1.22, 1.16, and 1.10 and associated apparent rate constants at 10°C of 1198 s⁻¹, 1408 s⁻¹, and 2207 s⁻¹ for type IIb, IIa, and I fibers, respectively were computed from the fit to the Arrhenius equation. Phase 2_slow, on the other hand, shows a complex dependence of rate on increasing temperature with a typical rate decline to a minimum value (centered between 10°C and 15°C) followed by a monotonic rate rise at higher temperatures with Q₁₀ values of 1.89, 11.41, and 21.92 for type IIb, IIa, and I fibers, respectively computed from the fit of the reduced data set to the Arrhenius equation. The very high Q₁₀ values indicate increased coupling to adjacent steps in the cross-bridge cycle. Overall, the rate of phase 2_slow declines in concert with fiber type from IIb to IIa to I with measured rates of 227 ± 19 s⁻¹, 109 ± 13 s⁻¹, and 20.4 ± 0.2 s⁻¹, respectively at 1°C. Data from between three and eight individual fibers were averaged at each temperature point. Error bars are SE.

TABLE 1.

Summary of the rates and temperature dependencies of phases 2_fast and 2_slow in different fiber types

	Type IIb	Type IIa	Type I
Phase 2fast rate (10°C)	1198 s−1	1408 s−1	2207 s−1
Phase 2fastQ10	1.22	1.16	1.10
Phase 2slow rate (1°C)	227 ± 19 s−1	109 ± 13 s−1	20.4 ± 0.2 s−1
Phase 2slowQ10 (above ∼10°C)	1.89	11.41	21.92

These data were obtained by fitting the temperature dependencies of rate shown in Fig. 2 to the Arrhenius equation. In the case the rate data for phase 2_slow the mean ± SE (n = 8) of the actual datum is reported.

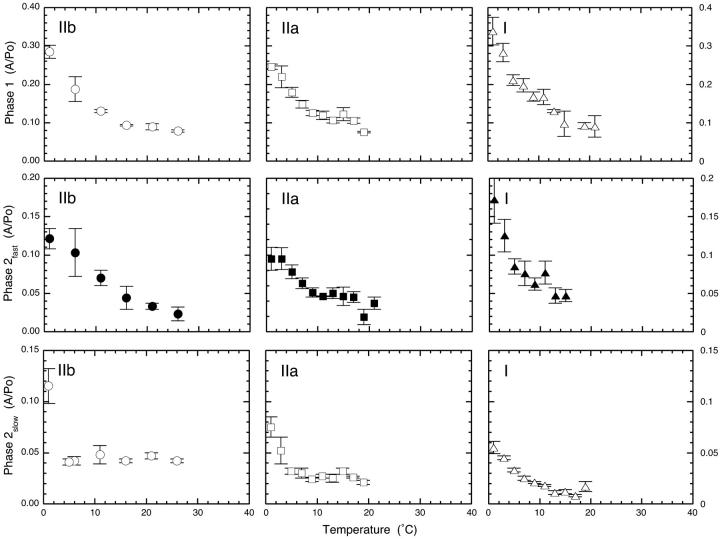
The temperature dependence of the normalized amplitude of phase 2_fast is shown in the center row of Fig. 3. The overall form of the temperature dependencies bear a close resemblance to the phase 1 data depicted in the upper row of the same figure. Note that the amplitude of phase 2_fast is approximately half that of phase 1, a feature highlighted by ordinate axes for phase 2_fast with half the range of the phase 1 plots. Quantitative aspects of the interrelationship between the amplitudes of phases 1 and 2_fast and isometric tension are explored later in detail.

FIGURE 3.

Temperature dependencies of the normalized amplitudes of phases 1, 2_fast, 2_slow in fast, medium speed, and slow fibers. The amplitude of phase 1, normalized (relative) to isometric tension at the temperature of the experiment, declines with increasing temperature to show that isometric tension increases more than stiffness as temperature is raised. The form (shape) and magnitude is similar in each panel irrespective of fiber type. Phase 2_fast versus temperature data resembles phase 1 save that the amplitudes are reduced ∼twofold, a relationship explored in Fig. 4. Phase 2_slow amplitude versus temperature data is different. In fast, but also in medium speed fibers, normalized amplitudes are constant at 5°C and higher temperatures. However, in slow fibers the response is different and normalized tension does not plateau, but declines with increasing temperature. Data from between three and eight individual fibers were averaged at each temperature. Error bars are SE.

Temperature dependencies of the rate and amplitude of phase 2_slow in different fiber types

Phase 2_slow is quite different. Its rate decreases in accord with fiber type in the L-jump tension transients of Fig. 1. Fig. 2 shows the temperature dependencies of the rate of phases 2_slow in fast, medium, and slow speed fibers plotted in Arrhenius form. All plots share the same basic dog's leg or biphasic form in which the apparent rate constant first declines to a minimum between 5° and 10°C and then increases monotonically with increasing temperature. Table 1 lists the Q₁₀ values obtained from a nonlinear least-squares fit to the positive segment of the Arrhenius plots show that type IIa and I fibers have 6- and 12-fold greater Q₁₀ values than the moderate 1.89 recorded for fast type IIb fibers, a value lower than the 2.8 reported in earlier work (Davis and Harrington, 1993b). Apparent rate constants, listed in the legend of Fig. 2 and Table 1 for phase 2_slow at a reference temperature of 1°C show that rates for type IIa and I mouse fibers are ∼2- and ∼10-fold slower than rabbit type IIb fibers. Thus changing from fast to medium to slow speed fibers correlates with a general decline in the rate of phase 2_slow at low to moderate temperatures. The markedly temperature-sensitive medium and slow speed fiber rate data at high temperatures are less relevant to the properties of phase 2_slow as defined in fast fibers and in Scheme 1 because the kinetics reflect the properties of adjacent coupled steps as well as step 7.

Amplitudes also change in specific ways with fiber type. The lower panels of Fig. 3 show changes in the normalized amplitude of phase 2_slow with temperature. As shown in earlier work on fast fibers (Davis and Harrington, 1993b), the phase 2_slow amplitude vs. temperature data is quite different from that of the stiffness-related phases 1 and 2_fast. Change of fiber type alters the form of the plot in several ways. Type IIb fibers serve as reference. With these fibers, the amplitude of phase 2_slow remains in fixed ratio to isometric tension at ∼5°C and above, a property indicative of the role of the phase in de novo tension generation (Davis and Harrington, 1993b). In type IIa fibers, the plateau is established later at ∼9°C and the contribution of phase 2_slow to the overall return to the prejump isometric tension is somewhat reduced. These progressive changes in the temperature dependencies observed in going from fast to slow fibers reach full expression in slow type I fibers. The plateau indicative of the fixed ratio between the amplitude of phase 2_slow and isometric tension, typical of faster fibers, is absent. In these fibers, the contribution of phase 2_slow declines progressively with increasing temperature and the overall contribution to the return to the prejump isometric tension is the lowest of the group.

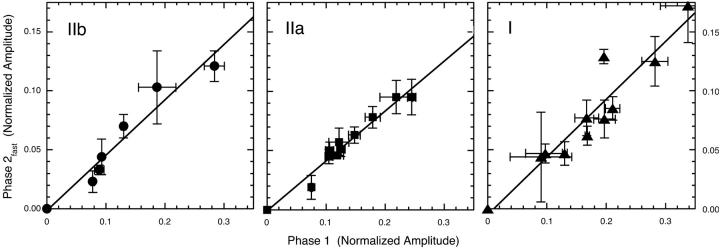
Linear interdependence of the amplitudes of phases 1 and 2_fast

Fig. 4 illustrates the direct relationship between the amplitudes of phases 1 and 2_fast. It is evident that phase 2_fast has approximately half the normalized amplitude of phase 1 in all fiber types and at all temperatures studied. Thus instantaneous stiffness (phase 1) of a fiber apparently arises from a common source in all fiber types studied, as does the viscoelastic contribution from phase 2_fast. Thus fast, medium speed, and slow fibers data have similar phase 2_fast amplitudes that are 0.47, 0.42, and 0.49 of amplitude of phase 1, respectively.

FIGURE 4.

Linear interdependence of the amplitudes of phases 1 and 2_fast in fast, medium speed and slow fibers. Normalized phases 1 and 2_fast amplitude data from Fig. 3 are replotted. The slopes of the linear fits to these fast, medium speed and slow fibers data are a similar 0.47, 0.42, and 0.49, respectively. This indicates a fixed relationship between the amplitudes of phase 1 and 2_fast that is independent of both fiber type and temperature. Error bars are SE.

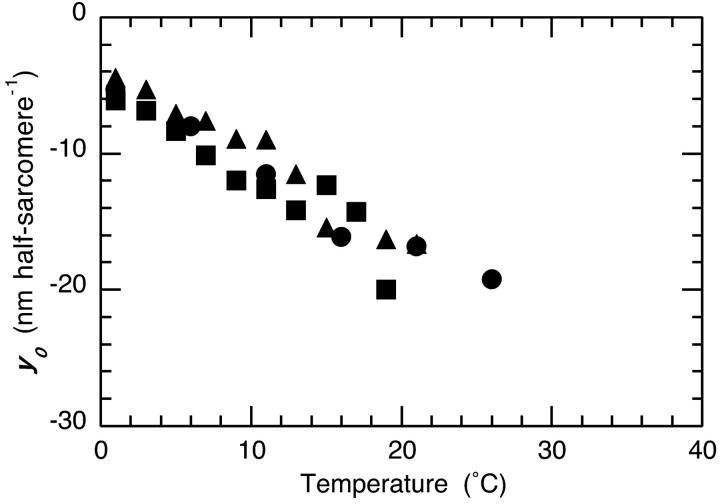
Effect of temperature on y₀

The size of the step release required to synchronously reduce fiber tension to zero is termed y₀. Its dependence on fiber type and temperature is illustrated in Fig. 5. It is evident that there is an approximately linear increase in y₀ with temperature for all fiber types, a relationship implicit in earlier experiments in which it was shown that fiber stiffness (phase 1 or the T₁ curve) has a lower temperature dependence than tension (Davis and Harrington, 1993b). The relationship was made explicit when a common linear dependence of y₀ on temperature was shown to hold for different fiber types of the rat (Galler and Hilber, 1998).

FIGURE 5.

Dependence of y₀ on fiber temperature. These data were obtained by extrapolating the Huxley-Simmons T1 (1 phase 1 amplitude) vs. the −1.5 nm/half-sarcomere length change data to zero tension and recording the value of y₀ at the intercept. Symbols for the three different fiber types are the same as used elsewhere.

Effect of temperature on fiber tension and stiffness

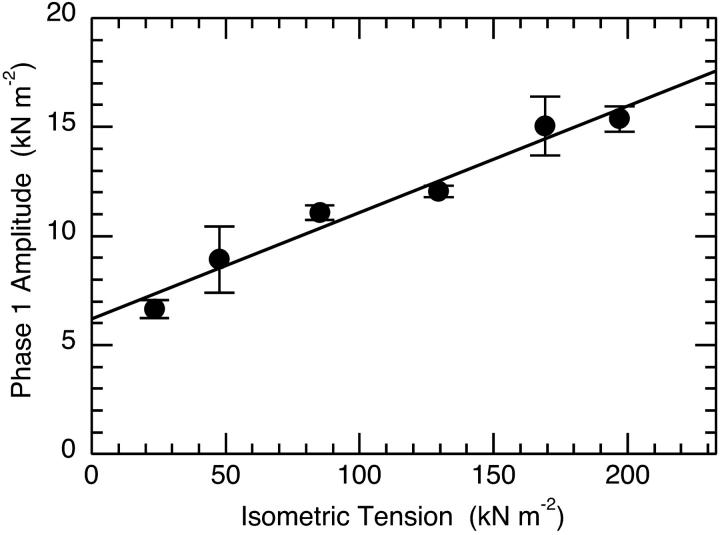
Measuring fiber tension and stiffness at one or two temperatures is relatively straightforward and reliable. This is because the experiments can be performed quickly before activation related fiber damage sets in. Calculating the temperature dependence of the stiffness/tension ratio requires absolute tension values. Fortunately, accurate temperature/tension data obtained under activating conditions identical to our own, with a fiber cell specifically designed for this type of experiment, is available in the literature (Ranatunga, 1994). The temperature/tension data we use here is the result of the a nonlinear least-squares fit we made to Ranatunga's data using the van't Hoff relationship and a two-state model (Davis, 1998). A plot of absolute stiffness versus absolute tension is shown in Fig. 6. Absolute tension data is obtained from the fit to Ranatunga's data. Absolute stiffness data is obtained by multiplying our phase 1 stiffness values, normalized to isometric tension at the temperature of the experiment, by the absolute tension of the fiber at that temperature. In this experiment, as in the fit of the van't Hoff equation to the tension-temperature data (Davis, 1998), tension is used as a measure of the concentration of the AMD^* tension generating state. This appears a reasonable assumption, because optical trap experiments show that the tension produced by a single head does not change significantly with temperature (Kawai et al., 2000). Fig. 6 shows that there is a simple linear relationship between fiber stiffness and tension. The important observation is that both fiber tension and stiffness rise in direct proportion to each other. Back extrapolation to zero tension and forward extrapolation to peak tension at physiological temperatures shows that fiber stiffness increases ∼2.8-fold from 4.1 kN m⁻² nm⁻¹ to 11.7 kN m⁻² nm⁻¹. Note that in our experiments, we obtain normalized tensions that are systematically ∼2.4-fold higher (59.7 ± 4.6 kN m⁻², n = 9 at 1°C; 117.4 ± 13.4 kN m⁻², n = 10 at 6°C; and 188.7 ± 17.7 kN m⁻², n = 5 at 11°C (mean ± SE)) than Ranatunga's data. Were our tension data used, the 2.8-fold increase in stiffness would not change because the sigmoidal form of the temperatures dependence of tension is the same, but the absolute stiffnesses at zero and maximum tension would both be 2.4-fold greater. In the Discussion we relate these values, through a model, to the stiffness of strongly attached cross-bridges that are in the preforce generating state at the zero tension limit, to the stiffness of strongly attached cross-bridges in the force generating state at the limit of peak tension.

FIGURE 6.

Linear dependence of phase1 stiffness on isometric tension. The plot shows that stiffness increases with temperature. Extrapolation to a limit stiffness at zero tension provides a stiffness of 4.1 kN m⁻² nm⁻¹ compared to a limit stiffness at maximum tension (233 kN m⁻²) of 11.7 kN m⁻² nm⁻¹. The temperature dependence of the normalized stiffness of fast rabbit psoas type IIb fibers determined with a −1.5 nm L-jump and the tension versus temperature data obtained from a three-parameter fit to the van't Hoff equation (see Fig. 1 of Davis, 1998) for the fit to the data of Ranatunga, 1994). Tension and stiffness were both determined under identical activating conditions employing the temperature insensitive buffer, glycerol 2-phosphate.

DISCUSSION

The results obtained support a heterogeneous biphasic phase 2 in all three fiber types. The experiments extend and confirm earlier work on fast fibers in which it was proposed that phase 2_fast had the properties of a damped elastic element (viscoelasticity) whereas phase 2_slow had the properties of a de novo tension generating transition in the cross-bridge (Davis and Harrington, 1993b). In interpreting these data we will make use of, and extend Scheme 1, a mechanism primarily based on small-perturbation L-jump, temperature-jump (T-jump), and concentration-jump kinetic data of our own and others.

The relationship of Scheme 1 to other mechanochemical models of muscle contraction

Discussion of the way in which the fast fiber mechanism of Scheme 1 with tension generation by phase 2_slow relates to other mechanisms is very limited. Information on the interrelationships of the various phases generated by different perturbation techniques is presented first, followed by a discussion on how Scheme 1 compares to the main alternative mechanism in which tension generation occurs within step 5 of Scheme 1, is associated with P_i release and phase 3 kinetics.

Phases generated by different perturbation techniques are summarized in Table 2, an update of a previously published version (Davis, 1998). These relationships are generally accepted, but there is debate over the important assignment of the equivalents of phases 2_slow and 3 in certain T-jump (Gutfreund and Ranatunga, 1999; Ranatunga, 1999) and P-jump experiments (Fortune et al., 1991; Vawda et al., 1999). Here, it appears that an apparent monoexponential (single phase) fit to the T and P-jump equivalents of phases 2_slow and 3 resulted in a hybrid phase in which the positive amplitude of the equivalent of phases 2_slow dominates, whereas the equivalent of phase 3 (present as a “shoulder” due to its negative amplitude) contributes phosphate sensitivity, thereby confounding interpretation. The similarity of these T- and P-jump tension transients where the two phases were not resolved, with a set of similar looking T-jump tension transients where these two phases were readily resolved is well illustrated in Fig. 2 of Davis and Rodgers (1995b). Thus, a shoulder in small-perturbation tension transients is a sure indicator of the negative amplitude of a phase 3 like kinetic component. This issue is important, because Scheme 1 requires phase 2_slow to be P_i insensitive in fast fibers.

TABLE 2.

Relationship between exponential phases recorded in small-perturbation kinetic experiments on skinned rabbit psoas muscle fibers contracting under isometric conditions.

Perturbation method	Cross correlation of kinetic phases
L-jump	Phase 2fast	Phase 2slow	Phase 3	Phase 4a	Phase 4b
Sinusoidal length changes	Process D	Process C	Process B	Process A
T-jump	(τ1)	τ2	τnegative		τ3
Pi-jump			kPi
ADP-jump					kADP

An update of correlations proposed by Davis and colleagues (see Davis, 1998) between their L-jump and T-jump phases and phases recorded by others in sinusoidal length change experiments (Zhao and Kawai, 1994), P_i-jump (caged phosphate) experiments (Dantzig et al., 1992) and ADP-jump (caged ADP) experiments (Lu et al., 1993). The phase τ₁ is bracketed because it arises indirectly from fiber expansion and not the T-jump (Davis and Harrington, 1993b). Limited data on pressure-jump (P-jump) kinetic phases precludes their inclusion in the table (Fortune et al., 1991; Vawda et al., 1999), however they appear to be qualitatively similar to T-jump data. Phases 4a and 4b are, respectively the temperature dependent and independent components of phase 4 (Davis and Rodgers, 1995a).

Constraints on space limit the discussion of phase 2_slow to its role of in tension generation and to its location within the Scheme 1 cycle. Experiments that point to a unique role for phase 2_slow as opposed to phase 3 in de novo tension generation are considered first: 1), According to Le Chatelier's principle tension generation in muscle is associated with all phases that mediate (i.e., do not oppose) the return to the postjump equilibrium. Accordingly, the negative amplitudes characteristic of phase 3 (Davis and Rodgers, 1995a; Davis, 1998) and the T-jump τ_negative (Davis and Rodgers, 1995b) cause both to fail the tension generation test. As discussed earlier (Table 2) it is generally agreed that both phases 3 and τ_negative are equivalent to k_Pi, the apparent rate constant determined by the step-release of phosphate from caged precursor. Accordingly, tension generation by a structural change coupled to P_i dissociation from actomyosin cross-bridges seems unlikely (Davis and Rodgers, 1995a); 2), Isometric tension increases when the temperature of muscle fiber is raised. Two laser T-jump phases, termed τ₂ and τ₃, add to give this temperature-dependent rise in isometric tension (Davis and Harrington, 1993b; Davis and Rodgers, 1995a; Ranatunga, 1996; Davis, 1998). Of these, only the rate of τ₂ (phase 2_slow equivalent) is temperature sensitive, rendering it the sole candidate to actively contribute to the tension rise; and 3), Strain sensitivity is a useful probe for tension generating transitions. Characteristically, the rate of a force generating transition slows on stretch as the cycle is reversed and increases on release as the cycle is accelerated. This response was first ascribed to phase 2 in the classical Huxley-Simmons L-jump experiments (Huxley and Simmons, 1971). As has been pointed out (Chaen et al., 1998), this type of strain sensitivity has proven quite distinct from the strain sensitivity of the kinetics of ligand (P_i and ADP) release where stretch and isometric fiber rates are the same. Rate changes are only recorded in releases where both the P_i (Homsher et al., 1997) and ADP release (Chaen et al., 1997) rates increase. These observations indicate that phase 2_slow rather than phase 3 has the requisite hallmarks of a tension generating transition.

Experiments to locate phase 2_slow in the cross-bridge cycle and Scheme 1 are considered next: 1), Redevelopment of tension generation by phase 2 after a large step release of −5 nm half-sarcomere⁻¹ of an isometrically contracting fiber occurs with the kinetics of phase 3 (Lombardi et al., 1992; Piazzesi et al., 1993). One plausible interpretation is that the repriming of the phase 2 (strictly speaking phase 2_slow) is the result of new cross-bridges entering the cross-bridge cycle to replace detached bridges (Davis and Rodgers, 1995b; Cooke, 1997; Huxley and Tideswell, 1997). This interpretation is in accord with Scheme 1, where the repopulation of the phase 2_slow equilibrium (step 7) is mediated by the kinetics of phase 3 and steps 4–6 (Davis and Rodgers, 1995b). It also explains why phase 3 (earlier in the cycle) is consistently slower than phase 2_slow (later in the cycle) and why all caged phosphate tension transients have a lag phase (Dantzig et al., 1992; Millar and Homsher, 1992); 2), It has been shown that P_i has no effect on the rate of phase 2_slow indicating insignificant back-coupling to earlier steps in the cycle (Davis and Rodgers, 1995b). Changing the concentration of P_i in fast fibers simply serves to increase or decrease the flux through to force generation and thus tension; and 3), Step release of ADP from caged precursor fails to induce a change in fiber tension with the kinetics of phase 2_slow by reversing step 8 (Lu et al., 1993; Davis and Rodgers, 1995a). Consequently, tension generation in fast fibers appears as a two state, single-step transition, i.e., step 7 appears isolated from kinetic coupling to structural changes associated with either upstream P_i or downstream ADP binding/release (see Davis, 1998). There is, of course, a continuous forward flux of cross-bridges through the steady-state cycle, each generating tension on passing through step 7. These experiments all suggest that phase 2_slow and tension generation occur after P_i release.

A biphasic phase 2 in all fiber types

The results show that a biphasic phase 2 is common to all three fiber types. This observation confirms and extends earlier L-jump and laser T-jump on fast fibers that led to the proposal that the Huxley-Simmons phase 2 is subdivisible into two distinct and different kinetic phases termed phases 2_fast and 2_slow and established a new mechanochemical model for tension generation (Davis and Harrington, 1993b).

Phase 2_fast is a stiffness related viscoelastic phase that changes little with fiber type

The experimental observations made on different fibers in this paper are in general agreement with data obtained earlier on rabbit fast fibers (Davis and Harrington, 1993b). Temperature dependencies of the rates and amplitudes of phase 2_fast appear to be independent of fiber type. The proposed direct proportionality between the amplitudes of phase 2_fast and phase 1 is investigated in greater detail here and is confirmed, leaving little doubt as to their common origin. It is a remarkably robust interrelationship, since it transcends both fiber type and temperature. These results confirm and extend earlier data on fast rabbit fibers where it was shown that the rate of phase 2_fast is remarkably temperature insensitive (Davis and Harrington, 1991, 1993b).

In earlier work, two possible sources of phase 2_fast viscoelasticity were considered (Davis and Harrington, 1993b): 1), a shortening of a slow responding elastic (viscoelastic) element resident in cross-bridges; or 2), detachment of negatively strained cross-bridges with the kinetics of the phase 2_fast. Here, under conditions that bias the ATPase reaction to the right (low P_i and ADP concentrations), phase 2_fast viscoelasticity appears to arise solely from the extensibility of the cross-bridge proteins and not from detachment of strained cross-bridges. Several observations support this interpretation: 1), It is generally accepted that instantaneous stiffness (phase 1), measured using small length changes (0.1% of the fiber length), arises from fiber elasticity and viscoelasticity and not from cross-bridge yield and detachment. An in depth discussion of assigning fiber stiffness to the mechanical properties of the proteins rather than to cross-bridge yield can be found elsewhere in Bagni et al. (1998). By analogy, the strict proportionality between the amplitudes of phases 1 and 2_fast recorded here implies a common origin for both phases; 2), In all fiber types, the rate of phase 2_fast has a Q₁₀ close to unity. This rather atypical response indicates a low activation energy typical of diffusion-limited reactions (e.g. changes in the length of protein random coil) rather than domain-domain interactions in proteins that are characterized by marked temperature dependence and significantly larger activation energies.

Note that phase 1 can itself be subdivided into additional exponential phases in high speed L-jump and rapid stretch experiments in the μs time domain (Linari et al., 1995; Bagni et al., 1998). These authors conclude that these ultra-fast exponential phases are stiffness related and arise from cross-bridge elasticity. Thus phase 2_fast recorded in the millisecond time domain can be regarded as the first described and slowest member of a spectrum (series) of stiffness-related viscoelastic exponential phases. Its primary effect on muscle mechanics is to halve fiber stiffness after a few milliseconds have elapsed.

A related observation is that fiber tension increases to a much greater extent than does stiffness as temperature is raised (Davis and Harrington, 1993a). This is evident in the decline of the normalized amplitudes of phases 1 and 2_fast with increasing temperature. Consequently, y₀, the size of the L-jump step release required to drop fiber tension to zero and once used as a measure of cross-bridge throw, will also increase with temperature. As made explicit (Galler and Hilber, 1998), we confirm that this relationship shows an approximately linear dependence on temperature and is independent of fiber type.

Phase 2_slow and tension generation become increasingly back coupled to P_i release the slower the fiber type

In fast fibers, the rate of phase 2_slow is typified by a dog's leg or biphasic Arrhenius plot in which the rate first slows somewhat and then increases as temperature is raised (Davis and Harrington, 1993b). All fiber types show this particular behavior. However, unlike phase 2_fast, phase 2_slow decreases in rate as fiber type is switched from IIb to IIa to I at low to moderate temperatures. In order to compare these rates across fiber types, myofilament and cross-bridge compliance (fiber stiffness) must be the same at each temperature. Similar temperature dependencies of the amplitudes of phases 1 and 2_fast, their direct proportionality to one another, and the superposition of the y₀ data from all three fiber types show that this requirement is met.

Kinetic evidence for reversibility and coupling to earlier steps in the cycle in medium and slow, but not in fast fibers comes from both rate and amplitude data. High Q₁₀ values recorded with medium and particularly slow speed fibers indicate increased coupling of step 7 to adjacent temperature sensitive steps (e.g. cross-bridge formation and step 4) in the cross-bridge cycle (for a general discussion, see Gutfreund, 1995). Changing from the fast-fiber mechanism of Scheme 1 to slow-fiber equilibrium coupling links tension generation (phase 2_slow) with its moderate Q₁₀ to the large Q₁₀ values known to be associated with P_i release (phase 3) (Dantzig et al., 1992; Zhao and Kawai, 1994). Thus, the marked increase in apparent rate constant of phase 2_slow in medium speed and slow fibers results from the contributions of adjacent steps to a once largely isolated fast-fiber phase 2_slow. The plateau in the amplitude data, showing a direct proportionality between tension and the amplitude of phase 2_slow, is established at ∼5°C in type IIb fibers, at ∼9°C in type IIa fibers and not at all in type I fibers. The fixed ratio between the amplitude of phase 2_slow and isometric tension that is the hallmark of an isolated two-state single-step tension generating step (Davis and Harrington, 1993b) is thus absent in slow fibers. A testable prediction of the hypothesis is that a change in fiber P_i concentration should alter the rate of phase 2_slow in slow, but not in fast fibers. This is indeed the case (Davis and Rodgers, 1995b; Wang and Kawai, 1997).

Another dramatic and direct manifestation of differences between fast- and slow-fiber cross-bridge cycle reversibility is seen in the different way in which fast and slow fibers respond to an L-jump stretch. In fast fibers, tension transients from small 0.1% step stretches consistently remain well above the prejump isometric tension whereas similar transients in slow fibers consistently dip well below the prejump isometric tension. Accordingly, the amplitude of phase 2_slow in fast fibers is ∼80% of phase 1 after a step stretch, whereas in slow fibers the amplitude of phase 2_slow increases to ∼100% of phase 1 (Davis et al., 2002). Add in the contribution from the amplitude of phase 2_fast and slow-fiber tension dips well below the prejump isometric level. As here, these data come from fibers with unphosphorylated regulatory light chains. Regulatory light chain phosphorylation up regulates P_i release and would therefore reduce cross-bridge cycle reversibility (Davis et al., 2002).

Thus, the window on the mechanism provided by fast-fiber data that enabled us to develop our self-consistent scheme for tension generation, changes with fiber type. The steps of the mechanism appear to remain the same, but the kinetic constants change. Changing from fast, to medium speed, to slow fibers causes phase 2_slow and step 7 of Scheme 1 to become increasingly coupled to P_i release and to other earlier steps in the cross-bridge cycle. The simple fast-fiber kinetics characteristic of phase 2_slow, arising primarily from step 7, changes and takes on the kinetic character of linked adjacent steps in the contractile cycle particularly at higher temperatures in medium speed and slow fibers.

Tension, stiffness, and two-state single-step tension generation

It requires little imagination to appreciate how useful it would be if tension generation in muscle fibers could be approximated by an endothermic two-state transition between largely isolated preforce-generating and force-generating states. At low temperatures the strongly bound preforce-generating state would predominate, and the force-generating state would predominate at high temperatures. Simple rules would determine the ratio of the two states at any selected temperature and various techniques could be applied to separately characterize these two very important structural states.

Several lines of evidence summarized earlier in the discussion of Scheme 1 indicate that tension generation can indeed be approximated by such a two-state transition in isometrically contracting fast fibers. One other related observation is that the temperature dependence of fiber isometric tension can itself be approximated as an apparent two-state transition with a ΔH of 106 ± 22 kJ mol⁻¹ and midpoint of 14.5 ± 1.6°C (Davis, 1998). In Scheme 1, this two-state transition is associated with an isomerization between a strongly attached preforce-generating and a strongly attached force-generating AMD states at step 7. The transition itself does not generate tension, rather it creates the AMD^* intermediate that is of itself capable of tension generation and movement (e.g. Hill, 1989). It is this very fast transition that is tracked in single molecule measurements of head movement and tension generation (e.g. Finer et al., 1994). It remains to be seen whether the similarity of the ΔH for ATP hydrolysis of 89 kJ mol⁻¹ and, more importantly, the 99 kJ mol⁻¹ for the associated structural change in which disorganized (open conformation) heads become ordered (closed conformation) in fibers (Xu et al., 1999, 2003) is in some way related to the similar ΔH we record for tension generation. Note that heating generates structural order, but thermodynamic analysis actually shows an overall increase in entropy (disorder) on heating. However, these authors favor a different mechanism in which the low-temperature disordered state might generate a drag on filament sliding, an effect that might underlie the release of the vanadate-mediated inhibition of V_max above 25°C (Pate et al., 1994).

The increase in fiber stiffness when the AMD state converts to the AMD^* tension-generating state in step 7 is considered next. We found that the cross-bridge/filament stiffness of the AMD state, obtained by back extrapolation to zero tension, was 4.1 kN m⁻² nm⁻¹, while that of the AMD^* state obtained by forward extrapolation to the maximum tension yielded a higher 11.7 kN m⁻² nm⁻¹. These absolute stiffness measurements are proportional to limit maximum tensions reached at high temperatures and have to be adjusted accordingly. For instance, we record tensions per cross-sectional area at three different temperatures some ∼2.4-fold higher than Ranatunga's data used to calculate the above stiffness values. These differences probably arise from the extent of swelling of the fiber lattice caused by the different protocols used to skin fibers. Note that had tension generation been mediated by the creation of a strongly attached state from a precursor weakly attached state of negligible stiffness, the plot would still have been linear, but with an origin at zero. Since fiber stiffness is partitioned between cross-bridges and the thick and thin filaments (Goldman and Huxley, 1994; Huxley et al., 1994; Wakabayashi et al., 1994), actual changes in cross-bridge stiffness caused by tension generation are likely to be higher than the 2.8-fold change recorded here.

X-ray T-jump experiments (Bershitsky et al., 1997; Tsaturyan et al., 1999) provide a structural basis for the increase in fiber stiffness we observe on tension generation. Their experiments show that tension generation occurs as a transition between preforce generating cross-bridges that are nonstereo-specifically attached to actin that convert to force generating cross-bridges that are stereo-specifically attached to actin. We assign these two structural intermediates to endothermic tension generation in step 7 of Scheme 1 where nonstereo-specifically attached cross-bridges of low stiffness (AMD) interconvert to high stiffness stereo-specifically attached and tension generating cross-bridges (AMD^*). Note that this heat-absorbing, tension-generating disorder-order structural change is a thermodynamic order-disorder (entropy driven) tension generating transition associated with an increase in disorder at the atomic level.

Physiological role for cross-bridge cycle reversibility

Phase 2_slow is closely associated with endothermic tension generation in muscle. In earlier work we reasoned that phase 2_slow is uncoupled from both upstream P_i release and downstream ADP release in fast fibers contracting isometrically (Davis and Harrington, 1993b; Davis and Rodgers, 1995a,b). Apparently the irreversibility of step 6 in Scheme 1 is not universal, since we have shown here that phase 2_slow is increasingly back coupled to earlier steps in the cross-bridge cycle the slower the fiber type. This reversibility has the potential to increase the efficiency of slower muscles when stretched under load (eccentric contraction). Good examples include activated muscles that are cyclically stretched during locomotion and cardiac function. During cardiac systole, for example, the papillary muscles, though activated, are stretched by other portions of the contracting heart (see Davis et al., 2001). All would benefit from a reversibility of the cross-bridge cycle to conserve energy. Interestingly, it has recently been shown that ultra-fast muscles have a quite different function-related adaptation of the cross-bridge cycle (Rome et al., 1999). Here, ADP release is accelerated, leading to a decay of the tension generating state, rapid movement, and low tensions. Apparently, function can be fine tuned by either reverse biasing or forward biasing the tension generating step.