Analysis of the Intrinsic Bend in the M13 Origin of Replication by Atomic Force Microscopy

Abstract

Atomic force microscopy (AFM) has been used to image a 471-bp bent DNA restriction fragment derived from the M13 origin of replication in plasmid LITMUS 28, and a 476-bp normal, unbent fragment from plasmid pUC19. The most probable angle of curvature of the 471-bp DNA fragment is 40–50°, in reasonably good agreement with the bend angle determined by transient electric birefringence, 38° ± 7°. The normal 476-bp DNA fragment exhibited a Gaussian distribution of bend angles centered at 0°, indicating that this fragment does not contain an intrinsic bend. The persistence length, P, was estimated to be 60 ± 8 and 62 ± 8 nm for the 471- and 476-bp fragments, respectively, from the observed mean-square end-to-end distances in the AFM images. Since the P-values of the normal and bent fragments are close to each other, the overall flexibility of DNA fragments of this size is only marginally affected by the presence of a stable bend. The close agreement of AFM and transient electric birefringence results validates the suitability of both methods for characterizing DNA bending and flexibility.

INTRODUCTION

DNA bending has been the subject of many experimental and theoretical studies (Olson and Zhurkin, 1996; McGill and Fisher, 1998; Bloomfield et al., 1999). It has been recognized widely that intrinsic bends existing in particular DNA sequences facilitate recognition and binding by specific proteins that are important for DNA transcription, replication, recombination, packaging, and repair processes (Koepsel and Khan, 1986; Werner et al., 1996; Perez-Martin and de Lorenzo, 1997; Bloomfield et al., 1999).

DNA replication is a coordinated and highly regulated process that requires the assembly of various nucleoprotein complexes (Bell, 2002). The key factor responsible for the assembly of the replication machinery is an initiator protein that recognizes a specific DNA sequence within the replication origin(s). In the filamentous coliphages (f1, M13, and fd), binding of 2–4 copies of the initiator protein gpII to the replication origin leads to bending of the helix axis, followed by strand separation and nicking of the plus strand if Mg²⁺ ions are present (Higashitani et al., 1994). Electron microscopy has shown that binding of gpII to the f1 origin causes the helix axis to bend by 90–160°, depending on the number of gpII molecules bound; in the absence of the initiator protein, the DNA appears to be relatively straight (Higashitani et al., 1994).

As shown in Fig. 1, the M13 origin of replication is a noncoding intergenic region ∼570 basepairs in length, containing several regulatory genes (Zagursky and Berman, 1984; Evans et al., 1995). DNA replication is activated by coinfection with a helper phage to generate a single-stranded DNA (van Wezenbeek et al., 1980).

FIGURE 1.

The noncoding intergenic M13 origin of replication, which is found in the plasmid LITMUS 28 from 1043 to 1545 bp (between the HpaI and HincII cut sites). Highlighted are the ribosome binding site at 1043–1056 bp, the Pribnow box (−10) and −35 hexamer, shown as boxes ∼8 bp and 35 bp from the gpII mRNA start site at 1077 bp, the start site for replication of complementary (minus) strand DNA synthesis ((−) ori RNA) at 1265 bp and the viral (plus) strand initiation site ((+) ori DNA) at 1291 bp, which are indicated by arrows, and the gpII nick site at 1266 bp. The sequence between 925 and 1042 bp belongs to the ampicillin resistance gene. The 471-bp fragment used in this study was obtained by using the restriction enzymes AhdI/BanII to digest the plasmid at 931 and 1402 bp.

Previous work in this laboratory (Strutz and Stellwagen, 1996; Lu et al., 2003) has indicated that a significant bend is located at ∼1153 bp in LITMUS 28, within the M13 origin of replication that has been cloned into this plasmid (Evans et al., 1995). Restriction fragments derived from this region migrate anomalously slowly in polyacrylamide gels, and an intrinsic bend of 30–70° can be estimated from the relative mobilities using an approximate equation given by Thompson and Landy (1988). Recently, the bend angle was determined more quantitatively, using transient electric birefringence (TEB) measurements (Lu et al., 2003). The bend angle in the M13 origin of replication was found to be 38° ± 7°, very similar to the bend of 33° observed in the λ-DNA replication origin by ligase-catalyzed cyclization measurements (Zahn and Blattner, 1987).

The conformation of the DNA molecule in solution is fluctuating constantly due to thermal perturbations. Unlike normal unbent DNA molecules, a DNA molecule containing a stable, sequence-dependent bend tends to adopt a preferred conformation (Crothers et al., 1990). Bent or curved DNA molecules are often identified by their anomalously slow electrophoretic mobilities in polyacrylamide gels (Wu and Crothers, 1984; Harrington, 1993; Strutz and Stellwagen, 1996); the bends can be characterized more quantitatively by TEB measurements (Hagerman, 1984; Levene et al., 1986; Lu et al., 2003). Many other techniques, such as x-ray crystallography (Dickerson and Chiu, 1997), electron microscopy (Bednar et al., 1995), and atomic force microscopy (AFM) (Lyubchenko et al., 1993; Hansma et al., 1994, 1996; Rivetti et al., 1998; Seong et al., 2002), have also been used to visualize DNA bends. AFM is particularly useful because it provides information on both the shapes of individual DNA molecules and the population density of molecules with each shape (Hansma et al., 1994; Seong et al., 2002).

A wormlike chain (WLC) model is often used to describe the conformation of DNA molecules in solution (Lu et al., 2002). The stiffness of the chain is usually described by its persistence length, P, or mean-square end-to-end distance, 〈R²〉. A normal, unbent DNA molecule will have a larger value of P or 〈R²〉 than an intrinsically bent one (Hansma et al., 1994). In TEB measurements, the rotational relaxation times (τ), which are approximately proportional to the third power of macromolecular length (Fredericq and Houssier, 1973; Hagerman, 1990; Lu et al., 2002), are measured. The rotational relaxation times are sensitive to DNA conformation because DNA molecules that are stably bent or curved have shorter end-to-end distances than unbent DNA fragments containing the same number of basepairs, and therefore exhibit shorter τ-values. Persistence lengths can be calculated for normal, unbent DNA molecules from the τ-values, if a specific WLC model is assumed (Lu et al., 2002, 2003). However, WLC models cannot be used to calculate the persistence length of bent DNA fragments because the models assume that the fragment has a single average conformation with a constant average flexibility. On the other hand, AFM makes it possible to directly image the conformations of DNA molecules deposited from a buffer solution onto a mica substrate. The images can then be used to analyze the statistical parameters of bent and unbent DNA molecules.

In this study, AFM was used to analyze the bend in the M13 origin of replication, which has been incorporated in LITMUS 28, a small multipurpose cloning/in vitro transcription phagemid vector (Evans et al., 1995). A 471-bp fragment with the bend region centrally located (Lu et al., 2003) was used as the bent DNA fragment for the AFM experiments, whereas a 476-bp fragment derived from a bend-free region of plasmid pUC19 (Strutz and Stellwagen, 1996) was used as the unbent normal control. Transient electric birefringence experiments (Lu et al., 2003) have shown that the 471-bp fragment contains an intrinsic bend of 38° ± 7° at its center, and that the control 476-bp fragment contains no intrinsic bend and has a persistence length close to that of normal, unbent DNA fragments. The statistical parameters calculated for the 471- and 476-bp fragments from the AFM analysis are in reasonable agreement with the results obtained by TEB measurements, thus validating the use of both methods to characterize DNA bending and flexibility.

MATERIALS AND METHODS

DNA restriction fragments

Two restriction fragments were used in this study: the 471-bp AhdI/BanII fragment derived from plasmid LITMUS 28, and the 476-bp TaqI fragment derived from plasmid pUC19, as shown in Table 1. The plasmids were purchased from New England Biolabs (Beverly, MA). Subcloning efficiency DH5α competent cells from Invitrogen (Carlsbad, CA) were transformed with the plasmids via the heat shock method and cultured using procedures described previously (Stellwagen, 1981; Lu et al., 2002). The plasmids were digested with AhdI and BanII (LITMUS 28) or TaqI (pUC19) for 90–180 min to generate the desired restriction fragments. The enzymes were denatured by heating the solutions at 65°C for 15 min.

TABLE 1.

DNA restriction fragments

Length (bp)	Source	Enzyme	Enzyme coordinates	% A + T	Bend position*
471	LITMUS 28	AhdI, BanII	931–1402 bp	60.3	1153 ± 1 bp
476	pUC19	TaqI	430–906 bp	46.0	Unbent

^*Lu et al. (2003).

The desired fragments were then isolated by electrophoresis in 1% agarose gels cast and run in TAE buffer (40 mM Tris/1 mM EDTA with pH 8.0 adjusted by adding glacial acetic acid) (Sambrook et al., 1987). The desired bands were excised from the gel, the agarose was dissolved using a chaotropic salt (QIAquick gel extraction kit, Qiagen, Valencia, CA), and the DNA was concentrated and desalted by adsorption on small DEAE columns, as described previously (Stellwagen, 1981). The restriction fragments were eluted from the columns, ethanol precipitated, redissolved in buffer F (1 mM Tris/0.1 mM MgCl₂, pH 8.0) at a concentration of ∼14 μg/mL and stored at −20°C until needed. All buffers were prepared using deionized water from the Barnstead Nanopure II Water System (GenTech Scientific, Arcade, NY).

AFM analysis

DNA adsorption on mica

DNA fragments in buffer F were diluted to a concentration of 1–2 ng/μl in Hepes-Mg buffer (20 mM Hepes, 5 mM MgCl₂, pH 7.6) (Lyubchenko et al., 1993; Hansma et al., 1994, 1996). An aliquot of 5 μl was deposited onto freshly cleaved mica (Pelco International, Redding, CA) and incubated for 3 min, rinsed ∼30 s with Barnstead Nanopure II deionized water, blown dry with compressed nitrogen, and then further dried in a desiccator for several hours before imaging in AFM.

AFM imaging

AFM imaging was carried out with the Nanoscope III system with multimode AFM (Digital Instruments, Santa Barbara, CA), used in the tapping mode. Standard 125-μm-long silicon cantilevers, with their reflective sides coated with aluminum, were purchased from MikroMasch (Portland, OR). The cantilevers had tips of radius 10 nm, height 15–20 mm, and resonant frequencies ranging from 265 to 400 kHz. Samples were imaged in air at a scan rate of 3 Hz at room temperature (23° ± 1°C), using the Nanoscope Software (version 4.42r8) from Digital Instruments. The 512 × 512 pixel images were collected with a scan size of 1 × 1 μm.

Image processing and statistical histograms

A flattening process was carried out for the images by using the functional commands provided in the Nanoscope Software, subtracting from each line a least-squares polynomial to remove the background slope in the images. The DNA molecules were randomly chosen for statistical analysis. The end-to-end distance was defined as the distance from one end of the molecule to the other. The bend angle was defined as the angle formed between lines tangent to the two ends of the individual molecules. The measured end-to-end distances and the bend angles were binned in 10% intervals, and graphed as histograms (Bednar et al., 1995). The end-to-end distances were converted to the percent of the measured DNA contour length.

Persistence lengths

To calculate the apparent persistence length, we used the equations derived by Rivetti et al. (1998) for the mean-square end-to-end distance, 〈R²〉:

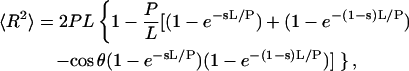(1)

where L is the contour length of the chain, P its persistence length, θ the bend angle, and s the fractional distance from the bend center to one end of the molecule.

For an unbent DNA fragment (θ = 0 and s = 0), Eq. 1 reduces to:

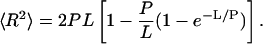(2)

Electrophoresis and TEB measurements

Gel mobility

The electrophoretic mobilities of the 471- and 476-bp fragments were measured in polyacrylamide gels containing 6.9% total acrylamide and 3% bis cross-linker, cast and run in TAE-Mg buffer (40 mM Tris/1 mM EDTA/39.2 mM MgCl₂ adjusted to pH 8.0 with glacial acetic acid), using the 50-bp ladder of Invitrogen as a mobility marker. The gels were run at room temperature ∼23°C, using an electric field strength of 3.33 V/cm. The methods used for the preparation and running of the polyacrylamide gels have been described previously (Strutz and Stellwagen, 1996; Lu et al., 2002).

TEB τ-values

The TEB measurement has been described previously (Lu et al., 2002, 2003). A pulse duration of 8 μs and an electric field strength of 5 kV/cm were used for the experiments. DNA samples with a concentration of 14 μg/mL were pulsed at 20.0 ± 0.1°C for 15 times in the single shot mode, and the field-free decay of each TEB signal was analyzed by fitting the decay curve to the sum of two exponentials, using a nonlinear least-squares fitting program (CurveFit) adapted from the program designed by Bevington (1969). The slower relaxation time (τ-value) was taken to be characteristic of the end-over-end rotation of the DNA molecules. The wormlike chain model of Hagerman-Zimm/Newman (Hagerman and Zimm, 1981; Newman et al., 1977) was used to calculate the persistence length of the normal, unbent 476-bp restriction fragment from the τ-values as described previously (Lu et al., 2002). The bend angle (θ) of the 471-bp fragment was determined from the ratio of the τ-value of this fragment to the τ-value expected for an unbent fragment of the same molecular weight (Vacano and Hagerman, 1997; Lu et al., 2003).

RESULTS

Fig. 2 a illustrates that the 471-bp DNA restriction fragment obtained from the M13 origin of replication in LITMUS 28 migrates anomalously slowly in polyacrylamide gels, suggesting that it is bent or curved. The 471-bp fragment also exhibits terminal birefringence relaxation times that are significantly smaller than those of the 476-bp normal fragment, or for a hypothetical normal fragment containing 471 basepairs, as shown in Fig. 2 b. For clarity, only the fitted curves are shown for the 476-bp fragment (solid line) and the normal, unbent 471-bp fragment (dashed-dot line).

FIGURE 2.

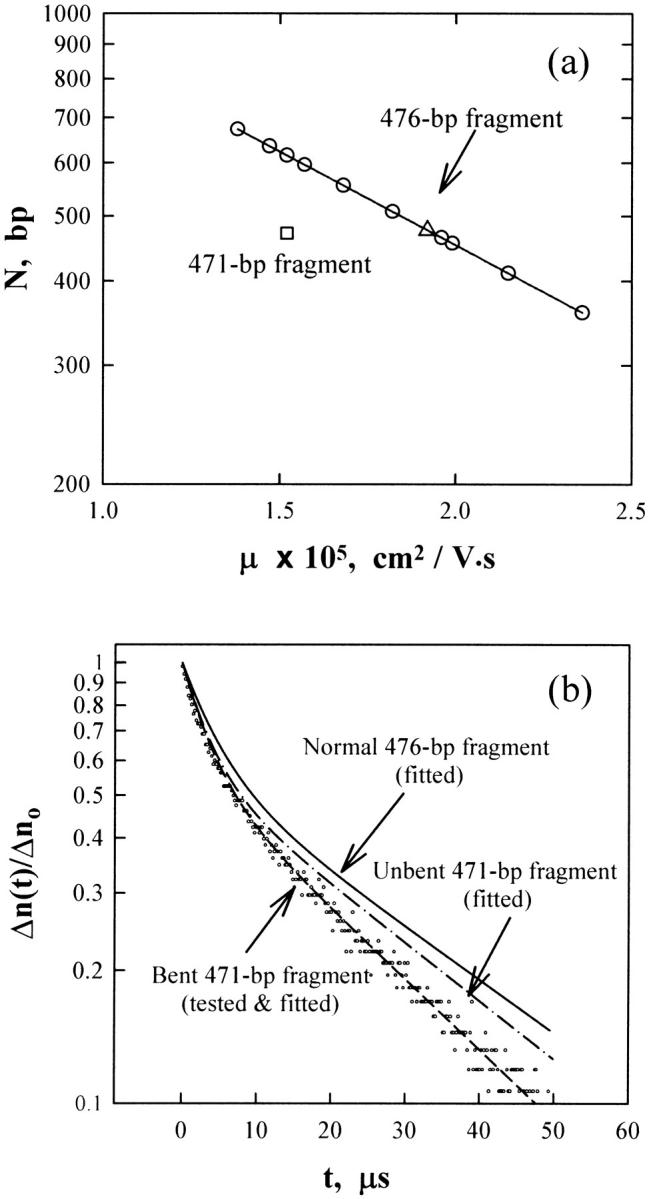
(a) The logarithm of DNA molecular weight, N, in basepairs, as a function of the absolute electrophoretic mobility, μ, observed for the 471-bp fragment (□) and the 476-bp fragment (Δ) in a 6.9% T, 3% C polyacrylamide gel cast and run in 40 mM Tris/1 mM EDTA/39.2 mM MgCl₂, pH 8.0 at 23°C using E = 3.33 V/cm. The solid line and circles correspond to the mobilities observed for a standard 50-bp ladder run in the same gel. (b) Semilogarithmic plot of the normalized decay of the birefringence as a function of time. The circles correspond to the measured data for the 471-bp fragment in the buffer (1 mM Tris/0.1 mM EDTA, pH 8.0) at 20°C. The dashed line corresponds to a two-exponential fit of the data points. Only the fitted curve is shown for the 476-bp fragment (solid line) and a normal, unbent 471-bp fragment (dashed-dot line).

The bent 471-bp fragment has a higher %A + T content (60.3%) than the normal 476-bp fragment (46.0%) and contains five A_n- or T_n-tracts (n ≥ 5), two of which occur in phase with the helix repeat and flank the observed bend center (Lu et al., 2003). The normal 476-bp fragment, which was obtained from a bend-free region in pUC19 (Strutz and Stellwagen, 1996), contains three unphased A₅- or T₅-tracts located close to one end. Gel electrophoresis studies have shown that phased A-tracts, runs of 5–6 adenine residues in a row separated by 10–11 bp (∼1 helical turn) cause significant bending of the DNA helix axis, whereas out-of-phase A-tracts do not (Koo et al., 1986). The results observed for the 471- and 476-bp fragments are consistent with these sequence patterns.

Because DNA molecules and the mica substrate are both negatively charged, divalent cations such as magnesium or nickel are often used to form a bridge between the two (Lyubchenko et al., 1993; Hansma et al., 1994). In the present study, a Hepes-Mg buffer was used for this purpose. Fig. 3 shows typical AFM images obtained for the 471- and 476-bp fragments. The occasional large white patches are due to buffer components. A high-pressure water rinse could have been used to remove these patches (Hansma et al., 1994); however, a high pressure rinse was not used because it caused a significant decrease in the number of DNA molecules bound to the mica. Some of the DNA molecules exhibit variable intensities along their contour lengths, presumably because the DNA molecules had a Gaussian distribution of conformations while in solution. Previous studies (Rivetti et al., 1998) have shown that DNA molecules deposited onto freshly cleaved mica equilibrate on the surface as if the surface were an ideal two-dimensional solution. The bright spots along the DNA contours are not due to protein impurities bound to the DNA, because the samples were isolated by agarose gel electrophoresis and purified by DEAE column chromatography, which would have removed such impurities.

FIGURE 3.

AFM images of DNA molecules in air in mica. Left, the 476-bp fragment; right, the 471-bp fragment. AFM was operated in tapping mode with a scan scale of 1 × 1 μm.

The average measured contour lengths were 152.7 and 157.0 nm for the 471- and 476-bp fragments, respectively. The rise per basepair in the normal 476-bp fragment, which was calculated by dividing the average measured contour length by the number of the basepairs of the fragment, was found to be 0.329 nm, very close to the value of 0.34 nm expected for canonical B-form DNA, but somewhat larger than the value of 0.307 nm obtained by Rivetti et al. (1998) for similar sized DNA fragments using AFM. Histograms of the frequency of occurrence of the end-to-end distances observed for the two DNA fragments, 〈R²〉, expressed as the percentage of the average measured contour length, 〈R²〉/L, %, are shown in Fig. 4. The most probable fractional extension of the 476-bp fragment is 75%, with the mean value ∼70% (Fig. 4 a). The most probable fractional extension of the 471-bp fragment is 65%, with the mean value ∼62% (Fig. 4 b). Hence, the 476-bp DNA fragments are more extended than the 471-bp fragments, as expected from the gel electrophoresis and TEB measurements (Lu et al., 2002, 2003).

FIGURE 4.

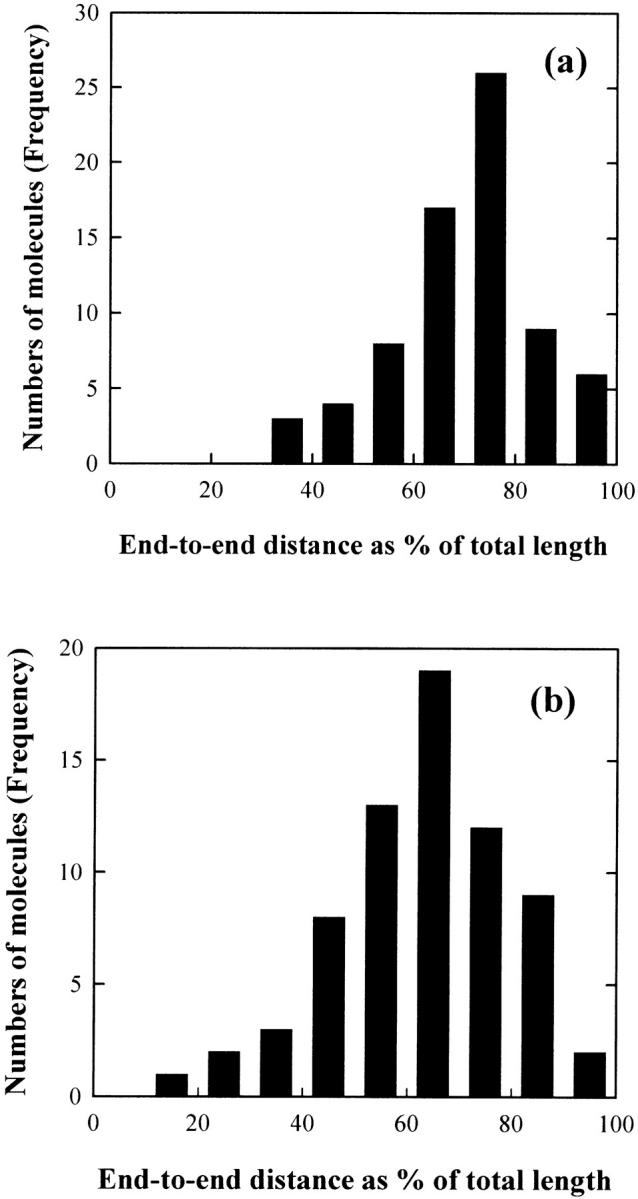
Histograms of the frequency of occurrence of end-to-end distances: (a) for the 476-bp fragment and (b) for the 471-bp fragment. The molecules measured for the analysis were 73 for the 476-bp fragment and 69 for the 471-bp fragment, respectively. The measured mean-square end-to-end distance, 〈R²〉, was converted into the percentage of the average measured contour length of the target DNA.

The degrees of curvature observed in the AFM images of the two DNA fragments yielded a distribution that is quantified in the histograms of Fig. 5. The 476-bp DNA molecules showed a Gaussian distribution centered at 0° (Fig. 5 a), indicating that this fragment does not contain an intrinsic bend. The most probable curvature angle of the 471-bp DNA fragment was observed to be 40°–50°. (Fig. 5 b).

FIGURE 5.

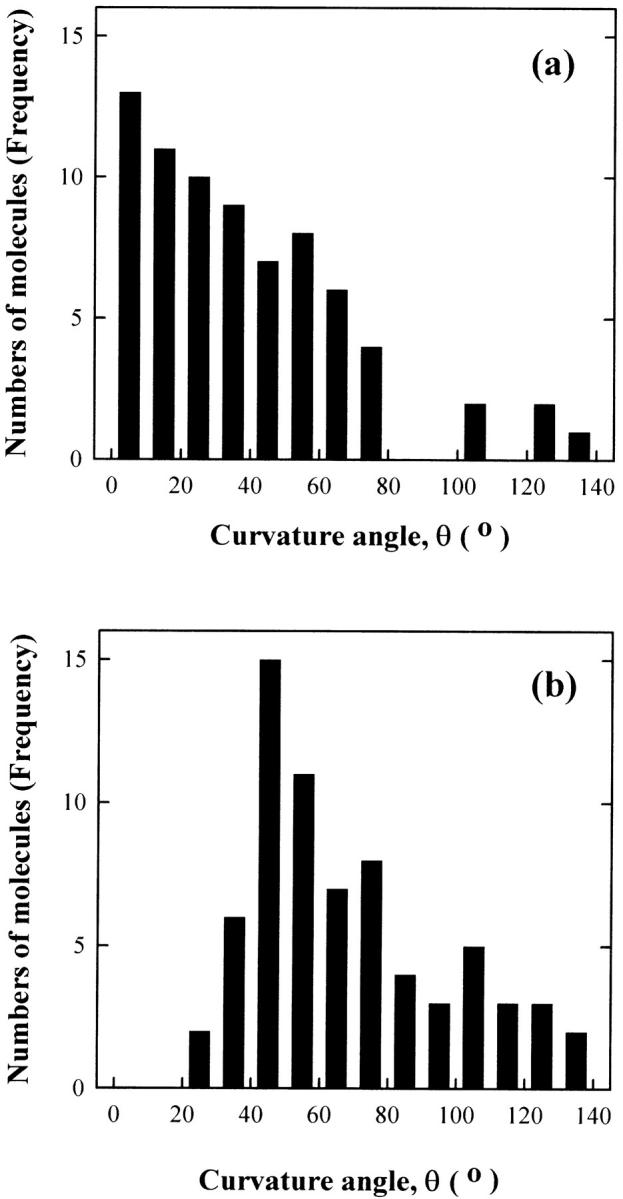
Histograms of the frequency of occurrence of bend angles: (a) for the 476-bp fragment and (b) for the 471-bp fragment. The same numbers of molecules were analyzed as given in Fig. 3.

Equations 1 and 2 were used to calculate the persistence lengths (P-values) of the 471- and 476-bp fragments, respectively, from the measured mean-square end-to-end distances, 〈R²〉, in the AFM images. The estimated persistence lengths of the 471- and 476-bp fragments are 60 ± 8 nm and 62 ± 8 nm, respectively, as shown in Table 2.

TABLE 2.

Estimation of bend angle (θ) and persistence length (P)

	AFM		TEB
	θ(°)	P(nm)	θ(°)	P(nm)
471 bp	40–50	60 ± 7	38 ± 7*	—
476 bp	0	62 ± 8	0	44 ± 2†

^*Average bend angles calculated from the ratios of the TEB τ-values of the bent 471-bp fragment and reference τ-values of normal fragments of the same molecular weight in several low ionic strength buffers (Lu et al., 2003).

^†Global P-value estimated from the TEB τ-values using the Hagerman-Zimm/Newman formalism for a set of normal, unbent fragments in a buffer containing 1 mM Tris/0.1 mM EDTA/0.2 mM MgCl₂ (Lu et al., 2002). The individual P-value calculated for the 476-bp fragment was 48 ± 3 nm, slightly higher than the global value.

DISCUSSION

The AFM technique makes it possible to visualize the conformations of individual DNA molecules, assuming only that the DNA molecules have retained their free solution conformation upon adsorption (Rivetti et al., 1998). A 471-bp DNA fragment containing a centrally located bend, and a 476-bp unbent DNA fragment, have been compared by AFM in this work.

Analysis of the images showed that the 471-bp fragment exhibits stable curvature of the helix backbone with a bend angle of 40°–50°, in reasonably good agreement with the bend angle of 38° ± 7° determined by TEB measurements of the same fragment (Lu et al., 2003). The AFM results thus provide independent evidence that the M13 origin contains a stable bend. The bend angle observed for the M13 origin of replication is similar to the bend of ∼33° observed for the core bend of the O-protein binding site in the λ-origin (Zahn and Blattner, 1987). In the λ-origin, as in the M13 origin of replication studied here, the bend sites are not located at the binding site of the initiator protein. However, the intrinsic bends may act as recognition signals for the binding of the initiator protein, because intrinsic bends tend to be found at the tips of hairpin loops in supercoiled DNAs (Yang et al., 1995; Laundon and Griffith, 1988). Alternatively, the intrinsic bend near the gpII binding site may facilitate wrapping the DNA around the gpII protein to form the initiation complex.

Persistence lengths were calculated for the 471- and 476-bp fragments from the mean-square end-to-end distance, 〈R²〉, using Eqs. 1 and 2. The values of 60 ± 8 nm and 62 ± 8 nm obtained for the 471- and 476-bp fragments, respectively, are not significantly different from each other, suggesting that the bent and unbent fragments have similar overall flexibilities.

Harvey and co-workers (Trifonov et al., 1987; Schellman and Harvey, 1995) have suggested that the observed persistence length of DNA, P, can be divided into static and dynamic persistence lengths, P_s and P_d in the form:

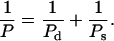(3)

This equation may be used to make an approximate evaluation of the contribution of the intrinsic bend to the overall persistence length of the 471-bp fragment. We assume that the 476-bp fragment contains no static bend, but is flexible because of thermal fluctuations that can be characterized by the dynamic persistence length, P_d. The 471-bp fragment has a static bend, which will contribute to the overall persistence length, along with the dynamic flexibility due to thermal fluctuations. Then we get:

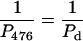(4)

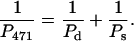(5)

Assuming that P_d is the same for the 471- and 476-bp fragments,

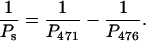(6)

Because the apparent persistence lengths calculated from the AFM images (Table 2) are P₄₇₆ = 62 nm and P₄₇₁ = 60 nm, P_s = 1860 nm. Hence, the bend in the 471-bp fragment makes a very limited contribution (smaller than 4%) to the overall persistence length. The results are consistent with those of Vologodskaia and Vologodskii (2002), who found that the contribution of an intrinsic bend to the overall persistence length of a 200-bp restriction fragment was at least 20 times smaller than that of the dynamic persistence length due to thermal fluctuations. The combined results indicate that the overall flexibility of DNA fragments containing 200–∼500 bp is only marginally affected by the presence of a stable bend. However, the contribution of small sequence-dependent local bends (e.g., in each basepair step) to thermal fluctuations of the helix axis (dynamic persistence length) may be substantial (Trifonov et al., 1987; Schellman and Harvey, 1995).

The persistence lengths obtained for the 471- and 476-bp fragments by AFM (60–62 nm) are ∼20–30% larger than obtained by TEB (44 nm) in a buffer containing 1 mM Tris/0.1 mM EDTA, pH 8.0, plus 0.2 mM MgCl₂. The imaging methodology could account for this difference, because the apparent persistence length of a chain equilibrated in two dimensions is larger than that of the same chain in free solution (three dimensions (Rivetti et al., 1998)). In addition, the buffer/salt solutions used in AFM and TEB studies were different; the persistence length is known to depend on buffer composition (Lu et al., 2002).

In summary, the AFM analysis of DNA conformation at the molecular level provides robust support for the validity of the bend angles and persistence lengths calculated from transient electric birefringence measurements of DNA molecules in solution.