Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jul;85(1):581–588. doi: 10.1016/S0006-3495(03)74502-0

Diffusion of Nerve Growth Factor in Rat Striatum as Determined by Multiphoton Microscopy

Mark Stroh *, Warren R Zipfel †, Rebecca M Williams †, Watt W Webb †, W Mark Saltzman *
PMCID: PMC1303113  PMID: 12829512

Abstract

Neurotrophins such as nerve growth factor (NGF) may be useful for treating diseases in the central nervous system; our ability to harness the potential therapeutic benefit of NGF is directly related to our understanding of the fate of exogenously supplied factors in brain tissue. We utilized multiphoton microscopy to quantify the dynamic behavior of NGF in coronal, 400-μm thick, fresh rat brain tissue slices. We administered a solution containing bioactive rhodamine nerve growth factor conjugate via pressure injection and monitored the dispersion in the striatal region of the coronal slices. Multiphoton microscopy facilitated repeated imaging deep (∼200 μm) into tissue slices with minimal photodamage of tissue and photobleaching of label. The pressure injection paradigm approximated diffusion from a point source, and we therefore used the corresponding solution to the diffusion equation to estimate an apparent diffusion coefficient in brain tissue (Db(34°C)) of 2.75 ± 0.24 × 10−7 cm2/s (average ± SE). In contrast, we determined a corresponding free diffusion coefficient in buffered solution (Df(34°C)) of 12.6 ± 0.9 × 10−7 cm2/s using multiphoton fluorescence photobleaching recovery. The tortuosity, defined as the square root of the ratio of Df to Db, was 2.14 and moderate in magnitude.

INTRODUCTION

Nerve growth factor (NGF) is a 130-kD protein homodimer with each monomer comprised of three subunits, α, β, and γ (Thoenen and Barde, 1980). The 26-kD β-subunit is responsible for the bioactivity of NGF. Exogenous supply of NGF to the brains of animals clearly demonstrates the capability of the neurotrophin to rescue septal cholinergic cells from both injury-induced (Gage et al., 1988) and spontaneous, age-related (Fischer et al., 1987) degeneration, giving rise to promise that NGF might be a potential treatment for Alzheimer's disease. Because NGF does not appreciably cross the blood-brain barrier and plasma half-lives are short, proposed treatment strategies involve direct administration of NGF to diseased brain tissue in Alzheimer's patients (Tuszynski and Kordower, 1999). As with normal cells, which secrete growth factors to convey information, so too in diseased tissue we utilize a source of diffusible factor to convey a trophic signal to degenerating neurons. A clear understanding of the transport phenomena involved is of paramount importance to ensure that NGF rescues diseased cells from degeneration while interfering minimally with normal tissue.

Much of what we know today about NGF transport in tissue is the result of a commonly used methodology: NGF is administered to the brain of an animal, the animal is sacrificed, the brain is sectioned, and the protein is detected generally through autoradiography or immunohistochemistry (Krewson et al., 1995; Morse et al., 1993; Yan et al., 1994). Although such a procedure is useful to learn end-point information, it is extremely difficult to use this methodology to get information about the dynamic behavior of the molecule in tissue. The distribution at each time point is obtained from an individual animal; the effect of time is confounded by variability between experiments and animals. Furthermore, the distribution at time points well after the initial administration is a result of simultaneous, competing processes that serve to disperse the protein (“transport processes”), and degrade and eliminate (“elimination mechanisms”) it from the tissue (Radomsky et al., 1990). Whether NGF supply is from a controlled-release polymer (Krewson and Saltzman, 1996), an infusion pump (Morse et al., 1993), or cells genetically modified to secrete NGF (Tuszynski et al., 1996), any final distribution determined from longtime, static snapshots is a consequence of both transport and elimination mechanisms. We must be able to account for both accurately to propose rational improvements in formulation design.

We studied the diffusive spread of a bioactive, rhodamine-βNGF conjugate (RNGF) in the striatal region of rat brain tissue slices over the course of 0.5–2.0 min using multiphoton microscopy (MPM). The use of brain tissue slices allowed imaging of the striatum—a uniform, approximately spherical domain deep within the rat brain (Paxinos and Watson, 1986). Two-photon imaging simplified our study; out-of-focus fluorescence did not blur the recorded image, and we could repeatedly image deep (∼200 μm) within the slice with both minimal photodamage to tissue and photobleaching of label. We selected specific timescales for delivery of agent and monitoring of dispersion to facilitate the subsequent analysis. We administered small, rapidly delivered (0.25–1.0 s) volumes of tracer from a micropipette, and monitored the dispersion for 20 s to 2.0 min. The span of time over which we monitored dispersion was much less than any previous estimates of NGF half-life in the brain (30 min (Krewson et al., 1995)); this further simplified the analysis because an elimination mechanism was not needed in the model. We modeled the dispersion of RNGF as diffusion after administration from a point source (“point-source diffusion”), for which the solution is well known (Berg, 1983). By considering a diffusion-only system, we could make statements concerning the relative ease of diffusive RNGF transport.

Cellular membranes and macromolecules of the extracellular space (ECS) act as physical barriers that increase the effective path length for diffusion (Radomsky et al., 1990; Rice and Nicholson, 1991; Sykova, 1997). Therefore, we expect a disparity between the free diffusion coefficient in solution (Df), and the apparent diffusion coefficient in tissue (Db). The ratio of Df to Db is defined as the square of the tortuosity (τ2); tortuosity increases as a molecule experiences greater difficulty in navigating the ECS. Other factors act to further impede diffusive transport in tissue, including molecular shape and size (Pluen et al., 1999; Prokopova-Kubinova et al., 2001), binding (Berk et al., 1997), and charge interactions (Nugent and Jain, 1984). The complexities of transport through the ECS hamper efforts at an accurate, predictive model for τ, necessitating robust, accurate techniques for experimental determination of Db and Df. The well-defined excitation volume characteristic of MPM not only assisted us in our efforts to determine Db, but also facilitated determination of Df via multiphoton fluorescence photobleaching recovery (MPFPR) (Brown et al., 1999; Zipfel and Webb, 2001). Briefly, in this technique the laser intensity was modulated to first photobleach and then monitor the same subvolume of solution containing RNGF. Recovery of the signal was due to the diffusion of unbleached molecules back into the previously bleached volume. We obtained Df by fitting the recovery data to the model described in Brown et al. (1999).

MATERIALS AND METHODS

Our study was comprised of both a trial to validate our new method and an effort to estimate transport constants for RNGF. We selected a FITC-conjugated 70 kD dextran (Molecular Probes, Eugene, OR) for our validation trial because there are literature estimates of Db for 70 kD dextran administered to the cortex of rats (Nicholson and Tao, 1993). Unless otherwise indicated, we utilized the Matlab (Mathworks, Natick, MA) environment for fitting models to data, and JMP (SAS Institute, Cary, NC) for all hypothesis testing and cluster analysis. We employed Matlab's “fmins” routine to minimize sum of squared errors between data and given nonlinear models, and the “regress” algorithm for linear regression analysis.

RNGF conjugate

A bioactive RNGF conjugate was prepared based upon a procedure by Levi (Levi et al., 1980). Murine βNGF (Harlan, Indianapolis, IN) at a concentration of 2 mg/ml in phosphate buffered saline (pH 7.2 PBS; 0.1 M sodium phosphate, 0.15 M sodium chloride) was reacted with cystamine (Sigma, St. Louis, MO) and 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide, hydrochloride (EDAC; Molecular Probes) at 10 and 50 times molar excess over NGF, respectively, for 2 h at room temperature. After an overnight dialysis against PBS at 4°C, 1.43 mM β-mercaptoethanol (Sigma) was added at 10 times molar excess over NGF. Tetramethylrhodamine-5-iodoacetamide dihydroiodide (5-TMRIA; Molecular Probes) was added at 10 times molar excess over the concentration of NGF and the mixture was reacted for 2 h at room temperature with continual shaking. The mixture was dialyzed using a 10-kD molecular weight cutoff dialysis cassette (Slide-A-Lyzer; Pierce, Rockford, IL) at 4°C against several complete changes of pH 7.4 PBS to ensure removal of unreacted 5-TMRIA. Any precipitates that were formed were removed by centrifugation at 14,000 × g for a period of 10 min.

The RNGF was subjected to several biochemical and biological assays. The concentration was determined using a total protein assay (Micro BCA; Pierce), and the product purity was verified by SDS-PAGE with silver staining. The RNGF was assayed for biological activity using the PC12 rat pheochromocytoma cell line based on the neurite regeneration assay of Greene (Greene et al., 1996). The PC12 cells were incubated with medium (84% RPMI 1640, 10% heat-inactivated horse serum, 5% fetal bovine serum, 1% penicillin/streptomycin; all from Invitrogen, Carlsbad, CA) supplemented with 50 ng/ml NGF. At the end of one week, neurite-bearing cells were harvested and washed repeatedly to facilitate removal of both neurites and NGF. The cells were transferred to collagen-coated six-well plates, and incubated with RNGF and NGF each at concentrations of 10, 100, and 500 ng/ml; three wells containing NGF-free medium were included for control. Cells were imaged using an inverted phase contrast microscope (Diaphot; Nikon, Tokyo, Japan) and the number of neurites with length of two cell bodies or greater were noted for each condition.

Slice preparation

The following procedure for rat brain harvest was approved by the Cornell University Animal Care and Use Committee. Male 35–40-day-old Fisher rats (Charles River, Wilmington, MA) were deeply anesthetized using a 3.5 ml/kg intraperitoneal injection of a ketamine/xylazine solution, and decapitated. Brains were quickly and carefully removed and chilled in ice-cold artificial cerebral spinal fluid (ACSF) with the following composition (in mM) (Clancy et al., 2001): NaCl, 125; KCl, 3.5; MgCl2, 1.3; CaCl2, 2.5; NaHCO3, 26; and glucose, 10; saturated with 95/5 O2/CO2 pH 7.4. The brains were blocked and glued to the chuck of an oscillating microtome (752M Vibroslice, Campden Instruments, Ltd., UK) using cyanoacrylate glue, and submerged in ice-cold ACSF that was continuously gassed with 95/5 O2/CO2. Four-hundred-micron thick coronal slices were obtained, and slices of interest were maintained in a room-temperature holding chamber. The custom-made chamber contained ACSF gassed with 95/5 O2/CO2 passed through a glass frit.

Pressure injection

After a 1-h period for slice equilibration, we transferred a slice of interest to a custom-built chamber that rested upon the stage of the multiphoton microscope. The chamber was comprised of a bath, a heating system, and a mesh for holding the slices. The bath included a 10-cm glass Petri dish to which tubing was affixed with cyanoacrylate glue. Continuously gassed ACSF was circulated through the chamber at a rate of ∼1 ml/min with a peristaltic pump. A heating system, comprised of a thermocouple, bench-top controller (both from Omega Engineering, Stamford, CT), and bath heater, maintained the bath at 34°C. The bath heater was comprised of a cartridge heater (Omega Engineering) placed in a custom-built, submersible heating fin. Slices were suspended in the chamber between two meshes comprised of nylon stockings. For the dextran validation trial, we used an external rather than a submersible heater, and the bottom supporting mesh was not used.

Injections were performed using prefabricated microcapillaries (Femtotips; Brinkmann Instruments, Westbury, NY) with a 0.5-μm inner diameter and 1.0-μm outer diameter. Capillaries were loaded with test compound and attached to the headstage of an Eppendorf Model 5242 pressure injector system. Capillary tubes in the headstage were positioned using a Burleigh micromanipulator (model PCS-5000) mounted on the microscope stage. The mass concentrations investigated were 1250 and 500 μg/ml in PBS for dextran and RNGF, respectively. The microcapillary tip was lowered ∼200 μm into the slice at a desired location within the striatum. We focused upon the tip using MPM with a 10×, 0.3 numerical aperture (NA) water-immersion and a 4×, 0.28 NA air-immersion lens for the RNGF and dextran studies, respectively. The excitation wavelength was 850 nm for RNGF and 800 nm for FITC-dextran. The multiphoton microscope was comprised of a Tsunami Ti:S laser pumped by a 10 W Millennia Nd:YVO4 laser (Spectra Physics, Mountain View, CA), a modified MRC-600 scanbox (Bio-Rad Microscience, Hemel Hempstead, UK), a Hamamatsu (Bridgewater, NJ) GaAsP H7421-40 photomultiplier tube (PMT), and an upright, fixed-stage AX-70 Olympus microscope; additional details are available elsewhere (Kloppenburg et al., 2000). The laser intensity was adjusted using a ConOptics 350-80 electro-optic modulator to ensure that the intensity data were within the linear range of the PMT. The modulator was also used to blank the laser during scanner fly-back to further reduce photobleaching during image acquisition. A scan was performed immediately after inserting the capillary to verify that no tracer entered the tissue before injection. The pressure injector system was preprogrammed to allow a pressure pulse delivery lasting 0.25–1.0 s, and a volume of test compound was administered to the slice. We collected from 20 to 60 images after pulse administration at time intervals of 1–2 s depending upon the experiment.

For the dextran validation and the initial NGF experiments, the injector capillary was left in the tissue for the duration of the recordings. The image of the diffusing molecules was obstructed by the presence of the injector; by removing the capillary, we could more readily analyze the entire area of the diffusing injection. We executed a controlled experiment with RNGF in which the only factor varied was the withdrawal of the injector cannula after NGF administration, and did not note an effect of injector withdrawal upon Db. We withdrew the injector immediately after injection for all subsequent trials, and pooled data from trials with and without injector withdrawal.

MPFPR

The apparatus and procedure used for MPFPR measurements are described in detail elsewhere (Brown et al., 1999; Zipfel and Webb, 2001). Briefly, the RNGF was loaded into deep-well slides and enclosed with number 1.5 coverslips. Although we used 500 μg/ml RNGF for Db determination, 5 μg/ml RNGF (∼190 nM) was used for MPFPR to help conserve conjugated protein. Although this resulted in reduced signal to noise in the MPFPR measurements, preliminary studies indicated no statistically significant difference between Df estimates obtained with 500 μg/ml and 5 μg/ml RNGF. The parked laser was focused within the sample using a 60×, 1.2 NA water-immersion lens. A 10-μs bleaching pulse was immediately followed by acquisition of the fluorescence recovery for 4 ms in 10-μs time bins. Due to the low concentration of RNGF we used a high QE GaAsP PMT and 10,000 photobleach-monitor cycles per experiment, with a slow enough repeat rate (50 Hz) to allow complete recovery of fluorescence signal between cycles.

Analysis

Pressure injection methodology

The rapid delivery of RNGF from a small diameter orifice allowed us to approximate the dispersion as point-source diffusion (Berg, 1983). The governing equation for this process is a function of radius, r, and time, t, as follows:

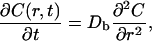graphic file with name M1.gif (1)

where C is the volume-averaged (Nicholson, 1985) concentration of NGF. The solution to Eq. 1 in the point-source approximation is well known and takes the form:

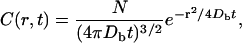graphic file with name M2.gif (2)

where N is the initial number of molecules administered. We used a slight modification of a two-step procedure to estimate Db (Nicholson and Tao, 1993). We executed a three-parameter fit of the intensity data to Eq. 3 for each of the extracted concentration profiles in the time series.

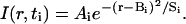graphic file with name M3.gif (3)

where I was the intensity at radial position r and time increment ti, and Ai, Bi, and Si were fit parameters. We included the parameter Bi to estimate the center of the dispersing molecules. By comparison of Eq. 3 with exact solution Eq. 2, Si is given by 4Dbti; for an ideal point source, a regression of Si/4 upon ti gives Db as the slope with zero intercept. In practice, tracer infiltrates the interstitial space during the injection (see Fig. 1 B). Although the initial distribution of injected material deviates from an ideal point source, the dispersing molecules behave as if they were released from a “virtual” point source at some time to before the actual injection (Nicholson and Tao, 1993; Prokopova-Kubinova et al., 2001). This discrepancy results in a negative time intercept in a regression of Si/4 upon ti; to explicitly account for a nonzero intercept, Si takes the form 4Db(ti + to). The entire optimization routine was repeated along each of two additional lines constructed at consecutive 120° intervals from the first line.

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Three centerlines constructed through dispersing sphere of RNGF molecules yield the intensity profiles that were fit to Eq. 3 for all times recorded in the sequence. (B) The data and fit of the intensity profiles are depicted at an initial time (open squares and dashed line, respectively) and at 42 s later (solid circles and solid line, respectively). (C) The calculated values of S/4 were plotted as a function of time for all images in the sequence to extract Db as the slope, indicated as 4.10 × 10−7 cm2/s in this case. The procedure was repeated for each of the three centerlines depicted in A.

MPFPR analysis

Fluorescence recovery data were fit to the single component simple diffusion model from Brown et al. (1999) using lab-written software:

graphic file with name M4.gif (4)

The 1/e2 beam dimensions ωxy and ωz were calculated as described in Zipfel and Webb (2001) and the fitting was carried out over the first eight terms of the summation. Values for the 1/e2 beam dimensions for both the MPFPR and imaging studies described in the previous section are listed in Table 1. We determined Df at 20°C, and corrected all values to 34°C using the Einstein relationship, Df(34°C)/Df(20°C) = [T(34°C)/T(20°C)] × [η(20°C)/η(34°C)], where T is the temperature in Kelvin and η is the viscosity of water. This facilitated direct comparison with Db as these estimates were obtained at 34°C.

TABLE 1.

1/e2 radii (μm) of the two-photon illumination point spread function calculated for wavelengths and objective lenses used

Wavelength (nm) NA ωxy ωz
800 0.28 1.65* 26.7*
850 0.30 0.91 13.2
850 1.2 0.23 0.60
Open in a new tab

Calculations carried out using the integral representation of Richards and Wolf (1959).

*

The 4× 0.28 NA macro lens used in the dextran studies had a 25-mm back aperture and was underfilled (beam diameter was ∼10 mm). Calculation was modified accordingly to account for the degree of underfilling resulting in values that were ∼2 larger than the diffraction limited case.

RESULTS

RNGF conjugate

The RNGF migrated as a single band under SDS-PAGE analysis of ∼13 kD (corresponding to the weight of the monomeric β-subunit). The native and conjugated NGF both stimulated neurite outgrowth at levels as low as 10 ng/ml.

Fit of models to experimental data

Hindered diffusion and Db

Fig. 1 B is a representative fit of Eq. 3 to the extracted intensity data for one of the three lines indicated in Fig. 1 A for both the initial image analyzed and an image recorded later in time. In Fig. 1 B the signal to noise appears low because the data is from a line of single pixels with only ∼10 photons per pixel maximum, and less at the edges of the diffusing spot. The low fluorescence intensity was due to the imaging depth into the tissue (∼200 μm) and the need to be at low excitation intensities to ensure that photobleaching was negligible over the course of the repeated scanning. Although the signal to noise could have been improved by using longer pixel integration times (pixel integration time was ∼6 μs), we were scanning a dispersing sphere of RNGF, and it was important to ensure that changes in the intensity profiles due to diffusion did not occur substantially while collecting each individual image (i.e., time point). The Gaussian distribution of intensity data as a function of position both flattens and spreads in time, as would be expected for point-source diffusion. As the spread of the intensity data increases, so does the estimate of Si returned by the optimization routine. Fig. 1 C is a least-squared regression fit of the estimates of S/4 as a function of t. The slope of the regression fit gives Db directly.

MPFPR and Df

A representative MPFPR trace is shown in Fig. 2 for one of the RNGF photobleaching experiments. The data represent 10,000 photobleaching-recovery cycles. As mentioned in Materials and Methods, we used a low concentration of RNGF (∼190 nM) for these studies to conserve protein, which resulted in reduced signal to noise relative to previous MPFPR work using more concentrated solutions (Brown et al., 1999). Although we show normalized data in Fig. 2, prebleach count rates were less than 100 KHz. For all of our measurements, the recovery was well described by a single coefficient model.

FIGURE 2.

FIGURE 2

Open in a new tab

Typical MPFPR curve for RNGF; fluorescence data were normalized to the average count value before the 10 μs photobleaching pulse at t = 0. Nonlinear fit of the recovery returns a value for Df (20°C) of 8.62 × 10−7 cm2/s. Excitation and bleaching wavelength was 850 nm delivered through a 60×, 1.2 NA water-immersion objective lens. Average power during bleaching pulse and monitoring was ∼10 mW and ∼1 mW, respectively.

Estimation of D

Table 2 gives a summary of the estimates for Db and Df. For Df, we report data from 24 photobleaching experiments. For Db, we include a validation trial with dextran, where we collected data from two rats, with one coronal section per rat and a maximum of three injections per slice. The RNGF study in tissue was more exhaustive and represents data collected from four rats, with up to two sections per animal and five injections per section. In some instances, the injected amount was barely detectable; this was attributed to injector clogging, and these data were omitted from further analysis. In all studies, we generated three replicate estimates of Db for each injection to give a total of 78 and 15 estimates of Db for RNGF and dextran, respectively.

TABLE 2.

Moment and parametric data for D (×107 cm2/s)

Species N Mean Standard deviation Median 75% quartile 25% quartile
*RNGF (free) 24 12.6 4.53 12.1 13.6 9.42
RNGF (brain) 78 2.75 2.13 2.14 3.63 1.08
†Dextran (brain) 15 0.84 0.43 0.63 1.23 0.50
Dextran (brain, literature) 12 0.75 0.16 – – –
Open in a new tab

Because the data are log-normal, we evaluated the logarithm of the individual data in a Tukey-Kramer test and determined all our estimates were significantly different from one another.

*

Df for RNGF was obtained at 20°C, and corrected to 34°C via the Einstein relationship.

†

Results for 70 kD FITC-dextran conjugate reflect measurements in brain tissue only, and are cited for both our study and from a literature source (Nicholson and Tao, 1993) (quartile data were not available from the literature for dextran).

For Db and Df, the mean values are greater than median values for each case, reflecting a slight positive skew in the data. The most likely source of the skew comes from a restriction on D; negative values of D are not physically realizable, and the distribution cannot be symmetric about the mean value (which is close to zero relative to the spread of the data). Accordingly, we compared means using log(D) as the independent variable in the model to account for the log-normal distribution. Results from a Tukey-Kramer Honestly Significant Difference test confirm that all pairs of our estimates are significantly different from one another (α = 0.05). The previously published Db(34°C) estimate for 70 kD dextran in rat cortex, 0.75 × 10−7 cm2/s (Nicholson and Tao, 1993), is lower than our estimate in the striatum, 0.84 × 10−7 cm2/s, although the literature value is within the 95% confidence interval spanning 0.60–1.08 × 10−7 cm2/s. The calculated values for RNGF in brain, 2.75 × 10−7 cm2/s, and in solution, 12.6 × 10−7 cm2/s, reflect the anticipated hindrance to diffusive transport in tissue.

DISCUSSION

From our previous investigations with long-term delivery to whole animals, NGF penetration through brain tissue is spatially restricted (Krewson et al., 1995; Mahoney and Saltzman, 1999). This earlier work provided motivation for this study: development and validation of a new method for estimating diffusion coefficients in brain tissue, and estimation of transport constants for NGF in free solution and in brain tissue. To make efficient use of our RNGF supply, we elected to use an injection, rather than photobleaching procedure to determine Db. In the derivation of Eq. 4, a uniform initial concentration of fluorophore is assumed and therefore large quantities of RNGF would have to be loaded into the tissue to achieve this initial condition. The replicate measurements required to perform statistical testing would further exacerbate the problem. In contrast, the injection paradigm allowed us to obtain multiple estimates of Db with nanoliter quantities of material.

Despite differences in methodology and site of administration, we note very good agreement between our Db estimate for 70 kD dextran and that from the literature. In our case, we studied diffusion in the striatum, whereas previous estimates were obtained with injections to cortical layers III, V, and VI (Nicholson and Tao, 1993). There is a discrepancy between τ estimates reported for these same cortical layers (τ = 1.62–1.65 in 90–120-day-old rats) (Lehmenkuhler et al., 1993) and the striatum (τ = 1.54) (Rice and Nicholson, 1991) with tetramethylammonium diffusion studies. It is reasonable to assume that domain-specific variability may account for some of the difference observed between our measurement and the previous result. Furthermore, we fit Eq. 3 directly to our extracted data, whereas literature estimates require further manipulations. Although there are no general models for prediction of Db, for globular proteins Df may be regressed upon the inverse cubic root of the molecular weight (1/M1/3) (Saltzman et al., 1994). We performed this regression using Df values from the literature (Sober, 1970), and superimposed our result for RNGF upon this plot (Fig. 3). Our estimate lies near the regression line and well within the 95% confidence intervals, lending credibility to our result.

FIGURE 3.

FIGURE 3

Open in a new tab

Various literature estimates (circles) of Df (×107 cm2/s) for globular proteins (Sober, 1970) at 20°C regressed upon M−1/3. Solid and dashed lines indicate regression fit and 95% individual confidence bands, respectively. Our superimposed estimate of Df(20°C) for RNGF (star), lies near the regression fit and well within the confidence intervals, indicating our estimate is within the expected range.

Whereas simple correlations exist that enable us to predict Df with some accuracy, the complexities of diffusion in tissue hamper efforts at a general, predictive model for τ. Nicholson has estimated τ in rat brain cortex for albumins (Tao and Nicholson, 1996), dextrans (Nicholson and Tao, 1993), poly[N-(2-hydroxypropyl)methacrylamide] (PHPMA) polymers and a PHPMA-bovine serum albumin (BSA) conjugate (Prokopova-Kubinova et al., 2001). For low molecular weight dextrans (3 and 10 kDa) and all of the PHPMA fractions considered (spanning from 7.8 to 1057 kDa), τ ranges from 1.46 to 1.70. The albumins (lactalbumin, ovalbumin, and BSA) suffer increased hindrance to diffusion, with τ values ranging from 2.24 to 2.50. The 70 kD dextran (postulated to occupy a spherical shape at this size) and the bulky 176 kD PMMA-BSA conjugate also experience relatively hampered diffusion, with reported τ values of 2.25 and 2.27, respectively. These findings led to the conclusion that diffusion in the ECS of normal brain tissue is dependent upon molecular configuration; linear molecules enjoy relative ease in navigating the ECS relative to more compact spherical or globular molecules. Reports in the literature confirm this hypothesis across several experimental platforms. Fox and Wayland (1979) noted the apparent D for rat serum albumin in the rat mesentery is approximately half that of a dextran with the same hydrodynamic radius. Nugent and Jain (1984) reported a similar disparity in D between BSA and dextrans of comparable size in both normal and tumor tissue. The authors postulated that BSA suffers hampered diffusion not only due to molecular configuration, but also possibly due to like-charge repulsion (negative charges associated with BSA and components of the ECM) and binding to tissue.

We calculated a τ value of 2.14 for RNGF and compared our results with previous estimates in normal rat brain tissue to ascertain the relative ease with which NGF navigated the interstitium. A k-means clustering analysis partitions the data into two groups: the first spans τ = [1.46, 1.70] and includes all PHPMA and low molecular-weight (3 and 10 kD) dextrans, whereas the second spans τ = [2.14, 2.50] and includes RNGF, the albumins, and high molecular weight dextrans (40 and 70 kD) (Fig. 4). The data are partitioned in the manner anticipated from the previous works in that compact molecules collectively experience greater hindrance than their more linear counterparts. Although assigned to the high-τ category, RNGF corresponds to the lowest τ of this group, indicating relatively facile diffusion among its peers. Of the albumins studied, lactalbumin has the Df (and hence hydrodynamic radius) closest to RNGF (11.9 (Tao and Nicholson, 1996) and 12.1 × 10−7 cm2/s, respectively). Despite the similarities in size, τ for RNGF (2.14) is slightly less than that reported for lactalbumin (2.24 (Tao and Nicholson, 1996)). This slightly enhanced diffusion mimics the general trend noted from our 70 kD dextran control study, where we note approximately a 12% enhancement in Db relative to literature values. Like the dextran control, this may be in part due to site-specific variability, in that our τ estimates were obtained in the striatum whereas literature values were measured in the cortex. We did not expect our comparison to be affected by differences in age between the animals investigated in our study and those used in the cited literature; a previous study reported no significant effect of rat age upon τ values obtained in cortex and white matter over a span of 2–120 postnatal days (Lehmenkuhler et al., 1993).

FIGURE 4.

FIGURE 4

Open in a new tab

Results from a k-means clustering analysis partitions τ values into two groups characterized by comparatively high- and low-τ values; our estimate of τ for RNGF is the lowest among the high-τ group, comprised of albumins and high molecular weight dextrans. From this analysis, RNGF experienced only intermediate difficulty in navigating the striatum.

We assumed negligible influence of elimination on the concentration profiles over the time span considered in this experiment (seconds to minutes). For long-duration studies (hours and greater), the final distribution of NGF in rat brain tissue is a result of a competition between diffusion and elimination mechanisms that serve to assist and hamper transport, respectively (Krewson et al., 1995; Krewson and Saltzman, 1996). Tissue NGF concentration profiles approach steady-state distributions in the vicinity of controlled-release polymeric intracranial implants (Mahoney and Saltzman, 1996). The steady concentration profile normalized to the concentration at the controlled release source-tissue interface (Co) is a function of a so-called elimination modulus, (φ). The modulus is in turn a function of Db, a first-order elimination constant ke, and the polymer half-width a (Radomsky et al., 1990):

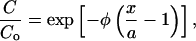graphic file with name M5.gif (5a)

where

graphic file with name M6.gif (5b)

The elimination constant, ke, is a lumped parameter that accounts for all mechanisms that may serve to clear the molecule from the brain, including degradation and blood-brain barrier permeation. From previous studies, NGF concentration profiles are characterized by a modulus value of approximately unity, which corresponds to very limited (2–3 mm) penetration of factor into surrounding tissue (Krewson and Saltzman, 1996). The modulus value is the lone fitted parameter from steady profiles; we consequently only learn the ratio of ke to Db, not the individual values of these parameters. We cannot be certain if abnormally slow diffusion or rapid elimination is the source of limited NGF penetration from steady-state profiles. With our independent estimate of Db and historical values for φ, we calculated a value for ke of 0.01/min, corresponding to an elimination half-life (t1/2) of 1.2 h. Comparison of characteristic times for diffusion (td) and elimination allows us to unlock the therapeutic potential of NGF through rational formulation design (Haller and Saltzman, 1998). We define td as the ratio of the square of a characteristic length to Db. Tissue penetration of NGF surrounding an implant is on the order of 1 mm (Krewson and Saltzman, 1996); using 1 mm as the characteristic length, we calculated a td of ∼10 h. The elimination process, characterized by t1/2 = 1.2 h, is rapid relative to diffusion over this length scale, suggesting one must circumvent this rapid elimination mechanism to extend the therapeutic reach of NGF in diseased brain tissue (Belcheva et al., 1999; Krewson et al., 1996).

Acknowledgments

We acknowledge Drs. Barbara Clancy, Karl Kasischke, and Karen Smith for their assistance with brain tissue slice preparation and chamber construction.

This work was supported by a grant from National Institutes of Health (NS-38470). This publication was made possible in part by the National Center for Research Resources, NIH (P41-RR04224) to RMW, WRZ, and WWW.

References

  1. Belcheva, N., K. Woodrow-Mumford, M. Mahoney, and W. M. Saltzman. 1999. Synthesis and biological activity of polyethylene glycol-mouse nerve growth factor conjugate. Bioconjug. Chem. 10:932–937. [DOI] [PubMed] [Google Scholar]
  2. Berg, H. C. 1983. Random Walks in Biology. Princeton University Press, Princeton.
  3. Berk, D. A., F. Yuan, M. Leunig, and R. K. Jain. 1997. Direct in vivo measurement of targeted binding in a human tumor xenograft. Proc. Natl. Acad. Sci. USA. 94:1785–1790. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brown, E. B., E. S. Wu, W. Zipfel, and W. W. Webb. 1999. Measurement of molecular diffusion in solution by multiphoton fluorescence photobleaching recovery. Biophys. J. 77:2837–2849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Clancy, B., M. Silva-Filho, and M. J. Friedlander. 2001. Structure and projections of white matter neurons in the postnatal rat visual cortex. J. Comp. Neurol. 434:233–252. [DOI] [PubMed] [Google Scholar]
  6. Fischer, W., K. Wictorin, A. Bjorklund, L. R. Williams, S. Varon, and F. H. Gage. 1987. Amelioration of cholinergic neuron atrophy and spatial memory impairment in aged rats by nerve growth factor. Nature. 329:65–68. [DOI] [PubMed] [Google Scholar]
  7. Fox, J. R., and H. Wayland. 1979. Interstitial diffusion of macromolecules in the rat mesentary. Microvasc. Res. 18:255–276. [DOI] [PubMed] [Google Scholar]
  8. Gage, F. H., D. M. Armstrong, L. R. Williams, and S. Varon. 1988. Morphological response of axotomized septal neurons to nerve growth factor. J. Comp. Neurol. 269:147–155. [DOI] [PubMed] [Google Scholar]
  9. Greene, L. A., M. M. Sobeih, and K. K. Teng. 1996. Methodologies for the culture and experimental use of the PC12 rat pheochromocytoma cell line. In Culturing Nerve Cells. G. Banker and K. Goslin, editors. MIT Press, Cambridge. 207–226.
  10. Haller, M. F., and W. M. Saltzman. 1998. Localized delivery of protein in the brain: can transport be customized? Pharm. Res. 15:377–385. [DOI] [PubMed] [Google Scholar]
  11. Kloppenburg, P., W. R. Zipfel, W. W. Webb, and R. M. Harris-Warrick. 2000. Highly localized Ca(2+) accumulation revealed by multiphoton microscopy in an identified motoneuron and its modulation by dopamine. J. Neurosci. 20:2523–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Krewson, C., M. Klarman, and W. M. Saltzman. 1995. Distribution of nerve growth factor following direct delivery to brain interstitium. Brain Res. 680:196–206. [DOI] [PubMed] [Google Scholar]
  13. Krewson, C. E., R. Dause, M. Mak, and W. M. Saltzman. 1996. Stabilization of nerve growth factor in controlled release polymers and in tissue. J. Biomater. Sci. Polym. Ed. 8:103–17. [DOI] [PubMed] [Google Scholar]
  14. Krewson, C. E., and W. M. Saltzman. 1996. Transport and elimination of recombinant human NGF during long-term delivery to the brain. Brain Res. 727:169–181. [DOI] [PubMed] [Google Scholar]
  15. Lehmenkuhler, A., E. Sykova, J. Svoboda, K. Zilles, and C. Nicholson. 1993. Extracellular space parameters in the rat neocortex and subcortical white matter during postnatal development determined by diffusion analysis. Neuroscience. 55:339–351. [DOI] [PubMed] [Google Scholar]
  16. Levi, A., Y. Shecter, E. J. Neufeld, and J. Schlessinger. 1980. Mobility, clustering, and transport of nerve growth factor in embryonal sensory cells and in a sympathetic neuronal cell line. Proc. Natl. Acad. Sci. USA. 77:3469–3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mahoney, M. J., and W. M. Saltzman. 1996. Controlled release of proteins to tissue implants for the treatment of neurodegenerative disorders. J. Pharm. Sci. 85:1276–1281. [DOI] [PubMed] [Google Scholar]
  18. Mahoney, M. J., and W. M. Saltzman. 1999. Millimeter-scale positioning of a nerve-growth-factor source and biological activity in the brain. Proc. Natl. Acad. Sci. USA. 96:4536–4539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Morse, J. K., S. J. Wiegand, K. Anderson, Y. You, N. Cai, J. Carnahan, J. Miller, P. S. DiStefano, C. A. Altar, and R. M. Lindsay. 1993. Brain-derived neurotrophic factor (BDNF) prevents the degeneration of medial septal cholinergic neurons following fimbria transection. J. Neurosci. 13:4146–4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Nicholson, C. 1985. Diffusion from an injected volume of a substance in brain tissue with arbitrary volume fraction and tortuosity. Brain Res. 333:325–329. [DOI] [PubMed] [Google Scholar]
  21. Nicholson, C., and L. Tao. 1993. Hindered diffusion of high molecular weight compounds in brain extracellular microenvironment measured with integrative optical imaging. Biophys. J. 65:2277–2290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Nugent, L. J., and R. K. Jain. 1984. Extravascular diffusion in normal and neoplastic tissues. Cancer Res. 44:238–244. [PubMed] [Google Scholar]
  23. Paxinos, G., and C. Watson. 1986. The Rat Brain in Stereotaxic Coordinates. Academic Press, San Diego.
  24. Pluen, A., P. A. Netti, R. K. Jain, and D. A. Berk. 1999. Diffusion of macromolecules in agarose gels: comparison of linear and globular configurations. Biophys. J. 77:542–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Prokopova-Kubinova, S., L. Vargova, L. Tao, K. Ulbrich, V. Subr, E. Sykova, and C. Nicholson. 2001. Poly[N-(2-hydroxypropyl)methacrylamide] polymers diffuse in brain extracellular space with same tortuosity as small molecules. Biophys. J. 80:542–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Radomsky, M. L., K. J. Whaley, R. A. Cone, and W. M. Saltzman. 1990. Macromolecules released from polymers: diffusion into unstirred fluids. Biomaterials. 11:619–624. [DOI] [PubMed] [Google Scholar]
  27. Rice, M. E., and C. Nicholson. 1991. Diffusion characteristics and extracellular volume fraction during normoxia and hypoxia in slices of rat neostriatum. J. Neurophysiol. 65:264–272. [DOI] [PubMed] [Google Scholar]
  28. Richards, B., and E. Wolf. 1959. Electromagnetic diffraction in optical systems II. Structure of the image field in an aplanatic system. Proc Roy Soc A. 253:358–379. [Google Scholar]
  29. Saltzman, W., M. Radomsky, K. Whaley, and R. Cone. 1994. Antibody diffusion in human cervical mucus. Biophys. J. 66:508–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sober, H. A. 1970. Handbook of Biochemistry. CRC Press, Boca Raton, FL.
  31. Sykova, E. 1997. The extracellular space in the CNS: its regulation, volume and geometry in normal and pathological neuronal function. Neuroscientist. 3:28–41. [Google Scholar]
  32. Tao, L., and C. Nicholson. 1996. Diffusion of albumins in rat cortical slices and relevance to volume transmission. Neuroscience. 75:839–847. [DOI] [PubMed] [Google Scholar]
  33. Thoenen, H., and Y. A. Barde. 1980. Physiology of nerve growth factor. Physiol. Rev. 60:1284–1335. [DOI] [PubMed] [Google Scholar]
  34. Tuszynski, M., and J. Kordower, editors. 1999. CNS Regeneration. Academic Press, San Diego.
  35. Tuszynski, M., J. Roberts, M. Senut, H. S. U, and F. Gage. 1996. Gene therapy in the adult primate brain: intraparenchymal grafts of cells genetically modified to produce nerve growth factor prevent cholinergic neuronal degeneration. Gene Ther. 3:305–314. [PubMed] [Google Scholar]
  36. Yan, Q., C. Matheson, J. Sun, M. Radeke, S. Feinstein, and J. Miller. 1994. Distribution of intracerebral ventricularly administered neurotrophins in rat brain and its correlation with trk receptor expression. Exp. Neurol. 127:23–26. [DOI] [PubMed] [Google Scholar]
  37. Zipfel, W. R., and W. W. Webb. 2001. In vivo diffusion measurements using multiphoton excited fluorescence photobleaching recovery (MPFPR) and fluorescence correlation spectroscopy (MPFCS). In Methods in Cellular Imaging. A. Periasamy, editor. Oxford University Press, Oxford. 216–235.

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES