Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Aug;85(2):686–694. doi: 10.1016/S0006-3495(03)74512-3

Specific Ion Effects: Why the Properties of Lysozyme in Salt Solutions Follow a Hofmeister Series

M Boström *,‡, D R M Williams *, B W Ninham *,†
PMCID: PMC1303194  PMID: 12885620

Abstract

Protein solubility in aqueous solutions depends in a complicated and not well understood way on pH, salt type, and salt concentration. Why for instance does the use of two different monovalent salts, potassium thiocyanate and potassium chloride, produce such different results? One important and previously neglected source of ion specificity is the ionic dispersion potential that acts between each ion and the protein. This attractive potential is found to be much stronger for SCN− than it is for Cl−. We present model calculations, performed within a modified ion-specific double-layer theory, that demonstrate the large effect of including these ionic dispersion potentials. The results are consistent with experiments performed on hen egg-white lysozymes and on neutral black lipid membranes. The calculated surface pH and net lysozyme charge depend strongly on the choice of anion. We demonstrate that the lysozyme net charge is larger, and the corresponding Debye length shorter, in a thiocyanate salt solution than in a chloride salt solution. Recent experiments have suggested that pKa values of histidines depend on salt concentration and on ionic species. We finally demonstrate that once ionic dispersion potentials are included in the theory these results can quantitatively be reinterpreted in terms of a highly specific surface pH (and a salt-independent pKa).

INTRODUCTION

Salt-induced precipitation is an important method frequently used as an initial step to purify proteins, for example to separate proteins from blood plasma. Although industrially a very important method, which has been used for more than 100 years (Hofmeister, 1888), protein solubility is certainly not well understood. Ion-specific salt-induced interactions play an important role in protein-protein interactions in aqueous solutions at biological and higher concentrations, i.e., at all concentrations relevant for protein precipitation. Lewith (Lewith, 1888) and Hofmeister demonstrated that the precipitation of proteins in salt solutions depends not only on the salt concentration, but also on protein concentration and the specific salt used. It has for a long time been a great mystery why protein-protein interactions, protein net charge, precipitation, and cloud-point temperature depend so critically on the choice of background salt (Baldwin, 1996; Melander and Horvath, 1977; Curtis et al., 1998, 2002; Grigsby et al., 2001; George and Wilson, 1994). The same phenomenon is observed for the formation and stability of protein-coupled receptors (Vogel et al., 2001) and for the apparent pKa values of histidine (Lee et al., 2002). Due to the lack of understanding for protein precipitation and crystallization it is difficult to select optimal conditions to target a specific protein. We demonstrate here that many of these phenomena can be better understood once we take into account the previously neglected ionic dispersion potential that acts between each salt ion and the protein.

It is well known that membrane (including protein membrane) biology often can be described surprisingly well using the electrostatic mean-field double-layer theory (Ninham and Parsegian, 1971; Parsegian, 1974; McLaughlin, 1989; Belloni, 1998; Ji et al., 1993) (and its extensions used to consider detailed molecular interactions (Ben-Tal et al., 1996; Pandit and Berkowitz, 2002) or nonuniform charge effects (Grant, 2001)). The only ionic property included in this theory is the ionic charge. There is nothing specific in this theory that can explain why proteins interact differently in thiocyanate than in chloride salt solutions. One important source of ion specificity missed in the classical double-layer theory is the ionic dispersion potential that acts between an ion and an interface. Ions have in general a different polarizability than the surrounding water (specific for each ion) and hence experience a very specific dispersion potential near an interface (Ninham and Yaminsky, 1997; Netz, 2001). At high salt concentrations, where electrostatic potentials become more and more screened, these ionic dispersion potentials dominate the interaction completely. We have in a series of publications demonstrated the importance of including these ionic dispersion potentials to obtain correct results for the highly ion specific surface tension increment with added salt at an air-water interface (Boström et al., 2001a; Karraker and Radke, 2002; Weissenborn and Pugh, 1996; Aveyard et al., 1977), double-layer forces (Boström et al., 2001b; Pashley et al., 1986; Dubois et al., 1998), ion condensation on micelles (Boström et al., 2002a; Brady et al., 1986) and polyelectrolytes (Boström et al., 2002b), binding of peptides to membranes (Boström et al., 2002c; Ben-Tal et al., 1996), and pH measurements (Boström et al., 2003.)

In this paper we examine how the dispersion force between a protein and the surrounding ion cloud affects the nature of this cloud, the protein charge, and the Debye length of the solution. This in turn gives us a partial understanding of the forces between two identical protein particles and allows a similar understanding of the Hofmeister series. We do not claim at this point, that ionic dispersion forces give a full picture in detail of the Hofmeister effect, but our calculations clearly show they are a very important part of the explanation, and probably contain all the basic physics needed. The outline is as follows. In the Theory section, we describe the ion specific double-layer theory that we use to model the electrostatic properties of a single globular protein (here hen egg-white lysozyme) in a salt solution. We then give an example of ion specificity, not for proteins but for the surface potential of neutral black-lipid membranes deduced from conductance measurements (McLaughlin et al., 1975). We calculate the lysozyme net charge and surface pH in the Lysozyme Hofmeister Effects section. We show why the protein net charge is different in the presence of chloride and thiocyanate salt solutions. The anions are attracted toward the protein surface by electrostatic forces. But ionic dispersion forces that are more attractive for thiocyanate than for chloride also influence them. As we will see this can explain why the lysozyme net charge (Curtis et al., 1998) and membrane potential (McLaughlin et al., 1975) are both larger in the presence of a thiocyanate salt than with a chloride salt. We then demonstrate that the difference in protein charges gives rise to highly ion specific Debye lengths in highly charged protein solutions (even at the lowest protein concentration used by Hofmeister). This is one reason why protein-protein interactions are more attractive in a thiocyanate salt than in a chloride salt (Curtis et al., 1998, 2002). It could also be one reason why the cloud-point temperature for lysozymes is higher in a NaNO3 solution than in a NaCl solution (Grigsby et al., 2001) (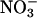Inline graphic is more polarizable than Cl−). The apparent experimental pKa values of ionizable groups (for example histidine) have been shown to depend on salt concentration and ionic species. We interpret the experimental observation in terms of concentration and ion specific surface pH (and a constant pKa). Finally, we end with a few concluding remarks.

THEORY

We consider an aqueous solution of negatively charged anions and positively charged cations each with bulk concentration c and charge e outside a globular protein. The protein is modeled as a dielectric sphere of radius rp (16.5 Å (Grant, 2001)) with ionizable surface groups. The electrostatic potential on the model protein is averaged over the spherical surface. On a real protein charges are localized and there will be distinct tangential variations in charge density. Counterions will cluster at the specific localized charges of a real protein. This is an effect that goes beyond the scope of the present paper.

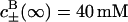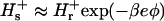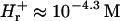The calculations that we present are for a hen egg-white lysozyme at 25 °C, in a sodium acetate buffer (Inline graphic), and pH 4.3. pH is defined as −log10(cH γH), where cH is the hydronium bulk concentration and γH is the activity coefficient. Following Parsegian (1974) we neglect any changes in the hydronium ion bulk activity coefficient (i.e., we take Inline graphic, and Inline graphic). The lysozyme has the following basic charge groups (Grant, 2001): 1 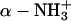Inline graphic (pKa = 9.2); 6 lysine (pKa = 10.8); 11 argines (pKa = 12.5); and 1 histidine (pKa = 6.0). The lysozyme furthermore has the following acid charge groups: 1 α-COO− (pKa = 2.0); 2 glutamic acids (pKa = 4.3); 7 aspartic acids (pKa = 3.9); and 3 tyrosines (pKa = 10.9). Although the pK values of the ionizable groups may well change with salt concentration (Lee et al., 2002; Kuehner et al. 1999), this effect is neglected since we here focus on other effects of added salt. We will demonstrate in “Are histidines pKa values really salt tolerant?” that the experimentally observed concentration and ion dependent pKa values to a large degree are a theoretical artifact. The average charge of an acid group (q−) is given by the fractional dissociation of the group 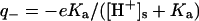Inline graphic. Similarly, the average charge of a basic group is 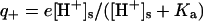Inline graphic. The net protein charge, and the surface concentration of hydronium ions ([H+]s), must be determined self-consistently with the nonlinear Poisson-Boltzmann equation,

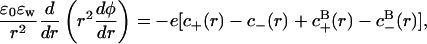graphic file with name M8.gif (1)

with the ion concentrations given by

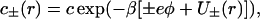graphic file with name M9.gif (2)

with similar expressions for the sodium acetate buffer (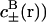Inline graphic. Here β = 1/kBT, kB is Boltzmann constant, T is temperature, and ɛw is the dielectric constant of salt solution. Furthermore, φ is the self-consistent electrostatic potential experienced by the ions, and U±(r) is the interaction potential experienced by the ions. The purpose here is to demonstrate qualitative effects of including previously ignored ionic dispersion potentials between the ions and the interface (in general there will also be contributions from image potentials, and from electrostatic, hard-core and ionic dispersion interactions between ions). Here we have included the dispersion potential that acts between an ion and the spherical interface. The boundary conditions follow from global charge neutrality. The first boundary condition is that the electric field vanishes at infinity faster than 1/r2. The second is that

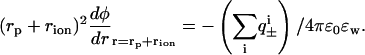graphic file with name M11.gif (3)

Here we have made the plausible assumption that the ions cannot get any closer to the effective protein surface than one ion radius (rion). Usually, the difference in ion size for similar ions is quite small, and to highlight the effects of dispersion potentials we take it to be the same for all ions (2 Å). The nonretarded dispersion interaction between a point particle and a sphere can within the pair summation approximation be written

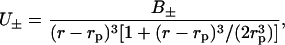graphic file with name M12.gif (4)

where the dispersion coefficient (B±) will be different for different combinations of ion and spherical protein membrane. When retardation is neglected we can calculate the dispersion coefficients from the corresponding planar interface as a sum over imaginary frequencies (iωn = i2πkBTn/ℏ, where ℏ is Planck's constant) (Ninham and Yaminsky, 1997)

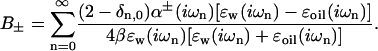graphic file with name M13.gif (5)

We have neglected the ionic dispersion potential acting on hydronium ions. The inclusion of this potential produces a small, constant shift in surface pH. We recently showed that the surface tension of different salts could be accounted for when ionic dispersion potentials were included (Boström et al., 2001a; Karraker and Radke, 2002). The increment of the refractive index of water when a salt solution is added is different for different salt solutions (Wolf et al., 1982). The refractive index of pure water is nw = 1.3333, for a 0.051 M KSCN solution the refractive index has increased to n = 1.3339. For a 0.067 M KCl solution the refractive index has increased to n = 1.3337. (Similarly, to increase the refractive index of a salt solution up to 1.3404 one must add 0.763 M KCl, whereas if KSCN is used it suffices to add 0.419 M). The sum of static excess polarizabilities for thiocyanate and potassium (or chloride and potassium) can then be estimated from the following approximation

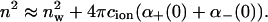graphic file with name M14.gif (6)

We find that the sum of static excess polarizabilities is ≈3.68 Å3 for KCl, and ≈6.22 Å3 for KSCN. Anions with additional electrons are expected to be more polarizable than cations (cations may well even have a negative excess polarizability). If we assume that the static excess polarizability of Cl− is at least as large as K+, the static excess polarizability of SCN− should be ∼4.4 to 6.2 Å3. We model the excess polarizability as

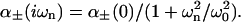graphic file with name M15.gif (7)

The effective resonance frequencies (ω0) for different ions are not known, but should typically be in the range 1–5 × 1016 rad/s (Mahan, 1982). Using the model dielectric functions given by Nir (1976) for calf serum protein (which should be similar to the hen egg-white lysozyme since most proteins have similar densities and composition) and for water we find that the dispersion coefficient for SCN− should be of the order −5 to −25 × 10−50 J m3. Similar but smaller values (in magnitude) are expected for potassium and chloride. Considering the many approximations used these values can obviously only give us an order of magnitude estimate. The point is that we can estimate the ionic dispersion potential acting on the different ions. There should be a reasonably large attractive dispersion potential acting on the SCN− ion, whereas the dispersion potentials acting on Cl− and K+ must be substantially smaller. Although the difference in van der Waals force due to changes in refractive index is very small indeed, the difference in the double-layer related properties (double-layer force, surface pH, net charge of the protein, and so on) due to ionic dispersion potentials can be very large. Here we first explore what happens in a model system, an uncharged spherical membrane. In the next section we explore how the inclusion of these ionic dispersion potentials influence the lysozyme net charge, lysozyme surface pH, and the Debye length of protein solutions.

We first consider an uncharged spherical membrane, in 0.25 M salt solution of the same size as the charged lysozyme that we consider later. This system is chosen, as an introduction to the protein problem, and because there are measurements for this kind of system by McLaughlin et al. (1975). These measurements are actually for flat membranes, but the differences caused by geometry will only be very slight. As in all calculations presented here there is also a 40 mM sodium acetate buffer. Acetate has a much smaller static excess polarizability than thiocyanate. The ionic dispersion potential acting on the acetate ion (with almost the same electron density as water) is neglected. We also assume that the ionic dispersion potential acting on the cations can be neglected. For the example considered here (an uncharged membrane) this approximation is certainly questionable. However, the dispersion potential acting on potassium should certainly be much smaller than the corresponding potential acting on thiocyanate. To neglect ionic dispersion potentials acting on the cations will be a much better approximation when we consider a highly charged protein in the next section (model calculations have revealed only minor co-ion (cation) effects). When anions and cations experience different ionic dispersion potentials near a charge-neutral membrane a double layer is set up. The self-consistent electrostatic potential is shown in Fig. 1. We consider three different cases: B− = −10 × 10−50 J m3 (dotted line); B− = −15 × 10−50 J m3 (dashed line); and B− = −20 × 10−50 J m3 (solid line). McLaughlin et al. (1975) used conductance measurements to deduce the electrostatic potential in planar black lipid membranes in different salt solutions. In a 0.25 M sodium perchlorate solution the deduced surface potential was −25 mV. Although sodium thiocyanate gave virtually the same surface potential, no surface potential was found in a sodium chloride solution (i.e., McLaughlin et al. observed no change in the conductance with added NaCl). They also measured the zeta potential for the same systems and found them to be −14 mV (perchlorate), −11 mV (thiocyanate), and −1 mV (chloride), respectively. Theoretically, it is quite common to compare the zeta potential with the electrostatic potential found a distance 2 Å away from the interface. As we see in Fig. 1 the experimentally deduced surface potential is only slightly lower than the surface potential calculated for the largest attractive ionic dispersion potential considered here (B− = −20 × 10−50 J m3). The experimental zeta potential compares better with the theoretical result if we take B− = −15×10−50 J m3. The important point is that both these ionic dispersion potentials have exactly the same magnitude and sign that we previously estimated for SCN− near a protein surface above. Since the optical properties of a black neutral lipid membrane (formed from phosphatidylcholine) and a hen egg-white lysozyme can clearly be different one should not have been surprised if there had been no agreement at all. Indeed, when lipid membranes (formed from either phosphatidylcholine or phosphatidylethanolamine) were replaced with glycerol mono-oleate membranes much smaller surface potentials were found. Although McLaughlin et al. at the time had no explanation for this, it is much easier to understand now. The ionic dispersion potential at different oil-water interfaces can be very different reflecting the fact that dielectric properties of different oils are different (it is for instance known that the chemical potential of oil on water can change sign as we go from long to short chain hydrocarbons (Richmond et al., 1973; Hauxwell and Ottewell, 1970)). The fact that we here considered a spherical membrane (rather than a planar) turns out to be of no real importance. We have done exactly the same calculation for a planar charge neutral membrane with virtually the same result. We observe that our result also should be relevant for the permeability of human red cell which follows the same Hofmeister series (Wieth, 1970).

FIGURE 1.

FIGURE 1

Open in a new tab

Theoretical electrostatic potential outside a charge neutral membrane in a 0.25 M salt solution set up by unequal ionic dispersion potentials acting on cations (B+ = 0 × 10−50 J m3) and anions. Three different examples of ionic dispersion potentials acting on the anions are considered here: B− = −10 × 10−50 J m3 (dotted line), B− = −15 × 10−50 J m3 (dashed line), and B− = −20 × 10−50 J m3 (solid line).

Lysozyme hofmeister effects: net charge, surface pH, and debye length

The pH-dependent lysozyme net charge in potassium chloride solutions has been deduced from titration experiments (Kuehner et al., 1999; Haynes et al., 1994). If allowance is made for changes in pKa values agreement can be found between the theoretical and experimental lysozyme net charge as a function of pH. However, there is nothing in the ordinary double-layer theory that explains why the lysozyme net charge at pH 4.5 is 10 for 0.1 M KCl and 10.5 for the same concentration of KSCN (Curtis et al., 1998), nor why the protein-protein interaction should be more attractive when it takes place in a thiocyanate salt than in a chloride salt. As we will demonstrate a new understanding begins to emerge when we include ionic dispersion potentials.

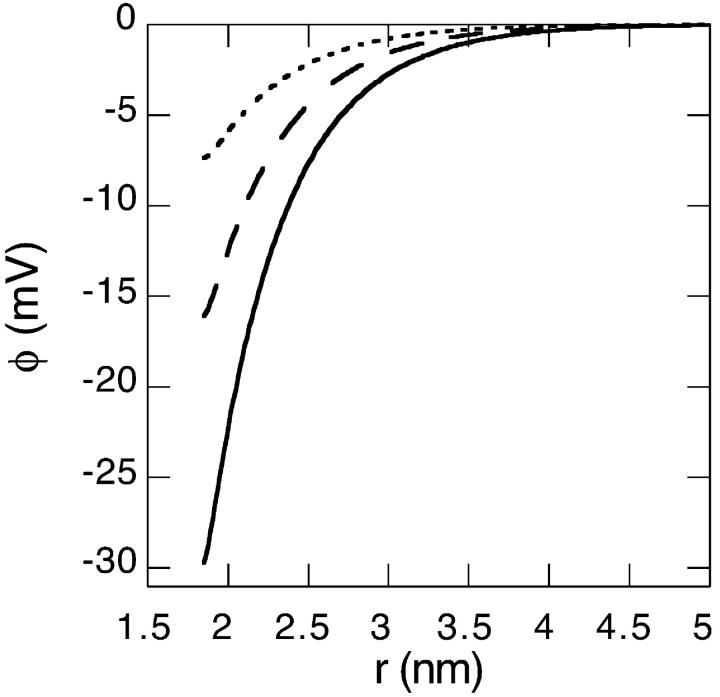
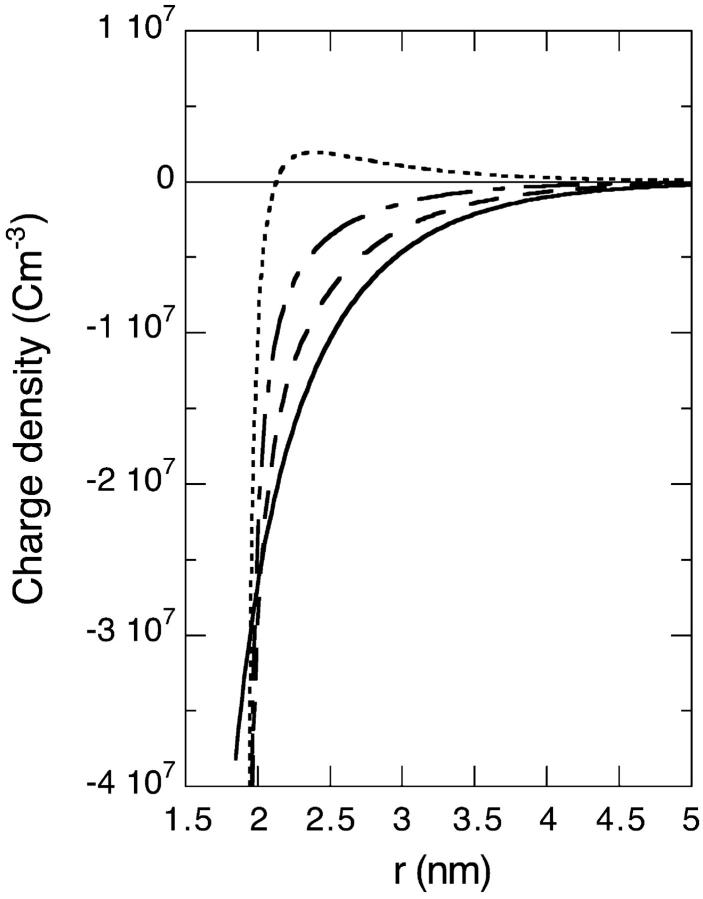
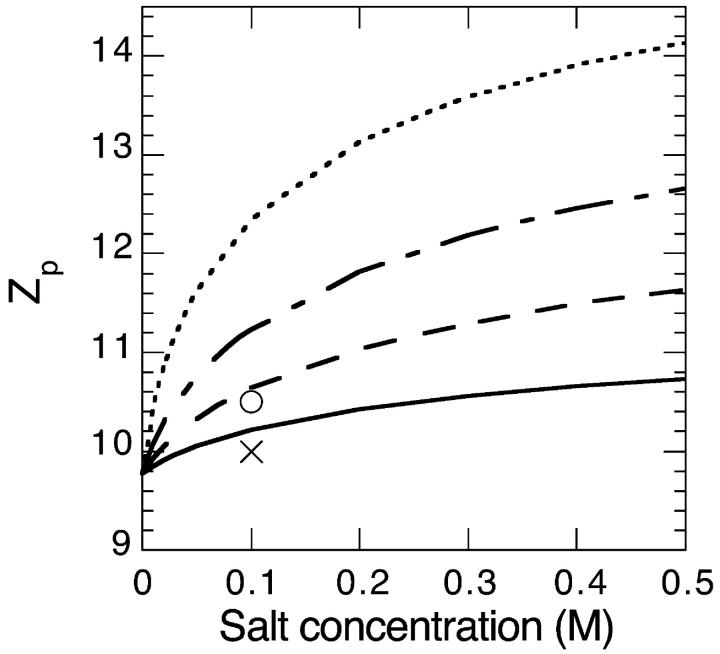
We now consider a charged lysozyme under the conditions described in Sec. 2. The electrostatic potential and charge distribution outside the lysozyme for a 0.1 M salt solution are shown in Figs. 2 and 3. We consider four different cases: B− = 0 × 10−50 J m3 (solid line); B− = −10 × 10−50 J m3 (dashed line); B− = −15 × 10−50 J m3 (dashed-dotted line); and B− = −20 × 10−50 J m3 (dotted line). Clearly the surface concentration of highly polarizable anions can be very large. Moderately large attractive ionic dispersion potentials acting on the anions can even cause a charge reversal in as far as the electrostatic potential and ionic charge distribution some distance away from the surface behave as if the protein is negatively charged (i.e., a negative electrostatic potential and positive charge distribution). The calculated surface pH and net protein valency (Zp) as a function of salt concentration are shown in Figs. 4 and 5 (for the same 4 model salts as in Figs. 2 and 3). At low concentrations we observe that the surface pH for all these salts are higher than the bulk pH of 4.3 (shown as a solid line in Fig. 4). But as the salt concentration enters the so-called biological regime (around 0.1 M and higher) some salts, such as thiocyanate, can produce a surface pH lower than the pH of the bulk reservoir. Also there is a very large degree of ion specificity found for the net protein charge. The cross (circle) in Fig. 5 represents the experimentally obtained net charge of lysozyme at pH 4.5 in a 0.1 M KCl (KSCN) salt solution. We see again that inclusion of the ionic dispersion potential acting on thiocyanate (with values in the range estimated in the previous section) can by itself explain the experimental ion specific results.

FIGURE 2.

FIGURE 2

Open in a new tab

Theoretical electrostatic potential outside a charged lysozyme (pHr = 4.3, 0.1 M salt concentration). Ionic dispersion potentials acting on cations are neglected. Four different examples of ionic dispersion potentials acting on the anions are considered here: B− = 0 × 10−50 J m3 (solid line), B− = −10 × 10−50 J m3 (dashed line), B− = −15 × 10−50 J m3 (dash-dotted line), and B− = −20 × 10−50 J m3 (dotted line). More details are given in the text.

FIGURE 3.

FIGURE 3

Open in a new tab

Theoretical ionic charge density distribution outside a charged lysozyme (pHr = 4.3, 0.1 M salt concentration) for the same system considered in Fig. 2.

FIGURE 4.

FIGURE 4

Open in a new tab

Theoretical surface pH of lysozyme as a function of salt concentration (pHr = 4.3). Ionic dispersion potentials acting on cations are neglected. Four different examples of ionic dispersion potentials acting on the anions are considered here: B− = 0 × 10−50 J m3 (solid line), B− = −10 × 10−50 J m3 (dashed line), B− = −15 × 10−50 J m3 (dash-dotted line), and B− = −20 × 10−50 J m3 (dotted line).

FIGURE 5.

FIGURE 5

Open in a new tab

Theoretical netcharge of a lysozyme globular protein as a function of salt concentration for the same system considered in Fig. 4. As comparison we have added two experimental data points (at pH = 4.5) for the netcharge in 0.1 M KCl (cross) and 0.1 M KSCN (circle).

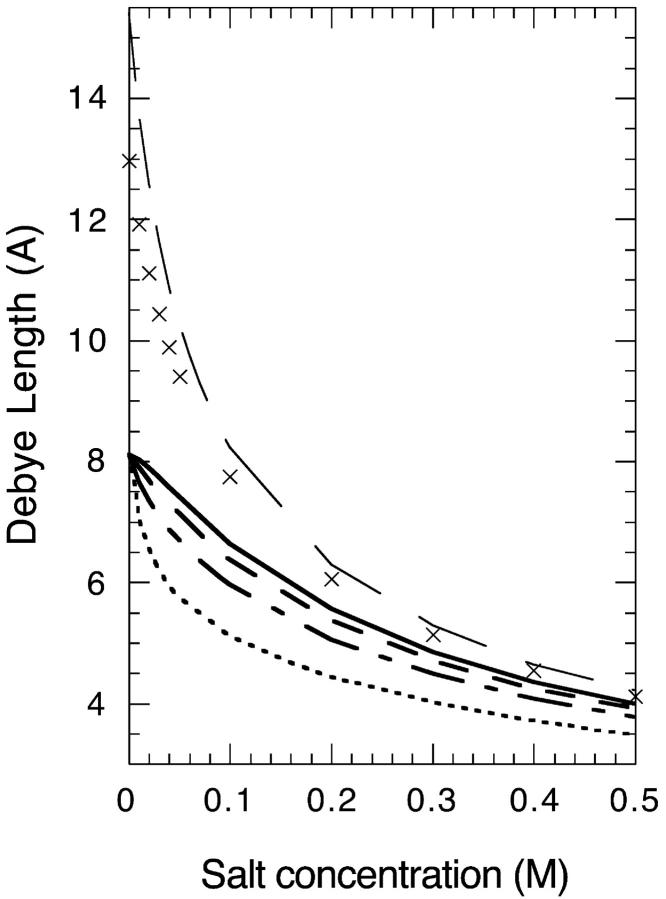
We can now explore, in the most primitive way, what these results mean for the forces between two proteins in solution. It is ultimately these forces that are needed for a full explanation of the Hofmeister effect, since a small double-layer repulsion will promote precipitation of the protein. We examine the forces by first calculating the Debye length. The measured Debye length in highly charged protein solutions has been found to be in close agreement with the asymptotic form derived by Mitchell and Ninham (Mitchell and Ninham, 1978; Kekicheff and Ninham, 1990; Nylander et al., 1994 Waninge et al., 1998). As an example Kekicheff and Ninham demonstrated that the experimental Debye length in a 4.1 × 10−6 M 12:1 electrolyte was 10.0 nm, in close agreement with the predicted value of 10.5 nm (Kekicheff and Ninham, 1990). The corresponding classical Debye length is substantially higher (17.0 nm). The sensitive dependence of the Debye length upon the protein charge has also been exploited to estimate the net protein charge (Nylander et al., 1994). We will here, for the purpose of demonstration only, assume that the protein charge on each protein does not change as we increase the protein concentration. This means that we can estimate the Debye length of protein solutions using the calculated net charge shown in Fig. 5. Expressed on a molar basis the decay length in an asymmetric electrolyte is (Mitchell and Ninham, 1978, Nylander et al., 1994)

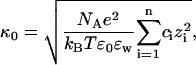graphic file with name M16.gif (9)

where NA is Avagadros number and 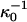Inline graphic is the classical Debye length. We show in Fig. 6 the Debye length, for the same model salt solutions as in Fig. 5, as a function of salt concentration in a 5 g/l (M = 14500 g/mol) lysozyme solution. This was the lowest protein concentration used in the classical Hofmeister experiment (Hofmeister, 1888). We have also added the Debye length at zero protein concentration (long dashed line). For comparison we also added the classical (but incorrect) Debye length (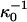Inline graphic) shown as crosses. All four salts gave very similar Debye lengths within this approximation and for the sake of clarity we only show the result for one of them.

FIGURE 6.

FIGURE 6

Open in a new tab

Debye length, for the same model salt solutions as in Fig. 5, as a function of salt concentration in a 5 g/l (M = 14500 g/mol) lysozyme solution. We also show the Debye length at zero protein concentration (long-dashed line), and for comparison the classical (but incorrect) Debye length (crosses). Details are given in the text.

The inclusion of ionic dispersion potentials, that is required for thermodynamic consistency, fundamentally alters the double-layer force (Boström et al., 2001b). It is not simply a matter of changing the charge of the proteins and Debye length of protein solutions to obtain the correct double-layer force between proteins. However, this is clearly one effect. The classical electrostatic double-layer repulsion between two proteins derived from Debye-Hückel theory is:

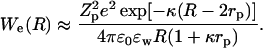graphic file with name M19.gif (10)

The salt specific increase in protein net charge, when we replace NaCl with NaSCN, has then (at least) two effects on the electrostatic repulsion. Since it increases the charge the repulsion is larger at small protein separations. However, it also decreases the Debye length which at any protein concentration relevant for precipitation leads to a reduced repulsion at large protein separations.

Are histidine pKa values really salt sensitive?

As we demonstrated in the previous section surface pH of proteins depends sensitively on salt concentration and on ionic species following a Hofmeister series. It is the surface pH, rather than bulk pH, that is important for groups localized to the surface (Gibson et al., 1999; Wang et al., 2002). Lee et al. (2002) carefully investigated experimentally the apparent pKa values of histidines. They found that it depends on both salt concentration and ionic species. Since we have demonstrated that surface pH depends on both salt concentration and ionic species it is natural to question the origin of the salt sensitivity of the pKa values. Table 1 shows the experimentally observed apparent pKa values from Lee et al. (Lee et al., 2002) for His-46 and His-121 in SNase, measured as a function of KCl and KSCN concentration. The last column of Table 1 shows the result of model calculations that will be described later. The apparent pKa increase with added salt for all considered histidines. The effect of adding 0.1 M KSCN is, for both histidines, very similar to that of adding 0.5 M KCl. As a preliminary comparison it is interesting to compare with the calculated surface pH presented in Fig. 4: adding 0.5 M of the salt represented by the solid line (which we can compare with chloride) had virtually the same effect as adding 0.1 M of the salt represented by the dashed line (to be compared with thiocyanate).

TABLE 1.

The experimental apparent pKa values of histidines in SNase as a function of KCl and KSCN concentration

Salt concentration His-46* His-121* Model calculation His-46
0.02 M KCl 5.71 ± 0.02 4.91 ± 0.03 5.70
0.10 M KCl 5.86 ± 0.04 5.30 ± 0.06 5.83
0.50 M KCl 5.95 ± 0.02 5.56 ± 0.02 5.99
1.50 M KCl 6.10 ± 0.04 5.85 ± 0.03 6.08
0.10 M KSCN 6.01 ± 0.04 5.53 ± 0.04 5.98
0.50 M KSCN 6.30 ± 0.03 6.12 ± 0.03 6.24
Open in a new tab
*

Values from Lee et al. (2002).

We have also added the result of model calculations described in the text. For the theoretical calculations the salt labeled KCl (KSCN) represents B− = 0 × 10−50 J m3 (B− = −10 × 10−50 J m3). In the theoretical calculations the actual (salt independent) pKa = 6.25 of histidine was chosen to get agreement with the experimental result for His-46 in 0.02 M KCl.

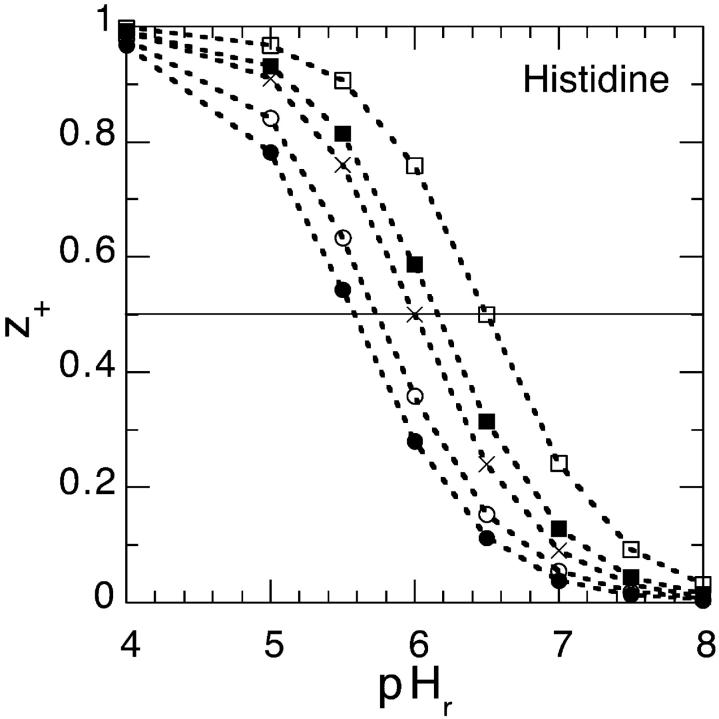
We will now explore in some detail how the average net valency (z+) of the histidine charge group in our model globular protein (lysozyme), as a function of bulk pH, varies with the choice of salt and with concentration. (Although one can expect some differences between lysozyme and SNase, they are both highly charged proteins with similar composition and density). The average net valency is

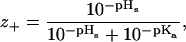graphic file with name M20.gif (11)

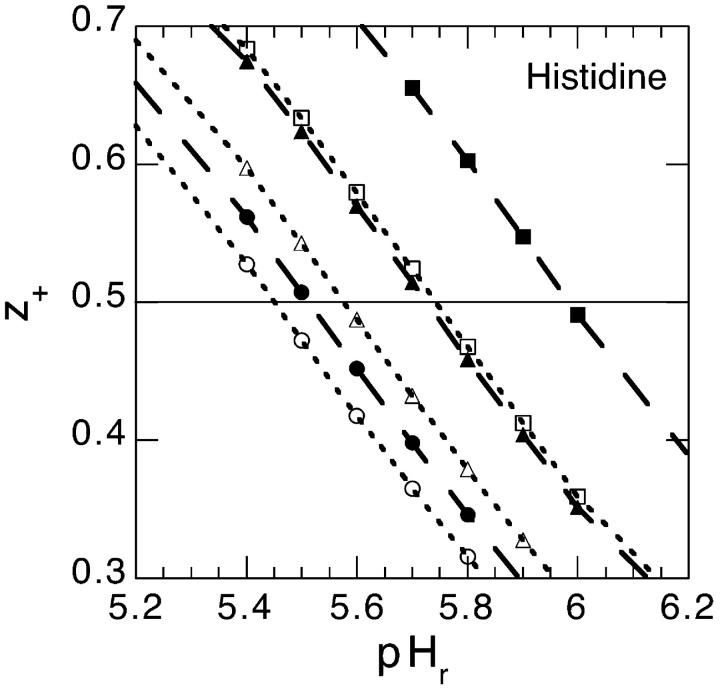
where as before we take the pKa = 6.0. The average net valency as a function of pH in the bulk reservoir is shown in Fig. 7. We consider two different model salt solutions (as before we take B+ = 0 × 10−50 J m3) and two different concentrations: B− = 0 × 10−50 J m3 (circles); B− = −20 × 10−50 J m3 (squares); 0.1 M (solid symbol) and 0.5 M (open symbol). For comparison we have also added the corresponding curve when the surface pH is replaced with the bulk pH (shown as crosses). If Fig. 7 had shown experimental titration curves the natural conclusion (Lee et al., 2002) would have been to assume that the histidine pKa (note: pHs = pKa when z+ = 1/2, the apparent pKa can be taken to be equal to pHr at this point) depend on concentration and on the ionic species. We now know better, but these curves are in fact even too salt sensitive compared to the experimental titration curves for chloride and thiocyanate salts. However, the values for B− that we found could accommodate the net charge of lysozyme much better, were −10 × 10−50 J m3 (shown as solid symbols in Fig. 8) for thiocyanate and 0 × 10−50 J m3 (shown as open symbols in Fig. 8) for chloride. It is unlikely that there should be no dispersion interaction acting on chloride, but for our purposes it suffices to know that it must be substantially less attractive than for thiocyanate. We show the calculated histidine net valency, for these two model salts, for three different concentrations in Fig. 8: 0.02 M (circle); 0.1 M (triangle); 0.5 M (square). The apparent pKa values deduced from our Fig. 8 are given in Table 2. We have also performed identical model calculations for the case that the anions experience a slightly more attractive ionic dispersion potential (B− = −15 × 10−50 J m3). The apparent pKa values from these calculations are also shown in Table 2. Considering that the experimental values given in Table 1 were measured under different experimental conditions (e.g., in SNasa rather than in a globular lysozyme) than our model calculations, and that none of their histidines even at low salt concentrations give exactly the same apparent pKa values as our model histidine, the agreement is really very good.

FIGURE 7.

FIGURE 7

Open in a new tab

The average net valency of histidine as a function of pH in the bulk reservoir. We consider two different model salt solutions (as before we take B+ = 0 × 10−50 J m3) and two different concentrations: B− = 0 × 10−50 J m3 (circles), B− = −20 × 10−50 J m3 (squares), 0.1 M (solid symbol), and 0.5 M (open symbol). For comparison we have also added the corresponding curve when the surface pH is replaced with the bulk pH (shown as crosses).

FIGURE 8.

FIGURE 8

Open in a new tab

The average net valency of histidine as a function of pH in the bulk reservoir. We show the result for two different ionic dispersion potentials acting on the anions: −10 × 10−50 J m3 (shown as solid symbols) and 0 × 10−50 J m3 (shown as open symbols). Three different concentrations are considered: 0.02 M (circle), 0.1 M (triangle), and 0.5 M (square).

TABLE 2.

Theoretical apparent pK values of a histidine in lysozyme as deduced from the pH that give z+ = 0.5

Salt concentration B− = 0 × 10−50 J m3 B− = −10 × 10−50 J m3 B− = −15 × 10−50 J m3
0.02 M 5.45 5.51 5.61
0.10 M 5.58 5.72 5.90
0.50 M 5.74 5.98 6.20
Open in a new tab

The actual pK value used to model the histidine was 6.0.

Let us pursue the comparison between theory and experiment in more detail. One can back out a theoretical pKa value for histidine (keeping the same pKa as before for the other ionizable groups) that gives exact agreement with the experimental result for His-46 in the presence of 0.02 M KCl. A simple way to do this is to first assume that surface pH does not change dramatically when we change pKa slightly. Within this approximation one can then use the previously obtained values for pHs to find which pKa value that reproduce the experimentally observed apparent pKa. Using this value for pKa we then repeated the calculation for the 0.02 M salt with B− = 0 × 10−50 J m3 and found that the result agreed well with the experimental result for KCl. One can then test this value for different salts and different concentrations. The result is shown in the last column of Table 1. Where the salts labeled KCl (KSCN) for the theoretical calculation represents B− = 0 × 10−50 J m3 (B− = −10 × 10−50 J m3). As can be seen we find a remarkably good agreement between theory and experiment for both salts at all concentrations considered if we take pKa = 6.25.

We are not saying that the pKa values of histidine and other ionizable charge groups on proteins never change with added salt, or that they cannot follow a Hofmeister series. But concentration and ion specific surface pH changes due to ionic dispersion potentials can clearly by itself account for the entire experimental observation. One very important reason that the apparent pKa values are consistently higher in thiocyanate than in chloride is that thiocyanate anions are much more attracted by ionic-dispersion potentials toward the protein surface than chloride. These attractive ionic-dispersion potentials reduce surface pH, so that one must go to a higher bulk pH to obtain the same effect. The importance of consistently including ionic-dispersion potentials becomes increasingly important as the salt concentration increases, consistent with the observation that Hofmeister effects become more and more important at biological and higher concentrations.

CONCLUSIONS

An understanding of the Hofmeister series is finally emerging when ionic-dispersion potentials are included in the theory of charged proteins. We have demonstrated that ionic-dispersion potentials (that are not only consistent with the surface potential of lipid bilayers, but also for example with surface tension of salt solutions and ion binding to micelles) can explain the observed ion specificity of globular proteins such as hen egg-white lysozyme. There may of course be other effects that can influence the Hofmeister effect. A few examples include: water structure (Marrink and Marcelja, 2001); different ion size; ion specific solvation energy; co-ion and counterion exclusion (Woelki and Kohler, 2000); and dissolved gas (Alfridson et al., 2000). However, our results have clearly demonstrated the important, and often dominating, role for ionic-dispersion potentials behind the Hofmeister effect.

Acknowledgments

Financial support from the Australian Research Council is gratefully acknowledged.

References

  1. Alfridson, M., B. W. Ninham, and S. Wall. 2000. Role of co-ion specificity and dissolved atmospheric gas in colloid interaction. Langmuir. 16:10087–10091. [Google Scholar]
  2. Aveyard, R., S. M. Saleem, and R. Heselden. 1977. Desorption of electrolytes at liquid-vapour and liquid-liquid interfaces. J. Chem. Soc. Faraday Trans. 173:84–94. [Google Scholar]
  3. Baldwin, R. L. 1996. How Hofmeister ion interaction affect protein stability. Biophys. J. 71:2056–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Belloni, L. 1998. Ionic condensation and charge renormalization in colloidal suspensions. Colloid Surf. A: Physicochem. Eng. Aspects. 140:227–243. [Google Scholar]
  5. Ben-Tal, N., B. Honig, R. M. Peitsch, G. Denisov, and S. McLaughlin. 1996. Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results. Biophys. J. 71:561–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boström, M., D. R. M. Williams, and B. W. Ninham. 2001a. Surface tension of electrolytes: specific ion effects explained by dispersion forces. Langmuir. 17:4475–4478. [Google Scholar]
  7. Boström, M., D. R. M. Williams, and B. W. Ninham. 2001b. Specific ion effects: why DLVO theory fails for biology and colloid science. Phys. Rev. Lett. 87:168103–168104. [DOI] [PubMed] [Google Scholar]
  8. Boström, M., D. R. M. Williams, and B. W. Ninham. 2002a. Ion specificity of micelles explained by ionic dispersion forces. Langmuir. 18:6010–6014. [Google Scholar]
  9. Boström, M., D. R. M. Williams, and B. W. Ninham. 2002b. The Influence of ionic dispersion potentials on counterion condensation on polyelectrolyte. J. Phys. Chem. B. 106:7908–7912. [Google Scholar]
  10. Boström, M., D. R. M. Williams, and B. W. Ninham. 2002c. Influence of Hofmeister effects on surface pH and binding of peptides to membrane. Langmuir. 18:8609–8615. [Google Scholar]
  11. Boström, M., V. S. J. Craig, R. Albion, D. R. M. Williams, and B. W. Ninham. 2003. Hofmeister effects in pH measurements: the role of added salt and co-ions. J. Phys. Chem. B. 107:2875–2878. [Google Scholar]
  12. Brady, J. E., D. F. Evans, G. G. Warr, F. Grieser, and B. W. Ninham. 1986. Counterions specificity as the determinant of surfactant aggregation. J. Phys. Chem. 90:1853–1859. [Google Scholar]
  13. Curtis, R. A., J. M. Prusnitz, and H. W. Blanch. 1998. Protein-Protein and protein-salt interactions in aqueous protein solutions containing concentrated electrolytes. Biotechnol. Bioeng. 57:11–21. [DOI] [PubMed] [Google Scholar]
  14. Curtis, R. A., J. Ulrich, A. Montaser, J. M. Prusnitz, and H. W. Blanch. 2002. Protein-protein interactions in concentrated electrolyte solutions. Biotechnol. Bioeng. 79:367–380. [DOI] [PubMed] [Google Scholar]
  15. Dubois, M., T. Zemb, N. M. Fuller, R. P. Rand, and V. A. Parsegian. 1998. Equation of state of charged bilayer system: measure of the entropy of the lamellar-lamellar transition in DDABR. J. Phys. Chem. 108:7855–7869. [Google Scholar]
  16. George, A., and W. W. Wilson. 1994. Predicting protein crystallization from a dilute solution properties. Acta Crystallogr. D. 50:361–365. [DOI] [PubMed] [Google Scholar]
  17. Gibson, S. K., J. H. Parkes, and P. A. Liebman. 1999. Phosphorylation alters the pH-dependent active state equilibrium of rhodopsin by modulating the membrane surface potential. Biochemistry. 38:11103–11114. [DOI] [PubMed] [Google Scholar]
  18. Grant, M. L. 2001. Nonuniform charge effects in protein-protein interactions. J. Phys. Chem. B. 105:2858–2863. [Google Scholar]
  19. Grigsby, J. J., H. W. Blanch, and J. M. Prausnitz. 2001. Cloud-point temperatures for lysozyme in electrolyte solutions: effect of salt type, salt concentration and pH. Biophys. Chem. 91:231–243. [DOI] [PubMed] [Google Scholar]
  20. Hauxwell, F., and R. H. Ottewell. 1970. A study of the surface of water by hydrocarbon adsorption. J. Colloid Interface Sci. 34:473–479. [Google Scholar]
  21. Haynes, C. A., E. Sliwinsky, and W. Norde. 1994. Structural and electrostatic properties of globular proteins at a polystyrene-water surface. J. Colloid Interface Sci. 164:394–409. [Google Scholar]
  22. Hofmeister, F. 1888. Zur lehre der wirkung der salze. Zweite mittheilung. Arch. Exp. Pathol. Pharmakol. 24:247–260. [Google Scholar]
  23. Ji, S., J. Weiss, and G. A. Langer. 1993. Modulation of voltage-dependent sodium and potassium currents by charged amphilies in cardiac ventricular myocytes. J. Gen. Physiol. 101:355–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Karraker, K. A., and C. Radke. 2002. Disjoining pressures, zeta potentials and surface tensions of aqueous non-ionic surfactant/ electrolyte solutions: theory and comparison to experiment. Adv. Colloid Interface Sci. 96:231–264. [DOI] [PubMed] [Google Scholar]
  25. Kekicheff, P., and B. W. Ninham. 1990. The double-layer interaction in asymmetric electrolytes. Europhys. Lett. 12:471–477. [Google Scholar]
  26. Kuehner, D. E., J. Engmann, F. Fergg, M. Wernick, H. W. Blanch, and J. M. Prausnitz. 1999. Lysozyme net charge and ion binding in concentrated aqueous electrolyte solutions. J. Phys. Chem. B. 103:1368–1374. [Google Scholar]
  27. Lee, K. K., C. A. Fitch, J. T. J. Lecomte, and E. B. Garcia-Moreno. 2002. Electrostatic effects in highly charged proteins: salt sensitivity of pKa values of histidines in staphylococcal nuclease. Biochemistry. 41:5656–5667. [DOI] [PubMed] [Google Scholar]
  28. Lewith, S. 1888. Zur lehre der wirkung der salze. Erste mittheilung. Arch. Exp. Pathol. Pharmakol. 24:1–16. [Google Scholar]
  29. Mahan, G. D. 1982. Van der Waals coefficient between closed shell ions. J. Chem. Phys. 76:493–497. [Google Scholar]
  30. Marrink, S. J., and S. Marcelja. 2001. Potential of mean force computations of ions approaching a surface. Langmuir. 17:7929–7934. [Google Scholar]
  31. McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
  32. McLaughlin, S., A. Bruder, S. Chen, and C. Moser. 1975. Chaotropic anions and the surface potential of bilayer membranes. Biochim. Biophys. Acta. 394:304–313. [DOI] [PubMed] [Google Scholar]
  33. Melander, W., and C. Horvath. 1977. Salt effects on hydrophobic interactions in precipitation and chromatography: an interpretation of the lyotropic series. Arch. Biochem. Biophys. 183:200–215. [DOI] [PubMed] [Google Scholar]
  34. Mitchell, D. J., and B. W. Ninham. 1978. Range of screened Coulumb interaction in electrolytes and double layer problems. Chem. Phys. Lett. 53:397–399. [Google Scholar]
  35. Netz, R. R. 2001. Static van der Waals interactions in electrolytes. Eur. Phys. J. E. 5:189–205. [Google Scholar]
  36. Ninham, B. W., and V. A. Parsegian. 1971. Electrostatic potential between surfaces bearing ionizable groups in ionic equilibrium with physiological saline solutions. J. Theor. Biol. 31:405–428. [DOI] [PubMed] [Google Scholar]
  37. Ninham, B. W., and V. Yaminsky. 1997. Ion binding and ion specificity: the Hofmeister effect and Onsager and Lifshitz theories. Langmuir. 13:2097–2108. [Google Scholar]
  38. Nir, S. 1976. Van der Waals interactions between surfaces of biological interest. Prog. Surf. Sci. 8:1–58. [Google Scholar]
  39. Nylander, T., P. Kekicheff, and B. W. Ninham. 1994. The effect of solution behaviour of insulin on interactions between adsorbed layers of insulin. J. Colloid Interface Sci. 164:136–150. [Google Scholar]
  40. Pandit, S. A., and M. L. Berkowitz. 2002. Molecular dynamics simulation of dipalmitoylphosphatidylserine bilayer with Na+ counterions. Biophys. J. 82:1818–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Parsegian, V. A. 1974. Possible modulation of reactions on the cell surface by changes in electrostatic potential that accompany cell contact. Ann. N. Y. Acad. Sci. 238:362–371. [DOI] [PubMed] [Google Scholar]
  42. Pashley, R. M., P. M. McGuiggan, B. W. Ninham, J. Brady, and D. F. Evans. 1986. Direct measurements of surface forces between bilayers of double-chained quaternary ammonium acetate and bromide surfactants. J. Phys. Chem. 90:1637–1642. [Google Scholar]
  43. Richmond, P., B. W. Ninham, and R. H. Ottewell. 1973. A theoretical study of hydrocarbon adsorption on water surfaces using Lifshitz theory. J. Colloid Interface Sci. 45:69–80. [Google Scholar]
  44. Vogel, R., G.-B. Fan, M. Sheves, and F. Siebert. 2001. Salt dependence of the formation and stability of the signaling state in G protein-coupled receptors: evidence for the involvement of the Hofmeister effect. Biochemistry. 40:483–493. [DOI] [PubMed] [Google Scholar]
  45. Wang, Y., A. V. Botelho, G. V. Martinez, and M. F. Brown. 2002. Electrostatic properties of membrane lipids coupled to metarhodopsin II formation in visual transduction. J. Am. Chem. Soc. 124:7690–7701. [DOI] [PubMed] [Google Scholar]
  46. Waninge, R., M. Paulsson, T. Nylander, B. W. Ninham, and P. Sellers. 1998. Binding of sodium dodecyl sulphate and dodecyl trimethyl ammonium chloride to β-lactoglobulin: a calorimetric study. Int. Dairy J. 8:141–148. [Google Scholar]
  47. Weissenborn, P. K., and R. J. Pugh. 1996. Surface tension of aqueous solutions of electrolytes: relationship with ion hydration, oxygen solubility, and bubble coalescence. J. Colloid Interface Sci. 184:550–563. [DOI] [PubMed] [Google Scholar]
  48. Wieth, J. O. 1970. Effect of some monovalent anions on chloride and sulphate permeability of human red cells. J. Physiol. 207:581–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Woelki, S., and H.-H. Kohler. 2000. A modified Poisson-Boltzmann equation I. Basic relations. Chem. Phys. 261:411–419. [Google Scholar]
  50. Wolf, A. V., M. G. Brown, and P. G. Prentiss. 1982. Concentrative properties of aqueous solutions: conversion tables. In CRC Handbook of Chemistry and Physics, 63 ed. The Chemical Rubber Co. Cleveland, USA.

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES