An Integrated Model of Epidermal Growth Factor Receptor Trafficking and Signal Transduction

Abstract

Endocytic trafficking of many types of receptors can have profound effects on subsequent signaling events. Quantitative models of these processes, however, have usually considered trafficking and signaling independently. Here, we present an integrated model of both the trafficking and signaling pathway of the epidermal growth factor receptor (EGFR) using a probability weighted-dynamic Monte Carlo simulation. Our model consists of hundreds of distinct endocytic compartments and ∼13,000 reactions/events that occur over a broad spatio-temporal range. By using a realistic multicompartment model, we can investigate the distribution of the receptors among cellular compartments as well as their potential signal transduction characteristics. Our new model also allows the incorporation of physiochemical aspects of ligand-receptor interactions, such as pH-dependent binding in different endosomal compartments. To determine the utility of this approach, we simulated the differential activation of the EGFR by two of its ligands, epidermal growth factor (EGF) and transforming growth factor-alpha (TGF-α). Our simulations predict that when EGFR is activated with TGF-α, receptor activation is biased toward the cell surface whereas EGF produces a signaling bias toward the endosomal compartment. Experiments confirm these predictions from our model and simulations. Our model accurately predicts the kinetics and extent of receptor downregulation induced by either EGF or TGF-α. Our results suggest that receptor trafficking controls the compartmental bias of signal transduction, rather than simply modulating signal magnitude. Our model provides a new approach to evaluating the complex effect of receptor trafficking on signal transduction. Importantly, the stochastic and compartmental nature of the simulation allows these models to be directly tested by high-throughput approaches, such as quantitative image analysis.

INTRODUCTION

The cells of all living organisms sense their environment and respond to environmental stimuli. Cellular signaling mechanisms govern how information from the environment is decoded, processed, and transferred to the appropriate locations within the cell. Signaling through the receptor tyrosine kinase (RTK) family of receptors regulates a wide range of biological phenomena, including cell proliferation and differentiation. Because of their importance, members of this receptor group, such as the epidermal growth factor receptor (EGFR), have been extensively studied (Lauffenburger and Linderman, 1993; Marshall, 1995; Weiss et al., 1997; Carpenter, 2000; Schlessinger, 2000; Sorkin, 2000; DiFiore and DeCamilli, 2001; Wiley and Burke, 2001; Yarden and Sliwkowski, 2001).

Signaling pathways of various RTK's are reasonably well described and have common underlying features such as receptor self-phosphorylation on tyrosine residues and their subsequent interactions with molecules containing the src homology 2 (SH2) and phosphotyrosine binding domains (Haugh and Lauffenburger, 1998; Kholodenko et al., 1999; Asthagiri and Lauffenburger, 2001; Resat et al., 2001a; Schoeberl et al., 2002). The signal from the receptor is transmitted to downstream effector molecules through a series of protein-protein interactions, such as the MAP kinase cascade (Seger and Krebs, 1995). The EGFR can be activated by the binding of any one of a number of different ligands, each of which appear to stimulate a somewhat different spectrum of biological responses (van der Geer et al., 1994). The effect of different ligands on EGFR activity appears to be quite similar at a biochemical level and thus the mechanisms responsible for their differential effect on cellular responses are unknown. After binding of any of its ligands, the EGFR is rapidly internalized by endocytosis (Sorkin and Waters, 1993; Lemmon and Schlessinger, 1994; Baulida et al., 1996; Sorkin, 2001). Although it has been shown that internalized receptors can stay active, the role of receptor internalization and endocytosis in receptor signaling is not well understood (Wada et al., 1992; Di Guglielmo et al., 1994; Haugh et al., 1999b).

Different EGFR ligands vary in their ability to bind to the receptor as a function of receptor microenvironment, such as intravesicular pH (French et al., 1995). After endocytosis, receptor-ligand complexes pass through several different compartments that vary in their intravesicular milieu. Receptor movement among cellular compartments, which is referred to as receptor trafficking in the rest of this article, can exert a significant effect on the activity of the complexes. The different intracellular compartments also vary in their access to some of the substrates of the EGFR kinase. The conjoined relationship between substrate access and ligand-dependent activity in different endocytic compartments suggests that trafficking could function to “decode” the information unique to each ligand. Furthermore, the persistence of ligand-receptor interactions controls receptor trafficking. Thus, trafficking can be expected to have three types of functional roles in receptor signal regulation: i), controlling the magnitude of the signal, ii), controlling the specificity of the response, and iii), controlling the duration of the response. Much of the current data suggest that all three aspects are important in regulation of the EGFR, but understanding their relative contributions for any given combination of cells, conditions, and ligands is very difficult.

Computational models of the EGF receptor system have been very useful in understanding complex interactions between different parts of the receptor pathway. Prior work in this area mainly followed two complementary approaches. Several groups concentrated their efforts on the trafficking and ligand-induced endocytosis of the EGFR (Wiley and Cunningham, 1981; Gex-Fabry and DeLisi, 1984; Bajzer et al., 1989; Lund et al., 1990; Sorkin et al., 1991; French and Lauffenburger, 1997; Haugh and Lauffenburger, 1998). These models were primarily focused on the dynamics of receptor trafficking and did not include mechanistic details of signaling through downstream elements such as Ras or MAP kinases. Qualitative differences in receptor signaling from either the cell surface or endosomes was generally not considered. In contrast, other models were focused on understanding the acute response characteristics of activated EGFR, i.e., the transmission of the signal from the receptor to the downstream elements on the signaling path. For example, a network model for EGFR signaling was developed by Kholodenko and co-workers to describe signal transduction from the receptor to the Ras GTPase (Kholodenko et al., 1999). This model included an experimentally based set of estimated rate constants of the biochemical reactions that take part in the signal transduction process. Another EGFR signaling network model has also been described by Asthagiri and Lauffenburger (2001) recently, and the same study also presents a detailed outline of the ERK activation pathway. These signaling models neglect the trafficking and compartmentalization of the EGFR and its substrates.

A comprehensive understanding of the EGFR signaling network will require inclusion of both trafficking and signaling processes into a single model. However, most approaches to building computational kinetic models have severe drawbacks when representing spatially heterogenous processes on a cellular scale. In the traditional approach, one starts with a set of coupled ordinary differential equations (reaction rate equations) that describe the time-dependent concentration of chemical species. One then uses some integrator to calculate the concentrations as a function of time given the rate constants and a set of initial concentrations. Gillespie has shown that this formal deterministic approach can be translated to a stochastic scheme, termed the Dynamic Monte Carlo (DMC) approach (Gillespie, 1977). Because the molecules forming the physical system are chemical entities, they must participate in the reactions as integer species. The traditional approach based on the continuum treatment of chemical kinetics ignores the discrete nature of the problem, and this can lead to misrepresentation of the physical system. This is particularly true when the number of reacting molecules is small, thus making the discrete nature of the system important. As argued by Gillespie and others, the use of a discrete representation is more appropriate in kinetic simulation studies in cellular systems (McAdams and Arkin, 1997; Resat et al., 2001b). This is particularly true when regulatory mechanisms are studied, because such networks are controlled by species which exist at very low concentrations in the cells and are produced in small quantities (Arkin et al., 1998). Therefore, stochastic approaches, such as the Dynamic Monte Carlo method, are better suited for the kinetic simulation of biological networks.

In the DMC method (Gillespie, 1977), reactions are considered events that occur with certain probabilities over set intervals of time. The event probabilities depend on the rate constant of the reaction and, generally, on the number of molecules participating in the reaction. In many interesting natural problems, the time scale of the events would cover a considerably large spectrum. This gives rise to the “multiple time scale” problem in kinetic simulations (Resat et al., 2001b). When the multiple time scale problem exists, the DMC method becomes computationally inefficient because all processes are scaled to the fastest individual reaction. Therefore, the usefulness of the DMC method has been rather limited. For example, the EGFR signaling network contains reactions ranging from almost instantaneous reactions (receptor phosphorylation after ligand binding) to reactions that occur over many minutes (vesicle formation or the sorting to lysosomes). To overcome the computational inefficiency problems associated with multiple time scales, we have developed the Probability Weighted-DMC method and have shown that it is an accurate and efficient algorithm (Resat et al., 2001b). The use of the Probability Weighted-DMC enables stochastic simulations of processes, such as endocytosis, to be run considerably faster, with typical speed-up factors of 20 to 100.

We have used our new approach to stochastic simulations to create an integrated model of the EGFR system incorporating both trafficking and downstream signal transduction. Because many of the factors controlling the activation of the EGFR signaling pathways are similar in other receptor systems, this integrated model should be a useful approach for the quantitative computational analysis of cellular networks. In addition, our stochastic model allows inclusion of realistic cell-based parameters that can be quantified by high-resolution image analysis. We have experimentally tested the predictions of the model, and then used it to investigate the possible roles of receptor sorting to activation of specific signaling pathways. Our initial results suggest that an important function of EGF receptor internalization and sorting is to control the cellular site from where different signals are generated.

COMPUTATIONAL MODELING AND SIMULATIONS

Trafficking model

Our trafficking model (Fig. 1) is a generalization of the trafficking model used by Lauffenburger, Wiley, and co-workers (Lund et al., 1990; Haugh and Lauffenburger, 1998; Resat et al., 2001a). Trafficking of the EGFR is regulated at multiple steps, including endocytosis, early endosomal sorting, and lysosome targeting. After internalization, the EGFR are either shuttled back to the plasma membrane or transported into late or multivesicular endosomes. The receptors in the late endosomes are further sorted to lysosomes for degradation or recycled back to the cell surface (Herbst et al., 1994). The occupancy of the receptors dictates their ability to participate in each step of the sorting process (French et al., 1994).

FIGURE 1.

Diagram showing the compartments involved in receptor trafficking and the receptor movement pathways within the cell.

In our model, EGF receptors are internalized by either an induced pathway or a constitutive pathway (Fig. 1) (Sorkin et al., 1991b)). We label the vesicles formed through the induced pathway as coated-pit mediated early endosome (EE) vesicles, to be consistent with the data in the literature. In the case of the constitutive pathway, vesicles are formed randomly at the plasma membrane. Such vesicles are labeled smooth-pit EE vesicles.

All EE vesicles go through a sorting stage and can either return to the cell surface or merge into the late endosomes (LE). When an EE vesicle recycles back to the plasma membrane (PM), all of its receptors become part of the PM and any unbound ligand is released into the extracellular medium. Similarly, when an EE vesicle merges into the LE, all of its contents get transferred to the LE. The rates of recycling to the plasma membrane and of merging into the late endosome can depend on the type of EE vesicle (Lund et al., 1990). This feature of our model accommodates for the experimental observations that endocytic vesicles are recycled back to the plasma membrane either at a very fast rate or after a time lag (i.e., slowly). In our model, coated-pit EE vesicles are assumed to recycle back to the plasma membrane slowly and, as a result, a considerable percentage of the coated-pit EE vesicles merge into the LE. In contrast, constitutive EE vesicles have a faster recycle rate and thus most of them return to the plasma membrane.

The receptors go through a second stage of sorting in the LE and either get tagged for degradation and sent to the lysosome or are recycled back to the cell surface (Herbst et al., 1994; Kurten et al., 1996). We modeled the receptor sorting in LE as follows: A small vesicle breaks away from the sorting endosome at a certain rate. This vesicle either fuses to the lysosome for its contents to be degraded or it recycles back toward the plasma membrane. Mechanistically, receptors recycling from the late endosomes are likely to pass through the golgi, but there is insufficient experimental data to estimate the relevant rate constants. We thus use a lumped recycling rate from the LE. It should be noted that inclusion of a secondary (i.e., golgi) sorting compartment would delay return of the receptors back to the surface. However, since the majority of the receptors that are recycled from the LE are nonactivated, our simplifying assumptions do not significantly affect the signaling dynamics.

Although cells may contain multiple copies of multivesicular sorting/late endosomes, in our model there is only a single late endosome, which can grow or shrink in size. The size of the LE increases by one “vesicle” unit when an EE vesicle merges into the LE. Similarly, the size of the LE compartment decreases by one unit when a small vesicle forms and recycles back toward the PM or gets targeted for lysosomal degradation. The rate of vesicle formation from the LE depends on the size of the LE, and this aspect of the model reasonably accommodates the likelihood that there are many multivesicular endosomes within a given cell.

Signal transduction model

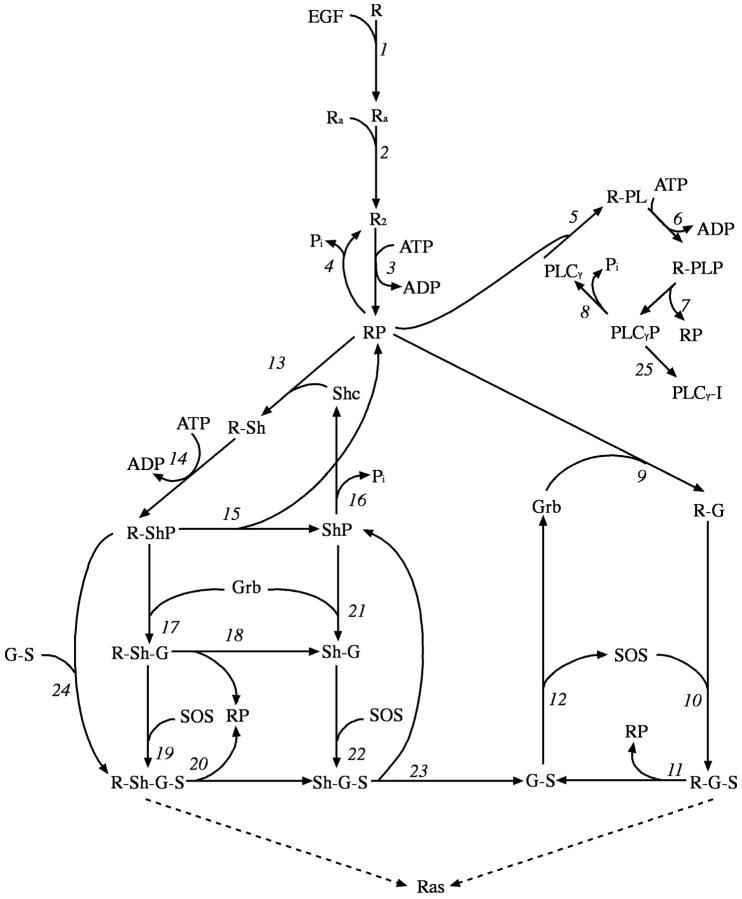
For modeling the signal transmission from the receptor to the downstream elements, we use the network model introduced by Kholodenko et al. (1999). This network of reactions of the receptor with its target proteins (Fig. 2) is composed of three coupled cycles of interactions with Grb2, PLC-γ, and Shc, respectively, and stops at the level of Sos activation. Although it was included in the calculations, because it does not directly lead to Sos recruitment, the loop leading to the PLC-γ and receptor interactions is not relevant to our investigation. In our analysis we mainly concentrated on the time dependent response of Sos recruitment (i.e., Ras activation), which controls the further downstream signaling events and is a control point for cellular growth. Sos binds to the receptor complex through Grb2. Association of Grb2 with the receptor either occurs directly or through the complex formation with Shc (Fig. 2). Therefore, Sos recruitment can proceed through two parallel but coupled pathways.

FIGURE 2.

Signal transduction model of the EGF receptor signaling pathway. This figure is adapted from Kholodenko et al. (1999). The rate constants of the reactions 3–25 are tabulated in Table II of Kholodenko et al. (1999). The rates for reactions 1 and 2 are tabulated in Table III.

Based on the experimental evidence (Haugh et al., 1999b; Burke et al., 2001), all of the receptors in our network model, regardless of their cellular location, can participate in the signal transduction. Thus, the set of molecular reactions included in the model (Fig. 2) can take place in all of the compartments of the cell, namely the EE vesicles, the late endosomes, and the plasma membrane. As each EE vesicle is included in the model explicitly, there are roughly 275 compartments in the simulated model, and a total of ∼13 thousand reactions need to be included in the kinetic simulations.

Construction of the simulation system

There are 23 distinct molecular species in the simulations. As listed in Table 1, 12 of the species are various forms of the receptors. The plasma membrane accessible to the cytoplasm is considered as the first compartment. This main compartment (PM) also includes the ligands in the extracellular medium (Fig. 1). There are many early endosomic (EE) vesicles, and their number fluctuates with time as they form and disappear. The two types of EE vesicles, coated and constitutive, have different receptor capture properties. There is only one late endosome pool and one lysosome pool in the model cell. The lysosome is a sink to remove degraded receptors and ligands. Although there is only one LE pool in the system, it can grow or shrink over time as EE vesicles merge into it or as small vesicles are removed from it.

TABLE 1.

List of species in the EGF receptor signaling model

Receptor forms
R	Unbound/free receptor
Ra	Ligand bound receptor, monomer
R2	Ligand bound, dimerized receptor
RP	Phosphorylated receptor dimer
R-PL	RP associated with PLC-γ
R-PLP	R-PL where PLC-γ is phosphorylated
R-Sh	RP bound by Shc
R-ShP	R-Sh where Shc is phosphorylated
R-Sh-G	R-ShP bound by Grb2
R-Sh-G-S	R-Sh-G bound by SOS
R-G	RP bound by Grb2
R-G-S	R-G bound by SOS
Other molecular species*
L	Ligand
Shc	Shc
ShP	Phosphorylated Shc
Grb	Grb2
SOS	Sos
PLCγ	PLC-γ
PLCγP	Phosphorylated PLC-γ
PLCγP-I	Cytoskeleton bound, inactivated PLCγP
G-S	Grb2:SOS complex
Sh-G	ShP:Grb2 complex
Sh-G-S	ShP:Grb2:SOS complex

^*The adaptor proteins Shc and Grb2 bind to the cytoplasmic tail of the receptor. Because the cytoplasmic tail of the receptor always faces the cytoplasm, the adaptor proteins (and Sos and PLC-γ) reside only in the cytoplasm. The adaptor proteins, or their complexes, may bind to the receptors that are on the early or late endosomes, but they return back to the cytoplasm when they dissociate from the receptor.

The simulation results were analyzed by defining grouped receptor and ligand quantities as shown in Table 2 (also see Fig. 2). By grouping various species, we can simplify comparison of the simulation results with experiments. The ligand bound forms of the receptors are grouped together to form the bound receptor group. Similarly, the forms of the receptors that are self-phosphorylated are classified as the phosphorylated receptor group. It should be noted that, with the exception of R and Ra, species representing different forms of the EGFR in the system correspond to dimerized complexes and contain two receptors and two ligands. It is assumed that both dimerized receptors are phosphorylated, and only one adaptor protein binds to the activated receptor complex.

TABLE 2.

Receptor and ligand group definitions

Group	Description	Definition
Runbound	Unbound receptor	R
Rbound	Bound receptor	Ra + 2 × (R2 + RP + R-PL + R-PLP + R-G + R-G-S + R-Sh + R-ShP + R-Sh-G + R-Sh-G-S)
Rphosphorylated or R*	Phosphorylated receptor	2 × (RP + R-PL + R-PLP + R-G + R-G-S + R-Sh + R-ShP + R-Sh-G + R-Sh-G-S)
Lfree	Free ligand	L
Lbound	Receptor bound ligand	Ra + 2 × (R2 + RP + R-PL + R-PLP + R-G + R-G-S + R-Sh + R-ShP + R-Sh-G + R-Sh-G-S)

Note that with these definitions R_bound = R^* + Ra + 2 × R2 and R_total = R_bound+R_unbound.

Ligand-receptor binding properties

The kinetic simulations were designed to investigate the response differences between EGFR activation with the ligands EGF and TGF-α. In a series of experiments, Reddy et al. (1996a,b, 1998) showed that ligand-receptor interaction characteristics are important factors that determine the relative potency of the ligands EGF and TGF-α. Their experiments studied the mitogenic response over a 3-day period with a 1-day time resolution. In the current study, we concentrated on determining the dynamic properties of the EGFR system within the first 2 h after ligand addition.

French et al. (1995) measured the binding properties of EGFR and its ligands TGF-α and EGF as a function of the medium's pH and tabulated the binding and dissociation rate constants at the extracellular and endosomal pH levels. It was determined that the binding affinities of these two ligands are similar at the pH (∼7.4) of the extracellular medium. However, TGF-α tends to dissociate from the receptor to a much larger extent than EGF in the acidic environment of the endosomes. To investigate the different response to activation of EGFR by different ligands, we performed kinetic simulations and assay experiments to measure the differences in the receptor phosphorylation levels upon activation of the EGFR by the ligands EGF and TGF-α.

Based on their experimental measurements, French et al. (1995) report a set of forward and reverse ligand:receptor binding rate constants at two different pH levels, and we have used these rate constants. However, to conserve the overall cohesiveness of the signal transduction model that we have chosen (Kholodenko et al., 1999), the rate constants reported by French et al. were scaled to make them compatible with the values tabulated by Kholodenko et al. In the first set of simulations, the scaling of the rate constants was done in such a way that the ratio of the values at different pH levels or between the different ligands was kept the same (Table 3). The second set of simulations is identical to the initial EGF simulations, but uses the more rapid dissociation rate of TGF-α to isolate the effect of its twofold higher dissociation. This fictitious ligand is labeled EGF-like in Table 3.

TABLE 3.

Rate constants of the ligand:receptor interactions

	Ligand and compartment
	EGF		TGF-α		EGF-like
Reaction	Plasma membrane	Endosomes	Plasma membrane	Endosomes	Plasma membrane	Endosomes
L + R→Ra	3.00 × 10−3	4.05 × 10−4	2.05 × 10−3	2.71 × 10−4	3.00 × 10−3	4.05 × 10−4
Ra→L + R	0.06	0.248	0.10	0.863	0.06	0.511
2 Ra→ R2	0.01	1.35 × 10−3	6.83 × 10−3	9.05 × 10−4	0.01	1.35 × 10−3
R2→2 Ra	0.1	0.413	0.169	1.438	0.10	0.852

Units of the first (Ra→L + R and R2→2 Ra) and the second (L + R→Ra and 2 Ra→ R2) order reactions are s⁻¹ and nM⁻¹ × s⁻¹, respectively.

Early endosomic vesicle formation and determination of vesicle's content

Based on the rate of fluid intake measurement experiments for fibroblast cells (McKinley and Wiley, 1988), we estimate the EE vesicle formation rate as 250 vesicles per min. The same set of experiments suggests that the coated-pit mediated and constitutive endocytosis pathways contribute roughly equally to the fluid intake of the extracellular solution. Assuming that the sizes of the EE vesicles are roughly the same for both vesicle types, the formation rates, λ_f, of the coated- and smooth-pit EE vesicles were set equal in our model, and the rate was 2.1 vesicles/s for both EE vesicle types.

Because the receptors that are ligand-bound have a higher affinity for coated-pits, the receptor internalization rate depends on the ligand bound state of the receptor (Lund et al., 1990). Experiments show that ∼2% of the unbound (ligand free) and 15% of the ligand-bound receptors on the PM get internalized per min. In the numerical implementation, the contents of the vesicles are determined by defining inclusion coefficients that reflect the internalization probabilities. How many molecules of a certain receptor type will go into an EE vesicle is found by multiplying the inclusion coefficient by the number of molecules of a particular receptor species. Inclusion coefficients, as shown in Table 4, were adjusted to yield the experimentally determined rates of ligand-free and ligand-bound receptor internalization. The endocytosis rate of the free ligands in the extracellular medium is very low and thus a very low ligand inclusion rate was used.

TABLE 4.

Early endosome inclusion coefficients

Molecule type	Coated-pit vesicles	Smooth-pit vesicles
Free ligand (L)	2.60 × 10−5	2.60 × 10−5
Free receptor (R)	7.94 × 10−3	7.94 × 10−3
Ligand bound receptor*	1.11 × 10−1	7.94 × 10−3

The reported values are the percentage of the number of molecules on the cell plasma membrane that go into an early endosomic vesicle that is formed.

^*These are the following receptor forms (see Table 1): Ra, R2, RP, R-PL, R-PLP, R-G, R-G-S, R-Sh, R-ShP, R-Sh-G, R-Sh-G-S.

Because we employ stochastic simulations, the percentage values given above are average values and the numbers of receptors internalized in the vesicles can fluctuate during the simulations. To better mimic the natural system, we have associated an uncertainty factor with the vesicle content determination. For example, the number of receptors that goes into an early endosome vesicle was set by multiplying the number of plasma membrane receptors at the time of vesicle formation by the inclusion coefficients discussed above. This value was further multiplied by a random number picked from a uniform distribution in the interval [0.8:1.2], i.e., up to an additional 20% uniform uncertainty was added into vesicle content determination. This allowed experimentally measured uncertainties to be included in our simulations.

Early endosome vesicle recycling and fusion with late endosomes

EE vesicles can either return back to the PM or merge into the LE. These processes are modeled as first order reactions with occurrence probabilities of λ × N_EE, where N_EE is the number of EE vesicles. As described above, coated- and smooth-pit type EE vesicles differ in their recycling characteristics where recycling back to the plasma membrane ratio is higher for the smooth-pit vesicles. The overall rates for EE vesicles to recycle back to the cell surface or merge with the late endosome were λ = 2.26 × 10⁻² and 1.85 × 10⁻² per s for the coated- and smooth-pit vesicles, respectively. During their trafficking, 48.7% and 96.2%, respectively, of the formed coated- and smooth-pit EE recycle back to the cell surface. We have chosen a high recycling ratio for the smooth-pit EE vesicles to be consistent with the experiments demonstrating that internalization through clathrin-coated pits is sufficient to account for the majority of fluid-phase endocytosis (McKinley and Wiley, 1988). Therefore, receptor internalization through the coated-pit EE vesicles is the dominant mechanism of receptor accumulation within cells, and this is particularly true when ligand is present in the system.

Modeling of the late endosome-receptor and ligand recycling and targeting for degradation

Although actual cells contain multiple copies of multivesicular endosomes, to keep this initial model simple, we have modeled the late/sorting endosome(s) as a single compartment that can grow or shrink in size. Receptor/ligand recycling from the LE or the transfer of the tagged receptors/ligands to the lysosome for degradation are modeled as a small vesicle segregating from the sorting endosome. Thus, a small part (most likely part of the tubular extensions of the LE; see, e.g., Lauffenburger and Linderman, 1993) of the LE becomes a separate vesicle. The size N_LE of the LE was monitored by counting how many EE vesicles undergo fusion or are produced by fission of the LE. The vesicle fission step was modeled as a first order reaction with a probability term λ × N_LE where the rate constant λ was 7.2 × 10⁻⁴ per s. Since N_LE is around 1560, ∼68 vesicles are formed from the LE per min on average. Trafficking parameters were chosen such that on average 2.8% of the formed vesicles are tagged for degradation in the lysosomes and the rest recycle back to the plasma membrane.

When a vesicle is removed from the LE, the vesicle's content is determined by the size of the sorting endosome N_SE and by the number of receptors and ligands in the LE at the time of vesicle formation. The number of molecules of a certain reactant species that goes into the vesicle is found by dividing the number of molecules of that species in the LE by its size N_LE. As in the case of early endocytic vesicle formation, the average value that is obtained is further multiplied by an uncertainty factor (20% in this study) to allow for random fluctuations. It has been experimentally observed that the degradation/recycle ratio of ligand-bound receptors in the LE is higher than the corresponding ratio of ligand-free receptors (French and Lauffenburger, 1997). This is apparently due to ligand occupancy facilitating interactions with endosomal retention components. As a simplifying first step to accommodating the relative differences in the recycling/degradation patterns of different receptor species (i.e., to include the role of sorting proteins) in the model, the number of ligand-bound receptors that go into a vesicle tagged for degradation in lysosome was further multiplied by a factor of 6. Thus, the fraction of the occupied receptors sorted to lysosomes was set at ∼17%.

Volume effects of the intravesicular compartments

Since the molar concentrations of the molecules depend on the volume, the small finite size of the intravesicular compartments will affect the ligand-receptor interaction properties. In our model, we have assumed that 5% of the cellular volume is found within endosomes (Lauffenburger and Linderman, 1993). With the average number of vesicles we have in our model, this corresponds to an early endosome vesicle volume of 1/36,600 of the cellular volume, and to a 1/23.5 of the cellular volume for the late endosome on average. Rates of the reactions in our model were volume corrected where appropriate.

Receptor synthesis and ligand input/loss

Receptors (in unbound form, R) are synthesized at a constant rate of 2.8 molecule/s (i.e., a zeroth order reaction). The synthesized receptors are added into one of the existing smooth-pit vesicles. Ligand appears in the extracellular medium at a constant rate for a given duration. This feature allows for the simulation to mimic a natural system where ligand would be generated by regulated proteolysis, or an artificial system where ligand would be provided as a bolus. In addition to internalization, a fraction of the free ligand is lost from the extracellular environment per unit time. This feature represents the presence of extracellular sinks, such as capillaries, competing cells, or binding to the extracellular matrix. We used a very slow escape rate in our calculations, k = 1.68 × 10⁻² percent/min.

Initial configurations and running the simulations

In many kinetic models, the initial condition of the system is often ignored, and the initial concentrations of many molecular species are initially set to zero. However, most experimental systems start at steady state and are perturbed by a change in some parameter, such as ligand concentration. To include this feature and to obtain a reasonable initial configuration, we ran a kinetic simulation in the absence of ligands until steady state was effectively achieved. The initial concentrations of Grb2 (85 nM), Shc (150 nM), and Sos (34 nM) were taken from literature (Kholodenko et al., 1999). Starting with these values, a 2-hour kinetic simulation was sufficient to obtain the steady state for the no-ligand condition. This steady state configuration was used as the starting point in our simulations.

Because a stochastic simulation approach was used, there were fluctuations around the average values in the computed quantities. Thus, obtaining reliable average quantities required simulations to be repeated multiple times. Our statistical tests showed that eight simulation runs were enough to achieve reliable average quantities. Increasing the number of simulation runs did not significantly lower the statistical fluctuations.

EXPERIMENTAL MATERIALS AND METHODS

Materials

Human EGF was purchased from PeproTech (Rocky Hill, NJ) and recombinant human transforming growth factor TGF-α was obtained from R&D Systems (Minneapolis, MN). Monoclonal antibody (mAb) 225 against the EGFR (Gill et al., 1984) was purified from hybridomas obtained from American Type Culture Collection (Manassas, VA). Anti-EGFR rabbit polyclonal antibody 1005 (sc-03) was purchased from Santa Cruz Biotechnology (Santa Cruz, CA). Anti-rabbit-alkaline phosphatase-conjugated secondary antibody was purchased from Sigma (St. Louis, MO). Anti-phosphotyrosine alkaline-phosphatase-conjugated antibody RC20AP was purchased from Becton-Dickson/Transduction Laboratories (Lexington, KY).

Cell culture and EGFR phosphorylation assay

The HMEC cell line 184A1 was provided by Dr. Martha Stampfer and was cultured in DFCI-1 medium supplemented with 12.5 ng/ml EGF (Stampfer, 1985; Band and Sager, 1989). Between 16 and 20 h before experiments, cells were washed twice with warmed phosphate buffered saline, the medium was replaced with bicarbonate-free DFHB minimal medium plus 1% bovine serum albumin (BSA), and transferred to a 37°C air incubator. Cells were treated with varying concentrations of TGF-α or EGF added to bicarbonate-free DFHB medium plus 1% BSA and incubated for varying periods on a 37°C water bath. The cells were placed on ice, washed three times with ice-cold PBS, and then treated with ice-cold acid-glycine strip buffer (50 mM glycine-HCl/100 mM NaCl/1 mg/ml polyvinylpyrrolidone, pH 3.0) (Haugh et al., 1999a). To allow the dephosphorylation of surface associated EGFR from which ligand had been stripped, cells were then washed three times with ice-cold PBS and incubated in bicarbonate-free DFCI-1 plus 1% BSA at 37°C for 5 min.

Both stripped and unstripped cells were lysed in extraction buffer (10% glycerol, 1% Triton X-100, 20 mM HEPES, pH 7.0, 0.02% azide, 0.1 mM orthovanadate, 2 mM sodium pyrophosphate, and 1 μg/ml each of pepstatin, chymostatin, leupeptin, and aprotinin) and lysates were cleared of debris by centrifugation at 16,000 × g for 10 min. The amount of EGFR per sample, and the extent to which EGFR in each sample was tyrosine phosphorylated, was determined using a ratiometric ELISA (Haugh et al., 1999a; Schooler and Wiley, 2000). A Molecular Devices microplate reader was used to take a single endpoint measurement after allowing the colorimetric reaction to incubate for 15 min.

RESULTS

After developing and testing our EGFR signaling pathway network model, we used it to study the receptor sorting dynamics as the receptor/available ligand ratio was varied. One still open question about EGFR signaling is what dictates the magnitude and specificity of the ligand activated mitogenic response. In a series of experiments, Reddy et al. (1996a,b, 1998) measured how different treatments of medium replenishment and serum levels affect the relative mitogenic potencies of different ligands. They showed, in particular, that, because it has a strong effect on the receptor downregulation and trafficking, ligand availability is an important factor in determining the overall mitogenic response. Modeling studies comparing the dynamical response of the EGFR signaling pathway when the available ligand per receptor per cell is systematically varied can reveal the important factors. To this effect, we ran our first series of simulations with the available EGF ligand per receptor ratio varied between 0.07 (0.2 nM ligand) and 6.8 (20 nM ligand). At the smaller end of this range, because the number of available ligands is low, degradation of the ligand and the receptor is not a major factor and nonspecific constitutive endocytosis dominates the receptor trafficking and sorting properties. At the other end of the spectrum, where there is an abundance of ligand, ligand-activated receptor properties dominate the overall cellular response.

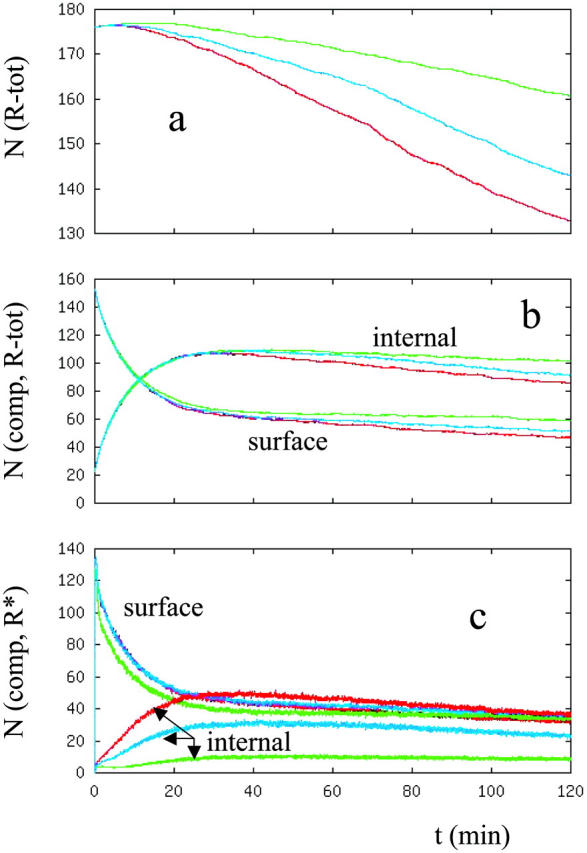
In the first set of simulations, starting from the steady state configuration with no ligand present, EGF in the dose amounts of 0.2 nM, 1 nM, 2 nM, 5 nM, 10nM, and 20 nM was added to the extracellular medium at time 0, and the temporal response of the system was followed. Fig. 3, a and b, respectively, show the decrease in the total number of phosphorylated receptors in the system and the ratio of the number of internalized receptors to the number of receptors that are on the plasma membrane (In/Sur ratio) after EGF is introduced. Results for the 5 nM and 10 nM ligand concentrations are omitted from Fig. 3 to make the figure less crowded. Results for these ligand concentrations fall in between the 2 nM and 20 nM results. As expected, the receptors are more phosphorylated and they are degraded faster as the ligand concentration increases (Fig. 3 a). Fig. 3 b shows that ligand availability can have a significant effect on the percentage distribution of the phosphorylated receptors between cellular compartments, especially at low EGF concentrations. Fig. 3 b also shows that the distribution of phosphorylated receptors among compartments does not change further when the ligand dose is raised above ∼2 nM, i.e., for a ligand/receptor ratio of ∼0.7. Saturation of the compartment distribution of phosphorylated receptors at such a relatively low ligand amount is somewhat surprising. However, as Table 5 and Fig. 3 c show, if the compartmental distribution of total number of receptors (phosphorylated + unphosphorylated) is monitored, the maximum of the In/Sur ratio keeps increasing with the ligand concentration up to a larger ligand dosage, ∼5 nM. The difference between the phosphorylated and total number of receptor distributions is due to the fact that the ligand-bound receptors are internalized and retained in the intravesicular compartments at larger ratios than the free receptors. As a result, when the amount of ligand in the system is high enough to activate most of the receptors, the In/Sur ratio of the phosphorylated receptors nearly reaches its maximum. Although not reported herein, similar results were observed when the ligand TGF-α was added to the system with the exception that it requires more than a 2 nM dose of TGF-α for the In/Sur distribution of the activated receptors to reach close to its maximum.

FIGURE 3.

(a) Total number of phosphorylated EGF receptors in the cell. Curves represent the number of activated receptors when the cell is stimulated with different ligand doses at the beginning. The y axis represents the number of receptors in thousands. (b) Ratio of the number of phosphorylated receptors that are internalized to that of the phosphorylated surface receptors (in the text this ratio is referred as the In/Sur ratio of the phosphorylated receptors). (c) Ratio of the number of internalized receptors to the number of surface receptors. Curves are colored as: [L] = 0.2 (magenta), 1 (blue), 2 (green), and 20 (red) nM.

TABLE 5.

Distribution of the receptors among cellular compartments

[L] (nM)	Phosphorylated receptors	Total number of receptors
0.2	0.23	0.18
1.0	0.80	0.39
2.0	1.11	0.82
5.0	1.09	1.60
10.0	1.14	1.76
20.0	1.13	1.76

Entries are the t = 40 min values of the In/Sur plots that are reported in Fig. 3, b and c. The t = 40 min point was chosen because at large ligand concentrations the In/Sur plots reach their maximum around this time point. This choice was, however, somewhat arbitrary.

Further sets of kinetic simulations were run to investigate the dependence of receptor activation on the two different ligands EGF and TGF-α. Because they control the receptor downregulation and trafficking, the ligand availability and ligand-receptor interaction characteristics are important factors that determine the relative mitogenic activity of the ligands EGF and TGF-α (Reddy et al., 1996a,b; 1998). French et al. (1995) studied the effect of medium's pH on the binding properties of EGFR and its ligands TGF-α and EGF. We have addressed similar questions in our kinetic simulations and investigated the response differences between the activation of the EGFR with its ligands EGF and TGF-α. We have complemented our computational studies with experiments measuring the cellular receptor activity in HME cells.

The second set of simulations addressed the differences in the EGFR signaling upon activation by two different ligands, EGF and TGF-α. In this set of simulations, the receptor binding properties of the ligands EGF and TGF-α were chosen in accordance with the experimental values (French et al., 1995), and the ligand-receptor interaction parameters are given in Table 3. TGF-α binds to the surface receptors with an affinity slightly lower than that of EGF. The receptor-binding affinity difference is, however, much larger for ligand-receptor interactions taking place in the intracellular compartments. Based on the ligand-receptor interaction characteristics, one can expect that TGF-α would dissociate to a greater extent in the late endosome, which would in turn lead to an increase in the receptor recycling. Thus, for activation of EGFR by TGF-α, such differences in the sorting properties would lead to a signal that would be strongly biased toward the surface. These expectations are supported by our simulation results.

Fig. 4 a shows the experimental and computational results for the total number of receptors in the cell when the cells are stimulated with 20 nM ligand. Due to the increased receptor recycling to the plasma membrane, as expected, the decrease in the number of receptors is slower when the ligand is TGF-α. Fig. 4, b and c, shows the compartment distribution of the receptors. The total numbers of receptors that are on the surface or within the cells are slightly higher for the TGF-α case (Fig. 4 b). Since they correspond to the activated forms, a better indicator of the effects of the receptor trafficking on the cellular response would be to investigate the dynamics of the phosphorylated receptors. Fig. 4 c shows the compartment distribution of the phosphorylated receptors as a function of time as computed in the simulations. Although the contribution of the surface receptors to cell signaling is roughly the same for both ligands, the contribution of the internalized receptors is very low for the TGF-α case. To further confirm this finding, we have experimentally measured the distribution of the phosphorylated receptors in HME cells. As discussed above, internalized to surface (In/Sur) ratio of the phosphorylated (i.e., activated) receptors is a good indicator of the cell signaling bias. To compare the signaling bias after stimulation with the ligands EGF and TGF-α, we computed the ratio of the receptor In/Sur ratios for these two ligands and compared our simulation results with experimental values (Fig. 5). Although the overall receptor distributions (ratios for the total number of receptors) are similar, the ratio of the In/Sur ratios for the phosphorylated receptor distribution, i.e., the cellular signal, differs from unity significantly. It is clear from Fig. 5 that, after enough time passes for receptor internalization, the cellular signal is highly biased toward the cell surface when the stimulating ligand is TGF-α. In this regard, there is good agreement between the computations and the experiments. The corresponding In/Sur ratios for the Sos-bound receptors are very similar to the In/Sur ratio of the phosphorylated receptors, and, therefore, are not reported.

FIGURE 4.

Comparison of the results when the EGFR signaling pathway is stimulated with its ligands EGF (red) and TGF-α (green). (a) Total number of receptors in the cell as a function of time after 20 nM ligand is added to the system. Red diamond (EGF) and green square (TGF-α) points show the experimental results. The experimental results at short times were normalized to overlap them with the computational results. (b) Distribution of the receptors between intravesicular compartments and the cell membrane. (c) Distribution of the phosphorylated receptors between intravesicular compartments and the cell membrane. In the figures, y axes represent the number of receptors in thousands.

FIGURE 5.

The ratio of the In/Sur ratios when the EGFR signaling pathway is stimulated with its ligands EGF and TGF-α at 20 nM ligand concentration. Comparison of the computational (solid lines) and experimental (points) results. Ratio of the ratios for the phosphorylated (i.e., activated) (blue), and total (phosphorylated + unphosphorylated) number (magenta) of receptors.

The results shown in Figs. 4 and 5 imply that trafficking of the EGF receptors that is dependent on the ligand type can introduce compartment specificity and bias the cellular signaling toward the plasma membrane or the intravesicular compartments. Due to the dependence of the contribution of the internalized receptors on the type of the stimulating ligand, the cellular response can become strongly biased toward signaling occurring at the plasma membrane, which would result in compartment specificity of the receptor signaling.

The third set of simulations addressed the following issue: Assume that there is a ligand of EGFR which has exactly the same association to the receptor properties of EGF; however, it dissociates from the receptor at a higher (2.06 times faster) rate when the pH is at the pH level of the endosomes. It was assumed that the only rates that change are the rates of ligand dissociation from the receptor (reaction 1 in Fig. 2) and of the reaction that separates a receptor dimer into monomers (reaction 2). The receptor binding affinities of the ligands depend on the ligand type and on the pH levels. Therefore, this set of simulations only partially implements the compartment and the ligand-type dependent properties of the receptor-ligand interactions. How much would EGFR signaling differ between this hypothetical (EGF-like) ligand and EGF? This is a simplistic but direct way of investigating the consequences of the pH dependence of the ligand/receptor dissociation properties for cell receptor signaling. This investigation allowed us to determine whether the response differences between EGF and TGF-α are solely due to the excess ligand/receptor unbinding in the late endosome.

The results of the third simulation set are reported in Fig. 6, a–c, and are to be compared to the results of the second simulation set (Fig. 4). As shown in Fig. 6, the results for the EGF-like ligand (blue curves) lie in between the results for EGF (red) and TGF-α (green). This means that excessive ligand dissociation in the intravesicular compartments can only partially explain the signaling differences between EGF and TGF-α and that the response differences due to the binding properties and the physical interaction parameters at the plasma membrane are also important in understanding the activation of EGFR by these two types of ligands.

FIGURE 6.

Comparison of the computed results for the hypothetical ligand (blue) that was investigated in the third set of simulations with the results for the ligands EGF (red) and TGF-α (green). Ligand concentration is 20 nM. Captions of the reported results are the same as in Fig. 4, a–c.

Because it controls the MAP kinase cascade further downstream in the signal transduction pathway, the Ras GTPase activation level provides another good point at which to monitor EGFR signaling properties (Fig. 7). In our model, in accordance with the experiments (Haugh et al., 1999b; Burke et al., 2001), Ras GTPase bound to the internalized receptor complexes is assumed to contribute to cellular signaling as do its counterparts bound to the surface receptor complexes. As Fig. 7 a shows, unless there is a critical Sos recruitment level in cells, the Sos/Receptor complex formation properties do not have a significant dependence on the ligand type. There are differences in Sos recruitment levels at long times but, unless there are critical response levels, these differences are not large enough to lead to significant differences in cellular response. In addition, the transient Sos activation levels have insignificant ligand-type dependence.

FIGURE 7.

Number of Sos molecules recruited to the receptor. (a) Dependence on the ligand type, EGF (red) and TGF-α (green) at 20-nM ligand concentration. (b) Dependence on the EGF ligand concentration, [L] = 0.2 (magenta), 1 (blue), 2 (green), and 20 (red) nM. In the figures, y axes represent the number of receptor:Sos complexes in thousands.

We have also looked at the dose-response characteristics of the Sos recruitment level. As Fig. 7 b shows, the level of Sos recruited to receptor complexes increases as the amount of stimulating EGF is increased, as expected. The most noticeable difference in the results at various EGF concentrations occurs at short-time transient activation levels of the signaling pathway (Fig. 7 b); the short-term response diminishes as the ligand concentration is reduced. Further increases in the ligand level above the basal amount change mainly the transient activation but contribute only insignificantly to the long-term growth response. Although the time scales studied in the experiments are much longer than the time range studied in this report, the experimental results obtained by Reddy et al. (1996a,b, 1998) support this conclusion.

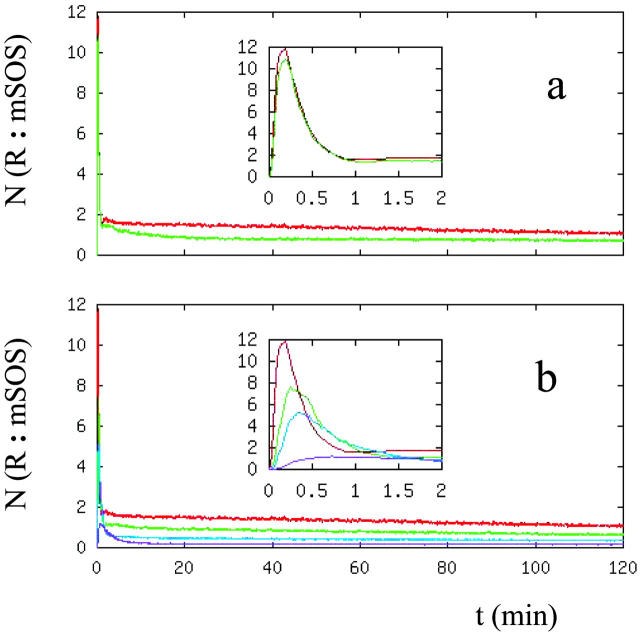
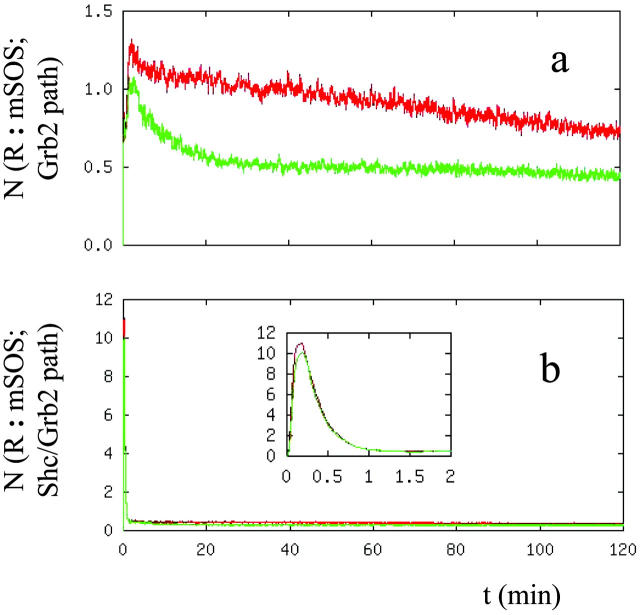
Recruitment of Sos to the receptor complexes can occur through two parallel pathways as shown in Fig. 2. Sos is recruited to the receptor by forming a complex with Grb2. Grb2 interacts with the phosphorylated receptor either directly or through the formation of Grb2/Shc complexes. Thus, we investigated the relative contribution of these parallel pathways to Sos recruitment. Fig. 8 shows the contribution of each of the two. The transient feature that occurs on the time scale of minutes is due to Sos activation through the Shc/Grb2 pathway. It has been observed that the SH2 domain of Grb2 has a higher affinity for the phosphorylated Shc, and therefore, it is more likely that the prominent mechanism of Ras membrane localization is through the intermediation of the Shc-Grb2-Sos complex (Sasaoka et al., 1994). Since the binding affinity of Shc toward the phosphorylated receptor is higher than that of Grb2 (compare the reaction rates of reactions 9, 13, and 21, Table II in Kholodenko et al., 1999), it can be expected from our model that the transient activation is due to the Sos recruitment through the Shc/Grb2 pathway. However, at long times the contribution of the Grb2 and Grb2/Shc pathways are at comparable levels.

FIGURE 8.

Number of Sos molecules recruited to the receptor complexes through (a) the Grb2 and (b) the Shc/Grb2 branch of the EGFR signal transduction network. Caption is the same as Figure 7 a.

DISCUSSION

Several groups have in the past constructed mathematical models to investigate various components of EGFR signaling, such as signal transduction and receptor downregulation through receptor trafficking. Although these studies complement each other, no single study has used a large-scale global model that includes both the signal transduction and receptor trafficking properties of EGFR signaling. The current study fills this gap and introduces our global model for the EGFR cellular signaling pathway. By using the new model, we have investigated various aspects of the EGFR signaling. We have also performed experiments to test the results of the simulations.

We have used the new model to investigate the ligand dose-response characteristics of EGFR signaling and the differences in cellular response upon activation of EGFR by its different ligands. Our findings can be summarized as follows: 1), The predictions of our model for the receptor downregulation and receptor distribution among cellular compartments are in very good agreement with the experiments. 2), The distribution of the total (phosphorylated plus unphosphorylated) number of receptors among cellular compartments has a monotonic dependence on the stimulating ligand concentrations. Due to the recycling and degradation patterns of the receptors, the distribution of the total number of receptors among cellular compartments does not saturate until large ligand doses are provided. 3), At low ligand concentrations, the distribution of the phosphorylated receptors among cellular compartments also has a monotonic dependence on ligand. However, the distribution of the phosphorylated receptors among cellular compartments levels off to a state that changes only insignificantly as the ligand dosage is further increased. The saturation level of the phosphorylated receptor distribution among cellular compartments occurs at a relatively low amount of EGF but, in the case of TGF-α, a higher dose is required. 4), In agreement with predictions based on experimental measurements, when EGF receptors are activated with TGF-α, the cellular response is biased toward the signal coming from the plasma membrane associated receptors. 5), Investigation of the cellular response characteristics using a hypothetical EGF-like ligand showed that the response differences upon activation by the ligands EGF and TGF-α is not solely due to the extensive dissociation of TGF-α from the receptors in the endosomic vesicles. The ligand-receptor interaction properties at the plasma membrane and the overall ligand-receptor binding properties also make a significant contribution to the differences in the response. 6), Comparison of the results showed that transient activation of the EGFR signal transduction pathway does not depend on the ligand type. Even at longer times, different ligand types recruit similar amounts of Sos to the receptor complexes. This observation, and the results for the ligand-type specific distribution of the activated receptors among cellular compartments, suggests that, rather than manipulating the magnitude of the signal, receptor trafficking controls the bias of the cellular response. 7), Transient activation of the EGFR signal transduction pathway is due to the interaction of Grb2 with the receptor through the protein Shc. However, Grb2 and Grb2/Shc pathways contribute at similar levels at long times.

In addition to the detailed investigation of the EGFR signaling network, our study also shows that large-scale simulations of the kinetics of biological signaling networks are possible. For example, the model studied in this report consists of hundreds of distinct compartments and ∼13,000 reactions/events that occur on a wide spatial-temporal range. This was made possible by the use of our recently developed kinetic Monte Carlo algorithm (Resat et al., 2001b). Such method development efforts are starting to make it possible to use large, global models in computational biology research.