Metabolic Switching in the Sugar Phosphotransferase System of Escherichia coli

Abstract

Bacteria grown in a mixture of multiple sugars will first metabolize a preferred sugar until it is nearly depleted, only then turning to other carbon sources in the medium. This sharp switching of metabolic preference is characteristic of systems that optimize fitness. Here we consider the mechanism by which switching can occur in the Escherichia coli phosphotransferase system (PTS), which regulates the uptake and metabolism of several sugars. Using a model combining the description of fast biochemical processes and slower genetic regulation, we derive metabolic phase diagrams for the uptake of two PTS sugars, indicating regions of distinct sugar preference as a function of external sugar concentrations. We then propose a classification of bacterial phenotypes based on the topology of the metabolic phase diagram, and enumerate the possible topologically distinct phenotypes that can be achieved through mutations of the PTS. This procedure reveals that there is only one nontrivial switching phenotype that is insensitive to large changes in biochemical parameters. This phenotype exhibits diauxic growth, a manifestation of the winner-take-all dynamics enforced by PTS architecture. Winner-take-all behavior is implemented by the induction of sugar-specific operons, combined with competition between sugars for limited phosphoryl flux. We propose that flux-limited competition could be a common mechanism for introducing repressive interactions in cellular networks, and we argue that switching behavior similar to that described here should occur generically in systems that implement such a mechanism.

INTRODUCTION

In the 1940s Jacques Monod discovered the phenomenon of “diauxie” (Monod, 1966): he found that bacterial growth in certain sugar mixtures consisted of two distinct exponential growth phases, separated by a lag phase during which growth was halted. Starting with such observations, Monod proposed that a bacterial cell does not simply take up various nutrients in proportion to their abundance, but instead actively controls their uptake by regulating its own enzymatic state. As the bacterium switches from one carbon source to another, a transient halting of growth occurs while the specific enzymes needed to metabolize alternative nutrients are synthesized.

Recent experiments on Escherichia coli suggest that this active control serves a very specific purpose: nutrient fluxes across the entire bacterial metabolic network seem to be adjusted so as to produce the maximum possible growth rate consistent with stoichiometry (Edwards et al., 2001). Very general considerations imply (see Analysis section) that such optimal flux distributions sometimes change discontinuously as the composition of the growth medium is varied. Therefore, if optimality is to be achieved, a small change in nutrient concentration must sometimes precipitate a large change in the enzymatic composition of the bacterium. A particularly well-studied system exhibiting such behavior is the E. coli lactose utilization network: expression of the lac operon, which codes for lactose-specific enzymes, is induced by the presence of lactose but repressed by the presence of glucose, the latter being the nutrient of choice for the bacterium (Müller-Hill, 1996). A detailed experimental (Novick and Weiner, 1957) and theoretical (Chung and Stephanopoulos, 1996) analysis reveals that the lac induction process is hysteretic in nature, typical of backward bifurcations (Strogatz, 1994) and first-order phase transitions (Ma, 1976) in physical systems. The hysteresis is characterized by a region of nutrient concentrations over which two alternative enzymatic states coexist, at the boundaries of which the enzymatic state can switch in a discontinuous fashion, leading to diauxic growth.

Here we investigate switching in the bacterial carbohydrate utilization network known as the phosphotransferase system (PTS), which carries out the uptake and phosphorylation of several sugars (Postma et al., 1993). PTS dynamics are determined by fast biochemical interactions, as well as by slower adaptation due to the induction of key PTS genes (see Analysis section). Competition between sugars for limited phosphoryl flux, together with positive feedback due to the induction of genes coding for sugar-specific channels, produces sharp switching between enzymatic states. We construct metabolic phase diagrams showing the transitions between these states as external sugar concentrations are varied (see Analysis section). Our approach is heuristic, and is of value even in the absence of accurate and complete biochemical data: we identify all of the topologically distinct phase diagrams that can occur over a range of biochemical parameters. That is, we classify phase diagrams based on qualitative properties, such as the various types of transitions they contain. This topological definition of phenotype is insensitive to the exact position of metabolic transition boundaries, and is therefore practical from an experimental standpoint. To the extent that parameter variation can be produced by mutations, the classification of phase diagrams provides a classification of possible bacterial phenotypes.

Surprisingly, of the many distinct nontrivial switching phenotypes that could occur, we find only one that is insensitive to large variations in the underlying biochemical parameters: the architecture of the PTS seems to be designed to implement one particular metabolic strategy. In our discussion we argue that this phenotype arises as a consequence of the winner-take-all (WTA) architecture of the PTS. We then discuss the parameters available to the cell to tune its metabolic response toward optimality, and we show how the topology of the metabolic phase diagrams can be studied experimentally.

ANALYSIS

Optimizing sugar metabolism

Techniques such as flux balance analysis and linear optimization can be applied to a comprehensive stoichiometric model of the E. coli metabolic network to calculate optimal flux distributions for growth on various substrates (Gombert and Nielsen, 2000; Schilling et al., 2001). Here, by way of a simple example, we derive the features of an optimal strategy for growth on multiple sugars based on linear constraints similar to the stoichiometric constraints underlying flux balance analysis (Danzig, 1963).

Consider a population of bacteria growing at a rate γ in a medium containing multiple sugar species with concentrations S_j. Let ɛ_j represent the enzymatic machinery that catalyzes the uptake and metabolism of sugar S_j. The rate of sugar uptake is most simply modeled as being proportional to both the external sugar concentration and to that of the sugar enzymatic machinery, ; the metabolism of these sugars will therefore lead to the production of free energy at a rate where ζ_j is the energy contribution of sugar S_j. The exponential growth of total cell volume at the rate γ will cause the concentrations of bacterial proteins to decay by dilution unless they are continually synthesized at some rate κ_j. These concentrations therefore evolve according to with ɛ_j = κ_j/γ in steady state. If α_j is the free energy required for the synthesis of one unit of ɛ_j, then the total rate of free energy consumption in steady state is given by 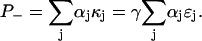Equating the rates of energy production and consumption, we find

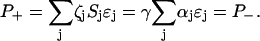(1)

The optimization problem involves maximizing the growth rate γ by suitably varying the enzyme concentrations ɛ_j:

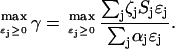(2)

The solution is straightforward: ɛ_j = 0 for all j except for the j = j^* with the highest value of ζ_jS_j/α_j. For example, if there are two metabolizable sugars S₁ and S₂ present in the medium, then across the line S₁/S₂ = ζ₂α₁/ζ₁α₂ the optimal choice of sugar switches discretely from S₂ to S₁, with 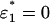on one side of the line, and 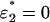on the other (see Fig. 3 E).

FIGURE 3.

Two-sugar uptake. We summarize operon induction levels as being either high, H, or low, L, for each sugar; we summarize system behavior by indicating all of the stable fixed points that obtain. For example, LH represents a state in which production of ɛ₂ alone is induced, so S₂ alone is metabolized; LL/HL/LH represents a state in which three distinct fixed points occur at once. (A) Independent hysteretic switches. A single hysteretic system goes through the states L, L/H, and H as S₁ is varied from 0 to ∞. If we assume a similar but independent control mechanism for the uptake of another sugar, S₂, the combined switching dynamics will be as shown in the figure. (B–D) PTS metabolic phase diagrams indicate operon expression levels as a function of external sugar concentrations. Discontinuous transitions occur across lines in {S₁,S₂} space. Diagrams are obtained by numerical solution for three parameter values {υ,β}: (B) {0.0625, 0.2}, (C) {0.077, 0.2}, and (D) {0.25, 0.25}. Stochastic effects will cause a population of bacteria to occupy all of the available fixed points simultaneously, but the majority of bacteria will occupy the most stable fixed point. In D, this creates a transition line (dashed) across which the most stable fixed point (indicated in circles) goes from HL to LH. (E) An optimal metabolic strategy for growth on two sugars. The optimal choice of sugar switches discontinuously across the dotted line, from S₁ below to S₂ above; the desired enzymatic state is therefore HL below the line, and LH above it. Note that the population-averaged switching behavior of the phenotype in D is consistent with the optimal metabolic strategy shown in E.

What has been derived here is the desired optimal metabolic strategy; what in fact occurs depends on how the enzyme synthesis rates κ_j are actually regulated. More detailed optimization functions might produce more complex desired strategies; however, the occurrence of discontinuous transitions is generic. Any actual regulatory mechanism must therefore include a means by which such switching can occur, if it is to achieve optimality. Moreover, it is insufficient to regulate the uptake of various sugars independently; what is required is some interaction between their uptake systems. As we shall show, the PTS is a source of such an interaction.

The phosphotransferase system

The phosphoenolpyruvate (PEP) carbohydrate phosphotransferase system (PTS) is central to several bacterial metabolic, sensory, and regulatory pathways (Postma et al., 1993). The system is responsible for the uptake and phosphorylation of a wide variety of sugars including glucose, fructose, mannitol, and mannose; for the control of their metabolism; for chemotaxis toward these sugars; and for a host of other regulatory interactions.

At the heart of the PTS is a cascade of phosphorylation and dephosphorylation reactions that serves to transfer a phosphoryl group, bucket-brigade style, from PEP to one of several substrate sugars (Fig. 1 A). Phosphorylation of the sugar makes its translocation across the bacterial membrane irreversible, both these reactions being driven by the free energy of conversion of PEP into pyruvate (Pyr). The first two steps in the PTS cascade are mediated by enzyme I (EI) and HPr, both cytoplasmic proteins that make up the general or nonspecific PTS system. In contrast, the next three phosphotransfer reactions are performed by sugar-specific enzymes collectively known as enzymes II (EII). EIIA is typically a cytoplasmic protein, whereas EIIB and EIIC form a membrane-bound complex (EIIBC) that is involved in the actual translocation of the sugar, and is therefore termed the sugar permease. Enzymes EIIA and EIIBC are typically transcribed from the same operon, so their concentrations are correlated.

FIGURE 1.

The PTS system. (A) The PTS cascade. The enzymes EI and HPr form the general PTS, whereas EIIA and EIIBC form the sugar-specific PTS. The cascade of PTS enzymes catalyzes the transfer of a phosphoryl group from PEP to a carbohydrate, glucose (G) in the case shown, and drives the transportation of that carbohydrate into the cytoplasm; in the process, PEP is converted into Pyr. Each phosphotransfer reaction is reversible, with forward rate constant k and backward rate constant but the final translocation of the carbohydrate is essentially irreversible. (B) The phosphotransfer branch point and flux-limited competition between different PTS sugars S_j. Total phosphoryl flux J is split into sugar-specific fluxes J_j (j = 1 … m). Flux-limited competition is mediated by the fraction f of phosphorylated HPr. Intracellular sugars induce their specific operons (local activation), but compete with each other for phosphoryl flux (global inhibition), thus creating a WTA-type network.

Let m be the number of distinct PTS sugar species; we will use the subscript notation […]_j, j = 1,…,m, to refer to rates, concentrations, and fluxes specific to sugar j. Let the extracellular concentrations of these sugars be S_j; these concentrations are parameters that can be varied in an experiment. Let ɛ_j represent the normalized concentration of enzymes specific to sugar j, so that [EIIA]_j,[EIIBC]_j ∝ ɛ_j; the quantities ɛ_j will be our dynamical variables.

The phosphorylation reactions of the PTS cascade are reversible but are not in equilibrium individually, because there is a net phosphotransfer flux J. Since the enzymes EIIA/BC are sugar-specific, the HPr→EIIA step is the phosphotransfer branch point: through this junction multiple PTS sugars compete for phosphoryl flux (Fig. 1 B). Balancing fluxes at the phosphotransfer branch point gives, in steady state,

(3)

where rate constants are as shown in Fig. 1 A. The detailed chemical-kinetic analysis involves applying such equations at each cascade step, and solving for steady-state fluxes as functions of external sugar concentrations (see Appendix). The results of such an analysis form the starting point for our discussion.

It is useful to define a quantity τ_j which measures the demand for phosphoryl flux by sugar j:

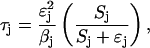(4)

where β_j is a sugar-specific parameter. We see that flux demand τ_j is an increasing function of sugar concentration S_j, and of sugar-specific operon expression level ɛ_j. (The 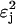term arises because the concentrations of enzymes EIIA and EIIBC are correlated; the hyperbolic term arises due to saturation of the sugar permease.) Note that τ_j depends only on quantities specific to sugar j. However, the limited availability of phosphoryl flux from PEP creates an effective interaction between the various sugar uptake mechanisms, so that the flux J_j actually received by any single sugar depends on the flux demands τ_i, i = 1,…,m, of all the sugars present. The resulting flux distribution is of a remarkably simple form. If J_max is the maximum possible flux through the PTS cascade (which occurs if each phosphotransfer reaction is driven entirely in the forward direction), then

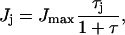(5)

where is th total flux demand. A large flux demand causes a dephosphorylation of the entire PTS cascade. The fraction f of HPr which is phosphorylated,

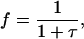(6)

is a direct readout of total flux demand, blind to which specific sugars are being taken up. As total demand becomes very large, the total phosphoryl flux 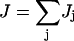approaches its maximum possible value, J_max, and f approaches zero. We see that f mediates the interaction between PTS sugars at the phosphotransfer branch point (Fig. 1 B). In a multiple sugar system, an increase in τ₁ alone will lead to an increase in J₁, but a decrease in J_j for all other sugars because of the decrease in f; we term this effect “flux-limited competition”.

We have so far dealt with PTS biochemistry, which equilibrates rapidly. It remains to specify the time dependence of the slower genetic variables, namely the enzyme concentrations {ɛ_j}. Sugar-specific operons are typically induced by their sugar substrates (Lin, 1993) (although certain operons, such as those relating to mannose and glucose, are not highly inducible). The intracellular concentration of a particular sugar equilibrates to a level proportional to its uptake rate, so and the expression level of the corresponding operon is typically a hyperbolic function of this quantity. (Although the hyperbola varies linearly with low sugar concentrations, operon expression levels are naturally nonlinear functions of the dynamical variables ɛ_j, due to the 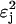term in Eq. 4; no ad hoc source of nonlinearity is necessary, such as might have been provided by the use of a sigmoid in place of the hyperbola.) For high values of ɛ_j, intracellular sugar concentrations saturate due to the limited availability of general PTS enzymes. We assume that this saturation occurs before that of the operon expression level, so that the hyperbola can be approximated by a linear function; the operon expression level is thus proportional to the intracellular sugar concentration. Assuming that enzyme concentrations decay by dilution, the resulting time evolution of ɛ_j is given by:

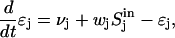(7)

where the unit of time has been chosen so that the dilution rate is unity. A basal transcription rate ν_j allows the bacterium to take up sugars whose operons are not, at some given moment, induced; a similar effect would be achieved by any leak mechanism that allowed a sugar to slowly enter the cell in the absence of sugar-specific permeases. The parameter w_j is a measure of the inducer efficiency (parameterizing the net interaction between the inducer, the corresponding repressor or transcription factor, and the DNA operator). After a rescaling of concentration units (see Appendix) we obtain our final dimensionless dynamical equations:

(8)

Here, β_j ∝ (J_max/w_j)², so τ_j can be thought of as measuring flux demand relative to the maximum supply possible from PEP. The system described by these equations is indicated schematically in Fig. 1 B.

Switching behavior and phenotypic classification

We now derive the cell's metabolic preference, as expressed by the degree of induction of different sugar specific operons, for one-sugar and two-sugar uptake. We solve Eq. 8 in steady state to find the operon induction profile {ɛ_j} as a function of extracellular sugar concentrations {S_j}, and summarize these results in metabolic phase diagrams.

Single-sugar uptake

We first discuss the simplest case, in which we follow the dynamics of uptake and operon expression for a single sugar j = 1. This analysis equally applies to the interaction between multiple PTS sugars, as long as only one of the operons is inducible. Equation 8 in steady state reduces to a three-parameter system, with solutions ɛ(S,β,ν) satisfying

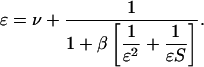(9)

Generically, this equation has one stable fixed point, or two stable and one unstable fixed points, with saddle-node bifurcations separating these two behaviors (Fig. 2). The onset of bistability occurs at a critical point C where the three solutions to Eq. 9 are degenerate (see Appendix). Once this bistable region appears, the system becomes hysteretic, and operon expression levels can change discontinuously as the sugar concentration crosses certain thresholds (Fig. 2 B).

FIGURE 2.

Single-sugar uptake. (A) Graphical solution to Eq. 9 for υ = 0.05, β = 0.2, and S = 1.0. Stable fixed points are labeled as high, H, or low, L. (B) System behavior for υ = 0.05. Discontinuous transitions can occur as the sugar concentration S is varied at fixed β (dashed line). For low sugar concentrations, only the low fixed point is present, so the operon expression ɛ is low, L; the concentration must pass some threshold S↑ before the operon can be induced to a high state, H. Similarly, S must fall below some S↓ before ɛ again switches to a low state. The region L/H is thus hysteretic, admitting two stable fixed points. Dynamical behaviors at various parameter values are shown in boxes; box labels and scale are as in Fig. 2 A. Note the critical point, C, that indicates the onset of bistability.

Two-sugar uptake

The competition between two PTS sugars produces a much richer variety of switching behaviors than seen in the one-sugar case: instead of the simple threshold points discussed above, metabolic preference can switch over an entire line in {S₁,S₂} space, producing complex metabolic phase diagrams.

For simplicity, we take the constants ν and β to be identical for both sugars; the metabolic phase diagrams are essentially unchanged when we go over to the slightly asymmetric parameter case. This gives

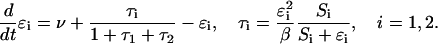(10)

We analyze the nullclines ɛ₂ = h₁(ɛ₁) and ɛ₁ = h₂(ɛ₂) defined by 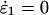and respectively (see Appendix). This analysis is analogous to that carried out for a single sugar above, although more involved. In the single-sugar case, the steady-state condition (Eq. 9) produces high (H) and low (L) induction stable fixed points (Fig. 2 A); for two sugars, particular intersections of the nullclines in {ɛ₁,ɛ₂} space define the stable fixed points of Eq. 10, which we can classify as being either H or L for each sugar, leading to such complex states as LL/HL/LH (Fig. 3).

For the purpose of comparison, Fig. 3 A shows the metabolic behavior that would result from regulation by two independent hysteretic switches. Fig. 3, B–D, shows three instances of PTS metabolic phase diagrams corresponding to three values of the parameters ν and β. The behavior shown in Fig. 3 B is very close to that of two independent switches, whereas that shown in Fig. 3 D is very different. Note, however, that the interaction mediated by flux-limited competition has completely eliminated the occurrence of the HH fixed point from all PTS phase diagrams. Fig. 4 shows the fine structure of the parameter space, indicating the twelve possible topologically distinct metabolic phase diagrams. For a given bacterial strain and a given choice of sugars, the underlying biochemical parameters are fixed; the resulting metabolic phase diagram therefore serves to characterize bacterial phenotype, with different strains displaying different switching behaviors.

FIGURE 4.

Phenotypic classification. Lines in {υ,β} space indicate transitions between topologically distinct metabolic phase diagrams, each of which can be associated with a possible bacterial phenotype. The 12 possible topologically distinct phase diagrams are indicated schematically in boxes, along with their corresponding parameter regions. The main graph shows a detailed portion of {υ,β} space so that fine transitions can be distinguished; the inset (showing the entire extent of transition lines in {υ,β} space) places emphasis on the three phenotypes that occupy the largest parameter regions. (A) The nonswitching phenotype. (B) The WTA phenotype. (C) The low basal transcription phenotype. The phenotype, B, shown in a bold box (and also in Fig. 3 D) is the only robust, nontrivial switching phenotype generated by the PTS.

DISCUSSION

Phenotypic robustness

The diversity of PTS switching behaviors is typical of the dynamics of all but the simplest nonlinear systems. What is surprising about the PTS is that a minority of switching phenotypes dominate most of parameter space, with the rest confined to very small regions (Fig. 4). Stochastic effects, which tend to coarse-grain transition boundaries, will eliminate fine-tuned phenotypes of the latter variety. Furthermore, phenotypes defined by small parameter regions are highly susceptible to mutation. The volume of parameter space that generates a particular phenotype can therefore be defined as a measure of its robustness: the greater that volume, the more stable the corresponding switching behavior will be against mutations and stochastic fluctuations.

We find that only three of the twelve switching phenotypes (Fig. 4, A–C) are significantly robust. The phenotype 4A, which occurs for most of parameter space, is a trivial case that displays no switching behavior at all. (For switching to occur, basal transcription ν and phosphoryl supply β must be low, so that competition between sugars is heightened.) The phenotype 4C corresponds to a region in which basal transcription is so low that it is possible to turn operons off, but not to turn them back on again; such behavior is likely to be selected against real systems. Therefore, 4B (also shown in Fig. 3 D) is the only robust, nontrivial switching phenotype generated by the PTS.

The switching properties discussed above are consequences of the structure of the PTS. The occurrence of discontinuous transitions is due to the nonlinear term 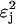in Eq. 8. This term arises because the concentrations of the two enzymes EIIA and EIIBC are correlated. Other sources of nonlinearity are also present, such as transcription factor dimerization, and would be equally sufficient to produce switching, even in those cases where enzyme EIIABC occurs as a single polypeptide. Local activation (by positive feedback from sugars to their specific operons) and global inhibition (by phosphoryl flux-limited competition) creates a winner-take-all (WTA) architecture (Hertz et al., 1991) which is responsible both for the absence of the HH state from all metabolic phase diagrams, and for the robustness of the particular phenotype 4B. This WTA behavior is preserved even when regulation by the CRP-cAMP complex (Botsford and Harman, 1992; Kolb et al., 1993) is considered, although the structure of the parameter space is more difficult to determine in this case (unpublished results). More generally, we would expect the WTA architecture of the PTS to ensure that a single sugar is metabolized over all others in a multisugar system. It is also reasonable to expect similar dynamics to arise in other systems which incorporate flux-limited competition.

Switching dynamics and experimental measurements

The switching behavior of the WTA phenotype is illustrated schematically in Fig. 5. The system is hysteretic: priming a bacterium in a medium containing a single sugar causes it to metabolize that sugar alone, even when it is transferred to a medium containing a mixture of sugars. However, biochemical noise (McAdams and Arkin, 1999) can cause single cells to switch operon induction levels stochastically. Such stochastic transitions tend to eliminate hysteresis at long timescales (Matheson et al., 1974), allowing a population of bacteria to occupy all of the accessible fixed points simultaneously, thus creating distinct subpopulations in equilibrium (Novick and Weiner, 1957; Siegele and Hu, 1997; Kepler and Elston, 2001). Slowly sweeping concentrations from a nonhysteretic range into a hysteretic one would therefore cause a unimodal population to become multimodal, with the number of subpopulations being equal to the number of stable fixed points of the system. The majority of bacteria would tend to occupy the most stable fixed point (that which is furthest from a switching threshold), so a population-averaged measurement would show a new switching line along which one fixed point becomes more stable than another (Figs. 3 D and 5 A).

FIGURE 5.

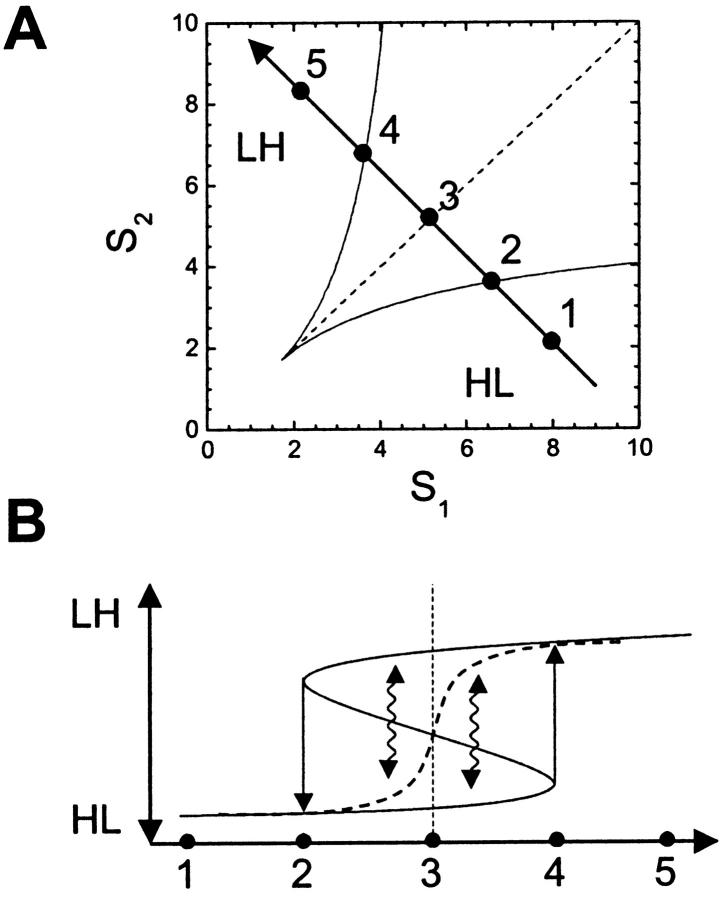
Switching dynamics of WTA phenotype: hysteresis and stochastic transitions. The dynamics along a cut in {S₁,S₂} space (A) are depicted schematically in B. The solid curve shows the fixed points obtained by solving Eq. 10; the upper, LH, and lower, HL, branches of this curve are the stable fixed points, whereas the middle branch is unstable. If the system begins in the HL state (1), then it will stay HL until it is moved to (4), where the HL fixed point vanishes, causing the system to transition to the LH state. Going in the opposite direction, a system that begins in the LH state (5) must be moved to (2) before it transitions back to the HL state. These hysteretic transitions (solid arrows) only occur when one or the other stable fixed point vanishes. However, stochastic fluctuations can cause transitions from one stable fixed point to another (wavy arrows). Hysteresis will only be observed if sugar concentrations are changed very fast so stochastic transitions do not have time to occur, or if stochastic fluctuations are small, making large transitions unlikely. Over time, these fluctuations will cause a population of bacteria to split into two subpopulations, one near each fixed point, and the majority of cells will occupy the most stable fixed point (that which is furthest from the unstable fixed point). The population average (dashed curve) will therefore switch sharply around (3), the point at which an equal number of cells occupy each fixed point. The position of the switching boundary (vertical dashed line) will be shifted if the subpopulations have different growth rates; for example, if cells in the LH state tend to grow faster, the transition line will be shifted to the left.

A bacterial population which is cultured in a continually refreshed medium at constant sugar concentrations will reach an equilibrium distribution after some period of time. At that time, a measurement of the population distribution of operon expression levels, using fluorescent reporters and single-cell-resolved imaging for example (Siegele and Hu, 1997), would indicate the number of stable fixed points of the system. Growing different samples at various concentrations would then enable the reconstruction of the metabolic phase diagram, and thereby, the determination of switching phenotype. The interpretation of experimental measurements is more complex if, as in Monod's early investigations of diauxie, the composition of the growth medium is allowed change over time as various nutrients are metabolized: flux-limited competition can then lead to diauxic growth in a mixture of PTS sugars (Fig. 6).

FIGURE 6.

Switching dynamics of WTA phenotype: diauxic growth. The complete hysteretic system can be visualized as a folded sheet, a slice of which was shown in Fig. 5 B. Bacteria on the topmost fold are in the LH state, metabolizing S₂ alone; those on the lowest fold are in the HL state, metabolizing S₁ alone. The folded sheet in the upper diagram is projected onto a two-dimensional surface in the lower diagram using our usual HL/LH notation; vertical lines connect points of equal {S₁,S₂} value. The depletion of sugars through metabolism causes sugar concentrations to change slowly over time. We follow two types of concentration trajectories (bold arrows): (1) a bacterial population that is initially entirely in the LH state metabolizes S₂ alone; concentrations therefore move parallel to the S₂ axis. When the system reaches the transition boundary at which the LH fixed point is lost, ɛ₁ must be newly synthesized to reach the HL fixed point; as the system “falls over the edge,” there is a lag in growth. Once in the HL state, the population metabolizes S₁ alone, and concentrations move parallel to the S₁ axis. The population thus achieves diauxic growth. (2) A population that is initially heterogenous, consisting of both HL and LH subpopulations, metabolizes both S₁ and S₂; this generates a diagonal concentration trajectory. The transition boundary is only reached at very low sugar concentrations, by which time the bacterial population is likely to be in stationary phase. Diauxie is therefore not observed. Note that it is possible to go from the HL to the LH state without switching at all, by employing a trajectory that goes around the cusp or critical point of the phase diagram.

Optimality and control

Natural selection operates at the level of populations: bacterial regulatory networks have evolved so as to produce populations that are optimal, rather than individuals. Indeed, we see that the population-averaged behavior of the robust switching phenotype (Fig. 3 D) is consistent with an optimal metabolic strategy (Fig. 3 E); specifically, the PTS has generated a sharp switching line in {S₁,S₂} space. However, true optimality requires that the positions of metabolic transitions be correct, not just their topology. What are the parameters that control the slope and extent of the PTS switching line?

Recall that β_j ∝ (J_max/w_j)² (Eq. 8). Increasing phosphoryl supply (J_max) increases all of the β_j values in proportion, moving the critical point further from the origin but leaving the slope of the switching line unchanged. This can be achieved by increasing the concentrations of the general PTS enzymes EI and HPr. In contrast, increasing the ratio of sugar-specific induction efficiencies w₁/w₂ changes the ratio β₁/β₂, causing the slope of the switching line to increase. (The switching line moves further from the S₁ axis since it now requires more S₂ to repress the S₁ operon.) This can be achieved by changing the expression of a single sugar-specific repressor, causing a sugar-specific operon to become more or less inducible. There is also a third, more subtle option for tuning the switching line. Increasing the concentration of CRP-cAMP, a global regulator, tends to increase the expression of various metabolic operons (Botsford and Harman, 1992; Kolb et al., 1993; Stülke and Hillen, 1999); in particular, this will cause phosphoryl supply to increase (since EI and HPr expression levels increase), and sugar-specific demand to increase (since the sugar-specific operons all become more inducible). However, the w_j values might not all increase in proportion, so the slope of the switching line might change. In certain cases (when two sugars require the same machinery for their metabolism, for example), it might be preferable to vary sugar uptake rates continuously instead of switching. This can be achieved by raising phosphoryl supply and basal transcription levels so that the nonswitching phenotype 4A occurs. A similar effect would be achieved by having a shared permease, which circumvents the competition between two sugars.

In summary, the robust WTA dynamics of the PTS provides a framework within which optimal metabolism may be achieved, while the availability of numerous adjustable parameters provides the flexibility for tuning switching positions. This type of robust-but-tunable response could be a common feature of biological sensory and regulatory systems. For example, a similar situation occurs in the adaptation response of the bacterial chemotaxis network: precise adaptation is a robust property of the system, while adaptation times can be tuned by modification of protein levels (Alon et al., 1999).

Suppression of cross talk during chemotaxis

Bacteria respond to chemical gradients in their environment by swimming up or down these gradients, a behavior known as chemotaxis. Current evidence (Postma et al., 1993) suggests that a change in the phosphorylated fraction f of HPr due to sugar uptake is the signal for PTS-dependent chemotaxis. Signals from the various sugar-specific permeases converge at the HPr branch point, so f responds to the total flux demand: it is blind to which sugar is being taken up (Eq. 6). However, the WTA architecture of the PTS ensures that only one sugar is taken up at any time, so only that sugar can be sensed. Thus, although signals from multiple sugar-specific systems are transmitted through a common pathway, the cross talk between independent signals is suppressed. This produces a very reasonable strategy for chemotaxis, in which the bacterium follows the concentration gradient of one sugar alone. Such a chemotactic strategy will ultimately lead the bacterium to the source of that sugar, whereas a blind search for total sugar concentration could trap it away from sources.

CONCLUSION

We have explored the dynamics of a central metabolic regulatory network, and predicted the variety of complex behaviors of which it is capable. We have found that the network, by virtue of its architecture, is designed to execute a very specific class of metabolic strategies; the resulting switching behavior could be consistent with optimal metabolism. It remains to carry out a quantitative experimental investigation of the competition between different sugars in bacterial metabolism. These experiments would build on Monod's pioneering work on diauxie (Monod, 1966) and the subsequent experimental studies of single sugar subsystems (Novick and Weiner, 1957; Siegele and Hu, 1997). The framework of metabolic phase diagrams presented here will aid in the design and interpretation of the future experiments.

APPENDIX

Short timescales: PTS chemical kinetics

The overall reaction mediated by the PTS is typified by the uptake of glucose and its conversion to glucose-6-phosphate, as shown in Fig. 1 A; similar reactions are involved in the case of other PTS sugars. The resulting intracellular carbohydrate phosphates are metabolized via glycolysis (Fraenkel, 1993; Stryer, 1995) to produce two molecules of PEP for each molecule of input monosaccharide. Thus, PEP is both a downstream product of PTS sugar metabolism and a requirement for sugar uptake: this creates a closed loop or self-priming structure. The final step in the glycolytic pathway, the production of ATP, is driven by the conversion of the remaining PEP to Pyr. (The various processes involving PEP and Pyr, and their effective rate constants, are shown in Fig. 7 A.) An interesting property of the closed loop structure of the PTS is that, in the absence of non-PTS sources of PEP, the steady state ratio [PEP]/[Pyr] becomes independent of external sugar concentrations.

FIGURE 7.

PTS chemical kinetics. (A) The PTS and glycolysis. Once transported into the cell, phosphorylated carbohydrates enter the glycolytic pathway with effective overall rate constant k_gly. This reaction produces two molecules of PEP for each molecule of input monosaccharide, thus closing the PTS loop. The conversion of PEP into Pyr by the enzyme pyruvate kinase produces one molecule of ATP; this reaction occurs with effective rate constant k_pyk. Both PEP and Pyr are subsequently converted into downstream metabolites in reactions with rate constants γ_PEP and γ_Pyr, respectively; Pyr, in particular, can participate in further energy synthesis. We show the reaction fluxes that are achieved in steady state, given a phosphoryl flux J through the PTS; the ratio f₀ = [PEP]/[Pyr] = γ_Pyr/(γ_PEP + 2k_pyk) is independent of J. (B) PTS modules. We represent the PTS components as a_i, and the corresponding phosphorylated species as A_i. The phosphotransfer reaction in the a₂→a₃ step is in equilibrium, so equal fractions f of HPr and EIIA are phosphorylated.

In our analysis, we designate PTS biochemical species as {a₀,a₁,a₂,…,a₅} with the corresponding phosphorylated species being {A₀,A₁,A₂,…,A₅}, with 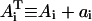(Fig. 7 B). Here, A₀ and a₀ are PEP and Pyr, respectively; A₅ and a₅ are the phosphorylated and the nonphosphorylated forms of the sugar; a₁ and a₂ are the general PTS enzymes EI and HPr; and a₃ and a₄ are the sugar-specific enzymes EIIA and EIIBC. Let m be the total number of distinct PTS sugars; we use the subscript notation […]_j (j = 1…m) to refer to quantities specific to sugar j. The phosphorylated fraction of a species is 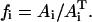Let the forward and backward rate constants of the five phosphotransfer reactions shown in Fig. 7 B be 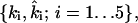and let 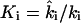be the phosphorylation equilibrium constants. These phosphorylation reactions are reversible but are not in equilibrium individually, since there is a net phosphotransfer flux J through the cascade:

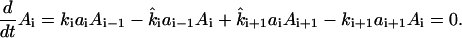(A1)

Physiological values of the equilibrium constants are shown in Table 1. For simplicity, we replace K_i by either 0 or 1. That is, the reactions are either irreversible, or have comparable backward and forward rate constants. (This approximation does not qualitatively change the results, but does simplify notation.) In addition, for physiological concentrations, the maximum possible flux through the HPr→EIIA step (i.e., the a₂→a₃ step) is very much greater than that through other cascade steps (due to the high values of k₃ and 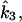and the high concentration of HPr). We therefore take this reaction to be in equilibrium, implying (within the K₃ = 1 approximation) that f₂ = f₃ ≡ f.

TABLE 1.

Physiological (K) and approximate (K_approx) values of PTS equilibrium constants

	K	Kapprox
1	0.667	1
2	0.04	0
3	0.771	1
4	0.364	1
5	0.0	0

Data taken from Rohwer et al. (2000).

Through the HPr→EIIA step, multiple carbohydrates [a₅]_j compete for phosphoryl flux (Fig. 1 B). The cascade divides into two equivalent modules, separated at this phosphotransfer branch point, the first of which satisfies

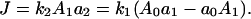(A2)

Using these two equations to eliminate f₁ gives

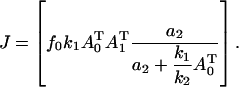(A3)

Similarly, the second module gives

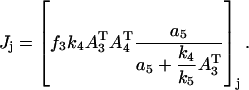(A4)

Applying f₂ = f₃ ≡ f and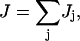

(A5)

this equation can be written as

(A6)

where and and can be solved uniquely for f. We now examine the stability of the solution obtained above, by incorporating the dynamics of PEP creation via glycolysis, and its degradation via cellular phosphate demand (Fig. 7 A). The intracellular sugar concentration equilibrates to 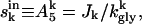and the rate of decay of is given by Then 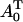evolves according to

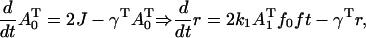(A7)

where r and t are as defined in Eq. A6. Setting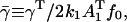

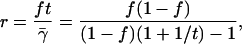(A8)

where the first equality arises from applying Eq. A7 in steady state, and the second directly from Eq. A6. This equation has a zero flux solution (f = 0) which is stable for The other solution, stable for is

(A9)

where we have set

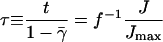(A10)

with 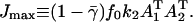This gives us Eq. 5 of the main text. The second-order transition from zero to nonzero flux can be understood as follows: 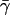is proportional to the cellular energy demand. When cellular demand becomes too high, not enough phosphate can be re-invested into the uptake of new carbohydrate raw material (that is, sugar demand cannot be satisfied). In this case, flux through the entire PTS pathway will be driven to zero. However, the system can be kick-started again once 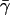drops below unity.

Long timescales: PTS gene regulation

A note about units: we have chosen the unit of time by setting the dilution rate γ = 1. The concentration-unit variables used in this analysis are related to the dimensionless variables of the main text by ɛ_j ≡ E_j/w_j, S_j ≡ s_j/w_j, β_j ≡ (B_j/w_j)², υ_j ≡ v_j/w_j, and ω_j ≡ w_j/w_j = 1.

The genes coding for EI, HPr, and EIIA^Glc (ptsI, ptsH, and crr, respectively) are located in the pts operon; the enzyme EIIBC^Glc is coded for by the ptsG gene (Postma et al., 1993). The expression of the pts operon is mildly upregulated during growth on PTS sugars. For sugars other than glucose, enzymes EIIA and EIIBC tend to be transcribed from the same operon. These sugar-specific operons are typically induced by their sugar substrates.

Since enzymes EIIA and EIIBC are transcribed from the same operon, their concentrations will be correlated, both being proportional to the operon expression level: of The quantities E_j will be our dynamical variables, slowly adapting over time; the rescaled extracellular sugar concentrations are parameters that can be varied in an experiment. All other quantities in our treatment, the internal parameters, will be absorbed into constants of proportionality: the biochemical rate constants (k_i, K_i, γ_Pyr, γ_PEP, k_pyk, and k_gly) are fixed; the concentrations of constitutively expressed general PTS enzymes and are constant; and the ratio f₀ = [PEP]/[Pyr] is constant, as mentioned earlier. Equations A4 and A10 then imply, introducing B_j ∝ J_max as a sugar-specific constant, that

(A11)

This is Eq. 4 of the main text. In steady state (Fig. 7 A) the intracellular sugar concentration equilibrates to 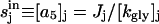. The time evolution of E_j is given by

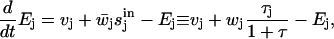(A12)

and the transformation to dimensionless variables gives Eqs. 7 and 8 of the main text.

Critical point for single-sugar uptake

Requiring that the three solutions to Eq. 9 are degenerate at the critical point corresponds to two constraints on a three-parameter system, producing a path parameterized by a single variable θ. Solving for the critical point, we find that

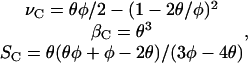(A13)

where we have introduced 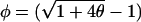for notational simplicity. Note that the cusps that appear in the phase diagrams are characteristic of the onset of saddle-node bifurcations. The lowest order function that produces this behavior is a general cubic f(x) = a₀ + a₁x + a₂x² + a₃x³ (see Fig. 2 A); linear transformation of the coefficients produces the following normal form: f(x) = Δ + ɛx − x³. The turning points of this function occur at f′(x) = ɛ − 3x² = 0, giving and f(x^*) = Δ + cɛ^3/2 (where c depends on the sign of the square root chosen). f(x) = 0 then gives the two saddle-node bifurcations at Δ ∝ ɛ^3/2, thus producing a cusp.

Metabolic phase diagrams for two-sugar uptake

The object of this section is to derive metabolic phase diagrams in {S₁,S₂} space, which will be symmetric since υ and β are identical for the two sugars. The topology of the phase diagrams can therefore be entirely determined by sampling along the following lines:

(A14)

We will first investigate the S₁ = S₂ = ∞ limit. The intersections of the nullclines ɛ₂ = h₁(ɛ₁) and ɛ₁ = h₂(ɛ₂) at give the fixed points of Eq. 10, which are stable for

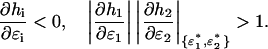(A15)

Along the line S₁ = S₂ ≡ S, the situation becomes completely symmetric, and Eq. 10 admits either symmetric or antisymmetric fixed points. The symmetric fixed points at 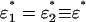satisfy the equation

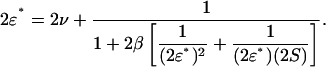(A16)

However, these solutions are not necessarily stable. The symmetric form of Eq. A15 (∂h/∂ɛ₁ < −1) implies the following necessary and sufficient condition for stability of a symmetric fixed point ɛ^*:

(A17)

For 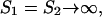the boundary of stability of the symmetric fixed point is given by υ = ɛ^*/2. Using this condition to substitute for ɛ^* in Eq. A16 implies that a symmetric stable fixed point exists for

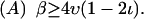(A18)

The emergence of the asymmetric fixed points in a saddle-node bifurcation can be analyzed perturbatively. Consider the fixed point at ɛ₂ ≈ υ ≈ 0. The nullcline h₁ is given by . Solving for the saddle-node tangency condition shows that the asymmetric fixed point exists for

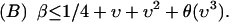(A19)

Conditions A and B completely determine the behavior for S₁ = S₂ = ∞. Line 1 can now be determined by considering the trajectory of a critical point; the required calculation is analogous to that carried out in the previous section, and the results will be similar to lowest order. Line 2 has been explicitly determined in the previous section: the critical point Eq. A13 shows the change in behavior as S₁ goes from 0 to ∞ while S₂ = 0. Line 3 is the most challenging case, in that the order of various topological transitions must be inferred from the difference in topology at several points along the line. We do not solve for such transitions explicitly, but show them with the correct connectivity and relative position. A careful examination of Fig. 4 reveals the nature of the topological transitions that define each line in parameter space; the figure shows schematic metabolic phase diagrams for the twelve different switching phenotypes that occur. Note that in the asymmetric sugar case, certain transitions (those whose switching lines intersect the S_j axes, for example) will no longer occur simultaneously.