Lateral Heterogeneity of Photosystems in Thylakoid Membranes Studied by Brownian Dynamics Simulations

Abstract

The aggregation and segregation of photosystems in higher plant thylakoid membranes as stromal cation-induced phenomena are studied by the Brownian dynamics method. A theoretical model of photosystems lateral movement within the membrane plane is developed, assuming their pairwise effective potential interaction in aqueous and lipid media and their diffusion. Along with the screened electrostatic repulsive interaction the model accounts for the van der Waals-type, elastic, and lipid-induced attractive forces between photosystems of different sizes and charges. Simulations with a priori estimated parameters demonstrate that all three studied repulsion-attraction alternatives might favor the local segregation of photosystems under physiologically reasonable conditions. However, only the lipid-induced potential combined with the size-corrected screened Coulomb interaction provides the segregated configurations with photosystems II localized in the central part of the grana-size simulation cell and photosystems I occupying its margins, as observed experimentally. Mapping of thermodynamic states reveals that the coexistence curves between isotropic and aggregated phases are the sigmoidlike functions regardless of the effective potential type. It correlates with measurements of the chlorophyll content of thylakoid fragments. Also the universality of the phase curves characterizes the aggregation and segregation of photosystems as order-disorder phase transitions with the Debye radius as a governing parameter.

INTRODUCTION

The thylakoid, a membranous body located in a chloroplast, hosts the light reactions of oxygenic photosynthesis. It has a high protein-lipid volume ratio, which is around unity in the green plants. The majority of thylakoid lipids are entirely nonionic (Murata et al., 1990; Nenonene and Fragata, 1998). Thylakoid proteins are organized into five types of integral membrane spanning complexes: Photosystems I (PSI), Photosystems II (PSII), light harvesting complex associated with PSII (LHCII), cytochrome b₆/f, and ATP synthase (Whitmarsh and Govindjee, 1999).

Thylakoid membranes of the higher plants reveal two distinct morphological components: the stacked region (granal lamellae) and the unstacked region (stromal lamellae) (Whitmarsh and Govindjee, 1999). Photosystems in the higher plant thylakoids are segregated in vivo, so that PSIIs mostly occupy appressed membrane regions and are localized in the central parts of grana while PSIs occupy nonappressed parts and are mostly localized within the grana periphery and lamellae (Whitmarsh and Govindjee, 1999).

Traditionally the segregation of photosystems is considered together with stacking of thylakoids (in the surface charge hypothesis, Barber, 1980; local charge hypothesis, Allen and Holmes, 1986; and molecular recognition hypothesis, Allen, 1992), both processes being reversible salt-sensitive phenomena. However, thorough examination of experimental data suggested that the segregation of photosystems and stacking of thylakoids are two distinct phenomena, each having its own dependence on ionic strength of stromal solution and cation composition (Wollman and Diner, 1980; Briantais et al., 1984; Stys, 1995). It was also found that segregation is the primary event responsible for creating the areas of low surface-charge density in thylakoids. Stacking was established to be a secondary event as a result of attraction between the protein enriched regions of distinct lamellae (Stys, 1995). Unlike the segregation, stacking requires the presence of LHCIIs, so that under certain cation conditions the hydrophobic interactions between their molecules favor the adjacent membrane appression (Staehelin and Arntzen, 1983).

Several speculations were made for the role of segregation of photosystems: minimizing the excitonic contacts between kinetically slow PSII and fast PSI (Trissl and Wilheim, 1993), resistance to the degradation of the PSII proteins (Anderson and Aro, 1994), and enhancement of noncyclic ATP synthesis in the vicinity of PSI (Chow, 1984, 1999). However, understanding of the segregation phenomenon and its driving forces is far from complete.

In Rojdestvenski et al. (2000, 2002), the lateral dynamics of PSIs and PSIIs was studied in computer simulations assuming the interactions between point particles moving in a viscous lipid medium. Postulated screened electrostatic and lipid-induced pair potentials with several free parameters were used to demonstrate the appearance of clustered and segregated configurations as a result of the interplay between repulsive and attractive forces.

Here we explore the lateral segregation of PSIs and PSIIs in the grana thylakoids using an advanced theoretical model. It is based on pairwise potential interactions between photosystems and comprises three alternatives. PSIs and PSIIs are viewed as colloids dissolved in a fluid lipid medium, as inclusions in an elastic lipid continuum, or as particles placed in a structured environment of small lipid molecules. In all three cases photosystems are allowed to diffuse. Parameters used in the model are estimated analytically based on the experimental data. We perform the Brownian dynamics simulations to study the system's time evolution considering its structural and dynamical properties.

The structure of the article is as follows. In the next section we briefly review different theories of the protein-protein interactions and formulate the effective pairwise potentials that mostly contribute to the PSI and PSII ordering. Then we present the model of photosystems' lateral dynamics in thylakoids, describe the computational techniques and modeling routine followed by discussion of the obtained results and conclusions.

NONSPECIFIC INTERACTIONS BETWEEN PHOTOSYSTEMS

The lateral aggregation and segregation of photosystems occurs in the granal disk with the diameter of 0.5–0.8 μm (Staehelin and van der Staay, 1996; Albertsson, 2001). Typical sizes and stoichiometric ratios for its lipid and protein components are represented in Table 1. Indicated spatial scales yield the certain assumptions that the aggregation and segregation of PSIs and PSIIs are the mesoscopic phenomena mostly determined by the long-range protein-protein interactions with lengths greater than the radius of gyration of the lipid molecule and about the protein size respectively. We may neglect the specific protein-lipid interactions because they are short-range and effectively perturb only the first lipid layer around the protein. Nonspecific protein-lipid interactions attributed to solvation and hydrophobic forces have longer range, but they only contribute to the effective change in Brownian motion of proteins within the membrane.

TABLE 1.

Model parameter estimates and used experimental data with references

Theoretical estimates	Measured data	References for data
Lipid and protein components of the grana thylakoid
The membrane volume fractions, φprotein/φlipid = 1.0; the protein component fractions, φPSI = 0.15, φPSII = 0.61, φLHCII = 0.12, φcyt b6f = 0.09, and φATPsyn = 0.03	The grana core area, 60%; The grana margin area, 40%; The protein-lipid ratio, 1:1; The PSI-PSII ratio, 7:3; 3 LHCII and 0.6 cyt b6f per PSII; 1 ATP synthase per PSI	Albertsson (2001); Staehelin and van der Staay (1996); Drepper et al. (1993)
Approximate spherical radii, σPSI = 60 Å; σPSII = 80 Å; σLHCII = 35 Å; σcyt b6f = 40 Å; and σATPsyn = 30 Å	Maximal sizes along membrane, 160 × 120 Å (PSI-monomer), 197 × 135 Å (PSII-dimer), 73 × 73 Å (LHCII-trimer), 83 × 44 Å (cyt b6f monomer), 65 × 65 Å (ATP syn)	van Roon et al. (2000); Kuhlbrandt et al. (1994); Boekema et al. (1994)
Lipid monomer number density, ρL = 1.56 × 10−3 Å−3	Bilayer thickness, Lbilayer = 50 Å; Lipid segment length, dL = 4.8 Å; Area per lipid molecule, a = 64 Å2	Thorne and Duniec (1983); Marsh (1997); Kleinschmidt and Marsh (1997)
Interaction and diffusion of the photosystems
The Bjerrum length,*rB = 0.0007 μm	Stromal dielectric constant, ɛ = 81	Thorne and Duniec (1983)
Effective electric charges,†q1 = −14.3 × 10−19 C; q2 = −9.29 × 10−19 C	Membrane surface charge densities,† −0.86 × 10−14 C/μm2 (the PSI vicinity); −1.3 × 10−14 C/μm2 (the PSII vicinity)	Itoh (1978, 1979)
The Hamaker constant, AH = 1.75 (in kT units)	Dielectric constants, ɛlipid = 2, ɛprotein = 3, ɛwater = 81; Refractive indices, nlipid = 1.41, nprotein = 1.55, nwater = 1.33	Haltia and Freire (1995); Israelachvili (1992)
The Brownian times,*τBr(1) = 0.31 s, τBr(2) = 0.72 s	Diffusion coefficients,*‡D1 = 1.17 × 10−4μm2/s, D2 = 0.88 × 10−4μm2/s	Drepper et al. (1993)

^*At temperature kT = 4.0 × 10⁻²¹ J in energy units.

^†At pH = 7.6.

^‡The Monte-Carlo simulation results with using experimental data.

Hence, in the theoretical treatment one may leave aside a detailed structure of the amphiphilic bilayer and consider protein complexes as macroscopic bodies placed in a continuous lipid medium. Two main theoretical approaches are applicable. One may treat proteins as colloids immersed in a lipid fluid medium or as inclusions embedded in a lipid elastic medium. Both concepts are widely used and yield results in accordance with experimental observations (Israelachvili, 1992; Gennis, 1989).

Within the framework of the above approximations, the Coulomb force (of electrostatic nature) and van der Waals (VDW)-type and elastic forces (of electrodynamic nature) are most important, together with the lipid-induced interactions between proteins. The latter comprise effects due to the entropic contributions from structured lipid environment as well as enthalpic ones from the fluctuations of lipid density and lipid orientations. They may be considered either in the elastic or colloidal approaches. Further we discuss some analytical expressions for the pairwise additive effective potentials of these nonspecific protein-protein interactions.

We stress that the lipid-induced and elastic are both indirect interactions between proteins and, in general, they partially overlap each other because of their relations with the membrane fluctuations. However, our separate consideration of these forces brings their distinct features into focus. In the case of the elastic interaction, we assume that inclusions as inhomogeneities are responsible for spatial variations of the elastic properties of the mixed membrane system—first of all, its bending rigidity and, possibly, its spontaneous curvature. In the case of the lipid-induced interaction we assume that inclusions influence only the properties of the lipid component changing the conformational freedom of lipid chains and enhancing lipid density fluctuations. Those distinct features lead to the different radial dependence of the lipid-induced and elastic pair potentials that will be considered below.

Coulomb repulsive interaction between charged bodies

Electrostatic interactions between the proteins are screened by interactions with counterions and dissolved salts (via the electrostatic mean field) as well as by the solvent properties (via the solvent medium dielectric constant). Usually the effective potential between charged bodies is represented in the Yukawa form, albeit the number of its parameters and their meaning essentially depend on the model (Alexander et al., 1984; Beresford-Smith et al., 1985; Levin, 1999; Sanyal and Sood, 1998).

We take a simple representation of the effective electrostatic interaction energy between the photosystems, assuming a purely repulsive, size-corrected Derjaguin-Landau-Verwey-Overbeek potential,

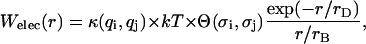(1)

where r is the center-to-center distance between any pair of particles of two sorts (i = 1,2 and j = 1,2). The dimensionless parameter κ(q_i,q_j) = q_iq_j/e² in Eq. 1 relates to bare charges q₁ and q₂ of PSI and PSII as spheres with radii σ_i and σ_j, respectively. 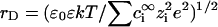and are the Debye and Bjerrum lengths, respectively, in a solvent medium with dielectric constant ɛ at temperature T. The Boltzmann constant k, elementary charge e, and permittivity constant ɛ₀ are used. Concentrations 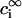and valences z_i of impurity ions at infinite distance from a particle provide the ionic strength 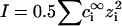of the stromal solution. The dimensionless geometric factor Θ(σ_i,σ_j) depends on σ_i and σ_j, as well as r_D, and is given by

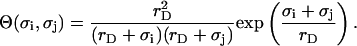VDW-type attractive interactions between colloids

The distance dependence of the VDW-type forces is mostly governed by the shape of the interacting surfaces (Parsegian, 2000). They are always attractive between similar particles in a medium and often repulsive between different types of polymers dissolved in an organic solvent. In the case of interacting photosystems they provide attraction between like-charged particles.

We take the VDW-type contribution to the effective interaction energy between PSI and PSII particles as the Hamaker potential,

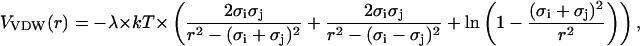(2)

where a dimensionless λ is proportional to the nonretarded Hamaker constant A₁₂₁. It regulates the strength of interaction between two spheres (medium 1) of radii σ_i and σ_j in a fluid (medium 2) at the distance r. For the symmetrical case of two interacting identical phases, it may be represented as follows (Israelachvili, 1992):

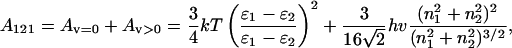where ɛ₁,ɛ₂ and n₁,n₂ are, respectively, the dielectric constants and the refractive indices of the media with polarizabilities as functions of frequency v. The zero-frequency part A_v=0 includes the Keesom and Debye dipolar interactions and accounts for the entropic contribution. The nonzero-frequency part A_v>0 is related to the London interaction and is responsible for the dispersion contribution.

Elastic attractive interactions between inclusions

When the lipid bilayer is treated as an elastic continuum, the consideration of protein-protein interactions is based on the free-energy functional for membrane deformations. Different modes of membrane distortions can be taken into account, including bending, surface tension, and compression-expansion (Huang, 1986; Helfrish and Jakobsson, 1990; Sens and Safran, 2000). Here we consider the bending-controlled interaction between inclusions assuming the thylakoid membrane as a rigidity-dominated surface.

The insertion of integral proteins into the lipid bilayer enhances thermal fluctuations of the membrane shape and imposes new boundary conditions for the membrane as a whole. It leads to the generic interactions between inclusions associated mostly with a bending and partially with a surface tension term to the free energy of a system (Netz, 1995; Netz and Pincus, 1995). If the separation between inclusions is much smaller than the bilayer scale, these long-range interactions fall off as 1/r⁴ with the distance, and may be repulsive or attractive (Goulian et al., 1993; Golestanian et al., 1996). They are always attractive if the inclusions are much stiffer than the membrane, and their energy scale is independent of the membrane rigidity and surface tension, under the assumption that inclusions are infinitely rigid. However, in the case of noncircular inclusions the sign of the shape-fluctuation-induced potential depends on interplay among their ellipticity (via their stiffness and shape factor) and the membrane roughness (via its background curvature) (Kim et al., 1998; Chou et al., 2001).

We take the elastic energy contribution to the effective potential interaction energy between PSI and PSII particles, assuming its pairwise additive, in the form

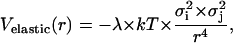(3)

where λ is a dimensionless constant. This equation is similar to that obtained analytically in Goulian et al. (1993) and Golestanian et al. (1996) for the stiff inclusions of the circular cross-sectional area.

Lipid-induced attractive interactions between proteins

To study the lipid-induced effective interactions between membrane proteins, computer simulations are typically used (Pink and Chapman, 1979; Sperotto and Mouritsen, 1991; Aranda-Espinoza et al., 1996). Proteins and lipids are considered as hard spheres, cylinders, or other objects of simple geometry, which interact via hard-core (excluded volume) potentials. Information about the effective potential energy U^eff(r) and forces between proteins is stored in their radial distribution function g(r) or probability distribution P(r) of interprotein distances. These functions are measured in computer experiments. Then, using the Ornstein-Zernike equation in the Percus-Yevick closure, hypernetted chain, or other approximations, it is possible to obtain U^eff(r) numerically (Lague et al., 2000). However, the analytical form of U^eff(r) is available either after fitting numerical data or making some additional assumptions when solving the integral equations (Pearson et al., 1984).

In Sintes and Baumgartner (1997), it was found that two cylindrical proteins embedded in a bilayer of ∼1000 lipid molecules, modeled as flexible chains of monomers with diameter d_L, exhibited two types of effective attraction. The first was a depletion-induced interaction in the range of r < d_L, which related to a depletion zone of thickness δ ≈ d_L around each cylinder, and originated from the steric interactions between lipids and proteins. The second was a fluctuation- induced interaction in the range of d_L < r < 6d_L that relates to the fluctuations of lipid density and lipid orientations. The effective lipid-induced attraction obtained by the analysis of the fluctuation plots demonstrates an exponential decay.

The exponential decay of interprotein attractive interaction was also numerically found in phenomenological models of lipid-protein interactions based on the Landau expansion of free energy in terms of the lipid order parameter (Marcelja, 1976; Schroder, 1977; Mouritsen and Bloom, 1984; Heimburg and Biltonen, 1996). The proteins were introduced as perturbing impurities in the pure lipid bilayer matrix. Those models involve different order parameters, such as hydrophobic thickness of lipid bilayer, the average hydrocarbon chain orientational parameter, and the lipid bilayer area, thus incorporating various contributions into the membrane free energy and using different phenomenological parameters.

We take the lipid-induced contribution to the effective potential interaction energy between PSI and PSII particles in the form

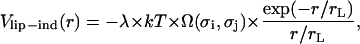(4)

with the two model parameters λ and r_L that characterize the strength and the decay of the interaction, respectively. They are considered as being related to the osmotic pressure of lipids and the correlation length of lipid density and orientation fluctuations. We introduce the dimensionless geometric factor Ω(σ_i, σ_j) by analogy with the electrostatic interaction (see Eq. 1) to consider r as the center-to-center distance between any pair of particles. It depends on σ_i and σ_j, as well as r_L, and is given by

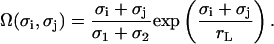To calculate λ we use the analytical expression from Mao et al. (1995) for the depletion interaction between hard spherical particles in the solution of smaller ones:

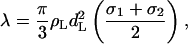where ρ_L is the bulk density of the small hard spheres of diameter d_L. The specific feature of this equation, obtained in the mean-field approach, is the linear dependence on the colloid size as predicted also by the scaling theory (de Gennes, 1992) and Monte-Carlo simulations (Dickman and Yethiraj, 1994).

To calculate r_L, we make an assumption that in thylakoids the lipid density fluctuation length is close to the sizes of the PSI and PSII particles, because it is determined by the membrane deformations caused by these proteins when incorporated in a lipid bilayer. It implies

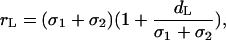reflecting that the lipid fluctuation length depends on both the lipid and protein particle sizes. This expression also appears in the exponential if one considers the depletion potential in the generalized Asakura-Oosawa model (Verma et al., 2000) as a truncated Taylor series.

MODEL OF PSIs AND PSIIs LATERAL MOVEMENT

The biophysical system comprises a low dielectric constant lipid bilayer with inserted protein complexes and high dielectric constant stromal and lumenal aqueous environment with salt ions. We consider a thylakoid membrane exposed to the stroma, assuming the flat surface of the lipid bilayer. In the thermodynamic equilibrium the ionic concentration gradient between the vicinities of protruding PSI and PSII complexes and the bulk phase in stroma is balanced by the electric potential gradient. When complexes are distributed randomly, the counterion diffuse layer associated with the uniformly charged membrane occupies the space up to 100–200 Å from the stromal face of the membrane under physiologically reasonable ionic conditions of 10–100 mM for both monovalent C⁺A⁻ (e.g., KCl) or divalent C²⁺A²⁻ (e.g., MgSO₄) salts (Barber, 1982). Here we do not consider the thylakoid lumen explicitly. The fact that PSII complexes protrude significantly into lumen may, in principle, modify the interparticle interactions. However, within the framework of the mesoscopic approach such modifications would be essentially reduced to renormalizations of the certain interaction parameters, without changing the interaction types.

Cation size and valence effects (Bostrom et al., 2001) on the dynamics of photosystems as well as their Coulomb attraction through the intermediary of counterions (Sogami and Ise, 1984) are beyond the scope of this article. Therefore, we account for the screening of PSI and PSII electrostatic interactions via electrolyte ionic strength I (or the Debye radius, r_D). In our simulations the reduction of r_D corresponds to increase of the divalent cation concentration, as is typical in the experiments on segregation and stacking (see, for example, Mullet and Arntzen, 1980).

The statistical system consists of two sorts of particles, PSIs and PSIIs. The motion of each particle is governed by two processes: the pair-wise interaction with all other model particles, and diffusion in a viscous lipid medium. The presence of the LHCII, cytochrome b₆f, and ATP synthase complexes hinders diffusion of PSIs and PSIIs.

In low ionic strength solvents, the electrostatic repulsions between the macroions are sufficient to stabilize the ordered structure for interparticle separations of ∼1 μm (Alexander et al., 1984). In thylakoids the average distance between photosystems is smaller by several orders of magnitude. Therefore, for exploring the ordering of PSIs and PSIIs we must, together with the repulsive term, introduce in the pair potential the attractive one.

Insofar that we consider protein lateral organization within the flat membrane, only the radial force dependence is of interest. We treat three alternatives for the effective potential. Its repulsive part W(r) is of electrostatic nature in all cases, while the attractive term V(r) is taken as the VDW-type, elastic or lipid-induced interaction, as discussed above:

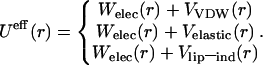(5–7)

Theoretical estimates for the model parameters are represented in Table 1. We use the same notation λ for the attraction strength of different interactions, keeping in mind, however, that it takes different values, and varies within different intervals, depending on the origin of the potential. Straightforward calculations for the VDW-type interaction give λ_VDW ∼ 0.20 ÷ 0.29. The typical values referred to the elastic interaction are λ_elastic ∼ 5.0 ÷ 6.0. For the lipid-induced interactions we obtain λ_lip-ind ∼ 1.0 ÷ 2.0.

Our main objective is to quantify ordering of the PSI and PSII particles for different pair potentials and establish which interactions can be responsible for their lateral segregation in thylakoid membrane. We are also interested in the generalized phase diagram for each of the three effective potentials, discussed above, i.e., to determine the critical values 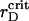for certain values of the model parameter λ. Such a phase diagram yields valuable information about the system's response to the environmental variations and, in particular, how the photosystems self-organize when exposed to changes in stromal cation concentration.

To fulfill our objectives, we need to resort to computer modeling, as the interactions in the system are too complex for further analytical treatment.

COMPUTATIONAL TECHNIQUES AND MODELING ROUTINE

We carry out Brownian dynamics simulations using the Ermak algorithm (Ermak, 1975) to convert the positional Langevin equation into the following equation of motion

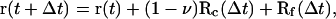where r(t) and r(t + Δt) are the positions of a given PSI (PSII) within a membrane plane at times t and t + Δt, respectively. Here, R_c(Δt) represents the random diffusive displacement due to multiple collisions with the lipids during the time Δt, and R_f(Δt) represents the displacement due to pairwise interactions with all other photosystems. The phenomenological coefficient 0 < v < 1 reflects the Brownian motion of a PSI (PSII) at the presence of obstacles (the LHCII, cytochrome b₆f, and ATP synthase complexes).

The rectangular simulation cell, L = 6000 Å, with the density conservation ensured by the periodic boundary conditions contains 240 + 560 = 800 PSIs and PSIIs. Timescales of our interest are considered to be long, comparing to the Brownian times of the PSI and PSII with the diffusion coefficients D₁ and D₂, respectively (see the Table). We set v = 0.69 to satisfy the fluctuation-dissipation theorem formulated for an extended many-particle system of five different protein components in a viscous lipid medium. Distances, times, and energies are measured in σ = (σ₁ + σ₂)/2, τ_Br = σ₁²/4D₁, and kT units, respectively.

We consider λ and r_D as free model parameters, whereas others in Eqs. 5–7 are assumed to be constant. Unless otherwise indicated, the system is prepared as follows. We generate a random configuration with N₁ and N₂ particles on the square lattice and equilibrate the system. The system is equilibrated at λ = 0 by melting the colloidal crystal into a liquid followed by cooling the colloidal liquid into a crystal (Sanyal and Sood, 1995). In this procedure, repulsion prevails and makes sure any overlaps between particles are avoided. Then the isotropic system is quenched at t = 0 to the state with the particular λ and r_D values.

Another route of PSIs and PSIIs dynamics is kept track of to establish the critical 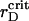values, which correspond to the particle aggregation, and obtain the generalized phase curves 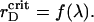The system with a particular λ is subsequently quenched at t = 0 from the isotropic to the ordered state (Soga et al., 1999) by gradual reduction of .

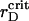To examine the structure, we calculate the pair distribution functions (PDF) for the PSI and PSII pairs, 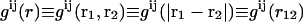(i = I,II and j = I,II),

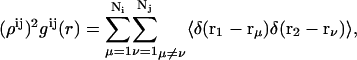where the implemented weights are ρ^I&I = N₁/L², ρ^II&II = N₂/L², and ρ^I&II = (N₁ + N₂)/L². The PDFs g^ij(r) are related to the spatial correlations of the component density fluctuations.

To examine the dynamics, we follow the time changes of the two order parameters. In the current configuration the first maxima of the PDFs , , 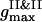, 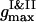and their locations 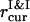, , 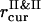and 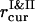, are used to compute the current values of the order parameters.

The instantaneous value of the aggregation order parameter is calculated as η_aggr = 1 − (a/b)², with 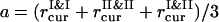and b = l, where l = L/(N₁ + N₂)^1/2 is the average interparticle distance in the uniform mixture of PSIs and PSIIs. When PSI and PSII particles aggregate, η_aggr → 1, even for a weak demixing of two components. If there is no particle density increase locally, then η_aggr = 0. It is worthwhile to mention that, due to the difference in the PSI and PSII occupation fractions, the aggregation ordering might be detected in any segregated configuration.

The instantaneous value of the segregation order parameter is calculated as η_segr = 1 − (c/d), with 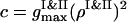and 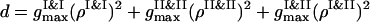. When the PSI and PSII particles are totally segregated, we have η_segr → 1. If the particles of two sorts are mixed well, even for the condensed configurations we have η_segr = 0.

Computer program, control units for tracing the code, and graphical modules to visualize the resulting configurations were developed in FORTRAN-90 and computed in the Microsoft Developer Studio (Microsoft, Seattle, WA) environment.

RESULTS AND DISCUSSION

We study two distinct aspects of the photosystems ordering. The first one relates to the local density variations in the two-component protein mixture due to particle aggregation in the lipid matrix provoked by stromal cation changes. This we term aggregation. The second aspect is demixing of two protein components dissolved in the lipid composition that is also activated by the stromal cation changes. This we term segregation.

VDW-type attraction

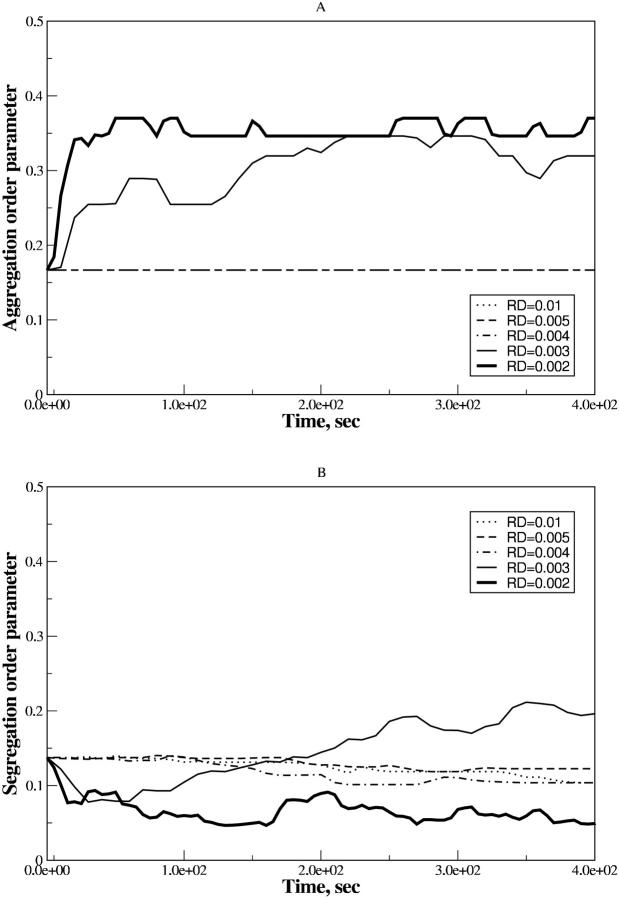
In Fig. 1, A and B, the results are shown for η_aggr and η_segr, respectively, as functions of time, in the case of the effective pairwise potential taken in the form of Eq. 5.

FIGURE 1.

Time dependence of the aggregation (A) and segregation (B) order parameters for the ensemble of PSI and PSII particles with the VDW-type attraction. Simulations are for the estimated attraction parameter, λ = 0.29, at different r_D values. Three dashed lines coincide in A. The thin solid line corresponds to .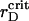

At all r_D values <0.0022 μm there are no structural changes in the system detected for the long time period. Three corresponding lines of η_aggr coincide in Fig. 1 A, so that no distinctions between them can be observed. η_aggr is a constant, and its relatively small value, in comparison with two other curves, shows that particles have no tendency to aggregate and preserve homogeneous distribution. Although three corresponding lines of η_segr in Fig. 1 B show small fluctuations, they do not exceed several percent of its average level. It means that particles of two components are still mixed well. In general, the system's structure in those cases does not differ significantly from that of the state used as equilibrated.

Starting from 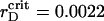μm (see enlarged circle in Fig. 2), we observe essential structural changes in the system monitored by the time variations of both order parameters. After a quiescent period of ∼10 s (∼32τ_Br), we see the aggregation onsets dramatically. A rapid increase of η_aggr is followed by the plateau with a lifetime of ∼5 s (∼16τ_Br) and then it diminishes rapidly to the same value. The plateau appearance in aggregation is preceded by the monotonic decrease in segregation. For a period about the aggregation plateau, lifetime η_segr undergoes the monotonic growth to its initial value. Oscillations of η_segr in Fig. 1 B have a slightly increased amplitude in comparison with the previous case.

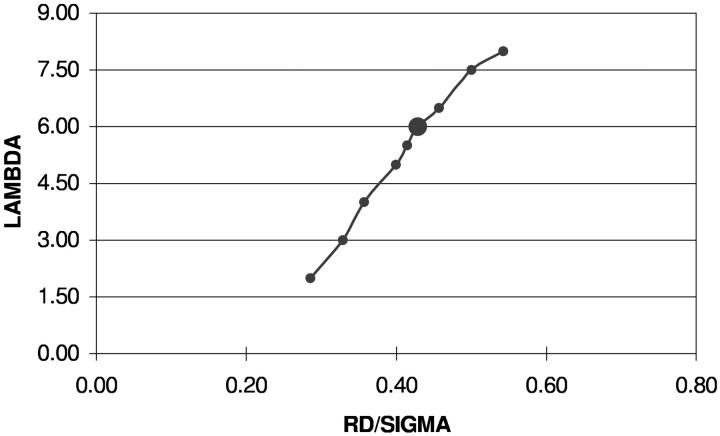
FIGURE 2.

Phase diagrams on the (r_D/σ, λ) plane for the VDW-type attraction. The enlarged circle denotes the segregated state with the theoretical estimate for λ.

Further lowering of r_D <0.0022 μm enhances the aggregation as well as the segregation. Both order parameters show a tendency to the monotonic growth up to certain limits. Also the quiescent period becomes shorter and the lifetime of a plateau of η_aggr reduces.

We attribute such behavior of the order parameters with the structural changes of the two-component system that evince the nucleation mechanism of the phase separation. In the vicinity of 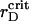, a nucleation with the denser phase abundant in the PSII component takes place. However, a coalescence of nuclei to form the large droplets at the expense of small ones is not detected even for later times, so that the PSII clusters seem frozen in the less dense phase of the PSI component. A typical spatial arrangement of particles is represented in Fig. 3 A. PSIIs form an ordered phase with the honeycomb patterns observed clearly, while the PSI component seems to belong to an isotropic phase. This notion is also supported by the general forms of three PDFs for the current configuration. In Fig. 3 B 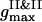is several times larger than 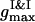. It corresponds to the PSII-component phase representing the small size nuclei randomly dispersed in the PSI-component phase sea. The split-second maximum of 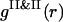gives evidence that nuclei are heterogeneous in their sizes. It seems there are no PSII particles in the liquid state in the vicinity of and <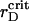, as follows from the particle arrangement represented in Fig. 3 A.

FIGURE 3.

(A) Segregated state of PSI (dark circles) and PSII (light circles) particles interacting via the VDW-type attraction. The PSI and PSII particles are depicted as dark and light spots, respectively. State variable values are λ = 0.29 and r_D = 0.0022 μm. (B) Relevant to this spatial configuration are the PDFs calculated for the PSI-PSI, PSII-PSII, and PSI-PSII pairs. The center-to-center distance between the PSI and PSII particles is used as a variable.

In general, we detect here a liquid-solid transition in the binary mixture accompanied by the phase separation. Also, due to the phase separation, the mixture undergoes a transition from the isotropic to the ordered state. Demixing of photosystems pre-empted by the nucleation results in ordering with PSIs and PSIIs segregated locally.

Thus, simulations with the estimated parameters show that the VDW-type interactions coupled with the electrostatic ones give the segregation of photosystems under the physiological cation concentrations. However, demixing of particles of two sorts has the appearance of numerous PSII clusters in the PSI component and cannot provide the arrangement with PSIs totally excluded from the central part of the grana. Nonetheless, the VDW-type attraction may contribute to the oligomeric aggregates of photosystems. Three- and four-particle nuclei of the PSII component as well as two- and three-particles agglomerates of the PSI component were observed in simulations with another set of parameters; in particular, with enlarged λ, but their quantitative description requires further studies.

Elastic attractive interaction

The time dependences of η_aggr and η_segr are shown in Fig. 4, A and B, respectively, in the case of the effective pairwise potential taken in the form of Eq. 6.

FIGURE 4.

Time dependence of the aggregation (A) and segregation (B) order parameters for the ensemble of PSI and PSII particles with the elastic attraction. Simulations are for the estimated attraction parameter, λ = 6.0, at different r_D values. Three dashed lines coincide in A. The thin solid line corresponds to .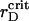

For all r_D values <0.003 μm there are no structural changes in the system detected for the time of observation up to ∼1300τ_Br. As in the previous case, three corresponding lines of η_aggr coincide in Fig. 4 A, so that no distinctions between them can be observed. η_aggr remains constant and particles have no tendency to aggregate. Again, three corresponding lines of η_segr in Fig. 4 B show small fluctuations that do not exceed several percent of its average level. The system's structure does not differ significantly from that of the state used as equilibrated. Here the effects of the PSI and PSII heterogeneity in charge and size are small enough, so that particles constitute the nearly homogeneous binary mixture.

In the vicinity of the critical value, 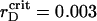μm (see enlarged circle in Fig. 5), we observe pronounced time variations of the order parameters, which bring out the essential structural changes in the system. The short quiescent period of ∼1.25 s (∼4.0τ_Br) is followed by the aggregation onsets. After passing through the plateau for several τ_Br, η_aggr keeps on growing to a certain value. In turn, η_segr undergoes monotonic decay for the aggregation quiescent period and aggregation plateau lifetime and then starts growing. Two order parameters show a tendency for sustained growth up to their certain limits with fluctuating amplitudes.

FIGURE 5.

Phase diagrams on the (r_D/σ, λ) plane for the elastic attraction. The enlarged circle denotes the segregated state with the theoretical estimate for λ.

Further lowering of r_D <0.003 μm speeds up the aggregation, so that the particles of the two components have no time to start the segregation. Indeed, whereas η_aggr increases several times in amplitude within just a few τ_Br and reaches its saturation value, η_segr demonstrates a slow decay to the lower limit in a fluctuating manner.

We attribute such a behavior of the order parameters with a transient gelation that causes the structural changes in the two-component system. In the vicinity of 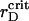we observe the appearance of several clusters, different in size, followed by their coalescence. Cluster-cluster aggregation proceeds gradually and results in a ramified structure. Small changes in the already formed spanning cluster proceed during the long time of observation up to ∼1300τ_Br. A typical spatial arrangement of the particles is represented in Fig. 6 A. In general, the transient gelation in the liquid-solid coexistence region detected here is accompanied by the partial phase separation. Apparently, in the vicinity of 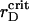all the PSII particles belong to the ordered phase, while the PSI component contributes in the ordered and isotropic phases. As it follows from the particle arrangement, Fig. 6 A, the PSIIs are found in the liquid and the PSIs in the liquid and solid states. The plots of three PDFs in Fig. 6 B for the current configuration partially support these statements. In comparison with the case of the VDW-type attraction, the ratio of 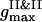to 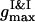is higher here, and the difference between their locations is smaller. The split secondary maxima of all three PDFs underline the ramified structure in the particle arrangement.

FIGURE 6.

(A) Segregated state of PSI (dark circles) and PSII (light circles) particles interacting via the elastic attraction. The PSI and PSII particles are depicted as dark and light spots, respectively. State variable values are λ = 6.0 and r_D = 0.003 μm. (B) Relevant to this spatial configuration are the PDFs calculated for the PSI-PSI, PSII-PSII, and PSI-PSII pairs. The center-to-center distance between the PSI and PSII particles is used as a variable.

In general, we detect here a liquid-solid coexistence in the binary mixture accompanied by the transient gelation. Separation of liquid and solid phases does not occur, but a ramified cluster is formed instead. Also, due to the transient gelation, the mixture undergoes an overextended transition from the isotropic to the ordered state. Some demixing pre-empted by the gelation results in ordering with PSIs and PSIIs partially segregated within a spanning cluster.

Thus, simulations with the estimated parameters show that the elastic interactions coupled with the electrostatic ones give the spanning cluster, which consists of two sorts of particles with most of the PSIs expelled to its periphery. This structure is not stable and undergoes spatial changes on microscopic and mesoscopic timescales. The observed irregular fluctuations of the time-dependent macroscopic functions, such as the order parameters, are the attributes of nonequilibrium behavior of the system with the transient gelation (Poon and Haw, 1997). Partial segregation of PSIs and PSIIs takes place simultaneously with the transient gelation. Maximal demixing of two sorts of particles occurs in the vicinity of 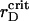being suppressed at larger r_D values and becomes inhibited significantly when further addition of cations increases screening. Certainly, the ramified structure prevents the arrangement of particles with PSIs totally excluded from the central part of the grana.

Lipid-induced attractive forces

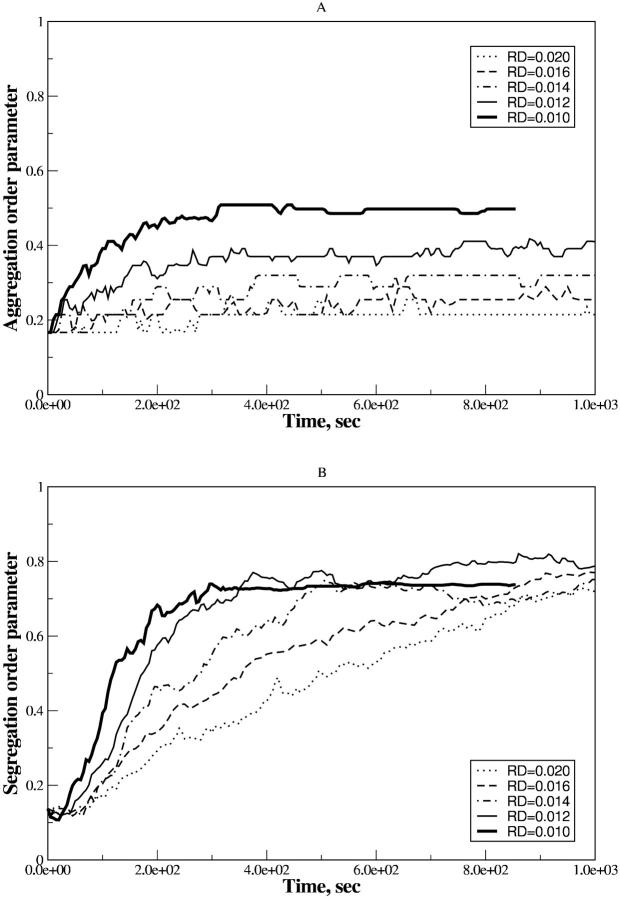
In the case of the effective pairwise potential taken in the form of Eq. 7, the time-dependent η_aggr and η_segr are depicted in Fig. 7, A and B, respectively. Here the structural changes in the system take place for early, intermediate, and late times, even at large r_D which exceeded 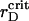2–4 times.

FIGURE 7.

Time dependence of the aggregation (A) and segregation (B) order parameters for the ensemble of PSI and PSII particles with the lipid-induced attraction. Simulations are for the estimated attraction parameter, λ = 1.0, at different r_D values. The thin solid line corresponds to .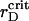

In Fig. 7 A, every η_aggr = η_aggr(t) represents a combination of monotonic growth with saturation and small but continuing oscillations. The threshold value increases with r_D, while the oscillations proceed with nearly the same amplitude. Here for η_aggr the absolute ratio of the average over τ_Br fluctuations to the mean value becomes smaller when r_D increases. Close to 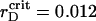μm the aggregation character does not display new features at lowered r_D values.

η_segr = η_segr(t) also shows the monotonic growth superposed by the quasiperiodic oscillations of small amplitudes. However, at any certain r_D value, each trajectory tends to the same saturation level. Also, the inflection point of η_segr(t) is shifted to later times in comparison with the function η_aggr(t). Nevertheless, the main distinct feature of the segregation is that η_segr approaches the saturation level faster at 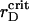(see enlarged circle in Fig. 8), rather than at reduced or increased values of r_D. Thus, with respect to the segregation, r_D has an optimal value, r_D ∼ 0.012 μm, that provides the maximal demixing of particles for the shortest time. Close to 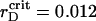μm, the segregation character does not show other new features at lowered r_D values.

FIGURE 8.

Phase diagrams on the (r_D/σ, λ) plane for the lipid-induced attraction. The enlarged circle denotes the segregated state with the theoretical estimate for λ.

We attribute such behavior of the order parameters with structural changes in the two-component system that evince the spinodal decomposition mechanism of the phase separation. In the vicinity of 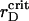we detect the total demixing of the PSI and PSII components after ∼1100 τ_Br. In the absence of the quiescent period, the appearance of mobile PSII-enriched domains of the prolate form with diffuse interfaces is observed, followed by their merging. After coarsening of the interface, we recognize the structure, with all PSIIs located within its core and all PSIs expelled into the peripheral zone. A typical spatial arrangement of particles is represented in Fig. 9 A. PSIIs form an ordered phase with the honeycomb patterns observed clearly and the PSIs do the same. However, the solid phase of the PSII component is denser than the solid phase composed from the PSI particles. In Fig. 9 B three PDFs for the current configuration confirm these notions. The graphs of g^I&I(r) and g^II&II(r) are similar except for a shift between their first maxima locations, reflecting the existence of more dense and less dense phases, and a relative difference between 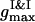and 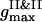due to a particle size mismatch. The expressive form of g^I&II(r) with decreased first maximum and increased envelope formed by the rest maxima certifies the pronounced segregation.

FIGURE 9.

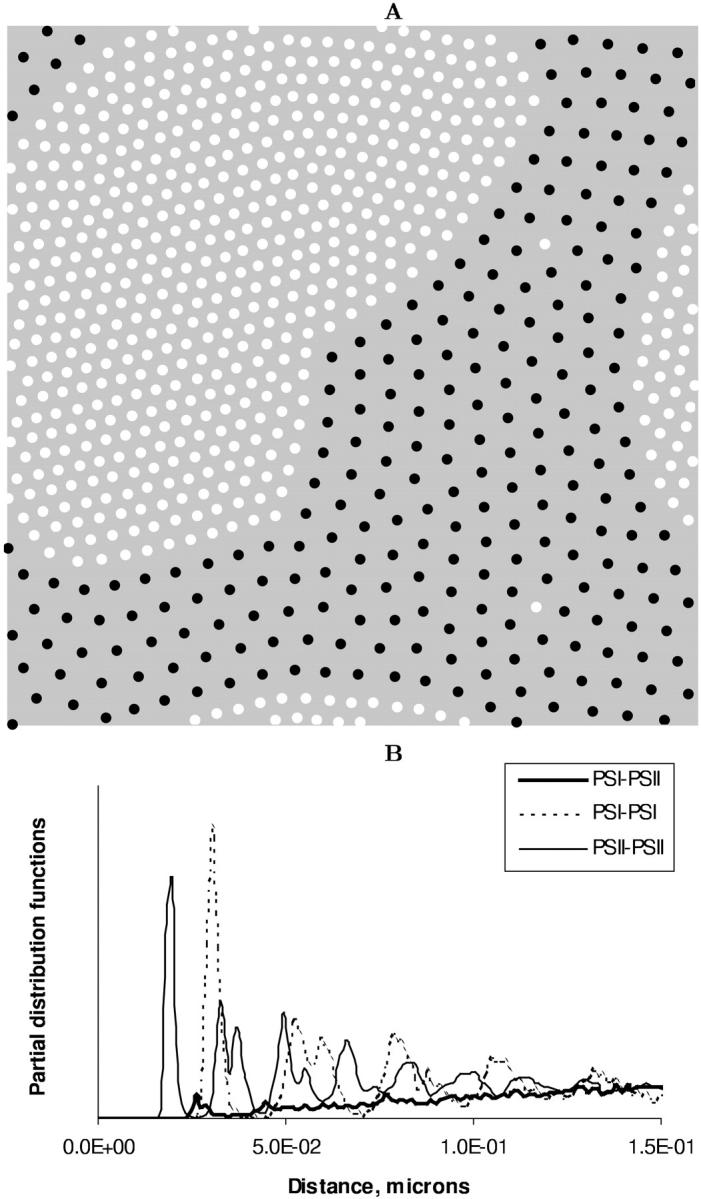
(A) Segregated state of PSI (dark circles) and PSII (light circles) particles interacting via the lipid-induced attraction. The PSI and PSII particles are depicted as dark and light spots, respectively. State variable values are λ = 1.0 and r_D = 0.016 μm. (B) Relevant to this spatial configuration are the PDFs calculated for the PSI-PSI, PSII-PSII, and PSI-PSII pairs. The center-to-center distance between the PSI and PSII particles is used as a variable.

In general, we detect here a liquid-solid coexistence in the binary mixture accompanied by the phase separation. Also, due to the phase separation the mixture undergoes a transition from the isotropic to the ordered state. Demixing of photosystems pre-empted by the spinodal decomposition results in ordering with PSIs and PSIIs segregated globally.

At further lowering of 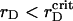, we observe that sustained growth of η_aggr(t) advances with fluctuations of reduced amplitude (see Fig. 7, A and B). Simultaneously, η_segr(t) grows faster at initial and intermediate timescales, but its saturated value is reduced. These confirm the idea that nucleation and growth superseded the spinodal decomposition. Indeed, while reducing r_D at the same λ ∼ 1.0 we observe the formation of several nuclei composed of the PSII component instead of a single cluster. However, they are less dense here than in nucleation process with the VDW-type attraction discussed above.

Thus, simulations with the estimated parameters show that the lipid-induced interactions coupled with the electrostatic ones give the segregation of photosystems under the physiological cation concentrations. Moreover, total demixing results in the arrangement of PSIs and PSIIs that clearly resembles the lateral heterogeneity of photosystems in higher plant thylakoids.

Lateral heterogeneity of photosystems as aggregated states

The dynamical behavior of the many particle system with any of considered interactions, Eqs. 5–7, is extremely complicated, so that detailed study of its phase behavior is a great challenge. For example, the potential, taken in the form of Eq. 7, is of the two-Yukawa-type with four parameters, λ, r_L/σ, κ, and r_D/σ, for the fixed sizes and charges of particles. Particle heterogeneity further complicates the situation. The statistical system with such a pairwise interaction possesses a broad spectrum of various states and covers a wide range of physical, chemical, and biological phenomena. Therefore, in pursuing our goals we restrict the consideration by a limiting set of parameters as well as a limiting class of phase states related to our system.

As the aggregation and segregation of photosystems in higher plant thylakoids are observed as salt-induced phenomena, at least two free adjustable parameters should be incorporated in any comprehensive model. One of them, certainly, is the external parameter related to the stromal solution; it is r_D/σ in the present consideration. Another one should somehow characterize the internal specificity of the two-component system; it is λ in our studies. These parameters (or their equivalents) form a limiting set of parameters related to the system.

Further, we accept the most general classification of equilibrium states when they belong to either ordered phases (segregated and mixed) or isotropic phase (nearly uniform distribution of mixed photosystems in the membrane plane). Such classification gives us a limiting class of phase states related to the system. The set of points on the plane (λ, r_D/σ) can be considered as a mapping of possible thermodynamics states of the given system, so that it might be identified as the generalized phase plane. Typical phase diagrams taken from results of the simulations with potentials of Eqs. 5–7 are presented in Figs. 2, 5, and 8, respectively. They were obtained for the different attractive interaction parameters from the expanded intervals that incorporate their analytically estimated λ-values (see Model of PSIs and PSIIs Lateral Movement). Every phase curve divides the phase plane (λ, r_D/σ) into two parts corresponding to the ordered or isotropic states in the ensemble of PSI and PSII particles.

The phase diagrams for all interactions yield 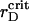from the interval that incorporates reasonable physiological r_D values, 0.002–0.02 μm (Barber, 1982; Thorne and Duniec, 1983), even if the values of the attractive parameters λ deviate from their theoretical estimates by up to several times. This observation supports the idea of the photosystems ordering in higher plant thylakoids due to the long-range nonspecific protein-protein interactions.

Regardless of the interaction type, all phase curves are monotonic functions of the governing parameter r_D. Upon increase of the divalent cation concentration, the electrostatic repulsion between protein complexes becomes more screened and weaker attractive forces suffice to stabilize the system at intermediate distances between particles. This is a direct consequence of the fact that r_D and λ characterize repulsive and attractive terms separately. In the case of salt-dependent attractive forces, a nonmonotonic behavior of the phase curves is admitted.

Regardless of the interaction type, all phase curves are sigmoidal. The strong attraction limit (upper saturated parts of the phase diagrams) represents the situation when ordering occurs at the upper physiological limit of the Debye radius values, which corresponds to the low cation concentrations. At this upper limit the system becomes very sensitive to changes in the cation concentrations, and, hence, may be unstable with respect to these concentrations. The lower part of the sigmoid phase diagram represents another physiologically interesting situation. At low values of the attraction parameter even relatively high counterion concentrations are not sufficient for ordering, and the photosystems remain uniformly distributed in the membrane plane. The absence of protein-rich domains in this case might prevent appression of membranes to form grana (Andersson and Anderson, 1980; Barber, 1980) although any direct conclusions are beyond the scope of our model.

The sigmoidal profile of the obtained phase curves correlates with measurements of the chlorophyll content of thylakoid fragments, a 10,000 × g pellet (Rubin et al., 1981; Barber, 1982). Chlorophyll percentage plots are the same type of functions of divalent cation concentration. Indeed, stacking of thylakoids demands some kind of membrane surface charge heterogeneity. When the particles are polydispersed in charge, this corresponds to their aggregation accompanied or not by segregation. In turn, the phase curves, presented here, elucidate that aggregation of photosystems, regulated by the dimensionless parameter κ/(λɛ) with κ ≡ q₁q₂/e², depends on another dimensionless parameter χ = σ²/r_D², which varies with the ionic strength of stromal solution, χ ∼ I/ɛ, in the same manner as the degree of stacking.

General remarks

Intuitively, one might expect that total demixing of the PSI and PSII particles within the grana should take place as the spinodal decomposition rather than nucleation and growth. Indeed, the spinodal decomposition as a phase transition is small in degree with respect to the composition change in time but large in extent with respect to the composition change in space. In segregation phenomena in higher plant thylakoids, local variations in polydisperse particle interactions cause the global rearrangement of particles.

Intuitively, it is also clear that for the total demixing of PSIs and PSIIs, the metastable region of the phase coexistence (fluid-solid) should have a wide band in stromal cation concentration, comparable with its physiological range. Indeed, the spinodal decomposition happens in the region between the coexistence curve and the stability curve located within the coexistence region. Phase separation in vivo will be guaranteed if the stability band in ionic strength (or the Debye radius) is wide enough.

We used in simulations the bare charges of PSI and PSII instead of effective ones, as charge renormalization leads to higher values of r_D (Sanghiran and Schmitz, 2000). Another source of increase in r_D is the additional attraction between PSI and PSII due to cation density fluctuation (Wu et al., 1998). Hence, the model requires the renormalized Debye length and the PSI-PSII charge ratio to be adjustable parameters. They should be fitted to experimental data on chlorophyll fluorescence yield under different salinity conditions. More generally, one might consider the two dimensionless parameters, κ/(λɛ), and χ, introduced above, as free.

CONCLUSIONS

In this article we have reported the Brownian dynamics simulation results on aggregation and segregation of photosystems in the grana thylakoids, considering different potential interactions between PSIs and PSIIs. The main results obtained are the following.

1. Cation-induced aggregation and segregation of photosystems in the higher plant thylakoid membrane were mesoscopic phenomena driven by the nonspecific protein-protein interactions between particles, that are distinct in the electric charge and size.

2. For the VDW-type and elastic attractions, the obtained configurations had no similarity with those detected experimentally. Aggregation took place at the small r_D values, which correspond to the stacking of thylakoids without passing through a preliminary stage of lateral heterogeneity of photosystems. Segregation was observed as nucleation in case of the VDW-type attraction or as a transient gelation in case of the elastic attraction, while such scenarios allowed only local demixing of PSIs and PSIIs.

3. At the same time, the lipid-induced attraction made a strategic balance to the electrostatic repulsion providing demixing on the grana scale. The obtained configurations clearly resembled the lateral heterogeneity of photosystems observed in the grana thylakoids. Aggregation took place at the intermediate r_D values, which correspond to the preliminary stage preceding the stacking of thylakoids. Segregation proceeded as a spinodal decomposition.

4. The phase curves obtained for different protein-protein interactions were monotonic functions of the governing parameter r_D and revealed the sigmoid shape. The similarity of the phase curves reflects the universality of the critical exponents (referred to as a phase transition of the second order), and scaling relations between them (Kadanoff, 1966; Halperin and Hohenberg, 1969). They depend only on the spatial dimension of the system and the tensor range of its order parameter, which can be chosen in various ways to characterize a transition of the system between the states of different ordering; in our case, nonaggregated and ordered ones.

The overall remark is about an explicit consideration of PSIs and PSIIs and implicit treatment of other thylakoid proteins. Large sizes and charges of photosystems, together with their high volume fractions, allow using the two-component model in case of the grana scale phenomena. Here we have studied the general features of the aggregation and segregation of photosystems, neglecting their fine structures, such as formation of the PSII-dimer-LHCII-trimer supercomplexes (Boekema et al., 2000), existence of mobile domains with several PSIIs, LHCIIs, and cytochrome b₆/f (Kirchhoff et al., 2000), etc. Certainly, the consideration of the dynamical arrangement of all photosynthetic units in thylakoids demands modeling a five-component system of interacting particles. However, it requires the new measurements, in particular, data on the thylakoid geometry, sizes of all protein complexes, and their stoichiometry, established for the same chloroplast at nearly the same experimental conditions.