Insights into Nucleic Acid Conformational Dynamics from Massively Parallel Stochastic Simulations

Abstract

The helical hairpin is one of the most ubiquitous and elementary secondary structural motifs in nucleic acids, capable of serving functional roles and participating in long-range tertiary contacts. Yet the self-assembly of these structures has not been well-characterized at the atomic level. With this in mind, the dynamics of nucleic acid hairpin formation and disruption have been studied using a novel computational tool: large-scale, parallel, atomistic molecular dynamics simulation employing an inhomogeneous distributed computer consisting of more than 40,000 processors. Using multiple methodologies, over 500 μs of atomistic simulation time has been collected for a large ensemble of hairpins (sequence 5′-GGGC[GCAA]GCCU-3′), allowing characterization of rare events not previously observable in simulation. From uncoupled ensemble dynamics simulations in unperturbed folding conditions, we report on 1), competing pathways between the folded and unfolded regions of the conformational space; 2), observed nonnative stacking and basepairing traps; and 3), a helix unwinding-rewinding mode that is differentiated from the unfolding and folding dynamics. A heterogeneous transition state ensemble is characterized structurally through calculations of conformer-specific folding probabilities and a multiplexed replica exchange stochastic dynamics algorithm is used to derive an approximate folding landscape. A comparison between the observed folding mechanism and that of a peptide β-hairpin analog suggests that although native topology defines the character of the folding landscape, the statistical weighting of potential folding pathways is determined by the chemical nature of the polymer.

INTRODUCTION

The hairpin-loop motif is a ubiquitous building block within the three dimensional structure of DNA and RNA, with loop regions known to participate in specific tertiary contacts or act as nucleation sites for RNA tertiary folding (Uhlenbeck, 1990), and hairpin structures taking part in various biomolecular processes (Bhasin et al., 1999; Froelich-Ammon et al., 1994; Kennedy et al., 1998; Roth et al., 1992; Suo and Johnson, 1997; Trinh and Sinden, 1993; Wilson and von Hippel, 1995; Zazopoulos et al., 1997). Understanding the folding dynamics of such species, which has been described previously as a potential paradigm for the folding of larger RNAs (Zhang and Chen, 2002), may be a precursor to understanding the assembly of larger nucleic acid structures (Ansari et al., 2001).

Experimental and theoretical techniques focusing primarily on statistical mechanical representations of RNA folding have recently been employed to elucidate the kinetics and thermodynamics for these events (Ansari et al., 2001; Bonnet et al., 1998; Chen and Dill, 2000; Cocco et al., 2001; Flamm et al., 2000; Goddard et al., 2000; Grunwell et al., 2001; Kuznetsov et al., 2001; Liphardt et al., 2001; Shen et al., 2001; Tostesen et al., 2001; Wallace et al., 2000, 2001; Zhang and Chen, 2001, 2002). Still, the coarse-grained nature of these models, although explaining some experimental observations and predicting macroscopic observables well, limits their ability to offer an atomistic description of conformational dynamics for nucleic acid hairpin structural formation and disruption. This lack of a well-resolved picture of hairpin conformational dynamics, in both the spatial and temporal senses, serves as the primary motivation of this study, which employs massively parallel stochastic dynamics simulations to probe and characterize hairpin structural changes.

This work reports on simulations using an all-atom model and a continuum representation of solvent effects that total more than 500 μs for an ensemble of small RNA hairpins that include 1), unfolding, misfolding, refolding, and unwinding/rewinding events; 2), calculations of conformer-specific folding probabilities (P_fold) to characterize the transition state (TS) within each observed pathway; and 3), thermodynamic sampling using a multiplexed replica exchange molecular dynamics (MREMD) algorithm. Preceding these results is an assessment of the atomistic model used. The caveats of the model of hairpin conformational dynamics employed and a comparison to the simulated folding of a peptide analog of this nucleic acid hairpin are then discussed.

METHODS

General simulation protocols

A simple, atomistic model (Sorin et al., 2002) is employed to investigate hairpin configurational dynamics using: Allen's stochastic (Langevin) integrator (Allen, 1980) within the TINKER molecular modeling package (available online at http://dasher.wustl.edu/tinker/) with viscosity γ = 91 ps⁻¹ for kinetic sampling; the AMBER95 force field (Cornell et al., 1995); the RATTLE algorithm (Andersen, 1983) to constrain only covalent bonds involving hydrogen atoms; no electrostatic truncation; and a 2.0-fs timestep, with molecular coordinates stored every 50–100 ps for all trajectories.

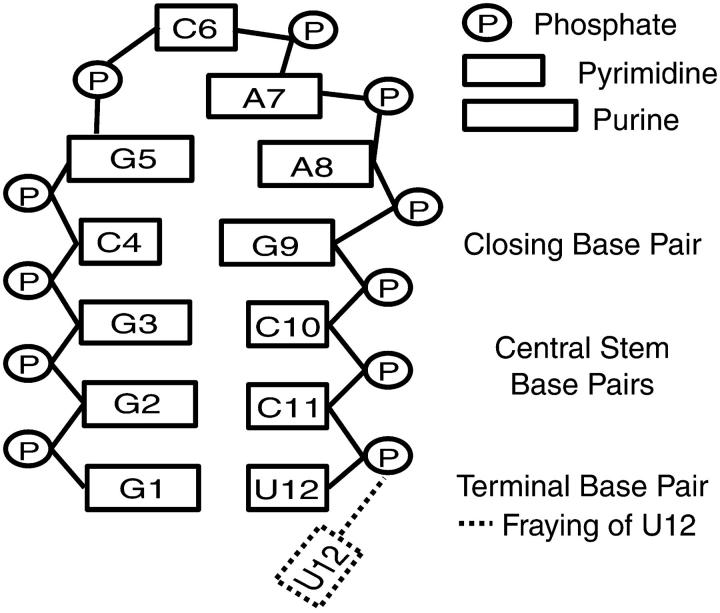
Employing a heterogeneous, massively distributed computer (Folding@Home online at http://folding.stanford.edu/) consisting of over 40,000 processors, >500 μs of simulation time was collected (outlined in Table 1) for the RNA hairpin 5′-GGGC[GCAA]GCCU-3′ (Scheme 1), the structure of which was previously characterized via nuclear magnetic resonance (NMR) (Jucker et al., 1996). All kinetic trajectories reported herein were collected in unperturbed folding conditions at 300 K following a 1-ns molecular dynamics relaxation period performed on the first refined NMR model (PDBID# 1ZIH). This relaxation period employed Beeman integration (zero solvent-induced friction) at 300 K, and resulted in a starting structure with an all-atom, root-mean-squared deviation (RMSD) of 1.62(±0.16) Å from the 10 refined NMR models. The academic distribution ProFit, available online at http://www.bioinf.org.uk/software/, was used for structural alignment and RMSD calculations.

TABLE 1.

Cumulative simulation times by project

Simulation series	∼Time (μs)
Uncoupled ensemble dynamics
Native state	200
Denatured state	175
Collapsed ensemble	40
MRESD
Native state	16
Denatured state	16
Pfold	73
Total	520

Figure 11.

Solvent model

The effects of solvation are approximated using the generalized Born surface area (GB/SA) continuum solvation model (Qiu et al., 1997), as implemented in the TINKER molecular modeling package, using a surface area prefactor of 7.0 cal/mol × Å². This is not the first work to report the application of the GB approximation to model nucleic acid dynamics. Indeed, numerous studies have reported positive results using GB as an implicit solvent model for small nucleic acid simulation. Case and co-workers have reported successful comparisons between GB simulations and explicit solvent simulations, and convergence of an A-form DNA duplex to proper B-form using the GB model, as well as studies of RNA and metal ion binding using GB (Tsui and Case, 2000, 2001a,b). Williams and Hall have reported nucleic acid hairpin studies using GB that mimic previous explicit solvent studies by the Kollman group and that maintain low RMSD values from the NMR structure (Williams and Hall, 1999). Zacharias and co-workers have studied tri-loop structure and RNA-metal ion binding using GB (Burkhardt and Zacharias, 2001; Zacharias, 2001). Furthermore, our previous work has included tabulated structural data on the stability of native state simulations of this tetraloop hairpin using the model presented in our current work (Sorin et al., 2002), and we include below a brief analysis of the stability of the native state using this model averaged over ∼200 μs of native state simulation. Of course, no model is without its limitations and we thus discuss the limitations of this model below.

Uncoupled ensemble dynamics

We have previously reported our method of coupled ensemble dynamics (Pande et al., 2003; Shirts and Pande, 2000; Zagrovic et al., 2001), which entails sampling a large number of constant temperature trajectories. In this case, when a single trajectory overcomes a detected free energy barrier, all trajectories in that simulation series are relocated in configurational space to the final locale of that trajectory and restarted with independent, random atomic velocities. Here we report a simpler variation on this idea, uncoupled ensemble dynamics, which does not include these relocating moves after detected barrier crossings. This method does not require, a priori, a definition of the relevant free energy barriers and, as all trajectories in a simulation series are fully independent, elucidating apparent transition rates follows directly from the relevant rate theory.

As an example, one can consider the conformational transition U → F over a complex free energy landscape with n pathways that exhibit single exponential kinetics with rates k_i and statistical weights C_i. The fraction of the population remaining in state U at short times t can be approximated by

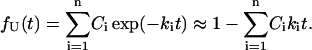(1)

The fraction that reaches state F in this same time is then

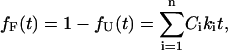(2)

with an apparent transition rate given by

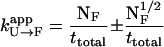(3)

for all processes that exhibit first-order kinetics (Zagrovic et al., 2001), where N_F transitions to state F occur in a total simulation time t_total.

We have previously demonstrated that this approximation holds for large ensembles of trajectories, thus allowing rates for long timescale dynamics (on the order of milliseconds) to be derived from many short trajectories (tens of nanoseconds each) based on ensemble principles (Shirts and Pande, 2001). Here we apply this approximation to uncoupled ensemble dynamics simulations at 300 K, resulting in a total of ∼200 μs of simulation starting with a relaxed native structure and ∼175 μs of simulation starting from the fully extended chain. Additionally, ∼40 μs of simulation time was collected to examine the dynamics of the collapsed state of the hairpin before proper formation of basepairing and stacking interactions: five conformers with low radii of gyration (R_g) and lacking native character were chosen from the ∼175 μs total simulation time of the unfolded state, and each was used as the starting point in 100 independent, parallel simulations.

P_fold calculations of TS

The TS for each observed pathway was determined by calculating P_fold values (Du et al., 1998; Pande and Rokhsar, 1999) for conformations around the relevant free energy barriers after conducting a large number of simulations starting from each of these conformations. The TS is defined as the region in configurational space between two free energy minima with P_fold = 0.5, equivalent to the stochastic separatrix (Klosek et al., 1991). By construction, P_fold is a natural, well-suited single reaction coordinate for monitoring conformational transitions, independent of the chemical nature of the polymer.

Here we have chosen windows of 4–5 ns around the detected transition barriers in the trajectories described below and started 100 independent simulations for each of 25 conformations within each window, totaling ∼73 μs of simulation time. Based on current and previous simulation results, each trajectory was then classified as folding or unfolding by defining boundaries on the RMSD from the relaxed native structure of <3 Å and >9 Å, respectively.

MREMD

The multiplexed replica exchange molecular dynamics algorithm (MREMD), as implemented by Rhee and Pande (2003), is a variant of the well-established temperature replica exchange molecular dynamics (REMD) algorithm (Hukushima and Nemoto, 1996; Sugita and Okamoto, 1999). Here we employ stochastic dynamics rather than molecular dynamics. As in REMD algorithms (Hukushima and Nemoto, 1996; Sugita and Okamoto, 1999), this variant is based on thermal jumps between a wide range of temperature levels with relatively small spacings, yet also includes random solvent derived frictional forces. These temperature jumps prevent trajectories from being kinetically trapped in local energetic minima, and thus enhance the sampling efficiency achievable by constant temperature simulations alone (Rhee and Pande, 2003).

The implementation of the MREMD algorithm is based on a series of Metropolis-style swap attempts (Metropolis et al., 1953) between atomic configurations (q) in neighboring temperature levels (T) at periodic time intervals according to the swap acceptance probability

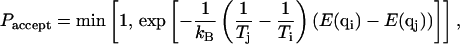(4)

where k_B is the Boltzmann constant, T_x is the absolute temperature of level x containing configuration q_x, and E(q_x) is the energy of that conformation. For the nonmultiplexed REMD situation, this swap criterion ensures that detailed balance is maintained for the Markov process given by

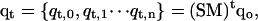(5)

where S is the swap operator, M is the molecular (or stochastic) dynamics operator, and q_t,x is the conformation at time t in temperature level x.

By multiplexing replicas in each temperature level, we allow swap attempts between levels i and j across a large number of simulations at temperatures T_i and T_j, thus increasing our sampling greatly. This multiplexing of levels also maintains the Markovian properties of the calculation with the simple inclusion of a rearrangement operator R, that acts to interlace the many temperature levels i with their many potential swapping partners j such that

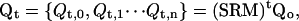(6)

where Q_t,x is a collective set of multiplexed conformations in temperature level x. Thus, in MREMD, exchanges between replicas in different multiplexed-replica layers, as well as swaps between replicas in the same layer, are allowed. This both enhances sampling by extending the work done during a single simulation series, and removes unnecessary waiting periods when conformations in neighboring temperature levels of the same layer are not available for swap attempts at the same time.

Here we have completed two such MREMD simulations, with one starting in the relaxed native configuration and the other in a fully extended configuration. Each employed 50 temperature levels exponentially distributed between 150 and 650 K, with a maximum of 200 parallel trajectories per level, totaling ∼32 μs. With swaps being attempted after every 250 ps of simulation, we obtain temperature-independent Metropolis swap ratios between 0.54 and 0.71. To further enhance sampling without eliminating the stochastic forces that can also “push” conformations out of local energetic minima, all MREMD trajectories were run with moderately low viscosity (γ = 5 ps⁻¹).

RESULTS

Stability of the atomistic model

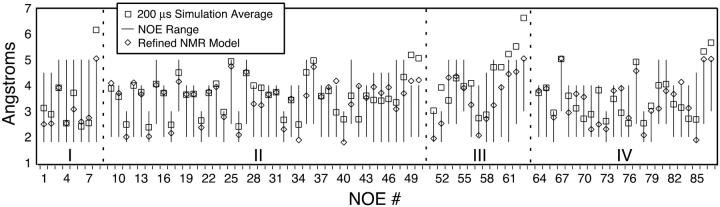
To assess the quality of the model employed herein, two measures of stability averaged across the ∼200-μs simulated ensemble of the native state are considered. With nanosecond temporal resolution, this averaging includes over 200,000 structures. Global native state stability is characterized by calculating the average atomic root-mean-squared deviation from the relaxed starting structure, 〈RMSD〉 = 1.89 Å, while agreement between our simulated ensemble and experimentally derived distance constraints is characterized by calculating average interproton distances throughout the hairpin. Weighting all such inter-proton distances as 〈r_ij⁻⁶〉^−1/6 allows direct comparison between simulation and experiment. As shown in Fig. 1, of the 50 constraints derived from nuclear Overhauser effects (NOEs) within the stem (regions I and II), only three minor violations of ∼1 Å or less were detected. These three violations coincide with distances in the refined NMR model used to generate our relaxed starting structure that are at or over the NOE range maximum.

FIGURE 1.

Ensemble average interproton distances (boxes) over ∼200 μs of simulation of the native hairpin, for the four types of constraints used to derive the refined NMR models, plotted alongside the NOE-derived constraint ranges (bars) and values for the refined model used to generate the relaxed starting structure (diamonds): (I) stem interstrand; (II) stem intrastrand; (III) stem-loop interface; and (IV) intraloop constraints.

Competing pathways in hairpin unfolding

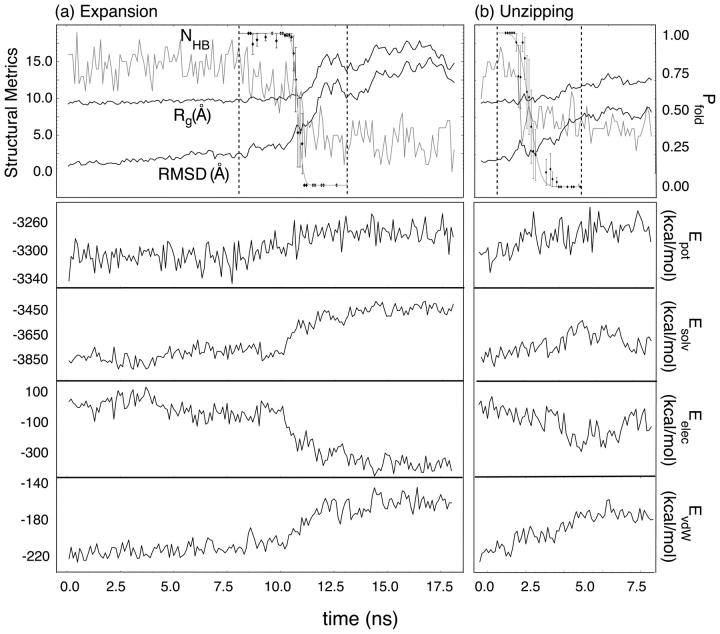
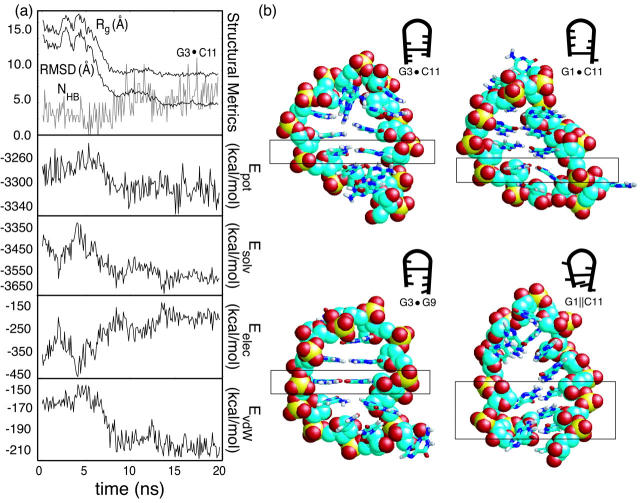
While unfolding under folding conditions (300 K, waterlike viscosity) is expected to be extremely rare, two such events were observed in our ∼200 μs of native state simulations, each demonstrating unique mechanistic behavior. Fig. 2 shows time-series of three structural measures for both pathways, referred to further herein as expansion and unzipping, including the RMSD from the relaxed native structure, the radius of gyration, and the total number of (native and nonnative) hydrogen bonds (N_HB, defined by an acceptor-donor distance of 2.5 Å or less and a bond angle of 110° or greater). P_fold values are shown between dashed lines for both pathways and are fit to the function

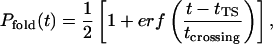(7)

where t_TS is the time at which the TS is reached and t_crossing represents the duration of the barrier crossing event. Four energy components are also included in the figure to illustrate the transitions from an energetics perspective.

FIGURE 2.

Unfolding pathways at 300 K: shown are the time-series for the expansion pathway (a), showing very discrete unfolding, and the unzipping pathway (b), which maintains a compact loop region after unfolding. P_fold calculations for a window around each free energy barrier in the unfolding events are shown between dashed lines. The total potential, solvation, electrostatic, and van der Waals energy components are also shown for each pathway.

Mechanistically, the expansion event (Fig. 2 a) begins with a slight loss of helicity in the stem region, followed by the buckling of the terminal and closing basepairs away from near-planar native basepairing geometry. As the backbone relaxes away from helical geometry, only the G3•C10 basepair remains intact. At this point, nearly all native stem hydrogen bonds are lost, with transient nonnative interactions holding the strands together. Final flattening of the backbone into a planar conformation occurs as the last intact basepair (G3•C10) protrudes away from the hairpin “core” and into solvent, resulting in a single native hydrogen bond between this pair. The transition state for this pathway (TS_exp), as identified by P_fold analysis, is characterized as compact (R_g ∼ 10.5 Å) and planar, with 1 native hydrogen bond between a single basepair in the hairpin stem. Moreover, charge interaction energy is decreasing more rapidly at this point than at any other. As the trajectory crosses the TS_exp, the loss of both native and nonnative base-base contacts between opposing strands and a departure from a global planar geometry toward random coil orientation are observed. Physically, this mechanism brings about an overall increase in R_g of 50% within 4 ns and an increase in RMSD from ∼2 Å to ∼10 Å in that same time period.

In contrast, R_g increases by only 25% in 4 ns during unzipping (Fig. 2 b), with a maximal RMSD ≈ 8 Å (though the hairpin has unfolded, the loop region remains compact). This event begins with fraying of the terminal basepair, followed by successive loss of basepairing continuing toward the loop region. The transition state for this pathway (TS_zip) determined by P_fold analysis maintains a nearly broken C•G closing basepair consisting of only 1–2 hydrogen bonds. As the TS_zip is reached, the bases in the partially broken second basepair extend away from one another rapidly: the closest atomic separation between G3 and C10 rises from ∼2.5 Å to ∼4.5 Å. Although the final unfolded structure retains stacking in the loop region, as illustrated by the solvation and electrostatic energy components, the total potential of the unfolded state agrees with that observed in the expansion pathway unfolding event.

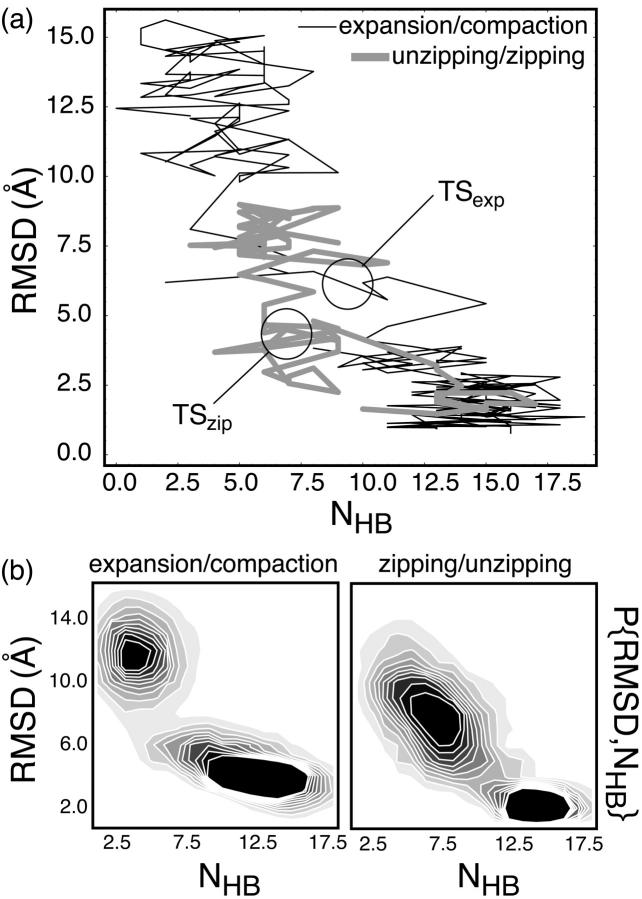
Fig. 3 a depicts the projections of these pathways onto the RMSD vs. N_HB surface, with the detected TS regions noted. While these two-dimensional projections likely oversimplify the actual dynamics, it is evident that these trajectories do not contribute to a single, generic pathway with multiple nucleation sites. Consistent with this model, the respective TS conformations are highly structurally differentiable: TS_exp is globally planar and involves multiple transient, nonnative interstrand hydrogen bonds, whereas TS_zip is nonplanar, having little nonnative hydrogen bonding character. As is the case for protein folding (Klimov and Thirumalai, 2001), simulation suggests that RNA folding at the most elementary level (hairpin or duplex formation) includes multiple nucleation sites and a heterogeneous TS ensemble.

FIGURE 3.

(a) Expansion (thin black) and unzipping (thick gray) trajectories projected onto the RMSD vs. N_HB surface with the respective TS regions noted. (b) Probability surfaces for both pathways that were determined from P_fold sampling around the relevant free energy barriers, which verify that both are bimodal in nature. Such sampling is analogous to umbrella sampling confined to the region of configurational space directly surrounding the folded and unfolded regimes.

The appearance of these individual trajectories might suggest pathway specific kinetics, and the unzipping pathway was initially interpreted as consisting of three energetic minima. To probe the landscape about these pathways, cumulative sampling about the relevant free energy barriers from P_fold trajectories was considered. Because P_fold trajectories were started from conformations near the detected free energy barriers, and therefore rapidly folded or unfolded, this sampling is comparable to umbrella sampling across only the most relevant portion of phase space. Verifying that both pathways follow two-state kinetics, Fig. 3 b shows histograms of the observed relative probabilities in this simplified representation. Although a statistically significant weighting between these pathways is not known, the two-state nature of both pathways explicitly allows the parallel rates to be summed in deriving the overall unfolding rate, which we thus approximate using Eq. 3: k_u = 10 (±7) ms⁻¹.

It is interesting to note that the thermal denaturation pathway reported in a previous computational study of this hairpin is consistent with the expansion pathway described above, whereas no unzipping events were observed at rapidly denaturing temperatures (Sorin et al., 2002). This suggests that increasing random thermal fluctuations, which can more easily disrupt multiple native contacts throughout the structure simultaneously, favors the expansion pathway, and highlights the fact that although thermal unfolding studies can allow the elucidation of potential folding pathways, the possibility of a temperature dependence of the folding and unfolding mechanism should be considered both experimentally and computationally.

Hairpin collapse and misfolding

To study hairpin collapse and misfolding, simulations were started from the fully extended, denatured state. A total of 21 trajectories had undergone a nativelike collapse within the ∼175 μs of the extended conformer simulation set, giving an average collapse rate of k_coll = 0.12 (±0.03) μs⁻¹, which yields a collapse time of τ_coll ≈ 8 μs, consistent with previous measurements of hairpin closing rates at or near 300 K (Ansari et al., 2001; Bonnet et al., 1998; Goddard et al., 2000; Shen et al., 2001; Wallace et al., 2000, 2001; Ying et al., 2001). The time-series for such a collapse is plotted in Fig. 4 a, with nativelike collapse defined according to two structural criteria: R_g < 11.0 Å (R_g, native ∼ 9.5 Å) and RMSD < 6.0 Å. The collapsed ensemble, as defined, is thus limited to structures with a hairpinlike bend occurring somewhere in the sequence and a relatively compact global size. Furthermore, these numeric limits on R_g and RMSD require our nativelike collapsed ensemble to share global similarity with the TS ensemble.

FIGURE 4.

(a) Time-series for a representative collapse and misfolding event. (b) Members of the misfolded trap ensemble observed in our simulations, including the observed non-native interstrand G1‖C11 stacking interaction. Schematic illustrations are shown for clarity, and boxes bound the interactions in the atomistic figures that are explicitly shown in the schematics.

Within these collapse events and further simulations of collapsed structures, a pattern of misfolding behavior that leads to off-pathway traps during the folding process has been identified. In labeling these intermediates, the conventions of Chen and Dill are followed (Chen and Dill, 2000), where off-pathway microstates involve primarily nonnative contacts and on-pathway conformers exhibit primarily native interactions. Four such traps are schematically illustrated in Fig. 4 b. Two of these involve complete Watson-Crick G•C basepairing in which C11 mispairs with the G nucleotides that neighbor its native pairing partner, G2. In the third, the G3•G9 pair attempts multiple possible pairing configurations, including a trans dual H1 to O6 scheme. It appears that this rather dynamic misfolded conformer may be a part of the G1•C11 trap state: in both cases the same misalignment of the two strands occurs.

One observed folding trajectory that included complete formation of the native G3•C10 basepair offers further insight into the energetic frustration expected of nucleic acids. During conformational sampling, the G1 base stacked with the C11 base directly below this fully formed native basepair (Fig. 4 b, G1‖C11). After some fluctuation, breaking of the basepair occurred, leaving only the nonnative stacking interaction. Simulation thus indicates that misfolding into conformational traps can result not only from non-native basepairing interactions, consistent with prior models of hairpin dynamics (Ansari et al., 2001; Shen et al., 2001; Zhang and Chen, 2002), but also from nonnative interstrand stacking and hydrogen bonding interactions that act to impede or destabilize native contact formation.

A dominant zipping mechanism

Within the ∼215 μs of simulation of the fully extended conformer and the resulting collapsed structures, a small number of trajectories fell to slightly above 3 Å RMSD (min = 3.06 Å), some of which included structures with native stacking, hydrogen bonding, and/or basepairing interactions. Although the global topology of these structures was very similar to the native state, none exhibited complete stem basepairing and global helicity, and they are therefore not considered as complete folding events. However, multiple refolding trajectories from on-pathway unfolded conformations (that had passed the TS region during unfolding) were observed during P_fold simulations. Although these refolding conformers were sampled near the apparent free energy barrier, and had therefore not reached a truly random-coil state, this signals a first in atomistic nucleic acid simulation: the unbiased reassembly of unfolded conformers into the native fold, as described below.

After brief conformational sampling of various base orientations (1–10 ns), a nucleation site is formed and these refolders follow the reverse unfolding pathways described above, denoted further herein as “compaction” and “zipping,” and illustrated in Fig. 5. Refolding trajectories started from unfolded conformers along the zipping/unzipping pathway reliably followed the zipping pathway during refolding, whereas those started from unfolded conformers along the compaction/expansion pathway exhibited variability in refolding route, with some following the zipping pathway and others developing nucleation centers in either of the central G•C basepairs. This suggests a preference for refolding via the zipping pathway. We speculate that this preference is structurally necessary unless a globally planar geometry is obtained, which would entail a significantly larger entropic penalty than that predicted for the zipping pathway: the compaction mechanism requires limited, planar strand orientations before and during nucleation.

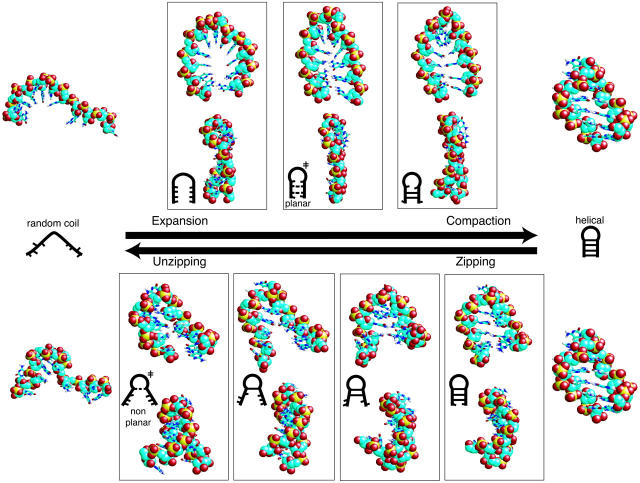
FIGURE 5.

Competing pathways in hairpin folding and unfolding are illustrated in atomic resolution, with each frame rotated ∼90° about the vertical to allow more accurate visualization. Schematic figures inset in each frame more clearly illustrate the interactions in each structure (dashed lines indicate partially formed basepairing interactions, with the compaction mechanism having multiple potential nucleation sites in the TS). The compaction/expansion mechanism includes a planar TS with favorable nonnative interstrand hydrogen bonding, whereas the zipping/unzipping mechanism includes a nonplanar TS with little nonnative hydrogen bonding character.

If we consider the initial collapse and reorganization of random interstrand contacts into the TS as rate-limiting, as is commonly assumed in fluorescence measurements of hairpin closing rates, and make the reasonable assumption that this collapse follows two-state kinetics (as suggested by the sharp transition in Fig. 4), the collapse rate serves as an upper bound on the folding rate, with τ_coll ≈ 8 μs being a lower bound on the folding time. Both this approximation and the apparent unfolding rate above are consistent with previous measurements for similar hairpins (Ansari et al., 2001; Bonnet et al., 1998; Goddard et al., 2000; Shen et al., 2001; Wallace et al., 2000, 2001; Ying et al., 2001). Furthermore, these apparent rates result in a free energy change of approximately ΔG_fold ≈ −1.5 kcal/mol for folding, which is in reasonable agreement with, but smaller in magnitude than, previously reported experimental values for this hairpin (Brion and Westhof, 1997; SantaLucia et al., 1992).

The folding/unfolding mechanisms reported herein are in agreement with the Ansari model of folding (Ansari et al., 2001; Kuznetsov et al., 2001; Shen et al., 2001), in which multiple nucleation sites are assumed and the TS is defined by any single, fully formed native basepair. We note that by the nature of their model, which employs the fraction of intact basepairs as the folding order parameter, it cannot elucidate an atomistic model of hairpin folding dynamics (such as partially formed basepairs), making their TS as consistent with our observations as can be expected.

Our model is only slightly inconsistent with the model of Zhang and Chen (2002), which employs a “stack-based” basepair measure of folding. With this metric, used in place of basepairing to simplify the enumeration of pathways, their calculated TS essentially requires a nucleation site containing two adjacent (stacked) basepairs. This contradicts both the observed TS determined by P_fold calculations, in which the nucleating basepair has minimally established one hydrogen bond, and the single basepair TS of the Ansari model. Support for the less structured TS reported here and by Ansari and co-workers may come from the experimental observation of DNA hairpins with stable stem regions consisting of only two basepairs (Hirao et al., 1994).

The dominance of a zipping mechanism predicted by the Zhang and Chen model near physiological temperatures, however, is consistent with our observations of folding as described above. Furthermore, as depicted in Fig. 5, TS_zip is more like the unfolded state than TS_exp, suggesting a smaller free energy barrier for zipping, again in agreement with the Zhang and Chen model (Zhang and Chen, 2002).

Defect-induced winding modes

An unwinding/rewinding mode has also been identified in simulations of the native hairpin that is mechanistically different than observed folding and unfolding events. As outlined by a single example in Fig. 6 a, these events are characterized by the loss and recapturing of global helicity, showing a departure from nativelike global structure (RMSD > 6 Å) while maintaining a relatively constant, compact size (R_g ∼ 10 Å). Four complete and eight additional, incomplete winding events occurred in ∼200 μs of native state simulation, resulting in apparent lower and upper bounds on the winding rate of 0.02 (±0.01) μs⁻¹ ≤ k_wind ≤ 0.06 (±0.02) μs⁻¹ and a characteristic mode period of 17 μs ≤ τ_wind ≤ 50 μs. Loop geometry appears to have no effect on unwinding and rewinding of the stem, consistent with previous simulation results in which the stem and loop were observed to behave independently (Sarzynska et al., 2000; Sorin et al., 2002; Zichi, 1995).

FIGURE 6.

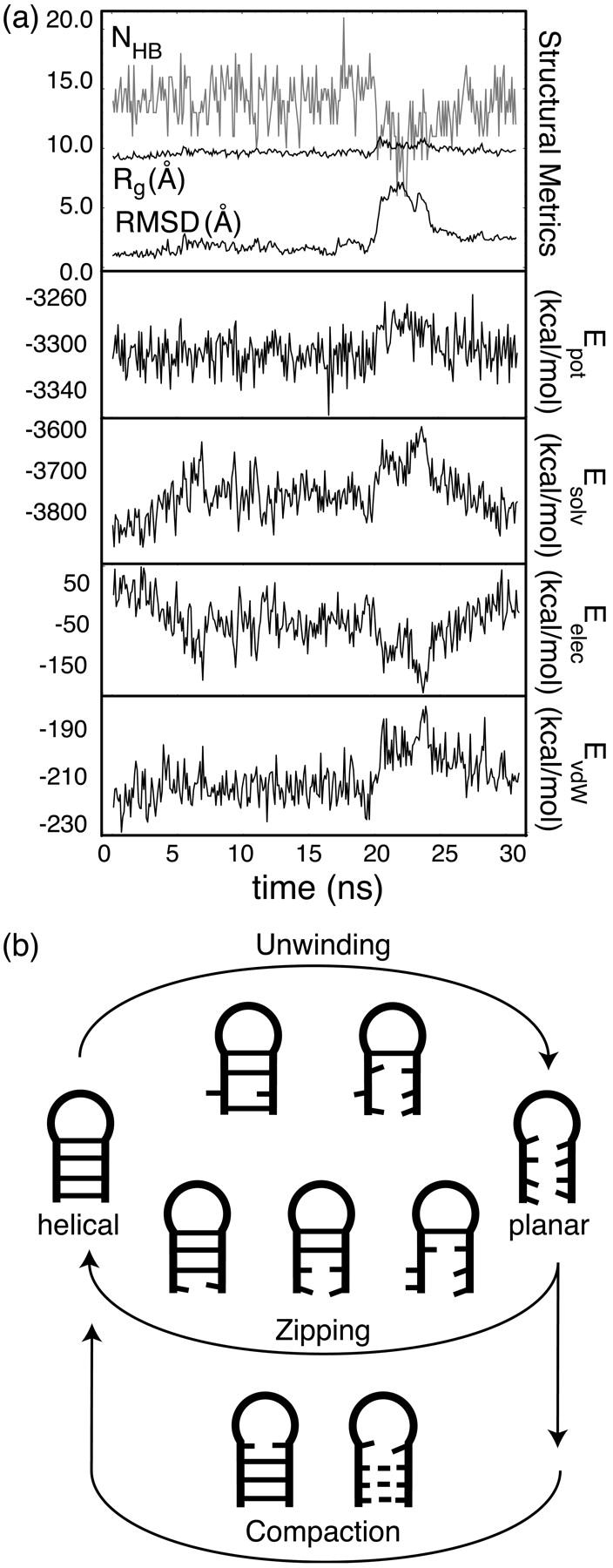
(a) Time-series for a representative hairpin winding mode event. (b) The observed unwinding and rewinding mechanisms in schematic form. As helicity is a function of basepairing, the schematics used represent both basepairing and local helical content; dashed lines in the nucleation step of compaction indicate alternate nucleation sites.

The mechanism of the observed winding modes is illustrated in Fig. 6 b. The event begins with the unexpected breaking of a central stem basepair as one of the bases drifts out of pairing position and removes local helicity in that region. Propagation of this unwinding occurs in both directions, resulting in a roughly planar global structure, not unlike TS_exp. Variability in unwound structures is apparent, as some maintain a fully or partially formed basepair, whereas others do not. This is in contrast to observed unfolding dynamics in which the closing and/or terminal basepairs break first and propagation occurs toward the central stem, rather than away from it.

Rewinding occurs less rapidly and also shows variability. In some rewinding events the closing C•G basepair reforms first, followed by a gradual regaining of global helicity during a zipping of basepairs down the hairpin. For unwound structures with one or more remaining native hydrogen bonds, rewinding follows the compaction mechanism with those native contacts acting as a nucleation site. We thus propose that local, conformational defects such as flipped-out solvent-exposed bases, although rare (Saenger, 1984), can result in such winding modes within nucleic acid helices, and that these events effectively relocate the hairpin to a point in the conformational space along one of the observed pathways near the folded region.

The collapse/misfolding and winding mode trajectories of Figs. 4 a and 6 a are shown in Fig. 7, as projected onto the RMSD vs. N_HB plane. Again using a simplified two-dimensional projection of these trajectories, the trap and unwound regions are not consistent with the apparent energetic minima observed in the folding and unfolding pathways shown in Fig. 3. The appearance of local minima within these dynamics offers evidence for a rough folding landscape, as suggested by the Ansari model (Ansari et al., 2001; Kuznetsov et al., 2001; Shen et al., 2001). Unlike previous experimental studies, however, which commonly measure only hairpin collapse rather than full formation of folding interactions (Bonnet et al., 1998; Goddard et al., 2000; Wallace et al., 2000; Ying et al., 2001), the dynamics observed suggest a complex landscape with multiple local minima.

FIGURE 7.

The collapse/misfolding (thin black) and unwinding/rewinding (thick gray) trajectories shown in Figs. 4 a and 6 a, respectively, as projected onto the RMSD vs. N_HB plane, with the misfolded trap and unwound regions noted.

Sampling conformational space

In an attempt to characterize this complex folding landscape, a multiplexed replica exchange stochastic dynamics algorithm was employed for thermodynamic sampling. Recently, numerous REMD applications have been reported in protein folding studies (Garcia and Sanbonmatsu, 2001; Sanbonmatsu and Garcia, 2002; Sugita et al., 2000; Zhou et al., 2001). Here we discuss the first application of replica exchange methodology to RNA folding. The incorporation of the replica exchange algorithm into a distributed computing architecture has allowed sampling on timescales that are orders-of-magnitude longer than previous reports. Still, with ∼32 μs of MREMD sampling time, the free energy surfaces derived from the native and denatured simulations do not converge (see Rhee and Pande, 2003, for a complete discussion of the inherent limitations of this method). Nevertheless, a qualitative description of the folding landscape can be extracted from MREMD simulations. To differentiate such qualitatively correct surfaces from the quantitatively exact ones, however, the resulting MREMD landscapes are referred to herein as statistical energy landscapes, as determined by the sampling achieved.

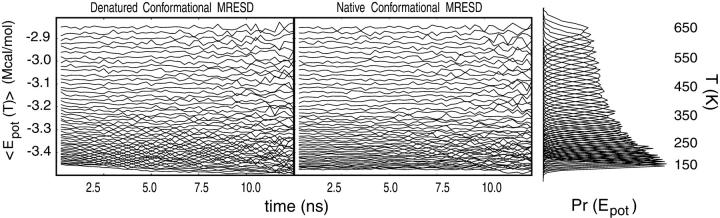
The thermally averaged potential energy 〈E_pot(T)〉 for each energy level in the native and denatured MREMD simulation series is plotted in Fig. 8, as are the potential energy probabilities for each temperature level. The drift in 〈E_pot(T)〉 for the coldest of temperature levels (<250 K) is not seen in higher temperatures, thus suggesting that the hairpin was well-relaxed into the modeling conditions employed before initiation of the first MREMD temperature level exchanges, thereby allowing the entire MREMD simulation time to be used in generating the statistical energy landscapes for higher temperatures (>250 K).

FIGURE 8.

The thermally averaged potential energies for each temperature level in the MREMD trajectories. (Right) The overlap of MREMD energy probabilities that results in relatively high acceptance ratios in Metropolis-style swap attempts.

Fig. 9 shows the resulting folding landscapes obtained from the native and denatured MREMD simulations (summed with equal weighting) at three temperatures, as projected onto the RMSD and N_HB order parameters. Approximate statistical energy difference contours are defined by

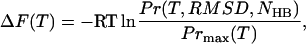(8)

where R = 1.9872 cal K⁻¹ mol⁻¹, a landscape grid size of 1 Å × 1 hydrogen bond was used, and Pr_max(T) is the relative probability of the most likely configuration in the temperature level.

FIGURE 9.

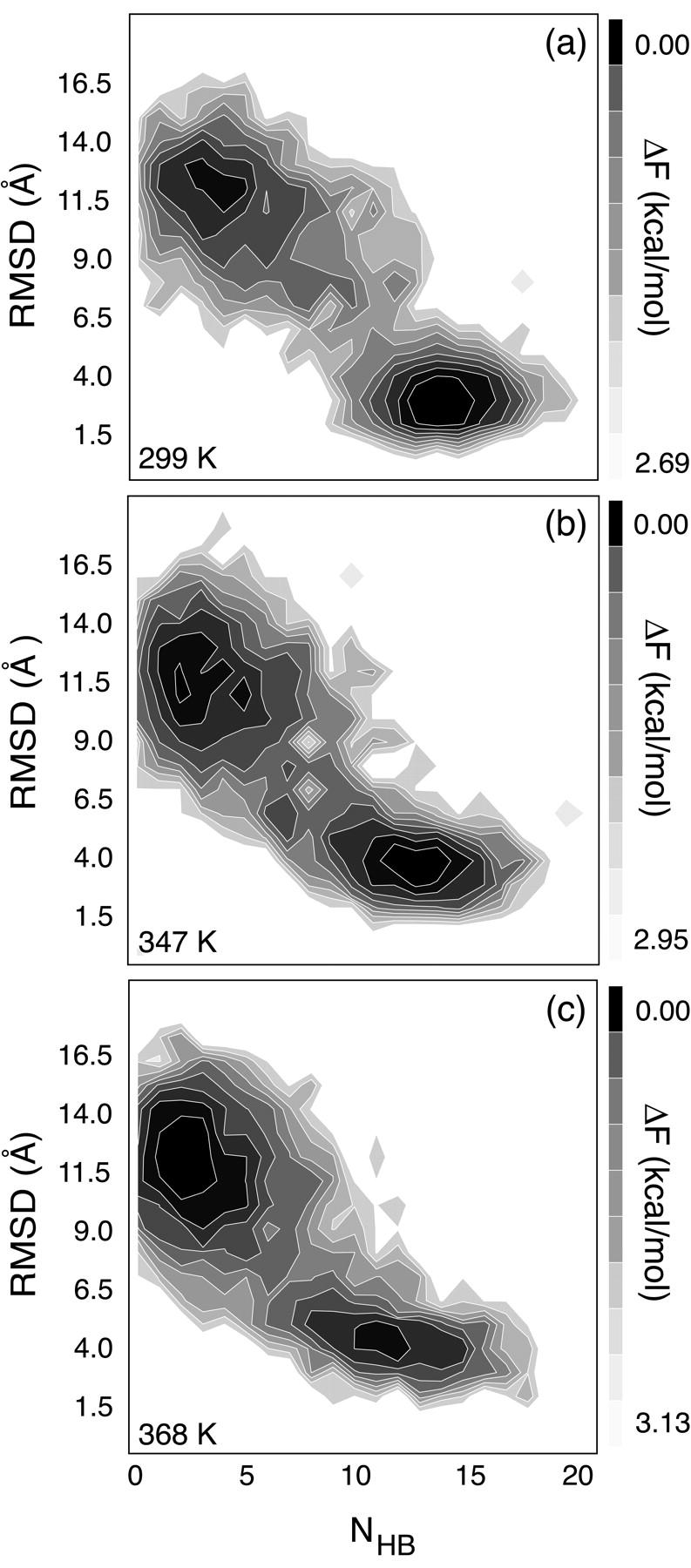
MREMD-derived approximate statistical energy landscapes for RNA hairpin conformational dynamics are shown at (a) 299 K, near the temperature of the reported dynamic trajectories (300 K); (b) 347 K, near, but slightly above, the experimental melting temperature; and (c) 368 K, above the melting temperature. Energetic contours are scaled linearly between the two values shown at each temperature.

As a result of both the temperature-dependent weighting of the folding and unfolding pathways and the lack of overall MREMD convergence described above, the observed sampling strongly favors the expansion/compaction pathway, as demonstrated in Fig. 10 a. Although this clearly limits the global accuracy of the resulting profiles shown in Fig. 9 (in terms of properly sampling the entire configurational space), we speculate that the general thermodynamic features elucidated by this method are applicable to many experimental conditions, such as those involving temperature jump perturbations and studies near the hairpin melting temperature.

FIGURE 10.

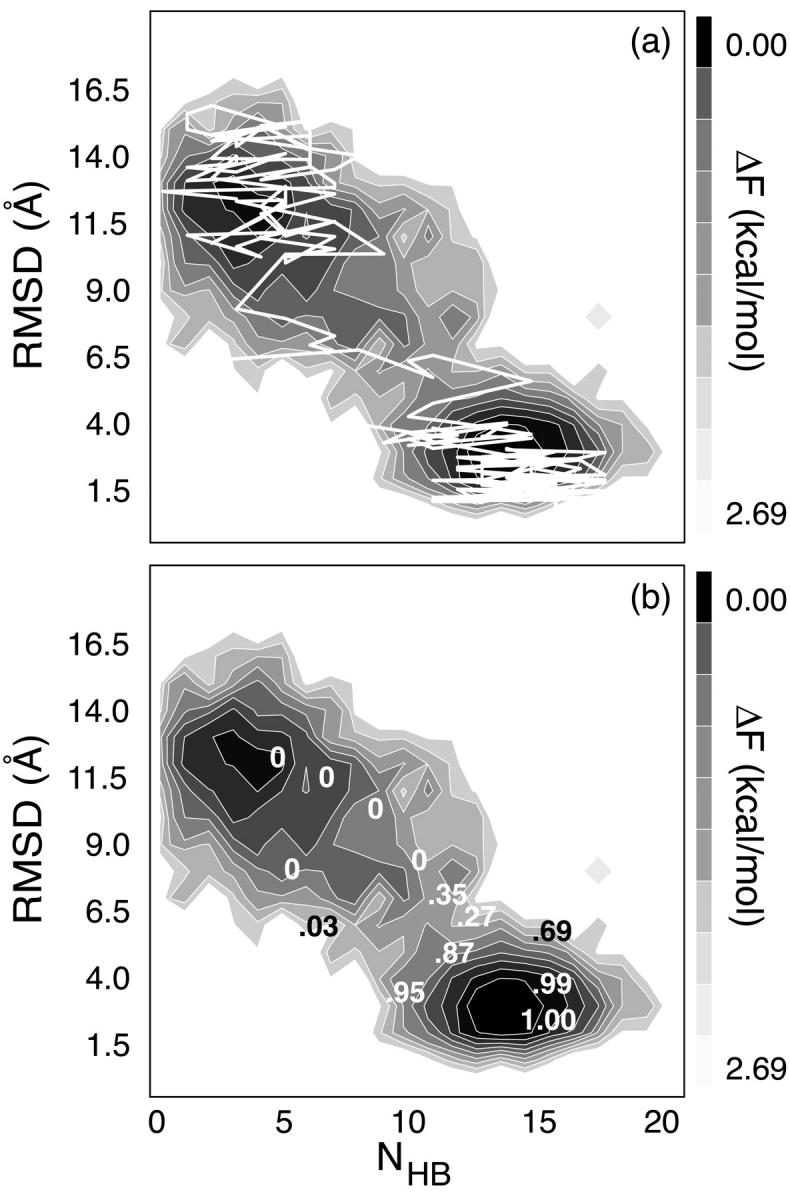
(a) The expansion/compaction trajectory overlaid on the 299 K folding landscape, demonstrating the temperature-dependent favoring of this pathway (in MREMD simulations) over the zipping/unzipping pathway that is expected to dominate at this temperature. (b) P_fold values for the expansion/compaction pathway are overlaid on the same landscape. Adjacent values have been removed for clarity without compromising the quality of the comparison.

Direct comparison of thermodynamic MREMD sampling to P_fold sampling is shown in Fig. 10 b. For clarity, adjacent P_fold values have been removed without altering the qualitative character of the comparison. The apparent TS for the expansion/compaction pathway (TS_exp) predicted by the MREMD sampling falls between low and high P_fold values, showing consistency between the two methods in locating the TS along the order parameters used. Consistent with previous experimental and theoretical assessments (Ansari et al., 2001; Bonnet et al., 1998; Goddard et al., 2000; Grunwell et al., 2001; Kuznetsov et al., 2001; Shen et al., 2001; Wallace et al., 2000; Ying et al., 2001; Zhang and Chen, 2002), our results indicate an essentially two-state energy surface. As noted above, however, the overall landscape near physiological temperature is expected to include various local minima corresponding to unwound and trap states that only considerably longer MREMD simulations could capture.

DISCUSSION

Using a simple atomistic model, we have observed two pathways in silico between the native and denatured regimes of conformational space for a small nucleic acid duplex capped by a well-characterized tetraloop region. In doing so, we have derived approximate rates, using a two-state model, that are consistent with experimental observations of hairpin closing rates for similar systems and a folding free energy based on these rates that is on the order of the experimental value. Our observation of multiple pathways agrees well with current models, as described above, and a temperature-dependent weighting of these pathways has been identified. Furthermore, simulations indicate the presence of a defect-induced winding dynamics not previously described. Two aspects of our results are considered in the discussion below: we first comment on the model applied herein, which is followed by a section discussing the relevance of this work to biomolecular folding theory in a generalized framework.

Caveats of the model

Although the model reported herein has allowed us to investigate nucleic acid hairpin conformational transitions on the submillisecond timescale, the caveats and limitations of our model have not yet been explicitly stated. We begin with the use of the GB/SA implicit solvent model, which has been heavily studied and parameterized many times in the last decade. We note that the primary method of assessing the accuracy of various GB models throughout this period has been based upon correlations between GB energies and those obtained from more analytically rigorous, and more computationally expensive, Poisson-Boltzmann (PB) solvers, such as Zap and DelPhi (Grant et al., 2000; Nicholls and Honig, 1991). The extent to which GB models are considered sufficiently accurate is therefore entirely dependent on the absolute accuracy of the PB calculations to which they are compared (Edinger et al., 1997; Onufriev et al., 2002; Srinivasan et al., 1999), which are expected to be most accurate for monovalent salt solutions at low ionic strength.

In the simulations reported herein, ions were not accounted for explicitly. To understand why this might be a reasonable model, first consider that the GB model tends to overestimate electrostatic screening for atoms far from the solvent-exposed surface (Srinivasan et al., 1999), causing inaccuracies for “core” atoms and being more accurate for atoms nearer the solute surface. Unlike larger polypeptides and proteins, small nucleic acid duplexes and hairpins do not have a dense core to which this effect would apply. More importantly, the GB model typically results in self-interaction energies (energy changes that result from moving a given atom from vacuum into the solute-solvent environment) that are lower than the analogous PB energies (Onufriev et al., 2002; Srinivasan et al., 1999). GB thus assigns greater overall stability, on average, than the PB model of solvation, as illustrated by the high hairpin melting temperature for this model predicted from both MREMD simulations (Fig. 9) and by evaluating the temperature dependence of the mean RMSD order parameter (data not shown). Therefore we suggest that it is redundant to include explicit co-ions in conjunction with current implementations of the GB model, and we speculate that doing so would cause a divergence from the behavior of the atomic force field (AMBER), not seen in our simulations.

We note also that the GB algorithm has not yet been parameterized for inclusion in periodic systems. Although previous studies have reported the use of GB in conjunction with explicit ions lacking periodic boundaries, the resulting trajectories lasted only a few nanoseconds. In longer simulations (tens of nanoseconds), a natural entropic drive for those ions to leave the vicinity of the RNA solute would result in an equilibrium situation analogous to the model employed (i.e., with explicit ions far from the nucleic acid solute).

In essence, we approximate a low ionic strength solution by using the GB/SA continuum solvent model to solvate and stabilize a small RNA hairpin. However, this approximation should be considered with caution: this additional GB stability is likely to become less effective as the size of the duplex or hairpin increases, and thus the number of non-neutralized net charges grows. In a prior study we reported a strong correlation between GB and PB solvation energies (R² = 0.997) for 1662 conformations of this same sequence across a wide range of temperatures (300–700 K) and spanning the range from fully extended to fully folded structures (Sorin et al., 2002). Similar correlations have been reported elsewhere for nucleic acid systems (Srinivasan et al., 1999).

Still, it is not evident that the GB model, or any other current solvation model (including both PB and explicit solvents), will determine the experimentally derived native structure to have the lowest energy in a given conformational ensemble. In fact, observed misfolded conformations within this study are energetically similar to the native state (compare Figs. 2 and 4), a phenomenon that has also been observed for protein conformations solvated in the implicit GB model. However, it remains to be shown through ample thermodynamic sampling whether such low energy nonnative structures are the direct result of GB solvation or simply artifacts of contemporary atomistic force fields, for which no sampling on the order of microseconds has yet been reported.

With these caveats in mind, the stability observed in our simulations of the native tetraloop hairpin supports the use of GB/SA as an implicit solvation environment for the simulation of small nucleic acids. Preparations are currently underway to integrate an explicit representation of the solvent and co-ions into simulations of this nature, however, and future comparisons of the GB/SA solvation model to explicit solvent representations across massive data sets should be enlightening.

Implications for folding theory

Having sampled both pathways on the microsecond timescale, we have characterized a heterogeneous transition state ensemble in which very little native structure is present: indeed, a single (partial or fully formed) basepair exists in the simulated TS ensemble. This suggests that surmounting the free energy barrier in helical hairpin formation requires proper loop formation, as seen in our refolding simulations.

Although two distinct folding/unfolding pathways were detected in the reported simulations, we cannot exclude the possibility of other pathways. When considering the observed refolding events, however, we speculate that additional unique pathways are much less likely to contribute to the experimental observables frequently examined. To be sure, consider the possible pathways such a limited topology can allow: we have observed unfolding and refolding events in which the closing basepair and the central stem basepairs acted as nucleation/anchoring sites within the chain, leaving only the possibility of a terminal nucleation center. This latter possibility seems remote at best, considering the rigidity inherent to the nucleic acid backbone and the less likely occurrence of terminal residue collision during stochastic movement of the unfolded chain.

Having also recently simulated β-hairpin folding in atomistic detail using a very similar model to that presented here, a natural extension of our analysis was to consider the apparent similarities and differences between the folding dynamics of these peptide and nucleic acid analogs, a consideration others have taken up in past works (Kuznetsov et al., 2001; Thirumalai et al., 2001; Wallace et al., 2001). We note that the fast-folding protein studied exhibits both negative activation enthalpies during folding and non-Arrhenius folding kinetics (Munoz et al., 1998), as has been observed for small nucleic acid hairpins.

In our previous study (Zagrovic et al., 2001), the primary driving force of β-hairpin folding was determined to be hydrophobic collapse and assembly of core residues. Of the eight direct, fully independent β-hairpin folding events previously described, one trajectory exhibited a zipperlike mechanism in which the loop and hydrophobic contacts nearest the loop formed first with the separated strand termini maintaining random orientations. This was followed by successive contact formation toward the hairpin termini with the strands slowly gaining a global hairpin conformation, consistent with the observed zipping pathway for nucleic acid hairpin folding described above. The remaining seven β-hairpin folding events followed a mechanism in which centralized hydrophobic interactions preceded global formation of a heterogeneous hydrogen bonding network, not unlike the expansion/compaction mechanism described above, in which proper basepairing occurs through a nucleation center and progresses to the duplex ends.

It is interesting to consider the intrinsic weighting of pathways for these two analogs. Nucleic acid hairpins, with a more rigid backbone than proteins, favor the zipping mechanism. In contrast, the more flexible β-hairpin peptide apparently folds predominantly via a compaction mechanism. We speculate that this inherent difference in rigidity is responsible for the observed difference in pathway preference: whereas the more flexible unfolded protein backbone may bend easily under global hydrophobic attraction, loop formation in nucleic acids appears to depend more prevalently upon hydrogen bonding and stacking interactions near the loop region to bring the strands together.

The presence of two strikingly similar pathways in both nucleic acid and peptide hairpin conformational dynamics suggests an intimate link between native topology and the general features of the conformational free energy landscape that may be generalizable beyond the chemical nature of the polymer. Numerous past studies have, in fact, recognized correlations between the folding mechanism (free energy landscapes, transition states, and kinetics) and protein topology/contact order (Baker, 2000; Debe and Goddard, 1999; Goldenberg, 1999; Klimov and Thirumalai, 2000; Makarov et al., 2002; Plaxco et al., 2000), and recent simulation studies by Caflisch and co-workers (Ferrara and Caflisch, 2001; Gsponer and Caflisch, 2001) suggest that “the folding mechanism is primarily defined by the native state topology, while specific interactions determine the statistically predominant folding route.” The observations reported herein strengthen this notion, breaking the boundary of the very chemical nature of the polymer: these analogs share a distinct topology with comparable folding pathways, yet each contains inherently different interatomic and interresidue interactions that result in unique statistical weighting of these available pathways.

CONCLUSIONS

The conformational dynamics of a small RNA hairpin have been studied using a novel computational tool: massively parallel stochastic dynamics simulation. For the first time, nucleic acid simulation on the order of hundreds of microseconds has been achieved, and has allowed us to characterize, in atomistic resolution, submillisecond conformational dynamics, including the refolding of unfolded conformers along multiple pathways, and the detection of previously unreported defect-induced unwinding and rewinding events. In doing so, we have avoided perturbing the system through temperature or force, thereby permitting elucidation of the unperturbed dynamics near both physiological and standard laboratory temperatures.

We find that nucleic acid hairpins exhibit heterogeneity in both folding mechanism and transition state ensemble, with two primary competing pathways between the native and denatured regions of the conformational space manifesting temperature-dependent relative weighting. We present approximate folding and unfolding rates that are consistent with previous experimental results, and our observations both agree with and extend recent models of nucleic acid hairpin conformational dynamics. In addition, we propose that native topology defines the folding landscape for nucleic acids in an analogous manner to that which has been suggested for proteins, with the specific interactions within the polymer determining the relative weighting between parallel pathways.

While hairpin folding is likely to be simple relative to larger molecules with native tertiary and dynamic secondary structure (Thirumalai, 1998; Wu and Tinoco, 1998), understanding these “simple” dynamics is a stepping stone to larger challenges. We have attempted to provide insights into the dynamics of nucleic acid hairpin folding that cannot currently be gleaned experimentally: our model provides an atomistic framework within which current coarse-grained theoretical models and experimental data fit well.