Structure-Based Prediction of Potential Binding and Nonbinding Peptides to HIV-1 Protease

Abstract

HIV-1 protease is a major drug target against AIDS as it permits viral maturation by processing the gag and pol polyproteins of the virus. The cleavage sites in these polyproteins do not have obvious sequence homology or a binding motif and the specificity of the protease is not easily determined. We used various threading approaches, together with the crystal structures of substrate complexes which served as template structures, to study the substrate specificity of HIV-1 protease with the aim of obtaining a better differentiation between binding and nonbinding sequences. The predictions from threading improved when distance-dependent interaction energy functions were used instead of contact matrices. To rank the peptides and properly account for the peptide's conformation in the total energy, the results from using short-range potentials on multiple template structures were averaged. Finally, a dynamic threading approach is introduced which is potentially useful for cases when there is only one template structure available. The conformational energy of the peptide—especially the term accounting for the side chains—was found to be important in differentiating between binding and nonbinding sequences. Hence, the substrate specificity, and thus the ability of the virus to mature, is affected by the compatibility of the substrate peptide to fit within the limited conformational space of the active site groove.

INTRODUCTION

HIV-1 protease cleaves the gag and pol polyproteins of the virus to release the structural proteins and enzymes required for virus structure and replication. This process is essential for the production of infectious virus particles; hence HIV protease has been a major target for drug design against AIDS. Structure-based drug design efforts resulted in six FDA-approved protease inhibitors, all of which are peptidomimetics. Unfortunately, treatment with protease inhibitors can lead to the selection of drug-resistant virus mutants. Understanding the basis of molecular recognition events in HIV-1 protease is of vital importance in the development of next-generation drugs against AIDS.

The protease is highly specific in catalyzing the cleavage of 10 sites in the gag and pol polyproteins. These sites, however, share little sequence homology and lack an obvious consensus binding motif. It is known that the protease can bind to a large variety of peptides but the principles governing and the physical parameters determining substrate recognition and specificity remain poorly understood.

Crystal structures of HIV-1 protease in complex with a variety of inhibitors are deposited in the Protein Data Bank (PDB). However, there was, until recently, a lack of structures with natural substrates. The crystal structures of an inactive (D25N) protease with six decameric peptides corresponding to the natural cleavage sites within the gag and pol polyproteins were solved (Prabu-Jeyabalan et al., 2002). The structural information obtained enables us to investigate how different sequences bind to the same molecule.

To understand the principles of substrate recognition, we applied an approach that has been used to address the inverse protein-folding problem. In this method, referred to as threading, the amino-acid sequence is threaded through known three-dimensional structures and the energy of the structure is evaluated based on pairwise contact potentials. The application of this approach to peptide complexes was originally proposed by Altuvia and co-workers and applied to the complexes of major histocompatibility complex (MHC) molecules (Altuvia et al., 1995, 1997; Schueler-Furman et al., 2000). In the present work, we expanded upon this approach to look at the substrate specificity of HIV-1 protease.

The recently solved structures of HIV-1 protease substrate complexes provide ideal structural information to be used in threading analysis. The number of conformations the peptide can adopt in the binding groove is limited and defined by the protease structure that imposes physical constraints on the peptide. We applied several different threading procedures to differentiate between binding and nonbinding sequences and determine which factors are important in peptide recognition of HIV-1 protease. The first method was that of Altuvia et al. (1995), where a statistical potential matrix was used to evaluate the interaction of peptide with the protease residues it contacts (Miyazawa and Jernigan, 1996). The residues were considered to be in contact or not according to three different distance criteria. This corresponds to approximating the interaction between residues by a square-well potential. In the second method, we employed distance-dependent statistical potentials (Bahar and Jernigan, 1997). Then, we further developed the force field to include the effect of peptide conformation in the energy evaluation. With all three methods, we investigated whether using multiple template structures and taking the average improves the predictions or not. Finally, we used a dynamic Monte Carlo relaxation procedure after threading a peptide sequence onto the template structure. After these analyses, we found that using distance-dependent, long-range potentials and taking multiple peptide conformations into consideration improves the threading procedure, and that dynamic threading is a potentially useful method when there is only one complex structure available. Besides the long-range potentials accounting for the interactions between the peptide and the protease, the side-chain short-range potentials of the peptide were found to be important in discriminating between binding and nonbinding peptides. Although the active site can also adapt to some extent depending on the sequence bound, there is a constrained conformational space accessible to the bound peptide. Hence, the compatibility of the peptide sequence with the space in the binding groove has an important role in molecular recognition. This is also in accordance with the idea that a shape rather than specific amino acid residues is recognized by the protease (Prabu-Jeyabalan et al., 2002), and implies that the peptide conformation should be taken into consideration to improve the predictions of threading methods.

MATERIALS AND METHODS

Template structures

The crystal structures of HIV-1 protease in complex with six of its natural substrates (Prabu-Jeyabalan et al., 2000, 2002) are used as the template structures. These structures are deposited in the Protein Data Bank (PDB) with codes 1f7a (ca-p2), 1kj4 (ma-ca), 1kj7 (p2-nc), 1kjf (p1-p6), 1kjg (rt-rh), and 1kjh (rh-in) (Bernstein et al., 1977; Berman et al., 2000).

Threading with a contact potential matrix

In this method, binding affinity of a peptide is predicted by the total energy of interaction with contact residues. The contacts of the peptide in the available template co-crystal structure are determined according to three different criteria: 1), α-carbon atoms are closer than 7.5 Å (Covell and Jernigan, 1990); 2), β-carbon atoms are closer than 7 Å (Altuvia et al., 1995); and 3) any two atoms are closer than 4 Å (Madden et al., 1993). Then, the amino-acid sequence of the query peptide is threaded onto the coordinates of the peptide in the template. The contacts are assumed to be conserved, and the total interaction energy is obtained by summing the interaction energy values of peptide residues using a contact potential matrix. The intraresidue energy for the host molecule (protease) amino acids is not included in the computation as it is considered to be constant for all the threaded peptides for a given template structure. The contacting residues are determined for the conformation in the known structure, and therefore are only approximate for different sequences threaded. Energy values for amino acid-to-amino acid interactions are taken from the table of statistical pairwise contact potentials derived by Miyazawa and Jernigan (1996).

Threading with distance-dependent potentials

The interaction energy of the peptide is calculated by employing distance-dependent interresidue potentials (Bahar and Jernigan, 1997). These potentials were derived using 302 structures from the PDB (Bernstein et al., 1977; Berman et al., 2000). They are not fit to functions, and are discrete instead, at 0.4 Å resolution. Bahar and Jernigan used both solvent-exposed and residue-exposed reference states, which correspond to formation of a specific residue-to-residue contact at the expense of contacts with the solvent and with an average residue, respectively. An effective set of parameters to be used in protein simulations were derived from the potentials with these reference states that operate at different environments. Bahar and Jernigan also presented effective contact potentials obtained from the integration of radial distributions over different distance ranges. They could reproduce Miyazawa and Jernigan potentials as one case of these integrations. Miyazawa and Jernigan potentials were discussed to have quite weak specificity as they have a high radius of interaction (6.5 Å). The dominance of highly specific hydrophilic interactions at close separations was demonstrated by Bahar and Jernigan potentials. Hence, these potentials are expected to better account for specific side-chain contacts that may be of great importance in peptide-to-protease interactions.

In the previous method of threading with a contact potential matrix, the interaction energy between residues was approximated by a square-well type potential. For any two residues, the depth of the well was determined by the corresponding potential value in a statistical scoring matrix, and the interaction was considered to be in or out of the well according to a distance criterion. Hence, the selection of the distance criterion was a major concern in this all-or-none approach. In this next method, we eliminated the need of such a tentative criterion by using distance-dependent potentials. Two effective interaction sites per residue (its α-carbon atom for the backbone and a residue-specific side-chain site) were considered, and the energy of interaction between any two interaction sites were evaluated depending on the distance in between, and the type, of amino acid that the sites belong to. The total interaction energy of the peptide is found by summation over all n peptide and N protease residues as

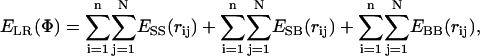(1)

where r_ij is the distance between sites i and j in conformation Φ. The terms account for potentials between side-chain sites (SS), side-chain and backbone sites (SB), and two backbone sites (BB) of residues i and j, respectively.

Threading with conformational potentials

In this method, the conformation of the peptide was taken into consideration in calculating the total energy. To evaluate the conformational energy of the backbone, the statistical potentials, as based on the virtual bond model given by Bahar et al. (1997a) for bond angle and bond torsions, are used as

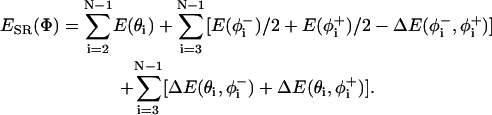(2)

Here, the first summation is to account for the bending of backbone bond angles; the second is for the torsion of bonds 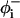and 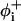referring to the rotational angles of the virtual backbone bonds preceding and succeeding the i^th α-carbon, respectively. The last term in this summation and the last summation account for the pairwise interdependence of the torsion and/or bond angle bending.

For the side chains, the probability distributions of Keskin and Bahar for packing of side chains in low-resolution models (Keskin and Bahar, 1998) were converted into statistical potentials using the Boltzmann relationship. The energy associated with a side-chain bond angle at state θ_i for a residue type A is evaluated from

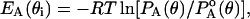(3)

where P_A(θ) is the statistical probability of finding that bond at angle θ and 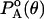is the background probability assuming uniform distribution probability. In the discrete state formalism adopted, the background probabilities are directly proportional to the mesh sizes. Analogous expressions were used for side-chain bond lengths and torsions. The side-chain conformational energy is summed up over all n side-chains in the peptide as

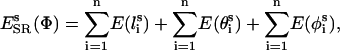(4)

where 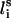, , 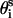and 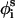are the bond length, bond angle, and torsion angle of side chain i.

The total energy of the peptide is found by the summation of its backbone and side-chain conformational energies, and the long-range interaction energy with the protease, which was evaluated using distance-dependent potentials as in the previous method.

Dynamic threading

The Monte Carlo (MC) minimization process used in dynamic threading is based on the reduced model and MC method previously used to simulate various protein structures (Bahar et al., 1997b; Haliloglu and Bahar, 1998; Kurt and Haliloglu, 1999; Haliloglu, 1999). The algorithm is as follows: both the protease and the threaded peptide are moved by a random combination of perturbations and the energy of the structure after each perturbation is checked. The protease and peptide are moved by randomly choosing a backbone or side-chain interaction site, and perturbing the Cartesian coordinates of the site by an amount Δx = k (2r − 1), where r is a random number 0 ≤ r ≤ 1, and k is a proportionality factor controlling the strength of perturbation. Here, k was chosen to be 0.8 Å (consistent with the above-cited previous applications in protein simulations), which allows the protein to move only in the neighborhood of the original conformation.

The acceptance of each move is controlled on the basis of the Metropolis criterion (Metropolis et al., 1953): conformations whose energy is lower than the previous one, or whose Boltzmann factor is greater than a random number between 0 and 1, are accepted. The total energy considered here is the combination of both short-range and long-range potentials summed over the entire structure,

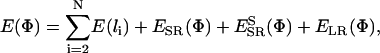(5)

where E_SR, 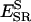, and E_LR are from Eqs. 2, 4, and 1, respectively. The term E(l_i) controls the stretching of the virtual backbone bonds by a stiff harmonic potential with a force constant of 10 RT/Ų, which allows only relatively small changes in the virtual bond lengths of the original structure.

In accordance with conventions, one Monte Carlo step (MCS) comprises the N perturbations, where N is the total number of residues in the structure. The structure of ca-p2 complex with PDB code 1f7a is used as the starting conformation.

System and programs

All programs for threading analysis are written in FORTRAN programming language and run on a Silicon Graphics R5000 workstation. Prediction results from threading programs can be obtained in seconds, whereas a run of 1000 Monte Carlo step relaxations takes ∼2–3 h of computational time. The programs can be run on UNIX operating systems and are available upon request.

RESULTS

The 10 natural substrates of HIV-1 protease from the gag and pol polyproteins and five peptides which were predicted to have the lowest affinity to protease (Chou 1996) were used as the test set. K. C. Chou used a discriminant function algorithm based on the Markov-chain theory for predicting the cleavability of peptides by HIV protease. The probabilities of amino acids to occur at various positions along the sequence were calculated using a training database consisting of 62 substrates and 239 noncleavable peptides taken from experimental data. Using these probabilities, the algorithm predicts a discriminant function which is a criterion for the affinity of a given peptide to HIV-1 protease. Here, we use five lowest-affinity peptides as predicted by this algorithm.

We also included the sequence of nc-p1 to the test set by shifting it one amino acid to the N-terminal side (called “nc-p1s”), as the sequence homology to the other substrates increases in this case (notice F and L residues in the P1 and P1′ sites of p1-p6 and rh-in), but nevertheless the original sequence is recognized by the protease. The sequences of the substrates and peptides are given in Table 1.

TABLE 1.

Ten natural substrates of HIV-1 protease and lower-affinity peptides used in threading experiments

Name*	P4	P3	P2	P1	P1′	P2′	P3′	P4′
ma-ca	Ser	Gln	Asn	Tyr	Pro	Ile	Val	Gln
ca-p2	Ala	Thr	Ile	Met	Met	Gln	Arg	Gly
p2-nc	Ala	Thr	Ile	Met	Met	Gln	Arg	Gly
nc-p1	Arg	Gln	Ala	Asn	Phe	Leu	Gly	Lys
p1-p6	Pro	Gly	Asn	Phe	Leu	Gln	Ser	Arg
tf-pr	Ser	Phe	Asn	Phe	Pro	Gln	Ile	Thr
pr-rt	Gln	Ile	Thr	Leu	Pro	Lys	Arg	Pro
rt-rh	Thr	Leu	Asn	Phe	Pro	Ile	Ser	Pro
rh-in	Ala	Glu	Thr	Phe	Tyr	Val	Asp	Gly
auto	Arg	Lys	Val	Leu	Phe	Leu	Asp	Gly
pep1	Trp	Arg	Asn	Arg	Cys	Lys	Gly	Thr
pep2	Met	Met	Lys	Ser	Arg	Asn	Leu	Thr
pep3	Leu	Ala	Ala	Ala	Met	Lys	Arg	His
pep4	Thr	Thr	Gln	Ala	Asn	Lys	His	Ile
pep5	Val	Asn	Cys	Ala	Lys	Lys	Ile	Val
nc-p1s	Gln	Ala	Asn	Phe	Leu	Gly	Lys	Ile

The names of substrates whose complex structures with HIV-1 protease are available are in bold, and those of the lower-affinity peptides are underlined.

^*The substrates are identified with the abbreviations of proteins released upon cleavage of the site: matrix (ma), capsid (ca), nucleocapsid (nc), trans-frame peptide (tf), protease (pr), autoproteolysis site (auto), reverse transcriptase (rt), RNase H (rh), and integrase (in).

The peptide sequences in the test set were threaded onto the crystal structures of the HIV-1 protease-substrate complexes (Prabu-Jeyabalan et al., 2000, 2002) (see Materials and Methods). Different methods were used to obtain an estimate of the binding affinity of the threaded sequences, with the goal of differentiating between binding and nonbinding sequences in the set.

Threading with a contact potential matrix

We applied the method of Altuvia et al. (1995) to score and rank the binding affinities of peptides in Table 1 to HIV-1 protease. The threading methodology was described in detail in the original reference and summarized here in Materials and Methods. Table 2 gives the ranking of peptides according to the binding affinities predicted by this threading algorithm and using the ca-p2 complex structure as the template with three different distance criteria to define the contacting residues. Although it is reasonable to use the same distance criterion as in the parameterization of the statistical contact potentials, we applied all three criteria of Altuvia et al. (1995) to enable a direct comparison of the results.

TABLE 2.

Ranking of peptides according to their predicted binding affinity by threading using a scoring matrix and ca-p2 (1f7a) substrate complex structure as the template

Cα < 7.5 Å		Cβ < 7.0 Å		Nearest atom < 4.0 Å
rh-in	−172.85	rh-in	−156.31	rh-in	−191.94
pr-rt	−160.60	nc-p1s	−136.52	ca-p2*	−183.82
ca-p2*	−150.18	p2-nc	−134.47	pr-rt	−181.67
nc-p1s	−149.88	pr-rt	−134.00	tf-pr	−180.32
p2-nc	−149.77	auto	−132.99	p2-nc	−175.01
auto	−148.94	ca-p2*	−130.85	auto	−173.49
tf-pr	−148.69	nc-p1	−130.70	nc-p1s	−173.32
rt-rh	−147.71	rt-rh	−130.47	pep1	−172.38
nc-p1	−144.34	p1-p6	−128.70	rt-rh	−167.89
ma-ca	−141.14	tf-pr	−124.45	ma-ca	−164.35
p1-p6	−137.59	pep4	−122.15	pep4	−160.65
pep1	−137.31	ma-ca	−118.21	pep3	−159.49
pep4	−136.83	pep1	−111.87	p1-p6	−158.99
pep3	−130.05	pep3	−105.73	nc-p1	−158.42
pep5	−119.28	pep2	−105.26	pep5	−148.15
pep2	−118.36	pep5	−101.65	pep2	−140.09

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The residues in the template were considered to be in contact according to three different criteria: their α-carbon atoms are closer than 7.5 Å; their β-carbons are closer than 7 Å; and any nearest atoms are closer than 4 Å.

^*Structure used as template.

In this threading method, determination of protease residues that are in contact with the peptide is a major concern. For the MHC system, the nearest atom criterion was found to give the best results (Altuvia et al., 1995). Here, we found that the criterion for α-carbon distances to determine the contacting residues gives a better prediction compared to others. Surprisingly, although it still ranks high, the template structure's own peptide (ca-p2) does not have the highest score, indicating that this force field may not have adequate precision. The shifted nc-p1s structure has a better score than the nc-p1 sequence, which is actually recognized by HIV-1 protease. Overall, there is a tendency that the nonbinding peptides are ranked lower than the binding ones, but it is not possible to differentiate the two using these rankings.

We performed the same analysis with another substrate (ma-ca) complex of HIV-1 protease (Prabu-Jeyabalan et al., 2002). Table 3 gives the ranking results with this template structure, and Table 4 gives the average of results from the two template structures. With the ma-ca complex structure as the template, the nearest atom criterion seems to work better. However, the template structure's own peptide (ma-ca) has a very bad score, and is predicted to have a binding affinity even lower than nonbinding peptides. The results of threading are very much dependent on the template structure used, as a peptide ranks high if its binding scheme is similar to the template peptide. Hence, using multiple templates potentially should provide a better fit for the binding peptides. However, when the results from two template structures were averaged, no improvement in ranking was seen. Even when five and six template structures were used, the results did not change much. Especially within the coarse-grained scale of the α-carbon criterion, the residues considered to be in contact are almost the same for different template structures. Therefore, this crude force field is not accurate enough to distinguish the subtle differences between the various peptide sequences.

TABLE 3.

Ranking of peptides according to their predicted binding affinity by threading using a scoring matrix and the ma-ca (1kj4) substrate complex structure as the template

Cα < 7.5 Å		Cβ < 7.0 Å		Nearest atom < 4.0 Å
rh-in	−173.56	rh-in	−180.21	rh-in	−142.58
p2-nc	−156.68	p2-nc	−151.93	pr-rt	−131.82
ca-p2	−155.97	nc-p1s	−150.58	tf-pr	−127.89
pr-rt	−155.65	nc-p1	−149.37	p2-nc	−125.64
nc-p1s	−154.98	rt-rh	−149.20	ca-p2	−125.50
auto	−154.88	ca-p2	−146.81	auto	−125.12
tf-pr	−153.93	p1-p6	−145.42	rt-rh	−124.53
rt-rh	−148.98	auto	−142.41	nc-p1s	−120.41
p1-p6	−146.54	pr-rt	−141.04	ma-ca*	−119.90
nc-p1	−143.82	pep4	−134.91	p1-p6	−117.01
pep4	−143.71	ma-ca*	−133.14	nc-p1	−116.39
pep1	−142.76	tf-pr	−130.51	pep1	−114.12
ma-ca*	−140.00	pep1	−124.79	pep4	−110.65
pep3	−135.36	pep2	−116.41	pep3	−107.73
pep2	−124.13	pep5	−110.87	pep2	−96.25
pep5	−121.53	pep3	−110.35	pep5	−94.45

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The residues in the template were considered to be in contact according to three different criteria: their α-carbon atoms are closer than 7.5 Å; their β-carbons are closer than 7 Å; and any nearest atoms are closer than 4 Å.

^*Structure used as template.

TABLE 4.

Ranking of peptides according to their predicted binding affinity by the average of threading results from two template structures, the substrate complexes: ca-p2 (1f7a) and ma-ca (1kj4)

Cα < 7.5 Å		Cβ < 7.0 Å		Nearest atom < 4.0 Å
rh-in	−173.21	rh-in	−168.26	rh-in	−167.26
pr-rt	−158.13	nc-p1s	−143.55	pr-rt	−156.75
p2-nc	−153.23	p2-nc	−143.20	ca-p2*	−154.66
ca-p2*	−153.08	nc-p1	−140.04	tr-pr	−154.11
nc-p1s	−152.43	rt-rh	−139.84	p2-nc	−150.33
auto	−151.91	ca-p2*	−138.83	auto	−149.31
tf-pr	−151.31	auto	−137.70	nc-p1s	−146.87
rt-rh	−148.35	pr-rt	−137.52	rt-rh	−146.21
nc-p1	−144.08	p1-p6	−128.53	pep1	−143.25
p1-p6	−142.07	pep4	−128.53	ma-ca*	−142.13
mc-ca*	−140.57	tf-pr	−127.48	p1-p6	−138.00
pep4	−140.27	ma-ca*	−125.68	nc-p1	−137.41
pep1	−140.04	pep1	−118.33	pep4	−135.65
pep3	−132.71	pep2	−110.84	pep3	−133.61
pep2	−121.25	pep3	−108.04	pep5	−121.30
pep5	−120.41	pep5	−106.26	pep2	−118.17

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The residues in the template were considered to be in contact according to three different criteria: their α-carbon atoms are closer than 7.5 Å; their β-carbons are closer than 7 Å; and any nearest atoms are closer than 4 Å.

^*Structure used as template.

Threading with distance-dependent potentials

We modified the calculation of interaction energy of the peptide in threading by employing distance-dependent interresidue potentials (Bahar and Jernigan, 1997). These structure-derived potential functions have been previously used in dynamic simulations and threading experiments to find the tertiary structures of proteins (Jernigan and Bahar, 1996; Bahar et al., 1997b). They provide a more detailed/precise force field for long-range interactions compared to contact potential matrices.

Table 5 gives the results of threading with distance-dependent interaction potentials using the two template structures and the average of results from the two. In the current energy evaluation scheme, there is no need for a criterion to decide on the contacting residues. Rather, a distance-dependent energy function is used with a less coarse-grained model, considering two sites per residue; one at its α-carbon atom and one at the side chain. This approach improves the accuracy of the threading. In this case, the template structure's own peptides have reasonable rankings; and, as expected, taking the average of two templates improves the ranking. This technique can even distinguish the subtly different nc-p1s sequence, which has a lower score than the real substrate. The nonbinding peptides rank worse, but the energy gap between the binding and nonbinding peptides is not yet significantly separated.

TABLE 5.

Ranking of peptides according to their predicted binding affinity by threading with distance-dependent interaction energies through different templates

rh-in	−86.33	pr-rt	−82.24	rh-in	−83.77
pr-rt	−83.58	rh-in	−81.21	pr-rt	−82.91
ca-p2*	−83.20	rt-rh	−80.43	rt-rh	−80.69
p2-nc	−81.04	nc-p1	−79.22	ca-p2*	−79.78
rt-rh	−80.96	ma-ca*	−77.57	nc-p1	−79.67
ma-ca	−80.64	p1-p6	−76.95	ma-ca*	−79.10
auto	−80.25	p2-nc	−76.75	p2-nc	−78.89
nc-p1	−80.13	ca-pa2	−76.37	p1-p6	−78.20
nc-p1s	−79.50	tf-pr	−75.92	auto	−77.72
p1-p6	−79.45	auto	−75.19	tf-pr	−77.56
tf-pr	−79.19	nc-p1s	−74.77	nc-p1s	−77.13
pep4	−78.04	pep4	−72.44	pep4	−75.24
pep5	−75.08	pep1	−66.78	pep5	−70.44
pep1	−73.55	pep5	−65.80	pep1	−70.17
pep2	−68.58	pep3	−64.80	pep3	−66.13
pep3	−67.46	pep2	−62.78	pep2	−65.68

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

^*Structure used as template.

Threading with conformational potentials

Besides the long-range interactions it makes with neighboring protease residues, the binding affinity of a peptide also depends on its own conformation. The consideration of the conformational energy gives a measure of how favorable the given conformation is for a peptide, and to account for this we incorporated short-range energies to the total energy. Statistical short-range potentials for bond angles and torsions were used to calculate the conformational energy of the backbone and side chains of the peptide.

The threading results with conformational potentials are given in Table 6 for two different template structures. When the conformation of the peptide in the template is taken into account in evaluating the energy, the template structure's own peptide has the best score in both cases. This results from using a more detailed force field which defines the energy of the peptide more precisely.

TABLE 6.

Ranking of peptides taking into account both the interaction energy with protease and the short-range conformational energy of the peptide

Name	bb	sc	lr	Total	Name	bb	sc	lr	Total
ca-p2*	2.02	−22.26	−83.20	−103.44	ma-ca*	−11.72	−5.89	−77.57	−95.18
rh-in	0.86	10.99	−86.33	−74.48	pr-rt	−11.14	15.14	−82.24	−78.24
p2-nc	0.07	12.75	−81.04	−68.22	tf-pr	−10.28	11.10	−75.92	−75.10
rt-rh	0.36	16.97	−80.96	−63.62	p1-p6	−8.95	19.82	−76.95	−66.09
p1-p6	−1.11	21.94	−79.45	−58.62	p2-nc	−10.14	24.84	−76.75	−62.05
nc-p1	0.90	21.55	−80.13	−57.69	rt-rh	−10.96	36.19	−80.43	−55.19
auto	−0.34	24.09	−80.25	−56.50	pep2	−9.38	20.00	−62.78	−52.16
ma-ca	−0.98	26.60	−80.64	−55.02	rh-in	−10.36	41.62	−81.21	−49.95
nc-p1s	−0.38	36.09	−79.49	−43.78	nc-p1	−9.63	40.36	−79.22	−48.49
pr-rt	−1.37	42.42	−83.58	−42.54	nc-p1s	−9.04	36.39	−74.77	−47.42
pep2	−0.69	26.95	−68.58	−42.33	pep5	−8.92	30.25	−65.80	−44.47
pep5	0.29	34.32	−75.08	−40.48	pep1	−9.59	35.31	−66.78	−41.07
tf-pr	−1.17	41.34	−79.19	−39.02	auto	−10.49	45.02	−75.19	−40.66
pep1	0.61	37.06	−73.55	−35.88	cap2	−9.65	49.66	−76.37	−36.37
pep4	1.97	43.24	−78.04	−32.83	pep3	−8.69	43.70	−64.80	−29.79
pep3	1.22	43.38	−67.46	−22.86	pep4	−7.91	54.18	−72.44	−26.17

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The total energy (total) used for ranking the peptides is the summation of backbone short-range energies (bb), side-chain short-range energies (sc), and energy associated with long-range interactions evaluated by distance-dependent potentials as before (lr).

^*Structure used as template.

For the other sequences, it is not possible to differentiate substrates and nonbinding peptides based on energy using a single template; however, some substrates have lower scores using one template and have high scores in the other (for example, pr-rt and tf-pr; these sequences fit better to the conformation of ma-ca, compared to that of ca-p2). Using multiple templates provides more possible conformations accessible in the binding groove than the binding sequences can possibly assume. Therefore, taking the average of results from the two templates improves the results as seen in Table 7. The shifted nc-p1s sequence is identified as having lower affinity than the real nc-p1 substrate, and ranked among the nonbinders. The nonbinders are ranked lower than the binding substrates, but once again, the energy difference between the binding and nonbinding peptides is not significant.

TABLE 7.

Ranking using the average of total energies in Tables 6 and the average of total energies from five templates

Name	bb	sc	lr	Total	Name	bb	sc	lr	Total
ma-ca*	−6.35	10.35	−79.10	−75.10	rt-rh*	−7.70	10.89	−83.30	−80.11
ca-p2*	−3.82	13.70	−79.78	−69.90	p2-nc*	−6.54	13.47	−80.23	−73.31
p2-nc	−5.04	18.79	−78.89	−65.14	rh-in*	−6.95	19.78	−85.18	−72.34
p1-p6	−5.03	20.88	−78.20	−62.36	p1-p6	−6.40	22.90	−80.82	−64.32
rh-in	−4.75	26.30	−83.77	−62.21	ca-p2*	−5.65	23.75	−80.51	−62.42
pr-rt	−6.26	28.78	−82.91	−60.39	pr-rt	−8.01	30.55	−84.81	−62.27
rt-rh	−5.30	26.58	−80.69	−59.41	ma-ca*	−7.99	26.05	−80.23	−62.16
tf-pr	−5.72	26.22	−77.56	−57.06	tf-pr	−7.44	28.33	−80.41	−59.52
nc-p1	−4.37	30.95	−79.67	−53.09	auto	−6.88	27.64	−79.53	−58.77
auto	−5.42	34.56	−77.72	−48.58	nc-p1	−5.99	27.98	−80.01	−58.01
pep2	−5.03	23.47	−65.68	−47.24	nc-p1s	−6.25	29.49	−80.73	−57.49
nc-p1s	−4.71	36.24	−77.13	−45.60	pep2	−6.50	26.90	−69.12	−48.72
pep5	−4.32	32.28	−70.44	−42.48	pep1	−6.38	30.73	−71.30	−46.96
pep1	−4.49	36.19	−70.17	−38.47	pep3	−5.48	28.36	−68.86	−45.99
pep4	−2.97	48.71	−75.24	−29.50	pep4	−4.60	37.54	−77.45	−44.51
pep3	−3.74	43.54	−66.13	−26.33	pep5	−6.03	36.83	−72.53	−41.73

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The total energy (total) used for ranking the peptides is the summation of backbone short-range energies (bb), side-chain short-range energies (sc), and energy associated with long-range interactions evaluated by distance-dependent potentials as before (lr).

^*Structure used as template.

However, when the five templates are averaged—we excluded p1-p6 complex structure here, as the peptide assumes a very different conformation than the others, as seen in the crystal structure, and its inclusion worsens the predictions as the peptide conformation is very important in this method—the results improve significantly as given in the right panel of Table 7. The only sequence that could not easily be distinguished is nc-p1s, which does not clearly belong to the nonbinders' group, but has a score comparable to the real sequence. This is likely because the sequence is highly homologous to other substrate sites, even though it is not itself a substrate. Otherwise, the energy gap between the binding and nonbinding peptides is now ∼10 RT, which would allow identifying the two groups efficiently without prior knowledge of their identities.

Dynamic threading

As a last method, we modified the threading methodology by introducing dynamics to allow the relaxation of the system to equilibrate and minimize its energy after threading the query amino-acid sequence onto the structure. This is potentially helpful when there are not multiple structures to be used as templates. We employed a Monte Carlo/Metropolis-type dynamic minimization process with a simplified coarse-grained model of the protein structure.

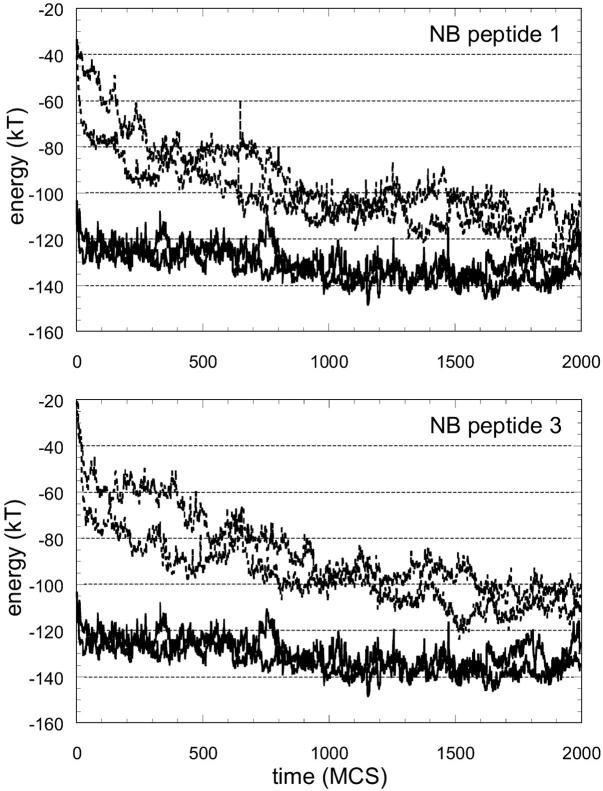
The total energy of the peptide, comprising long- and short-range potentials throughout a minimization of 2000 MC steps (MCS), is given for three of the natural substrates in Fig. 1. Two independent runs are made for each threaded sequence. The results from both are given in the graphs as separate curves in broken lines and they are quite similar. For the threaded substrates in Fig. 1, there is a rapid relaxation and decrease in energy to approach the energy of the template's own peptide. The results for two of the nonbinding peptides are given in Fig. 2 in the same format as Fig. 1. In this case, there is not a rapid relaxation of the energy and the energy does not converge to the reference energy during the simulation. The results are promising in differentiating between binders and nonbinders; therefore, we carried out the relaxation process for all the sequences in the test set.

FIGURE 1.

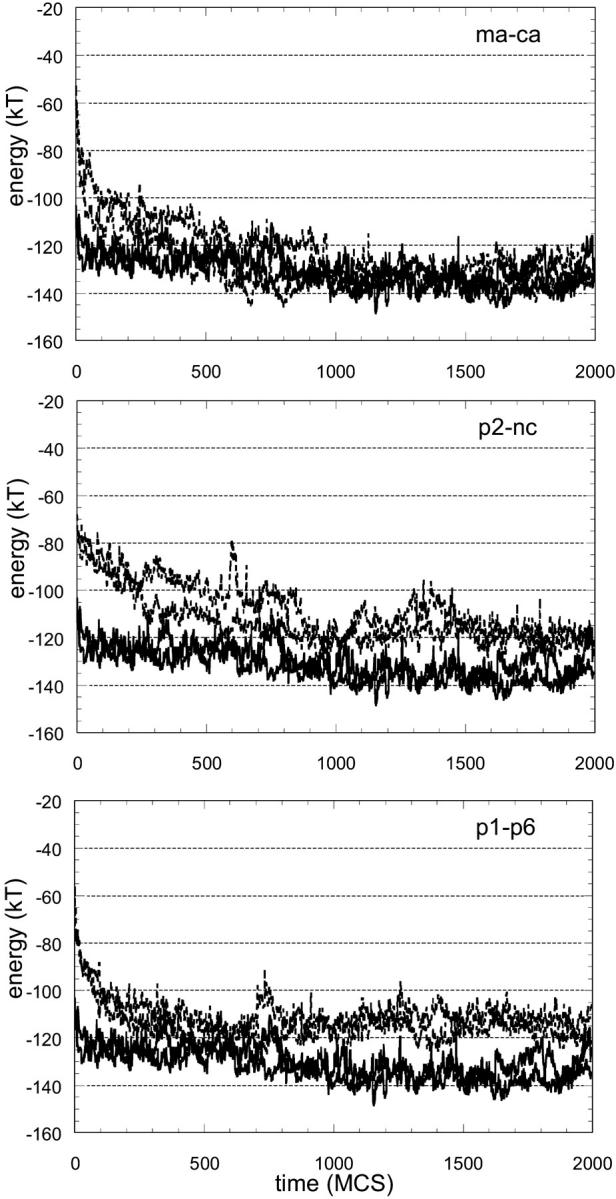
Total energy of the substrate during energy minimization after threading onto ca-p2 complex structure. The total energy comprises long-range interactions of the substrate with protease and short-range energies to account for its backbone and side-chain conformation. Note that the initial energy value at time zero corresponds to the total energy given in Table 6 for that sequence. Two solid lines (the same in all graphs) are from the simulations with the structure's own substrate, ca-p2, which can be regarded as the reference. With a rapid relaxation, the energy decreases to approach the energy of the template's own peptide.

FIGURE 2.

Total energy of two of the nonbinding peptide sequences during energy minimization after threading onto ca-p2 complex structure. Refer to the caption to Fig. 1 for explanation. Contrary to substrates, the difference between the reference energy is maintained throughout the simulation.

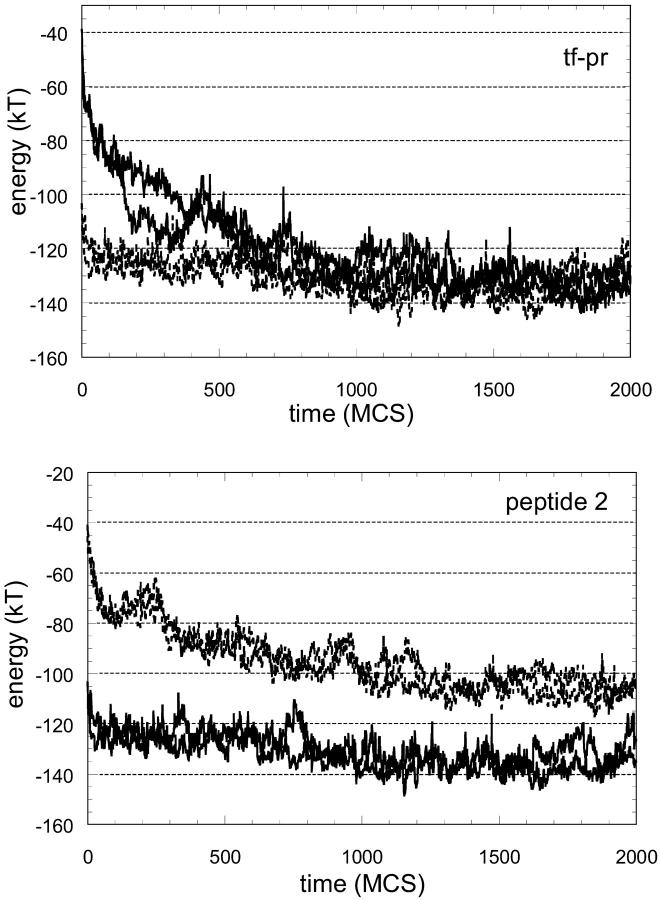
One case clearly demonstrated the efficacy of introducing relaxation into threading. Fig. 3 gives the results for one of the substrates (tf-pr) and one of the nonbinding peptides. This substrate was predicted to have lower affinity than the nonbinding peptide when threaded onto the ca-p2 structure (see Table 6). Hence, the energy value at time zero in the graphs is higher for the substrate. When the systems were allowed to move with the force field, the energy of the substrate relaxed quickly and became favorable (as with the other substrates given in Fig. 1), whereas the nonbinding peptide did not relax as fast, nor did it converge.

FIGURE 3.

Energy minimization for a substrate and a peptide. When the sequences are threaded onto the template, the nonbinding peptide is predicted to have higher affinity than the substrate (see Table 6). Hence, the starting energy value at time zero is more favorable for the nonbinding peptide. However, the substrate relaxes rapidly to minimize its energy whereas the energy difference of the nonbinding peptide with the reference is maintained throughout the simulation.

We calculated the mean total energy of the threaded peptide during the simulations in various time windows, and ranked them accordingly. In all time windows, the substrates ranked higher than the nonbinding peptides, with the exceptions of the autoproteolysis site and the nc-p1s. A larger energy difference was obtained between the binders and nonbinders when the time window was in the first-half of relaxation. The rankings of threaded peptides according to their mean energy in different time windows of relaxation are given in Table 8. Despite the high degree of similarity in two independent runs, the fluctuations in the energy reduces the reliability on the rankings if the differences are only a few RT. When the two sequences mentioned above are not considered, the differences between the mean energy value of the worst ranking substrates and the best ranking nonbinding peptides are in the order of 10 RT. Hence, a significant energy gap is achieved between the two groups of sequences.

TABLE 8.

Ranking of peptides according to their mean energies in various time windows during relaxation simulations, using a single (ca-p2 complex) structure as the template

t = 250–500 MCS		t = 250–750 MCS		t = 250–1000 MCS		t = 500–1000 MCS
ca-p2*	−125	ca-p2*	−126	ca-p2*	−128	ca-p2*	−129
ma-ca	−116	ma-ca	−121	ma-ca	−123	ma-ca	−127
rt-rh	−114	rt-rh	−118	rt-rh	−119	tf-pr	−122
p1-p6	−113	p1-p6	−114	tf-pr	−117	rt-rh	−121
rh-in	−108	tf-pr	−112	p1-p6	−115	p1-p6	−115
pr-rt	−107	rh-in	−111	rh-in	−112	rh-in	−114
nc-p1	−106	p2-nc	−105	p2-nc	−109	p2-nc	−112
tf-pr	−106	pr-rt	−105	nc-p1	−105	nc-p1	−105
p2-nc	−102	nc-p1	−104	pr-rt	−105	pr-rt	−103
nc-p1s	−102	nc-p1s	−100	nc-p1s	−102	auto	−103
auto	−90	auto	−95	auto	−98	nc-p1s	−102
pep1	−86	pep2	−89	pep1	−93	pep1	−96
pep2	−85	pep1	−89	pep4	−92	pep4	−96
pep4	−84	pep4	−87	pep2	−91	pep2	−93
pep3	−75	pep5	−79	pep3	−84	pep3	−88
pep5	−74	pep3	−79	pep5	−81	pep5	−84

The predicted contact energies are given in dimensionless units of RT, where R is the gas constant and T the absolute temperature. The nonbinding peptides are underlined.

The total energy (total) used for ranking the peptides is the summation of backbone short-range energies (bb), side-chain short-range energies (sc), and energy associated with long-range interactions evaluated by distance-dependent potentials as before (lr).

^*Structure used as template.

When the results of the dynamic threading (Table 8) are compared to the conventional static threading with a single template (Table 6), there is a significant improvement in prediction of binders and nonbinders. A short relaxation of 1000 MCS is enough for this improvement, and it takes computationally very reasonable times (∼2–3 h per sequence on an R5000 SGI workstation).

DISCUSSION AND CONCLUSIONS

Different threading methodologies employing force fields of various levels of detail were applied to HIV-1 protease with a test set consisting of both its natural substrate sequences and nonbinding peptides. The aim was to find which method gives better predictions to differentiate between the two groups in the test set, and hence determine which factors are important in the substrate recognition in HIV-1 protease. We found that using a more detailed force field and using the average of results from multiple template structures resulted in better predictions.

In the first method applied, the interactions between the peptide and protease residues in close proximity were approximated by square-well-type long-range potentials. The depth of the well was determined by the type of amino acids in contact, and taken from a statistical contact potential matrix. The important point in this approach is to determine the distance parameter of the square-well potential; that is, the maximum distance, between atoms of the residues, that is required to consider their interaction (a constant value) or not. We tried using three different criteria to answer this question as was done for the MHC system (Altuvia et al., 1995). Nevertheless, we could not obtain results that could separate the binders from the nonbinders in the test set even when we used multiple templates.

Employing distance-dependent potentials as a second method of evaluating the long-range interaction of the peptide, we obtained improvement in the results. Instead of the square-well potential, here we used distance-dependent statistical potentials specific for the type of interacting amino acids. This approach eliminates the need of choosing a distance criterion to determine which residues are in contact and which are not. Instead, the potential energy function gives a certain value depending on the distance. The residues were represented by two effective interaction sites, one for the backbone and one for the side chain specific to the amino-acid type. Introducing a more detailed representation of the long-range interactions and using multiple templates enabled predictions to separate the binders and nonbinders in the test set.

When the structures of six substrate complexes of HIV-1 protease were solved, it was seen that superposition of the structures of any three substrates defines a consensus volume where the substrates fit (Prabu-Jeyabalan et al., 2002). This leads to the idea that a shape, rather than certain amino acids, are recognized by the protease. Although the protease also adapts to bind different sequences, the binding groove restricts the conformations accessible to the bound peptide. The affinity of the peptide is thus affected by how well it can fit into the volume defined by the binding groove. To account for this restriction, we added conformational short-range potentials to the energy evaluation scheme in threading. In this approach, one has to consider different conformations accessible to the peptide, and thus it is very important to use multiple template structures. In accordance with these notions, we obtained a clear differentiation between binders and nonbinders in the test set with the employment of conformational potentials in addition to distance-dependent long-range potentials and multiple templates. This finding suggests that the “fitness” of a given peptide to the conformations accessible in the bound form is an important determinant of its binding affinity; hence short-range as well as long-range potentials should be considered in the evaluation of energy in threading methods. In the general field of protein structure prediction, there have been works to include extra terms to the score or force field accounting for local information, by secondary structure predictions (Russell et al., 1996; Rost et al., 1997) or experimental data such as nuclear magnetic resonance (Ayers et al., 1999). Wolynes and co-workers demonstrated that including local environmental preferences and residue contacts refined their screening technique in correctly discriminating correct folds (Goldstein et al., 1992). There have also been some approaches with emphasis on the local aspects of conformation and forces that operate on the short range of a polypeptide backbone (Jones, 1999; Sippl, 1990). Our results indicate that short-range potentials are important in protein-to-protein interactions, where the conformation of the side chains is expected to play an important role.

In another test to justify the improvement obtained in the threading methods, we evaluated their performances using the rank analysis: how are the binding potentials of the natural cleavage site sequences ranked among all the possible 8-mer sequences derived from the overlapping peptides in the gag-pol polyproteins? We would expect that the sequences that best fit to the binding site will be recognized and cleaved by HIV-1 protease, and therefore threaded all possible 8-mers in the polyproteins onto the known peptide complexes to see if the cleavage sites could be found. The structure of the polypeptides when they are cleaved by the protease is not known and this could also affect the recognition events. Nevertheless, consistent with the results for the test set, there was an improvement in the rankings of the cleavage sites as the force field was improved, and as multiple templates were used (Fig. 4). Applying the most accurate method, where both short- and long-range potentials are used, the template structure's own peptide always ranks the first among all possible 8-mers in the polyproteins. This indicates that the force field precisely defines the energy of the peptide when the exact conformation is available. Other sites within the polyprotein, which are not known to be cleavage sites, also score well; however, local secondary and tertiary structure may prevent them from being cleaved.

FIGURE 4.

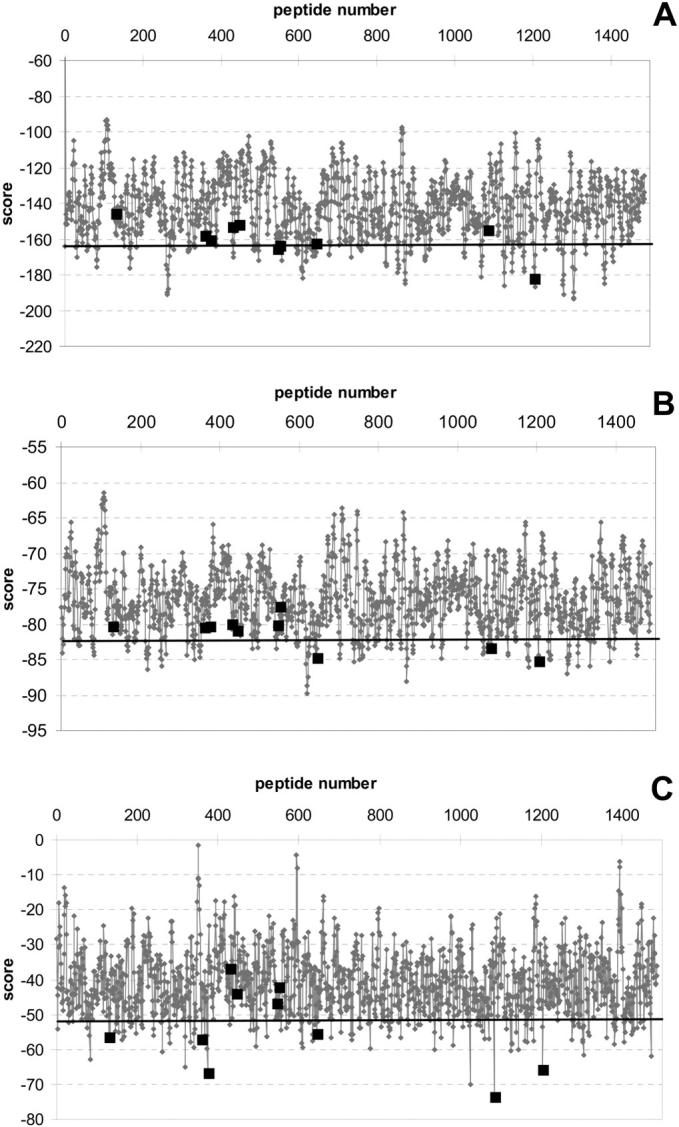
The scores for all possible 8-mers in the gag-pol polypeptide using threading with contact potential matrix (A), distance-dependent potentials (B), and distance-dependent and conformational potentials (C). The black squares show the actual cleavage sites. A horizontal line is drawn to indicate the peptide sequences ranking in the top 10%.

In all the threading methods discussed so far, the coordinates in the available co-crystal structure were used to evaluate the binding affinities of peptides whose complex structures with the protease are not available. Therefore, the results are only approximations for the different sequences threaded, assuming that there is a unique spatial path possible for the peptide in the active site. However, both the peptide and the protease can adapt for recognition (Prabu-Jeyabalan et al., 2002). To take into account this adaptation, multiple templates were used as representatives of different possible conformations of both the peptide and the protease. Also, the dynamic-threading method, where a short dynamic simulation is performed to allow the system to move and equilibrate after threading the peptide sequence, allows for this adaptation. The structures moved with a root-mean-square deviation of 2.0 ± 0.2 Å on the average, at the end of MC runs. In the simulation scheme used here, we allowed both the peptide and the protease to move as the protease also adapts to recognize its substrates, and we obtained a significant improvement in the predictions using a single template when dynamics were introduced into threading. This method is therefore potentially useful for systems for which multiple complex structures are not available.

Threading should enable a computationally fast and less expensive screening of candidate sequences using a rough estimate of the binding affinity. Although the threading predictions improve upon employment of more detailed energy evaluations, all-atom representations and force fields such as in MD simulations and detailed structure predictions are not appropriate for threading. Hence, an optimum should be found by balancing the detail and speed of the method, taking into account the nature of the problem. Here we found that a threading method using conformational short-range and distance-dependent long-range potentials with two effective interaction sites per residue gives good enough predictions to differentiate between substrates and nonbinding sequences, when either multiple template structures are used or dynamic threading algorithm is applied with a single template. Both of these methods are computationally fast and effective. In this postgenomic era, they are potentially useful for screening a library of potential binding sequences to the newly discovered proteins.