A Computer Simulation Study of the Hydrated Proton in a Synthetic Proton Channel

Abstract

Classical molecular dynamics simulations using the multistate empirical valence bond model for aqueous proton transport were performed to characterize the hydration structure of an excess proton inside a leucine-serine synthetic ion channel, LS2. For such a nonuniform pore size ion channel, it is found that the Zundel ion (H₅O₂⁺) solvation structure is generally more stable in narrow channel regions than in wider channel regions, which is in agreement with a recent study on idealized hydrophobic proton channels. However, considerable diversity in the relative stability of the Zundel to Eigen cation (H₉O₄⁺) was observed. Three of the five wide channel regions, one located at the channel's center and the other two located near the channel mouths, are found to show extraordinary preference for the Eigen solvation structure. This implies that proton hopping is inhibited in these regions and therefore suggests that these regions may behave as barriers in the proton conducting pathway inside the channel. The proton solvation is also greatly influenced by the local molecular environment of the protein. In particular, the polar side chains of the Ser residues, which are intimately involved in the solvation structure, can greatly influence proton solvation. However, no preference of the influence by the various Ser side chains was found; they can either promote or prevent the formation of certain solvation structures.

INTRODUCTION

Proton channels are passages formed by proteins that selectively allow protons to be transported across a membrane or from the exterior solution to the interior reaction center of an enzyme (Oliver and Deamer, 1994; DeCoursey and Cherny, 2000; Durrant, 2001). They are intimately involved in a fundamental phenomenon—proton transport (PT) in biological systems—and are thus very important structural-functional domains deserving of detailed investigation.

Several relatively simple but interesting membrane proton channels, such as the gramicidin A and the influenza A M2 channels, have been extensively investigated in experiments. Important channel properties, such as gating, blocking, current-voltage relations, and ion selectivity, can be characterized through electrophysiological experiments; modern biochemical and structural techniques can further help to determine channel structures and to deduce the structure-function relationships. Molecular dynamics (MD) simulation is a theoretical methodology that can be used to directly calculate the dynamics of the molecules of interest at the atomic level, and thus it is capable of revealing both microstructural dynamical fluctuations and detailed averaged molecular interactions. Furthermore, methods such as umbrella sampling can be implemented in the MD approach to help explore long-timescale dynamical processes. Macroscale properties can also be derived through statistical mechanics based on the MD simulations. This technology is extremely useful in exploring the molecular details that are difficult or impossible to observe directly using experimental methods alone.

Although the MD methodology has been extensively used in studies of various biological systems including ion channels, directly simulating an excess proton in the system remains a challenge. This is largely due to the peculiar nature of proton solvation. According to the Grotthuss hypothesis (Agmon, 1995), proton transport (PT) consists of successive proton transfer reactions (hops) between adjacent water molecules; specifically, in each hop, an O-H covalent bond is broken and transformed to an O-H hydrogen bond, while simultaneously another O-H covalent bond is formed:

where “…” denotes a hydrogen bond. This hypothesis implies an unusual dynamics of the proton solvation structure.

Two proton solvation structures in bulk water have been proposed by experimentalists. One is the Eigen cation, , in which the hydronium (H₃O⁺) is symmetrically hydrogen-bonded to three water molecules; the other is the Zundel cation, 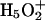, in which the proton is equally shared between two water molecules (for a diagram of the two hydration structures, see Schmitt and Voth, 1999a). The existence of two distinct solvation species implies that if there is a transformation of the proton solvation structure, it must happen via the aforementioned rearrangement of bonding topology. Detailed discussions of PT can be found in some theoretical studies of an excess proton in water clusters, “wires,” and bulk water (Tuckerman et al., 1995a,b; Mei et al., 1998; Marx et al., 1999; Schmitt and Voth, 1999a,b; Day et al., 2000, 2002; Brewer et al., 2001). These studies revealed that the actual proton solvation structure fluctuates between the Eigen and Zundel cations with the latter having a slightly higher free energy. The proton transfer is always associated with transformation of the solvation structure; therefore the concept of structural diffusion has been proposed for the PT mechanism (Tuckerman et al., 1995a,b; Day et al., 2000, 2002). For these reasons it is critical to have an MD model capable of treating the proton transfer reaction in an accurate and computationally efficient way.

Previous MD simulation studies of an excess proton in channels have relied on either a nonreactive hydronium model (Sagnella and Voth, 1996) or some reactive but not especially accurate models (Pomès and Roux, 1996, 1998, 2002), such as the PM6 model (Stillinger and David, 1978). Though these studies have provided insights into some issues of PT, their limitations are also obvious. An accurate PT model for detailed simulations of proton behavior in condensed phase is the multistate empirical valence bond (MS-EVB) model of Schmitt and Voth (1998, 1999a), and its second generation has recently been formulated (Day et al., 2002). This model allows the proton to diffuse along the three-dimensional hydrogen-bonded network of water molecules. It can describe many aspects of the process in good agreement with both experimental and ab initio MD results (Marx et al., 1999). Examples are the geometries and energetics of protonated water clusters, the proton hopping rate (Schmitt and Voth, 2000), the spectroscopy and density of vibrational states (Kim et al., 2002), and the relative stabilities of the Eigen and Zundel cations in bulk water. One feature of this model is that quantitative measures for discriminating the Eigen and Zundel cations are readily available from the simulation, thus making it very convenient to analyze the proton solvation structure. The model is also completely deterministic (based on molecular forces) and much more computationally efficient compared to the ab initio MD methods. It is therefore ideal for use in simulations of biological systems. For a discussion of other MD approaches for studying PT, see Day et al. (2002).

In a recent article from our group (Brewer et al., 2001), an excess proton in channels with different radii was simulated using the MS-EVB model. The channels were hydrophobic and simulated using a repulsive potential as introduced by Lynden-Bell and Rasaiah (1996). This study investigated the effects of pore radii and channel length on the equilibrium and dynamic properties of the excess proton. It found that the relative stability of the Zundel cation with respect to the Eigen cation increases as hydrophobic pore radius narrows to 2.0 Å. An interesting phenomenon was observed that when the pore radius decreases to 2.0 Å, the proton diffusion constant increases by more than an order of magnitude, which implies that the greatly enhanced proton diffusion is a result of the single-file “water wire” formed in the narrow channel.

The previous study treats the channel structure as a cylindrical region that is periodic along the channel axis. Furthermore, the channels were hydrophobic and uniform in pore size, which is, of course, quite different from real channels. Therefore, numerous questions remain unanswered—for example, how the proton behaves in a more realistic model that includes molecular details from the protein, and how the channel and the proton interact with each other.

To address these issues in the present study, we require the model channel to contain the most important features of an ion channel, but also to be relatively simple to avoid less important but complicating factors. Since we are interested in the previously observed narrow-channel phenomenon, we also require the channel to be relatively narrow. For these reasons, a synthetic leucine-serine channel, LS2, was chosen. This channel is voltage-gated and highly proton-selective (Lear et al., 1988). Its primary structure contains only leucine and serine residues: (LSLLLSL)₃NH₃. Though its detailed structure is not available, a model has been proposed with the aid of molecular modeling (Lear et al., 1988). This model, as was supported by later experimental and MD simulation work (DeGrado and Lear, 1990; Åkerfeldt et al., 1993; Mitton and Sansom, 1996; Zhong et al., 1998; Randa et al., 1999), is a parallel bundle of four identical α-helices, which can support a thin water column across the bilayer. The bundle has a pseudo-C₄ symmetric or dimer-of-dimers structure with their polar side chains directed toward the lumen. This channel includes many more realistic features than the hydrophobic tube model used by Brewer et al. (2001). First, the protein atoms (except the nonpolar hydrogens) are explicitly included. Second, the pore size is nonuniform along the channel. Third, the channel is not periodic in the channel axis direction, and the cap waters at each end of the channel are explicitly included. Finally, the channel is hydrophilic due to the Ser residues' side chains. The present study therefore shows how the proton hydration structure may be affected by the explicit protein environment. For a related discussion of the role of the protein electrostatic environment in the PT process, see Sham et al. (1999).

In the next section, the MS-EVB model and related concepts will be briefly introduced, followed by the protocols for constructing the LS2 channel systems as well as the simulation details. The results of the simulations are presented and discussed in the third section, followed by the conclusions.

METHODS

The MS-EVB model for PT in aqueous systems

The Empirical Valence Bond (EVB) approach is one of the most effective approaches to modeling chemical reactions (Warshel, 1991). In an EVB model, the state of a chemical reaction process is described as a linear combination of a small number of independent, empirically-motivated valence bond (VB) “states”:

(1)

The rule for combining the “N” VB states is given by the equation

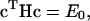(2)

where c is the eigenvector with elements c_i [i = 1, N] for the lowest eigenvalue, E₀, and H is the Hamiltonian matrix with elements h_ij = 〈i|H|j〉. Each matrix element is a function of the nuclear degrees of freedom of the molecular system under consideration; the forms and parameters of the functions can be chosen to reproduce key aspects of the actual potential energy surface, usually determined from ab initio calculations or experimental results. Conventionally, two VB states, namely the reactantlike and productlike VB states, are used in an EVB model for describing the potential energy surface of a single chemical process. To describe a number of chemical reactions that are tightly coupled together, such as the case of proton hopping in water, it is essential to consider these reactions simultaneously and couple their states' changes, since each reaction's state can affect the others. The multistate EVB (MS-EVB) approach realizes this treatment.

In the MS-EVB model for an excess proton in water, any VB state is a hydronium-like structure that is formed by a water molecule and any third hydrogen in the system. Therefore, there are a larger number of VB states in bulk water, but, in fact, only a limited number (usually ∼15 for bulk water phase) of VB states contribute significantly to the Hamiltonian; the others can be safely ignored. In the MS-EVB2 model used in the current study, the VB states are constructed for waters within the first three solvation shells of the pivot hydronium, which is the one in the VB state that has the largest contribution to the Hamiltonian. More detailed information can be found in the literature (Schmitt and Voth, 1998, 1999a,b; Čuma et al., 2000, 2001; Day et al., 2002; Brewer et al., 2001; Smondyrev and Voth, 2002a,b).

Here, it is desirable to point out that the MS-EVB approach provides convenient ways for identifying proton solvation species and for describing PT reactions. For example, since the EVB amplitude () is proportional to the Hamiltonian contribution of the corresponding VB state, this quantity can be used as a measurement of hydronium-likeness of the structure. The first two largest EVB amplitudes are often of the most interest since they can reflect the overall solvation structure of the excess proton. The sum of all EVB amplitudes is 1, whereas the largest amplitude (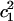) usually ranges from 0.4 to 0.9 and the second largest () from 0.01 to 0.5. In bulk water, an Eigen structure, which is more hydronium-like, usually has ≈ 0.65 and/or 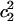≈ 0.1; as the structure is more and more Zundel-like, the two quantities will go closer and closer, and a typical Zundel structure usually has values of roughly 0.46 for both and . The EVB amplitudes are calculated for each time step in an MD simulation, so their distributions and relative free energies can be readily calculated from simulations.

Because of the delocalized nature of the positive charge of the excess proton, its position cannot be assigned to any individual hydrogen nucleus. A more general description for its position is the center of excess charge (CEC) (Brewer et al., 2001), defined as

(3)

where r_i(t) are vectors of the center of charge of the hydronium in the i^th EVB state at time t, while the EVB amplitudes [i = 1, N] are obtained from Eq. 1. This quantity is essentially the expectation value of the excess proton position in the time-evolving MS-EVB state space.

Construction of a reduced LS2 channel system

To make the simulations computationally less demanding, we constructed a reduced LS2 channel system using the following protocol:

1. An LS2 channel system embedded in 1-palmitoyl-2-oleoyl-sn-glycerol-3-phosphatidylcholine (POPC) bilayer was built by truncating the box of a snapshot from an equilibrated trajectory of a large LS2 channel system containing the LS2 channel, 158 POPC lipids, and 4961 water molecules. The box size was then reduced in the membrane lateral directions (i.e., x- and y-directions), resulting in a central rectangular region containing the LS2 channel, 88 POPC, and 2821 water molecules. This is called the composite system.

2. The new structure was energy-minimized for 2000 steps using the steepest descent method to remove bad contacts near the box boundaries as caused by the truncation.

3. Two-nanosecond constant pressure and temperature MD simulation was then performed with this energy-minimized system under the following conditions:

   • The 300 K constant temperature was maintained with a Berendsen thermostat.
   • A pressure of 1 atm was applied independently in the normal and lateral directions of the membrane using the Berendsen barostat method (Berendsen et al., 1984).
   • The coupling constants for the thermostat and barostat were 0.1 ps and 1.0 ps, respectively.
   • The system was treated periodically in all three directions.
   • Long-range contributions of the Lennard-Jones interactions were corrected using the standard method, whereas Coulomb interactions were treated using the particle mesh Ewald method.
   • The cutoff radii for both Lennard-Jones interactions and the real-space Coulomb interactions were 10 Å.
   • The force field was the same one as used before (Randa et al., 1999), except that the SPC water model was replaced with the TIP3P model.
   • The bond lengths of the molecules in the system were constrained using the LINCS method (Hess et al., 1997), and the MD time step was 2 fs.
   • The system appeared to be equilibrated within the initial 1 ns (see Results and Discussion).

4. The final structure from the above MD simulation (Fig. 1 A) was then used to construct the initial structure of the reduced system. Both the lipid and water molecules in the cap regions were discarded, leaving only the protein and the pore waters. Then the size of box was adjusted as follows: the z-dimension was set to the length of the channel plus 20 Å, giving 52.74 Å in total; the box size in the x- and y-directions was reduced to be slightly larger than the diameter of the channel, which gives 29.2 Å and 27.7 Å for the x- and y-directions, respectively. Finally, a patch of equilibrated water with the same sizes in the x- and y-directions, 10-Å thick in the z-direction, was added to each end of the channel to form the water caps.

5. Bad contacts in the new system were removed by 500 steps of energy minimization using the steepest descent method. To keep the integrity of the channel structure in MD simulations, harmonic position restraints with force constants of 1000 kJ/(mol Ų) were applied to the backbone atoms. The equilibrium positions of the position restraints were derived from the average backbone structure over the last 1-ns trajectory obtained in step 3. The system was simulated for 1.5 ns under the same conditions except that no pressure was coupled.

All the above simulations were carried out using the GROMACS 2.0 package (Berendsen et al., 1995; van der Spoel et al., 1999). The simulation trajectories were analyzed with tools either from the package or coded in-house.

FIGURE 1.

The structures of the composite and reduced LS2 systems. (A) A snapshot of the composite system. The water molecules are displayed in space-fill mode, whereas lipid molecules are shown in stick mode between the two water layers. The protein embedded in the lipid bilayer is represented by its backbone shown in tube mode. (B) A snapshot of the reduced system. The water molecules are displayed in space-fill mode, whereas the protein, which surrounds a thin water column, is shown in stick mode, with its backbone emphasized by thicker sticks. Lipid molecules are not included in the reduced system.

MD simulations with the MS-EVB model

The simulations of an excess proton in the channel were carried out with a modified DL_POLY 2.12 software (Smith and Forester, 1999) incorporating the MS-EVB2 algorithm (Smondyrev and Voth, 2002a). The system was simulated under the constant volume and temperature condition. The 300-K constant temperature was maintained using the Nosé-Hoover thermostat with a relaxation constant of 0.1 ps. Long-range correction for Lennard-Jones interactions followed the normal method, and Coulomb interactions were calculated with the Ewald method. The cutoff radii for both Lennard-Jones and real space Coulomb interactions were 10 Å. The time step was 1 fs, and the velocity of the whole system was removed every 5 time steps. The force field parameters for both the protein and the water are the same as the MD simulations described above with the exception of the MS-EVB interactions.

The structure of the reduced system was derived from the final structure of the MD simulation of step 5, described in the previous subsection. An excess proton was placed into the channel by replacing a pore water near a specified position with a hydronium. A Cl⁻ ion was added into the bulk water region to maintain charge neutrality of the system. This ion did not enter the channel in any of our simulations.

To characterize the properties of the solvation states of the excess proton in different channel regions, a series of MD simulations were performed in which an artificial harmonic potential applied on the z-coordinate of the CEC (Eq. 3) was introduced to prevent the CEC from diffusing out of the region. The force constant of this restraining potential was 5–15 kcal/(mol Ų), and the CEC was confined within roughly 0.4 Å around the equilibrium position of the restraining potential.

The hydrophilicity effects of the protein on the hydration of the excess proton in the channel were examined via simulations with so-called charge-off LS2 mutants, in which the partial charges of the side chain atoms (–CH₂OH) of the nearby Ser residues were set to zero, while keeping the other parameters, such as those for intramolecular and the Lennard-Jones interactions, unchanged. The mutated serine residues were those within roughly 4 Å to the equilibrium point of the CEC restraining potential. Other simulation conditions were the same as described above.

All of the MS-EVB simulations lasted for roughly 1 ns. The analyzing tools for these simulations are C++ programs coded in-house. Unless specified otherwise, the equilibrium properties were calculated from the data after the initial 400 ps of the simulation.

RESULTS AND DISCUSSION

Stability of the composite system

Our previous MD simulations on the LS2 channel were performed using the SPC water model (Randa et al., 1999). Since the MS-EVB2 model was parameterized for the TIP3P water model, the water model in the LS2 system needs to be changed and the stability of the system needs to be re-evaluated. For this purpose, a 2-ns MD simulation was performed on the composite system, and the following quantities were calculated as functions of time.

Fig. 2 shows the changes in box size and the total potential energy of the system versus time. The overall changes are small. Relatively large fluctuations (up to 2 Å) of the box dimensions in both the membrane normal (z) and the lateral (x- and y-) directions are observed over the initial 1 ns. The total potential energy also decreases slightly during this period. After the initial 1 ns, the system seems to stabilize with little fluctuation in box size and very little drift in the total potential energy. Given that the system was obtained by box truncation, it is not surprising to see some relaxation during the initial 1 ns.

FIGURE 2.

The evolution of the box size (A) and the total potential energy (B) of the simulation of the composite system.

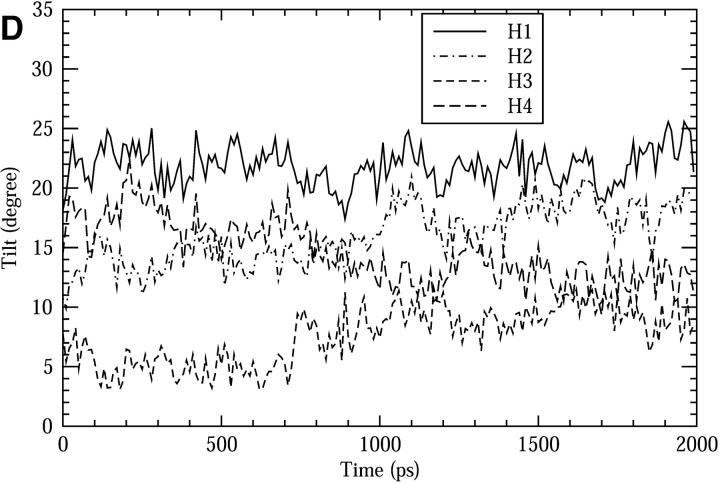
The structural stability of the channel protein was examined through the following quantities: Fig. 3 A shows the root mean square of deviation (RMSD) of the protein backbone with respect to the initial structure from previous simulation. The overall deviation from the initial structure is very small (∼1 Å), and most of the observed deviation happens during the initial 1 ns (∼0.8 Å), indicating the protein structure is very stable and no substantial change occurs after 1 ns of equilibration. The overall packing stability of the helix bundle can be examined through the distances (D) between pairs of centers-of-masses (COMs) of the helices (H1, H2, H3, and H4) as shown in Fig. 3 B. These quantities change very little during the whole simulation. The largest noticeable changes are ∼0.2 Å for H1-H2, H1-H3, and H3-H4, and again those changes were largely within the initial 1 ns. The cross angles (Ω) between the neighboring helices are shown in Fig. 3 C. Divergences after 1 ns from 18° to 22.5° (for H1-H2 and H3-H4) and to 17° (for H2-H3 and H4-H1) were noticed. This may indicate that the protein packing changes slightly from a tetramer-like conformation to a dimer-of-dimers-like conformation. Similar conformation changes have been observed in another LS2 simulation (Zhong et al., 1998). It is still unclear whether this change is an intrinsic long-term fluctuation of the packing pattern or a simulation artifact caused by unknown factors. The tilt angles of the helices with respect to the membrane normal are shown in Fig. 3 D as functions of time. Again, small changes (up to 5°) were noticed for H2, H3, and H4 during the first 1 ns, but they are stable in the last 1 ns.

FIGURE 3.

The structural change of the LS2 channel during the simulation of the composite system. (A) The RMSD of the backbone atoms. (B) The distances between each pair of the COMs of the α-helices. (C) The cross angles between two neighboring α-helices. (D) The tilt angles of the helices with respect to the membrane normal.

To follow the stability of the volume of the pore, the number of pore waters as a function of time was calculated and is shown in Fig. 4. The LS2 pore water region is defined as a cylindrical region whose center is at the protein's COM with a fixed radius of 3 Å and whose length is determined by the distance between the COMs of the NH₂ groups at both ends of the channel. Fig. 4 shows this quantity fluctuates between 16 and 30, but it does not show noticeable drift in the full time, suggesting that the channel's lumen is basically not changed. The average number of pore water molecules is ∼22.

FIGURE 4.

The change of the number of pore water molecules during the simulation of the composite system.

All the above results show that the system is very stable despite changes to the system size by box truncation and to the water model from SPC to TIP3P. Most of the noticeable changes happen within the initial 1-ns equilibration time. Thus, we are confident that the LS2 composite system is a stable channel. Furthermore, the high protein stability implies that the approximation of using position restraints on the protein backbone to replace the stabilizing effects from the lipid bilayer in the reduced system may be acceptable.

Comparisons between the composite and reduced systems

The reduced system was constructed to decrease the computational expense, reflecting the tradeoff between the realism of the model and the sampling size of the simulations. Due to the missing lipid bilayer, the channel protein must be treated specially to maintain its structural integrity without dramatically changing its dynamics. In this study, this was achieved in our reduced system by applying harmonic position restraints on the backbone atoms with respect to the average structure derived from the equilibrium trajectory of the composite system, while allowing the protein's side chains to move freely.

Some rationale for this treatment is as follows. First, the protein is basically embedded in the hydrocarbon region of the lipid bilayer. The forces from this region on the pore water are small and short-ranged, therefore they may be reasonably ignored as long as the protein's natural structure is preserved. Second, the α-helical structure of peptides is quite rigid by their nature, as is evident from the above simulation results concerning the protein's stability in the composite system. Thus the introduction of position restraints on the backbone atoms seems reasonable. Another advantage of this treatment is that it allows us to carry out the charge-off mutations without worrying if they could substantially affect the protein's overall structure. However, on the other hand, this treatment may bring some problems. For example, the membrane potential at the lipid-water interface is not present in the reduced system, so the pore water behavior near the channel mouth will probably be altered. The “breathing motion” effect of the channel might be much inhibited by the position restraints. Furthermore, some artifacts may arise due to the small size of the reduced system and the Ewald method.

To measure how the reduced system approximates the more realistic composite system, we compared the following aspects of the two systems.

Root mean square fluctuation (RMSF) of the protein backbone, which reflects the flexibility of the protein, is compared in Fig. 5 A. The shapes of the curves are similar to each other. However, due to the position restraints, the RMSF for the reduced system is ∼30% smaller. Decreasing the force constants may achieve the same RMSF, but it is unclear whether or not a smaller RMSF would also make the system behave better in other aspects.

FIGURE 5.

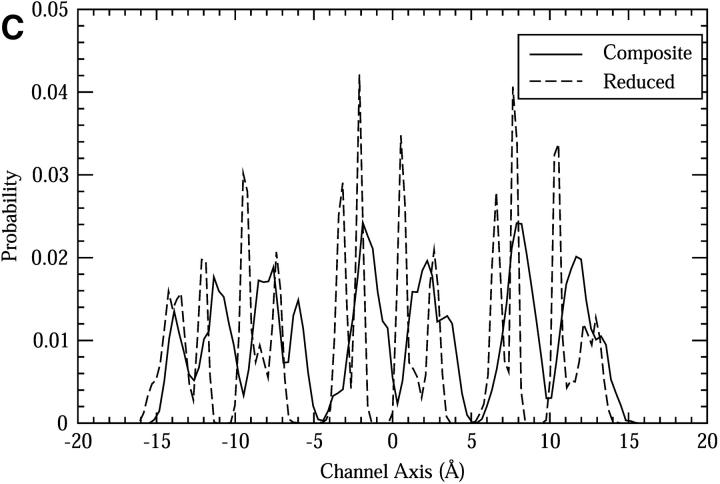
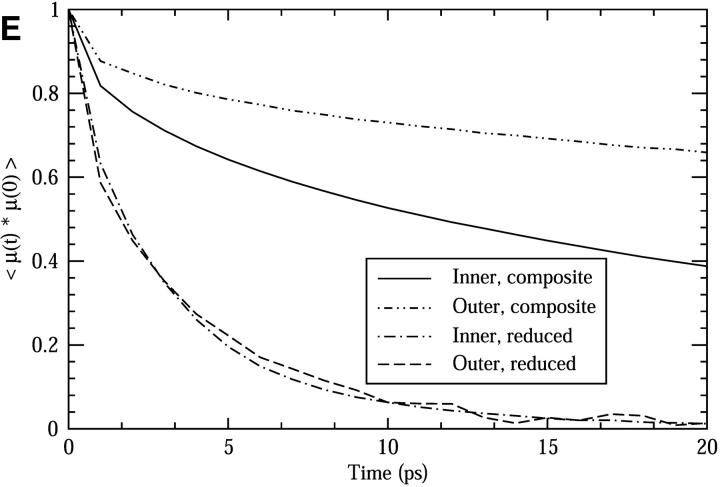
Comparisons between the composite and reduced systems. (A) The RMSF of the backbone atoms. (B) The pore radii as functions of the channel axis (see text for details). (C) The spatial distribution of the oxygen atoms of the Ser side chains along the z-axis. (D) The functions of the mean squared displacement in the z-direction for pore water molecules. (E) The dipole orientational correlation functions for pore water molecules.

Fig. 5 B shows the average channel pore radii calculated as functions of the channel axis for three systems: the composite system, the reduced system, and the reduced system with a hydronium in the lumen. The method for estimating the pore sizes is that by Smart et al. (1993, 1997), and the calculations were done with the HOLE program with the van der Waals radii derived from the same force field as used in the simulations. This method assumes that the intersection of the channel lumen has a roughly spherical shape; thus the pore size can be obtained by searching for the maximal radius of a hard spherical object that can fit into the lumen without causing bad contacts with the protein. In Fig. 5 B, the zero of the channel axis corresponds to the position of the protein's COM, and the channel ranges from roughly −15 Å to 15 Å with the N-terminus at the left end and C-terminus at the right end. The upper three curves are the pore radii for the three systems, whereas the lower three are the corresponding standard deviations of the upper curves. Along the channel axis, narrow and wide regions appear alternatively with a period of roughly 5 Å, attributed mainly to the periodicity of the helical structure. As one can see, this characteristic is very well-preserved in the reduced systems, giving a nearly identical curve to that of the composite system. A small, but noticeable change in the pore size arises when a hydronium is placed inside the channel. The standard deviations for the three systems are also comparable.

The spatial distribution of the side chains is affected by the backbone restraints. This is shown in Fig. 5 C, which is the distribution of the oxygen atoms of the Ser side chains as functions of the z-axis. The positions of the peaks and valleys generally match between the two systems, but most of the broad peaks in the composite system split into two or more sharp peaks in the reduced system; the valleys are also wider in the reduced system. The difference suggests that the accessible space of the side chain atoms seems significantly restricted in the reduced system.

The diffusion constants of the pore water in the z-direction for both systems were calculated using the Einstein equation

(4)

where D_z is the one-dimensional diffusion constant, z(t) is the z-position coordinate of the particle(s) under consideration at time t, and the angle brackets (〈 〉) denote the ensemble average. We divide the full channel range (roughly 30 Å) into two parts: the inner 20 Å region and the outer 5 Å regions near each mouth of the channel. Based on previous qualitative results for the diffusion constant (Randa et al., 1999), the inner part has a small and almost uniform value, whereas the outer parts have an increasing and relatively large value. Calculating the diffusion constants for these two parts, rather than as a function of the channel axis, can significantly reduce the statistical error in the results for a narrow channel like LS2. The mean square displacements are shown in Fig. 5 D. The diffusion constants were obtained by linear fits over the 20–60 ps part of the curves, giving the values 0.101 Ų/ps and 0.105 Ų/ps for the outer regions in the composite and reduced systems, respectively; and 0.037 Ų/ps and 0.047 Ų/ps for the inner region in the composite and reduced systems, respectively (the standard errors for these values are normally within 0.005 obtained by fitting into different ranges of the mean square displacement curves).

The pore water dipole correlation functions were calculated for both the outer and inner channel regions. As shown in Fig. 5 E, the pore water in the reduced system has a significantly shorter relaxation time than in the composite system. Furthermore, there is no difference in the relaxation time in the reduced system between the outer and inner pore waters, whereas in the composite system, the relaxation time for the outer water is longer than that for the inner pore water. The lack of a difference between the outer and inner pore water in the reduced system is probably mainly due to the missing membrane potential, present near the channel mouth.

The above comparisons show that the major differences are in the protein's flexibility and the pore water's orientational dynamics. These differences are probably due to the enhanced rigidity of the protein and the absence of the membrane interface potential. The possible artifacts caused by the Ewald method is considered less significant, because these artifacts should constrain the pore water dynamics, which is not observed in above results. Despite the differences, some important features are well-preserved in the reduced system, such as the channel's geometry and pore water diffusion constant. Based on these comparison results, we believe the reduced system can serve as a good channel model for the purposes of this study.

The effects of the pore size on the hydration state of the excess proton

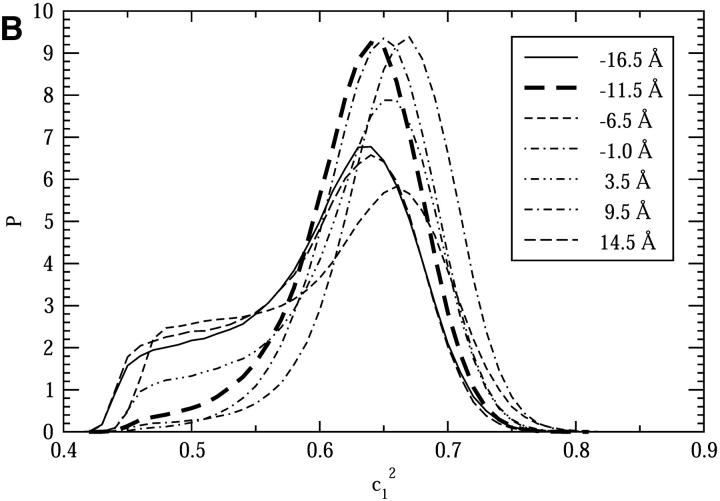
To examine the pore size effects of a nonuniform pore radius channel, we carried out a number of simulations with the CEC restrained to different points along the channel axis (the coordinate is same as that in Fig. 5 B): −14.5 Å, −8.5 Å, −3.5 Å, 1.5 Å, 6.5 Å, and 12.0 Å for the narrow channel regions (NCRs); and −16.5 Å, −11.5 Å, −6.5 Å, −1.0 Å, 3.5 Å, 9.5 Å, and 14.5 Å for the wide channel regions (WCRs). As shown in Fig. 5 B, the NCRs have pore radii of roughly 1.6 Å, whereas the WRCs have radii of roughly 2.1 Å. The restraint acts only on the z-coordinate of the CEC. Note that the CEC restraints should not significantly affect the properties we show here, since they depend on degrees of freedom other than the CEC spatial coordinates.

As mentioned in the Methods section, the solvation state of an excess proton can be identified by examining the first two largest EVB amplitudes, and 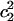. Fig. 6, A and B, show the possibility distributions of the largest amplitude () for NCRs and WCRs, respectively.

FIGURE 6.

The probability distributions of when the CEC is restrained to different points on the channel axis. A is for different narrow channel regions; B is for different wide channel regions. See text for details.

For NCRs, some degree of diversity in the proton solvation state is seen (Fig. 6 A). In some regions, such as at 1.5 Å and 12.0 Å, the distributions show peaks at 0.5 and shoulders at 0.65–0.7, which indicates that the excess proton is nearly equally well-hydrogen-bonded by two pore water molecules, thus exhibiting a Zundel-like hydration structure. In contrast, in the other NCRs, the distributions show peaks at 0.65 and shoulders at 0.5, which is quite similar to that for the bulk water (Day et al., 2002) and indicate at an Eigen-like solvation structure. Some interesting differences in details of these distributions can also be noticed. For example, compared to the similar ones, the shoulder of the distribution for −8.5 Å is less apparent, and its peak shifts somewhat to the left; whereas in contrast, the distribution for −3.5 Å shifts toward the right, giving a peak at roughly 0.67, and its shoulder is also roughly 2× smaller than the similar cases.

For WCRs, it is evident that the proton solvation state is all Eigen-like (Fig. 6 B). Differences in the details of the distributions also exist. The most pronounced are those for −11.5 Å, −1.0 Å, and 9.5 Å, which, compared to the others, show very high probability at 0.65 and diminishing shoulders at 0.5, indicating the Eigen-like species is favored in these regions.

Comparing the results for NCRs and WCRs, it is clear that the Zundel-like solvation species is more favorable in the NCRs than in the WCRs, which is in agreement with the previous study by Brewer et al. (2001). However, the considerable diversity in the probability distributions suggests that the solvation state in such a narrow channel is probably a property sensitive to the local structures; a subtle difference in the local structures can bring change to the proton's solvation state.

The influence can further be examined by calculating the relative free energy, given by the equation

(5)

where ΔF is the relative free energy for a 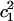value, k_B is the Boltzmann constant, T is the absolute temperature, and P(q) is the probability of 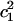from Fig. 6.

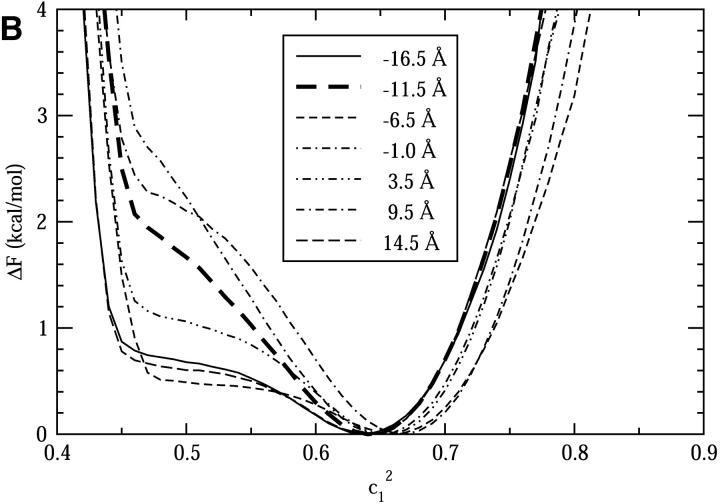
Fig. 7, A and B, show the free energy profiles for the NCRs and the WCRs, respectively. Again, for each curve in Fig. 7, values close to 0.46 represent the Zundel-like solvation states, whereas values at 0.65 or larger represent the Eigen-like solvation states. The free energy difference between the Zundel and Eigen solvation states can be obtained from the curves. In the NCRs at −1.5 Å and 12.0 Å on the channel axis, where the Zundel-like species dominates, the Zundel solvation state is more stable by roughly 0.3 kcal/mol; in contrast, in the WCRs at −11.5 Å, −1.0 Å, and 9.5 Å, the Eigen-like species is more stable by roughly 2.4 kcal/mol. We also notice that for some NCRs (from −3.5 Å to 12.0 Å) the free energy curves at = 0.8 are much shallower than those for the WCRs, indicating a more poorly solvated hydronium, which is understandable since the space available for solvation water is much smaller in those regions. This is probably one reason that the relative free energy of the Zundel-like species is decreased with respect to that of the Eigen-like species in these regions.

FIGURE 7.

The free energies of when the CEC is restrained to different points on the channel axis. A is for different narrow channel regions; B is for different wide channel regions. See text for details.

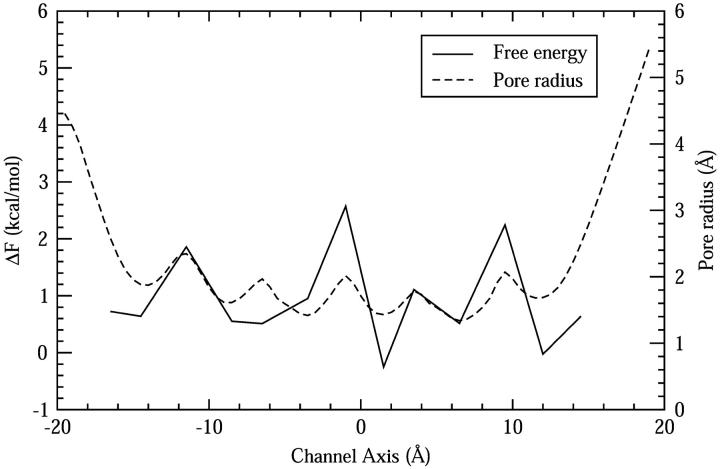
To see more clearly how the relative stability changes with the channel pore radius, in Fig. 8 we plot the free energy differences between the Zundel and Eigen cations obtained from Fig. 7 along with the pore radius curve obtained from Fig. 5 B (the one for the reduced system with an excess proton inside the channel). It can be seen that the stability of Zundel cation is generally increased in the NCRs. Three WCRs, one at the center of the channel and the other two near the channel mouths, are found to favor the Eigen cation with a free energy difference of 2–3 kcal/mol, considerably more than that in the bulk water (0.9 kcal/mol) (Day et al., 2002).

FIGURE 8.

The relative free energy difference between the Zundel and Eigen hydration structures when the CEC is restrained to different points on the channel axis. The pore radius profile for the reduced system with a hydronium in the channel is also shown.

Hydrophilicity effects on PT

An examination of the hydrophilicity effects on the PT was carried out via comparisons between the simulation results for the normal LS2 and its hydrophobic mutants. The hydrophobic mutants were prepared by the charge-off mutation as mentioned earlier. Since the pore size is primarily determined by the Lennard-Jones parameters, which are not changed in the charge-off mutation, the pore radii were essentially unchanged.

The free energy differences between the Zundel and Eigen cations were calculated for a number of different mutants. Together with those for the normal channel, the data are listed in Table 1. The hydrophilicity dramatically affects the free energy difference between the Zundel and Eigen cations. However, this change also exhibits considerable diversity, ranging in absolute value from 0.52 kcal/mol to 3.85 kcal/mol. Furthermore, the direction of the change is not uniform: the mutations can either promote or reduce the relative stabilization of the Zundel cation. Further analysis using two-dimensional free energy profiles (data not shown) demonstrates that changes in relative stability are associated with the change of the proton's first solvation shell structure. This result suggests that the Ser residues, which are the only residues with polar side chains in the channel, are intimately involved in the solvation of the excess proton.

TABLE 1.

Free energy of the Zundel cation (in kcal/mol)

ZCEC	ΔFnormal*	ΔFmutant†	ΔΔF‡
−11.5	2.1	0.3	−1.8
−3.5	1.35	−2.5	−3.85
−1.0	2.8	6	3.2
1.5	−0.35	0.17	0.52
3.5	1.2	3.5	2.3
6.5	0.53	2.5	1.97
12.0	−0.25	0.67	0.92

^*The free energy with respect to that of the Eigen cation. Values are calculated based on Eq. 5 and are for the normal LS2 channel.

^†The free energy with respect to that of the Eigen cation. Values are calculated based on Eq. 5 and are for the hydrophobic mutants LS2 channel.

^‡The free energy change as obtained by ΔF_mutant − ΔF_normal.

Discussion and further analysis on the channel effects

Combining all of the above results, it may be concluded that proton solvation is highly sensitive to its local microenvironment and can be affected by many factors, including the pore radius and the polar side chains. This in turn suggests that the movement of the proton inside channels may, to a large degree, rely on the dynamical fluctuation of the local microenvironment formed by the protein. This conclusion has also been suggested in a recent simulation study of PT in the M2 channel (Smondyrev and Voth, 2002b). For similar conclusions related to other proteins, see Sham et al. (1999) and references cited therein.

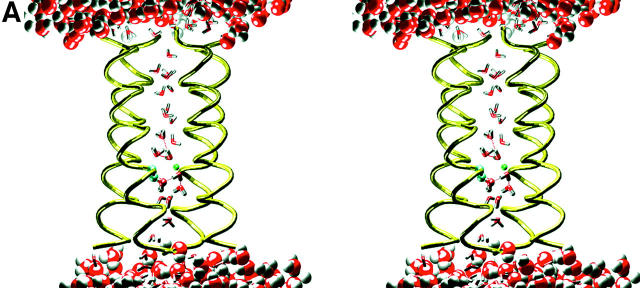
To further illustrate how the local microenvironment can affect proton solvation, the hydrogen bonds between the polar side chains and the water molecules in the first solvation shell of the excess proton were analyzed. It was found that the distances between the hydrogens and their acceptors were distributed at 1.65 Å, whereas the donor-hydrogen-acceptor angles were distributed from 10° to 25°. This indicates that strong hydrogen bonds are formed between the polar side chains and the water molecules and they may last for a long time in the simulations. A visual examination of the trajectories reveals how these hydrogen bonds can affect the proton solvation structure. Two representative snapshots from the simulations with the CEC restrained at −3.5 Å (Fig. 9 A) and 1.5 Å (Fig. 9 B) are shown. In Fig. 9 A, it can be seen that the proton donor water is hydrogen-bonded to a Ser side chain, whereas the acceptor is not. The hydrogen bond between the proton donor water and the Ser side chain is so strong that the donor water is well-solvated. The acceptor water is hydrogen-bonded with two water molecules. The water molecules cannot provide hydrogen bonds as strong as does the Ser side chain, thus the acceptor is not equally well-solvated. This imbalance makes the proton tend to adhere to the better solvated water molecule (the donor) to lower its potential energy, thus resulting in an Eigen proton solvation structure. By contrast, in Fig. 9 B, the proton donor and acceptor water molecules are nearly equally well-solvated; each forms one hydrogen bond with a water molecule and another hydrogen bond with a Ser side chain. In this case, as shown by the simulation trajectory, the excess proton can freely shuttle between the donor and acceptor water molecules and even oscillates around the middle point between the two oxygens, resulting in a stabilized Zundel cation.

FIGURE 9.

Simulation snapshots showing two representative hydration structures of the excess proton in the LS2 channel. The bulk water molecules are represented in space-fill mode, whereas pore waters are displayed in stick mode. The protein is represented by its backbone displayed in tube mode. The Ser side chains involved in the proton solvation structure are shown in ball-and-stick mode. The transferring hydrogen is shown as a small green ball. The dashed lines show the hydrogen bonds. (A) A stereo view of the snapshot taken from the simulation with the CEC restrained at −3.5 Å at 884 ps. (B) A stereo view of the snapshot taken from the simulation with the CEC restrained at 1.5 Å at 808 ps.

CONCLUSIONS

In this study, classical MD simulations with the MS-EVB2 model for aqueous PT were carried out with a reduced LS2 channel system, in which the explicit bilayer is omitted and the channel structure was stabilized by position restraints on the backbone atoms of the transmembrane protein. This treatment allows us to obtain longer simulation trajectories with relatively less computational expense. To validate the approach, comparisons between the reduced system and a larger, more realistic system with explicit lipid bilayers were carried out on the RMSF of the backbone atoms, the channel's pore size, the spatial distribution of the side chain of the Ser residues along the z-axis, the diffusion constants of the pore water, and the correlation function of the water dipole orientation. The analysis shows some deviations from the composite system, inasmuch as the RMSF of backbone atoms is reduced due to the position restraints used, the spatial distribution of the side chains were restricted, and the water's linear and rotational motions are also altered (although the change of the linear motion is small). The geometry of the channel, such as the pore size, is well-preserved in the reduced system. These results demonstrate the reduced system can represent the composite system qualitatively well, while incorporating many important channel features that were missing in the previous study with idealized channel models (Brewer et al., 2001).

The hydration of an excess proton inside the LS2 channel were studied by means of classical MD simulations using the MS-EVB2 model. In the previous study by Brewer and co-workers, an association of increased stability of the Zundel cation with decreased pore radius was observed for idealized uniform pore radius channels (Brewer et al., 2001). In the present study, the data shows that the Zundel cation is generally more stable in NCRs. This is in agreement with the previous study; however, on the other hand, the data also demonstrates the complexity of the solvation of an excess proton in a realistic channel environment. In particular, the Zundel cation is not always as stable as it is in an idealized channel and its stability varies in different regions of the channel even when the pore radii are similar. Interestingly, three wider channel regions with a strikingly high preference for the Eigen cation solvation structure were found. One of them is located at the center of the channel, and the other two are near the channel mouths. The strong preference for the Eigen cation implies that the Grotthuss type of PT can be considerably inhibited in these channel regions, so these regions may behave as effective barriers in the conducting pathway. This significant difference from the ideal hydrophobic channel suggests there exist “proton bumpers” in real channels like LS2. In addition to the geometrical aspects, the present study also investigated the possibility for some chemical factors to affect proton solvation. This was done by the simulations of the LS2 hydrophobic mutants, in which the side chains of the Ser residues that are near the CEC were modified to take zero partial charges. Our data shows that the change in relative stability of the proton solvation structure due to the mutation can be great, which in turn suggests that the Ser side chains can have a large contribution to the solvation of the excess proton. Further structural analysis demonstrates that strong hydrogen bonds can be formed between the proton-solvation water and the Ser side chains and that the Zundel cation may be favored if these types of hydrogen bonds exist on both proton donor and acceptor sides. These results suggest that the Ser side chains are possibly directly involved in the proton relay system inside the channel. Furthermore, considerable diversity of the effects of the pore size and channel hydrophilicity on the proton solvation state were noticed. This is probably due to some unidentified structural and/or chemical factors.

In all, our results suggest that the proton hydration state in the LS2 channel is highly sensitive to its local microenvironment. It is therefore expected that the dynamical fluctuations of the protein's structure, such as breaking or formation of hydrogen bonds with the pore water, can have significant impacts on the transport of the excess proton in the LS2 channel. A more detailed examination of the explicit proton transport in this and other channels will be the topic of future research.