Abstract
We studied the interaction of the cell-penetrating peptide penetratin with mixed dioleoylphosphatidylcholine/dioleoylphoshatidylglycerol (DOPC/DOPG) unilamellar vesicles as a function of the molar fraction of anionic lipid, XPG, by means of isothermal titration calorimetry. The work was aimed at getting a better understanding of factors that affect the peptide binding to lipid membranes and its permeation through the bilayer. The binding was well described by a surface partitioning equilibrium using an effective charge of the peptide of zP ≈ 5.1 ± 0.5. The peptide first binds to the outer surface of the vesicles, the effective binding capacity of which increases with XPG. At XPG ≈ 0.5 and a molar ratio of bound peptide-to-lipid of ∼1/20 the membranes become permeable and penetratin binds also to the inner monolayer after internalization. The results were rationalized in terms of an “electroporation-like” mechanism, according to which the asymmetrical distribution of the peptide between the outer and inner surfaces of the charged bilayer causes a transmembrane electrical field, which alters the lateral and the curvature stress acting within the membrane. At a threshold value these effects induce internalization of penetratin presumably via inversely curved transient structures.
INTRODUCTION
Homeoproteins are transcription factors discovered in Drosophila melanogaster, which are involved in multiple morphological processes (Gehring et al., 1994a). A 60-residue DNA-binding domain was identified in these proteins (Gehring et al., 1994b). This so-called homeodomain consists of three α-helices and one β-turn between helices 2 and 3. The homeodomain of Antennapedia was shown to translocate through the plasma membrane of cultured cells, to reach the nucleus and to induce changes in the cellular morphology (Joliot et al., 1991; Le Roux et al., 1993). The translocation properties of helix 3 are similar to those of the entire homeodomain (Derossi et al., 1994). It was proposed to use the so-called pAntp peptide, corresponding to residues 43–58 of the homeodomain, as a vehicle for the intracellular delivery of hydrophilic cargo molecules such as oligopeptides, oligonucleotides, and peptidic nucleic acids (PNA) (Derossi et al., 1998; Prochiantz, 1996, 1998; Theodore et al., 1995).
The pAntp peptide, known as penetratin, was the first member of a rapidly expanding family of peptide-based cellular transporters called cell penetration peptides originating from either natural or synthetic sources. They are also called Trojan peptides because they are able to enter the cells in an energy- and receptor-independent manner and to bring macromolecules such as small proteins, DNA (Prochiantz, 1996), and PNA oligomers into cells (Pooga et al., 1998). It should be noted that Trojan peptides spontaneously cross cell membranes with high efficiency and low lytic activity although they are water soluble.
The interaction between penetratin and the phospholipid matrix of the plasma membrane seems to be an essential step involved in the translocation mechanism. Due to its primary sequence related to its DNA-binding ability in the Antennapedia homeodomain-DNA complex, penetratin does not belong to the amphipathic helical peptide family, whose members are able to translocate membranes by pore formation. It was shown experimentally and by molecular modeling that penetratin is not sufficiently hydrophobic to insert deeply into the phospholipid model membranes (Drin et al., 2001). Instead, penetratin preferentially remains at the interface between the phospholipid bilayer and the aqueous environment. It was suggested that the peptide translocates through the lipid bilayer by transiently forming inverted micelles (Derossi et al., 1998; Prochiantz, 1996). Although this mechanism appears simplistic it possibly gives a first idea of the rationale of penetratin internalization.
Targeting hydrophilic compounds to the cytoplasm and nucleus of cells is, in principle, difficult because it requires the hydrophobic environment of the bilayer to be crossed. Classically this is obtained through a temporary disruption of the membranes. The peptide penetratin has recently been shown to translocate across neural cell membranes without damaging them, even when coupled to drugs. This surprising 16-amino-acid peptide interacts directly with the lipids of the membrane, although it is not yet known how the lipids reorganize around the peptide to let it pass across the membrane without any leakage. The transport mechanism is important to understand because of their potential use in drug delivery. For example, penetratin has been shown to be functional for experimental pancreatic cancer therapy (Hosotani et al., 2002). Structure/function studies have been carried out on penetratin to define the structural requirements and the mechanism of the cell penetration and to improve the carrier efficiency of the peptides (Christiaens et al., 2002; Derossi et al., 1994; Drin et al., 2001; Hällbrink et al., 2001; Lindgren et al., 2000; Magzoub et al., 2002, 2001; Persson et al., 2003, 2001; Salamon et al., 2003; Thoren et al., 2000). However, no systematic experiments have been realized to study the particular effect of the surface charge of the lipid membranes on the ability of the peptide to translocate through the bilayer.
Isothermal titration calorimetry (ITC) is highly sensitive in detecting the binding of peptides to lipid membranes (see Seelig (1997) for a review). So far this method has not been applied to study the interaction of penetratin with lipid membranes. We used the ITC technique to characterize factors that affect its internalization into lipid vesicles. Penetratin contains four lysines and three arginines nominally providing seven positive charges. Hence, electrostatics possibly plays a key role not only for the interaction of penetratin with membranes but also for the internalization process. Therefore, we studied penetratin binding to vesicles of anionic and zwitterionic lipids as a function of the surface charge density. The results indicate that both the cationic charge of the peptide and the anionic charge of the membrane are indeed essential for the ability of Trojan peptides to translocate across lipid bilayers. In addition, the ITC data provide insights into thermodynamic aspects of the association of cargo peptides with membranes owing to lipid-peptide interactions, hydration and changes of secondary structure of the peptide. We will separately deal with these issues in a forthcoming publication.
MATERIALS AND METHODS
Materials
Penetratin (Arg-Gln-Ile-Lys-Ile-Trp-Phe-Gln-Asn-Arg-Arg-Met-Lys-Trp-Lys-Lys; molecular weight 2246.7, amidated carboxy terminus), was solid-phase synthesized by Dr. Å. Engström at Uppsala University (Sweden). The zwitterionic, neutral phospholipid dioleoylphosphatidylcholine (DOPC), and the anionic phospholipid dioleoylphosphatidylglycerol (DOPG) were purchased from Avanti Polar Lipids (Alabaster, AL). The lipids and the peptide were used without further purification. The experiments were carried out at 25°C using 10 mM TRIS buffer containing 0.5 EDTA (pH 7.8) and NaCl (0.01–1 M).
Preparation of samples
Penetratin was weighed and directly dissolved in definite amounts of buffer to give stock solutions, which were further diluted to obtain the desired sample solutions of the nominal peptide concentration. Studies of the cationic peptide penetratin are complicated by extensive adsorption to charged and hydrophobic surfaces such as quartz and plastic materials during sample preparation and the experiments (Persson et al., 2003). This effect could hinder a proper quantification of peptide concentrations in the samples. Teflon stirring bars and polypropylene pipette tips are most dangerous candidates for extensive binding of penetratin from buffer solutions. To reduce the problems associated with peptide adhesion only glass vessels and Hamilton syringes were used for sample preparation. The sample solutions were degassed before the ITC experiments without use of Teflon stirring bars.
The final concentrations of penetratin in the samples were determined by ultraviolet absorption spectroscopy (Christiaens et al., 2002). No substantial loss of penetratin during sample preparation was established.
Vesicle suspensions were prepared as follows: stock solutions of the pure lipids DOPC and DOPG in chloroform:methanol (3:1 v/v) were mixed in definite amounts to give the desired composition of neutral and anionic lipids in terms of the molar fraction of DOPG, XPG. The organic solvent was removed with a rotary evaporator and subsequently under high vacuum for several hours at room temperature in the dark. The dried lipid films were resuspended in defined buffer volumes by vortexing to give the final lipid concentration, L = CDOPC + CDOPG. After five freeze-thaw cycles, the lipid suspension was either passed at least 15 times through two stacked Osmonics polycarbonate membranes of 100-nm pore size in a 1-ml mini-Liposo-Fast-Pneumatic extruder (Avestin, Canada), or it was sonicated in cold water for 20 min using a titanium tip ultrasonicator followed by 10-min ultracentrifugation (3000 g) to prepare large and small unilamellar vesicles, LUV and SUV, respectively.
Isothermal titration calorimetry
The measurements were performed using a VP isothermal titration calorimeter produced by MicroCal Inc. (Northampton, MA). Data handling (baseline subtraction, peak integration, sample dilution) procedures were performed with MicroCal Origin software.
In the lipid-to-peptide titration (L-to-P) experiment aliquots (δVsyr = 7 or 10 μl) of a lipid solution (Lsyr = 10–30 mM) were titrated into the sample cell of volume Vcell = 1.42 ml that initially contains the penetratin buffer solution (P0 = 7–20 μM). The L-to-P experiment represents the standard titration protocol to characterize the binding of charged peptides to lipid membranes (see e.g., Seelig (1997) and Wenk and Seelig (1998) for details). Each injection j produces a differential heat, qLj (in kJ/mol of injected lipid), mainly because free peptide binds to the injected lipid. The qLj values decrease in (absolute) magnitude with consecutive injections because the amount of (free) peptide that binds to the vesicles progressively decreases with increasing lipid concentration.
In the peptide-to-lipid titration (P-to-L) experiment aliquots of a peptide solution (δVsyr = 7 or 10 μl; Psyr = 0.2–0.5 mM) were titrated into the sample cell that initially contains only lipid vesicles (L0 = 0.2–0.5 mM). The integral over each heat peak provides the differential heat of reaction caused by injection j, qPj (in kJ/mol of injected peptide). The qP values decrease in absolute magnitude if the membranes become saturated with bound peptide because further addition of peptide provides no reaction.
RESULTS
Lipid-to-peptide titration experiments
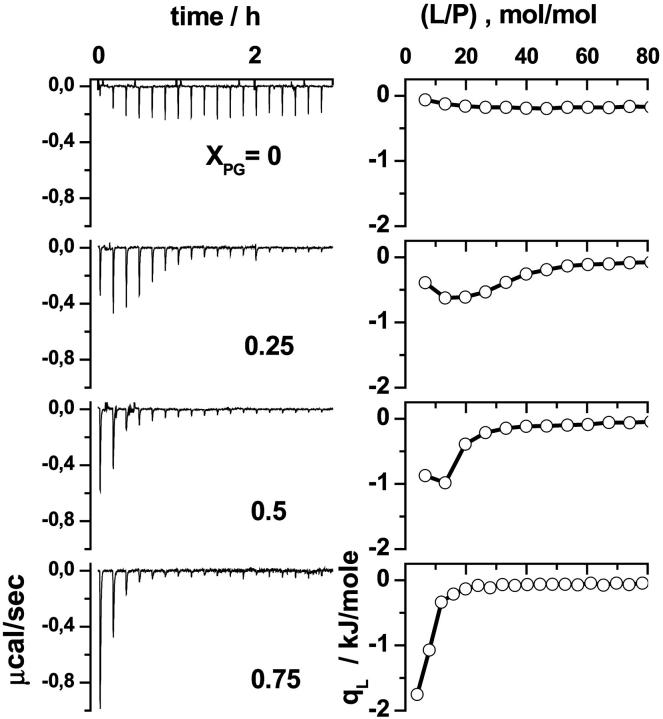
The left part of Fig. 1 shows the ITC traces of a series of L-to-P titration experiments. Integration of the exothermic heat pulses recorded after each injection yields the differential reaction heat, qL, in units of kJ/mol of injectant shown in the right part of Fig. 1. The released heat results from the binding reaction of a certain amount of penetratin with the injected lipid. After each injection, the concentration of free, available peptide decreases owing to progressive membrane binding. Consequently, the absolute value of the differential heat continuously decreases with increasing injection number, because less penetratin binds to the vesicles in consecutive injections. After a certain number of injections almost all peptide is bound and further addition of lipid entails no further reaction. The remaining small differential heat can be mainly attributed to dilution effects.
FIGURE 1.
Lipid-to-peptide experiments for mixed DOPC/DOPG SUV of different composition. The molar fraction of DOPG, XPG, is given in the figure. Calorimeter tracings are shown in the left panel (δVsyr = 7 μl, SUV in TRIS + 100 mM NaCl; Lsyr = 15 mM, P0 = 0.0125 mM). The right panel displays the differential heats, qL, as a function of the molar ratio lipid-to-peptide in the sample cell.
Penetratin, formally carrying seven positive charges, is expected to interact with negatively charged membranes via Coulombic forces. We therefore varied the surface charge of membranes by varying the fraction between the zwitterionic DOPC and the anionic DOPG. The absolute value of the differential heat, qL, of the first injections decreases whereas the number of injections that are necessary to bind the dissolved peptide increases with decreasing molar fraction of anionic DOPG, XPG (Fig. 1). Weak but significant binding was also observed at XPG = 0. The respective reaction heat could be explained to only ∼50% by dilution effects.
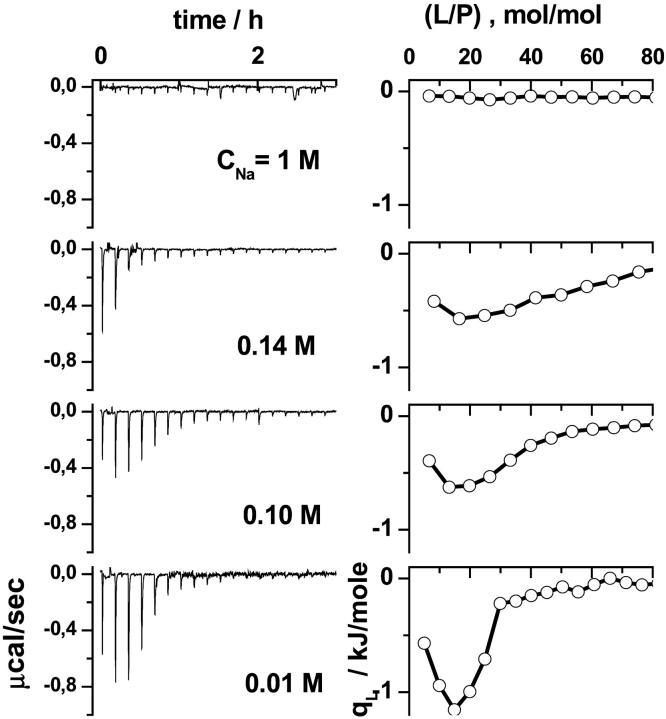
Further indications of a charge dependent binding mode were obtained in experiments with different amounts of NaCl in the buffer solution (Fig. 2). The salt ions screen the surface charge of the membrane and of the peptide. Consequently, an increased ionic strength reduces the electrostatic interactions between the compounds, and thus weakens the binding of the peptide to the membranes.
FIGURE 2.
Lipid-to-peptide experiments for mixed DOPC/DOPG SUV (XPG = 0.25) at different electrolyte concentration (NaCl) of the buffer. Calorimeter tracings are shown in the left panel (δVsyr = 7 μl, SUV in TRIS + NaCl; Lsyr = 15 mM, P0 = 0.01 mM, and 0.0125 mM). The right panel displays the differential heats, qL, as a function of the molar ratio lipid-to-peptide in the sample cell.
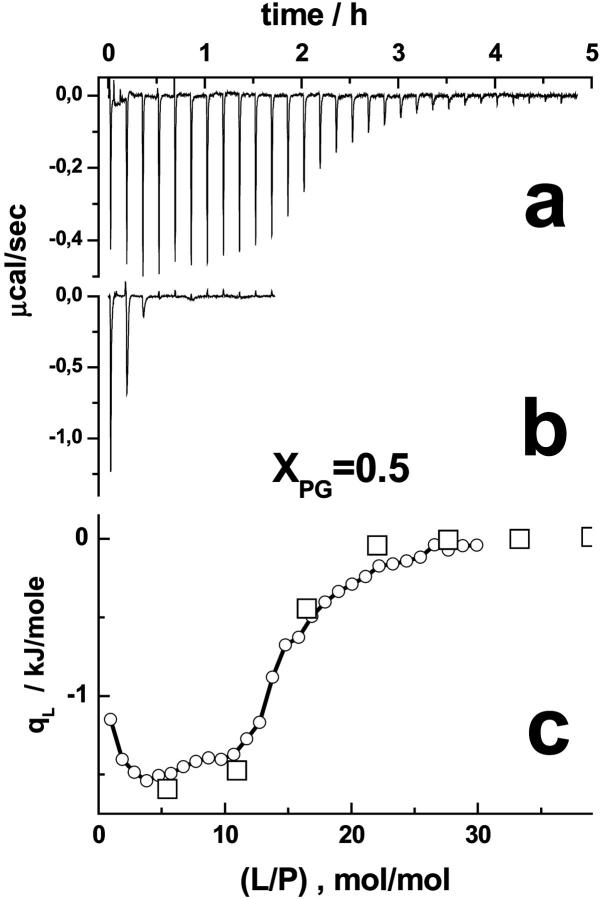
Fig. 3 compares two L-to-P experiments that run at different time- and concentration scales. The results of both experiments agree well if one plots qL versus the molar ratio lipid-to-peptide, (L/P). Let us discuss this result in terms of a binding equilibrium (see appendix, Eqs. A1–A4). The binding behavior is determined by the amount of bound lipid, (Pb/L). Fig. 3 implies (Pb/L) ≈ (P/L), and thus Kapp ≫ (γL)−1, because the observed heats are virtually independent of the chosen concentrations P and L. With a relevant lipid concentration of L < 0.4 mM, corresponding to the inflection point of the heat course at which qL reaches ∼50% of its initial value, the data are compatible with K50% ≡ Kapp ≫ 5 mM−1 using an accessible factor of γ = 0.5 (vide infra).
FIGURE 3.
Lipid-to-peptide titration experiment of lipid SUV (XPG = 0.5) to penetratin. The calorimeter traces in the a and b were obtained with Lsyr = 3 mM/P0 = 0.025 mM, and Lsyr = 15 mM/P0 = 0.0125 mM, respectively. Because of the smaller lipid concentration in the syringe, 6–7 times more injections, and a longer time span are necessary in the former experiment to adjust a certain lipid-to-peptide molar ratio, (L/P), in the calorimeter cell. Panel c shows the differential heat of reaction as a function of (L/P). The circles and squares refer to the traces shown in a and b.
Titration of smaller increments of (L/P) reveals an initial plateau of qP followed by a sigmoidal drop (Fig. 3). This behavior suggests that the amount of free peptide in the cell exceeds the binding capacity of available lipid in the range of small (L/P). The binding equilibrium is obviously strongly shifted toward the bound state and thus it reveals saturation characteristics.
Both experiments also differ considerably in the number of injections and thus also in the time range to achieve a certain effect, e.g., the change of qL by 50%. This result suggests that the samples behave identically in the considered time window ranging from several tens of minutes to several hours. Consequently, kinetic effects such as the binding of penetratin to the membrane surfaces and/or its permeation through the bilayers proceed with characteristic times that are either considerably smaller or considerably longer than the time window of the experiments.
Peptide-to-lipid titration experiments
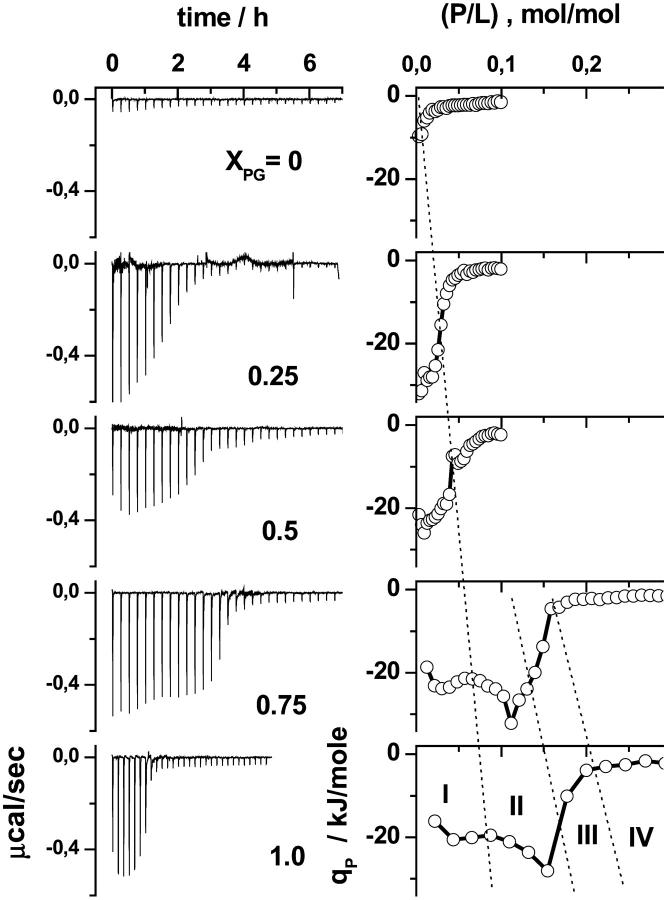
Fig. 4 shows the calorimetric traces and the differential heats, qP, for titrating DOPC/DOPG vesicles with penetratin. The molar fraction of DOPG in the vesicles was varied between XPG = 0 and 1. The heat effect observed upon titration with penetratin to neutral DOPC (XPG = 0) is much weaker than for anionic membranes (XPG > 0). This result confirms the charge dependent interaction of penetratin with the membranes stated above. The decreasing absolute value of qP with increasing peptide content for XPG ≤ 0.5 reflects the fact that with each titration less of the injected peptide binds to the vesicles presumably because the positive charges of bound penetratin progressively hamper further binding of the peptide. The membrane surface obviously saturates with penetratin.
FIGURE 4.
Peptide-to-lipid titration experiments of penetratin into mixed DOPC/DOPG LUV of different molar fraction of DOPG, XPG (see figure). Aliquots (δVsyr) of penetratin solution (Psyr) were titrated into a lipid dispersion. The left panel shows the calorimeter tracings. The right panel shows the differential heat of reaction as a function of the molar ratio peptide-to-lipid, (P/L), in the sample cell. The experimental conditions are Psyr = 0.2 mM, L0 = 0.4 mM, δVsyr = 10 μl (XPG = 0, 0.25, 0.5); Psyr = 0.4 mM, L0 = 0.2 mM, δVsyr = 7 μl (XPG = 0.75), and Psyr = 0.4 mM, L0 = 0.17 mM, δVsyr = 10 μl (XPG = 1.0). The ranges I–IV indicated by dotted lines are defined in Fig. 9. See text.
Let us empirically define an apparent binding capacity as the lipid-to-peptide molar ratio, (P/L)50% at which the absolute value of qP reaches 50% of its initial value. With increasing XPG, and thus with the negative surface charge density of the membranes, the apparent binding capacity, (P/L)50%, markedly increases (Fig. 4).
Repeated P-to-L experiments, which were performed at different time- and concentration scales indicate that qP depends only on the molar ratio peptide-to-lipid, (P/L) = (L/P)−1, in the sample cell and not on the binding kinetics (not shown). This result agrees with that of the analogous L-to-P experiments (see above).
The qP versus (P/L) curves exhibit a more structured course for XPG ≥ 0.5 than for XPG < 0.5. The differential reaction heat first increases, then it turns to decrease before its absolute value drops to values near zero. The shape of the heat peaks distinctly changes in the latter range (Figs. 5 and 6). The peaks become broader at the basis or may even split into two peaks. These subtle effects were reliably reproduced in repeated experiments.
FIGURE 5.
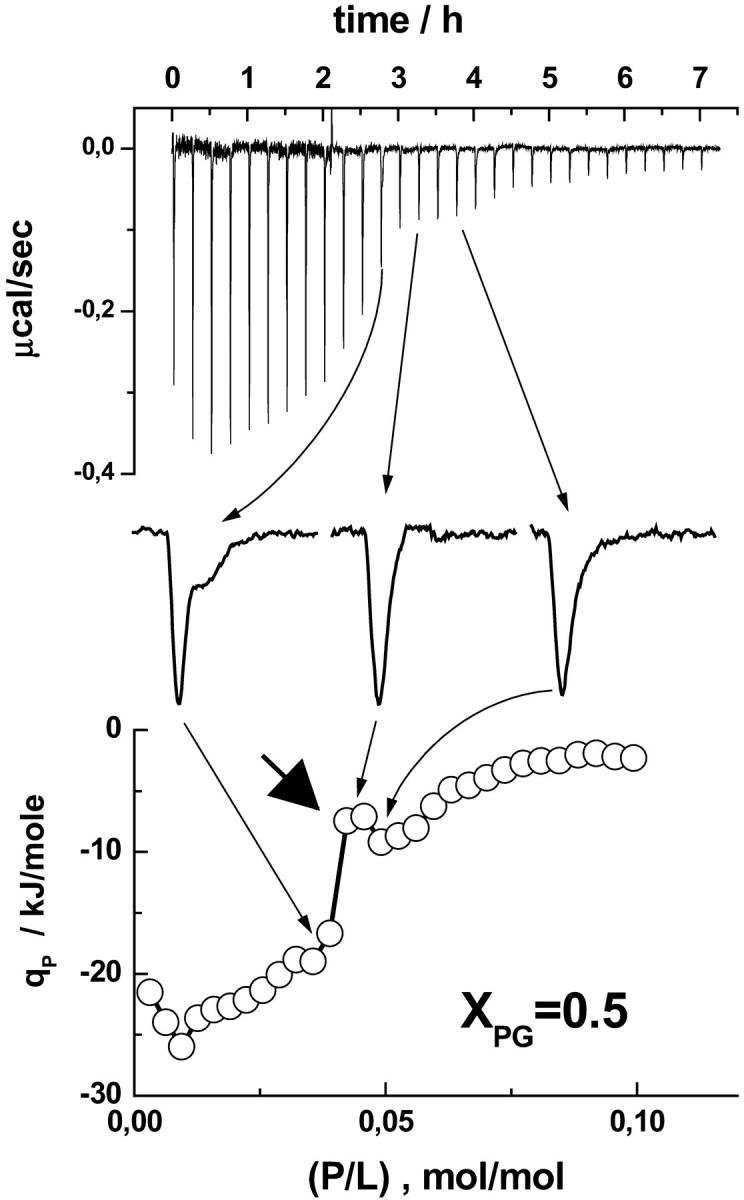
Enlarged view of selected heat peaks of a P-to-L titration experiment of penetratin into an equimolar DOPC/DOPG mixture (XPG = 0.5). The calorimeter tracing is shown in the top panel. The bottom panel shows the respective differential heat of reaction. The peak becomes broader with indications of a second heat event near (P/L) ≈ 0.05 (left peak, see arrows for assignment). The thick arrow points to the local minimum of absolute qp values that has been attributed to the onset of internalization of penetratin.
FIGURE 6.
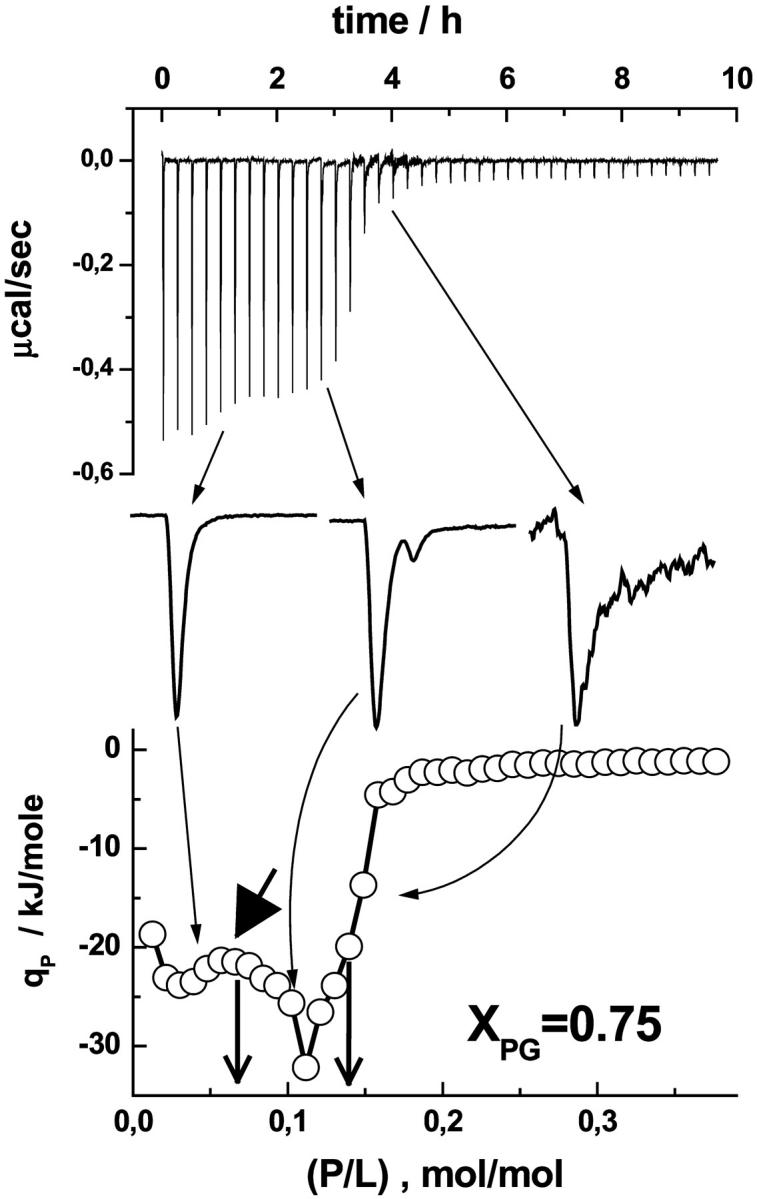
Enlarged view of selected heat peaks of a P-to-L titration experiment of penetratin into a DOPC/DOPG mixture (XPG = 0.75). The thick arrow points to the local minimum of absolute qp values that has been attributed to the onset of internalization of penetratin. The vertical arrows indicate the critical concentrations (P/L)50%γ=0.5 (left) and (P/L)50%γ=1 (right). See text and also Fig. 5 legend for details.
Charge-dependent binding of penetratin to membranes
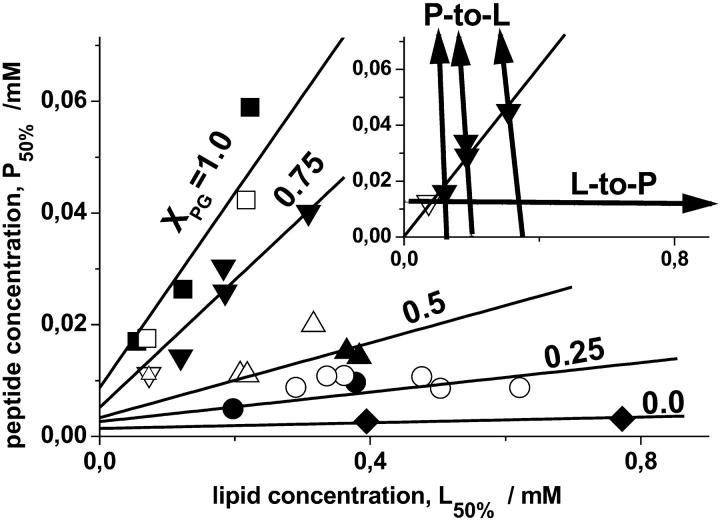
The arrows in the insert in Fig. 7 show the concentration courses of typical L-to-P and P-to-L titration experiments covering different concentration ranges of the compounds. The appropriate critical concentrations, P50% and L50%, at which the absolute values of the ITC heats drop to ∼50% compared with their initial value in the first injections of the respective titration experiment (vide supra) are indicated by symbols. Respective values of the critical concentrations, P50% and L50%, were analogously determined for selected molar fractions of the anionic DOPG in the vesicles.
FIGURE 7.
Critical concentrations of the peptide and of the lipid for vesicles containing different molar fractions of DOPG, XPG = 0.0 (diamonds), 0.25 (circles), 0.50 (up triangles), 0.75 (down triangles), and 1.0 (squares). The solid and open symbols refer to P-to-L and L-to-P ITC experiments, respectively. The lines were calculated according to Eq. A8 with zP = 5.1, K50% = 20 mM−1, fNa = 0.15, ξ = 0.08 (XPG > 0.25), K50% = 10 mM−1, fNa = 0.13, ξ = 0.07 (XPG = 0.25), and γ = 0.5 for 0 < XPG ≤ 0.5, and γ = 1.0 for XPG > 0.5. The line through the data for XPG = 0.0 was drawn as a guide for the eyes. The arrows in the insert (with the same designations of the axes as in the main figure) show the concentration courses of the titration experiments for XPG = 0.75. The critical peptide concentrations at which the absolute value of the differential heat decreases to 50% of its initial value are indicated by the symbols.
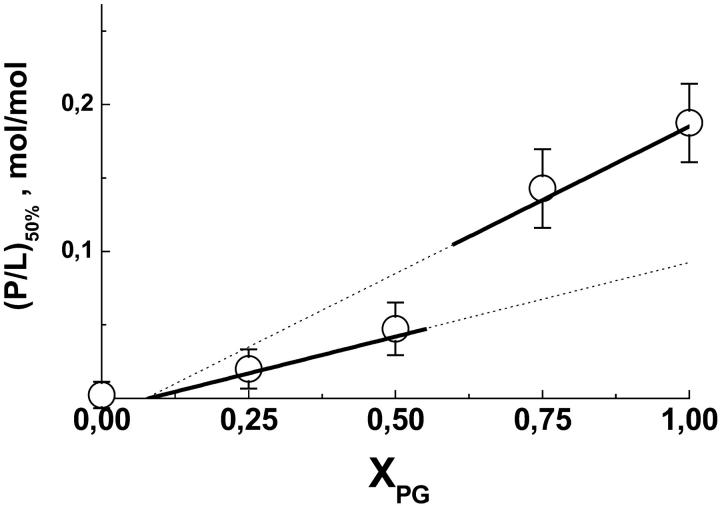
In a first step of analysis we correlate the respective critical concentrations P50% with the respective L50% data (Fig. 7). The data pairs corresponding to each XPG were well fitted by a linear regression line through the origin of the coordinates (see e.g., insert in Fig. 7), the slope of which provides a reasonable estimation of the mean critical molar ratios of peptide-to-lipid, (P/L)50%. Note that this analysis presumes K50% ≫ (γL50%)−1 in accordance with our first estimation of K50% ≫ 5 mM−1 given above (vide supra and Eq. A2). In a second step the obtained (P/L)50% values were plotted as a function of XPG (Fig. 8).
FIGURE 8.
Critical peptide-to-lipid molar ratio as a function of the molar fraction of DOPG in the vesicles (○). The lines are calculated according to Eq. A7 (thick lines) with zP = 5.3 ± 0.5 (γ = 0.5, 0 < XPG ≤ 0.5) and zP = 4.9 ± 0.4 (γ = 1, XPG > 0.5).
The critical molar ratio (P/L)50% and the critical peptide concentration P50% are functions of the effective peptide charge, zP, of the accessibility factor, γ, of the critical apparent binding constant, K50%, and of the respective fraction of not compensated lipid charges, ξ, according to the surface partition model given in the appendix (Eqs. A7 and A8). Relevant values of these parameters were estimated using an iterative algorithm as described in the appendix (see also Figs. 7 and 8 legends). The respective fits are shown by lines in Figs. 7 and 8.
The critical concentrations P50% and L50% are compatible with an apparent binding constant of K50% ≈ 20 mM−1 (XPG > 0.25) and 10 mM−1 (XPG = 0.25) that exceed the respective intrinsic binding constant, Kb ≈ 80 M−1 (Persson et al., 2003) by more than two orders of magnitude. The critical binding constant, K50%, is related to a residual anionic surface charge density of the membrane, σ50%, (see appendix). The obtained values of σ50% refer to a molar fraction of anionic lipid with not compensated charges of ξ = 0.07–0.08. They refer to a reduction of the original anionic surface charge density by ∼70% at XPG = 0.25 and by more than 90% at XPG = 1. Hence, the surface charge of the pure lipid membranes becomes largely compensated by bound peptide at critical conditions.
The data shown in Fig. 8 provide an effective peptide charge of zP ≈ 5.1 ± 0.5 assuming that either 100% of the lipid (γ = 1) or only 50% (γ = 0.5) is accessible for association with penetratin at XPG > 0.5 and XPG ≤ 0.5, respectively. In other words, the observed binding capacities are compatible with peptide binding only to the outer surface of the vesicles at XPG ≤ 0.5 and with the binding of penetratin with the inner and outer bilayer surface at XPG > 0.5. At small DOPG concentration penetratin obviously binds only to the outer surface of the bilayer vesicles. The interaction with the inner surface at higher DOPG content of the membranes presumes the transbilayer distribution of penetratin. Consequently, penetratin must either translocate through the vesicle membranes and/or it must disrupt the integrity of the vesicles to access all lipids present in the samples.
Note that the effective peptide charge of zP ≈ 5.1 ± 0.5 is distinctly smaller than its formal charge (z = +7). Similar differences were reported in studies on a number of other charged peptides (Ladokhin and White, 2001b) and also for penetratin (Persson et al., 2003). The discrepancy has been attributed to discrete charge effects (Schwarz and Beschiaschvili, 1989; Stankowski, 1991), to charge separation in the peptide (Carnie and McLaughlin, 1983; Seelig and Macdonald, 1989), and to associated counterions (Schwarz and Beschiaschvili, 1989).
The effective charge of penetratin potentially depends on the secondary structure of the peptide, and thus on the DOPG content of the membrane that possibly affects the equilibrium between α-helical and β-sheet structures of penetratin (Magzoub et al., 2002). Therefore, the obtained effective charge of zP ≈ 5.1 should be interpreted as a mean value averaged over the range of considered surface charge densities and related peptide conformations. On the other hand, the linear relation between the surface charge density of the membrane and the critical peptide-to-lipid molar ratio gives no indication of a significant change of zP with XPG within the frame of the considered model (see Fig. 8).
According to the observed effect, there is no doubt that electrostatic effects dominate the binding of penetratin to charged vesicles. The peptide has a high affinity toward negatively charged membranes because the peptide accumulates in the aqueous lipid-water interface by electrostatic attraction, and not because it binds specifically to anionic lipids. The apparent binding constant for the pure lipid membranes with the maximum negative charge density exceeds K50% by several orders of magnitude. Hence, at peptide concentrations P < P50% (i.e., in the area below the lines in Fig. 7) penetratin nearly completely binds to the membranes whereas at P > P50% the binding reaches saturation, i.e., newly injected peptide remains virtually dissolved in the aqueous phase.
DISCUSSION
The internalization threshold of penetratin and vesicle aggregation
The negative surface charge of the DOPC/DOPG vesicles increases with increasing molar ratio of total peptide to lipid owing to the increasing fraction of negative lipid charges that are compensated by bound cationic penetratin until the remaining anionic surface charge reaches some critical value. Beyond this point further binding of the peptide is hampered because electrostatic attraction between dissolved peptide and the membrane and thus the apparent binding constant considerably decrease. The steep drop of the exothermic reaction heat to values near zero in the P-to-L experiments with vesicles of high DOPG content (XPG ≥ 0.75) reflects this effect (Fig. 4). The two vertical arrows in Fig. 6 indicate critical conditions at (P/L)50%γ=0.5 and (P/L)50%γ=1 = 2(P/L)50%γ=0.5 for γ = 0.5 and 1, respectively (see Eq. A8, zP = 5.1). As discussed above the experimental data are clearly compatible with (P/L)50%γ=1. This result implies that the peptide binds to the outer and inner surface of the vesicles.
Obviously, the peptide is able to penetrate the vesicle membranes in the course of the titration experiment at (P/L) < (P/L)50%γ=1. Interestingly, the absolute qP values exhibit a local minimum near (P/L)50%γ=0.5, the critical molar ratio corresponding to impermeable vesicles (γ = 0.5, thick arrow in Fig. 6, see also Eq. A7). We suggest that this enthalpic event reflects the onset of internalization of the peptide into the vesicles.
A similar behavior of the absolute values of the ITC reaction heat, namely a minimum followed by a maximum at concentrations near to the saturation threshold, was observed upon titration of detergents such as bile salts and alkyl maltoside to lipid vesicles (Heerklotz, 2001; Hildebrand et al., 2002). The authors argued that an increase in the effective concentration of the additive in the outer monolayer leads first to a decrease in the heat effect. Further addition of the detergent renders the membrane more permeable. As a consequence the additive can flip-flop to the inner monolayer and the heat effect increases again. Also previous lipid-to-peptide (Magainin 2 and PGLa) titration experiments, showing a complicated pattern of reaction heats, were interpreted in terms of a pore formation, i.e., of flip-flop of the lipids combined with a rapid peptide translocation across the membrane, owing to membrane perturbation at high peptide concentrations (Wenk and Seelig, 1998; Wieprecht et al., 2000).
According to these results we assume that penetratin binds only to the outer surface of the vesicles until the (P/L) ratio reaches a critical value, (P/L)threshold ≈ (P/L)50%γ=0.5 (range I in Fig. 4). At peptide concentrations above this threshold value penetratin becomes able to translocate across the lipid membrane and it binds also to the inner vesicle surface (range II). This interpretation is fairly compatible with the shape of the titration curves. At (P/L) > (P/L)threshold the peaks become broader at the basis or even split into two peaks, where a second weaker peak follows the first one (Fig. 6). The main peak can be tentatively assigned to an outside incorporation of the peptide and the second event to the translocation through the bilayer succeeded by peptide binding to the inner monolayer. In terms of kinetics, the detection of the internalization event in the ITC experiment reflects the situation that this process, at least partly, gets fast enough to occur within some tens of minutes.
Time-dependent light scattering experiments showed that the addition of penetratin to DOPG vesicle suspensions with lipid-to-peptide molar ratios above (P/L) ≈ 0.07 induces vesicle aggregation within a few minutes (Persson et al., 2001). The concentration at this aggregation threshold roughly corresponds to critical conditions for the outer surface of pure DOPG vesicles according to our estimation of (P/L)50%γ=0.5 ≈ 0.09 ± 0.03. Note that the predominate fraction of anionic lipid charges becomes neutralized by bound peptide at critical conditions (vide supra). One could suggest that fluctuations of the local concentration of bound peptide at critical conditions leads to alternating positively and negatively charged areas at the outer vesicle surfaces, which will force the vesicles to aggregate owing to electrostatic attraction. The aggregation process is followed by spontaneous, slow disaggregation of the vesicles (Persson et al., 2001). This process could be the result of depletion of the peptide from the outer vesicle surfaces as a consequence of its translocation through the membranes. Dissociation of the aggregated vesicles, however, no longer occurs at peptide concentrations, exceeding the aggregation threshold concentration by a factor of two, i.e., at (P/L) > 0.14 (Persson et al., 2001). This result can be rationalized if the peptide equally distributes between both halves of the bilayer and mostly compensates the anionic surface charge at (P/L)50%γ=1 ≈ 2(P/L)50%γ=0.5. Then, the aggregated state of the vesicles refers to the stationary state of thermodynamic equilibrium in agreement with the observations.
To answer the question if vesicle aggregation also takes place in our experiments, we checked the turbidity of the cell content after finishing the P-to-L titrations by visual inspection. The vesicle suspensions with a fraction of anionic lipid of XPG ≥ 0.5 are highly turbid whereas those with XPG < 0.5 remain transparent. The turbidity originates from large lipid aggregates that precipitate in the course of minutes. We conclude that penetratin must translocate the membranes at XPG ≥ 0.5 because the titrations end in stable, aggregated vesicles with a peptide content of (P/L) > (P/L)50%γ=1. A similar check of the cell content of the L-to-P experiments reveals transparent solutions at all conditions. This result shows that aggregation is reversible, because these titrations start at (P/L) > (P/L)50%γ=1 and end at low peptide concentrations, (P/L) < (P/L)50%γ=0.5. Disruption of the vesicle membranes accompanied by the formation large multilamellar aggregates seems not to take place. This interpretation agrees with the results of previous light scattering experiments (Persson et al., 2001).
Internalization of penetratin is related to electrostatics
One hypothesis proposes that the internalization mechanism for membrane permeabilization of antibiotic peptides such as magainin and PGLa involves the formation of short-lived toroidal pores composed of peptides and lipids. However, direct evidence for the existence of a pore with a well-defined structure in fluid bilayers seems not to exist to date. Peptide-induced permeabilization is coupled to peptide translocation through the membrane and lipid flip-flop. The term “pore” thus solely indicates the existence of an active peptide-lipid structural state leading to enhanced membrane permeability.
Alternatively, a “detergent-like” permeabilization mechanism is assumed for selected amphipatic peptides such as melittin (Ladokhin and White, 2001a) and surfactin (Heerklotz and Seelig, 2001). Although the details are only vaguely understood one suggests that permeabilization involves steps such as reorientation and self-aggregation of the peptide paralleled by the formation of transient, inversely curved structures. Also interpretation in terms of an asymmetry-controlled permeability threshold of lipid membranes presumably reflects an important aspect of the permeation mechanism (Heerklotz, 2001).
Both “pore formation” and “detergent-like” actions presume a substantial perturbation of the membrane that is induced by deep insertion of the additives into the hydrophobic region of the bilayer. These peptides are amphipathic, and thus this step is mainly driven by the hydrophobic effect accompanied by changes of their secondary structure. Hence, the amphipathicity of the peptide has been implied as an important factor in peptide-mediated membrane disturbance. Measures of the amphipathicity such as the hydrophobic moment or the change of the Gibbs free energy upon transfer from the aqueous phase into the membrane interface often correlate with the efficiency of a given peptide to permeabilize lipid bilayers (Hällbrink et al., 2001).
In contrast, penetratin possesses a small hydrophobic moment (Hällbrink et al., 2001). Also the intrinsic constant for penetratin binding to DOPC/DOPG membranes, Kb ≈ 80 M−1, is typical for weakly hydrophobic peptides (Persson et al., 2003). It refers to a relatively small free energy of binding of ΔG = −RTln(Kb × W) ≈ −20.8 kJ/mol (W = 55.5 M is the concentration of water in dilute solutions). Note that the single residue transfer energy of penetratin of ΔGw→if = +7.5 kJ/mol is even unfavorable for membrane insertion. The latter value was calculated using single residue values without considering the contribution of the peptide bonds (White and Wimley, 1998). Hence, penetratin is weakly hydrophobic or even hydrophilic according to these parameters. There are no indications that penetratin significantly affects the hydrophobic region of the bilayer upon membrane binding (Berlose et al., 1996; Binder and Lindblom, in preparation; Drin et al., 2001; Salamon et al., 2003). Also theoretical simulations indicate that helical penetratin does not penetrate deeply into the bilayer but remains at the water-lipid interface in a parallel or more oblique orientation relatively to the membrane plane (Drin et al., 2001; Lindgren et al., 2000). Hence, amphipathicity does not seem to be related as the main parameter to the cell uptake potency of penetratin.
On the other hand, penetratin and other cargo peptides such as Tat (48–60, z = +8) and HIV Rev (34–50, z = +10) are highly charged owing to a relatively large number of lysine and/or arginine residues. Not only these virus-derived cationic peptides but also oligoarginines and oligolysines of 4–16 residues were able to transfect cells with high efficiency (Futaki et al., 2001). We suggest that electrostatic interactions are crucial not only for the accumulation of the peptide near the polar interface, but also to destabilize the bilayer as a prerequisite for internalization.
The anionic lipid content of the membrane and the peptide concentration trigger internalization
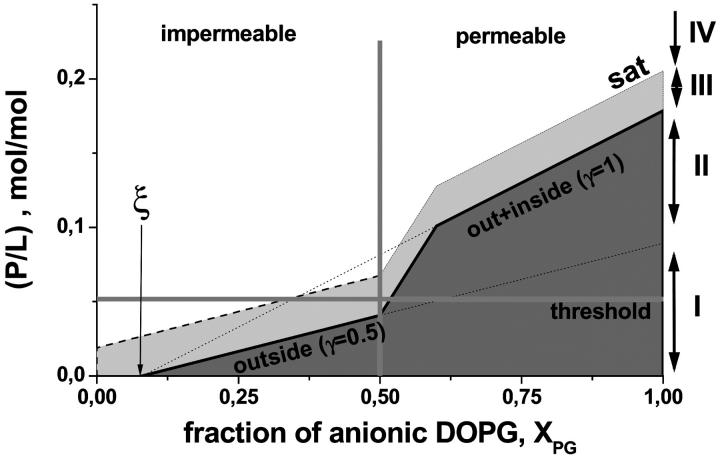
Fig. 9 schematically illustrates how the peptide binding affects the permeability of the membranes as a function of the fraction of anionic lipid in the bilayer. At XPG < 0.5 the outer surface of the vesicles becomes saturated with penetratin at (P/L) ratios below the internalization threshold (range IV, see also Fig. 9 legend for explanations). This situation corresponds to (P/L)threshold > (P/L)50%γ=0.5. In other words, zwitterionic and weakly charged membranes are obviously unable to bind a sufficiently high amount of penetratin that would be necessary to induce permeabilization. In contrast, the peptide content in the outer monolayers of highly charged membranes (XPG > 0.5) reaches the threshold concentration before these saturate with bound peptide (range I). This situation corresponds to (P/L)threshold < (P/L)50%γ=0.5. Consequently, after internalization penetratin binds also to the inner vesicle surfaces up to their complete saturation.
FIGURE 9.
Peptide binding to DOPC/DOPG vesicles and its permeabilization through the membranes. The horizontal and vertical lines define the internalization threshold, (P/L)threshold and XPGthreshold , respectively. The diagonal “50%” line is given by (P/L)50% (see Eq. A7). The parameter ξ defines the respective fraction of not compensated lipid charges. The dark gray region refers to the strong binding regime where virtually all peptide binds to the negatively charged surface of the vesicles. At critical conditions the binding affinity of the membranes markedly drops, and thus added penetratin distributes between the aqueous and lipid phase. The respective binding constant further decreases and the membranes effectively saturate at an arbitrarily chosen saturation limit, (P/L)sat = (P/L)50% + 0.03 (dashed line). At (P/L) > (P/L)sat the membrane surface is saturated and peptide that exceeds (P/L)sat remains virtually free. The “step” in the course of the “50%” and “sat” lines refers to the onset of internalization where the system turns from exclusive peptide binding to the outer monolayer (γ = 0.5) to peptide binding to both monolayers (γ = 1) after internalization. The regions I–IV were shown in Fig. 4 for XPG = 0.75. See text.
According to this scenario, the peptide concentration, which ensures critical conditions of the outer monolayer, is expected to cross the threshold line in Fig. 9 roughly at an equimolar content of anionic lipid (i.e., (P/L)threshold ≈ (P/L)50%γ=0.5). The analysis based on the inflection points, (P/L)50% and (L/P)50%, according to Eq. A7 is compatible with γ ≈ 0.5 at XPG = 0.5 (see Fig. 8). The sigmoidal decrease of the absolute qP values of the P-to-L experiments however shows a complicated pattern, and thus the used (P/L)50% value is relatively uncertain (see Fig. 5). Particularly, a local minimum is followed by a maximum (see thick arrow in Fig. 5). The calorimetric traces broaden in the same P/L region. We interpreted both effects as characteristic signatures of peptide internalization. Internalization of penetratin in this system was further confirmed by the detection of aggregated vesicles after finishing the P-to-L experiment (i.e., at (P/L) > (P/L)sat, vide supra). We suggest that the bilayer becomes permeable at (P/L) values slightly above (P/L)50%γ=0.5. Internalization remains however incomplete because peptide binding virtually stops in the range of progressive internalization (range II). We assume that the bilayer becomes impermeable before penetratin completely equilibrates between the inner and outer vesicle surfaces. Note that the broad decay range of the qP data shown in Fig. 5 is also compatible with slightly increased values of the accessibility factor γ ≤ 0.8 in agreement with the hypothesis of partial internalization. Alternatively, also slow kinetics of internalization at these conditions can mask complete equilibration in the ITC experiment (vide supra).
In summary, all these findings can be rationalized in terms of an internalization threshold. It is given by a threshold molar ratio of peptide-to-lipid that is met slightly above critical conditions but below the saturation limit (P/L)sat > (P/L)threshold ≈ 0.05 > (P/L)50%γ=0.5 and by the respective threshold molar fraction of anionic lipid XPGthreshold = ξ + zP·(P/L)threshold/γ ≈ 0.5 (see Eq. A7 and Fig. 9).
“Electroporation-like” internalization of penetratin
The asymmetric adsorption of the peptide to the headgroup region of the outer monolayer at concentrations below the internalization threshold causes an electric field between the differently charged outer and inner monolayers of E = (σin − σout)/2 × ɛm × ɛ0 under the assumption of a planar membrane. Here σ denotes the respective surface charge density (see Eq. A5). The relative permittivity, ɛm, refers to the membrane region, which is sandwiched between the charged interface of both monolayers. It includes the glycerol and carbonyl groups and the hydrocarbon chains of the lipid. We used an effective value of ɛm ≈ 10–20 (vide infra). Making use of Eq. A5 with (P/L)bin = 0 and (P/L)bout = P/γL and the approximations fNa ≈ 0 and (AP/AL) × (P/L)b ≪ 1, where AL and AP denote the partial molecular area of lipid and peptide within the membrane plane, respectively, one obtains a transmembrane electric field strength of
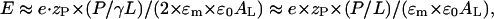 |
(1) |
where the right side of the equation refers to γ = 0.5. With zP·(P/L)threshold ≈ 0.5 (XPGthreshold − ξ) ≈ 0.2 (see Eq. A7) Eq. 1 provides the respective threshold value of the electric field strength, Ethreshold. It corresponds to a transmembrane voltage of ΔUthreshold ≈ 1.1 V according to ΔUthreshold = Ethreshold×dm, where dm ≈ 3.5 nm is the thickness of the part of the membrane sandwiched between the headgroup regions of opposite monolayers (Binder and Gawrisch, 2001).
Accordingly, the membrane becomes permeable at this threshold concentration and peptide molecules can translocate the bilayer. Equilibration of the peptide concentration through the membrane reduces the electric field and possibly reestablishes the stability of the membrane until new peptide binds to the outer monolayer. In this case, the electric field strength is given by Eq. 1 with the substitution (P/γL)→Δ(P/L)b ≡ (P/L)bin − (P/L)bout. This mechanism partly explains gradual internalization that was discussed above on a qualitative basis.
Diederich et al. (1998) investigated the voltage induced rupture of planar anionic black lipid membranes (electroporation) of diphytanoylphosphatidylserine covered with electrostatically adsorbed polylysines to obtain information about its mechanical stability. They found breakdown voltages of ∼0.5 V, which agree with our estimation in its order of magnitude. Moreover, it was shown that adsorption of polylysine on one side of the membrane leads to an asymmetric transmembrane potential, which adds to the external applied voltage, and in this way decreases the critical breakdown threshold. These results confirm our hypothesis that asymmetrically bound cationic compounds affect membrane stability via a transbilayer electric field.
Note that the used continuum model neglects discrete charge effects and the effect of the electrical double layer on the transmembrane potential, and thus it must be viewed as a rough approximation. Nevertheless, it appears reasonable to conclude that the content of anionic lipid in the membrane and the effective charge of the peptide determine the strength of the transmembrane electric field that is generated upon asymmetrical association of the peptide with the outer monolayer. The electric field in turn destabilizes the bilayer, and thus induces internalization. This electroporation-like process is triggered by a subtle interplay between the anionic surface charge density and the effective cationic charge of the peptide.
Penetratin affects the lateral pressure profile
The existence of an electric field causes the so-called Maxwell stresses, which depend quadratically on the field strength according to (Pawlowski et al., 1998)
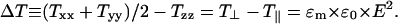 |
(2) |
ΔT defines the extensil stress of the mechanical, uniaxial stress tensor (T⊥ = Txx = Tyy, T‖ = Tzz). The x and y coordinate axes point perpendicular to the electric field vector that is oriented along the membrane normal. We assume that the extensil stress potentially leads to transient rupture of the bilayer if it exceeds the critical limit, ΔTthreshold, which is related to the threshold value of the electrical field (see Eq. 2).
The extensil tension, ΔT (given in units of N/m2), represents a three-dimensional pressure that refers to the whole thickness of the membrane. It can be transformed into the two-dimensional excess pressure induced by Maxwell stresses (in units of N/m) according to (see also Eq. 1)
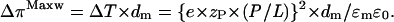 |
(3) |
The threshold concentration, zP·(P/L)threshold ≈ 0.5 (XPGthreshold − ξ) ≈ 0.2, provides a threshold value of the lateral excess pressure of ΔπthresholdMaxw ≈ 60 mN/m. This excess pressure is comparable with the critical lateral pressure of ∼40–50 mN/m at which lipid systems typically undergo a phase transition between different fluid phases (Binder and Gawrisch, 2001).
The bilayer is not a homogeneous film, but its chemical composition and molecular structure distinctly varies along the membrane normal. The profile of the lateral pressure along the membrane normal, p(z) ≡ ∂π/∂z, reflects this heterogeneous architecture. It is defined as the contribution of an infinitely thin layer at position z to the lateral pressure π. The stability and self-organizing ability of the bilayer is closely related to the amphiphilic nature of its constituents, which implies a polarity gradient across the bilayer. Consequently, the relative permittivity represents a function of the coordinate along the bilayer normal z, ɛm(z). Differentiation of Eq. 3 provides the contribution of the Maxwell stresses to the pressure profile due to the absorption of penetratin
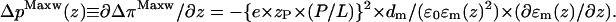 |
(4) |
Let us assume that the relative permittivity changes from values near ɛm(water) ≈ 70–80 at the water interface over ɛm(carbonyl) ≈ 20–30 in the carbonyl region to ɛm(chains) ≈ 5–10 in the membrane center. The inverse quadratic dependence between ΔpMaxw(z) and ɛm(z) (Eq. 4) predicts an increase in the amplitude of the pressure profile by factors of ∼10 and 200 in the carbonyl and methyl region of the membrane, relatively to its value in the headgroup region, assuming ∂ɛm(z)/∂z ≈ const. This simple estimation shows that the lateral pressure profile in the center of the bilayer can exceed its amplitude in the headgroup region by more than two orders of magnitude. As a consequence the excess pressure, which effectively acts in the hydrophobic core of the membrane, potentially induces a considerable inverse curvature stress in both halves of the bilayer that tends to bend the monolayers into inversely curved (water inside) structures. We assume that the inverse curvature stress reaches a critical stability limit at the internalization threshold followed by the destabilization of the bilayer architecture.
The inverse curvature stress before destabilization facilitates the formation of inversely curved structures (Binder et al., 1999). Such structures are capable of shielding the polar residues of the peptide from the hydrocarbon chains of the lipids and thus to minimize unfavorable contacts between polar and apolar moieties upon translocation of the peptide across the hydrophobic core of the bilayer. The translocation of penetratin through the membrane via transiently formed inversely curved lipid structures may explain why polar compounds such as peptides (Bardelli et al., 1999; Hall et al., 1996; Mutoh et al., 1999) or oligonucleotides (Pooga et al., 1998; Troy et al., 1996) covalently tagged to penetratin enter into cells.
Penetratin induces area inbalance between both halves of the membrane
Electrostatic repulsion within one monolayer force lipid films to dilate (Jähnig et al., 1979), creating such a destabilizing electrostatic tension, which measures as the decrease in mechanical tension that induces vesicle rupture with increasing anionic lipid fraction (Shoemaker and Vanderlick, 2002). The destabilizing electrostatic tension within each of the monolayers is proportional to the surface charge density in a first-order approximation, ∼4RT σ/NA (Shoemaker and Vanderlick, 2002). This effect gives rise to two possible consequences for membrane stability:
The membrane destabilizes with increasing XPG, and thus the threshold of internalization in terms of critical electric field strength and critical peptide to lipid molar ratio decreases. The destabilizing effect is expected to affect mostly the inner monolayer because the anionic lipid charges are not compensated by bound cationic peptide.
- The asymmetric binding of penetratin to the membrane results in a difference of the lateral pressure between the inner and outer monolayers of
using a first-order approximation of electrostatic dilation (Shoemaker and Vanderlick, 2002) and similar arguments as upon derivation of Eq. 1. In the right side of the equation it is assumed that γ = 0.5. The different lateral pressures acting within the outer and inner monolayers are expected to cause an area imbalance between both halves of the bilayer of ΔALin-out/AL ≈ Δπin-out/KA, where KA ≡ AL × ∂π/∂AL is the lateral compressibility modulus of the bilayer. Using the threshold composition zP·(P/L)threshold ≈ 0.2 one obtains Δπin-out ≈ 11 mN/m and a corresponding area imbalance of ΔALin-out/AL ≈ 0.06 assuming a value of KA ≈ 200 mN/m (Rawicz et al., 2000). Note that the electrostatic dilation causes an expansion of the outer monolayer relative to the inner monolayer leading to a bending moment that tends to curve the whole bilayer. This is in contrast to the alteration of the pressure profile, which tends to bend both monolayers into opposite directions.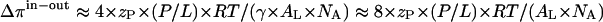
(5)
Also the asymmetric incorporation of detergents into vesicle membranes has been shown to induce an area imbalance between their outer and inner surfaces (Heerklotz, 2001). At a value of ΔALin-out/AL ≈ 0.15 the vesicle membranes reach an asymmetry-controlled permeability threshold, at which the system equilibrates by permeation of the detergent across the bilayer.
In summary, the asymmetric electrostatic dilation of the inner and outer monolayer of lipid vesicles induces an area imbalance with subsequent stress, which finally may facilitate the permeation of the peptide across the membrane.
SUMMARY AND CONCLUSIONS
We studied the interaction of the cell-penetrating peptide penetratin with lipid membranes as a function of the content of an anionic lipid by means of isothermal titration calorimetry. The work was aimed at understanding factors, which affect peptide binding to the membranes and its permeation through the bilayer. The experimental results could be rationalized in the following scenario:
The aqueous concentration of cationic penetratin carrying an effective charge of zP ≈ 5.1 ± 0.5 markedly enriches near the anionic membrane surface because of electrostatic attraction.
The high surface concentration facilitates binding of the peptide to the membrane.
The peptide first binds to the outer surface of the vesicles. Its binding capacity increases with the content of anionic lipid in the membrane. The asymmetrical distribution of the peptide between the outer and inner surfaces of the charged bilayer causes a transmembrane electrical field that alters the lateral and curvature stresses acting within the membrane by means of so-called Maxwell stresses and/or asymmetrical electrostatic dilation.
At a certain fraction of bound peptide, the electric field reaches a critical threshold value followed by an “electroporation-like” permeabilization of the membrane. Hence, further binding of peptide destabilizes the membrane and induces its internalization by means of inversely curved transient structures.
Internalization is triggered by a subtle interplay between the anionic surface charge density and the effective cationic charge of the peptide. On one hand, the fraction of anionic lipid must be large enough to bind a sufficiently high amount of peptide and to enable the sufficient high electric field strength to reach the internalization threshold. On the other hand, the effective charge of the peptide must be high enough to enable a sufficient compensation of the lipid charges at relatively small peptide concentrations in the outer monolayer. The minimum fraction of DOPG to induce internalization is ∼50% of the total lipid content. The threshold concentration of penetratin amounts roughly to one peptide per 20 lipids. Hence, the mechanism of internalization should be seen not only as an inherent feature of penetratin but it depends in a crucial fashion on the properties of the lipid bilayer.
We conclude that the relatively high cationic charge of cell penetrating peptides accomplishes a threefold role concerning its ability to permeate cell membranes: Firstly, it assures membrane selectivity by electrostatic interactions to anionic regions of the lipid bilayer. Secondly, it facilitates enrichment near and binding to the lipid-water interface. Thirdly, it destabilizes the bilayer architecture by electrostatic effects. We suppose that the charge-controlled internalization mechanism is of general importance for the translocation of other cationic Trojan peptides as well. The ability to translocate across cell membranes without damaging them may be essential to maintain its physiological state because it minimizes perturbations of the bilayer architecture contrarily to amphipathic detergent-like and pore-forming peptides. These substances with an antibiotic function have molecular properties that maximize their activity to perturb the membrane.
The relative small fraction of charged lipids in biomembranes and their nonhomogeneous distribution between the inner and outer leaflets suggests that the role of electrostatic interactions in native systems is much more complex than in simplified experimental models such as lipid vesicles studied here (see (Langner and Kubica, 1999) and references cited therein). For example, the fraction of charged lipids in the plasma membrane of eukaryote cells is typically smaller (less than 20% in rat liver cell membranes) than the critical permeability threshold of penetratin in DOPC/DOPG mixed vesicles. On the other hand, charged lipids are usually not randomly distributed in the membrane plane and can accumulate in domains (Murray et al., 1999). Calculations suggest that the local concentration of anionic lipid considerably increases in the vicinity of cationic peptides (May et al., 2000). Especially in the case of low molar fractions of charged lipids and low densities of highly charged peptides the extent of local charge modulation of the membrane is substantial. Previous experiments reveal that in prokaryote cells with a significant content of phosphatidylglyceroles this lipids facilitates the translocation of proteins through the membrane (De Vrije et al., 1988).
Although our results indicate that electrostatics play a key role for penetratin internalization, we propose that a certain charge-independent affinity to lipid membranes is also essential for the translocation of cargo peptides across lipid membranes. Note that the lipid-induced secondary structure that the peptide adopts at the membrane interface affects its hydrophobicity, and thus also its insertion mode before internalization. These issues will be addressed in a forthcoming publication.
APPENDIX
Surface partitioning and compensation of the surface charge
The surface partitioning model of Beschiaschvili and Seelig (1990) describes the association of charged peptides with the surface of lipid membranes by means of a partitioning equilibrium of free and bound additives between the aqueous and the lipid phase, respectively. The apparent binding constant is defined as
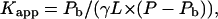 |
(A1) |
where γ is the fraction of accessible lipid, L and P denote the concentrations of lipid and peptide, respectively, and Pb is the concentration of membrane-bound peptide. Rearrangement provides the molar ratio of bound peptide to (total) lipid as a function of the molar ratio peptide to lipid
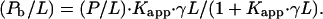 |
(A2) |
We assume that only a fraction γ of the lipid, L, is accessible to peptide binding. Consequently, the effective molar ratio of bound peptide to lipid in the respective leaflet of the bilayer is given by
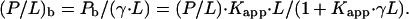 |
(A3) |
The apparent binding constant,
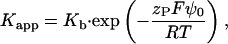 |
(A4) |
divides into two factors: the intrinsic binding constant, Kb, characterizes the “true”, chemical binding of the additive to the membrane whereas the exponential term describes the enrichment (or depletion) of dissolved additive in the immediate vicinity of the surface owing to attractive (or repulsive) electrostatic interactions with the charged membrane. The effective charge of the peptide, the Faraday constant, the gas constant, and the temperature are denoted by zP, F, R, and T, respectively.
The surface charge density, σ, of the DOPC/DOPG membrane with bound cationic peptide is given by (Beschiaschvili and Seelig, 1990)
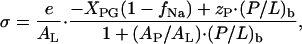 |
(A5) |
where e is the elementary charge, AL and AP denote the partial molecular area of lipid and peptide within the membrane plane, respectively. XPG is the molar fraction of the anionic lipid DOPG in the mixed DOPC/DOPG membrane. Counterion binding according to a Langmuir isotherm neutralizes a fraction of DOPG associated with Na+, fNa = KNa·CNa·exp(−ψ0F/RT)/(1 + KNa·CNa·exp(−ψ0F/RT)), and thus reduces the surface charge density of the membrane. Here KNa is the Na+ binding constant, taken as 0.6 M−1 (Eisenberg et al., 1979) and CNa is the concentration of Na+. An area requirement of AP = 1.5 nm2 was previously used for amphipatic peptides (see, e.g., Beschiaschvili and Seelig (1990)). Probably this value overestimates the (unknown) partial molecular area of penetratin owing to its superficial association with the membrane. This estimation together with AL ≈ 0.7 nm2 implies that the second term in the denominator of Eq. A5 can be neglected at the relevant peptide to lipid molar ratios.
The surface charge density and the respective surface potential, ψ0, are related each to another by means of the Guy-Chapman theory (see, e.g., Beschiaschvili and Seelig (1990)),
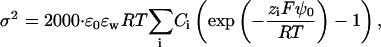 |
(A6) |
where ɛ0 and ɛw denote the permittivity in vacuum and the relative permittivity of water, respectively. The sum runs over the dissolved ionic species of equilibrium concentration Ci and signed valency zi.
The negative surface charge of the membrane increases with the amount of bound peptide. Let us define σ50% as the surface charge density corresponding to the inflection point of the ITC heats at which the absolute value of the observed titration heat decreases to 50% of its initial value. It refers to the surface potential ψ0 = ψ50% (see Eq. A6) and to the apparent binding constant K50% ≡ Kapp(ψ0 = ψ50%) (see Eq. A4). Making use of Eqs. A3 and A5, one obtains the respective molar ratio peptide to lipid
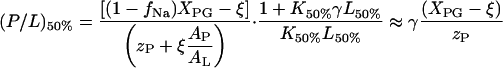 |
(A7) |
with 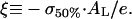
The parameter ξ defines the effective fraction of anionic lipid charges that remain not compensated by bound cationic peptide. The approximation at the right side of Eq. A7 assumes strong binding of the peptide (K50%L50% ≫ 1), and neglects Na+ binding (fNa = 0) and the area requirement of the peptide in the membrane plane. Note that the critical molar ratio (P/L)50% ensures the complete neutralization of lipid charges by bound peptide for K50% = Kb (isoelectric conditions: ψ50% = ξ = 0) (Lau et al., 1981).
With (P/L)50% ≡ P50%/L50% Eq. A7 transform into
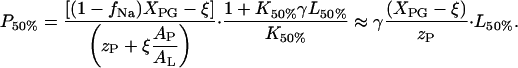 |
(A8) |
According to Eq. A8, the total peptide and lipid concentrations at the inflection point of the ITC heat traces are directly related each to another. A plot of P50% versus L50% virtually crosses the coordinate origin for K50%L50% ≫ 1.
Relevant values of the effective peptide charge, zP, of the accessibility factor, γ, of the critical apparent binding constant, K50%, and of the respective fraction of not compensated lipid charges, ξ, were estimated using an iterative algorithm: i), First approximations of zP and γ were obtained by linear fits of (P/L)50% as a function of XPG using the right side of Eq. A7 with ξ = 0; ii), Fits of Eq. A8 with ξ = 0 to the data shown in Fig. 8 provide first values of K50%; iii), Then, Eq. A4 gives an estimation of ψ50% using the intrinsic binding constant of Kb = 80 M−1 (Persson et al., 2003); iv), Eq. A6 provides the respective surface charge density, σ50%, and thus a first value ξ ≠ 0 (see also Eq. A7). It is used in a second cycle of steps i–iv instead of ξ = 0 providing the next estimation of the respective parameters. Their values converge after a few further iterations of steps i–iv.
References
- Bardelli, A., P. Longati, T. A. Williams, S. Benvenuti, and P. M. Comoglio. 1999. A peptide representing the carboxyl-terminal tail of the Met receptor inhibits kinase activity and invasive growth. J. Biol. Chem. 274:29274–29281. [DOI] [PubMed] [Google Scholar]
- Berlose, J. P., O. Convert, D. Derossi, A. Brunissen, and G. Chaissaing. 1996. Conformational and associative behavior of the third helix of antennapedia homeodomain in membrane-mimetic environment. Eur. J. Biochem. 242:372–386. [DOI] [PubMed] [Google Scholar]
- Beschiaschvili, G., and J. Seelig. 1990. Peptide binding to lipid bilayers. Binding isotherms and zeta-potential of a cyclic somatostatin analogue. Biochemistry. 29:10995–11000. [DOI] [PubMed] [Google Scholar]
- Binder, H., U. Dietrich, M. Schalke, and H. Pfeiffer. 1999. Hydration Induced Deformation of Lipid Aggregates before and after Polymerization. Langmuir. 15:4857–4866. [Google Scholar]
- Binder, H., and K. Gawrisch. 2001. Effect of unsaturated lipid chains on dimensions, molecular order and hydration of membranes. J. Phys. Chem. B. 105:12378–12390. [Google Scholar]
- Carnie, S., and S. McLaughlin. 1983. Large divalent cations and electrostatic potentials adjacent to membranes. A theoretical calculation. Biophys. J. 44:325–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christiaens, B., S. Symoens, S. Vanderheyden, Y. Engelborghs, A. Joliot, A. Prochiantz, J. Vanderkerckhove, M. Rosseneu, and B. Vanloo. 2002. Tryptophan fluorescence study of the interaction of penetratin peptides with model membranes. Eur. J. Biochem. 269:2918–2926. [DOI] [PubMed] [Google Scholar]
- De Vrije, T., R. L. De Swart, W. Dowhan, J. Tommassen, and B. De Kruijff. 1988. Phosphatidylglycerol is involved in protein translocation across E. coli inner membrane. Nature. 334:173–175. [DOI] [PubMed] [Google Scholar]
- Derossi, D., G. Chassaing, and A. Prochiantz. 1998. Trojan peptides: the penetratin system for intracellular delivery. Trends Cell Biol. 8:84–87. [PubMed] [Google Scholar]
- Derossi, D., A. H. Joliot, G. Chassaing, and A. Prochiantz. 1994. The third helix of the antennapedia homodomain translocates through biological membranes. J. Biol. Chem. 269:10444–10450. [PubMed] [Google Scholar]
- Diederich, A., G. Bähr, and M. Winterhalter. 1998. Influence of polylysine on the rupture of negatively charged membranes. Langmuir. 14:4597–4605. [Google Scholar]
- Drin, G., H. Demene, J. Temsamani, and R. Brasseur. 2001. Translocation of the pAntp peptide and its amphipathic analogue AP-2AL. Biochemistry. 40:1824–1834. [DOI] [PubMed] [Google Scholar]
- Eisenberg, M., T. Gresalfi, T. Riccio, and S. McLaughlin. 1979. Adsorption of monovalent cations to bilayer membranes containing negative phospholipids. Biochemistry. 18:5213–5223. [DOI] [PubMed] [Google Scholar]
- Futaki, S., W. Ohashi, T. Suzuki, M. Niwa, S. Tanaka, K. Ueda, H. Harashima, and Y. Sugiura. 2001. Stearylated arginine-rich peptides: a new class of transfection systems. Bioconjug. Chem. 12:1005–1011. [DOI] [PubMed] [Google Scholar]
- Gehring, W. J., M. Affolter, and T. Burglin. 1994a. Homeodomain proteins. Annu. Rev. Biochem. 63:487–526. [DOI] [PubMed] [Google Scholar]
- Gehring, W. J., Y. Q. Quian, M. Billeter, K. Furukubo-Togunaka, A. F. Schier, D. Resendez-Perez, M. Affolter, G. Otting, and K. Wuthrich. 1994b. Homeodomain-DNA recognition. Cell. 78:211–223. [DOI] [PubMed] [Google Scholar]
- Hall, H., E. J. Williams, S. E. Moore, F. Walsh, A. Prochiantz, and P. Doherty. 1996. Inhibition of FGF-stimulated phosphatidylinositol hydrolysis and neurite outgrowth by a cell-membrane permeable phosphopeptide. Curr. Biol. 6:580–587. [DOI] [PubMed] [Google Scholar]
- Hällbrink, M., A. Floren, A. Eomquist, M. Pooga, T. Bartfai, and Ü. Langel. 2001. Cargo delivery kinetics of cell-penetrating peptides. Biochim. Biophys. Acta. 1515:101–109. [DOI] [PubMed] [Google Scholar]
- Heerklotz, H., and J. Seelig. 2001. Detergent-like action of the antibiotic peptide surfactin on lipid membranes. Biophys. J. 81:1547–1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heerklotz, H. H. 2001. Membrane stress and permeabilization induced by asymmetric incorporation of compounds. Biophys. J. 81:184–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hildebrand, A., R. Neubert, P. Garidel, and A. Blume. 2002. Bile salt induced silubilization of synthetic phosphatidylcholine vesicles studied by isothermal titration calorimetry. Langmuir. 18:2836–2847. [Google Scholar]
- Hosotani, R., Y. Miyamoto, K. Fujimoto, R. Doi, A. Otaka, N. Fukii, and M. Imamura. 2002. Trojan p16 peptide suppresses pancreatic cancer growth and prolongs survival in mice. Clin. Cancer Res. 8:1271–1276. [PubMed] [Google Scholar]
- Jähnig, F., K. Harlos, H. Vogel, and H. Eibl. 1979. Electrostatic interactions at charged lipid membranes. Electrostatically induced tilt. Biochemistry. 18:1459–1468. [DOI] [PubMed] [Google Scholar]
- Joliot, A. H., A. Triller, M. Volovich, C. Pernelle, and A. Prochianz. 1991. alpha-2,8-Polysialic acid is the neuronal surface receptor of antennapedia homeobox peptide. New Biol. 3:1121–1134. [PubMed] [Google Scholar]
- Ladokhin, A. S., and S. White. 2001a. ‘Detergent-like’ permeabilization of anionic vesicles by melittin. Biochim. Biophys. Acta. 1514:253–260. [DOI] [PubMed] [Google Scholar]
- Ladokhin, A. S., and S. H. White. 2001b. Protein chemistry at membrane interfaces: non-additivity of electrostatic and hydrophobic interactions. J. Mol. Biol. 309:543–552. [DOI] [PubMed] [Google Scholar]
- Langner, M., and K. Kubica. 1999. The electrostatics of lipid surfaces. Chem. Phys. Lipids. 101:3–35. [DOI] [PubMed] [Google Scholar]
- Lau, A., A. McLaughlin, and S. McLaughlin. 1981. The adsorption of divalent cations to phospatidylglycerol bilayer membranes. Biochim. Biophys. Acta. 645:279–292. [DOI] [PubMed] [Google Scholar]
- Le Roux, I., A. Joliot, E. Bloch-Gallego, A. Prochiantz, and M. Volovitch. 1993. Neurotrophic activity of the antennapedia homeodomain depends on its specific DNA-binding properties. Proc. Natl. Acad. Sci. USA. 90:9120–9124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindgren, M., X. Gallet, U. Soomets, M. Hällbrink, E. Brakenhielm, M. Pooga, R. Brasseur, and U. Langel. 2000. Translocation properties of novel cell penetrating transportan and penetratin analogues. Bioconjug. Chem. 11:619–626. [DOI] [PubMed] [Google Scholar]
- Magzoub, M., L. E. Erikson, and A. Gräslund. 2002. Conformational states of the cell-penetrating peptide penetratin when interacting with phospholipid vesicles: effects of surface charge and peptide concentration. Biochim. Biophys. Acta. 1563:53–63. [DOI] [PubMed] [Google Scholar]
- Magzoub, M., K. Kilk, L. E. Erikson, Ü. Langel, and A. Gräslund. 2001. Interaction and structure induction of cell-penetrating peptides in the presence of phospholipid vesicles. Biochim. Biophys. Acta. 1512:77–89. [DOI] [PubMed] [Google Scholar]
- May, S., D. Harries, and A. Ben-Shoul. 2000. Lipid demixing and protein-protein interactions in the adsorption of charged proteins on mixed membranes. Biophys. J. 79:1747–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, D., A. Arbuzova, G. Hangyas-Mihalyne, A. Gambhir, N. Ben-Tal, B. Honig, and S. McLaughlin. 1999. Electrostatic properties of membranes containing acidic lipids and adsorbed basic peptides: theory and experiment. Biophys. J. 77:3176–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutoh, M., F. D. Lung, Y. D. Long, P. P. Roller, R. S. Sikorski, and P. M. O'Connor. 1999. A p21Waf1/Cip1 carboxyl-terminal peptide exhibited cyclin-dependent kinase-inhibitory activity and cytotoxicity when introduced into human cells. Cancer Res. 59:3480–3488. [PubMed] [Google Scholar]
- Pawlowski, P., S. A. Gallo, P. G. Johnson, and S. W. Hui. 1998. Electrorheological modeling of the permeabilization of the stratum corneum: theory and experiment. Biophys. J. 75:2721–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persson, D., P. E. G. Thoren, M. Herner, P. Lincoln, and B. Norden. 2003. Application of a novel analysis to measure the binding of the membrane-translocating peptide penetratin to negatively charged liposomes. Biochemistry. 42:421–429. [DOI] [PubMed] [Google Scholar]
- Persson, D., P. E. G. Thoren, and B. Norden. 2001. Penetratin-induced aggregation and subsequent dissociation of negatively charged phospholipid vesicles. FEBS Lett. 505:307–312. [DOI] [PubMed] [Google Scholar]
- Pooga, M., U. Soomets, M. Hällbrink, A. Valkna, K. Saar, K. Rezai, U. Kahl, J. Hao, X. Xu, Z. Wiesenfeld-Hallin, T. Hokfelt, T. Bartfai, and U. Langel. 1998. Cell penetrating PNA constructs regulate galanin receptor levels and modify pain transmission in vivo. Nat. Biotechnol. 16:857–861. [DOI] [PubMed] [Google Scholar]
- Prochiantz, A. 1996. Getting hydrophilic compounds into cells: lessons from homeopeptides. Curr. Opin. Neurobiol. 6:629–634. [DOI] [PubMed] [Google Scholar]
- Prochiantz, A. 1998. Peptide nucleic acid smugglers. Nat. Biotechnol. 16:819–820. [DOI] [PubMed] [Google Scholar]
- Rawicz, W., K. C. Olbrich, T. McIntosh, D. Needham, and E. Evans. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79:328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salamon, Z., G. Lindblom, and G. Tollin. 2003. Plasmon-waveguide resonance and impedance spectroscopy studies of the interaction between penetratin and supported lipid bilayer membranes. Biophys. J. 84. [DOI] [PMC free article] [PubMed]
- Schwarz, G., and G. Beschiaschvili. 1989. Thermodynamic and kinetic studies on the association of melittin with a phospholipid bilayer. Biochim. Biophys. Acta. 979:82–90. [DOI] [PubMed] [Google Scholar]
- Seelig, A., and P. M. Macdonald. 1989. Binding of a neuropeptide, substance P, to neutral and negatively charged lipids. Biochemistry. 28. [DOI] [PubMed]
- Seelig, J. 1997. Titration calorimetry of lipid–peptide interactions. Biochim. Biophys. Acta. 1331:103–116. [DOI] [PubMed] [Google Scholar]
- Shoemaker, S. D., and T. K. Vanderlick. 2002. Intramembrane electrostatic interactions destabilize lipid vesicles. Biophys. J. 83:2007–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stankowski, S. 1991. Surface charging by large multivalent molecules. Extending the standard Gouy-Chapman treatment. Biophys. J. 60:341–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theodore, L., D. Derossi, G. Chassaing, B. Llirbat, M. Kubes, P. Jordan, H. Cheiweiss, H. Godement, and A. Prochiantz. 1995. Intraneuronal delivery of protein kinase pseudosubstrate leads to growth cone collapse. J. Neurosci. 15:7158–7167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoren, P. E. G., D. Persson, M. Karlsson, and B. Norden. 2000. The Antennapedia peptide penetratin translocates across lipid bilayers -the first direct observation. FEBS Lett. 482:265–268. [DOI] [PubMed] [Google Scholar]
- Troy, C. M., D. Derossi, A. Prochiantz, L. A. Greene, and M. L. Shelanski. 1996. Downregulation of Cu/Zn superoxide dismutase leads to cell death via the nitric oxide-peroxynitrite pathway. J. Neurosci. 16:253–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenk, M. R., and J. Seelig. 1998. Magainin 2 amide interaction with lipid membranes: calorimetric detection of peptide binding and pore formation. Biochemistry. 37:3909–3916. [DOI] [PubMed] [Google Scholar]
- White, S. H., and W. C. Wimley. 1998. Hydrophobic interactions of peptides with membrane interfaces. Biochim. Biophys. Acta. 1376:339–352. [DOI] [PubMed] [Google Scholar]
- Wieprecht, T., O. Apostolov, M. Beyermann, and J. Seelig. 2000. Membrane binding and pore formation of the antibacterial peptide PGLa: thermodynamic and mechanistic aspects. Biochemistry. 39:442–452. [DOI] [PubMed] [Google Scholar]