The Pressure-Dependence of the Size of Extruded Vesicles

Abstract

Variations in the size of vesicles formed by extrusion through small pores are discussed in terms of a simple model. Our model predicts that the radius should decrease as the square root of the applied pressure, consistent with data for vesicles extruded under various conditions. The model also predicts dependencies on the pore size used and on the lysis tension of the vesicles being extruded that are consistent with our data. The pore size was varied by using track-etched polycarbonate membranes with average pore diameters ranging from 50 to 200 nm. To vary the lysis tension, vesicles made from POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine), mixtures of POPC and cholesterol, and mixtures of POPC and C₁₆-ceramide were studied. The lysis tension, as measured by an extrusion-based technique, of POPC:cholesterol vesicles is higher than that of pure POPC vesicles whereas POPC:ceramide vesicles have lower lysis tensions than POPC vesicles.

INTRODUCTION

Vesicles are quasispherical shells consisting of lipid bilayers that encapsulate an aqueous environment. They are ubiquitous in cells where they participate in intra- and intercellular transport of cellular material. They are also produced by several methods in the laboratory where they are used as model membranes or as nanoscale containers (New, 1990). One popular method of vesicle production is extrusion (Hope et al., 1993) where solutions containing large multilamellar vesicles are forced or extruded through small pores in track-etched polycarbonate filter membranes, using either a pressurized gas (Hope et al., 1985) or a syringe-based plunger system (MacDonald et al., 1993). This method produces a relatively monodisperse solution of vesicles of controlled average size without the addition of organic solvents or detergents.

Although the use of extrusion to produce unilamellar vesicles is extensive, the actual mechanism by which large multilamellar vesicles (MLVs) break up into smaller vesicles comparable to the pore size remains speculative. Understanding exactly what happens in this process should lead to better control of the vesicles produced and wider application of the method. Several studies have been made to characterize the vesicles produced by this method. Early studies showed that multiple passes are required to reduce the size and multilamellarity of extruded vesicles, and that their size depends on the pore size (Hope et al., 1993). Extrusion was found to be unsuccessful below the gel-fluid transition temperature, an effect that has been attributed to decreased fluidity of the membrane below the transition temperature (Nayer et al., 1989). Later studies of the size of the extruded vesicles as a function of concentration and pressure indicated that the size of the vesicles decreases slightly as the extrusion pressure is increased (Kölchens et al., 1993). More recently, we characterized the effect of extrusion pressure and lipid properties on vesicle size and polydispersity in more detail (Hunter and Frisken, 1998). We found that there is a minimum pressure below which vesicles cannot be extruded successfully and confirmed that the average size of the extruded vesicles decreases with applied pressure. We were able to show that the minimum pressure is related to the lysis tension, the tension required to rupture a vesicle, and proposed a method (Frisken et al., 2000) to determine the lysis tension of vesicles using this characteristic of the extrusion process. Results using this method were shown to be consistent with those obtained using micropipette methods.

In this article, we concentrate on the pressure-dependence of the size of the extruded vesicles. One mechanism for vesicle formation by extrusion has been proposed (Clerc and Thompson, 1994); it is based on the Rayleigh instability, which predicts that a cylinder of water or a soap film of radius R will break up into smaller pieces to minimize surface energy, where the dominant wavelength of the instability is λ = 2πR. Clerc and Thompson predicted that long cylinders of phospholipid bilayer with a radius comparable to the pore size R_p would break up either inside the pore or at the pore exit in a similar way. Clerc and Thompson's analysis predicts a vesicle size given by π^1/2 R_p. Obviously more detailed analysis is necessary to explain variations of the vesicle size under different conditions. In equilibrium, the surface tension of a vesicle is zero (Seifert, 1994), but surface tension is induced in the bilayer as it flows through the pore (Bruinsma, 1996). Presumably, since the surface tension induced depends on the shear rate, or equivalently the flow rate of vesicle solution through the pores, more detailed analysis based on this model would predict a flow-rate-dependent vesicle size. However, we have shown (Frisken et al., 2000) that the radius depends on the pressure applied rather than the flow rate induced.

Instead, we propose that large vesicles block the entrance to the pores of the polycarbonate membrane and break up because the applied pressure induces a surface tension that exceeds the rupture tension of the membrane. We use a simple model based on blowing bubbles through a circular opening to explain the observed decrease in vesicle radius as a function of extrusion pressure. This model predicts that the vesicle radius should be inversely proportional to the square root of the applied pressure and that the vesicle size should depend on the size of the pores used and the lysis tension of the vesicles extruded. We show that this model is consistent with data for vesicles made with polycarbonate membranes of different pore size, except for the largest pore size, and for vesicles of different lysis tension.

To vary the lysis tension of the vesicles, we have used vesicles of different lipid composition. In particular, we have made vesicles from POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphati-dylcholine), POPC:cholesterol, and POPC:C₁₆-ceramide. POPC, an unsaturated lipid that has a double bond between C9 and C10 on one of its chains, is a typical example of a naturally occurring phospholipid. We investigated POPC:cholesterol because cholesterol is known to increase the lysis tension of phospholipid membranes (Needham and Nunn, 1990). We chose to investigate the effect of ceramide on bilayer properties because there has been recent interest in the presence of ceramide in biological membranes, but the mechanical strength of ceramide lipid membranes has not yet been investigated. This seemed like it would be an interesting property, especially in consideration of the role of ceramides in apoptosis, or cell death (Quintans et al., 1994). This family of molecules is also involved in cellular signaling for growth and differentiation (Hannun, 1994) and is ubiquitous in the stratum corneum (Williams and Barry, 1992), the outermost layer of mammalian skin that functions as a permeability barrier. Other properties of ceramide lipid membranes that have been investigated include possible channel formation (Siskind and Colombini, 2000; Siskind et al., 2002), effects on the gel-liquid crystalline phase transition (Hsueh et al., 2002), and mixing (Holopainen et al., 1997, 1998; Hsueh et al., 2002). C₁₆-ceramide was chosen because its chain length is comparable to that of POPC.

In this paper, we first introduce our model, describe materials and methods, and then discuss our results. Although the model predicts a pressure-dependence consistent with our data and is in agreement with data for different lipid mixtures and most pore sizes, it is not able to predict that the vesicle radius is comparable to the pore size at high pressures, and there is incomplete agreement with vesicles extruded through the largest pores. These shortcomings are discussed.

THEORY

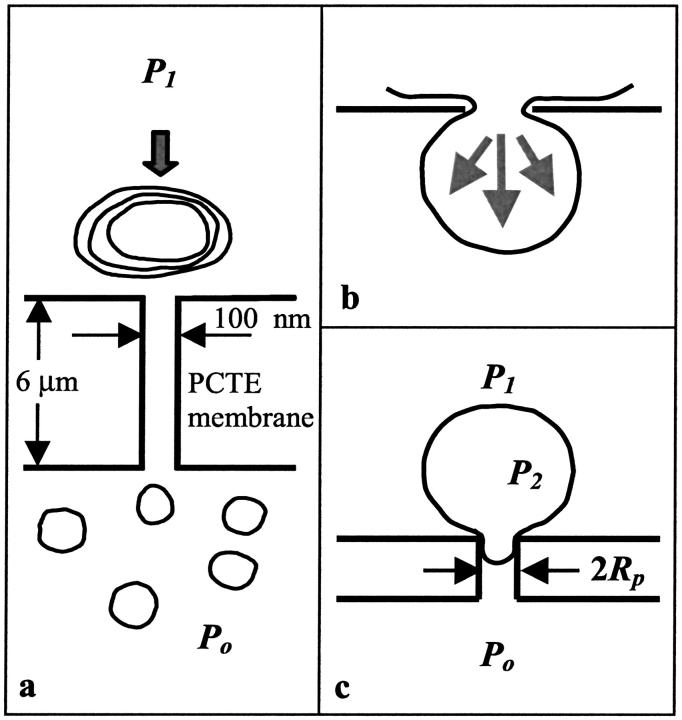
Vesicle extrusion involves pushing a solution of large MLVs through polycarbonate membrane filters several times. Although the extrusion process is fast, flow is still laminar (Clerc and Thompson, 1994). The polycarbonate membranes used for extrusion have roughly cylindrical pores formed by chemical etching along ion tracks (Fleischer et al., 1975). The pores are long and narrow; they can be made with a large range of nominal diameters, where 100 nm is typical for extrusion, and have lengths of 6 μm. In practice, the nominal pore size is an upper bound and the average pore size is somewhat smaller. As the MLVs are pushed through these pores, they break up into smaller vesicles, as shown schematically in Fig. 1 a. Both the average vesicle size and the width of the size distribution decrease on subsequent passes through the membrane filters to a final distribution of vesicle sizes that is characteristic of the applied pressure and lipid used. The mean of the final distribution is comparable to the pore size.

FIGURE 1.

(a) Schematic diagram of the extrusion process. Large multilamellar vesicles are pushed or extruded through polycarbonate membrane filters at least 10 times resulting in small unilamellar vesicles whose size is comparable to the pore size. (b) Schematic diagram depicting vesicle extrusion in terms of blowing bubbles through circular pores. The force due to the applied pressure is balanced by a force caused by line tension around the neck of the vesicle. (c) Schematic diagram of a vesicle at the entrance of the pore. The small fragment of the vesicle pulled into the pore has radius equal to the radius of the pore R_p, whereas the large fragment of the vesicle outside the pore has radius comparable to the original radius of the vesicle R_o. P₂ is the pressure inside the vesicle and the difference between P₁ and P_o is the applied pressure.

An important consideration in trying to model this process is whether the radius is flow-rate dependent or pressure dependent. Flow of the vesicle through the pore results in shear-induced tension in the bilayer (Bruinsma, 1996) and could lead to an instability inside the pore or at the pore exit that would result in vesicle formation (Clerc and Thompson, 1994). In this case, the size of the vesicles should depend on the flow rate. Alternatively, a pressure-induced breakup mechanism could occur at the pore entrance. The pressure and flow rate are related; the flow rate Q for laminar flow through a cylindrical pore of radius R_p is given by Darcy's law

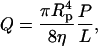(1)

where P is the pressure difference and L is the distance over which it is applied. However, it is possible to vary the flow rate and the pressure independently by changing L. We performed experiments where we used one filter membrane instead of two so that we were able to double the flow rate while keeping the pressure constant. Although each individual pore is not elongated in this way, the flow resistance is doubled and the flow rate halved. Even in the pressure range where the radius is most sensitive to these conditions, we saw no difference in vesicle radius (Frisken et al., 2000). From these experiments, we concluded that vesicle breakup due to some pressure-dependent mechanism is more likely.

To explain the observed pressure-dependence of the radius of the extruded vesicles, we have developed a simple model based on blowing bubbles as shown in Fig. 1 b. The lipid bilayer is pushed into a small circular opening and a bubble forms on the low pressure side of the opening. There is a force F_ℓ due to the line tension around the neck of the bubble given by

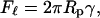(2)

where R_p is the radius of the pore and γ is the surface tension. The surface tension is induced by the applied pressure. This is balanced by a force due to the applied pressure F_p where

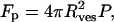(3)

where R_ves is the radius of the final vesicle. When the induced tension exceeds the lysis or rupture tension γ = γ_ℓ of the bilayer, the small vesicle fragments and separates from the main vesicle. Using Eqs. 2 and 3, we can derive a relation between the applied pressure and the size of the final vesicle

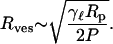(4)

We concede that, in deriving Eq. 4, we have ignored both the influence of the long cylindrical pore on the formation of the vesicles and the vector nature of the forces; however, this simple picture does lead to a reasonable prediction of the system's behavior. The model not only predicts a relationship between the radius and the applied pressure but also predicts that the vesicle radius will depend on the lysis tension of the bilayer and on the pore size. We expect that this model is not sufficiently precise to predict numerical factors and that these will be determined by detailed analysis of the pore shape, etc. A more serious shortcoming is that it predicts that the radius of the vesicles will approach zero as the pressure increases; our observations indicate that the radius approaches the pore size at high pressure. However, the model is not really valid in this limit because vesicles comparable to the pore size are able to slip through without distortion, and thus without breakage, so that the vesicles should not reduce further after they have reached sizes smaller than the pore size.

MATERIALS AND METHODS

Materials

POPC, cholesterol, and C₁₆-ceramide were purchased in powder form from Northern Lipids (Vancouver, BC). POPC and cholesterol and POPC and ceramide were mixed at ratios of 30 mol % cholesterol, and 10 and 15 mol % ceramide, respectively. Each mixture was then added to a 4:1 benzene:methanol mixture and was vortexed until all of the powder had dissolved. Finally the solution was “lyophilized”, i.e., it was frozen in liquid nitrogen and then evaporated under vacuum for ∼6 h. This process produces a well-mixed powder form of the lipid mixture and has been found to effectively remove the solvent from the mixture (Y.-W. Hsueh and J. Thewalt, private communication).

Sample preparation and extrusion

Lipid vesicle preparation began by hydrating each sample using purified water from a Milli-Q Plus water purification system (Millipore, Bedford, MA) to a concentration of 1 mg/ml. The use of purified water ensures the production of spherical vesicles (Mui et al., 1993); the vesicles are nonspherical after extrusion but swell to quasispherical shapes unless there are solutes present. If there are solutes present, swelling leads to concentration gradients across the bilayer and the resulting osmotic pressures oppose the swelling. The mixture was then taken through a freeze-thaw-vortex process, freezing by immersion in liquid nitrogen, thawing by immersion in a bath at 50°C and then vortexing. Each step was continued for 5 min and the cycle was repeated five times. This process is used to help break up multilamellar vesicles and to promote the mixing of the enclosed contents with the exterior solution (Mayer et al., 1985). After the freeze-thaw-vortex process, the vesicle suspension was extruded through two polycarbonate membrane filters (Osmonics, Livermore, CA) with nominal pore diameters of 400 nm held in an extruder (Northern Lipids) using pressurized nitrogen gas. We call this first extrusion through large pores preextrusion; we have found that it improves the reproducibility of vesicle size and extrusion flow-rate measurements (Hunter and Frisken, 1998). At this stage, the vesicles have a radius of ∼200 nm and are generally fairly polydisperse.

The sample of preextruded vesicles was then diluted to the required concentration and extruded through two final polycarbonate membrane filters of the required pore size. Samples generally had concentrations of 0.1 mg/ml for pressures up to 100 psi (where 1 psi = 6895 Pa) and 1 mg/ml for pressures higher than 100 psi. When low concentration samples are extruded at high pressure, high flow rates make it difficult to contain the samples. Previous measurements (Frisken et al., 2000) have shown that vesicle size is independent of concentration at low concentration. Multiple passes of the sample were made through the extruder until a final size distribution was reached. The number of times the solution was extruded varied with the applied pressure; at low pressures more extrusions are required to reach a size distribution that does not change on further passes through the extruder. We generally monitor the flow rate as an indicator of changes in the vesicle solution; we have found (Hunter and Frisken, 1998) that the flow rate, radius, and polydispersity stop changing after about the same number of passes. All solutions were extruded at least 10 times; samples extruded at lower pressures required up to 20 passes through the extruder to reach a flow rate that did not change from pass to pass. The flow rate of vesicle solution through the extruder was measured each time by weighing the solution extruded in a known time interval. The pore diameters of the filter membranes as provided by the manufacturer are shown in Table 1.

TABLE 1.

Pore diameters of the polycarbonate membrane filters used in extrusion

Lot number	Lipid	Measurement	Pore diameter (nm)
AG83CC11A	POPC	Radius	161
AE84G11D031	POPC	Radius	98.5
75423	POPC	Radius	80*
AE86AQ12B	POPC	Radius	47
K01CP02500 78856	POPC	Lysis tension	88.5
K01CP02500 78856	POPC:cholesterol	Lysis tension	88.5
K01CP02500 74298	POPC:ceramide	Lysis tension	88.5

^*Measured value not available—nominal value used in all calculations.

During extrusion, the temperature of the extruder was maintained by a water bath. After the solution was placed in the extruder, it was allowed to equilibrate for several minutes before extrusion. The temperatures used for extrusion were 25°C, 35°C, and 70°C for POPC, POPC:cholesterol, and POPC:ceramide samples, respectively. These temperatures were chosen to ensure that all samples were in the fluid phase when extruded. A higher temperature was used for POPC:ceramide samples due to the fact that POPC:ceramide mixtures phase separate into coexisting gel and fluid phases below 31°C and 38°C for 10 and 15 mol % ceramide, respectively (Hsueh et al., 2002). We found we needed to keep the solution at 70°C to extrude successfully. We checked the possibility of ceramide content reduction through extrusion using high pressure liquid chromatography and found that there was no significant reduction of either ceramide or POPC after extrusion. The recovery of lipid composition for lipid:ceramide vesicles after extrusion has also been shown by other authors (Hatfield and Fung, 1995).

Vesicle size measurements

The average radius and polydispersity of the suspended vesicles were measured using dynamic light scattering (DLS). The apparatus used for these measurements was an ALV DLS/SLS-5000 spectrometer/goniometer (ALV-Laser GmbH, Langen, Germany). The light scattered from the sample was detected by a photomultiplier tube at a scattering angle of 90° from the transmitted beam. The temperature of the sample bath was maintained by a water bath controlled at 25°C, 35°C, and 55°C for samples of POPC, POPC:cholesterol and POPC:ceramide, respectively. Five measurements were made for each sample.

The mean decay rate Γ̄ and the standard deviation of the decay rate distribution σ were determined by fitting a function of the form

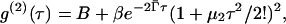(5)

where B is the baseline 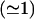and μ₂ ≡ σ² is the variance of the distribution, to the measured intensity-intensity correlation function g⁽²⁾(τ). As is the case for the standard expansion in terms of cumulants (Koppel, 1972), Eq. 5 is also the result of a moments-based derivation (Frisken, 2001). However, the use of fewer assumptions results in a more robust function that can be fit to the data over a larger range of delay time τ. Terms involving higher moments can be incorporated in the function; however, they were not required to find good fits to the vesicle data. In fact, this relationship was consistent with our data for all cases; no systematic deviations from the fits were observed. This, by itself, is a good indication that the distributions are unimodal; moments analysis is valid only for distributions of this type. Further analysis using Laplace inversion routines supplied with the ALV instrument confirmed that the distributions were monomodal. The vesicle samples are generally polydisperse, with relative standard deviations ranging from 20% for the smaller pore sizes to 30% for the larger ones.

Lysis tension

The lysis tension γ_ℓ is the tension required to rupture a bilayer. This can be determined from the minimum pressure P_min required for extrusion of lipid solutions at low lipid concentration (Frisken et al., 2000). Below this pressure, the flow rate of lipid solution through the extruder and the number of vesicles produced goes to zero. This is because large vesicles block the pores of the polycarbonate membrane, as shown schematically in Fig. 1 c. To enter the pores, they must reduce their volume by bursting or lysing. As a large vesicle of radius R_o is pulled into a pore of radius R_p, a surface tension γ is induced in the membrane. The vesicle bursts when the induced surface tension is greater than the lysis or bursting tension of the bilayer. A relation between the applied pressure difference P, γ, R_p, and R_o can be derived using Laplace's law between the pressure difference across a curved interface and the surface tension of the interface and assuming uniform tension throughout the membrane (Hunter and Frisken, 1998):

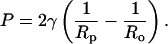(6)

Similar expressions have been derived to describe vesicle aspiration by micropipettes (Kwok and Evans, 1981). If the pressure is too small, the induced tension is smaller than the lysis tension and the vesicle cannot burst and the pore remains blocked. The minimum pressure P_min for vesicle extrusion (where the flow rate is equal to zero) can then be associated with the lysis tension through Eq. 6. The lysis tension of the vesicle can be determined if P_min, the radius of the pore, and the radius of the preextruded vesicle are known.

This simple picture is most accurate during the first pass of the vesicle solution through the extruder because the vesicles are largest at this stage. We have found (Frisken et al., 2000) that measuring the flow rate during the first pass results in a flow rate that is linear in the applied pressure at lipid concentrations of ∼0.1 mg/ml. The slope is comparable to the slope measured for the flow rate of water through the polycarbonate membrane, and we use the nonzero pressure intercept to calculate the lysis tension. Choice of concentration is important; at lower and higher concentrations there is evidence of leakage of water through empty pores and crowding, respectively.

RESULTS AND ANALYSIS

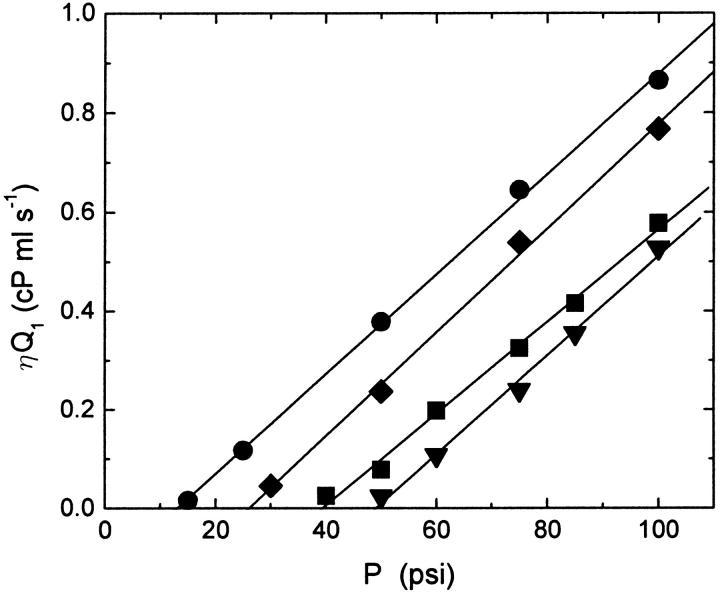
To determine the lysis tension of the lipid mixtures used in these experiments, the product of the flow rate of the first extrusion pass and the viscosity of water for the temperature at which the sample was extruded, ηQ₁, was plotted as a function of extrusion pressure, and a linear equation was fit to the data to determine P_min. Fig. 2 shows a plot of the first pass viscosity-corrected flow rate as a function of extrusion pressure for POPC, POPC:cholesterol, and POPC:ceramide solutions with concentrations of 0.1 mg/ml. The data confirm a linear relationship between the viscosity-corrected flow rate and the applied pressure as predicted by Darcy's law. As expected, the slopes of all four sets of data are consistent; as can be seen in Eq. 1, the slope contains only geometrical factors and should be lipid-independent. The figure also shows the fits of a linear equation to the data to determine the minimum pressure; the minimum pressure depends on vesicle composition and is largest for POPC:cholesterol vesicles and smallest for POPC:ceramide vesicles.

FIGURE 2.

Plot of the viscosity-corrected flow rate, ηQ₁, of vesicle solution during the first pass through the polycarbonate filter membrane as a function of extrusion pressure for solutions of POPC (▪), POPC:cholesterol (70:30) (▾), POPC:ceramide (90:10) (♦), and POPC:ceramide (85:15) (•) in water at concentrations of 0.1 mg/ml. The solutions were extruded through two polycarbonate membrane filters with nominal pore diameters of 100 nm. The flow rate increases linearly with the applied pressure, and there is a nonzero pressure below which the flow rate is negligible. The fit (lines) of a linear equation to the data for each sample is also shown.

The minimum pressure resulting from the fits, the radius of the preextruded vesicles measured using DLS, and the lysis tension calculated using Eq. 6 for POPC, POPC:cholesterol, and POPC:ceramide samples are summarized in Table 2. The results show an increase in the lysis tension of POPC vesicles with the presence of cholesterol confirming that cholesterol increases the mechanical strength of POPC vesicles, but a decrease in the lysis tension with the addition of ceramide showing that the presence of ceramide weakens POPC vesicles.

TABLE 2.

Minimum pressure for extrusion P_min, average size of preextruded vesicles R_o, and lysis tension calculated from Eq. 6 γ_ℓ for POPC, POPC:cholesterol, and POPC:ceramide samples

Lipid composition	Pmin (psi)	Ro (nm)	γℓ (mN/m)
POPC	39.3 ± 2.9	228.7	7.4 ± 1.1
POPC:cholesterol (70:30)	49.2 ± 5.9	218.0	9.4 ± 1.4
POPC:ceramide (90:10)	26.0 ± 2.9	161.9	5.5 ± 0.97
POPC:ceramide (85:15)	13.0 ± 1.2	143.7	2.9 ± 0.50

The dependence of the lysis tension on temperature should be considered at this stage due to the fact that different samples were extruded at different temperatures. To check the temperature dependence of the lysis tension, POPC samples were extruded at temperatures of 25°C, 50°C, and 70°C at different pressures. The minimum pressures resulting from these measurements (data not shown) vary between 34 and 38 psi, but the results agree within experimental uncertainty and there is no systematic trend with temperature.

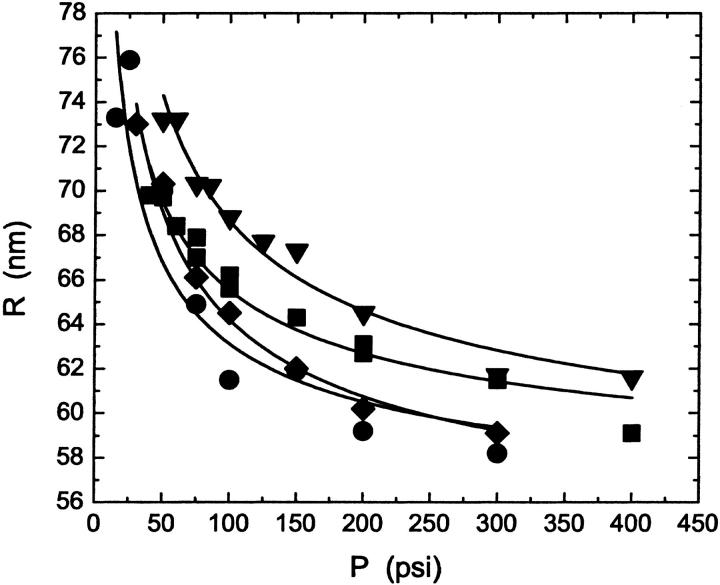
Results of DLS measurements show that the pressure-dependence of the vesicle radius depends on the lipid composition of the vesicles and on the pore size. Fig. 3 shows a plot of the average hydrodynamic radius of the extruded vesicles for each lipid composition as a function of the pressure applied during the extrusion. All vesicles were extruded through the same batch of polycarbonate membranes with nominally 100 nm pores. The figure shows that the radius decreases as the pressure is increased and that the behavior varies with the lipid composition of the vesicles. To produce the same size of vesicles, POPC samples must be extruded at higher pressures than POPC:ceramide samples, but at smaller pressures than are required for POPC:cholesterol samples. As predicted by Eq. 4, the variation in vesicle size with lipid composition corresponds to the variation of the lysis tension; the higher the lysis tension, the larger the size of the vesicles. The curves are fits to each set of data of the function

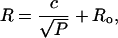(7)

where R is the average hydrodynamic radius of the vesicles, P is the applied pressure, and c and R_o are constants. It is clear that all of the data are consistent with a radius that decreases as the inverse square root of the applied pressure. The constant R_o is comparable to the pore size.

FIGURE 3.

Average radius, R, of extruded vesicles as a function of extrusion pressure, P, for vesicles made from POPC (▪), POPC:cholesterol (70:30) (▾), POPC:ceramide (90:10) (♦), and POPC:ceramide (85:15) (•) after at least 10 passes through the extruder. The solutions were extruded at 25°C, 35°C, 70°C, and 70°C, respectively, through two polycarbonate membrane filters with nominal pore diameters of 100 nm. The fit (lines) of the empirical function given in Eq. 7 to the data for each sample is also shown.

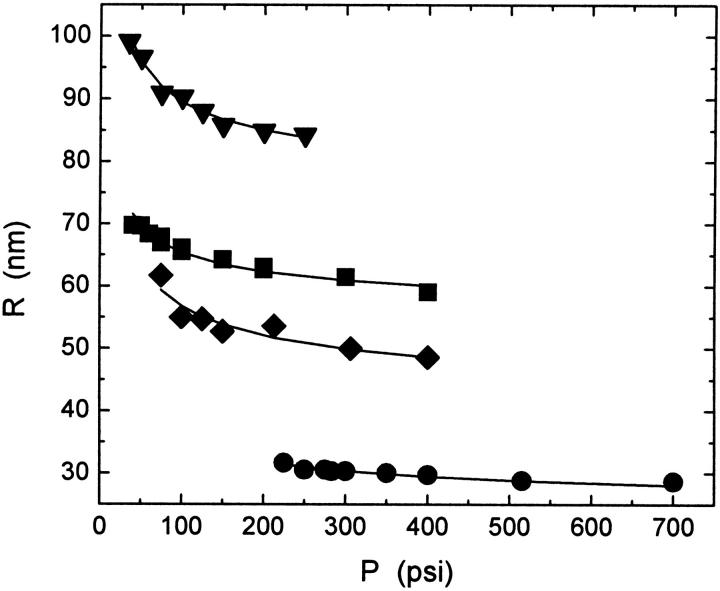
Data for vesicles made with filter membranes of different pore size but using the same lipid also show that the average vesicle size decreases as the applied pressure is increased as shown in Fig. 4. The curves are fits of Eq. 7 to the data. The constant R_o is comparable to the pore size for the nominally 50, 80, and 100 nm membranes and somewhat smaller for the 200 nm membranes.

FIGURE 4.

Average radius, R, of extruded vesicles made from POPC as a function of extrusion pressure for samples extruded at 25°C using polycarbonate membrane filters with different pore diameters, 50 nm (•), 80 nm (♦), 100 nm (▪), and 200 nm (▾). The fit (lines) of the empirical function given in Eq. 7 to the data for each sample is also shown.

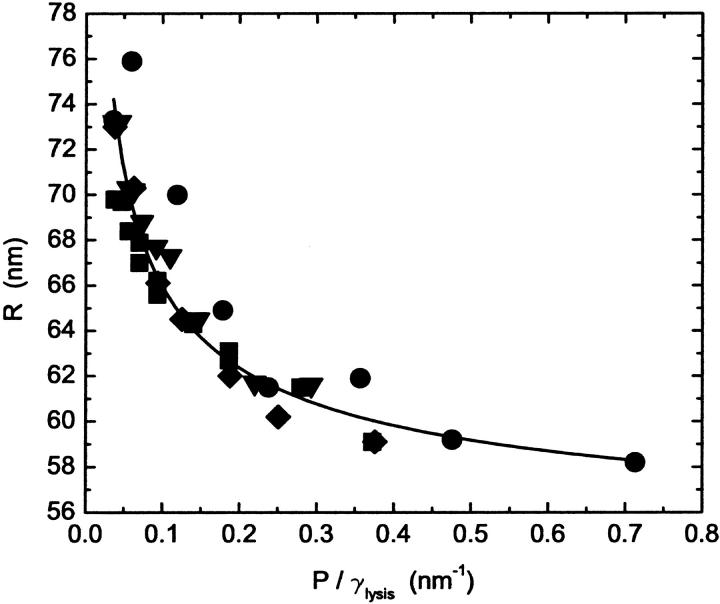
Fig. 5 tests the predicted dependence of the radius on lysis tension. The data shown in Fig. 3 is replotted as a function of the ratio of the pressure to the lysis tension P/γ_ℓ. The data collapse nicely. Obviously, the vesicle radius does not tend to zero at infinite pressure as predicted by the model, but approaches a finite value. Thus the curve is a fit to a function of the form

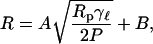(8)

which is clearly consistent with all the data. The asymptotic value of the radius is ∼10% larger than the pore size of the polycarbonate membranes.

FIGURE 5.

Plot of the data shown in Fig. 3 as a function of the ratio of the pressure to the lysis tension, P/γ, for vesicles made from POPC (▪), POPC:cholesterol (70:30) (▾), POPC:ceramide (90:10) (♦), and POPC:ceramide (85:15) (•). The lysis tension values used are shown in Table 2. The fit (line) of the function given in Eq. 8 to all of the data is also shown.

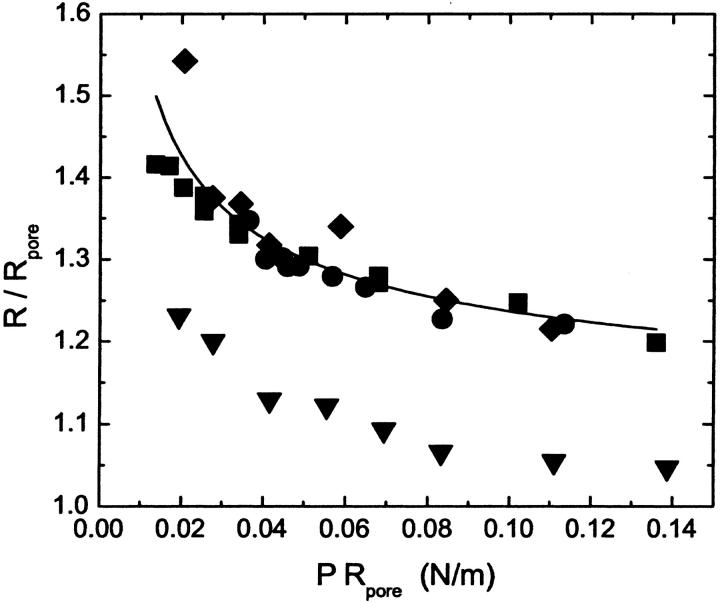
Fig. 6 tests the predicted dependence of the radius on pore size. The data shown in Fig. 4 is replotted to show the size of the vesicles relative to the reported pore size as a function of the pressure multiplied by the pore size. The data for nominally 50, 80, and 100 nm filter membranes collapse to a single curve consistent with the model, whereas data for 200 nm filter membranes is too low. The 200 nm filter data can also be collapsed if a pore size of 70 nm is used to scale the data. The curve is a fit of a function of the form

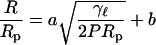(9)

to the data for the three smaller pore sizes, which is clearly consistent with the data.

FIGURE 6.

Plot of the ratio of the average radius of the POPC vesicles shown in Fig. 4 to the radius of the pore as a function of the product of the pressure and pore radius, PR_p. The samples were extruded at 25°C using polycarbonate membrane filters with different pore diameters, 50 nm (•), 80 nm (♦), 100 nm (▪), and 200 nm (▾). Three of the four data sets show the collapse predicted by the model. The fit (line) of the function given in Eq. 9 to the data for these three data sets is also shown.

DISCUSSION

Lysis tension

The lysis tension of 7.4 ± 1.1 mN/m for pure POPC vesicles measured by extrusion methods is consistent with the result of 8.3 ± 0.5 mN/m from micropipette measurements (Rawicz and Evans, unpublished). We have found that the lysis tension of POPC vesicles containing 30 mol % cholesterol (measured at 35°C) increases from 7.4 to 9.4 mN/m. In contrast, we have found that the lysis tension of POPC vesicles containing 10 and 15 mol % C₁₆-ceramide (measured at 70°C) decreases from 7.4 to 5.5 and 2.9 mN/m, respectively. We do not believe that these differences in lysis tension are due to temperature because our results for POPC show that its lysis tension is independent of temperature between 25°C and 70°C, within the accuracy of our measurements. The higher mechanical strength of POPC:cholesterol vesicles is consistent with other results showing that cholesterol increases the mechanical strength of phospholipid vesicles. For example, Needham and Nunn (1990) used micropipette methods to measure increases in lysis tension from 5.7 to 12.6 mN/m as the nominal cholesterol content in SOPC (1-stearoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine) vesicles was increased from 0 to 28 mol %. Ceramide, on the other hand, appears to decrease the mechanical strength of POPC vesicles.

It is generally accepted that rupture or lysis of the membrane requires the formation of pores and that in the process of rupture there is competition between the applied tension and the edge energy associated with pore formation (Olbrich et al., 2000). The exact material parameters that control the edge energy do not seem to be well understood but probably include the membrane thickness and compressibility and the presence of defects in the membrane. The addition of cholesterol affects several material parameters that may be involved in pore formation. For example, cholesterol decreases acyl chain motion and has a significant ordering effect on POPC in bilayers (Thewalt and Bloom, 1992). This leads to a less compressible surface and a more cohesive membrane (Bloom et al., 1991). The addition of cholesterol also leads to a thicker membrane (Nezil and Bloom, 1992), which should make pore formation more difficult because of increased edge energy. However, the fact that lysis tension for our POPC vesicles does not change significantly over 45°C suggests that this may not be a crucial factor. We estimate that the change in thickness of the POPC bilayer with temperature should be comparable to that observed with the addition of cholesterol, assuming that the change in volume is negligible and that there is a fractional change in area of 3 × 10⁻³/°C (Evans and Needham, 1987). This change in area was measured for SOPC (1-stearoyl-2-oleoyl-phosphatidylcholine) at 15°C. As far as we know, the fractional change in area for POPC between 25°C and 70°C has not been measured.

The decrease of lysis tension due to the presence of ceramide is probably not due to either reduced order or reduced thickness but may be related to a tendency toward pore formation in lipid:ceramide systems. Recent NMR studies (Hsueh et al., 2001) indicate that ceramide has an ordering effect on the acyl chains in POPC bilayers. The thickness of POPC:ceramide bilayers is not known. However, increased acyl chain order suggests that the bilayer should be thicker in the presence of C₁₆-ceramide as more ordered chains are longer. Thus the observation of increased order suggests that ceramide would increase the lysis tension, not decrease it, if lysis tension were thickness or order dependent. On the other hand, ceramide may weaken the bilayer because of heterogeneities in membrane composition. We have worked at high temperatures (70°C) to ensure that we are far above the gel-fluid coexistence region where the POPC:ceramide is well mixed. It is possible that there is a region of fluid-fluid coexistence, as exists in cholesterol:lipid phase diagrams (Thewalt and Bloom, 1992). Phase coexistence or even concentration fluctuations above a region of coexistence could lead to defects and a weakening of the membrane. However, Needham and Nunn (1990) measured lysis tension for 0–80 mol % cholesterol in SOPC with a linear increase in lysis tension from 0 to 60 mol %. These measurements were made ∼10° above the gel transition in a region where fluid-fluid coexistence is expected, i.e., they observed no evidence of weakening of the membrane near a liquid-liquid coexistence region. There are recent reports suggesting the formation of stable pores in ceramide phospholipid bilayers (Siskind and Colombini, 2000; Siskind et al., 2002), and pore formation could lead to reduced lysis tension. However, these measurements were done in a region of the phase diagram where the lipids were most likely within the gel-fluid coexistence region and may not be relevant at higher temperatures where the membrane is in a fluid state.

Size of extruded vesicles

Figs. 3 and 4 show that the average final radius of the vesicles decreases by ∼20% over the range of pressures applied in these studies. The figures also show a significant difference between vesicles of different composition and vesicles made by extrusion through different pores. The rescaled versions of these plots (Figs. 5 and 6) show that our data is consistent with the pressure, lysis tension, and pore size dependence of the model presented in the Theory section. Expressing the results of the fits to the data in Figs. 5 and 6 in terms of the parameters in Eq. 9 shows that parameters from the fits to the two sets of data are also consistent. These results are shown in Table 3. The dimensionless parameter a = A/R_p may be a geometrical factor related to the fact that the vesicle breaks up at the mouth of a long cylindrical pore rather than at a circular opening, or it may be associated with the exact hydrodynamics of the vesicle-pore interaction. The dimensionless parameter b = B/R_p is consistent with a high pressure limit to vesicle size that is ∼10% larger than the reported pore size. It is clear that the model does not predict the high pressure limit of the radius—this appears to be a vesicle size consistent with the pore size rather than zero as predicted by the model. A high pressure size limit comparable to the pore size is consistent with the fact that vesicles smaller than the pore size will not distort in the pore and will be unlikely to break up further. The fact that these two parameters are the same (within experimental uncertainty) for the two data sets further justifies the use of this model.

TABLE 3.

Values of the fitting parameters a and b resulting from fitting the function given in Eq. 9 to the radius-pressure data for the scaled lipid composition data (Fig. 5) and the scaled data for different pore sizes (Fig. 6)

Data	a	b
Lipid composition	0.61 ± 0.04	1.09 ± 0.02
Pore size	0.64 ± 0.06	1.08 ± 0.02

There are several reasons why the model may not be consistent with data for vesicles extruded through nominally 200 nm pores. The reported pore size may be incorrect. We are currently working on methods of characterizing the pore size independently. The preextruded vesicles may not be large enough, compared to the pore size, to validate using our simple bubble blowing model. However, using MLVs that were not preextruded (and thus larger) did not result in significant changes to the pressure dependence.

Multilamellarity

Vesicles made by extrusion can be multilamellar. However, use of the freeze-thaw process to prepare the lipid solution before extrusion should minimize both the extent of lamellarity and its influence. For example, NMR studies (Mayer et al., 1985) of the ³¹P NMR signal of extruded MLVs before and after the addition of external Mn²⁺ have shown that, for MLVs that have been subjected to the freeze-thaw process, 52, 44, and 32% of the ³¹P NMR signal originates from the outer monolayer for MLVs extruded through 100, 200, and 400 nm pores, respectively. If only uni- and bilamellar vesicles are considered, these samples should be 100, 86, and 44% unilamellar, respectively. These studies have also shown that frozen and thawed MLVs have larger interlamellar spacings, which should minimize the impact of multilamellarity on membrane properties.

We had expected that multilamellarity might affect our results for lysis tension where the minimum pressure required to extrude MLVs preextruded through 400 nm pores is measured. However, agreement between our results for POPC and those of Rawicz and Evans (unpublished) suggests that this is not a factor. This may be because the bilayers are separated in the freeze-thaw process. Furthermore, the fact that the data for the pressure dependence of vesicles of different composition, measured during their last pass through the extruder where they are predominantly unilamellar, can be collapsed using our lysis tension results, measured during the first pass of the vesicles through the extruder when they are multilamellar, also confirms that multilamellarity does not play a major role either in the measurement of lysis tension by extrusion through 100 nm pores or in the radius of the vesicles produced.

CONCLUSIONS

We have proposed a simple model based on blowing bubbles to explain the pressure dependence of extruded vesicles. The model predicts that the radius will also depend on the lysis tension of the lipid bilayer and on the pore size through which the vesicles are extruded. The model predicts pressure, lysis tension, and pore size dependencies that are consistent with data for vesicles with lysis tensions ranging from 2.9 to 9.4 nN/m and for vesicles extruded through pore sizes ranging from 50 to 100 nm. It is not sufficiently precise to predict the exact numerical relation between these quantities, but that may be determined by detailed analysis of the pore shape, etc. However, the numerical factors determined from the lysis tension and pore size data are consistent. The model is not valid in the high pressure limit where the radius of the vesicles approaches the pore size and the vesicles are able to slip into the pores without breaking.

The results of the lysis tension measurements of vesicles made from POPC, POPC:cholesterol, and POPC:ceramide confirm that cholesterol increases bilayer strength and show for the first time that ceramide decreases bilayer strength. Weakening of the bilayer in the presence of ceramide is probably not due to a thinning of the bilayer but may be due to heterogeneities in the lipid composition within the bilayer or a propensity for pore formation in lipid:ceramide mixtures.