The Conformation of Myosin Head Domains in Rigor Muscle Determined by X-Ray Interference

Abstract

In the absence of adenosine triphosphate, the head domains of myosin cross-bridges in muscle bind to actin filaments in a rigor conformation that is expected to mimic that following the working stroke during active contraction. We used x-ray interference between the two head arrays in opposite halves of each myosin filament to determine the rigor head conformation in single fibers from frog skeletal muscle. During isometric contraction (force T₀), the interference effect splits the M3 x-ray reflection from the axial repeat of the heads into two peaks with relative intensity (higher angle/lower angle peak) 0.76. In demembranated fibers in rigor at low force (<0.05 T₀), the relative intensity was 4.0, showing that the center of mass of the heads had moved 4.5 nm closer to the midpoint of the myosin filament. When rigor fibers were stretched, increasing the force to 0.55 T₀, the heads' center of mass moved back by 1.1–1.6 nm. These motions can be explained by tilting of the light chain domain of the head so that the mean angle between the Cys⁷⁰⁷–Lys⁸⁴³ vector and the filament axis increases by ∼36° between isometric contraction and low-force rigor, and decreases by 7–10° when the rigor fiber is stretched to 0.55 T₀.

INTRODUCTION

Muscle contraction is thought to be driven by a structural change or working stroke in the head domain of myosin while it is bound to an adjacent actin filament in the muscle sarcomere. Adenosine triphosphate (ATP) hydrolysis provides the free energy for contraction, and several lines of evidence have associated the working stroke with release of the ATP hydrolysis products from the active site of myosin (Reedy et al., 1965; Lymn and Taylor, 1971; Hibberd and Trentham, 1986; Geeves and Holmes, 1999). Some of the earliest and most direct evidence in support of this hypothesis came from electron microscope studies of the conformation of the myosin heads or cross-bridges in muscle fibers that had been permeabilized and depleted of ATP, i.e., in rigor (Reedy et al., 1965). In these conditions the myosin heads are tilted so that the end that is attached to actin is closer to the midpoint of the myosin filament—the M-line. This is the direction of tilt expected from a working stroke that shortens the muscle sarcomeres by driving actin filaments toward the M-line.

Subsequent electron microscopic work on isolated myosin head domains bound to actin filaments in the absence of ATP (Moore et al., 1970; Milligan and Flicker, 1987; Volkmann et al., 2000) led to higher resolution structures of the actin-myosin head complex in vitro and, in combination with crystallographic data, to atomic models of the rigor complex (Rayment et al., 1993b; Whittaker et al., 1995; Volkmann et al., 2000). However, little is known about the structure of two-headed myosin bound to actin in rigor in the sarcomeric lattice of actin and myosin filaments. This structure is likely to be distinct from that of single actin-bound myosin heads in vitro, because of the incommensurate periodicities of the actin and myosin filaments and the steric constraints imposed by the filament lattice. Moreover, since both heads of each myosin molecule bind to an actin monomer in vertebrate muscle in rigor (Cooke and Franks, 1980; Thomas and Cooke, 1980; Lovell et al., 1981), but share a junction with the myosin rod, they cannot have the same conformation.

X-ray diffraction has been used extensively to investigate myosin conformation in rigor muscle (Reedy et al., 1965; Huxley and Brown, 1967; Haselgrove, 1975; Squire and Harford, 1988; Takezawa et al., 1999). The x-ray diffraction diagram from rigor muscle is dominated by a series of layer-line reflections that index on the ∼38 nm repeat of the actin helix, but the meridional axis of the pattern exhibits a series of reflections that index on the ∼43 nm axial repeat of the myosin filament. The intensities of both these sets of reflections are sensitive to the conformation of the myosin heads, but the complexity and disorder of the structure have so far prevented a definitive structural interpretation (Holmes et al., 1980; Squire and Harford, 1988; Takezawa et al., 1999; Koubassova and Tsaturyan, 2002).

Recently it became clear that an extension of the x-ray technique can provide a precise and unambiguous measure of the axial motions of myosin heads with respect to the midpoint of the myosin filament in an intact muscle fiber (Linari et al., 2000; Piazzesi et al., 2002). The method depends on interference between the oppositely directed arrays of myosin heads in the two halves of each myosin filament, which produces a finely spaced modulation of the axial x-ray reflections associated with the myosin filament periodicity. Although this phenomenon was apparent in early x-ray studies of muscle (Huxley and Brown, 1967; Rome et al., 1973; Haselgrove, 1975), recent developments in synchrotron x-ray beams and detectors have greatly increased the effective resolution of the technique, and enabled its application to a wide range of structure-function studies on muscle.

Here we used the x-ray interference method to measure the axial motion of the myosin heads between the states of active isometric contraction and rigor in isolated single muscle fibers. We then used previous estimates of the conformation of the heads in isometric contraction (Irving et al., 2000; Piazzesi et al., 2002) to deduce the rigor conformation. To further constrain the interpretation and conclusions, we measured the changes in the interference fine structure produced by slowly stretching the rigor fibers to impose elastic distortion on the myosin heads.

METHODS

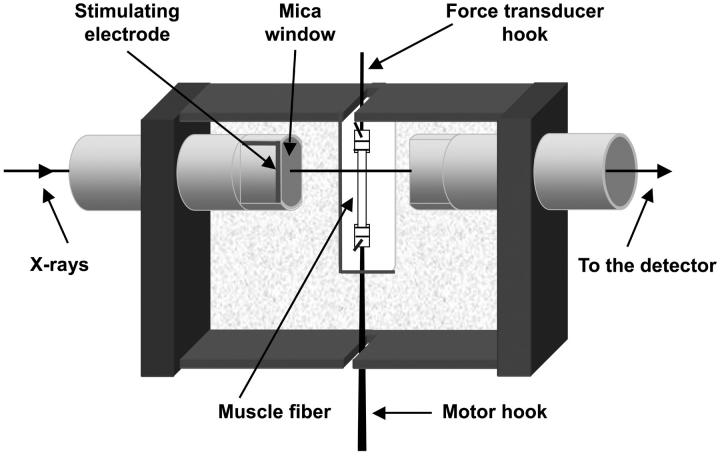
Preparation and mounting of muscle fibers

Frogs (Rana temporaria) were cooled to 2–4°C and killed by decapitation followed by destruction of the spinal cord, following the official guidelines of the European Community Council (directive 86/609/EEC). Single fibers were dissected from the tibialis anterior muscle and mounted by means of aluminum foil clips between a capacitance force transducer and a loudspeaker-coil motor in a thermoregulated trough containing Ringer's solution (115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, 3 mM phosphate buffer at pH 7.1) at 4°C. The sarcomere length was set at 2.1 μm. Details of procedures for mounting and measuring the fibers and of the mechanical apparatus have been described (Lombardi and Piazzesi, 1990, and references therein). Two mica windows, carrying the stimulating electrodes (Fig. 1), were moved as close as possible to the fiber to minimize the x-ray path through the solution. The gap between the windows was typically 600 μm. For x-ray measurements at beam line ID2 of the European Synchrotron Radiation Facility (ESRF, Grenoble, France), the trough was mounted vertically, with the force transducer at the top and the motor at the bottom as shown in Fig. 1, so that the fiber axis was parallel to the smaller (vertical) dimension of the x-ray beam. A perspex cover sealed with silicone grease ensured that the Ringer's solution did not leak from the trough. Some x-ray measurements were also made at beam line 16.1 of the CLRC Daresbury Laboratory, UK, with the trough and fiber mounted horizontally.

FIGURE 1.

Vertical mounting of muscle fibers for x-ray and mechanical measurements. The gap between the mica windows has been greatly increased from the 600 μm used in the experiments to show the muscle fiber. The two stimulating electrodes were attached to opposite edges of the windows; only the front electrode is shown here.

X-ray data collection and experimental protocol

Most of the x-ray data were collected at ID2, ESRF, which provides a well-collimated monochromatic x-ray beam of wavelength 0.1 nm with a flux of up to 10¹³ photons s⁻¹ (Boesecke et al., 1995). The beam size at the fiber, measured by scanning a small pinhole, was 0.4 mm horizontally and 0.15 mm vertically (full width half-maximum). Beam divergence was 0.069 mrad horizontally and 0.025 mrad vertically. X-ray diffraction patterns were recorded on storage phosphor image plates (IP, A3 size, Molecular Dynamics, Sunnyvale, CA) placed in an evacuated tube 10 m from the fiber (Linari et al., 2000).

Fibers were stimulated under isometric conditions for 2.3 s at the optimal frequency (20–30 Hz) for a fused tetanus. X-ray data were collected in 2-s exposures in the resting fiber and from 0.3 to 2.3 s after the start of stimulation, when the force had attained its plateau value (T₀). X-ray exposure of the fiber was controlled by a fast shutter (switch time ∼1 ms). Three 2-s exposures were accumulated on the same image plate in each condition. After the measurements on the intact fiber, it was transferred to a drop of Ringer's solution in a multitrough apparatus used for experiments on demembranated fibers (Linari et al., 1993). The fiber was chemically demembranated in 0.5% Triton X-100, then aluminum clips were attached to an ∼3-mm segment of the fiber, which was mounted between another motor and force transducer. To preserve sarcomere order during the transition to the rigor state, ATP was removed from the fiber in the presence of 2,3-butanedione monoxime (20 mM), which prevents development of rigor force (Linari et al., 1998). Sarcomere length varied by <±3% along each fiber in rigor, and local sarcomere length was always in the range 2.04–2.17 μm. The rigor fiber was remounted in the trough used for the x-ray measurements and stretched slightly to a force ∼0.05 T₀.

X-ray diffraction data were collected from rigor fibers at this low force level (low-force rigor) by accumulating several 5-s exposures on a single image plate. X-ray data at a steady force of ∼0.5 T₀ (high-force rigor) were collected in one 20-s exposure starting 500 ms after a slow stretch of the rigor fiber by ∼2% fiber length (Fig. 4 A). This produced an increase in half-sarcomere length of only ∼4 nm in the fiber segment in the x-ray beam, because of end compliance and yielding of the fiber attachments (Linari et al., 1998).

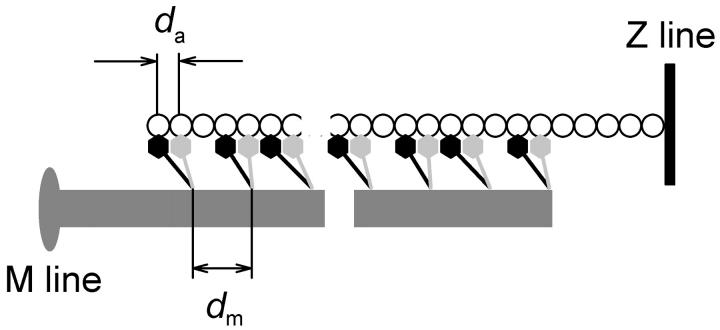
FIGURE 4.

Effect of stretch on the M2 and M3 x-ray reflections in rigor; Daresbury Synchrotron. (A) Length and force records from one fiber. Blue and red segments indicate the periods when the shutter opened to collect the low-force and high-force x-ray data, respectively. (B) Axial intensity distribution at low-force (blue) and high-force (red) from three fibers. (C) Radial intensity distribution in the region of the M3 reflection (axial integration limits 0.061–0.077 nm⁻¹).

In x-ray measurements on the resting, active, and low-force rigor states, the fiber was shifted vertically by 400 μm between each 2-s (resting, active) or 5-s (low-force rigor) exposure, to minimize the effects of radiation damage. In the high-force rigor measurements, the fiber was moved continuously up and down at a velocity of 0.1 mm/s over a vertical range of ∼2.5 mm during the x-ray exposure. The combination of strain and long x-ray exposure led to irreversible damage of the fiber, as indicated by a reduction in the intensity of the M3 reflection in x-ray patterns obtained a few minutes after the initial high-force measurements (the minimum time required for exchange of the image plate). Consequently only one x-ray exposure for high-force rigor could be made in each fiber in the experiments at ESRF.

Repeated x-ray measurements on the same fiber in low- and high-force rigor were made at beam line 16.1 at the CCLRC, Daresbury, UK, using a 20 × 20 cm gas-filled detector (Towns-Andrews et al., 1989) and 3-m camera. This facility provided a lower x-ray flux than in the ESRF experiments, and did not allow resolution of the interference fine structure of the axial x-ray reflections, but it enabled accurate measurements of the intensities of these reflections in the same fiber at rest, during active contraction, and in low- and high-force rigor. Rigor patterns were collected in pairs of 5-s frames just before and 500 ms after the imposition of a slow ramp stretch that increased the steady force to ∼0.5 T₀ (see Fig. 4 A). Typically, three pairs of low-/high-force rigor patterns could be collected from each fiber at beam line 16.1 without significant radiation damage.

X-ray data analysis

Image plates exposed at ESRF were scanned at 100 μm nominal spatial resolution with a Molecular Dynamics Storm 840 scanner. X-ray diffraction images were analyzed using the program HV (Dr A. Stewart, Brandeis University, Waltham, MA) and the Peakfit software package (SPSS, Chicago, IL). Images were centered and aligned using the centers of the M3 reflections. The axial intensity distribution was calculated by integrating the region from 0.013 nm⁻¹ on either side of the meridional axis of the x-ray pattern. The background intensity distribution was fitted by a polynomial function in the regions between the x-ray reflections, and subtracted. The fine structure of each reflection was analyzed with a multi-Gaussian fitting program (Peakfit) that provided the intensity and the peak position (reciprocal spacing) of each of its components. The total intensity of the reflection was determined as the sum of those of the component peaks. The mean spacing of the reflection was calculated as the mean of the spacings of the component peaks weighted by their intensities. Spacings were calibrated using the resting spacing of the M3 reflection, 14.34 nm (Haselgrove, 1975). For some measurements it was necessary to add intensity distributions from several fibers before the Gaussian fitting; in such cases the fitted parameters are given without estimates of their variability. The intensity distribution of the x-ray reflections was broadened by the finite size of the x-ray beam and by the limited spatial resolution of the image plate and scanner. The combined point spread function (PSF) of the beam and detection system was estimated by recording the undiffracted x-ray beam attenuated by a 50-μm Rhodium sheet on an image plate, and its vertical full width at half-maximum was 0.44 mm. The signal/noise of the intensity distributions recorded from single muscle fibers was generally too low for deconvolution of the PSF, so we used the alternative approach of convoluting the intensity distributions calculated from structural models with the PSF before comparison with the experimental data.

X-ray data collected on the gas-filled detector at CCLRC were analyzed using the BSL and XOTOKO software provided by CCLRC via Collaborative Computational Project 13 (CCP13). After correcting for the detector response and camera background, the axial intensity distribution was calculated by integrating the diffraction pattern between 0.005 nm⁻¹ on either side of the meridian. The background of the axial intensity distribution in the region of the M2 and M3 reflections was subtracted using HV.

RESULTS

The axial x-ray reflections at rest, during isometric contraction and in rigor

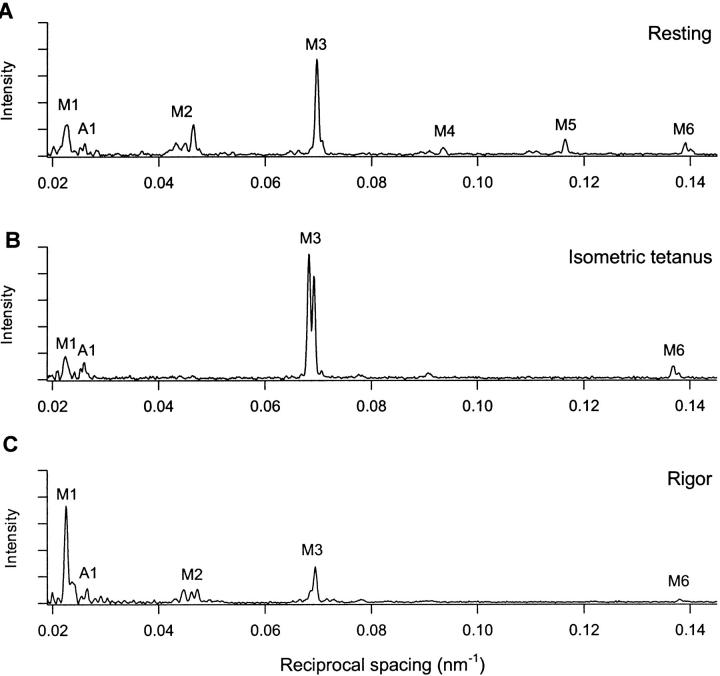
The axial diffraction pattern from a resting muscle fiber (Figs. 2 A and 3 A) is dominated by a series of reflections (labeled M1, M2, etc. in Fig. 3 A) that index on the ∼43 nm quasihelical periodicity of the myosin heads in the thick filaments (Huxley and Brown, 1967). The most intense of these is the M3 reflection, with a spacing of 14.34 nm in resting fibers, corresponding to the axial repeat of levels of heads along the three-stranded filament. The myosin-based axial reflections were generally composed of multiple peaks, separated by ∼1/1000 nm⁻¹, that result from interference between the two arrays of myosin heads in each thick filament (Rome et al., 1973; Haselgrove, 1975; Malinchik and Lednev, 1992; Linari et al., 2000; Juanhuix et al., 2001). The spacings of the main component peak of each reflection were 44.3 nm (M1), 21.51 nm (M2), 14.35 nm (M3), 10.70 nm (M4), 8.59 nm (M5), and 7.19 nm (M6). An axial component of the first actin-based layer line was visible at 38.4 nm (A1).

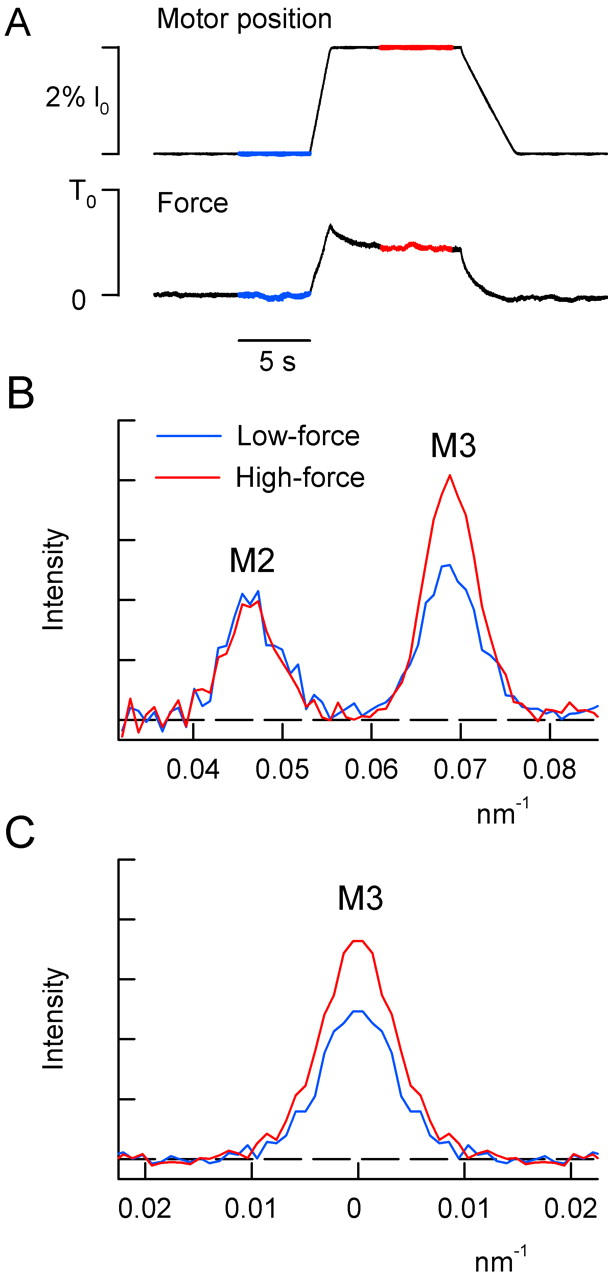
FIGURE 2.

Axial region of the x-ray diffraction pattern recorded at the European Synchrotron Radiation Facility from a single muscle fiber: A, at rest; B, isometric tetanus plateau (force T₀); and C, low-force rigor (force <0.05 T₀). The top of each panel corresponds to a reciprocal spacing of 0.16 nm⁻¹, the bottom to 0.015 nm⁻¹. Resting sarcomere length, 2.14 μm; cross-sectional area, 19,000 μm².

FIGURE 3.

Axial x-ray intensity distributions: A, at rest; B, isometric tetanus plateau; and C, low-force rigor. Intensity data from the fiber in Fig. 2, integrated from 0.013 nm⁻¹ on either side of the meridional axis and normalized by exposure time in each condition. M1, M2, M3, M4, M5, and M6 indicate the myosin-based axial reflections. A1 indicates the actin-based axial reflection at 38.4 nm.

At the plateau of an isometric tetanus the M1, M3, and M6 reflections had roughly the same intensities as in the resting fiber, but the M2, M4, and M5 reflections became very weak (Figs. 2 B and 3 B). The M3 reflection was clearly split into two peaks during isometric contraction (Figs. 2 B and 3 B; Linari et al., 2000). The intensity of the higher angle peak at 14.462 nm was 76% of that of the lower angle peak at 14.661 nm (Table 1). The mean spacing of the M3 reflection (S_M3), calculated as the intensity-weighed mean of its component peaks, was 14.575 nm, 1.6% larger than that at rest, 14.34 nm (Huxley and Brown, 1967; Linari et al., 2000). The M6 reflection was also split into two peaks during isometric contraction (Fig. 3 B), and the intensity of its higher angle peak was 55% of that of the lower angle peak, similar to the ratio at rest (Fig. 3 A; Linari et al., 2000). The mean spacing of the M6 reflection (S_M6) during isometric contraction was 7.29 nm (Table 1), 1.7% larger than that at rest, 7.17 nm.

TABLE 1.

Spacings (nm) of the component peaks of the M2, M3, and M6 reflections: European Synchrotron Radiation Facility

	M2			M3			M6
	Peak 1	Peak 2	Peak 3	Peak 1	Peak 2	Peak 3	SM3	Peak 1	Peak 2	SM6
Isometric contraction				14.462 0.011	14.661 0.012		14.575 0.012	7.261 0.005	7.312 0.003	7.293 0.004
Low-force rigor	21.171 0.009	21.657 0.011	22.396 0.010		14.407 0.006	14.600 0.008	14.444 0.006			7.247
High-force rigor	21.207 0.026	21.711 0.038	22.433 0.021	14.321 0.040	14.461 0.021	14.619 0.040	14.461 0.023			7.265

Numbers in italics are standard deviations for five, eight, and two fibers in isometric contraction (T₀), low-force rigor (<0.1 T₀), and high-force rigor (0.55 T₀), respectively. S_M3 and S_M6 are the intensity-weighted means of the component peaks of the M3 and M6 reflections, respectively. In rigor, S_M6 could be determined reliably only from the sum of the intensity distributions from all the fibers studied, and no standard deviation is given.

In low-force rigor (Figs. 2 C and 3 C), the M3 and M6 reflections were weaker than during isometric contraction, but the M2 was almost as intense as at rest. The ratio of the intensity of the M3 reflection (I_M3) in low-force rigor to that during isometric contraction was 0.32 ± 0.14 (n = 6 fibers, mean ± SD). The radial width of the reflection was 20% smaller in rigor (Fig. 2, B and C), suggesting a greater degree of axial alignment between neighboring myosin filaments in the myofibril. The product of the observed axial intensity and the radial width of the M3 reflection in each condition was used to estimate the change in I_M3 associated with the mass distribution along an individual filament (Huxley et al., 1982). This corrected I_M3 value in low-force rigor was 0.25 ± 0.10 of that in isometric contraction.

The main peak of the M3 reflection in low-force rigor had a spacing of 14.407 nm, and there was a second peak, with intensity 24% of that of the main peak, at 14.600 nm (Table 1). S_M3 was 14.444 ± 0.006 nm in low-force rigor, intermediate between the values at rest, 14.34 nm, and in isometric contraction, 14.575 nm, and clearly distinct from both. S_M3 was 0.9% smaller in low-force rigor than during isometric contraction. The M6 reflection was weak in low-force rigor (Fig. 3 C), but appeared as a single peak with mean spacing (S_M6) of 7.247 nm (Table 1), which is 0.6% less than that during isometric contraction.

Effect of stretch on the axial x-ray reflections in rigor

The effect of stretch on the intensities of the axial x-ray reflections in rigor was measured using a gas-filled detector at beam line 16.1 (CCLRC). When fibers were stretched by ∼4 nm per half-sarcomere (Fig. 4 A) so that the force increased to 0.45 ± 0.15 (mean ± SD, three fibers) of the active isometric force (T₀), I_M3 increased to 137 ± 2% of its low-force value (Fig. 4 B). This increase occurred without significant change in the radial width of the reflection (Fig. 4 C). A similar increase in I_M3 was reported previously for the stretch phase of a 3-kHz length oscillation of isolated rigor fibers (Dobbie et al., 1998) and after slow stretch of whole muscles (Takezawa et al., 1999). This increase in I_M3 is likely to be due to elastic strain of the myosin head that results in a narrowing of its axial mass projection. The intensity of the M2 reflection (I_M2), did not change significantly when fibers were stretched to 0.45 T₀ in rigor (Fig. 4 B); I_M2 at the higher force was 0.97 ± 0.04 of that at low force.

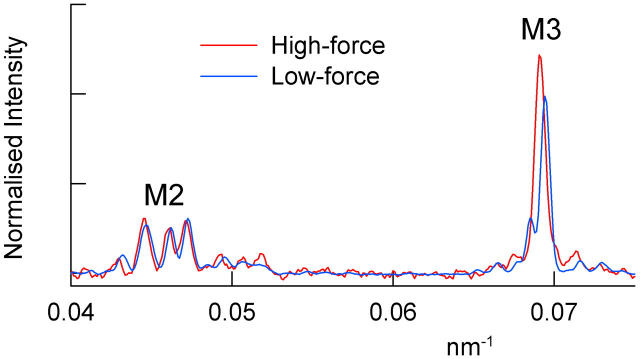
The effect of stretch on the fine structure of the axial x-ray reflections from fibers in rigor was investigated using the higher spatial resolution of the ID2 beam line at ESRF, Grenoble, with an image plate detector (Fig. 5). This facility did not allow precise measurements of the relative intensities of each reflection before and after the stretch, so the axial intensity distributions at low force (Fig. 5, blue) and high force (red) were scaled by the total intensity of the M2 reflection, based on the results obtained at Daresbury (Fig. 4).

FIGURE 5.

Effect of stretch on the fine structure of the M2 and M3 reflections in rigor; European Synchrotron Radiation Facility. Blue, low-force (<0.05 T₀; five fibers); red, high-force (0.55 T₀; 2 fibers). Intensities scaled by the total intensity of the M2 reflection. The intensity of the M3 reflection was 27% greater at high force, slightly less than in the more reliable comparison from paired measurements in Fig. 4.

Stretching fibers in rigor from low force (∼0.05 T₀; Fig. 5, blue) to high force (0.55 T₀; Fig. 5, red) altered the interference fine structure of the M3 reflection. The minor peak at 14.600 nm that was observed on the low angle side of the main peak at low force was less prominent at the higher force. The axial intensity distribution of the M3 reflection in high-force rigor was well-fitted by a major Gaussian peak at 14.461 nm and two almost symmetrically disposed minor peaks with intensities <10% of that of the main peak, at 14.321 and 14.619 nm (Table 1). These changes in the fine structure of the M3 reflection are in the direction expected from an increase in the interference distance as actin-attached myosin heads are pulled away from the midpoint of the myosin filament, as shown in detail below.

The mean spacing of the M3 reflection (S_M3) increased from 14.444 nm at low force to 14.461 nm at 0.55 T₀ (Table 1). This spacing change corresponds to a myosin filament compliance (〈S_M〉; Piazzesi et al., 2002) of ∼0.2%/T₀ in rigor. This is similar to the value measured by applying slow stretch to whole muscles of Rana catesbiana in the rigor state, 0.26%/T₀ (Takezawa et al., 1999). Both these values are intermediate between that measured during a 100-μs length step in active contraction of intact single fibers from R. temporaria, 0.14 ± 0.03%/T₀, and that measured ∼1 ms later after the rapid force response to the step, 0.34 ± 0.05%/T₀ (Piazzesi et al., 2002).

The higher resolution of the ESRF beam line also revealed several component peaks in the M2 reflection in rigor (Fig. 5). The three most prominent peaks had spacings of 21.171, 21.657, and 22.396 nm at low force (Table 1). Since these peaks are not uniformly spaced, they are unlikely to be due to a simple interference effect between myosin heads in the two halves of the myosin filament. When the fiber was stretched to 0.55 T₀, the spacing of each of the three peaks increased by about the same amount (Table 1), corresponding to an apparent compliance of ∼0.4%/T₀, twice that inferred from the corresponding change in S_M3 (Table 1). Moreover, the relative amplitudes of the three M2 peaks were not affected by stretch, in contrast with the behavior of the M3 reflection. These results suggest that the M2 and M3 reflections observed in fibers in rigor arise from different structural components (see Discussion).

Axial motions of myosin heads

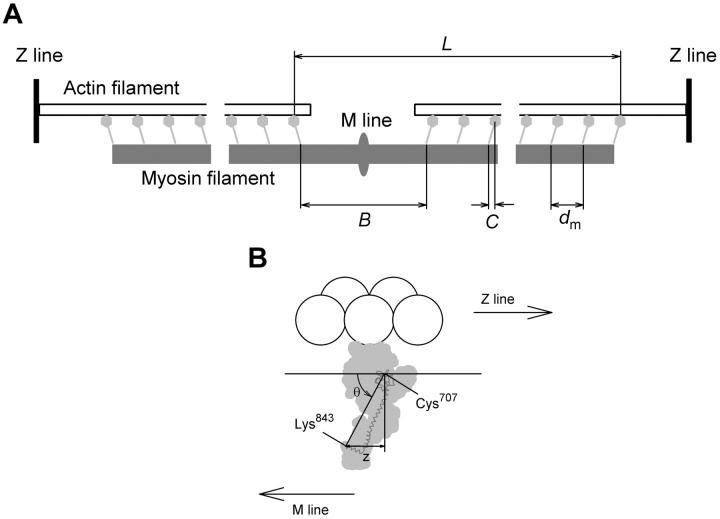
Center of mass analysis

The fine structure of the M3 reflection in isometric contraction and in rigor was analyzed in terms of interference between the two arrays of myosin heads in each myosin filament (Fig. 6 A). Each half-filament contains 49 levels of myosin heads with an axial spacing (d_m) of ∼14.5 nm. At the midpoint of the filament is a bare zone of length B, defined as the separation between the head-rod junctions of the pair of heads nearest the midpoint of the myosin filament, or M-line. There is an axial displacement C between the center of mass of each level of myosin heads and their head-rod junctions. The mass distribution along the filament can then be considered in terms of 49 pairs of head levels, where the centers of mass of each pair are separated by an interference distance L = B + 48d_m + 2C (Fig. 6 A). To a good approximation, the interference fine structure of the M3 reflection is determined solely by the mean axial position of the centers of mass of the myosin heads; for a given mean axial position the conformation and disorder of the heads have little effect (Linari et al., 2000; Piazzesi et al., 2002). Thus the axial intensity distribution of the M3 reflection may be calculated as the product of 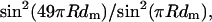from the Fourier transform of an array of 49 points with spacing d_m, multiplied by an interference fringe pattern proportional to cos² πRL, where R is the reciprocal space parameter in the region of the M3 reflection.

FIGURE 6.

Sarcomeric location and conformation of myosin head domains. (A) Myosin heads (light gray) with head-rod junctions (Lys⁸⁴³) connected to the myosin filament backbone (dark gray) at axial periodicity d_m, except for the central bare zone of length B. The center of mass of each level of myosin heads is displaced from its head-rod junction by a distance C. The interference distance (L) is defined in the text. (B) Myosin head (light gray) with catalytic domain (residues 1–707 of the chicken skeletal myosin heavy chain sequence) attached to an actin monomer (white sphere) in the conformation of Rayment et al. (1993a,b), and light chain domain (residues 707–843 of the myosin heavy chain (dark gray) and both light chains) rotated around Cys⁷⁰⁷ so that the Cys⁷⁰⁷–Lys⁸⁴³ axis makes an angle θ with the filament axis. z denotes the axial displacement of the catalytic domain (with Cys⁷⁰⁷ as reference residue) with respect to Lys⁸⁴³.

At the plateau of an isometric tetanus, the ratio of the intensity of the higher angle peak of the M3 reflection to that of the lower angle peak (I_HA/I_LA) was 0.76, and the mean spacing of the reflection (S_M3) was 14.575 nm (Table 1). According to the equations given above, these values require B_i + 2C_i = 166.68 nm, d_mi = 14.573 nm, where the subscript i denotes isometric contraction.

In low-force rigor (lfr), I_HA/I_LA was 4.0 and S_M3 was 14.444 nm. These values can be reproduced by d_mlfr = 14.446 nm and B_lfr + 2C_lfr = 155.95 nm. In practice the interference method cannot distinguish between this value of B_lfr + 2C_lfr and values that are larger or smaller by d_mlfr. The value B_lfr + 2C_lfr = 155.95 nm was chosen because it is smaller than B_i + 2C_i, as expected for myosin heads tilting so that their actin-bound ends move toward the midpoint of the myosin filament in the transition between isometric contraction and low-force rigor (Reedy et al., 1965; Dobbie et al., 1998). It follows that the decrease in B + 2C associated with this transition must be large, almost 11 nm. Changes in B related to changes in the axial periodicity of the myosin filament make a small contribution to this decrease. B is expected to be slightly smaller in low-force rigor than at the plateau of the isometric tetanus (at T₀) because of the compliance of the myosin filament. Assuming that mean myosin filament compliance is 0.14%/T₀ (Piazzesi et al., 2002) and that the strain in the bare zone is twice the average strain in the overlap region (Linari et al., 1998), the effect of filament compliance would be to make B smaller by 0.28%, or 0.5 nm, in low-force rigor. However, the observed difference in myosin filament periodicity between low-force rigor (d_mlfr = 14.446 nm) and the plateau of the isometric tetanus (d_mi = 14.573 nm) is greater than expected from the instantaneous compliance of the myosin filament and the difference in force; if this change in d_m were due to a separate structural change distributed uniformly along the myosin filament, it would cause an additional decrease in B of 1.2 nm. Thus we estimate that only (1.2 + 0.5 = 1.7 nm) of the observed 10.8 nm decrease in B + 2C is due to changes in B, so the term 2C accounts for the remaining 9.1 nm, and C_i − C_lfr = 4.5 nm. The change in conformation of the myosin heads between isometric contraction and low-force rigor involves an axial motion of their centers of mass, measured with respect to their head-rod junctions, by 4.5 nm toward the midpoint of the myosin filament.

A similar analysis was applied to the comparison between low-force and high-force rigor. In the latter state (hfr) the M3 reflection is dominated by a single peak, with spacing 14.461 nm, which we take as the best estimate of S_M3 (Fig. 5). Although it was difficult to measure the value of I_HA/I_LA precisely in high-force rigor, the interference distance can be estimated from the observation that the intensities of both the low- and high-angle side peaks of the reflection were <10% of that of the main peak. This experimental constraint corresponds to a range of B_hfr + 2C_hfr from 158.57 to 159.57 nm, with d_mhfr = 14.461 nm. Stretching the rigor fiber produced an increase in B + 2C of 2.6–3.6 nm. Of this, only 0.4 nm can be explained by the increase in B corresponding to the observed increase in filament periodicity from d_mlfr = 14.446 nm to d_mhfr = 14.461 nm, so 2C changes by 2.2–3.2 nm, and C_hfr − C_lfr is in the range 1.1–1.6 nm. Stretching the rigor fiber by ∼4 nm/half-sarcomere to increase the rigor force by 0.55 T₀ moved the centers of mass of the myosin heads 1.1–1.6 nm farther from the midpoint of the myosin filament with respect to their head-rod junctions.

Conformations of the myosin heads

The changes in myosin head conformation corresponding to these axial motions of their centers of mass were calculated using a crystallographic model of the myosin head structure (Fig. 6 B). The catalytic domain of each head was assumed to bind to actin in the conformation determined by cryoelectron microscopy of the nucleotide-free complex (Rayment et al., 1993b). The light chain domain was assumed to pivot at Cys⁷⁰⁷ (Dominguez et al., 1998; Houdusse et al., 2000) to allow axial tilting of actin-attached heads during filament sliding. This model of the conformational change in the myosin head can be used to calculate the relationship between the axial motion of the center of mass of the myosin head (ΔC, the change of C in Fig. 6 A) and that of Cys⁷⁰⁷ and the whole catalytic domain of the myosin head (Δz, the change of z in Fig. 6 B). Both ΔC and Δz are defined with respect to the axial position of the head-rod junction (Lys⁸⁴³). For a given tilting of the light chain domain of the myosin head in this model, Δz is 29% larger than ΔC.

In the transition between isometric contraction and low-force rigor, we found that the centers of mass of the myosin heads moved by C_i − C_lfr = 4.5 nm. According to the crystallographic model in Fig. 6 B, z_i − z_lfr is therefore 4.5 × 1.29 = 5.8 nm. During isometric contraction, C_i is 2.8 nm and the angle θ between the Cys⁷⁰⁷–Lys⁸⁴³ vector and the filament axis is ∼65° (Irving et al., 2000; Piazzesi et al., 2002). The 5.8-nm motion of the catalytic domain toward the M-line in low-force rigor requires an increase in θ of 36°, so the mean angle between the Cys⁷⁰⁷–Lys⁸⁴³ vector and the filament axis in low-force rigor can be estimated as 101°. This is essentially identical to the value, 102°, measured by cryoelectron microscopy of myosin head fragments bound to isolated actin filaments in the absence of ATP (Rayment et al., 1993b).

In high-force rigor, the center of mass of the heads was 1.1–1.6 nm farther from the midpoint of the myosin filament, corresponding to θ = 91–94°. Comparison with the value of θ in low-force rigor suggests that stretching the rigor fiber to produce a force increase of 0.55 T₀ tilted the light chain domain of the myosin heads by 7–10°. The associated change in form factor of the heads in this structural model would produce an increase in the total intensity of the M3 reflection of 33–50%, similar to the intensity increase, 37%, that we observed for a slightly smaller force increase, 0.45 T₀ (Fig. 4).

Two-headed models for myosin

So far we have neglected the fact that each myosin molecule has two head domains, both of which are bound to actin in rigor (Cooke and Franks, 1980; Thomas and Cooke, 1980; Lovell et al., 1981). Since the two heads share a junction with the myosin rod, they are both likely to contribute to the M3 reflection. We therefore constructed a structural model for the myosin filament that included the two heads of each myosin molecule, and calculated the intensity profile in the region of the M3 reflection from the Fourier transform of the axial mass projection of this model.

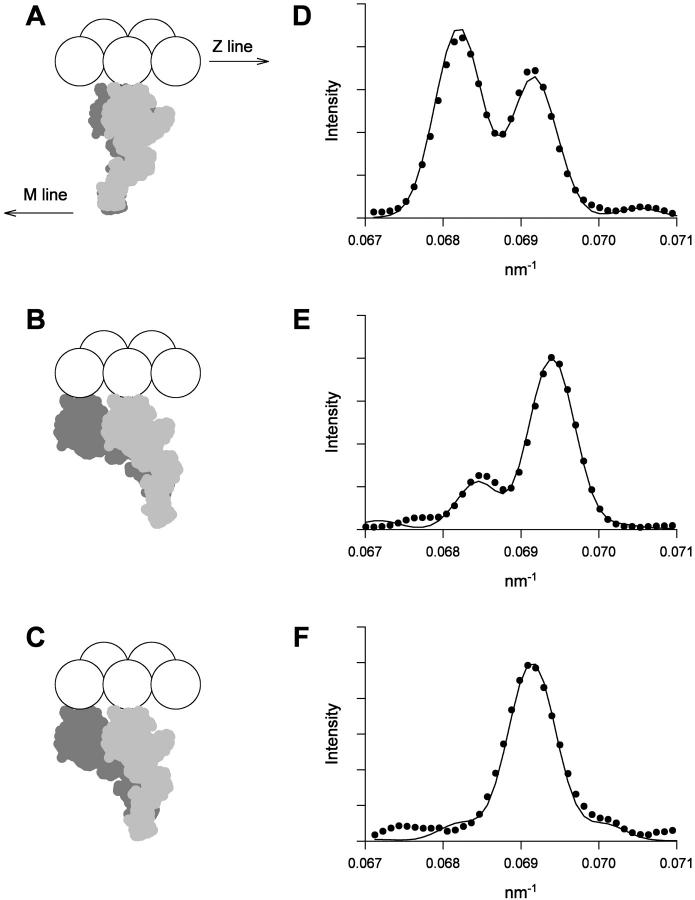
In the model for isometric contraction (Fig. 7 A) each myosin molecule has one head with θ = 60° (dark gray) and one with θ = 70° (light gray), as deduced from our previous studies of the change in the M3 reflection during rapid length changes applied to actively contracting muscle fibers (Irving et al., 2000; Piazzesi et al., 2002). Only one of these heads, that with θ = 60°, is strongly bound to actin (Piazzesi et al., 2002). The values of B_i + 2C_i (166.68 nm) and d_mi (14.573 nm) were taken from the center-of-mass analysis described above, giving B_i = 161.14 nm. The slight discrepancy between the calculated axial intensity distribution in the region of the M3 reflection (Fig. 7 D, continuous line) and the observed distribution (circles) is due to the approximation in the center of mass analysis arising from the assumption that each myosin molecule diffracted as a point mass.

FIGURE 7.

M3 intensity profiles calculated from the two-head model. (A and D) Isometric contraction. (B and E) Low-force rigor. (C and F). High-force rigor. In A–C, the two heads of one myosin molecule are shown in light and dark gray; actin monomers are shown as white spheres. In D–F, the experimental intensity profiles are shown as black circles and the profiles calculated from the two-head model convolved with the point-spread function of the x-ray beam and detector are shown as continuous lines.

In rigor (Fig. 7, B and C) we assumed that the two heads of each myosin again share a head-rod junction, but attach to adjacent monomers on one strand of the actin filament, with axial separation 5.46 nm (Huxley and Brown, 1967). The value of B in low-force rigor, B_lfr, was calculated as 159.51 nm by correcting the value of B_i in the previous paragraph for small changes in filament periodicity as described for the center-of-mass model, and the value of d_m in low-force rigor, d_mlfr, was 14.446 nm as before. Since the two heads are assumed to share a head-rod junction, a single adjustable parameter describes the orientations of the light chain domains of the pair of heads. The observed fine structure of the M3 reflection in low-force rigor (Fig. 7 E, circles) was reasonably well fit with θ values 92° and 127° for the two heads (Fig. 7, B and E, continuous line). These values bracket that (101°) inferred above from the center-of-mass analysis, and that (102°) from cryoelectron microscopy of isolated myosin heads bound to actin in the absence of nucleotide (Rayment et al., 1993b).

In high-force rigor (Fig. 7, C and F), B_hfr was 159.84 nm and d_mhfr was 14.461 nm. The observed fine structure of the M3 reflection (Fig. 7 F, circles) was quite well reproduced with θ = 80° and 113° for the two heads (Fig. 7 C). Applying the constraint that the intensities of both the low- and high-angle side peaks of the reflection are <10% of that of the main peak, as in the center-of-mass analysis, the range of θ values in high-force rigor was 78–82° for one head and 111–115° for the other. Thus the tilt of both light chain domains produced by an increase in the rigor force of 0.55 T₀ was 10–14°, slightly greater than the 7–10° estimated above from the center-of-mass analysis in conjunction with the single head model. According to the two-head model, the rigor stretch would produce an increase in the total intensity of the M3 reflection, I_M3, of 107–150%, much larger than the 37% increase observed for the slightly smaller stretch that increased the rigor force by 0.45 T₀ (Fig. 4).

Long-range order of the actin filament

The effect of the long-range order of the actin filament on the myosin-based axial reflections was assessed using a model in which the catalytic domains of myosin heads bind to actin monomers with axial periodicity d_a, while their head-rod junctions retain the myosin filament periodicity d_m (Fig. 8). The helical nature of the filaments and their arrangement in the transverse filament lattice are neglected in this one-dimensional model. The catalytic domains of the heads were assumed to bind to actin monomers in the conformation of Rayment et al. (1993b), as before, and the incommensurate periodicities of the myosin and actin filaments are accommodated by tilting of the light chain domain. At the plateau of an isometric contraction (force T₀), we assumed that one head of each myosin in each of the 49 levels of heads in a half-sarcomere binds to the nearest actin monomer, i.e., the binding site that requires the smallest axial displacement of its catalytic domain. The other head of each myosin is not bound to actin, and has θ = 70° as in Fig. 7 A. In rigor, we assumed that the two heads of each myosin bind to adjacent actin monomers on the same strand of the actin filament. The orientation of the light chain domain of the myosin heads in either isometric contraction, low- or high-force rigor, averaged over the 49 levels, was fixed at that obtained from the two-head model and described in the previous section (Fig. 7, A, B, and C, respectively). For simplicity, the distribution of head conformations was assumed to be symmetrical about the M-line.

FIGURE 8.

Sarcomeric location of myosin heads; model with long-range order of the actin filament. The two heads of each myosin (black and light gray) bind to adjacent actin monomers (circles) with axial periodicity d_a, but share a head-rod junction with the axial periodicity (d_m) of the myosin filament (dark gray). Only half the sarcomere is shown; axial intensity distributions were calculated from this model under the assumption that the sarcomere was symmetrical across the M-line.

The fine structure of the M3 reflection in isometric contraction calculated from this model (Fig. 9 A, continuous line) was in reasonably good agreement with the experimental intensity distribution (Fig. 9 A, circles), although the relative amplitude of the two component peaks of the M3 reflection was slightly different from that calculated without taking into account the long-range order of the actin filament (Fig. 7 D). In low-force rigor (Fig. 9 B), the model with long-range actin order (continuous line) again reproduced the main features of the fine structure of the M3 reflection (circles), although the relative amplitude of the low-angle side peak was too low, and the best fit to this parameter required θ values ∼5° greater than those obtained from the model without long-range actin order (Fig. 7 E).

FIGURE 9.

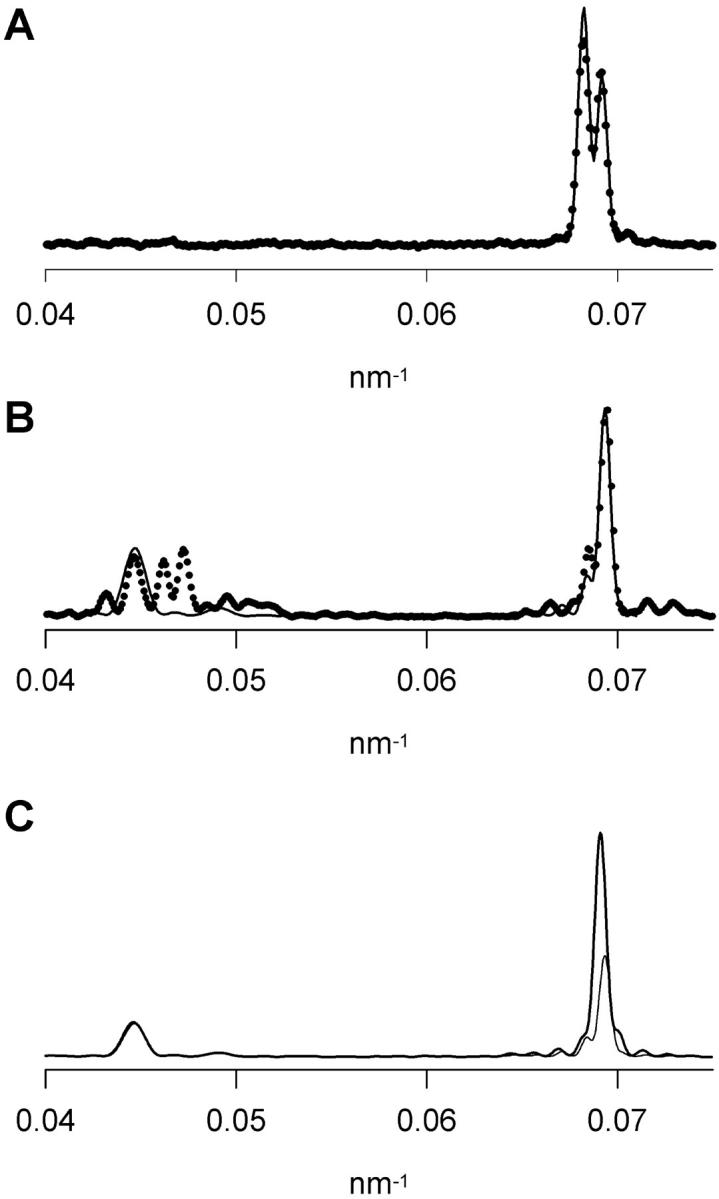
Axial intensity profiles of the M2 and M3 reflections calculated from models with long-range actin order. (A) Isometric contraction; circles, experimental intensity distribution; continuous line, calculated intensity distribution. (B) Low-force rigor; circles, experimental intensity distribution; continuous line, calculated intensity distribution. (C) Comparison of calculated distributions for low-force rigor (thin line) and high-force rigor (thick line).

The axial intensity distribution calculated from this model for low-force rigor (Fig. 9 B, continuous line) shows an extra reflection at 22.4 nm, coinciding with one of the components of the M2 reflection observed in rigor (Fig. 9 B, circles). The relative intensity of the 22.4-nm and M3 reflections calculated from the model was similar to that of the observed reflections. In a variant of the model in which the constraint that the two heads of each myosin bind to adjacent actin monomers was removed, the relative intensity of the 22.4-nm reflection was reduced by ∼50%. In contrast with the behavior of the M3 reflection, the 22.4-nm reflection is not sensitive to tilting of the myosin heads; the calculated intensity and profile of the 22.4-nm reflection was the same in low-force and high-force rigor (Fig. 9 C), in agreement with the experimental results (Figs. 4 and 5).

During isometric contraction, the relative intensity of the 22.4-nm and M3 reflections calculated from the model of Piazzesi et al. (2002), in which only one of the two heads of each myosin is strongly bound to actin, was 0.02, consistent with the very low intensity observed at 22.4 nm under these conditions (Fig. 9 A). These results provide further support for the myosin head conformations during isometric contraction proposed by Piazzesi et al. (2002).

DISCUSSION

X-ray interference measurement of the axial motions of myosin heads

The axial x-ray reflections from the myosin filaments in skeletal muscle are modulated by a series of finely spaced fringes that arise from interference between the two arrays of myosin heads in each filament (Haselgrove, 1975; Linari et al., 2000). This interference effect can be precisely characterized in single muscle fibers using the M3 x-ray reflection from the axial periodicity of the myosin heads along the filaments, and provides an extremely sensitive measure of axial motions of the myosin heads toward or away from the midpoint of the myosin filament, the M-line of the sarcomere (Linari et al., 2000; Piazzesi et al., 2002). The interference modulation of the M3 x-ray reflection depends primarily on the axial separation of the centers of mass of the myosin heads and, for a given center-of-mass separation, is almost independent of the shape of the heads, their orientation with respect to the filament axis, and their axial disorder. For the purpose of investigating the structural changes in the myosin heads that drive muscle contraction, this feature is both a limitation and an advantage. The limitation is that it is not possible to calculate the conformation or orientation of the myosin heads in a particular contractile state solely from the interference fine structure of the M3 reflection in that state. The advantage is that the average axial motion of the center of mass of the heads can be measured precisely in the presence of unknown changes in head conformation, orientation, and/or disorder. With a suitable protocol, this measurement can distinguish between alternative mechanisms for the action of myosin heads (Piazzesi et al., 2002).

In the present work we used the x-ray interference method to measure the axial motion of the center of mass of the myosin heads between the well defined steady states of isometric contraction and rigor. There was a large change in the interference fine structure of the M3 reflection between these two states, corresponding to an axial motion of the center of mass of the myosin heads by 4.5 nm toward the midpoint of the myosin filament. Although the transition was also accompanied by a small change in the axial periodicity of the myosin filament, the effect of the periodicity change on the interference fine structure was an order of magnitude smaller than that of the motion of the myosin heads with respect to their myosin filament attachments. We used the measured motion of the center of mass of the heads, in combination with previous estimates of their conformation during isometric contraction (Irving et al., 2000; Piazzesi et al., 2002), to deduce the conformation of the myosin heads in rigor.

The conformation of the myosin heads in low-force rigor

Myosin head conformations were calculated under the assumption that the catalytic domain of each head binds to actin as determined by cryoelectron microscopy of the nucleotide-free complex (Rayment et al., 1993b), but that the light chain domain can pivot at Cys⁷⁰⁷ (Dominguez et al., 1998; Houdusse et al., 2000). Although this model is based on in vitro studies, dipole probes attached to the catalytic domain in rigor muscle fibers have shown that the two catalytic domains of each myosin have the same orientation with respect to the fiber axis, and that this orientation is the same as that in isolated myosin head fragments bound to actin in the absence of ATP (Thomas and Cooke, 1980). Moreover, the orientation of the catalytic domain probes is not altered by stretching a muscle fiber in rigor (Cooke, 1981; Berger et al., 1996). Thus the conformation of each myosin head in a rigor muscle fiber can conveniently be described by a single parameter, the angle θ between the Cys⁷⁰⁷–Lys⁸⁴³ vector and the filament axis (Fig. 6 B).

We also assumed that the catalytic domain of the myosin head has the same orientation in isometric contraction and in rigor (Irving et al., 2000; Piazzesi et al., 2002). This is an oversimplification (Cooke et al., 1982; Taylor et al., 1999). However, because the interference fine structure of the M3 reflection is almost independent of myosin head conformation per se, this assumption has little effect on the 4.5-nm estimate of the axial motion of the center of mass of the myosin heads between isometric contraction and rigor. Our estimates of head conformation in rigor do depend on the axial displacement between the center of mass of the head and the head-rod junction during isometric contraction (C_i, Fig. 6 A). This was estimated from the changes in the total intensity of the M3 reflection (I_M3) during rapid (submillisecond) changes of fiber length imposed in isometric contraction (Dobbie et al., 1998; Irving et al., 2000; Piazzesi et al., 2002). Those experiments showed that the myosin heads tilt during small shortening steps so that I_M3 reaches its maximum value, corresponding to the head conformation with the narrowest axial mass projection, for shortening steps of 1–2 nm. If the catalytic domain of the myosin head binds to actin in the same orientation during isometric contraction and in rigor, the value of C_i deduced from these I_M3 data is 2.8 nm. The exact value of C_i will depend on the distribution of myosin head conformations during isometric contraction, which remains to be characterized in detail.

In the simplest model for the conformation of the myosin heads in rigor, the light chain domains of all the myosin heads were assumed to have the same orientation θ, defined as the angle between the Cys⁷⁰⁷–Lys⁸⁴³ vector and the filament axis (Fig. 6 B). With this model, the observed interference fine structure of the M3 x-ray reflection in low-force rigor was reproduced with θ = 101°. When the model was extended to consider two heads of each myosin binding to adjacent monomers of the same strand of the actin filament, the best-fit values of θ for the two heads were 92° and 127°, respectively. When the long-range order of the actin filament was taken into account, the corresponding best-fit values of θ were 97° and 132°.

The value of θ deduced from the single-head model is close to that, 102°, determined by docking the crystallographic structure of the myosin head into cryoelectron microscopic reconstructions of the actin-myosin head complex in the absence of ATP (Rayment et al., 1993b). In the two-head models, the values of θ for the two heads bracket that in the Rayment et al. (1993b) model. Thus the average orientation of the light chain domain in native myosin heads in rigor muscle fibers is close to that in the isolated actin-myosin rigor complex. This conclusion is consistent with the changes in the intensities of axial and layer-line x-ray reflections produced by stretching frog muscle fibers in rigor (Dobbie et al., 1998; Takezawa et al., 1999).

The rigor orientation of the light chain domain in single fibers from rabbit psoas muscle has been estimated from the polarized fluorescence from bifunctional rhodamine probes on the myosin regulatory light chain (Corrie et al., 1999; Hopkins et al., 2002). Although Corrie et al. (1999) used different reference axes to describe the orientation of the light chain domain, their results correspond to an average value of θ as defined here of 77° for native myosin heads in rigor, and 82° for exogenous myosin head fragments bound to actin filaments in the absence of ATP. Hopkins et al. (2002), using the same probe technique, interpreted the fluorescence changes produced by applying small stretches to rigor fibers in terms of two roughly equal populations of myosin heads, centered on θ values of 70° and 97°, with only the 97° population tilting in response to the length steps. In both sets of results, there was considerable disorder about these mean orientations, corresponding to a Gaussian standard deviation of ∼20°.

The polarized fluorescence technique measures the twist or rotation (γ) of the light chain domain around the Cys⁷⁰⁷–Lys⁸⁴³ axis in addition to θ. Because the light chain domain is bent, its mass is not arranged symmetrically around the Cys⁷⁰⁷–Lys⁸⁴³ axis, and the axial mass distribution of the myosin heads bound to actin in rigor depends on γ as well as θ. The mean value of γ in rigor muscle fibers (Corrie et al., 1999) is more than 30° greater than in the Rayment et al. (1993b) model used here to interpret the x-ray interference data. This may explain at least part of the difference between the mean values of θ in rigor deduced from the polarized fluorescence and x-ray interference data.

The conformation of the light chain domains of native myosin heads in insect flight muscle in rigor was recently described in detail by electron tomography and molecular modeling (Chen et al., 2002). The catalytic domain of the myosin heads was assumed to bind to actin in the conformation of Rayment et al. (1993b), as in the present work. The light chain domain was modeled as six rigid bodies, but the mean angle θ between the Cys⁷⁰⁷–Lys⁸⁴³ axis and the filament axis was 100°, close to the average value calculated here from the x-ray interference data. The average twist angle γ determined by Chen et al. (2002) was ∼40° smaller than that of Corrie et al. (1999).

The comparison with dipole probe and electron imaging techniques highlights the essentially one-dimensional character of structural measurements by x-ray interference. The latter is uniquely sensitive to the axial motions of myosin heads, but detailed interpretation of these motions in terms of myosin head conformations requires three-dimensional structural data from other methods. At present, such data are ambiguous or incomplete for myosin heads in situ. Despite this, there is a broad consensus between x-ray interference, dipole probe, and electron microscopical studies that the tilt angle of the light chain domain of native myosin heads in rigor muscle at low force is similar to that in the isolated actin-myosin head complex in the absence of ATP. This similarity may be related to the fact that the mean elastic strain in the myosin heads is close to zero in both conditions.

Effect of strain on the conformation of the rigor heads

When muscle fibers in rigor were stretched to a force of 0.55 times that in isometric contraction (T₀), the change in the interference fine structure of the M3 reflection showed that the center of mass of the myosin heads moved 1.1–1.6 nm away from the midpoint of the myosin filament (the M-line of the sarcomere). If the orientation of the light chain domain is the same in all the myosin heads (one-head model), this corresponds to a decrease in θ of 7–10°. In the two-head model the corresponding decrease was 10–14° in each head.

The total intensity of the M3 reflection (I_M3) increased by 37% for a stretch of 0.45 T₀ (Fig. 4), within the range expected for the one-head model, 33–50%, but considerably smaller than that expected for the two-head model, 107–150%. This large discrepancy arises from the relatively small difference between the average values of θ in low-force rigor: 102° in the one-head model and 109° in the two-head model. If the average θ in low-force rigor in the two-head model is reduced to 102°, the 10° decrease in θ associated with the transition to high-force rigor increases I_M3 by 50%, similar to that calculated using the one-head model. Thus we do not consider that the observed I_M3 changes provide strong evidence to favor this model over the two-head model. The estimates of head conformations from the interference fine structure of the M3 reflection are likely to be more reliable than those based on I_M3, because the latter depends on the axial order of the myosin heads as well as on θ.

The axial motion C of the center of mass of the myosin heads produced by stretching a rigor fiber to 0.55 T₀ was 1.1–1.6 nm. According to the tilting light chain domain model, the relative motion (z) of the catalytic domain of the myosin head with respect to its junction with the myosin rod is 1.29 times larger, i.e., 1.4–2.1 nm. Assuming that the axial motion is linearly related to the force change, this corresponds to 2.6–3.8 nm/T₀, which is larger than expected from the instantaneous compliance of the half-sarcomere and filaments. The total compliance of the half-sarcomere in rigor, measured with submillisecond length steps or 3 kHz sinusoidal length oscillations, is 2.6–4.3 nm/T₀ (Linari et al., 1998; Dobbie et al., 1998). More than half of this compliance is in the actin and myosin filaments, and the instantaneous compliance associated with the myosin heads is only 1.2–1.9 nm/T₀ (Linari et al., 1998; Dobbie et al., 1998). However, during the relatively slow ramp stretches used in the present experiments, the apparent compliance of the half-sarcomere is ∼6 nm/T₀, considerably larger than the instantaneous compliance (Linari et al., 1998). After correcting for filament compliance as before, these mechanical measurements suggest that the apparent myosin head compliance during a slow ramp stretch in rigor is ∼3 nm/T₀, similar to the 2.6–3.8 nm/T₀ range estimated above from the x-ray interference data.

The observation that the apparent mechanical compliance of myosin heads is larger during slow than during fast length changes of a rigor fiber suggests either that myosin heads slip between actin monomers during a slow stretch, or that there is a slow mechanical relaxation within the actin-attached head. The x-ray interference data are inconsistent with the first of these hypotheses, because slippage between actin monomers would reduce the net axial motion of the myosin heads during slow stretch (Piazzesi et al., 2002). The present results suggest that stretching myosin heads in rigor produces both an instantaneous distortion (Dobbie et al., 1998) and a delayed conformational change in the same direction—the slow mechanical relaxation within the attached head. This would also explain why the increase in I_M3 during the stretch phase of a 3kHz oscillation (∼14% for a force increase of ∼0.55 T₀; Dobbie et al., 1998) is smaller than that during slow ramp stretch (37% for a force increase of 0.45 T₀; Fig. 4). The kinetics and structural basis of the delayed conformational change in the rigor head and its relationship to the working stroke in active contraction will be the subject of future x-ray interference studies.

The origin of the M2 reflection in rigor muscle

The M2 reflection in rigor muscle exhibits three relatively intense peaks (Fig. 5). One of these, with a spacing of ∼22.4 nm, was reproduced by a structural model in which the two heads of each myosin molecule bind to actin monomers with axial periodicity 5.46 nm on the long-pitched strand of the actin filament, while the head-rod junction retains the myosin filament periodicity. The calculated relative intensity of the 22.4-nm and M3 reflections in rigor was larger when the two heads of each myosin were assumed to bind to adjacent monomers along the 5.46-nm periodicity of the actin filament, and this model reproduced the relative intensities observed in rigor fibers quite well (Fig. 9 B). In the model with long-range actin order, the 22.4-nm reflection is dominated by the axial mass distribution of the catalytic domains of the myosin heads. This distribution is not altered by tilt of the light chain domain of the head, which explains why the intensity of the 22.4-nm reflection is not affected by stretch of the rigor fiber (Fig. 4).

The other components of the M2 reflection observed in rigor were not reproduced by the model, and their origin is unknown. It is likely that the M2 reflection in resting muscle also contains components with different structural origins, since the intensities of the higher- and lower-angle components of the M2 decrease with different time courses during development of isometric force at the start of stimulation (Martin-Fernandez et al., 1994). All these M2 components are very weak during active contraction in single muscle fibers (Fig. 3). As far as the 22.4-nm component is concerned, this is consistent with the idea that only one head of each myosin bears the force of active contraction (Piazzesi et al., 2002).