Solvation of Nucleosides in Aqueous Mixtures of Organic Solvents: Relevance to DNA Open Basepairs

Abstract

Toward the goal of understanding how open basepairs in DNA interact with their heterogeneous environment, we have studied the steady-state intrinsic fluorescence properties of the purine and pyrimidine deoxynucleosides in organic solvents in the presence of small amounts of water. The organic solvents used in the present study were: n-butanol, acetonitrile, methanol, n-propanol, isopropanol, and isobutanol. For n-butanol and acetonitrile, which have a high degree of amphiphilicity and weak hydrogen bonding ability, respectively, the fluorescence spectral properties of the purines are found to depend on the sequence of steps in which the aqueous mixtures were formed. By contrast, no such dependence was observed in the mixtures with any of the other solvents used in the present study. Moreover, no such dependence was observed for the pyrimidines. These findings suggest that the final solvation network around the purines is dependent on the nature of the environment to which they were initially exposed. This would tend to present an impediment to the closing of AT or GC basepairs in DNA that become open as a result of structural fluctuations, DNA bending, or protein-DNA interactions.

INTRODUCTION

Water is generally considered to be an integral part of DNA and a major determinant of its structure (Franklin and Gosling, 1953; Saenger, 1987; Westhof, 1988; Berman, 1994). It also appears to play a role in protein-DNA recognition (Otwinowski et al., 1988; Robinson and Sligar, 1993; Qian et al., 1993; Shakked et al., 1994) and DNA-ligands (e.g., drugs) interactions (Kopka et al., 1985; Chalikian et al., 1994). X-ray crystallographic and NMR spectroscopic measurements reported the presence of an ordered spine of hydration in narrow minor grooves (Drew and Dickerson, 1981; Liepinsh et al., 1992; Kubinec and Wemmer, 1992). Furthermore, less structured hydration patterns around the bases were found to be local (Schneider and Berman, 1995).

Structural fluctuations in DNA could result in broken interbase hydrogen bonds and open basepairs. The environment of such bases is heterogeneous as it includes, in addition to interactions with hydrating water, nonpolar, polar, and stacking interactions with adjacent bases and sugars. Basepair opening may play a role in sequence recognition by proteins, DNA replication and transcription, interactions with ligands (e.g., drugs), and DNA photodamage. Consequently, the open state has been extensively studied both experimentally (Mandal et al., 1979; Hartmann et al., 1986; Kochoyan et al., 1987; Guéron et al., 1987; Leroy et al., 1988a,b; Dornberger et al., 1999; Wärmländer et al., 2000) and theoretically (Ramstein and Lavery, 1988, 1990; Briki et al., 1991; Bernet et al., 1997; Chen et al., 1991; Kryachko and Volkov, 2001; Giudice et al., 2001). However, the formation and the nature of the open state are not well understood. Basepair opening and exposure of imino protons to the aqueous environment were reported to occur on the millisecond timescale (Guéron et al., 1987; Leroy et al., 1988a; Dornberger et al., 1999). On the other hand, the internal dynamics of DNA take place on the picosecond-nanosecond timescales (Georghiou et al., 1996). The much slower timescale of basepair opening may be understood on the basis of a mechanism that invokes buildup of such fast fluctuations to rupture the interbase hydrogen bonds (Briki et al., 1991). Theory as well as experiment find that basepairs open one at a time (Gralla and Crothers, 1973; Lukashin et al., 1976; Guéron et al., 1987; Leroy et al., 1988a; Ramstein and Lavery, 1988), and theory suggests that there is a family of open states (Ramstein and Lavery, 1990; Kryachko and Volkov, 2001). DNA bending represents an additional process through which basepair opening can take place (Manning, 1983; Ramstein and Lavery, 1988). The values of the fraction of open basepairs reported in the literature vary over a considerable range, ∼10⁻⁵–10⁻² (Gralla and Crothers, 1973; McGhee and von Hippel, 1977; Wartell and Benight, 1982; Wilcoxon and Schurr, 1983; Wilcoxon et al., 1984; Frank-Kamenetskii, 1985; Chen et al., 1991; Chen and Prohofsky, 1992). This is the result of limitations and uncertainties associated with the experimental and theoretical methods employed, as well as of the fact that different methods probe different open states that range from configurations with exchangeable amino/imino protons with the solvent to completely unstacked basepairs (Wartell and Benight, 1985).

The interaction of open bases with the aqueous environment was investigated mainly with NMR spectroscopic techniques using catalyzed exchange of the imino proton, which have yielded apparent lifetimes of open basepairs that are in general on the nanosecond timescale (Leroy et al., 1988a,b; Guéron and Leroy, 1992; Dornberger et al., 1999; Wärmländer et al., 2000). However, the actual lifetimes may be much longer if, because of steric hindrance, the accessibility of the imino group to the catalyst in the open pair is considerably reduced relative to that in the mononucleoside.

To obtain insights into the interaction of open basepairs with their environment and their ability to reform efficiently, we have investigated the effect of small amounts of water on the fluorescence properties of the purine nucleosides (2′-deoxyguanosine (dG) and 2′-deoxyadenosine (dA)) and the pyrimidine nucleosides (2′-deoxythymidine (dT) and 2′-deoxycytidine (dC)) in organic solvents. The exposure of the nucleosides to water was done in three different ways that gave them initial full exposure to water, initial partial exposure to water, or initial full shielding from water. Whereas the fluorescence spectral properties of both purines and pyrimidines are found to be quite sensitive to the nature of their environment, in solvents of high amphiphilicity or weak hydrogen bonding ability these properties of the purines are found to be also dependent on the nature of the environment to which they were initially exposed. This implied formation of a distribution of solvation networks around the purines is discussed in connection with the closing of basepairs in DNA that are opened by structural fluctuations, DNA bending, or protein-DNA interactions.

MATERIALS AND METHODS

The deoxynucleosides were obtained from the following sources: dA from USB (Cleveland, OH), dG from Sigma (St. Louis, MO), and dT and dC from Calbiochem (La Jolla, CA). Spectral grade methanol was a product of Malinkcrodt (Paris, KY). High purity acetonitrile, isopropanol, isobutanol, and n-butanol manufactured by Burdick and Jackson were obtained from VWR Scientific (Suwanee, GA). HPLC grade n-propanol was obtained from Aldrich (Milwaukee, WI). Triply distilled water was obtained from Carolina Biological Supply (Burlington, NC). These solvents were chosen on the basis of their transmission in the ultraviolet region and the solubility of water and of the nucleosides in them. All nucleosides and organic solvents were checked for fluorescence impurities and were used without further purification. (It is noted for the sake of completeness that the fluorescence of the nucleosides is very weak, quantum yield ∼10⁻⁴ in water (Cadet and Vigny, 1990).)

Absorption measurements were performed in 1 cm quartz cuvettes using a Shimadzu UV-254 spectrophotometer (Columbia, MD). Fluorescence measurements were made in 1 cm quartz cuvettes at right angle to the incident light using a spectrofluorometer that employed the following components: a 1 kW Xe-Hg lamp (Spectral Energy, Hillsdale, NJ), a 0.5 m focal length Bausch and Lomb monochromator (Rochester, NJ), a 0.32 m focal length HR-320 Instruments SA monochromator (Metuchen, NJ), a thermoelectrically cooled 9558 QB EMI photomultiplier (Fairfield, NJ), a Stanford Research Systems SR440 preamplifier (Sunnyvale, CA), and a Stanford Research Systems SR400 photon counter (Sunnyvale, CA). In all measurements, the excitation wavelength was 265 nm. The excitation and emission bandwidths were 5.0 nm and 1.7 nm, respectively. The fluorescence spectra were corrected for the variation of the sensitivity of the photomultiplier-monochromator combination with emission wavelength and for absorbance differences. The estimated uncertainty in the wavelength of the fluorescence spectral peak was ±2 nm, and that in the wavelength of the absorption spectral peak was ±0.25 nm.

Solutions of nucleosides in water-organic solvent mixtures were prepared in three different methods designated as “premixed” solution, “carry its own water” solution, and “injected water” solution. In the “premixed” solution, the water and the organic solvent were first mixed in the desired proportion before dissolving the nucleoside in their mixture. In the “carry its own water” solution, the nucleoside was dissolved in water at a high enough concentration so that an absorbance of ∼0.05 was obtained when a small amount from it was diluted in the organic solvent. Finally, in the “injected water” solution, the nucleoside was first dissolved in the organic solvent and then a small amount of water was added to it. In all the fluorescence measurements, the absorbance of the solutions was kept at ∼0.05 at the excitation wavelength of 265 nm. We have inquired as to whether stacking of these mononucleosides can take place under the conditions of the present experiments. Based on the values of ∼0.05 for the absorbance and ∼11.8 × 10³ M⁻¹ cm⁻¹ for the average molar extinction coefficient (in aqueous buffer) (Voet et al., 1963), the purine concentration is calculated to be ∼4 μM. It is known that purines in aqueous solution undergo stacking interactions for concentrations >∼0.01 M (Bloomfield et al., 1974), a value that is much greater than the concentration of ∼4 μM employed in the present study. It is also known that mononucleosides do not undergo stacking interactions in organic solvents (Ts'o, 1974). These considerations indicate that stacking of purine mononucleosides in the solutions employed in the present study is very unlikely. This should also be the case for the pyrimidine mononucleosides that are known to stack less than the purine mononucleosides in aqueous solution (Bloomfield et al., 1974; Ts'o, 1974). (Their average molar extinction coefficient at 265 nm is ∼8.9 × 10³ M⁻¹ cm⁻¹ (Voet et al., 1963), which yields for their concentration a value of ∼6 μM that is similar to that of the purine mononucleosides.)

All fluorescence measurements were made at room temperature under steady-state conditions. Test measurements were made at the peak fluorescence wavelength within ∼2 min after solution preparation. These were followed by scanning of the full spectrum, which took ∼33 min. No difference was found between the test fluorescence intensity and that obtained after a full spectral scan.

For the temperature studies, the sample was heated for 20 min at the desired incubation temperature and then allowed to cool to room temperature before making absorption and fluorescence measurements. No change was observed in the absorption spectra (data not shown) in the n-butanol-water mixtures for either dA or dG for the maximum incubation temperature of 49°C. This was found to be also the case for the acetonitrile-water mixtures of both dA and dG for the maximum incubation temperature of 55°C.

The full width at half maximum (FWHM) (in cm⁻¹) of the fluorescence spectra was calculated using the relationship

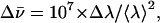(1)

where Δλ is the bandwidth (in nm) at half maximum and 〈λ〉 is the average wavelength of the band (in nm). For dG, the full width at two-third maximum (FWTTM) was used to calculate 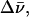where Δλ in this case is the bandwidth at two-third maximum, to eliminate contributions from the long tail of the fluorescence spectra.

RESULTS

We prepared water-organic solvent mixtures in three different methods designated as “premixed”, “carry its own water”, and “injected water” solutions as is described under Materials and Methods. The organic solvents used in the present study were n-butanol, acetonitrile, methanol, n-propanol, isopropanol, and isobutanol. The choice of these solvents was dictated by their transmission at the excitation wavelength of 265 nm and by the solubility of water and of the nucleosides in them. For n-butanol and acetonitrile, which have a high degree of amphiphilicity and weak hydrogen bonding ability (Marcus, 1998), respectively, the fluorescence spectral properties of the purines were found to depend on the sequence of steps in which the aqueous mixtures were formed. On the other hand, the absorption spectra were found to be independent of the sequence of steps of solution preparation and to be very similar to those in the neat solvents. The fluorescence spectral properties of solutions that were left overnight (24–30 h) were found to remain unchanged.

2′-deoxyadenosine (dA)

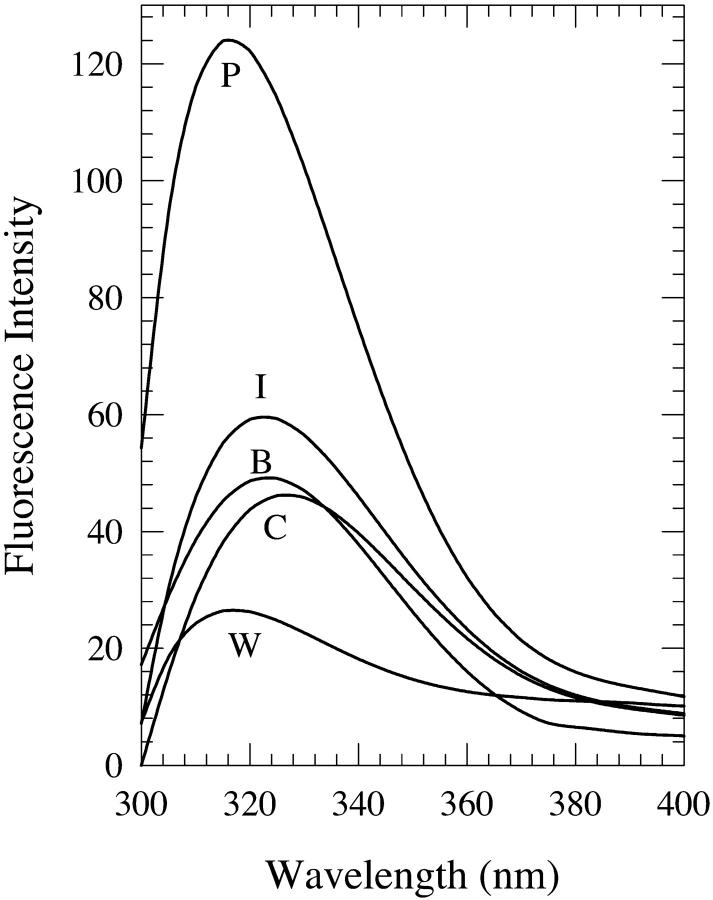
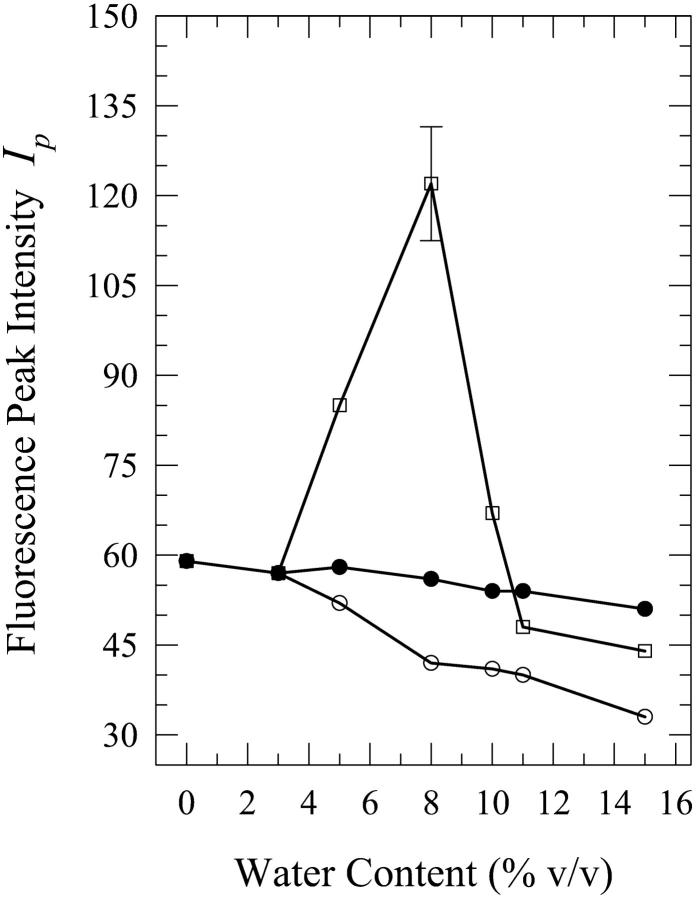
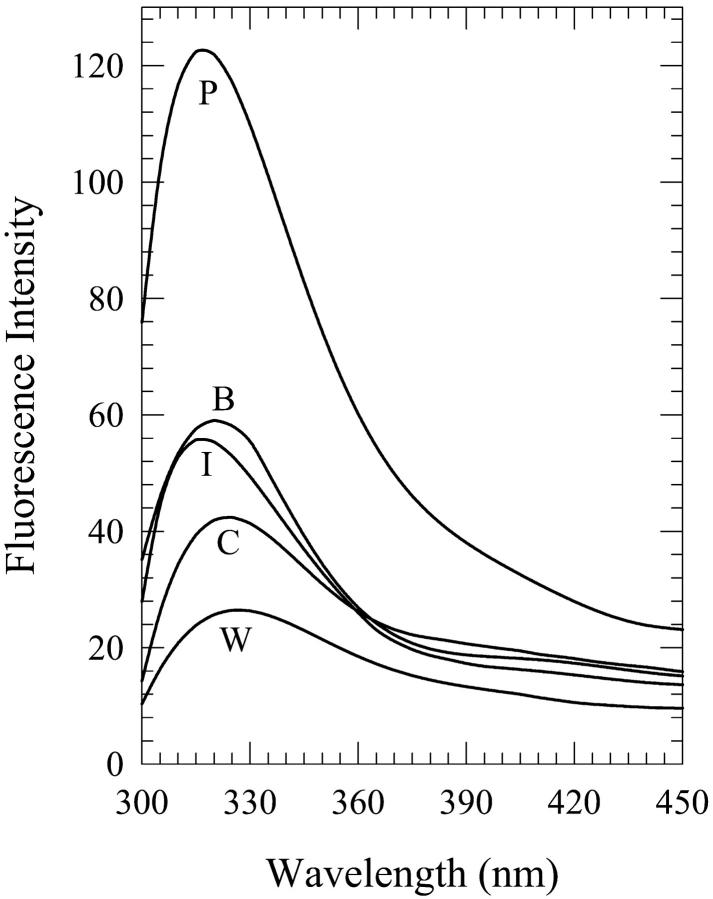
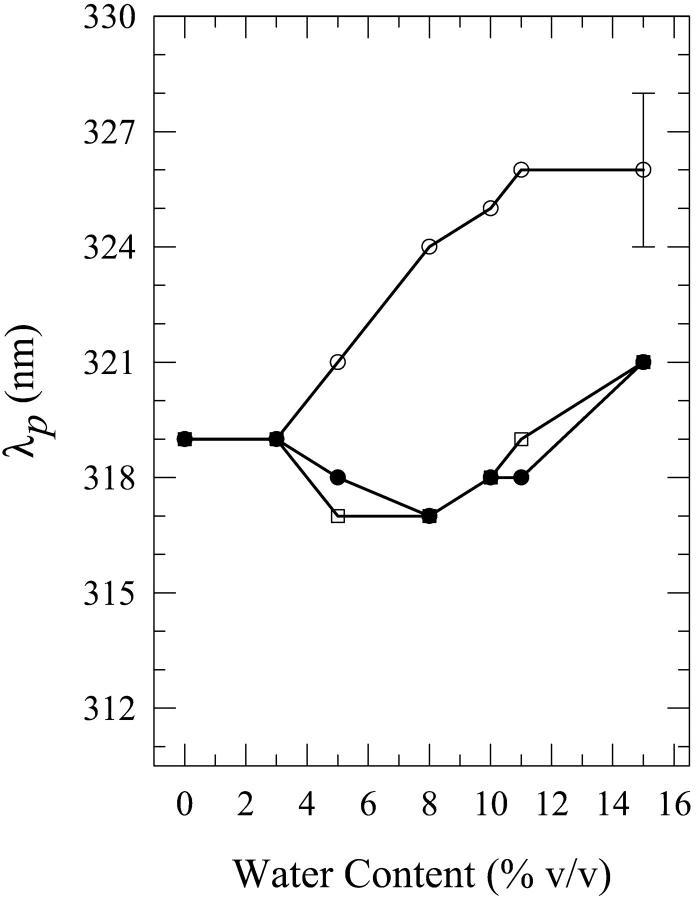
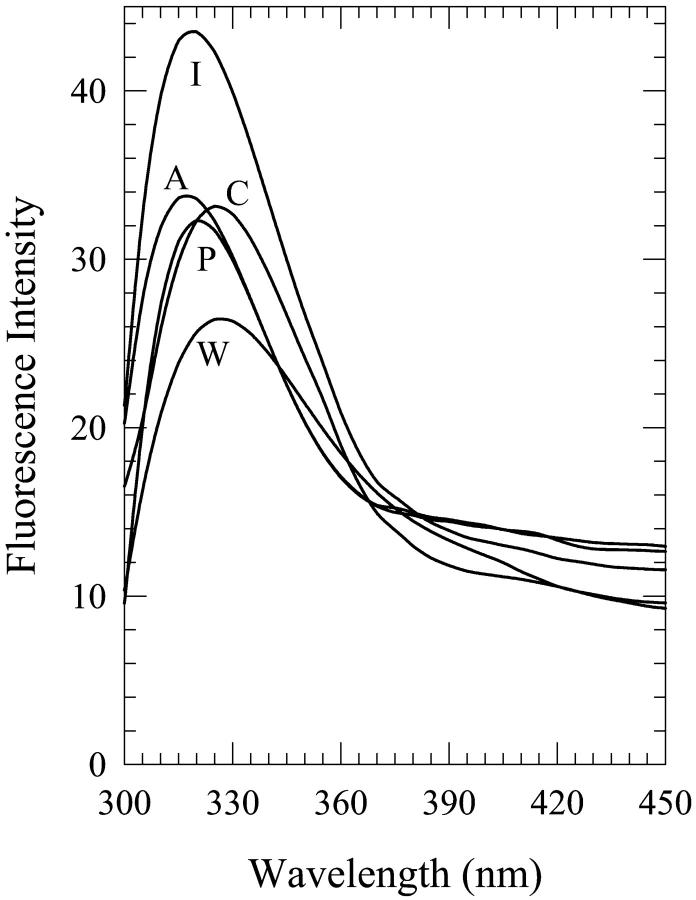
Solutions of dA in water-n-butanol mixtures with water contents of 3–15% by volume were investigated. The onset of this phenomenon for dA is at ∼3% water content. Fig. 1 shows the fluorescence spectra in 8% water-n-butanol mixtures prepared in the three different methods described above. Fig. 2 shows a comparison of the fluorescence peak intensities I_p as a function of the water content for the three methods of solution preparation. For solutions containing 6–10% water, the “premixed” solutions have a much larger peak intensity than those of the “carry its own water” and “injected water” solutions. However, for water contents >12%, fluorescence quenching is observed relative to the fluorescence in neat n-butanol for the “premixed” and the “carry its own water” solutions, with the latter exhibiting the largest quenching; this is consistent with the quenching observed in bulk water (Fig. 1). Fig. 3 shows a comparison of the wavelengths of the fluorescence spectral peak λ_p for the three solutions. For all water contents used in the present study, λ_p for the “carry its own water” solution is the longest, whereas that for the “premixed” solution is the shortest. The shift between the wavelengths of the fluorescence spectral peak for these two solutions ranges from ∼6–12 nm; the maximum shift of ∼12 ± 3 nm is observed in solutions with a water content in the range of ∼7–10%. This water content range is comparable to that of 6–10% for which the “premixed” solution exhibits the largest enhancement (Fig. 2), indicating that the large fluorescence enhancement is accompanied with shifts to shorter wavelengths. The shapes of the spectra, as described by their widths (FWHM), do not depend strongly on the method of solution preparation (data not shown). Below, the effect of increasing the water content on the fluorescence properties of dA is presented for each method of solution preparation individually.

FIGURE 1.

Fluorescence spectra of 2′-deoxyadenosine (dA) in 8% (v/v) water-n-butanol mixtures designated as “premixed” (P), “carry its own water” (C), and “injected water” (I) solutions. (The preparation of these solutions was done as described under Materials and Methods). Also shown are the spectra in neat n-butanol (B) and water (W).

FIGURE 2.

Plot of the fluorescence peak intensity I_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyadenosine (dA) in n-butanol aqueous mixtures as a function of the water content (% v/v). The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

FIGURE 3.

Plot of the wavelength of the fluorescence spectral peak λ_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyadenosine (dA) in n-butanol aqueous mixtures as a function of the water content (% v/v). For dA in water, λ_p = 319 ± 2 nm. The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

For dA in “premixed” solutions, the fluorescence peak intensity is seen to increase relative to that in neat n-butanol upon increasing the water content and to reach a maximum by a factor of ∼2.5 ± 0.3 for the 8% solution (Fig. 2). For larger water contents, the intensity drops below that of the 8% solution and a fluorescence intensity quenching is observed relative to the fluorescence intensity in neat n-butanol for the 12–15% solutions: for the 15% solution, quenching by a factor of ∼1.3 ± 0.1 is observed. It is also observed that the wavelength of the fluorescence spectral peak is shifted to shorter wavelengths where it reaches a minimum value of 315 nm (a shift by ∼7 nm from that in neat n-butanol) for the 6% and 7% solutions (Fig. 3). Further addition of water shifts the spectral peak to longer wavelengths relative to that minimum, and a value of 324 ± 2 nm is reached for the 15% solution, which is not very different from that in neat n-butanol (322 ± 2 nm; Fig. 3). The FWHM does not exhibit a strong dependence on the water content, with the spectra for the 8–11% water solutions being slightly narrower than those for the other water contents (data not shown).

For the “carry its own water” solutions, the fluorescence intensity remains virtually constant up to 7% water, and fluorescence quenching is observed for greater water contents relative to the fluorescence in neat n-butanol (Fig. 2): this decrease is by a factor of ∼1.5 ± 0.2 for the 15% solution, which is similar to that of 1.3 ± 0.1 for the “premixed” solution. A shift to longer wavelengths is observed upon increasing the water content, which for the 15% solution is by ∼9 ± 3 nm relative to that in neat n-butanol (Fig. 3). The changes in the widths of the spectra are very small and slight broadening is observed only for large water contents: by ∼480 ± 300 cm⁻¹ for the 15% solution (data not shown).

For the “injected water” solutions, the observed changes are small, with a maximum fluorescence enhancement by a factor of ∼1.2 ± 0.1 for the 5–8% solutions (Fig. 2). For larger water contents, a continuous decrease in the intensity (Fig. 2) and small shifts to longer wavelengths in the spectral peak are observed (Fig. 3). For the 15% solution, the shift is by ∼4 nm (Fig. 3). No significant changes are observed in the widths of the spectra (data not shown).

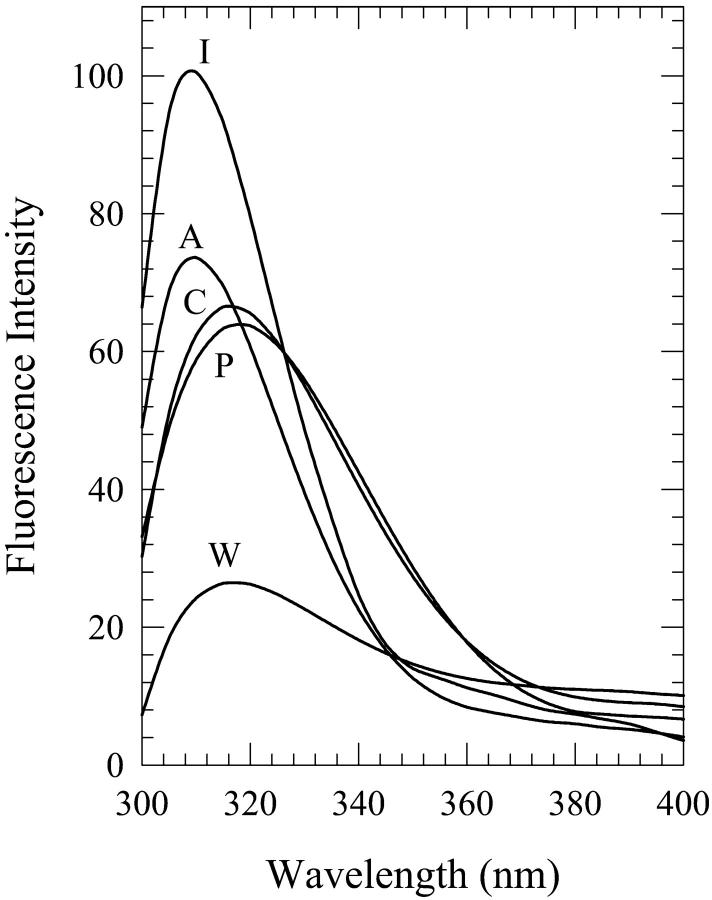
We have also carried out measurements with mixtures of water and acetonitrile, a solvent that is a hydrogen bond acceptor. Mixtures of 5–25% water contents show a dependence of the fluorescence spectral properties on the method of solution preparation. Fig. 4 shows the spectra for the 8% water-acetonitrile mixtures. The onset of this dependence is at ∼3% water content and its cessation is at ∼30%. The most pronounced spectral difference is exhibited by the fluorescence peak intensity shown in Fig. 5.

FIGURE 4.

Fluorescence spectra of 2′-deoxyadenosine (dA) in 8% (v/v) water-acetonitrile mixtures designated as “premixed” (P), “carry its own water” (C), and “injected water” (I) solutions. Also shown are the spectra in neat acetonitrile (A) and water (W).

FIGURE 5.

Plot of the fluorescence peak intensity I_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyadenosine (dA) in acetonitrile aqueous mixtures as a function of the water content (% v/v). The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

The spectra for the 5% aqueous solutions are very similar in their widths and in the wavelengths of their peaks; however, they are shifted to longer wavelengths by ∼3–5 nm relative to that in neat acetonitrile (spectra not shown). The fluorescence peak intensities for the “carry its own water” and the “premixed” solutions are slightly quenched, by a factor of ∼1.2 ± 0.1, compared to that for the “injected water” solution (Fig. 5). For the 8% water content, the spectrum for the “injected water” solution has a shape that is very similar to that in neat acetonitrile, whereas those for the “carry its own water” and “premixed” solutions are considerably broader, by ∼30% and 20%, respectively; the latter two spectra are shifted to longer wavelengths by ∼7 ± 3 nm (Fig. 4). However, the fluorescence spectrum for the “injected water” solution is enhanced by a factor of ∼1.4 ± 0.1 relative to that in neat acetonitrile. For the 15% solutions, all three spectra have very similar shapes and are shifted to longer wavelengths by ∼4–5 nm as compared to that in neat acetonitrile (spectra not shown), with the peak intensity for the “injected water” solution being enhanced by a factor of ∼1.4 ± 0.1 (Fig. 5). Further addition of water, 25% (spectra not shown), has little effect on the fluorescence properties of the three solutions, with the fluorescence peak intensity for the “injected water” solution being slightly reduced (Fig. 5).

We have also made measurements in aqueous mixtures with four other alcohols: methanol, n-propanol, isopropanol, and isobutanol. None of these mixtures exhibited this phenomenon (i.e., the dependence of the fluorescence properties on the sequence of steps of solution preparation). The observed spectral changes are listed in Table 1.

TABLE 1.

Fluorescence spectral parameters of 2′-deoxyadenosine (dA) in aqueous mixtures of methanol, isopropanol, n-propanol, and isobutanol with water contents of 8% and 15%: ratio f of the fluorescence peak intensity for the aqueous mixture to that for the neat organic solvent, wavelength of the fluorescence spectral peak λ_p (in nm), and full width at half maximum (FWHM) (in cm⁻¹) as defined in Eq. 1

	0% water			8% water			15% water
Solvent	f	λp (nm)	FWHM (cm−1)	f	λp (nm)	FWHM (cm−1)	f	λp (nm)	FWHM (cm−1)
Methanol	1	315	4244	1.1	313	4102	1.2	314	4076
Isopropanol	1	320	4301	1.5	320	4705	0.7	320	3764
n-propanol	1	322	4853	1.1	327	4882	1.6	323	4794
Isobutanol	1	318	4125	1.0	325	4833	1.0*	317*	3696*

For dA in water, λ_p = 319 ± 2 nm and FWHM = 4570 ± 270 cm⁻¹. The errors are: ∼±10% for f, ∼±2 nm for λ_p, and ∼±6% for FWHM.

^*For isobutanol, the maximum water content used was 12% by volume due to the low solubility of water in isobutanol, 14% (Marcus, 1998).

2′-deoxyguanosine (dG)

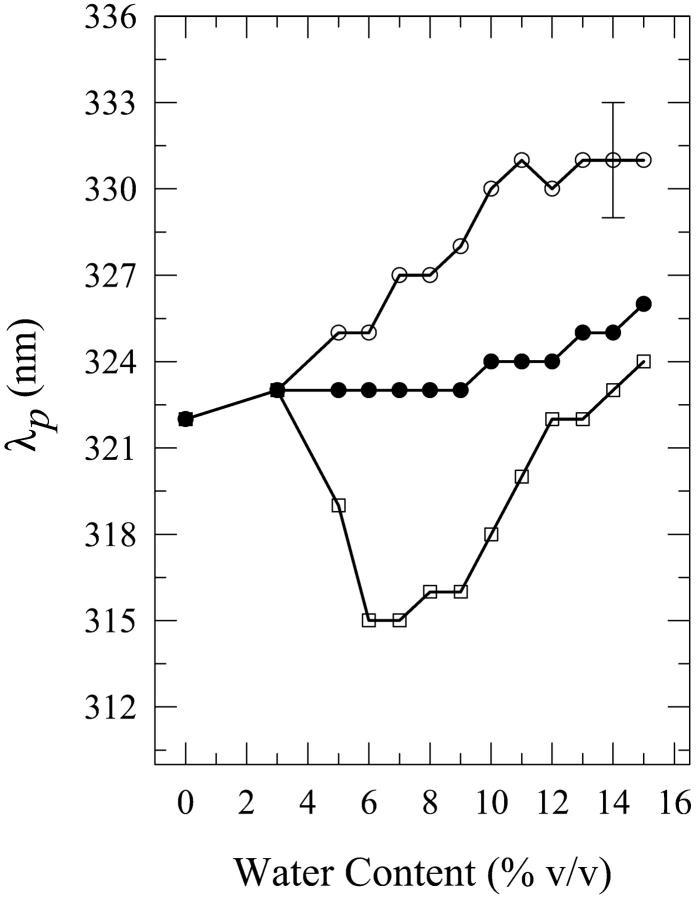
As was the case for dA, the present phenomenon also occurs for dG, the other purine, in aqueous mixtures of n-butanol and acetonitrile. We first describe the results for water-n-butanol mixtures. Water contents of 3% (onset of this phenomenon), 5%, 8%, 10%, 11%, and 15% by volume were used. The occurrence of this phenomenon is seen from the plots of the fluorescence spectral parameters as a function of the water content (Figs. 6–8). Fig. 9 shows the spectra for the 8% solution. As is the case for the dA solutions in water-n-butanol mixtures (Fig. 2), the spectra of the “premixed” solutions have the largest peak intensity for water contents in the range of 5–10%, whereas those for the “carry its own water” solutions have the lowest intensity (Fig. 6). But, unlike the case of dA (Fig. 3), the spectral peak wavelengths for the “premixed” and the “injected water” solutions are very similar (Fig. 7). The spectra for the “carry its own water” solutions are shifted to longer wavelengths relative to those of the other two solutions by ∼4–7 nm (Fig. 7) and are considerably broader (Fig. 8). The largest shift of 7 nm, which is smaller than that of 12 nm observed for the dA solutions (Fig. 3), is reached for water contents of 8–11% (a range that is comparable to that for dA). The dependence of the fluorescence properties on the amount of water for each individual method of solution preparation is described below.

FIGURE 6.

Plot of the fluorescence peak intensity I_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyguanosine (dG) in n-butanol aqueous mixtures as a function of the water content (% v/v). The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

FIGURE 8.

Plot of the full width at two-third maximum (FWTTM) for the fluorescence spectra of “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyguanosine (dG) in n-butanol aqueous mixtures as a function of the water content (% v/v). For dG in water, FWTTM = 5040 ± 260 cm⁻¹. The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

FIGURE 9.

Fluorescence spectra of 2′-deoxyguanosine (dG) in 8% (v/v) water-n-butanol mixtures designated as “premixed” (P), “carry its own water” (C), and “injected water” (I) solutions. Also shown are the spectra in neat n-butanol (B) and water (W).

FIGURE 7.

Plot of the wavelength of the fluorescence spectral peak λ_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyguanosine (dG) in n-butanol aqueous mixtures as a function of the water content (% v/v). For dG in water, λ_p = 327 ± 2 nm. The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

For the “premixed” solutions, the fluorescence intensity increases relative to that in neat n-butanol (as is the case for dA (Fig. 2)) and reaches a maximum by a factor of ∼2.1 ± 0.2 for the 8% solution (Fig. 6). For larger water contents, the fluorescence intensity decreases and an actual quenching is observed for the 11% and 15% solutions relative to the fluorescence in neat n-butanol; for the 15% solution, the quenching is by a factor of ∼1.3 ± 0.1 (Fig. 6). However, addition of water has very little effect on either the wavelength of the spectral peak (Fig. 7) or the width of the spectra for the “premixed” solutions (Fig. 8), with the exception of the 15% solution that is broader by ∼600 ± 300 cm⁻¹ relative to the “premixed” solutions for the other water contents (Fig. 8). For the “carry its own water” solutions, a gradual quenching is observed upon increasing the water content (Fig. 6) that reaches a maximum by a factor of ∼1.7 ± 0.2 for the 15% solution. It is also observed that increasing the water content has the effect of gradually shifting the spectrum of the “carry its own water” solution to longer wavelengths (Fig. 7) as well as broadening it relative to that in neat n-butanol (Fig. 8). For the 15% solution, the shift is by ∼7 ± 3 nm (Fig. 7) and the broadening is by ∼1200 ± 300 cm⁻¹ (Fig. 8). It is worth noting that this shift moves the spectrum of the “carry its own water” solution closer to that in water, which is shifted to longer wavelengths by ∼8 nm and is broader by ∼900 cm⁻¹ relative to that in neat n-butanol (Fig. 9). For the “injected water” solutions, a very weak quenching is observed (Fig. 6), by a factor of ∼1.1 ± 0.1 for the 10–15% solutions, with no significant changes in either the wavelength of the fluorescence spectral peak (Fig. 7) or in the width of the spectra (Fig. 8).

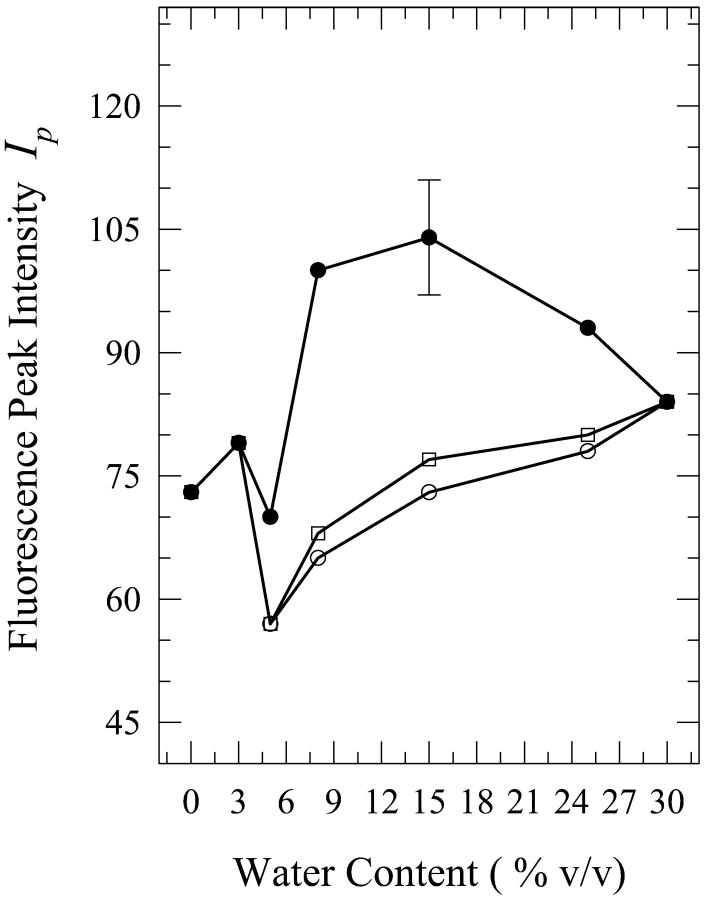
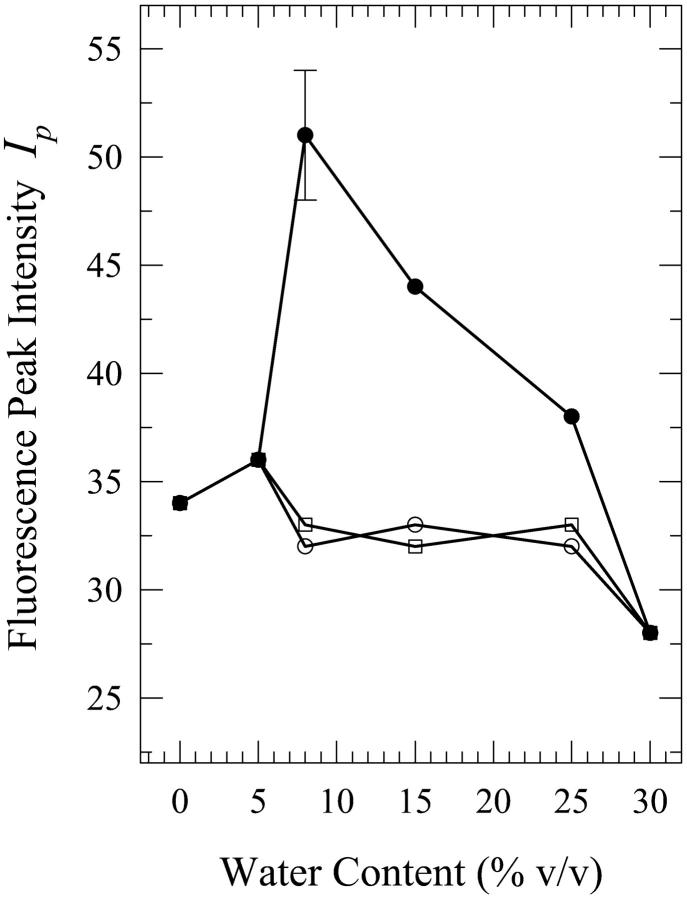
Solutions of dG in aqueous mixtures of acetonitrile were prepared for the water contents of 5%, 8%, 15%, 25%, and 30% by volume. The spectra for the solutions that contain 8%, 15%, and 25% water show a dependence on the method of solution preparation. The onset and the cessation of the present phenomenon is at ∼5% and 30% water contents, respectively (spectra not shown). Fig. 10 shows a plot of the fluorescence peak intensity as a function of the water content, which is seen to be qualitatively similar to that of dA in these mixtures (Fig. 5). It is seen from this figure that the fluorescence peak intensity is enhanced considerably for the “injected water” solution for the water contents of 8% and 15%. The spectra for the 15% solutions are shown in Fig. 11. Although the shapes of the fluorescence spectra for the 15% “premixed” and “injected water” solutions are very similar, the spectrum for the “carry its own water” solution is shifted to longer wavelengths by ∼5 nm and is broader by ∼400 cm⁻¹ (Fig. 11). The fluorescence peak intensity for the “injected water” solution is, however, enhanced by a factor of ∼1.3 ± 0.1 relative to that in neat acetonitrile (Fig. 10). Further addition of water to 25% has little effect on the widths of the spectra and the wavelengths of their peaks (data not shown). The intensity for the “injected water” solution is, however, reduced relative to that for the 15% solution by a factor of ∼1.2 (Fig. 10). The spectra for the 8% solutions (not shown) exhibit trends similar to those for the 15% solutions, and all three spectra (for the “premixed”, “carry its own water”, and “injected water” solutions) are shifted to shorter wavelengths by ∼3–5 nm relative to those for the 15% solutions (data not shown). The enhancement in the fluorescence peak intensity for the “injected water” solution is by a factor of ∼1.5 ± 0.2 (Fig. 10). (It should be noted here that plots of the fluorescence quantum yield versus the water content exhibit trends similar to those of the fluorescence peak intensity for all the solutions of dG as well as dA.)

FIGURE 10.

Plot of the fluorescence peak intensity I_p for “premixed” (open squares), “carry its own water” (open circles), and “injected water” (filled circles) solutions of 2′-deoxyguanosine (dG) in acetonitrile aqueous mixtures as a function of the water content (% v/v). The lines do not represent fits to the data; they have been drawn to guide the eye. The error bars indicate the largest standard deviation for these data.

FIGURE 11.

Fluorescence spectra of 2′-deoxyguanosine (dG) in 15% (v/v) water-acetonitrile mixtures designated as “premixed” (P), “carry its own water” (C), and “injected water” (I) solutions. Also shown are the spectra in neat acetonitrile (A) and water (W).

As is the case for dA, aqueous mixtures of dG in methanol, n-propanol, isopropanol, and isobutanol were found not to exhibit this phenomenon (i.e., the dependence of the fluorescence parameters on the method of solution preparation). The corresponding spectral changes are listed in Table 2.

TABLE 2.

Fluorescence spectral parameters of 2′-deoxyguanosine (dG) in aqueous mixtures of methanol, isopropanol, n-propanol, and isobutanol with water contents of 8% and 15%: ratio f of the fluorescence peak intensity for the aqueous mixture to that for the neat organic solvent, wavelength of the fluorescence spectral peak λ_p (in nm), and full width at two-third maximum FWTTM (in cm⁻¹)

	0% water			8% water			15% water
Solvent	f	λp (nm)	FWTTM (cm−1)	f	λp (nm)	FWTTM (cm−1)	f	λp (nm)	FWTTM (cm−1)
Methanol	1	329	4290	1.1	330	4226	1.3	332	4277
Isopropanol	1	333	4945	1.5	328	4212	1.3	332	4366
n-propanol	1	324	4689	1.3	334	4325	1.2	336	6791
Isobutanol	1	326	3961	1.0	327	3857	1.4*	326*	3840*

For dG in water, λ_p = 327 ± 2 nm and FWTTM = 5040 ± 260 cm⁻¹.

^*For isobutanol, the maximum water content used was 12% by volume due to the low solubility of water in isobutanol, 14% (Marcus, 1998).

For dT, this phenomenon was not observed for any of the solvent mixtures used in the present study. We have observed changes in the shape and/or in the intensity of the fluorescence spectrum upon varying the water content in the mixtures, but these changes were found to be independent of the sequence of steps in which the solutions were prepared; this implies that the phenomenon observed for dA and dG does not operate for dT. That was also found to be the case for the other pyrimidine, dC. The data for these two nucleosides are not shown here for the sake of brevity and also because of their limited utility in assessing the origin of the present phenomenon.

DISCUSSION

Solvation plays an important role in the function of DNA, and thus there is considerable interest in understanding the solvation networks of its constituent components. This is particularly important when studying the closing of open basepairs, the hydrogen bonds of which have been disrupted as a result of structural fluctuations or protein-DNA interactions. The open base can undergo polar as well as nonpolar interactions with its heterogeneous environment. The question then arises as to how the open bases interact with such an environment and to what extent these interactions affect the closing of these bases.

In an attempt to shed light on this matter, we have studied the intrinsic fluorescence properties of the purine and pyrimidine nucleosides dA, dG, dT, and dC in organic solvents in the presence of small amounts of water. In the process, we have found that these properties vary with the sequence of the steps in which the solutions were prepared in a nucleoside- and solvent-dependent fashion. This variation was observed for the purines, but not for the pyrimidines, only when dissolved in aqueous mixtures with n-butanol and acetonitrile. With regard to this solvent selectivity, acetonitrile is completely miscible in water but forms very weak hydrogen bonds in its capacity as a hydrogen bond acceptor (Marcus, 1998). The significance of these bonds with regard to this phenomenon will be discussed later on. We will first address the water-n-butanol mixtures.

n-butanol

Alcohols have an aliphatic chain and a hydroxyl group, and thus they have an amphiphilic nature. Even methanol, which possesses the shortest aliphatic chain, does not form a homogeneous solution in water at a water:methanol ratio of ∼19% by volume (Dixit et al., 2002). Instead, water tends to form clusters or strings with a structure similar to that in neat water. The high amphiphilicity of n-butanol, which has the longest aliphatic chain of all the alcohols employed in the present study, allows a water solubility in it of only ∼17% by volume (Marcus, 1998); this, despite the fact that its hydrogen bonding ability is very good (Table 3), as is the case for all the other alcohols employed in the present study.

TABLE 3.

The structures and some physical parameters for the solvents used in the present study: log P, where P is the octanol/water partition constant, α-scale for the hydrogen-bond donor acidity, and β-scale for the hydrogen-bond acceptor basicity

Solvent	Structure	Log P*	α*	β*
Methanol	CH3 (OH)	−0.7	0.98	0.66
	CH3 – CH – CH3
Isopropanol	|	0.13	0.76	0.84
	OH
n-propanol	CH3 – CH2 – CH2 (OH)	0.28	0.84	0.9
	CH3 – CH – CH2 (OH)
Isobutanol	|	0.75	0.79	0.84
	CH3
n-butanol	CH3 – CH2 – CH2 – CH2 (OH)	0.75	0.84	0.84
Acetonitrile	CH3 (CN)	−0.34	0.19	0.4
Water	H (OH)	–	1.17	0.47

^*Marcus (1998).

An empirical measure of solvent hydrophobicity is provided by the log P, where P is the partition constant of the solvent between 1-octanol and water (Marcus, 1998). The values of log P for the solvents used in the present study are listed in Table 3. It is seen that the hydrophobicity of the alcohols increases in the order of methanol, isopropanol, n-propanol, isobutanol, and n-butanol. Isobutanol and n-butanol, which have identical hydrophobicities, are by far the most hydrophobic. The length of the alcohol aliphatic chain, and not the hydrophobicity of the alcohol alone, apparently plays an important role in the manifestation of the present solvation phenomenon. This is seen from the fact that n-butanol, which exhibits the phenomenon, has the longest chain, whereas isobutanol does not exhibit the phenomenon despite the fact that it is as hydrophobic as n-butanol and allows a water solubility in it of only ∼14%, which is even slightly lower than that of 17% in n-butanol (Marcus, 1998). This suggests that the occurrence of the phenomenon necessitates the formation of a rather elaborate solvent network around the purines, which will be further discussed later on.

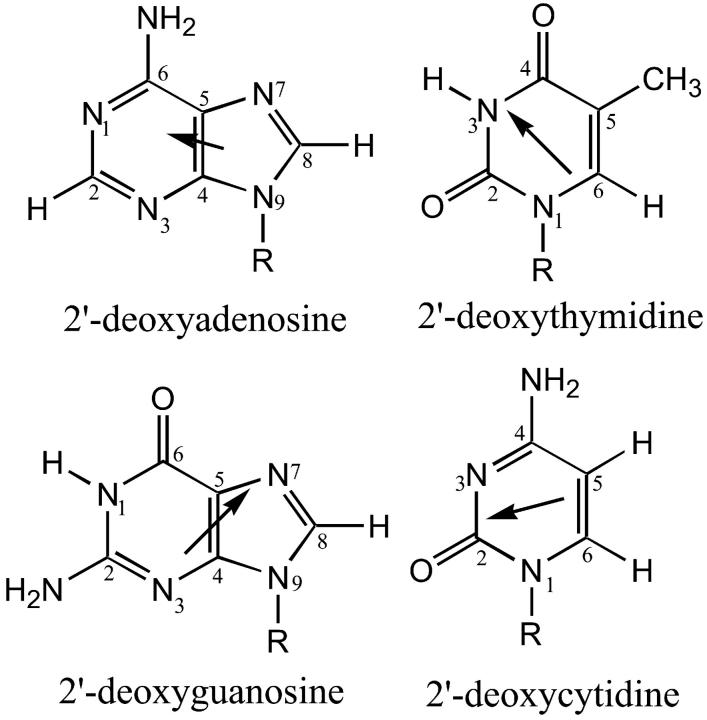
As to the question of why the current phenomenon was not observed for the pyrimidines in water-n-butanol mixtures, we note here that because of the more localized polar groups of the pyrimidines, such an elaborate network cannot be potentially formed in that case. It is seen from Fig. 12 that, in addition to the contiguous polar groups that participate in interbase hydrogen bonding in DNA, the purines have the N3 and N7 ring nitrogen atoms, which have been reported to have considerable hydration occupancies (Schneider and Berman, 1995), whereas the pyrimidines have no such additional atoms. Thus, these two nitrogen atoms are likely to participate in the solvent network around the purines. Below, we address the possible solvation/hydration networks in the three solutions, “injected water”, “carry its own water”, and “premixed”.

FIGURE 12.

Structures of the four deoxynucleosides used in the present study: 2′-deoxyadenosine (dA), 2′-deoxyguanosine (dG), 2′-deoxythymidine (dT), and 2′-deoxycytidine (dC). Also shown are the directions of the permanent dipole moments of the nucleosides (Clementi et al., 1969; Bloomfield et al., 1974).

In the “injected water” solution, a purine molecule would be initially solvated by n-butanol. Hydrophobic interactions are expected to dominate when water is injected into the solution. In this regard, neutron diffraction studies on aqueous mixtures of tert-butanol (Bowron et al., 1998, 2001; Finney et al., 2000) have reported that the behavior of tert-butanol molecules is predominantly driven by hydrophobic interactions that bring their methyl groups into direct contact and that there is no significant hydrogen bonding between these molecules. Because of the large polarizabilities of the DNA bases, average value ≈ 13.1 ų (Guckian et al., 2000), and the sizable polarizability of n-butanol, 8.9 ų (Lide, 2000), the contribution of dispersion interactions would also need to be considered. These arise from interactions between a transient dipole in one molecule, of polarizability α₁, and an induced dipole at a neighboring molecule, of polarizability α₂. The interaction energy U_dis is given by (Israelachvili, 1992)

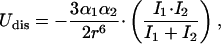(2)

where r is the distance between the interacting molecules, the ionization potentials of which are I₁ and I₂, respectively. The values of the polarizabilities of dA and dG are very similar, 13.7 ų and 15.0 ų (Guckian et al., 2000), respectively, and therefore their average value of 14.4 ų will be used in the calculations. Also, their ionization potentials are very similar, 8.9 eV and 8.6 eV (Alyoubi and Hilal, 1995), and their average value of 8.8 eV will be used. The ionization potential of n-butanol is 10.0 eV (Lide, 2000). Equation 2 then yields U_dis ≈ −8 kcal/mol for a butanol-purine distance r ≈ 3.7 Å. (The choice of r ≈ 3.7 Å is based on the thickness of the DNA bases, ∼3.4 Å (Yanagi et al., 1991), and the diameter of the aliphatic chain of n-butanol ∼4 Å (Israelachvili, 1992).) This would suggest a considerable dispersion attraction between purine and n-butanol molecules that could give rise to a stacking interaction between them. (This is reminiscent of stacking in DNA that is known to be dominated by dispersion interactions (Sowers et al., 1987).)

These considerations taken together suggest that a likely configuration for the solvation of the purines by n-butanol would involve i), hydrogen bonding interactions between the hydroxyl group of n-butanol and polar sites of the purines, with the aliphatic chains of neighboring n-butanol molecules making contact, and ii), stacking interactions between the purines and n-butanol. In this fashion, the long aliphatic chains of n-butanol may result in a solvation network that would encapsulate the purine. (For the case of pyrimidines, this extended network would not be favored as was discussed above.) Thus, when water is injected into the solution, the tendency of water molecules to avoid the aliphatic chains of n-butanol molecules that are solvating the purines would not allow them to participate in the solvation network, and consequently the fluorescence spectrum would be expected to be very similar to that in neat n-butanol. This expectation is borne out by the results of the present study (Figs. 2 and 3).

It is noted that a potential contribution to the solvation of purines in a stacked configuration might be made by dipole-dipole interactions. However, these are considered below and found to be ineffective. For dG, two plausible configurations would involve the CH₃ group of n-butanol interacting with the CH group at position 8 and its OH group either interacting with the NH₂ group or with the NH group at position 1. Values of ∼6 Å and ∼5.1 Å, respectively, are then estimated for the distances between the dipole of dG (Fig. 12) and the dipole of n-butanol in these configurations. Without a detailed geometry, Eq. 3 is used that is valid under statistical mixing (Israelachvili, 1992) to estimate the dipole-dipole interaction energy U_d−d for the average distance r ∼ 5.6 Å

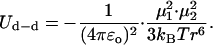(3)

Here, k_B = 1.38 × 10⁻²³ J/K is Boltzmann's constant, ɛ_o = 8.85 × 10⁻¹² C²/N·m² is the permittivity of free space, T is the absolute temperature (295 K), and μ₁ and μ₂ are the interacting permanent dipole moments. The dipole moments of guanine (G) and adenine (A) are 6.6 D and 2.3 D, respectively (Guckian et al., 2000), and the dipole moment of n-butanol is 1.7 D (Lide, 2000). Equation 3 then yields U_d−d ≈ −0.5 kcal/mol for dG. For dA, two plausible configurations would involve the CH₃ group of n-butanol interacting with the CH group at position 2 of dA and its OH group interacting with the N7 position, or the CH₃ group interacting with the CH group at position 8 and the OH group interacting with the N1 position. Values of ∼4.4 Å and 4.8 Å, respectively, are then estimated for the dipole-dipole distances in these configurations. For the average distance of ∼4.6 Å, Eq. 3 yields U_d−d ≈ −0.2 kcal/mol. These values of U_d−d are seen to be much smaller than that of ∼−8 kcal/mol for the average dispersion interaction energy for dG and dA discussed above. (It is noted that the dispersion and the dipole-dipole (orientation) interactions are the two major contributors to the van der Waals interaction, whereas the third one, the dipole-induced dipole interaction (induction), is typically very weak (Israelachvili, 1992).)

In the “carry its own water” solution, the purine is first hydrated. The extent to which the purine would retain its hydration when diluted in n-butanol would be dependent on the strength of its hydration as well as on the level of connectivity that water can retain upon dilution; the latter would be high when the cosolvent is hydrophobic. Upon increasing the amount of water, the fluorescence properties of dG, in the absence of bulk solvent effects, would then be expected to approach those in neat water on account of the fact that this is the most strongly hydrated nucleoside as deduced from the high value of the hydration free energy of guanine (G), ∼−21 kcal/mol (Mohan et al., 1992; Elcock and Richards, 1993; Miller and Kollman, 1996) as well as from volumetric measurements (Lee and Chalikian, 2001). (The values of the hydration free energies, in kcal/mol, of the other bases are: ∼−18 for cytosine (C), ∼−12 for adenine (A), and ∼−12 for thymine (T).) The present observations bear this out. The fluorescence peak intensity decreases monotonously (Fig. 6), the width of the spectrum increases (Fig. 8), and its peak wavelength shifts to longer wavelengths (Fig. 7); all of these parameters approach those in neat water: 33 vs. 26, 5320 cm⁻¹ vs. 5040 cm⁻¹, and 326 nm vs. 327 nm for the 15% solution and for neat water, respectively. On the other hand, because of the fact that dA is much more weakly hydrated than dG, formation of a mixed water-n-butanol solvation network around dA is possible. The trend observed for the fluorescence properties of dG in the “carry its own water” solutions upon increasing the amount of water, relative to those in neat water, is not observed for the dA solutions. Although the fluorescence peak intensity approaches closely that in neat water (Fig. 2), a large shift in the wavelength of the fluorescence spectral peak to longer wavelengths relative to that in neat water (Fig. 3) and a broadening of the spectrum are observed (data not shown): for the 15% solution, the shift is by ∼12 nm (Fig. 3) and the broadening is by ∼600 cm⁻¹. These differences suggest the formation of a mixed solvation network around dA.

In the “premixed” solution, a purine would be initially exposed to both water and n-butanol. The interaction would depend on the affinity of the different sites in the purine. The mixture of n-butanol and water is expected to be heterogeneous in view of the incomplete mixing at the molecular level that was observed for the water-methanol system in which water appeared as clusters or strings of varying sizes (Pálinkás et al., 1991; Laaksonen et al., 1997; Venables and Schmuttenmaer, 2000; Dixit et al., 2002). Furthermore, because of strong cooperative interactions in water, its hydrogen bonding ability is considerably enhanced (Keutsch and Saykally, 2001) and thus there could be a preference for water cluster-nucleoside interaction than for individual water molecule-nucleoside interaction. These considerations suggest that different solvation and hydration patterns would be formed in which some of the purine molecules would be either exclusively hydrated or solvated by n-butanol or would have a mixed solvent network. The fraction of each network formed would depend on the water content. The large fluorescence enhancement that is observed upon increasing the water content up to 9% (Figs. 2 and 6 for dA and dG, respectively) probably stems from increasing the fraction of the “mixed” solvation network. This inference is reached on the basis of the observation that the fluorescence intensity is much larger than those in neat n-butanol or in the “carry its own water” solutions (Figs. 2 and 6). Studies on binary mixtures of water with alcohols (Ferrario et al., 1990; Venables and Schmuttenmaer, 2000) showed that the formation of mixed hydrogen bonds between water and alcohols depends on the water content; the population of the different hydrogen bonding configurations was found to peak at different water contents. Presumably, this would also be the case for tertiary systems like the ones under study here.

Acetonitrile

Acetonitrile is completely miscible with water, but is only a hydrogen bond acceptor and a very weak one at that (Marcus, 1998). Thus, regarding the hydrogen bonding interaction, the solvation network would be more local than the networks in the case of alcohols. For the pyrimidines, only the amino group of dC and the imino group of dT would be sites of interaction (Fig. 12). For the purines, the sites would be the amino and the imino groups of dG and the amino group of dA.

A number of studies have reported the existence of microheterogeneity in water-acetonitrile mixtures over a wide range of water contents (Kovacs and Laaksonen, 1991; Marcus and Migron, 1991; Bertie and Lan, 1997; Bergman and Laaksonen, 1998; Takamuku et al., 1998; Mountain, 1999; Venables and Schmuttenmaer, 2000), even for an as low as 0.15 mol fraction (∼6% v/v), which is at the lower end of the range of water contents used in the present study. This heterogeneity results in the formation of clusters of water and acetonitrile. In “premixed” solutions of water and acetonitrile, the solvation preference of a purine would be a function of its hydrogen bonding affinity for the two solvents as well as of the strength of dipole-dipole interactions with them; the latter interactions arise from the sizable dipole moments of purines, acetonitrile, and water. Since the dipole moment of guanine (G) is much larger than that of adenine (A) (6.6 D and 2.3 D, respectively (Guckian et al., 2000), and the dipole moment of acetonitrile is larger than that of water (3.9 D and. 1.85 D, respectively (Lide, 2000)), G would experience much stronger dipole-dipole interactions with acetonitrile (AN) than A would, and these interactions would be stronger than those with water. By using Eq. 3 with r ≈ 5 Å, the strengths of these interactions at room temperature are: U_d−d (G − AN) ≈ −5 kcal/mol, U_d−d (G − H₂O) ≈ −1.1 kcal/mol, U_d−d (A − AN) ≈ −0.6 kcal/mol, and U_d−d (A − H₂O) ≈ −0.1 kcal/mol. (The value of r ≈ 5 Å is based on the average distance between the bases and the hydrating water, ∼4.8 Å (Schneider and Berman, 1995).) With the ionization potential I = 12.2 eV and the polarizability α = 4.4 ų for acetonitrile (Lide, 2000), the energy of the purine-acetonitrile dispersion interaction is calculated from Eq. 2 to be −0.7 kcal/mol for a distance r ≈ 5 Å. The above considerations point to the dominance of the dipole-dipole interactions in the solvation of dG by acetonitrile. (An additional contribution can be made by the dipole-dipole interaction between acetonitrile and the sugar of dG and dA. The dipole moment of the sugar is ∼2.5 D (Pechenaya, 1993). This would yield a value of ∼−0.7 kcal/mol for U_d−d, which is only ∼14% of that for the guanine-acetonitrile interaction energy and very similar to that for the adenine-acetonitrile interaction.) Another interaction arises from hydrogen bond formation, the energy of which is ∼−1 kcal/mol (Freier et al., 1986; Turner et al., 1987). This is discussed below.

Water would form a much more extended hydrogen-bonding network around the purines than acetonitrile would because of its much greater hydrogen bonding ability and the fact that it is both a hydrogen bond donor as well as an acceptor. Moreover, because of strong cooperative interactions in water, its hydrogen bonding ability is considerably enhanced (Keutsch and Saykally, 2001), and therefore there could be a preference for water cluster-nucleoside interactions than for individual water molecule-nucleoside interactions; these interactions would contribute to the heterogeneity of the solvation network. These considerations taken together suggest that in “premixed” solutions, mixed solvation networks would be formed around dA or dG in which water and acetonitrile molecules would participate. These networks would have purines that are either exclusively hydrated by the water clusters formed in the heterogeneous water-acetonitrile mixture or exclusively solvated (with acetonitrile) or have a mixed network in which they are interacting with both water and acetonitrile.

In the “carry its own water” solution, a hydration network would be formed around the purine in the initial step of dissolving it in water. The degree to which this network would be retained upon dilution in acetonitrile would be dependent on the affinity of the purine for water, which is much greater in the case of dG as was discussed above, and on the level of connectivity that water can retain after dilution. This suggests that the participation of acetonitrile in the solvation network around dA is more likely than in the network around dG. The fluorescence spectral properties of dA in the “carry its own water” solution are very similar to those in the “premixed” solution (Figs. 4 and 5, and data not shown), an observation that suggests that the mixed networks formed in these two solutions are very similar. The spectra are broader by ∼20%–30% and are shifted to longer wavelengths by ∼4–7 nm, depending on the water content, relative to those in neat acetonitrile (data not shown). By contrast, in the case of dG for the “carry its own water” solution, the spectrum is shifted to longer wavelengths by ∼5 nm and is broader by ∼20% relative to that in the “premixed” solution (data not shown). These differences suggest the formation of different solvation networks in these two dG solutions. In the networks formed in the “carry its own water” solutions, because of the strong hydration of dG, one would expect less participation of acetonitrile molecules in the solvation network around it and thus greater hydration than in the “premixed” solutions.

Before the addition of water in the “injected water” solution, dG is expected to be more stabilized than dA through dipole-dipole interactions with acetonitrile because of its much larger dipole moment (6.6 D vs. 2.3 D), as was discussed above. Another potential interaction in the formation of the solvation network in neat acetonitrile is hydrogen bonding. However, hydrogen bonding interactions are not expected to contribute significantly to the solvation of either dG or dA, because of the fact that acetonitrile is a very weak hydrogen bond acceptor (Table 3) and of the limited number of purine polar groups that are hydrogen bond donors (Fig. 12).

Upon water addition in the “injected water” solution, the observed relatively large fluorescence enhancement for both dA and dG (Figs. 5 and 10, respectively) suggests that the stabilization in neat acetonitrile is disturbed with water participating in the solvation network and forming a mixed network. The strong hydrogen bonding ability of water relative to that of acetonitrile most likely plays a significant role in the formation of such a network. This mixed network is, however, different from that formed in the “premixed” solution, as is suggested by the observation that the fluorescence peak intensities are very different in the two cases (Figs. 5 and 10). The network formed around purines in the “injected water” solutions is most likely dominated by configurations in which both acetonitrile and water participate because of the affinity of purine polar groups for water, whose hydrogen bonding is not satisfied by acetonitrile. Yet, it would be rather difficult for water, when injected, to completely dislodge acetonitrile from around the purine because of stabilizing acetonitrile-purine dipole-dipole interactions, especially in the case of dG (see above). The large fluorescence enhancement and its strong dependence on the water content observed in the 8–15% “injected water” solutions (Figs. 5 and 10) are most likely related to the number of such mixed networks. In this regard, the number of mixed water-acetonitrile hydrogen bonding structures has been reported to peak at a water content range of ∼4–13% depending on the hydrogen bond configuration (Venables and Schmuttenmaer, 2000). It is possible that in the tertiary mixtures studied in the present work, the number of mixed water-acetonitrile networks around purines peaks at a larger water content than that in the binary mixtures because of hydrogen bonds that are lost to the purine.

The question arises as to why the final solvation networks formed around the purines in water-acetonitrile mixtures are dependent on their initial exposure, whereas those formed around the pyrimidines are not. Because of the large dipole moment of acetonitrile, 3.9 D, one might consider the possibility that differences between the magnitudes of the dipole moments of purines and pyrimidines would result in differences in the strength of the dipole-dipole interactions with acetonitrile. However, the magnitudes of the dipole moments of the four bases, 6.6 D for guanine, 2.3 D for adenine, 4.5 D for thymine, and 6.0 D for cytosine (Guckian et al., 2000) do not reveal a distinction between purines and pyrimidines. Moreover, there is no differential pattern in the directions of the dipole moments of purines and pyrimidines (Fig. 12). These considerations suggest no clear rationale for the operation of the present phenomenon in terms of dipole-dipole interactions. It is significant to observe that, whereas the purines have polar groups widely distributed on their rings, the pyrimidines have two contiguous positions, 5 and 6, with nonpolar groups (Fig. 12). On the other hand, dG has only one nonpolar group, a CH at position 8, and dA has, in addition, the noncontiguous CH group at position 2 (Fig. 12). These considerations suggest that the nonpolar regions of dC and dT would promote hydrophobic interactions with acetonitrile through its methyl group. Thus, in water-acetonitrile mixtures, a mixed solvation network would be formed around the pyrimidines with acetonitrile tending to solvate the nonpolar groups and water tending to hydrate the polar groups. In the “carry its own water” solution, acetonitrile would have access to the nonpolar region of the purine because of its poor hydration. In the “premixed” solution, the solvation network would be determined on the basis of the affinity of the sites, with the polar groups of the pyrimidines having preference for hydration and their nonpolar region interacting with acetonitrile through its methyl group. In the “injected water” solution, a mixed network would also be formed because of the affinity of the polar groups for water and the tendency of water to avoid the hydrophobic region of the pyrimidines. Thus, the formation of the network around the pyrimidines in these three solutions is not expected to be dependent on the sequence of steps in which the mixture is prepared. This expectation is borne out by the experimental results reported here.

Solvent effects on the spectral properties

The observed differences in the spectral properties of the aqueous mixtures for the three solutions most probably are the consequence of nucleoside-solvent specific effects rather than solvent bulk effects in view of the fact that all three solutions have the same solvent composition. The direction of the shift of the wavelength of the spectral peak relative to that in a nonhydrogen bonding solvent signifies a difference in the strength of the hydrogen bond in the ground state from that in the excited state (Pimentel, 1957; Georghiou, 1981). However, this difference cannot be quantified in the present study because none of the nucleosides is soluble in a nonhydrogen bonding solvent. Also, hydrogen bonding in general is known to affect the fluorescence quantum yield, but the actual mechanism has not been established (Mataga and Kubota, 1970).

We should note that solvent effects on the two ππ^* electronic states in the long-wavelength absorption band of the purines (Callis, 1983; Ge et al., 1990) or on the nπ^* electronic states of the purines and the pyrimidines (Clark and Tinoco, 1965; Voelter et al., 1968; Kaito and Hatano, 1980; Callis, 1983; Broo, 1998) cannot provide an explanation for the present solvation phenomenon because, even in that case, the spectral properties would be expected to be independent of the sequence of steps in which the solution was formed.

With regard to the observed changes in the spectral properties of the nucleosides in neat solvents, these may be the result of interactions that stem from solvent polarity, polarizability, or specific effects (Reichardt, 1988). Depending on the nucleoside, correlations have been found in the present study with either the solvent polarity (according to the empirical parameter of solvent polarity 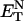(Reichardt, 1994; Suppan and Ghoneim, 1997)) or the solvent polarizability, and these will be presented elsewhere.

Temperature effects on the spectral properties

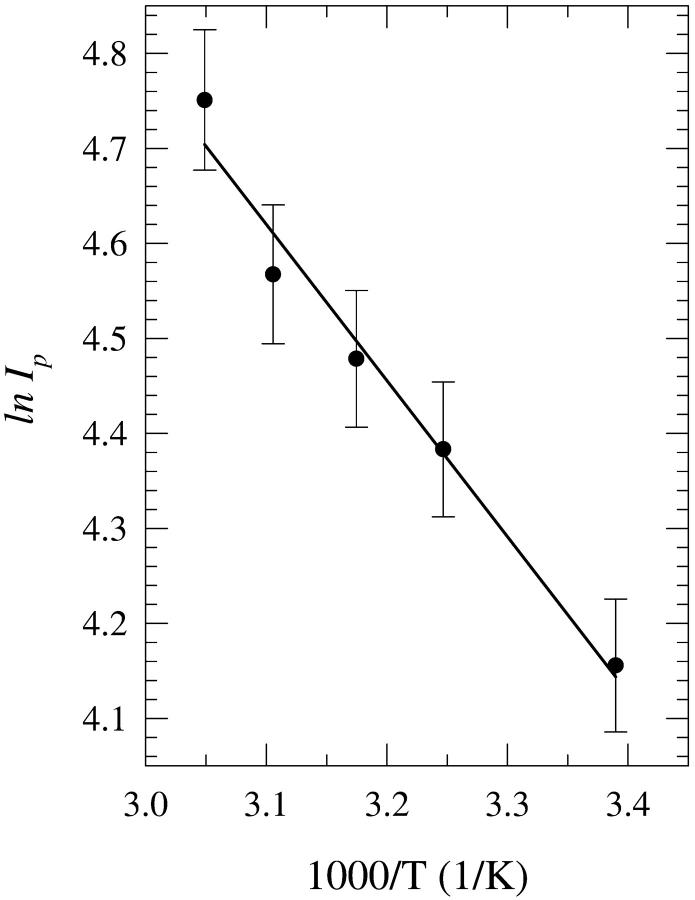
The disruption of the final solvation network formed around the purines in aqueous mixtures of n-butanol and acetonitrile has been investigated for the three solutions, i.e., “premixed”, “carry its own water”, and “injected water”. The solutions were heated over the temperature range of 22°C up to 55°C for 20 min and allowed to cool to room temperature before measuring their fluorescence spectra. In general, no significant changes have been observed in either the spectral width or the wavelength of the fluorescence spectral peak (data not shown). However, changes in the fluorescence peak intensity I_p have been observed. Fig. 13 shows a plot of ln I_p as a function of 1/T, where T is the absolute incubation temperature, for dA in an 8% “carry its own water” solution in acetonitrile. It is seen that I_p increases as T is increased, which most likely results from disruption of the hydration network around dA. The plot in Fig. 13 follows an Arrhenius behavior of the form

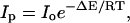(4)

where R is the gas constant = 1.987 × 10⁻³ kcal/mol · K, ΔE is the activation energy, and I_o is a constant. The plot is linear and yields ΔE = 3.4 ± 0.5 kcal/mol. In the thermodynamic relationship

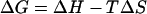(5)

for the “carry its own water” solution, ΔG can be identified with the free energy of partial dehydration. In the temperature ranges used, one would not expect a complete removal of water from around the purines; the solvation energies for purines are ∼−21 kcal/mol for G and ∼−12 kcal/mol for A (Mohan et al., 1992; Elcock and Richards, 1993; Miller and Kollman, 1996). Schweitzer and Kool (1995) reported a dehydration free energy of ∼5 kcal/mol for position N1 and for the N6 amino group of adenine. In this regard, it was reported (Kharakoz, 1991; Chalikian and Breslauer, 1998) that the hydration of adjacent polar groups is strongly enhanced relative to that of distant ones. It would therefore be expected that the hydration at N1 and N6 would be considerably stronger than that at N3 and N7. Thus, partial dehydration of dA would more likely involve N3 and N7, and the value of 5 kcal/mol would be the maximum ΔG for this process. The activation energy ΔE would represent the maximum value of the enthalpy ΔH_max = 3.4 kcal/mol. Equation 5 then yields TΔS = −1.6 kcal/mol. A similar value was obtained for the 15% water solution, −1.8 kcal/mol (Table 4). A value of ∼−3.0 kcal/mol was obtained for the mixtures in n-butanol (Table 4). The negative sign of these entropy changes suggests that the disruption of the water network around dA is accompanied by an increase in the order of the organic solvent around it. The larger increase in the order observed in n-butanol relative to that in acetonitrile is most likely due to the greater hydrophobicity of n-butanol (Table 3): log P of n-butanol is 0.75 whereas that of acetonitrile is −0.34. Information on the ΔG value for the partial dehydration of dG is not available from the literature. If we were to use the aforementioned value of 5 kcal/mol that was reported for the partial dehydration of dA, we obtain TΔS values of ≈−2.1 kcal/mol and −3.1 kcal/mol for the 8% and 15% “carry its own water” solutions in acetonitrile, respectively. The respective values in n-butanol mixtures are −2.5 kcal/mol and −3.6 kcal/mol. The greater increase in the order of acetonitrile around dG as compared to that around dA (Table 4) may be the result of stronger dipole-dipole interactions in the former case because of the larger dipole moment of dG (see above). These considerations suggest that both enthalpy and entropy changes make contributions to the processes involved in the manifestation of the retention of the hydration network in the “carry its own water” solutions.

FIGURE 13.

Plot of the natural logarithm of the fluorescence peak intensity I_p of the spectra of 2′-deoxyadenosine (dA) in 8% (v/v) “carry its own water” solutions in acetonitrile as a function of 1/T, where T is the absolute incubation temperature. The solutions were heated for 20 min and were then allowed to cool to room temperature before the fluorescence spectra were measured. The error bars indicate the standard deviation.

TABLE 4.

Activation energies ΔE (in kcal/mol) for purines in aqueous mixtures in acetonitrile and in n-butanol

	dA				dG
	Acetonitrile		n-butanol		Acetonitrile		n-butanol
	8%	15%	8%	15%	8%	15%	8%	15%
“Carry its own water”	3.4 (−1.6)*	3.2 (−1.8)	2.0 (−3.0)	1.9 (−3.1)	2.9 (−2.1)	1.9 (−3.1)	2.5 (−2.5)	1.4 (−3.6)
“Injected water”	-†	-	1.5	2.1	-	-	2.1	2.5
“Premixed”	2.5	2.5	-	-	-	-	-	-

^*In parentheses are the TΔS values (in kcal/mol) calculated from Eq. 5 (see text).

^†Dash indicates that the changes in the fluorescence intensity were too small to allow the construction of a meaningful Arrhenius plot, from which ΔE would be calculated.

For the “injected water” solutions in the case of n-butanol, ΔG in Eq. 5 can be identified with the free energy of partial desolvation, which is not known, whereas in the case of acetonitrile, a mixed network is formed (see above) that prevents the identification of ΔG. In any case, the activation energies could not be calculated for these solutions because of the very small changes observed in their fluorescence intensity upon heating (data not shown). Also, the “premixed” solutions exhibit rather small changes in the fluorescence intensity upon heating with the exception of dA in acetonitrile (data not shown).

Implications for open basepairs in DNA

The findings of the present study have ramifications for the closing of open basepairs in DNA. Transient breaking of the hydrogen bonds because of thermal fluctuations is known to take place on the millisecond timescale (Guéron et al., 1987; Leroy et al., 1988a; Dornberger et al., 1999). An additional mechanism for opening of basepairs in DNA is through DNA bending, which has been found to require a very small amount of energy, ∼0.2 kcal/mol (Jeltsch, 1998). Significantly, theory finds that DNA bending is coupled to opening of its basepairs (Manning, 1983; Ramstein and Lavery, 1988). After the local breaking of the interbase hydrogen bonds as a result of thermal fluctuations and/or DNA bending, the chemical groups that were participating in these bonds, as well as other polar and nonpolar groups of the bases, would be exposed to a heterogeneous environment that would include chemical groups of adjacent bases, sugars, and the surrounding aqueous environment. The considerable freedom of unpaired bases would allow them to undergo interactions that were not possible or were not of the same strength as in the hydrogen-bonded structure. These may include intrastrand base-base dipole-dipole interactions that may be of considerable strength not only because of the large dipole moments of the bases but also because of the favorable dipole orientations that would become possible as a result of the freedom of the unpaired bases. Moreover, hydrogen bonding as well as partial stacking between unpaired and paired bases could take place. These interactions may occur not only locally but over more distant DNA segments as well in view of the finding that once a basepair is open, DNA becomes very flexible over a wide range of radii of curvature (Ramstein and Lavery, 1988). Theoretical calculations suggest that there is no unique open state but rather a family of open states (Ramstein and Lavery, 1990; Kryachko and Volkov, 2001). Currently, these states are poorly understood.

Depending on the extent to which an open base in DNA is exposed to the surrounding water, one can envision configurations of purine-environment interactions that bear some resemblance to the interactions with purine mononucleosides in the water-organic solvent mixtures.

1. The case of initial full exposure to water would resemble that of the “carry its own water” solution. As was discussed above, hydration forces would tend to preserve this configuration, especially for dG, in the case of interactions with molecular components that have a high degree of amphiphilicity. On the other hand, if hydrogen bonding interactions with other molecular components are weaker than those with water, this configuration would tend to lead to partial exposure to water (as is suggested by the similarity between the fluorescence properties of the “carry its water” and “premixed” solutions, especially for dA (see above)). The degree of exposure to water would be greater in the case of dG because of its much greater hydration free energy as compared to that of dA, ∼−21 kcal/mol vs. ∼−12 kcal/mol (see above).

2. The case of initial full shielding from water would resemble that of the “injected water” solution. This configuration would be dependent on the nature of the shielding interactions. If these interactions involve a high degree of amphiphilicity, this configuration would tend to be preserved. On the other hand, if the shielding interactions stem from weak hydrogen bonding, this configuration would tend to transform into one in which water would participate in the solvation of the purine.

3. The case of initial partial exposure to water would resemble that of the “premixed” solution. As for the probability of this configuration occurring at the DNA level, theoretical calculations find the interaction between the bases of a partially opened AT pair through a bridging water molecule to be quite probable and to stabilize such a pair (Kryachko and Volkov, 2001; Giudice et al., 2001).

The results with the mononucleosides suggest that when the chemical groups of open purines, which in the double-stranded DNA structure are involved in interbase hydrogen bonding, find themselves in a weakly hydrogen bonding or highly amphiphilic environment, the solvation network formed around them would be dependent on the nature of the environment to which they were initially exposed following basepair opening. As a consequence, reformation of the interbase hydrogen bonds to yield a double-stranded DNA structure would tend to be a not very efficient process. This would prolong the open basepair lifetime and thereby allow access of macromolecules (e.g., proteins and enzymes) and ligands (e.g., drugs) to the DNA interior. However, reformation of the interbase hydrogen bonds would be favored by hydrophobic interactions, which would tend to bring the aromatic rings of the bases into the DNA interior, as well as by base-stacking interactions. Thus, the efficiency of this process would be determined by these competing tendencies.

With regard to the state of open basepairs in DNA, NMR measurements of the imino proton exchange yield an apparent lifetime τ′ of the open state, which is the product of its lifetime τ and an accessibility factor that accounts for differences in the accessibility of the imino group to the catalyst in the open pair and in the mononucleoside (Guéron and Leroy, 1992). For a series of oligonucleotides, apparent lifetimes τ′ of the open state were found to be in the range of 10–100 ns (Guéron and Leroy, 1992). Wärmländer et al. (2000) have recently reported for an AT basepair centrally located in a dodecamer the occurrence of a long-lived open state that constituted ∼10% of the open states with an apparent lifetime τ′ ∼ 1 μs. Steric hindrance may allow very limited access or even virtually no access of the catalyst to some of the open bases in DNA, and this would result in a very small value of the accessibility factor and, consequently, in a very long lifetime for those open states.

As was stated above, one situation in which the present solvation phenomenon manifests itself is when purine mononucleosides are involved in weak hydrogen bonding interactions. In the present study, this has been found to be the case in aqueous solutions of acetonitrile, a solvent that is known to form weak hydrogen bonds (Marcus, 1998). At the DNA level, likely weak hydrogen bonds could be formed between amino or imino groups of open bases and the rings of adjacent bases, with the rings functioning as hydrogen bond acceptors. This type of hydrogen bond points toward the plane of the ring and is referred to in the literature as the N-H···π bond. Many examples have appeared in the literature that involve such bonds with aromatic amino acid side chains of proteins (see e.g., the reviews by Burley and Petsko (1988) and by Perutz (1993) as well as the book by Desiraju and Steiner (1999) and the comprehensive analysis of a large number of protein crystal structures by Steiner and Koellner (2001)). They have also been found to be involved in sequence-specific protein-DNA recognition (Parkinson et al., 1996). The two-ring system of tryptophan has been found to be more likely to participate in N-H···π hydrogen bonding than the one-ring system of tyrosine or phenylalanine because of ring area considerations and conjugation effects that are known to strengthen such bonding (Steiner and Koellner, 2001; Gilli et al., 1996); this suggests by analogy that the purines may be more likely candidates for hydrogen bond acceptors in DNA than the pyrimidines. Also, open purines may tend to be more likely candidates for hydrogen bond donors in DNA because their amino and imino groups, being parts of two-ring systems, would be more likely to reach the rings of adjacent bases. Another potential case of weak hydrogen bond formation by the amino and imino groups in DNA would be with the N3 position of the purines, which is a weak hydrogen bond acceptor (Jeffrey and Saenger, 1991). These considerations suggest that purines of open basepairs in DNA can preferentially participate in weak hydrogen bond formation. The strong hydrogen bonding ability of water would allow it to compete efficiently with the N3 position of purines and with the aromatic ring systems in forming hydrogen bonds with the amino and imino groups of open purines in DNA. This competition parallels that between water and acetonitrile in forming hydrogen bonds with the latter groups of purine mononucleosides. This suggests that the present solvation phenomenon, regarding the dependence of the solvation network of purine mononucleosides on their initial environment, likely operates with purines of open basepairs in DNA as well.

Another situation in which the solvation phenomenon has been found in the present study to operate is in aqueous mixtures of n-butanol, which is a highly amphiphilic solvent having a rather long aliphatic chain and a hydroxyl group. In such mixtures, purines tend to retain the solvation network that is initially formed around them. As was discussed above, alcohols that have an aliphatic chain that is shorter than that of n-butanol (methanol, n-propanol, isopropanol, or isobutanol) do not exhibit this solvation retention tendency. The hydrogen bonding abilities of these alcohols (Marcus, 1998) as well as their dipole moments (Lide, 2000) are very similar to those of n-butanol. It has also been found in the present study that arguments based on hydrophobicity considerations fail to account for this solvent selectivity. These considerations suggest that the length of the aliphatic chain is critical in the formation of an elaborate solvation network around purines. This is clearly illustrated by comparing the results of purine mononucleosides in aqueous mixtures of n-butanol with those of isobutanol. These two alcohols have virtually identical hydrogen bonding abilities (Table 3), dipole moments (Lide, 2000), hydrophobicities (Table 3), and polarizabilities (Lide, 2000), but differ in the length of the aliphatic chain. The present study finds that for isobutanol, which has a shorter branched aliphatic chain, the solvation phenomenon does not operate. Aliphatic chains similar to that of n-butanol would not be present in naked DNA, but most likely would be present during protein-DNA interactions. In fact, the length of the aliphatic chain of lysine is the same as that of n-butanol. Moreover, like n-butanol, lysine possesses a high degree of amphiphilicity as it has an ɛ-amino group in addition to the relatively long aliphatic chain. Thus, after the opening of basepairs through protein-DNA interactions, lysine side chains could form a “solvation” network around the purines of open basepairs, which the solvation retention phenomenon suggests that would tend to be preserved. This would keep the purines from reforming the interbase hydrogen bonds, thus making them accessible to enzymatic interactions. As was noted above, theory finds that DNA bending is coupled to opening of its basepairs (Manning, 1983; Ramstein and Lavery, 1988). Thus, the observed high frequency of DNA bending in protein-DNA complexes (Dickerson, 1998) implies the occurrence of a high frequency of basepair opening in such complexes. The nucleosome presents a quite pertinent case of protein-DNA interactions of special interest. Covalent modifications of the lysines of the very flexible histone N-terminal tails are known to play a very important role in transcription regulation (Turner, 2001). Such modifications (in particular acetylation or methylation) would alter the amphiphilicity of lysines, which, on the basis of the solvation retention phenomenon reported here, would in turn alter their ability to retain basepairs in their open states and thus make them accessible to the transcription machinery. These considerations will be discussed elsewhere (Georghiou and Ababneh, unpublished).

We finally note that the solvation phenomenon observed here, in which purines have the tendency to retain certain solvation as well as hydration networks formed initially around them, is reminiscent of the reported “molecular memory” effect exhibited by the catalytic activity of enzymes suspended in organic solvents in the presence of small amounts of water (Dai and Klibanov, 1999). Those workers reported that enzymes have a much greater catalytic activity when added in a small amount from an aqueous enzyme solution to the organic solvent rather than when suspending the enzyme directly in the organic solvent that contained the same small amount of water as in the former method of solution preparation. These methods of suspension of enzymes in organic solvents resemble the methods used in the present study for preparations of “carry its own water” and “premixed” solutions, respectively. The operation of this molecular memory effect was found to depend on the nature of the solvent and the enzyme.