TOUCHSTONE II: A New Approach to Ab Initio Protein Structure Prediction

Abstract

We have developed a new combined approach for ab initio protein structure prediction. The protein conformation is described as a lattice chain connecting C_α atoms, with attached C_β atoms and side-chain centers of mass. The model force field includes various short-range and long-range knowledge-based potentials derived from a statistical analysis of the regularities of protein structures. The combination of these energy terms is optimized through the maximization of correlation for 30 × 60,000 decoys between the root mean square deviation (RMSD) to native and energies, as well as the energy gap between native and the decoy ensemble. To accelerate the conformational search, a newly developed parallel hyperbolic sampling algorithm with a composite movement set is used in the Monte Carlo simulation processes. We exploit this strategy to successfully fold 41/100 small proteins (36 ∼ 120 residues) with predicted structures having a RMSD from native below 6.5 Å in the top five cluster centroids. To fold larger-size proteins as well as to improve the folding yield of small proteins, we incorporate into the basic force field side-chain contact predictions from our threading program PROSPECTOR where homologous proteins were excluded from the data base. With these threading-based restraints, the program can fold 83/125 test proteins (36 ∼ 174 residues) with structures having a RMSD to native below 6.5 Å in the top five cluster centroids. This shows the significant improvement of folding by using predicted tertiary restraints, especially when the accuracy of side-chain contact prediction is >20%. For native fold selection, we introduce quantities dependent on the cluster density and the combination of energy and free energy, which show a higher discriminative power to select the native structure than the previously used cluster energy or cluster size, and which can be used in native structure identification in blind simulations. These procedures are readily automated and are being implemented on a genomic scale.

INTRODUCTION

As second half of the genetic code, the prediction of tertiary structure of proteins from their primary amino acid sequence is one of the most important and challenging problems in contemporary structural biology. There are three classes of theoretical approaches to the problem in the recent literature (Murzin, 2001): homology modeling (Guex and Peitsch, 1997; Sanchez and Sali, 1997); threading (Bowie et al., 1991; Panchenko et al., 2000; Skolnick and Kihara, 2001); and ab initio folding (Pillardy et al., 2001; Simons et al., 2001; Kolinski and Skolnick, 1998). Although homology modeling aims to find a template protein whose sequence is clearly evolutionarily related to the query sequence, the aim of threading is to detect both evolutionary-related sequences and analogous folds, which adopt very similar structures to the query protein. Both threading and homology modeling, in principle, are capable of producing high-resolution folds based on the identified template proteins, but they suffer from the fundamental limitation that the native topology for the sequence of interest must have already been solved; and new folds cannot be predicted by these approaches. To address this issue, the most difficult and general approach is ab initio folding, where one attempts to fold a protein from a random conformation.

In principle, ab initio approaches are based on the thermodynamic hypothesis formulated by Anfinsen (Anfinsen, 1973), according to which the native structure corresponds to the global free energy minimum under the given set of conditions. The success of the approach therefore relies on the effectiveness of the following factors: 1), An implicit representation of the protein with sufficient structural fidelity and computational tractability. 2), A force field having near-native structures as its global minimum. 3), A protocol to effectively search the important regions of conformational phase space in a reasonable amount of CPU time. 4), A methodology to correctly identify near-native structure from the decoys produced by the simulation.

In this article, we will present our efforts to address all of these four issues that extend and improve our previous TOUCHSTONE approach (Kihara et al., 2001). Here, we exploit a new lattice representation for the protein structure, in which three united atom groups of C_α, C_β, and the side-group (SG) center of mass of the remaining (non-C_β) heavy atoms (CABS) are specified. Compared with our previous side-chain-only (SICHO) model (Kolinski and Skolnick, 1998) where only the side-chain centers of mass are treated, the CABS model has higher geometric fidelity.

Similar to the SICHO model (Kolinski and Skolnick, 1998), the basic force field includes energy terms describing short-range structural correlations, hydrogen-bond interactions, long-range pairwise potentials, one-body burial interactions, and a residue-contact-based environmental profile. All interactions are reconstructed in a more specific way in the new lattice model. For example, the H-bond and proteinlike conformational stiffness are more precisely constructed because of the inclusion of explicit C_α atoms in the model. The combination of C_α-C_α and SG-SG correlations provides for short-range interactions of higher amino acid specificity than the SICHO model. We also incorporate electrostatic interactions for the charged residues and a global propensity to the predicted contact order and contact number. Because these energy terms are not independent, some interactions are overcounted. To combine all of these energies, we create 60,000 decoys for each of 30 training proteins of diverse lengths (47 ∼ 146 residues) and topologies. We obtain their weight factors by maximizing the correlation between the total energy and the structural similarity of decoys to the native structure, and by maximizing the energy gap between native structure and decoy ensembles. Decoy-based optimization of force fields has been exploited in previous studies that either maximize the correlation of the energy (scoring) function and RMSD to native (Simons et al., 1999) or require a lower energy of the native structure than the ensemble of decoys (Vendruscolo et al., 1999; Tobi and Elber, 2000). Here, we find that their combination provides for a better folding yield than when using either one alone. The optimized force field has a significantly improved energy versus RMSD correlation in favor of the native structure, compared to the naïve uniformly weighted combination of all the energy terms.

To effectively search the resultant energy landscape, we exploit the recently developed parallel hyperbolic sampling algorithm in our Monte Carlo (MC) simulations (Zhang et al., 2002). Previously, this protocol was shown to be more effective than general replica sampling in searching for low-energy structures, especially for proteins of large size where the energy landscape is significantly more rugged than the energy landscape of small proteins. To identify near-native structures from decoys generated in the MC simulations, we exploit the structure-clustering algorithm (SCAR) (Betancourt and Skolnick, 2001) to cluster the low-energy trajectories. We introduce two quantities dependent on the cluster density and the combination Y of energy and free energy, which are more discriminative than the generally used average energy and cluster size for the identification of near-native structures.

We apply our approach to a test set of 125 proteins (65 proteins that are the same as used in the original TOUCHSTONE paper (Kihara et al., 2001) plus an additional, harder 60-protein test set that covers a larger range of protein sizes). Using only protein sequence information, we can fold 41 cases that have structures with root mean square deviation (RMSD) from native of 1.79 ∼ 6.5 Å in the top five clusters. All these foldable cases are restricted to small proteins (36 ∼ 120 residues). To fold proteins of larger size and to improve the folding yield of the small proteins as well, we take the threading-based predictions of side-chain contacts as loose restraints in our force field to guide the folding simulations. These restraints are collected from consensus contacts hit by PROSPECTOR (Skolnick and Kihara, 2001). Their inclusion results in a significant improvement in the overall folding performance. There are 83 cases (70 cases with length less than 120 residues plus 13 cases with 120 ∼ 174 residues) in the restraint-guided simulations that have at least one structure with a RMSD to native below 6.5 Å in the top five clusters. Especially, for the 60 harder representative proteins, the fraction of foldable cases (defined as having one of the top five clusters with RMSD from native below 6.5 Å) by the SICHO and CABS models are 1/3 and 1/2, respectively (i.e., 20/60 and 32/60), indicating a qualitative improvement of the new CABS model over the SICHO model. This improvement may, however, be partly due to the force-field optimization procedure used for the CABS model.

This article is organized as follows: we first describe the lattice representation of protein structure. Second, we give a detailed discussion of the interaction scheme and the procedure used to optimize the force field. This is followed by a description of the conformational search engine and the secondary structure prediction scheme. Then, we present the results of our approach applied to representative proteins, and our method for the evaluation of the simulation results. Finally, we summarize the key results.

METHODS

Reduced protein representation

Each amino acid is represented by up to three united atom groups (Fig. 1). In the main chain, only the alpha carbon (C_α) atoms are treated explicitly, and the C_α trace is restricted to a three-dimensional underlying cubic lattice system with a lattice spacing of 0.87 Å. To keep sufficient facility for the conformational movements and geometric fidelity of structure representation, we allow the model's backbone length to fluctuate from 3.26 Å to 4.35 Å. As a result, we have 312 basis vectors representing the virtual C_α-C_α bonds (see Table 1). The average vector length is ∼3.8 Å, which coincides with the value of real proteins. To reduce the configurational entropy, we also restrict the virtual C_α-C_α bond angle to the experimental range [65°,165°].

FIGURE 1.

Schematic representation of a three-residue fragment of polypeptide chain in the CABS model. The C_α trace is confined to the underlying cubic lattice system, whereas the C_β atom and side-group rotamers are off-latticed and specified by the positions of three adjacent C_α atoms.

TABLE 1.

The lattice vectors employed in the representation of the main chain C_α trace

Vector type*	Number of vectors	Squared length in lattices	Length [Å]†
[±3,±2,±1]	48	14	3.26
[±4,0,0]	6	16	3.48
[±3,±2,±2]	24	17	3.59
[±4,±1,0]	24	17	3.59
[±3,±3,0]	12	18	3.69
[±4,±1,±1]	24	18	3.69
[±3,±3,±1]	24	19	3.79
[±4,±2,0]	24	20	3.89
[±4,±2,±1]	48	21	3.99
[±3,±3,±2]	24	22	4.08
[±4,±2,±2]	24	24	4.26
[±4,±3,0]	24	25	4.35
[±5,0,0]	6	25	4.35
			〈r〉 = 3.81 Å

^*Includes all permutations of the coordinates and signs.

^†One lattice unit corresponds to 0.87 Å.

The positions of three consecutive C_αs define the local coordinate system used for the determination of the remaining two interaction units: the β-carbon (C_β) (except glycine), and the center of mass of remaining side-group heavy atoms (except glycine and alanine). A two-rotamer approximation has been assumed, depending on whether the configuration of the main chain is expanded (for instance in a β-sheet) or compact (for instance in an α-helix). The secondary structure-dependent numerical parameters for the determination of the C_β and SG positions are extracted from the protein data bank (PDB) (Berman et al., 2000).

The excluded volume of the envelope of the C_α and C_β atoms are represented as identical size hard spheres (infinite energy of overlap) of diameter 3.25 Å plus a 1/r type of soft-core potential in the range [3.25 Å, 5.0 Å]. This mimics the minimal observed cutoff distance of 4.0 Å in real proteins, and allows a few atoms to approach closer than the reality at a penalty, thereby partly remedying the coarseness of the discrete lattice model. The excluded volume of the SG units is approximated by a strong energy penalty when the distance of a side group from other units is below cutoff values specific to the interacting pair of amino acids. With the above geometric restrictions, all PDB structures can be represented with an average RMSD of 0.4 Å from native, better than that of 0.8 Å via the SICHO model (Kolinski and Skolnick, 1998). This geometric fidelity does not show any systematic dependence on protein length.

Energy terms in the force field

The force field consists of a variety of terms based on or derived from the regularities seen in PDB structures. They contain a generic bias to proteinlike conformational stiffness, amino acid-dependent interactions, and protein-specific restraints predicted from evolutionary information. According to the distance along the sequence between the involved amino acid pairs, these interactions can roughly be classified into two categories: long-range tertiary interactions and short-range secondary structural correlations, based on which our following descriptions are separated.

The different energy terms achieve various effects on the generation of nativelike states. The most important factors for overall folding in our force field are the secondary structure prediction propensities, hydrogen bonding, and tertiary contact restraints derived from threading. The first two terms provide a basic folding framework; the contact restraints are of critical importance in modifying the energy landscape to guide the simulations to near native states, especially for large proteins where the general proteinlike potential cannot distinguish the native state among a huge number of possible topologies.

The other terms describing short-range correlations, environment profiles, burial, and long-range pairwise interactions are helpful for refining the packing of side chains and local fragments; the bias toward predicted contact order and contact number also helps somewhat to speed up the folding processes.

Some of the above energy terms are similar to that in the SICHO model (Kolinski and Skolnick, 1998); however, the implementation is different in the new lattice model. For the sake of completeness, we present all the energy terms used in the CABS model. Below, we first describe the short-range interactions and then the long-range terms. Next, we will determine the relative weights of the energy terms in the combined force field, based on the correlation between the energy and structure quality of the decoys.

Short-range interactions

Multiple short-range correlations

The potential contains both C_α-C_α and SG-SG local structure correlations derived from the PDB as the negative logarithm of the relative frequency histogram:

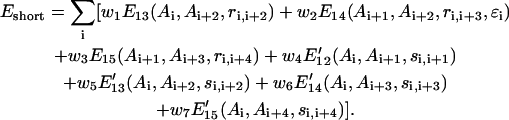(1)

Here, A_i denotes the amino acid identity of the ith residue; r_i,j (s_i,j) is the C_α (SG) distance between the ith residue and the jth residue; ɛ_i denotes the local chain chirality of three consecutive C_α-C_α vectors from i to i + 3. E_i,j represents the C_α-C_α correlation of the ith and jth residues extracted from a statistical analysis of a structural data base of nonhomologous proteins (Kolinski and Skolnick, 1994, 1998). E₁₃ includes only two bins depending on the distance of r_i,i+2, which correspond to local extended and compact structures, respectively. E₁₄ and E₁₅ include more bins because more distant interactions are involved. When the predicted secondary structure is assigned in the fragments, both E₁₄ and E₁₅ are half/half combinations of the general and secondary structure specific parts extracted from generic and secondary structure specific fragments of the PDB, respectively.

E′_ij in Eq. 1 represents the local side-group correlation from the ith residue to jth residue and is derived from a set of PDB structures that have certain levels of sequence similarity to the query proteins and where homologous proteins of more than 25% sequence identity to the query proteins are excluded from the structural data base (Kolinski et al., 1998). When predicted secondary structure is assigned, E′_ij is also combined with a SG-SG correlation potential derived from secondary structure specific fragments of PDB data base. The w_i values in Eq. 1 and the equations below are the relative scale factors of these interactions that will be determined in the next section.

Local conformational stiffness

This potential describes the characteristic local stiffness of global proteins and the general tendency toward regular arrangements of (predicted and nonpredicted) secondary structure:

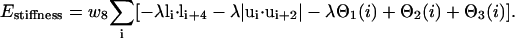(2)

Here, the unit tangent vector 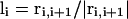, and bisector vector 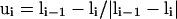, where r_i,i+1 is the C_α-C_α bond vector from vertex i to vertex i + 1. The first two terms represent the general propensities to common bond-vector orientations of α-helical and β-sheet structures as shown in Fig. 2. The third term is designed to impose further structure biases to the individual regularities of α-helical and β-sheet structures and is written as

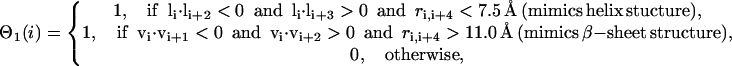(3)

where the unit normal vector 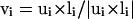(see Fig. 2). It should be noted that in Eq. 3, a helical bias is not applied to the residues predicted to be in an extended secondary structure, and vice versa. λ is a stiffness modulation factor for the first three terms, equal to 1 or 0.5, depending on whether the involved residues are inside or outside the radius of gyration of the protein respectively.

FIGURE 2.

Schematic illustration of the virtual C_α-C_α vectors for regular helical and sheet structures. 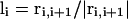, , 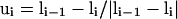, 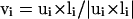where r_i,i+1 is the C_α-C_α bond vector from vertex i to vertex i + 1. As demonstrated in the first two terms of Eq. 2, for both helical and sheet structures, l_i and l_i+4 are oriented in parallel whereas u_i and u_i+2 are either antiparallel (helix) or parallel (sheet).

Θ₂ denotes the strong tendency to form predicted secondary structures, which are taken from the combined PSIPRED (Jones, 1999) and SAM-T99 (Karplus et al., 1998) secondary structure prediction algorithms (discussed in “Secondary structure prediction”).

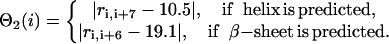(4)

Θ₃ imposes a penalty to the irregular crumpled structures, i.e.

(5)

where r_i,j is the vector from the ith C_α vertex to the jth C_α vertex.

Hydrogen bonds

Hydrogen bond interactions can be short range or long range depending on the secondary structures of the involved residues, although we list it here in the short-range category of interactions. Only main chain hydrogen bonds are considered. Due to the lack of the explicit positions for the peptide bond atoms, the effect of hydrogen bonds is translated into C_α packing preferences:

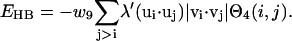(6)

Here 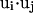and 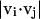impose a bias to the specific vertex orientation of regular H-bonds. 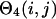defines the conditions when the ith residue is hydrogen bonded to the jth residue, i.e.,

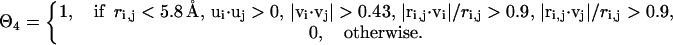(7)

Secondary structure assignments (when predicted) modify the formation of H-bonds: H-bonds between extended-assigned and helical-assigned residues and long-range H-bonds between helical-assigned residues are prohibited. Moreover, to enhance the H-bond in the better assigned secondary structure regions, we set the stiffness modulation factor λ′ to 1.5 or 1, respectively, depending on whether or not regular helix and sheet structures are predicted.

Local distant restraints

The consensus local distance predictions for pairs of C_αs less than six residues along the sequence are collected from the templates and short fragments hit by our threading program PROSPECTOR (Skolnick and Kihara, 2001). These protein-specific predictions are incorporated in the force field as loose restraints on the local structure:

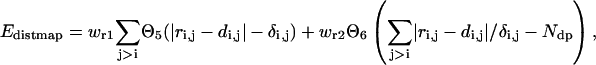(8)

where d_i,j is the predicted distance of the ith residue and jth residue, and δ_i,j is the mean square deviation of the prediction. The step functions 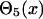and 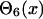are defined as

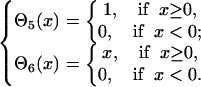(9)

The accumulated normalized deviations to the predicted distant map enter into the force field as a penalty when they exceed the number of predictions, N_dp. This penalty term allows for the significant violation of a small fraction of unreasonable predictions.

Long-range interactions

Pairwise interactions

The long-range pairwise interactions of C_α(_β)-C_α(_β) and that of SG-C_α(_β) are essentially the general excluded volume interactions, which as mentioned above are represented by a smaller hard-sphere potential plus a 1/r type of soft-core potential with a slightly larger range. The SG-SG interaction is written as

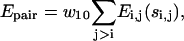(10)

where

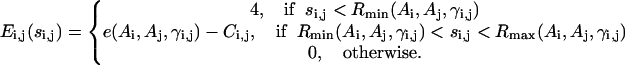(11)

Here, γ_i,j denotes the relative orientations of the bisector vectors of the backbone vertices, i.e., parallel (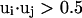), antiparallel (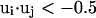), and perpendicular (). 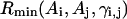and 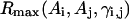are the cutoff values for the hard-core excluded volume interactions and the soft-core square-well interactions, respectively. The pairwise potential 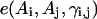is derived from a structural data base (Skolnick et al., 1997). 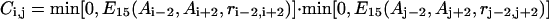aims to enhance the contact interactions of the short fragments that have favorable short-range correlations and therefore stabilize their local structures.

Burial interactions

This potential represents the general propensity of amino acids to be buried or exposed to solvent and is only applicable to single-domain proteins. It includes contributions from both the C_αs and the SGs:

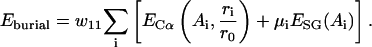(12)

Here r_i is the radial distance of the ith C_α related to the protein center, r₀ is the average radius of gyration, which has an approximate relationship with the length of protein N, i.e., 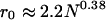. 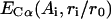is a statistical potential derived from PDB data base, where r_i was divided into five bins for each amino acid A_i. 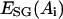is a half/half combination of the two most commonly used hydrophilicity scales of Kyte-Doolittle (Kyte and Doolittle, 1982) and Hopp-Woods (Hopp and Woods, 1981). μ_i is the burial factor relative to hydrophobic core defined as

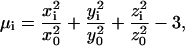(13)

where (x_i, y_i, z_i) and (x₀, y₀, z₀) are the coordinates of the SG in the center of mass coordinate system and the lengths of principal axes of the protein ellipsoid, respectively.

Electrostatic interactions

We consider electrostatic interactions among four charged residues, i.e., Asp (−), Glu (−), Lys (+), and Arg (+), in a Debye-Huckel form:

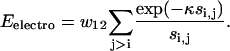(14)

Here, κ is the inverse Debye length that is sensitive to solvent conditions (Zhang et al., 2001). Through examination of the potential on structure decoys, we found that a value of 1/κ ∼ 15 Å produces the best correlation between the RMSD and energy.

Environment profile

The potential describing the contact environment of individual residues is written as

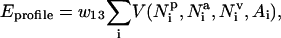(15)

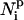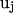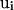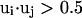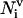is the number of residues that are in contact with the ith residue, whose vertex vectors ('s) are parallel to , i.e., ; and are defined in a similar way but with 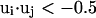(antiparallel) and 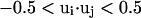(perpendicular), respectively. Residues are regarded as being in contact when the distance between their side groups is below 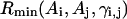. (For a list of all parameters see http://bioinformatics.buffalo.edu/abinitio.) Again, the amino acid-specific potential 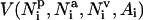is derived from the protein structure data base as the negative logarithm of the relative frequency histogram.

Contact order and contact number

We also include biases to the expected contact order and contact number:

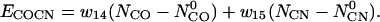(16)

Here, 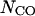is the contact order of the given structure, defined as average sequence separation of residues in contact (Baker, 2000). The expected contact order has an approximately linear dependence on protein length N, i.e., 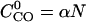, where α is a protein secondary structure specific parameter that is derived from the PDB data base, which was divided into three categories of helix, sheet, and helix/sheet proteins. 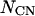is the number of contacting residues, and 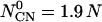is an approximate estimate of the contact number according to the PDB.

Contact restraints

Consensus tertiary contact predictions are collected from templates hit by the threading program PROSPECTOR (Skolnick and Kihara, 2001), where sequence homologs have been excluded from the data base. These predictions are incorporated into the force field as

(17)

where step functions 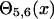are defined as in Eq. 9. The summation of 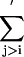is done only for N_cp residue pairs that are predicted in PROSPECTOR as having side-chain center of mass contacts. A penalty is invoked when the distance of a side-group pair predicted as being in contact is beyond 6 Å. An additional penalty enters when the total violation against the prediction is beyond a threshold value of N_cp. Because only a portion of the predictions is exactly correct and some predicted contacts may even be in geometric contradiction to each other, this threshold cutoff is designed to tolerate some significant violations of a small portion of the contact restraints.

Optimization of force field

Our total force field is a combination of all above energy terms, i.e.:

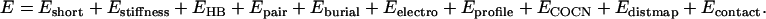(18)

There are 19 parameters in Eq. 18, which dictate the relative weights of the different energy terms. We could not combine them naïvely, i.e., let all w_i = 1, because the energy terms are not independent and some interactions are multiply counted. For example, the short-range five-residue correlation energy E₁₅ partly includes the contributions of lower-order correlation energies E_1i (i < 5); the former is also incorporated in the calculations of pairwise interactions. The propensity to regular secondary structure is implemented in different energy terms such as hydrogen bonding, conformational stiffness, and pairwise interactions. Thus in the following, we will first generate a set of nonredundant decoys, and then determine the parameters by maximizing the correlation between the energy and the structural similarity of the decoys to native.

Generation of decoy structures

To generate decoys, we selected 30 nonhomologous protein sequences from the PDB (Berman et al., 2000), which cover a variety of lengths (47 ∼ 146) and topologies (see proteins marked with ^⋆ in Table 6). We make Monte Carlo runs based on both the SICHO (Kolinski et al., 1998) and CABS force fields using the parallel hyperbolic sampling algorithm (Zhang et al., 2002). To perform the CABS runs, we made a temporary initial estimate of the force field parameters. These simulations start from the native structure. For reasonable force fields, the low temperature replicas stay around the near-native state and the higher temperature replicas move away and generate structures further away from native. If the model force field is not good enough and even low temperature replicas go far away from native, we intermittently stop and restart the simulation from native structures to ensure that a sufficient number of decoys are near native.

TABLE 6.

Summary of fold results on 125 benchmark proteins

ID*	Str†	N‡	Clusterwo§	Clusterw¶	Comb‖	E1**	M1††	Y1‡‡	D1§§	Bests¶¶
Set65‖‖
1a32_	α	64	4.63(3/3)	6.30(1/3)	6.30	6.30★	6.30★	6.30★	6.30★	4.57(435)
1ah9_	β	63	6.20(1/11)	5.09(1/5)	5.09	5.09★	5.09★	5.09★	5.09★	3.18(324)
1aoy_⋆	α	65	6.84(4/5)	4.68(1/9)	4.68	4.68★	4.68★	4.68★	4.68★	2.22(325)
1bq9A	β	53	7.05(7/19)	4.82(1/13)	4.82	4.82★	4.82★	4.82★	4.82★	2.87(123)
1bw6A	α	56	4.79(2/3)	4.22(1/8)	4.22	4.22★	4.22★	4.22★	4.22★	2.96(699)
1c5a_⋆	α	65	4.28(2/7)	4.25(2/4)	4.25	8.25	8.25	8.25	8.25	3.16(554)
1cewI	αβ	108	10.96(1/14)	6.33(2/7)	6.33	9.02	9.02	9.02	9.02	3.82(763)
1cis_⋆	αβ	66	5.12(4/9)	5.92(3/3)	5.92	6.65	6.65	6.65	6.65	3.96(493)
1csp_	β	67	6.37(4/11)	3.84(2/5)	3.84	10.57	4.32	4.32	4.32	3.36(211)
1ctf_⋆	αβ	68	5.54(3/4)	5.24(2/11)	5.24	9.91	9.91	9.91	9.91	3.94(777)
1erv_⋆	αβ	105	6.01(3/6)	2.09(1/8)	2.09	2.09★	2.09★	2.09★	2.09★	1.86(187)
1fas_⋆	β	61	6.81(5/29)	3.21(1/4)	3.21	3.21★	3.21★	3.21★	3.21★	2.42(676)
1fc2C	α	43	3.61(1/4)	3.92(1/4)	3.61	3.92★	3.92★	3.92★	3.92★	2.58(93)
1ftz_⋆	α	48	5.07(1/2)	1.66(1/7)	1.66	1.66★	1.66★	1.66★	1.66★	1.20(311)
1gpt_⋆	αβ	47	6.30(1/25)	3.96(1/10)	3.96	3.96★	3.96★	3.96★	3.96★	2.19(214)
1hlb_	α	157	7.02(8/11)	4.68(1/10)	4.68	4.68★	4.68★	4.68★	4.68★	3.36(65)
1hmdA⋆	α	113	7.58(1/6)	9.12(5/9)	7.58	13.99	9.12★	9.12★	9.12★	6.59(270)
1hp8_	α	68	4.67(2/3)	5.26(1/4)	5.26	5.26★	5.26★	5.26★	5.26★	4.14(319)
1ife_	αβ	91	4.60(1/5)	8.76(4/4)	4.60	11.68	11.68	11.68	11.68	3.93(427)
1ixa_	β	39	6.04(4/31)	4.30(1/5)	4.30	4.30★	4.30★	4.30★	4.30★	2.40(648)
1iyv_	β	74	8.43(1/15)	7.60(2/9)	7.60	9.69	7.60★	7.60★	7.60★	6.28(407)
1kjs_⋆	α	74	5.54(1/4)	8.23(2/3)	5.54	10.03	10.03	10.03	10.03	5.34(119)
1ksr_⋆	β	100	8.03(5/16)	5.82(1/8)	5.82	5.82★	5.82★	5.82★	5.82★	4.57(133)
1lea_⋆	α	72	5.69(5/5)	4.22(1/8)	4.22	4.22★	4.22★	4.22★	4.22★	2.92(79)
1mba_⋆	α	146	10.25(3/11)	2.51(1/6)	2.51	2.51★	2.51★	2.51★	2.51★	2.10(804)
1ner_	α	64	6.35(2/8)	2.70(1/11)	2.70	2.70★	2.70★	2.70★	2.70★	2.28(174)
1ngr_	α	83	5.19(5/6)	3.39(1/7)	3.39	3.39★	4.80	3.39★	4.80	2.57(524)
1nkl_	α	77	5.50(2/7)	3.89(1/6)	3.89	3.89★	3.89★	3.89★	3.89★	2.91(356)
1nxb_⋆	β	62	6.08(3/19)	2.35(1/7)	2.35	2.35★	2.35★	2.35★	2.35★	2.13(393)
1pdo_⋆	αβ	124	6.98(2/15)	6.66(1/3)	6.66	6.66★	8.56	6.66★	6.66★	5.34(102)
1pgx_	αβ	59	5.62(3/7)	5.96(5/7)	9.30	10.80	9.31	9.31	5.96★	4.22(24)
1poh_	αβ	85	9.10(5/9)	12.71(4/6)	12.71	12.74	12.74	12.74	12.74	9.93(10)
1pou_	α	69	4.41(5/9)	4.22(4/7)	4.22	9.57	9.57	9.57	9.57	3.38(47)
1pse_⋆	β	68	9.55(2/13)	7.88(9/11)	9.15	10.81	10.81	10.81	10.81	5.81(682)
1rip_	β	76	7.97(5/8)	8.53(2/7)	8.53	9.41	9.41	9.41	9.41	7.21(236)
1rpo_	α	61	5.47(1/3)	4.55(1/2)	4.55	4.55★	24.82	4.55★	4.55★	3.18(456)
1shaA⋆	αβ	103	8.66(7/13)	4.05(1/10)	4.05	4.05★	4.05★	4.05★	4.05★	2.95(595)
1shg_	β	57	7.62(7/8)	4.59(2/8)	4.59	9.89	10.40	10.40	10.40	3.54(499)
1sro_⋆	β	71	7.65(1/7)	4.27(1/8)	4.27	4.27★	4.27★	4.27★	4.27★	3.21(107)
1stfI	αβ	98	8.79(1/12)	4.92(1/9)	4.92	4.92★	4.92★	4.92★	4.92★	2.91(551)
1stu_⋆	αβ	68	7.68(2/6)	6.31(2/6)	6.31	6.72	6.72	6.72	6.72	4.97(101)
1tfi_⋆	β	47	6.79(2/2)	6.22(2/7)	6.22	10.23	6.22★	6.22★	6.22★	4.35(526)
1thx_	β	108	6.22(3/10)	2.33(1/6)	2.33	2.33★	2.33★	2.33★	2.33★	2.10(547)
1tit_	β	89	7.88(7/15)	1.88(1/10)	1.88	1.88★	5.45	1.88★	1.88★	1.71(896)
1tlk_	β	95	9.27(4/21)	2.24(1/6)	2.24	2.24★	2.24★	2.24★	2.24★	1.99(868)
1tsg_	αβ	98	8.19(15/18)	9.08(3/9)	9.08	12.49	9.08★	9.08★	9.08★	6.64(840)
1ubi_⋆	αβ	72	6.60(3/7)	1.74(1/11)	1.74	1.74★	1.74★	1.74★	1.74★	1.54(821)
1vcc_	αβ	76	7.07(3/16)	7.29(12/15)	7.42	7.42	10.70	10.70	10.70	6.54(68)
1vif_	β	52	6.87(9/12)	7.93(3/9)	7.12	8.58	7.93★	7.93★	7.93★	5.33(215)
1wiu_	β	93	9.95(2/10)	2.22(1/8)	2.22	2.22★	2.22★	2.22★	2.22★	1.96(619)
256bA⋆	α	106	3.61(2/3)	3.18(2/7)	3.18	8.60	3.19★	3.19★	3.19★	2.17(685)
2af8_⋆	α	86	11.07(5/6)	3.68(1/9)	3.68	3.69★	6.87	3.69★	3.69★	3.19(463)
2azaA⋆	β	129	10.20(38/51)	2.79(1/13)	2.79	2.79★	2.79★	2.79★	2.79★	2.66(475)
2bby_⋆	α	67	9.10(4/6)	6.65(2/6)	6.65	9.71	9.71	9.71	9.71	4.34(35)
2ezh_⋆	α	65	5.78(3/3)	4.74(3/5)	4.74	8.69	4.74★	4.74★	4.74★	3.13(377)
2ezk_⋆	α	90	8.06(4/7)	8.98(4/6)	8.98	12.59	12.39	12.39	12.39	7.28(278)
2fdn_⋆	αβ	55	5.73(1/41)	2.27(1/12)	2.27	2.27★	2.27★	2.27★	2.27★	1.97(542)
2fmr_	αβ	64	5.66(5/9)	4.97(1/9)	4.97	4.96★	4.96★	4.96★	4.96★	3.98(216)
2lfb_	α	70	7.47(2/5)	6.37(4/7)	6.37	10.29	10.29	10.29	10.29	5.95(35)
2pcy_	β	99	8.00(4/36)	4.25(1/11)	4.25	4.25★	4.25★	4.25★	4.25★	3.47(135)
2ptl_⋆	αβ	61	3.32(1/5)	2.63(1/6)	2.63	2.63★	2.63★	2.63★	2.63★	2.02(528)
2sarA⋆	αβ	96	9.57(11/36)	7.55(4/7)	7.55	11.36	11.36	11.36	11.36	5.35(666)
4fgf_	β	124	10.40(29/49)	3.75(2/13)	3.75	6.11	3.75★	6.11	3.75★	3.11(492)
5fd1_	αβ	106	9.19(3/8)	5.79(1/6)	5.79	5.79★	10.69	5.79★	5.79★	4.76(303)
6pti_	αβ	56	5.02(2/8)	4.04(5/9)	6.31	6.31	4.04★	4.04★	4.04★	3.48(545)
Set60***
1ail_	α	70	7.31(1/3)	4.01(2/5)	4.01	8.44	8.44	8.44	8.44	2.77(565)
1aiw_	β	62	8.75(4/34)	8.07(4/19)	8.07	8.74	9.76	8.74	9.76	6.95(269)
1amm_	αβ	174	12.86(62/62)	10.08(1/6)	10.08	10.08★	13.84	13.84	13.84	9.06(998)
1apf_	β	49	6.04(5/27)	4.43(2/10)	4.43	9.31	6.59	9.31	9.31	4.31(228)
1b2pA	β	119	12.52(31/56)	11.39(19/32)	12.09	13.93	12.31	12.60	12.31	10.53(613)
1bd8_	α	156	13.36(3/8)	3.03(1/11)	3.03	3.03★	3.03★	3.03★	3.03★	2.22(629)
1bfg_	β	126	10.71(32/54)	3.72(1/13)	3.72	3.72★	3.72★	3.72★	3.72★	3.20(831)
1bkf_	αβ	107	8.49(5/24)	7.52(3/16)	7.52	14.21	12.45	12.45	12.45	6.65(973)
1bkrA	α	108	7.82(3/7)	2.12(1/14)	2.12	2.12★	2.12★	2.12★	2.12★	1.76(785)
1bm8_	αβ	99	8.11(8/19)	8.98(2/11)	8.98	11.91	9.84	9.84	9.84	8.53(399)
1c3mA	β	145	11.02(27/36)	10.53(5/20)	12.96	14.98	10.53★	12.96	10.53★	9.55(551)
1c8cA	αβ	64	8.97(26)	8.72(5/7)	10.24	10.24	11.87	11.87	11.87	8.41(4)
1cpq_	α	129	9.76(3/7)	6.26(5/5)	10.90	15.43	10.90	10.90	6.26★	5.16(498)
1cy5A	α	92	11.60(3/5)	1.76(1/9)	1.76	1.76★	1.76★	1.76★	1.76★	1.47(711)
1dhn_	αβ	121	9.47(1/14)	2.91(1/11)	2.91	2.91★	2.91★	2.91★	2.91★	2.41(554)
1dxgA	β	36	6.46(3/11)	4.46(3/7)	4.46	7.44	6.15	6.15	6.15	3.46(143)
1e6iA	α	110	8.42(4/7)	12.07(2/3)	12.00	22.98	12.07★	12.07★	12.07★	10.28(2)
1eca_	α	136	10.12(3/10)	3.37(1/10)	3.37	3.37★	3.37★	3.37★	3.37★	2.67(862)
1eq7A	α	56	7.01(3/3)	3.72(2/5)	3.72	17.15	17.15	17.15	17.15	1.89(84)
1ezgA	β	82	11.03(40/44)	9.38(4/9)	9.38	11.22	9.38★	9.38★	9.38★	9.13(24)
1f4pA	αβ	147	7.83(2/13)	2.80(1/14)	2.80	2.80★	2.80★	2.80★	2.80★	2.64(880)
1f94A	β	63	8.22(13/24)	3.92(1/12)	3.92	3.92★	3.92★	3.92★	3.92★	3.56(601)
1fazA	α	122	9.01(3/11)	10.84(3/12)	10.84	12.82	12.24	12.24	12.24	8.59(477)
1fk5A	α	93	4.10(2/9)	5.05(2/5)	5.05	9.21	5.05★	5.05★	5.05★	4.07(421)
1fna_	β	91	5.11(1/9)	3.06(1/11)	3.06	3.06★	3.06★	3.06★	3.06★	2.74(367)
1fw9A	αβ	164	14.11(13/20)	13.71(5/22)	14.26	14.26	13.77	13.77	13.77	12.78(866)
1gnuA	αβ	117	10.79(3/12)	9.34(11/13)	11.76	14.72	14.72	14.72	14.72	9.07(56)
1hbkA	α	89	8.19(4/9)	8.52(2/7)	8.52	14.54	14.84	14.54	14.84	7.45(329)
1hoe_	β	74	9.39(5/13)	8.57(1/12)	8.57	8.57★	10.19	10.19	10.19	6.91(216)
1i27A	αβ	73	9.11(3/6)	5.60(2/7)	5.60	7.79	7.79	7.79	7.79	4.45(305)
1i2tA	α	61	3.64(1/6)	2.49(2/6)	2.49	10.20	10.20	2.49★	2.49★	1.80(151)
1isuA	α	62	5.54(6/22)	2.65(1/14)	2.65	2.65★	2.65★	2.65★	2.65★	2.02(538)
1koe_	αβ	172	13.02(22/50)	14.45(5/8)	15.22	16.18	16.35	16.35	16.35	13.67(15)
1kp6A	αβ	79	10.01(8/14)	9.69(2/15)	9.69	9.73	9.73	9.73	9.73	8.10(909)
1lid_	αβ	131	11.42(2/47)	2.32(1/13)	2.32	2.32★	2.32★	2.32★	2.32★	2.22(530)
1lkkA	αβ	105	7.57(9/20)	3.87(1/11)	3.87	3.87★	3.87★	3.87★	3.87★	2.85(854)
1msi_	β	66	7.72(19/28)	4.40(5/26)	9.22	10.94	8.85	10.25	4.40★	3.96(947)
1nbcA	αβ	155	12.60(14/45)	5.77(1/13)	5.77	5.77★	5.77★	5.77★	5.77★	4.97(903)
1nkd_	α	59	1.78(1/2)	4.21(2/2)	1.78	23.81	23.81	23.81	23.81	3.15(212)
1npsA	αβ	88	6.89(33/34)	3.42(1/13)	3.42	3.42★	3.42★	3.42★	3.42★	3.09(880)
1opd_	αβ	85	3.55(1/9)	10.21(4/8)	3.55	13.24	13.24	13.24	13.24	8.81(9)
1ppt_	α	36	1.92(1/2)	7.00(3/5)	1.92	7.64	7.64	7.64	7.64	3.25(7)
1qj8A	β	148	12.00(8/43)	12.13(2/10)	12.13	17.99	12.13★	12.13★	12.13★	11.00(1)
1qqhA	αβ	144	13.58(8/30)	14.46(15/16)	16.68	17.08	16.68	17.08	16.68	13.02(9)
1qstA	αβ	160	9.09(6/20)	7.50(1/3)	7.50	7.50★	7.50★	7.50★	7.50★	5.38(497)
1sfp_	β	111	7.48(2/18)	6.00(1/13)	6.00	6.00★	13.26	6.00★	13.26	5.75(625)
1sra_	α	151	10.71(3/12)	11.09(1/10)	11.09	11.09★	11.09★	11.09★	11.09★	8.64(144)
1t1dA	αβ	100	8.96(7/13)	3.63(1/13)	3.63	3.63★	3.63★	3.63★	3.63★	2.72(357)
1tul_	β	102	6.87(6/19)	8.13(3/12)	8.13	10.41	9.49	9.49	9.49	6.11(977)
1utg_	α	70	6.24(3/5)	4.93(3/5)	4.93	12.87	12.87	12.87	12.87	4.26(138)
1who_	β	94	5.24(4/24)	5.29(1/12)	5.29	5.29★	5.29★	5.29★	5.29★	3.10(887)
1wkt_	β	88	6.75(14/47)	10.92(4/23)	10.92	11.47	10.92★	10.92★	10.92★	9.95(464)
2a0b_	α	118	4.25(1/6)	12.76(3/9)	4.25	13.22	13.22	13.22	13.22	9.90(63)
2cdx_	β	60	6.98(7/16)	3.61(1/7)	3.61	3.61★	3.61★	3.61★	3.61★	3.04(913)
2erl_	α	40	6.51(2/2)	6.08(4/4)	6.08	8.91	8.59	8.59	8.59	4.79(101)
2hbg_	α	147	10.19(4/9)	1.72(1/11)	1.72	1.72★	1.72★	1.72★	1.72★	1.73(904)
2i1b_	β	153	12.18(10/43)	11.85(1/21)	11.85	11.85	11.85	11.85	11.85	10.94(398)
2mcm_	β	112	9.46(4/20)	9.75(2/11)	9.75	13.89	13.89	13.89	13.89	8.27(461)
2sak_	αβ	121	9.17(9/29)	11.23(12/24)	11.86	11.86	11.25	14.19	11.25	8.02(913)
3ebx_	β	62	7.35(3/26)	2.24(1/15)	2.24	2.24★	2.24★	2.24★	2.24★	1.53(734)
Average			7.72(6.4/16.1)	5.90(2.5/9.4)	5.84	7.82	7.59	7.31	7.26	4.72(434)
Total number†††:
RMSD<6.5:			42(41)	83(83)	85	58	60	65	67	94
RMSD<6.0:			31(29)	75(75)	77	55	57	61	63	92
RMSD<5.5:			22(21)	69(69)	71	51	55	57	59	89
RMSD<5.0:			15(14)	64(64)	66	48	50	53	55	83
RMSD<4.5:			11(10)	55(55)	56	42	43	46	47	77
RMSD<4.0:			7(7)	41(41)	44	36	35	38	38	69
RMSD<3.5:			3(3)	29(29)	31	27	26	29	28	61
RMSD<3.0:			2(2)	22(22)	24	21	20	22	22	42

^*PDB code of test proteins. The 30 proteins marked with ^⋆ are those used in training for the force-field optimization.

^†The structure type assigned by DSSP (Kabsch and Sander, 1983).

^‡Protein length.

^§RMSD of the best cluster by the simulations without using protein-specific restraints. The first number in parentheses denotes the rank of the best cluster produced by SCAR (Betancourt and Skolnick, 2001), and the second number in parentheses is the total number of produced clusters. The cluster rank is obtained from the average energy of the structures in the cluster.

^¶RMSD of the best cluster by the simulation with the use of threading-based restraints by PROSPECTOR (Skolnick and Kihara, 2001). The first number in parentheses denotes the rank of the best cluster produced by SCAR, and the second number in parentheses is the total number of produced clusters. The cluster number is obtained from the average energy of the structures in the cluster.

^‖RMSD of the best cluster among the five combination clusters, i.e., the four lowest energy clusters from Cluster_w plus the single lowest energy cluster from Cluster_wo.

^**RMSD of the cluster centroid of the lowest energy E. ^★ denotes that the lowest cluster is the cluster with the lowest RMSD to native.

^††RMSD of the cluster centroid of the biggest size M. ^★ denotes that the biggest cluster is the cluster with the lowest RMSD to native.

^‡‡RMSD of the cluster centroid of the lowest Y. ^★ denotes that the cluster of lowest Y is the cluster with the lowest RMSD to native.

^§§RMSD of the cluster centroid of the highest density D. ^★ denotes that the cluster of highest density is the cluster with the lowest RMSD to native.

^¶¶RMSD of the best structure in the structure pool that is picked up from Monte Carlo trajectories and submitted to clustering processes. The number in parentheses is the number of MC steps when the best structure is produced.

^‖‖The 65-protein set that was used in our previous studies (Kihara et al., 2001; Zhang et al., 2002).

^***The 60 harder-protein set selected in the PISCES server (G. Wang and R. L. Dunbrack, unpublished results).

^†††The number of the proteins with RMSD below a threshold value. The number in parentheses is the number of the proteins if we only count the top five clusters.

The decoys are collected from the structure trajectories in all high- and low-temperature replicas. To avoid the overaccumulation of some structure clusters, we introduce a cutoff on the RMSD of structure pairs and ensure that the RMSD of any pair of decoy structures are larger than 3.5 Å. The decoys produced in this way retain their secondary structure and side-chain packing pattern in the low- and middle-temperature replicas. To neglect bad random coil structures present in the high temperature replicas, we remove structures whose radii of gyration are larger than 3N^1/3. The simulation continues until 60,000 decoys are generated for each protein.

Because the force fields are different in the SICHO and CABS models, these two simulations cover different regions of configurational phase space; this is helpful for the divergence of the decoy sets. As shown in Fig. 3 a, the rank of native structure in the decoys produced by the SICHO model is poor if the decoys are evaluated by the SICHO force field; however, if the same decoys are evaluated by the CABS force field, the rank of native structure is much better (Fig. 3 b). Similarly, if the decoys produced by the CABS model simulation are evaluated by CABS force field itself, the rank of native structure is poor (Fig. 3 d); however, if these same decoys are evaluated by the SICHO force field, the rank of native structure is much better (Fig. 3 c). This is a general feature seen in all the decoy sets on the 30 selected proteins; this means that, when the force field used for structure evaluation is different from the force field used for structure generation, it is possible that we can get better identification of native structure than if both force fields are the same. This is understandable because the Monte Carlo simulations always detect the so-called “important phase space” regions that are of low energy. Because of imperfections of the force field, this lowest energy basin usually does not correspond to the native state in most cases (see Fig. 3 e), so the rank of native structure in those decoys produced by the force field itself is poor. Because of the differences in the two force fields, the states in the lowest energy basin of the first force field can be of high energy in the second force field. But the idea is that native structure should be of relatively low energy in a reasonable force field. Therefore, the rank of native structure can be relatively better when ranked by the second force field (Fig. 3 e).

FIGURE 3.

Energy versus RMSD of decoys to native structure of protein 1cis_. (a) Decoys generated by Monte Carlo simulations of the SICHO model, energies of decoys are evaluated by the SICHO force field. (b) The same decoys as in a but the energies are evaluated by the CABS force field. (c) The decoys generated by Monte Carlo simulations of the CABS model, energies of decoys are evaluated by the SICHO force field. (d) The same decoys as in c but the energies are evaluated by the CABS force field. (e) A schematic illustration of landscape of the SICHO and CABS models. Due to differences in potential energy functions, the important regions of phase space in the two simulations do not match, and the lowest energy state may be nonnative.

Parameter optimization

The aim of our parameter optimization procedure is: i), to maximize the correlation between the energy function of the decoys and the RMSD to the native structure; and ii), to maximize the energy gap between the native state and the ensemble of unfolded states. For the 30 × 60,000 decoy structures, we try to find a set of parameters to minimize the following equation:

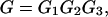(19a)

where

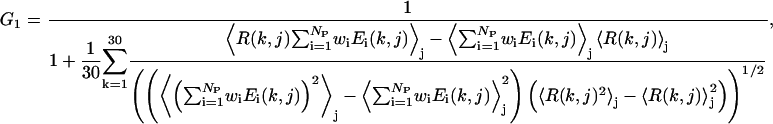(19b)

(19c)

and

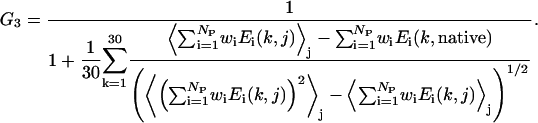(19d)

Here 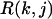is the RMSD of jth decoy structure of kth training protein. We have a cutoff on the RMSD, i.e., 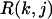= 4 if RMSD < 4 Å, = 10 if RMSD > 10 Å, because we consider any decoy with a RMSD < 4 Å as good and a RMSD > 10 Å as poor. N_p is the number of undetermined parameters (w_i values) of force fields, 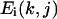is the energy term conjugate to the parameter w_i. 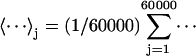denotes the average over the decoys.

The first term G₁, of Eq. 19 b, aims to maximize the correlation coefficient between the RMSD and the total energy. The second term G₂ of Eq. 19 c acts to minimize the χ² between a linear regression (R_k = ηE + b_k) and the energy versus RMSD, where b_k is the individual intercept for the kth training protein, η is the slope of the fit line. Although b_k and η are irrelevant for the determination of the best force field, η decides the scale of the energy function that is related to the temperature range using MC simulations. We will determine η from the simulations. Although both G₁ and G₂ try to enhance the correlation of the energy function to the RMSD from native, the combination of these two terms speeds up the convergence of the optimization procedure and gives better results than when using either one of them alone. Finally, the aim of the third term G₃ is to maximize the relative gap between the native structures and the ensemble of the decoys of all 30 training proteins.

Because the weight parameters w_ri in Eqs. 8 and 17 depend on the results from threading, based on Eq. 19 a we at first optimize the 15 inherent parameters of w_i of the intrinsic force field with the threading-based restraint parameters w_ri = 0. In the second step, we have the 15 w_i values fixed at their optimized values and we optimize the remaining four threading parameters w_ri. To obtain the optimized values of 30 + N_P parameters in Eq. 19, we develop a minimization approach based on the CERN MINUIT package (James, 1998), which can handle and find the global minimum of a generation function of up to 100 variable parameters. To avoid some unphysical subminima and to speed up the optimization processes, we have put a loose physical restriction on each parameter.

In Fig. 4 a, we show an example of the energy versus RMSD correlation for 1fas_. If we simply add all the subenergy items with naïve weight factor w_i = 1, the global minimum of the force field is ∼8.5 Å away from native structure and the correlation coefficient of total energy and RMSD is 0.44 (Fig. 4 b). With the optimization of the weight factors, the global minimum state is much closer to native and the energy versus RMSD correlation coefficient equals to 0.69 (Fig. 4 c).

FIGURE 4.

The energy versus RMSD for the decoy structures of 1fas_ produced by the CABS model. (a) Correlations of 19 subenergy terms with the RMSD to native. (b) Combined energy with w_i = 1. (c) Combined energy with optimized weight parameters.

In Table 2, we show the average correlation coefficients and z-scores of the different energy terms over 30 × 60,000 decoys. It is shown that the combined energy with optimized weight factors has higher correlation coefficients and nativelike recognition capability than the naïve combination of energy and each of the single energy terms alone.

TABLE 2.

Summary of the CABS force-field weights

Energy terms	Correlation coefficient*	z-score†
E13: 3-Cα correlation	0.27	−0.36
E14: 4-Cα correlation	0.56	−0.78
E15: 5-Cα correlation	0.33	−0.42
E′12: 2-SG correlation	0.23	−0.10
E′13: 3-SG correlation	0.32	−0.31
E′14: 4-SG correlation	0.47	−0.62
E′15: 5-SG correlation	0.14	−0.48
Estiffness: local stiffness	0.25	−0.22
EHB: hydrogen bonds	0.51	−0.83
Epair: pairwise interaction	0.38	−0.51
Eburial: burial interaction	0.46	−0.47
Eelectro: electric interaction	0.27	−0.23
Eprofile: environment profile	0.34	−0.47
ECO: contact order	0.02	−0.07
ECN: contact number	0.31	−0.52
Edistmap1: distant map	0.43	−0.60
Edistmap2: accumulate distant map	0.47	−0.55
Econtact1: contact restraints	0.53	−0.74
Econtact2: accumulate contacts	0.50	−0.60
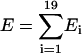: naïve combination	0.54	−0.64
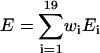: optimized combination	0.65	−1.01

^*The correlation coefficient of energy (E) and RMSD (R), i.e., 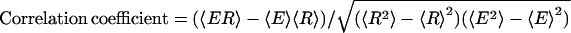, where 〈⋯〉 denotes the average over the 60,000 decoy structures. The values shown in the table are the average over 30 training proteins.

^†The z-score is defined as 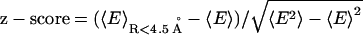, where 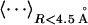denotes the average on the near-native structure of RMSD < 4.5 Å. The values shown in the table are the average over 30 training proteins.

Conformational search engine

Because of the extremely large configuration phase space of protein molecules and the significant roughness of the energy landscape, it is of vital importance to have a powerful search engine to scan the “important” regions of conformational phase space. The efficiency of a Monte Carlo-based search engine depends on interplay of the energy update protocol and the type of conformational movements used to modify a given conformation.

Because the energy barriers can be too high for the simulation to cross, it is well known that the canonical Metropolis protocol usually results in the simulations being trapped in local energy minima in rugged force fields (Newman and Barkema, 1999). In recent work (Zhang et al., 2002), we developed a new parallel hyperbolic sampling (PHS) algorithm to alleviate the problem of “ergodicity breaking.” The point of this algorithm is that the local high-energy barriers are flattened by a nonlinear transformation, i.e.:

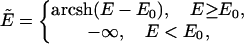(20)

where E₀ is the protein energy of the current structure and arcsh is the inverse hyperbolic sine function. Thus, the locations of all local energy minima are preserved, and the simulation is allowed to tunnel more efficiently through energetically inaccessible regions to low-energy valleys. We implement the simulations in a composite replica ensemble, with each replica at a different temperature. By allowing global swaps between replicas (say i and j) with a probability 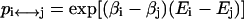, the larger-scale conformational jumps for the low-temperature replicas can be achieved by the aid of the higher-temperature replicas. We applied the PHS algorithm to the SICHO model and found that it can fold proteins faster and identify lower energy structures in the same CPU time, as compared to the general replica sampling (RS) method (Zhang et al., 2002).

In this work, we will use the PHS algorithm as the energy update protocol for the CABS model. The conformational update is first applied on the C_α chain. Then positions of C_β and SG units are determined accordingly. Five kinds of C_α-chain movements are used in our simulations.

• Movement 1: Basic 2-bond and 3-bond movements (Fig. 5 a), in which a 2- or 3-bond fragment is replaced by a fragment of the same length, but with a new conformation. Because of the limited number of conformations of 2- and 3-bond fragments on the lattice, all basic moves can be prefabricated, i.e., they are calculated only once and then randomly selected during the simulation. With the current lattice, we have 67,272 2-bond fragments and 14,507,376 3-bond fragments.

• Movement 2: 4-, 5-, and 6-bond movements (Fig. 5 b), which consist of consecutive 2- and 3-bond moves.

• Movement 3: 6- to 12-bond translation (Fig. 5 c), in which a randomly chosen fragment of 6–12 bonds is translated over a small distance.

• Movement 4: Multibond sequence shift (Fig. 5 d), which is performed through a permutation of a randomly chosen 2-bond piece and another randomly chosen 3-bond piece. Because the conformation of the fragment between the permutation points is not modified, the net result of this permutation is a sequence shift along the modeling chain as marked by the arrows in Fig. 5 d. Although the acceptance probability of this movement can be quite low, it can substantially increase the probability of extrusion and resorption of tangled structures and help the simulation get out of some local energy traps.

• Movement 5: Extremity movements (Fig. 5 e), which reconstruct the conformation of the N-or C-terminus through a random walk from a chosen point to the extremity.

FIGURE 5.

Schematic diagrams of the movements employed in the Monte Carlo simulations. The C_α-traces before and after movements are denoted by the solid and dashed lines, respectively. (a) A basic prefabricated 3-bond update of the fragment [i, i + 3] in the simulations. (b) A 5-bond update of the fragment [i, i + 5] consists of two consecutive 3-bond movements. The first 3-bond movement updates the interval of [i, i + 3], and the second 3-bond movement updates the piece of [i + 2, i + 5]. (c) An 8-bond translation of the fragment in [i, i + 8] over a small distance l. (d) A permutation of a 3-bond piece of [i, i + 3] and a 2-bond piece of [j, j + 2]. The thin arrows denote the shift orientation of the amino acid sequence. (e) Examples of random walks from i to the N-terminus or from j to the C-terminus.

In each of the above randomly chosen movements, a geometric restriction on the virtual C_α-C_α bond angles to lie in the range of [65°, 165°] is put on all new conformations. The smaller moves with higher acceptance rates are performed with greater frequency, which lead to a better simulation of the process of the fine repacking of side chains after a larger change of the main chain local geometry.

Because only the energy difference between two conformations is involved in Eq. 20, in each step of updates we only need to calculate the energies of the fragments whose conformation changed to save CPU time. Before any energy computation, the test for excluded volume violation of the C_α and C_βs are always performed, and trial conformations that would lead to steric collisions of chain units are rejected.

Table 3 shows the lowest energies identified by different algorithms using different move sets for the same CPU time and demonstrates how the two aspects of the energy update protocol and movements influence the efficiency of Monte Carlo simulations. The 20 test cases cover protein lengths from 36 to 174 residues. For the same algorithm, the simulations with a more comprehensive move set always do better than these including only basic 2- and 3-bond movements, because the larger moves can cross over local energy barriers more efficiently. When using simple movements, the PHS algorithm does significantly better than the RS algorithm, because the local energy obstacles, which are difficult to surmount by simple movements, are flattened in the PHS simulation. When using combined move sets, there is no obvious difference in the performance of the PHS and RS simulations for small proteins (say, <100 residues). However, for larger proteins, the PHS simulations almost always identify lower energy structures than the RS simulations do. This may mean that the roughness of energy landscape is correlated with protein length. For small proteins, the local energy barriers are not too high and can be surmounted when using a larger set of movements. For large proteins, however, the local energy barriers are still difficult to surmount with the combined movements. So the flattening of energy landscape improves the sampling.

TABLE 3.

Lowest energies found in test simulations of different algorithms and move sets

		Simple move set‡				Combined move set§
		〈E1〉¶		Emin‖		〈E1〉		Emin
IP*	N†	PHS**	RS††	PHS	RS	PHS	RS	PHS	RS
1ppt_	36	−676.9	−666.4	−704.2	−699.2	−700.8	−700.2	−713.1	−712.2
1eq7A	56	−1123.6	−1091.1	−1147.5	−1116.0	−1140.3	−1131.8	−1170.7	−1168.7
2cdx_	60	−1047.4	−1032.9	−1116.6	−1111.2	−1062.1	−1082.1	−1149.1	−1154.6
1aiw_	62	−1144.7	−1130.3	−1199.8	−1177.5	−1149.0	−1176.9	−1205.9	−1220.1
1ail_	70	−1534.0	−1505.0	−1594.0	−1554.1	−1583.8	−1571.6	−1642.8	−1612.3
1kp6A	79	−1669.0	−1658.5	−1725.5	−1731.8	−1669.8	−1669.7	−1734.7	−1737.9
1npsA	88	−1719.0	−1714.1	−1799.5	−1797.6	−1745.3	−1747.8	−1835.6	−1843.6
1fna_	91	−1924.1	1945.2	−2018.4	−2018.8	−1984.9	−1986.6	−2068.2	−2077.7
1t1dA	100	−2152.1	−2142.5	−2265.5	−2281.0	−2188.5	−2163.3	−2288.7	−2279.5
1tul_	102	−1836.1	−1809.9	−1950.3	−1925.2	−1940.1	−1928.7	−2022.0	−2042.0
1bkf_	107	−1769.5	−1730.9	−1895.6	−1842.9	−1867.7	−1867.6	−1989.3	−1971.8
2mcm_	112	−1902.8	−1861.1	−2025.5	−1986.9	−1912.8	−1910.7	−2109.9	−2109.3
1dhn_	121	−2621.5	−2600.6	−2740.5	−2694.6	−2647.5	−2646.7	−2733.0	−2734.3
1bfg_	126	−2231.5	−2157.8	−2407.4	−2352.9	−2297.4	−2298.2	−2410.3	2411.0
1lid_	131	−2527.2	−2467.7	−2699.2	−2638.9	−2618.7	−2603.2	−2708.4	−2701.6
1f4pA	147	−3516.3	−3534.8	−3673.8	−3663.2	−3555.0	−3555.2	−3703.7	−3701.1
2i1b_	153	−2856.9	−2852.3	−3038.2	−3011.1	−2918.9	−2905.7	−3110.6	−3101.2
1qstA	160	−3483.0	−3481.5	−3708.8	−3689.0	−3533.7	−3532.3	−3727.2	−3701.8
1koe_	172	−3029.0	−2974.4	−3225.2	−3167.9	−3081.4	−3069.4	−3278.5	−3255.2
1amm_	174	−2877.3	−2758.6	−3129.0	−3003.1	−3027.1	−3007.0	−3288.9	−3217.3
〈⋯〉		−2081.9	−2055.8	−2203.2	−2173.1	−2131.2	−2127.7	−2244.5	−2237.7

The underlines denote the lower energies between PHS and RS simulations.

^*PDB code of test proteins.

^†Length of test protein.

^‡Simulations using only basic 2- and 3-bond movements.

^§Simulations using all the movements in the text.

^¶The average energy in the trajectory of the lowest-temperature replica.

^‖The lowest energy found in the simulation.

^**Parallel hyperbolic sampling method.

^††Replica sampling method.

Secondary structure prediction

Our force field has imposed strong conformational biases to the predicted secondary structures for both short- and long-range interactions. Thus, highly accurate secondary structure prediction is extremely important for successful tertiary structure prediction.

The prediction accuracy of secondary structures has been considerably improved with the utilization of the multiple sequence alignments (Benner and Gerloff, 1991). It was found that the secondary structure information can be extracted from the sequence evolutionary information (Branden and Tooze, 1999). In Table 4, we show the results of secondary structure predictions on 125 test proteins based on the three most-often-used sequence-based predictors: PHD (Rost and Sander, 1994), SAM-T99 (Karplus et al., 1998), and PSIPRED (Jones, 1999). The average prediction accuracy of the single predictor for the 125 proteins fluctuates from 73.4% to 81.0%, depending on the cutoff of the confidence level for α-helix and β-strand assignments. The accuracy of PSIPRED is slightly better than SAM-99 in our test set, and the accuracy of both prediction methods is better than PHD. The highest prediction accuracy comes from the combination of PSIPRED and SAM-T99 results, where two ways of combination of “overlap” and “consensus” are defined as in Table 5. We have done test runs using six sets of highest secondary structure prediction accuracy (see italic bold numbers in Table 4) in our fold simulations, after the optimization of the force field. The tertiary structure prediction results depend on both the accuracy and the coverage of the secondary structure predictions. The overlap set with a cutoff equaling to 5 and 0.49 for PSIPRED and SAM-T99, respectively (see italic bold numbers in Table 4) works the best. This is used in all subsequent simulations.

TABLE 4.

Accuracy and coverage of secondary structure prediction by different predictors

Cut1*	Cut2†	PHD	PSIPRED	SAM-T99	Overlap‡	Consensus§
0	0.23	76.6	80.8	80.1	79.2	81.3
1	0.33	76.6	81.0	80.1	79.6	81.0
2	0.37	76.9	80.8	80.1	79.9	80.7
3	0.41	76.7	80.6	80.2	80.4	80.0
4	0.45	76.2	79.9	80.1	80.8	78.9
5	0.49	75.8	78.7	79.5	81.1	77.0
6	0.53	75.1	77.3	77.6	80.4	74.4
7	0.57	73.4	74.6	75.5	78.9	71.2
0	0.23	52.1	51.6	51.7	57.3	44.9
1	0.33	51.9	48.9	51.7	56.2	43.4
2	0.37	49.0	46.5	51.2	55.1	41.9
3	0.41	46.0	43.7	49.4	53.3	39.4
4	0.45	42.7	41.2	45.9	50.3	36.6
5	0.49	39.3	38.4	41.7	46.5	33.5
6	0.53	35.8	35.1	37.2	42.4	29.9
7	0.57	32.0	31.0	32.5	38.1	25.5

Averaged on 125 test proteins. The upper part of the table is the percentage of accuracy defined as, 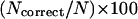, where 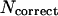is the number of residues that are correctly assigned to either α-helix, β-strand or loop state, and N is the length of the sequence. The secondary structure elements in native structures are classified according to DSSP (Kabsch and Sander, 1983). The lower part of the table is the average number of residues that are assigned as α-helix or β-strand. The bold and italic bold numbers denote those used in our test runs for the evaluations of the secondary structure predictions in our fold simulations. The italic bold numbers are used in our final fold simulations.

^*The threshold of confidence level (0 = low, 9 = high) for PHD and PSIPRED predictors.

^†The threshold of confidence level for SAM-T99. The confidence level for SAM-T99 is defined as the difference of the possibilities of the two highest confident assignments.

^‡§The definitions of “overlap” and “consensus” are in Table 5.

TABLE 5.

Combinations of two secondary structure predictors

Predictor1	Predictor2	Overlap	Consensus
α	α	α	α
β	β	β	β
α	β	α or β*	α or β†
α	loop	α	loop
β	loop	β	loop
loop	loop	loop	loop

^*†Take the assignment of higher confidence.

RESULTS AND DISCUSSION

In this section, we will report the results of applying our methodology to a test set of 125 proteins. We first check the folding ability and convergence of our basic force field (without restraints) on 100 small proteins. Then, we use the methodology on the whole set of proteins under the guide of threading-based restraints. Finally, we describe the protocol of selecting structures from the generated trajectories.

Test set selection

The test protein set employed in this work consists of two subsets. The first subset includes 65 proteins used in previous studies (Simons et al., 2001; Kihara et al., 2001; Zhang et al., 2002); the second subset contains 60 proteins selected from the PISCES server (G. Wang and R. L. Dunbrack, unpublished results), which have a pairwise sequence identity below 30% and a resolution cutoff better than 1.6 Å. This subset includes more proteins of larger size and much more diverse topology than the first 65-protein set. It also turns out to be harder to fold than the first protein set by our approach. The combined 125-protein set ranges in length from 36 to 174 residues and has 43 α-helical proteins, 41 β-sheet proteins, and 41 mixed α/β proteins, as assigned by DSSP (Kabsch and Sander, 1983).

Folding results

We performed PHS Monte Carlo simulations with N_rep replicas. N_rep is dependent on the size of the simulated protein and is a compromise of saving CPU time and keeping sufficient communication between adjacent replicas. We take N_rep = 30 for small proteins of length N < 100; N_rep = 35 for 100 < N < 150; and N_rep = 40 for N > 150. For each protein, two Monte Carlo runs are made, each including 1000 MC sweeps and using ∼48 h of CPU time on a 1.26-GHz Pentium III processor for a protein of 150 residues. We select one snapshot after each MC sweep from the 12 lowest-temperature replicas. The collected 24,000 structures are then submitted to SCAR (Betancourt and Skolnick, 2001) for clustering, which takes ∼1 additional hour of CPU time.

In column four of Table 6, we list the folding results of the CABS model without using predicted protein-specific local and tertiary restraints provided by our threading program. If we define a “successful” fold as one in which at least one of the top five clusters has the RMSD to native below 6.5 Å, we can successfully fold 41 cases using the basic force field. There is an obvious bias of fold success to the protein secondary structure class: 21 foldable cases are α-helical proteins, nine are β-sheet proteins, and 11 are mixed α/β proteins. All the successful folds occur on the 100 small proteins of length N < 120 amino acids. The dependence of RMSD on protein size is shown in Fig. 6 a with both testing (denoted as solid circles) and training (denoted as open circles) protein sets. It shows that the folding results have no obvious bias to the training protein set (13 foldable cases belong to the 30 training proteins, compared with 41 foldable cases to 100 proteins in total). This may mean that the training set of 30 proteins is sufficiently large and representative for a general optimization of the force field.

FIGURE 6.

(a) RMSD of the best cluster in the top five clusters versus protein length N in the CABS simulations without using protein-specific restraints. The solid circles denote the training proteins that are used in the optimization of force field. The open circles are the test proteins. All the successful fold cases are small proteins with N < 120 amino acids. (b) RMSD of the best cluster in top five clusters versus protein length N in the CABS simulations with threading-based restraints. The large proteins (>120 residues) can be folded only when appropriate restraints are incorporated in the simulations.

To fold proteins longer than 120 residues and to improve the yield of small proteins, we exploit the predicted local and tertiary restraints in our force field (see Eqs. 8 and 17). These restraints are collected from consensus substructures found by our threading program PROSPECTOR (Skolnick and Kihara, 2001), where homologous sequences to the query protein are entirely excluded from the data base. Although a portion of the predicted restraints may be incorrect, it is indeed helpful to guide the simulations to near-native states and significantly improve the folding results in the majority of cases. In column five of Table 6, we list the results of the simulations with restraints. There are 83 cases with a RMSD of the best cluster centroid below 6.5 Å to native, all within the top five clusters. Fifty-one successful cases are from the 65-protein set and 32 are from the harder 60-protein set (The trajectories and cluster centroids of all the 125 proteins are available on our website: http://www.bioinformatics.buffalo.edu/abinitio/125).

The improvement using tertiary restraints occurs on both small and large proteins (see Fig. 6 b). For the 100 small proteins of lengths less than 120 residues, the number of foldable cases with restraints increases to 70 (compared to 41 without restraints). Without restraints especially, the program can never fold proteins of lengths longer than 120 residues. Under the guide of restraints, we can fold 13 of the 25 large proteins; none can be folded without predicted side chain contacts. Moreover, within all 83 cases, 33 cases belong to α-helical proteins, 27 cases to β-sheet proteins, and 23 to mixed α/β proteins, which show a considerably reduced folding bias to the secondary structure class, compared to the pure ab initio results.

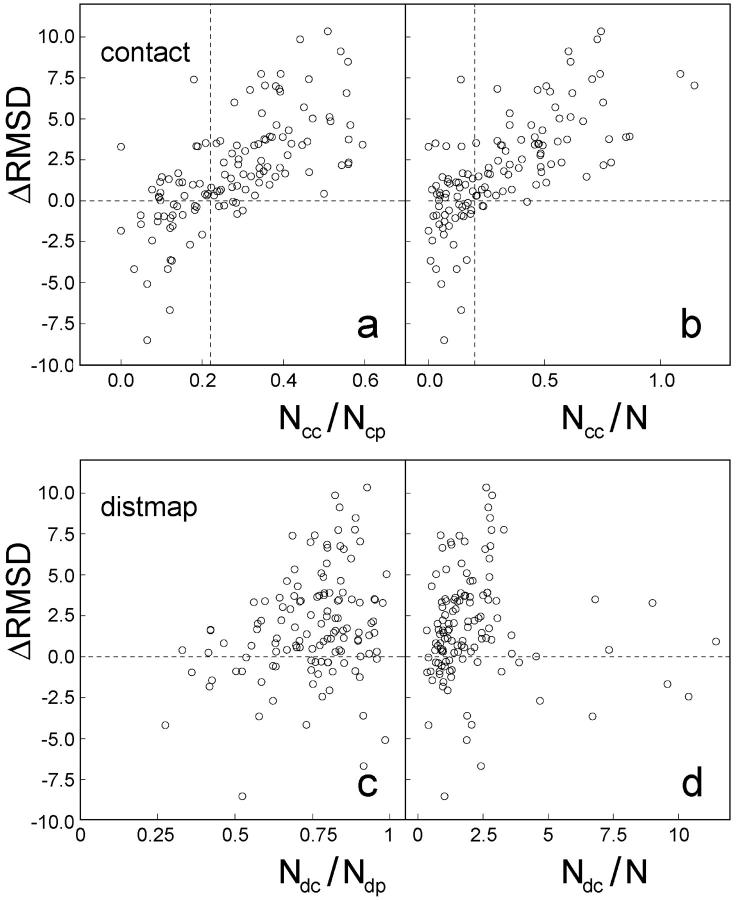
The effect of restraints on the degree of folding success depends on its accuracy. In Fig. 7, we show the dependence of the fold improvement on the accuracy of the predicted contacts and local distant restraints. There is a strong correlation between the RMSD improvement and the accuracy of long-range contact restraints. This correlation is much less obvious for the local distance restraints, which seems to indicate that the local short-range restraints are less important. This may be due to the fact that the information of short-range correlations has been included due to the relatively high accurate secondary structure prediction and the short-range distance restraints do not provide much additional information. However, our simulations show that appropriate short-range restraints indeed considerably speed up the formation of local structures.

FIGURE 7.

RMSD improvement on including the threading-based tertiary and secondary restraints versus the accuracy of the restraints. 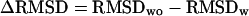, where RMSD_wo and RMSD_w are the RMSD of the best clusters to native structures in the simulations without and with using the threading-based restraints. N is the number of the amino acids of proteins, N_cc the number of correct contact restraints, N_cp the number of total predicted contact restraints, N_dc the number of correct short-range distant restraints, and N_dp the number of total predicted distant restraints.

As expected, when the accuracy of contact restraints is too low, a successful fold from a “pure” ab initio simulation can be spoiled by inclusion of poorly predicted restraints. According to Fig. 7, when accuracy of contact restraints is higher than 22% or the ratio of the number of correct restraints to protein length is larger than 0.2, the restraints almost always have a positive effect on folding. To alleviate the negative influence of the bad restraints, we combine the clusters from both simulations as follows: The best cluster is the lowest energy cluster in most of the successful pure ab initio simulations because only a good ab initio force field can fold a protein without restraints. Thus, we take the lowest energy cluster from the pure ab initio simulations and combine it with the four lowest energy clusters from restraint-based simulations. As shown in column six of Table 6, this combination converts all the significant spoiled cases by the inclusion of poorly predicted restraints into successful folds. Moreover, we retain all the successful folding cases in the restraint-based simulation set.

As a comparison, we also made Monte Carlo runs of the SICHO model on the harder subset of proteins with similar CPU times. The results are shown in the histogram in Fig. 8. It should be noted that these 60 proteins represent diverse structure categories, and no protein from this set was used in the training of either the CABS or the SICHO force field. The folding rate is 1/3 for the SICHO model and 1/2 for the CABS model. However, in fairness, the SICHO model has not yet been subjected to the same optimization procedure as done in the CABS model.

FIGURE 8.

Comparison of the folding results by the SICHO and CABS models on the 60-nonhomologous-protein set. The shown data are the number of proteins that have their best cluster below a given RMSD threshold versus the RMSD threshold.

Identification of correct folds

An important step in ab initio structure prediction is the evaluation of the folding results. There are two relevant problems involved in the evaluation process. At first, because of imperfections of the force field, the global energy minimum usually does not correspond to native state. Thus it is a nontrivial task to identify the best fold (i.e., closest to native) from the simulation trajectories. Secondly, unlike homology modeling or threading where the sequence identity of the target to the template and the z-score of sequence alignments are important parameters to indicate the likelihood of success of the predictions, we lack a reliable indicator of the likelihood of success of the blind ab initio structure predictions. This problem is especially relevant when multiple ab initio simulations are performed with different force fields (for example, using different sets of threading-based restraints in our case). Although some sets of restraints can help the simulation to generate correct folds and some other sets do not, it is important to choose the simulation of highest likelihood of success based on the output of the ab initio simulations.

In what follows, we first address the issues of how to select the best structure from an individual simulation trajectory. We introduce several quantities that are highly correlated with the likelihood of successful fold selection. We perform five sets of simulations under different restraints, and present an automatic procedure to select the best structures from the multiple simulations by combining appropriate fold selection criteria.

Selecting the best fold from an individual simulation

In previous approaches to ab initio structure predictions, the authors usually cluster the generated structures (Shortle et al., 1998; Betancourt and Skolnick, 2001) and choose the cluster with the lowest energy (Kolinski et al., 2001; Kihara et al., 2001). Although clustering has considerable success in selecting the correct folds (Simons et al., 2001; Kihara et al., 2001), this approach can have an inherent contradiction. Although the aim of clustering is to identify the low free energy structures, the selection of the lowest energy structure neglects the configurational entropy, because the structure of lowest energy is not necessary that of lowest free energy. Thus, we consider a combination of the energy and free energy

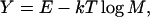(21)

where E is the average energy of the structures in a cluster, and M is the multiplicity of the cluster (number of structures in the cluster). We found that the discriminative ability of Y to choose native structures is better than either E or M. As shown in Table 6, by selecting the cluster of lowest energy E, in 61 of 125 cases, we chose the best cluster (i.e., the lowest RMSD cluster to native structure among all the produced clusters) and 58 of the lowest energy clusters have a RMSD below 6.5 Å (see column seven of Table 6). By selecting the cluster of largest multiplicity M, in 67 cases the best cluster is chosen, and 60 of the selected clusters have a RMSD below 6.5 Å (see column eight of Table 6). By selecting the cluster of lowest Y, in 73 cases, the best cluster is chosen and 65 of the selected clusters have a RMSD below 6.5 Å (see column nine of Table 6).

Another relevant indicator of the quality of the predicted structures is the normalized structure density of cluster defined as

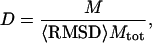(22)

where M is the multiplicity of structures in the cluster, M_tot is the total number of structures submitted to the clustering processes, and 〈RMSD〉 denotes the average RMSD to the cluster centroid of the structures in the given cluster. D reflects the degree of structure convergence in the simulations, and it is also related to the coordination among the different terms in the force field. If a conformation is favored by the majority of terms in the force field, the local minima of different energy terms will reinforce each other; this results in a deeper energy basin in the total energy landscape. The corresponding structural cluster therefore has a higher density D. On the other hand, if a conformation is favored by a part of the energy terms but “contradicted” by other terms, the energy basin of the total energy landscape will be frustrated. The structure cluster will be less convergent and therefore have a lower structure density. This can occur, when, for example, the threading-predicted restraints have some “contradictions” with the general intrinsic potentials in the CABS model or when restraints themselves are divergent (collected from inconsistent templates). Alternatively the nonrestraint parts of the force field may be in contradiction.

In Fig. 9, we show the RMSD to native of all the cluster centroids versus their normalized structure density. There is a strong correlation between the fold quality and the structure density. If we define the best cluster as a cluster of lowest RMSD, most of the best clusters (denoted by solid circles) have higher structure density as compared to the high RMSD clusters. As shown in column 10 of Table 6, by selecting the highest-density cluster, we choose the best fold in 76 of 125 cases and 67 of the chosen clusters have a RMSD below 6.5 Å.

FIGURE 9.

RMSD to native of all cluster centroids for 125 proteins versus the normalized structure density. The solid circles denote the best clusters of lowest RMSD to native in each of the 125 proteins.

Indicator of likelihood of success of the folding simulation

Now we turn to the issue of how to judge the likelihood of success of a blind simulation. As mentioned above, if the force field is a combination of consistent and reinforcing energy subterms, the resultant landscape tends to have a funnellike shape with deep energy basins, which results in convergent structure clusters in the fold simulation. Recent experimental studies of denatured state showed that this funnellike landscape is a basic and necessary characteristic of real proteins to keep the native structure as a stable and unique state (Shea and Brooks, III, 2001). This funneling characteristic can be quantitatively evaluated by the maximum cluster density D_max, or the maximum multiplicity rate of clusters 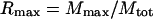, where M_max is the multiplicity of the largest cluster. It can also be a represented by the normalized Y-gap between the energy basin of lowest Y and other basins, i.e.:

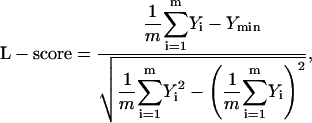(23)

where Y is defined in Eq. 21 and Y_min is the lowest Y among all m clusters.

In Fig. 10, we show the dependence of the RMSD of the best cluster on D_max, R_max, and L-score, respectively, demonstrating that these parameters can be considered as indicators of the likelihood of success of the simulations.

FIGURE 10.

RMSD of the best cluster to native versus different funneling parameters of the energy landscape. (a) The maximum structure density D_max. (b) The maximum multiplicity R_max. (c) L-score of energy landscape (defined in Eq. 23).

In Fig. 11, we show the successful folding rate and average RMSD of best clusters versus the threshold values of maximum cluster density. With higher density cutoff, we have higher rate of successful folds and lower average RMSD. For example, for the simulations with D_max > 0.18, 95% of cases (63 of 66 cases) are successfully folded, and the average RMSD is 3.92 Å. This is dramatically better than the overall fold rate 66% (83 of 125) and the overall average RMSD of 5.90 Å. Furthermore, if we select the highest D cluster in these 66 cases of D_max > 0.18, 82% of them (54 cases) have RMSD below 6.5Å.

FIGURE 11.

(a) Rate of successful fold (best RMSD < 6.5 Å) versus the cutoff of maximum density (D_max > D_cut). (b) Average RMSD versus the cutoff of maximum density.

Automatic procedure of selecting top five clusters from multiple simulations

To demonstrate the usage of the combination of above-defined parameters, we make five sets of simulations on the 60 hard proteins, each set taking different restraints that were obtained by using different threading procedures and cutoff parameters. On average, there are ∼10 clusters for each protein in each individual run. To select the five best clusters for each protein from these roughly 50 clusters, we at first sort the clusters in each simulation according to Y and D, and the different simulation sets according to D_max. Then, we choose the five clusters according to following automatic procedures:

1. Select the five clusters of highest D from five sets of simulations.

2. If any pair of clusters is of the same fold (<2 Å), displace the cluster selected from lower D_max simulation with the cluster of lowest Y from the simulation of higher D_max.

3. Repeat step 2 until five different clusters are chosen.

In column three of Table 7 we show the selection result according to the automatic procedure. Compared with the absolutely best clusters in column four, this procedure allows us to select almost all the best folds in the top five clusters (all 37 successful cases with a RMSD < 6.5Å). Column two shows the selection of five clusters if we choose them just according to cluster energy E in different sets of simulations, which is much worse than that by above combined selection procedure.

TABLE 7.

Selection of top five clusters from multiple simulation runs

	Nbest†	NlowE‡	Ncomb§	Nabs¶
RMSD < 6.5Å*	32	33	37	37
RMSD < 6.0Å	29	30	35	35
RMSD < 5.5Å	28	29	31	32
RMSD < 5.0Å	26	26	28	30
RMSD < 4.5Å	24	25	28	28
RMSD < 4.0Å	22	23	26	27
RMSD < 3.5Å	19	19	21	21
RMSD < 3.0Å	12	12	15	15

^*Number of proteins with a RMSD below a threshold value in the top five selected clusters.

^†Selection of the top five clusters according to energy from the best set of simulations.

^‡Selection of the top five clusters from all five sets of simulation runs according to energy.

^§Selection of the top five clusters from all five sets of simulation runs according to the combination of Y, D, and D_max (see text).

^¶The absolutely best clusters among the five sets of simulation runs.

SUMMARY

In this work, we have developed a new ab initio modeling approach to the tertiary protein structure prediction, based on a simplified lattice representation of the C_α, C_β, and center of side group of protein chains. This new lattice description has a high geometric fidelity. The basic energy function consists of general short-range correlations biased to regular and predicted secondary structures, amino acid-dependent short- and long-range interactions derived from the PDB data base, hydrogen bonds, electrostatic interactions, one-body burial interactions, and a general bias to the expected contact order and contact number that depends on protein size and secondary structure. These energy terms from different sources are combined and optimized by a set of 30 × 60,000 nonredundant structure decoys, by maximizing both the correlation of RMSD of decoys to native and their energies, and the relative energy gap between native and decoy ensemble. This combined force field provides a basic working platform for further assembly and optimization of tertiary structures when threading information (i.e., predicted side-chain contact restraints) are available. It has also shown to be able to successfully assemble structures from sparse NMR experimental NOE data (Li et al., 2002). Here, we used the intrinsic platform (without restraints) on the folding experiment of 100 small proteins (<120 amino acids). 41% of them can be successfully folded with the best RMSD of the top five clusters below 6.5 Å. Twenty-one foldable cases are α-helical proteins, nine are β-sheet proteins, and 11 are mixed α/β-proteins. There is no obvious bias to the training set (13/30 foldable cases for training proteins compared to 41/100 foldable cases in total), which demonstrates that the training set of decoys is large enough for a universal derivation of the force field.

The long-range contact prediction and short-range distance prediction are collected from templates found by our threading program PROSPECTOR (Skolnick and Kihara, 2001). These data are incorporated into our CABS force field as loose side-chain pairwise and local distance restraints. It should be mentioned that, even when no template is hit with significant z-scores in the threading program, some useful information could still be extracted from the consensus substructures with weak z-score hits. These threading-based restraints in most cases can significantly improve the folding results, even if the prediction accuracy is low. More specifically, when the accuracy of contact prediction is higher than 22% or the ratio of correctly predicted contact number to protein length is larger than 20%, the effect of restraints on the folding is almost always positive. There is no obvious sensitivity on the accuracy of local short-range distance predictions. This may be because short-range interactions are already dictated by the high accurate secondary structure predictions (the combination of the PSIPRED (Jones, 1999) and SAM-T99 (Karplus et al., 1998) secondary structure predictors) that have been incorporated in our force field, and therefore the short-range restraints do not provide much additional information.

The improvement by including the tertiary restraints occurs for both small- and large-size proteins. For 100 small proteins <120 residues, the program can fold 70 cases with restraints compared to 41 in pure ab initio folding. The intrinsic force field, especially, can never fold proteins >120 residues in length. Under the guide of restraints, however, the program can fold 13 cases of the 25 larger proteins with lengths ranging from 120 to 174 residues. Overall, in the restraint-based simulations, 33 foldable cases belong to α-helical proteins, 27 belong to β-sheet cases, and 23 belong to α/β-proteins, which shows a less obvious bias toward the protein topology category than the pure ab initio simulations.

We found that the structure density of cluster D and combination of energy and free energy Y are more discriminative than the often-used energy E or cluster size M in the selecting of best-folded structures. In the folding of 125 proteins, if we select one cluster according to the lowest E, or biggest M, or lowest Y, or highest D, the numbers of cases that select the lowest RMSD are 61, 67, 73, and 76, respectively. The numbers of cases that have a RMSD below 6.5 Å in the first cluster in these selections are 58, 60, 65, and 67, respectively.

The coherence of the energy terms in the force field and the funnellike characteristics of the energy landscape can be quantitatively evaluated by the maximum cluster density, maximum multiplicity rate, or L-score. There are strong correlations between the best RMSD and these funneling parameters, which demonstrate that the parameters can be used as indicators of the likelihood of success of fold simulations. For the simulations of 125 proteins, if we take a cutoff of maximum density D_max > 0.18, 95% of cases (63 of 66) are successfully folded, which is much larger than the overall folding rate of 66% (83 of 125).

The combination of the discriminative parameters and the indicator parameters of likelihood of success folds can be used for selection of the best structures from multiple simulations that are run using different force fields (e.g., based on different tertiary restraints). In an evaluation of five sets of test simulation runs, by sorting the simulations according to the indicator parameters and sorting the clusters according to the discriminative parameters, we can select almost all the absolute best structures in the top five chosen clusters. This could not be achieved by the selection based on traditional average energy or cluster size. Because our procedures are fully automatic from the trajectory generation to the identification of final structures, these approaches can be applied to large-scale structure predictions. A comprehensive prediction survey of PDB structure data base and the subsequent genome-scale structure predictions based on these approaches are in progress.