Recovery, Visualization, and Analysis of Actin and Tubulin Polymer Flow in Live Cells: A Fluorescent Speckle Microscopy Study

Abstract

Fluorescent speckle microscopy (FSM) is becoming the technique of choice for analyzing in vivo the dynamics of polymer assemblies, such as the cytoskeleton. The massive amount of data produced by this method calls for computational approaches to recover the quantities of interest; namely, the polymerization and depolymerization activities and the motions undergone by the cytoskeleton over time. Attempts toward this goal have been hampered by the limited signal-to-noise ratio of typical FSM data, by the constant appearance and disappearance of speckles due to polymer turnover, and by the presence of flow singularities characteristic of many cytoskeletal polymer assemblies. To deal with these problems, we present a particle-based method for tracking fluorescent speckles in time-lapse FSM image series, based on ideas from operational research and graph theory. Our software delivers the displacements of thousands of speckles between consecutive frames, taking into account that speckles may appear and disappear. In this article we exploit this information to recover the speckle flow field. First, the software is tested on synthetic data to validate our methods. We then apply it to mapping filamentous actin retrograde flow at the front edge of migrating newt lung epithelial cells. Our results confirm findings from previously published kymograph analyses and manual tracking of such FSM data and illustrate the power of automated tracking for generating complete and quantitative flow measurements. Third, we analyze microtubule poleward flux in mitotic metaphase spindles assembled in Xenopus egg extracts, bringing new insight into the dynamics of microtubule assemblies in this system.

INTRODUCTION

Extended polymeric structures such as the actin and microtubule cytoskeletons are pervasive in eukaryotic cells. They are in particular responsible for the generation of cell polarity, movement, and morphogenesis, for organizing cell division and cellular organelle transport, as well as for ensuring cell mechanical integrity (Alberts et al., 2002). In addition, defects in cytoskeletal function have been implicated in many diseases, for example in vascular diseases (Wesselman and De Mey, 2002), neuronal degeneration (Brandt, 2001; Garcia and Cleveland, 2001), and cancer (Condeelis et al., 2001; Thiery and Chopin, 1999).

When very low amounts of a fluorescent derivate of the monomer forming actin filaments and microtubules (G-actin and tubulin, respectively) are introduced into a living cell, the cytoskeletal polymer assembled from the mixture of endogenous and fluorescent monomers acquires a speckled appearance in high-resolution, high-magnification fluorescence microscopy digital images (Waterman-Storer and Danuser, 2002). The speckles correspond to diffraction-limited regions where, statistically, more labeled monomers have polymerized into the underlying structure than in the immediate neighborhood. In time-lapse fluorescent speckle microscopy (FSM), the movement and appearance/disappearance of speckles act as local reporters for the translocation (i.e., flow), and assembly/disassembly (i.e., turnover) of polymer. Since the discovery of this effect (Waterman-Storer et al., 1998), FSM has been applied in various contexts, including: in vitro analysis of microtubule treadmilling (Grego et al., 2001); in vivo studies of mitotic spindles in cells and cell extracts (Maddox et al., 2000; Waterman-Storer et al., 1998); the analysis of microtubule transport along axonal shafts (Chang et al., 1999); investigations of the actin cytoskeleton dynamics in stationary and migrating cells (Watanabe and Mitchison, 2002; Waterman-Storer et al., 2000b); the dynamic relationship of the actin and tubulin cytoskeletons (Gupton et al., 2002; Salmon et al., 2002; Schaefer et al., 2002; Waterman-Storer et al., 2000a); and the study of microtubule-associated proteins (Bulinski et al., 2001; Kapoor and Mitchison, 2001; Perez et al., 1999).

There are at present no techniques besides FSM having a similar potential to deliver dynamic information on cytoskeletal flow and turnover activities over extended areas of the cell. FSM, however, is still in its infancy. A particular challenge consists in the complexity and sheer volume of the data. In time-lapse FSM image series, thousands of weak contrast speckles exhibit movement. Also, new speckles may pop up unexpectedly or speckles can disappear at any time. Speckle appearance and disappearance can potentially be exploited to analyze local polymer turnover, but they interfere heavily with our ability to recover flow information. The relationship existing between the true, continuous flow of the viscoelastic cytoskeletal media and a set of time-lapse speckle images, perturbed by the various effects enumerated above, is far from trivial. Hence, we use the term “flow recovery” throughout this contribution.

FSM of filamentous actin flow at the leading edge of migrating cells

Migrating cells in culture are polarized, with a broad flat lamellum that terminates in a ruffling lamellipodia facing the direction of migration (the leading edge). A meshwork of actin polymerizes at the leading edge and flows retrogradely toward the cell body (Wang, 1985). The nucleation and growth of actin filaments (F-actin) into a cross-linked and branched meshwork is thought to drive forward protrusion of the cell membrane (Mogilner and Oster, 1996), whereas retrograde flow, if coupled to substrate adhesion, is thought to generate lamellipodial traction.

Recently, we proposed a computational framework for the analysis of F-actin turnover in nonmigrating, contact-inhibited cells (Ponti et al., 2003), where the leading edge F-actin assembly and retrograde flow are shut down. Nevertheless, FSM movies of such cells still showed a photometric activity of fluorescent speckles in the nonmoving cortical actin, indicating that F-actin is undergoing steady turnover (Waterman-Storer et al., 2000b). The algorithm relied on the statistical evaluation of speckle intensity fluctuations coupled with speckle appearance and disappearance.

In the present contribution, we address how speckle movements can be exploited to map the retrograde F-actin flow in a migrating cell. The task is complicated by the high variability of the speckle signal, which is typically near the noise level of the imaging system, and by the presence of speckle sources and sinks, associated with either regions of polymerization and depolymerization, or contractile centers formed by myosin motor proteins. Such singularities are clearly visible in the results produced by our new tracker. We are also able to confirm findings concerning the organization of F-actin flow in migrating newt lung epithelial cells, which were up to now only inferences from sparse kymograph analyses on small data sets. Finally, we show that significant, coherent changes in the flow pattern can occur on a timescale of seconds; a result that is not surprising considering the ability of motile cells to respond remarkably rapidly to changes in their environment.

FSM of poleward microtubule flux in mitotic spindles

Another exciting application of FSM is the study of microtubule dynamics in the mitotic spindle. This is a complex machine composed of two polar arrays of microtubules, motor proteins, and other molecules (Karsenti and Vernos, 2001; Wittmann et al., 2001). During mitosis, the spindle assembles around the duplicated chromosomes and distributes them equally to the daughter cells. Each of the two spindle poles initiates the growth of microtubules that overlap to form the central spindle. Growth occurs at microtubule plus ends oriented distal from the poles. Some overlapping microtubules form bundles of interpolar spindle fibers (cf. also Fig. 6 A). A second class of bundles link chromosomes to the spindle poles. The plus ends of these microtubules attach to the centromeric DNA via a specialized organelle, known as the kinetochore (Bloom, 1993). At metaphase, chromosomes become aligned at the spindle equator with kinetochore bundles symmetrically extending from sister chromatids toward the corresponding pole. The mitotic checkpoint senses the bipolar attachment for all pairs of sister chromatids and regulates the onset of anaphase, when sisters separate and are moved by their kinetochore microtubule bundles to opposite poles.

FIGURE 6.

Tracking microtubule speckles in the mitotic spindle from Xenopus leavis egg extracts. (A) Schematic diagram of the microtubule organization in a metaphase spindle. Microtubules radiate from the two spindle poles (SPs). At metaphase, kinetochore microtubules establish bipolar attachment of the chromosomes via kinetochores (green dots; label 1), located in the metaphase plate (MP). Non-kinetochore fibers (label 2) are formed from bundles of overlapping microtubules extending from opposite poles and cross-linked by motors and other microtubule associated proteins. For a microtubule system emanating from one SP, all speckles flow poleward. Thus, in the bipolar system, the speckle flow direction is a signature of which subsystem the associated microtubule belongs to. (B) Speckle matches as recovered by the tracker aggregated over 10 frames. The populations moving upward (blue) and downward (red) are separated automatically before further filtering (see C). The number of matches and the trajectory lengths are seen to increase as speckles approach their home pole. Both effects are discussed in more detail in the text. (C) An FSM image of metaphase spindle, overlaid by the filtered vector map of upward microtubule flux (blue matches in B; side length of interpolation grid, 1 μm). The width of the Gaussian convolution kernel was 15 pixels (0.9 μm in the object domain). Time averaging was performed over four frames. The flow speed is almost constant across the whole spindle and amounts to 2.5 ± 0.2 μm/min. (D) Number density of speckles moving toward the upper SP (blue) and toward the lower SP (red) as a function of the position along the mitotic axis. See text for a further interpretation of this data.

A major dynamic aspect of microtubule assembly in the spindle is a steady poleward flux of microtubules toward their poles that occurs at the same rate as minus end depolymerization (Mitchison, 1989; Mitchison and Salmon, 1992; Sawin and Mitchison, 1991). At metaphase, the net rate of polymerization at plus ends equals the flux rate and the spindle achieves a constant steady-state length. Flux may be produced by microtubule treadmilling mechanisms (Margolis and Wilson, 1991) or driven by one or more of the many microtubule motors associated with the spindle (Desai et al., 1998; Kapoor and Mitchison, 2001; Mitchison, 1989). Flux appears important for aligning chromosomes at the spindle equator during metaphase and for generating the tension required to inactivate the spindle checkpoint (Kapoor and Compton, 2002). In anaphase, polymerization at kinetochores mostly ceases and flux can make a major contribution to the movement of chromosomes to their poles (Desai et al., 1998; Maddox et al., 2000).

Although microtubule flux is now easily visible with time-lapse FSM (Waterman-Storer et al., 1998), most of the information captured by such movies has remained unexploited because of a lack of appropriate data processing tools. Indeed, analyzing the kinematics of poleward microtubule flux in mitosis is particularly challenging because of the complex and densely interleaved, antiparallel motion of fluorescent speckles associated with the two opposing and overlapping bipolar arrays. Hence, flow recovery has to be achieved at the level of single speckles. Each speckle is treated as a local reporter of microtubule flux, independent of any other speckle in the neighborhood. Ambiguities during tracking are the rule rather than the exception, and a framework able to resolve these conflicts for thousands of speckles simultaneously has to be used. As with FSM of actin, a speckle tracker has to cope with disappearances and the formation of new speckles. These demands exceed the capability of any existing single-particle tracking method, justifying the developments presented in this contribution.

Scope of the article

In this article we present the first results obtained with our novel single-particle tracking algorithm. The software proceeds in four steps: i), particle generation, i.e., the selection of significant speckles; ii), generation of candidate matches, i.e., a set of possible speckle displacement vectors between successive frames; iii), scoring of candidate matches based on rules defining the variability of speckles in position and intensity—probable matches get high scores, improbable ones get low scores; and iv), selection of the candidate subset with maximum global score and no topological ambiguity, i.e., none of the speckles is allowed to participate in two trajectories. In the current state, the program delivers the displacements of thousands of speckles between consecutive frames while coping with the unexpected appearance and disappearance of speckles. The algorithm can also deal with antiparallel motion of proximate speckles. This allows us not only to quantify the interleaved flux fields of bipolar spindles, but also to resolve shear flow in contraction areas of actin meshworks.

An obvious next use of the speckle tracker will be to combine displacement data with appearance and disappearance data to calculate trajectories for every speckle and to perform speckle lifetime analysis for moving polymers in the manner we have shown for spatially stationary F-actin assemblies (Ponti et al., 2003). This development is currently under way. Here we focus on the recovery of flow fields from the tracking data. Detected displacement matches are averaged in space and time to map the overall polymer transport, reducing the effect of various random displacements superimposed at the single speckle level.

To demonstrate the power of the data from the tracker for future applications of quantitative FSM, we include various statistical analyses of the bipolar speckle flow within the spindle. In particular, the classification of speckles with respect to their direction of movement reveals the spatial distribution of the two overlapping microtubule subarrays. This is a piece of information hitherto inaccessible and prototypical of what can now be systematically examined with single speckle tracking. We also obtained measurements indicating that flux is slower for kinetochore microtubules than for non-kinetochore microtubules. We interpret this heterogeneity as the result of tension at kinetochores. Such findings augur a new era in the exploitation of FSM data for quantitative cytoskeleton biology.

MATERIALS AND METHODS

FSM of actin in migrating newt lung epithelial cells

Primary cultures of epithelial cells were established on 22 × 22 mm No. 1.5 coverslips from Taricha granulosa lung tissue and maintained in Rose Chambers as previously described (Rieder and Hard, 1990). X-rhodamine-labeled chicken skeletal muscle actin was prepared as described (Waterman-Storer, 2002). Migrating cells at the edge of the epithelial sheet that extends from the lung explant were microinjected with 1 mg/ml X-rhodamine G-actin in G-buffer (2 mM Tris, 0.2 mM CaCl₂, 0.2 mM MgATP, 0.5 mM β-mercaptoethanol, pH = 8). After microinjection, cells were allowed to recover for 1–2 h in the dark before being mounted on slides with double stick tape in culture media containing 0.3–0.6 U/ml Oxyrase (Oxyrase, Mansfield OH) to inhibit photobleaching during imaging. Digital images were obtained at 10-s intervals with a 12-bit Hamamatsu C-4880 camera containing a Texas Instruments TC-215 charge coupled device (with 12 μm² pixels) cooled to −40°C on the multimode microscope described in (Salmon et al., 1998) using a 60×, 1.4 NA objective, a 1.25× body tube magnifier, and a 1.5× optavar and epifluorescence filters for X-rhodamine. Excitation illumination was blocked between camera exposures with an electronic shutter.

FSM of mitotic spindle in Xenopus eggs extracts

Metaphase spindles with replicated mitotic chromosomes were assembled in meiotic Xenopus egg extracts as described (Desai et al., 1998; Murray et al., 1996; Waterman-Storer et al., 1998). For FSM of microtubules, a low level of X-rhodamine-labeled tubulin was introduced into the Xenopus egg extracts before spindle assembly, and FSM was performed as described (Waterman-Storer et al., 1998) by wide field microscopy using a Nikon (Melville, NY) E600 upright microscope equipped with a 60×, 1.4 NA Plan-Apochromat bright field objective lens with no intermediate magnification and a multiple bandpass dichromatic filter that allowed sequential acquisition of blue (DAPI stained chromosomes) and red (X-rhodamine-labeled tubulin in microtubules) fluorescent images in register on the detector of a Hamamatsu Orca 1 cooled charge coupled device camera. Metamorph software (Universal Imaging, West Chester, PA) was used to control illumination through a dual filter wheel (excitation wavelength and intensity) and shutter, specimen focus via a stepping motor (Nikon), and image acquisition. Pairs of fluorescence images were collected at 10-s intervals with exposure times of 500 ms.

ALGORITHM

Signal preconditioning

Because the resolution of optical microscopes is limited to ∼250 nm due to diffraction, signals displaying significant variations over distances shorter than this limit must originate from noise of e.g., electronic origin. This noise can be removed without compromising the speckle signal by low-pass filtering every image with a Gaussian convolution kernel of a full width at half maximum equal to 250 nm, expressed in pixel dimensions (Ponti et al., 2003). Note that speckles represent the diffraction-limited image of a random distribution of fluorophores. Thus, the pattern does not contain significant spatial frequencies beyond the optical cutoff, i.e., our low-pass filter strictly suppresses noisy features only. Omitting this preconditioning, the number of local intensity maxima in the image, later identified as potential speckles, would be much higher. Moreover the apparent movement of the noisy features removed would bear no connection with the physical flow.

Particle generation

In particle-tracking methods, the complexity inherent to an image is condensed into a set of discrete features with associated properties. Here, these properties are the speckle coordinates and their intensities. We generated these particles from the images by applying a local maximum detector, such that a particular pixel is detected as a maximum whenever its intensity is higher than every pixel around it. Each particle was stored in an array, containing the coordinates and the corresponding intensities.

Particle selection

Particles produced up to this point are still likely to be the result of noise. In the preconditioning step, we have only suppressed noise components corresponding to spatial frequencies higher than the diffraction limit. The components with spatial frequencies below this limit are still present and interfere with the speckle signal. Thus, a further selection is performed. We apply a statistical selection scheme to only keep those speckles (here, particle and speckle are equivalent terms), whose peak intensities are significantly higher than the local background intensity. Details on how we estimate the local background of each speckle and how we test the significance of peak intensities against noise are described in Ponti et al. (2003).

Generation of candidate matches

Over time, speckles move continuously along with the intracellular cytoskeletal flow. Because time-lapse images deliver only discrete snapshots of this flow, speckles in one frame have to be reidentified in the consecutive frame. Because speckles can appear, disappear, fuse, and split, this correspondence search is far from trivial, even at high image sampling rates. The speckle flow has a finite maximum speed over the duration of an FSM movie. Together with the sampling rate, this defines the maximum displacement d that a speckle can undergo from one frame to the next. It is fairly easy to visually estimate an upper limit for this distance. Omitting the use of this a priori information, the number of potential matches to consider would be overwhelmingly large. Hence, for each speckle, we store every neighboring speckle within the distance d in an array M, such that each row of this array consists of the two position vectors [r_k, r_k+1], with r_k = [r_k,x, r_k,y]. Here, r_k denotes the position of a source speckle in frame k, and r_k+1 denotes the position of a potential target speckle in the frame indexed by k + 1.

Selection of matches

The essence of particle-tracking methods is that particles are indivisible and that they retain their individuality even when they come very close. In that sense, the notion of a particle does not capture every aspect of a speckle because nothing prevents two speckles from fusing in an FSM sequence. This happens particularly in regions of flow convergence, where speckles are squeezed into a volume below the optical resolution of the microscope, compelled to do so, for example, by cytoskeleton contraction.

However, by analyzing some sample data manually, it appeared that fusion or splitting of speckles were rather rare events in the polymer assemblies we studied. Moreover, ignoring fusion and division allowed us to use a standard method from operational research to recover the speckle correspondences between frames. Specifically, the correspondence search selects a subarray of M such that:

1. A source speckle at time k is matched with at most one target speckle at time k + 1.

2. A target speckle at time k + 1 is matched with at most one source speckle at time k.

3. The matches are selected according to heuristic rules, describing the a priori likelihood of potential actions of speckles between consecutive frames.

Condition c determines the quality of particle-to-particle correspondence, and thus imposes local constraints on the selection of matches. Items a and b formulate conditions for the global topology of all matches. Whereas many particle-tracking systems employ some sort of similarity measure to define the correspondence, they resolve topological conflicts at best with an ad hoc scheme. Topological conflicts occur, for example, when two speckles in frame k would have their best match with the same speckle in k + 1, violating rule a above. In this case, the algorithm has to decide which of the two is permitted to link to the overbooked target speckle, and how the losing speckle reparticipates in the competition for another speckle.

Another example of a topological conflict is illustrated in Fig. 1 A. Three speckles, indexed by r_1,k, r_2,k, and r_3,k, translate to their new positions, indexed by r_1,k+1, r_2,k+1, and r_3,k+1. Frequently, particle tracking methods use a nearest-neighbor criterion to describe the quality of a match. In the example given, r_2,k would therefore be linked to r_1,k+1, and r_3,k to r_2,k+1, whereas r_1,k and r_3,k+1 would have no correspondents in frame k + 1 and k, respectively. This would represent a false speckle disappearance and appearance, and more critical for flow recovery, would yield the wrong selection of matches.

FIGURE 1.

Applying graph concepts to tracking problems. (A) Speckles at time point k (small circles), move to new positions (squares) at time point k + 1. (B) Translation of candidate matches into edges of a graph that defines all possible topologies for linking the speckles. In terms of graph theory, speckles represent vertices arranged in two layers. Only those matches are considered that fall into the search area of the corresponding speckle (dashed circles in A). Costs equal to the distance separating speckles are attached to the graph edges (numbers in regular font). Capacities of edges are all equal to one (first number in italic font). Not more than one unit of flow can leave from any of the source vertices or flow into a target vertex. Pushing a maximum amount of flow through the graph at minimal cost yields the matches selected by the tracker. In the case shown, the correct solution is chosen (edges with an effective flow 1, see second number in bold italic font), at a cost of 29. A nearest-neighbor matching scheme would result in a cost of 9, but would violate the condition of maximum flow.

In the following, we propose a solution to this challenging tracking problem, using the terminology and methods of graph theory (Sedgewick, 2002). Speckles are identified with graph vertices and candidate matches with graph edges. Different time points correspond to separate graph layers, and the matching topology is defined by a subgraph in which the edges connect corresponding speckles. We explain the computation of the “best” subgraph first for the simple example in Fig. 1 A, which can be translated into a two-layer graph. Then, we indicate the weaknesses of the two-layer approach, mainly in presence of antiparallel speckle movements, and outline the extension of the method to a three-layer graph.

Tracking with two-layer graphs

The relation between speckles (circles for frame k, squares for frame k + 1) and candidate matches (arrows), and their representation as graph vertices and graph edges, respectively, are illustrated in Fig. 1, A and B. The speckles r_2,k and r_3,k have two candidate matches within their search areas (defined by the dashed circles with radius d). Thus, in the corresponding graph (Fig. 1 B), two edges start from each of these positions. For r_1,k, only one vertex in frame k + 1 falls into the search area, and accordingly, only one edge leaves the corresponding vertex in layer k. Notice that the limitation of candidate matches to a certain search area reduces the graph complexity and thus the computation time. This is critical when running the procedure on thousands of speckles. As long as the areas enclose the maximum expected displacement of a speckle, this restriction has no effect on the final solution. Each graph edge is attributed an integer capacity that represents the maximum flow that can be transferred across a single edge (the use of the term flow in graph theory is unrelated to the cytoskeletal flow we aim at recovering with the tracking). In our graphs, each edge has a capacity 1 (cf. first italic number assigned to each edge of the graph in Fig. 1 B). Graph edges are also attributed a cost, reflecting the likelihood of the candidate match. In the example of Fig. 1, we simply assign the vector length of the match, rounded to an integer value, as a cost to the edge (cf. regular numbers assigned to each edge of the graph in Fig. 1 B).

According to graph theory, optimal matches with no topological conflicts are obtained by maximizing the flow crossing the graph, while minimizing the overall cost. The latter is calculated as the sum of the cost of all edges multiplied by the flow crossing them. Algorithms to achieve this are available either commercially or in the public domain (Goldberg, 1997; Sedgewick, 2002). In Fig. 1 A, the requirement of maximum flow forces the solution to the correct topology. The overall cost of the solution amounts to 10 + 11 + 8 = 29. Although there are many other subgraphs with lower cost, including the nearest-neighbor match, associated with a cost of 5 + 4 = 9, none of them sustains the maximum flow of 3. The requirement of minimal cost and maximum flow yields an optimal solution to the assignment problem.

For any particle tracker, the appearance and disappearance of particles represent major sources of perturbation for the reliable recovery of particle motion. This is how this problem is addressed in the presented scheme: The optimal subgraph is selected in a two-step procedure. First, a so-called network flow algorithm is run, followed by a so-called mincost algorithm. The outcome of the network flow algorithm is a configuration of edges, each one assigned an effective flow value (cf. bold italic number in Fig. 1 B). In our case the effective flow values are either 0 or 1. In terms of graph theory, this means that edges are either empty (0) or full (1). Full edges now define the topology of a subgraph that maximizes the flow across the entire graph. They connect a source speckle in frame k with a target speckle in frame k + 1, whereas empty edges represent candidate matches discarded by the network flow algorithm because of a violation of the topological constraints. Importantly, not more than one unit of flow can leave from any of the vertices in layer k, or flow into a target vertex in layer k + 1.

The search for maximum flow is ambiguous. The larger the graph, the more subgraphs exist that can sustain the maximum flow. Which of those is associated with the best matches is determined by the mincost algorithm. It uses the output graph of the network flow algorithm as an initial solution and seeks other subgraphs with the same flow but lower overall cost. The final subgraph returned by the mincost algorithm again labels the selected speckle matches with an effective flow 1, the others with an effective cost 0. Notice that the subgraph may or may not be equal to the initial one obtained by the maxflow algorithm. In the example of Fig. 1 B, there is obviously no reassignment of edge flows, as there is only one solution supporting the maximum flow of 3.

Given the output of the combined maxflow and mincost algorithms, speckle appearances and disappearances are readily found. Disappearing speckles correspond to vertices in layer k for which no edge leaves with an effective flow 1. Speckle appearances correspond to vertices in layer k + 1 for which no edge arrives with an effective flow 1. These considerations will become central in the future when we make a detailed speckle lifetime analysis, but they are not critical here. For the scope of this article, it is sufficient that the matches used for flow recovery are minimally perturbed by speckle appearances and disappearances.

Tracking with three-layer graphs

In the case of speckles moving in antiparallel flows, the recovery of correct matches is particularly difficult. Fig. 2 A displays the result of a two-layer graph algorithm run on data comprising two interleaved, rotating flow fields with opposite directions of rotation. The match selection frequently fails in areas with proximate antiparallel trajectories. To enhance the tracking performance, we modified our graph to be able to exploit the information contained in three frames simultaneously. This allowed us to exploit the notion of trajectory smoothness. Such heuristics have proved very powerful for solving the motion correspondence problem in other contexts (Veenman et al., 2001). Following (Sethi and Jain, 1987), we express the cost of a candidate match as

(1)

The first term is equal to zero for displacement vectors that are aligned, whereas the second term is zero for displacement vectors whose magnitude does not change over time. The sum of the two terms is therefore a measure of trajectory smoothness over three frames. The weights γ₁ and γ₂ tune the relative contribution of changes in direction versus changes in magnitude. Although Sethi and Jain (1987) propose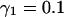d and 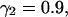we found that for our application, weight factors of 0.4 and 0.6 yielded better results.

FIGURE 2.

Tracking antiparallel flow. (A) Difficulties encountered with tracking antiparallel flow using a two-layer graph. (B) Improvement of the performance using a three-layer graph, which can account for the smoothness of speckle trajectories. See text for a discussion of the highlighted areas. (C) Illustration of the selection process in real data exhibiting antiparallel flow (FSM data of bipolar microtubule flux in a mitotic spindle, Fig. 6). Solid black vectors are candidate matches between frame k and frame k + 1, dotted black vectors are those between frame k + 1 and frame k + 2. The algorithm associates solid vectors with dotted vectors to form trajectories linking speckle positions at time k, k + 1, and k + 2, such that the overall cost of the selected paths is minimal. According to the cost function in Eq. 2, the algorithm tends to select smooth trajectories with minimal speckle intensity variation. The red vectors indicate the matches selected by the algorithm. In agreement with the bipolar flux arrays, they outline a densely interleaved antiparallel flow (see, for example, the trajectories indicated by labels 1 and 2, pointing toward the upper and lower spindle poles, respectively).

With the cost function of Eq. 1, we do not only introduce a third graph layer, but the costs of the edges between the layers k and k + 1 are now coupled to those of the edges between the layers k − 1 and k. This requires a nonstandard restructuring of the graph, which will be discussed in a more dedicated publication. Here we confine ourselves to demonstrating the improvement in tracking performance.

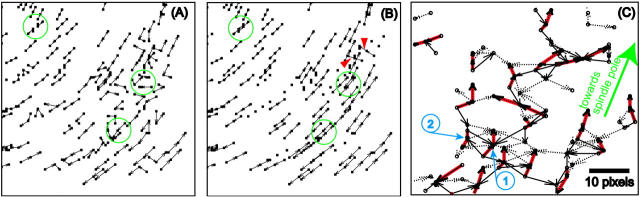
Fig. 2 B shows the same flow field as Fig. 2 A, but now tracked with a three-layer graph. With the exception of two false matches (red arrowheads), the algorithm returns the correct solutions. We highlight three locations (green circles) where antiparallel trajectories are particularly close. As evident in Fig. 2 B, the algorithm cannot guarantee the selection of all matches. This will have to be improved for complete lifetime analysis but is irrelevant for the flow evaluation aimed at in this contribution. As explained in the paragraph “Flow Recovery by Filtering and Interpolation” below and the Results section, missing matches do not affect the reconstruction of flow fields.

Nevertheless, to maximize the number of matches and to make the selection as robust as possible, the cost function should incorporate as much prior knowledge of the speckle action between consecutive frames as available. A further information we have is that speckles largely conserve their intensity. Therefore, we seek matches with minimal variation in speckle intensity. To achieve this, the term 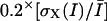was added to the cost c in Eq. 1, where is the standard deviation of the intensities of the speckles at r_k−1, r_k, and r_k+1, and is the mean intensity over all three frames:

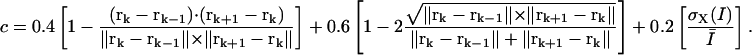(2)

Fig. 2 C shows an example of the graph selection process on real data. We present a zoom-up of a small region near one pole of the mitotic spindle, analyzed in more detail in the Results section (see frame of inset B-I in Fig. 6 B). Here, speckles mark an interspersed scaffold of microtubules, which flow in opposite directions. The panel displays candidate matches shorter than the radius (d = 10 pixel) of the circular search region centered at each of the speckles of frame k. Candidates between the frames k − 1 and k are shown as solid black vectors; those between k and k + 1 as dotted black vectors. According to the explanations above, the goal of the graph selection algorithm is to optimally pair solid vectors with dotted vectors. The possible combinations of vectors are bewildering, even for the very small example shown. The red vectors indicate the selected matches. As the region under scrutiny is near the upper spindle pole, the majority of matches points in the direction of the pole, located above and to the right of the zoom-in window (see green arrow). Most of the remaining matches point in the opposite direction indicating that these speckles belong to long microtubules reaching into this area from the opposite pole. We will revisit this phenomenon in the Results section with more emphasis on the biological significance. For now, we remark that e.g., the two antiparallel vector pairs, highlighted by the blue labels 1 and 2 in Fig. 2 C, are only 6 pixels apart, which is in the range of the actual speckle displacements. A global resolution of topological conflicts, as it is achieved with the proposed selection of matches using graphs, is essential to cope with such a densely interleaved antiparallel flow.

Relaxing the condition of nonfusing and nonsplitting speckles in a next version of the tracking scheme

Despite our finding that fusion and splitting are relatively rare, we aim at overcoming this limitation of the current scheme (see above) with a future version. Fusion and splitting of speckles can be addressed in two ways: i), by relaxing conditions a and b, which demands a restructuring of the graph such that multiple edges with an effective flow equal 1 can leave a vertex in layer k, and vertices in layer k + 1 can receive several edges with an effective flow equal 1. For graphs with thousands of vertices per layer this procedure will be ambiguous and computationally not affordable; ii), by resolving signal overlaps during particle generation. This bears the advantage that the graph structure is unaffected and all the core modules of the current software package are applicable without modifications. Near colocation of two or more significant speckles can e.g., be resolved by mixture model fitting (Thomann et al., 2002). As a result, several speckle positions and intensities are obtained for what is currently detected as only one local maximum. This procedure will also be computationally expensive, but in contrast to the restructuring of the graph, it can be implemented in a framework for parallel computing.

Flow recovery by filtering and interpolation

As mentioned in the Introduction, the first utilization of the extracted matches consists in the reconstruction of speckle flow. Because speckle intensities and positions are stochastic variables subjected, among other effects, to the influence of thermal fluctuations (Ponti et al., 2003), their displacements are only in a statistical sense related to the underlying average cytoskeletal flow. Flow recovery is therefore achieved by spatial filtering of the map of matches delivered by the graph algorithm, using convolution. At the same time, we obtain interpolated flow on a regular grid, which mainly serves the purpose of flow visualization. In addition to spatial filtering, steady-state flow components are retrieved by filtering the maps of matches in time.

The amount of filtering is determined by the spatial and temporal correlation lengths of the filter. In our case, we chose an isotropic Gaussian convolution kernel in space, multiplied with another Gaussian in the time domain, describing the correlation of flow between any two frames of the movie. In the current version of the software, the correlation lengths are set globally, i.e., the same lengths are applied throughout the entire field of view for all frames. They are tuned by the operator based on an educated guess. Obviously, the parameter choice depends on the focus of the study, and thus on some prior knowledge of the flow structure. For example, if an average, global measure of cytoskeletal motion is to be obtained, the spatial and temporal correlation lengths ought to be set relatively large, e.g., in the range of the persistence length of the studied polymer (∼1–2 μm for actin). On the other hand, if flow needs to be studied around a pole in the vector field, e.g., associated with an area of meshwork contraction or depolymerization, the correlation length has to be lowered to pick up the details. This is, of course, done at the risk of including more random components, which are unrelated to the meshwork flow into the pole.

In future versions of the software, we will relax the need for operator input. Prior knowledge of the flow structure can, for example, be extracted from the flow field itself. Borrowing ideas from edge-preserving filtering in computer vision, a filtering framework will be implemented where the correlation lengths are iteratively adjusted to the local convergence or divergence of flow. This will permit the combined recovery of global flow in areas of coherent speckle movement and of details of poleward or shear flow in areas with singularities in the movement field. Alternatively, the computation of correlation lengths can be supported with a mechanical model of the cytoskeleton. Initial tests with such approaches deliver promising results. However, their discussion goes beyond the scope of this article and we confine the presentation of results to flow fields computed with one globally and manually defined set of correlation lengths.

An application where global filtering is inappropriat e arises with the densely interleaved antiparallel tubulin flow present in the mitotic spindle. Here, global filtering would result in vectors of zero length approximately everywhere. In this case, the algorithm starts with a sorting procedure before filtering, where matches pointing toward one pole are separated from those pointing to the opposite pole. This operation is straightforward and robustly performed without further user interaction (see Results and Fig. 6 B).

RESULTS AND DISCUSSION

The scope of this section is to demonstrate the potential of our new single speckle tracker to extract flow information in different situations. We present three types of data: i), Simulated flow fields where artificial particles are tracked and the recovered matches are compared with the known displacement vectors. ii), The speckle flow at the front edge of a migrating cell is analyzed to indicate the power of computational FSM to unravel the dynamics of lamellipodial and lamellar F-actin meshworks. Intentionally, we perform our study on FSM data already published and manually analyzed to point out the gain of high-content information achieved with our new computational schemes. iii), Speckle flow representing interleaved microtubule flux in mitotic spindles is analyzed to emphasize the ability of our tracker to cope with antiparallel movement. In addition, the spindle data is attractive to demonstrate the new possibilities we obtain with the wealth of quantitative information we can now extract. We present two statistical population analyses of single speckle matches that provide novel insights of the microtubule organization and dynamic behavior inside the spindle.

Performance analysis on simulated flow fields

Data of the type “peas in a rotating dish” are traditionally used for testing tracking approaches and we have adhered to this practice here. For such data, the magnitude of the displacement depends heavily on the position, a feature shared with data from biological samples. We have generated at time point k a spatially random planar distribution of particles with random intensities. In the following, we always mean “obeying a uniform distribution” when we say “random”. Then, these particles were twice subjected to a rotation of 3° to generate the particles at time point k + 1 and at time point k + 2. The particle sets were distributed over an area of 200 × 200 pixels and the first frame contained ∼200 particles. From one frame to the next, random intensity variations with a maximum of 0.5 times the intensity of the corresponding particle in the previous frame were imposed. These variations are significantly above those we could observe for real data and therefore constitute a demanding benchmark for the tracker. The parameters mentioned above were applied to all simulations, except when explicitly stated otherwise.

The quality of tracking was measured as the proportion between false matches and the number of recovered matches. As a rule of thumb, error rates below 20% do not seriously affect flow recovery and thus are acceptable. The average density of speckles in real FSM images generally guarantees five matches or more falling into the support area of the convolution kernel applied for flow filtering and interpolation. Consequently, with an error rate of 20%, one out of five matches would deteriorate the convolution as an outlier. Since the correspondence search area is limited to the user-defined radius d, the magnitudes of outlier matches are also limited. In a strict mathematical sense, this moves the break point of the convolution to infinity (Rousseeuw and Leroy, 1987). In practical terms, this means that, in the worst case, filtered and interpolated flow vectors near outlier matches are biased by d/5.

In the same spirit, missing matches do not need to be counted as errors as they do not contribute to the recovery of filtered flow. Unless stated otherwise, the number of matches recovered was above 90% for all of the following tests on synthetic data.

Influence of positional fluctuations

In real data, speckle trajectories are perturbed by various effects, including thermal fluctuations, local cytoskeleton contractions, and positional fluctuations due to photometric changes (see Ponti et al., 2003, for a discussion of these effects). Hence, we have evaluated the influence of positional fluctuations by subjecting the speckles in every frame to random perturbation displacements of variable mean. The proportion of mistakes committed by the matching algorithm changed from 1.8% ± 0.75% to 5.3% ± 1.6% (n = 3), when progressively increasing the maximum perturbation displacement from 0 to 3 pixels imposed independently on both image directions.

Influence of particle appearance and disappearance

We have also evaluated the influence of speckle appearance and disappearance, which in real FSM data is associated with polymer turnover (Ponti et al., 2003). We ran separate tests for appearance and disappearance. To mimic appearance, new particles with random intensities were added to the particle sets in time point k + 1 and k + 2 at random positions. The rate of appearance is expressed as the number ratio between new particles and existing particles in the previous time point. To mimic disappearance, a certain fraction of existing particles were randomly deleted from the sets in time point k + 1 and k + 2. The rate of disappearance is expressed as the number of particles removed, divided by the number of particles present before their elimination in the next frame.

The proportion of mistakes committed by the algorithm when varying the appearance rate from 0% to 80% increased progressively from 1.8% ± 0.75% to 11.5% ± 2.7% (n = 3); the one associated with disappearance rates between 0% and 60% from 1.8% ± 0.75% to 2.5% ± 0.5% (n = 3). These results indicate that the tracker performs robustly in the presence of this type of perturbation.

Influence of the magnitude of the displacement

To examine the performance of the tracker as a function of the mean displacement, we varied the rotation angle from 0° to 7°. The results clearly depend on the density of particles, so the latter was kept constant. In these simulations, the search distance d for candidate matches (see paragraph “Generation of Candidate Matches” in Algorithm section) was set to the maximum displacement across the images. The proportion of mistakes committed by the algorithm when going from 0° to 7° increased progressively from 1.8% ± 0.75% to 9.7% ± 3.7% (n = 3).

Influence of antiparallel flow

Antiparallel flow is a distinctive characteristic of the mitotic spindle or of contracting actin/myosin assemblies. Hence, we tested our algorithm on a data set where two sets of particles were rotating in opposite directions. This was done by superposing two sets of data of the type used up to this point, where rotations were taking place in opposite directions (the total number of particles in each frame was ∼400). The results are shown in Fig. 3 A, and indicate that the tracker is not confused excessively with shear flow. The figure inset points at one of three particle clusters, where errors occur in the selection of matches.

FIGURE 3.

Performance tests of the algorithm using synthetic data sets. (A) Tracking of two interleaved and antiparallel flow fields of ∼200 particles each, rotating at an angular velocity of 3° per frame. Particles belonging to the first, second, and third frame are represented by black, blue, and red circles, respectively. The recovered matches are indicated by arrows connecting the particles. The inset shows a region containing matching mistakes. Speckle intensity variations are also used for selecting the trajectories, sometimes leading to inappropriate matches. In the case of a rotating field, the true trajectory is not the smoothest of all possible, which is another source of mistakes. (B) Tracking a rotating flow field when multiple perturbations are applied. The rate of appearance between successive frames was 10% of the number of existing particles, whereas 10% of existing particles were deleted between each pair of frames. The amplitude of random positional fluctuations in each frame was 2 pixels in both the horizontal and the vertical image direction. The width of the filter kernel was set to 20 pixels (cf. text for further parameters). Continuous thin arrows represent the recovered matches, whereas thick arrows represent the filtered vector field. The average recovered rotation angle was 2.5° ± 0.3°, only slightly underestimating the nominal rotation angle of 3°. (C) Tracking a standard test data set for particle tracking methods (Veenman et al., 2001). The few mismatches correspond to trajectories, which are smoother than the correct ones (i.e., linked points are in almost perfect alignment). No intensity information was available for this data set.

Fig. 3 A shows the recovery without perturbation from displacement fluctuations, particle appearance, or disappearance. We have also tested the influence of these parameters in the presence of shear flow (results not shown). To our surprise, the results were similar to those presented before with only parallel flow.

Influence of various effects applied simultaneously

Ultimately, a speckle tracker has to deal with multiple sources of perturbation simultaneously. To conclude these simulations, we show one example of flow estimation where the effects of speckle appearance, speckle disappearance, speckle intensity variation, and positional fluctuations are simultaneously present (Fig. 3 B). As can be recognized in Fig. 3 B, the global flow is recovered accurately. Moreover, the average rotation angle estimated from the recovered flow was equal to 2.5° ± 0.3°, underestimating the nominal value of 3° only slightly.

Comparative evaluation

The goal of this article is not to systematically compare our approach with other tracking algorithms, but to apply it to solve important biological problems. However, for a very partial, comparative evaluation of our software, we have tested it on a data set accepted as a benchmark in the computer vision community (Veenman et al., 2001). The centroid coordinates of these particles were provided with the data set, and no other information than that was exploited to recover the trajectories. We have tracked the particles between the first three frames of the sequence, as shown in Fig. 3 C.

Although there are algorithms reported to be able to track this data without a single mistake, most of them experience difficulties with it (Veenman et al., 2001). Moreover, our algorithm can handle data sets containing thousands of particles, whereas the rather complete panel of algorithms tested by Veenman et al. (2001) tends to fail for more than 100 particles. Finally, except for the fact that we have adjusted the parameter d (see paragraph “Generation of Candidate Matches” in Algorithm section), we have used our algorithm without tuning it for this particular data set. In conclusion, our algorithm seems unique in being able to match thousands of particles, and performs well compared to other trackers on smaller problems.

F-actin flow recovery in a migrating newt lung epithelial cell

A cross-linked meshwork of F-actin continuously polymerizes in a highly regulated manner at the edge of migrating cells (Pollard et al., 2000). Polymerization is thought to generate protrusive forces that push forth a lamellipodium and begin the cell motility cycle (Mogilner and Oster, 1996). Often, the growth of the polymerizing meshwork is compensated by myosin-driven rearward pulling of the meshwork, such that the F-actin cytoskeleton exhibits a retrograde flow (Lin and Forscher, 1995). In addition to myosin motor activity, the polymerization of the meshwork itself may contribute to pushing forces against the leading edge plasma membrane, promoting F-actin transport away from the edge. Spatial perturbations of the balance between polymerization and retrograde transport produce macroscopic shape changes in the cell boundary, which ultimately lead to a forward or backward movement of the lamellipodium. To understand the mechanics of cell migration, it is therefore essential to quantify the spatial modulation of F-actin retrograde flow and to relate it to molecular factors controlling motor activity, polymer turnover, and meshwork mechanical properties (Cramer, 1997; Lauffenburger and Horwitz, 1996). The direct coupling of cell shape variations and F-actin flow was demonstrated in Danuser and Oldenbourg (2000), where spatial changes in a high-resolution map of retrograde flow were accompanied by deformations of the cell outline. However, for technical reasons, this study was limited to a steady-state analysis. To understand how F-actin flow contributes to cell migratory and morphogenic responses, dynamic maps of the flow are required. As will be demonstrated in the following, FSM appears to be the ideal tool for this purpose.

Recovery of complete F-actin flow maps at the front edge of a migrating cell

We have analyzed newt lung epithelial cells microinjected with fluorescently labeled actin during their migratory wound-healing response in tissue culture. In FSM images, the actin meshwork appears in these cells as an approximately even distribution of fluorescent speckles with brighter areas representing regions of high F-actin concentration (Salmon et al., 2002). The data set we analyzed was published in Fig. 3 A of Waterman-Storer et al. (2000b) and the QuickTime movie is available as Supplementary Material of this article (actinFlow.mov). Fig. 4 B shows the filtered flow obtained by convolving matches from the first seven frames of the FSM movie, overlaid on the first frame. In the original publication, the analysis of F-actin flow was restricted to visual inspection or kymographs, such as shown in Fig. 4 A (see also Fig. 3 C of Waterman-Storer et al., 2000b). With our new tool, we can now recover a complete vector field representing the flow in every point of the meshwork (Fig. 4 B). For the sake of visualization, interpolated flow vectors are plotted on a grid (raster size 1 μm). Vector lengths are proportional to the flow velocity, and their direction indicates the locally averaged direction of speckle movements. Spatial filtering was performed with a correlation length of 1.6 μm (see “Flow Recovery by Filtering and Interpolation” in Algorithm section), chosen in consideration of the shear modulus of a cross-linked F-actin meshwork (Tseng and Wirtz, 2001). The overall pattern of flow in our map corresponds closely to the visual impression one gains from simply watching the movie. However, there were regions that initially did not draw our attention in the movie, such as the anterograde flow near label A, or the flow converging toward a “pole” (label P). The use of our algorithm uncovered such patterns, and, upon closer visual inspection, it became apparent that in this case computer vision outperformed the human eye not only in terms of quantification and objectivity, but also in terms of sensitivity in detection. This is a rather rare situation, as computer vision algorithms typically lag behind human vision in qualitative analyses of complex scenes. We speculate that the complexity inherent to the movements of the actin cytoskeleton and associated FSM data obscures significant details to the human observer.

FIGURE 4.

F-actin speckle flow in a migrating newt lung epithelial cell. (A) Kymograph analysis (cf. text for more details) in the region indicated by a narrow yellow box in panel B. The slopes of the streaks in the kymograph permit the measurement of the average speckle flow velocity along the vertical axis of the box, as indicated by two dashed lines highlighting streaks from two different populations of speckles. In the lamellipodium and lamellum, a retrograde flow of 0.45 ± 0.05 μm/min is measured (label R). Farther away from the leading edge, the flow stops and the horizontal streaks indicate a flow of 0.0 ± 0.05 μm/min (label 0). (B) Flow analysis of the entire cell front using the new single speckle tracker. The presented flow field is averaged over seven frames and spatially filtered with a correlation length of 1.6 μm. The flow vectors are interpolated on a grid with 1 μm side length, and overlaid on the first frame of the movie. The flow appears to be organized in three main regions: i), retrograde flow (R); ii), converging (C) and poleward (P) flow; and iii), anterograde flow (A). Velocity vectors with an origin on the axis of the kymograph report a flow speed of 0.40 ± 0.05 μm/min (R) with a transient slowdown to 0.02 ± 0.05 μm/min, in agreement with the kymograph. Farther down on this axis, an anterograde flow of 0.08 ± 0.04 μm/min is measured, which is not detectable with kymograph analysis. Flow speeds in other areas of the mapped field are higher than 0.40 μm/min, e.g., at the very front (see zoom-up). See text for further discussion of the flow map.

F-actin flow is organized in three distinct zones

Three distinct zones can easily be distinguished in the flow map: i), the lamellipodium and lamellum at the cell edge, where a prominent retrograde flow away from the cell edge is present (label R in Fig. 4 B). ii), further down in the direction of the cell body, a laminar convergence region, where most speckles coalesce and subsequently move parallel to the cell edge (label C in Fig. 4 B). As mentioned before, in the same zone we also find poles where speckles converge toward one point (label P in Fig. 4 B). iii), behind the convergence region, a flow of smaller magnitude is on average directed anterograde (toward the cell edge; label A in Fig. 4 B). The vector map presented here illustrates strikingly the spatial complexity of F-actin meshwork flow.

F-actin flow is dynamically modulated

By matching successive frames over time, complete movies of the flow can be constructed, revealing not only spatial but also interesting temporal modulations of F-actin flow. In Fig. 5, we map the temporal evolution of the vector field for a window in area C in Fig. 4 B where retrograde and anterograde flows converge. The anterograde flow is seen to turn its direction within a period as short as 40 s. We speculate that this could be induced by very local modulations of the myosin activity in this area. In summary, our FSM analysis technique gives us access to a new body of knowledge on F-actin dynamics. Such mapping can potentially uncover how the dynamics are affected by upstream molecular control factors, and how it correlates with downstream responses such as cell migration events. This new tool can be used to investigate and quantify F-actin dynamic responses to perturbations in actin-related signaling (Wittmann and Waterman-Storer, 2003), to drug application (Ponti et al., 2003), and to spatially modulated cell adhesion (Csucs et al., 2003).

FIGURE 5.

Dynamic changes in the actin cytoskeleton flow in the area C of Fig. 4 B, where we suspect increased myosin concentration and activity (cf. text for more details). Dynamic maps are obtained by filtering the matches of every frame separately in the spatial domain only. The vector fields are then concatenated into movies with the same temporal resolution as the raw data.

Comparison with previous kymograph analyses

The presence of the three regions, as revealed by Fig. 4 B, agrees well with a comparatively sparse kymograph analysis of the flow in the same cell system (Salmon et al., 2002). Although much less detailed and subject to potential artifacts, kymographs generated at a few critical locations were able to recover some of the main features of actin flow characteristics. An example of such a kymograph is given in Fig. 4 A. Image slices (the position of the slice is shown by a yellow box in Fig. 4 B) of 5 pixels in width have been copied from the first 50 frames of the movie and have been pasted side by side to form the kymograph. Speckles that move along the long axis of the box for a sufficiently long period become visible as bright streaks in the kymograph. Their slope is a measure of speckle speed, as indicated by dashed lines in Fig. 4 A. The speeds estimated for the lamellum and at the pole were equal to 0.45 ± 0.05 μm/min, and 0.0 ± 0.05 μm/min, respectively. In good agreement, our method delivered for the same locations and time period speeds of 0.40 ± 0.05 μm/min, and 0.02 ± 0.05 μm/min, respectively. As manifest in the kymograph of Fig. 4 A and the flow map of Fig. 4 B, there is a difference in the flow speed between the lamellipodium proximal to the leading edge and the inner lamellum, suggesting that the flow in these two areas is driven by distinct molecular mechanisms (Waterman-Storer and Salmon, 1997; Waterman-Storer et al., 2000b; Salmon et al., 2002). Our new vector map permits the investigation of this apparent transition along the entire cell edge. In some regions we indeed find this same behavior. The lamellipodial speed (white ellipse and zoom-up in Fig. 4 B) can be up to two times faster than the fastest rates in the lamellum (around R label in Fig. 4 B). In other regions the difference is not as clear, indicating that there is substantial variation of flow velocity along the edge. However, at this point we are cautious not to draw too far-reaching conclusions. Because the lamellipodium is very narrow in these cells, i.e., in many locations less than the support area of the convolution kernel, and naturally fluctuates in width (Waterman-Storer and Salmon, 1997), our flow filtering probably obscures some details of the velocity variations along the edge and in the transition zone between lamellipodium and lamellum. Here, adaptive adjustment of the correlation lengths according to the underlying flow structure will likely reveal further insights. There is evidence that the retrograde actin flow in the lamellipodium is driven solely by forces associated with actin polymerization pushing on the leading edge plasma membrane, whereas actin flow in the lamellum is myosin dependent (Waterman-Storer and Salmon, 1997). Thus, a more precise spatial mapping of the velocity vectors with less filtering may uncover where exactly in the lamellipodium/lamellum junction myosin motors begin to engage actin filaments, a piece of information that cannot be obtained by any other means.

Recovery of microtubule flux in a mitotic spindle

We have applied our single speckle tracker to an FSM movie of microtubules in metaphase spindles with replicated mitotic chromosomes assembled in meiotic Xenopus egg extracts as described in Desai et al. (1998), Murray et al. (1996), and Waterman-Storer et al. (1998). Previous studies using fluorescence photoactivation (Desai et al., 1998; Sawin and Mitchison, 1994) or fluorescent speckles to mark the microtubule lattice have reported poleward flux rates of 2.0–2.5 μm/min. Measurements by fluorescence photoactivation are of low resolution and yield only averages over the whole spindle. Previous FSM measurements were done by kymograph analysis along the spindle axis and represent only a narrow sample of speckle movements within the spindle. In contrast, our particle tracking algorithm provides detailed velocity information throughout an optical section of the spindle as shown in Fig. 6. Fig. 6 A displays a cartoon of the microtubule organization in a metaphase mitotic spindle, which is formed from microtubules extending from opposite spindle poles (SPs) with plus ends distal and minus ends proximal to the associated pole. Kinetochore microtubule bundles link sister chromosomes to the poles (population 1). Most spindle microtubules are non-kinetochore microtubules, and interpolar spindle fibers are formed from bundles of overlapping non-kinetochore microtubules extending from opposite poles (population 2). The links between overlapping microtubules from opposite poles include microtubule associated motors (Sharp et al., 2000), rendering the spindle a complex motile scaffold (Wittmann et al., 2001). Also indicated is the position of the metaphase plate (MP) where chromosome pairs align under balanced bipolar forces, before they start to segregate after inactivation of the mitotic checkpoint (see Introduction).

Single speckle tracking reveals bipolar flux

In the metaphase arrangement, poleward microtubule flux coupled to minus end depolymerization produces a bipolar flow pattern with antiparallel components. When observed by FSM, this gives rise to a complicated speckle trajectory field with opposing velocity vectors (see QuickTime movie spindleFlow.mov in Supplementary Material). Indeed, the speckle flow recovered from the present FSM data is clearly bipolar. Fig. 6 B shows the speckle matches found by the tracker for 10 consecutive frames. For visual clarity, the figure contains two speckle populations, as automatically sorted by the flow filtering algorithm (see “Flow Recovery by Filtering and Interpolation” in Algorithm section). Speckle matches in blue point toward the upper pole, those in red point toward the lower pole (see also cartoon in panel A). The single speckle vector map indicates the ability of the tracker to reconstruct antiparallel movements, which is imperative in this case. This is confirmed in more detail by the zoom-ups of insets B-I and B-II. Although this article does not exploit speckle matches for lifetime analysis, the data presentation draws one's attention to a phenomenon related to the lifetime: The lengths of connected speckle matches increase, the closer the speckles are located to their “home pole.” This finding can easily be understood by examination of the cartoon in Fig. 6 A. Non-kinetochore microtubules undergo dynamic instability where their plus ends rapidly switch between phases of growth and shrinkage. Therefore, speckles generated by fluorophore incorporation during growth will disappear again when the microtubule end reaches their position during shrinkage. The more distant speckles are from the microtubule plus end, the lower is the probability of disappearing by disassembly, as reflected by the more stable trajectories toward the pole. The short trajectories of front speckles (see red trajectories in B-I, respectively blue trajectories in B-II) of 2–3 frames suggest rates of catastrophe (switch from growth to shrinkage) and rescue (switch from shrinkage to growth) in the range of 20–30 s, as expected for the dynamic instability of these microtubules (Sawin and Mitchison, 1991). The tendency for prolonged speckle trajectories toward the “home pole” is further amplified by the kinetochore microtubules, which only reach the MP, and in vertebrates are more stable than the non-kinetochore microtubules that have free plus ends (Zhai et al., 1995).

The velocity of microtubule flux is constant along the mitotic axis

Fig. 6 C visualizes the filtered and grid-interpolated flow (1 μm² raster) of the blue speckle population in Fig. 6 B. The vectors were filtered over four frames and with a convolution kernel with a width of 0.9 μm. The vector data are overlaid on the first image of the movie. As indicated by the vector map, the flow speed is almost constant along the pole-to-pole axis, with an average equal to 2.5 ± 0.2 μm/min. This value agrees well with previous measurements in kymographs (Mitchison and Salmon, 2001; Waterman-Storer et al., 1998).

At the single speckle level, some tracks do not head toward the poles but have a variable lateral component, or can even transiently reverse their direction (data not shown). Most of these events do not constitute matching mistakes, as verified by manual tracking of some of the implicated speckles. They only confirm that the spindle is a dynamic structure subjected to forces of multiple origins, including thermal bending fluctuations of microtubules. Analyzing the statistical properties of the speckle micromovement should allow us in the future to recover information about the nature of the forces acting at this scale.

Histograms of the speckle number density along the mitotic axis reveal the microtubule organization and the spatial extension of the spindle poles

Visual observation of FSM movies cannot provide quantitative answers to questions like: what is the density of microtubules, as measured by the density of speckles moving toward one pole or toward the opposite pole, as a function of the distance along the mitotic axis? In Fig. 6 D, the blue line indicates the distribution of speckles moving upward, whereas the red line shows the distribution of those moving in the opposite direction. Note from Fig. 6 A that the flux direction is a signature identifying which microtubule subsystem a specific speckle belongs to. Therefore, Fig. 6 D also displays the distribution of distances reached by microtubule plus ends emanating from one pole toward the other pole. At metaphase, kinetochore microtubules radiating from one pole reach only to the midzone, where they attach to chromosomes, whereas non-kinetochore microtubules can extend further toward the other pole. Consequently, one would expect for one microtubule subsystem that the density of microtubules suddenly decreases when going from one pole toward the other pole. In fact, this is what our measurements indicate and the most significant decrease occurs, as expected, at the position of the MP (Fig. 6 D). The symmetry of decrease in the two subsystems suggests that bipolar attachment of chromosomes by their sister kinetochores to microtubules from opposite spindle poles must be complete in the present image data. In agreement with our expectation that only few non-kinetochore microtubules reach the opposite pole, the distributions progressively decrease beyond the MP.

A second remarkable conclusion that can be drawn from this distribution is the outreach of the pole region. After a peak in the speckle number ∼10 μm away from the MP (arrowheads in Fig. 6 D), the number of speckles drops, on average, monotonically toward the poles (see dashed lines). This suggests that the distribution of minus ends where microtubules depolymerize and thus, the pole itself, extends over a large area.

Flux in non-kinetochore microtubules is higher than in kinetochore microtubules

Based on histograms constructed from the set of all speckle displacements, we have attempted to distinguish between two microtubule populations with putatively different flux behavior (Fig. 7). It could be expected that speckle velocities are higher for non-kinetochore microtubules as compared to kinetochore microtubules because the latter are linked to chromosomes, thereby introducing mechanical tension opposing the flux direction. To test this hypothesis, we considered the speckle population moving toward the upper spindle pole (represented by blue matches in Fig. 6 B). We then reasoned that, within this population, speckles starting their trajectory below the MP ought to belong to non-kinetochore microtubules. In contrast, both kinetochore and non-kinetochore microtubules are present between the MP and the pole. If kinetochore microtubules flowed more slowly than non-kinetochore microtubules, we would expect the two histograms of the speckle speed for these halves be shifted relative to one another. Indeed, a Kolmogoroff-Smirnov test, performed on ∼20,000 speckle matches over 25 frames of the movie, showed that non-kinetochore microtubules flow faster (2.57 μm/min on average) than the mixed population (2.46 μm/min) of non-kinetochore and kinetochore microtubules (p-value: 0.0004).

FIGURE 7.

Distinguishing kinetochore microtubules from non-kinetochore microtubules, based on differences in flux. The two histograms represent the velocity distribution of the complete speckle population moving upward (solid line) and of speckles located below the MP only (dashed line), respectively. The second population therefore contains only non-kinetochore microtubules. The two velocity distributions are very similar, but the population containing only non-kinetochore microtubules exhibits slightly higher velocities, making the distributions significantly different, as judged by a Kolmogorov-Smirnov statistical test (p-value = 0.0004).

We have repeated the analysis for speckles moving toward the lower spindle pole (represented by red matches in Fig. 6 B) and have obtained almost identical values: non-kinetochore microtubules flow at 2.64 μm/min vs. 2.5 μm/min for the mixed population.

Qualitative validation of tracking quality by speckle signal subtraction

The fraction of signal exploited for tracking can be evaluated by subtracting the signals of all speckles tracked from the raw image data. Visual inspection of the residual movies reveals in a qualitative sense how much of the speckle flow is “missed” by the software. Note that missed speckle flow does not necessarily add a new component to the overall flow field, but there is a certain probability that they could. On the other hand, if the residual images do not exhibit perceivable texture translocation, this is a sign that most of the information present in the images is exploited to recover the flow. Supplementary movies show a comparison for both actin retrograde flow and microtubule flux between the original time-lapse FSM images (see left half of the supplementary movie) and the corresponding residual images (see right half of the supplementary movie). Compared to the original data, little texture remains in the speckle-subtracted movies, and in almost all areas the signal is reduced to random flicker.

CONCLUSION

We have presented a new tool extending the possibilities of FSM as a quantitative method for analyzing protein dynamics in live cells. This tool was applied to two problems of biological relevance: the analysis of the F-actin flow pattern in a migrating cell and of the bidirectional microtubule poleward flux in a mitotic spindle. The exciting biological conclusions drawn from these analyses should be considered with care because in both cases they relied on the processing of a single movie, and systematic experimental controls supporting the findings are missing. Our intent with these two biological applications was merely to illustrate the performance of a new computational technique, which will finally allow exploitation of the full power of FSM, as proposed four years ago by Waterman-Storer et al. (1998). Now that these techniques are available, we plan to process extensive experimental data sets and to begin testing specific hypotheses in cytoskeleton biology, some of which are alluded to in the text. To do so, we face a few additional technical challenges. Currently, the processing of one movie of ∼200 frames takes ∼50 h on a high-end, newest generation personal computer. To deal with several data sets, and to compare them quantitatively, we will have to modify our software for distributed computing in a computer network. As indicated in the text, the analyses presented in this article represent only the tip of the iceberg in terms of the potential of this technique for FSM analysis.

The development of a novel tracking system was necessary to cope with the specific challenges of FSM

In both fields of computer vision and pattern recognition, the problem of particle flow analysis is very actively studied for innumerable applications (see Grant, 1997; Veenman et al., 2001; and references therein). In the biophysics community, the problem has drawn significant attention over the past 10 years as well (see Cheezum et al., 2001, for a comparative study of single particle tracking methods in light microscopy and its various applications to biophysical experiments). This begs the question whether we could have used an existing solution to solve our problem of speckle tracking in FSM. We have chosen to develop our own framework because on the one hand, we are not aware of an existing tracker capable of recovering reliably thousands of speckle trajectories simultaneously, and on the other hand because it was critical to be able to fine-tune the program, for example to exploit intensity information for the correspondence search, which is typically neglected by other approaches. In the case of FSM, exploiting intensity information is critical as the average distance between the particles lies frequently in the range of the particle displacements themselves, making the correspondence search highly ambiguous. The solution to this problem must, therefore, rely on additional information cues.

The chosen particle tracking approach outperforms alternative, pattern-based tracking methods

Alternative tracking approaches, which are often exploited in applications with image data containing a high density of features, are pattern- or window-based methods (see Corpetti et al., 2002; Haussecker and Fleet, 2001, for most recent examples of tracking algorithms of this kind). This approach is especially powerful when the features are weak in contrast and proper feature extraction before tracking is difficult (Danuser, 2000). The basic concept of window-based tracking is to determine for a small image subwindow (e.g., an area of 25 × 25 pixels) two transition models that describe the positional and photometric evolution between subsequent frames for each pixel forming the texture of the window (Danuser, 2000). The parameters of the transition models are then estimated by maximizing an objective function, defining the similarity between the pattern in frame k, and the transformed pattern in frame k + 1. This bears the advantage that correspondences do not have to be sought between thousands of features, but only a few parameters per window have to be calculated for an optimal mapping of one pattern upon another. Indeed, we and others (Perlman et al., 2001) have attempted to apply such algorithms to FSM data with the hope that a window-based tracking would allow us to circumvent some of the difficulties mentioned for particle-based methods. The result of such an analysis is shown in Fig. 8 where a speckle flow field has been recovered for the same movie as the one analyzed in Fig. 4. The weaknesses of this kind of analysis are evident: The window-based tracker fails; i), in areas where the number of speckles per window changes dramatically (i.e., with strong polymer turnover); and ii), where speckle trajectories are antiparallel, crisscross, or converge. For the F-actin meshwork displayed in Fig. 8, case i occurs at the leading edge (zone 1), where polymerization causes a constant appearance of new speckles. Case ii occurs in areas of meshwork contraction, yielding convergent (zone 2) or antiparallel (zone 3) speckle flow. Similar problems were encountered when applying such a tracker to the mitotic spindle data, where the antiparallel flow of speckles made a reliable tracking of the microtubule flux impossible (data not shown). We conclude from these comparative experiments that only particle-based methods can cope with the generally complex conditions of FSM data, and that the resolution necessary for relevant biological findings, e.g., the examination of cytoskeleton contraction, requires tracking at the level of single speckles.

FIGURE 8.

F-actin flow as recovered by a window-based tracker. Where recovered, the flow agrees well in speed and direction with the flow field recovered by our new tracker (cf. Fig. 4 B). However, the flow cannot be recovered in some parts of the cell, and no information at the single speckle level is available. See text for a more detailed comparison of the two methods, and the specific sources of failure in the zones 1–3.

Single speckle tracking can reveal local polymer events and delivers extensive data for statistical analysis of cytoskeletal events

A key feature of the solution we have presented in this work is that the displacements of individual speckles are accessible. This allowed us to validate the software on real data by visual inspection and hand tracking, and to perform statistical analyses at the single speckle level. In particular, we plan to extend the current framework to compute full trajectories to combine it with the kinetic analysis by Ponti et al. (2003). We will then be able to quantify depolymerization and polymerization activities that occur concurrently with flow, a project impossible to envision with a window-based tracking.

Another interesting element of a single speckle tracker is that we can determine whether a speckle population is homogeneous or heterogeneous for a property like velocity. In that way, the heterogeneity of the corresponding cytoskeletal structures becomes accessible. In general, with this novel tracker, each speckle can now be considered a local reporter of polymer movement.

The new speckle tracker overcomes the limitations of previous kymograph analyses

The method used until now to extract some quantitative flow information from FSM data was the kymograph analysis (Kapoor and Mitchison, 2001; Salmon et al., 2002; Waterman-Storer, 2002; Waterman-Storer et al., 1998). In a kymograph, successive images of the same thin rectangular image region, chosen with its long axis parallel to the average flow direction, are pasted side by side. The result of this operation displays diagonal bright streaks, whose slopes relate to the speed of the speckle flow (see Fig. 4 A). The nature of this relationship, however, is unambiguous only for simple cases. The component of the velocity perpendicular to the slice causes speckles to appear and disappear from the kymograph and also leads to underestimated speckle velocities. Nevertheless, when the amplitude of Brownian motion is limited and when the flow is coherent along the kymograph axis, such analysis and our tracking approach deliver identical results (see Fig. 4 A). Kymographs have further limits, however. For example, a kymograph cannot distinguish between a laminar convergence region and a pole, although the real nature of these flows is immediately visible in the complete mapping as shown in Fig. 4 B (C and P regions, respectively).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.