Bacterial Flagellar Microhydrodynamics: Laminar Flow over Complex Flagellar Filaments, Analog Archimedean Screws and Cylinders, and Its Perturbations

Abstract

The flagellar filament, the bacterial organelle of motility, is the smallest rotary propeller known. It consists of 1), a basal body (part of which is the proton driven rotary motor), 2), a hook (universal joint—allowing for off-axial transmission of rotary motion), and 3), a filament (propeller—a long, rigid, supercoiled helical assembly allowing for the conversion of rotary motion into linear thrust). Helically perturbed (so-called “complex”) filaments have a coarse surface composed of deep grooves and ridges following the three-start helical lines. These surface structures, reminiscent of a turbine or Archimedean screw, originate from symmetry reduction along the six-start helical lines due to dimerization of the flagellin monomers from which the filament self assembles. Using high-resolution electron microscopy and helical image reconstruction methods, we calculated three-dimensional density maps of the complex filament of Rhizobium lupini H13-3 and determined its surface pattern and boundaries. The helical symmetry of the filament allows viewing it as a stack of identical slices spaced axially and rotated by constant increments. Here we use the closed outlines of these slices to explore, in two dimensions, the hydrodynamic effect of the turbine-like boundaries of the flagellar filament. In particular, we try to determine if, and under what conditions, transitions from laminar to turbulent flow (or perturbations of the laminar flow) may occur on or near the surface of the bacterial propeller. To address these questions, we apply the boundary element method in a manner allowing the handling of convoluted boundaries. We tested the method on several simple, well-characterized cylindrical structures before applying it to real, highly convoluted biological surfaces and to simplified mechanical analogs. Our results indicate that under extreme structural and functional conditions, and at low Reynolds numbers, a deviation from laminar flow might occur on the flagellar surface. These transitions, and the conditions enabling them, may affect flagellar polymorphism and the formation and dispersion of flagellar bundles—factors important in the chemotactic response.

INTRODUCTION

Bacteria are the only cells known to swim using rotating propellers. The flagellum, the bacterial organelle of motility, consists of 1), a rotary motor largely embedded in the cell envelope and driven by a proton or sodium ion gradient generated across the cell membrane, 2), a relatively flexible, curved, short hook functioning as a universal coupler (or universal joint) enabling the transmission of rotary motion in directions off axial to the motor's shaft, and 3), a rigid, superhelical filament that functions as a propeller, i.e., converting the rotary motion of the motor into linear thrust (DePamphilis and Adler, 1971a,b; Berg and Anderson, 1973; Silverman and Simon, 1974). The hook and the filament are self-assembling helical polymers constructed from monomers of the protein flagellin (Asakura, 1970).

The ability of the monomers to coexist in two stable and switchable conformations and the initial helical symmetry of the straight polymer allow for filament polymorphism (for reviews, see Asakura (1970), Calladine (1983), and Kamiya et al. (1982); for a more recent view, see Coombs et al. (2002)), i.e., to supercoil reversibly into a variety of helical forms with changing amplitude, wavelength, and helical sense. These dynamic helical parameters may affect the overall hydrodynamic properties of the propeller, allowing it to adapt to changing environmental conditions (e.g., viscosity, flow, and mechanical stress). The hydrodynamics of rotating propellers in the form of smooth, rigid, corkscrew-like tubes or lines is well established (see, e.g., Berg (1993), Bray (2001), Brennen and Winet (1977), Holwill and Burge (1963), Lighthill (1976), and Schreiner (1971)). One would assume that, given the small dimensions (∼1–2 × 10⁻⁴ cm) and, consequently, low Reynolds numbers of bacteria (10⁻⁴–10⁻⁵), the flow associated with them is completely laminar (Purcell, 1977, 1997).

Although being the largest and most diverse phylogenetic group, eubacteria have only two types of flagellar filaments (propellers): “plain” and “complex” (see Schmitt et al., 1974a,b). The “complex” filaments are structurally perturbed forms of the “plain” ones. The perturbation is a result of symmetry reduction due to flagellin dimerization. The reduction of symmetry occurs along the right-handed six-start helical lines (resulting in a helical perturbation (Trachtenberg et al., 1986)) or along the left-handed five-start helical lines (resulting in a nonhelical perturbation (Trachtenberg et al., 1998)). (The six-, five-, and three-start families mentioned can be viewed, at least at low resolution, as six-, five-, and three-stranded helical bundles or densities). Only two bacterial species are known to have helically perturbed filaments—Rhizobium and Pseudomonas (Schmitt et al., 1974a,b). We have been studying the three-dimensional molecular structure (Trachtenberg et al., 1986, 1987, 1998; Cohen-Krausz and Trachtenberg, 1998; 2003a,b) and the physical properties (Trachtenberg and Hammel, 1992) of the complex bacterial propellers using high-resolution electron microscopy and image reconstruction techniques. These studies resulted in detailed density maps whose surface patterns are of particular interest here.

Helically perturbed (“complex”) filaments have a rather coarse surface with deep grooves and ridges along the right-handed three-start helical lines, reminiscent of an Archimedean screw or turbine. The concomitant propelling function of these organelles and their unique hydrodynamic shape is intriguing. Here, we attempt to study the hydrodynamics of bacterial motility at the level of molecular dimensions. Rather than treating the helical propeller in its entirety as a smooth, featureless tube (or helical line), we explore whether the turbine-like surface pattern of the “complex” filament might make a potential contribution to the propeller's hydrodynamics. We do so on a local scale, i.e., not on the entire superhelical filament, but on a straight segment or, rather, on a cross section of it (see below). In viscous, gel-like environments (e.g., Trachtenberg, 1986) bacteria can bore their way through the medium. An overall screw-like shape is helpful (see Gilad et al. (2002) and references therein). In fluid environments of low viscosity, a modified surface pattern would also help and the deviation from laminar flow might be of importance. The deviation from pure laminar flow, to any extent and even only under extreme conditions, may initiate a disturbance leading to a flagellar polymorphic switch and effect flagellar bundle formation and dispersion—a key element in controlling the direction of swimming and the chemotactic response (Larsen et al., 1974). It is sufficient to initiate a local perturbation in flow at the tip of the filament. The perturbation, or, rather, its structural effect, may, then, propagate along the filament or the flagellar bundle (see Macnab and Ornston, 1977, for examples of polymorphic transitions propagating from and to the cell proximal end of the filament).

Here we use the boundary element method (BEM), which we extend and refine to handle complex surfaces (see below) beyond what has been previously applied to studies on smooth tubular flagella. In particular we explore whether the unique, turbine-like, coarse and convoluted surface structure of the “complex” bacterial propeller affects its microhydrodynamics, i.e., may cause deviation from pure laminar flow, and to what extent.

Due to the helical symmetry of the propeller, all its cross-sectional slices are identical (at a resolution lower than the rise-per-subunit), but rotated and shifted axially by a constant amount. At this stage, we reduce the analysis to two dimensions and apply it to the actual closed contour of single cross-sectional density maps as generated by electron microscopy and helical image reconstruction. For comparison, we apply the method to a smooth cylindrical cross section and to a reduced and simplified mechanical model (Archimedean screw) with helical and dimensional parameters of a flagellar filament. Such a comparison might single out the unique contribution of the different structural components and, in particular, the complex flagellar surface pattern.

The BEM enables to approximate solutions of differential equations, which can be represented as integrals along the boundary (Brebbia, 1984; Powel and Wrobel, 1995; Pozrikidis, 2002). The advantage of such a representation is that it may be readily applied to problems with complex geometries. In our case, we attempt to model the flow using the Stokes equation. Here, the solution may be written as integrals along the boundary and, therefore, the BEM may be easily implemented. Moreover, the BEM has a definite advantage over other methods (e.g., finite difference or spectral methods) in cases where the domain has a convoluted boundary. A similar representation holds for time-dependent problems. However, the BEM becomes limited if we want to include nonlinear effects (i.e., model the flow by the Navier-Stokes equations). For these applications, the use of finite-difference, finite-volume, or finite-element methods, where nonlinear terms are handled more efficiently, is preferred (see Ben-Artzi et al. (2001) for a detailed discussion and applications).

Although this analysis is concerned with and applied to an extreme case of potential biological importance, it might have broad implications on nanotechnological problems.

THEORY AND DATA ANALYSIS

The boundary element method is a numerical technique for solving differential problems by invoking their integral representation, which involves integrals along the boundary of the computational domain. The BEM is an efficient way to handle problems with complicated boundaries, especially in the case where the solution of the differential problem can be constructed only from boundary integrals. We include here some of the essential formulas and refer to Brebbia (1984), Powel and Wrobel (1995), and Pozrikidis (2002) for more details.

The boundary element method

Since the fluid is highly viscous and can be regarded as being in its steady state, the Stokes equation

(1)

serves as an adequate model. Here u is the fluid velocity, p is the pressure field, is the incompressibility condition, and η is the viscosity coefficient. It is known that Eq. 1 has solutions subject to appropriate boundary conditions, typically the no-slip condition on Ω. In the BEM, one expresses the solution in Ω by its values on the boundary. A crucial ingredient of the method is the evaluation of certain combinations of the derivatives of the unknowns at the boundary. To do this, we first prove the following:

Lemma 1

If u and v are incompressible, namely then

(2)

where

is the boundary of Ω, is a surface measure on 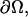and

is the unit normal to the boundary. (See Proof in Appendix 1.)

Now, let us choose three pairs of solutions 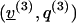that solve, respectively,

(3)

where

and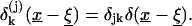

Here

is the Kronecker delta and is the delta function.

The three pairs 1≤j≤3 constitute the fundamental solution.

The construction of such solutions is provided below. They serve for the representation of any solution in terms of its boundary values as follows:

Lemma 2

Let u, p be a solution of Eq. 1. Then for any interior point

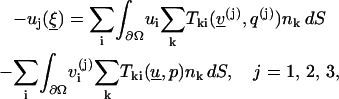(4)

where (See proof in Appendix 2.)

We point out that this Lemma represents the essential feature of the BEM. Note that the boundary elements 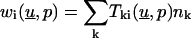depend on the derivatives of the unknown solution on In Lemma 4 below, we show how they are evaluated in terms of the given boundary values of u.

Fundamental solutions

The next step is to construct the fundamental solution, i.e., the three pairs of solutions to Eq. 3. We will actually do that in two dimensions. The three-dimensional case may be treated similarly. We denote here We choose, without loss of generality, j = 1 in Eq. 3 and thus seek solutions of

(5a)

(5b)

Taking the divergence of both sides of Eq. 5a, using Eq. 5b, we have

Let where we require

As is well-known (Roach, 1982), so that

By Eq. 5a, for

we have:

(6a)

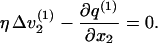(6b)

Since there exists a function ψ such that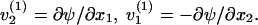

From Eq. 6b, it follows that 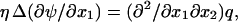which is a condition that must be satisfied by ψ.

Looking for ψ of the form we get

Assuming that is radially symmetric about ξ, 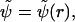we find that

By integration, Integrating once again yields

Now,

so that

We may ignore the constant 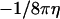and obtain

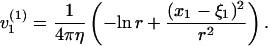To summarize, we have for j = 1, 2,

(7)

(8)

As a corollary we can now compute the terms in Eq. 4.

Lemma 3

For the fundamental solution, the terms 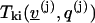may be written in the following form:

(See proof in Appendix 3.)

Following the discussion after Lemma 2, we finally express 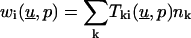in terms of the given boundary values.

Lemma 4

Suppose is smooth, then for

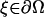
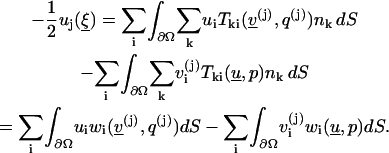(9)

(See proof in Appendix 4.)

TEST PROBLEMS

Here we assess the BEM theory, applied to simple, well-defined objects for which solutions are available:

Test problem 1: Stokes equations for flow over a cylinder with radius R = 10 and v = 1

The boundary conditions are given on

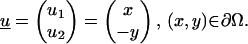In this case the exact solution is known. It is given by 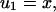in By Eq. 9

(10)

where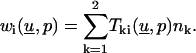

It can be shown that 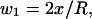therefore, 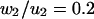whenever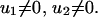

After discretizing by a 24-node polygon, and choosing linear approximations to the functions involved, Eq. 10 reduces to a set of algebraic linear equations.

Table 1 A presents the solutions (columns 4 and 5) at the nodal points (column 2) on the first quarter of the boundary Columns 6 and 7 of Table 1 contain the numerical ratios 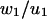and 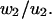These values should be compared with the exact values, both of which are 0.2.

TABLE 1A.

Computed where at selected points on in the first quarter, computed to be compared with the exact values 0.2 and 0.2, respectively

Node	x	y	w1	w2	w1/u1	w2/u2
1	10	0	2.0152	0	.2015	NA
2	9.6593	2.5882	1.9457	−.5183	.2014	.2003
3	8.6603	5	1.7425	−1.0023	.2012	.2005
4	7.0711	7.0711	1.4206	−1.4198	.2009	.2008
5	2.5882	8.6603	1.0030	−1.7413	.2006	.2011
6	2.5882	9.6593	.5186	−1.9444	.2004	.2013

The number of grid points on the boundary is 24.

Table 1 B presents the errors in the computed tractions for various points on the boundary and for various number of grid points. The computed rate of the convergence is defined by where are the errors in the traction for two different grids with meshes Since the boundary is approximated by a polygon, first order convergence is expected.

TABLE 1B.

Computed 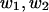with 48 points on the boundary, at the same selected points as in Table 1 A, computed 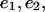to be compared with the exact values, are the rate of convergence when compared to the coarser grid

Node	w1	w2	e1	e2	r1	r2	q1	q2
1	2.000149	−0.000091	1.49(−4)	0.91(−4)	5.63	0.53	8.40	0.5
2	1.931862	−0.518158	1.04(−5)	5.20(−4)	9.25	0.94
3	1.731796	−1.001094	2.55(−4)	1.09(−3)	3.84	1.07	1.76	5.03
4	1.413760	−1.416040	4.54(−4)	1.83(−3)	0.65	0.62
5	0.999445	−1.734516	5.55(−4)	2.47(−3)	0.96	0.85	4.33	1.49
6	0.517242	−1.934964	3.96(−4)	3.11(−3)	1.55	1.20

are the rate of convergence when a grid of 24 points is compared to a grid with 12 points. For example, the computed error in the fourth column means that The rates of convergence are 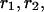when compared to the coarser grid. The computed rate of the convergence is defined by 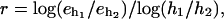where are the errors in the traction for two different grids with meshes Here are the meshes that correspond to 24 and 48 points, respectively. are the rate of convergence when a grid of 24 points is compared to a grid with 12 points.

Test problem 2: uniform flow over a circular cylinder

This is equivalent to a cylinder moving with velocity 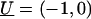relative to the fluid that surrounds it, where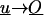as as

The total force, F_i, acting on the cylinder is: where F₁, F₂ are forces in the x, y directions, respectively. We denote D = F₁ the total drag and L = F₂ the total lift on the cylinder.

The drag for low to moderate Reynolds numbers (high to moderate viscosity) is known to behave as 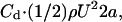where U is the norm of the velocity field at infinity, a is the cylinder's radius, ρ is the density, and is the Reynolds number (Lamb, 1932; Batchelor, 1967).

In Table 2 A, we show the computed drag (column 2) and lift (column 5) with 150 points on the cylinder. In column 2 we represent the expected drag as calculated by Batchelor (1967, page 246), i.e., where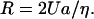

TABLE 2A.

Computed drag for various values of viscosity, compared with Batchelor's; their computed ratio appears in the third column

Viscosity	Computed drag	Drag	Ratio	Computed lift
50	134.3	120.3	1.11	0.018
75	184.8	176.5	1.10	0.011
80	185.8	176.7	1.05	0.011
90	187.6	194.7	0.96	0.011
100	233.0	215.5	1.09	0.007

The last column contains the computed lift, which should be compared with exact lift—zero.

The ratio between our computed drag and the expected value by Batchelor (1967) is presented in column 4 and is shown be around 1. The computed lift is shown in column 5, and is shown to be around zero—its expected value.

Table 2 B presents the errors in the computed tractions for various values of viscosity and for various number of grid points. The computed rate of the convergence is defined by 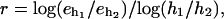where are the errors in the traction for two different grids with meshes The computed rate of convergence ranges from 1.05 to 17.5, where first order accuracy is expected.

TABLE 2B.

Computed drag error and rates of convergence for various number of grid points on the boundary (n = 75, 100, 125, and 150) for different values of viscosity = 80, 90, and 100

Viscosity	Batchelor's drag	Error_75	Rate	Error_100	Rate	Error_125	Rate	Error_150
80	176.7	63.6	1.81	37.7	4.57	13.6	2.70	8.3
90	194.7	81.0	1.35	54.8	2.66	30.3	7.96	7.1
100	215.5	101.4	1.05	74.9	1.81	50.0	5.75	17.5

The convergence rate is defined by 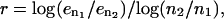where 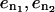are the errors in the drag for two different number of mesh points, on the boundary.

THE BACTERIAL FLAGELLAR FILAMENT

Native and reduced filament structures

The bacterial flagellar filament is a helical, self-assembling polymer of flagellin monomers. The helical symmetry is used to calculate the three-dimensional reconstruction of the filament by Fourier-Bessel methods (DeRosier and Moore, 1970). At a resolution lower than one rise-per-subunit (∼9.7 Å for complex filaments; see Trachtenberg et al. (1986, 1987)), the reconstruction can be viewed as a stack of identical slices, raised and rotated relative to each other by constant increments (9.7 Å; 132°). Thus, the problems posed here can be treated, stepwise, as two-dimensional (per cross section) and three-dimensional (per stack). For a full account on the three-dimensional structures of complex flagellar filaments, see Trachtenberg et al. (1986, 1987, 1998) and Cohen-Krausz and Trachtenberg (1998, 2003a,b).

Here, we confine our analysis to the two-dimensional case. We compare single cross sections of the actual three-dimensional density maps of Rhizobium to a circular cross section of a cylinder of similar diameter (see “test problems”) and to a cross section through an idealized Archimedean screw of the same helical parameters (see below).

The surface topology of the three-dimensional density map is defined by the outermost contour line. We lowered the contour level so that a closed, continuous line defines the outer surface of the cross section and represents ∼100% of the protein's volume. To reduce the structure to an idealized mechanical analog and simplify it, the internal densities (see Cohen-Krausz and Trachtenberg (1998); Trachtenberg et al. (1987)) were reduced to a solid cylinder. The external three-start, right-handed helical windings were taken as external, continuous, smooth blades protruding from the central shaft with helical dimensions of pitch, off-axial tilt, and radial depth similar to those of Rhizobium. In three dimensions, such a reduced form becomes a three-start Archimedean screw. In cross section it is a symmetrical structure of three blades protruding from a central, solid shaft. The leading and trailing edges of the blades were shaped so as to optimize hydrodynamic performance.

A surface view of a three-dimensional reconstruction of R. lupini is shown in Fig. 1 A. Its mechanical analog is shown next to it in Fig. 1 B. The respective cross sections are shown in Fig. 2, A and B. The corresponding cylinder analyzed would be the solid body from which the Archimedean screw was carved out.

FIGURE 1.

(A) Surface view of a segment from a reconstruction of the flagellar filament of Rhizobium lupini. The three-dimensional density map is displayed at a relatively high contour level (see Fig. 2 A) to demonstrate interior details and connectivities. (B) The simplified, mechanical analog in the form of a right-handed Archimedean screw. The diameter of the structures is ∼200 Å.

FIGURE 2.

Cross sections through the three-dimensional reconstruction of Rhizobium lupini (A) and its mechanical analog (B). The density map of R. lupini is contoured so that it represents 100% of the protein volume and has a continuous outer contour line (the only useful line in our analysis). The corresponding cylindrical cross section is the full circle containing B.

A schematic model depicting a bacterium with one supercoiled flagellum aligned axially is shown in Fig. 3, left. In this case, a point on the filament would follow a circle equal to the diameter of the filament's supercoil. The curved hook may position the filament off axially (Fig. 3, right) such that it precesses. In this case, a point on the filament would follow a conical cross section. The tip of the filament follows a larger circle and, when rotated by the motor at a given frequency, moves at a higher velocity relative to cell proximal points.

FIGURE 3.

Flagellar shape and orientation. (Left) The superhelical filament can coincide with the cell's axis and rotate about it. (Right) The curved hook can reorient the filament off-axially in which case it precesses about a conical surface. The relative circular path of the flagellar tip is indicated for both cases. Note that D = 2L sin α and may increase dramatically with the filament's off-axial tilt. The cell body is depicted as a gray ellipse.

Extreme conditions of flagellar geometry and rotation

An average complex flagellar filament of, e.g., Rhizobium lupini has a pitch, P = 2.28 × 10⁻⁴ cm, a diameter, D = 6 × 10⁻⁵ cm, and a tubular diameter, d = 2 × 10⁻⁶ cm. A typical cell has 2–3 filaments with ∼2–3 helical repeats each and a typical swimming velocity of 5.24 × 10⁻³ cm/s (Trachtenberg et al., 1987).

The length, L, of an average helical repeat is: L = [P²+(πD)²]^1/2 = 2.96 × 10⁻⁴ cm. The supercoiled filament is at its maximal diameter, = 9.42 × 10⁻⁵ cm, when it is tightly coiled, i.e., when P = d. Note that D_max increases as the filament, L, is tilted by an angle α (D = 2L sin α; see Fig. 3, right). At α = 30°, it may increase about fivefold. Such off-axial filament tilts were observed in dark-field images (S. Trachtenberg, unpublished) and in images of fluorescently labeled filaments (Scharf, 2002; Turner et al., 2000) of R. lupini.

Bacterial propellers have been reported to rotate at frequencies, f, up to ∼1700 Hz (∼1 × 10⁵ rpm (McCarter, 2001)). Thus, the velocity, v, of a point on the propeller's surface would be: v = πDf. Under these conditions (L ∼ 10⁻³ cm, α = 30°) the flow over a point on the surface at the filament's end would be ∼5.92 cm/s. For comparison, the velocity, v, of a point on an axial filament of typical parameters (D = 6 × 10⁻⁵ cm, f = 100 Hz) would be ∼1.9 × 10⁻² cm/s.

The fluid environment in which the propeller rotates is defined by its density, ρ, and viscosity, η. Here we use, for simplicity, the values for water at 37°C, which are very similar to those of the dilute broth in which bacteria are cultured: ρ = 0.99299 gr./cm³ and η = 6.915 × 10⁻³ gr./cm × s. The Reynolds number, Re, under these conditions would be: Re = (Dρv)/η.

Under these conditions, the Reynolds number would be ∼0.051. At a tilt of ∼30°, Re might reach ∼0.26. For comparison, Re of a typical filament (see above) is ∼1.6 × 10⁻⁴, indicating the extremity of the case we analyze.

Laminar and turbulent flow over flagellar surfaces

We now apply the BEM method, as described and tested in previous sections, to cross sections of idealized and actual flagellar and circular boundaries. The most crucial factor (ignoring, for the moment, the convolution and complexity of the boundary) determining the transition from laminar to turbulent flow is the Reynolds number (composed of D, v, ρ, and η). In this regard, the parameters we can vary in our model (of fixed viscosity, density, and temperature) are the propeller's frequency of rotation, off-axial inclination, and supercoiled diameter. These parameters determine, actually, the relative velocity of the incompressible fluid over the boundary. Given the realistic combinations of dimensions, velocities, and viscosities involved, the corresponding Reynolds numbers are in the order of ∼0.05–0.25.

What we show below are a series of cross-sectional, scaled maps for each of the three structures studied (cylinder, Archimedean screw, and complex flagellar filament). Each panel corresponds to a given Reynolds number. The fluid flows over each boundary from left to right and is indicated with vectors whose direction and magnitude indicate local direction and velocity of flow. The boundary is sampled at 24 boundary points for a cylinder, 144 points for the Archimedean screw, and 410 points for the flagellar filament. The arrows are layered concentrically at radial intervals of 10 units, i.e., 2 × 10⁻⁶ cm, indicating the behavior of the flow at various distances from the boundary. For clarity, normalization of vectors was carried out for the Archimedean screw and flagellar filament.

The flow over a straight cylinder

The first case we test is a circular cross section through a straight, smooth cylinder equal in diameter to a flagellar filament. The flow regimes at Reynolds numbers, Re = 0.2, 1, 10, and 100 are shown. The flow is laminar under all conditions (Fig. 4). See also “test problems”.

FIGURE 4.

Flow patterns over a smooth cylinder (presented as a circular cross section) at Reynolds numbers Re = 0.2, 1, 10, and 100. The flow is from left to right. The vectors indicate scaled speed and direction of flow. Three vector layers, spaced 10 units apart, i.e., around 2 × 10⁻⁶ cm, are shown. The x, y axes are in nondimensional units. Note that the flow is laminar throughout the entire range.

The flow over an idealized Archimedean screw

The flow over an idealized Archimedean screw, having the helical parameters of R. lupine, is shown in Fig. 5. A complete laminar flow is seen at Re = 0.01.Very slight disturbances in flow can be detected at Re = 0.05. The disturbances become noticeable at Re = 0.3–0.5.

FIGURE 5.

Flow patterns over an idealized, three-start, right-handed Archimedean screw having helical parameters identical to those of the complex filament of Rhizobium lupini. The flow is sampled at Reynolds numbers Re = 0.01, 0.05, 0.3, 0.5, 1, and 10. The flow is completely laminar until Re = 0.05. Slight turbulence is detected at Re = 0.3 near the leading edges of the blades; it becomes noticeable beyond Re = 0.5. The vectors are normalized for clarity.

The flow over the filament of R. lupini

The filament of R. lupini, having the same dimensions and proportions as the idealized screw and smooth cylinder, is presented in the same manner for Reynolds numbers Re = 0.01, 0.015, 0.2, 1, and 10 (Fig. 6). At Re = 0.01, the flow is completely laminar as suggested from all vectors being parallel in all layers presented. Deviation from laminar flow is first detected at Re = 0.015. A reversal in flow can be detected in part of the structure, which is changed again at Re = 0.02 with an increase in turbulence from there on.

FIGURE 6.

Flow over the flagellar surface of Rhizobium lupini sampled at Reynolds numbers Re = 0.01, 0.015, 0.2, 1, and 10. The flow is completely laminar at Re = 0.01. First signs of turbulence are detected at Re = 0.015. The turbulence occurs at the leading edges of the outer windings as in the Archimedean screw. The vectors are normalized for clarity.

It is apparent from the data shown that the deviation from laminar flow differs between the structures analyzed. Within the tested range, the flow over a smooth cylinder remains laminar throughout. Fluctuations around the smooth Archimedean screw are detected at higher Reynolds numbers. The interesting finding is that in the flagellar structure, the initiation of turbulence occurs within the Reynolds number regime applicable to realistic, although extreme, flagellar environments and motility conditions. Since the only difference between the structures tested is the degree of surface complexity, we can only assume that this is the crucial factor in initiating the earlier transitions from laminar to turbulent flow. The easiest way to increase the Reynolds number, the crucial factor in determining the nature of flow over the surface, is to control the extent of the precession of the filament and, therefore, the flow velocity at its tip. The initiation of a disturbance at the filament's tip will probably propagate toward the cell proximal end as is often seen in high-intensity dark-field videomicroscopy.

Microhydrodynamic studies on flagellar propulsion

The hydrodynamics of swimming cells has been studied analytically and quantitatively by applying various methods (for review, see e.g., Kim and Karilla (1991). Slender body theory (SBT) (Brennen and Winet, 1977; Hancock, 1953) was applied to cilia and flagella. Myerscough and Swan (1989) and Ramia (1991) applied this method to bacteria with a spiral cell body. Resistive force theory (RFT) has been applied to spermatozoa, propagating planar sinusoidal waves (e.g., Gray and Hancock, 1955) as well as to bacteria with rigid rotating propellers (Chwang and Wu, 1971; Schreiner, 1971). The boundary element method has been applied to the study of microbial swimming (Phan-Thien et al., 1987), the results being in good agreement with both the SBT method (Higdon, 1979) and experimental observations. The BEM proved best when dealing with bulky, nonslender bacteria, such as Spirillum (Phan-Thien et al., 1987), whereas the SBT method failed to agree with experimental observations (Myerscough and Swan, 1989). Ramia et al. (1993) refined and generalized the BEM to the study of bacterial motility.

Here we report on a higher-resolution application of the boundary element method. We analyze the of actual three-dimensional reconstructions of bacterial flagellar filaments (propellers) rather than treating them as smooth, coiled cylinders or their center lines, as has been done in previous applications of the method. We confined our study to the structural and molecular surface (boundary) details and restricted the analysis to the two-dimensional cross sections taking advantage of the helical symmetry of the propeller. We assumed, in our analysis, that the structures are rigid—this is reasonable on a local scale. We also ignored in our maps the potential hydration shell on the protein surface; the thickness of an adsorbed molecular water layer would be only ∼3 Å.

We find that the convoluted surface of the “complex” flagellar filament is, under identical conditions, more effective in causing a transition from laminar to turbulent flow than smooth cylinders or analog Archimedean screws of similar dimensions.

The initiation of turbulence at extreme conditions of flagellar function, orientation, and structure suggests its potential involvement in bundle formation and dispersion, switching of helical sense, and polymorphic transitions.

Complex filaments are believed to be an adaptation to motility in highly viscous environments. The thick and dense mucilage layers that these bacteria have to swim across to infect cells are highly structured. Under these circumstances, a rigid filament with a screw-like surface might be helpful. The outer windings seem to provide both the extra rigidity needed for motility in structured media and better propulsion in low viscosity media.

Although this high-resolution, surface-pattern-dependent flow analysis was applied to an extremely small structure at an extreme functional state (and simulated translationally rather than rotationally), the sensitivity of the method points toward its potential in analyzing larger structures in the nanotechnology scale domain.

APPENDIX 1: PROOF OF LEMMA 1

Proof

Denote by I the left-hand side of Eq. 2. We clearly have, since

which can be rewritten as

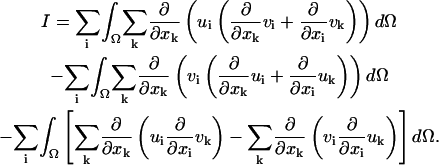Applying the divergence theorem to the first and second integrals, we get,

The two last integrals vanish; the third by symmetry and the fourth since

APPENDIX 2: PROOF OF LEMMA 2

Proof

Define

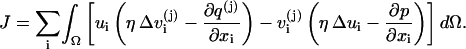By Eqs. 1 and 3, and by the incompressibility condition

On the other hand, by Lemma 1 and the divergence theorem,

which is precisely the right-hand side of Eq. 4.

APPENDIX 3: PROOF OF LEMMA 3

Proof

Applying Eqs. 7 and 8 to the definition of we have

APPENDIX 4: PROOF OF LEMMA 4

Proof

When the functions given in Lemma 3, seem to be singular when 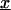approaches 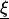in ∂Ω. However, since n_k are the components of the normal, it is clear that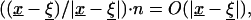 (since approaches the tangent at ). In particular, multiplying by we get and since we see that is continuous even as and the integrals on the right-hand side of Eq. 9 are all well defined.

Next, take an interior point and apply Lemma 2 with the constant function and p ≡ 0. Take instead of Ω a (solid) ball K_ɛ centered at We get, by Eq. 4,

By symmetry, if we take half of the solid sphere, we obtain −(1/2)δ_ij for the integral.

Now, we repeat the proof of Lemma 2 (in Appendix 2), but replace Ω by Ω\K_ɛ (i.e., we cut out from Ω the part of the ball K_ɛ, centered at 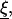which is in Ω). Then J = 0 (since is outside of Ω\K_ɛ) and hence, repeating the calculations of the right-hand side in Appendix 2,

On the part ∂K_ɛ the normal is directed inside. Inspecting Eq. 8 for 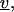we see that the contribution of this part in the second integral is O(ɛ). As approaches a point on the boundary, the part ∂K_ɛ approaches a half-sphere, and since on ∂K_ɛ can be replaced by (with O(ɛ) error) we get for using the above derivation

where the normal 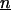is directed inward,

By letting ɛ→0 we obtain Lemma 4.