A Model of Calcium Waves in Pancreatic and Parotid Acinar Cells

Abstract

We construct a mathematical model of Ca²⁺ wave propagation in pancreatic and parotid acinar cells. Ca²⁺ release is via inositol trisphosphate receptors and ryanodine receptors that are distributed heterogeneously through the cell. The apical and basal regions are separated by a region containing the mitochondria. In response to a whole-cell, homogeneous application of inositol trisphosphate (IP₃), the model predicts that 1), at lower concentrations of IP₃, the intracellular waves in pancreatic cells begin in the apical region and are actively propagated across the basal region by Ca²⁺ release through ryanodine receptors; 2), at higher [IP₃], the waves in pancreatic and parotid cells are not true waves but rather apparent waves, formed as the result of sequential activation of inositol trisphosphate receptors in the apical and basal regions; 3), the differences in wave propagation in pancreatic and parotid cells can be explained in part by differences in inositol trisphosphate receptor density; 4), in pancreatic cells, increased Ca²⁺ uptake by the mitochondria is capable of restricting Ca²⁺ responses to the apical region, but that this happens only for a relatively narrow range of [IP₃]; and 5), at higher [IP₃], the apical and basal regions of the cell act as coupled Ca²⁺ oscillators, with the basal region partially entrained to the apical region.

INTRODUCTION

Exocrine cells are highly ordered epithelial cells which exhibit functional and morphological polarity. This specialization allows distinct physiological processes to occur in specific regions of the cell. Many of these processes are initiated by an increase in cytosolic calcium. In response to agonist stimulation, resulting in the generation of inositol trisphosphate (IP₃), exocrine cells from the pancreas or parotid display a rich variety of calcium responses. Calcium waves that are initiated in the apical region can spread across the entire cell to form a global intracellular wave, or remain isolated to the apical region (Thorn et al., 1993a,b). Calcium oscillations in the apical and basal regions can take a wide variety of shapes, from baseline spikes, to sinusoidal oscillations upon a raised baseline (Yule et al., 1991), and can form periodic global waves (Nathanson et al., 1992; Kasai, 1995; Yule et al., 1996). To match the wide variety of observed responses, acinar cells express a variety of calcium handling mechanisms, including inositol trisphosphate receptors (IPR), ryanodine receptors (RyR), and mitochondria. Furthermore, these release mechanisms have well-characterized spatial distributions, which are most likely related to the spatial characteristics of the various kinds of Ca²⁺ signals observed (Kasai et al., 1993; Petersen, 1995; Xu et al., 1996; Petersen et al., 1999; Straub et al., 2000).

Despite a great deal of experimental data, the exact mechanisms underlying Ca²⁺ wave propagation in a single acinar cell remain unclear, and the interactions between IPR and RyR in wave propagation are not well understood. Whole-cell application of agonists such as acetylcholine cause different types of waves, depending on the agonist concentration. At threshold agonist concentrations the Ca²⁺ responses can be confined to the apical region, whereas at higher physiological agonist concentrations the apical response appears to be propagated throughout the cell. Local uncaging of Ca²⁺ (in either the apical or basal regions) can also stimulate waves that travel from the apical to the basal region (Ashby et al., 2002). Thus, homogeneous stimulation results in heterogeneous wave responses, whereas localized stimulation can cause waves that propagate in a nonintuitive direction. Although some of the basic mechanisms appear clear (for instance, a higher concentration of IPR in the apical region appears to be the reason for the apical region acting as a trigger zone), there are still a number of unanswered questions. In particular, it is not yet clear how waves propagate across the basal region. Are they propagated by the diffusion of Ca²⁺ between release sites (an active mechanism) and are those release sites IPR or RyR? Or do basal waves result rather from the inherent timing difference between the apical and basal responses, being only weakly modulated by Ca²⁺ diffusion (a kinematic mechanism)? Based on experimental work we have previously suggested (Giovannucci et al., 2002) that, depending on the exact circumstances, both mechanisms can operate. However, as yet there has been no detailed quantitative investigation of whether both wave mechanisms are actually present, how they interact, and how their relative importance depends on agonist concentration.

Our goal is to develop a model that can help us understand the variety of Ca²⁺ waves in pancreatic and parotid acinar cells. In particular, we aim to investigate the interaction of active and kinematic wave mechanisms, and their relative importance. To do this we determine the crucial model parameters by fitting to previously published experimental data (Giovannucci et al., 2002) and then perform a theoretical investigation of the wave properties of the model with those parameters. Because of the complexity of acinar cells, our model incorporates detailed models of both RyR and IPR as well as a simplified model of mitochondrial uptake, and, importantly, is spatially heterogeneous to reflect the functional and morphological polarity of these cell types. Ultimately we wish to understand intercellular wave propagation in an entire acinus, but we begin with a model in one spatial dimension to study the complex calcium dynamics in a simpler setting.

MODEL CONSTRUCTION

The model is complex, and requires considerable explanation and justification. We shall approach this in the following steps:

1. The details of the IPR model (Sneyd and Dufour, 2002).

2. The details of the RyR model (Keizer and Levine, 1996).

3. How the two models are combined into a whole-cell model.

4. The heterogeneous spatial distribution of the receptor types and the spatial model.

5. Mitochondrial transport (Colegrove et al., 2000).

The IPR model

Sneyd and Dufour (2002) constructed a detailed model of the type-2 IPR, and determined the model parameters by fitting to experimental data from hepatocytes. This IPR model has a number of advantages over previous models. Most importantly, it incorporates transitions between receptor states having rates that are saturating functions of [Ca²⁺], so that, for example, binding of Ca²⁺ to the IPR does not happen too quickly at high [Ca²⁺].

Although it is known that pancreatic and parotid cells contain both type-II and type-III IPR (Nathanson et al., 1994; Wojcikiewicz, 1995; Thorn, 1996; Yule et al., 1997), it is probable that the use of a type-II IPR model only will not have a significant impact on our results. In simulations of this type, the steady-state behavior of the IPR is much less important than the dynamic response of the IPR to changing [Ca²⁺] and [IP₃]. (Of course, the steady-state receptor properties are important in determining the resting Ca²⁺ levels in the cytoplasm and the ER, which will in turn have an effect on the dynamic responses, but such effects are indirect.) Hence, although there appear to be significant differences in steady-state behavior between the IPR subtypes, it is the sequential activation and inactivation of the receptor that plays a greater role in the control of oscillatory and wave behavior (LeBeau et al., 1999; Sneyd and Dufour, 2002). This is a common feature of a wide range of physiological models, many of which are discussed in detail in Keener and Sneyd (1998). There is little available data on the dynamic responses of the different IPR subtypes, and even less on the functional importance of any such differences, but what data there are (Finch et al., 1991; Dufour et al., 1997; Marchant and Taylor, 1997) indicate that the dynamic responses of the IPR subtypes are similar.

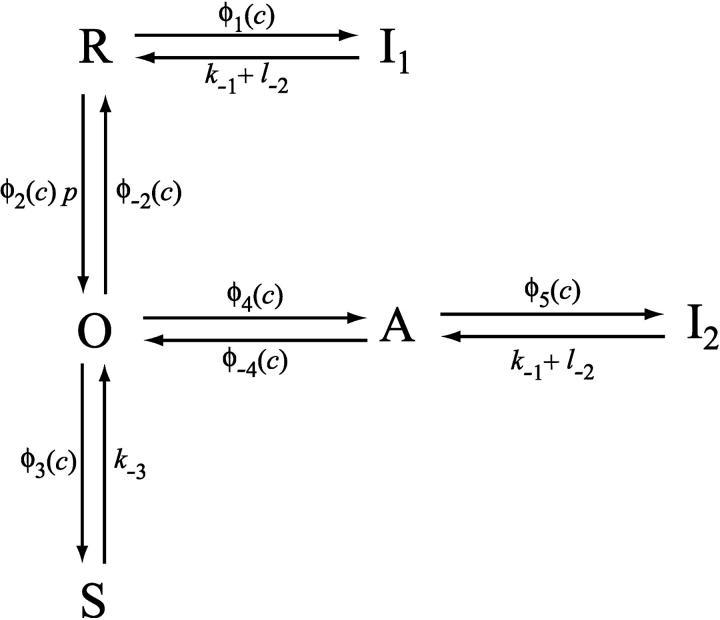
For completeness, we summarize the IPR model here. More complete details may be found in Sneyd and Dufour (2002). We assume that the IPR can exist in one of six states: R (resting state), O (open), S (shut), A (activated), and I₁ and I₂ (inactivated states). Movement between the receptor states is sequential, with rates that are saturating functions of [Ca²⁺] (Fig. 1). Each of the receptor states was mandated by experimental data, and parameter values were obtained by fitting to experimental data (Sneyd and Dufour, 2002). In construction, this model is similar to previous models of DeYoung and Keizer (1992), Othmer and Tang (1993), and LeBeau et al. (1999), with the major difference being that the parameters were determined by fitting to dynamic IPR data. Thus, although we cannot be sure that the structure of the model is a faithful reflection of the actual states of the type-II IPR, we can be reasonably confident that the model responds correctly to changes in [Ca²⁺] and [IP₃].

FIGURE 1.

Diagram of the model of the IPR. Adapted from Sneyd and Dufour (2002).

Let c denote [Ca²⁺], p denote [IP₃], R denote the fraction of receptors in state R, and similarly for the other receptor states. Using mass-action kinetics, we see that the equations for the transitions between the receptor states are

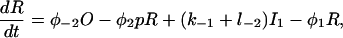(1)

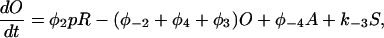(2)

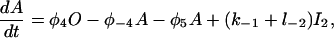(3)

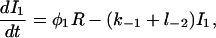(4)

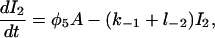(5)

where each φ is a function of c and is given in detail in the Appendix.

We assume the IPR consists of four independent and identical subunits, and allows Ca²⁺ current when all four subunits are in state O, or all four are in state A, or some intermediate combination. Furthermore, we shall assume that the more subunits there are in state A, the greater the open probability of the receptor. With these assumptions, the open probability of the IPR, P_IPR, is most conveniently written as

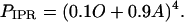(6)

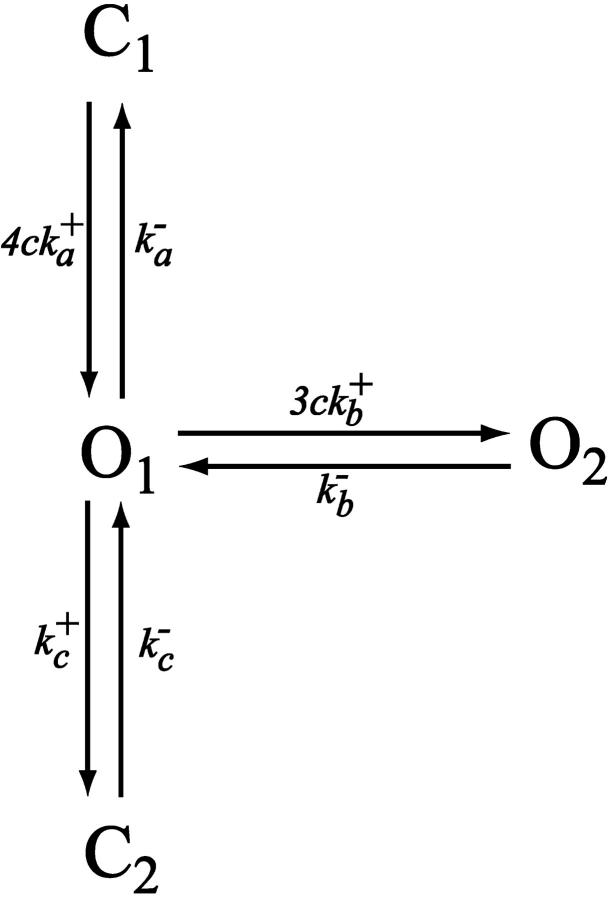
The RyR model

To model the ryanodine receptor we use the model of Keizer and Levine (1996), developed originally for cardiac cells. The model assumes that the RyR can exist in one of four states, two open (O₁ and O₂) and two closed (C₁ and C₂), as illustrated in Fig. 2. The parameters were determined by fitting to the dynamic data of Györke and Fill (1993), and thus the model reproduces the time course of the RyR open probability after step increases in [Ca²⁺]. Assuming that the O₁→C₁ and O₁→O₂ transitions are fast, Keizer and Levine showed that the open probability takes the form

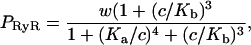(7)

where w is the fraction of RyR not in state C₂, and where 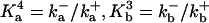and 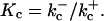The equation for w is

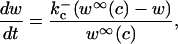(8)

where w^∞(c) is given in the Appendix.

FIGURE 2.

Diagram of the model of the RyR. Adapted from Keizer and Levine (1996).

The whole-cell model

Next we include the action of SERCA pumps and plasma membrane Ca²⁺ ATPases. We model the endoplasmic reticulum (and all pumps and receptors) as continuously distributed through the interior of the cell. In addition we assume that the fluxes of Ca²⁺ through the IPR and RyR, as well as the leak from the ER, are proportional to the difference in [Ca²⁺] between the endoplasmic reticulum and the cytoplasm.

Finally, we include two linear leaks—one from outside the cell into the cytoplasm (J_in), the other from the endoplasmic reticulum into the cytoplasm (J_er). Such leaks are necessary to balance the pump fluxes in the absence of any IPR or RyR fluxes. Thus, if we let c_e denote the concentration of Ca²⁺ in the endoplasmic reticulum, we get

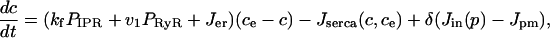(9)

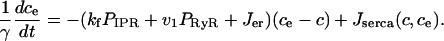(10)

The constant γ is the ratio of the cytoplasmic volume to the ER volume, whereas δ, although not strictly necessary, is a useful parameter inasmuch as it controls the magnitude of the trans-membrane fluxes relative to the trans-ER fluxes, without changing the resting [Ca²⁺].

The plasma membrane calcium pump is modeled by a Hill equation, with a Hill coefficient of 2. This is less than the coefficient of 3 found by Camello et al. (1996), but is in agreement with the value of 1.9 given by Albrecht et al. (2002). Thus,

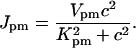(11)

We chose K_pm = 0.425 μM, which is higher than the experimental figure of 0.2 μM from pancreatic acinar cells (Camello et al., 1996), but lower than the figure used by Keizer and Levine (1996). This change in the value of K_pm was necessary to get a reasonable resting cytosolic Ca²⁺ concentration in addition to retaining oscillatory behavior at higher IP₃ concentrations.

The SERCA pump model is slightly more complicated. Experimental evidence indicates that the rate of SERCA pumping is modulated by c_e (Favre et al., 1996; Mogami et al., 1998) and thus we let

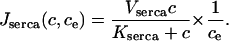(12)

The term 1/c_e is a simplified version of the model discussed in Favre et al. (1996), and ensures that the rate of the SERCA pump increases as c_e decreases. It is valid only when c_e is bounded away from zero, which is always the case in model simulations. The functional form of our model of the SERCA pump is considered in more detail in the Discussion.

The flux J_in must be an increasing function of p, as otherwise the steady-state [Ca²⁺] is independent of [IP₃], which conflicts with experimental results. This necessity was first recognized theoretically by Dupont and Goldbeter (1993). We do not make any assumption about the mechanism of this increase, whether via the arachidonic acid pathway (Shuttleworth, 1999) or via capacitative entry (Berridge, 1995). We model merely the effect (see Eq. 26 in the Appendix).

The spatial model

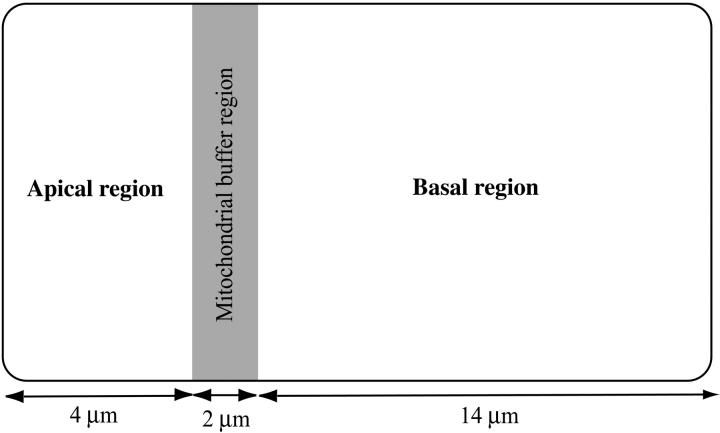
One crucial feature of acinar cells is their spatial polarization. The apical and basal regions of the cell have different densities of IPR and RyR, and (at least in pancreatic acinar cells) are separated by a mitochondrial buffer layer (Tinel et al., 1999; Straub et al., 2000). We build this spatial heterogeneity into our model by assuming spatially heterogeneous IPR and RyR densities.

A schematic diagram of our acinar cell is given in Fig. 3. The cell is assumed to be spatially homogeneous in the y-direction, resulting in an effectively one-dimensional cell. The leftmost 4 μm of the cell (the apical region) is assumed to have different densities of IPR and RyR than the rightmost 14 μm of the cell (the basal region). The IPR and RyR densities chosen for these two regions are determined by fitting to experimental data, as discussed later. Morphological and functional data (Tinel et al., 1999; Straub et al., 2000) indicate that, at least in pancreatic acinar cells, a band of mitochondria around the apical region plays a role in restricting some Ca²⁺ responses to the apical region. We thus include a mitochondrial buffer region in the model, between the apical and basal regions—one-tenth the length of the cell. The mitochondrial buffer region is assumed to contain both mitochondria and RyR.

FIGURE 3.

Schematic diagram of the model of the acinar cell.

The variations in receptor densities are controlled by the parameters k_f (which controls the density of IPR) and v₁ (which controls the density of RyR), which are themselves determined by fitting to experimental data, as described below. In the mitochondrial buffer region k_f is assumed to be zero, while v₁ is fixed (i.e., not determined by the fitting procedure). The exact values are given in Table 1.

TABLE 1.

Parameter values of the model

Pancreatic cells
kf (apical)	0.71 s−1	kf (basal)	0.32 s−1
v1 (apical)	0.098 s−1	v1 (basal)	0.04 s−1
v1 (buffer region)	0.08 s−1	Vmito (buffer region)	100 s−1
Parotid cells
kf (apical)	5.9 s−1	kf (basal)	1.2 s−1
v1 (apical)	0.24 s−1	v1 (basal)	0 s−1
v1 (buffer region)	0.08 s−1	Vmito (buffer region)	100 s−1
Transport parameters
Jer	0.002 s−1	γ	5.405
Vserca	120 (μM)2s−1	Kserca	0.18 μM
Vpm	28 μM s−1	Kpm	0.425 μM
δ	0.1	Dc	20 (μm)2 s−1
IPR parameters
k1	0.64 s−1 (μM)−1	k−1	0.04 s−1
k2	37.4 s−1 (μM)−1	k−2	1.4 s−1
k3	0.11 s−1 (μM)−1	k−3	29.8 s−1
k4	4.0 s−1 (μM)−1	k−4	0.54 s−1
L1	0.12 μM	l2	1.7 s−1
L3	0.025 μM	l4	1.7 (μM)−1 s−1
L5	54.7 μM	l6	4707 s−1
RyR parameters
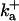
	1500 (μM)4 s−1		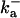28.8 s−1
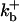
	1500 (μM)3s−1		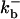385.9 s−1
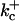
	1.75 s−1		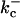0.1 s−1

The IPR parameters were determined by fitting to model data from type-II hepatocyte IPR (Sneyd and Dufour, 2002). The RyR parameters were determined by fitting to model data from cardiac cells (Keizer and Levine, 1996). The transport parameters came from a variety of previous modeling work, as discussed in the text. The remaining parameters were determined by fitting to experimental data from pancreatic and parotid cells (Fig. 4).

Finally, Ca²⁺ is assumed to diffuse, with a constant diffusion coefficient of D_c. We thus ignore the complications introduced by mobile calcium buffers.

Mitochondrial transport

We model the mitochondria simply as providing an additional Ca²⁺ uptake term, using the model of Colegrove et al. (2000). We assume that mitochondrial Ca²⁺ uptake, J_mito, is given by

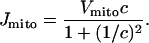(13)

The rate of mitochondrial uptake, V_mito, is assumed to be zero everywhere except in the buffer region. Although the form of this function is the same as that derived by Colegrove et al. (2000), the parameter values are altered, so that the mitochondria provide a Ca²⁺ buffering effect at physiological concentrations in pancreatic acinar cells. The parameters derived by Colegrove et al. (for bullfrog sympathetic neurons) give essentially zero Ca²⁺ uptake by the mitochondria in the present model.

IP₃ dynamics

One goal is to understand experimental results obtained by photoreleasing IP₃ simultaneously over the entire cell (Giovannucci et al., 2002). Under such conditions the diffusion of IP₃ will be minimized. We mimic this by setting [IP₃] to be constant across the cell, with an initial value of p₀ and decreasing with a time constant of 1/0.8 s. Thus,

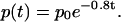(14)

The initial value, p₀, controls the amount of photoreleased IP₃.

Calcium buffering

Calcium buffering is included implicitly in the model (in both the cytoplasm and the ER) by treating all fluxes as effective fluxes, and using a small diffusion coefficient for Ca²⁺. This is equivalent to assuming that all the calcium buffers are fast, immobile, and unsaturated (Wagner and Keizer, 1994; Sneyd et al., 1998; Keener and Sneyd, 1998). There has been little work done on the model equations for the transport of Ca²⁺ by mobile buffers. It is known that inclusion of mobile buffers will not eliminate an existing wave (Sneyd et al., 1998), and can cause the appearance of two stable waves in some cases (Slepchenko et al., 2000) but little else is known about their effects on qualitative wave properties. Some recent work has indicated that buffer mobility has only a limited effect on the wave properties (Sneyd and Tsaneva-Atanasova, Lecture Notes in Physics, in press), and thus it is likely that inclusion of mobile buffers would have no qualitative effects on the results here. However, there is still only very limited theoretical understanding of the effects of mobile buffers on the wave properties of a model, and further work is required on this question.

Detailed models of calcium buffering have been studied by Neher and Augustine (1992), Nowycky and Pinter (1993), Jafri and Keizer (1995), and Sala and Hernández-Cruz (1990). Nowycky and Pinter, in particular, did a highly detailed study of the effects of various types of calcium buffers. However, although the effects of Ca²⁺ buffering are relatively well understood, the validity of the rapid buffering approximation in any particular situation is less well understood. Removing the assumption of rapid buffering from our model will affect the wave properties (Kupferman et al., 1997) but, over the timescales and speeds we consider here, is unlikely to affect the qualitative results of the model. The finite speed of Ca²⁺ buffering is more important for the fast timescale modeling of Ca²⁺ concentration close to a point source (Smith et al., 1996). Neher (1998) provides an excellent discussion of the benefits and limitations of the rapid buffering approximation.

In addition, the addition of exogeneous Ca²⁺ buffers in the form of fluorescent dyes will affect the Ca²⁺ responses (Neher and Augustine, 1992; Noble and Powell, 1991). We do not take this into account, assuming instead that, although the exact responses will not be a precise reflection of cellular behavior, the apical and basal regions retain the same relative responses, and thus our conclusions still hold.

Summary of the model

For convenience, the model equations are collected in the Appendix, and the complete list of parameter values is given in Table 1.

Numerical simulations

The model equations were solved using a partially implicit backward Euler scheme in one spatial dimension, with no-flux boundary conditions. Before the application of IP₃ all the model variables were set to the steady state obtained for p = 0. It is important to note that the resting Ca²⁺ concentrations in the ER and the cytoplasm will be spatially heterogeneous, even when p = 0. Firstly, the different RyR densities in the apical and basal regions give different resting leaks from the ER, resulting in different resting ER Ca²⁺ concentrations. Secondly, the increased Ca²⁺ uptake in the buffer region will cause a lower resting cytosolic Ca²⁺ concentration there, with higher Ca²⁺ concentrations in the apical and basal regions. Ca²⁺ diffusion smooths out these differences but cannot entirely eliminate them, leading to a spatially heterogeneous steady state. Hence, the steady state was found by solving the differential equations (for p = 0) until an approximate steady state was reached. This was then used as the starting point for the simulation of IP₃ addition. Although it is important to use the correct steady state as the initial condition for the model, the fact that the resting state is spatially heterogeneous is probably not physiologically significant, or even easily detectable.

The cell was 20-μm length, discretized by 50 grid points. The leftmost 10 gridpoints (i.e., one-fifth of the cell) were considered the apical region, whereas the next five gridpoints were considered the mitochondrial buffer region.

Parameter values

Parameters for the IPR and RyR models were determined by fits to experimental data (Sneyd and Dufour, 2002; Keizer and Levine, 1996), whereas the transport parameters were taken from previous modeling work, as described in the text, and adjusted where necessary to ensure a physiologically plausible steady state. The parameters k_f and v₁ were determined by fitting to the experimental data shown in Fig. 4. A least-squares fitting procedure was used, and fits to the basal and apical data were done separately for each cell type. The parameters shown are at a local minimum of the least-squares objective function, but no exhaustive studies were performed to ensure that a global minimum was found. The parameters k_f and v₁ were not, in general, determined precisely; varying them by 10% (or often more) makes no qualitative change to the model behavior. Finally, the parameter V_mito was set, somewhat arbitrarily, to be 100 s⁻¹. The results were insensitive to changes in V_mito. The parameters are summarized in Table 1.

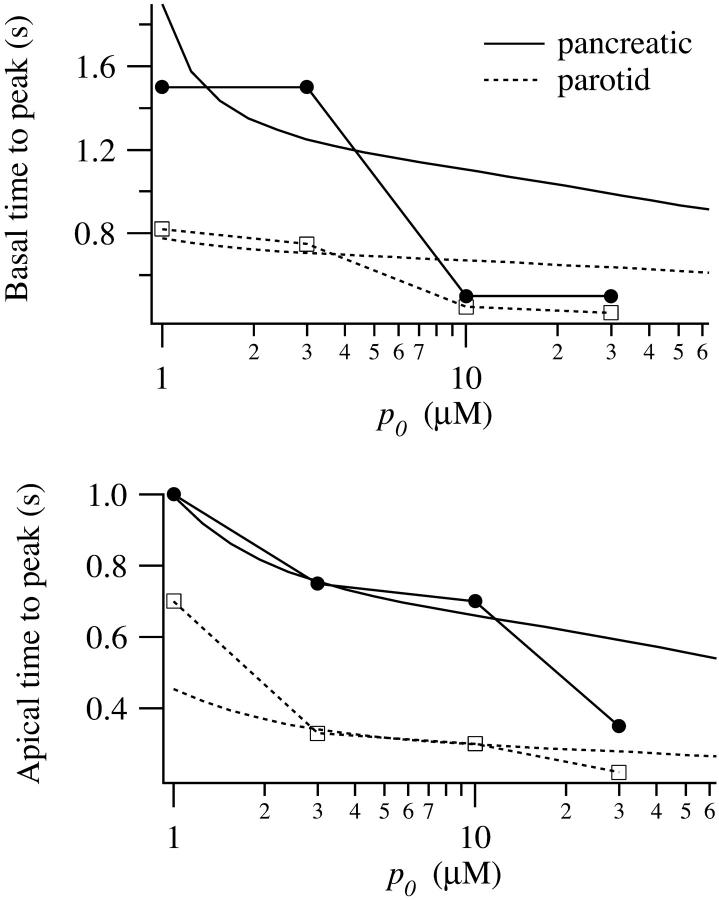
FIGURE 4.

Experimental data (symbols) and model simulations (smooth curves). The solid curves correspond to data and simulations from pancreatic cells; the dotted lines from parotid cells. The experimental method is described in detail in Giovannucci et al. (2002). (Upper panel) Time to the peak of the calcium response in the basal region, measured from the time of the IP₃ release. (Lower panel) Time to peak of the calcium response in the apical region, measured from the time of the IP₃ release.

RESULTS

Parameter values

The results of the fitting procedure are shown in Table 1 and Fig. 4. In both pancreatic and parotid cells the estimated apical densities of IPR and RyR were greater than the estimated basal densities. (Our model cannot be used to infer absolute receptor densities, only relative ones.) Densities of IPR and RyR were mostly greater in parotid cells than in pancreatic cells, with the exception of the basal RyR density. According to our fit the basal RyR density in parotid cells was very small. However, although this was a local minimum of the fit; increasing v₁ (basal) to 0.02 in parotid cells made little visual difference to the fit.

Responses to addition of IP₃

We have previously published data on the speed and amplitude of the intracellular wave as a function of the amount of photoreleased IP₃ (Giovannucci et al., 2002). To collect these data, IP₃ was photoreleased across the whole cell simultaneously and the time to the peak of the Ca²⁺ response was measured in the apical and basal regions. From this the apparent wave speed was calculated.

We simulated these experiments numerically by setting the initial conditions across the whole cell to be those corresponding to p = 0. We then raised p to p₀ over the entire cell instantaneously, and then let p decay to zero with a time constant of 1.25 s (see Eq. 14). Because of their differing concentrations of IPR and RyR, the apical and basal regions responded quite differently to such stimuli.

Results from model simulations are shown in Fig. 4, where they are compared to experimental data (presented in detail in Giovannucci et al., 2002). The time from the IP₃ stimulus to the peak of the Ca²⁺ response in the apical region is a decreasing function of p₀, and is greater for pancreatic cells than for parotid cells. Similarly, the time to the peak Ca²⁺ response in the basal region is greater than in the apical region, and also a decreasing function of p₀. In the apical region the decrease in the time to peak is a reflection of the kinetics of the IPR, which show a decreasing time to peak (in the open probability) with increasing p (Sneyd and Dufour, 2002). In the basal region the time to peak is considerably more complicated, and reflects the wave propagation properties also. No oscillations are observed in these simulations because the IP₃ decays too rapidly.

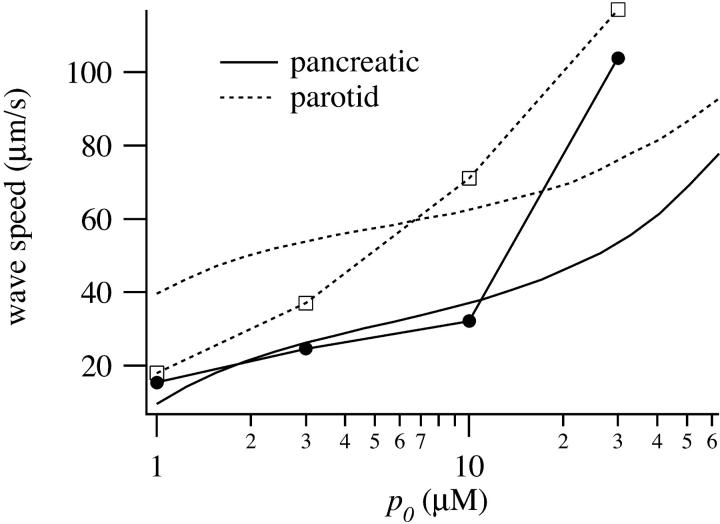
The speed of the wave across the cell is shown in Fig. 5. After an initial relatively flat portion, the wave speed rises steeply with p₀. This is a pronounced feature in both experimental and simulation results from pancreatic cells, but is not so apparent in the data from parotid cells.

FIGURE 5.

Speed of the wave across pancreatic and parotid cells, as a function of magnitude of the IP₃ stimulus. Experimental data (symbols) and model simulations (smooth curves). The solid curves correspond to data and simulations from pancreatic cells; the dotted lines from parotid cells.

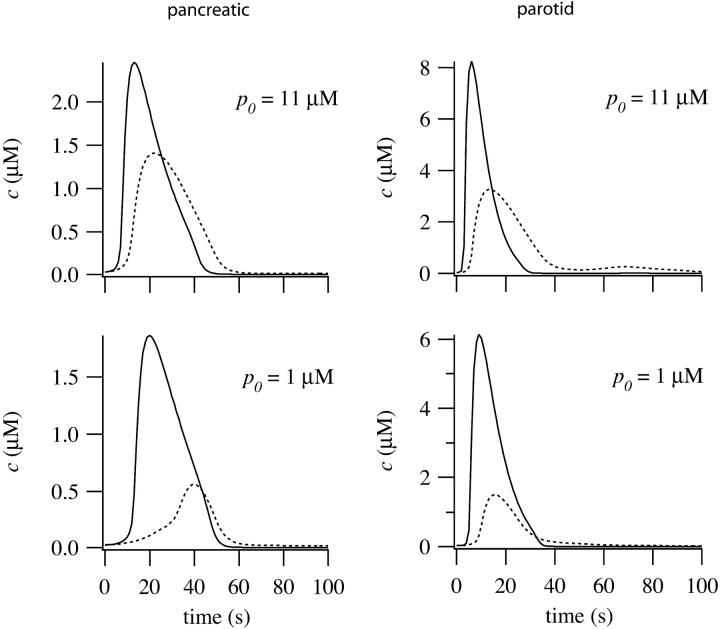
In Fig. 6 we show simulated time courses of c from the apical and basal regions of pancreatic and parotid cells. Due to the lower receptor densities, the peak basal responses are smaller than in the apical region. This is a common feature of experimental data (Kasai et al., 1993; Straub et al., 2000).

FIGURE 6.

Simulated time courses of Ca²⁺ from the apical (smooth curve) and basal (dotted curve) regions of pancreatic and parotid cells, for two different values of p₀.

At low [IP₃] the basal wave in pancreatic cells is initiated by the apical response, and actively propagated by Ca²⁺ release through RyR. This follows from the fact that at low p₀ the wave is eliminated by setting D_c = 0 or by removing RyR from the basal region (computations not shown). In addition, a numerical bifurcation analysis (computations not shown) indicates the existence of traveling wave solutions to the model equations when the basal parameters are used and when p ≈ 1. Hence, the long latency at low p₀ is a result of the time taken for the wave to propagate across the basal region of the pancreatic cell. At higher p₀ the basal wave does not depend on Ca²⁺ diffusion (although it is modulated by it). Both apical and basal regions respond to the IP₃, but the apical region responds more quickly because of its higher IPR density. This difference in response times gives rise to an apparent wave. There are thus two quite different wave regimes in the pancreatic responses. At low p₀ we get an initial apical response transmitted across the cell by active propagation, whereas at high p₀ we get an apparent wave, caused by the time difference in the responses in the apical and basal regions.

In parotid cells the model predicts a low basal RyR density. Thus, parotid cells cannot propagate a basal wave by active Ca²⁺ release through RyR, and so do not exhibit such high times to peak at low [IP₃], or such low wave speeds. Neither do they exhibit the two wave regimes exhibited by pancreatic cells. In parotid cells the waves are always apparent waves, driven by the difference in apical and basal response times, which is driven in turn by the different apical and basal IPR densities.

Temporal dynamics

To understand wave propagation in the model it is necessary first to understand how the model behaves in the absence of Ca²⁺ diffusion. We begin by studying how the model responds to a constant value of p. Because the apical and basal regions have different parameter values we study each region separately, restricting our discussion to pancreatic cells.

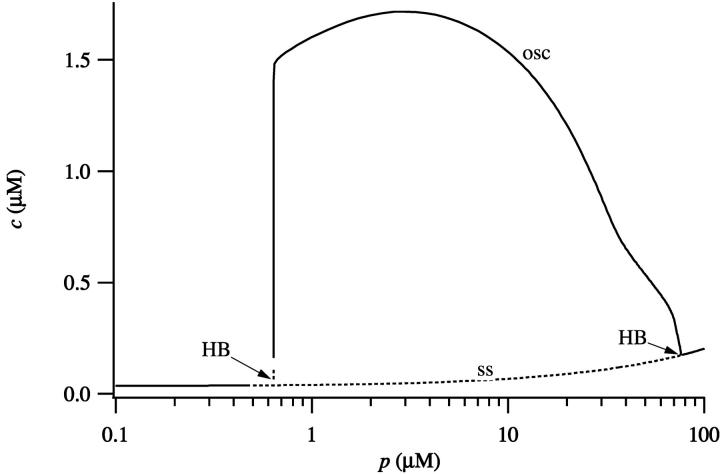
The behavior of the model without diffusion, at different values of p and using the parameters of the pancreatic apical region, is summarized in Fig. 7. As p increases, the steady state loses stability and a branch of stable periodic orbits appears. The periodic orbits disappear at high p, and thus there is an intermediate range of p that supports stable oscillations in c. This behavior is common to many previous models of Ca²⁺ oscillations (Sneyd et al., 1995; Tang et al., 1996; Keener and Sneyd, 1998).

FIGURE 7.

Bifurcation diagram of the model, using the parameters corresponding to the apical region of a pancreatic cell. Dotted lines denote unstable branches and HB denotes a Hopf bifurcation. The curve of steady states is labeled ss; maximum value of c, over an oscillation, is labeled osc.

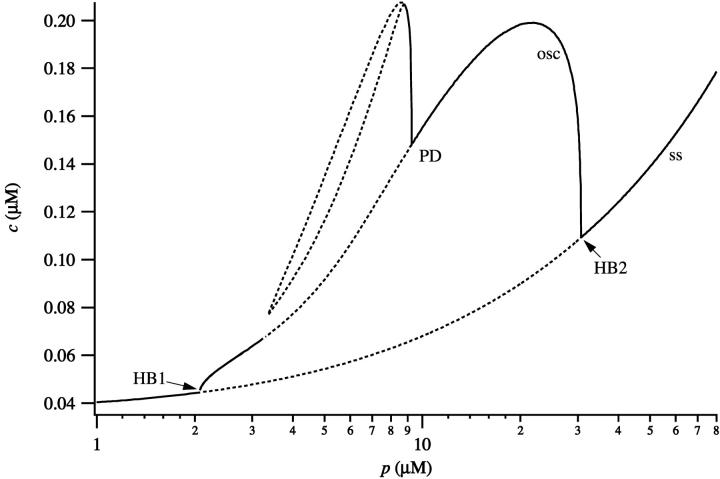
If the basal parameters are used (Fig. 8) the behavior of the model is slightly different. Oscillations now occur for a smaller range of values of p and their amplitude is smaller. In addition, period doubling bifurcations occur, leading to more complicated oscillatory behavior. By comparing Figs. 7 and 8 we see that there is an intermediate range of IP₃ concentrations (∼2 < [IP₃] < 30 μM) such that both the apical and basal regions are oscillatory. However, for [IP₃] approximately in the range 0.6–2 μM, the apical region is oscillatory, but the basal region is not.

FIGURE 8.

Bifurcation diagram of the model, using the parameters corresponding to the basal region of a pancreatic cell. Dotted lines denote unstable branches and HB denotes a Hopf bifurcation. The curve of steady states is labeled ss; maximum value of c, over an oscillation, is labeled osc.

Coupling of the apical and basal regions

If p is held fixed after being raised, c oscillates with a period dependent on the value of p (as shown in Figs. 7 and 8). However, even though p is raised homogeneously across the entire cell, because of the differing receptor densities in the apical and basal regions the oscillations are not spatially homogeneous. Furthermore, the band of mitochondria can affect the propagation of waves between the apical and basal regions.

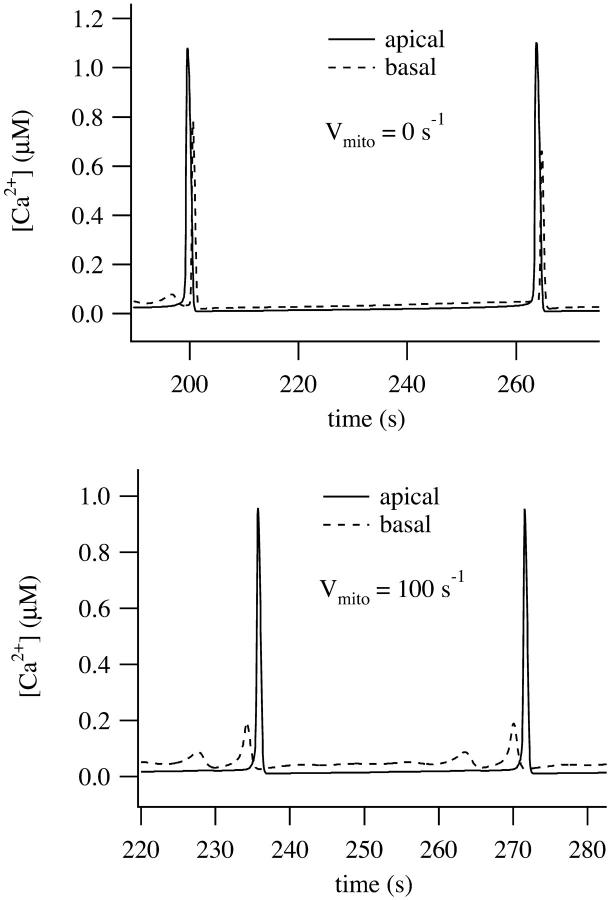
In Fig. 9 we show simulations using the parameters from pancreatic acinar cells. When p is raised to 2 μM in the absence of the mitochondrial buffer region, i.e., with V_mito = 0 (Fig. 9, upper panel), the apical oscillations are transmitted across the basal region in an intracellular wave. The intracellular wave disappears when D_c = 0 or when the RyR are removed, and thus is actively propagated by the diffusion of Ca²⁺ between the RyR release sites (computations not shown). However, when V_mito = 100 (Fig. 9, lower panel), the apical oscillations are not converted to global waves.

FIGURE 9.

Oscillatory responses computed with p = 2 μM. Time traces were taken from two places in the cell, one in the apical region (solid line; x = 2 μm) and the other in the basal region (dashed line; x = 15 μm). (Upper panel) No mitochondria (V_mito = 0). (Lower panel) With mitochondria (V_mito = 100).

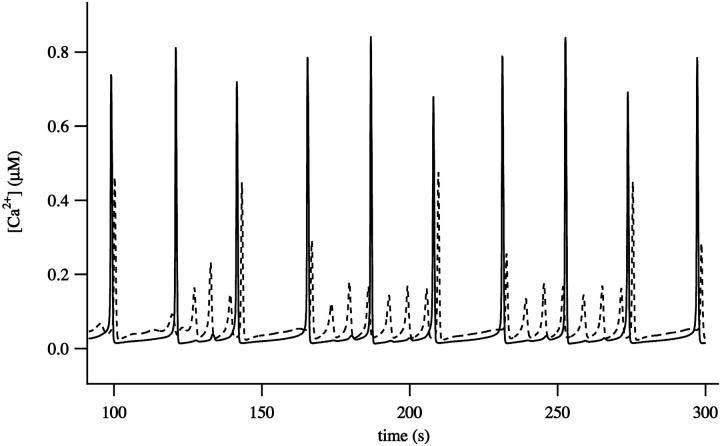
Although the mitochondria can eliminate an intracellular wave, p must be in a relatively narrow range for this to occur. This prediction is consistent with experimental data which demonstrates the narrow [IP₃] range in which local apical Ca²⁺ signals are observed in pancreatic acinar cells (Straub et al., 2000). More typically both apical and basal regions can oscillate independently and thus the pancreatic cell behaves like two coupled oscillators. This is illustrated in Fig. 10. The larger oscillations in the apical region have partially entrained the basal oscillations, but the basal region can also exhibit Ca²⁺ oscillations of higher frequency and lower amplitude that occur between the peaks of the apically-induced responses. In the absence of Ca²⁺ diffusion the basal and apical regions are independent oscillators (when p = 10), and thus the entrainment between the apical and basal regions is the result of calcium diffusion, even in the presence of a mitochondrial buffer region.

FIGURE 10.

Oscillatory responses computed with p = 10 μM. Time traces were taken from two places in the cell, one in the apical region (solid line) and the other in the basal region (dashed line).

DISCUSSION

The spatial heterogeneity assumed in our model is based on morphological data, which indicate that the apical and basal regions have different concentrations of both IPR and RyR, and that they are separated by a buffer region with a high mitochondrial density and a high RyR density (Kasai et al., 1993; Nathanson et al., 1994; Lee et al., 1997; Tinel et al., 1999; Straub et al., 2000; Fogarty et al., 2000). The actual figures for receptor density were chosen by fitting the model to the peak response data of Giovannucci et al. (2002), as discussed above. The results of the fitting procedure indicated that, in both pancreatic and parotid cells, the apical regions had higher receptor densities than the basal regions, a result consistent with experimental data (Wojcikiewicz, 1995; Thorn, 1996; Yule et al., 1997). In addition, the model is consistent with experimental data indicating higher receptor densities in parotid cells than in pancreatic cells (Giovannucci et al., 2002). It is important to note that our model cannot give reliable estimates of exact receptor densities, as such estimates rely crucially on a host of other parameters such as single-channel flux, open probability, or intraluminal Ca²⁺ levels, many of which are not specified precisely here. However, the model can estimate relative receptor densities.

The major prediction arising from the model is that there are two different ways in which the waves propagate, with an active mechanism operating at low agonist concentration, and a kinematic mechanism at high concentrations. In other words, at low agonist concentration the wave is propagated by the diffusion of Ca²⁺ between release sites. At higher agonist concentrations the basal region responds later than the apical region, giving the appearance of a wave that travels across the cell. This apparent wave is independent of Ca²⁺ diffusion. This conclusion is a direct result of the relative receptor densities determined by the fit to data. Calcium waves at both high [IP₃] and low [IP₃] are initiated by Ca²⁺ release through the IPR, and extended by Ca²⁺ release through the RyR. That Ca²⁺ waves in pancreatic acinar cells begin in an apical zone, spreading thence across the cell, has been widely accepted for some years (Nathanson et al., 1992; Thorn et al., 1993a,b; Kasai et al., 1993; Lawrie et al., 1993; Thorn, 1996; Straub et al., 2000; Leite et al., 2002). Our results are essentially similar to these earlier conclusions. However, our results indicate the possible presence of two distinct wave regimes. At lower [IP₃], the pancreatic apical responses are transmitted across the basal region by a process of active Ca²⁺ release through RyR and diffusion of Ca²⁺ between release sites. At higher [IP₃] the intracellular waves are the result of the differing phase of oscillation in the apical and basal regions, and occur in the absence of Ca²⁺ diffusion. Such apparent waves are sometimes called kinematic waves (Murray, 1989). In neither pancreatic nor parotid cells could RyR alone propagate a wave, in agreement with Ashby et al. (2002).

It is known that parotid cells have higher densities of IPR in both the apical and basal regions than do pancreatic cells (Giovannucci et al., 2002). Our model simulations support the hypothesis that the observed differences in the properties of Ca²⁺ waves in pancreatic and parotid cells are the result principally of differences in IPR density. Simulations predict that an increased IPR density results in faster waves and decreased times to peak, and that a lower basal RyR density prevents the active propagation of parotid Ca²⁺ waves.

In our simulations, the mitochondria seem to play little role in shaping the initial response of the cell. The parameter V_mito can be varied from 200 to 0, without making any significant change to the results shown in Figs. 4–6. Thus, the spatially heterogenous Ca²⁺ responses are almost entirely the result of the heterogeneous receptor distributions, rather than the result of the localized mitochondrial distribution. However, as long as [IP₃] lies in a relatively narrow range, the additional Ca²⁺ buffering by the mitochondria can prevent the spread of a global signal (Fig. 9). These simulations agree with some experiments (Tinel et al., 1999; Park et al., 2001; Johnson et al., 2002; Camello-Almaraz et al., 2002), although there are conflicting data (Gonzalez et al., 2000). The model suggests a way these conflicting reports could possibly be reconciled. Although the mitochondria can cause a spatial restriction of the responses, this effect is very sensitive to the background IP₃ concentration. It is thus not surprising that different experimental groups have made different observations.

However, they also indicate that the role of mitochondrial buffering may be more complex than simply blocking the diffusion of Ca²⁺ and preventing wave propagation. Fig. 8 shows how the basal region can itself generate autonomous oscillations. Thus, when p is high enough there is a complex interplay between two oscillatory regions (apical and basal) connected by a region of higher calcium uptake and release (the mitochondrial buffer region). Because of its higher density of IPR, the apical region tends to have a shorter period, and thus drive the combined behavior, but the response is not always so simple. At these higher values of p both basal and apical regions are capable of autonomous oscillations, but the basal region is not completely entrained to the apical region. Thus, we see not only global waves, initiated in the apical region and propagating across the basal region (Fig. 10), but also waves that are initiated in the basal region, and not entrained to the apical region. Such waves have been seen experimentally by Xu et al. (1996), who observed that, although mostly waves were initiated in the apical region, they could also originate from the lateral-basal region. Although, experimentally, the type of wave was agonist-dependent, our results indicate that different concentrations of IP₃ would also be expected to generate qualitatively different wave patterns.

The fit to the data shows some quantitative discrepancies. At high agonist concentration the model does not attain low enough times to peak, and this is reflected in wave speeds which are too low. This is most likely because the IPR and RyR respond too slowly in this regime. However, better agreement with the data would serve only to reinforce our conclusion that the waves are driven by a kinematic mechanism at high agonist concentration. The model predicts that active waves, driven by Ca²⁺ release through the RyR, travel at much lower speeds (∼15–20 μm s⁻¹, a figure that agrees extremely well with the experimental data of Straub et al., 2000). Hence, a wave speed of ∼100 μm s⁻¹ most likely results from a kinematic mechanism.

As always with these kinds of complex models, one most consider carefully the assumptions underlying the model construction. Unfortunately it is not yet possible to construct a model using parameters determined from only pancreatic acinar cells. Thus, to understand the complexities of wave propagation in these cell types it is necessary to construct a model using data from other sources.

Our model for the IPR is based on a recent detailed model of the type-II IPR (Sneyd and Dufour, 2002). The parameters of this model were determined by fitting the model to time course data from type-II IPR from hepatocytes. The majority of IPR in mouse pancreatic acinar cells are type-II and type-III, and are concentrated in the apical region (Wojcikiewicz, 1995; Thorn, 1996; Yule et al., 1997). This raises the question of how well a model for a type-II receptor reflects the dynamic behavior of a type-III receptor. It is not yet possible to answer this question, as there is not yet enough kinetic data from the IPR subtypes to do a detailed quantitative comparison between them. What we can say with confidence is that the steady-state behavior of the receptor subtypes has little relevance for its dynamic behavior. Whether or not the steady-state curve is biphasic, for instance, has nothing to do with whether or not the receptor subtype can generate Ca²⁺ oscillations, or how it controls such oscillations (LeBeau et al., 1999). Since there is no detailed dynamic model of type-III IPR, we use instead the most detailed available IPR model, which happens to be of a type-II IPR. It is possible that the IPR subtypes do not differ greatly in their dynamic responses. For instance, type-I IPR (Finch et al., 1991) seem to have similar dynamic properties to type-II IPR (Dufour et al., 1997).

There is as yet no detailed model of the dynamical behavior of RyR in either pancreatic or parotid acinar cells. The model we use here (Keizer and Levine, 1996) was originally developed for cardiac cells, and reproduces the measured peak and plateau responses in that cell type. However, the extent to which such results are applicable to acinar cells is not clear. Although other isoforms are present (Fitzsimmons et al., 2000), rat pancreatic acinar cells have a predominance of type-2 RyR (Leite et al., 1999), the same isoform that is found in cardiac cells, but this does not necessarily mean that their behavior, in situ, is the same. Stern et al. (1999) have performed a detailed comparison of a number of different models of the cardiac RyR, including the model of Keizer and Levine that we use here. Their results show that the Keizer and Levine model is not locally stable, i.e., with the given parameters it does not provide sufficient inactivation of Ca²⁺ release to generate the correct behavior in the RyR microdomain. This problem with the model does not affect our results as we rely entirely upon a macroscopic, not a local control, description.

Our model of Ca²⁺ entry is highly simplified, being merely a linearly increasing function of p, as was used by Dupont and Goldbeter (1993). There is general agreement that the application of agonists leads, ultimately, to an increase in Ca²⁺ influx into the cell, and even general agreement that, at high agonist concentrations when the ER is partially or wholly depleted, this increased influx is the result of signaling from the ER to the plasma membrane (Berridge, 1995). However, there is evidence that, at lower agonist concentrations, the increased Ca²⁺ influx may be the result of a more direct pathway mediated by arachidonic acid (Shuttleworth, 1999), with the depletion-activated influx becoming significant only at higher agonist concentrations. In the model here we do not make either assumption, modeling merely the overall effect, that an increase in p is associated with increased influx. Essentially, we have so little information about the mechanisms that modulate Ca²⁺ influx that a more detailed model is not realistically possible.

We have not used a cooperative model for the SERCA pump, an assumption that disagrees with some experimental evidence. Camello et al. (1996) have shown that the SERCA pumps in pancreatic acinar cells are steeply dependent on the Ca²⁺ concentration, activating quickly when Ca²⁺ is raised only slightly. Lytton et al. (1992) also measured a Hill coefficient of 2 for the SERCA pump. On the other hand, our SERCA model (Eq. 25), assuming a constant c_e, gives an excellent fit to the data in Fig. 2 C of Albrecht et al. (2002). Since Albrecht et al. measured the Ca²⁺-dependence of SERCA pump fluxes in intact cells, this is a strong indication that SERCA pumps in situ may be accurately modeled by a Hill equation with a Hill coefficient of 1. Furthermore, computations show that if the SERCA pump is modeled as a cooperative pump the oscillatory nature of this IPR model is destroyed (Tsaneva-Atanasova and Sneyd, unpublished results). Indeed, as with all models of Ca²⁺ oscillations, the model's behavior is highly sensitive to the exact form of the SERCA pump. There is still very little theoretical understanding of exactly how the Ca²⁺-dependence of the SERCA pumps interacts with the Ca²⁺-dependence of release through the IPR and RyR, to give oscillatory release and reuptake. We shall not address this question here, leaving it instead for analysis in a future publication.

We have assumed that the Ca²⁺ ATPase pumps in the plasma membrane and the ER are distributed homogeneously, and that their activity is unaffected by agonist concentration. These assumptions conflict with some experimental data. Zhang et al. (1992) have shown how, in pancreatic acinar cells, agonists activate the plasma membrane Ca²⁺ pumps independently of the Ca²⁺ concentration, whereas Lee et al. (1997) have showed that the SERCA2b ATPases are preferentially expressed in the basal region, with SERCA2a being preferentially expressed in the apical region. It is not clear what effect these omissions have on the model results. It is likely that detailed modulation of ATPase activity and distribution will have significant effects on the shape of the oscillations but little effect on the qualitative properties of wave propagation. However, detailed consideration of these complications will have to wait for future work.

When modeling the mitochondria, we included only Ca²⁺ uptake, not Ca²⁺ release, and followed the functional form derived by Colegrove et al. (2000). In their model, Ca²⁺ release from the mitochondria was modulated by the internal mitochondrial Ca²⁺ concentration, a variable that does not appear in our model. In effect, we are assuming that the mitochondrial Ca²⁺ is never significantly depleted, and Ca²⁺ efflux from the mitochondria is unimportant. We have no direct measurements of the total rate of Ca²⁺ uptake by the mitochondria in the buffer region of our model. Instead, we chose a value for V_mito such that the buffer region was able to prevent the global propagation of acinar responses at low [IP₃]. Neglect of efflux from the mitochondria is obviously a crude simplification that is not valid over the entire time course of a wave. However, we wished to investigate the effects of mitochondrial uptake on wave propagation, and thus on the rising phase of the wave front. The details of how the Ca²⁺ concentration returns to rest, including the effects of Ca²⁺ efflux from the mitochondria, are not of central interest to the present study. In addition, since mitochondrial uptake is typically ineffective at restricting Ca²⁺ responses to the apical region (although this can happen, as shown in Fig. 9), it follows that the inclusion of Ca²⁺ release from the mitochondria will make them even less effective at causing a spatial restriction of the Ca²⁺ responses. Thus, the general conclusions arising from the model will be unchanged by the addition of mitochondrial efflux.

APPENDIX: SUMMARY OF THE MODEL EQUATIONS

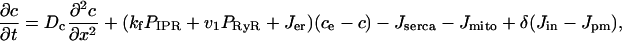(15)

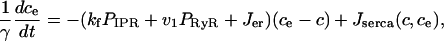(16)

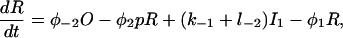(17)

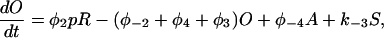(18)

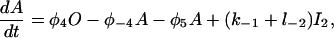(19)

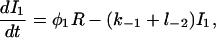(20)

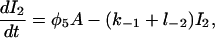(21)

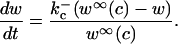(22)

where

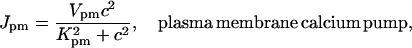(23)

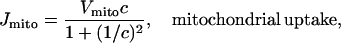(24)

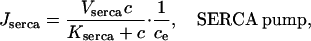(25)

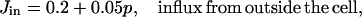(26)

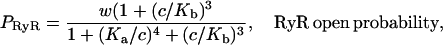(27)

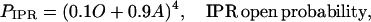(28)

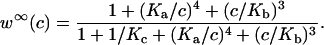(29)

The functions φ are derived in detail in Sneyd and Dufour (2002). For completeness we give them here:

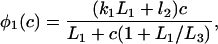(30)

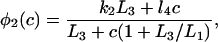(31)

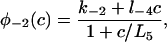(32)

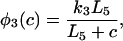(33)

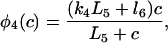(34)

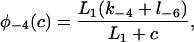(35)

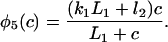(36)

All the k, l, and L values are positive constants. Although it appears that there are more constants than necessary for the model, they appear because this model was obtained by simplification of a more complex model (Sneyd and Dufour, 2002). We leave all the constants in here to facilitate comparison with the full model.

All the model parameters are given in Table 1.