Concerted Simulations Reveal How Peroxidase Compound III Formation Results in Cellular Oscillations

Abstract

A major problem in mathematical modeling of the dynamics of complex biological systems is the frequent lack of knowledge of kinetic parameters. Here, we apply Brownian dynamics simulations, based on protein three-dimensional structures, to estimate a previously undetermined kinetic parameter, which is then used in biochemical network simulations. The peroxidase-oxidase reaction involves many elementary steps and displays oscillatory dynamics important for immune response. Brownian dynamics simulations were performed for three different peroxidases to estimate the rate constant for one of the elementary steps crucial for oscillations in the peroxidase-oxidase reaction, the association of superoxide with peroxidase. Computed second-order rate constants agree well with available experimental data and permit prediction of rate constants at physiological conditions. The simulations show that electrostatic interactions depress the rate of superoxide association with myeloperoxidase, bringing it into the range necessary for oscillatory behavior in activated neutrophils. Such negative electrostatic steering of enzyme-substrate association presents a novel control mechanism and lies in sharp contrast to the electrostatically-steered fast association of superoxide and Cu/Zn superoxide dismutase, which is also simulated here. The results demonstrate the potential of an integrated and concerted application of structure-based simulations and biochemical network simulations in cellular systems biology.

INTRODUCTION

There are a burgeoning number of programs aimed at creation of a “virtual cell” by simulation of cellular biochemical and signaling dynamics. Macroscopic kinetic simulations are used to model the complex multistep dynamics. However, experimental data on kinetic parameters are often missing, and this hinders construction and validation of models. With advances in protein structure determination, in particular arising from structural genomics programs, it is increasingly likely that macromolecular structural data will be available for proteins in the simulated cellular pathways. Here we demonstrate how this protein structure data can be exploited, by means of atomic-detail molecular simulations, to compute kinetic parameters that are fed into macroscopic biochemical network simulations. We show the value of this concerted simulation approach by applying it to the PO reaction.

The PO reaction (Scheeline et al., 1997), which displays oscillatory dynamics important for immune response (Olsen et al., 2003), involves many elementary steps and five different oxidation states of the peroxidase enzyme (see Fig. 1). It thus provides a good model system for complex biochemical behavior. In addition to the classical peroxidase reaction, peroxidase catalyzes the PO reaction. This involves the oxidation of an organic electron donor (typically NADH) by molecular oxygen. Referring to Scheeline et al. (1997), the overall reaction can be written as

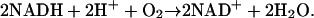(1)

The electron transfer can be mediated by aromatic compounds such as melatonin that react with the enzyme to form radicals that in turn oxidize NADH (Olsen et al., 2001). When NADH and O₂ are supplied continuously to a stirred aqueous solution at pH 5.0–6.5 containing peroxidase, a suitable aromatic compound, and methylene blue, the concentrations of the reactants and five enzyme intermediates oscillate (Nakamura et al., 1969) (see Fig. 2). The reaction intermediates include hydrogen peroxide and superoxide (Scheeline et al.). These reactive oxygen species were previously considered undesirable in cellular metabolism, but have recently been suggested to function as secondary messengers in certain cell signaling processes (Amit et al., 1999). The oscillatory dynamics appear to protect peroxidase from the harmful effects of the superoxide radical (Hauser et al., 2001) and, in the case of myeloperoxidase (MPO), to be involved in the activation of neutrophilic leukocytes and, therefore, of immune response (Olsen et al., 2003). The importance of the oscillatory dynamics due to MPO is highlighted by the observation that changes in the oscillations in activated neutrophils are associated with medical conditions such as septic shock and myocardial infarction (Kindzelskii and Petty, 2002). Therefore, an understanding of the determinants of cellular oscillations that reaches from the macroscopic level down to the detailed level of protein structure would aid rational, targeted drug design.

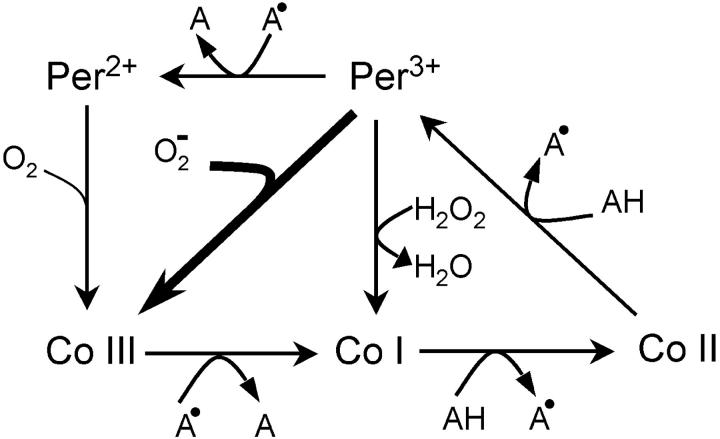
FIGURE 1.

Schematic representation of the elementary steps involving enzymatic intermediates in the peroxidase-oxidase reaction. Several additional nonenzymatic steps also take place. AH represents NADH or certain aromatic compounds such as melatonin. The enzyme can adopt one of five states: Per²⁺ and Per³⁺, and compounds (co) I to III with a bound ligand. The step shown by the thick arrow (binding of superoxide to form compound III) is simulated by Brownian dynamics to compute the second-order rate constant. The complete set of reactions is given, together with rate constants, in Table A1 of Appendix A.

FIGURE 2.

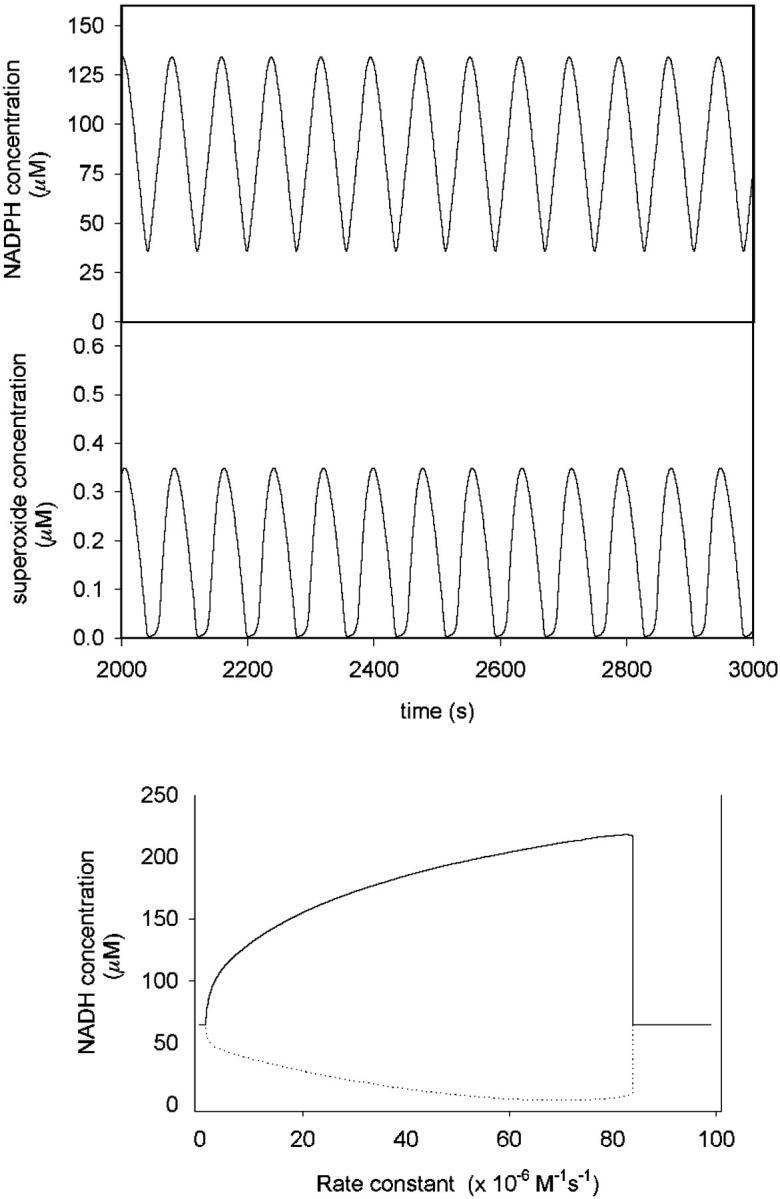
Time series from biochemical network simulations showing oscillation of the concentrations of NAD(P)H and superoxide using the parameters given in Table A1. Initial concentrations of myeloperoxidase and melatonin were 200 and 300 μM, respectively. All other initial concentrations were zero. The bottom figure shows the envelope of the oscillations of NAD(P)H plotted against the second-order rate constant for the association of ferric myeloperoxidase and superoxide.

The rate constants of most of the elementary steps of the PO reaction have been measured experimentally and, by fitting the few unknown constants, it is possible to perform simulations of the biochemical network (Scheeline et al., 1997). Such simulations have been performed primarily for horseradish peroxidase (HRP), but recently also for MPO, the focus of the present study, in the context of neutrophil activation (Olsen et al., 2003). Thus, the PO reaction is suitable for investigating the incorporation of kinetic parameters estimated from protein structure-based simulations. Experimental measurements of kinetic parameters can be costly and time-consuming, especially when they are fast and involve highly reactive compounds like the radical intermediates in this reaction. Therefore, we focus here on using structure-based BD simulations to estimate the association rate constant for superoxide binding to peroxidase. The rate constant for this elementary step has been determined experimentally for HRP (Scheeline et al., 1997), and for MPO at pH 7.8 (Kettle et al., 1988) but not at the physiological pH of 5. So far, a fitted value has been used for this rate constant when simulating the overall network (Olsen et al., 2003).

The rate of diffusional association of two molecules places an upper limit on the rate of a reaction between them. The rate constant for diffusional association can be computed by combining an analytical solution to the diffusion equation for two spherical particles (Smoluchowski, 1917) with data on the probability of reaction of the two molecules from BD simulations (Northrup et al., 1983). The BD simulations provide a means to account for the nonuniform shape, charge distribution, and reactivity of biomolecules when computing association rate constants. In the present BD simulations, the diffusion of superoxide to the enzyme active site was simulated.

We first carried out BD simulations for superoxide dismutases from two species, bovine (SOD-B) and Photobacterium leiognahi (SOD-P). These SODs are diffusion-controlled and well-characterized experimentally. Consequently, BD simulations for these SODs permitted calibration of our simulation method and provided a point of reference for the simulations with peroxidases. We then performed BD simulations for three peroxidases: MPO, the homologous lactoperoxidase (LPO), and the nonhomologous HRP. The rate constants computed for the peroxidases were entered into macroscopic biochemical network simulations. These showed oscillatory dynamics consistent with experimental measurements. Comparison of the determinants of the rate constants in the five enzymes revealed a novel enzymatic control mechanism: negative steering by the electrostatic potential of MPO depressed the rate constant for its association with superoxide, bringing the rate constant for this reaction into the range necessary for oscillatory behavior.

MATERIALS AND METHODS

Biochemical network model

The model is shown in Table A1 in Appendix A and was derived as described in Olsen et al. (2003). Simulations were performed with the MADONNA software (www.berkeleymadonna.com) using the Rosenbrock routine for the numerical solution of stiff differential equations.

Molecular modeling

Protein crystal structures were taken from the PDB for bovine (2sod) and photobacterium leiognahi (1yai) Cu/Zn SOD and for HRP (7atj) and human MPO (1d2v). The structure of human LPO has not yet been determined experimentally. It was modeled by homology using the SwissModel automated modeling server (www.expasy.ch/swissmod). The LPO sequence has 67% and 56% identity to chains A and C, respectively, of MPO in the structure files 1d2v (human), 1mhl (human), and 1myp (dog), which were used as templates. The SODs were modeled as homodimers, each monomer having one Cu²⁺ and one Zn²⁺ ion. MPO was modeled as a homodimer with a heme and one bound Ca²⁺ ion (Shin et al., 2001). HRP was modeled as a monomer with a heme and two bound Ca²⁺ atoms (Shiro et al., 1986). LPO was modeled as a homodimer with a heme but without bound ions.

Polar hydrogen atom coordinates were added using the WHATIF software (Hooft et al., 1996) after assigning titration states as follows. For SOD, His41 was doubly protonated and His61, which ligates both Cu and Zn ions was unprotonated (−1 e charge). For the peroxidases, protonation states were assigned on the basis of pK_a values computed with the UHBD program (Madura et al., 1994) using a Poisson-Boltzmann electrostatic model (Demchuk and Wade, 1996; Raquet et al., 1997); see Table B1 of Appendix B.

Brownian dynamics simulations

Simulations were carried out with the SDA software (Gabdoulline and Wade, 1998) using forces derived from protein electrostatic potential grids computed with the UHBD program (Madura et al., 1994) by numerical solution of the finite difference linearized Poisson-Boltzmann equation.

OPLS (Jorgensen and Tirado-Rives, 1988) atomic radii and partial charges were assigned to protein atoms. The charges on the metal ions and their ligating residues in SOD were assigned following Shen et al. (1990). Parameters for ferric heme were taken from Kuczera et al. (1990).

The superoxide ion was modeled as two spheres, each having a charge of −0.5 e and radius of 1.5 Å, at 1.5 Å separation. The motion of the ion in the presence of a fixed enzyme was simulated. Superoxide was assigned a translational diffusion constant of 0.1283 Ų/ps, which corresponds to a hydrodynamic radius of 1.62 Å, as used in Sergi et al. (1994). The rotational diffusion constant assigned of 3.9 10⁻² rad²/ps was derived with this hydrodynamic radius using the Stokes-Einstein equation.

Electrostatic forces were computed from the protein electrostatic potential grids and the charges on superoxide atoms, taking into account the desolvation penalties (Elcock et al., 1999) that occur when a charged ligand approaches a protein's low dielectric cavity. The parameters used were the same as in a recent study of protein-protein association (Gabdoulline and Wade, 2001).

The enzyme was fixed and the diffusion of superoxide, in a continuum ionic solution exerting frictional and stochastic forces on the solute, was simulated by Brownian dynamics (Ermak and McCammon, 1978). Association was monitored by measuring the distance between the oxygen atoms of superoxide and the Cu or Fe ions.

RESULTS AND DISCUSSION

Validation of the Brownian dynamics protocol for the calculation of diffusional association rate constants

The rate of the reaction of superoxide with the diffusion-controlled enzyme, SOD, has been studied extensively by BD simulation (Folcarelli et al., 1999; Sergi et al., 1994; Sines et al., 1990) and experiment (Getzoff et al., 1992; Tainer et al., 1983). Consequently, we first performed simulations of superoxide association with SODs from two species, bovine (SOD-B) and Photobacterium leiognahi (SOD-P), that show different arrangements of the SOD monomer in the active homodimer (Bourne et al., 1996). This permitted us to define a reaction criterion for rate constant determination from our BD simulations that reproduced the experimental rates for SOD well (see Table 1). This “reaction criterion” is consistent with those that we have used previously (Gabdoulline and Wade, 2001). The rate constants are calculated by requiring approach of a superoxide atom to within 8 Å of the metal ion for a BD trajectory to be considered reactive. The computed rate constant is then divided by a scaling factor of 1.3. A distance of 8 Å to the Cu of SOD-B, for example, corresponds to a distance of <6 Å to one of the side-chain hydrogen bond donors of Arg141, Lys134, Thr135, and some of the main-chain atoms. The “reaction distance” of 8 Å to the Cu differs significantly from the distance of 4 Å used in some other SOD simulations (Sergi et al., 1994). This difference is due to several factors. First, we use desolvation penalties (Elcock et al., 1999) while computing the interaction of superoxide with a protein. Second, a 2-atom rather than 1-atom representation of superoxide is used; this effectively makes superoxide larger and hinders its approach to the copper ion. Third, we model charge redistribution between the metal ions and their ligands. This weakens the electrostatic steering of the superoxide specifically to the Cu, thus increasing the derived “reaction distance” value. Test simulations with these factors eliminated show that experimental rates are reproduced with a reaction distance of 4–4.5 Å from the Cu.

TABLE 1.

Computed and experimental rate constants for the binding of superoxide to different enzymes

Enzyme	Ionic strength (mM)	pH	Experimental (107 M−1s−1)	Calculated (error)† (107 M−1s−1)
SOD-B	20	7.0	380	380 (75)
	∞		<170*	140 (25)
SOD-P	20	7.0	850	850 (150)
	∞		–	140 (30)
HRP	100	5.0	1.7	1.2 (0.4)
	∞		–	0.8 (0.4)
MPO	100	8.0	0.11	0.08 (0.05)
	100	5.0	–	1.1 (0.4)
	∞		–	18 (2)
LPO	100	7.0	–	5.8 (1.0)
	100	5.0	–	26 (3)
	∞		–	12 (3)

^*Value measured at 150 mM ionic strength.

^†Calculated values are rate constants for approach of a superoxide atom to within 8 Å of the metal ion, divided by 1.3 (See text for details).

Application of the Brownian dynamics protocol to calculate diffusional association rate constants for peroxidases

We then applied an identical procedure and reaction criterion to simulate the association of superoxide with the three peroxidases: HRP, MPO, and LPO. The results are reported in Table 1. The rate constant for HRP at 100 mM ionic strength, which is ∼2 orders-of-magnitude lower than that for SOD at 20 mM ionic strength, was correctly computed as 1.2 × 10⁷ M⁻¹s⁻¹. The rate constant for MPO at pH 8 was computed as 8 × 10⁵ M⁻¹s⁻¹, in agreement with the experimental determination (Kettle et al., 1988). The estimated rate constant for MPO at pH 5 was almost the same as that for HRP (1.1 × 10⁷ M⁻¹s⁻¹), whereas the rate constant for LPO was higher (2.6 × 10⁸ M⁻¹s⁻¹).

Dependence of the association rate constant on protein electrostatics

Comparison of the rate constants computed at low ionic strength and at infinite ionic strength (modeled by neglecting electrostatic interactions) shows that the rate of association of superoxide and SOD is enhanced by electrostatic steering, reaching 8.5 × 10⁹ M⁻¹s⁻¹ at 20 mM ionic strength. This electrostatic steering has been seen in previous BD simulations for SOD (Folcarelli et al., 1999; Sergi et al., 1994; Sines et al., 1990) and other diffusion-influenced enzymes such as triose phosphate isomerase (Wade et al., 1998). HRP and LPO, on the other hand, show only modest electrostatic enhancement of their association rate with superoxide. This is compatible with their much lower rate constants. MPO has approximately the same rate as HRP at 100 mM but, surprisingly, shows electrostatic depression of its rate, which is an order-of-magnitude lower at 100 mM ionic strength than in the absence of electrostatic interactions.

Dependence of oscillatory behavior on the rate constant for peroxidase compound III formation

Simulation of the time-dependence of all the concentrations in the biochemical network model for MPO displayed in Table A1 of Appendix A reveals that the depression of the rate constant for superoxide binding to MPO has a crucial impact on the overall behavior of the system. In this model, MPO is located in a different compartment from one of its substrates (NAD(P)H). The rate constant computed at pH 5 is within the range of (0.4–8) × 10⁷ M⁻¹s⁻¹ for oscillatory dynamics to occur, whereas the rate at pH 8 is below the lower border of this range and the rate in the absence of electrostatic interactions is well above the upper border (see Fig. 2).

Analysis of the sensitivity of oscillatory behavior to all the individual kinetic parameters reveals that the rate constant for association of superoxide to peroxidase (k₄) is one of the most crucial parameters for oscillatory behavior (see Table 2). Only two out of the other 10 kinetic parameters show similar importance (the reaction of compound II with melatonin, k₃, and the reaction of the NADP-radical with oxygen, k₈). This comparison also reveals the robustness of the oscillatory behavior in this system to the other parameters, most of which can be changed by many orders of magnitude without destroying the system's ability to display oscillatory behavior. Therefore, a few crucial parameters have to be more strictly controlled (as is shown here for the case of superoxide association to peroxidase), whereas other parameters can be adjusted flexibly according to the needs of other parts of the system.

TABLE 2.

Sensitivity of the oscillatory behavior toward the individual kinetic constants

Kinetic parameter	Range within which oscillations occur (M−1s−1)
k1	8 × 106–8.2 × 108
k2	5 × 104–∞
k3	2 × 103–1.1 × 104
k4	4 × 106–8 × 107
k5	0–3 × 109
k6	1 × 103–3.2 × 105
k7	0–7.6 × 102
k8	1 × 107–1.6 × 108
k9	3 × 104–∞
k10	8 × 103–∞
k11	7 × 106–2.2 × 109

Parameters were changed one at a time, resulting in an analysis of the local sensitivity of the system. The parameters are defined in Table A1 of Appendix A.

Structural comparison of the active sites of SOD and the peroxidases

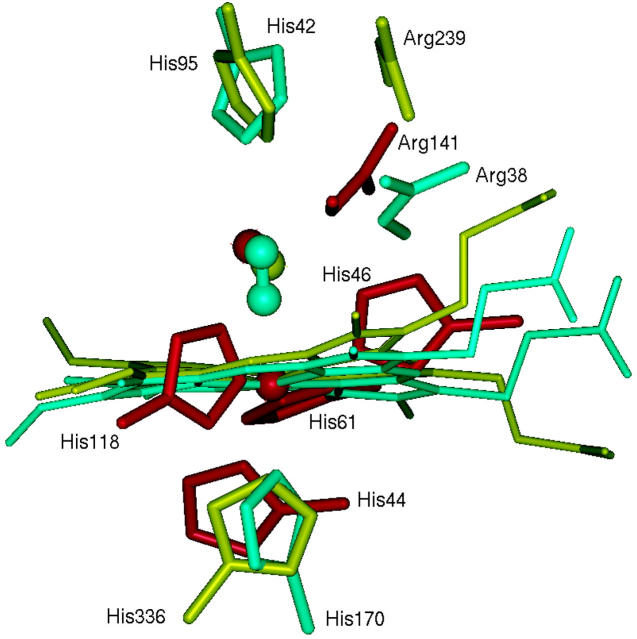
Despite both being peroxidases, HRP and MPO have negligible sequence identity. Thus, it appears puzzling that the two proteins can achieve approximately the same rate constant for the superoxide binding step. However, even though the overall structures are very different, the active sites show key similarities in the region around the superoxide binding site. This suggests that postdiffusional-encounter events may be similar (see Fig. 3). In particular, MPO, HRP, and SOD-B have a catalytic arginine with a guanadinium nitrogen atom ∼6 Å from the metal ion. This arginine is thought to be crucial for the dismutation reaction in SOD (Fisher et al., 1994; Folcarelli et al., 1999; Wade et al., 1998).

FIGURE 3.

Superposition of the active sites of Cu/Zn SOD-B (red) and the MPO (yellow) and HRP (blue) heme proteins. A conserved water site is shown by a sphere in the SOD and MPO structures. A cyanide molecule is shown in the same location in the HRP structure where a recent crystal structure shows superoxide binds (Berglund et al., 2002). Despite lack of sequence similarity, there are similar features in the active sites, such as the location of the guanadinium group of an arginine. The distal histidines of MPO and HRP superimpose well, even though the entrance channels to the active sites of these two peroxidases have completely different shapes and orientations. The channel in MPO extends into the page behind and to the right of the distal histidine, whereas that in HRP extends out of the page in front of the distal histidine.

Sequence and structural comparison of the peroxidases to reveal features important for determining rate constants for compound III formation

A structural superposition also yields insights into the different factors governing diffusional association rates. The active site entrance channels are oriented in different directions in the two proteins. MPO appears to have a larger entrance channel than HRP, and therefore the rates of diffusional association of uncharged substrates to MPO are larger. However, due to the presence of negatively charged residues near the active site entrance of MPO, the association rate for the negatively charged superoxide is depressed by a factor of 10 (see Fig. 4). These negatively charged residues are also present in eosinophil peroxidase, which has a 70% sequence identity to MPO and is likely to function in eosinophils in a similar way to MPO in neutrophils. On the other hand, these negatively charged residues are not conserved in other structurally similar peroxidases, such as LPO with a 56% sequence identity. Indeed, as a result of the more positive charge in this region (+5 e more), BD simulations show that the rate constant for association of superoxide with LPO should be approximately an order-of-magnitude greater than for MPO (see Table 1). This is consistent with the observation that LPO catalyzes an oscillating reaction in vitro at very low enzyme concentrations (Kummer et al., 1996).

FIGURE 4.

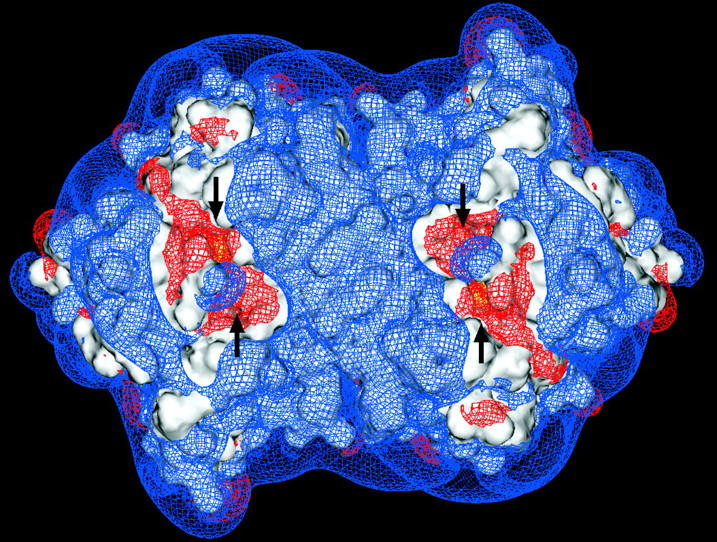
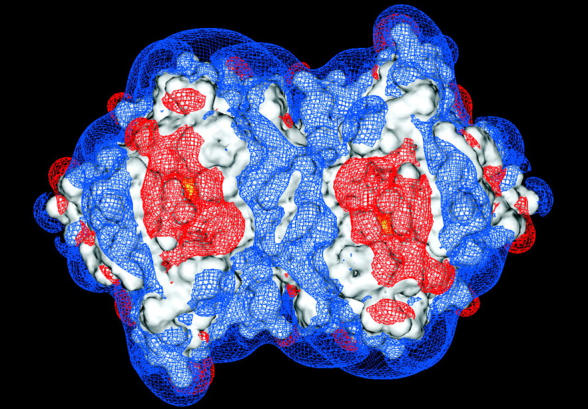
Electrostatic potential of the MPO homodimer at pH 5 (a) and pH 8 (b) contoured at + 0.5 (blue) and − 0.5 (red) kT/e. The black arrows show the locations of channels into the active sites. The yellow contours represent the reaction criterion for superoxide binding and are 8 Å from the Fe atom. The difference in the region of negative contours near the active sites at the two pHs is due to a histidine residue that changes protonation state between these pHs.

The discovery of the use of negative electrostatic steering to depress a reaction rate is unlikely to be limited to MPO alone. Investigation of how widespread such an electrostatic control mechanism is should be facilitated by the increasing availability of kinetic parameters from high-throughput experiments and the use of combined structural and kinetic simulation techniques.

APPENDIX A

TABLE A1.

Elementary reaction steps and rate constants of the model of the peroxidase-oxidase reaction in activated neutrophils

Reaction	Rate expression (Ri)	Rate constant
Reactions occurring in phagosome
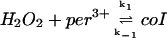
1.	k1[H2O2]p[Per3+]p − k−1[coI]p	k1 = 5.0 × 107 M−1 s−1
		k−1 = 58 s−1
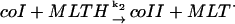
2.	k2[coI]p[MLTH]p	k2 = 1.0 × 107 M−1 s−1
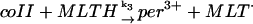
3.	k3[coII]p[MLTH]p	k3 = 4.0 × 103 M−1 s−1
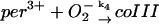
4.		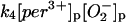k4 = 1.1 × 107 M−1 s−1
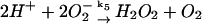
5.		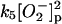k5 = 1.0 × 107 M−1 s−1
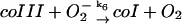
6.		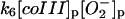k6 = 1.0 × 105 M−1 s−1
Reactions occurring in cytoplasm
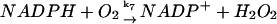
7.	k7[NADPH]c[O2]c	k7 = 1 M−1 s−1
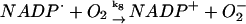
8.		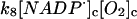k8 = 5.0 × 107 M−1 s−1
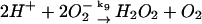
9.		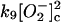k9 = 5.0 × 108 M−1 s−1
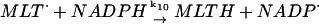
10.		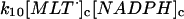k10 = 1.0 × 107 M−1 s−1
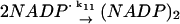
11.		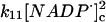k11 = 6.0 × 107 M−1 s−1
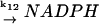
12.	k12	k12 = 22–35 μM s−1
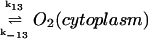
13.	k13 − k−13[O2]c	k13 = 12.5 μM s−1
		k−13 = 4.5 × 10−2 s−1
Diffusion terms
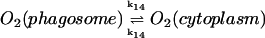
14.	k14([O2]p − [O2]c)	k14 = 30 s−1
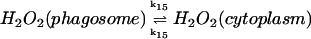
15.	k15([H2O2]p − [H2O2]c)	k15 = 30 s−1
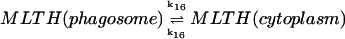
16.	k16([MLTH]p − [MLTH]c)	k16 = 10 s−1
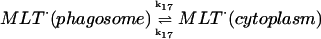
17.		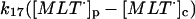k17 = 10 s−1
18.		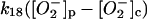k18 = <0.01 s−1
NADPH oxidase
19. NADPH (cytoplasm) + 2O2 (phagosome) → NADP+ (cytoplasm) + 2O2− (phagosome)

MLTH, melatonin; MLT^·, melatonin free radical; per³⁺, ferric peroxidase; and coI–III, compounds I–III.

The value of the rate constant for reaction 4 is computed from structure-based Brownian dynamics simulations.

APPENDIX B

TABLE B1.

Computed pK_a values and assigned net charges for titratable residues in the peroxidases

Enzyme	Residue*	pKa†	Charge (e) at pH 5	Charge (e) at pH 7	Charge (e) at pH 8
HRP	Glu238	4.7	−0.5
	Glu249	5.0	−0.5
	His40	5.1	+1.0
MPO	Asp98	6.8	0.0		0.0
	Glu102	5.5	−0.5		−1.0
	Glu116	5.5	−0.5		−1.0
	Glu242	5.2	−0.5		−1.0
	Glu245	5.1	−0.5		−1.0
	His95	5.6	+0.5		0.0
	His217	6.7	+1.0		0.0
	His250	5.2	+0.5		0.0
	Ntrm1	7.5	+1.0		+0.5
	Ntrm113	7.8	+1.0		+0.5
LPO	Asp227	5.4	−0.5	−1.0
	Asp229	6.9	0.0	0.0
	Asp659	4.7	−0.5	−1.0
	Glu235	4.9	−0.5	−1.0
	His226	6.0	+0.5	+0.5
	His339	6.3	+1.0	+0.0
	His383	5.3	+0.5	0.0
	His390	5.7	+1.0	0.0
	His437	6.0	+1.0	0.0
	His543	6.5	+1.0	+0.5
	Ntrm132	7.9	+1.0	+1.0
	Ntrm245	7.7	+1.0	+1.0

^*In MPO, numeration of residues is according to that in the pdb file 1d2v. In LPO, numeration of residues is according to the SwissProt sequence PERL_HUMAN.

^†pK_a values were computed as an average over the pH range 4–8 (Demchuk and Wade, 1996; Raquet et al., 1997) using the UHBD program (Madura et al., 1994), assigning a protein dielectric constant of 15 (see Methods).