Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Sep;85(3):1457–1465. doi: 10.1016/S0006-3495(03)74578-0

Two-State Folding over a Weak Free-Energy Barrier

Giorgio Favrin 1, Anders Irbäck 1, Björn Samuelsson 1, Stefan Wallin 1
PMCID: PMC1303322  PMID: 12944263

Abstract

We present a Monte Carlo study of a model protein with 54 amino acids that folds directly to its native three-helix-bundle state without forming any well-defined intermediate state. The free-energy barrier separating the native and unfolded states of this protein is found to be weak, even at the folding temperature. Nevertheless, we find that melting curves to a good approximation can be described in terms of a simple two-state system, and that the relaxation behavior is close to single exponential. The motion along individual reaction coordinates is roughly diffusive on timescales beyond the reconfiguration time for a single helix. A simple estimate based on diffusion in a square-well potential predicts the relaxation time within a factor of two.

INTRODUCTION

In a landmark paper in 1991, Jackson and Fersht (1991) demonstrated that chymotrypsin inhibitor twofolds without significantly populating any metastable intermediate state. Since then, it has become clear that this protein is far from unique; the same behavior has been observed for many small single-domain proteins (Jackson, 1998). It is tempting to interpret the apparent two-state behavior of these proteins in terms of a simple free-energy landscape with two minima separated by a single barrier, where the minima represent the native and unfolded states, respectively. If the barrier is high, this picture provides an explanation of why the folding kinetics are single exponential, and why the folding thermodynamics show two-state character.

However, it is well known that the free-energy barrier, ΔF, is not high for all these proteins. In fact, assuming the folding time τf to be given by τf = τ0 exp(ΔF/kT) with τ0 ∼ 1 μs (Hagen et al., 1996), it is easy to find examples of proteins with ΔF values of a few kT (Jackson, 1998; k is Boltzmann's constant and T the temperature). It should also be mentioned that Garcia-Mira et al. (2002) recently found a protein that appears to fold without crossing any free-energy barrier.

Suppose the native and unfolded states coexist at the folding temperature and that there is no well-defined intermediate state, but that a clear free-energy barrier is missing. What type of folding behavior should one then expect? In particular, would such a protein, due to the lack of a clear free-energy barrier, show easily detectable deviations from two-state thermodynamics and single-exponential kinetics? Here we investigate this question based on Monte Carlo simulations of a designed three-helix-bundle protein (Irbäck et al., 2000, 2001; Favrin et al., 2002).

Our study consists of three parts. First, we investigate whether or not melting curves for this model protein show two-state character. Second, we ask whether the relaxation behavior is single exponential or not, based on ensemble kinetics at the folding temperature. Third, inspired by energy-landscape theory (recently reviewed by Plotkin and Onuchic (2002a,b)), we try to interpret the folding dynamics of this system in terms of simple diffusive motion in a low-dimensional free-energy landscape.

MODEL AND METHODS

The model

Simulating atomic models for protein folding remains a challenge, although progress is currently being made in this area (Kussell et al., 2002; Shen and Freed, 2002; Zhou and Berne, 2002; Shea et al., 2002; Zagrovic et al., 2002; Clementi et al., 2003; Irbäck et al., 2003). Here, for computational efficiency, we consider a reduced model with 5–6 atoms per amino acid (Irbäck et al., 2000), in which the side chains are replaced by large Cβ atoms. Using this model, we study a designed three-helix-bundle protein with 54 amino acids.

The model has the Ramachandran torsion angles φi, ψi as its degrees of freedom, and is sequence-based with three amino acid types: hydrophobic (H), polar (P), and glycine (G). The sequence studied consists of three identical H/P segments with 16 amino acids each (PPHPPHHPPHPPHHPP), separated by two short GGG segments (Guo and Thirumalai, 1996; Takada et al., 1999). The H/P segment is such that it can make an α-helix with all the hydrophobic amino acids on the same side.

The interaction potential

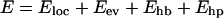graphic file with name M1.gif (1)

is composed of four terms. The local potential Eloc has a standard form with threefold symmetry,

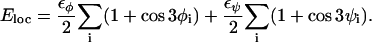graphic file with name M2.gif (2)

The excluded-volume term Eev is given by a hard-sphere potential of the form

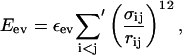graphic file with name M3.gif (3)

where the sum runs over all possible atom pairs except those consisting of two hydrophobic Cβ. The parameter σij is given by σij = σi + σj + Δσij, where Δσij = 0.625 Å for CβC′, CβN, and CβO pairs that are connected by a sequence of three covalent bonds, and Δσij = 0 Å otherwise. The introduction of the parameter Δσij can be thought of as a change of the local potential.

The hydrogen-bond term Ehb has the form

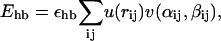graphic file with name M4.gif (4)

where the functions u(r) and v(α, β) are given by

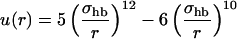graphic file with name M5.gif (5)
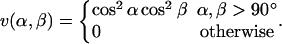graphic file with name M6.gif (6)

The sum in Eq. 4 runs over all possible HO pairs, and rij denotes the HO distance, αij the NHO angle, and βij the HOC′ angle. The last term of the potential, the hydrophobicity term Ehp, is given by

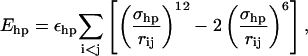graphic file with name M7.gif (7)

where the sum runs over all pairs of hydrophobic Cβ.

To speed up the calculations, a cutoff radius rc is used, which is taken to be 4.5 Å for Eev and Ehb, and 8 Å for Ehp. Numerical values of all energy and geometry parameters can be found elsewhere (Irbäck et al., 2000).

The thermodynamic behavior of this three-helix-bundle protein has been studied before (Irbäck et al., 2000, 2001). These studies demonstrated that this model protein has the following properties:

  • It does form a stable three-helix bundle, except for a twofold topological degeneracy. These two topologically distinct states both contain three right-handed helices. They differ in how the helices are arranged. If we let the first two helices form a U, then the third helix is in front of the U in one case (FU), and behind the U in the other case (BU). The reason that the model is unable to discriminate between these two states is that their contact maps are effectively very similar (Wallin et al., 2003).

  • It makes more stable helices than the corresponding one- and two-helix sequences, which is in accord with the experimental fact that tertiary interactions generally are needed for secondary structure to become stable.

  • It undergoes a first-order-like folding transition directly from an expanded state to the three-helix-bundle state, without any detectable intermediate state. At the folding temperature Tf, there is a pronounced peak in the specific heat.

Here we analyze the folding dynamics of this protein in more detail, through an extended study of both thermodynamics and kinetics.

As a measure of structural similarity with the native state, we monitor a parameter Q that we call nativeness (the same as in our earlier studies (Irbäck et al., 2000, 2001; Favrin et al., 2002)). To calculate Q, we use representative conformations for the FU and BU topologies, respectively, obtained by energy minimization. For a given conformation, we compute the root-mean-square deviations δFU and δBU from these two representative conformations (calculated over all backbone atoms). The nativeness Q is then obtained as

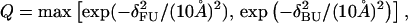graphic file with name M8.gif (8)

which makes Q a dimensionless number between 0 and 1.

Energies are quoted in units of kTf, with the folding temperature Tf defined as the specific heat maximum. In the dimensionless energy unit used in our previous study (Irbäck et al., 2000), this temperature is given by kTf = 0.6585 ± 0.0006.

Monte Carlo methods

To simulate the thermodynamic behavior of this model, we use simulated tempering (Lyubartsev et al., 1992; Marinari and Parisi, 1992; Irbäck and Potthast, 1995), in which the temperature is a dynamic variable. This method is chosen to speed up the calculations at low temperatures. Our simulations are started from random configurations. The temperatures studied range from 0.95Tf to 1.37Tf.

The temperature update is a standard Metropolis step. In conformation space we use two different elementary moves: first, the pivot move in which a single torsion angle is turned; and second, a semilocal method (Favrin et al., 2001) that works with seven or eight adjacent torsion angles, which are turned in a coordinated manner. The nonlocal pivot move is included in our calculations to accelerate the evolution of the system at high temperatures.

Our kinetic simulations are also Monte Carlo based, and only meant to mimic the time evolution of the system in a qualitative sense. They differ from our thermodynamic simulations in two ways: first, the temperature is held constant; and second, the nonlocal pivot update is not used, but only the semilocal method (Favrin et al., 2001). This restriction is needed to avoid large unphysical deformations of the chain.

Statistical errors on thermodynamic results are obtained by jackknife analysis (Miller, 1974) of results from ten or more independent runs, each containing several folding/unfolding events. All errors quoted are 1σ errors. Statistical errors on relaxation times are difficult to determine due to uncertainties about where the large-time behavior sets in and are therefore omitted. We estimate that the uncertainties on our calculated relaxation times are ∼10%. The statistical errors on the results obtained by numerical solution of the diffusion equation are, however, significantly smaller than this.

All fits of data discussed below are carried out by using a Levenberg-Marquardt procedure (Press et al., 1992).

Analysis

Melting curves for proteins are often described in terms of a two-state picture. In the two-state approximation, the average of a quantity X at temperature T is given by

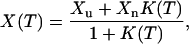graphic file with name M9.gif (9)

where K(T) = Pn(T)/Pu(T), Pn(T) and Pu(T) being the populations of the native and unfolded states, respectively. Likewise, Xn and Xu denote the respective values of X in the native and unfolded states. The effective equilibrium constant K(T) is to leading order given by K(T) = exp[(1/kT − 1/kTm)ΔE], where Tm is the midpoint temperature and ΔE the energy difference between the two states. With this K(T), a fit to Eq. 9 has four parameters: ΔE, Tm, and the two baselines Xu and Xn.

A simple but powerful method for quantitative analysis of the folding dynamics is obtained by assuming the motion along different reaction coordinates to be diffusive (Bryngelson et al., 1995; Socci et al., 1996). The folding process is then modeled as one-dimensional Brownian motion in an external potential given by the free energy F(r) = −kT ln Peq(r), where Peq(r) denotes the equilibrium distribution of r. Thus, it is assumed that the probability distribution of r at time t, P(r, t), obeys Smoluchowski's diffusion equation

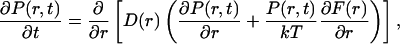graphic file with name M10.gif (10)

where D(r) is the diffusion coefficient.

This picture is not expected to hold on short timescales, due to the projection onto a single coordinate r, but may still be useful provided that the diffusive behavior sets in on a timescale that is small compared to the relaxation time. By estimating D(r) and F(r), it is then possible to predict the relaxation time from Eq. 10. Such an analysis has been successfully carried through for a lattice protein (Socci et al., 1996).

The relaxation behavior predicted by Eq. 10 is well understood when F(r) has the shape of a double well with a clear barrier. In this situation, the relaxation is single exponential with a rate constant given by Kramers' well-known result (Kramers, 1940). However, this result cannot be applied to our model, in which the free-energy barrier is small or absent, depending on which reaction coordinate is used. Therefore, we perform a detailed study of Eq. 10 for some relevant choices of D(r) and F(r), using analytical as well as numerical methods.

RESULTS

Thermodynamics

In our thermodynamic analysis, we study the five different quantities listed in Table 1. The first question we ask is to what extent the temperature dependence of these quantities can be described in terms of a first-order two-state system (see Eq. 9).

TABLE 1.

Parameters ΔE and Tm

ΔE/kTf Tm/Tf
E 40.1 ± 3.3 1.0050 ± 0.0020
Ehb 41.0 ± 2.6 1.0024 ± 0.0017
Ehp 45.4 ± 3.3 1.0056 ± 0.0017
Rg 45.7 ± 3.8 1.0099 ± 0.0018
Q 53.6 ± 2.1 0.9989 ± 0.0008
Open in a new tab

Parameters ΔE and Tm obtained by fitting results from our thermodynamic simulations to the two-state expression in Eq. 9. This is done individually for each of the quantities in the first column; the energy E, the hydrogen-bond energy Ehb, the hydrophobicity energy Ehp, the radius of gyration Rg (calculated over all backbone atoms), and the nativeness Q (see Eq. 8). The fits are performed using seven data points in the temperature interval 0.95 Tf ≤ T ≤ 1.11 Tf.

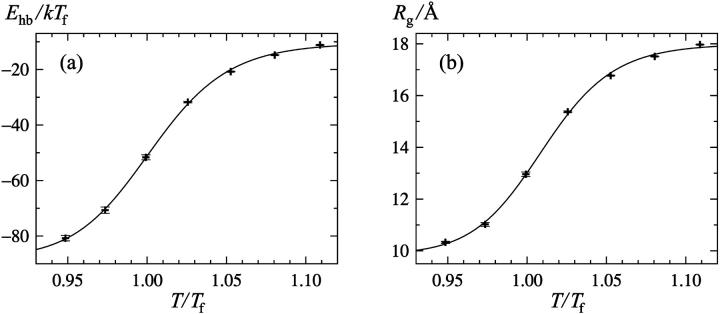
Fits of our data to this equation show that the simple two-state picture is not perfect (χ2 per degree of freedom, dof, of ∼10), but this can be detected only because the statistical errors are very small at high temperatures (<0.1%). In fact, if we assign artificial statistical errors of 1% to our data points, an error size that is not uncommon for experimental data, then the fits become perfect with a χ2/dof close to unity. Fig. 1 shows the temperature dependence of the hydrogen-bond energy Ehb and the radius of gyration Rg, along with our two-state fits.

FIGURE 1.

FIGURE 1

Open in a new tab

Temperature dependence of (a) the hydrogen-bond energy Ehb and (b) the radius of gyration Rg. The lines are fits to Eq. 9.

Table 1 gives a summary of our two-state fits. In particular, we see that the fitted values of both the energy change ΔE and the midpoint temperature Tm are similar for the different quantities. It is also worth noting that the Tm values fall close to the folding temperature Tf, defined as the maximum of the specific heat. The difference between the highest and lowest values of Tm is less than 1%. There is a somewhat larger spread in ΔE, but this parameter has a larger statistical error.

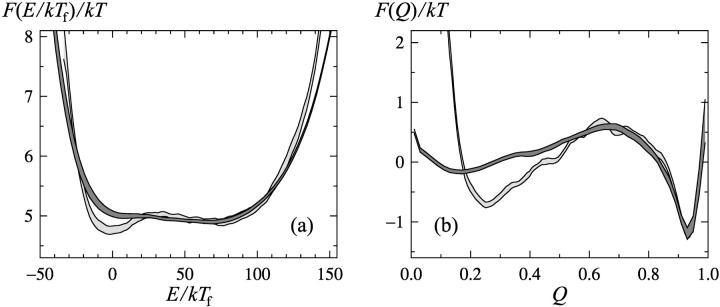
So, the melting curves show two-state character, and the fitted parameters ΔE and Tm are similar for different quantities. From this it may be tempting to conclude that the thermodynamic behavior of this protein can be fully understood in terms of a two-state system. The two-state picture is, nevertheless, an oversimplification, as can be seen from the shapes of the free-energy profiles F(E) and F(Q). Fig. 2 shows these profiles at T = Tf. First of all, these profiles show that the native and unfolded states coexist at T = Tf, so the folding transition is first order like. However, there is no clear free-energy barrier separating the two states; F(Q) exhibits a very weak barrier, <1 kT, whereas F(E) shows no barrier at all. In fact, F(E) has the shape of a square well rather than a double well.

FIGURE 2.

FIGURE 2

Open in a new tab

Free-energy profiles at T = Tf for (a) the energy E and (b) the nativeness Q (dark bands). The light-gray bands show free energies Fb for block averages (see Eq. 12), using a block size of τb = 106 MC steps. Each band is centered around the expected value and shows statistical 1σ errors.

Phase transition terminology is, by necessity, ambiguous for a finite system like this, but if states with markedly different E or Q coexist it does make sense to call the transition first order like, even if a free-energy barrier is missing. At a second-order phase transition, the free-energy profile is wide, but the minimum remains unique.

Kinetics

Our kinetic study is performed at T = Tf. Using Monte Carlo dynamics (see Model and Methods), we study the relaxation of ensemble averages of various quantities. For this purpose, we performed a set of 3000 folding simulations, starting from equilibrium conformations at temperature T0 ≈ 1.06Tf. At this temperature, the chain is extended and has a relatively low secondary-structure content (see Fig. 1).

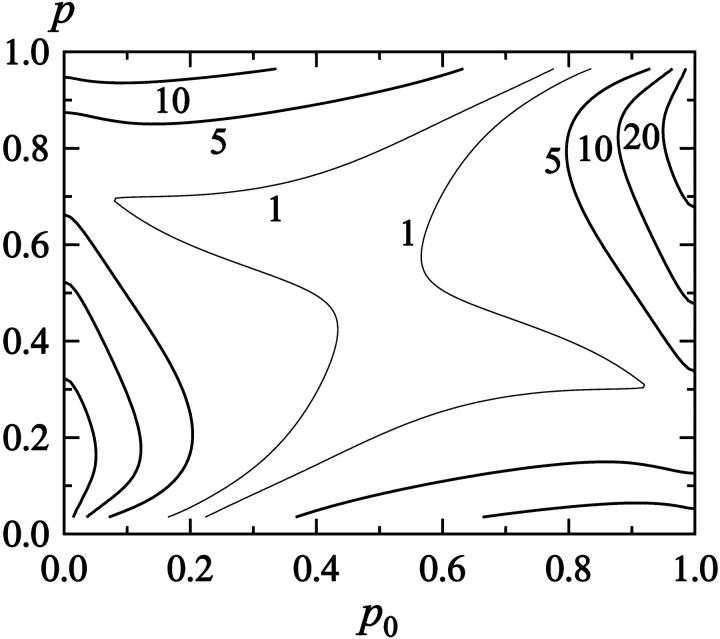
In the absence of a clear free-energy barrier (see Fig. 2), it is not obvious whether or not the relaxation should be single exponential. To get an idea of what to expect for a system like this, we consider the relaxation of the energy E in a potential F(E) that has the form of a perfect square well at T = Tf. For this idealized F(E) and a constant diffusion coefficient D(E), it is possible to solve Eq. 10 analytically for relaxation at an arbitrary temperature T. This solution is given in Appendix A, for the initial condition that P(E, t = 0) is the equilibrium distribution at temperature T0. Using this result, the deviation from single-exponential behavior can be mapped out as a function of T0 and T, as is illustrated in Fig. 3. The size of the deviation depends on both T0 and T, but is found to be small for a wide range of (T0,T) values. This clearly demonstrates that the existence of a free-energy barrier is not a prerequisite to observe single-exponential relaxation.

FIGURE 3.

FIGURE 3

Open in a new tab

Level diagram showing the deviation (in %) from a single exponential for diffusion in energy in a square well, based on the exact solution in Appendix A. The system relaxes at temperature T, starting from the equilibrium distribution at temperature T0. p is defined as p = (〈E〉 − En)/ΔEsw, where 〈E〉 is the average energy at temperature T, and En and ΔEsw denote the lower edge and the width, respectively, of the square well. p can be viewed as a measure of the unfolded population at temperature T, and is 0.5 if T = Tf. p0 is the the corresponding quantity at temperature T0. As a measure of the deviation from a single exponential, we take δmax/δE(t0), where δmax is the maximum deviation from a fitted exponential and δE(t0) = E(t0) − 〈E〉, E(t0) being the mean at the smallest time included in the fit, t0. Data at times shorter than 1% of the relaxation time were excluded from the fit.

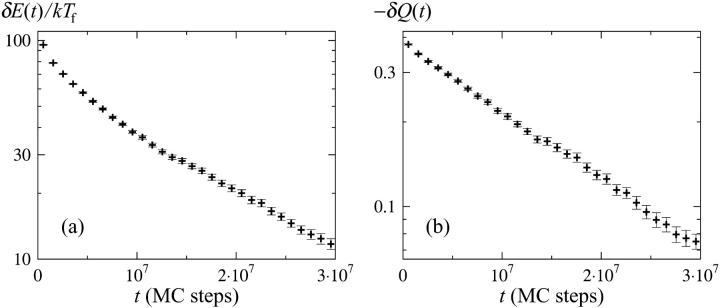
Let us now turn to the results of our simulations. Fig. 4 shows the relaxation of the average energy E and the average nativeness Q in Monte Carlo (MC) time. In both cases, the large-time data can be fitted to a single exponential, which gives relaxation times of τ ≈ 1.7 × 107 and τ ≈ 1.8 × 107 for E and Q, respectively, in units of elementary MC steps. The corresponding fits for the radius of gyration and the hydrogen-bond energy (data not shown) give relaxation times of τ ≈ 2.1 × 107 and τ ≈ 1.8 × 107, respectively. The fit for the radius of gyration has a larger uncertainty than the others, because the data points have larger errors in this case.

FIGURE 4.

FIGURE 4

Open in a new tab

Relaxation behavior of the three-helix-bundle protein at the folding temperature Tf, starting from the equilibrium ensemble at T0 ≈ 1.06Tf. (a) δE(t) = E(t) − 〈E〉 against simulation time t, where E(t) is the average E after t MC steps (3000 runs) and 〈E〉 denotes the equilibrium average (at Tf). (b) Same plot for the nativeness Q.

The differences between our four fitted τ values are small and most probably due to limited statistics for the large-time behavior. Averaging over the four different variables, we obtain a relaxation time of τ ≈ 1.8 × 107 MC steps for this protein. The fact that the relaxation times for the hydrogen-bond energy and the radius of gyration are approximately the same shows that helix formation and chain collapse proceed in parallel for this protein. This finding is in nice agreement with recent experimental results for small helical proteins (Krantz et al., 2002).

For Q, it is necessary to go to very short times to see any significant deviation from a single exponential (see Fig. 4). For E, we find that the single-exponential behavior sets in at roughly τ/3, which means that the deviation from this behavior is larger than in the analytical calculation above. On the other hand, for comparisons with experimental data, we expect the behavior of Q to be more relevant than that of E. The simulations confirm that the relaxation can be approximately single exponential even if there is no clear free-energy barrier.

To translate the relaxation time for this protein into physical units, we compare with the reconfiguration time for the corresponding one-helix segment. To that end, we performed a kinetic simulation of this 16-amino acid segment at the same temperature, T = Tf. This temperature is above the midpoint temperature for the one-helix segment, which is 0.95Tf (Irbäck et al., 2000). So, the isolated one-helix segment is unstable at T = Tf, but makes frequent visits to helical states with low hydrogen-bond energy, Ehb. To obtain the reconfiguration time, we fitted the large-time behavior of the autocorrelation function for Ehb,

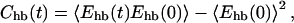graphic file with name M11.gif (11)

to an exponential. The exponential autocorrelation time, which can be viewed as a reconfiguration time, turned out to be τh ≈ 1.0 × 106 MC steps. This is roughly a factor of 20 shorter than the relaxation time τ for the full three-helix bundle. Assuming the reconfiguration time for an individual helix to be ∼0.2 μs (Williams et al., 1996; Thompson et al., 1997), we obtain relaxation and folding times of ∼4 μs and ∼8 μs, respectively, for the three-helix bundle. This is fast but not inconceivable for a small helical protein (Jackson, 1998). In fact, the B domain of staphylococcal protein A is a three-helix-bundle protein that has been found to fold in <10 μs, at 37°C (Myers and Oas, 2001).

Relaxation-time predictions

We now turn to the question of whether the observed relaxation time can be predicted based on the diffusion equation, Eq. 10. For that purpose, we need to know not only the free energy F(r), but also the diffusion coefficient D(r). Socci et al. (1996) successfully performed this analysis for a lattice protein that exhibited a relatively clear free-energy barrier. Their estimate of D(r) involved an autocorrelation time for the unfolded state. The absence of a clear barrier separating the native and unfolded states makes it necessary to take a different approach in our case.

The one-dimensional diffusion picture is not expected to hold on short timescales, but only after coarse graining in time. A computationally convenient way to implement this coarse graining in time is to study block averages b(t) defined by

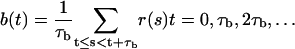graphic file with name M12.gif (12)

where τb is the block size and r is the reaction coordinate considered. The diffusion coefficient can then be estimated using Db(r) = 〈(δb)2〉/2τb, where the numerator is the mean-square difference between two consecutive block averages, given that the first of them has the value r.

In our calculations, we use a block size of τb = 106 MC steps, corresponding to the reconfiguration time τh for an individual helix. We do not expect the dynamics to be diffusive on timescales shorter than this, due to steric traps that can occur in the formation of a helix. In order for the dynamics to be diffusive, the timescale should be such that the system can escape from these traps.

Using this block size, we first make rough estimates of the relaxation times for E and Q based on the result in Appendix A for a square-well potential and a constant diffusion coefficient. These estimates are given by 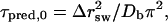Inline graphic where Δrsw is the width of the potential and Db is the average diffusion coefficient. (Eq. 15 in Appendix A can be applied to other observables than E if T = Tm. The predicted relaxation time τpred,0 is given by τ1). Our estimates of Δrsw and Db can be found in Table 2, along with the resulting predictions τpred,0. We find that these simple predictions agree with the observed relaxation times τ within a factor of two.

TABLE 2.

Predictions for τpred,0 and τpred

Δrsw Db τpred,0 τpred τ
E: 140kTf (9.3 ± 0.2) × 10−5(kTf)2 2.1 × 107 1.9 × 107 1.7 × 107
Q: 1.0 (1.00 ± 0.02) × 10−8 1.0 × 107 0.8 × 107 1.8 × 107
Open in a new tab

The predictions τpred,0 and τpred (see text) along with the observed relaxation time τ, as obtained from the data in Fig. 4, for the energy E and the nativeness Q. Δrsw is the width of the square-well potential and Db is the average diffusion coefficient.

We also did the same calculation for smaller block sizes, τb = 100, 101, …, 105 MC steps. This gave τpred,0 values smaller or much smaller than the observed τ, signaling nondiffusive dynamics. This confirms that for b(t) to show diffusive dynamics, τb should not be smaller than the reconfiguration time for an individual helix.

Having seen the quite good results obtained by this simple calculation, we now turn to a more detailed analysis, illustrated in Fig. 5 a. The block size is the same as before, τb = 106 MC steps, but the space dependence of the diffusion coefficient Db(r) is now taken into account, and the potential, Fb(r), reflects the actual distribution of block averages. The potential Fb(r), shown in Fig. 2, is not identical to that for the unblocked variables. At a first-order-like transition, we expect free-energy minima to become more pronounced when going to the block variables, provided that the block size τb is small compared with the relaxation time, because when forming the block variables one effectively integrates out fluctuations about the respective states. The results in Fig. 2 do show this tendency, although the effect is not very strong. Fig. 5 b shows the diffusion coefficient Db(E), which is largest at intermediate values between the native and unfolded states. The behavior of Db(Q) (not shown) is the same in this respect. Hence, there is no sign of a kinetic bottleneck to folding for this protein.

FIGURE 5.

FIGURE 5

Open in a new tab

(a) Numerical solution of Eq. 10 with the energy as reaction coordinate. The distribution P(E, t) is shown for t = 0, τ/3, τ and 2τ (solid lines), where τ is the relaxation time. The dashed line is the equilibrium distribution. The diffusion coefficient Db(E) and the potential Fb(E) (light gray band in Fig. 2 a) were both determined from numerical simulations, using a block size of τb = 106 MC steps (see Eq. 12). (b) The space dependence of the diffusion coefficient Db(E). The band is centered around the expected value and shows the statistical 1σ error.

Given Db(r) and Fb(r), we solve Eq. 10 for P(r, t) by using the finite-difference scheme in Appendix B. The initial distribution P(r, t = 0) is taken to be the same as in the kinetic simulations. We find that the mean of P(r, t) shows single-exponential relaxation to a good approximation. An exponential fit of these data gives us a new prediction, τpred, for the relaxation time.

From Table 2 it can be seen that the prediction obtained through this more elaborate calculation, τpred, is not better than the previous one, τpred,0, at least not in Q, despite that there exists a weak barrier in this coordinate (see Fig. 2 b). This means that the barrier in Q is too weak to be important for the relaxation rate. If the underlying diffusion picture, Eq. 10, had been perfect, τpred would have been equal to τ, as obtained from the kinetic simulations. Our results show that this is not the case. At least in Q, there are significant deviations from the behavior predicted by this equation.

If more accurate relaxation time predictions are needed, there are different ways to proceed. One possible way is to simply increase the block size. However, for the calculation to be useful, the block size must remain small compared to the relaxation time. A more interesting possibility is to refine the simple diffusion picture defined by Eq. 10, in which, in particular, non-Markovian effects are ignored. Such effects may indeed affect folding times (Plotkin and Wolynes, 1998; Plotkin and Onuchic, 2002b). Yet another possibility is to use a combination of a few different variables, perhaps E and Q, instead of a single reaction coordinate (Du et al., 1998; Socci et al., 1998; Plotkin and Onuchic, 2002b). With a multidimensional representation of the folding process, non-Markovian effects could become smaller.

SUMMARY AND DISCUSSION

We have analyzed the thermodynamics and kinetics of a designed three-helix-bundle protein, based on Monte Carlo calculations. We found that this model protein shows two-state behavior, in the sense that melting curves to a good approximation can be described by a simple two-state system and that the relaxation behavior is close to single exponential. A simple two-state picture is, nevertheless, an oversimplification, as the free-energy barrier separating the native and unfolded states is weak (≲1kT). The weakness of the barrier implies that a fitted two-state parameter such as ΔE has no clear physical meaning, despite that the two-state fit looks good.

Reduced (Kolinski et al., 1998; Takada et al., 1999; Zhou and Karplus, 1999; Shea et al., 1999; Berriz and Shakhnovich, 2001) and all-atom (Guo et al., 1997; Duan and Kollman, 1998; Shen and Freed, 2002; Kussell et al., 2002; Zagrovic et al., 2002; Linhananta and Zhou, 2003) models for small helical proteins have been studied by many other groups. Most of these studies relied on so-called Gō-type (Gō and Abe, 1981) potentials. It should therefore be pointed out that our model is sequence based.

Using an extended version of this model that includes all atoms, we recently found similar results for two peptides, an α-helix and a β-hairpin (Irbäck et al., 2003). Here the calculated melting curves could be directly compared with experimental data, and a reasonable quantitative agreement was found.

The smallness of the free-energy barrier prompted us to perform an analytical study of diffusion in a square-well potential. Here we studied the relaxation behavior at temperature T, starting from the equilibrium distribution at temperature T0, for arbitrary T and T0. We found that this system shows a relaxation behavior that is close to single exponential for a wide range of T0, T values, despite the absence of a free-energy barrier. We also made relaxation-time predictions based on this square-well approximation. Here we took the diffusion coefficient to be constant. It was determined assuming the dynamics to be diffusive on timescales beyond the reconfiguration time for an individual helix. The predictions obtained this way were found to agree within a factor of two with observed relaxation times, as obtained from the kinetic simulations. So, this calculation, based on the two simplifying assumptions that the potential is a square well and that the diffusion coefficient is constant, gave quite good results. A more detailed calculation, in which these two additional assumptions were removed, did not give better results. This shows that the underlying diffusion picture leaves room for improvement.

Our kinetic study focused on the behavior at the folding temperature Tf, where the native and unfolded states, although not separated by a clear barrier, are very different, which makes the folding mechanism transparent. In particular, we found that helix formation and chain collapse could not be separated, which is in accord with experimental data by Krantz et al. (2002). The difference between the native and unfolded states is much smaller at the lowest temperature we studied, 0.95Tf, because the unfolded state is much more nativelike here. Mayor et al. (2003) recently reported experimental results on a three-helix-bundle protein, the engrailed homeodomain (Clarke et al., 1994), including a characterization of its unfolded state. In particular, the unfolded state was found to have a high helix content. This study was performed at a temperature below 0.95Tf. It would be very interesting to see what the unfolded state of this protein looks like near Tf. In our model, there is a significant decrease in helix content of the unfolded state as the temperature increases from 0.95Tf to Tf.

It is instructive to compare our results with those of Zhou and Karplus (1999), who discussed two folding scenarios for helical proteins, based on a Gō-type Cα model. In their first scenario, folding is fast, without any obligatory intermediate, and helix formation occurs before chain collapse. In the second scenario, folding is slow with an obligatory intermediate on the folding pathway, and helix formation and chain collapse occur simultaneously. The behavior we find does not match any of these two scenarios. In our case, helix formation and chain collapse occur in parallel but folding is nevertheless fast and without any well-defined intermediate state.

Acknowledgments

This work was supported in part by the Swedish Foundation for Strategic Research and the Swedish Research Council.

APPENDIX A: DIFFUSION IN A SQUARE WELL

Here we discuss Eq. 10 in the situation when the reaction coordinate r is the energy E, and the potential F(E) is a square well of width ΔEsw at T = Tf. This means that the equilibrium distribution is given by Peq(E) ∝ exp(−δβE) if E is in the square well and Peq(E) = 0 otherwise, where δβ = 1/kT − 1/kTf. Eq. 10 then becomes

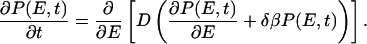graphic file with name M14.gif (13)

For simplicity, the diffusion coefficient is assumed to be constant, D(E) = D. The initial distribution P(E, t = 0) is taken to be the equilibrium distribution at some temperature T0, and we put δβ0 = 1/kT0 − 1/kTf.

By separation of variables, it is possible to solve Eq. 13 with this initial condition analytically for arbitrary values of the initial and final temperatures T0 and T, respectively. In particular, this solution gives us the relaxation behavior of the average energy. The average energy at time t, E(t), can be expressed in the form

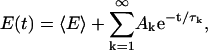graphic file with name M15.gif (14)

where 〈E〉 denotes the equilibrium average at temperature T. A straightforward calculation shows that the decay constants in this equation are given by

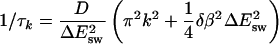graphic file with name M16.gif (15)

and the expansion coefficients by

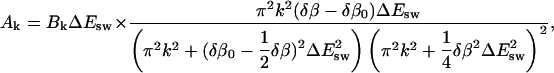graphic file with name M17.gif (16)

where

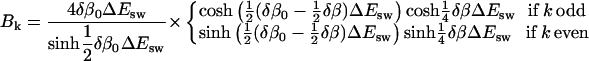graphic file with name M18.gif (17)

Finally, the equilibrium average is

graphic file with name M19.gif (18)

where En and Eu are the lower and upper edges of the square well, respectively.

It is instructive to consider the behavior of this solution when |δβ−δβ0| ≪ 1/ΔEsw. The expression for the expansion coefficients can then be simplified to

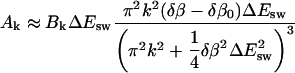graphic file with name M20.gif (19)

with

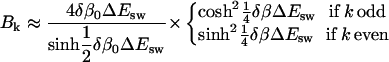graphic file with name M21.gif (20)

Note that Ak scales as k2 if 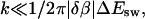Inline graphic and as 1/k4 if 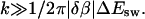Inline graphic Note also that the last factor in Bk suppresses Ak for even k if T is close to Tf. From these two facts it follows that |A1| is much larger than the other |Ak| if T is near Tf. This makes the deviation from a single exponential small.

APPENDIX B: NUMERICAL SOLUTION OF THE DIFFUSION EQUATION

To solve Eq. 10 numerically for arbitrary D(r) and F(r), we choose a finite-difference scheme of Crank-Nicolson type with good stability properties. To obtain this scheme we first discretize r. Put rj = jΔr, Dj = D(rj) and Fj = F(rj), and let p(t) be the vector with components pj(t) = P(rj, t). Approximating the RHS of Eq. 10 with suitable finite differences, we obtain

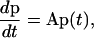graphic file with name M24.gif (21)

where A is a tridiagonal matrix given by

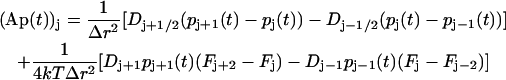graphic file with name M25.gif (22)

Let now pn = p(tn), where tn = nΔt. By applying the trapezoidal rule for integration to Eq. 21, we obtain

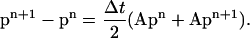graphic file with name M26.gif (23)

This equation can be used to calculate how P(r, t) evolves with time. It can be readily solved for pn+1 because the matrix A is tridiagonal.

References

  1. Berriz, G. F., and E. I. Shakhnovich. 2001. Characterization of the folding kinetics of a three-helix bundle protein via a minimalist Langevin model. J. Mol. Biol. 310:673–685. [DOI] [PubMed] [Google Scholar]
  2. Bryngelson, J. D., J. N. Onuchic, N. D. Socci, and P. G. Wolynes. 1995. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 21:167–195. [DOI] [PubMed] [Google Scholar]
  3. Clarke, N. D., C. R. Kissinger, J. Desjarlais, G. L. Gilliland, and C. O. Pabo. 1994. Structural studies of the engrailed homeodomain. Protein Sci. 3:1779–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Clementi, C., A. E. García, and J. N. Onuchic. 2003. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: all-atom representation study of protein L. J. Mol. Biol. 326:933–954. [DOI] [PubMed] [Google Scholar]
  5. Du, R., V. S. Pande, A. Y. Grosberg, T. Tanaka, and E. I. Shakhnovich. 1998. On the transition coordinate for protein folding. J. Chem. Phys. 108:334–350. [Google Scholar]
  6. Duan, Y., and P. A. Kollman. 1998. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science. 282:740–744. [DOI] [PubMed] [Google Scholar]
  7. Favrin, G., A. Irbäck, and F. Sjunnesson. 2001. Monte Carlo update for chain molecules: biased Gaussian steps in torsional space. J. Chem. Phys. 114:8154–8158. [Google Scholar]
  8. Favrin, G., A. Irbäck, and S. Wallin. 2002. Folding of a small helical protein using hydrogen bonds and hydrophobicity forces. Proteins. 47:99–105. [DOI] [PubMed] [Google Scholar]
  9. Garcia-Mira, M. M., M. Sadqi, N. Fischer, J. M. Sanchez-Ruiz, and V. Muñoz. 2002. Experimental identification of downhill protein folding. Science. 298:2191–2195. [DOI] [PubMed] [Google Scholar]
  10. Gō, N., and H. Abe. 1981. Non-interacting local-structure model of folding and unfolding transition in globular proteins. Biopolymers. 20:991–1011. [DOI] [PubMed] [Google Scholar]
  11. Guo, Z., C. L. Brooks III, and E. M. Boczko. 1997. Exploring the folding free energy surface of a three-helix bundle protein. Proc. Natl. Acad. Sci. USA. 94:10161–10166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Guo, Z., and D. Thirumalai. 1996. Kinetics and thermodynamics of folding of a de novo designed four-helix bundle protein. J. Mol. Biol. 263:323–343. [DOI] [PubMed] [Google Scholar]
  13. Hagen, S. J., J. Hofrichter, A. Szabo, and W. A. Eaton. 1996. Diffusion-limited contact formation in unfolded cytochrome C: estimating the maximum rate of protein folding. Proc. Natl. Acad. Sci. USA. 93:11615–11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Irbäck, A., and F. Potthast. 1995. Studies of an off-lattice model for protein folding: sequence dependence and improved sampling at finite temperature. J. Chem. Phys. 103:10298–10305. [Google Scholar]
  15. Irbäck, A., B. Samuelsson, F. Sjunnesson, and S. Wallin. 2003. Thermodynamics of α- and β-structure formation in proteins. Biophys. J. 85:1466–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Irbäck, A., F. Sjunnesson, and S. Wallin. 2000. Three-helix-bundle protein in a Ramachandran model. Proc. Natl. Acad. Sci. USA. 97:13614–13618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Irbäck, A., F. Sjunnesson, and S. Wallin. 2001. Hydrogen bonds, hydrophobicity forces and the character of the collapse transition. J. Biol. Phys. 27:169–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jackson, S. E. 1998. How do small single-domain proteins fold? Fold. Des. 3:R81–R91. [DOI] [PubMed] [Google Scholar]
  19. Jackson, S. E., and A. R. Fersht. 1991. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry. 30:10428–10435. [DOI] [PubMed] [Google Scholar]
  20. Kolinski, A., W. Galazka, and J. Skolnick. 1998. Monte Carlo studies of the thermodynamics and kinetics of reduced protein models: application to small helical, β, and α/β proteins. J. Chem. Phys. 108:2608–2617. [Google Scholar]
  21. Kramers, H. A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 7:284–304. [Google Scholar]
  22. Krantz, B. A., A. K. Srivastava, S. Nauli, D. Baker, R. T. Sauer, and T. R. Sosnick. 2002. Understanding protein hydrogen bond formation with kinetic H/D amide isotope effects. Nat. Struct. Biol. 9:458–463. [DOI] [PubMed] [Google Scholar]
  23. Kussell, E., J. Shimada, and E. I. Shakhnovich. 2002. A structure-based method for derivation of all-atom potentials for protein folding. Proc. Natl. Acad. Sci. USA. 99:5343–5348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Linhananta, A., and Y. Zhou. 2003. The role of sidechain packing and native contact interactions in folding: discontinuous molecular dynamics folding simulations of an all-atom Gō model of fragment B of staphylococcal protein A. J. Chem. Phys. 117:8983–8995. [Google Scholar]
  25. Lyubartsev, A. P., A. A. Martsinovski, S. V. Shevkunov, and P. N. Vorontsov-Velyaminov. 1992. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys. 96:1776–1783. [Google Scholar]
  26. Marinari, E., and G. Parisi. 1992. Simulated tempering: a new Monte Carlo scheme. Europhys. Lett. 19:451–458. [Google Scholar]
  27. Mayor, U., N. R. Guydosh, C. M. Johnson, J. G. Grossman, S. Sato, G. S. Jas, S. M. V. Freund, D. O. V. Alonso, V. Daggett, and A. R. Fersht. 2003. The complete folding pathway of a protein from nanoseconds to microseconds. Nature. 421:863–867. [DOI] [PubMed] [Google Scholar]
  28. Miller, R. G. 1974. The jackknife—a review. Biometrika. 61:1–15. [Google Scholar]
  29. Myers, J. K., and T. G. Oas. 2001. Preorganized secondary structure as an important determinant of fast folding. Nat. Struct. Biol. 8:552–558. [DOI] [PubMed] [Google Scholar]
  30. Plotkin, S. S., and J. N. Onuchic. 2002a. Understanding protein folding with energy landscape theory. Part I: basic concepts. Q. Rev. Biophys. 35:111–167. [DOI] [PubMed] [Google Scholar]
  31. Plotkin, S. S., and J. N. Onuchic. 2002b. Understanding protein folding with energy landscape theory. Part II: quantitative aspects. Q. Rev. Biophys. 35:205–286. [DOI] [PubMed] [Google Scholar]
  32. Plotkin, S. S., and P. G. Wolynes. 1998. Non-Markovian configurational diffusion and reaction coordinates for protein folding. Phys. Rev. Lett. 80:5015–5018. [Google Scholar]
  33. Press, W. H., B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling. 1992. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
  34. Shea, J.-E., J. N. Onuchic, and C. L. Brooks, III. 1999. Exploring the origins of topological frustration: design of a minimally frustrated model of fragment B of protein A. Proc. Natl. Acad. Sci. USA. 96:12512–12517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shea, J.-E., J. N. Onuchic, and C. L. Brooks, III. 2002. Probing the folding free energy landscape of the src-SH3 protein domain. Proc. Natl. Acad. Sci. USA. 99:16064–16068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Shen, M. Y., and K. F. Freed. 2002. All-atom fast protein folding simulations: the villin headpiece. Proteins. 49:439–445. [DOI] [PubMed] [Google Scholar]
  37. Socci, N. D., J. N. Onuchic, and P. G. Wolynes. 1996. Diffusive dynamics of the reaction coordinate for protein folding funnels. J. Chem. Phys. 104:5860–5868. [Google Scholar]
  38. Socci, N. D., J. N. Onuchic, and P. G. Wolynes. 1998. Protein folding mechanisms and the multidimensional folding funnel. Proteins. 32:136–158. [PubMed] [Google Scholar]
  39. Takada, S., Z. Luthey-Schulten, and P. G. Wolynes. 1999. Folding dynamics with nonadditive forces: a simulation study of a designed helical protein and a random heteropolymer. J. Chem. Phys. 110:11616–11629. [Google Scholar]
  40. Thompson, P. A., W. A. Eaton, and J. Hofrichter. 1997. Laser temperature jump study of the helix⇆coil kinetics of an alanine peptide interpreted with ‘kinetic zipper’ model. Biochemistry. 36:9200–9210. [DOI] [PubMed] [Google Scholar]
  41. Wallin, S., J. Farwer, and U. Bastolla. 2003. Testing similarity measures with continuous and discrete protein models. Proteins. 50:144–157. [DOI] [PubMed] [Google Scholar]
  42. Williams, S., T. P. Causgrove, R. Gilmanshin, K. S. Fang, R. H. Callender, W. H. Woodruff, and R. B. Dyer. 1996. Fast events in protein folding: helix melting and formation in a small peptide. Biochemistry. 35:691–697. [DOI] [PubMed] [Google Scholar]
  43. Zagrovic, B., C. D. Snow, M. R. Shirts, and V. S. Pande. 2002. Simulation of folding of a small alpha-helical protein in atomistic detail using worldwide-distributed computing. J. Mol. Biol. 323:927–937. [DOI] [PubMed] [Google Scholar]
  44. Zhou, R., and B. J. Berne. 2002. Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water? Proc. Natl. Acad. Sci. USA. 99:12777–12782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhou, Y., and M. Karplus. 1999. Interpreting the folding kinetics of helical proteins. Nature. 401:400–403. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES