Abstract
Ceramides are known to play a major regulatory role in apoptosis by inducing cytochrome c release from mitochondria. We have previously reported that ceramide, but not dihydroceramide, forms large and stable channels in phospholipid membranes and outer membranes of isolated mitochondria. C2-ceramide channel formation is characterized by conductance increments ranging from <1 to >200 nS. These conductance increments often represent the enlargement and contracture of channels rather than the opening and closure of independent channels. Enlargement is supported by the observation that many small conductance increments can lead to a large decrement. Also the initial conductances favor cations, but this selectivity drops dramatically with increasing total conductance. La+3 causes rapid ceramide channel disassembly in a manner indicative of large conducting structures. These channels have a propensity to contract by a defined size (often multiples of 4 nS) indicating the formation of cylindrical channels with preferred diameters rather than a continuum of sizes. The results are consistent with ceramides forming barrel-stave channels whose size can change by loss or insertion of multiple ceramide columns.
INTRODUCTION
Apoptosis, programmed cell death, is a physiological process required for normal development and tissue homeostasis in multicellular organisms. Disregulation of apoptosis is fundamental to many diseases, such as cancer, stroke, heart disease, neurodegenerative disorders, autoimmune disorders, and viral diseases. Mitochondria have been shown to play a major regulatory role in apoptosis (for review see Bernardi et al. (1999); Crompton (1999); Kroemer et al. (1998); Susin et al. (1998); Green and Reed (1998)). Early in apoptosis, there is an increase in the permeability of the mitochondrial outer membrane that leads to the release of intermembrane space proteins, including cytochrome c, apoptosis-inducing factor (AIF), procaspases, and heat shock proteins (Bernardi et al., 1999; Crompton, 1999; Kroemer et al., 1998; Susin et al., 1998; Narula et al., 1999). The release of mitochondrial intermembrane space proteins into the cytoplasm is crucial for the activation of specific caspases and DNases that are responsible for the execution of apoptosis. The mechanism(s) by which proapoptotic intermembrane space proteins are released from mitochondria is a topic of much debate. Several mechanisms have been proposed, including the permeability transition (Crompton, 1999), channels formed by Bax oligomers (Antonsson et al., 2000, 2001; Saito et al., 2000), the mitochondrial apoptosis-induced channel (MAC) (Pavlov et al., 2001), Bax induced lipidic pores (Basañez et al., 1999), BH3/Bax/cardiolipin interactions that induce supramolecular openings/lipidic pores (Kuwana et al., 2002), an interaction between Bax and ceramide (Lee et al., 2002; Belaud-Rotureau et al., 2000; Pastorino et al., 1999), and ceramide channels (Siskind and Colombini, 2000; Siskind et al., 2002).
Ceramide, a sphingosine-based lipid, is known to be involved in the regulation of apoptosis (for a review see Radin, 2001; Kolesnick et al., 2000; Kolesnick and Hannun, 1999; Kolesnick and Krönke, 1998; Ariga et al., 1998; Hannun, 1996). Ceramide can be generated in cells via de novo synthesis from sphingosine and acyl-CoA or hydrolysis of sphingomyelin. Several inducers of cellular stress leading to apoptosis have been shown to cause a net increase in cellular ceramide levels (Kolesnick and Krönke, 1998; Ariga et al., 1998; Hannun, 1996) that often precedes the mitochondrial phase of apoptosis (Bose et al., 1995; Witty et al., 1996; Thomas et al., 1999; Raisova et al., 2000; Perry et al., 2000; Charles et al., 2001; Rodriguez-Lafrasse et al., 2001; Kroesen et al., 2001). Addition of ceramide to whole cells (Zamzami et al., 1995; Castedo et al., 1996; Susin et al., 1997a,b; De-Maria et al., 1997; Zhang et al., 1997; Amarante-Mendes et al., 1998) or isolated mitochondria (Arora et al., 1997; Di Paola et al., 2000; Ghafourifar et al., 1999) induces cytochrome c release. However, the molecular mechanism by which ceramide induces cytochrome c release is still under intense investigation.
We propose that ceramide channels forming in the outer mitochondrial membrane are responsible for the ceramide-induced cytochrome c release. We have previously shown that short- and long-chain ceramides form large and stable (nontransient) channels in membranes, whereas the biologically inactive dihydroceramides do not (Siskind and Colombini, 2000). The addition of either N-acetyl-D-erythro-sphingosine (C2-ceramide) or N-palmitoyl-D-erythro-sphingosine (C16-Ceramide) to the aqueous phase on either one or both sides of a planar phospholipid membrane results in pore formation as indicated by discrete stepwise current increases (Siskind and Colombini, 2000; Siskind et al., 2002). These discrete increments in conductance are, by definition, channels, reflecting the formation of continuous water-filled pathways through the membrane. Others have reported ceramide-induced increases in the permeability of liposomes (Ruiz-Argüello et al., 1996; Simon and Gear, 1998; Montes et al., 2002).
We proposed a structural model to explain the ability of ceramides, despite being lipids, to form large channels in membranes (Siskind and Colombini, 2000). This model is based on the formation of intermolecular hydrogen bonds between hydrogen bond donating and accepting groups in the ceramide molecule. The number of ceramides molecules making up the pore determines the pore size. Because the ceramide channels are composed of many ceramide monomers, their formation is exceedingly sensitive to the free ceramide concentration in the membrane. According to a mathematical model, both the individual conductance of the channels and the overall membrane conductance are directly related to the overall concentration of ceramide in the membrane (Siskind and Colombini, 2000). Slight changes in concentration have dramatic effects on the size of the channels formed (Siskind and Colombini, 2000). De novo synthesis (ceramide synthase) and hydrolysis (ceramidase) enzymes are found in mitochondria (Shimeno et al., 1998; El Bawab et al., 2000). Altering the activity of one or both of these enzymes would change the steady-state level of ceramide, increasing or decreasing the propensity for channel formation and regulating the permeability of the outer membrane to small proteins.
It has been suggested that C2-ceramide can cause unspecific increases in membrane permeability in a detergent-like manner (Radin, 2001; Di Paola et al., 2000; Simon and Gear, 1998; Hofmann and Dixit, 1999). However, our studies utilizing isolated mitochondria have shown that the ceramide-induced increase in the permeability of the outer mitochondrial membrane is due to ceramide channels and not a detergent-like effect (Siskind et al., 2002). Both C2- and C16-ceramide channels allow the bidirectional flux of cytochrome c across the outer mitochondrial membrane, not just cytochrome c release (Siskind et al., 2002). C2-ceramide channels can be reversed with bovine serum albumin thus restoring the permeability barrier of the outer mitochondrial membrane (Siskind et al., 2002). In addition, C2- and C16-ceramide channels allowed the release of other intermembrane space proteins, not just cytochrome c, and had a distinct molecular weight cutoff of 60,000 (Siskind et al., 2002). This sharp cutoff is diagnostic of a channel and distinguishes ceramide channels from a detergent-like effect. In addition, the fact that ceramides do not destabilize solvent-free planar membranes and form channels in said membranes (Siskind and Colombini, 2000) also demonstrates that they are not detergent-like.
The distinct molecular-weight cutoff for ceramide channels in the mitochondrial outer membrane (Siskind et al., 2002) differs from the behavior of ceramide channels in planar membranes where a wide range of single channel conductances is thought to be observed (Siskind and Colombini, 2000). In this study, we performed a detailed analysis of C2-ceramide channel formation and disassembly in planar membranes to explore the possibility that the conductance transition increases often represent enlargements of preformed ceramide channels, rather than the formation of new ceramide channels.
MATERIALS AND METHODS
Materials
The following reagents were purchased from Avanti Polar Lipids (Alabaster, AL): N-acetyl-D-erythro-sphingosine (C2-ceramide), asolectin (polar extract of soybean phospholipids), and diphytanoylphosphatidylcholine (DiPhyPC). All other reagents were purchased from either Fischer Scientific (Pittsburgh, PA) or Sigma Chemical Co. (St. Louis, MO).
Electrophysiological recordings
Planar membranes were formed by the monolayer method (Montal and Mueller, 1972) as modified, (Colombini, 1987), across a 100-μm-diameter hole in a Saran partition using a solution of either 1% (w/v) asolectin (soybean phospholipids), 0.2% (w/v) cholesterol; 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, 0.1% (w/v) cholesterol; or 1% (w/v) DiPhyPC, 0.1% (w/v) cholesterol in hexane to form the monolayers. Except for the reversal potential experiments, the aqueous solution contained 1.0 M KCl, 1 mM MgCl2, and 5mM HEPES (pH 7.0) or 5mM Tris (pH 7.5). The voltage was clamped (trans side was ground) and the current recorded. C2-ceramide was stirred into the water phase from a Me2SO solution to have a final concentration of vehicle not >0.5%.
Reversal potential measurements
Planar membranes were formed as above using a 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, 0.1% (w/v) cholesterol in hexane solution. The aqueous solution on the trans side contained 100 mM KCl, 1 mM MgCl2, and 5 mM PIPES (pH 7.0) and on the cis side 1.0 M KCl, 1 mM MgCl2, and 5 mM PIPES (pH 7.0). The voltage was clamped at 10 mV and the current recorded. C2-ceramide was stirred into the water phase on the cis side to achieve a final concentration of 5 μM. As the ceramide channels started to insert, the voltage required to achieve a zero net current across the membrane was frequently measured.
La+3 reversal experiments
Planar membranes were made as above using 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, 0.1% (w/v) cholesterol in hexane solution. The aqueous solution contained 1 M KCl, 1 mM MgCl2, 5 mM HEPES or Tris (pH 7.5). C2-ceramide (5 μM) was added to the cis side. After the ceramide channels formed and reached a total membrane conductance that remained constant for several minutes, LaCl3 or a La+3 buffer (see below) was added to the cis side of the membrane. When a known free [La+3] was not required, LaCl3 was added to the cis side of the membrane (from a stock solution of LaCl3 made up in the same aqueous solution bathing the membrane) to achieve a final total [La+3] of 1–35 μM. After the La+3 induced complete disassembly of the C2-ceramide channel(s) (the membrane conductance returned to the baseline level), additional buffer was added to the aqueous solution to increase the concentration to 10 mM so that EDTA could be added to chelate the La+3 without a change in pH (protons are released when EDTA chelates La+3 or Mg+2). Throughout the experiment, the voltage was held constant at 10 mV and the current recorded.
La+3 is known to bind to phospholipids and surfaces (Reed and Bygrave, 1974; Hammoudah et al., 1979; Akutsu and Seelig, 1981; Seelig et al., 1987; Bentz et al., 1988; Petersheim and Sun, 1989; Tanaka et al., 2001). Thus when LaCl3 is added to the aqueous solution bathing the planar membrane, the actual free [La+3] is lower than the total La+3 concentration. When a known and constant free [La+3] was desired, a La+3 buffering solution was employed using the chelator ethylene diamine-n,n′-diacetic acid (EDDA). See appendix for details on the calculations and binding constants required for preparing the stock solutions of this La+3-buffer system to achieve a given free [La+3] at a particular pH. The La+3-buffer EDDA exists in different protonated forms and binds other cations such as Mg+2. Thus, the free [La+3] is extremely sensitive to pH and the [Mg+2] must be accurately known. Upon completion of the experiment, the pH of the aqueous solution bathing the membrane was measured to verify that in fact it was at the level used in the calculations of free [La+3]. The pH was occasionally different. In those cases, the free [La+3] was recalculated at the final pH of the medium.
RESULTS
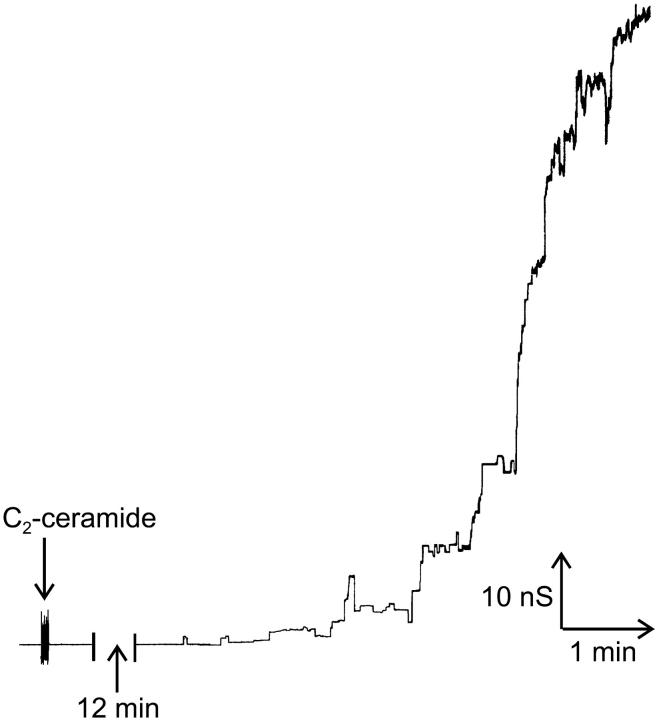
We have previously reported that C2- and C16-ceramides form large channels in solvent free phospholipid membranes (Siskind and Colombini, 2000), whereas the biologically inactive C2- and C18-dihydroceramides do not (Siskind and Colombini, 2000). Addition of 5 μM C2-ceramide to the aqueous phase on one side of a planar phospholipid membrane results in pore formation as indicated by discrete stepwise current increases (Fig. 1 and see Siskind and Colombini, 2000; Siskind et al., 2002). These discontinuous changes, diagnostic of channel formation, have a wide distribution of conductance values (Siskind and Colombini, 2000; Siskind et al., 2002; and Fig. 1), ranging from 1 nS to >200 nS, which, according to the bulk electrolyte properties, would have estimated diameters ranging from 0.4 to 11.4 nm, respectively. Some of these are likely to be large enough to allow cytochrome c (3.4 nm in diameter) to cross the membrane. Small channels are seen early on when the total membrane conductance is low. With time, larger discrete conductance increases are evident, which suggests the formation of larger structures (The possibility that many channels are inserting simultaneously is statistically insignificant). The conductance increments do not increase monotonically indefinitely with time. Eventually the conductance grows with fluctuations of current overlapping into current noise. Depicted in Fig. 1 are representative examples of discrete conductance increases observed with C2-ceramide.
FIGURE 1.
A wide range of discrete conductance increases observed after the addition of C2-ceramide (25 nmol into 5 ml) to the aqueous solution on the cis side of a solvent-free planar phospholipid membrane as described in Materials and Methods. The monolayers were formed using 1% (w/v) asolectin, 0.2% (w/v) cholesterol in hexane and the aqueous buffer consisted of 1.0 M KCl, 1 mM MgCl2, 5 mM Tris (pH 7.5). The applied voltage was clamped at 10 mV (trans side is ground).
Evidence for channel expansion
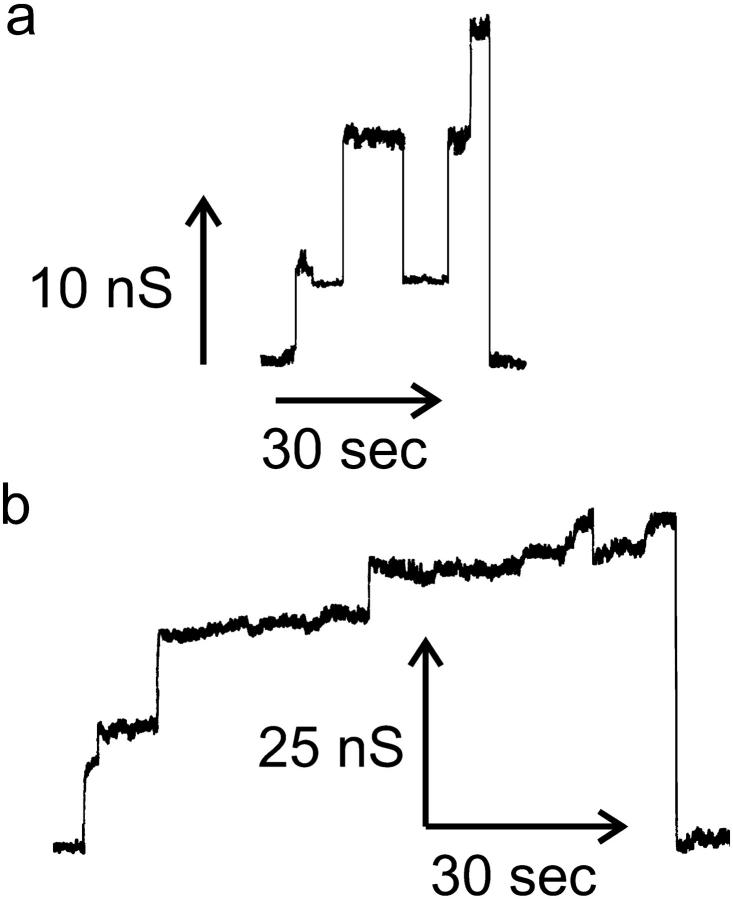
Originally, it was thought that each conductance increment represented the formation of a distinct ceramide channel and that sizes of the ceramide channels could be directly estimated from the distribution of conductance increments (Siskind and Colombini, 2000; Siskind et al., 2002). However, more detailed examinations indicate that this straightforward interpretation is probably incorrect. At least some of these increments represent the increase in size of previously formed channels. For example, we have at times observed a series of small increases in conductance followed by one large conductance drop (Fig. 2). Either all the channels are cooperatively closing simultaneously or they are, in fact, one channel and the increments are merely ceramide aggregates combining with an already-formed channel, resulting in a sudden increase in size and therefore conductance. Although it is possible that ceramide forms arrays of small channels that gate cooperatively, it seems more likely that the individual conductance increments were enlargements of a single ceramide channel that subsequently disassembled.
FIGURE 2.
Evidence of channel enlargement from observations of small increases in conductance followed by one large conductance drop. The conditions were the same as in Fig. 1 except for the lipid composition used to form the monolayers was 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, and 0.1% (w/v) cholesterol in hexane.
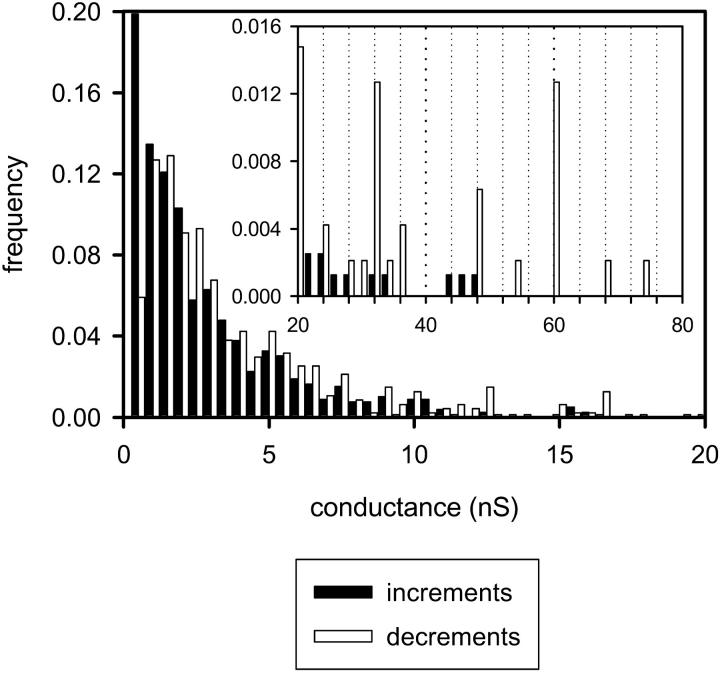
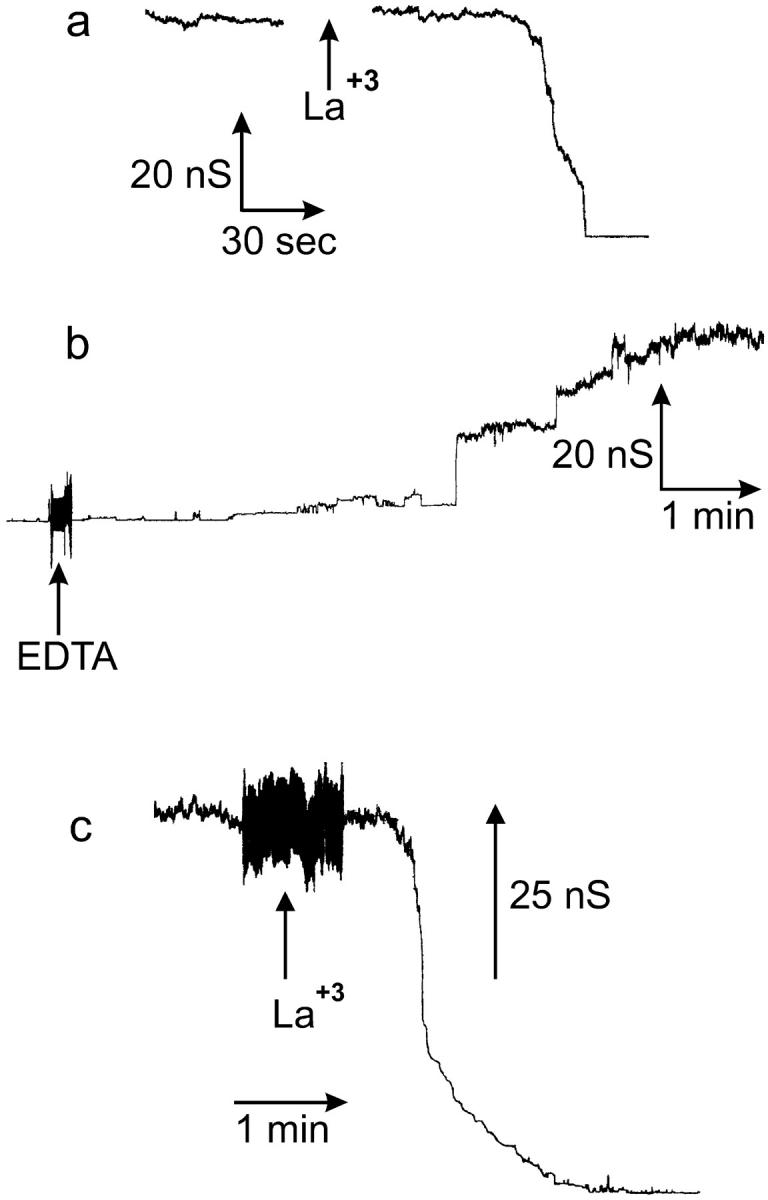
Certain types of distributions of conductance increments and decrements can only be explained by enlargement and contracture of channels, not by channels opening and closing through the same states. Presented in Fig. 3 are the distributions of conductance increments and decrements observed for C2-ceramide channel(s). The mean conductance increment is smaller than the mean conductance decrement (Fig. 3). This is what would be expected if some of the conductance increments represented the enlargement of preexisting ceramide channels. In order for the mean decrement to be larger than the mean increment, some increments would have to add to existing channels, not simply create new ones. If each conductance increment represented the opening of a new channel, then the distribution of decrements could contain only steps equal to or less than the steps seen in the distribution of increments. Rather, the larger decrements are more prevalent than the larger increments and many of the steps seen in the distribution of decrements are larger than the steps seen in the distribution of increments (Fig. 3). Therefore, the decrements, in addition to representing the collapse of ceramide channels, also represent the disassembly of ceramide channels that previously enlarged or the shrinkage of larger ceramide channels to smaller sizes (see next section). The ceramide channels are at least as large as the decrement sizes indicate; although it is possible that even larger channels are forming that do not disassemble. Note that the mean conductance increment presented in the distribution in Fig. 3 is somewhat smaller than the one previously reported (Siskind and Colombini, 2000). This is most likely due to the fact that the membrane and aqueous solutions had different compositions. We are currently exploring the influence of lipid composition, cholesterol content, pH, and Mg+2 on the ceramide channels.
FIGURE 3.
A comparison of the distribution of conductance increments and decrements observed after the addition of C2-ceramide to the aqueous solution bathing planar phospholipid membranes. Conductance changes <20 nS are depicted in the larger figure, whereas the larger ones are depicted in the inset. Conditions were identical to those in Fig. 2. The bin size was 0.5 nS for the main figure and 1.5 nS for the inset. The data was compiled from 18 separate experiments. The vertical dotted lines are placed at conductance values that are multiples of 4.0 nS (20, 24, 28 nS, etc.).
Indications of channel shrinkage
Some of the decrements could also represent the shrinkage of larger ceramide channels to smaller sizes. We have at times observed an increment in conductance that is followed by a decrement to a lower conductance level (Fig. 4). The initial conductance increments presented in the example traces in Fig. 4, a and b, originated from the baseline conductance and thus represent the formation of new channels. The subsequent conductance decrements must therefore represent the shrinkage in size of the channel. Alternatively, the initial conductance increment may represent multiple channels simultaneously inserting and the subsequent smaller decrements may represent the collapse of one of these channels. A more likely explanation is that the decrements represent the shrinkage of a ceramide channel. This is consistent with a multimeric channel that can shrink in size as well as enlarge.
FIGURE 4.
Evidence of channel shrinkage from observations of a single conductance increment from baseline and subsequent decrement(s) to a lower conductance level. The conditions were identical to those in Fig. 2.
Note in Fig. 3 that some of the decrements often occur at very distinct conductance values. Because of the highly complex nature of ceramide channel assembly and disassembly, one would expect that, after combining data from eighteen separate experiments, the decrements would occur over a broad range of conductance values. However, the larger decrements (≥16 nS) tend to occur at distinct conductance values (Fig. 3). The decrements of a particular transition size (conductance) were observed in several experiments and thus are not repeats from the same experiment. Most of these decrements are higher in conductance than the largest increment. In addition, notice in the inset of Fig. 3 that many of these larger decrements are of conductance values that are multiples of 4.0 nS (i.e., 16, 20, 24 nS, etc.). These distinct decrement sizes indicate that the ceramide channels enlarge to certain sizes that are particularly energetically stable. The decreases in conductance of defined sizes may represent losses of monomers in large domain-like units or structural deformations to specific energy-favorable states of lower conductance (more in discussion).
Evidence of channel expansion from selectivity measurements
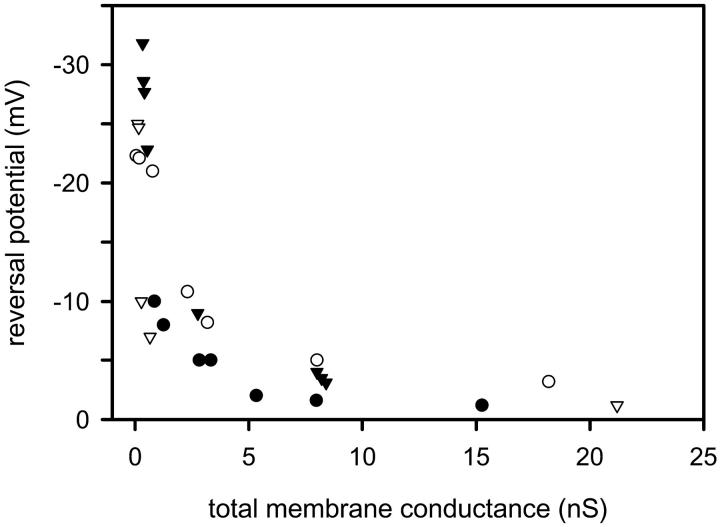
From the observed conductance increments, channel growth seems to be an important process in ceramide channel formation. The alternative, although less likely possibility, that individual channels are cooperating and gating in unison, can be tested by monitoring channel selectivity at the same time as channel insertion. By performing the recordings in the presence of an ion gradient one assesses selectivity by measuring the reversal potential (zero-current potential). This can be measured frequently as the recorded current changes to detect changes in selectivity. Increases in channel size are usually accompanied by a decrease in ion selectivity whereas channels conducting in parallel have the same selectivity. (If the channels are very close there is the possibility of cross talk between them but effects on selectivity in these cases are minor.).
We have recorded significant cation selectivity in small C2-ceramide channels in the presence of a 10-fold KCl gradient (Fig. 5). With increasing total membrane conductance, the reversal potential of the membrane became less negative and eventually approached zero (Fig. 5). This change in reversal potential with increasing total membrane conductance demonstrates a decrease in the selectivity of the channel(s) with increased conductance and thus an increase in their diameter. At large total membrane conductances, the C2-ceramide channel(s) are no longer selective.
FIGURE 5.
Evidence of channel expansion from selectivity measurements made after C2-ceramide addition as the conductance increased. Experiments were performed in the presence of a 10-fold KCl gradient (see Materials and Methods). The monolayers were formed with 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, 0.1% (w/v) cholesterol in hexane. The reversal potential (zero-current potential) was frequently measured as the recorded current changed to detect changes in selectivity. Results are representative of combined data from three separate experiments.
An alternative interpretation might be that the first channels formed are small due to the low free ceramide concentration in the membrane and subsequent channels are larger as more ceramide monomers insert. The larger channels are both more conductive and have lower selectivity resulting in a rapid decline in the overall membrane selectivity. We measured the reversal potential following each of a series of conductance increments and calculated the reversal potential for each increment assuming they were independent channels. The total current, I, is given by:
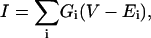 |
where Gi and Ei are the conductance and reversal potential of the ith event respectively and V is the transmembrane potential. These calculations showed that the selectivity was not related to the magnitude of the conductance increment, but rather that the most selective channels always insert first irrespective of their conductance. In one case it would have required a channel with anion selectivity to insert into the membrane to account for the sudden decrease in selectivity. Because no single anion selective ceramide channel has been observed, channel expansion must have taken place.
La+3-induced channel disassembly
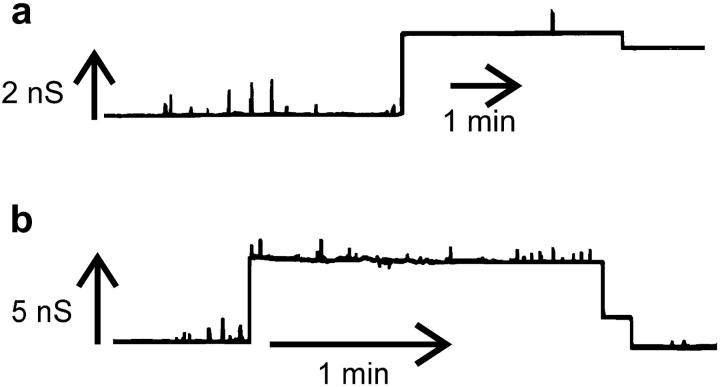
If the ceramide conductance increments reflect the enlargement of one or a few ceramide channels, then the addition of agents that caused channel closure or disassembly may reveal the presence of one or a few large channels. La+3 is a known inhibitor of various types of channels and transporters (Takata et al., 1966; Reed and Bygrave, 1974; Armstrong and Cota, 1990; Sparagna et al., 1995; Colvin, 1998; Colvin et al., 2000; Gincel et al., 2001). La+3 eliminates ceramide conductance (Fig. 6, a and c). The inhibition by La+3 is reversible because removal of La+3 by addition of the chelator, EDTA, allows for the reformation of the ceramide channels (Fig. 6 b). In addition, La+3 inhibition of ceramide channels was not dependent on the membrane composition; we observed inhibition in membranes using solutions of 0.5% (w/v) DiPhyPC, 0.5% (w/v) asolectin, 0.1% (w/v) cholesterol; 1% (w/v) DiPhyPC, 0.2% (w/v) cholesterol; and 1% (w/v) asolectin, 0.2% (w/v) cholesterol in hexane to form the monolayers (data not shown). We interpret this inhibition by La+3 as channel disassembly.
FIGURE 6.
La+3 eliminates C2-ceramide conductance. (a–c) Planar phospholipid membranes were formed from monolayers using a solution of 0.5% (w/v) asolectin, 0.5% (w/v) DiPhyPC, 0.1% (w/v) cholesterol in hexane, and the aqueous solution consisted of 1 M KCl, 1 mM MgCl2, 5 mM HEPES (a, b) or Tris (c) pH (7.0). C2-ceramide (5 μM) (25 nmol into 5 ml) was added to aqueous solution on the cis side of the membrane and the voltage was held constant at 10 mV. (a) LaCl3 added to the cis side (10 μM final) rapidly eliminated the C2-ceramide-induced conductance. (b) EDTA addition (10 μM final) restored ceramide conductance (HEPES concentration increased to 10 mM before addition of EDTA). (c) C2-ceramide-induced conductance is eliminated by a 150-nM free La+3 concentration. The free [La+3] was held constant by the La+3-buffer EDDA as described in the Materials and Methods section and the Appendix.
To observe, in more detail, the process of channel disassembly after La+3 addition, lower amounts of La+3 were added so that the process could proceed at a slower rate. However, La+3 is known to bind to phospholipids and various types of surfaces (Reed and Bygrave, 1974; Hammoudah et al., 1979; Akutsu and Seelig, 1981; Seelig et al., 1987; Bentz et al., 1988; Petersheim and Sun, 1989; Tanaka et al., 2001). Therefore, the free concentration of La+3 in the chamber was both unknown and, worse still, probably changing during the experiment. This sometimes resulted in channel reassembly presumably as the [La+3] dropped below the effective value. To maintain a constant and known free [La+3], we developed a La+3-buffering system utilizing the compound ethylene diamine-n,n′-diacetic acid (EDDA; see appendix for details of pK values for binding constants and calculations).
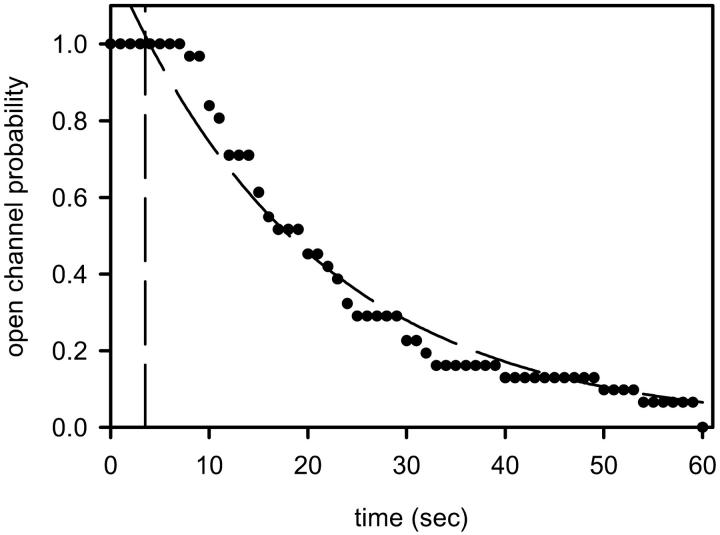
Using the La+3 buffer, we found that 75–225 nM of free La+3 (depending on the experiment) was sufficient to totally or almost totally eliminate the ceramide conductance. These experiments revealed evidence of the disassembly or closure of large structures. As depicted in Fig. 6 c, addition of the La+3-buffering system (addition is made while solution is being stirred) is followed by a brief delay, in which the total membrane conductance remains essentially constant, and then a sudden decrease in the total conductance to baseline. This is distinctly different from the exponential conductance decrease that is expected for the inhibition of a population of channels. In addition, the observed delay times ranged from 8 to 60 s; these delay times are much longer than the time it takes for diffusion through the unstirred layer in these chambers (estimated at 3.5 s for the measured thickness of 55 μm; Negrete et al., 1996). It is highly unlikely that many ceramide channels would be inhibited synchronously by La+3 (i.e., disassemble simultaneously). It is much more likely that the total membrane conductance is comprised of only one or a few large channels rather than many small ones. Although individual experiments do not show an exponential conductance decrease after La+3 addition, pooling the results from many experiments leads to an exponential decay. As illustrated in Fig. 7, the observed likelihood of the conductance being unchanged after La+3 addition (the open channel probability) decayed essentially in an exponential manner when the data was pooled from several experiments.
FIGURE 7.
The observed likelihood of the C2-ceramide-induced conductance being unchanged after La+3 addition decays in essentially an exponential manner. For each time point after the addition of La+3, experiments were given ratings of one or zero, indicating no change or a decrease in conductance respectively. The values for each particular time point were combined between experiments and plotted against time. Results are a combination of data from 31 separate experiments. The vertical dashed line at 3.5 s represents the calculated diffusion time through the unstirred layers. The dashed line through the data is an exponential fit through data. The time constant is 29 s.
In addition, a comparison of the distributions of decrements observed after the La+3 addition for low (<25 nS), medium (>25–100 nS), and high (>100 nS) total membrane conductances (at the time of the La+3 addition) is made in Fig. 8. When the La+3 is added at higher total membrane conductances, the decrements are significantly larger (Fig. 8 c) than when it is added at medium (Fig. 8 b) or low (Fig. 8 a) total membrane conductances. If at higher total membrane conductances there is an increase in the number of channels rather than an increase in the size of preexisting channels, then after the La+3 addition, the mean decrement in the distribution would be of similar size to the mean decrement size of the distributions at low and medium total membrane conductances. However, this is not the case (Fig. 8), further confirming ceramide channel enlargement. Note that the larger decrements (>16 nS; Fig. 8 c) are consistent in size with the ones observed earlier (Fig. 3) in that they occur at very distinct conductances that are often multiples of 4.0 nS.
FIGURE 8.
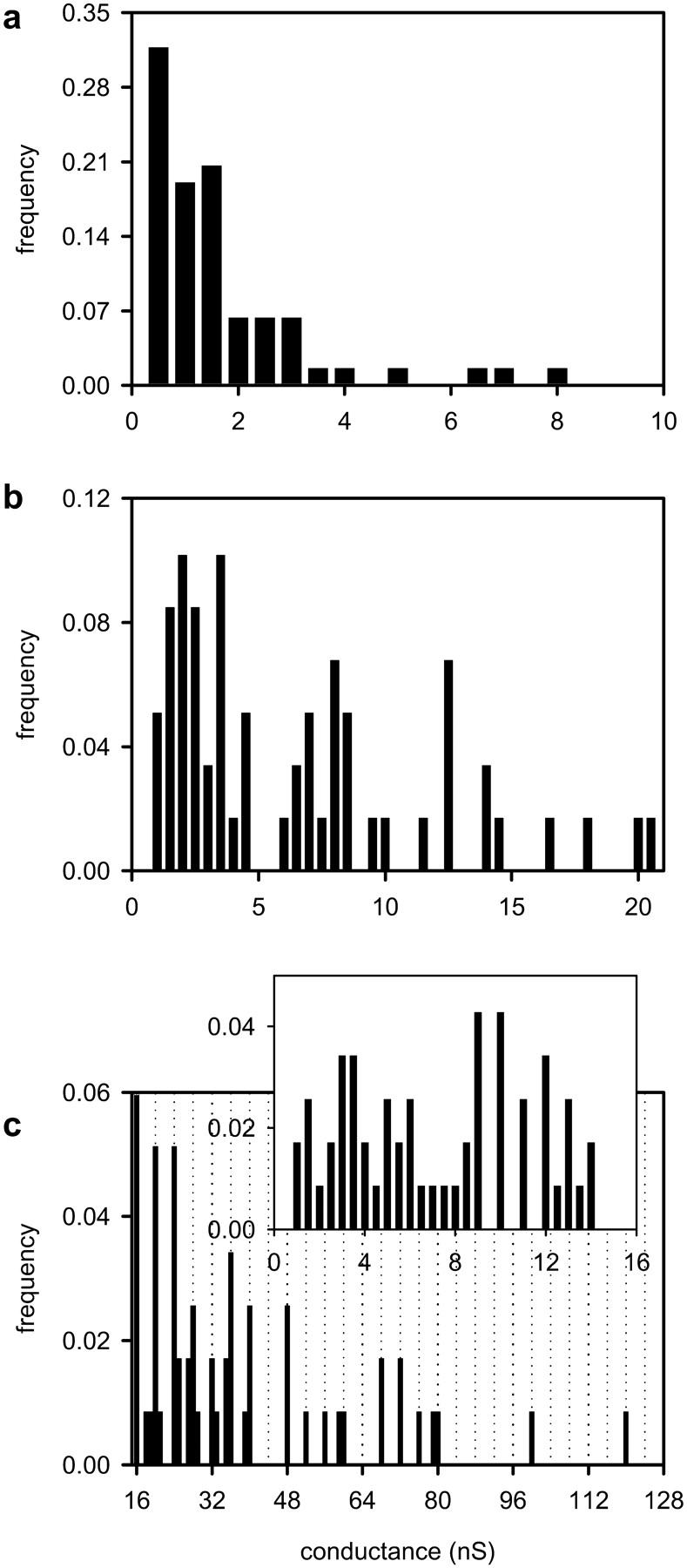
A comparison of the distributions of decrements observed after the La+3 addition for (a) low (<25 nS), (b) medium (from 25 to <100 nS), and (c) high (>100 nS) total initial membrane conductance. In c the decrements <16 nS are depicted in the inset, whereas those larger are depicted in the main figure. The vertical dotted lines are placed at conductance values that are multiples of 4.0 nS (i.e., 16, 20, 24 nS, etc.).
DISCUSSION
The conductance increments in a phospholipid membrane after ceramide addition are not multiples of a fundamental conductance. A broad range of events is observed. (Siskind and Colombini, 2000; Siskind et al., 2002). It was originally thought that each discrete conductance increase represented the formation of a new ceramide channel and that the size of ceramide channels could be directly estimated from the sizes of the discrete conductance increases (Siskind and Colombini, 2000). However, the results of this study show that this straightforward interpretation was incorrect. Ceramide channels enlarge in size; the size of the channels is much larger than can be predicted by the individual conductance increments. The discrete conductance increases and decreases represent, in addition to the formation and disassembly of novel channels, the enlargement and shrinkage of these channels. The results of this paper show that channel enlargement is a fundamental process in ceramide channel assembly.
Structure of the ceramide channel
The primary evidence for channel enlargement is the observation of multiple conductance increments followed by a large conductance decrement. This is supported by histograms of all the increments and decrements observed under a given set of conditions showing that the mean decrement size is of larger conductance than the mean increment size. The reduction in selectivity with increased conductance also shows that the ceramide channels are enlarging. Finally, La+3-induced channel disassembly shows the type of cooperativity expected for the disassembly of large channels.
The ability of ceramide channels to enlarge and shrink in size can be explained by our previously proposed ceramide channel structural model (Siskind and Colombini, 2000; and see Fig. 9). Each ceramide molecule contains several hydrogen bond donating and accepting groups, namely the two hydroxyls (on carbons 1 and 3 of the sphingoid base backbone), the amide nitrogen, and the carbonyl group (see Fig. 9 a for ceramide structure). The molecular model for ceramide channels is based on the ability of ceramide molecules to form intermolecular hydrogen bonds (Pascher, 1976; Moore et al., 1997). We propose the formation of columns of ceramides on the membrane surface held together by intermolecular hydrogen bonds between amide nitrogens and carbonyl groups located on opposite surfaces of the ceramide molecule (Fig. 9 b). These columns could swing into the membrane, forming an annulus stabilized by hydrogen bonding of the hydroxyl groups lining the channel (Fig. 9, c and d). This hydrogen-bonded network would be similar to the structure of ice and thus should form a good interface between the water in the channel and the nonpolar portion of the ceramide molecule (Fig. 9, c and d, for a top and a cut-away longitudinal view, respectively). Each transmembrane column would consist of six to seven individual ceramide molecules (sufficient to span the membrane). This column has a dipole moment due to the alignment of the amide linkages and thus we propose that adjacent columns are oriented in opposite directions so that the dipoles attract. The number of columns in the annulus determines the size of the channel. This is essentially a barrel-stave model for the channel; the insertion or removal of columns or groups of columns would result in channel enlargement or contracture, respectively. We propose that the curvature of the headgroups of the surrounding phospholipids at the outer edge of the channel is such that they minimize the exposure of the hydrophobic regions of the channel edge (Fig. 9 d).
FIGURE 9.
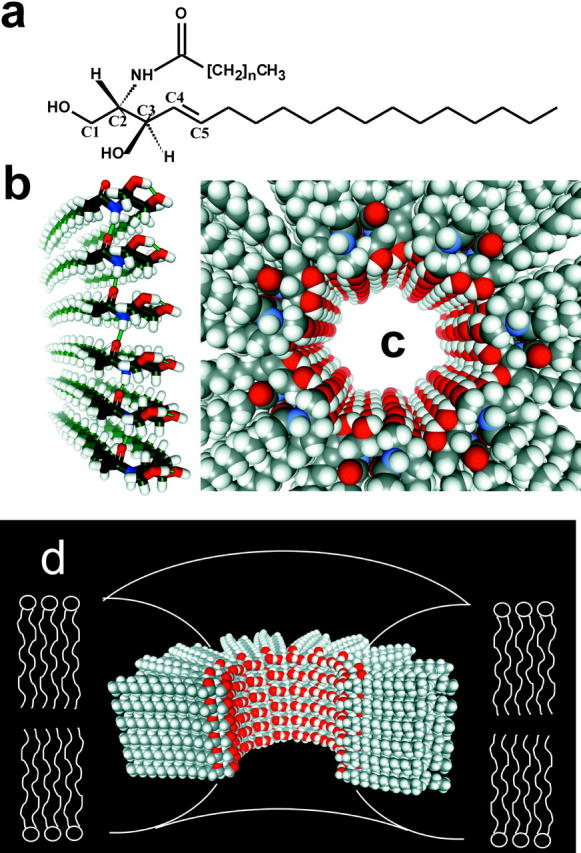
Structural model for ceramide channels. (a) C2-ceramide structure. (b) A column of ceramide residues held together by intermolecular hydrogen bonds between amide nitrogens and carbonyl groups. This column would span the hydrophobic portion of the membrane and in association with other columns would form pores of varying sizes. (c) Top view of a ceramide channel, consisting of 14 columns of ceramide molecules. Adjacent columns are oriented in an antiparallel fashion so that amide dipoles attract. The columns are held together via intermolecular hydrogen bonds between hydroxyl groups proposed to line the channel lumen. (d) A longitudinal cutaway of a ceramide channel, consisting of 14 columns of ceramide molecules, where four columns have been removed to show the interior of the channel. The curvature of the phospholipids of the membrane at the channel interface would minimize the exposure of the hydrophobic regions of the outer surface of the channel to the aqueous solution.
Ceramide channel formation is similar to a polymerization process and, like the polymerization of actin or tubulin, there seems to be a kinetic barrier to nucleation. After the addition of C2-ceramide to the aqueous solution bathing the membrane, there is a long delay period before the appearance of the first channel (ranging from ∼2 to 45 min) followed by a lag period in which total membrane conductance initially increases at a very slow rate (Fig. 1). During this period, small channels often form and disassemble multiple times. The conductance then increases at a faster rate with a concomitant increase in the size of the increments and decrements. The slow initial progression may indicate both a slow rate of formation of the initial channel(s) and an inherent instability of small channels. The faster subsequent increase in conductance may reflect the faster rate of channel growth. Channel growth beyond a certain size may be a much faster process that competes effectively with the formation of new channels. This may explain why the disassembly of channels after La+3 addition indicates the presence of only a single large channel (Figs. 6, 7, and 8). The long delay time (long compared to the diffusion time through the unstirred layer) before disassembly (Figs. 6 and 7) demonstrates the cooperative nature of the process and is best explained in terms of one or a few large structures.
Larger channels must be either kinetically or energetically favored over the formation of new channels. The interaction energy of the proposed hydrogen-bonded network lining the pore (hydrogen bond lengths and angles) may depend on the radius of curvature of the wall of the pore which, in turn, depends on the number of columns forming the channel. Thus, the orientation of ceramide molecules in larger channels may allow for the formation of stronger hydrogen bonds. In addition, the packing of the ceramide hydrocarbon chains may favor larger channels. At some point, however, the wedge-shaped structure of ceramide may limit the size of the pore. The repulsive forces between the ceramide hydrophobic chains may lead to an optimal size range for these channels.
Indeed, the data supports the notion that certain sizes/conformations of ceramide channels are preferred over others. Fig. 3 shows that the larger decrements occurred predominantly at distinct conductance levels. Similarly, the larger decrements (>16 nS) that were observed after the addition of La+3 at high total membrane conductance (>100 nS; Fig. 8 c) also occurred with high frequency at distinct conductance levels. Interestingly, the majority of these high frequency decrements are of conductances that are multiples of 4 nS (Figs. 3 and 8 c).
Multiplicity of 4.0 nS and the mechanism of channel contracture
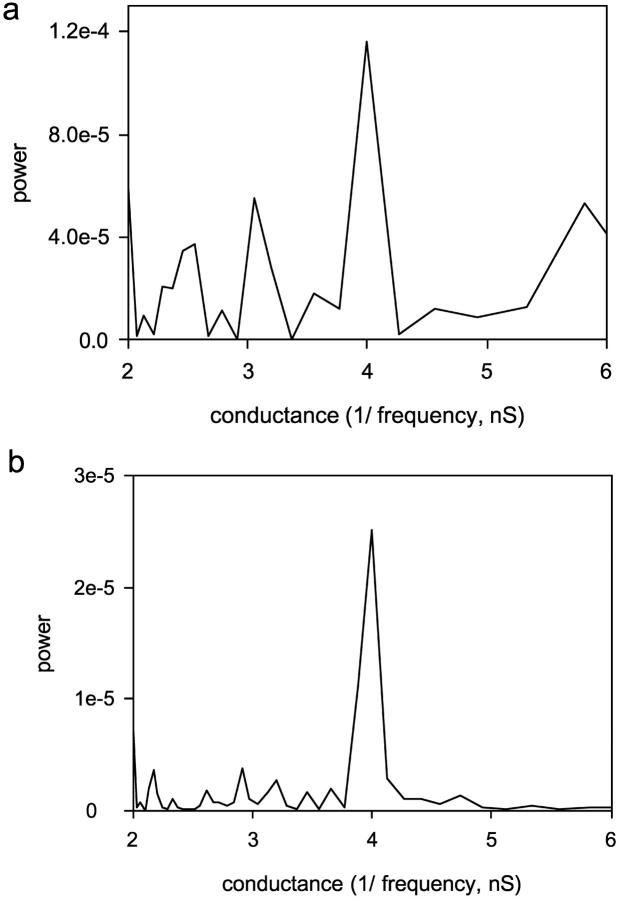
A visual inspection of the histograms in Figs. 3 (spontaneous decrements) and 8 c (La+3-induced decrements) shows that the large decrements (>12 nS) tend to occur at multiples of 4 nS. To confirm and amplify this unusual observation, a fast Fourier transform analysis of the channel size distributions was performed using Origin software. The conductance replaced the time axis and the smallest resolvable unit was taken as 0.25 nS. The power spectra (Fig. 10) show a sharp peak at 0.25 Hz. There are other peaks including higher harmonics (not shown). The peak at 0.25 Hz is indeed so sharp as to justify the use of two significant digits, i.e., 4.0 nS, demonstrating a remarkably precise multiplicity (i.e., 12, 16, 20 nS, etc.).
FIGURE 10.
A fast Fourier transform analysis of conductance decrements ≥12 nS from the distributions in Fig. 3 (panel a) and in Fig. 8 c (panel b). The power spectrum of the fast Fourier transform (using the program Origin 6.1) was performed on all observed decrements ≥12 nS. Only a portion of the spectrum is shown with the x axis presented as the inverse of the frequency (in this case the conductance in nS).
This multiplicity of 4 nS demonstrates that the disassembly process occurs by means of multiples of a fundamental structural unit. The structural unit cannot be a single ceramide molecule. However, a barrel-stave model of the ceramide channel presents a larger unit, the single ceramide column or perhaps a pair of columns. This unit could naturally slide out of the channel to the membrane surface. However, one expects that the conductance is related to the area of the channel, not the circumference. As we shall see, this expectation disappears for large channels. We used a theoretical model to test whether a mechanism, where channel disassembly consists of removal of columns, could result in conductance decrements that are multiples of 4 nS.
For large channels, the conductance (G) of a channel can be calculated from the radius and length of the channel as follows (Hille, 1992):
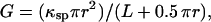 |
(1) |
where r is the radius of the channel, κsp the specific conductance (equal to 112 for 1.0 M KCl; Robinson and Stokes, 1965), and L the length of the channel (estimated at ∼5 nm). The channel length (L) is increased by 0.5 (π r) to take into account the access resistance. Thus, the conductance in nS (r in nm) is:
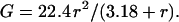 |
(2) |
The radius can be replaced by (n d) / (2 π), where n is the number of columns and d the thickness of a column or fundamental column multiple (in nm). Thus, the change in conductance (in nS) becomes:
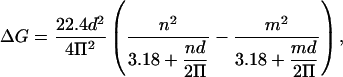 |
(3) |
where m represents the number of columns remaining in the channel after the decrease in conductance. For very large channels, 3.18 is small compared to the radius and can be eliminated. This approximation has a 10-fold smaller impact when changes in conductance are calculated. Using this approximation, the change in conductance (in nS) is:
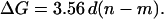 |
(4) |
Because term (n − m) must always be an integer, ΔG would occur as multiples of 4.0 nS if d were equal to 1.12 nm. This size is compatible with the dimension of two ceramide columns indicating that the fundamental unit of disassembly is a two-column unit. This is consistent with two columns interacting by the favorable dipole-dipole interaction of adjacent amide linkages oriented in opposite directions (Fig. 9 c).
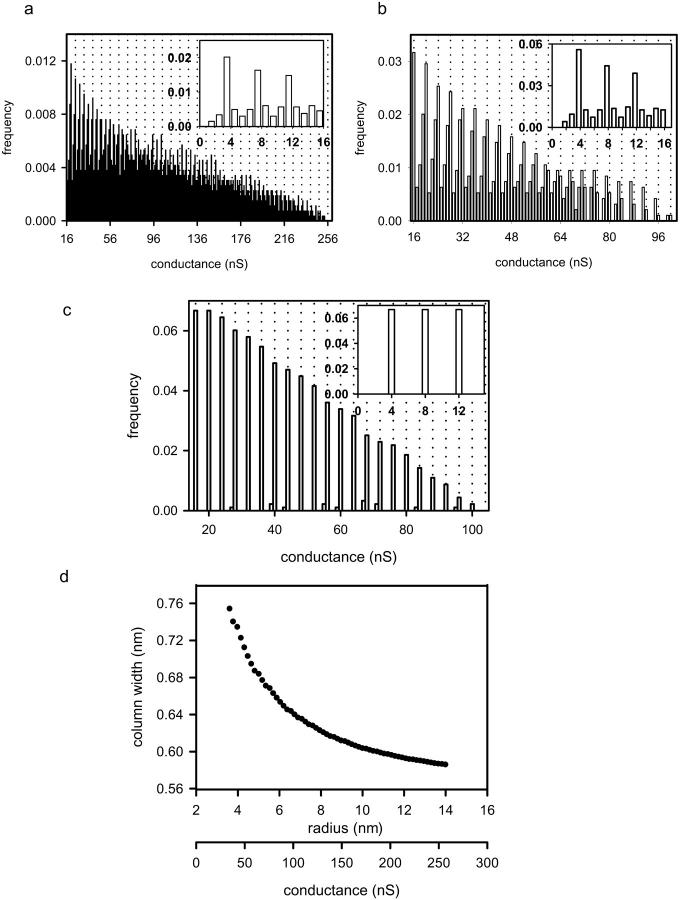
The elimination of 3.18 from the denominator would only be valid for large channels. For channels less than ∼100 nS, this simplification results in a >10% error. If the large-channel assumption is eliminated and a theoretical model channel of 150 columns is employed, then calculations, using Eq. 3 above, of all possible decrements from the disassembly of the channel by the removal of two-column units results in the distribution presented in Fig. 11 a. This theoretical model assumes that the smallest possible channel consists of six columns and utilizes a fixed column width of 0.586 nm. Notice that this theoretical distribution presented in Fig. 11 a differs greatly from that which is observed in Figs. 3 and 8 c. A broad range of conductance decrements is observed in the theoretical distribution in Fig. 11 a and the decrements do not occur as multiples of 4.0 nS. This is distinctly different from that which is experimentally observed in the distributions of spontaneous (Fig. 3) and La+3-induced decrements (Fig. 8 c). However, the model assumes that there is no upper limit to the number of two-column units that can be removed in a single event in the disassembly process. When the model was constrained by assuming that the maximum number of two-column units that can be removed from a channel in any one event is one-third of the total columns in the channel, the decrements in the distribution sharpen at multiples of 4.0 nS (Fig. 11 b). However, the peaks are not as distinct as in the experimental results. A further refinement would be to allow the column width to vary. It may be that the column thickness changes as the radius of curvature of the channel changes in the disassembly process yielding the observed multiplicity of exactly 4.0 nS. When the column width was allowed to vary, exact multiples of 4.0 nS could be generated (Fig. 11 c). Fig. 11 d depicts the relationship between the column width and the radius/conductance of the channel that generates a periodicity of 4.0 nS. Note that as the channel radius (or conductance) decreases, the column width required to achieve decrements with a periodicity of four, increases. This is somewhat counterintuitive in that one would expect the column width to decrease, rather than increase, as the channel radius decreases. The answer may lie in the structure of the hydrogen-bonded network. Molecular dynamic simulations may provide insight into this issue.
FIGURE 11.
All possible decrements that would result from the disassembly of a theoretical model ceramide channel consisting initially of 150 columns by the removal of two-column units were calculated utilizing Eq. 3 (see text). (a) Fixed column width of 0.586 nm; (b) fixed column width of 0.586 nm and the upper limit of one-third for the fraction of columns lost in any single decrement event; (c) the same constraint as in b but with the column width adjusted to yield multiples of four; (d) the relationship between column width and channel radius/conductance from c required to achieve a periodicity of four.
Small ceramide channels may disassemble by a more complicated process than the constraints placed on the model. The data show a continuum in the size of small decrements (<12 nS). For channels with smaller radii of curvature single columns, rather than pairs of columns, may come out of the channel. In addition, the length of the channel has a much greater impact on the conductance of channels with smaller radii than it does for channels with larger radii. If the disassembly process included changes in channel length, this would result in conductance changes more easily detected with small channels. These processes would result in a broad distribution of decrements for smaller channels, as is observed (Figs. 3 and 8).
A major difference between the decrements in the theoretical distribution and that obtained experimentally is that the larger decrements of Fig. 11 c occur at every multiple of 4.0 nS, whereas the decrements that are observed experimentally occur preferentially at particular multiples of 4.0 nS and not at others. This theoretical model does not include the energetics of the channel disassembly process. Regardless, the larger decrements occurring at conductance values that are multiples of 4.0 nS are evidence of a barrel-stave model for ceramide channel structure. Indeed, the model requires that the channel be essentially a perfect cylinder rather than a defect in the membrane.
Ceramide channel enlargement
Ceramide channel enlargement could also occur by the addition of columns or pairs of columns even though the increments do not appear to be of conductances that are multiples of 2.0 or 4.0 nS. This is most likely due to the fact that the increments are smaller in size than the decrements, which indicates that the channels increase by smaller changes in size. In addition, it is interesting that after a given decrement when a segment comes out of the channel an equal-sized increment is not usually observed, reflecting the reinsertion of the segment into the channel. (Rarely one sees conductance oscillations between two levels.) This fundamental asymmetry can be explained in terms of the difference between the radius of curvature of the inside of the channel and the membrane surface.
According to a simple barrel-stave arrangement of columns, the channel could theoretically grow indefinitely with the size limited only by the concentration of ceramide monomers in the membrane. However, the observations indicate some upper limit to the channel size. This is in agreement with the previous work on intact mitochondria (Siskind et al., 2002). Clearly, as the channel grows, the radius of curvature of the channel also grows. The energetics of the hydrogen-bonded network lining the channel and the steric nature of the ceramide packing may depend on the radius of curvature resulting in an optimal size. Therefore, when a multicolumn segment leaves the channel, the infinite radius of curvature on the surface may break up the segment into smaller units (fewer columns). This would make conductance increments smaller than decrements. Future molecular modeling simulations will hopefully provide insights into the energetics behind this process.
Channel budding and fusion?
An alternative model for the origin of conductance changes is channel fusion and budding. Two channels could fuse to become one larger channel. The intermediate structure would initially have an oblong/oval shape before becoming a circular pore. This oblong-shaped channel would be of lower conductance than the final circular cylinder. In fact, just before a large increment in conductance, we often observe a smaller decrement (for example in Fig. 1). This could be evidence for a fusion model for channel enlargement. The reverse process, budding (several columns could bud off a large channel, leaving two smaller channels), could account for conductance drops. However, theoretical calculations show that a budding process does not yield conductance drops that are multiples of a fundamental unit. Needless to say, other models that propose that ceramides act by simply disrupting the membrane or forming rafts that result in defects between these and the surrounding phospholipids are all in sharp disagreement with the findings of this paper. Indeed, the results strongly argue that the channels are not flaccid structures but rather rigid cylinders whose structure is determined by the hydrogen-bonded network forming the inner lining of the channel.
La+3-induced channel disassembly
We hypothesize that La+3-induced disassembly of ceramide channels occurs through interaction with hydroxyl and/or carbonyl oxygen atoms of the ceramides causing disruption of hydrogen bonds that hold the channel together. An alternative hypothesis involves an effect of lanthanides on the phospholipids thereby indirectly inducing channel disassembly. The high-affinity binding of lanthanides to negatively charged phospholipid headgroups has been shown to affect the physical properties of phospholipid membranes (Ermakov et al., 2001; Tanaka et al., 2001). Lanthanides have been reported to cause phase transitions (Hammoudah et al., 1979; Li et al., 1994; Verstraeten et al., 1997; Tanaka et al., 2001), vesicle fusion (Hammoudah et al., 1979; Bentz et al., 1988; Petersheim and Sun, 1989), conformation changes in the headgroups of phosphatidylcholine membranes (Akutsu and Seelig, 1981; Seelig et al., 1987), and even pore formation in erythrocytes (Cheng et al., 1999). Lanthanides have been shown to interact with and inhibit a variety of membrane proteins and ion channels, including mechanogated channels (Gustin et al., 1988; Yang and Sachs, 1989; Zhou and Kung, 1992; Hamill and McBride, 1996; Caldwell et al., 1998; Lee et al., 1999), the voltage-gated sodium channel (Takata et al., 1966; Armstrong and Cota, 1990), the mitochondrial outer membrane channel, VDAC (Gincel et al., 2001), the nonselective cation channel, from human placental microvillous membranes (Grosman and Reisin, 2000), the mitochondrial Ca+2 uniporter (Nicholls and Akerman, 1982) and the plasma membrane zinc exporter (Colvin, 1998; Colvin et al., 2000). It has been proposed that lanthanide binding to membrane lipids indirectly influences the properties of membrane proteins (Tanaka et al., 2001; Ermakov et al., 2001). Because we observed La+3 disassembly of ceramide channels in membranes composed of only uncharged lipids at a total concentration of 3 μM, we are leaning toward a direct action of La+3 on the channels.
Irrespective of lanthanum's mechanism of action, the results of the lanthanum experiments strongly support the conclusion that single large channels grow in size rather than the formation of many small channels. The observed long delay period (nonexponential decay for the individual experiments) before a decrease in conductance indicates the disassembly of a single structure. When the results from many experiments were pooled, an exponential decay was observed as expected for a population of channels. The lanthanum results also argue that the observed conductance arises from an organized ceramide channel structure rather than ceramide-induced structural changes in the phospholipid membrane. Note that La+3 has been shown to induce the Lα to HII phase transition and stabilize the hexagonal II (HII) phase (Tanaka et al., 2001). However, ceramide alone has been shown to facilitate the lamellar-to-hexagonal transition in lipid bilayers (Ruiz-Argüello et al., 1996; Veiga et al., 1999). It has been proposed that the ability of ceramide to induce lamellar-to-hexagonal transitions in lipid bilayers explains its ability to increase the permeability of membranes (Ruiz-Argüello et al., 1996; Veiga et al., 1999; Montes et al., 2002). However, the ability of La+3 to disassemble ceramide channels, given its effects on the physical properties of membranes, argues against this possibility.
As with any effector, the potency of La3+ is related to the free concentration required to achieve a half-maximal response. With La3+, this is difficult to determine because La+3 binds to surfaces in general and phospholipids in particular (Reed and Bygrave, 1974; Hammoudah et al., 1979; Akutsu and Seelig, 1981; Seelig et al., 1987; Bentz et al., 1988; Petersheim and Sun, 1989; Tanaka et al., 2001). In some of our experiments, the free La+3 concentration was held at a constant known level by the use of a La+3 buffer system. As far as the authors are aware, this is the only method to date that allows for a constant and known free concentration of La+3 in the nanomolar range. Existing methods for the measurement of the free [La+3] are not sensitive enough. For example, the metallochromic dye murexide spectrophotometrically detects changes in [Ca+2] or [La+3] in the presence of subcellular particles (Lehninger and Carafoli, 1971; Reed and Bygrave, 1974; Tapia et al., 1985), but is limited to the micromolar range. This new method may allow the determination of the potency of the effects of La+3 and help distinguish between direct effects on channels as opposed to indirect effects on membrane properties.
Comparison with other channels formed from many monomers
Ceramide is not the only channel to exhibit nonintegral conductance increments nor is it the only channel that can enlarge in size. Extensive studies utilizing membrane-active peptides have increased our understanding of ion-channel structure, self-assembly of inactive monomers into active channel-forming aggregates, and peptide-lipid interactions and the role that these interactions play in biological function (for review see Sansom (1993); Shai (1999); Chugh and Wallace (2001)). Many membrane-active peptides are amphipathic in nature, which allows them to self-oligomerize into channel-forming assemblies that span the width of phospholipid membranes. In addition, many membrane-active peptides form pores of varying conductance whose size depends on the number of aggregates making up the pore, including alamethicin (e.g., Hanke and Boheim, 1980; Fox and Richards, 1982; Spach et al., 1989; Sansom, 1991, 1993; Woolley and Wallace, 1992; Keller et al., 1993; Vodyanoy et al., 1993; Bezrukov and Vodyanoy, 1993; Cafiso, 1994; Helluin et al., 1997) subtilin (Schuller et al., 1989), melittin (Hanke et al., 1983), pardaxin (Ehrenstein and Lecar, 1977; Rapaport and Shai, 1992; Shai, 1994), the pore-forming protein from Entamoeba histolytica (Keller et al., 1989), and several members of the trichorzianine family (Molle et al., 1987). These channels are thought to have “barrel-stave” arrangements; peptide monomers oligimerize to form a helix bundle surrounding a central aqueous pore whose size depends on the number of helices in the bundle (Shai, 1999).
CONCLUSION
From the results of this paper, it is evident that channel enlargement is a fundamental process for ceramide channel formation. It is clear that the channels are distinct structures with preferred sizes; enlargement and contracture allow channels to preferentially adopt low energy states. The sizes of ceramide channels in planar phospholipid membranes cannot be directly estimated from individual conductance increments and decrements. The channels may enlarge to optimal sizes that may correspond to the 60,000 molecular weight cutoff observed in isolated mitochondria (Siskind et al., 2002). It is evident that ceramide channel kinetics is complex and requires further investigation for increased understanding.
Recent studies of ceramide channel formation in isolated mitochondria showed that ceramide channels have the right biophysical properties to be responsible for the release of proapoptotic factors from mitochondria (Siskind et al., 2002). When added to isolated mitochondria they increase the permeability of the outer membrane in a way that is consistent with the formation of dynamic channels. The appropriate enzymes capable of regulating ceramide levels are located in mitochondria. There is evidence that the activity of synthetic enzymes is elevated early in apoptosis (Kroesen et al., 2001; Lee et al., 2002). Because ceramide channels are good candidates for the pathway in the outer membrane that is responsible for the release of proapoptotic factors leading to irreversible apoptosis, an understanding of the energetics and kinetics of ceramide channels is essential. Further understanding of ceramide channel energetics and kinetics will allow us to investigate and understand how biologically relevant external factors influence channel enlargement or disassembly. A full understanding of the energetics, kinetics, and mechanics of ceramide channels is thus essential for the development of pharmacological tools that can be used to promote either ceramide channel enlargement or disassembly for the control of apoptosis and hence treatment of disease.
Acknowledgments
This work was supported by National Institutes of Health grant NS042025, a National Institutes of Health predoctoral fellowship to L.S., and an undergraduate fellowship to A.D. from a Howard Hughes Medical Institute grant to the University of Maryland.
APPENDIX
Calculations of the free lanthanum ion concentration using the binding constants of the compound, ethylene diamine-n,n′-diacetic acid
The buffer ethylene diamine-n,n′-diacetic acid (EDDA) was utilized to maintain a constant and known free La+3 concentration. The binding constants for the EDDA complexes were obtained from a program put out by the National Institute of Standards and Technology (NIST), namely the NIST Standard Reference Database 46, NIST Critically Selected Stability Constants of Metal Complexes: Version 6.0. The pK values for the binding constants of relevant complexes are listed in Table 1. These pK values were used to calculate the concentrations of the complexes between EDDA and H+, Mg+2, and La+3 (ions designated as “A”) according to the following relationship:
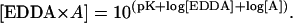 |
(A1) |
A spreadsheet program was used to calculate the concentrations of all involved species to find conditions that would yield the desired free concentration of La+3 at the desired pH. The free concentrations of Mg+2 and EDDA−2 were adjusted to yield the total concentrations of MgCl2, EDDA, and LaCl3 that would result in the desired conditions. To generate a free [La+3] of 149 nM, the final concentrations of the ingredients were: 6.02 mM EDDA, 1.27 mM MgCl2, 0.596 mM LaCl3 neutralized with potassium hydroxide to a final concentration of 7.55 mM. The pH was 8.0. A concentrated solution was produced and an appropriate aliquot added to the chamber to achieve the indicated final concentrations.
TABLE 1.
Stability constants for the relevant EDDA complexes
| Complex | pK Value |
|---|---|
| LaEDDA+ | 6.95 |
| LaHEDDA+2 | 4.5 |
| LaEDDA2− | 11.56 |
| LaH2EDDA+3 | 10.7 |
| HEDDA− | 9.64 |
| H2EDDA | 6.7 |
| H3EDDA+ | 2.35 |
| H4EDDA+2 | 1.75 |
| MgEDDA | 3.95 |
Note that in our experimental conditions, we used an aqueous buffer bathing the planar membranes that consisted of 1 M KCl, 1 mM MgCl2, 5 mM Tris (pH 7.5). The concentration of Mg+2 already present is taken into consideration as part of the total [Mg+2]. The pH was measured at the end of the experiment and the [La+3]free recalculated. We used Tris buffer even though it has been suggested that Tris has an affinity for La+3. A literature search revealed no evidence for such an affinity.
References
- Akutsu, H., and J. Seelig. 1981. Interaction of metal ions with phosphatidylcholine bilayer membranes. Biochemistry. 20:7366–7373. [DOI] [PubMed] [Google Scholar]
- Amarante-Mendes, G. P., C. Naekyung Kim, L. Liu, Y. Huang, C. L. Perkins, D. R. Green, and K. Bhalla. 1998. Bcr-Abl exerts its antiapoptotic effect against diverse apoptotic stimuli through blockage of mitochondrial release of cytochrome c and activation of caspase-3. Blood. 91:1700–1705. [PubMed] [Google Scholar]
- Antonsson, B., S. Montessuit, S. Lauper, R. Eskes, and J. C. Martinou. 2000. Bax oligomerization is required for channel-forming activity in liposomes and to trigger cytochrome c release from mitochondria. Biochem. J. 345:271–278. [PMC free article] [PubMed] [Google Scholar]
- Antonsson, B., S. Montessuit, B. Sanchez, and J. C. Martinou. 2001. Bax is present as a high molecular weight oligomer/complex in the mitochondrial membrane of apoptotic cells. J. Biol. Chem. 276:11615–11623. [DOI] [PubMed] [Google Scholar]
- Ariga, T., W. D. Jarvis, and R. K. Yu. 1998. Role of sphingolipid-mediated cell death in neurodegenerative diseases. J. Lipid Res. 39:1–16. [PubMed] [Google Scholar]
- Armstrong, C. M., and G. Cota. 1990. Modification of sodium channel gating by lanthanum. Some effects cannot be explained by surface charge theory. J. Gen. Physiol. 96:1129–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arora, A. S., B. J. Jones, T. C. Patel, S. F. Bronk, and G. J. Gores. 1997. Ceramide induces hepatocyte cell death through disruption of mitochondrial function in the rat. Hepatology. 25:958–963. [DOI] [PubMed] [Google Scholar]
- Basañez, G., A. Nechushtan, O. Drozhinin, A. Chanturiya, E. Choe, S. Tutt, K. A. Wood, Y.-T. Hsu, J. Zimmerberg, and R. J. Youle. 1999. Bax, but not Bcl-xL, decreases the lifetime of planar phospholipid bilayer membranes at subnanomolar concentrations. Proc. Natl. Acad. Sci. USA. 96:5492–5497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belaud-Rotureau, M. A., N. Leducq, F. Macouillard Poulletier de Gannes, P. Diolez, L. Lacoste, F. Lacombe, P. Bernard, and F. Belloc. 2000. Early transitory rise in intracellular pH leads to Bax conformational change during ceramide-induced apoptosis. Apoptosis. 5:551–560. [DOI] [PubMed] [Google Scholar]
- Bentz, J., D. Alford, J. Cohen, and N. Düzgünes. 1988. La3+-induced fusion of phosphatidylserine liposomes. Close approach, intermembrane intermediates, and the electrostatic surface potential. Biophys. J. 53:593–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi, P., L. Scorrano, R. Colonna, V. Petronilli, and F. Di Lisa. 1999. Mitochondria and cell death. Mechanistic aspects and methodological issues. Eur. J. Biochem. 264:687–701. [DOI] [PubMed] [Google Scholar]
- Bezrukov, S. M., and I. Vodyanoy. 1993. Probing alamethicin channels with water-soluble polymers. Effect on conductance of channel states. Biophys. J. 64:16–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bose, R., M. Verheij, A. Haimovitz-Friedman, K. Scotto, Z. Fuks, and R. Kolesnick. 1995. Ceramide synthase mediates daunorubicin-induced apoptosis: an alternative mechanism for generating death signals. Cell. 82:405–414. [DOI] [PubMed] [Google Scholar]
- Cafiso, D. S. 1994. Alamethicin: a peptide model for voltage-gating and protein-membrane interactions. Annu. Rev. Biophys. Biomol. Struct. 23:141–165. [DOI] [PubMed] [Google Scholar]
- Caldwell, R. A., H. F. Clemo, and C. M. Baumgarten. 1998. Using gadolinium to identify stretch-activated channels: technical considerations. Am. J. Physiol. 275:C619–C621. [DOI] [PubMed] [Google Scholar]
- Castedo, M., T. Hirsch, S. A. Susin, N. Zamzami, P. Marchetti, A. Macho, and G. Kroemer. 1996. Sequential acquisition of mitochondrial and plasma membrane alterations during early lymphocyte apoptosis. J. Immunol. 157:512–521. [PubMed] [Google Scholar]
- Charles, A. G., T. Y. Han, Y. Y. Liu, N. Hansen, A. E. Giuliano, and M. C. Cabot. 2001. Taxol-induced ceramide generation and apoptosis in human breast cancer cells. Cancer Chemother. Pharmacol. 47:444–450. [DOI] [PubMed] [Google Scholar]
- Cheng, Y., M. Liu, R. Li, C. Wang, C. Bai, and K. Wang. 1999. Gadolinium induces domain and pore formation of human erythrocyte membrane: an atomic force microscopic study. Biochim. Biophys. Acta. 1421:249–260. [DOI] [PubMed] [Google Scholar]
- Chugh, J. K., and B. A. Wallace. 2001. Peptaibols: models for ion channels. Biochem. Soc. Trans. 29:565–570. [DOI] [PubMed] [Google Scholar]
- Colombini, M. 1987. Characterization of channels isolated from plant mitochondria. Method. Enzymol. 148:465–475. [DOI] [PubMed] [Google Scholar]
- Colvin, R. A. 1998. Characterization of a membrane zinc transporter in rat brain. Neurosci. Lett. 247:147–150. [DOI] [PubMed] [Google Scholar]
- Colvin, R. A., N. Davis, R. W. Nipper, and P. A. Carter. 2000. Evidence for a zinc/proton antiporter in rat brain. Neurochem. Int. 36:539–547. [DOI] [PubMed] [Google Scholar]
- Crompton, M. 1999. The mitochondrial permeability transition pore and its role in cell death. Biochem. J. 341:233–249. [PMC free article] [PubMed] [Google Scholar]
- De-Maria, R., L. Lenti, F. Malisan, F. d'Agostino, B. Tomassini, A. Zeuner, M. R. Rippo, and R. Testi. 1997. Requirement for GD3 ganglioside in CD95- and ceramide-induced apoptosis. Science. 277:1652–1655. [DOI] [PubMed] [Google Scholar]
- Di Paola, M., T. Cocco, and M. Lorusso. 2000. Ceramide interaction with the respiratory chain of heart mitochondria. Biochemistry. 39:6660–6668. [DOI] [PubMed] [Google Scholar]
- Ehrenstein, G., and H. Lecar. 1977. Electrically gated ionic channels in lipid bilayers. Q. Rev. Biophys. 10:1–34. [DOI] [PubMed] [Google Scholar]
- El Bawab, S., P. Roddy, T. Qian, A. Bielawska, J. J. Lemasters, and Y. A. Hannun. 2000. Molecular cloning and characterization of a human mitochondrial ceramidase. J. Biol. Chem. 275:21508–21513. [DOI] [PubMed] [Google Scholar]
- Ermakov, Y. A., A. Z. Averbakh, A. I. Yusipovich, and S. Sukharev. 2001. Dipole potentials indicate that restructuring of the membrane interface induced by gadolinium and beryllium ions. Biophys. J. 80:1851–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox, R. O., and F. M. Richards. 1982. A voltage-gated ion channel model interred from the crystal structure of alamethicin at 1.5 Å resolution. Nature. 300:325–330. [DOI] [PubMed] [Google Scholar]
- Ghafourifar, P., S. D. Klein, O. Schucht, U. Schenk, M. Pruschy, S. Rocha, and C. Richter. 1999. Ceramide induces cytochrome c release from isolated mitochondria. Importance of mitochondrial redox state. J. Biol. Chem. 274:6080–6084. [DOI] [PubMed] [Google Scholar]
- Gincel, D., H. Zaid, and V. Shoshan-Barmatz. 2001. Calcium binding and translocation by the voltage-dependent anion channel: a possible regulatory mechanism in mitochondrial function. Biochem. J. 358:147–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green, D. R., and J. C. Reed. 1998. Mitochondria and apoptosis. Science. 281:1309–1312. [DOI] [PubMed] [Google Scholar]
- Grosman, C., and I. L. Reisin. 2000. Single-channel characterization of a nonselective cation channel from human placental microvillous membranes. Large conductance, multiplicity of conductance states, and inhibition by lanthanides. J. Membr. Biol. 174:59–70. [DOI] [PubMed] [Google Scholar]
- Gustin, M., X.-L. Zhou, B. Martinac, and C. Kung. 1988. A mechanosensitive ion channel in the yeast plasma membrane. Science. 242:762–765. [DOI] [PubMed] [Google Scholar]
- Hamill, O. P., and D. W. McBride, Jr. 1996. The pharmacology of mechanogated membrane ion channels. Pharmacol. Rev. 48:231–252. [PubMed] [Google Scholar]
- Hammoudah, M. M., S. Nir, T. Isac, R. Kornhauser, T. P. Stewart, S. W. Hui, and W. L. C. Vaz. 1979. Interaction of La3+ with phosphatidylserine vesicles: binding, phase transition, leakage, and fusion. Biochim. Biophys. Acta. 558:338–343. [DOI] [PubMed] [Google Scholar]
- Hanke, W., and G. Boheim. 1980. The lowest conductance state of the alamethicin pore. Biochim. Biophys. Acta. 596:456–462. [DOI] [PubMed] [Google Scholar]
- Hanke, W., C. Methfessel, H. U. Wilmsen, E. Katz, G. Jung, and G. Boheim. 1983. Melittin and a chemically modified trichotoxin form alamethicin-type multi-state pores. Biochim. Biophys. Acta. 727:108–114. [DOI] [PubMed] [Google Scholar]
- Hannun, Y. A. 1996. Functions of ceramide in coordinating cellular responses to stress. Science. 274:1855–1859. [DOI] [PubMed] [Google Scholar]
- Helluin, O., J.-Y. Dugast, G. Molle, A. R. Machie, S. Ladha, and H. Doclohier. 1997. Lateral diffusion and conductance properties of a fluorescein-labelled alamethicin in planar lipid bilayers. Biochim. Biophys. Acta. 1330:284–292. [DOI] [PubMed] [Google Scholar]
- Hille, B. 1992. Ionic Channels of Excitable Membranes, 2nd ed. Sinauer Assoc., Sunderland, MA. 59.
- Hofmann, K., and V. M. Dixit. 1999. Reply to Kolesnick and Hannun, and Perry and Hannun. Trends Biochem. Sci. 24:227. [DOI] [PubMed] [Google Scholar]
- Keller, F., W. Hanke, D. Trissl, and T. Bakker-Grunwald. 1989. Pore-forming protein from Entamoeba histolytica forms voltage- and pH-controlled multi-state channels with properties similar to those of the barrel-stave aggregates. Biochim. Biophys. Acta. 982:89–93. [DOI] [PubMed] [Google Scholar]
- Keller, S. L., S. M. Bezrukov, S. M. Gruner, M. W. Tate, I. Vodyanoy, and V. A. Parsegian. 1993. Probability of alamethicin conductance states varies with nonlamellar tendency of bilayer phospholipids. Biophys. J. 65:23–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolesnick, R. N., F. M. Goñi, and A. Alonoso. 2000. Compartmentalization of ceramide signaling: physical foundations and biological effects. J. Cell. Physiol. 184:285–300. [DOI] [PubMed] [Google Scholar]
- Kolesnick, R., and Y. A. Hannun. 1999. Ceramide and apoptosis. Trends Biochem. Sci. 24:224–227. [DOI] [PubMed] [Google Scholar]
- Kolesnick, R. N., and M. Krönke. 1998. Regulation of ceramide production and apoptosis. Annu. Rev. Physiol. 60:643–665. [DOI] [PubMed] [Google Scholar]
- Kroemer, G., B. Dallaporta, and M. Resche-Rigon. 1998. The mitochondrial death/life regulator in apoptosis and necrosis. Annu. Rev. Physiol. 60:619–642. [DOI] [PubMed] [Google Scholar]
- Kroesen, B. J., B. Pettus, C. Luberto, M. Busman, H. Sietsma, L. de Leij, and Y. A. Hannun. 2001. Induction of apoptosis through B-cell receptor cross-linking occurs via de novo generated C16-ceramide and involves mitochondria. J. Biol. Chem. 276:13606–13614. [DOI] [PubMed] [Google Scholar]
- Kuwana, T., M. R. Mackey, G. Perkins, M. H. Ellisman, M. Latterich, R. Schneiter, D. R. Green, and D. D. Newmeyer. 2002. Bid, bax, and lipids cooperate to form supramolecular openings in the outer mitochondrial membrane. Cell. 111:331–342. [DOI] [PubMed] [Google Scholar]
- Lee, H., Z. Fuks, A. Rimner, D. Ehleiter, J. Reed, W.-C. Liao, and R. Kolesnick. 2002. Ionizing radiation remodels mitochondrial membranes to facilitate Bax insertion. In preparation.
- Lee, J., A. Ishihama, G. Oxford, B. Johnson, and K. Jacobson. 1999. Regulation of cell movement is mediated by stretch-activated calcium channels. Nature. 400:382–386. [DOI] [PubMed] [Google Scholar]
- Lehninger, A. L., and E. Carafoli. 1971. The interaction of La+3 with mitochondria in relation to respiration-coupled Ca2+ transport. Arch. Biochem. Biophys. 143:506–515. [DOI] [PubMed] [Google Scholar]
- Li, X., Y. Zhang, J. Ni, J. Chen, and F. Hwang. 1994. Effect of lanthanide ions on the phase behavior of dipalmitoylphosphatidylcholine multilamellar liposomes. J. Inorg. Biochem. 53:139–149. [DOI] [PubMed] [Google Scholar]
- Molle, G., H. Duclohier, and G. Spach. 1987. Voltage-dependent and multi-state ionic channels induced by trichorzianines, anti-fungal peptides related to alamethicin. FEBS Lett. 224:208–212. [DOI] [PubMed] [Google Scholar]
- Montal, M., and P. Mueller. 1972. Formation of bimolecular membranes from lipid monolayers, and a study of their electrical properties. Proc. Natl. Acad. Sci. USA. 69:3561–3566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montes, L. R., M. B. Ruiz-Argüello, F. M. Goñi, and A. Alonoso. 2002. Membrane restructuring via ceramide results in enhanced solute efflux. J. Biol. Chem. 277:11788–11794. [DOI] [PubMed] [Google Scholar]
- Moore, D. J., M. E. Rerek, and R. Mendelsohn. 1997. FTIR spectroscopy studies of the conformational order and phase behavior of ceramides. J. Phys. Chem. B. 101:8933–8940. [Google Scholar]
- Narula, J., P. Pandey, E. Arbustini, N. Haider, N. Narula, F. D. Kolodgie, B. Dal Bello, M. J. Semigran, A. Bielsa-Masdeu, G. W. Dec, S. Israels, M. Ballester, R. Virmani, S. Saxna, and S. Kharbanda. 1999. Apoptosis in heart failure: release of cytochrome c from mitochondria and activation of caspase-3 in human cardiomyopathy. Proc. Natl. Acad. Sci. USA. 96:8144–8149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negrete, H., R. Rivers, A. H. Gough, M. Colombini, and M. L. Zeidel. 1996. Individual leaflets of a membrane bilayer can independently regulate permeability. J. Biol. Chem. 271:11627–11630. [DOI] [PubMed] [Google Scholar]
- Nicholls, D., and K. Akerman. 1982. Mitochondrial calcium transport. Biochim. Biophys. Acta. 683:57–88. [DOI] [PubMed] [Google Scholar]
- Pascher, I. 1976. Molecular arrangements in sphingolipids. Conformation and hydrogen bonding of ceramide and their implication on membrane stability and permeability. Biochim. Biophys. Acta. 455:433–451. [DOI] [PubMed] [Google Scholar]
- Pastorino, J. G., M. Tafani, R. J. Rothman, A. Marcineviciute, J. B. Hoek, and J. L. Farber. 1999. Functional consequences of the sustained or transient activation by Bax of the mitochondrial permeability transition pore. J. Biol. Chem. 274:31734–31739. [DOI] [PubMed] [Google Scholar]
- Pavlov, E. V., M. Priault, D. Pietkiewicz, E. H.-Y. Cheng, B. Antonsson, S. Manon, S. J. Korsmeyer, C. A. Mannella, and K. W. Kinnally. 2001. A novel, high conductance channel of mitochondria linked to apoptosis in mammalian cells and Bax expression in yeast. J. Cell Biol. 155:725–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersheim, M., and J. Sun. 1989. On the coordination of La3+ by phosphatidylserine. Biophys. J. 55:631–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perry, D. K., J. Carton, A. K. Shah, F. Meredith, D. J. Uhlinger, and Y. A. Hannun. 2000. Serine palmitoyltransferase regulates de novo ceramide generation during etoposide-induced apoptosis. J. Biol. Chem. 275:9078–9084. [DOI] [PubMed] [Google Scholar]
- Radin, N. S. 2001. Killing cancer cells by poly-drug elevation of ceramide levels: a hypothesis whose time has come? Eur. J. Biochem. 268:193–204. [DOI] [PubMed] [Google Scholar]
- Raisova, M., M. Bektas, T. Wieder, P. Daniel, P. Eberle, C. E. Orfanos, and C. C. Geilen. 2000. Resistance to CD95/Fas-induced and ceramide-mediated apoptosis of human melanoma cells is caused by a defective mitochondrial cytochrome c release. FEBS Lett. 473:27–32. [DOI] [PubMed] [Google Scholar]
- Rapaport, D., and Y. Shai. 1992. Aggregation and organization of pardaxin in phospholipid membranes. A fluorescence energy transfer study. J. Biol. Chem. 267:6502–6509. [PubMed] [Google Scholar]
- Reed, K. C., and F. L. Bygrave. 1974. The inhibition of mitochondrial calcium transport by lanthanides and ruthenium red. Biochem. J. 140:143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson, R. A., and R. H. Stokes. 1965. Electrolyte Solutions. Butterworths, London, England. 466.
- Rodriguez-Lafrasse, C., G. Alphonse, P. Broquet, M.-T. Aloy, P. Louisot, and R. Rousson. 2001. Temporal relationships between ceramide production, caspase activation, and mitochondrial dysfunction in cell lines with varying sensitivity to anti-Fas-induced apoptosis. Biochem. J. 357:407–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruiz-Argüello, M. B., G. Basañez, F. M. Goñi, and A. Alonoso. 1996. Different effects of enzyme-generated ceramides and diacylglycerols in phospholipid membrane fusion and leakage. J. Biol. Chem. 271:26616–26621. [DOI] [PubMed] [Google Scholar]
- Saito, M., S. J. Korsmeyer, and P. H. Schlesinger. 2000. BAX-dependent transport of cytochrome c reconstituted in pure liposomes. Nat. Cell Biol. 2:553–555. [DOI] [PubMed] [Google Scholar]
- Sansom, M. S. P. 1991. The biophysics of peptide models of ion channels. Prog. Biophys. Mol. Biol. 55:139–236. [DOI] [PubMed] [Google Scholar]
- Sansom, M. S. P. 1993. Alamethicin and related peptaibols-model ion channels. Eur. Biophys. J. 22:105–124. [DOI] [PubMed] [Google Scholar]
- Schuller, F., R. Benz, and H. G. Sahl. 1989. The peptide antibiotic subtilin acts by formation of voltage-dependent multi-state pores in bacterial and artificial membranes. Eur. J. Biochem. 182:181–186. [DOI] [PubMed] [Google Scholar]
- Seelig, J., P. M. Macdonald, and P. G. Scherer. 1987. Phospholipid head groups as sensors of electric charge in membranes. Biochemistry. 26:7535–7541. [DOI] [PubMed] [Google Scholar]
- Shai, Y. 1994. Pardaxin: channel formation by a shark repellant peptide from fish. Toxicology. 87:109–129. [DOI] [PubMed] [Google Scholar]
- Shai, Y. 1999. Mechanism of the binding, insertion and destabilization of phospholipid bilayer membranes by α-helical antimicrobial and cell non-selective membrane-lytic peptides. Biochim. Biophys. Acta. 1462:55–70. [DOI] [PubMed] [Google Scholar]
- Shimeno, H., S. Soeda, M. Sakamoto, T. Kouchi, T. Kowakame, and T. Kihara. 1998. Partial purification and characterization of sphingosine N-acyltransferase (ceramide synthase) from bovine liver mitochondrion-rich fraction. Lipids. 33:601–605. [DOI] [PubMed] [Google Scholar]
- Simon, C. G., and A. R. Gear. 1998. Membrane-destabilizing properties of C2-ceramide may be responsible for its ability to inhibit platelet aggregation. Biochemistry. 37:2059–2069. [DOI] [PubMed] [Google Scholar]
- Siskind, L. J., and M. Colombini. 2000. The lipids C2- and C16-ceramide form large stable channels. Implications for apoptosis. J. Biol. Chem. 275:38640–38644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siskind, L. J., R. N. Kolesnick, and M. Colombini. 2002. Ceramide channels increase the permeability of the mitochondrial outer membrane to small proteins. J. Biol. Chem. 277:26796–26803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spach, G., H. Duclohier, G. Molle, and J.-M. Valleton. 1989. Structure and supramolecular architecture of membrane channel-forming peptides. Biochimie. 71:11–21. [DOI] [PubMed] [Google Scholar]
- Sparagna, G. C., K. K. Gunter, S. S. Sheu, and T. E. Gunter. 1995. Mitochondrial calcium uptake from physiological-type pulses of calcium. A description of the rapid uptake mode. J. Biol. Chem. 270:27510–27515. [DOI] [PubMed] [Google Scholar]
- Susin, S. A., N. Zamzami, and G. Kroemer. 1998. Mitochondria as regulators of apoptosis: doubt no more. Biochim. Biophys. Acta. 1366:151–165. [DOI] [PubMed] [Google Scholar]
- Susin, S. A., N. Zamzami, M. Castedo, E. Daugas, E. G. Wang, S. Geley, F. Fassy, J. C. Reed, and G. Kroemer. 1997a. The central executioner in apoptosis: multiple connections between protease activation and mitochondria in Fas/APO-1/CD95 and ceramide induced cell death. J. Exp. Med. 186:25–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Susin, S. A., N. Zamzami, N. Larochette, B. Dallaporta, I. Marzo, C. Brenner, T. Hirsch, P. X. Petit, M. Geuskens, and G. Kroemer. 1997b. A cytofluorometric assay of nuclear apoptosis is induced in a cell-free system: application to ceramide induced apoptosis. Exp. Cell Res. 236:397–403. [DOI] [PubMed] [Google Scholar]
- Takata, M., W. F. Pickard, J. Y. Lettvin, and J. W. Moore. 1966. Ionic conductance changes in lobster axon membrane when lanthanum is substituted for calcium. J. Gen. Physiol. 50:461–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka, T., S. J. Li, K. Kinoshita, and M. Yamazaki. 2001. La3+ stabilizes the hexagonal II (HII) phase in phosphatidylethanolamine membranes. Biochim. Biophys. Acta. 1515:189–201. [DOI] [PubMed] [Google Scholar]
- Tapia, R., C. Arias, and E. Morales. 1985. Binding of lanthanum ions and ruthenium red to synaptosomes and its effects on neurotransmitter release. J. Neurochem. 45:1464–1470. [DOI] [PubMed] [Google Scholar]
- Thomas, R. L., Jr., C. M. Matsko, M. T. Lotze, and A. A. Amoscato. 1999. Mass spectrometric identification of increased C16-ceramide levels during apoptosis. J. Biol. Chem. 274:30580–30588. [DOI] [PubMed] [Google Scholar]
- Veiga, M. P., J. L. Arrondo, F. M. Goñi, and A. Alonoso. 1999. Ceramides in phospholipid membranes: effects on bilayer stability and transition to nonlamellar phases. Biophys. J. 76:342–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verstraeten, S. V., L. V. Nogueira, S. Schreier, and P. I. Oteiza. 1997. Effect of trivalent metal ions on phase separation and membrane lipid packing: role in lipid peroxidation. Arch. Biochem. Biophys. 338:121–127. [DOI] [PubMed] [Google Scholar]
- Vodyanoy, I., S. M. Bezrukov, and V. A. Parsegian. 1993. Probing alamethicin channels with water-soluble polymers. Size-modulated osmotic action. Biophys. J. 65:2097–2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witty, J. P., J. T. Bridgham, and A. L. Johnson. 1996. Induction of apoptotic cell death in hen granulosa cells by ceramide. Endocrinology. 137:5269–5277. [DOI] [PubMed] [Google Scholar]
- Woolley, G. A., and B. A. Wallace. 1992. Model ion channels: gramicidin and alamethicin. J. Membr. Biol. 129:109–136. [DOI] [PubMed] [Google Scholar]
- Yang, X. C., and F. Sachs. 1989. Block of stretch-activated ion channels in Xenopus oocytes by gadolinium and calcium ions. Science. 243:1068–1071. [DOI] [PubMed] [Google Scholar]
- Zamzami, N., P. Marchetti, M. Castedo, D. Decaudin, A. Macho, T. Hirsh, S. A. Susin, P. X. Petit, B. Mignotte, and G. Kroemer. 1995. Sequential reduction of mitochondrial transmembrane potential and generation of reactive oxygen species in early programmed cell death. J. Exp. Med. 182:367–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, P., B. Liu, S. W. Kang, M. S. Seo, S. G. Rhee, and L. M. Obeid. 1997. Thioredoxin peroxidase is a novel inhibitor of apoptosis with a mechanism distinct from that of Bcl-2. J. Biol. Chem. 272:30615–30618. [DOI] [PubMed] [Google Scholar]
- Zhou, X.-L., and C. Kung. 1992. A mechanosensitive ion channel in Schizosaccharomyces pombe. EMBO J. 11:2869–2875. [DOI] [PMC free article] [PubMed] [Google Scholar]