Formation Pathways of a Guanine-Quadruplex DNA Revealed by Molecular Dynamics and Thermodynamic Analysis of the Substates

Abstract

The formation of a cation-stabilized guanine quadruplex (G-DNA) stem is an exceptionally slow process involving complex kinetics that has not yet been characterized at atomic resolution. Here, we investigate the formation of a parallel stranded G-DNA stem consisting of four strands of d(GGGG) using molecular dynamics simulations with explicit inclusion of counterions and solvent. Due to the limitations imposed by the nanosecond timescale of the simulations, rather than watching for the spontaneous formation of G-DNA, our approach probes the stability of possible supramolecular intermediates (including two-, three-, and four-stranded assemblies with out-of-register basepairing between guanines) on the formation pathway. The simulations suggest that “cross-like” two-stranded assemblies may serve as nucleation centers in the initial formation of parallel stranded G-DNA quadruplexes, proceeding through a series of rearrangements involving trapping of cations, association of additional strands, and progressive slippage of strands toward the full stem. To supplement the analysis, approximate free energies of the models are obtained with explicit consideration of the integral cations. The approach applied here serves as a prototype for qualitatively investigating other G-DNA molecules using molecular dynamics simulation and free-energy analysis.

INTRODUCTION

Since the discovery of the B-DNA double helix, it has become increasingly clear that DNA is highly polymorphic in its nature. In the early days of DNA structural analysis, two distinct conformations of DNA—the canonical A- and B-DNA duplexes—were observed depending on the hydration state of DNA fibers used for x-ray analysis (Arnott and Hukins, 1972). Since then, and predominantly based on structural analysis of DNA oligonucleotides in vitro by biophysical and biochemical methods, a flurry of DNA structural motifs have been discovered including the left-handed Z-DNA duplex (Wang et al., 1979) and multistranded DNA structures with three, four, or five hydrogen-bonded strands (Saenger, 1984). Among these, the guanine (G) quadruplex DNA (G-DNA) has gained particular attention for a variety of reasons, including its potential use as a target for cancer therapy (Arthanari and Bolton, 1999; Bearss et al., 2000; Guittat et al., 2001; Han et al., 1999, 2001; Han and Hurley, 2000; Hurley et al., 2000a, 2000b; Izbicka et al., 1999; Lane and Jenkins, 2001; Mergny et al., 2001, 1999; Neidle et al., 2000; Read et al., 2001, 1999; Sun and Hurley, 2001) and its proposed role in the maintenance of the very ends of chromosomes, the telomeres (Henderson et al., 1987) as observed in eukaryotic nuclei in vivo (Schaffitzel et al., 2001). Sequences with stretches of guanine residues occur not only at the telomeres, but also in many other regions in the genome of cells, including the regulatory region of the insulin gene, fragile X-syndrome triplet repeats, and the promoter region of the c-myc gene (Simonsson et al., 1998). In each of these cases, G-quadruplex structures readily form in cell-free systems (Hammond-Kosack et al., 1993; Nadel et al., 1995; Simonsson et al., 1998). Moreover, it has been shown that specific proteins promote the formation of G-quadruplexes (Arimondo et al., 2000; Fang and Cech, 1993). Therefore it is likely that guanine quadruplex structures play an important role in a variety of cellular processes including transcription, replication, and recombination. In each of these processes, transient separation of the regular DNA duplex occurs, allowing a strand containing stretches of guanine residues to fold into a guanine quadruplex structure.

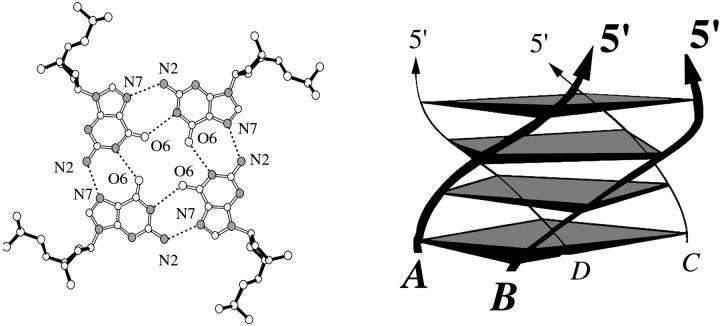
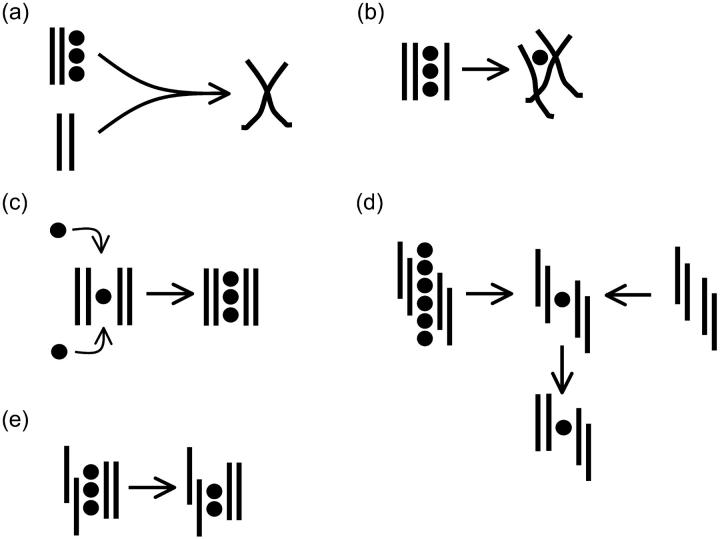
Guanine quadruplexes are stabilized by quartet layers of Hoogsteen paired guanine residues (Fig. 1 A), and they are readily formed by DNA sequences containing stretches of guanines under physiological conditions. Although atomic resolution data exist now for many guanine quadruplex structures adopted by a variety of DNA sequences (Bouaziz et al., 1998; Horvath and Schultz, 2001; Hud et al., 1996; Kettani et al., 1998; Laughlan et al., 1994; Macaya et al., 1993; Phillips et al., 1997; Smith and Feigon, 1992, 1993; Strahan et al., 1998), including direct visualization of localized monovalent cations centered between the planes of the quartets (Haider et al., 2002; Horvath and Schultz, 2001; Hud et al., 1999; Laughlan et al., 1994), the actual process of how these sequences fold into guanine quadruplexes is not clear. The formation process is a long timescale event with complicated kinetics that can take from hours to days. Experimental insight into G-DNA folding is very limited and mainly comes from spectroscopic studies (Hardin et al., 1997, 1991, 2000). As simultaneous and spontaneous association of four strands of d(GGGG) and three ions is unlikely, other rather straightforward models of the quadruplex stem formation can be envisioned (Fig. 2). One of these models assumes that the strands are coming together in a step-by-step strand addition process (Fig. 2 A), first involving formation of a duplex stabilized by G-G Hoogsteen pairs followed by recruitment of a third strand to form a triplex, and finally the last strand to complete the entire quadruplex. An alternative model could involve dimerization of two duplexes to form the stem in a bimolecular fashion (Fig. 2 B) (Hardin et al., 2000). A further possible pathway of guanine quadruplex formation has also been proposed (Hardin et al., 1997) that is essentially a triplex dissociation process. Here, two three-stranded assemblies would interact with each other and dissociate to yield a quadruplex and a duplex assembly. Further, a central question with regarding G-DNA formation is at which stage monovalent cations are integrated into the structure. The formation of quadruplex DNA likely involves a combination of different paths (Hardin et al., 1997). Moreover, the formation process likely varies with different sequences and experimental conditions, given the many different intra- and intermolecular conformers of guanine quadruplex DNA and the possibilities of both parallel and antiparallel strand orientations (for review, see Gilbert and Feigon, 1999).

FIGURE 1.

Schematic drawing of a guanine quadruplex stem formed by d(GGGG)₄. This structure is stabilized by four stacked guanine quartet layers (left) and has all strands oriented in parallel (arrows) (right) with all anti glycosidic bonds.

FIGURE 2.

Two predominant hypothetical models proposed for G-DNA formation from experiments (Hardin et al., 1991): (A) stepwise strand addition and (B) duplex dimerization.

Recent advances in biomolecular simulation methodologies now allow us to investigate G-DNA molecules using state-of-the-art computational tools (Chowdhury and Bansal, 2000, 2001a, 2001b; Gu and Leszczynski, 2000; Han et al., 2001; Meyer et al., 2001a, 2001b; Read et al., 2001, 1999; Spackova et al., 1998, 2001; Stefl et al., 2001a; Strahan et al., 1998). In the present study, we probe the formation of a parallel-stranded d(GGGG)₄ quadruplex stem with four stacked guanine quartet layers stabilized by Na⁺ cations. This molecule is well described by atomic resolution x-ray data (Phillips et al., 1997) and is relatively simple. Unlike other quadruplex structures that may occur in the context of the genome, this structure lacks connective loop regions between the strands of the quadruplex stem. Careful examination of the sequences interspersed between guanine stretches that may adopt guanine quadruplex structures in vivo, however, shows that although the connecting stretches are highly conserved in the telomeric regions (-TTTT- in the case of ciliates, -TTA- in the case of humans), there is little conservation of these loop-forming sequences to those of other regions such as the immunoglobulin heavy chain switch regions or the insulin-linked polymorphic region ILPR (Simonsson et al., 1998). Further, in atomic resolution studies of quadruplexes formed by the human telomeric repeat, it was shown that the -TTA- regions could adopt loops spanning either the diagonal of the guanine quartet layers (in the presence of Na⁺) or bulging out to the side (in the presence of K⁺) of a parallel G-quadruplex stem (Parkinson et al., 2002; Wang and Patel, 1993). Interestingly, the guanine quadruplex stem structure with bulged loops (Parkinson et al., 2002) closely resembles the quadruplex in the structure of d(TGGGGT) solved earlier at atomic resolution (Laughlan et al., 1994), which lacks loop regions. Thus, the parallel stranded models studied here are relevant and provide general insight into the formation process of G-quadruplex molecules that may occur in cell nuclei.

As spontaneous aggregation of the four strands and formation of the stem in nanosecond-scale molecular dynamics (MD) simulations is unrealistic, we adopted the following two-step modeling approach. First we carried out MD simulation including explicit solvent on a set of four-strand, three-strand, and double-stranded structures that conceivably represent intermediates in the folding process. With the exception of the complete cation-stabilized four-quartet layer d(GGGG)₄ quadruplex stem structure, the present computational study deals with nucleic acid molecules that have not (yet) been described by atomic-resolution experiments. Properties of the intermediates are nevertheless of primary importance for formation and function of G-DNA molecules.

Although nanosecond-scale MD simulations are sufficient to explore the short-term stability of model G-DNA structures, the simulations do not reveal the relative stability of a given model. Thus, we have complemented the simulations by estimating the relative free energies of all structures studied by well-known technologies that combine molecular mechanical and continuum electrostatic energy analysis of representative snapshots from a stable simulation to give estimates of the (relative) free energies (Kollman et al., 2000; Srinivasan et al., 1998; Vorobjev et al., 1998). Although our simulations are obviously far from being capable to provide a complete sampling of the conformational space of the studied formation process (see also Discussion) and the free-energy estimates are qualitative, they nevertheless provide surprisingly clear suggestions regarding which intermediate structures may or may not be involved. Our study reveals the existence of a wide range of four-stranded molecules with shifted strands and indicate their capability to undergo spontaneous transitions toward the four-quartet stem. The simulations and free-energy calculations unambiguously show that once a single quartet is present in the structure, the molecule is stabilized by monovalent cations and these cations are retrieved from the solvent on the nanosecond timescale. Thus, monovalent cations are involved in the early stages of the quadruplex stem assembly. Those parts of the preformed stem that remain outside the quartet area primarily rely on guanine hydrogen bonding. On the other hand, parallel stranded duplexes and triplexes hydrogen-bonded in a quadruplex-like manner have been ruled out as possible intermediates with a reasonable confidence. Instead, a stable intermediate structure that we find is a “cross-like” dimer structure formed by two roughly perpendicular dG₄ strands. Although the structure is stabilized through hydrogen bonds involving the central guanines, the terminal guanines are free and thus capable to establish hydrogen bonding with additional strands. The simulations further suggest that this cross-like dimer structure can, for example, be involved in a coil-like trimer arrangement stabilized by a single Na⁺ ion. Structures of this kind might represent genuine early-stage nuclei in the formation of G-DNA stems, though their further characterization is beyond the scope of this article.

METHODS

General

All simulations were carried out using the AMBER 6.0 program (Pearlman et al., 1995) with the Cornell et al. (1995) force field. This force field has been applied extensively in studies of four-stranded nucleic acids (Chowdhury and Bansal, 2000, 2001a, 2001b; Spackova et al., 1998, 1999, 2001; Stefl et al., 2001a; Strahan et al., 1998) and performs well. In addition to giving a good representation of the structure and dynamics, this force field also provides a balanced description of base stacking and hydrogen bonding interactions of nucleic acid bases (Hobza et al., 1997). We have also tested the performance of the newer parm98 modifications of this force field (Cheatham et al., 1999) and found no substantial differences or obvious structural artifacts (data not shown). All of the molecular dynamics simulations were performed using all-atom nucleic acid models solvated with a buffer of at least 10 Å of TIP3P waters (Jorgensen et al., 1983) surrounding the solute with explicit net-neutralizing Na⁺ counterions (placed by LEaP at points of favorable electrostatic potential). The ion parameters used are AMBER adapted (for Lorentz-Bertholet combining rules) Aqvist ion parameters (Aqvist, 1990). Molecular manipulation and visualization were done using the programs AMBER xLEaP, MidasPlus (Ferrin et al., 1988), and MOLMOL (Koradi et al., 1996). Several simulations (G-DNA vacant, G-DNA native, and slipped_D_3ions (Spackova et al., 1999) were carried out previously with the same force field as used here, albeit with an older but compatible version of AMBER. All of the equilibration and production molecular dynamics simulations used standard protocols and applied the particle mesh Ewald method (Essmann et al., 1995) with a heuristic pair list update (and 1.0 Å nonbonded pair list buffer), a 9 Å cutoff, an Ewald coefficient (κ) of 0.30768, an FFT grid size of the next largest product of powers of 2, 3, or 5 that is larger than the box size, and a uniform bulk density long-range van der Waals correction. During the dynamics, the center of mass translation was removed every 5 ps (Chiu et al., 2000; Harvey et al., 1998) and a 2 fs time step was applied. In the MD simulations, SHAKE was applied with a tolerance of 10^–8 (Ryckaert et al., 1977). Constant pressure and temperature (300 K) was maintained with Berendsen coupling (Berendsen et al., 1984) and 0.2 time constants during equilibration and 2.0 ps time constants during production. Despite an overall shrinking of the periodic box size by a small amount, the simulated structures were sufficiently solvated, even after free rotation, to avoid artifacts from direct interaction with the periodic images.

Starting structures

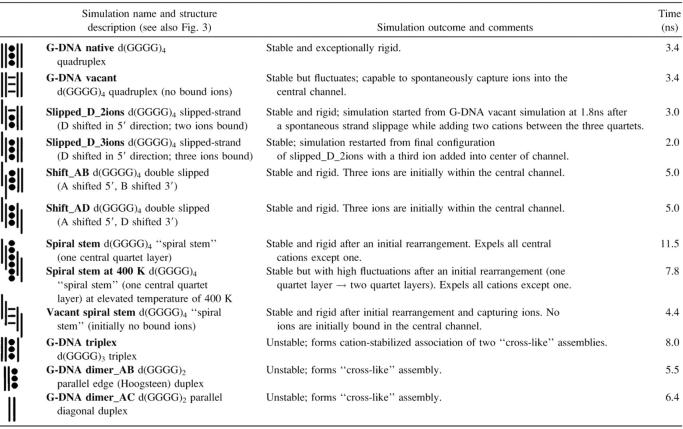
Most simulations were carried out assuming hypothetical structures as starting geometries and were hand built based on experimental structures where possible. In some cases, the model structures explored were found to occur spontaneously during earlier simulation. In other cases, shifts of the single strands were forced. In this case, idealized geometries were assumed and strands were shifted by performing all-atom root mean-squared deviation (RMSD) fits to effectively move a strand up or down by one step. The simulations performed are summarized in Table 1. Initial models were based on the 0.95 Å resolution crystal structure of the d(TGGGGT)₄ quadruplex (Phillips et al., 1997) omitting the terminal thymines. Model structures in addition to the native quadruplex structure, with and without ions, included models with one or two of the stands shifted by one step. Additionally, various dimer and trimer model structures, based on the quadruplex geometries, were built and simulated. More details on how the model structures were built and more details regarding the simulation protocol are provided in the supplementary material.

TABLE 1.

Summary of the parallel d(GGGG)_n models investigated including a description of the initial models, simulation name, and the outcomes and length of the MD simulation

All simulations were performed in explicit solvent with explicit Na⁺ ions. Trajectories of the first four simulations are discussed in more detail in our previous work (Spackova et al., 1999).

Analyses of the trajectories

The results were analyzed using the ptraj and carnal modules of AMBER 6.0 (Pearlman et al., 1995). The average structures were obtained by RMSD fit coordinates averaged over all atoms, at 1 ps intervals, over stable portions of the trajectories. No extra processing of the averaged structures was performed. Hydrogen bonding and ion occupancies were calculated using ptraj to bin and analyze selected molecular interactions.

Free-energy analysis

Free-energy analysis was performed using the MM-PBSA scripts supplied with AMBER 6.0 (Kollman et al., 2000; Srinivasan et al., 1998). This analysis is equivalent to the explicit solvent/implicit solvent method of Vorobjev and Hermans (Vorobjev et al., 1998), similar in spirit to the linear interaction energy approaches (Hansson et al., 1998; Marelius et al., 1998), and a direct extension of well-known methods for estimating free energies (Froloff et al., 1997; Misra and Honig, 1996; Misra et al., 1994) that involve averaging over configurations sampled in an MD simulation. Solute entropic contributions for the G-DNA models were estimated using a subset of these structures (at 250 ps intervals), including three explicitly bound ions (as discussed below), based on a harmonic approximation to the normal modes, and standard (quantum) formulas at 300 K (McQuarrie, 1976). For this, a subset of the structures was minimized, first with the generalized Born method in AMBER 6.0 (1000 steps total, 75 steepest descent, 100 Å cutoff), followed by in vacuo minimization with a distance-dependent dielectric function (with a dielectric constant of ɛ = 4 r, where r is the interatomic distance in Å and up to 10,000 steps, the first 100 of which are steepest descent followed by conjugate gradient, unless the RMS gradient drops below 10⁻⁴). After this, Newton-Raphson minimizations (maximum of 5000 steps) were carried out on a series of structures until the root mean-square of the elements of the gradient vector was <10⁻⁴ kcal/mol/Å. As discussed in the next section, it should be noted that these estimates neglect some of the entropic components due to the ions, in particular the loss of translational freedom upon ion binding. Additionally, these entropic estimates based on gas-phase minimization of representative structures are relatively static and do not properly represent the dynamic fluctuations within the accessible substates; for more accurate estimates, methods based on analysis of the covariance of the structures in the MD simulation are recommended (Andricioaei and Karplus, 2001; Harris et al., 2001; Karplus and Kushick, 1981; Schafer et al., 2000; Schlitter, 1993). Preliminary analysis of the current data using these methods is similar (data not shown). In this work, since we are only interested in crude estimates of the relative free-energy differences, the estimates herein are sufficient for ranking the observed models.

Solvation free-energy components are estimated with a Poisson-Boltzmann electrostatic continuum method, Delphi (Sharp and Honig, 1990), with a hydrophobic component from a surface area-dependent term. This procedure, along with a more thorough theoretical background, is discussed in much greater detail in related work (Srinivasan et al., 1998) and recent reviews (Kollman et al., 2000). As discussed in the previous work, the solute and molecular mechanical dielectric constant was ɛ = 1. This is consistent with the use of a nonpolarizable molecular mechanical force field and also consistent with the use of explicit averaging of conformations to represent the response of the solute to charge fluctuations. Although this may not be sufficient to fully capture the electronic response of the macromolecule, we justify the use of ɛ = 1 in the current study since 1), we are mainly interested in ranking the relative importance of the various models (which seems to be retained anyways when a dielectric constant of ɛ = 2 or 4 is applied) and 2), less accurate estimates of binding free energies and relative stabilities are obtained with these parameters and the MM-PBSA protocol when ɛ > 1. This has been shown in a wide variety of nucleic acid systems (Kollman et al., 2000) investigating DNA duplex stability (Srinivasan et al., 1998), drug binding in the minor groove of DNA (Spackova et al., 2003), and ion binding in RNA (Tsui and Case, 2001). For the Poisson-Boltzmann calculations, the Delphi II program was used (Gilson et al., 1987; Nicholls and Honig, 1991). A cubic lattice with linear dimensions ∼50% larger than the longest dimension was applied with a 0.25 Å grid spacing; potentials at the boundaries of the finite-difference lattice were set to a sum of Debye-Huckel potentials (Gilson et al., 1987). Salt effects were not included implicitly in the continuum model. Our past experience shows these effects to be small and not tremendously sensitive to conformation. Instead, however, our present experience suggests it is critical to include explicitly the effect of bound integral ions (see below). To estimate the nonpolar contributions to solvation, ΔG_nonpolar, the solvent accessible surface area (SASA) algorithm of Sanner (Sanner et al., 1996) was used in a parameterization where ΔG_nonpolar = γ(SASA) + β, where γ = 0.00542 kcal/Ų and β = 0.92 kcal/mol.

Explicit inclusion of integral ions

Unlike other DNA molecules, G-DNA contains bound cations that are integral to its structure. These important elements of G-DNA structure cannot be accurately treated with an implicit salt model. Thus, we adapted the MM-PBSA methodology to include explicit ions (similar to what has been done previously by Jayaram and co-workers (Jayaram et al., 1998)). As discussed in the Results section, the significant differences in estimated free energies observed when explicit ions are included have serious implications for the MM-PBSA methodology and suggest that integral ions and hydration need to be explicitly considered. A minimal subset of explicit ions were included as an initial test to avoid large fluctuations in the overall (free) energetics. To obtain meaningful evaluations, it is necessary to only compare data between calculations that have the same number of explicitly treated Na⁺ ions. To facilitate this, if structures were compared that had fewer than three integral cations, additional (unbound) ions in the vicinity (closest to any of the O6 atoms of the guanine in the central channel) were included.

To provide balanced free energetics, the continuum radii for Na⁺ ions were set to be 1.656 Å. This gives an electrostatic contribution to the ΔG_solvation of −99.7 kcal/mol and an overall −98.2 kcal/mol ΔG_solvation (from Poisson-Boltzmann), which is consistent with some experiment and other theoretical work (Hummer et al., 1996; Marcus, 1994). As mentioned previously, the applied protocol for estimating free energies neglects translational entropy losses for the Na⁺ ions. Although for typical drug-like molecule binding the rotational and translational entropy losses can be fairly significant (in the 3–30 kcal/mol range at 300 K (Gilson et al., 1997; Hermans and Wang, 1997; Lazaridis et al., 2002; Luo and Gilson, 2000; Page and Jencks, 1971; Schwarzl et al., 2002; Tidor and Karplus, 1994; Yu et al., 2001)), for Na⁺ ions in solution, these components are fairly small. As discussed in related work by Jayaram, Beveridge, and co-workers (Jayaram et al., 1998), when excluding the electrostatic contribution to the entropy of solvation for Na⁺ from its gas phase value, an estimate of the entropic component for free Na⁺ ions in water is on the order of 2–3 kcal/mol at 300 K (Friedman and Krishnan, 1973; Krestov, 1991). This component of the free energies was not included in the tables shown in the Results section but can be easily considered by subtracting 2–3 kcal/mol for each “free” ion from the set of three ions explicitly considered. In addition, the results do not include the (small) standard state volume correction (BenNaim, 1987; Vitha and Carr, 2000).

For the free energetic analysis, 200 configurations (including the three closest explicit ions) at equally spaced intervals from two nanosecond portions of each trajectory were analyzed. For each trajectory they are:

• G-DNA native: 0.5–2.5 ns at 10 ps intervals (200 frames); each 200 ps for entropy.

• G-DNA vacant: 0.5–2.5 ns at 10 ps intervals (200 frames); each 250 ps for entropy.

• Slipped_D_3ions: 0–2.0 ns at 10 ps intervals (200 frames).

• Slipped_D_2ions: 1.0–3.0 ns at 10 ps intervals (200 frames); each 250 ps for entropy.

• Shift_AB: 1–3 ns at 10 ps intervals (200 frames); each 250 ps for entropy.

• Shift_AD: 1–3 ns at 10 ps intervals (200 frames).

• Spiral stem: 2–4 ns and 7–9 ns at 10 ps intervals; each 200 ps for entropy.

• G-DNA triplex: 6–8 ns at 10 ps intervals.

• G-DNA dimer_AB: 3–5 ns at 10 ps intervals.

• G-DNA dimer_AD: 3–5 ns at 10 ps intervals; each 200 ps for entropy.

RESULTS

The purpose of this study is to characterize the structural dynamics and relative free energies of a variety of molecules that may be involved in the formation of a parallel stranded d(GGGG)₄ quadruplex stem (Table 1 and Fig. 3). The applied technology can serve as a prototype for investigation of other models representative of G-DNA assembly including quadruplexes with loops. The subsequent parts of the paper are organized in the following way. We first introduce the atomic-resolution behavior of a wide range of four-, three-, and double-stranded model structures studied by explicit solvent MD simulations. After this, we evaluate their relative free energies as revealed by the MM-PBSA procedure. Then, we use the dynamics and free-energy data to suggest possible scenarios in the formation of parallel-stranded quadruplex stems. Finally, we discuss the performance and limitations of our computational approaches.

FIGURE 3.

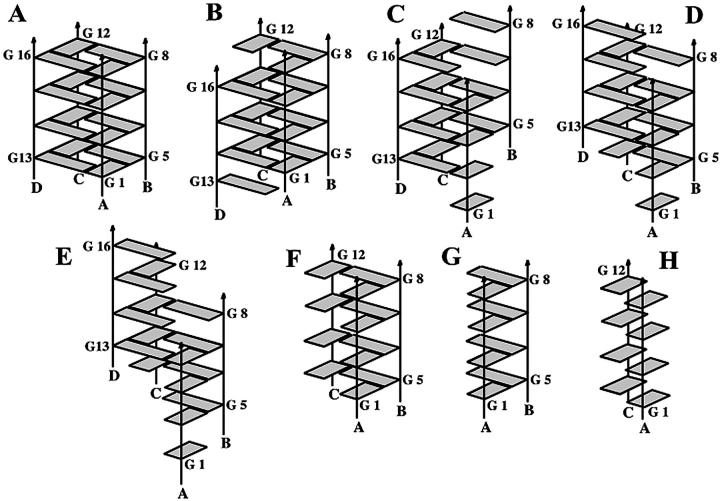
Molecular structures of the parallel d(GGGG)₄ stem, G-DNA native, (A), and intermediates studied here: (B) slipped_D_2ions, G-DNA stem with one strand shifted (from Spackova et al. (1999)); (C) shift_AB with A and B strands shifted down and up, respectively; (D) shift_AD with A and D strands shifted down and up respectively; and (E) d(GGGG)₄ as a spiral stem with one central guanine quartet (F) d(GGGG)₃ triplex, (G) parallel d(GGGG)₂ edge duplex (G-DNA dimer_AB), and (H) parallel d(GGGG)₂ diagonal duplex (G-DNA dimer_AC). See text for further details.

Molecular dynamics of selected parallel d(GGGG)₄ quadruplex assemblies

The native cation-stabilized stem

The native parallel-stranded quadruplex stem d(GGGG)₄ (Fig. 3 A) (Spackova et al., 1999) consists of four consecutively stacked guanine quartet layers and a central channel lined by the guanine O6 keto groups. This central channel is occupied by three sodium cations placed along the central axis of the molecule between the guanine quartet layers. The native quadruplex stem is an extremely stable and rigid molecule that does not show significant geometrical movements during nanosecond-scale simulations. Overall, during 3+ ns of simulation, the structure remains incredibly close (<1.0 Å) to the experimental structure (see Supplementary Material for a plot of RMSD versus time for each of the trajectories). The G-DNA native model studied in MD simulation is in excellent agreement with the 0.95 Å resolution crystal structure of d(TGGGGT)₄, including hydration patterns and occupancies of substate populations of phosphate group conformations. Nevertheless, subtle structural differences exist between the x-ray structure and the simulated molecule, and these have been ascribed to force field approximations and specifically the imperfect description of the short-range cation-DNA interactions (Spackova et al., 1999). Additional simulations suggest no significant structural destabilization when the number of monovalent cations in the channel is reduced to two (Spackova et al., 1999). This implies that a smooth exchange of cations between the G-DNA and surrounding solvent is possible.

A metastable G-DNA quadruplex in the absence of bound ions (G-DNA vacant)

As shown previously, the d(GGGG)₄ stem reveals a pronounced instability and enhanced dynamics when all cations are removed from its channel (Spackova et al., 1999). The increased flexibility is characterized by greater motion of the bases and backbone, including some terminal basepair fraying and even complete strand slippage. Despite these marked fluctuations, the molecule does not dissociate. Quite to the contrary, MD simulations show that these vacant G-DNA stems are capable of spontaneously incorporating a cation from the bulk solvent into the central ion channel on a scale of ∼10 ns. This binding of cation leads to an immediate rigidification and stabilization of the molecule (Chowdhury and Bansal, 2001a; Spackova et al., 2001) and suggests that given sufficient sampling in longer scale MD simulations, an initially vacant stem may convert into the fully cation-stabilized native quadruplex stem.

Potential intermediates on the folding pathways; parallel d(GGGG)₄ quadruplexes with one strand shifted

Based on the observation of spontaneous strand slippage in our previous simulations with no cations in the quadruplex core (G-DNA vacant) (Spackova et al., 1999), two simulations of slipped-strand d(GGGG)₄ models consisting of three guanine quartets enveloped at one end by a guanine triad and an isolated stacked guanine at the other (Fig. 3 B) were performed. These models contained two (slipped_D_2ions) and three (slipped_D_3ions) sodium ions bound in the central channel. In these structures, one strand is out of register by one base-stacking distance with respect to the other three strands of the molecule. In multi-nanosecond length MD simulation, the structures are stable as characterized by reasonably low RMSD values. For the final nanosecond of each simulation, the RMSD values to the average structures are 0.82 ± 0.15 Å for the slipped_D_2ions and 0.73 ± 0.12 Å for the slipped_D_3ions simulations.

Further intermediates on the folding pathway; G-DNA with two slipped strands

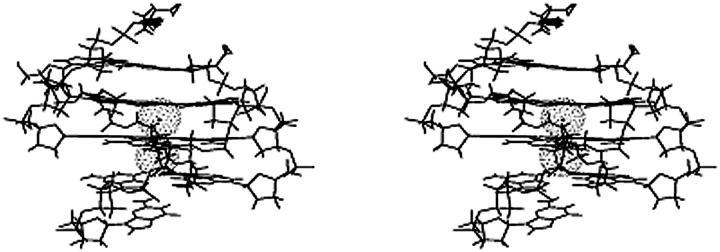
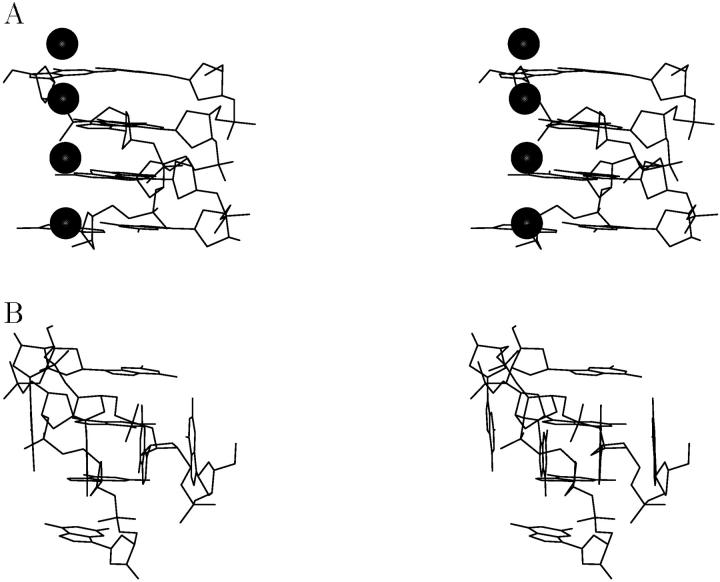
Given that the single slipped strands are stable in nanosecond-scale MD simulation, we decided to investigate slipped models involving the shift of two strands in opposite directions. This involved the shifting down and up of strands A and B (shift_AB, Fig. 3 C) and the shifting down and up of strands A and D (shift_AD, Fig. 3 D). Single 5-ns length simulations were performed on each model and both model structures were stable over the entire simulation. The stability is evident by low RMS deviations of the average structures to those sampled at 1 ps intervals over the simulation of only 1.7 ± 0.25 Å and 2.3 ± 0.22 Å for the shift_AB and shift_AD models, respectively. Despite the inherent differences related to which strand is shifted, the two models are remarkably similar. Although both simulations were started with three ions bound in the central channel, rather quickly in the simulations the top-most (5′) bound ion, sitting between the first triad and first quartet, moves into the surrounding solvent. On the other hand, the remaining two ions, one between the two quartets and the other between the bottom-most (3′) quartet and triad, were stable throughout the simulation in each case. Shown in Fig. 4 is a stereo view of the 2–5 ns straight-coordinate averaged structure of the shift_AB simulation. The structure retains the central two quartets, flanked by base triad and finally single unpaired bases. The terminal 5′ unpaired base (top) appears as a blob in the figure due to conformational averaging.

FIGURE 4.

Stereo view of the 2–5 ns average structure from the shift_AB simulation.

Two different configurations of the triad bases are observed consistently in both simulations. Whereas the bottom-most triad in the structure retains a quartet-like geometry (Fig. 5, left), the top-most triad (Fig. 5, right) adopts a different structure in the absence of coordinated ions that allows an additional hydrogen bonding interaction between the bases.

FIGURE 5.

View of the triad bases from the two ends of the shift_AB structure, including a representation of the hydrogen bonding between the bases. The triad geometry is regulated by the position of the cations stabilizing the adjacent quartet region.

Spiral stem

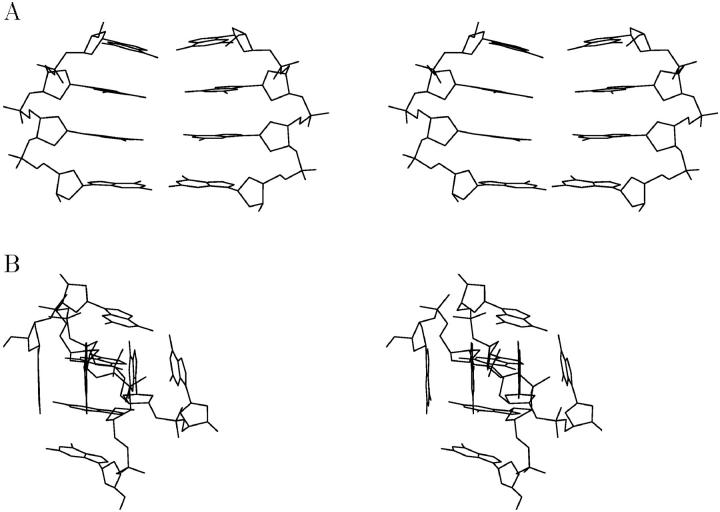
To probe structures even farther away from the native quadruplex stem and as an extreme case of slippage, we investigated a model structure in which strand slippage has progressed as far as possible from the native stem. This is a structure (spiral stem, Fig. 3 E) in which the individual strands are shifted such that only one complete quartet layer in the center of the molecule remains, successively enveloped by a guanine base triad, a G-G Hoogsteen pair, and finally a stacked isolated guanine residue toward either end of the molecule (see Methods section and Supplementary Material).

This spiral stem model structure, initially filled with six sodium ions along its central axis (each between two consecutive base planes, see Fig. 6 A), was subjected to equilibration and 11.5 ns MD simulation. The simulated structure was surprisingly stable (with RMSD values of values of 2.3 Å or less between block averaged structures over each nanosecond interval). At the beginning, conformational adjustments with respect to the initial geometry were observed. The two terminal ions were released to the bulk solvent, which led to an increase in flexibility of the terminal bases and G-G basepairs. Additionally, three cations were expelled later, leaving only a single cation coordinated in the plane of the central quartet for the entire simulation. After the surplus cations were freed to solvent, the terminal parts of the strands became more flexible and engaged in mutual hydrogen bonding interactions with nearby guanine residues (Fig. 6, B and C). Nevertheless, despite the increase in flexibility and structural reorganization, the structure did not disintegrate and remained stable on the nanosecond scale.

FIGURE 6.

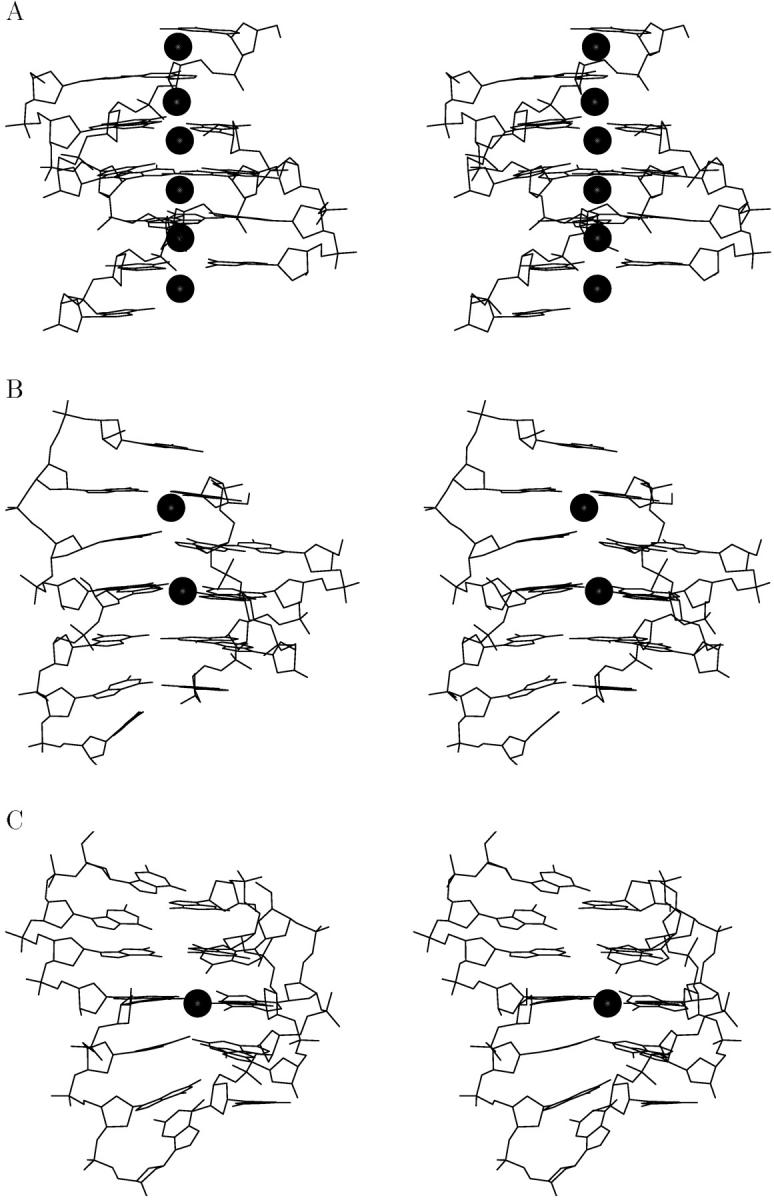
Line drawing stereo representation of the simulated “spiral stem” structure: (A) starting model, (B) average structure at 7–9 ns, and (C) average structure at 10–11 ns of simulation. Only nonhydrogen atoms are depicted along with coordinated sodium ions along the helical axis of the four-stranded molecule (molecules are not shown in the same side view).

We performed an additional 4.4 ns MD simulation of the spiral stem model structure initially without any cations in the central channel (vacant spiral), in analogy to the simulation of a vacant four-quartet d(GGGG)₄. However, immediately during the simulation, the vacant spiral stem attracted two ions from the bulk solvent. One sodium ion was coordinated between the central base quartet and the adjacent base triad, and the second sodium ion was coordinated between this base triad and the adjacent G-G Hoogsteen pair. The sodium ions remained in these positions throughout the 4.4 ns simulation. This is again a clear example that molecules containing G-quartets are capable to swiftly retrieve cations from the bulk solvent when substantially deficient of cations on nanosecond length MD simulation. The coordination rendered the lower part of the spiral structure more stable than the upper half without ions, where higher fluctuations were observed. Although the lower part of the spiral stem maintained the quartet, triad, pair, and isolated base arrangement in largely planar stacks, the upper part of the spiral (5′ end of C- and D-strands, see Fig. 3) showed again stabilization via interbase hydrogen bonding.

Potential early intermediates on the formation pathway: dimers and trimers

To form the G-DNA stem, one needs to consider also double-and triple-stranded structures. In the absence of any atomic resolution data, we assumed reasonable models may be obtained from the native stem simply by removing one or two of the G-DNA quadruplex strands. To our surprise and as shown below, these parallel triplex and duplex models are markedly unstable on the nanosecond timescale and swiftly convert into other types of structures.

Molecular dynamics of a parallel edge (AB) d(GGGG)₂ Hoogsteen duplex

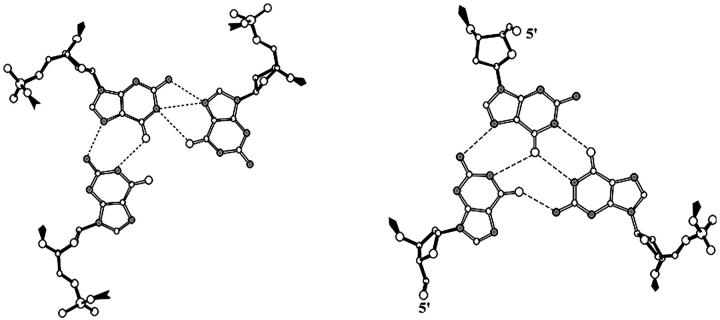
A possible metastable state that may occur at the early stages of G-DNA formation is a dimer of two d(GGGG) strands. Toward this end, we designed a d(GGGG)₂ duplex with Hoogsteen-type hydrogen bonds (Fig. 1) that is half of the original quadruplex stem, built from two strands on one edge of the quadruplex. Ions were kept initially in the positions described in the x-ray structure (Fig. 7 A).

FIGURE 7.

Stereo representation of the simulated parallel d(GGGG)₂ “edge duplex”: (A) starting model; (B) average structure (last ns). Only nonhydrogen atoms are depicted along with coordinated sodium ions.

This edge duplex (A- and B-strands, Fig. 1 and Fig. 3 G) was subjected to equilibration and 5.5 ns molecular dynamics simulation. After releasing all the ions, the structure gradually lost its cohesiveness during the initial 2 ns of the simulation. As the terminal basepairs came apart, the two strands were rotated in such a way that they adopted, at around 2 ns, a perpendicular position. This “cross-like” assembly was stable during the rest of the simulation and displayed surprisingly low geometrical fluctuations. This stability can be attributed to the extended network of hydrogen bonds involving residues G1–G3 and G5–G7. This involves basepairing interactions from one base on one strand to two bases on the other strand via O6•H1 hydrogen bonding. Although the two strands are oriented nearly perpendicular, the bases still have a sufficiently favorable orientation toward each other as to establish such hydrogen bonds; all donors or acceptors of the bases of one strand are close to their counterparts on the other strand. Despite the presence of sodium ions initially, no sodium ions are coordinated to this “cross-like” structure after it forms.

Molecular dynamics of parallel d(GGGG)₂ “diagonal duplex”

Another duplex that could potentially be formed by dimerization of two d(GGGG) strands is a parallel d(GGGG)₂ “diagonal duplex” stabilized by two symmetric O6•H1 hydrogen bonds (see Fig. 1 and Fig. 3 H). This molecular assembly (Fig. 8 A) was built and subjected to equilibration and a 6.4 ns production run. Its behavior was strikingly similar to that seen for the simulation started as an edge duplex. The A- and C-strands gradually rotated to form the “cross-like” assembly (Fig. 8 B) within 2 ns and retained this structure for the remainder of the simulation. The resulting duplex is almost identical to that in the “edge duplex” simulation, with an RMS deviation of ∼1.7–2.1 Å between the average structures. When only the central four nucleotides are considered, the RMSD drops to 1.6 Å when comparing the 3–5 ns average structure for the edge duplex simulation to the 2–5 ns average structure for the second simulation. Given the convergence to a common model structure from two different starting points in such short simulations, it is conceivable that this is a molecular architecture that is commonly encountered on the nanosecond timescale in simulations of partial G-DNA stems.

FIGURE 8.

Stereo view of the simulated parallel d(GGGG)₂ “diagonal duplex”: (A) starting model; (B) average structure at 3–4 ns of simulation. Only nonhydrogen atoms are depicted.

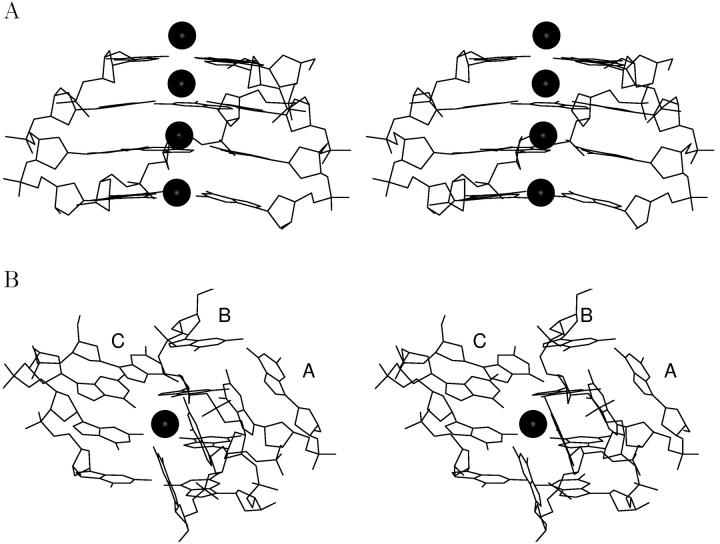
Molecular dynamics of a parallel d(GGGG)₃ triplex

After investigating the stability of possible four-stranded and two-stranded intermediates, we designed a parallel d(GGGG)₃ triplex (Fig. 3 F). This triplex initially had three ions in its partially exposed channel (Fig. 9 A) and was subjected to equilibration and 8.1 ns molecular dynamics simulation. In a striking contrast to all simulations involving four d(GGGG) strands, the triplex assembly is not stable in the simulation. The integrity of the d(GGGG)₃ triplex is closely correlated with base-cation interactions in the channel. During the first nanosecond of MD simulation, the overall triplex conformation is retained (similar to the triplex structure observed in the quadruplex) and the sodium ions remain in the incomplete channel. However, significantly larger fluctuations are observed, in sharp contrast to the rigid native quadruplex stem, especially for the outermost sodium ions. The terminal sodium ions were expelled from the channel at around 1 ns and simultaneously the overall triplex structure swiftly disintegrated. The collapse led to a coiled-up structure formed by the three strands with an ion coordinated between the two innermost triplets. This structure remains stable throughout the simulation. A detailed inspection of this molecular coil reveals a duplex arrangement where two sets of strands (initially strands A and B and strands B and C, see Fig. 1) are oriented almost perpendicular (Fig. 9 B).

FIGURE 9.

Stereo view of the simulated parallel d(GGGG)₃ triplex structure: (A) starting model; (B) average structure at 4–8 ns of simulation. Only nonhydrogen atoms are depicted along with coordinated sodium ions in the molecule center.

Comparing these pair interactions to the cross-like dimer discussed in the previous section, we see profound similarity. In the case of the A-B strand interaction, the RMSD of the central four nucleotides to the cross-like duplexes is 1.7 Å (compared to 1.6 Å between the two above cross-like duplexes). The B-C interaction also has some cross-like features, albeit less apparent, with an RMSD of 2.1 Å for the internal four nucleotides or 3.0 Å overall. The larger differences to the cross-like duplex result from the C strand interaction where it partially interacts with the other strand in a classic quadruplex manner mediated by a bound sodium ion in the major shallow groove of the A-B “cross-like” duplex (Fig. 9 B).

Fig. 10 qualitatively summarizes the basic dynamic behavior of the simulations molecules as revealed by all the above simulations.

FIGURE 10.

Cartoon representation of the simulations performed and structural changes observed in various models on the G-DNA formation pathway. (A) Creation of the “cross-like” dimer from G-DNA parallel- and edge-like duplex models. (B) Creation of the ion-stabilized trimer structure from the G-DNA like triplex model. (C) Spontaneous capture of ions from the solvent by the vacant G-DNA quadruplex. (D) Creation of the single cation stabilized “spiral stem” and spontaneous strand slippage closer to the native quadruplex. (E) Only two ions appear necessary to stabilize the double slipped G-DNA quadruplex model structures.

Estimating the relative importance of various G-DNA d(GGGG)₄ assemblies

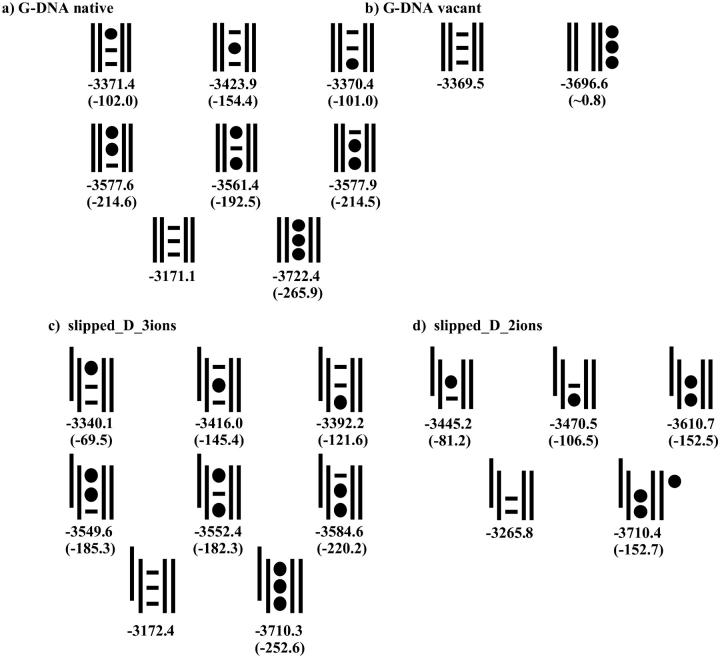
To obtain a better understanding of the relative importance of each different G-DNA assembly studied, we applied the MM-PBSA technology (Kollman et al., 2000; Srinivasan et al., 1998) to obtain crude estimates of the relative free energies between the various model structures (Table 2). The goal is to give a qualitative ranking of the relative importance or validity of the various models. Estimates of the free energy for each model were obtained over at least 2 ns portions of each trajectory with sampling at 10 ps intervals to give averages over 200 configurations. Similar numbers are obtained if we use finer sampling for the average free energies (not shown). As demonstrated in the following, to obtain meaningful results it is necessary to explicitly include the integral structural cations into the calculations.

TABLE 2.

Estimated free energies for the various d(GGGG)₄ models calculated using the MM-PBSA methodology (Srinivasan et al., 1998)

Model	G (no ions) (kcal/mol)	G (3 ions) (kcal/mol)	Gbinding ion d(GGGG)4	ΔGnative (kcal/mol)	−TΔS, 300 K (kcal/mol)
G-DNA native	−3171.2	−3722.4	−265.9	0.0	0.0
	(23.3)	(15.0)	(19.2)
G-DNA vacant	−3369.5	−3696.6	∼0.8*	+25.8	−5.4
	(15.8)	(16.1)	(4.5)
Slipped_D_2ions	−3265.8	−3710.4	−152.7	+12.0	−2.2
	(23.2)	(16.3)	(16.6)
Slipped_D_3ions	−3172.4	−3710.3	−252.6	+12.1	–
	(27.5)	(16.6)	(24.2)
Shift_AB	−3264.9	−3710.9	−154.0	+11.3	−4.8
	(24.5)	(16.6)	(20.7)
Spiral stem (2–4 ns)	−3353.7	−3659.5	∼−9.1*	+62.9	∼−4.2
	(20.4)	(19.9)	(5.0)
Spiral stem (7–9 ns)	−3372.9	−3672.8	∼−3.3*	+49.6	∼−2.8
	(21.4)	(21.3)	(5.4)

Total free energies do not include the solute entropic components. These are shown in the last column and represent the difference in total (rotational, translational, and vibrational) entropy, thermally weighted at 300 K, to the native G-DNA model with three explicitly bound ions. As discussed in Methods, translational entropic components of the “free” ions (representing 2–3 kcal/mol per free ion) are not included. Column 2 displays free energies neglecting any explicitly bound ions. Column 3 represents the absolute free energy of the d(GGGG)₄ model including three ions. Column 4 presents the interaction free energies for the three bound ions. The difference in the free energies (relative) of the G (3 ions) to the native G-DNA quadruplex are shown in column 5. Standard deviations are shown in parentheses. Standard deviations for the −TΔS term are on the order of 1–4 kcal/mol with higher values obtained when ions are included.

^*Numbers are approximate in that, due to ion motion, the solvent-accessible surface area calculation failed and therefore approximate values for this (small) energy component were used.

The importance of bound ions

As can be seen in the second column of Table 2, G (no ions), the free energies evaluated without explicit inclusion of the integral bound ions are misleading. These results would suggest that the native G-DNA quadruplex is more than 100.0 kcal/mol less stable than the ion free “vacant” G-DNA quadruplex or even the fully slipped spiral stem structures! This is a direct artifact of not including the explicitly bound ions into the (free) energy analysis. To get around this, we included the explicitly bound ions. The procedure employed always included all the channel-bound ions and then eventually additional “free” ions nearest any of the O6 atoms of the guanines such that the total number of ions included was three. This data is shown in Table 2, column 3 (in bold), and represents the absolute free energy of the d(GGGG)₄ model including three ions. The data are the main outcome of our MM-PBSA analysis and display a remarkable consistency in the estimated free energetics. A case in point is the reported free energies for the two distinct single slipped strand simulations with two or three bound ions (slipped_D_2ions and slipped_D_3ions) that are virtually identical, even though there is a considerable difference in the ion-G-DNA interaction free energy (as expected since in the case of the slipped_D_2ions simulation only two ions are bound inside the channel). This suggests amazing consistency of the total free energies despite the large differences in cation-solute interaction free energies (column 4). It should be noted that the reported free energies neglect the translational entropy loss upon binding of the third Na⁺ ion (2–5 kcal/mol at 300 K). If this entropy is included, along with an additional small favorable free energy due to the higher configurational entropy as estimated by quasiharmonic analysis (data not shown), this suggests that the slipped assembly is slightly more stable with two bound channel cations.

DISCUSSION AND CONCLUSIONS

In the following paragraphs, we first summarize what our results suggest about possible mechanism of the formation of parallel stranded G-DNA stem, and then we provide assessment of the reliability of our computations.

Implications for the formation of parallel stranded G-DNA quadruplexes

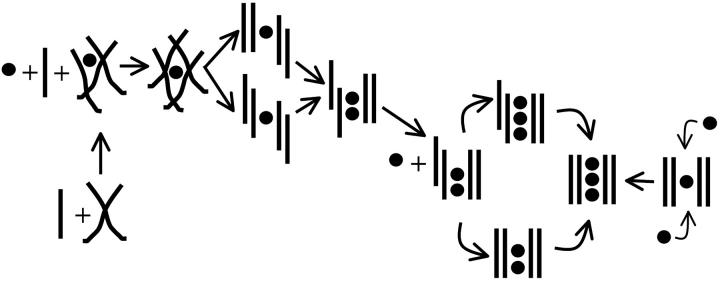
The simulated structures can be divided into two groups. The first group comprises molecules that are completely stable (some with minor initial rearrangements) on the timescale of the simulations. All these structures could in principle be involved in the stem formation. The second set of structures disintegrates on the nanosecond timescale, a timescale that is very short compared to the anticipated formation time of G-DNA. All structures that disintegrate on the nanosecond timescale are considered to be unstable and thus are not likely involved in G-DNA formation. It is our belief that this remarkable instability does not originate from force field artifacts. The force field utilized here has been extensively applied in the past for simulations of G-DNA (Chowdhury and Bansal, 2001a, 2001b; Spackova et al., 1999; Stefl et al., 2001a) and other noncanonical nucleic acid structures (Cubero et al., 2002, 2001; Shields et al., 1997, 1998; Spackova et al., 1998, 2000), and there has not been a single case reported demonstrating unstable structure in MD simulation of atomic-resolution experimental geometries. This is by no means proper evidence that the force field is perfect; however, its approximations have been well discussed (Cheatham et al., 1999; Cheatham and Kollman, 2000; Feig and Pettitt, 1998; Spackova et al., 1999; Stefl et al., 2001a). The force field has been shown to reliably represent G-DNA structures and it is highly unlikely that the force field approximation would lead to artifactual disintegration of a truly stable structure on a nanosecond timescale. Fig. 11 displays the hypothetical path toward quadruplex formation suggested by our simulation results.

FIGURE 11.

Cartoon representation of a possible folding pathway as suggested by the simulations. The key intermediates are the following: 1), cross-like hydrogen-bonded duplexes that do not interact with ions and that possess free base hydrogen bonds capable of intercepting additional strands; 2), cross-like hydrogen-bonded triplexes that are modestly stabilized by a cation and still possess free base hydrogen bonds to intercept additional strands; and 3), a wide range of stable four-stranded intermediates with structured quartets stabilized by monovalent cations.

On a direct path to the stem: four-stranded structures with slipped strands

The simulations show that d(GGGG)₄ can adopt a number of alternative parallel four-stranded structures with slipped strands that are completely stable during nanosecond-scale simulations. We have simulated a number of these (Fig. 11) including “slipped-strand” structures having one or two out-of-register strands with just three or two intact G-quartets. We further studied a “spiral stem” model with all strands progressively shifted, leaving just one central G-quartet intact. The latter structure can be considered an extreme case of “slipped” structures.

The data in column 5 of Table 2 (ΔG_native) that shows the relative free energy of the models (including the bound ions) confirms this picture. The experimentally observed native cation-stabilized stem is the free-energy minimum, and as strands slip, the free energy goes up (i.e., it is an unfavorable process). Similarly, absence of the cations to stabilize the G-quartets is unfavorable. The spiral structure clearly is the least stable assembly and this is significantly less stable than the four-quartet vacant stem. However, note that as the 300 K simulation of the spiral stem continues, its free energy improves by ∼10 kcal/mol, such that we may not have sampled sufficiently long to converge to a fully equilibrated spiral stem structure. The vacant quadruplex (including the three closest ions in bulk) is significantly destabilized (20.4 kcal/mol when considering solute entropy) compared to the native quadruplex. This suggests that four-quartet quadruplexes are never devoid of bound cations. When considering the single slipped strand model structures, it is apparent that the models are nearly equally stable with two or three bound ions. Interestingly, the single and double slipped structures are virtually isoenergetic and considerably more stable than the vacant stem and thus the vacant stem is unlikely to be an intermediate in the folding process. On the other hand, even the single-slipped structures are rather significantly less stable compared to the native stem and thus they are not supposed to be observed once the formation process is completed and equilibrium is reached.

Given the range of slipped structures sampled, we did not explore any further four-stranded intermediate structures with strand slippage closer to the native d(GGGG)₄ geometry. We assume that the stability of “spiral stem” points toward the existence of a large number of additional stable four-stranded structures of d(GGGG)₄ showing various degrees of strand slippage.

We have previously proposed that the “strand-slippage” mechanism may occur during G-DNA quadruplex stem formation (Spackova et al., 1999) and we identified the “slipped strand” structure as a possible metastable state involved in the very last stages of the native stem formation. The present simulations allow us to suggest that formation of the native stem is likely to occur after any of the four stranded assemblies with slipped strands is formed. After any of these slipped four-stranded d(GGGG)₄ structures assembles, the process could continue, albeit on a timescale much longer than affordable in our simulations, as a gradual step-by-step and sometimes perhaps back-and-forth process involving progressive reduction of strand-slippage, formation of additional G-quartets, and trapping of additional cations. Actually, a nanosecond-scale rearrangement of the “spiral stem”—one step toward the native structure—has been achieved and observed spontaneously in MD simulation by increasing the temperature of the simulation to 400 K. In this simulation, the same equilibrated spiral stem model structure (filled with six sodium ions along its central axis, see Fig. 6 A) was used as a starting point. Then the structure was slowly heated up to 400 K during the first 50 ps. All the ions were expelled within 300 ps except for one that remained coordinated in-plane with the central quartet, in close analogy to the room temperature simulation of the same molecule. However, contrary to the 300 K simulations, higher thermal fluctuation associated with the elevated temperature induced a shift of one strand to form two quartet layers at ∼1 ns one step closer to the native stem. These two quartets (with one sodium ion coordinated between them) remained stable until the end of simulation (7.8 ns) and no further slippage events were observed. This simulation suggests that the spiral stem intermediate is able to rearrange its geometry toward the native G-DNA stem. We further suggest that as the structure is approaching the four-quartet quadruplex stem, it becomes more and more structurally rigid with integral bound ions. It is to be noted that the final stages of G-DNA stem formation may actually be quite slow since cation stabilized intermediates with several quartets are assumed to be very rigid and their further movement toward the final stem is likely to occur during the exchange of cations between solute and bulk solvent.

Involvement of integral cations

The simulations clearly suggest that all “slipped” four-stranded structures are stabilized by monovalent cations interacting predominantly with intact G-quartets. The four-stranded structures containing at least one G-quartet, when lacking integrally bound cations stabilizing their quartets, are capable of swiftly retrieving cations from the bulk solvent. This principle is well demonstrated by the “spiral stem” simulation where the molecular assembly was stable in the presence or absence of ions in the channel at the beginning of the simulation. When initially excessively soaked by ions, the “spiral stem” molecule expelled all the ions except for a single one that remained coordinated in plane of the central quartet. When having a vacant quartet at the beginning, the molecule swiftly trapped two ions in the channel from the bulk solvent. Similarly, vacant intact 6-DNA stems retrieve a cation from the bulk solvent within few nanoseconds (Chowdhury and Bansal, 2001a; Spackova et al., 2001), and similarly the coil-like trimer model is significantly stabilized by its lone bound cation (see below).

Further insights into the role of bound cations in four selected trajectories can be obtained from Fig. 12, showing a comparison of the calculated free energies with no, one, two, or three explicitly included ions along with interaction energies for the ions to the DNA. These numbers allow approximate comparison of the stability of individual cation-binding sites inside the channel. Considering the values in Fig. 12 A for the native G-DNA quadruplex, there is a remarkable consistency in the numbers on both halves of the quadruplex. Specifically, ions are equally favored at the 5′ and 3′ side of the quadruplex with stronger ion interaction between the central quartets. The stronger interaction at the center favors having one of the ions at the center, when two ions are bound, rather than having the central binding site vacant. This provides an impetus upon ion binding for the shuttling of ions from the outside into the center of the quadruplex (Chowdhury and Bansal, 2001a). When no ions are bound (Fig. 12 B, vacant G-DNA qaudruplex), there is little free energy of ion binding, implying that the ions outside the channel are only weakly and transiently associated to the quadruplex. Considering the slipped structures, the picture changes somewhat and no longer is the central position always favored. When two ions are bound, there is a clear preference for leaving the 5′ position open. This is evident by Fig. 12 C, center, and by Fig. 12 D, where it is seen that the binding of a third ion and shifting it into the channel does not lead to a more stable structure (as shown in the last items of Fig. 12, C and D). The current energetic results suggest a preference for ion binding starting from the 3′ direction in slipped structures.

FIGURE 12.

Schematic representation of the free energy of individual ion binding sites extracted from four-stranded d(GGGG)₄ model trajectories: native and vacant stem, and single-slipped stems with two or three cations. Solid balls inside the double vertical lines (representing the DNA structure where the 5′ end is up) represent bound ions whereas those outside the DNA are free but associated ions (those closest to and outside the channel). Horizontal lines represent empty ion positions in the various models. Below each schematic model is the total free energy of the d(GGGG)₄ model including the ions shown by solid balls, and in parentheses is the (total) ion-DNA interaction energy (defined as the absolute free energy of the d(GGGG)₄-ion complex minus the free energies of the d(GGGG)₄ model and ions calculated separately). All the free energies are in kcal/mol. Solute entropic components are not included. Note that for a reasonable comparison of the absolute free energies, the same number of explicit cations must be included into the analysis.

Considering all the results, our study supports the view that monovalent cations are involved in the early stages of the process of the stem formation, and the quartet-cation interactions represent major stabilization contributions. Nevertheless, intermediates with a small number of quartets may heavily rely on base stacking and H-bonding of bases not yet involved in the quartets, as seen in the “spiral stem” simulations. As pointed out elsewhere, those structures utilizing H-bonding for stabilization may be sensitive, for example, to guanosine to inosine substitution. This is because the absence of the N2 amino group, although it does not affect the stabilization of the quartets by ions, significantly reduces the H-bonding capability of the strands in the absence of ions. Thus, extensive guanosine to inosine substitutions may alter the formation path and substantially destabilize some of the possible intermediates (Stefl et al., 2001a).

Farther away from the native stem: three and double-stranded assemblies

We could not locate any three-stranded or duplex structure that conserved the interaction patterns seen in the quadruplex. We simulated a Hoogsteen duplex with N7•H21 and O6•H1 hydrogen bonds, and a diagonal duplex with two symmetrical O6•H1 hydrogen bonds (Figs. 1 and 3). Both duplexes are very unstable and convert to virtually identical “cross-like” shapes stabilized by extensive nonplanar interbase hydrogen bonding but apparently not by monovalent ion association. The estimated free energy of strand association, neglecting entropic components, suggests that the association of strands is favored by ∼7–8 kcal/mol. Although the entropic penalty for loss of rotational and translational degrees from the free strands is significant, and likely in the range of 2.0–4.0 kcal/mol (for an ion) to ∼15 kcal/mol (for an ideal gas) at 300 K, it is partially offset by the greater vibrational freedom of the dimer (4 kcal/mol). The approximate free-energy analysis, and spontaneous formation of the “cross-like dimers” in short simulations, suggests that formation of a cross-like duplex is favorable and that ions do not further stabilize the structure. Note that the stability of this H-bonding could be further enhanced when allowing the guanine amino group to adopt a partial sp³ pyramidalization and to form out-of-plane H-bonds. This effect is not included in the present force field but has been well documented by recent ab initio quantum chemical studies (Hobza and Sponer, 1999, 1994; Sponer et al., 1996).

The same “cross-like” structure was also formed by sets of two strands when attempting simulation of a parallel d(GGGG)₃ triplex. After the initial disintegration of the triplex model, the “cross-like” duplex remains to interact with the third strand via a sodium cation (“coil-like” structure). Thermodynamics calculations reveal that the coil-like structure is likely stabilized by the presence of this cation, whereas the cross-like duplex itself is not stabilized by cation coordination. Table 3 shows the approximate free-energy decomposition for the G-DNA coil-like triplex structure and indicates that the bound ion is necessary to stabilize the structure. Without the bound ion, the interstrand interaction free energies (neglecting solute entropic components) are significantly positive (18–19 kcal/mol, marked at asterisk entry in the table, and likely even higher with entropic effects included). However, when the ion is bound, there is a net stabilization that overcomes the penalty of bringing a third strand to the dimer structure. In row 2 of Table 3, the separate duplex free energies for the AB and BC dimer closely match the corresponding energies of the free cross-like duplexes (see above). This is not seen for the AC dimer. The ion-dimer interaction energies, in contrast to the ion-trimer one, show essentially no stabilization by the tightly associated ion (since adding in the entropic loss for the ion on binding essentially negates the favorable interaction free energy), consistent with the results for the free dimers. In summary, the calculations suggest the following picture: formation of cross-like duplexes is favorable in the absence of bound cations, whereas keeping three strands together, at least in this particular case, requires the presence of a bound cation.

TABLE 3.

Decomposition of the free energies in the triplex models and association free energies for the various substructures in the triplex

A	B	C	Ion
−849.2	−847.0	−841.4	−99.7
A-B	B-C	A-C
−1690.6	−1690.1	−1683.4
(−0.7)	(−1.7)	(+0.9)
A-ion	B-ion	C-ion
−941.5	−944.8	−938.2
(−0.3)	(+0.4)	(+1.4)
AB-ion	AC-ion	BC-ion	ABC
−1795.4	−1783.0	−1792.0	−2512.8
(−6.5)	(−1.4)	(−4.4)	(+17.6–+19.0)*
ABC-ion
−2645.3
(−34.2)

Absolute free energies, and in parentheses, the effective binding energy for each model, where relevant (interacting subsystems are separated by the dash). All the sampled structures are from the triplex model trajectory. The heading in each table entry represents the portion of the model evaluated in the free-energy analysis. For example, A represents the free energy of the isolated A-strand from the triplex simulation, and ABC-ion represents the free energy of the A-, B-, and C-strand complex including the bound ion from the triplex simulation. For the interaction energy, the dash signifies how the interaction is split; for example, A-B represents the interaction of the A-strand with the B-strand (in the triplex structure). All the energies are in kcal/mol. Note that solute entropic effects are not included; these likely span the range of ∼2–3 (for an individual ion) to ∼10–15 kcal/mol (for strands) at 300 K disfavoring association (as discussed in Methods). For the sake of comparison, the free energies of the duplex simulations dimer_AB and dimer_AD are –1694.0 and –1689.4, respectively.

^*Range of association free energies for the triplex assembly ABC for A-BC, B-AC, and C-AB association in the absence of ions.

Both the “cross-like” dimer and “coil-like” triplex are stable and contain unpaired guanines capable of intercepting other single strands and/or similar “cross-like” dimer structures via hydrogen bonding of bases, allowing then a preformation of four-stranded structures. These could than serve as “nucleation” centers for a further buildup of the stem (Fig. 11). One can imagine, for example, two “cross-like” assemblies aggregating together, stabilized by an ion, with a slippage mechanism completing the formation into a fully paired quadruplex stem, similar to the proposed duplex-dimerization mechanism. A similar process could be initiated when adding the fourth strand to the cation-stabilized coil-like triplex with a mechanism similar to the strand addition formation process. Simulation of these processes is obviously out of the range of contemporary nanosecond timescale simulations.

Interestingly, the individual d(GGGG) strands in “cross-like” and “coil-like” structures keep their intrastrand geometries largely unchanged. This observation is actually consistent with the concept of an invariant guanine stacking geometry (Stefl et al., 2001b; Trantirek et al., 2000).

Comparison with experiments

Experimental kinetic and thermodynamic data indicate that G-DNA formation proceeds in discrete steps progressing through stable intermediate states (Hardin et al., 1997, 1991). Experiments indirectly suggest that the formation process might proceed by three mechanisms, that is: stepwise strand addition, duplex dimerization, or further by a triplex-triplex disproportionation (Hardin et al., 1997, 1991). If this were the case, the first and third of these mechanisms must involve a stable triplex substate. When considering “cross-like” duplexes and “coil-like” triplexes, our set of intermediates is already sufficient to follow all three paths. A combination of different paths and intermediates is obviously not ruled out and a more detailed insight is apparently beyond the currently available simulation techniques. We certainly do not suggest that the “coil-like” cation stabilized triplexes and “cross-like” duplexes represent the only possibilities how to assemble three and two d(GGGG) strands together. Nevertheless, they likely are representative examples of such structures. We suggest that in the later stages of the quadruplex formation, the process proceeds through step-by-step structuralization of cation-stabilized four-stranded intermediates.

Limitations of the present results

The goal of this work was to propose atomic resolution models of intermediate structures that may occur during the formation of a G-DNA quadruplex stem, using explicit solvent simulations followed by implicit solvent free-energy evaluations. The first significant limitation relates to the lack of completeness in the set of possible intermediate structures studied. Obviously, our search should be considered an investigation of a subset of possible models on the path between a single d(GGGG) strand and the four-quartet quadruplex stem. Nevertheless, we suggest that our range of structures allows some suggestions to be made and that these conclusions regarding the whole class of parallel slipped four-stranded structures are not affected substantially by the sampling limitations. The simulation capped both ends of the conformational space of four-stranded slipped structures and the results are very consistent. There exist a number of metastable parallel stranded slipped structures of d(GGGG)₄ having from one up to three quartets. The four-quartet stem is the global free-energy minimum with respect to them (Table 2) and the slipped structures are capable to spontaneously convert to the four-quartet stem. The simulations as well as the thermodynamics data suggest very clearly that the G-quartets are always stabilized by integral monovalent cations. We did not investigate four-stranded assemblies other than the partly structured “slipped” parallel stems. A vast number of such structures obviously can exist; nevertheless, we believe that when gradually converting the structures toward the native stem, the molecules would sooner or later transform into some partly structured parallel stems of the type investigated here. We did not investigate the antiparallel structures that may compete with the parallel ones; however, these will be considered in forthcoming work.

Regarding the three- and two-stranded intermediates, we obviously face further limitations: no stable three-stranded or duplex structure conserving native quadruplex-type basepairing patterns have been found. This does not rule that there might exist stable parallel guanine triplex or duplex geometries substantially different than the molecules investigated in our simulations. However, we consider this possibility to be rather remote, especially since we saw spontaneous conversion of different duplex models to a common cross-like duplex structure.

We did not investigate additional mismatch basepairing patterns, in which a combination of syn and anti orientations of glycosidic bonds would be required. The reason is that it is not entirely straightforward to imagine an anti-to-syn transition during the formation of a G-G paired duplex followed by a further syn-to-anti transition to form the parallel quadruplex. The G•G basepairs in which one base has syn and the other anti orientation of the glycosidic bond are relevant for G-DNA quadruplex conformers with antiparallel strand polarity, and investigation of these quadruplexes is currently in progress in our laboratories.

The present simulations were carried out to investigate primarily the parallel stranded d(GGGG)₄ and its possible intermediates. Obviously, the path of the quadruplex formation will be affected by factors such as the stem length, quadruplex topology including presence and composition of the loops, etc. Nevertheless, it is rather straightforward to extend the present approach to other quadruplex types. Also, formation of the stem might be largely affected by interactions with other molecules, such as proteins and drugs. Based on experimental data, we speculate that the process of strand shifts toward the four-quartet stem could be accelerated by stacking of large planar molecules on the top or bottom of the four-stranded assemblies (Han et al., 2001).

Reliability of free-energy calculations

As discussed in greater detail in the Supplementary Material, specific attention should be paid to understand the reliability of the MM-PBSA thermodynamics calculations (Marelius et al., 1998; Srinivasan et al., 1998; Vorobjev et al., 1998). A major point of the present study is finding that, for G-DNA molecules, meaningful MM-PBSA results are achieved only if ions are included in the analysis explicitly. To date, except for the work by Beveridge and co-workers (Jayaram et al., 1998; Sprous et al., 1998) and analysis of bound ions by Tsui and Case (2001), salt effects in this type of analysis have only been included implicitly where the effect on the free energy tends to be small. However, in the current work, if the bound ions are not explicitly included, the free-energy numbers do not make sense. This finding should have serious implications for future studies of nucleic acid molecules with tightly bound ions.

Although there are significant sampling limitations, we believe that the trends seen with our free-energy estimates are reasonable and based on significant free-energy differences. This gives us a qualitative ranking of the relative importance of different structures and clear insights into the cation binding. However, the limits of sampling in MM-PBSA evaluations can be considerably more important for some particularly subtle results of our study, mainly the 3′ preference for ion binding in the slipped structures. The sampling issue is a difficult problem, as highlighted in some recent work that shows that even 10 ns length MD simulations may not be sufficient to fully sample the interaction of monovalent ions with DNA (Cheatham and Young, 2001; Spackova et al., 2001). Even in the current set of state-of-the-art spiral stem simulations, as shown in Table 2, we see incomplete sampling as clearly evidenced by conformational transitions during the simulation that lead to free-energy drops of >10.0 kcal/mol.

It is also to be noted that the free energies of ion binding to the solute reported in column 4 of Table 2 and Fig. 12 are overestimated since they are derived from single trajectories of the whole complex. Thus, the solute relaxation upon cation binding/release is neglected.

CONCLUDING REMARKS

Recent years have been characterized by an unprecedented advance of the quality of computational tools available to study structure, dynamics, and molecular interactions of nucleic acids (Beveridge and McConnell, 2000; Cheatham and Kollman, 2000; Cheatham and Young, 2001; Hobza and Sponer, 1999). Specifically, modern classical molecular dynamics techniques were applied to study a wide variety of structures and processes and often demonstrate very substantial improvements toward reproducing and complementing available experimental data, including atomic resolution structures. Further refinements of these techniques, proper and careful consideration of their advantages and limitations, and increasing computer power give us more and more confidence that these tools can be, in selected cases, useful for predictions. The present study, suggesting and exploring at the atomic resolution level intermediate assemblies that could be involved in a G-DNA stem formation, is one of the most extended qualitative predictive attempts carried out so far. We believe that our study illustrates that use of advanced computational MD tools supplemented by techniques such as MM-PBSA for predictions will become one of the major tasks for computational chemistry of nucleic acids in the next decade.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.