Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Sep;85(3):1876–1881. doi: 10.1016/S0006-3495(03)74615-3

A Novel Method for Study of Protein Folding Kinetics by Monitoring Diffusion Coefficient in Time Domain

Tomokazu Nada 1, Masahide Terazima 1
PMCID: PMC1303359  PMID: 12944300

Abstract

Molecular diffusion process after the photo-induced electron injection to ferric cytochrome c (Fe(III) cyt c) in guanidine hydrochloride (GdnHCl) 3.5 M buffer solution is studied by the time-resolved transient grating technique. Circular dichroism studies have revealed that Fe(III) cyt c is unfolded under this condition but the reduced form, Fe(II) cyt c, is folded. Hence, this pulsed laser-induced reduction should initiate the folding process of cyt c. The observed transient grating signal shows prominent features, which have never been observed before. Based on several characteristic points, we concluded that the apparent diffusion coefficient (D) of Fe(II) cyt c after the reduction is time dependent, which must be associated with the protein folding dynamics. This time-dependent apparent D should reflect either the continuous time development of the hydrodynamic radius or population change of the unfolded and folded states during the folding dynamics. This is the first observation of the time-dependent apparent D during any chemical reaction, and this time-dependent measurement of D should be a unique and powerful way to study the protein folding kinetics from a viewpoint of the protein's shape or the protein-water intermolecular interaction.

INTRODUCTION

The diffusion coefficient is one of the important physical properties characterizing the nature of molecules in solution phase. Based on extensive research on the diffusion process over more than 100 years in chemistry, it is now well recognized that the diffusion coefficient (D) reflects not only the molecular size or solution viscosity but also the shape of the molecule as well as the intermolecular interaction (Cussler, 1984; Tyrrell and Harris, 1984). During the long history until now, D always has been considered to be a static character, partly because of rather time-consuming experimental techniques. Recently, a pulsed laser-based spectroscopy, transient grating (TG) method, opens a way to measurements of D in milliseconds to the tens of microseconds time range (Terazima and Hirota, 1993;Terazima et al., 1993, 1995; Okamoto et al.,1995, 1997, 1998; Ukai et al., 2000a,b; Terazima, 2000). Using this method, D of transient species, e.g., unstable radicals, have been reported, although D has still been a constant parameter in these works. In this paper, we report the first observation of the time-dependent apparent D during the protein folding kinetics using the time-resolved TG technique.

The folding and unfolding kinetics of proteins have been the subject of extensive studies using various methodologies for triggering and detection of the dynamics (Pain, 2000). For triggering the folding dynamics, a stopped flow and a rapid mixing have been used. Recently, several methods utilizing a pulsed laser, laser-induced temperature jump, or light-induced electron injection methods become gradually powerful technique for the studies. For the detection, the extent of the denaturation of the protein has been frequently monitored by circular dichroism (CD) method, emission detection, absorbance change in visible or infrared region, resonance Raman scattering, and so on. The emission intensity or absorbance change provides us information on rather local protein structural changes around the chromophores associated with the optical transition. The formation of the secondary structure (e.g., α-helices or β-sheets) can be monitored by the CD signal intensity. However, to understand the nature or the mechanism of the protein folding, it would be essential to monitor the global protein structure change or the protein-solvent interaction, e.g., hydrophobic or hydrogen-bonding interaction. In this respect, D is certainly a useful quantity to monitor the folding dynamics. Despite this expected usefulness, there has been no attempt to monitor the folding dynamics using D. Here we studied the folding kinetics of chytochrome c (cyt c) by the TG method combined with the pulsed laser-induced electron injection from β-nicotinamide adenine dinucleotide (NADH) to cyt c.

Cyt c is a small protein (104 residues) with a heme group covalently bound to residues Cys-14 and Cys-17.This protein has been a prototype of the protein folding studies(Pascher et al., 1996; Telford et al., 1998; Hagen et al., 1997; Takahashi et al., 1997; Yeh et al., 1997; Englander et al., 1998; Shastry and Roder, 1998; Shastry et al., 1998; Godbole and Bowler, 1999; Segal et al., 1999; Chen et al., 1999; Telford et al., 1999; Okuno et al., 2000; Abbruzzettri et al., 2001, Bhuyan and Udgaonkar, 2001). The protein stability depends on the metal oxidation state. Reduced cyt c (Fe(II) cyt c) is more stable than oxidized cyt c (Fe(III) cyt c) against guanidine hydrochloride (GdnHCl). For example, in 3.5 M GdnHCl solution, oxidized cyt c is unfolded, whereas the reduced form is folded. Thus, under these conditions, rapid electron injection into the unfolded Fe(III) cyt c initiates the folding dynamics (Jones et al., 1993; Pascher et al., 1996; Telford et al., 1998). We found that apparent diffusion coefficient of cyt c is changing in millisecond time range after photoexcitation of NADH. This change may be interpreted in terms of the time development of either the intermolecular interactions that affect the hydrodynamic radius or population change of the unfolded and folded states with different D during the folding dynamics.

EXPERIMENTAL

The experimental setup and the principle of the measurement were similar to that reported previously (Terazima and Hirota, 1993; Terazima et al., 1993, 1995; Okamoto et al., 1995, 1997, 1998; Ukai et al., 2000a,b; Terazima, 2000). Briefly, the third harmonic of a Nd-YAG laser (Spectra-Physics Quantum-Ray Model GCR-170-10) with a 10-ns pulse was used as an excitation beam and a photodiode laser (840 nm) as a probe beam. The diffraction of the probe beam was isolated from the excitation laser beam with a glass filter and a pinhole, detected by a photomultiplier tube. All measurements were carried out at room temperature under the oxygen-purged condition. Horse heart cyt c and ultrapure GdnHCl were purchased from Nakalai Tesque Co. and NADH was obtained from Sigma (St. Louis, MO). They were used without further purification. Cyt c (66 μM) with NADH (650 μM) sample was prepared in a 100 mM phosphate buffer (pH = 7). Because NADH is very sensitive to the light irradiation, the sample solution was changed to a fresh one after ∼150 shots of the excitation laser pulses. The photo-induced reduction of Fe(III) cyt c was confirmed by the transient absorption signal monitored at 550 nm. The unfolded and folded conformations of Fe(III) and Fe(II) cyt c, respectively, under this condition was checked by the CD spectrum.

The principle of the TG measurement and the method of the determination of diffusion coefficient have been well established. A photoinduced reaction takes place by the sinusoidal modulated light intensity that is produced by the interference of two excitation light waves. The spatial modulation of the concentration of reactant and the product leads to the sinusoidal modulation in the refractive index (δn), and this modulation can be monitored by the diffraction efficiency of a probe beam (TG signal). The refractive index change mainly comes from the thermal energy releasing (thermal grating) and created (or depleted) chemical species by the photo reaction (species grating). The signal intensity becomes weaker as the spatial modulations of the refractive index become uniform, which is accomplished by the translational diffusion. Hence the decay rate constant of the thermal grating signal should be Dthq2 (Dth; thermal diffusivity of the solution, q; grating wavenumber). The species grating signal decays with a rate constant of Dq2, where D is the diffusion coefficient of the chemical species. When D of the reactant (Dr) and the product (Dp) are constants, the time development of the TG signal can be expressed by a biexponential function (Terazima and Hirota, 1993; Terazima et al., 1993, 1995; Okamoto et al., 1995, 1997, 1998; Ukai et al., 2000a,b; Terazima, 2000).

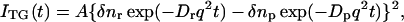graphic file with name M1.gif (1)

where A is a constant, q is a grating wavenumber, and δnr(>0) and δnp(>0) are, respectively, the refractive index changes due to the presence of the reactant and the product. The sign of δnp is negative because the phase of the spatial concentration modulation is shifted 180° from that of the reactant. It may be important to note here that once the spatial distribution of the chemical species becomes uniform by the diffusion, the signal should disappear. Hence, the time range during which we can observe the TG signal depends on Drq2 or Dpq2 (smaller one). In other words, the observation time range is determined by the magnitude of q2 for a given D.

RESULTS AND DISCUSSION

Photochemistry of NADH has been investigated previously. After the photoexcitation of NADH, it ejects the electron to finally produce the dimer (NAD)2 (Orii, 1993). The reaction scheme of NADH after the two-photon excitation at 355 nm was reported as (Orii, 1993):

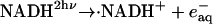graphic file with name M2.gif
graphic file with name M3.gif
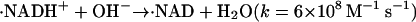graphic file with name M4.gif
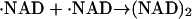graphic file with name M5.gif

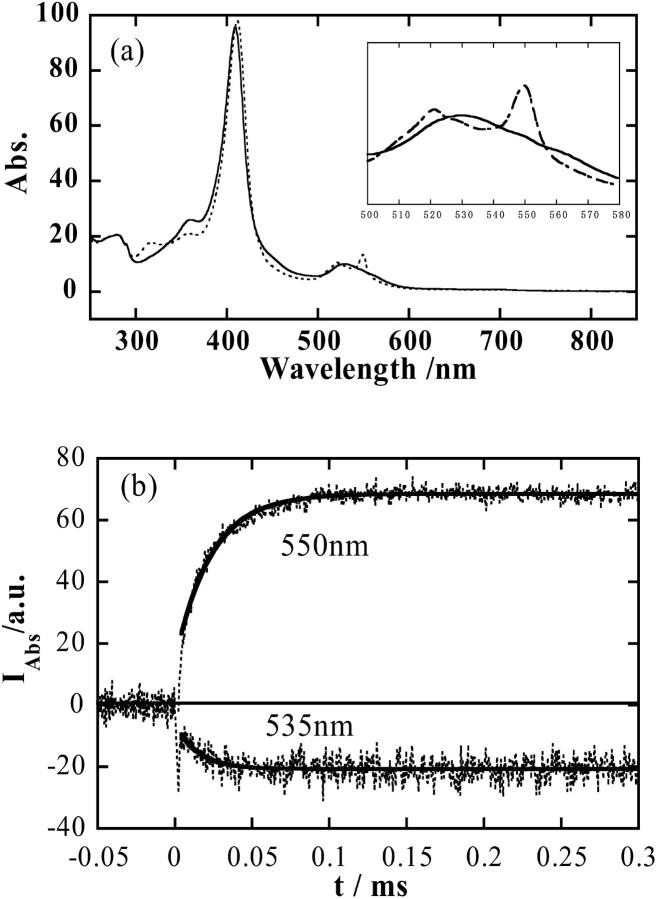
The solvated electron (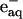Inline graphic) and NAD radical (·NAD) can efficiently reduce cyt c. Fig. 1 a shows the absorption spectra of oxidized and reduced forms of cyt c. The time profiles of the transient absorption signals of cyt c monitored at 535 nm and 550 nm after the photoexcitation of NADH are shown in Fig.1 b. The time dependence of the signal at these wavelengths indicates the reduction of cyt c with a rate constant of 3 × 104 s−1. It clearly shows that cyt c is reduced within ∼100 μs after the photoexcitation.

FIGURE 1.

FIGURE 1

Open in a new tab

(a) Absorption spectra of oxidized cyt c (solid line) and reduced cyt c (dotted line). (b) Time profile of the transient absorption signal of cyt c (dotted lines) monitored at 550 nm and 535 nm after the photoexcitation of NADH in phosphate (100 mM) buffer under nitrogen saturated condition. Fitted lines with a single exponential function are shown by the solid lines.

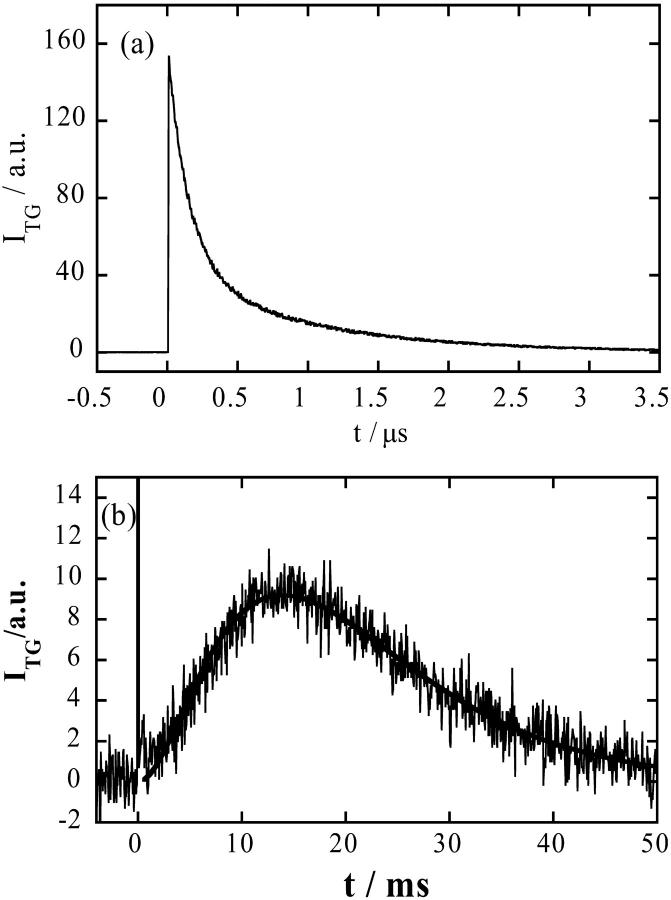
Fig. 2 a shows the TG signal after the photoexcitation of NADH/buffer solution. The TG signal rises with our instrumental response time (∼10 ns) and it decays with a lifetime of 200 ns and 1.8 μs under this condition in this short time range. The fast decay component does not depend on the grating wavenumber and the lifetime agrees well with the lifetime of the solvated electron monitored by the transient absorption method at 800 nm. Therefore, this component is assigned to the electron released from NADH. The longer lifetime depends on q2 and it agrees well with Dthq2. This is the thermal grating component created by the heating due to the nonradiative transition from the excited state. The temperature of the solution is inhomogeneous within this time range but after ∼5 μs, the temperature should be uniform because of this thermal diffusion process. Therefore, the temperature in homogeneity cannot affect the molecular dynamics on a much longer timescale.

FIGURE 2.

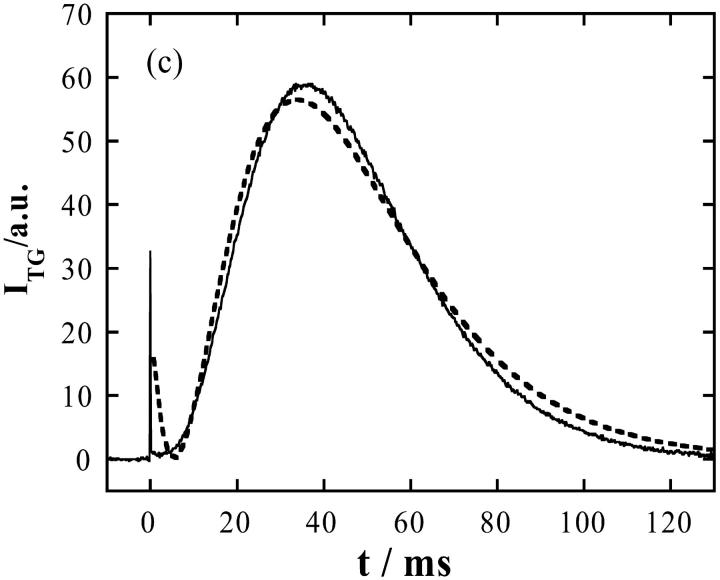
FIGURE 2

FIGURE 2

Open in a new tab

Time profile of the TG signal after the photoexcitation of NADH in phosphate (100 mM) buffer under nitrogen saturated condition with q2 = 2.5 × 1011 m−2 in (a) a short time region and (b) longer time region. The main contribution of a and the sharp spikelike signal at t ∼ 0 in b is the thermal grating signal, which comes from the thermal energy by the nonradiative transition. The smooth line in b is the best fitted curve by Eq. 1. (c) Time profile of the TG signal after the photoexcitation of NADH with Fe(III) cyt c (66 mM) and GdnHCl (3.5 M) in phosphate (100 mM) buffer under the same condition. The dotted line is the best fitted curve by Eq. 1.

We found that the time profile of the grating signal in the millisecond time range (Fig. 2 b) can be reproduced well by a biexponential function (Eq. 1), and the rate constants of the rise and decay components are proportional to q2. These facts clearly indicate that observed kinetics is controlled by the diffusion process of the reactant (NADH) and the product ((NAD)2). From the slopes of the plots of the decay rate constants versus q2, D of the these species were determined (D(NADH) = 4.0 ± 0.4 × 10−10 m2/s and D((NAD)2) = 2.5 ± 0.3 × 10−10 m2/s). These values are reasonable as D of a molecule of this size in water. Furthermore, the signal intensity is not sensitive to q2. This is a typical TG signal for diffusion species with a constant (time-independent) D.

When NADH in cyt c + GdnHCl (3.5 M)/buffer solution was photoexcited, a much stronger signal was observed on a much longer timescale (Fig. 2 c). There are several points we should note for the assignment of the origin of the signal. First, this signal was not observed without NADH. Hence, we can neglect the effect of direct photoexcitation of cyt c. Second, because the time range of this signal is much longer than that expected from D of NADH or (NAD)2, the chemical species contributed to the signal cannot be NADH but it should be much larger one, i.e., cyt c. Third, the rise-decay curve clearly indicates that two species having different D contribute to the signal. We find that the rise and decay components consist of positive and negative δn components, respectively. Hence, we can conclude from Eq. 1 that the rise and decay components correspond to the presence of the product (Fe(II) cyt c) and the reactant (Fe(III) cyt c), respectively (Eq. 1). Furthermore, this signal does not appear at a low concentration of GdnHCl and the intensity gradually increases in a range of 2.5 M < [GdnHCl] < 3.5 M. This range coincides with a range where Fe(III) cyt c is unfolded and Fe(II) cyt c is folded (Pascher et al., 1996; Telford et al., 1998). The signal intensity becomes gradually weaker with increasing the GdnHCl concentration further and almost disappeared in a range of [GdnHCl] > 6 M, under which cyt c is fully denatured. Based on these facts, we can conclude that the rise and decay components, respectively, consist of the faster (Fe(II) cyt c) and slower (Fe(III) cyt c) diffusing proteins, which should be induced by the folding reaction.

At the first glance, we may consider that the signal can be explained by two diffusing species with a constant D (Eq. 1). However, there are mainly two characteristic features to indicate that this signal does not represent the simple diffusion process. First, the time profile cannot be expressed by Eq. 1. The difference between the signal and the best fitted curve indicates that the signal at a faster timescale is much weaker (Fig. 2 c). Second, the time profile and the signal intensity depends on the observation time range (Fig. 3 a). The TG signal in a fast timescale (with a large q2) is weak, but it increases when increasing the observation time. Considering a condition of δnp ∼ δnr in Eq. 1, one may understand that the rise-decay signal intensity at the peak increases when increasing the difference between Dp and Dr. For Dp ∼ Dr, the signal should be very weak because of the cancellation of these two terms in Eq. 1. Roughly speaking, the signal intensity is a good indicator of the difference in D. Because D of the reactant (Fe(III) cytc: Dr) should be constant, the time dependence of the signal intensity should come from the time dependence of apparent D of Fe(II) cyt c (Dp), i.e., D of Fe(II) cyt c increases when increasing the observation timescale. Not only the signal intensity but also the time profile depends on the observation timescale.

FIGURE 3.

FIGURE 3

Open in a new tab

(a) The q2-dependence of the TG signals after the photoexcitation of NADH with Fe(III) cyt c (66 mM) and GdnHCl (3.5 M) in phosphate (100 mM) buffer under nitrogen saturated condition. q2 = (1) 9.6 × 1013 m−2, (2) 1.4 × 1012 m−2, (3) 5.7 × 1011 m−2, (4) 5.7 × 1010 m−2, and (5) 1.3 × 1010 m−2. (b) A geometric mean of the diffusion coefficients of the reactant (Fe(III) cyt c) and the product (Fe(II) cyt c) at various times determined from the curvature at the maximum intensity of the TG signal. The line is a guide for the eyes.

Here, it is important to note that there are two possible models to explain the time-dependent apparent D; the time-dependent D is caused by continuous change in the protein structure (hydrodynamic radius) with this speed, or the kinetics of apparent D reflects the population change between two (or more) states that have different D. In the former case, the kinetics of D represents the kinetics of structural change or the intermolecular interaction directly. In the latter case, the time dependence of the observed D does not represent the time course of the molecular structure itself but it represents the time dependence of averaged D of the mixture. In this case, if the kinetics can be expressed by the two state model having different diffusion coefficients of D (unfolded) and D (folded), which are not time dependent, the observed D (D (obs)) may be expressed by

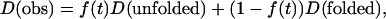graphic file with name M7.gif

where f(t) is a time-dependent fraction of (unfolded) species, which has a diffusion coefficient of D(unfolded). It is worthy to stress that the kinetics of f(t) observed in this experiment represents the population kinetics between two states with different D. Hence, the rate from this experiment should not be the same as the rate obtained by another experiment that does not probe the diffusion; i.e., the structural change that does not change D should not appear as the TG signal. Only the population change between chemical species having different size and shape, and the intermolecular interaction such as the hydrogen-bonding interaction or hydrophobic interaction (which is usually very difficult to probe in time domain) manifests itself. In either case (continuous change in D or discrete population change), we have no doubt that we are monitoring the time-dependent (either intrinsic or apparent) D and this is the first observation of the time-dependent apparent D in this timescale.

To distinguish which model is suitable to describe this time-dependent apparent D, we have to analyze the TG signal in whole time region and it is currently underway. In this paper, we qualitatively analyze the signal to show the time dependence of apparent D clearly as follows. Previously, it has been pointed out that the curvature of a biexponential function at the maximum intensity provides a geometric mean of two D (Spiegel et al., 1998).

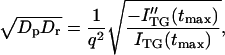graphic file with name M8.gif (2)

where ITG(tmax) is the signal intensity at the peak and ITG″(tmax) is the second derivative at this time. Fig. 3 b shows (DpDr)1/2 versus the peak time. It clearly indicates that Dr gradually increases with time after the reduction. Although the whole signal cannot be fitted by Eq. 1, the value from Eq. 2 is considered to represent (DpDr)1/2 at the time of the peak. The increase of Dp is reasonable for the folding reaction, because D of the folded cyt c should be larger than that of the unfolded cyt c due to the different conformation and different intermolecular interaction (Choi and Terazima, 2002).

The time dependence of apparent D was not detected in a submillisecond timescale, usually called the burst phase range in the cyt c folding studies. This result seems to be contradictory to the previous time-resolved small angle x-ray scattering study showing the decrease of the radius of gyration in 500 μs and 15-ms lifetime (Akiyama et al., 2002). This inconsistency may be due to the different experimental condition; the small angle x-ray scattering experiments were performed on oxidized cyt c at low denaturant concentrations. Furthermore, it should be noted that D reflects not only the size of the molecule but also the intermolecular interaction. Frequently, the D value is converted to the hydrodynamic radius based on the Stoke-Einstein relationship and discussed in terms of the molecular “size”. However, contrary to the radius of gyration that is defined solely from the geometric structure, many factors contribute to the hydrodynamic radius. For example, even when the molecular size is the same, D (or the hydrodynamic radius) could be different depending on the intermolecular interaction between the solute and the solvent (Terazima and Hirota, 1993; Terazima et al., 1993, 1995; Okamoto et al., 1995, 1997, 1998; Ukai et al., 2000a,b; Terazima, 2000). The surface roughness may also affect the diffusion process. Because, for the protein cases, the hydrophobic interaction or hydrogen bonding interaction are two major intermolecular interactions, the hydrodynamic radius in this study should be considered as the indicator of these interactions and the shape, not just the size of the protein. Hence the study of the time-dependent D provides a unique opportunity to study the time development of the destruction (or formation) of hydrophobic or hydrogen bonding interaction during the folding dynamics. The quantitative analysis of this time-dependent TG signal will be published in the future.

In conclusion, we have observed time-dependent apparent diffusion coefficient for the first time during a protein folding process. The signal clearly showed that apparent D increases with time, which suggests that the protein becomes compact and the intermolecular interaction between protein and water becomes weaker. This time-dependent apparent D can be interpreted in terms of either the continuous change of D with time by changing the conformation and/or the intermolecular interaction, or population change among two or several conformations with different diffusion coefficients. This technique will open new kinetic studies not only for the protein folding reaction but also any protein reaction dynamics that will change the hydrodynamic radius.

Acknowledgments

A part of this study was supported by the Grant-in-Aid (No. 13853002) from the Ministry of Education, Science, Sports and Culture in Japan and Scientific Research Grants from Mitsubishi Foundation.

References

  1. Abbruzzettri, S., C. Viappiani, J. R. Small, L. J. Libertini, and E. W. Small. 2001. Kinetics of histidine deligation from the heme in GuHCl-unfolded Fe(III) cytochrome c studied by a laser induced pH-jump technique. J. Am. Chem. Soc. 123:6649–6653. [DOI] [PubMed] [Google Scholar]
  2. Akiyama, S., S. Takahashi, T. Kimura, K. Ishimori, I. Morishima, Y. Nishikawa, and T. Fujisawa. 2002. Conformational landscape of cytochrome c folding studied by microsecond-resolved small angle x-ray scattering. Proc. Nat. Sci. Acad. 99:1329–1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bhuyan, A. K., and J. B. Udgaonkar. 2001. Folding of horse cytochrome c in the reduced state. J. Mol. Biol. 312:1135–1160. [DOI] [PubMed] [Google Scholar]
  4. Chen, E., P. Wittung-Stefshede, and D. S. Kliger. 1999. Far-UV time-resolved circular dichroism detection of electron-transfer-triggered cytochrome c folding. J. Am. Chem. Soc. 121:3811–3817. [Google Scholar]
  5. Choi, J., and M. Terazima. 2002. Denaturation of a protein monitored by diffusion coefficients: myoglobin. J. Phys. Chem. B. 106:6587–6593. [Google Scholar]
  6. Cussler, E. L. 1984. Diffusion. Cambridge University Press, Cambridge.
  7. Englander, S. W., T. R. Sosnick, L. C. Mayne, M. Shtilerman, P. X. Qi, and Y. Bai. 1998. Fast and slow folding in cytochrome c. Acc. Chem. Res. 31:737–744. [Google Scholar]
  8. Godbole, S., and B. E. Bowler. 1999. Effect of pH on formation of a nativelike intermediate on the unfolding pathway of a Lys73->His variant of yeast iso-1-cytochrome c. Biochemistry. 38:487–495. [DOI] [PubMed] [Google Scholar]
  9. Hagen, S. J., J. Hofrichter, and W. A. Eaton. 1997. Rate of intrachain diffusion of unfolded cytochrome c. J. Phys. Chem. B101:2352–2365. [Google Scholar]
  10. Jones, C. M., E. R. Henry, Y. Hu, C. Chan, S. D. Luck, A. Bhuyan, H. Roder, J. Hofrichter, and W. A. Eaton. 1993. Fast events in protein folding initiated by nanosecond laser photolysis. Proc. Nat. Acad. Sci. 90:11860–11864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Okamoto, K., M. Terazima, and N. Hirota. 1995. Temperature dependence of diffusion processes of radical intermediates probed by the transient grating method. J. Chem. Phys. 103:10445–10452. [Google Scholar]
  12. Okamoto, K., N. Hirota, and M. Terazima. 1998. Diffusion of photochemical intermediate radicals in water/ethanol mixed solvents. J. Phys. Chem. A. 102:3447–3454. [Google Scholar]
  13. Okamoto, K., N. Hirota, and M. Terazima. 1997. Diffusion process of the benzyl radical created by photodissociation probed by the transient grating method. J. Phys. Chem. A. 101:5269–5277. [Google Scholar]
  14. Okuno, T., S. Hirota, and O. Yamauchi. 2000. Folding character of cytochrome c studied by o-nitrobenzyl modification of methionine 65 and subsequent ultraviolet light irradiation. Biochemistry. 39:7538–7545. [DOI] [PubMed] [Google Scholar]
  15. Orii, Y. 1993. Immediate reduction of cytochrome c by photoexcited NADH: reaction mechanism as revealed by flow-flash and rapid-scan studies. Biochemistry. 32:11910–11914. [DOI] [PubMed] [Google Scholar]
  16. Pain, R. H. 2000. Mechanism of Protein Folding, 2nd ed. Oxford University Press, Oxford.
  17. Pascher, T., J. P. Chesick, J. R. Winkler, and H. B. Gray. 1996. Protein folding triggered by electron transfer. Science. 271:1558–1560. [DOI] [PubMed] [Google Scholar]
  18. Segal, D. J., D. Eliezer, V. Uversky, A. L. Fink, K. O. Hodgson, and S. Doniach. 1999. Transient dimer in the refolding kinetics of cytochrome c characterized by small angle X-ray scattering. Biochemistry. 38:15352–15359. [DOI] [PubMed] [Google Scholar]
  19. Shastry, M. C. R., and H. Roder. 1998. Evidence for barrier-limited protein folding kinetics on the microsecond time scale. Nat. Struct. Biol. 5:385–392. [DOI] [PubMed] [Google Scholar]
  20. Shastry, M. C. R., J. M. Sauder, and H. Roder. 1998. Kinetic and structural analysis of submillisecond folding events in cytochrome c. Acc. Chem. Res. 31:717–725. [Google Scholar]
  21. Spiegel, D. R., A. H. Marshall, N. T. Jukam, H. S. Park, and T. Chang. 1998. Measurement of mass diffusion coefficients using nonexponential forced Rayleigh scattering signals. J. Chem. Phys. 109:267. [Google Scholar]
  22. Takahashi, S., S.-R. Yeh, T. K. Das, C.-K. Chan, D. S. Gettfried, and D. L. Rousseau. 1997. Folding of cytochrome c initiated by submillisecond mixing. Nat. Struct. Biol. 4:44–50. [DOI] [PubMed] [Google Scholar]
  23. Telford, J. R., P. Wittung-Stafshede, H. B. Gray, and J. R. Winkler. 1998. Protein folding triggered by electron transfer. Acc. Chem. Res. 31:755–763. [Google Scholar]
  24. Telford, J. R., F. A. Tezcan, H. B. Gray, and J. R. Winkler. 1999. Role of ligand substitution in ferrocytochrome c folding. Biochemistry. 38:1944–1949. [DOI] [PubMed] [Google Scholar]
  25. Terazima, M., and N. Hirota. 1993. Translational diffusion of a transient radical studied by the transient grating method; pyrazinyl radical in 2-propanol. J. Chem. Phys. 98:6257–6262. [Google Scholar]
  26. Terazima, M., K. Okamoto, and N. Hirota. 1993. Transient radical diffusion in photoinduced hydrogen abstraction reactions of benzophenone probed by the transient grating method. J. Phys. Chem. 97:13387–13393. [Google Scholar]
  27. Terazima, M., K. Okamoto, and N. Hirota. 1995. Translational diffusion of transient radicals created by the photo-induced hydrogen abstraction reaction in solution; anomalous size dependence in the radical diffusion. J. Chem. Phys. 102:2506–2515. [Google Scholar]
  28. Terazima, M. 2000. Translational diffusion of organic radicals in solution. Acc. Chem. Res. 33:687–694. [DOI] [PubMed] [Google Scholar]
  29. Tyrrell, H. J. V., and K. R. Harris. 1984. Diffusion in Liquids. Butterworth, London.
  30. Ukai, A., N. Hirota, and M. Terazima. 2000a. Radical diffusion measured by the transient grating in a short time scale. Chem. Phys. Lett. 319:427–433. [Google Scholar]
  31. Ukai, A., N. Hirota, and M. Terazima. 2000b. Diffusion of organic molecules in the excited triplet states detected by the transient grating with a high wavenumber. J. Phys. Chem. A. 104:6681–6688. [Google Scholar]
  32. Yeh, S.-R., S. Takahashi, B. Fan, and D. L. Rousseau. 1997. Ligand exchange during cytochrome c folding. Nat. Struct. Biol. 4:51–56. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES