Dehydron: A Structurally Encoded Signal for Protein Interaction

Abstract

We introduce a quantifiable structural motif, called dehydron, that is shown to be central to protein-protein interactions. A dehydron is a defectively packed backbone hydrogen bond suggesting preformed monomeric structure whose Coulomb energy is highly sensitive to binding-induced water exclusion. Such preformed hydrogen bonds are effectively adhesive, since water removal from their vicinity contributes to their stability. At the structural level, a significant correlation is established between dehydrons and sites for protein complexation, with the HIV-1 capsid protein P24 complexed with antibody light-chain FAB25.3 providing the most dramatic correlation. Furthermore, the number of dehydrons in homologous similar-fold proteins from different species is shown to be a signature of proteomic complexity. The techniques are then applied to higher levels of organization: The formation of the capsid and its organization in picornaviruses correlates strongly with the distribution of dehydrons on the rim of the virus unit. Furthermore, antibody contacts and crystal contacts may be assigned to dehydrons still prevalent after the capsid has been assembled. The implications of the dehydron as an encoded signal in proteomics, bioinformatics, and inhibitor drug design are emphasized.

INTRODUCTION

Protein associations are at the core of biological processes, from signal transduction to enzymatic activity, and are central to the proteomics endeavor. Their physical basis, often attributed to favorable pairwise interactions between protein groups, remains elusive (Ringe, 1995; Clackson and Wells, 1995; Bogan and Thorn, 1998; Jones and Thornton, 1996; Lo Conte et al., 1999; Norel et al., 2001; Freire, 1999; Momany et al., 1996): hydrophobic-polar mismatches at protein-protein interfaces are all too common and difficult to properly account for. The prediction and rationalization of binding sites for soluble proteins require that we quantify pairwise energy contributions, and concurrently, the extent to which surrounding water is immobilized or excluded from the interactive residue pairs. In a broad sense, as proteins associate, their local solvent environments become modified in ways that can dramatically affect the intramolecular energy (Norel et al., 2001; Fernández, 2001; Fernández et al., 2002a,b; Nemethy et al., 1963; Fernández and Boland, 2002; Avbelj et al., 2000). This prompts us to deal systematically with the question: Where on a protein surface is it energetically most favorable or least unfavorable to remove surrounding water?

To answer this question, we take into account the fact that a proper “hydrophobic wrapping” of dielectric-dependent pairwise interactions is as important in energetic terms as the interactions themselves (Fernández, 2001; Fernández et al., 2002a,b; Nemethy et al., 1963; Fernández and Boland, 2002; Avbelj et al., 2000). By hydrophobic wrapping we mean the clustering of hydrophobic groups around an electrostatic interaction that enhances it by expelling the surrounding—dielectric—water. An illustrative extreme example is provided by the salt bridge, an important determinant of structural stability when it occurs in a desolvated environment. Thus, we show here how and why packing defects in the monomeric states have a significant bearing on the way in which proteins interact. We propose that the enhancement due to modifications in the solvent environment of preformed but insufficiently desolvated—“under-wrapped”—interactions is a crucial factor in protein associations which must and can be systematically investigated.

It is well known that water removal from hydrophobic patches on the protein surface results in a high thermodynamic benefit (Ringe, 1995; Clackson and Wells, 1995; Bogan and Thorn, 1998; Jones and Thornton, 1996; Lo Conte et al., 1999; Norel et al., 2001; Freire, 1999; Momany et al., 1996) due to an entropic gain by the solvent. Thus, hydrophobic patches might become suitable binding regions provided a geometric match on the binding partner is obtained. However, such patches are rare: most protein surfaces have the expected high ratios (typically 7:1 to 10:1) of hydrophilic to hydrophobic residues. Furthermore, even if overexposed hydrophobic patches become involved in associations, the resulting interface often presents hydrophobic-polar mismatches (Sondermann et al., 2000).

To explain this, we noticed that solvent-overexposed hydrophobes are not the only moieties for which the removal of surrounding water might entail a thermodynamic and energetic benefit. Here we show that certain intramolecular packing defects might also be compensated by exogenous removal of surrounding water; thus they are in effect “adhesive” and might constitute binding regions if an appropriate geometric fit arises in the binding partner.

In thermodynamic terms, it is well known that the desolvation of a preformed amide-carbonyl hydrogen bond contributes to its inherent stability, and this is so because the corresponding nonbonded state has exposed polar moieties, which, as a result of the solvation hindrance, would have a high self-energy (Fernández, 2001; Fernández et al., 2002a,b; Nemethy et al., 1963; Fernández and Boland, 2002; Avbelj et al., 2000). In other words, the desolvation of hydrogen bonds protects them from water attack. In fact, most backbone hydrogen bonds are sufficiently dehydrated in over 94% of stable soluble proteins (cf. Fernández and Scheraga (2003)). This leads us to assert that an insufficiently desolvated preformed hydrogen bond might be stabilized as the result of the exogenous (intermolecular) removal of surrounding water. These observations prompt us to pose the following questions: Which preformed hydrogen bonds in a given structure gain the most extra stabilization or strength by exogenous exclusion of water? What is the role of such bonds in protein-protein associations and higher-level organizations?

To address these questions, we need to identify deficiently packed backbone hydrogen bonds based on the assessment of their surrounding environments and determine the sensitivity of the Coulomb energy of such bonds to changes in their environment: i.e., those changes induced by the approach of an external hydrophobe from a binding partner. We adopt a continuous approach to deal with the solvent (Norel et al., 2001; Fernández and Berry, 2002; Fernández and Scheraga, 2003; Warshel and Papazyan, 1998; Bryant, 1996; Ooi, 1994; Honig and Yang, 1995), and introduce an equation that describes the dependence of the local dielectric coefficient on the positions of surrounding hydrophobic, carbonaceous groups (CH_i, i = 1,2,3).

In previous treatments of the problem, we established the importance of keeping the hydrogen-bond pattern “dry in water” if the structure is to prevail, and evaluated the “dryness” of the microenvironment of a hydrogen bond by merely counting vicinal carbonaceous hydrophobes (Fernández and Scheraga, 2003). Often such a crude approach yields good results in terms of identifying the hydrogen bonds most sensitive to water removal. This approach fails in <10% of the cases, as described below. It fails when the sensitivity is due to a very uneven distribution of desolvators around the bond—rather than an insufficient number of them—as shown in this work. Large yet structured looped regions in the peptide subunits of virus capsids (Zhou et al., 1998, 2000) are the most conspicuous illustrations where the more sophisticated approach presented in this work is required to identify hot spots for supramolecular assembly.

The continuous approach is explained in the first part of the paper, where previously derived relations (Fernández et al., 2002b; Fernández and Berry, 2002) estimating the changes in solvent polarizability depending on the arrangements of surrounding hydrophobic groups are adopted. Since dielectric and refractive properties are directly related (Fernández et al., 2002b; Fernández and Berry, 2002), this requires that we show how hydrophobic groups perturb the local refractive index on account of the fact that a solvent cavity must be made around the hydrophobic groups, and thus up to three layers of water dipoles become partially immobilized. Thus, hydrophobes perturb the environment producing a decrease in polarizability that has a quantifiable effect in enhancing the Coulomb energy.

We then proceed to identify the defectively packed backbone hydrogen bonds of the monomeric state where water exclusion upon binding would bring about the most significant decrease in Coulomb energy. Such bonds are here named dehydrons. To benchmark our method, we have utilized the full spectrum of proteomic data available, including annotations on the interactive context of proteins, structurally encoded propensities for aggregation and rearrangement, molecular evolution data, complexation, and supramolecular organization. To begin with, the dehydrons of two soluble proteins representing extreme examples of near-perfect and highly defective packing are determined and their relation to their interactive context is established. Then, dehydron sites are contrasted with the binding interfaces in 23 highly diverse protein complexes. In 18 cases, a strong correlation has been found, with the strongest correlation associated with the HIV-1 capsid protein P24 complexed with antibody light chain FAB25.3 (Momany et al., 1996).

The extent of incompleteness in the desolvation or hydrophobic wrapping of a preformed hydrogen bond determines a field acting on a test hydrophobe (Fernández et al., 2002b; Fernández and Berry, 2002): a hydrophobe is dragged toward a dehydron because, in approaching it, it causes a decrease in the local dielectric coefficient, thus enhancing the electrostatics of the hydrogen bond. This “field” contributes critically to determine the binding sites of proteins, as shown in the second part of the paper.

The number of dehydrons of a given protein may be also used as a marker of the complexity of its interactive context in different organisms: in homologous similar-fold proteins, the number of dehydrons appears to be a signature of proteomic complexity across species, as revealed by our results.

Finally, we analyze higher levels of structural organization. Thus, we show that the formation of the capsid in picornaviruses is essentially determined by the distribution of dehydrons in the individual virus-peptide (VP) subunits. This distribution concentrates at the symmetry centers of the capsid and edge-to-edge subunit positioning. Furthermore, antibody contacts and crystal contacts may be readily attributed to dehydrons still prevalent after the capsid has been assembled.

The implications of the dehydron concept for information processing in bioinformatics and proteomics and its possible impact for inhibitor design become readily apparent, as emphasized at the end of this work.

METHODS

The identification of the dehydrons in protein structure uses as sole input the atomic coordinates of the Protein Data Bank (PDB) structure. It is a local computation that requires the expression of the effective dielectric coefficient as a function of the coordinates of surrounding hydrophobic groups (CH_n, n = 1,2,3), as indicated in Eqs. 1–3 (Fernández et al., 2002b; Fernández and Boland, 2002; Fernández and Berry, 2002). Paramount to the identification of dehydrons is the assessment of the sensitivity of the hydrogen-bond electrostatic energy to exogenously induced water removal, immobilization, or structuring, given a fixed configuration of surrounding hydrophobic residues in the monomeric structure. Thus, we determine the changes in the electrostatic energy with respect to infinitesimal changes in the position vector of a “test” hydrophobic group. The only factor in the Coulomb expression that is affected by such a perturbation of the environment is ɛ⁻¹, the reciprocal of the permittivity coefficient. The gradients are computed along directions of approach orthogonal to the hydrogen-bond line and passing through its center, and thus their respective norms constitute a monoparametric family of values, indexed by a single angle. The circle associated with each hydrogen bond is thus defined by the intersection of the two 7 Å-desolvation shells centered at the paired α-carbons (Fig. 1 a).

FIGURE 1.

(a) Scheme of the desolvation shell of a backbone hydrogen bond representing an elementary motif in protein structure. The desolvation domain of the hydrogen bond consists of the reunion of two spheres of radius 7 Å centered at the α-carbons of the paired residues. The extent of desolvation, ρ, is generally given as the number of hydrophobic groups within the desolvation domain. (b) Relative abundance of hydrogen bonds in a nonredundant PDB sample (see main text) grouped in classes according to their sensitivity to water removal: 1, (λ × 10⁻⁶ < M_k < λ × 10⁻⁵); 2, (λ × 10⁻⁵ < M_k < λ × 10⁻⁴); 3, (λ × 10⁻⁴ < M_k < λ × 10⁻³); 4, (λ × 10⁻³ < M_k < λ × 10⁻²); 5, (λ × 10⁻² < M_k < λ × 10⁻¹); and 6, (λ × 10⁻¹ < M_k). (c) The ξ(n) plot for human hemoglobin β-subunit, representing the sensitivity to exogenous water exclusion from the vicinity of residue n and location of dehydrons (green segments joining α-carbons) for human hemoglobin β-subunit (pdb.1bz0, chain B). The desensitized backbone hydrogen bonds are denoted by gray segments joining α-carbons, the virtual-bond polygonal in blue represents the backbone, and the ribbon display is an aid to the eye. (d) ξ(n) Plot for the cellular human prion protein (pdb.1qm0) and location of dehydrons for the cellular human prion protein.

To coarse-grain—and simplify—the calculation, the sensitivity of the hydrogen bond is computed by dividing its associated circle in identical 10° sectors, and computing 36 gradients per hydrogen bond. For the kth hydrogen bond, the maximum norm, M_k, of the gradient is picked from its associated 36 nonnegative numbers. According to the statistical analysis displayed in Fig. 1 b, the kth hydrogen bond is a dehydron if and only if M_k > (ɛ_o⁻¹ − ɛ_w⁻¹)/2 Å, where ɛ_o and ɛ_w are the permittivity coefficients of vacuum and bulk water, respectively.

RESULTS

Defining dehydrons as structurally encoded signals

The enhancement of backbone hydrogen-bond strength and stability depends on the partial structuring, immobilization, or removal of surrounding water. In this section, we quantify this effect by adopting a continuous treatment of the local solvent environment surrounding backbone hydrogen bonds (Fernández et al., 2002b; Fernández and Berry, 2002; Honig and Yang, 1995). The aim here is to estimate the changes in the permittivity (or dielectric coefficient) of such environments and the sensitivity of the Coulomb energy to local environmental perturbations caused by protein interactions. Induced-fit distortions of monomeric structures are beyond the scope of this study.

We introduce here a sensitivity parameter M_k assessing the net decrease in the Coulomb energy contribution of the kth hydrogen bond that would result from a structuring or removal of water due to the approach by a hydrophobic group. This perturbation causes a net decrease in the permittivity of the surrounding environment, which becomes more or less pronounced, depending on the pre-existing configuration of surrounding hydrophobes in the monomeric state of the protein.

In general, nearby hydrophobic groups induce a structuring of the solvent needed to create a cavity around them and the net effect of this structuring is a localized reduction in the solvent polarizability with respect to reference bulk levels. This structuring of the solvent environment should be reflected in a decrease of the local dielectric coefficient ɛ. This effect has been quantified in recent work, where we delineated the role of hydrophobic clustering in the enhancement of dielectric-dependent intramolecular interactions. Thus, we have estimated ɛ as a function of the fixed positions {r_j, j = 1, 2,…, n} of surrounding hydrophobic groups (in our case of interest here, such groups are CH_n, with n = 1,2,3), placing the origin of intrinsic or local coordinates at the carbonyl oxygen atom.

Based on the fixed atomic framework for the monomeric structure, we now identify Coulomb energy contributions from intramolecular hydrogen bonds that are most sensitive to local environmental perturbations by subsuming the effect of the perturbations as changes in ɛ. Within the fixed coordinate system described above, we place the partner hydrogen net charge at fixed position r_o with respect to the carbonyl oxygen atom. Thus, we get (Fernández et al., 2002b; Fernández and Berry, 2002):

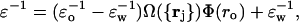(1)

where ɛ_w, ɛ_o are the permittivity coefficients of bulk water and vacuum, respectively, and

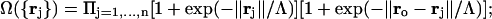(2)

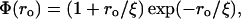(3)

where ‖·‖ denotes vector norm, r_o = ‖r_o‖, ξ = 5 Å is a water dipole-dipole correlation length; and Λ = 1.8 Å is the characteristic length associated with the water-structuring effect induced by the solvent organization around the hydrophobic groups. The derivation of Eqs. 1–3 is based on the relation between refraction and dielectric, and takes into account the perturbation of the water structure brought about by the incorporation of hydrophobic groups, which partially immobilize or structure the surrounding dipoles as they become engaged in the cavity formation.

Equations 1–3 reveal that the spatial distribution of the hydrophobic groups around the charge is responsible for an enhancement of the electric field when their distances to the carbonyl oxygen are comparable to the characteristic length ξ. Thus, Eqs. 1–3 quantify the local inhibition of solvent polarizability due to the presence of the hydrophobic groups, resulting in a net decrease in electrostatic shielding.

To identify the “hot spots” for water exclusion on the surface of native structures, we need to first cast the problem within the continuous approach, taking into account that 1/ɛ is the factor in the electrostatic energy that subsumes the influence of the environment. Thus to identify the dehydrons, we need to determine for which Coulombic contributions the exclusion or structuring of surrounding water due to the proximity of a hydrophobic “test” group produces the most dramatic increase in 1/ɛ.

It is convenient to introduce the quantity M_k, which describes the sensitivity of the Coulombic energy for the kth backbone hydrogen bond to variations in the dielectric. For the kth backbone hydrogen bond, this sensitivity is quantified as follows: a), define a desolvation domain D_k with border ∂D_k circumscribing the local environment around the kth backbone hydrogen bond. An operational definition of the desolvation domain has been introduced in previous work (Fernández et al., 2002b), and consists of two intersecting spheres of radius 7 Å, the typical cutoff distance in defining pairwise interactions between residues, centered at the α-carbons of the residues paired by the hydrogen bond, as shown in Fig. 1 a; b), introduce an extra “test” hydrophobic group at position R, so that the set of vector positions of the n_k hydrophobic groups surrounding the hydrogen bond is extended from {r_j, j = 1, 2,…, n_k} to {r_j, j = 1, 2,…, n_k; R}; c), compute the gradient ∇_R(1/ɛ)|_R=Ro, taken with respect to a perpendicular approach by the test hydrophobe to the center of the hydrogen bond at the point R = R_o located at the intersection C of the plane perpendicular to the hydrogen bond with ∂D_k; and d), for each k determine the number

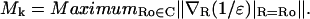(4)

The number M_k quantifies the maximum alteration in the local permittivity due to the approach of the test hydrophobe. The quantity M_k may be interpreted in physical terms as follows:

The electrostatic energy contribution E_coul(k, R) for the kth hydrogen bond within a fixed atomic frame for the protein, i.e., fixed r_o(k), {r_j(k)}, is given by:

(5)

where q and q′ are the net charges involved and r_o(k) = fixed O-H distance in the kth hydrogen bond. (Notice that r_o is a fixed parameter, and thus, the energy is not expected to have an R⁻¹ dependence, since R denotes the hydrophobe position and not the charge position). Thus, we get:

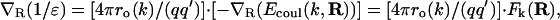(6)

where F_k(R) = −∇_R(E_coul(k, R)) is a net force exerted on the hydrophobe by the fixed preformed kth hydrogen bond. This drag represents a net three-body effect, whereby the hydrophobe is attracted to the hydrogen bond because in so doing, it decreases the value of E_coul(k, R). Thus, M_k measures the maximum possible attractive force—named the dehydronic force—exerted on the test hydrophobic group by the preformed hydrogen bond.

A sensitivity threshold for hydrogen bonds may be established by statistical analysis on a sample of native structures for soluble proteins, as shown on Fig. 1 b. Only 8% of backbone hydrogen bonds from a sample of 702 proteins of moderate sizes (52 < N <110, N = number of amino acids) and free from sequence redundancies (Hobohm et al., 1993) are highly sensitive in the sense that

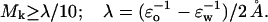(7)

The scaling λ factor is conveniently defined as measuring an extreme (ideal) sensitivity that would result if a completely exposed hydrogen bond (ɛ = ɛ_w) would be completely dehydrated (ɛ = ɛ_o) by a 2-Å displacement of a neighboring hydrophobic moiety.

On the other hand, 91.60% of backbone hydrogen bonds are relatively insensitive to water removal, since:

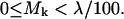(8)

This remarkable separation in the (nearly bimodal) distribution of sensitivities leads us to rigorously define a dehydron as a backbone hydrogen bond satisfying Eq. 7.

Thus, the condition given by Eq. 7 allows us to identify dehydrons as those preformed hydrogen bonds for which the change in Coulomb energy associated with the presence of a new hydrophobe from a binding partner is actually dramatic.

The most important soluble proteins constituting an exception to the statistics presented above are the cellular prion proteins (Fernández, 2002): given their typical sizes, their number of dehydrons is significantly larger, as shown in the next section.

A simpler, less precise treatment, based on mere counting of desolvators around hydrogen bonds, has also been introduced to identify adhesive sites (Fernández and Scheraga, 2003). As expected, this treatment fails to predict an adhesive site when it is produced by an uneven distribution of desolvators surrounding a hydrogen bond, rather than an insufficient number of such desolvators. To accurately compare both approaches, an exhaustive nonredundant structural sub-database of 2808 entries including 902 monomeric structures was constructed (cf. Fernández and Berry (2002)). In ∼91% of the complexes and monomeric proteins examined, there is 100% coincidence between the preformed hydrogen bonds most sensitive to exogenous water removal and the imperfectly wrapped or underdehydrated hydrogen bonds defined in Fernández and Scheraga (2003). However, within the remaining 9% of the cases, conspicuous exceptions arose: In contrast with the treatment presented here, the adhesive site responsible for the single contact between the HIV-1 capsid protein P24 and the antibody light chain FAB25.3 discussed in this work is not captured using the Fernández-Scheraga method. The latter method does not identify any underdehydrated hydrogen bond at the interface. This discrepancy justifies the more accurate treatment described here because the P24-FAB25.3 complex represents the most dramatic example of the guiding role of dehydrons in driving protein-protein association, as discussed below. Furthermore, the large number of dehydrons concentrated at the virus capsid symmetry centers reported in this work was invariably underestimated by ∼60–80% using the Fernández-Scheraga method. This is so since the hydrophobic wrapping of such hydrogen bonds is very unevenly distributed, typically exposing one side of the hydrogen bonds. This discrepancy is significant since it is well known that most virus capsids assemble spontaneously (Voet and Voet, 1990), and thus require a large enthalpic benefit to overcome the entropic cost associated with the immobilization of its constituent units. Thus it is expected that a large number of dehydrons should occur at the symmetry centers if they are to become organizing centers bringing together the virus units.

Dehydrons and protein interactions

The purpose of this section is to identify dehydrons using as input the all-atom PDB structures with resolution better than 3 Å, and contrast such “hot spots” with the interactive context of individual proteins and with the binding sites in protein complexes. An amide-carbonyl hydrogen bond is operationally defined as satisfying the following two constraints: a), N-O distance smaller than 3.45 Å, and b), smallest angle between the N-H, O=C vectors within 60° range.

The sensitivity ξ(n) to water exclusion for residue n is defined as the maximum of the M_k values for the hydrogen bonds engaging residue n. Thus, Fig. 1 c identifies the residues with largest ξ(n) for the hemoglobin β-subunit (pdb.1bz0, chain B), i.e., those involved in forming dehydrons. The 96 insensitive backbone hydrogen bonds (gray segments joining α-carbons) and three dehydrons (green segments) are also shown in Fig. 1 c, together with the ribbon representation as an aid to the eye. Within the natural interactive context of the Hb subunit, the dehydrons signal crucial binding sites: dehydrons (90, 94), (90, 95) are associated with the β-FG corner involved in the quaternary α₁β₂ interface, whereas dehydron (5, 9) is adjacent to Glu6, which in sickle cell anemia mutates to Val6, and is located at the protein-protein Glu6-(Phe85, Leu88) interface in the deoxyHbS fiber (Voet and Voet, 1990).

By contrast, the cellular prion structure for the human prion pdb.1qm0 (Prusiner, 1998; Zahn et al., 2000) is much more sensitive to environmental perturbations, as Fig. 1 d reveals (residues in ξ(n) plots are listed consecutively on the abscissas starting from n = 1 at the N-terminus). Its large number of dehydrons places the cellular prion structure far into the tail of the statistical distribution described in the previous section. The 30 insensitive hydrogen bonds and 28 dehydrons of the prion pdb.1qm0 are also depicted in Fig. 1 d. The vastly higher proportion of dehydrons signals a structure altogether vulnerable to water attack, and thus prone to rearrangement, especially in helix 1 (residues 143–156), where 100% of the hydrogen bonds are dehydrons. This observation agrees with current knowledge in the sense that the transition to the “scrapie” form of the prion entails a rearrangement of helix 1 with accretion onto the budding β-sheet (Prusiner, 1998; Zahn et al., 2000). Furthermore, helix 3 (residues 199–228) contains a significant number of dehydrons at the C-terminus, a region assumed to define the epitope for protein-X binding (Prusiner, 1998; Zahn et al., 2000). The remaining dehydrons occur at the helix-loop juncture, which can thus be easily distorted, bestowing the needed flexibility required by an eventual overall rearrangement.

This analysis might possibly have implications in inhibitor design, as the dehydrons at the extremity of helix 2, not being directly engaged in binding or rearrangement, might provide a target with a high propensity for association.

Although the NMR means of elucidating structure might occasionally imply less rigidity or looser packing than what would be required to obtain suitable crystals, the low wrapping of scrapie-inducing prions is certainly an aberration never found in any other NMR structure reported in the PDB.

To understand the role of dehydrons in protein associations, we computed the M_k's of hydrogen bonds at the protein-protein interface on individual monomers and complexes and on the entire surface of the binding partners for 23 complexes with resolution 3 Å or better from the PDB database, keeping in mind the difficulties in explaining and predicting binding sites on the basis of standard pairwise (p-p or h-h) interactions.

The complexes analyzed are identifiable by their PDB accession codes: 1a30, 1afv, 1as4, 1bm7, 1bxi, 1cph, 1cse, 1d5s, 1dfn, 1e4k, 1emv, 1fqw, 1hgu, 1i4f, 1im9 (chains A-D and A-C), 6ins, 1jvk, 1pon, 1prl, 1qp6, 1siv, 2spc. The overall (δ) and interface (δ_int) density of dehydrons on the protein surfaces were computed by calculating the total exposed surface area (ESA) of the separated binding partners and the interface surface area (by subtracting the ESA of the complex from that of the two separated monomers (Fraczkiewicz and Braun, 1998)). In 18 out of the 23 complexes (Table 1), we found a significantly higher value for the interface density of dehydrons: δ_int/δ > 1.5, whereas in the remaining four complexes, the ratio of densities was found to be less significant: 1.02 < δ_int/δ < 1.31. In some cases, the density of dehydrons at the interface was seven times higher than the average density (Table 1). In all cases, the interface dehydrons were desensitized upon binding (M_k > λ/10 → M_k < λ/100), as described below.

TABLE 1.

Complex name – PDB Code	Yint	Y	δint 10−3[Å−2]	δ 10−3[Å−2]
HIV-1 capsid protein (P24) + antibody-1afv	1	3 (4?)	8.33	0.19
HLA antigen A-2 + β2-microglobulin-1i4f	6	31	3.21	1.58
Ig-light chain dimer-1jvk	8	25	3.54	1.78
Transthyretin dimer-1bm7	5	12	3.55	1.01
Insulin dimer-6ins	4	12	4.61	2.80
HIV-1 protease dimer + inhibitor-1a30	7	11	4.91	1.87
SIV protease dimer-1siv	4	14	2.65	1.06
CheY complex-1fqw	4	10	6.07	1.02
Defensin dimer-1dfn	4	8	7.05	2.72
Antitrypsin polymers-1d5s	12	22	2.76	1.01
FcγRIII receptor + Ig-1e4k, B-C	6	22	7.08	0.97
Colicin + ligand-lbxi	6	12	3.97	0.92
Colicin + ligand-1emv	5	11	3.60	0.86
Serpin + ligand-1as4	10	31	2.02	1.40
Troponin heterodimer-1pon	6	10	4.54	1.34
MHC, antigen + receptor-1im9, A-D	4	39	2.21	0.84
MHC, antigen + ligand-1im9, A-C	3	33	6.12	2.00
De novo protein of α-2D-1qp6	6	12	3.67	1.65

Data on 18 selected complexes extracted from the nonredundant structural database described in the main text. Each complex is identified by its PDB code, and its association is defined by the following parameters: Y = number of dehydrons in the separated partners, Y_int = number of dehydrons at the interface which become desensitized to further water removal upon binding, δ = average density of dehydrons given as number of dehydrons per 1000 Ų for the solvent-exposed surface area of both separated binding partners, and δ_int = density of dehydrons at the binding interface desensitized upon association.

The most dramatic illustration of the guiding role in binding played by dehydrons is given in Fig. 2, a–c, where the complexation of the HIV-1 capsid protein P24 to the antibody light chain FAB25.3 (Momany et al., 1996) is displayed. In the monomeric state, the capsid protein has two dehydrons, but one of them may be attributed to an artifact of the free energy minimization algorithm used for the loop disordered region (Fig. 2 c), whereas the other appears in a crystallographically well-determined helix. The binding interface for this complex is the smallest of all complexes examined (∼120 Ų) and yet the single helical dehydron of the HIV-1 capsid protein lies precisely at the interface.

FIGURE 2.

Three illustrative complexes and separated binding partners for the HIV-1 capsid protein-antibody complex (pdb.1afv) (a) Ribbon representation. (b) Complex. (c) Separated partners showing a dehydron arising at the binding site). (d) CheY complex (pdb.1fqw) and (e) MHC antigen + ligand peptide (pdb.1im9, chains A and C). The binding partners are represented by blue or red virtual-bond backbone chains, the hydrophobic residues containing more than one carbonaceous group are denoted as α-carbon spheres. The backbone hydrogen bonds are indicated as lines joining α-carbons, gray if the bond is sufficiently desolvated with M_k < λ/100, green if it is a dehydron. A thin blue line joining an α-carbon with a hydrogen-bond center indicates that one or more aliphatic group from the side chain in one molecule attached to the α-carbon penetrates upon binding the desolvation domain of the hydrogen bond of its binding partner. In all interfaces analyzed, the former dehydron becomes desensitized upon complexation.

The results shown in Table 1 imply that the exclusion of water from dehydrons is an important factor in defining protein-protein associations. These “hot spots” should be distinguished from the exposed hydrophobic patches, although both are determined by the possibility of excluding water intermolecularly where it most counts in thermodynamic terms. In both cases, the lowering of the local permittivity entails a free energy decrease.

Fig. 2 displays three complexes and the separated (monomeric) binding partners. In all cases we see that the desolvation domains of the interface dehydrons are further filled with carbonaceous groups upon binding: the overexposed carbonaceous groups of the binding partner penetrate the desolvation domain of intramolecular dehydrons, desensitizing them. As the M_k values at the interface are recalculated after complexation, incorporating the carbonaceous groups from the binding partner's side chains, we invariably find a shift from satisfying Eq. 7 to obeying Eq. 8 upon complexation.

Number of dehydrons as an indicator of proteomic complexity

A PDB search for proteins with similar fold and function interrogated across species with diverse levels of evolutionary complexity was found to be revealing. Seven groups of proteins, each with homology across species, were chosen for this analysis: dehydrofolate reductase (DHFR), the scaffold for cytochrome c (heme-free), lysozyme, myoglobin, cellular prion protein (PrP^C), reverse transcriptase, and ubiquitin. The average extent of wrapping or desolvation of hydrogen bonds (Fernández and Scheraga, 2003), ρ, the number of dehydrons, Y, and the ratio of dehydrons to hydrogen bonds, r_d/HB, were calculated for homologous proteins in different species and are displayed in Table 2. The extent of wrapping ρ measures the average number of carbonaceous groups that lie in the desolvation domain of a backbone hydrogen bond and gives a crude but simple estimate of the packing efficiency of the structure. A clear picture emerges: one marker of biological complexity is provided by the proteomic or interactive complexity measured by either ρ⁻¹ or the ratio r_d/HB. Thus, species with a rich interactive complexity for a particular protein are singled out by the higher number of dehydrons (to be fully wrapped upon association) or low average extent of wrapping of their structure. On the other hand, in more archaic species, the homologous proteins are shown to be far less interactive. A clear illustration of this trend is provided in Fig. 3, where three different versions of myoglobin corresponding to aplysia limacina (gastropode, mollusc), whale, and human are displayed and their respective distribution of dehydrons is highlighted. It should be noted here that, with ρ = 24.02, the myoglobin from aplysia limacina is the best wrapper of hydrogen bonds in the entire PDB.

TABLE 2.

Protein homology	Species / PDB code	G [Mb]	N	NHB	ρ	Y	rd/HB
DHFR	Haloferax volcanii (archaea) / 1vdr	∼2	157	82	21.84	4	0.05
DHFR	Escherichia coli / 1dra	4.6	159	84	21.11	6	0.07
DHFR	Lactobacillus casei / 3dfr		162	90	19.62	11	0.12
DHFR	Homo sapiens / 1hfp	∼3000	186	95	18.21	17	0.18
Cytochrome c	Chlamydomonas reinhardtii (algae) / 1cyi	∼100	89	52	19.74	6	0.12
Cytochrome c	Rodophila globiformis (bacteria) / 1hro		105	50	17.52	7	0.14
Cytochrome c	Oryza sativa (rice) / 1ccr	430	111	55	14.94	11	0.20
Cytochrome c	Tuna / 5cyt		103	53	14.25	13	0.25
Cytochrome c	Katsuo (bonito) / 1cyc		103	44	14.03	15	0.34
Cytochrome c	Equus caballus / 1giw	∼3000	104	44	13.29	17	0.39
Lysozyme	Coliphage T4 (phage) / 109L	4–5	160	120	6.21	18	0.15
Lysozyme	Gallus gallus (hen egg-white) / 132L		129	85	5.82	19	0.22
Lysozyme	Canis familiaris (dog) / 1el1	∼3000	130	90	5.81	20	0.22
Lysozyme	Homo sapiens / 133L	∼3000	130	86	5.47	29	0.34
Myoglobin	Aplysia limacina (molluscum) /1mba		146	106	24.02	0	0
Myoglobin	Chironomas thummi thummi (insect) / 1eca	∼200	136	101	21.31	3	0.03
Myoglobin	Thunnus albacares (tuna) / 1myt		146	110	21.15	8	0.07
Myoglobin	Caretta caretta (sea turtle) / 1lht		153	110	21.09	11	0.10
Myoglobin	Physeter catodon (whale) / 1bz6		153	113	20.98	11	0.10
Myoglobin	Sus scrofa (pig) / 1mwc	∼2700	153	113	19.95	12	0.11
Myoglobin	Equus caballus (horse) / 1dwr	∼3000	152	112	18.90	14	0.13
Myoglobin	Elephas maximus (Asian elephant) / 1emy		153	115	18.90	15	0.13
Myoglobin	Phoca vitulina (seal) / 1mbs		153	109	18.84	16	0.15
Myoglobin	Homo sapiens / 2hbc	∼3000	146	102	18.80	16	0.16
PrPC	Saccharomices cerevisiae (yeast) / 1koa	12.1	233	148	22.33	13	0.09
PrPC	Saccharomices cerevisiae (yeast) / 1kod	12.1	220	137	22.95	10	0.07
PrPC	Mus musculus (mouse) / 1ag2	∼3000	103	53	12.42	29	0.55
PrPC	Mesocricetus (Syrian hamster) / 1b10		104	59	11.79	35	0.59
PrPC	Bos taurus (cow) / 1dwy	∼3000	104	59	11.76	35	0.59
PrPC	Homo sapiens / 1qm0	∼3000	104	59	11.71	35	0.59
Reverse transcriptase	Moloney murine leukemia virus / 1mml	∼10−2	251	158	19.71	12	0.076
Reverse transcriptase	HIV-1 (RT domains 1,2) / 1rth	∼10−2	209	120	16.68	21	0.175
Ubiquitin	Escherichia coli / 1foz	4.6	66	39	18.69	4	0.10
Ubiquitin	Mus musculus / 1u9b	∼3000	158	104	18.54	19	0.18
Ubiquitin	Homo sapiens / 1ubi	∼3000	76	48	16,26	12	0.25

Number of backbone hydrogen bonds (N_HB), extent of wrapping of hydrogen bonds (ρ), number of dehydrons (Y), and ratio of dehydrons-to-backbone hydrogen bonds (r_d/HB) for homologous similarfold proteins associated with different species. Since both ρ and r_d/HB are associated with the extent of protein complexation, these parameters give an estimation of the proteomic (or interactive) complexity across species. Also provided are the estimated genome sizes in Mb's (G) wherever known, and the number of amino acids (N) of the protein chain.

FIGURE 3.

Three versions of myoglobin corresponding to aplysia limacina (molluscum) (a), whale (b), and human (c). The first molecule is the best wrapper of hydrogen bonds in the PDB.

Dehydrons in higher-order levels of protein organization

In this section, we focus on illustrative higher levels of molecular organization, involving multiple protein-protein associations: the capsid assemblies of three picornaviruses (Fry et al., 1993; Kim et al., 1989; Krishnaswamy and Rossmann, 1990). The aim of this section is to show how the distribution of dehydrons on virus protein units correlates with the supramolecular arrangements and their interactions.

As a first step, we determine the distribution of dehydrons on the three individual VP (virus peptide) subunits that assemble into a virus unit for the foot-and-mouth disease virus (FMDV) (Kim et al., 1989). Following the previous convention on the unit labeling, the ξ(n) plots and dehydron location for subunits VP1-VP3 are displayed in Fig. 4, a–c, respectively. The atomic coordinates correspond to PDB entry 1bbt. Regions of high concentration of dehydrons are found at the symmetry centers of the capsid, and those dehydrons become desensitized upon unit associations (Fig. 5 a). ∼67% of the dehydrons involved in domain-swapping and unit assembly become desensitized upon formation of the unit. However, the unit has four remaining regions with a high concentration (δ > 4 dehydrons/(10³ Ų)) of dehydrons.

FIGURE 4.

(a–c) Respective ξ(n) plots and location of dehydrons for VP1, VP2, and VP3 subunits of the foot-and-mouth disease virus (FMDV) (pdb.1bbt).

FIGURE 5.

(a) Ribbon display of the FMDV unit and location of dehydrons in the assembled FMDV unit. Notice the distribution of highly concentrated dehydrons along the unit rim. (b) Organization of capsomeres in the FMDV vis-à-vis the distribution of dehydrons in the FMDV-unit. (c) Detail of VP3 hexamer organization center and adjacent dehydrons assigned to crystal contacts.

A comparison between Fig. 5 a and the capsid organization (Fig. 5 b) reveals that the four regions in the unit with a high dehydron density can be readily associated either with the centers of symmetry of the capsid or to what we have termed the interunit edge-to-edge assembly of VP2 and VP3. Thus, the FMDV unit presents two loop regions highly sensitive to water removal on VP1 and VP3, which are directly engaged in nucleating other units at the pentamer and hexamer (with threefold symmetry) centers of the capsid. Furthermore, a helical region on VP2 is severely underwrapped (δ = 5 dehydrons/(10³ Ų)) and occupies the central dimeric center (Fig. 5 b).

The dehydrons (Fig. 4) not directly engaged in shaping the attractive centers of symmetry of the capsid or signaling crystal contacts (Fig. 5) are desensitized upon assembly of the FMDV unit. However, the higher density of dehydrons at the centers of symmetry of the capsid (Fig. 5 a) suggests that there might be synergy between the assembly of the unit and the assembly of the capsid directly from the subunits (in a nonhierarchical fashion), with the latter, to some extent guiding the former.

Perhaps the most revealing design feature is the structurally defective “handle” region on FMDV-VP2, an underwrapped β-hairpin near the N-terminus (12–27 region), which is actually present in the VP2 subunits of all the picornaviruses. Because of its high density of dehydrons (δ > 6 dehydrons/(10³ Ų)), this region is the strongest organizing center in the capsid and should probably be targeted in the design of therapeutical drugs aimed at preventing the virus capsid assembling.

Some dehydrons still prevail after the units are assembled in the capsid; thus it becomes natural to investigate their role. Four dehydrons adjacent to the hexamer organizing center (Fig. 5 c) account for eight of the 10 residues involved in the crystal contacts of FMDV crystallized capsid (Fry et al., 1993): such residues belong to the desolvation domain of the dehydrons.

Similar roles for dehydrons are seen in the human rhinovirus (pdb.1r1a) (Kim et al., 1989). The ξ(n) plot for the VP1-subunit, containing the majority (80%) of the crystal contact sites is displayed in Fig. 6 a. Although most dehydrons can be attributed to the unit assembly, there are three particular sites with high dehydron density (δ > 4 dehydrons/(10³ Ų)) that are not desensitized either after the formation of the unit or after the assembly of the whole capsid. The respective sites have been individualized and are displayed on Fig. 6 b, and also indicated on Fig. 6 a. Two of them (I and II) correspond to antibody binding sites, although II, zoomed in Fig. 6 c, has also been identified as a site rich in crystal contacts (Kim et al., 1989). The other site (Fig. 6 b), lies under the so-called canyon of the VP1 structure and has been known to be the target region for the drug WIN 51711 used to treat the common cold (Kim et al., 1989).

FIGURE 6.

(a) ξ(n) Plot for the VP1 subunit of human rhinovirus (pdb.1r1a). The putative target region for the drug WIN 51711 used to treat the common cold (Kim et al., 1989) is indicated. (b) Localization of dehydrons in the VP1 subunit. (c) Detail of a region (identified by residue numbers) with a high concentration of dehydrons assigned to crystal contacts or antibody binding.

The Mengo encephalomyocarditis virus (pdb.2mev) (Krishnaswamy and Rossmann, 1990) has a large number of crystal contacts. The unit assembly is shown in ribbon display together with its pattern of dehydrons on Fig. 7. This unit has only two very strong dehydron centers on its rim: the pentamer center located in VP1, with density δ = 7.4 dehydrons/(10³ Ų)), and the ubiquitous VP2-VP3 edge-to-edge region (δ > 6 dehydrons/(10³ Ų)) located in VP2. The remaining 15 dehydrons are not involved in the organization of the capsid. The residues engaged in such dehydrons are marked by yellow α-carbon virtual bonds in Fig. 7. Of the 60 residues known to be engaged in crystal contacts for this virus (Krishnaswamy and Rossmann, 1990), 54 of them have side-chain carbonaceous groups in the desolvation domains of the 15 dehydrons marked in Fig. 7. Thus, the dehydrons not involved in capsid organization correlate with the crystal packing.

FIGURE 7.

Ribbon display of the unit for Mengo encephalomyocarditis virus (pdb.2mev) and location of dehydrons on the unit. A yellow virtual bond from residue n-1 to n indicates that residue n is engaged in a dehydron attributed to a crystal contact.

DISCUSSION

This work identifies a factor for protein association and supramolecular organization by determining a structurally encoded marker, the dehydron, which signals a packing defect in the monomeric structure. This signal becomes a means to systematically locate the spots on the surface of preformed protein structure that are most sensitive to perturbations in the solvent environment, specifically to the exogenous removal of water. The dehydron represents a defectively packed and preformed backbone hydrogen bond such that further water removal from its surroundings has a significant bond-stabilizing effect.

Dehydrons are identified by quantifying the sensitivity of Coulomb energetic contributions to the externally induced exclusion of water. This sensitivity can be conveniently regarded as measuring the drag on an external hydrophobic group. The relative abundance of native backbone hydrogen bonds grouped according to their sensitivities is sharply bimodal: native hydrogen bonds in monomeric structure are either highly sensitive or nearly insensitive. This important fact is at the crux of the site-selectivity of protein interactions and provides a solid justification for their rationalization in terms of dehydrons. Thus, a systematic study of known structures of individual proteins, protein complexes, and virus coats leads us to establish that the structural defects related to dehydrons play a significant role in determining protein associations and the organization of supramolecular assemblies.

To obtain a complete picture of protein interactions, the dehydron contribution should be complemented with the usual assessments of in situ geometric hindrances or fittings and pairwise matches. Furthermore, in an effort to clarify the dynamic functioning of dehydrons, we are now performing all-atom MD simulations with explicit solvent to examine the interactions of a hydrophobic test particle with the surface of the protein.

Since the dehydron is adhesive, it could become a useful concept to develop models of supramolecular organization of proteins within large-scale assemblies. For example, such models could be used together with data stemming from electron cryomicroscopy (Zhou et al., 1998) to infer and model virus organization and virus-host interactions (Zhou et al., 2000, 2001).

The potential use of dehydrons in functional genomics and proteomics has been to some extent assessed in this work. The number of dehydrons for homologous proteins with identical fold and function across species with diverse levels of evolutionary ancestry have been shown to provide a good marker for the proteomic complexity of the species. These findings suggest that the notion of function might need to be cast in terms of systems biology concepts.

Finally, inhibitor drug design benefits from the identification of suitable target regions on protein surfaces. Thus, adhesive spots arising from packing defects in the form of dehydrons are obvious sites to focus on.