The Photon Counting Histogram in Fluorescence Fluctuation Spectroscopy with Non-Ideal Photodetectors

Abstract

Fluorescence fluctuation spectroscopy utilizes the signal fluctuations of single molecules for studying biological processes. Information about the biological system is extracted from the raw data by statistical methods such as used in fluctuation correlation spectroscopy or photon counting histogram (PCH) analysis. Since detectors are never ideal, it is crucial to understand the influence of photodetectors on signal statistics to correctly interpret the experimental data. Here we focus on the effects of afterpulsing and detector dead-time on PCH statistics. We determine the dead-time and afterpulse probability for our detectors experimentally and show that afterpulsing can be neglected for most experiments. Dead-time effects on the PCH are concentration-dependent and become significant when more than one molecule is present in the excitation volume. We develop a new PCH theory that includes dead-time effects and verify it experimentally. Additionally, we derive a simple analytical expression that accurately predicts the effect of dead-time on the molecular brightness. Corrections for non-ideal detector effects extend the useful concentration range of PCH experiments and are crucial for the interpretation of titration and dilution experiments.

INTRODUCTION

Fluorescence fluctuation spectroscopy (FFS) exploits fluorescence fluctuations to study various physical and biological systems at the single molecule level. FFS has become a powerful tool for studying proteins and other biomolecules because information about dynamic processes and heterogeneity are determined from signal fluctuations with single molecule sensitivity (Berland et al., 1995; Qian and Elson, 1991; Webb, 2001). The technique has been used to study oligomerization of proteins (Berland et al., 1996; Palmer and Thompson, 1989; Wisemann and Squier, 2001), translational diffusion (Hink et al., 1999; Koppel et al., 1976; Rigler et al., 1993), flow (Foquet et al., 2002; Gosch et al., 2000; Magde et al., 1978), transport processes (Elson, 2001; Terada et al., 2000), and chemical reactions (Bonnet et al., 1998; Icenogle and Elson, 1983; Schwille et al., 1997) both in vitro and in vivo. FFS encompasses both fluctuation correlation spectroscopy (FCS) and the photon counting histogram (PCH) approach to analyzing signal fluctuations. FCS analyzes the temporal behavior of the fluctuations using the autocorrelation function, whereas PCH captures the amplitude distribution of the fluctuations.

The resolution of a mixture of species is an important biological application of FFS. The autocorrelation function relies on differences in the diffusion coefficient to resolve mixtures. The PCH is given by the histogram of photon counts and captures the distribution of molecular brightness values (Chen et al., 1999). It resolves mixtures of species by differences in brightness. While both methods can resolve multiple species, the autocorrelation function is, in practice, of limited use in resolving the association of proteins, particularly monomer-dimer assembly, because the difference in the diffusion time between a monomer and dimmer is too small (Meseth et al., 1999). However, PCH can resolve a monomer-dimer mixture since the dimer has twice the molecular brightness as the monomer (Müller et al., 2000).

The theory of PCH described in the literature has considered the case of ideal photo-detection (Chen et al., 1999; Kask et al., 1999). Unfortunately, photodetectors are never ideal and are typically plagued with at least two effects: dead-time and afterpulses. Dead-time is a fixed period of time after the registration of a photon during which the detector cannot accept another photon (Fig. 1 A). Afterpulses are spurious pulses following genuine output pulses (Fig. 1 B). The mechanisms of afterpulse generation depend on detector type (Höbel and Ricka, 1994). With respect to dead-time, detectors can exhibit nonparalyzable or paralyzable behavior. In paralyzable detectors, a photon reaching the detector during the dead-time leads to an elongation of the dead-time period. A photon reaching the detector during the dead-time in a nonparalyzable detector does not cause the dead-time period to be extended. We specifically consider the case of actively-quenched avalanche photodiodes (APD), because this detector is widely used in FFS experiments. Actively quenched APDs exhibit nonparalyzable behavior and constant dead-time with a typical duration of 50 ns (Sergio Cova, private communication).

FIGURE 1.

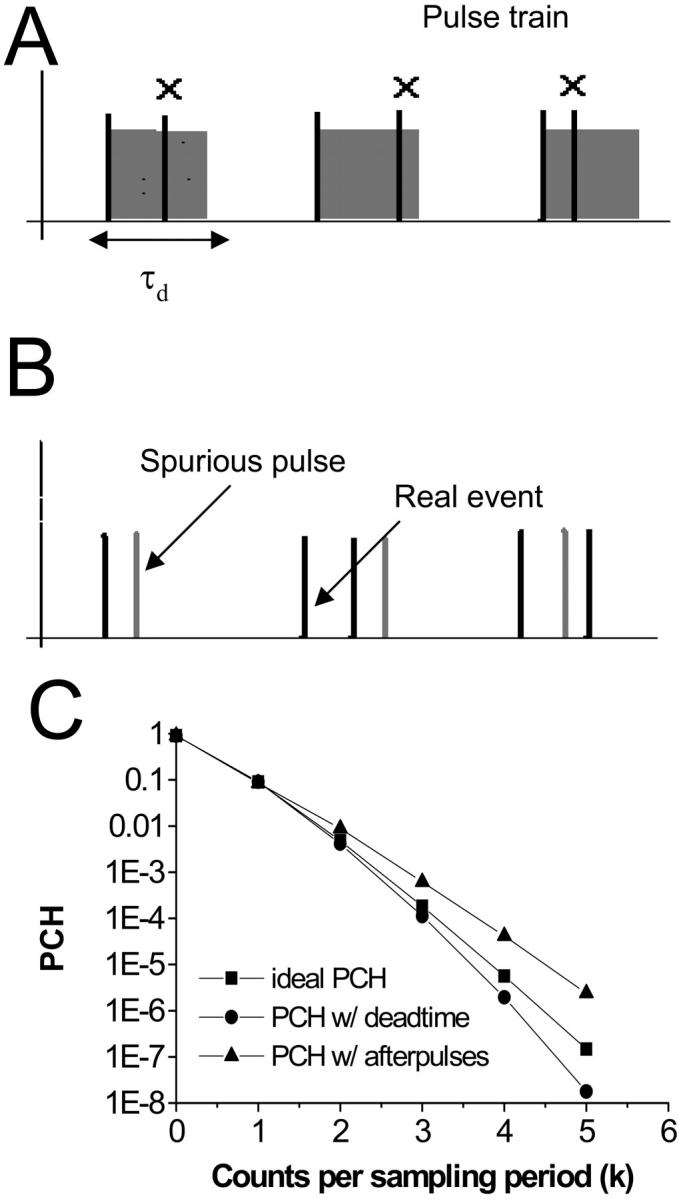
Non-ideal detector effects such as dead-time (A) and afterpulses (B) and their affect on the PCH (C). When a photon is counted by the detector, a dead-time of duration τ_d is initiated and any further photons reaching the detector during that time are lost. Afterpulses are spurious pulses that are generated with a probability p_a by the detection of a real event. Dead-time decreases the counts in the higher channels leading to a narrowing of the PCH (circles) as compared to the ideal PCH (squares). Afterpulses increase counts in the higher channels causing the PCH to broaden (triangles). Simulated data shown.

The qualitative influence of these two non-ideal detector effects on the photon count distribution is easy to understand. Since each detected photon is followed by a period in which the detector is “blind,” at high count rates many photons are lost in the dead-time. Thus, dead-time affects the PCH more strongly at high count rates, and causes the distribution to narrow since channels corresponding to higher counts will be preferentially affected compared to lower channels (Fig. 1 C). Here we use channel to refer to the number of photons detected in a sampling period. For example, the zero^th channel corresponds to zero photons detected during the sampling period. The overall effect of afterpulses, on the other hand, is to broaden the distribution. With each real pulse, there is a certain probability that an afterpulse follows. Channels corresponding to a high number of counts are more likely to contain afterpulses than channels with low counts (Fig 1 C). Dead-time and afterpulses have no affect on the zero^th channel of the PCH.

PCH experiments completely rely on photon count statistics and the non-ideal behavior of detectors modifies those signal statistics. This article investigates the effects of dead-time and afterpulses on PCH experiments. We found that the effect of afterpulses on PCH analysis is typically of no concern for most applications. However, dead-time introduces significant errors in PCH analysis at surprisingly low concentrations—even when only a few molecules are present in the observation volume. Thus, neglecting detector dead-time would severely limit the practical use of the PCH technique.

We therefore develop a new theory of PCH that analytically incorporates dead-time affects and significantly extends the concentration range accessible to PCH analysis. We first derive an expression for PCH in the presence of dead-time and find a simple analytical expression that determines the relative error in molecular brightness due to dead-time. The dead-time and afterpulse probability of our system is characterized and these parameters are subsequently used to model dead-time and afterpulse effects on the PCH for a range of concentrations and molecular brightness values. We will show that afterpulse effects can be safely ignored in almost all circumstances. We present experimental data and demonstrate that dead-time effects are accurately modeled by our theory. The modified PCH theory allows us to accurately study biological systems over a wide concentration range. It also opens the possibility to perform a global analysis of PCH experiments taken at many different conditions, since the photon count statistics are accurately described by our modified theory.

THEORY

Both PCH analysis and autocorrelation analysis return the number of molecules in the excitation volume. But PCH analysis also returns the molecular brightness ɛ of the fluorescent species. Molecular brightness is the fluorescence intensity produced by a single particle in the observation volume and depends on the physical properties of the fluorophore and the experimental setup. It is usually defined as the photon counts per molecule per sampling period (cpm). It may also be normalized according to the sampling period and given as counts per molecule per second (cpsm). The PCH yields the brightness in cpm, so we will use that convention in this article. We are particularly concerned with how the narrowing or broadening of the PCH due to dead-time and afterpulses changes the apparent molecular brightness and number of molecules, as it is these parameters which we use to make inferences about the biological system in question.

PCH analysis

A brief note on terminology and notation will be helpful at the outset. In this article, we use the terms photon count distribution and photon counting histogram (PCH). The first is a generic theoretical description that applies to any photon counting experiment and is denoted by p(k) or p′(k). The second term refers to photon count distributions particular to FFS experiments. The experimental PCH will be denoted π(k), whereas the theoretical PCH will be denoted either Π(k;ɛ,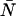) or Π′(k;ɛ,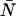,δ). The unprimed quantities refer to those measured by an ideal detector (e.g., ɛ). Primed quantities refer to those measured by detectors with dead-time (e.g., ɛ′). Quantities denoted with an asterisk refer to those obtained from detectors with afterpulsing (e.g., ɛ^*). The average number of molecules in the observation volume is given by .

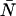The photon count distribution p(k) of any fluctuating light source incident on an ideal detector is given by Mandel's formula (Mandel, 1958),

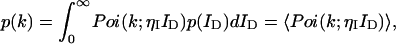(1)

where Poi(k,〈k〉) is the Poisson distribution with expectation value 〈k〉 and k is the number of photon counts in a time interval. The average photons counts 〈k〉 is given by the proportionality factor η_I, which incorporates the detection efficiency and sampling time interval, and the intensity at the detector I_D (〈k〉 = η_I I_D). The angular brackets denote the average of the Poissonian shot noise contribution over the intensity distribution p(I_D). We arrive at the PCH function that describes fluorescence fluctuation experiments by evaluating Eq. 1 with the corresponding intensity probability function p(I_D). The distribution p(I_D) depends on the specific illumination profile of the excitation volume. The exact derivation of the PCH function Π(k) for a number of different point spread functions (PSFs) has been described previously (Chen et al., 1999; Müller et al., 2000, 2001),

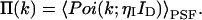(2)

Typical point spread functions for FFS experiments are Gaussian-Lorentzian or 3-dimensional Gaussian. The PCH for a single species as measured by an ideal detector is described by two parameters: the molecular brightness ɛ in cpm and the average number of molecules in the excitation volume 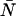, and is denoted by Π(k;ɛ,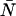). The average number of photon counts is then just the product of the molecular brightness and the average number of molecules inside the PSF volume, 〈k〉 = ɛ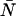. For multiple species, the PCH is a convolution of the individual species PCHs (Chen et al., 1999; Müller et al., 2000, 2001).

The discussion of the photon counting distribution so far has assumed that photon detectors are ideal. In reality, this assumption is violated and the non-idealities of the detector should be accounted for in the theoretical description of the photon count distribution whenever necessary. The effect of dead-time on the photon count distribution for a nonparalyzable detector has been addressed in the literature (Bedard, 1967; O'Donnell, 1986). See Teich and Vannucci (1978) for a discussion of the effect of dead-time on the photon count distribution for paralyzable detectors. The effect of dead-time on the data depends on the sampling time interval and is described by the parameter δ = τ_d/T_s = τ_df_s, where τ_d is the dead-time, T_s the sampling time interval, and f_s the sampling frequency. Typically, sampling time intervals are between 50 μs and 100 ns. Dead-time takes up a larger proportion of the time interval at high sampling frequencies and thus should affect data taken at those frequencies more strongly than data taken at lower frequencies.

A fluctuating light source measured by a detector with dead-time leads to a photon count distribution p′(k) given by Bedard (1967),

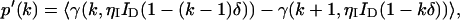(3)

where γ(k,x) is the incomplete γ-function,

(4)

Equation 3 is valid for a nonparalyzable photodetector that is active at the beginning of each sampling period. One could in principle evaluate Eq. 3 with the proper probability distribution function p(I_D) to arrive at the PCH function in the presence of detector dead-time. However, it is easier to transform the equation and express the new PCH function that includes dead-time effects as a mathematical series of ideal PCH functions. We first rewrite the incomplete gamma function as a series of Poisson distributions (Abramowitz and Stegun, 1964):

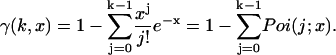(5)

Then, inserting Eq. 5 into Eq. 3 yields

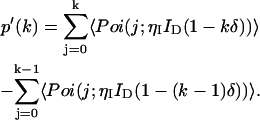(6)

We see from Eqs. 1 and 6 that the photon count distribution in the presence of dead-time is expressed as a sum over ideal distributions with reduced mean values. Thus, by inserting the definition of the PCH function (see Eq. 2) into Eq. 6, we arrive at an expression of the dead-time modified PCH Π′(k;ɛ,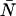,δ),

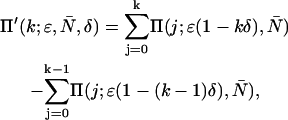(7)

where Π(j;ɛ,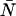) are ideal PCH functions with modified mean values. This analytical correction, which is exact, was incorporated into our PCH algorithm as part of our global fitting model.

Moment analysis

Upon inspection, Eq. 7 does not yield any insight into the magnitude of the effect of dead-time on the PCH. Specifically, it does not yield, directly, an analytical correction for the molecular brightness. Probability distributions are characterized by their moments and these represent another useful way to describe fluctuations (Chen et al., 2000; Qian and Elson, 1990a). We turned to moments to find a way to quantify the effect of dead-time on the molecular brightness. Additionally, moment analysis has the advantage of being computationally easier and faster than a fit to the theoretical PCH.

The two most important moments are the first ordinary moment, which provides the mean of the distribution, and the second central moment, which yields the variance of the distribution. Another useful quantity, which incorporates these two moments, is the normalized variance of the photon count distribution G(0) (Chen et al., 2000):

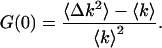(8)

G(0) is also by definition the time zero value of the autocorrelation function. Its value is inversely proportional to the average number of molecules in the excitation volume (Thompson, 1991),

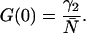(9)

The shape factor γ₂ depends on the geometry of the PSF and a general expression is given by (Thompson, 1991),

(10)

where 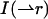describes the intensity beam profile. For a Gaussian-Lorentzian PSF, which describes the beam profile of our two-photon excitation setup, γ₂ = 3/4π².

Mandel's Q factor is used to characterize photon count distributions (Mandel, 1979). It is given by

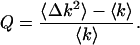(11)

For a Poisson distribution Q = 0 because the variance is equal to the mean. Sub-Poissonian distributions in which the variance is less than the mean are characterized by Q < 0, while Q > 0 corresponds to a super-Poissonian distribution (i.e., 〈Δk²〉 > 〈k〉). Comparing Eqs. 8, 9, and 11, we see that Q = 〈k〉 × G(0) = γ₂ɛ. We also see that fluctuations correspond to a positive Q and thus lead to super-Poissonian behavior. Note that ɛ refers to the molecular brightness as measured by an ideal detector.

We first derive an expression for the effect of dead-time on Q and use that to estimate our error in the molecular brightness. Since Q = γ₂ɛ in the absence of dead-time and afterpulses, we can define Q′, which includes dead-time effects, similarly as

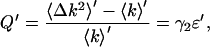(12)

where ɛ′ is the dead-time-affected brightness, 〈k〉′ denotes the dead-time modified first moment, and 〈Δk²〉′ = 〈k²〉′ − 〈k〉′² is the dead-time modified variance. The Q parameter is a measure of the width of the photon count distribution, and since dead-time narrows the photon count distribution, Q′ < Q.

The dead-time-effected photon count distribution in Eq. 3 can be expanded as a power series in δ in terms of the unaffected distribution p(k) (O'Donnell, 1986):

(13)

It is important to note that the expansion is valid only when δ × 〈k〉 ≪ 1. Using the Taylor expansion above, we calculated the dead-time-affected first and second moments in terms of δ and the ideal FFS parameters ɛ and (see Appendix). From the expressions for first two moments we derived an expression, to first order in δ, for the relative error in Q due to dead-time,

(14)

where γ₃ = 35/24π⁴ for a Gaussian-Lorentzian PSF. Note that the relative error in Q due to dead-time is equal to the relative error in ɛ due to dead-time,

(14a)

The dead-time-affected mean of the photon counts is given by

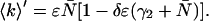(15)

Effect of afterpulsing on the PCH and its moments

The theoretical description developed thus far has only included the effects of dead-time on the PCH and its moments. A correction algorithm for the effect of afterpulses on the photon count distribution has been developed (Campbell, 1992). We inverted the algorithm to generate afterpulse-modified histograms from ideal histograms. It was assumed that a real event generates only one afterpulse with a probability p_a and that an afterpulse does not generate more afterpulses. For single afterpulses, the afterpulse-affected photon count distribution p^*(k) is given by

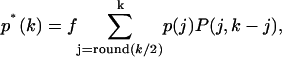(16)

where p(j) is the photon count distribution in the absence of afterpulsing, and P(j,k–j) the probability of k–j afterpulses after j events. P(j,k–j) is given by the binomial distribution,

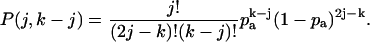(17)

The factor f is used to normalize the distribution p^*(k), so that 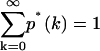. Since the afterpulse probability is small (p_a ≪ 1), Eq. 16 can be expanded as a power series in terms of p_a and afterpulse-affected moments can be derived in the same manner as the dead-time-affected moments are derived. Keeping only terms of order O(p_a), the first moment with afterpulses 〈k〉^* is given by

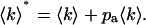(18)

And the relative error in Q due to afterpulses is

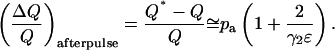(19)

As with dead-time, the relative error in Q due to afterpulses is equal to the relative error in ɛ due to afterpulses:

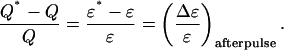(19a)

MATERIALS AND METHODS

Instrumentation

The instrumentation for two-photon fluorescence fluctuation experiments consisted of a two-photon excitation source and a Zeiss Axiovert 200 microscope (Thornwood, NY). A mode-locked Ti:sapphire laser (Tsunami, Spectra-Physics, Mountain View, CA) pumped by intracavity doubled Nd:YVO₄ laser (Millennia Vs, Spectra-Physics, Mountain View, CA) served as the two-photon excitation source. The dilution experiments were performed using a 63× C-Apochromat water immersion objective (NA = 1.2). The measurement of τ_d and p_a was carried out using a 10× Achroplan air objective (NA = 0.25). An excitation wavelength of 780 nm was used in all measurements. Under our experimental conditions, no photobleaching was detected for any of the samples measured. Photon counts were detected with an avalanche photodiode (APD) (SPCM-AQ-14, PerkinElmer, Dumberry, Québec). The output of the APD, which produces TTL pulses, was directly connected to a data acquisition card (ISS, Champagne, IL). The sampling frequency was 50 kHz for all measurements. The recorded photon counts were stored and later analyzed with programs written for IDL version 5.4 (Research Systems, Boulder, CO).

Sample preparation

Alexa 488 and fluorescein were purchased from Molecular Probes (Eugene, OR). Alexa 488 was dissolved in dH₂O and fluorescein in a pH 8 solution of 50 mM potassium phosphate. The dye concentration of the stock solutions (1–5 μM) was determined by optical absorption measurements using the extinction coefficient provided by Molecular Probes. Alexa 488 was diluted into dH₂O to a concentration of ∼100 nM and subsequently diluted by factors of two successively until a concentration of ∼0.1 nM was reached. The stock solution of fluorescein (5 μM) was used directly. Background counts were ∼200 cps.

Data analysis

The histogram of the experimental data is calculated from the recorded photon counts and then normalized to obtain the experimental probability distribution of photon counts π(k). To fit the experimental PCH to the PCH model, we must weigh each element of the PCH with its standard deviation σ_k. The probability of observing k counts n times out of M trials is given by the Binomial distribution function, so the standard deviation is given by 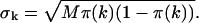The theoretical PCH, denoted Π(k;ɛ,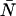) is then calculated and the reduced χ² determined by

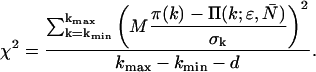(20)

The experimental photon counts range from a minimum value k_min, which is typically zero, to a maximum number k_max. The number of fitting parameters is given by d. Because a typical data set contains on the order of M = 10⁶ data points, the resulting binomial distribution is well approximated by a normal distribution. Thus, the quality of the model can be estimated by the reduced χ² and by the normalized residuals 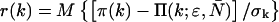from the fit.

RESULTS & DISCUSSION

Measurement of τ_d and p_a

To determine the quantitative affect of dead-time and afterpulses on our system, we first measured the dead-time τ_d and afterpulse probability p_a. A useful way to gauge these parameters is utilizing Mandel's Q parameter. If a constant light source is incident on an ideal detector, we obtain a Poisson probability distribution and thus Q = 0. Dead-time of the detector narrows the photon count distribution and leads to sub-Poissonian behavior (Q > 0). Afterpulses broaden the photon count distribution and lead to a super-Poisson probability distribution (Q > 0). But in a real experiment, intensity fluctuations, dead-time, and afterpulses are simultaneously present, so Q depends on the relative strengths of the individual effects. Mathematically, the effects of dead-time and afterpulses on the photon count distribution of constant light source is given by the following expression (Finn et al., 1988):

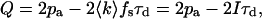(21)

where I = 〈k〉 × f_s is the photon count rate in counts per second (cps) and Q is given by Eq. 11. A plot of Q vs. count rate will be linear with a slope of −2τ_d and a y-intercept of 2p_a.

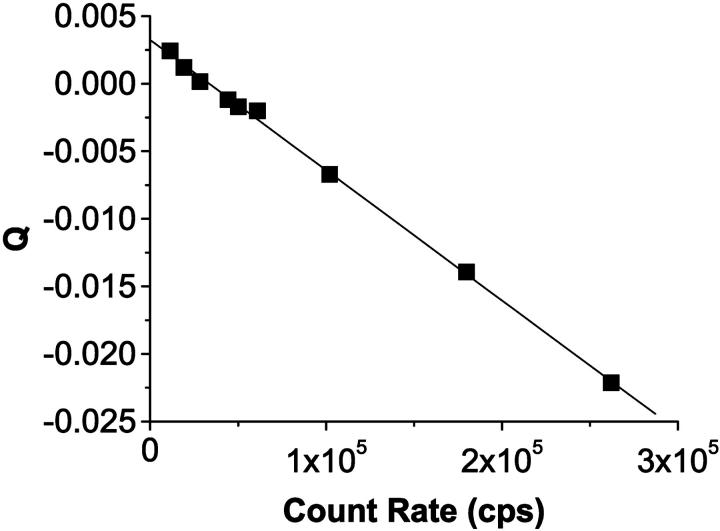
To approximate the conditions of a constant light source on our instrument, we measure at a high fluorophore concentration. The intensity fluctuations, which are caused by individual molecules leaving and entering the observation volume by diffusion, are negligible under these conditions. An ideal detector is then only limited by shot noise and would measure a Poisson distribution. A detector with dead-time and afterpulses is described by Eq. 21. We measured a concentrated solution of fluorescein (5 μM) and varied the intensity by changing the excitation power. The data was fit to Eq. 21, and a dead-time τ_d = 48.2 ± 0.7 ns and an afterpulse probability p_a = 0.0016 ± 0.0001 were obtained (Fig. 2). According to the manufacturer, the dead-time of the APD is 49.4 ns and the typical afterpulse probability for that model of APD is 0.003.

FIGURE 2.

A plot of Mandel's Q parameter for a constant light source, in this case a highly concentrated fluorescein sample, as a function of the photon count rate and a fit to Eq. 21. The slope is a measure of the dead-time of the system and the y-intercept is related to the afterpulse probability. The dead-time and afterpulse probability for our system were 48.2 ± 0.7 ns and 0.0016 ± 0.0001 ns, respectively.

Evaluation of dead-time and afterpulsing effects on PCH

As a starting point, we performed calculations to see if and how a δ-value of 0.0025, corresponding to τ_d = 50 ns and f_s = 50 kHz (a typical sampling frequency for our experiments), affects the PCH. More specifically, we wanted to know whether a dead-time-affected histogram could still be fit with the ideal PCH model and whether it would affect the ɛ- and 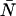-values returned by the fit. In the calculation, we generated several ideal PCHs (ɛ = 0.1–10.0 cpm, 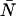= 0.01–10.00) and then used Eq. 7 to calculate a dead-time-affected PCH for each ideal PCH. When the ideal model was used to fit the modified histograms, we found that at low concentrations, the ɛ-values were unaffected, whereas at high concentrations the ɛ-values decreased. When the brightness decreased, the number of molecules increased. As an example, for an ideal PCH with ɛ = 1 cpm and 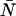= 3 (〈k〉 = 3), the corresponding dead-time-affected PCH showed only a slight narrowing of the distribution, but when fit to the ideal model, the modified PCH yielded ɛ = 0.777 cpm and 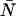= 3.829 (〈k〉 = 2.977). These results are summarized in Table 1. Although the average number of counts hardly changed, there was a significant change in the fit values of the molecular brightness and the number of molecules. Moreover, we found that the deviation in molecular brightness increases as the concentration increases, so in a dilution or titration experiment, the relative error in brightness due to dead-time (Δɛ/ɛ)_dead-time is not constant throughout the experiment.

TABLE 1.

Dead-time effects on the PCH parameters

δ	ɛ (cpm)		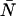〈k〉 (counts/Ts)
0	1.0	3.0	3.0
0.0025	0.777 (↓22%)	3.829 (↑28%)	2.977 (↓0.8%)

Two histograms with the same brightness and number of molecules (ɛ = 1.0 cpm and 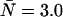), one with no dead-time and another with relatively small dead-time, were generated and fit to a PCH model that assumes an ideal detector. The results of the fit of the ideal histogram (δ = 0) are shown in the first line. The same parameters used to generate the histogram are returned by the fit. When the dead-time-affected histogram (δ = 0.0025) is fit to the ideal PCH model, the molecular brightness returned is significantly reduced whereas the concentration has increased. Since the changes in brightness and concentration offset each other, only a small decrease in the average counts in a sampling period is observed.

Since we were generating the data, reduced χ²-values were zero for all ideal histograms and very close to zero for fits of the dead-time modified histograms to the ideal PCH model. This implies that, experimentally, the ideal PCH model describes dead-time modified PCHs within experimental error. However, the molecular brightness and number of molecules returned from such a fit are wrong. The reason for this lies in how the PCH captures intensity fluctuations. A bright molecule passing through the excitation volume produces stronger intensity fluctuations than a dimmer molecule. The bright molecule's PCH is therefore broader than the PCH produced by its dimmer counterpart. Dead-time narrows the distribution and thus mimics the effect of a dimmer species. However, the average counts decrease only slightly in the presence of dead-time, so to obtain the correct mean counts per time interval, a higher number of molecules is needed to offset the decrease in brightness. Another way to understand this effect is to look at the moments of the PCH. The first moment gives the mean value of the distribution which changes only slightly in the presence of dead-time. The second and higher moments are required to adequately describe the tail of the distribution, and since the tail is affected more strongly by dead-time, it is these moments that suffer large deviations from ideal. Recall that Q is proportional to the brightness, and that Q involves the second as well as the first moment. Since the second moment is affected more strongly by dead-time than the first, we would expect that the brightness would also show larger deviations from ideal than the average counts would.

We have thus far only considered the effects of dead-time on the PCH and neglected afterpulsing. Since our afterpulse probability is quite low, we expected that afterpulses would have little or no effect on the PCH. Following a similar procedure as the dead-time modeling, we generated ideal and afterpulse-modified PCHs for a variety of ɛ- and 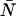-values using Eq. 16 with p_a set to 0.0016 and fit them using the ideal model. We found that the effect of afterpulses on PCH parameters is opposite that of dead-time, namely, molecular brightness increases and the average number of molecules decreases. More importantly, the relative error in the brightness due to afterpulsing (Δɛ/ɛ)_afterpulse depended only on the brightness and not on the average number of molecules. The size of that error increases as brightness decreases, and for our system, afterpulsing introduces an error of 10% when ɛ < 0.4 cpm. Therefore, in a dilution or titration experiment, afterpulsing introduces a small constant error that cannot be distinguished from other sources of experimental uncertainty. We rarely measure in this region because signal statistics, which depend on the brightness, are poor.

The cumulative effects of dead-time and afterpulsing for our system were calculated from Eqs. 14 and 19 and are shown in Fig. 3. The contour plot, which shows the relative error Δɛ/ɛ as a function of ɛ and 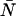, suggests we are correct to neglect afterpulse effects for most of our experiments and that dead-time corrections need to be made for concentrations where 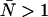. If afterpulses are neglected entirely, the contours are flat except at high concentrations where there is a slight dip (Fig. 3 A). Dead-time effects depend on the number of molecules in the excitation volume much more strongly than on the molecular brightness of the molecules. Corrections for non-ideal detector effects extend the useful concentration range for PCH experiments. If we did not make corrections for dead-time, we would be restricted to concentrations corresponding to an average of less than 1 molecule in the observation volume, where the relative error in the brightness due to dead-time is less than 10% (Fig. 3 B) when the sampling frequency is 50 kHz. At higher sampling frequencies, dead-time corrections would be necessary at even lower concentrations, whereas at lower sampling frequencies the concentration limit would be higher. The choice of sampling frequency depends on the diffusion coefficient of the molecule of interest. While lowering the sampling frequency will reduce the δ-value, it may also introduce undersampling effects if the diffusion coefficient is too high. For most in vitro experiments, a sampling frequency <20 kHz will introduce significant undersampling effects. At this sampling frequency and with a dead-time of 50 ns, the concentration limit at which dead-time corrections are necessary occurs when .

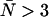FIGURE 3.

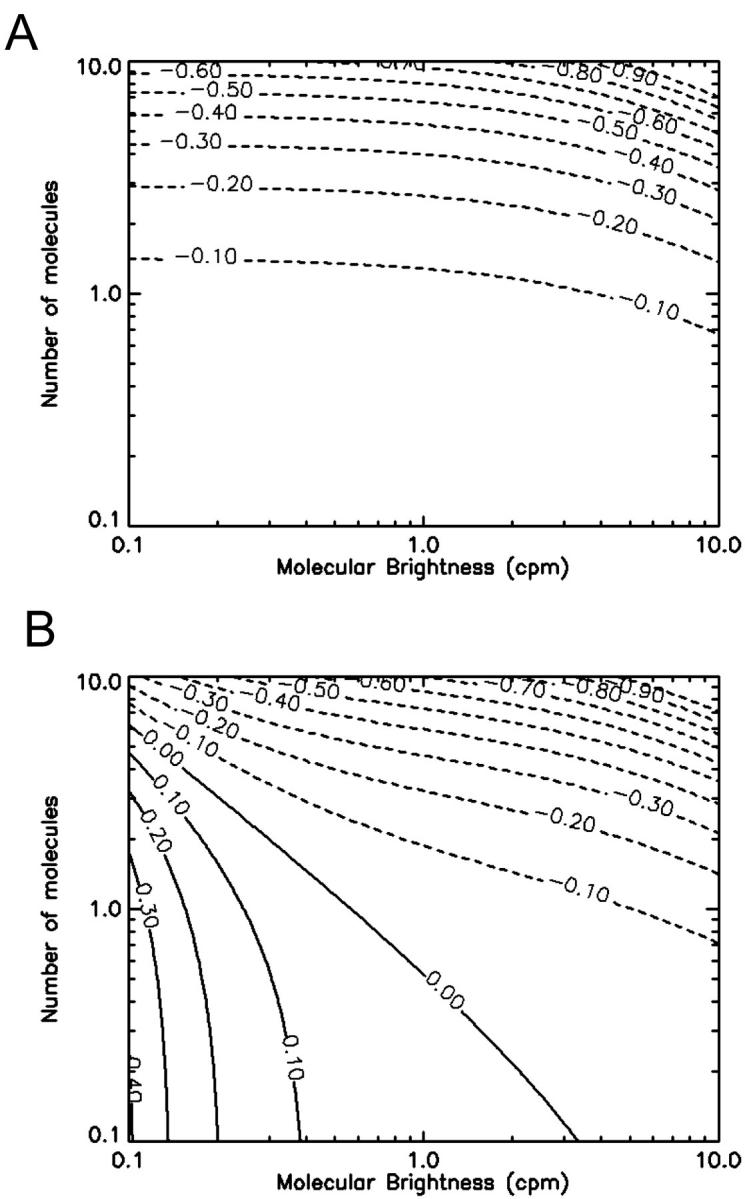
Contour plots showing the relative error in the molecular brightness due to dead-time only (A) and both dead-time and afterpulses (B) as a function of ɛ and 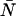. Dashed lines denote negative contours and solid lines denote positive contours. The contours were generated using a dead-time of 50 ns, sampling frequency of 50 kHz, and afterpulse probability of 0.0016. For low concentrations of 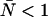little or no corrections are required for non-ideal detector effects as long as ɛ > 0.4 cpm. Dead-time introduces a relative error of greater than 10% when 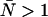and must be corrected for. Afterpulses can safely be ignored for our system as their effects are restricted to low ɛ- and 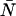-values where we do not typically measure, due to poor signal statistics.

In the preceding discussion, we treated dead-time and afterpulsing as statistically independent effects (i.e., Δɛ/ɛ = (Δɛ/ɛ)_dead-time + (Δɛ/ɛ)_afterpulse). However, each afterpulse generates dead-time in the detector, and thus treating both effects as independent is an approximation. Afterpulses occur with a probability p_a and the leading order of correction of afterpulsing to PCH is of order O(p_a). Similarly, dead-time effects give rise to corrections with leading order O(δ). The corrections due to the interdependency of afterpulses and dead-time is of order O(p_aδ). Since both p_a and δ are small numbers the correction is of higher order and we neglect it, as we are only interested in first-order effects. A higher order correction of dead-time and afterpulses on PCH requires the explicit treatment of the entanglement of both effects. In addition, such higher-order corrections require a more sophisticated model for describing afterpulses. In our model, we assumed that a real event could cause one afterpulse and no further afterpulses are generated. This is a reasonable assumption since the probability to produce two afterpulses from a real event would be on the order O(p_a²) or 10⁻⁶. Thus, our approximation of treating dead-time and afterpulses as statistically independent is justified based on the limitations of the model used to describe afterpulsing.

Experimental test of theory

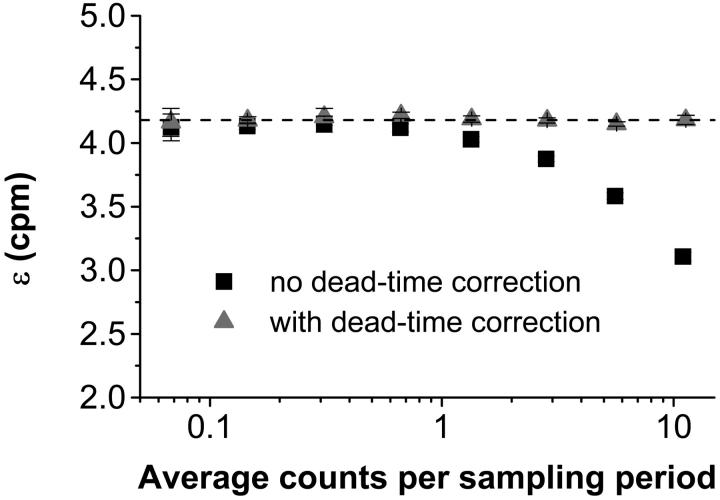
The theory predicts that in the presence of dead-time, a fit of the experimental PCH to the ideal model would yield a molecular brightness that would be less than that obtained without dead-time and that the effect on the molecular brightness would be stronger at higher count rates. To test this prediction, we performed a dilution experiment so that the brightness was held constant as the concentration, and thus the photon count rate, was varied. Diluting the sample should have no effect on the brightness; it simply reduces the number of molecules in the volume. We started with ∼100 nM Alexa 488 and sequentially reduced the concentration by factors of two. The experimental histograms from each dilution step were fit to the ideal PCH model and to the PCH model with dead-time. Our results are shown in Fig. 4. Using the ideal PCH model to fit the experimental histograms, we saw that dead-time effects showed up more strongly as the count rate increased as indicated by the measured brightness curve. As in the simulation, we also observed that ɛ decreased and 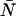increased when the experimental PCH was fit to a PCH model that assumed an ideal detector. All such fits returned reduced χ²-values between 0.58 and 2.85. More importantly, by including the effects of dead-time in our fitting model we obtained ɛ-values that were constant over the course of the dilution. The reduced χ²-values of the fits of the experimental PCHs to the modified PCH model were between 0.86 and 2.87. Notice also that the average counts were nearly the same regardless of which model was used for fitting. We also performed a global fit in which the histograms of the dilutions were linked together by requiring that all histograms have the same brightness and the same δ-value. From the global fit, we obtained δ = 0.0025 ± 0.0002 which corresponds to τ_d = 50 ± 4 ns (χ² = 2.21). All data sets were corrected for background counts by including a second species fixed to the brightness value obtained from a PCH fit to a solvent-only sample.

FIGURE 4.

The molecular brightness as a function of photon count rate in a dilution experiment. Alexa 488 was diluted in dH₂O sequentially by factors of two from a concentration of ∼100 nM. In such an experiment, the brightness should remain constant although the number of molecules changes. When the experimental histograms are fit to an ideal PCH model the brightness decreases dramatically at high concentrations (squares). When the histograms are fit to a modified PCH model that incorporates dead-time effects, the brightness is constant over the entire concentration range (triangles). The dashed line indicates the brightness obtained in a global fit to the modified model of all of the experimental histograms simultaneously (ɛ = 4.18 ± 0.02 cpm).

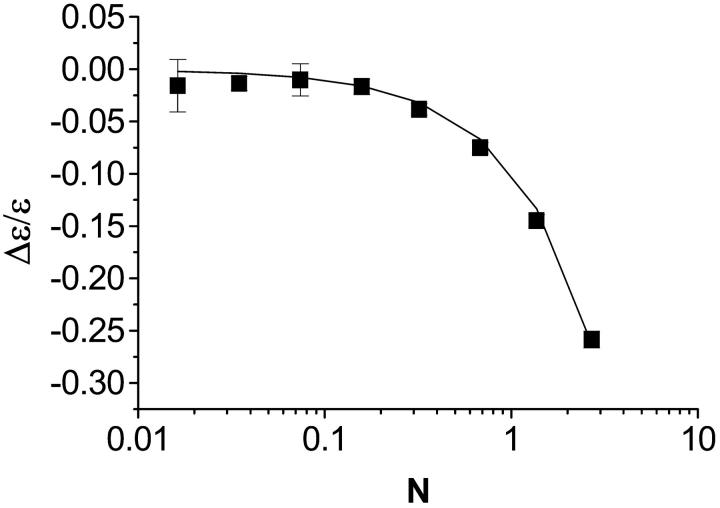
PCH analysis requires a nonlinear least squares fit and therefore does not lend itself to the fast, diagnostic data analysis often used when taking measurements. Moment analysis, on the other hand, provides a useful way to gauge data and it should produce results equivalent to those obtained from PCH analysis. From the Taylor expansion of the dead-time-affected PCH, we obtained an expression (Eq. 14) that predicts the relative error in molecular brightness when dead-time effects are not taken into account. A comparison of the relative error in ɛ from the experimental dilution data in Fig. 4 and that predicted from Eq. 14 is shown in Fig. 5. The Taylor expansion describes the experimental data very well. It is important to note that to use Eq. 14 to approximate (Δɛ/ɛ)_dead-time, one has to have prior knowledge of what the ideal brightness ɛ and average counts 〈k〉 are, which in turn requires that PCH analysis be performed. To recover the ideal brightness without using PCH analysis, Eq. 14 can be inverted and solved quadratically for ɛ as a function of 〈k〉 and ɛ′ as

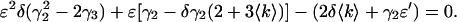(22)

However, we measure 〈k〉′ and ɛ′ and not 〈k〉 and ɛ. Eq. 16 can also be inverted and solved quadratically for 〈k〉 as a function of 〈k〉′ as

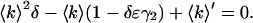(23)

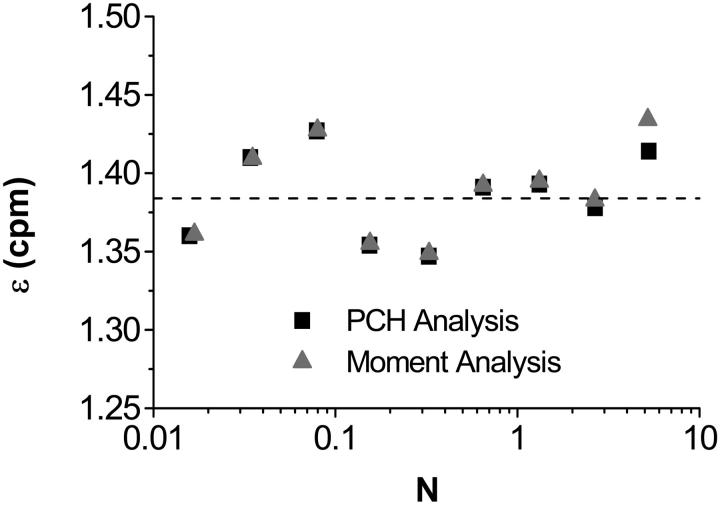
Equations. 22 and 23 are coupled and so we solve them in an iterative process. Since the average counts decrease only slightly in the presence of dead-time, we first use Eq. 22 to find an ɛ-value by making the approximation 〈k〉′ ≈ 〈k〉. Using this ɛ-value, we then find a new approximation for 〈k〉 using Eq. 23. This new value of 〈k〉 is then reinserted into Eq. 22 to find the ideal brightness. This procedure can be repeated iteratively until the ɛ-values converge, although usually only a few iterations are necessary. Fig. 6 compares data corrected for dead-time using PCH analysis and data corrected using the moment analysis just described. Only two iterations were required to obtain the excellent agreement shown.

FIGURE 5.

The relative error in the molecular brightness as a function of concentration for the dilution experiment in Fig. 4. The relative error was calculated by comparing the ɛ-value obtained from a fit of the experimental histogram to the ideal PCH model to that obtained from a global fit to the modified PCH model. Overlaid on the experimental data is the prediction of Δɛ/ɛ from the Taylor expansion (Eq. 14), which describes our data very well.

FIGURE 6.

A comparison of the dead-time-corrected molecular brightness obtained from PCH (squares) and moment analysis (triangles). This is the same dilution series as shown in Figs. 4 and 5, but with an additional neutral density filter inserted in the emission path which reduces the brightness. The results of moment and PCH analysis agree well with one another. The dashed line indicates the brightness obtained in a global fit of all the experimental histograms simultaneously (ɛ = 1.38 ± 0.01 cpm).

The moment corrections were developed with the assumption that δ × 〈k〉 ≪ 1. Our modeling and data suggest that when δ × 〈k〉 ∼ 0.05 the dead-time-affected moments calculated from the Taylor expansion differ by greater than 10% from the actual moments of the dead-time-affected distribution. However, with the corrections, we can measure up to as many as 10 molecules in the observation volume reliably, and even 100 molecules depending on the sampling frequency and brightness of the fluorophore . Another way to look at the limit given above is in terms of the intensity I. The limit then becomes I × τ_d ∼ 0.05. For a dead-time of 50 ns, we see that Eq. 14 will begin to break down when the count rate is on the order of 1 Mcps, which is close to the limit of most photon counting experiments. Although including second and higher order terms of δ in the Taylor expansion would improve the model, the first-order expression is sufficient to cover the range of useful fluctuation experiments. The correction algorithm developed for PCH theory itself is exact and not subject to the assumption noted above; thus, the dead-time-corrected PCH model should work for all ɛ- and 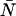-values.

The correction for dead-time effects is necessary for an exact and quantitative analysis of titration and dilution experiments. These experiments are important for studying biological systems. For example, consider a protein that assembles to form a homodimer. If there are ∼3 monomers, with ɛ = 1 cpm, for example, in the excitation volume and one dimer, the monomers' brightness is reduced by ∼20%, whereas the dimer's brightness is unaffected. The level of oligomerization is determined from the ratio of the brightnesses of the different species. In this case, we should obtain a ratio of two indicating a dimer, but instead we would obtain a ratio of 2.5, making it very difficult to interpret the level of oligomerization. Worse, if we were to measure at lower and higher concentrations of monomer, we would obtain ratios closer to two and three respectively, thus perhaps leading us to surmise that the oligomerization of the protein is concentration-dependent when, in fact, it is not. We have successfully used our model to measure protein-protein interactions in living cells over a wide concentration range. Including dead-time effects in our theory was crucial for analyzing the in vivo experiments. We will report these results in a future publication.

As part of this project, we also developed a global fitting routine in which multiple histograms can be fit and common parameters, such as the ɛ- and δ-values in dilution experiments, can be linked together. Global analysis is a very powerful tool because it is much more sensitive in resolving species than analyzing individual histograms. PCH analysis resolves mixtures directly from a single histogram provided the signal statistics of the data is sufficient (Müller et al., 2000). However, in many experimental situations a single PCH measurement is not sufficient in separating species. In particular, the presence of a dim minority species in a bright majority species is very difficult to detect by PCH analysis of a single histogram. For example, consider a FFS dilution experiment of a monomer-dimer mixture in which only a small fraction of the total number of molecules is monomer. Since we change the concentration, the equilibrium between the monomer and dimer forms shift. Analyzing the histograms individually will not resolve the presence of a monomer species in the mixture. However, if we perform a global analysis of the histograms and require that the brightness of each species remains constant, we would be able to resolve the mixture provided that no small systematic errors are present. We demonstrated that PCH analysis without corrections for dead-time leads to relative errors in the molecular brightness that exceed 10% if more than one molecule is present in the observation volume. This concentration-dependent error affects each histogram in a dilution or titration experiment to a different degree. Thus, the ideal PCH model is not suitable for global analysis. Only with the development of the dead-time-corrected PCH model are we able to exploit the advantages of global analysis.

CONCLUSIONS

FFS experiments rely on statistics for extracting information from experiments. Non-ideal detector effects, which are an unavoidable part of every experimental measurement, alter the signal statistics. Here we characterized the effects of afterpulsing and dead-time on PCH analysis. We specifically considered the case of actively quenched APD detectors, which are commonly used for FFS experiments. While it is typically safe to ignore afterpulsing, dead-time influences PCH data at surprisingly low concentrations. We have derived a quantitative expression for the relative error in the molecular brightness and verified it experimentally. More importantly, we arrived at an exact solution for dead-time correction and incorporated this into our global fitting model. This improved model describes our data within experimental error. By accounting for dead-time effects, we significantly extended the useful concentration range for FFS experiments utilizing PCH analysis.

Titration and dilution experiments are extremely useful ways of understanding biological systems. However, these types of experiments are especially prone to erroneous inferences about the behavior of the sample from the data due to non-ideal detector effects. Analysis with the ideal PCH model fits the experimental data; however, the brightness returned is reduced, whereas the number of molecules is too high. Dead-time effects are primarily dependent on concentration so some concentrations are only slightly affected, whereas others are severely so. Failure to recognize this problem will lead to an incorrect interpretation of PCH experiments and thus accounting for the dead-time effect in PCH is crucial for understanding biological titration and dilution experiments.

APPENDIX A

Probability distributions are described by several different types of moments, including ordinary moments, central moments, factorial moments, and cumulants. A discussion of these moments, their relation to each other, and the probability distribution can be found in Saleh (1978). We begin first with the ordinary moments of the PCH. The moments of an ideal histogram are given by

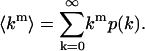(A1)

The dead-time-affected moments are given by

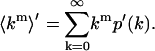(A2)

Evaluating Eq. A2 after expressing the distribution p′(k) in a Taylor expansion (Eq. 13) determines the moments of the photon count distribution in the presence of dead-time.

The first moment of the photon count distribution in the presence of dead-time is

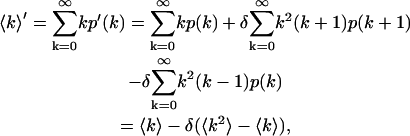(A3)

where in the second term we have made the substitution 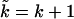and evaluated the following expression,

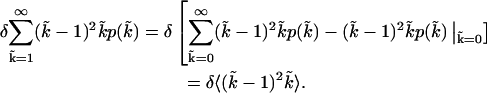(A4)

Following the same procedure, we determined the second moment of the photon count distribution in the presence of dead-time effects,

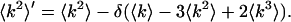(A5)

These expressions yield the dead-time-affected moments in terms of the ideal moments. However, we need expressions for the dead-time-affected moments in terms of the parameters ɛ and 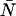. To transform Eqs. A3 and A5, we need to express the ideal ordinary moments of the photon counts in terms of intensity cumulants, which in turn, are functions of ɛ and 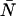(Qian and Elson, 1990a,b). First, the intensity cumulants are related to the central and ordinary moments of the intensity distribution. The first three cumulants are given below,

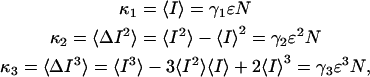(A6)

where γ_n is defined in Eq. 10. Next the intensity moments must be related to the photon count moments. In fact, the ordinary moments of the intensity distribution are given by the factorial moments of the photon count distribution (van Kampen, 1981),

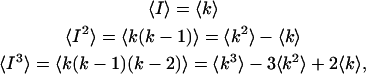(A7)

Combining Eqs. A6 and A7, we express the ordinary ideal moments of the photon count distribution in terms of the intensity cumulants and thus in terms of ɛ and ,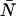

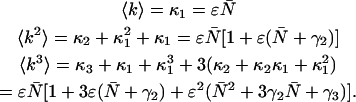(A8)

We have inserted γ₁ = 1 into Eq. A8 and in the expressions that follow. With the relationships in Eq. A8, we can now express the dead-time-affected moments in Eqs. A3 and A5 in terms of molecular brightness ɛ and the number of molecules ,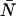

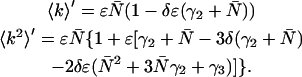(A9)

The derivation of Eq. 15 from Eqs. A8 and A9 is now straightforward. Inserting Eqs. A8 and A9 into Eqs. 11 and 12 respectively leads to an expression of the relative error in Q:

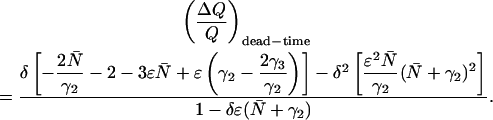(A10)

A Taylor expansion of Eq. A10 to order O(δ) yields Eq. 14.