ASTRO-FOLD: A Combinatorial and Global Optimization Framework for Ab Initio Prediction of Three-Dimensional Structures of Proteins from the Amino Acid Sequence

Abstract

The field of computational biology has been revolutionized by recent advances in genomics. The completion of a number of genome projects, including that of the human genome, has paved the way toward a variety of challenges and opportunities in bioinformatics and biological systems engineering. One of the first challenges has been the determination of the structures of proteins encoded by the individual genes. This problem, which represents the progression from sequence to structure (genomics to structural genomics), has been widely known as the structure-prediction-in-protein-folding problem. We present the development and application of ASTRO-FOLD, a novel and complete approach for the ab initio prediction of protein structures given only the amino acid sequences of the proteins. The approach exhibits many novel components and the merits of its application are examined for a suite of protein systems, including a number of targets from several critical-assessment-of-structure-prediction experiments.

INTRODUCTION

Structure prediction of proteins from their amino acid sequences is regarded as a holy grail in the computational chemistry, molecular, and structural biology communities. The basic premise, according to the thermodynamic hypothesis, is that the native structure of a protein in a given environment corresponds to the global minimum free energy of the system. Despite pioneering contributions and decades of effort, the ab initio prediction of the folded structure of a protein remains a very challenging problem. The challenge is a result of the complex relationships between both the accurate modeling and sufficient conformational sampling of these protein systems.

To avoid the difficult task of full ab initio structure prediction of proteins, database-driven methods have received considerable attention. Database-driven methods differ fundamentally from physics-based ab initio approaches in that they utilize knowledge-based information from structural databases. For purposes of critical assessment of structure prediction (i.e., CASP; CASP meetings held at Asilomar, in California, every two years), existing approaches for protein structure prediction are commonly classified as 1), comparative modeling; 2), fold recognition; or 3), ab initio methods. Although these general classifications exist, the distinction for many protein structure prediction approaches has become blurred. This is especially true for the so-called ab initio approaches since several of such denoted ab initio approaches actually rely on structural and statistical databases. In addition, these methods typically build upon or borrow concepts from other techniques, and only a handful of approaches can truly be classified as ab initio according to a full physiochemical denotation.

To understand this important distinction, it is useful to examine the application of several approaches to the prediction of a three-dimensional structure for a target sequence. A complementary classification scheme, which parallels the classification of prediction approaches, may involve the following identification of targets as discussed at the recent CASP5 meeting: 1), template refinement for methods in which the homology and sequence alignments are not difficult and the main goal becomes positioning of side chains; 2), template modeling, which must handle difficulties in both the detection of correct homology, alignment of sequence, and generation of correct template; and 3), free modeling, which is a general class for targets for which no discernible template exists. The classification of targets in this way facilitates the discussion of methods for determining accurate protein structures.

Database information is used most directly in the application of traditional comparative modeling methods for template refinement. Generally, classic comparative modeling is applied when the similarity between the target and parent structures is extensive and the problem becomes the refinement of an easily (relatively) identifiable template. Comparative modeling methods identify database templates by employing BLAST or PSI-BLAST searches against sequence databases (Altschul et al., 1997). When the homology between the parent and target sequences is high, the sequence-structure alignments can be derived directly from the PSI-BLAST results (with possibly some manual adjustments around insertion and deletion regions). Other multiple sequence alignment methods can also be used to examine the confidence of the sequence structure alignments (Notredame et al., 2000; Thompson et al., 1994). It is interesting to note that the fundamental problems of template refinement, such as loop closure and side-chain refinement, remain a challenge (Fiser et al., 2000; Tosatto et al., 2002; Xiang et al., 2002). However, many comparative modeling and fold recognition methods neglect these details and employ well-known algorithms for model generation (Sali and Blundell, 1993) and side-chain rebuilding (Bower et al., 1997). Classic methods for comparative modeling remain largely unchanged and have been applied with success to template refinement targets at multiple rounds of the CASP competition (Venclovas, 2001). An extensive review of comparative modeling can be found elsewhere (Moult et al., 2001).

As the name suggests, fold recognition approaches attempt to address the difficulties with remote detection of the correct fold for a target sequence. Such template modeling is necessary when the structural template of a protein in the database has very subtle or no obvious sequence relation to the target protein. The ability to effectively apply a fold recognition technique relies on the fact that structure is more evolutionary conserved than sequence. However, for distantly related proteins, the amount of similar structure may be relatively small. Thus, successful prediction of the target structure hinges not only on the alignment of regions of similar structure but also on the prediction of dissimilar regions. By extending this template modeling philosophy it may be possible to identify a composite structure from the fragments of different templates, which can then be used in combination to approximate the target structure. Of course this is where the distinction between fold recognition and so-called ab initio methods becomes vague because, for targets requiring template modeling, virtually all ab initio methods utilize information from sequence and structural databases. For the limit in which the correct fold of the target protein is a new fold, fold recognition methods are often complemented with or replaced by certain statistical techniques and thereby evolve into an ab initio counterpart.

The first step in locating remote low sequence identity structural homologs from the protein structure databases usually involves a check for evolutionary-related sequences using methods such as PSI-BLAST (Altschul et al., 1997). Multiple profiles from sequences with the same fold can be used to compute local and global alignments with a position-specific scoring matrix. The use of such sequence profiles aims at identifying the most evolutionarily distant homologs. However, sequence considerations alone will fail to link possible structural homologs with no common sequence patterning. Threading, an extension of the classic fold recognition approaches, attempts to identify such linkages by focusing on the possibility of shared structural motifs in the absence of detectable sequence homology.

The utilization of structural information is a significant feature of many fold recognition approaches. One particular strategy involves the inclusion of secondary structure predictions into fold recognition algorithms. An important observation supporting this technique is that pairwise secondary structure similarity can exceed 80% for certain pairs of sequences exhibiting <10% sequence similarity. Of course, the success of these types of approaches then also relies on the accuracy of secondary structure prediction for the target sequence. Given that recent methods for secondary structure prediction have reached 75% accuracy (although not comparably nor consistently for helix and strand predictions; see Cuff et al., 1998; Jones, 1999b; Rost and Sander, 1994), the use of predicted secondary structure for template modeling has become a significant component of successful fold recognition approaches. The form of this information can be as a string identifying the three-state prediction of the target sequence (DiFrancesco et al., 1997; Koretke et al., 1999), or as a map of the segments of α-helical and β-strands (Russell et al., 1996). Initial methods have relied on single secondary structure predictions for the target sequence; however, the finding that the combination of different predictions can create an exactly matched target has led to the development of methods for template alignment and modeling based on composite secondary structure predictions (An and Friesner, 2002).

Regardless of the incorporation of composite structural information for template alignment and modeling in fold recognition approaches, there remain problems with defining boundaries and insertions for the predicted models. For example, two proteins can share quite similar secondary structure motifs but differ dramatically in their overall three-dimensional structure. This is especially problematic when composite models are built, and is in part a consequence of the difference in length of the aligned sequence segments. In particular, a small sequence or segment may match very well within an overall longer template sequence, although the topology of the template may be very different and more complex due to the larger size of the overall template domain. This can be handled by penalizing sequence length differences, but will only be effective when combined with accurate domain parsing (Contreras-Moreira and Bates, 2002). A related problem is the correct identification of sequence insertions, which may represent domain boundaries or topological differences in the target sequence. Overall, the extent of success for fold recognition approaches is characterized by several features that belie some of the limitations of these techniques. As both the LIVEBENCH and CASP5 results demonstrate, the most successful predictions are often based on consensus prediction servers (metaservers) that attempt to select the best model according to the a ranking of independent fold recognition methods (Lundstrom et al., 2001). Beyond that, there are often concerted efforts and needs for human intervention to manually adjust the results of the template alignments and models generated by these database methods. These observations hint at the limits under which the database-dependent approaches operate. Other analyses of some of these methods can be found elsewhere (Moult et al., 2001; Murzin, 2001).

The blurry transition from fold recognition to ab initio approaches using structural databases can be understood by closer examination of the features of certain ab initio approaches. By definition, when considering new folds, ab initio approaches must not require the databases to possess proteins with global structural similarity to the new fold topology. Composite fold recognition approaches may also identify new fold topologies, although the designs of fold recognition techniques are better suited for matching of longer sequence fragments with modest insertion modeling. In practice, many ab initio approaches using databases represent the confluence of insertion modeling on a larger scale with fold recognition on a smaller scale. With this in mind, these approaches build template models through the extraction of fragments from general or tailored databases. This extraction process may involve the use of fragments with sequence similarity to fragments of the target sequence, or the use of fragments with structural similarity (secondary structure) to the predicted structure of fragments of the target sequence.

Fragment-based ab initio approaches have become extremely popular methods for exploiting database information. For small fragments the dependences on local conformational preferences are exploited, and the buildup of fragments has been implemented through a Monte Carlo procedure with a scoring function based on the Bayesian probability of sequence and structure matches (Simons et al., 1997, 1999). These ideas have been enhanced through the incorporation of secondary structure predictions as well as the addition of terms to favor the assembly of β-sheets (Bonneau et al., 2001). Another novel method uses the hierarchical application of multiple sequence alignment and threading to produce template fragments from which starting lattice models are built (Skolnick and Kihara, 2001; Skolnick et al., 2001). In this case, the hierarchical component reflects the obvious link between fold recognition and ab initio modeling. Several other outstanding methods employ predicted secondary structure, and thereby focus on the assembly of these predefined elements of structure, which are themselves obtained by predictions of methods based on databases (Eyrich et al., 1999a,b; Xia et al., 2000). One such method illustrates the utility of the deterministic αBB global optimization method for prediction of tertiary structure models (Eyrich et al., 1999a; Standley et al., 1999).

Discussion of these approaches also highlights another point, which is that the examination of the importance of certain features among ab initio methods using databases is difficult because of the inherent variability with which these methods depend on the database information (as related to sequence and structure similarity to proteins in these databases). On the other hand, the physics-based ab initio approaches lend themselves to, and even demand for, identical application for all types of target sequences. It is only under these conditions that the success and general application of an ab initio approach can be accurately assessed.

From the physiochemical point of view, there is a clear distinction between a true ab initio approach and an ab initio approach relying on sequence and structural databases. In the case of a true ab initio approach, the fundamental and driving principles for understanding protein folding rely upon Anfinsen's observation that the native tertiary structure of a protein corresponds to the conformation which minimizes the free energy of the system. This free energy of the protein depends upon the different interactions within the protein system—ionic interactions, nonbonded interactions, hydrogen bonding, hydrophobic interactions, steric and torsional effects, protein-solvent interactions, and entropic effects. Each energetic effect can be modeled mathematically, using fundamental knowledge of electrostatics and physical chemistry. As a result, the free energy of a protein can be expressed as a function of the positions of the atoms making up that protein. The native conformation of the protein then corresponds to the set of atomic locations providing the minimum possible value of the free energy function. Mathematically, ab initio protein folding is treated as a global optimization problem—a problem in which the goal is to locate the values of a variable set (in this case, the locations of the atoms in the protein) that describe the minimum possible value of a certain function (in this case, the free energy function).

A series of pioneering ab initio methods have been based on the hierarchical prediction of protein structures using detailed physics-based models (Liwo et al., 1998, 1999, 1997a,b; Pillardy et al., 2001). These approaches begin with reduced models of an all-atom force field, and subsequent conversion and refinement of the coarse model to an all-atom model. Recent work has involved the inclusion of multibody terms to improve the modeling of β-sheet formation. Unlike the database-driven methods, these physical (ab initio) models avoid the difficulties of coordinating insertions and deletions, as well as the associated unreliabilities in template alignment and side-chain positioning. One major advantage is that ab initio methods tend to be generic in how the physical processes of protein folding are modeled. This generality allows for not only the application of an ab initio approach to the structure prediction of any protein sequence, but may also lead to the understanding of the pathways that lead to the folded structure.

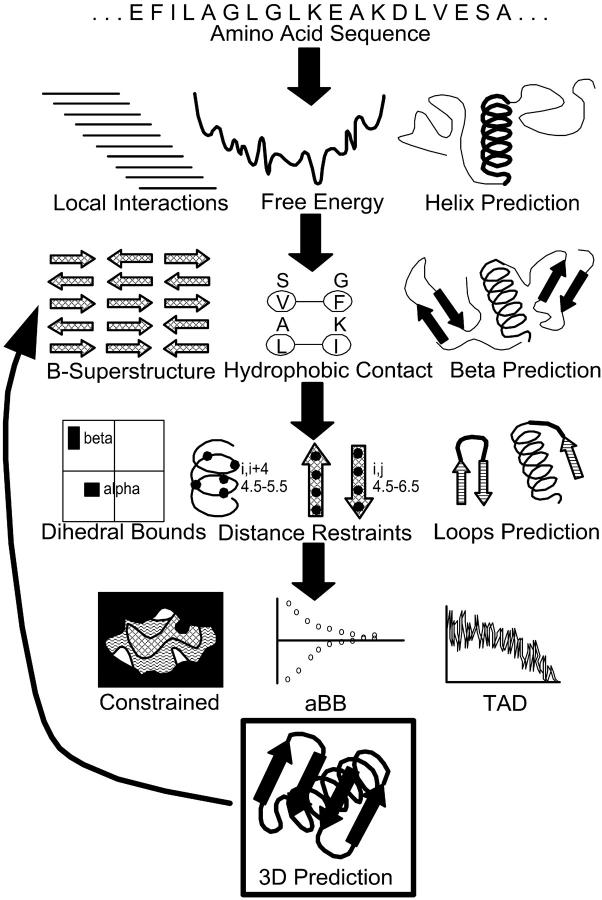
In this article a method true to the physiochemical perspective of ab initio structure prediction is presented. Underlying the structure prediction framework is the reconciliation of two competing views of protein folding. First, the predominance of local interactions in the fast formation of helical segments is used as a basis in detailed free energy calculations for subsequences of the overall target sequence. These calculations are used to identify initiation and termination sites of helices. In the second stage a model of hydrophobicity is employed in the simultaneous identification of β-strands and prediction of a β-sheet topology through the solution of a combinatorial optimization problem to maximize hydrophobic contacts. After deriving constraints on the system based on the previous stages and after additional calculations for loop segments, an overall three-dimensional structure is predicted using a combination of deterministic global optimization, stochastic optimization, and torsion-angle dynamics. This approach, known as ASTRO-FOLD, represents a combinatorial and global optimization framework for the ab initio prediction of three-dimensional structures of proteins. An overall schematic of the approach is provided in Fig. 1. The next four sections outline the stages of the overall approach, which are then followed by two sections describing the results for several benchmark systems including a variety of targets from recent CASP experiments.

FIGURE 1.

Overall schematic of ASTRO-FOLD approach for three-dimensional structure prediction of proteins.

α-HELIX PREDICTION

As a first step in the ASTRO-FOLD prediction framework, the principles of hierarchical folding are used to develop a method for the prediction of α-helices in protein systems (Klepeis and Floudas, 2002). The suitability of this method for α-helix determination is based on observations that nativelike segments of helical secondary structure form rapidly. The ability for helices to fold rapidly suggests that α-helix formation can occur during the earliest stages of protein folding. Such a mechanism for the helix-coil transition is based on local interactions which induce nucleation and propagation of the helix (Honig and Yang, 1995).

To isolate the prediction of α-helical elements to only local interactions, the overall protein is typically segmented into overlapping pentapeptide segments. In principle, longer peptide segments could be employed. As a minimum, a length of five residues is chosen because of the ability to observe the nucleation of a three-residue helix core within the fragment, which allows for the formation of a stabilizing backbone hydrogen bond. For a protein with N residues, the decomposition of the overall protein sequence into five residue segments corresponds to the analyses of a total of N-4 pentapeptides. For larger oligopeptides, such as heptapeptides or nonapeptides, the result would be either N-6 or N-8 subsequences, respectively. Theoretically, any fragments less than the total length of the target sequence could be simulated, although in practice the largest length should be the longest observed length for contiguous helices.

The helical propensity for an individual oligopeptide is determined through rigorous probability calculations using detailed atomistic level modeling. In the current implementation, the atomistic level modeling is based on the ECEPP/3 semiempirical force-field model (Némethy et al., 1992). For this force field, it is assumed that the covalent bond lengths and bond angles are fixed at their equilibrium values, so that the conformation is only a function of the independent torsional angles of the system. The total force field energy, E_forcefield, is calculated as the sum of electrostatic, nonbonded, hydrogen-bonded, and torsional contributions. The main energy contributions (electrostatic, nonbonded, hydrogen-bonded) are computed as the sum of terms for each atom pair (i,j) whose interatomic distance is a function of at least one dihedral angle.

With the amino-acid subsequences defined and the energy model selected, the ability to predict the preferred (or native) conformation for a given peptide translates into a global optimization problem in which the goal is to identify the global minimum free energy of the system. A wide variety of methods exist for tackling this problem, although generic guarantees for finding a global minimum energy conformation, even for pentapeptides, are not available. A deterministically-based global optimization method has been identified for solving these problems, although other stochastic methods have also been shown to be efficient (Floudas et al., 1998).

An additional consideration must be made when evaluating the entropic contributions for these systems. These entropic effects are necessary for calculating free energies (Klepeis and Floudas, 1999), which are the true gauges of conformational stability at equilibrium. A number of methods based on conformational sampling have been developed to approximate these effects. In this work, information regarding metastable states of the system is used in conjunction with the harmonic approximation to determine the accessibility of a given metastable state (Klepeis and Floudas, 1999). An attractive consequence of this approach is the identification of a significant ensemble of low free energy conformations, including the global minimum free energy structure. Rather than rely on the prediction of a single conformer (i.e., the global minimum free energy), the ensemble can be used to calculate occupational probabilities for representative conformational state of the system.

The analysis of the free energy of these oligopeptides therefore requires efficient methods for locating not only the global minimum energy structure but also large numbers of low energy conformers. A variety of methods have been used to find such stationary points on potential energy surfaces. For example, periodic quenching during a Monte Carlo or molecular dynamics trajectory can be used to identify local minima (Stillinger and Weber, 1988). In this work two algorithms are advocated for generating low energy ensembles for oligopeptide sequences. The first is based on modifications of a deterministic branch-and-bound algorithm, αBB (Adjiman et al., 1998a,b; Floudas, 2000; Klepeis et al., 1998, 2002; Klepeis and Floudas, 1999). The second is based on the principles of conformation space annealing (CSA) (Lee et al., 2000, 1998, 1997; Lee and Scheraga, 1999; Ripoll et al., 1998), an efficient yet stochastic method that does not provide the deterministic guarantees of the αBB approach. The implementation of the CSA-based method involves the combination of genetic algorithms and simulated annealing protocols (Lee et al., 1997). The details of these two approaches will be given in a later section.

Once an ensemble of low energy conformations (along with the global minimum energy conformation) has been identified for each oligopeptide, the free energy of each unique conformer is evaluated at 298 K using the harmonic approximation for entropic effects, and these free energy values are used to calculate individual occupational probabilities for each metastable state. Clustering of these states is based on the classification of the backbone torsion angles of the core residues. Specifically, the probabilities of conformers exhibiting identical Zimmerman codes for the core residues are summed and ranked to provide an ordered list of conformational propensities. The first iteration of the helix prediction approach is used to identify α-helical clusters for neutral oligopeptides. When the probability of the α-helical cluster (AAA for core residues of a helical pentapeptide) is greater than ∼85–90% for more than three consecutive sets of core residues, the marked oligopeptides are considered for further analysis.

For those subsequences including ionizable residues, α-helix propensities are refined according to detailed electrostatic and ionization energy calculations obtained through the solution of the Poisson-Boltzmann equation. Specifically, for the set of potential α-helical pentapeptides containing ionizable residues, probabilities are recalculated for a subset of conformers using a combination of the vacuum free energy calculations at 298 K and polarization and ionization free energies at pH 7. The final α-helix propensity for each residue are assigned according to the average AAA probability.

β-SHEET PREDICTION

Once the locations of α-helices have been predicted, the remaining residues are further analyzed to simultaneously identify and predict the location of β-strands and β-sheets. The procedure relies on hydrophobic information and the prediction of tertiary hydrophobic contacts to identify parallel and antiparallel β-sheets (Klepeis and Floudas, 2003b), as well as the location of disulfide contacts. In addition, the approach can identify a rank-ordered list of competitive β-sheet arrangements.

The principal feature of the β-sheet prediction is the modeling of the desolvation forces that govern hydrophobic collapse. The importance of the hydrophobic collapse, rather than just hydrogen bonding forces, in the formation of β-sheets has received growing theoretical support. One controversy regarding the validity of this hypothesis extends from the debate over hierarchical folding. In the case of hierarchical folding, it is believed that the β-sheet nucleates at the hairpin turn and proceeds to form through a zippering model that includes stabilization through hydrogen-bond formation (Munoz et al., 1997). The alternative view promotes a model in which β-sheet formation is driven by the hydrophobic collapse and is independent of hydrogen-bond formation. Recent simulations have demonstrated and supported the dominant role of hydrophobic forces in driving β-sheet formation (Bryant et al., 2000; Dinner et al., 1999; Pande and Rokhsar, 1999; Westerberg and Floudas, unpublished results).

The modeling of hydrophobic interactions between β-strand residues is used to formulate several problems that are globally optimized to produce a rank-ordered list of β-sheet arrangements with decreasing hydrophobic interaction energies. Each formulation produces an integer linear programming (ILP) problem in which the hydrophobic contact energy must be maximized.

The first formulation, a residue-to-residue contact problem, is based on iterative solution to effectively build an optimal set of hydrophobic contacts. The set of hydrophobic residues

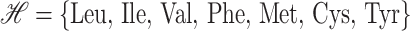in the target sequence is identified, and the relative positions of these residues are used to define a position-dependent parameter, P(i). Hydrophobicity parameters (H_i) are assigned to each residue based on experimentally derived free energy of transfer of amino acids from organic solvents to water (Karplus, 1997; Lesser and Rose, 1990; Radzicka and Wolfenden, 1988). The interaction energy for a potential hydrophobic contact is assumed to be additive, and the possible formations of these contacts are represented by binary variables, y_ij.

The objective function for the ILP formulation becomes

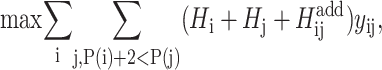(1)

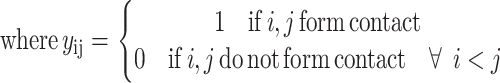(2)

For cystine-to-cystine contacts, an additional energy contribution is based on the addition of the interaction energy for all hydrophobic residues between the potential disulfide bonding pair. The contribution is normalized based on the length of the intervening segment.

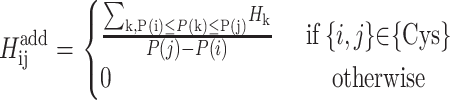(3)

A number of constraints are included in the formulation to provide physically consistent arrangements.

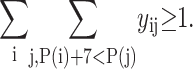(4)

The above constraint requires that at least one contact must form in which at least seven residues fall between residues i and j.

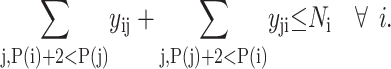(5)

Here N_i represents the total number of possible contacts for hydrophobic residue i. Initially this value is set equal to 1 for all residues so that each residue may participate in only one contact.

The next set of constraints define the allowable β-sheet configurations. For the case of antiparallel β-sheet formation, symmetric nonintersecting loops must be enforced. The following constraints provide the necessary conditions for antiparallel β-sheet formation:

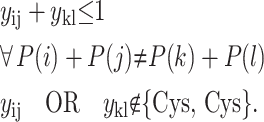(6)

The set of conditions implies that the sum of the contact position parameters must be equal and cannot be intersecting. In addition, the constraint is not included if a potential contact, either ij or kl, represents the formation of a disulfide bridge. In this way, disulfide bridge contacts are allowed to form nonsymmetric, intersecting loops. For the case of parallel β-sheet formation, the contacts must involve symmetric intersecting loops, which provides a similar set of constraints.

Finally, when disulfide bridge formation is allowed, an inequality constraint can be used to set the maximum allowable number of cystine-to-cystine contacts, such that the parameter N_SS represents an upper bound on the possible number of disulfide bridges.

The resulting ILP must be solved to global optimality to identify the set of contacts which maximize the hydrophobic interaction energy defined by the objective function. In general, MILP formulations belong to the class of NP complete problems (Floudas, 1995; Nemhausser and Wolsey, 1988), and available codes typically employ a branch-and-bound technique to find the optimal integer solution through the identification of a sequence of related LP relaxations.

The optimal set of hydrophobic residue-to-residue contacts is generated by solving the ILP formulation iteratively, with the identification of disulfide bonding pairs being included during the first iteration. For each subsequent iteration, the global optimal solution can be identified along with a rank-ordered list of possible antiparallel or parallel β-sheet configurations.

Three alternative formulations rely on the identification of potential β-strands, rather than just individual hydrophobic residues. These potential β-strands can be used to solve residue-to-residue contact or strand-to-strand contact ILP problems, or a combination of the two. The benefit of these approaches is the ability to identify the full β-sheet configuration simultaneously. Except for those simple systems that can be studied in detail using the residue-to-residue contact formulation, the strand-to-strand formulations represent the preferred technique for β-sheet predictions.

First, a protocol to identify potential β-strands is applied (Klepeis and Floudas, 2003b). This set of postulated strands represents a superstructure since the protocol typically leads to an overprediction of the true number of β-strands. In other words, the solution of the hydrophobic contact formulation may exclude certain postulated β-strands from the predicted β-sheet topology. Once the potential strands have been identified, each strand is assigned a position-dependent parameter, Q(si). The parameter is equal to the strand number by counting sequentially from the N-terminus to the C-terminus of the sequence. Each strand is also described by a start and end residue whose positions are denoted as P^beg(si) and P^end(si), respectively, and the number of hydrophobic residues within the strand is defined by N_H(si). A hydrophobicity value is assigned to each strand (S_si), according to the average hydrophobicity of the hydrophobic residues in that strand:

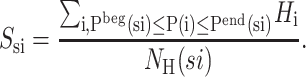(7)

The objective function for the strand-to-strand ILP formulation becomes that of maximizing the hydrophobicity by identifying the activation of those binary w_si,sj variables representing a particular strand-to-strand contact. The hydrophobicity gained by a particular contact is assumed to be an additive combination of the S_si and S_sj hydrophobicity values.

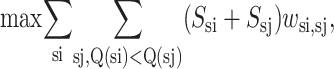(8)

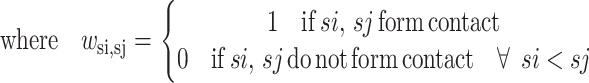(9)

A number of constraints are included in the formulation to provide physically realistic strand arrangements.

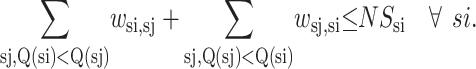(10)

Here NS_si represents the total number of possible contacts for strand si. In general, this value is set equal to 2 for all strands, although the proximity of helices may require a reduction of this value to 1. Another general constraint can be used to turn off certain disallowed strand-to-strand contacts.

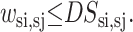(11)

A particular strand-to-strand contact is disallowed when the DS_si,sj parameter is set to zero for that combination.

Additional sets of constraints can be used to impose a maximum value on the number of consecutive strand-to-strand matches and to disallow more than one strand-to-strand match from one side of strand si. In addition, to maintain physically meaningful configurations the formation of β-sheet topologies with double intersecting strand-to-strand contacts are also disallowed (Klepeis and Floudas, 2003b).

A second formulation uses these strand definitions to solve the full β-sheet configuration problem. The objective function is based on the residue-to-residue contact energies, as given by Formulation 1. The set of constraints defined by Eqs. 4 and 5 are included in the formulation, and the constraints enforcing the formation of antisymmetric and symmetric loops are relaxed to include only individual strand pairings. The constraints included in the strand configuration problem are also enforced in this formulation. Finally, connections between strands and residue contacts are provided by the following set of constraints.

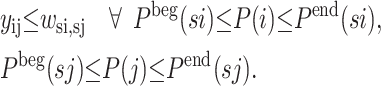(12)

These constraints link the y_ij and w_si,sj variables and can be complemented by additional constraints that serve to enhance the performance of the solver through tightening of the feasible search space. The linked problem can be thought of as a bilevel optimization problem in which the inner problem represents the maximization of given strand-to-strand contact registration, while these solutions are then suitable for an outer optimization problem that maximizes the hydrophobicity of the overall strand-to-strand arrangement.

A third and final formulation combines the objective functions from both the residue-to-residue and strand-to-strand formulations. This allows both contact energies to influence the prediction of the β-sheet configuration through the following objective function:

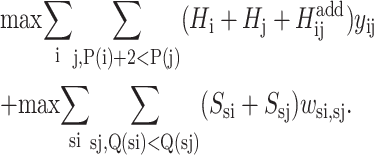(13)

As this formulation combines both strand and residue contact terms, the constraint set is identical to that of the previous formulation. It is important to note that multiple global solutions are also possible and that these β-sheet configurations may include both different strand-to-strand contacts as well as identical strand-to-strand contacts with varying strand-to-strand registrations. A full set of competitive solutions can be identified using integer cut constraints and iterative solution of the ILP formulations.

RESTRAINTS AND LOOP MODELING

Before progressing to the final stage of the ASTRO-FOLD approach, which involves the prediction of the tertiary structure of the full protein (Klepeis and Floudas, 2003a), the structure prediction problem is formulated based on the development of atomic distance and dihedral-angle restraints derived from the α-helix and β-sheet prediction results. In its final form, this formulation requires the use of constrained nonlinear global optimization techniques. This problem is solved through a combination of the deterministically-based αBB global optimization approach, stochastic global optimization, and molecular dynamics in torsion-angle space (Klepeis and Floudas, 2003a).

First, dihedral-angle bounds are assigned according to the predicted structure class, α-helical, β-strand, or unassigned, for each residue. The corresponding bounds on the values of the backbone torsion angles are given in Table 1. For α-helices, C^α-C^α distances can be restrained between each pair of i and i + 4 residues, which anticipates the formation of the α-helix hydrogen bond network. In a similar fashion, C^α-C^α restraints can be developed for residues in opposing strands of a β-sheet fold, so that hydrogen bond formation between strands is enforced. The β-strand restraints include both hydrophobic residues and intervening residues over the full extent of the matching strands in the β-sheet. The corresponding upper and lower distance limits are given in Table 2.

TABLE 1.

Dihedral angle bounds, lower and upper, for α-helix and β-strand residues

Conformer	φL	φU	ψL	ψU
α	−90	−40	−60	−10
β	−180	−80	80	180
unassigned	−180	180	−180	180

TABLE 2.

C^α-C^α distance bounds, lower and upper, for α-helix and β-strand residues

Conformer	dL	dU
α	5.50	6.50
β	4.50	6.50

Additional restraints can be generated through analysis of the unassigned loop residues in the protein sequence. Loops, those segments which connect elements of secondary structure in the protein fold, are often exposed or surfacial features of the protein structure. As a result, these segments can be important for defining differences in binding and activity characteristics for a fold family because functional variability is often related to the structural differences in the exposed regions.

Exploring the conformational space of a loop segment is a difficult undertaking given the large structural variability often observed in the loop regions of experimentally determined protein structures. For example, it is not unusual for loop fragments with the identical seven- or nine-residue sequence to exhibit highly dissimilar structures. These difficulties are compounded by the typically low sequence identities among the loop segments, which makes the application of comparative modeling techniques often inaccurate.

In this work, the prediction of loop conformations is treated in a manner similar to physics-based ab initio protein structure prediction (Klepeis and Floudas, 2003a). The goal of the approach is to aid in the ab initio treatment of the overall protein folding problem using only minimal information regarding the structure of the residues that flank the loop segment. Most importantly, an inherent assumption common to existing loop models—that is, the requirement of fixing the flanking and terminal loop residue positions—is not imposed.

Loop modeling follows the identification of secondary structure elements and β-sheet topology from the first two stages of the ASTRO-FOLD approach (Klepeis and Floudas, unpublished data). In the absence of threading such predictions onto a structural template, these results merely define the sequence (and not structural) location of loop fragments between two consecutive segments of secondary structure. The applied optimization approaches aim at deriving additional restraints, such as distance and torsional restraints, through systematic analysis of detailed all-atom, free energy simulations. The first method relies on the ability of local conformational preferences to define loop conformations and, in this spirit, a series of free energy calculations are performed for the overlapping oligopeptides (including portions of the flanking units) defining the loop segment. Structural probabilities are built for the dihedral angle space and used to define reduced bounds for subsequent simulations of larger portions of the loop fragment. This methodology culminates in a free energy simulation of the entire loop fragment. A second approach begins by dissecting the distance space over larger segments of the loop fragment such that longer range loop interactions are included. Distance domains are enforced via nonconvex constraints in the torsion space and simulations are conducted for all combinations of the dissected domains. Consolidation of the simulation results is used to define appropriate distance bounds to be imposed during a simulation of the overall loop fragment. In their final stages, both approaches provide energy-based predictions from models of the entire loop segment, although the progression of each approach is based on the emphasis of different structural descriptors.

These approaches play an important role in restraining and focusing the conformational searches used in treating the overall three-dimensional structure prediction problem. In particular, these restraints take the form of reduced φ- and ψ-domains as well as internal interatomic distance restraints for those residues connecting consecutive elements of secondary structure. The bounds are extracted from the set of low free energy conformers identified for oligopeptides representing these loop residue segments.

TERTIARY STRUCTURE PREDICTION

Once appropriate bounds on dihedral angles and interatomic distances have been determined, a combination of the deterministically-based αBB global optimization algorithm, stochastic global optimization, and molecular dynamics in torsion-angle space is used to solve a constrained tertiary structure prediction problem (Klepeis and Floudas, 2003a). The basic formulation begins as

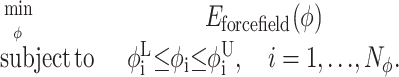(14)

Here the φ represents the variables used to describe protein conformations in the torsion-angle space, while φ^L and φ^U indicate the lower and upper bounds on these variables (which include both backbone and side-chain degrees of freedom). The energy function, E_forcefield(φ), is based on the atomistic level ECEPP/3 force field. This detailed energy modeling greatly increases the complexity of the objective function, as does the transformation from Cartesian to internal coordinates. However, one advantage of working in dihedral angle space is the reduction in the dimensionality of the independent variable set.

To solve the formulation given by Eq. 14 powerful global optimization-based search techniques must be utilized. Although many such methods have been developed, the major limitation is that the majority of the methods depend strongly on heuristics and initial point selection. To circumvent such difficulties, deterministically-based global optimization approaches can be employed. One such powerful method, the αBB global optimization approach (Adjiman et al., 1996, 1997, 1998a,b; Androulakis et al., 1995), has been extended to identifying global minimum energy conformations of peptides. This particular branch-and-bound method provides guarantees of convergence to the global minimum of nonlinear optimization problems with twice-differentiable functions (Floudas, 1997, 2000). The application of the αBB to the minimization of potential energy functions was first introduced for microclusters (Maranas and Floudas, 1992, 1993), and small acyclic molecules (Maranas and Floudas, 1994a,b). The αBB approach has also been applied to general constrained optimization problems (Adjiman et al., 1996, 1998a,b; Androulakis et al., 1995). In more recent work, the algorithm has been shown to be successful for isolated peptide systems using the ECEPP/3 potential energy model (Androulakis et al., 1997; Maranas et al., 1996), and including several solvation models (Klepeis et al., 1998; Klepeis and Floudas, 1999). αBB-based global optimization techniques have also been applied to NMR-type structure prediction problems (Eyrich et al., 1999a; Klepeis et al., 1999; Standley et al., 1999).

The αBB global optimization approach effectively brackets the global minimum by developing converging sequences of lower and upper bounds. These bounds are refined by iteratively partitioning the initial domain. Upper bounds on the global minimum are obtained by local minimizations of the original nonconvex problem. Lower bounds belong to the set of solutions of the convex lower bounding problems, which are constructed by augmenting the objective and constraint functions through the addition of separable quadratic terms. The lower bounding formulation can be expressed in the following manner:

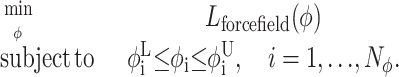(15)

In this formulation, variable bounds are specific to the subdomain for which the lower bounding functions are constructed. L_forcefield refers to the convex representation of the objective function, as given by

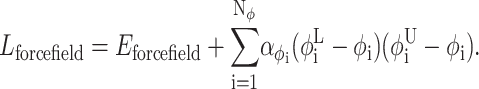(16)

The α-parameters represent nonnegative parameters which must be greater or equal to the negative one-half of the minimum eigenvalue of the Hessian of E_forcefield over the defined domain. Rigorous bounds on the α-parameters can be obtained through a variety of approaches (Adjiman et al., 1998a,b; Adjiman and Floudas, 1996; Hertz et al., 1999; Maranas and Floudas, 1994a). The overall effect of these terms is to overpower the nonconvexities of the original terms by adding the value of 2α to the eigenvalues of the Hessian of E_forcefield.

The same αBB principles can also be applied to more general formulations involving nonlinear constraint sets. Traditionally, restraints in the form of torsion-angle and interatomic-distance bounds (as derived in the previous stages) are formulated as unconstrained energy minimization problems. The lower and upper bounds on the torsion angles and interatomic distances are imposed through the use of weighted penalty terms that are minimized to zero while subsequently minimizing an overall energy objective. However, when reformulating these restraints as independent nonlinear constraints, both the E_dihedral and E_distance penalty terms are removed from the target function, leaving only E_forcefield:

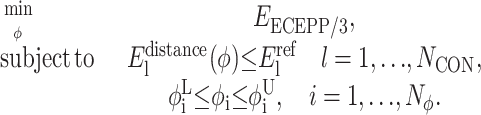(17)

As before, i = 1,…,N_φ corresponds to the set of dihedral angles, φ_i, with 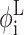and 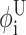representing lower and upper bounds on these dihedral angles. In general, the lower and upper bounds for these variables reflect full rotation although the reduced bounds (derived from the previous stage of the ASTRO-FOLD approach) are equally suitable. 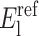are reference parameters for the N_CON constraints. The set of constraints are completely general, and can represent either the full combination of distance restraints or smaller subsets of the defined distance restraints. The maximum and average violation for each structural element can be controlled separately through the use of individual constraints, while an overall constraint including all distance can also be enforced to limit the violations over the entire structure.

These constraints, through reduction of the feasible search space, help to correct any discrepancies in the energy model, as well as focus the efforts of the global optimization algorithm. However, the highly nonlinear form of the potential energy function, coupled with the nonconvexities of the constraints, substantially increases the difficulty in identifying low energy feasible points for the αBB approach. To alleviate these difficulties a relatively fast torsion-angle dynamics module is implemented as a preprocessing step to the local minimization of the upper bounding problem. As a result, the performance of the αBB approach is improved significantly through the rapid determination of good approximations to feasible low energy minima.

Once the ability to formulate and effectively solve the upper and lower bounding problems has been established, the next step is to modify these problems for the next iteration. This is accomplished by successively partitioning the initial domain into smaller subdomains. For the protein conformation problems, it has been found that an effective partitioning strategy involves bisecting the same variable dimension across all nodes at a given level. To ensure nondecreasing lower bounds, the hyper-rectangle to be bisected is chosen by selecting the region which contains the infimum of the minima of lower bounds. A nonincreasing sequence for the upper bound is found by solving the nonconvex problem locally and selecting it to be the minimum among all conformers in the upper bound list. If the single minimum of L_forcefield for any hyper-rectangle is greater than the current upper bound, the global minimum cannot exist within this region and the entire subdomain can be deleted from the list of searchable regions (fathoming step). The computational requirement of the αBB algorithm depends on the number of variables (global) on which branching occurs.

The use of the αBB method is also amenable to the integration of other stochastic or heuristic search techniques for enhancing and improving the identification of low energy conformations. In other words, the solution of the upper bounding problem (i.e., the original nonconvex problem) is not limited to the use of nonlinear local minimization techniques. Such methods are known as hybrid global optimization methods and the ultimate goal of these methods is to combine the beneficial features of two or more algorithms. In particular, novel classes of hybrid global optimization methods, termed alternating hybrids, have been recently introduced for application as a tool in treating the protein structure prediction problems (Klepeis et al., 2003a,b). These new optimization methods take the form of hybrids between the deterministic global optimization algorithm, the αBB (Adjiman et al., 1998a,b; Floudas, 2000; Klepeis et al., 1998, 1999, 2002; Klepeis and Floudas, 1999), and a stochastically-based method, conformational space annealing (CSA) (Lee et al., 1997, 1998, 2000; Lee and Scheraga, 1999; Ripoll et al., 1998). The αBB method, as a theoretically proven global optimization approach, exhibits consistency, as it guarantees convergence to the global minimum for twice-continuously differentiable constrained nonlinear programming problems, but can benefit from enhanced computational efficiency. On the other hand, the independent CSA algorithm is highly efficient, though the method lacks theoretical guarantees of convergence. Furthermore, both the αBB method and the CSA method are found to identify ensembles of low-energy conformers, an important feature for determining the true free energy minimum of the system.

The CSA algorithm itself is a hybrid global optimization algorithm that combines genetic and simulated annealing algorithms (Kirkpatrick et al., 1983). The fundamental precept of the CSA algorithm is to anneal within the conformation space to converge upon the global minimum energy conformer. Initially, the entire conformation space is accessible, but as the algorithm proceeds the search region collapses around the lowest energy conformers. The process for reducing the search space is based on the concepts of simulated annealing, while the search for low energy conformers is influenced by the ideas of genetic algorithms.

To implement the CSA, the search begins with a bank of N_bank conformers generated randomly throughout the torsion-angle space. The separation between these conformers is quantified according to their pairwise deviation in torsion-angle space,

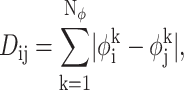(18)

where N_φ is the number of torsion angles in the protein, and 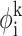is the value of torsion angle k in conformer i. At the start of the algorithm each conformer in the bank represents a region of conformation space with radius D_cut,o and centered on the point. The value of D_cut,o is calculated to be the average deviation among all conformers:

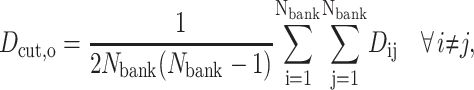(19)

where D_ij is the deviation given by Eq. 18. The value of D_cut is annealed according to an exponential schedule to reduce D_cut,o to a small value after a set number of iterations.

As the value of D_cut is annealed the conformation space is also searched according to a set of heuristics. These heuristics involve the alteration of variable values in a seed conformation according to random and crossover-based criteria. The mutated conformers are subjected to local minimization and then rejected or inserted into the current bank of active conformers with the stipulation that the size of the bank remains unchanged. Several scenarios are possible following the local minimization of the mutated conformer. In all cases, if the energy is above the highest energy conformer in the bank, the conformer is rejected and requires no further analysis. Otherwise, the value for D_ij is calculated for the combinations of the mutated conformers and those conformers in the bank. If the value of D_ij is greater than the current value for D_cut for all conformers, then the conformers are inserted in the bank and the highest energy conformer is removed to maintain the size of the bank. If the conformer falls within a defined region, then the conformer can be used to redefine the region if the energy is lower than the conformer already describing this region.

At each iteration a set number of mutations are performed before further reducing the value of D_cut. Each set of mutations is performed for one seed conformation taken from the bank. The seed conformations are chosen so that each conformer is not selected more than once until all conformers in the bank have been selected at least once. This process is repeated for a set number of iterations. In total, four types of mutations are performed, including both random and crossover-based substitutions using different sets of independent and connected variables.

With regard to the αBB/CSA hybrids, the algorithm alternates between large blocks of αBB iterations and large blocks of CSA iterations. In other words, for the hybrid global optimization approach, the αBB and CSA portions of the algorithm are not integrated (that is, one iteration of αBB is not followed by one iteration of CSA), but rather the two sides of the hybrid take turns dominating the behavior of the algorithm. First, the αBB branch-and-bound tree is set up, and the αBB portion of the algorithm is run for N_bank iterations. At each iteration, one of the local minima of the potential energy function generated in solving the upper-bounding problem is stored in a queue. Once N_bank iterations are complete, the queue is emptied into the initial CSA bank. At this point, the αBB algorithm shuts down temporarily, and the CSA portion of the hybrid takes over. One conformation is withdrawn at random from the CSA bank to serve as the seed conformation, and the offspring generated from this conformation are subjected to local minimization and entered into the bank (if applicable). This process is repeated for N_CSA iterations (with restrictions on the choice of a seed to ensure that every element in the bank is chosen once as a seed before any element is chosen a second time).

At this point, if the global optimum has not been located, the CSA portion of the algorithm shuts down temporarily, and control returns to the αBB portion. This proceeds through N_add more iterations to produce N_add more local minima. These minima are then added to the CSA bank, thus increasing its size by N_add. Control then returns to the CSA portion of the algorithm, and the cycle repeats. Care is taken to ensure that all of the new minima added to the CSA bank are used as seed conformations at least once before any of the conformers that were already in the bank are again selected as seed conformations.

COMPUTATIONAL COMPLEXITY

The application of the ASTRO-FOLD approach to the structure prediction of medium-sized proteins is made possible through the use of a distributed computing environment. Since the prediction approach is hierarchical in nature, the parallelized implementation is customized both to the type of problem being solved and the algorithm being employed at each stage of the approach.

First, the prediction of α-helices requires the decomposition of the full protein into smaller segments, and this approach is amenable to parallelization due to the independent nature of the analyses for the overlapping subsequences. The major computational expense for the α-helix prediction stage involves the calculation of accurate solvation and ionization energies for a subset of the overall oligopeptides (Klepeis and Floudas, 2002). The computational effort depends strongly on the number of times the Poisson-Boltzmann equation solver must be invoked, and is a function of the number of ionizable groups. In all cases, a finite difference solution to the Poisson-Boltzmann equation is implemented through the DELPHI package (Gilson and Honig, 1988; Honig and Nicholls, 1995). The calculation of solvation energy, namely the polarization energy of the neutral system, requires two calls to DELPHI, and is independent of the number of titratable groups in the system. For each ionizable group six additional DELPHI calls are required, which correspond to four reaction field calculations and two permanent dipole calculations. Two of the six calculations involve only single residue conformations, rather than the full protein system. When multiple titratable groups are present, four additional DELPHI calls must be made for each pair of ionizable groups. The computational effort in terms of the number of required DELPHI calls varies according to 2(N + 1)², where N is the number of ionizable groups (Klepeis and Floudas, 2002). These calculations are performed in parallel using a variation on a ring-based architecture system; in other words, processors communicate with nearest neighbors without the need for a master processor. After evenly dividing the static workload among all processors, load balancing is achieved through nearest-neighbor communication between processors in the ring structure. Termination is detected once the appropriate token has completed a full cycle through all idle processors.

For a given oligopeptide, the set of DELPHI calls is performed for an ensemble of the lowest free energy conformers. In the typical case of 5000 oligopeptide conformers, the total CPU requirement is on the order of ∼0.5 wallclock hour on a 128 parallel processor machine. However, the computational requirements are dependent on the specific size and charge distribution of the system. When considering systems with multiple titration sites, the computational cost increases significantly. For a two-titratable group oligopeptide, ∼1.5 wallclock hours are needed on the same parallel machine, whereas ∼3 wallclock hours are required for a system with three ionizable groups. These values can be used to estimate the total time to calculate free energies for oligopeptides of larger protein systems. For the in vacuo free energy calculations the total wallclock time will always be ∼6 h as long as the number of processors exceeds the total number of oligopeptides, since each oligopeptide can then be processed sequentially. When considering the DELPHI calculations, although the number of calculations varies linearly, the actual computational time varies according to the number of residues with titratable side chains and their occurrence in the set of oligopeptides. For a 100-residue sequence with average composition, a total of two wallclock days on a 128 parallel processor is needed to complete the ab initio prediction of helices.

After the identification of helices using rigorous free energy calculations, a combinatorial optimization problem is solved as part of the second stage of the ASTRO-FOLD approach. In particular, this second stage, which involves the prediction of β-sheet configurations, necessitates the optimization of several integer linear optimization, ILP, problems. In this work, a powerful software package, CPLEX (CPLEX, 1997), is used to identify globally optimal ILP solutions. The computational effort requires ∼1–2 h on a single processor, while simultaneously providing a rank-ordered list of competitive β-sheet topologies.

The final and computationally most expensive part of the ASTRO-FOLD approach is the solution of the constrained tertiary structure problem to produce a complete prediction of the three-dimensional structure of the target sequence. The nature of the alternating hybrid algorithm is also especially suitable to parallelization. Because the αBB and CSA elements of the algorithm are essentially totally separate, several plausible parallelization schemes present themselves, and these have been tested elsewhere (Klepeis et al., 2003a). The basic premise involves setting up two “master” nodes—an αBB master and a CSA master node. The slave nodes are then dedicated to one of these two masters—that is, a given slave node would perform either only αBB iterations, or only CSA iterations. Under this setup, while the CSA nodes are carrying out generation of trail conformations and bank updates, the αBB nodes could be working independently to solve enough lower-bounding problems to prepare for the next required update of the CSA bank. The parallel hybrid algorithm provides an efficient method for tackling the full structure prediction problem within the framework of the αBB deterministic global optimization approach.

Several factors affect the computational requirements for solving this constrained tertiary structure prediction problem. Most notable are the form of the energetic model, the form of the constraint functions, and the number of global variables for the system. For a system of ∼100 residues, the tertiary structure prediction phase, solved using the parallel hybrid algorithm described above, requires three wall clock days of CPU time on a 128 parallel processor distributed computing environment.

COMPUTATIONAL STUDIES

The ASTRO-FOLD methodology has been validated for several benchmark protein systems, as well as an ex post facto analysis for several CASP3 and CASP4 targets. A detailed analysis of blind CASP5 prediction results is presented in the subsection below. In addition, a significantly larger number of examples have been studied independently for both the α-helix (Klepeis and Floudas, 2002) and β-sheet (Klepeis and Floudas, 2003b) stages of the approach. Tables 3 and 4 provide a comparison of predicted and experimental results for eight computational studies after complete application of the ASTRO-FOLD approach.

TABLE 3.

Predicted and experimental values for location of helices

System	NRES		Predicted			Experimental
1GB1	56	H1 (23–34)			h1 (22–35)
BPTI	58	H1 (2–5)	H2 (47–54)		h1 (3–6)	h2 (48–55)
3CI2	63	H1 (12–21)	h1 (12–22)
R69	68	H1 (2–11)	H2 (16–22)	H3 (31–34)	h1 (1–12)	h2 (16–22)	h3 (28–35)
		H4 (48–50)	H5 (56–61)		h4 (45–50)	h5 (56–61)
T59	75	H1 (6–11)			h1 (6–13)
T114	87	none			none
T105	95	H1 (23–28)	H2 (48–53)	H3 (60–66)	h1 (26–29)	h2 (48–54)	h3 (62–65)
		H4 (73–79)			h4 (72–79)
T52	101	none			none

TABLE 4.

Predicted and experimental values for location and topology of β-sheets

System	Predicted strands		Predicted matches		Experimental matches
1GB1	S1 (1–7)	S2 (16–21)	S1–S2	S1–S4	S1–S2	S1–S4
	S3 (42–45)	S4 (50–55)	S3–S4		S3–S4
BPTI	S1 (17–23)	S2 (29–35)	S1–S2	S2–S3	S1–S2	S2–S3
	S3 (44–46)		C5–C55	C14–C38	C5–C55	C14–C38
			C30–C51		C30–C51
3CI2	S1 (27–33)	S2 (36–43)	S1–S3	S3–S4	S1–S3	S3–S4
	S3 (45–50)	S4 (56–59)	S2 not strand		s1(3–4)–S4
R69	None	None	None
T59	S1 (16–20)	S2 (26–28)	S1–S2	S1–S8	S1–S2	S1–S8
	S3 (31–33)	S4 (39–43)	S2–S5	S3–S4	S2–S5	S3–S4
	S5 (46–51)	S6 (54–58)	S4–S7	S5–S6	S4–S7	S5–S6
	S7 (61–63)	S8 (68–73)
T114	S1 (12–15)	S2 (23–26)	S1–S2	S1–S4	S1–S2	S1–S4
	S3 (31–37)	S4 (39–42)	S3–S7	S5–S6	S3–S7	S5–S6
	S5 (48–54)	S6 (61–70)	S5–S7	C7–C25	S5–S7	C7–C25
	S7 (77–86)				s1(3–4)–S2	s2(71–73)–S4
T105	S1 (10–15)	S2 (21–23)	S1–S2	S1–S5	S1–S2	S1–S5
	S3 (34–36)	S4 (42–45)	S2–S3	S3–S4	S2–S3	S3–S4
	S5 (65–67)	S6 (70–72)	S5–S6
T52	S1 (8–14)	S2 (17–23)	S1–S2	S2–S3	S1–S2	S2–S3
	S3 (31–33)	S4 (39–41)	S4–S5	S7–S8	S4–S5	S7–S8
	S5 (47–50)	S6 (54–59)	S8–S9	S10–S11	S8–S9	S10–S11
	S7 (62–64)	S8 (68–73)	C8–C22	C58–C73	C8–C22	C58–C73
	S9 (79–85)	S10 (90–94)	S6 not strand
	S11 (97–100)

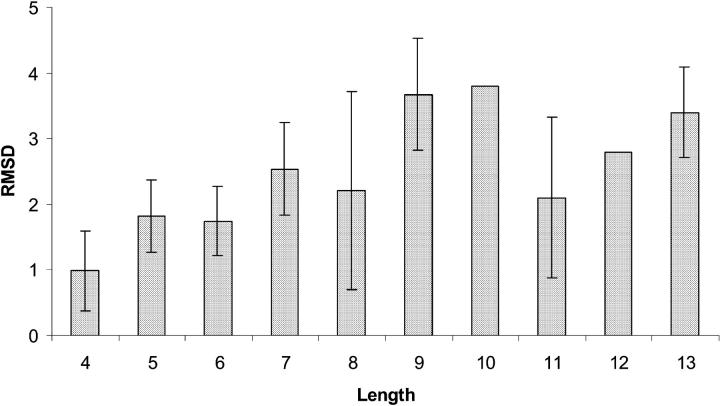
In general, the results of the ASTRO-FOLD approach are in excellent agreement with experiment for these systems (<100 residues). When considering the number and location of α-helices, the predictions are extremely accurate, with only slight variation in the initiation and termination sites of the individual helices. More impressive are the results for the β-strand and β-sheet predictions, shown in Table 4, which exhibit only small discrepancies for some of the larger targets (T114, T105, and T52). The agreement is also evidenced by the root mean square deviation (RMSD) values shown in Table 5 which indicate the difference of backbone atom placement between the experimental and predicted three-dimensional structures. It is interesting to note that the largest RMSDs are observed in the predicted structure of an all-α-helical protein (R69) and an all-β-sheet protein. This deviation is more pronounced for the α-helical system, as it is 30% shorter in sequence than the all-β-sheet protein (T52), which highlights the efficacy of the β-sheet prediction approach that lies at the heart of the ASTRO-FOLD methodology. It also suggests that a method for predicting restraints on helical topologies may aid in the structure prediction of predominantly α-helical targets.

TABLE 5.

Summary of predicted and experimental values for number of helices, strands, β-sheets, and disulfide bridges

	Predicted				Experimental
System	Helices	Strands	Sheets	SS	Helices	Strands	Sheets	SS	Overall backbone RMSD
1GB1	1	4	3	0	1	4	3	0	4.2
BPTI	2	3	2	4	2	3	2	4	4.1
3CI2	1	4	2	0	1	4	3	0	5.4
R69	5	0	0	0	5	0	0	0	6.2
T59	1	8	6	0	1	8	6	0	5.4
T114	0	7	5	1	0	9	7	1	4.5
T105	4	6	5	0	4	4	5	4	5.8
T52	0	11	6	2	0	10	6	2	6.9

The last column provides the backbone RMSD values between the predicted and experimental structures.

To better understand these results and the underlying predictions, two examples will be closely examined in the sequel: 1), the CASP3 target T59; and 2), the CASP4 target T114.

T59

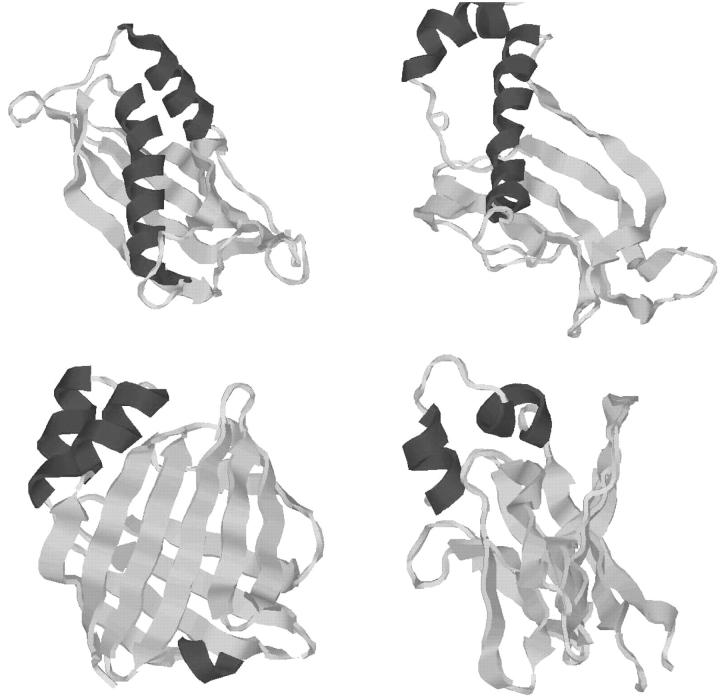
T59 is a representative of the target sequences introduced during the CASP3 experiment. The structure of the Sm D3 protein is consistent with the common core of typical Sm proteins. This structure involves a short N-terminal helix and a set of β-strands forming antiparallel β-sheets that fold upon themselves to produce a barrel-like structure. The overall topology resembles the common SH3 fold.

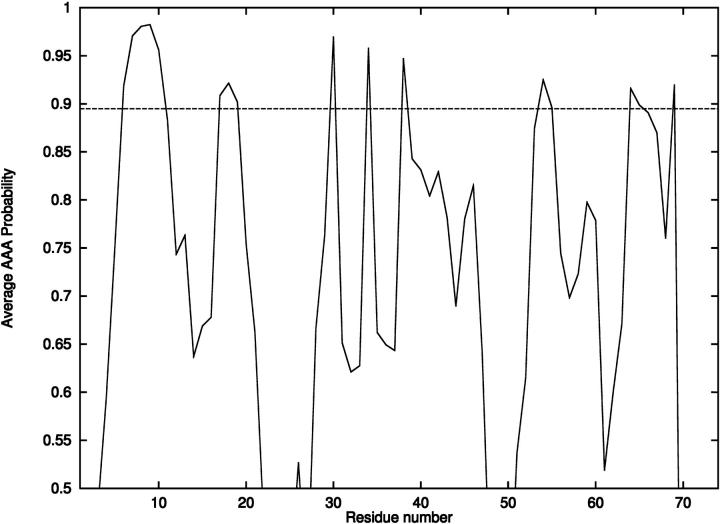
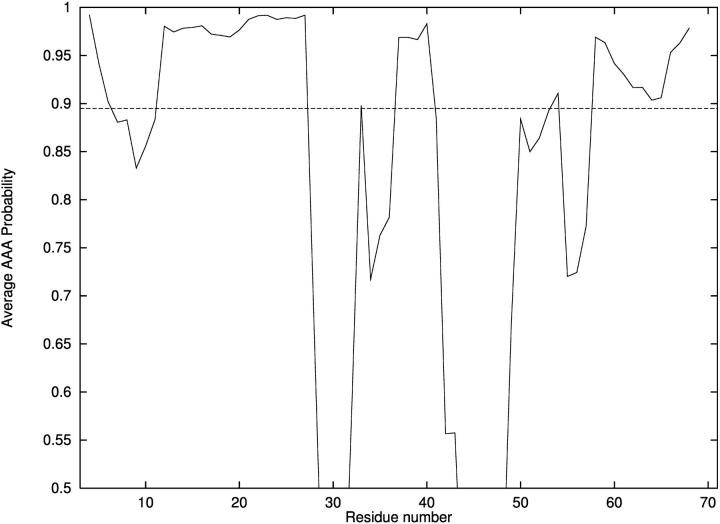
As a first step, helix predictions were made using free energy calculations for the 71 overlapping pentapeptides. For each pentapeptide, a series of free energy calculations was performed to identify low energy conformational ensembles. Energy modeling first included standard potential energy components based on the ECEPP/3 force field, as well as configurational entropic contributions using the harmonic approximation. Refinement of α-helix probabilities was based on detailed electrostatic and ionization energy calculations obtained through the solution of the Poisson-Boltzmann equation. For the set of possible α-helical pentapeptides containing ionizable residues, probabilities were recalculated for a subset of conformers using a combination of the free energy at 298 K and the polarization and ionization free energy at pH 7. Finally, α-helical propensity for each residue was assigned according to the average AAA probability. The results are presented in Fig. 2. The prediction of an α-helix corresponds to average AAA probabilities >∼85–90% for more than three consecutive residues. For T59, a single α-helix is predicted between residues 6 and 11, whereas the experimental findings place a helix between residues 6 and 13.

FIGURE 2.

Probability of α-helix formation for T59.

With the helical segments identified, the second stage of the ASTRO-FOLD methodology is used for the prediction of the β-sheet topology of T59 through application of the residue-based and strand-based formulations. For T59, the location of the postulated strands, shown in Table 6, almost exactly mimics the β-strand arrangement in the experimental structure. Eight individual strands are identified, and for three pairs of strands, the juxtapositioning of the two strands hint at the topology of the overall β-sheet topology. The common element for these strands is the separation between the two strands; that is, only two residues form the connection between the β-strands. The combination of the intervening residues clearly indicates the breakdown of the strands; in these cases, NT, TT, and NN.

TABLE 6.

Prediction of potential β-strands for small nuclear ribonucleoprotein Sm D3 (T59 from CASP 3)

1234567890	1234567890	1234567890	1234567890	1234567890
MSIGVPIKVL	HEAEGHIVTC	ETNTGEVYRG	KLIEAEDNMN	CQMSNITVTY
HTHT------	---NTNHHBH	NBTBTNHHNT	NHHNBNTTHT	HNHTTHBHBH
----------	------OOOO	OO----OOOO	OO-OO-----	OOOO-OOOO-
----------	-----XXXXX	X----XXXX-	XXXX----XX	XXX--XXXXX
1234567890	1234567890	12345
RDGRVAQLEQ	VYIRGCKIRF	LILPD
NTTNHBNHNN	HHHN---HNH	HHHTT
----OOOO-O	OOO------O	OO---
X-XXXXX---	XXXX---XXX	XXX--

The first row provides the single letter code for the amino acid sequence. The second row provides the classification, of ℋ, ℬ, 𝒯, and 𝒩 residues. The third row provides the location of the experimentally determined strands as depicted by contiguous blocks of O characters. A contiguous block of X characters shows the predicted β-strands in the fourth row.

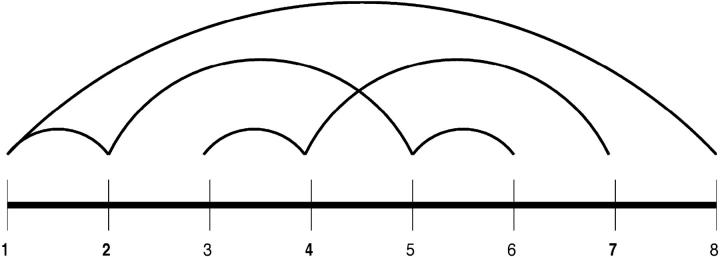
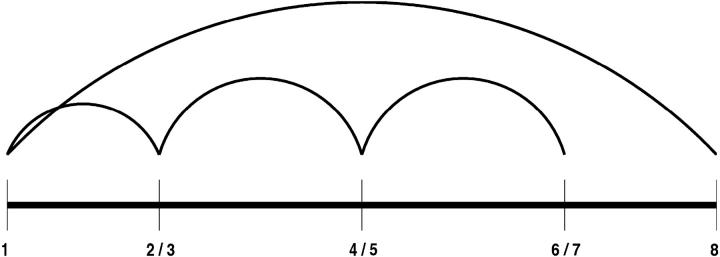
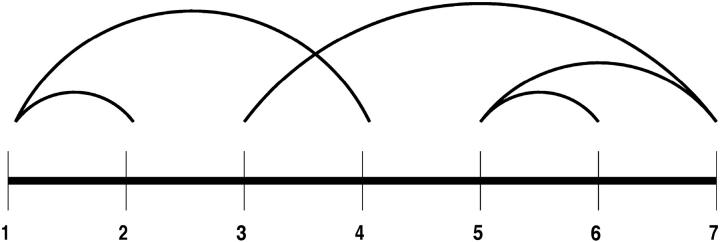
The solution of the strand-to-strand contact formulation identifies multiple global optima, with one of the seven globally optimal solutions corresponding to the true β-sheet topology shown in Figs. 3 and 4. Table 7 shows the strand-to-strand contacts for all seven global optima. Several common characteristics are evident. For example, strand connections always form between strand 1 and strands 2 and 8. In addition, since the strand probabilities are additive, the number of occurrences of each strand is the same for each solution. Since these solutions can be used as a starting point for further analysis, it should be noted that these common characteristics between different solutions can be used as a consistent set of restraints in the overall structure prediction.

FIGURE 3.

Contact diagram for global optimum of strand contact formulation for protein Sm D3 (T59).

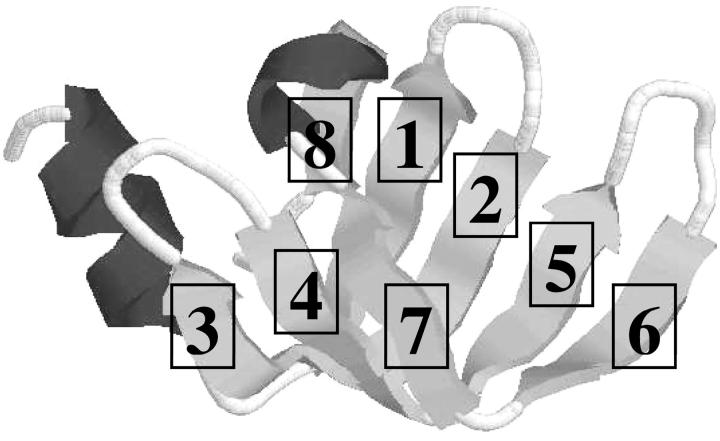
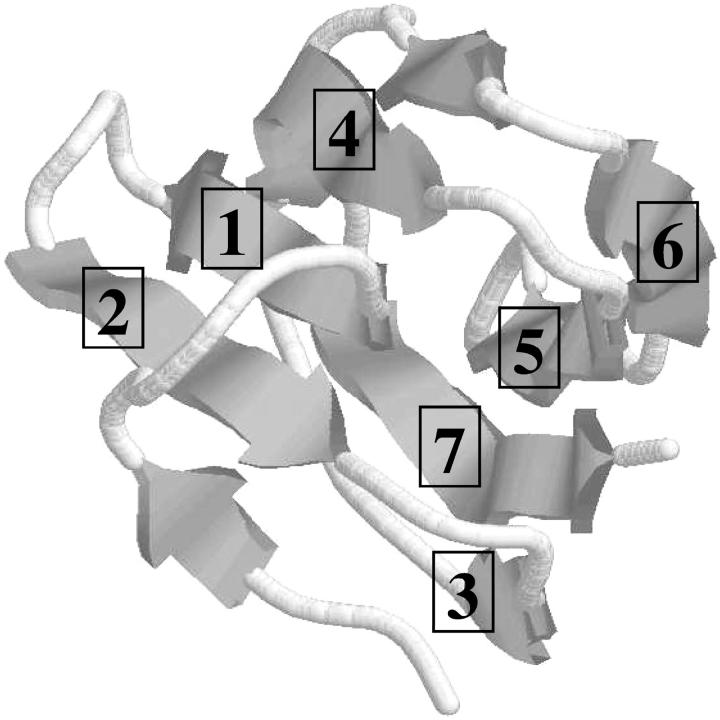
FIGURE 4.

Qualitative mapping of predicted β-strand to experimental structure of T59.

TABLE 7.

Strand-to-strand contacts for multiple global optima of T59

Optimum	1	2	3	4	5	6	7
Match 1	1-2	1-2	1-2	1-2	1-2	1-2	1-2
Match 2	1-8	1-8	1-8	1-8	1-8	1-8	1-8
Match 3	2-5	2-6	2-4	2-4	2-4	2-4	2-5
Match 4	3-4	3-4	3-7	3-6	3-5	3-5	3-4
Match 5	5-6	4-5	4-5	4-5	4-6	4-7	4-6
Match 6	4-7	5-7	5-6	5-7	5-7	5-6	5-7

The depiction of the strand-to-strand contact diagram can be used to visualize the overall topology of the T59 fold. Specifically, the symmetry of the intersecting loop between strands 2 and 7 represents the two β-ladders that comprise each side of the overall β-barrel. The periodic absence of connectivity between strands 2 and 3, strands 4 and 5, and strands 6 and 7 further dictates the positioning of these strands. In fact, the breakdown between these residues represents the formation of the β-wedge, within the flanking β-ladders. As referred to above, one possible configuration requires the extension of the strands to form a single extended region of β-structure from strands 2 to 3, strands 4 to 5, and strands 6 to 7. In this way, the symmetric intersecting topology is reduced to a single β-ladder, which represents the connection between the opposing sides of the β-wedge. This topology is illustrated in Fig. 5.

FIGURE 5.

Contact diagram for strand contact formulation with modified β-strand prediction for protein Sm D3 (T59).

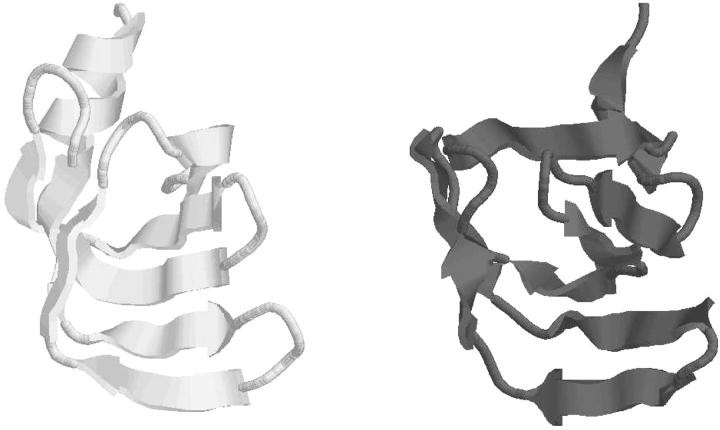
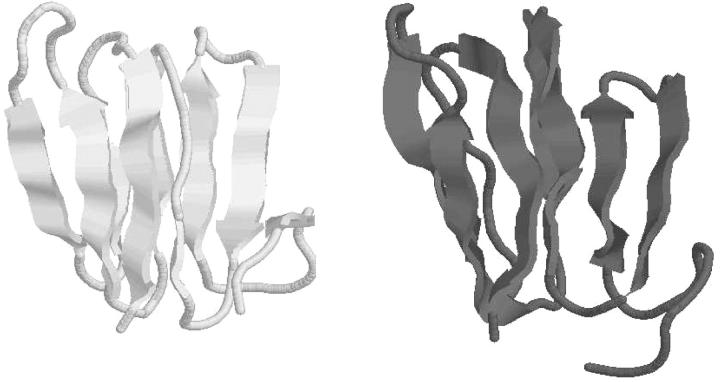
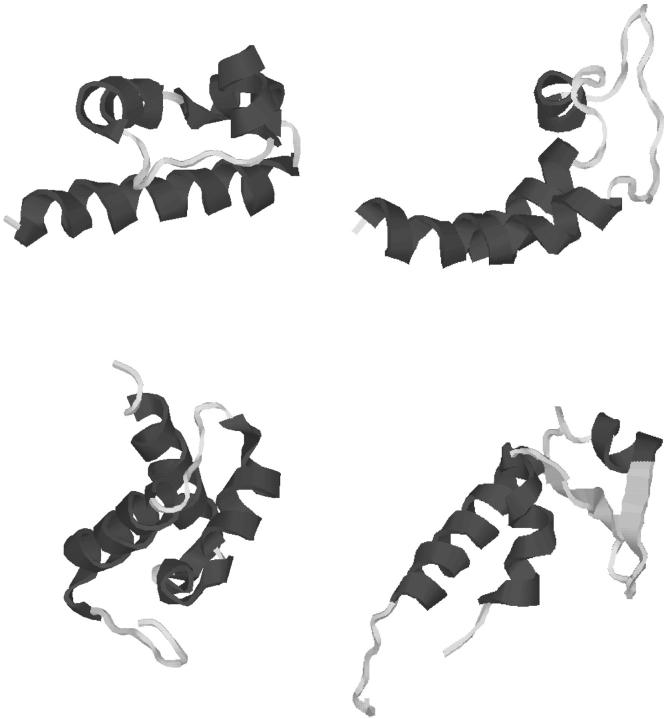
The final stage of the approach is then applied to predict the overall three-dimensional structure using the global optimal topologies listed in Table 7. For the scenario that matches the experimentally observed β-sheet topology, a total of 30 upper and lower distance bounds are identified. These interatomic distance constraints, along with the dihedral angle bounds, constrain the system according to the predicted topology and secondary structure content. Using the best overall energy as the single criterion, this structure, with an ECEPP/3 energy of −395 kcal/mol, possesses only a 5.4 Å deviation from the experimentally determined structure. A comparative plot of these two structures is given in Fig. 6.

FIGURE 6.

Comparison of predicted lowest energy tertiary structure (black) of T59 and experimentally determined structure (gray). All images generated with the RASMOL molecular visualization package (Sayle and Milner-White, 1995).

T114

T114 was released as a protein target for the CASP4 competition. The protein, an antifungal protein AFP-1 of Streptomyces tendae, is relatively small with a sequence length of only 87 amino acids. Using NMR techniques the structure of T114 was determined to possess a G-crystallin-like fold (Campos-Olivas et al., 2001), and although the classic crystallin sequence and structure motifs are absent from the structure of T114, the two folds are likely to be evolutionarily related. Shortly after the CASP4 competition, the killer-toxin-like protein SKLP was published and exhibited a similar structure and function.

As a target in the CASP4 competition the T114 system caused some difficulties for various structure prediction methods. Because of its structural relationships with existing proteins, the T114 target was classified as a fold recognition target without sequence homology. Overall, the structure of the protein exhibits a complex two layer β-sandwich topology, with some rare structural features; it is exactly these β-type proteins which consistently elude accurate structure prediction. T114 therefore represents a well-suited target to test the ASTRO-FOLD methodology and its novel techniques for the prediction of β-sheet topologies.

Helix prediction results indicated the absence of any contiguous helical segments. For this reason, the next stage began immediately with the application of the protocol for potential β-strand identification over the entire sequence of T114. The protocol identifies eight distinct strands, as shown in Table 8. In this study, the set of postulated β-strands is missing two additional strands observed in the experimental structure: 1), a short strand between residues 3 and 4; and 2), a three-residue strand between residues 71 and 73. It interesting to note that the PSIPRED method for secondary structure prediction not only misses these two strands, but also incorrectly joins the third and fourth strands in addition to predicting a helix over part of the last strand.

TABLE 8.

Prediction of potential β-strands for T114

1234567890	1234567890	1234567890	1234567890	1234567890
MINRTDCNEN	SYLEIHNNEG	RDTLCFANAG	TMPVAIYGVN	WVESGNNVVT
HHTNBTHTNT	THHNHNTTNT	NTBHHHBTBT	BHTHBHHTHT	HHNTTTTHHB
--OO------	-OOOOO----	-OOOOOO---	-O---OO---	OOOO----OO
------S---	-XXXXX----	-XXSXX----	XXXXXXX-XX	XX-----XXX
1234567890	1234567890	1234567890	1234567
LQFQRNLSDP	RLETITLQKW	GSWNPGHIHE	ILSIRIY
HNHNNTHTTT	NHNBHBHNNH	TTHTTTNHNN	HHTHNHH
OOOO------	-OOOOOO---	OOO------O	OOOOOO-
XXXX------	XXXXXXXXXX	------XXXX	XXXXXX-

The first row provides the single letter code for the amino acid sequence. The second row provides the classification of ℋ, ℬ, 𝒯, and 𝒩 residues. A contiguous block of O and X characters shows the experimental and predicted β-strands in the third and fourth rows, respectively.

Using the set of postulated β-strands, the combined residue-to-residue and strand-to-strand contact formulation is applied to jointly determine β-sheet connectivity, residue-to-residue contacts and possible disulfide bridge formation. The global optimum solution provides a disulfide bridge contact between the cystine residues at positions 7 and 25, as well as a β-sheet topology in which all postulated β-strands participate. All strand-to-strand contacts are predicted to be in antiparallel registration, and the overall configuration represents a nonsequential topology, as illustrated in Fig. 7. Although this global optimum provides strong agreement with experiment since all predicted strand-to-strand contacts are present in the experimental structure, there is a general underprediction in the number of β-sheet contacts. This is evidenced by a mapping of the predicted strands onto a three-dimensional cartoon representation of the experimental structure as shown in Fig. 8. In particular, the missing strands between residues 3 and 4, and 71 and 73, represent edge strands in the β-sheet architecture of the experimental structure.

FIGURE 7.

Contact diagram for global optimum strand-to-strand prediction for T114.

FIGURE 8.

Qualitative mapping of predicted β-strand to experimental structure of T114.

The derivation of restraints resulted in a set of 40 residues for which the backbone torsion-angle variables are constrained to extended β-sheet-like conformations. These 40 residues denote the locations of the seven predicted β-strands. The five predicted β-sheet contacts provided a set of 34 distances for which lower and upper bound constraints were imposed. Additional lower and upper bounds on the S^γ interatomic distance were enforced for the predicted disulfide bridge between residues 7 and 25. After solving the constrained global optimization formulation, the lowest energy structure for T114 provided an ECEPP/3 energy of −530 kcal/mol and possessed a 4.5 Å deviation from the experimental structure, as shown in Fig. 9. These results are promising in light of both the sparse set of constraints as well as the general difficulty with which accurate β-protein predictions are made.

FIGURE 9.

Comparison of predicted lowest energy tertiary structure (black) of T114 and experimentally determined structure (gray). All images generated with the RASMOL molecular visualization package (Sayle and Milner-White, 1995).

CASP5

In this section a comprehensive review is presented on the results from 11 of our blind predictions in the CASP5 experiment, for which experimental results were later made available. As our first participation in the CASP experiment, the target selection was based both on the size of the targets and the resources available for predictions. In general, we focused on targets smaller than 150 residues in length, and our sample is biased toward the earlier released targets since more time was typically available for these systems. Our target selection did not include evaluations of the sequence or structural homology of a given target sequence, as our goal was to examine the performance of the approach in a unbiased manner. For this reason, knowledge of “new-fold” classifications, which may have enhanced the performance of the ASTRO-FOLD approach in comparison to other database-driven approaches, was not exploited. The targets discussed here are listed in Table 9. The selection is skewed, unintentionally and unknowingly, toward comparative modeling and fold recognition targets, which reflects the general statistics of the overall set of the CASP5 targets.

TABLE 9.

List of CASP5 targets

Target	Start	End	NAA	Class
T0137	1	133	133	CM
T0150	−1	96	97	CM
T0153	2	135	134	CM
T0160	−1	125	126	CM
T0188	1	107	107	CM
T0130	6	105	100	CM/FR
T0132	6	151	147	CM/FR
T0138	1	135	135	FR(H)
T0157	2 (101)	119 (138)	120	FR(H)
T0170	3	71	69	NF/FR
T0139	239	300	62	NF

The start and end residues for the experimental structure are given, along with the overall number of amino acids (NAA) and the classification according to CASP5 postanalysis. CM indicates a comparative modeling target, CM/FR a comparative modeling/fold recognition target, FR(H) a homologous fold recognition target, NF/FR a new fold/fold recognition target, and NF a new fold target.

After application of the helix prediction stage, helices were present in all but one target sequence, as shown in Table 10. For this one sequence, T153, the experimental structure is characterized by only one short helix from residues 66–71. In other systems, the number of predicted helices varied from two to as many as five helices. For only one case, T160, the predictions overestimated the location of helices by predicting a small helix between residues 82–87. For two systems, T150 and T157, the helix predictions were almost in exact agreement with experiment. The most consistent inaccuracy with the approach was the tendency to underpredict small helical turns, which was the case for six separate target systems. Fortunately, these regions represent a very small number of amino acids, and even the classifications of these regions are somewhat ambiguous (in this case, the FSSP classification system was used to define individual residues as helix, strand, or coil). In only two cases, T139 and T170, were larger helical segments underpredicted. Both targets were classified as all-α-helical, relatively hard protein systems. In addition, as evidenced by the plot in Fig. 10, the probabilities in the region of underprediction for T170 (between residues 47–52 in Fig. 10), were not far below the cutoff value for helix prediction. However, since the goal of this stage is to determine the strongest helix nucleation sites, the underprediction of helical segments can be remedied in the final stage of the tertiary structure prediction.

TABLE 10.

Predicted and experimental values for location of helices

System		Experimental			Predicted
T130	H1(11–24)	H2(59–71)	H3(83–85)	h1(6–24)	h2(59–72)	h3(83–95)
	H4(89–96)
T132	H1(25–27)	H2(36–55)	H3(140–150)	h1(34–53)	h2(138–150)
T137	H1(2–4)	H2(16–23)	H3(27–35)	h1(17–22)	h2(40–45)
T138	H1(13–24)	H2(37–45)	H3(62–74)	h1(14–23)	h2(37–45)	h3(63–71)
	H4(95–99)	H5(107–111)	H6(113–128)	h4(108–127)
T139	H1(239–246)	H2(256–265)	H3(267–275)	h1(239–249)	h2(258–263)	h3(282–299)
	H4(278–299)
T150	H1(3–13)	H2(20–28)	H3(43–56)	h1(1–11)	h2(21–27)	h3(45–54)
	H4(67–73)	H5(93–95)		h4(68–73)	h5(92–95)
T153	H1(66–71)			None
T157	H1(42–52)	H2(73–87)	H3(119–135)	h1(42–50)	h2(73–84)	h3(119–135)
T160	H1(49–51)	H2(102–107)	H3(111–113)	h1(82–87)	h2(102–107)
T170	H1(14–28)	H2(36–45)	H3(47–52)	h1(12–27)	h2(36–40)	h3(58–68)
	H4(55–69)
T188	H1(12–14)	H2(46–48)	H3(56–62)	h1(57–62)	h2(76–83)	h3(96–103)
	H4(75–83)	H5(96–104)

FIGURE 10.

Probability of α-helix formation for T170.

Table 11 summarizes the β-strand predictions obtained from the second stage of the ASTRO-FOLD approach (and subsequently used in the final stage of the approach to identify the lowest energy configuration). The predictions are in excellent agreement with the experimental observations, as evidenced by the seven target sequences for which there is an essential one-to-one correspondence between the predicted strand locations and the experimental observations. These successful predictions include many mixed α- and β-protein systems. In addition, for two systems, namely T130 and T160, the only discrepancy between prediction and experiment is the underprediction of one β-strand. For another relatively large system, T153, the prediction misses one strand and mispredicts the location of a strand, with both errors occurring in close proximity. In addition, for this system, the β-strand prediction protocol identifies a long β-strand as two smaller separate strands. This is due to the lack of continuity of the hydrophobic patterning in this region of the target sequence. Finally, the prediction for one of the smaller systems, T170, erroneously identifies two β-strands within an all-helical protein. These secondary structure prediction results are summarized graphically in Fig. 11.

TABLE 11.

Predicted and experimental values for location of β-strands

System		Experimental			Predicted
T130	S1(29–33)	S2(47–52)	S3(78–82)	s1(28–33)	s2(47–52)	s3(74–81)
	S4(99–102)
T132	S1(16–22)	S2(59–64)	S3(78–88)	s1(16–24)	s2(58–70)	s3(78–88)
	S4(92–102)	S5(112–125)		s4(93–104)	s5(112–125)
T137	S1(6–14)	S2(39–46)	S3(49–55)	s1(4–11)	s2(40–45)	s3(49–53)
	S4(60–66)	S5(71–74)	S6(80–88)	s4(62–67)	s5(70–75)	s6(80–87)
	S7(91–97)	S8(102–110)	S9(113–120)	s7(90–93)	s8(100–110)	s9(113–120)
	S10(123–131)			s10(123–129)
T138	S1(5–10)	S2(29–34)	S3(53–57)	s1(2–11)	s2(29–34)	s3(51–57)
	S4(79–82)	S5(104–106)		s4(75–82)	s5(98–106)
T139	None			None
T150	S1(15–18)	S2(34–38)	S3(60–63)	s1(15–19)	s2(33–38)	s3(60–64)
	S4(82–87)			s4(80–86)
T153	S1(6–9)	S2(26–30)	S3(35–37)	s1(3–10)	s2(27–31)	s3(35–38)
	S4(42–52)	S5(57–62)	S6(73–75)	s4(42–45)	s5(49–53)	s6(57–61)
	S7(80–82)	S8(89–96)	S9(103–105)	s7(67–71)	s8(73–76)	s9(89–97)
	S10(110–118)			s10(103–106)	s11(111–122)
T157	S1(4–9)	S2(14–21)	S3(26–34)	s1(4–10)	s2(14–19)	s3(30–34)
	S4(56–63)	S5(91–96)		s4(56–61)	s5(89–94)
T160	S1(9–11)	S2(15–19)	S3(26–33)	s1(6–11)	s2(16–19)	s3(25–33)
	S4(40–46)	S5(52–55)	S6(58–61)	s4(39–45)	s5(51–54)	s6(66–74)
	S7(66–73)	S8(87–94)	S9(115–117)	s7(88–95)	s8(113–115)	s9(120–124)
	S10(120–124)
T170	None			s1(41–45)	s2(51–56)
T188	S1(2–7)	S2(26–33)	S3(36–44)	s1(1–7)	s2(26–32)	s3(37–43)
	S4(67–69)	S5(87–89)		s4(66–71)	s5(88–90)

FIGURE 11.

Comparison of predictions for helix and β-strand locations with respect to the experimental observations. For each target, the top line represents the secondary structure content of the experimentally determined structure, whereas the second line identifies the subsequent prediction results.

Quantitative evaluation of secondary structure prediction accuracy is a nontrivial task. Traditionally, a Q3 measure has been used to give an overall number of residues predicted correctly; however, this evaluation can be misleading. A measure that evaluates how secondary structure elements are predicted instead of individual residues has been found to be a better indicator of overall structure prediction accuracy. One particular measure that has received considerable attention is the segment overlap measure (SOV) (Rost et al., 1994; Zemla et al., 1999). The SOV evaluation is performed for overall three-state (helix, strand, and coil) and for each single conformational state. For a single conformational state i, SOV is defined as:

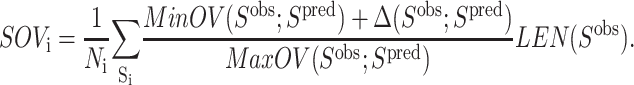(20)

Here S^obs and S^pred indicate the observed and predicted secondary structure segments in state i, which can be helix, strand, or coil. Len(S^obs) indicates the number of residues in the segment S^obs. MinOV(S^obs; S^pred) is the length of actual overlap of S^obs and S^pred, whereas MaxOV(S^obs; S^pred) is the total number of residues for which either of the segments has a residue in state i. Finally, Δ(S^obs; S^pred) is an integer value defined as

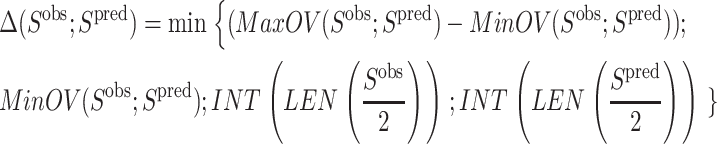(21)

The sum in Eq. 20 is taken over all pairs of segments in which S^obs and S^pred have at least one residue in state i in common, and the value for N_i is equal to the sum of length of all pairs of segments in which segments S^obs and S^pred have at least one residue in state i in common in addition to the length of the segments S^obs that do not provide any segment pair. The SOV measure for all three states is given by

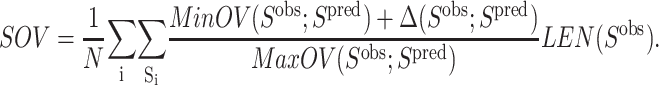(22)

In this case the value for N is taken as the sum of N_i over all three conformational states.

Quantitative evaluation of the predicted secondary structure content is computed using the SOV measure, and these results are presented in Table 12. In addition, the SOV analysis is used to compare the ASTRO-FOLD results to those obtained using the PSIPRED method for secondary structure prediction (McGuffin et al., 2000). PSIPRED utilizes two feed-forward neural networks to perform an analysis on output obtained from PSI-BLAST (Position Specific Iterated - BLAST; Altschul et al., 1997). Cross-validation of the method indicates that PSIPRED is capable of achieving an average Q3 score of nearly 77%, which is the highest result for any published secondary structure prediction method. The PSIPRED predictions are based on a standard three-state model to indicate the location of helix, strand, and coil fragments for a given sequence. It is important to note that PSIPRED can only predict the location of secondary structure in the overall sequence. In contrast, the presented ab initio approach predicts the location of potential β-strands as well the configuration of the overall β-sheet network.

TABLE 12.

Overall and three-state SOV evaluations for both the ASTRO-FOLD predictions and those obtained from the PSIPRED prediction server (McGuffin et al., 2000)

	ASTRO-FOLD SOV				PSIPRED SOV
Target	All	Helix	Strand	Coil	All	Helix	Strand	Coil
T0130	75.8	91.4	71.7	62.9	86.0	90.7	93.1	78.0
T0132	92.0	91.2	96.2	89.2	88.1	91.2	100.0	79.3
T0137	88.2	85.0	95.5	74.4	96.0	85.0	100.0	93.7
T0138	84.5	85.6	88.9	81.0	83.3	85.6	86.3	79.1
T0139	78.3	79.6	100.0	73.6	80.6	81.6	100.0	76.7
T0150	81.4	79.5	94.7	76.5	90.8	97.1	96.5	79.4
T0153	80.2	0.0	77.0	89.5	77.9	0.0	80.7	81.1
T0157	94.2	100.0	92.6	89.5	93.7	100.0	91.9	88.7
T0160	82.6	50.0	87.6	84.5	79.9	50.0	89.7	77.4
T0170	82.9	80.4	100.0	87.8	93.8	93.5	100.0	94.6
T0188	84.7	80.6	94.5	81.4	87.7	80.6	97.9	86.1

In general, the SOV values for all targets are relatively high, with most overall SOV values above 80% accuracy. In addition, the results are somewhat unusual in the sense that the β-strand predictions exhibit high accuracy, which reflects the fact that these particular targets are well-represented in the sequence and structural databases. Nevertheless, the results for the ASTRO-FOLD ab initio predictions perform well when compared to the PSIPRED database method. Out of the 11 total targets, the ASTRO-FOLD method predicts secondary structure content to a higher degree of accuracy for five of the targets.

Although the ab initio secondary structure predictions agree quite well with experimental observations, the true benefit of the β-sheet prediction approach is the identification of a three-dimensional topology for the connectivity of the β-strands. These strand-to-strand matches are summarized in Table 13. For five targets, the predicted strand-to-strand contacts identically match those observed in the corresponding experimental structures. In general, the predicted secondary structure for these five targets also exhibit relatively good correspondence when compared to the order and location of the observed secondary structure elements. This is indicated in Fig. 11 for the five targets: T132, T138, T139, T150, and T188. However, when compared to the quantitative evaluation provided by the SOV measure, only predictions for targets T132 and T138 were assessed to be better than the PSIPRED predictions. This emphasizes the importance of not only assessing secondary structure prediction accuracy, but also the need for identifying correct topological connections.

TABLE 13.

Predicted and experimental values for β-sheet topology

	Experimental			Predicted
System	Strand 1	Strand 2	Type	Strand 1	Strand 2	Type	Agree (Y/N)
T130	S1	S2	A	s1	s2	A	Y
	S2	S3	P	s2	s3	A	N
	S1	S4	A		None		N
T132	S1	S3	A	s1	s3	A	Y
	S3	S4	A	s3	s4	A	Y
	S4	S5	A	s4	s5	A	Y
	S2	S5	A	s2	s5	A	Y
T137	S1	S2	A	s1	s2	A	Y
	S3	S4	A	s3	s4	A	Y
	S6	S7	A	s6	s7	A	Y
	S7	S8	A	s7	s8	A	Y
	S8	S9	A	s8	s9	A	Y
	S9	S10	A	s9	s10	A	Y
	S2	S3	A		None		N
		None		s4	s5	A	N
	S5	S6	A		None		N
	S1	S10	A		None		N
T138	S1	S2	P	s1	s2	P	Y
	S1	S3	P	s1	s3	P	Y
	S3	S4	P	s3	s4	P	Y
	S4	S5	P	s4	s5	P	Y
T139		None			None		Y
T150	S1	S4	A	s1	s4	A	Y
	S2	S3	P	s2	s3	P	Y
	S2	S4	A	s2	s4	A	Y
T153	S1	S4	A	s1	s5	A	Y
	S2	S10	A	s2	s11	A	Y
	S3	S9	A	s3	s10	A	Y
	S4	S8	A	s4	s9	A	Y
	S5	S10	A	s6	s11	A	Y
	S5	S7	A	s6	s8	A	N
	S6	S8	A	s7	s9	A	N
T157	S1	S2	A	s1	s2	A	Y
	S4	S5	P	s4	s5	P	Y
	S2	S3	A	s2	s4	P	N
	S1	S4	P	s1	s3	P	N
T160	S1	S2/S3	A	s1	s3	A	Y
	S3	S7	A	s3	s6	A	Y
	S5	S7	A	s5	s6	A	Y
	S4	S6	A	s4	s5	A	N
	S8	S9	A	s7	s9	A	N
	S2	S10	P		None		N
T170		None		s1	s2	A	N
T188	S1	S2	A	s1	s2	A	Y
	S2	S3	A	s2	s3	A	Y
	S1	S4	P	s1	s4	P	Y
	S4	S5	P	s4	s5	P	Y

These results can be interpreted more exactly by examining individual predictions. For example, when considering overall secondary structure, the ASTRO-FOLD predictions for both T157 and T160 provide excellent agreement with experiment and the SOV evaluations are better than those provided by the PSIPRED predictions. In both cases, the predicted β-sheet topologies exhibit both consistent and inconsistent characteristics when compared to the experimental structures. For T157, these inaccuracies correspond to both a switch in the β-strand matches and also a difference in the antiparallel and parallel nature of one of the matches. In contrast, for T160, there exists a shift in the corresponding matches along the sequence, although the antiparallel nature of the matches remains correct. In addition, the T160 β-sheet prediction misses a potential parallel strand-to-strand contact. As will be shown, the T160 inconsistencies do not seriously affect the final three-dimensional structure prediction.

The final evaluation of structure prediction accuracy is the assessment of the overall three-dimensional structure as compared to the observed experimental structure. It should be noted that for all comparisons, the ASTRO-FOLD-based predictions represent the results for the lowest energy structure. In fact, the ASTRO-FOLD method does not rely on clustering of low energy structures nor additional energetic or structural criteria, and the evaluations reflect only the results of the single lowest energy structure. Several evaluation measures exist, although the performance of a given method may be judged differently depending on the choice of these evaluation criteria. This problem becomes compounded when visual evaluations are used, such as during the CASP experiments, and reflects the fact that the prediction results are generally not good. In other words, the generic structure prediction problem has not yet been solved.

To correctly evaluate the structure prediction problem several criteria must be used. In particular, one type of evaluation may involve the assessment of the prediction of the correct fold topology, including the β-sheet contacts as presented in Table 12. A step toward a more quantitative assessment of fold prediction accuracy is the evaluation of contact maps which indicate the interatomic distances between all C^α atoms in either the predicted or experimental structures. The relative coverage on a contact map can be used to evaluate accuracy in the topology of secondary structure contacts not predicted through the β-sheet prediction approach, such as those contacts between α-helices and β-strands, or α-helices with other α-helices.

Fig. 12 depicts comparative contact maps for four CASP5 targets: T0130, T0138, T0150, and T0160. The individual graphs were constructed by computing the interatomic distances and then plotting the appropriate color-scaled values for both the experimentally observed and ASTRO-FOLD predicted structures in the upper left and lower right triangles of the plot, respectively. The graphs are colored such that the shading progresses from dark to light when moving from short to long interatomic distances. Examination of the image for T130 reveals several significant pieces of information regarding the three-dimensional structure of the predicted and experimental structures. For example, the presence of an antiparallel β-sheet between the first two β-strands in each structure is indicated by the dark line perpendicular to the diagonal in this region of the contact map (30–35 for strand 1 and 45–50 for strand 2). As expected, the misprediction of an antiparallel rather than parallel match between strands 2 and 3 in the predicted β-sheet topology is also evident in this graph. This antiparallel match corresponds to a dark line perpendicular to the diagonal between residues 45–50 of strand 2 and residues 75–80 of strand 3. In contrast, the same region for the experimental structure features a dark line characteristically parallel to the diagonal. However, the contact maps also allow for assessment of topological features not identified through the β-sheet prediction. In particular, for T130, the experimental structure exhibits an antiparallel contact between the first and second helices, as evidenced by the dark line antiparallel to the diagonal between residues 10–20 and residues 60–70. In contrast, such a contact is totally absent in the contact map for the predicted structure as evidenced by the light region along the bottom line in this portion of the contact map.

FIGURE 12.

Contact map comparisons (clockwise from top left) for T130, T138, T160, and T150. The upper left triangle corresponds to interatomic distances calculated from the experimental structure, whereas the lower right triangle corresponds to those derived from the predicted structure. An upper distance cutoff of 30 Å was used to emphasize small interatomic distances. The progression from small to large distances follows the dark to light shading.

The comparative contact maps also offer information about those systems in which the predicted β-sheet topology matches experimental observations. For example, the β-sheet topology for T138 is correctly predicted to contain four parallel β-sheet matches. Comparison of the two triangles for T138 in Fig. 12 identifies these consistencies between the two structures, but also indicates a lack of short-range interactions between the N- and C-termini in the predicted structure. This observation is evidenced by the lack of any dark regions in the lower-right-hand corner of the T138 contact map, which stands in opposition to the apparent parallel contact between the first helix (residues 15–25) and the last helix (residues 115–120) in the experimental structure. Differences between experimentally observed and predicted contact maps are much less pronounced for other targets, such as T150 and T160. For T150, this agreement complements the prediction of the correct β-sheet topology. On the other hand, although the prediction of the β-sheet topology for T160 is not in exact agreement with experiment, the contact map agreement suggests that these discrepancies are not likely to affect the accuracy of the overall three-dimensional structure.

A more quantitative assessment is to compute the backbone RMSD between the experimentally observed and computationally predicted structures. Several measures for assessment employ RMSD values, although many times these measures are not stringent. For example, a sequence-independent RMSD analysis allows for shifting of the structure-to-structure alignment along the corresponding target sequence. In addition, other RMSD measures do not enforce that the set of compared residues are contiguous. One objective analysis involves the simple determination of the longest contiguous segment (LCS) that falls within a certain RMSD cutoff value. For the structure predictions of the CASP5 targets, 5 out of 11 predicted structures possessed at least 50 contiguous residues with RMSD values between 4–6 Å. When requiring at least a 40-residue LCS within the 4–6 Å RMSD cutoff, this set included 9 out of the 11 targets. For larger RMSD (6–8 Å) cutoffs, a 50-residue contiguous segment was predicted for 8 out of 11 targets. Finally, for both T138 and T160, an LCS of at least 100 residues was found within RMSD cutoffs of 6–8 Å.

Systematic analyses of the predicted three-dimensional structures can also be insightful in identifying potential improvements for the ASTRO-FOLD approach. Using the experimentally determined structures as a guide for the location of helices and strands, structural RMSDs were calculated between predicted and experimental structures for regions defined as helix, strand, or loop. These results were grouped according to the length of the regions, and average RMSDs along with the corresponding standard deviations were computed. Graphs of this information are provided in Fig. 13 for regular secondary structure elements (helices and strands) and in Fig. 14 for loop regions.

FIGURE 13.

Average backbone RMSDs from experimental structure for helical (top) and β-strand (bottom) regions (length given by values on x-axis) of all CASP targets. Helix and strand locations defined as in experimental structures. Standard deviations are also provided.

FIGURE 14.

Average backbone RMSDs from experimental structure for loop regions (length given by values on x-axis) of all CASP targets. Loop locations defined as in experimental structures. Standard deviations are also provided.

As Fig. 13 shows, the average RMSDs between predicted and experimental structures are essentially invariant with respect to the length of the helical segment. That is, although small helices have somewhat smaller RMSDs, even relatively large helices, in excess of 20 residues, also tend to have equally small RMSDs. This reflects the fact that when the location of a helical region is predicted correctly, the three-dimensional structure that emerges matches well with the actual experimental structure. In certain cases, the RMSD may be inordinately large, but this is due to the incorrect specification of that helical region. An illustration of this case is the incorrect prediction of one particular helical region of six amino acids in length, which resulted in the large standard deviation for this group of helices. In general, however, helices are predicted with deviations <2–2.5 Å, regardless of the length of the helix. The three-dimensional structures of β-strand regions tend to be predicted equally well. As shown in Fig. 13, strands of any length are predicted to within 2–2.5 Å RMSDs from the corresponding experimental structures.

The situation is not quite as impressive when considering the predictions for loop regions. The average RMSDs for small loops are quite good, as given in Fig. 14, although there is a decline in the accuracy of the predictions as loop length increases. In particular, it is not uncommon for loops longer than eight residues to have RMSD values in excess of 3 Å. This is important because the loop predictions are expected to become more difficult as loop lengths increase further. It should be noted that for these ab initio predictions, the loop prediction problem is compounded further because the locations of the stem regions are not specified, as is the case for the comparative modeling and template-based approaches. In this regard, these predictions are quite competitive given the additional flexibility of the loop stem regions. Nevertheless, it is expected that improvements in the prediction of loop regions can contribute significantly to further advancements in treating the protein structure prediction problem.

A more complete view on the accuracy of the three-dimensional predictions is given in Fig. 15. These graphs plot all-backbone atom RMSDs between the predicted and experimental structures for all CASP targets in the test set. In particular, the curves traces the best RMSDs for a continuous fragment of the sequence (sequence-dependent), which is plotted versus the fraction of the sequence for that particular fragment (exhibiting the best RMSD). A crucial observation is that for all CASP sequences, the ASTRO-FOLD predictions identify a fragment of no less than 50% of the entire sequence that does not deviate from the experimental structure by >9 Å. In addition, in more than half the cases, the deviation of such a fragment is within ∼6 Å of the same fragment in the experimental structure. In addition, for the vast majority of the CASP targets, the accuracy of the prediction for a fragment of >75% of the sequence matched the same part of the experimental structure to within a 12 Å deviation.

FIGURE 15.

Smallest RMSDs for longest continuous segment between predicted and experimental structures of CASP targets. The RMS values are plotted versus the fraction of the total sequence represented by the longest continuous segments providing that RMS value. The top plot is for sequences with lengths <110 amino acids, whereas the bottom plot is for the remaining longer length sequences.

To supplement these quantitative analyses, visual assessments of six CASP5 targets are shown in Figs. 16–18. These figures were constructed following full atom superpositioning of the experimental and predicted structures. For T132, the exact agreement between the antiparallel β-sheet networks becomes apparent, although the relative positioning of the α-helices is decidedly different. In addition, the α-helices in the predicted structure are less packed against the β-sheet network, an indication of the sparsity of information regarding the interplay between α- and β-structural elements. Another important observation is illustrated through visual comparison of the T137 structures. In particular, the β-sheet predictions for T137 identify a β-sheet topology similar to the experimentally observed system, with the major difference being an underprediction in the number of β-sheet contacts. However, the overall predicted structure does not exactly resemble the characteristic β-sandwich fold of the experimental structure, although significant portions of the overall structure produce relatively low RMSD values. As the structural plot indicates, these discrepancies are most likely related to the irregularity of the hydrogen bonding between the β-sheets. In fact, although not a component in the current ASTRO-FOLD methodology, the refinement of structures to improve hydrogen bonding networks is an important consideration in a variety of fold prediction methodologies.

FIGURE 16.

Comparison of predicted lowest energy tertiary structure (left) and experimentally determined structure (right) for T132 and T137 (top to bottom). All images generated with the RASMOL molecular visualization package (Sayle and Milner-White, 1995).

FIGURE 18.

Comparison of predicted lowest energy tertiary structure (left) and experimentally determined structure (right) for T138 and T160 (top to bottom). All images generated with the RASMOL molecular visualization package (Sayle and Milner-White, 1995).

Fig. 17 illustrates the predicted and experimental structures for two CASP targets classified as “new-fold” systems. Both systems are relatively small, and the experimental structures contain only helical segments. For target T170, the predicted structure is identified as having a small β-hairpin supersecondary structure. Although the antiparallel packing of this part of the sequence is satisfactory, the overall helix packing is not captured. In the case of T139, the ASTRO-FOLD prediction correctly identifies the majority of the helical regions. However, the packing of these helices is not predicted with high accuracy. These observations highlight the difference between the ASTRO-FOLD approach and other ab initio approaches. That is, although most ab initio approaches perform best for small all-helical proteins, the lack of tertiary restraints for such systems actually hinders the performance of ASTRO-FOLD methodology. In contrast, the ASTRO-FOLD approach performs well when the protein contains β-structure or mixed α-β structure, systems that have typically been bottlenecks for existing ab initio approaches. For this reason, an avenue for improvement would include the ability to predict packing constraints for helices, and current research is exploring these possibilities.

FIGURE 17.

Comparison of predicted lowest energy tertiary structure (left) and experimentally determined structure (right) for T139 and T170 (top to bottom). All images generated with the RASMOL molecular visualization package (Sayle and Milner-White, 1995).

Fig. 18 depicts two systems with very good agreement between experimental and predicted structures. In the case of T138, the parallel β-sheet topology is an important element that dominates the accuracy of the predicted structure. However, as the contact map analysis indicated, a discrepancy exists between the relative placement of the first and last helices in the experimental and predicted structures. Nevertheless, the accuracy of several loop fragments in combination with the correct β-sheet network results in an extremely accurate overall structure. For T160, the visual assessment also affirms the accuracy of the predicted structure. In fact, although the β-sheet predictions excluded a potential strand-to-strand contact, the final topology of the predicted structure closely mimics the experimentally observed packing.

Since the ultimate goal of successful structure prediction is to provide experimentalists with biologically relevant structures, other assessment criteria can be envisioned. For example, the predicted structures could be used to assess the functionality of the targets using a structural comparison to an available structural database. Although these criteria were not considered as part of the exclusively ab initio prediction (without databases) using ASTRO-FOLD, a postanalysis can be easily implemented to evaluate the quality of the predicted structures. In fact, a variety of methods exist for the structure-to-structure alignment of proteins (Holm and Park, 2000; Holm and Sander, 1996; Russell and Barton, 1992). The underlying premise is that structural matches between a predicted structure and a structure in the database may indicate the functional equivalence of the two systems. This analysis was completed for two systems, namely T138 and T160, using the DALI method for structure comparison (Holm and Sander, 1993). In the case of T160, the highest confidence match belonged to the major sperm protein (1msp-A), which possesses an overall length of 124 residues. Using a PSI-BLAST search, the 1msp-A also provided the highest ranked match for T160, which is indicative of its classification as a comparative modeling target for the purposes of CASP5 assessment. On the other hand, T138 was classified as a homologous fold recognition target by CASP5 evaluators. The predicted structure for T138 was accurate enough to provide a wide variety of structural matches, with the highest rank coming from 2dhq-A, a 3-dehydroquinate dehydratase protein. As with T160, the overall lengths of this system (136 amino acids) and the target sequence (135 amino acids) are almost identical. In addition, a fold recognition search using GenTHREADER (Jones, 1999a) identified 2dhq-A among the top matches for this system. Although this analysis relies on the use of database information for functional annotation, the underlying predictions are based on a pure ab initio structure prediction methodology. That is, although database approaches could be used to provide the same information, these results indicate that purely ab initio predictions can perform comparably. Of course, functional annotation of “new-fold” targets may not be possible, but these findings are significant because ab initio functional annotation is possible without the additional requirement of initially finding the correct database match. These results highlight the promise of ASTRO-FOLD as a method to unambiguously and generically address the structure prediction problem.

CONCLUSIONS

In the postgenomic era, the revolution in bioinformatics deals with the problem of structural genomics. To tackle this problem a variety of approaches have been developed to predict the three-dimensional structure of a protein given its amino-acid sequence. A basic premise for most methods is that they rely on the content of sequence and structural databases to guide the structure prediction for the target sequences. However, as the results from the CASP experiments indicate, the generic structure prediction problem has not yet been solved.

The development of a true ab initio methodology that can accurately predict protein structures holds the key to success in the field of generic structure prediction. We work toward this goal by presenting ASTRO-FOLD, a method true to the tenets of ab initio structure prediction. The approach is based on novel methods for modeling protein systems by combining concepts from two competing views regarding the folding of proteins. One component involves the modeling of local interactions and free energy calculations to predict regions of strong helix nucleation. The second component relies on the modeling of long-range hydrophobic forces and the principles of combinatorial optimization to predict the β-sheet and disulfide bridge topology for a protein structure. Finally, these results are combined in a hierarchical way to formulate a constrained global optimization problem that is solved via a combination of deterministic and stochastic algorithms to predict the final tertiary structure.

Both the validation and blind prediction results highlight the merits of the ASTRO-FOLD approach. In addition to accurately predicting the location of secondary structure elements as assessed via SOV evaluations, the approach provides specific information regarding the β-sheet topology of the protein. These results are extremely powerful, and form the basis for the overall accuracy of the final three-dimensional structure predictions. The assessments of the results through contact maps, LCS (RMSDs), and visual observations emphasize these successes as well as indicate avenues for potential improvement. Additional analysis also suggests that these ab initio predicted structures are accurate enough to link structure to function, which has important implications for genome-wide functional annotation (Brenner and Levitt, 2000; Baker and Sali, 2001).