Robust Biased Brownian Dynamics for Rate Constant Calculation

Abstract

A reaction probability is required to calculate the rate constant of a diffusion-dominated reaction. Due to the complicated geometry and potentially high dimension of the reaction probability problem, it is usually solved by a Brownian dynamics simulation, also known as a random walk or path integral method, instead of solving the equivalent partial differential equation by a discretization method. Building on earlier work, this article completes the development of a robust importance sampling algorithm for Brownian dynamics—i.e., biased Brownian dynamics with weight control—to overcome the high energy and entropy barriers in biomolecular association reactions. The biased Brownian dynamics steers sampling by a bias force, and the weight control algorithm controls sampling by a target weight. This algorithm is optimal if the bias force and the target weight are constructed from the solution of the reaction probability problem. In reality, an approximate reaction probability has to be used to construct the bias force and the target weight. Thus, the performance of the algorithm depends on the quality of the approximation. Given here is a method to calculate a good approximation, which is based on the selection of a reaction coordinate and the variational formulation of the reaction probability problem. The numerically approximated reaction probability is shown by computer experiments to give a factor-of-two speedup over the use of a purely heuristic approximation. Also, the fully developed method is compared to unbiased Brownian dynamics. The tests for human superoxide dismutase, Escherichia coli superoxide dismutase, and antisweetener antibody NC6.8, show speedups of 17, 35, and 39, respectively. The test for reactions between two model proteins with orientations shows speedups of 2578 for one set of configurations and 3341 for another set of configurations.

INTRODUCTION

This article considers an elliptic partial differential equation for reaction probability in high dimensions and constructs path integral, or random walk, methods for solving it. The methods are oriented toward the calculation of rate constants for diffusion-limited reactions. The challenge of the random walk method is variance reduction. An importance sampling method for random walk methods, biased Brownian dynamics, is proposed in an earlier article (Zou et al., 2000). That method makes use of weighted averages, but unfortunately the possibility of large weights sometimes cancels the benefit of importance sampling. To avoid this problem, a method of weight control has been developed (Zou, 2002) and submitted to SIAM J. Sci. Comput. for publication (G. Zou and R. D. Skeel, “Robust Variance Reduction for Random Walk Methods,” http://bionum.cs.uiuc.edu/p.html). The main contribution of this present work is to give an effective and systematic technique to approximate the reaction probability, from which the bias force in biased Brownian dynamics and the target weight in weight control are constructed. We demonstrate the effectiveness of the algorithm with four numerical tests.

The application considered here is the rate constant computation for diffusion-limited reactions, for which the encounter of the reactants is the time-limiting stage of the reaction. Biochemical reactions such as enzyme-substrate and antibody-antigen association fit well in this category. Brownian dynamics (BD) simulation is widely used in this area (Antosiewicz et al., 1995; Brune and Kim, 1994; Getzoff et al., 1992; Guddat et al., 1994; Kozack et al., 1995; Northrup et al., 1993; Wade et al., 1994). Northrup, Allison, and McCammon (NAM) developed a method for rate constant calculation for diffusion-limited reactions in 1984. The NAM method connects the reaction rate with a reaction probability, which is the solution of the Smoluchowski equation, an elliptic partial differential equation (PDE), in a finite domain (Zhou, 1990). Solving the PDE by a discretization method is difficult due to the possible high dimension and the complicated geometry of configuration space. Instead, the random walk method is used, which involves the calculation of the expectation of an exit value for a stochastic differential equation (SDE). A BD simulation code for biomolecules, University of Houston Brownian Dynamics (UHBD), that calculates biomolecular rates of association with the NAM method, is distributed by McCammon and co-workers (Davis et al., 1991). Our rate constant computation is based mainly on the NAM method and UHBD.

Standard BD samples only a few reacted trajectories, especially for problems with high dimensions or with high energy barriers. Thus it gives a large variance for the random exit value. To reduce the variance, an enhanced sampling method—weighted ensemble Brownian dynamics (WEBD)—was developed by Huber and Kim (1996). WEBD maintains an ensemble of particles (in configuration space) and associates a probability weight with each particle. All particles carry out Brownian motion without influencing each other. Periodically, WEBD splits and merges particles according to their position and weight. This procedure enables better sampling in regions inaccessible to standard BD. Thus, particles are sampled more frequently near reaction regions and the variance is reduced. WEBD was originally proposed for use with the flux-over-population method (Hänggi et al., 1990, p. 258), but it has also been combined with the NAM method (Rojnuckarin et al., 2000).

However, WEBD is a fairly complicated algorithm, and biased BD (Zou et al., 2000) is offered as a simpler, and delightfully parallel, alternative. Biased BD does importance sampling by 1), introducing a bias force in addition to the existing force; and 2), associating a weight with the particle. The expectation of the weighted exit value—the product of the exit value and the weight at the exit time—gives an unbiased estimate of the reaction probability of standard BD. The variance of the weighted exit value is related to the bias force. It turns out there is an optimal bias force that makes the variance of the weighted exit value 0, but in practice a rough approximation must be used.

One difficulty that biased BD faces is that the particle weight can grow without bound due to the imperfect choice of the bias force and the approximation in the numerical integration. The large weight fluctuations result in a large variance of the weighted exit value. Under the optimal bias force, the particle has an ideal weight, which is not trajectory-dependent, but a function only of the current configuration. This is the basis of a weight control algorithm (Zou, 2002), which uses a target weight and a tolerance range to force the particle weight into a range. The weight control algorithm operates as follows. At the beginning of each time step, the particle weight is checked. If the weight exceeds the upper limit, the particle splits into two, each with one-half the weight, and they are simulated independently. The final result is the sum of the two weighted exit values. Conversely, if the weight falls below the lower limit, the weight is doubled with 50% probability and zeroed out (and the trajectory abandoned) otherwise. Thus, the expectation of the exit value is unchanged.

In practice, an approximate reaction probability function is used to construct the bias force and the target weight. Hence, the quality of the approximation determines the performance of the algorithm. Given in the section “Construction of bias force” of this article is a method to calculate a good approximation, based on the selection of a reaction coordinate and the variational formulation of the reaction probability problem.

The benefit of using a partly numerical rather than a purely heuristic estimate of reaction probability is investigated for a model of Escherichia coli superoxide dismutase (SOD) 1eso. The speedup is 1.8 without weight control and 2.0 with it. Also, the fully developed method is compared to unbiased Brownian dynamics for this and two other systems. A Homo sapiens SOD 1spd test shows a speedup of 17, the SOD 1eso test shows a speedup of 35, and an antisweetener antibody NC6.8 test shows a speedup of 39.

Results are also obtained for a more difficult test problem of a reaction between two model proteins with orientations. The speedup due to a partly numerical estimate of reaction probability is 2.3 without weight control and 1.3 with it. The speedup for the fully developed method over unbiased Brownian dynamics is a factor of 2578 for one set of configurations and a factor of 3341 for another set.

Discussion

The partly numerical estimate of the reaction probability gives a worthwhile speedup and may serve as a safeguard against a poor heuristic estimate. The overall method is shown by numerical experiments to be a great success and as fast as WEBD. The relative simplicity of biased BD makes implementation easier and facilitates analysis and improvement of the method. In any case, these dramatic reductions in the cost of calculating rate constants make it practical to employ more detailed models of the biomolecular system and thus to close the gap between experiment and computation.

RATE CONSTANTS OF DIFFUSION-LIMITED REACTIONS

Equations of motion

Consider two types of molecules, enzyme and substrate, diffusing in solvent. Assume dilute concentrations, and, therefore, consider the movement between a pair of molecules. Model the enzyme by a set of atoms that moves like a rigid body, and neglect its rotational movement. Each atom has a partial charge and van der Waals parameter. Model the substrate by a set of spherical subunits with partial charges and van der Waals parameters and with subunits connected by constraints or bonded forces. Neglect the rotational movement of each subunit. Electrostatic and excluded volume forces act between subunits of the substrate, and between the substrate and the enzyme.

Let r₁, r₂, …, and r_N be the coordinates of the subunits of the substrate relative to the geometry center of all atoms of the enzyme. These coordinates describe a configuration of the system, represented by a column vector R of dimension 3N. Specify a set of reacted configurations Ω_rc such that if the particle diffuses to the reaction surface ∂Ω_rc, a reaction happens and motion terminates. Assume, as in UHBD, that reaction happens if, and only if, a certain number of distance criteria are satisfied, say, m out of n distances are less than a distance ξ_rc.

Define a potential energy function U(R) and a 3N × 3N symmetric positive definite diffusion tensor D(R). The movement of the substrate relative to the enzyme is described by a stochastic differential equation

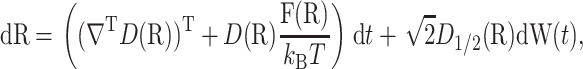(1)

where D_1/2 satisfies D_1/2D_1/2^T = D, ∇ is the column vector of 3N partial derivative operators, F(R) = −∇U(R) are the forces, W(t) is a 3N-dimensional canonical Wiener process, k_B is the Boltzmann constant, and T is the temperature. A canonical Wiener process W(t) has a Gaussian distribution with mean zero and covariance EW_i(s)W_j(t) = min {s, t}δ_ij. A typical choice for the tensor D(R) is the Rotne-Prager tensor, whose diagonal blocks are

(2)

and whose off-diagonal blocks are

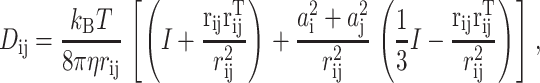(3)

where η is the viscosity of the solvent, a_i is the radius of the i^th subunit, a_mol is the radius of the enzyme, and I is the 3 × 3 identity matrix.

Rate constant calculation

Select a center r_c for the substrate. In UHBD, r_c is the geometry center of all subunits. The rate constant k is approximated by the formula (Northrup et al., 1984)

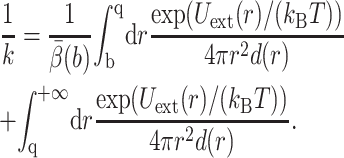(4)

where b < q are two values for |r_c|, d(|r_c|) is the diffusion coefficient of the center r_c, and 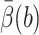is defined shortly. Assume that the 3N-dimensional set defined by |r_c| ≤ b contains Ω_rc, and let Ω_q be the 3N-dimensional set defined by |r_c| ≤ q. For a high-dimensional problem, UHBD computes d(|r_c|) during the BD simulation by collecting the mobility information of the center r_c. The term U_ext(|r_c|) is usually computed by treating the enzyme as a Debye-Hückel sphere with its net charge at the center and treating the substrate as a point charge.

The value 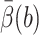is defined in terms of a reaction probability β(R), which satisfies the PDE and boundary condition (Zhou, 1990),

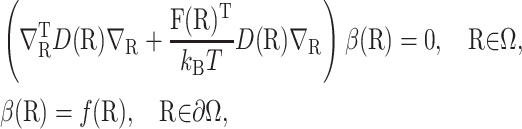(5)

where ∇_R acts on all that follows it, the domain Ω = Ω_q\Ω_rc, and the function f(R) is defined to be 0 on the escape surface ∂Ω_q and 1 on the reaction surface ∂Ω_rc.

In terms of SDEs, the reaction probability β(R) is (see Appendix) the path integral

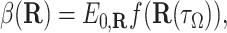where R(t) is a trajectory of the Brownian particle governed by Eq. 1 with initial condition R(0) = R, τ_Ω is the first exit time from domain Ω, and E_0,R is the expectation with respect to the probability law for the random trajectory R(t) starting at R(0) = R.

The average reaction probability on the b-surface for high-dimensional problems is taken as the average of β(R) with respect to some distribution p_b(R) on the b-surface, in which the center r_c is uniformly distributed on the |r_c| = b spherical surface and conformations are Boltzmann-distributed.

In practice, Eq. 1 is approximated by the scheme

(6)

where Δt is the time step and Zⁿ⁺¹ is a vector of 3N independent standard Gaussian random numbers (of mean 0 and variance 1).

BIASED BROWNIAN DYNAMICS WITH WEIGHT CONTROL

The expectation of f(R(τ_Ω)) can be estimated with smaller relative statistical error if reactions are more numerous. This motivates the addition of a bias force F_b(R):

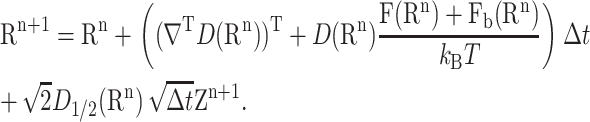(7)

The bias thus introduced is compensated for perfectly if the exit value is multiplied by the appropriate weight: the weight associated with Rⁿ is expressed as exp uⁿ where u⁰ = 0 and

(8)

In the continuum limit Δt → 0, E_0,R exp u(τ_Ω)f(R(τ_Ω)) = β(R), where u(t) satisfies the Δt → 0 limit of Eq. 8 (Milstein, 1988).

The purpose of the bias force is to reduce the variance of the estimate. Remarkably, in the continuum limit Δt → 0, there is an optimal bias force,

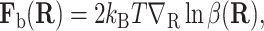(9)

that reduces the variance to zero (Milstein, 1988). In practice, the bias force is constructed from an estimate of β(R).

In the continuum limit Δt → 0, the use of the optimal bias force produces an ideal weight

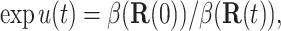(10)

that does not depend on the history of the trajectory. An estimate 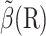of β(R) can be used to define a target weight and an acceptable range of weights, and this can be used to control the weight as described in the Introduction. The numerical tests reported here use the range u^*(Rⁿ) − 2 ≤ uⁿ ≤ u^*(Rⁿ) + 1.

The actual calculation is that of an average 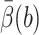on the b-surface, not that of a value β(R⁰) at a single point. A better target weight is given by

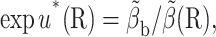(11)

where 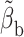approximates

CONSTRUCTION OF BIAS FORCE

Biased BD with weight control requires a bias force and a target weight, which can be constructed from an approximate solution 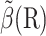using Eqs. 9 and 10. In particular, the bias force is

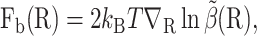(12)

which is computed by one-sided finite differences applied to

The method proposed here for computing 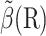uses a reaction coordinate ξ = ξ(R) that is easy to evaluate for every configuration R and that correlates well with β, in particular, 1), there is a value ξ_rc for which the set of configurations with ξ(R) < ξ_rc is exactly Ω_rc; and 2), there is a value ξ_q for which the set of configurations with ξ(R) ≤ ξ_q encloses Ω_q and equals Ω_q approximately. See Fig. 1 for an illustration. The reaction probability β(R) is approximated by where is to be determined.

FIGURE 1.

Reaction coordinate.

The choice of reaction coordinate is discussed first. Then a two-point boundary value problem is obtained for 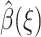by minimizing a functional. Finally, a Monte Carlo method is described for computing a density function ρ(ξ), which is required to compute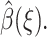

A single reaction coordinate ξ = ξ(R) is theoretically sufficient for representing β(R). The closer the constant ξ hyper-surfaces are to the constant β hyper-surfaces, the better is the choice of reaction coordinate. The reaction coordinate should attempt to measure closeness to reaction in the same way that β does, particularly near the binding site, which is most important for sampling. That is also why ξ(R) = ξ_rc is required to be the exact boundary of Ω_rc.

As stated earlier, the reaction condition in the test problems is that m out of n distances be less than the reaction distance ξ_rc. Hence, the reaction coordinate ξ(R) is defined as the m^th smallest of n distances.

The value ξ_q is defined as the maximum of ξ(R) on the q-surface. The ξ(R) = ξ_q surface is not the same as the q-surface, but is close to it. It is enough that 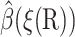satisfies the boundary condition on the q-surface only approximately, because this does not affect 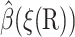much for the more interesting configurations with small reaction coordinates.

To determine 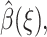we use the variational formulation of Eq. 5, namely, that β(R) minimize the functional

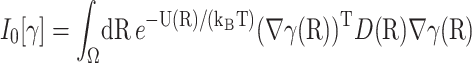for all functions γ(R) satisfying the same boundary condition as β(R), which is 0 at the q-surface ∂Ω_q, and 1 at the reaction site ∂Ω_rc. We seek a function 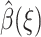that minimizes the much more restricted and slightly different functional

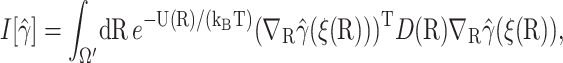(13)

subject to the boundary condition and 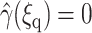where Ω′ is the set of configurations with ξ_rc ≤ ξ(R) ≤ ξ_q. Noting that 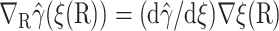and inserting into the right-hand side of Eq. 13, where δ(x) is the one-dimensional Dirac delta function, we obtain

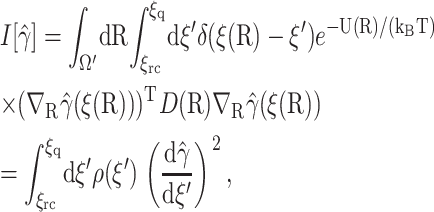(14)

where the density function is

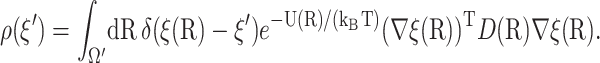(15)

To minimize the functional in Eq. 14, 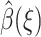must satisfy 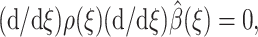with boundary condition 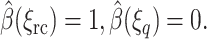The solution is

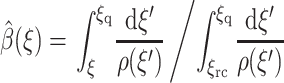(16)

To compute the density function ρ(ξ′) defined in Eq. 15 numerically, let ξ_rc = ξ₀ < … < ξ_n = ξ_q be a partition of the reaction coordinate and use the piecewise constant approximation

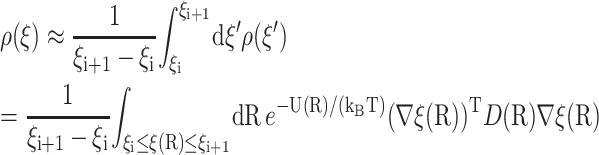(17)

for ξ_i ≤ ξ ≤ ξ_i+1. The above integral is computed using Monte Carlo trials. Note that a uniform scaling for ρ(ξ) does not affect the solution 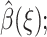only the relative magnitude for different ξ matters. Uniformly distributed random configurations R are generated, and for every such configuration, the reaction coordinate ξ(R) and the integrand in Eq. 17 are evaluated. A sum of integrand values is accumulated for each range of reaction coordinates. A rough piecewise constant function ρ(ξ) is obtained through millions of such Monte Carlo trials and is stored as a set of (ln ξ, ln ρ(ξ)) pairs.

A single Monte Carlo simulation usually does not give enough samples in the region with small ξ-values because of its small volume. Therefore, in practice, several Monte Carlo simulations with nested ranges are performed. As shown in the figures for the test problems, each Monte Carlo simulation gives a set of (ln ξ, ln ρ(ξ)) pairs that is “good” in a certain range of ξ. The sets of (ln ξ, ln ρ(ξ)) pairs from different Monte Carlo simulations are aligned to each other to form a merged density that is defined in the full range [ξ_rc, ξ_q], which is further smoothed to obtain a smoothed density.

The smoothing for (ln ξ, ln ρ(ξ)) is done by least-squares fitting ln ρ(ξ) to piecewise linear functions of ln ξ to obtain a set of (ln ξ, ln ρ(ξ), d ln ρ(ξ)/d ln ξ) triples, which are then used with Hermite interpolation to obtain a smoothed function. The reason to use linear functions to fit (ln ξ, ln ρ(ξ)) is that there is an approximate power relation between ξ and ρ(ξ), i.e., ρ(ξ) ∝ ξ^α, for small and for large ξ.

Alignment of two sets of (ln ξ, ln ρ(ξ)) pairs is done by computing an offset between the two sets of data. An offset is computed as the following: select a range of ξ such that both sets are “good” in this range. Smooth both sets in the range. The average difference between the smoothed data in this range is then used as the offset.

RATE CONSTANTS FOR SOD AND NC6.8

Implementation details and cost measurement

The simulations reported here are performed by a C program written by the first author, which uses methods from UHBD. Bonded forces are implemented as constraints and excluded volume forces as hard sphere bumping. The hard spheres representing the enzyme have radii equal to their van der Waals radii. When an integration step results in penetration, one simply retries the step with another random vector. Intermolecular electrostatic forces use a test charge approximation, where the force on the subunit is the product of its charge and the gradient of an electrostatic potential for the enzyme only. The potential for the enzyme's point charges in surrounding ionized solvent is modeled by the Poisson-Boltzmann equation and precomputed by UHBD on a three-dimensional grid.

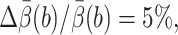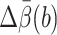The computational cost is measured by t_method, the CPU hours needed to make the relative error where is the 95% confidence interval of the estimate Let N′_trials be the required number of trajectories to make 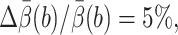t_step be the CPU seconds per integration step of the SDE, 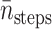be the average number of integration steps per trajectory, 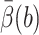be our best estimate of the average reaction probability on the b-surface (obtained as a weighted average of the available estimates with weights proportional to the reciprocals of the variances), and VarB be the estimated variance of the exit value B = exp u(τ_Ω)f(R(τ_Ω)) whose expectation Then

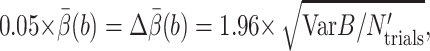so

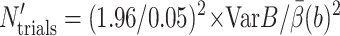(for standard BD, is used instead of VarB), and

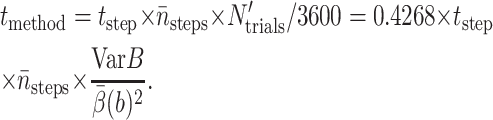(18)

To get t_method for a 10% relative error, one simply divides it by 4. All tests in this and the next section were run on Linux clusters of dual-processor Pentium III 1-GHz machines.

The relative error for is a good measure of the relative error of the rate constant k, because the second term on the right-hand side of Eq. 4 is usually much smaller than the first.

SOD tests

The enzyme CuZn SOD converts toxic O₂⁻ ions to oxygen and hydrogen peroxide. SOD is extremely reactive with a rate constant close to that obtained in the diffusion limit. SOD has been extensively studied by BD simulations (e.g., Sines et al., 1990; Getzoff et al., 1992). The experimental rate constant of SOD of bovine Bos taurus and shark Prionace glauca is reported to be 3.92 × 10⁹ M⁻¹s⁻¹ (Polticelli et al., 1994) compared to a calculated value of 5 × 10⁹ M⁻¹s⁻¹ (Rojnuckarin et al., 2000). Two types of SOD are examined here, H. sapiens SOD 1spd and E. coli SOD 1eso. The computed rate constant of SOD 1spd is ∼1.4 × 10⁹ M⁻¹s⁻¹. The computed rate constant of SOD 1eso is one order of magnitude less.

Coordinate data for SOD are taken from the Protein Data Bank (http://www.rcsb.org/pdb) and the partial charge and van der Waals parameter tables are taken from the standard CHARMM force field (Brooks et al., 1983) incorporated into UHBD. The substrate O₂⁻ is modeled by a subunit with a hard-sphere radius 1.5 Å and a charge of −e. Reaction is said to happen when O₂⁻ is within 7 Å of the copper atom of SOD. The diffusion tensor D is diagonal as in Eq. 2 where T = 300 K, water viscosity η = 0.89 g m⁻¹s⁻¹, the O₂⁻ hydrodynamic radius a₁ = 2.05 Å, and that of SOD is a_mol = 25 Å. The simulations use b = 80 Å and q = 400 Å.

Fig. 2 shows the Monte Carlo simulation results for ρ(ξ) for SOD 1spd. In the figure, each of the three original densities is valid for a certain range of ξ-values. They are aligned to each other by shifting vertically to form a merged density that is valid in the full range. This merged density is then smoothed to form a smoothed density in the full range by the process given in the preceding section.

FIGURE 2.

Monte Carlo simulations for SOD 1spd give three original densities for differing ξ-ranges. These are merged and smoothed to determine ρ(ξ).

The 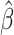function is computed from the smoothed ρ(ξ) with Eq. 16. The bias potential as a function of reaction coordinate ξ is shown in Fig. 3. The turning point of the curve is at ∼ξ = 20 Å where U_b(ξ) = 5k_BT. The magnitude of the bias potential indicates the strength of the free energy barrier needed to be overcome for the substrate to get to the reaction site of the enzyme. Compared to results for the tests that follow, the value 5k_BT is relatively low. The corresponding reaction probability and rate constant are also large compared to those in other tests. Near ξ = ξ_q, the bias potential prevents the particle from reaching the ξ = ξ_q surface.

FIGURE 3.

The bias potential for SPD 1spd with escape distance q = 400 Å.

Table 1 shows the rate constants of SOD 1spd and computing costs for biased BD and standard BD. In addition to the quantities defined earlier, the tabulated value N_trials is the actual number of trajectories, EB_est is the estimate produced for 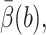and CPU is the actual CPU time. The CPU cost per integration step of biased BD is 2.7× that of the standard BD. The number of integration steps per trajectory of biased BD is 43% of that of the standard BD due to the weight control algorithm. The variance of biased BD is only 5% of that of the standard BD. The overall speedup of biased BD relative to standard BD is 17. It is interesting to compare this speedup with the sevenfold speedup obtained for biased BD without weight control several years ago (Zou et al., 2000).

TABLE 1.

Results for unbiased and full-featured biased Brownian dynamics

	Unbiased BD			Biased BD
System	SOD 1spd	SOD 1eso	NC6.8	SOD 1spd	NC6.8
tstep(s)	2.55 × 10−6	2.58 × 10−6	7.86 × 10−6	6.83 × 10−6	1.65 × 10−5
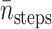	1.94 × 105	1.96 × 105	1.29 × 105	8.32 × 104	7.58 × 104
Ntrials	200,000	200,000	160,000	200,000	80,000
CPU(h)	27.5	28.2	45.1	31.6	27.8
EBest	1.49 × 10−2	1.73 × 10−3	6.50 × 10−4	1.45 × 10−2	6.82 × 10−4
VarB	1.47 × 10−2	1.73 × 10−3	6.50 × 10−4	7.21 × 10−4	1.40 × 10−5
k(M−1s−1)	1.46 × 109	1.71 × 108	5.85 × 107	1.42 × 109	6.13 × 107
Δk(M−1s−1)	5.19 × 107	1.79 × 107	1.12 × 107	1.15 × 107	2.33 × 106
tmethod(h)	14.4	123.3	635.5	0.8	16.1

E. coli SOD 1eso has a lower attractive force to steer the O₂⁻ ions to its binding site, which results in a higher energy barrier for association and a lower rate constant. Its bias potential has a graph that is qualitatively similar to that in Fig. 3. The turning point of the curve is at ∼ξ = 20 Å where U_b(ξ) = 7k_BT. This is larger than that of SOD 1spd and the rate constant is smaller as a result. The effect of using partly numerical instead of heuristic estimates of the reaction probability is shown for SOD 1eso in Table 2. The heuristic choice is 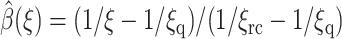where ξ_rc = 7 Å and ξ_q = 405.26545 Å (Zou, 2002). The best result in this table is 35× that of unbiased BD given in Table 1.

TABLE 2.

Results for SOD 1eso with heuristic and partly numerical estimates of reaction probability

	Heuristic		Partly numerical
wt ctl?	No	Yes	No	Yes
tstep(s)	5.50 × 10−6	6.91 × 10−6	5.59 × 10−6	6.83 × 10−6
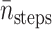	6.14 × 105	1.01 × 105	1.57 × 105	8.78 × 104
Ntrials	200,000	200,000	200,000	200,000
CPU(h)	187.8	38.9	48.7	33.3
EB	1.74 × 10−3	1.74 × 10−3	1.74 × 10−3	1.75 × 10−3
VarB	6.86 × 10−5	7.20 × 10−5	1.46 × 10−4	4.16 × 10−5
k(M−1s−1)	1.71 × 108	1.71 × 108	1.72 × 108	1.72 × 108
Δk(M−1s−1)	3.57 × 106	3.66 × 106	5.21 × 106	2.78 × 106
tmethod(h)	32.9	7.1	18.0	3.5

NC6.8 test

This section considers the antibody-antigen binding reaction between the antisweetener antibody NC6.8 (Protein Data Bank entry 2cgr) and the sweet-tasting ligand n-(p-cyanophenyl)-n′-(diphenylmethyl)-guanidinium acetic acid, formula C₂₃H₂₀N₄O₂). The antibody is the enzyme and the ligand is the substrate. The NC6.8 binding reaction was previously studied for the WEBD (Rojnuckarin et al., 2000). Here we follow the same setup and test for biased BD.

The NC6.8 antibody and the sweet-tasting ligand structure files are from the Protein Data Bank. In the simulation, only the Fv fragment of NC6.8 is used. The setup is similar to that of SOD except the following: the sweet-tasting ligand is modeled as a two-subunit dumbbell with a distance constraint of 4.374 Å between subunit centers. The negative subunit, centered at the carbonyl carbon (C19), has a radius of 1.5 Å and a charge of −e. The positive subunit, centered at the most cationic guanidinium nitrogen (N16), has a radius of 2.0 Å and a charge of +e. The reaction condition is that the positive subunit is within 5.0 Å of Glu H:162 OE2 (H:50), and the negative subunit is within 5.0 Å of Arg H:169 NH1 (H:57). The diffusion tensor D is a Rotne-Prager tensor as in Eqs. 2 and 3 where the hydrodynamic radius of the positive subunit a₁ = 2.0 Å, that of the negative subunit a₂ = 1.5 Å, and that of the enzyme a_mol = 25 Å. The values b = 80 Å and q = 300 Å are used.

The bias potential U_b(ξ) for NC6.8 is again qualitatively similar to that in Fig. 3. The turning point of the curve is at ∼ξ = 20 Å where U_b(ξ) = 8k_BT, which is larger than for both SOD tests and results in a smaller rate constant. Table 1 shows a 39× speedup of biased BD over standard BD for the NC6.8 test. A speedup of 8 is obtained from the WEBD/NAM method of Rojnuckarin et al. (2000).

ARTIFICIAL TEST PROBLEM

Problem description

The model problem described here is proposed in a 1992 article by Northrup and Erickson. It is later used by Huber and Kim in 1996 to show the speedup of the WEBD algorithm. Although this problem is outside the class of problems defined previously, the modification is straightforward.

In solvent are two types of proteins, each modeled as a sphere of radius 18 Å. For the purpose of defining a reaction condition, imagine that 17 Å × 17 Å squares are attached at their centers tangentially to each sphere as shown in Fig. 4. The set of reacted configurations Ω_rc consists of those configurations with a position and orientation such that at least three of the four vertex pairs, A₁A₂, B₁B₂, C₁C₂, and D₁D₂, between the two squares, are within 2 Å.

FIGURE 4.

Model protein diagram.

For i = 1, 2, let r_i be the center of protein i, Q_i be an orthogonal matrix describing the orientation of protein i, and a_i = 18 Å be the radius of protein i. Although the orthogonal matrix Q_i contains nine entries, it has only 3 degrees of freedom because of the constraints Q_i^TQ_i = I. Any point fixed in the body frame of protein i can be converted to lab frame coordinates with r_lab = Q_ir_body + r_i.

The tangent space for the three-dimensional manifold Q_i^TQ_i = I at a particular point Q_i has as a basis 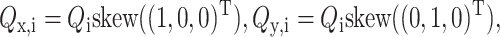and 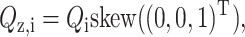where skew is the mapping

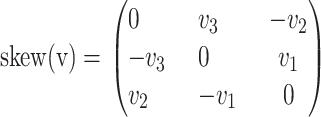from a vector to a skew matrix. The basis is orthogonal with respect to the double-dot inner product (A:C = tr(A^TC)) for matrices. Hence, the motion of two proteins is described by their translational and rotational diffusion in the liquid,

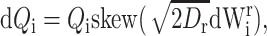(19)

for i = 1, 2, where D_t and D_r are translational and rotational diffusion coefficients given by the Stokes-Einstein relations D_t = k_BT/6πηa_i = 1.36 × 10⁻¹⁰ m² s⁻¹; D_r = k_BT/8πηa_i³ = 3.16 × 10⁷ s⁻¹ for T = 298 K; η = 0.89g m⁻¹s⁻¹; and where W₁, W₂, W₁^r, and W₂^r are independent canonical three-dimensional Wiener processes. There is no interaction between the proteins except hard sphere bumping.

Consider the relative position r_c = r₁ − r₂. We have

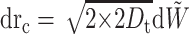(20)

where is a canonical Wiener process. The b-surface and q-surface are the set of configurations with |r_c| = b and |r_c| = q, respectively. The distribution of starting points on the b-surface is uniform for the center r_c and uniform with respect to the orientation of protein 1.

We compute the rate constant k with Eq. 4, where U_ext(r) = 0 and d(r) = 2D_t, although rigorous justification is not given here.

Numerical integration and bias force

For the r_c coordinates, there is no difference from previous sections for the numerical integration, bias force evaluation, and weight computation. However, these are all slightly different for the Q_i coordinates.

Directly applying a numerical integration method to Eq. 19 for Q_i usually does not preserve the orthogonality constraints of Q_i. To preserve the constraints, we update Q_i by multiplying it by orthogonal matrices. Let

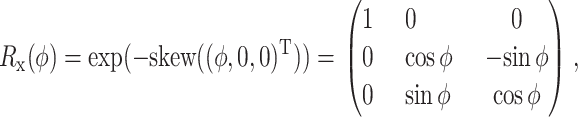in which R_x(φ) is the matrix that rotates an angle φ about the x-axis. Similarly define R_y and R_z. For a finite time step Δt, let be the Wiener increment W_i^r(t + Δt) − W_i^r(t), and let

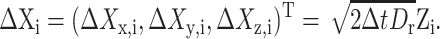Then to integrate Q_i numerically, use

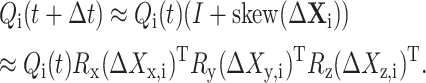Let

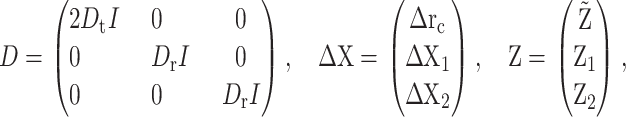where Δr_c is the increment of r_c during the time period [t, t + Δt] and 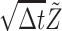is the increment of 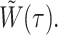The unbiased BD numerical scheme is thus

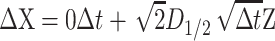where D_1/2D_1/2^T = D.

Similar to Eqs. 7 and 8 for biased BD, here we add a bias vector to the stochastic increment and associate a weight exp(u) with the system. Let 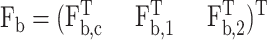where F_b,c, F_b,1, and F_b,2 are the bias forces for r_c, Q₁, and Q₂, respectively. The unbiased numerical scheme changes to the biased scheme

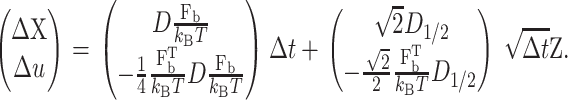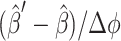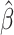The bias force F_b/(k_BT) is computed numerically from Eq. 12. For example, to compute the derivative of the approximate reaction probability in the direction of Q_x,i, use where is the approximate solution for the current configuration and 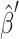is the approximate solution for the configuration obtained by replacing Q_i by Q_iR_x(Δφ)^T for some small angle Δφ.

Reaction coordinates and Monte Carlo calculation

Uniformly distributed random configurations are generated by randomly placing protein 1 at a distance r with probability density ∝ r², and rotating protein 1 with Euler angles φ, θ, ψ, where φ is the angle of self-rotation along the z-axis, θ is the angle of nutation along the x-axis, and ψ is the angle of precession along the z-axis. The positive z-axis goes through the center of the square on the protein. Angles φ and ψ are uniformly distributed in [0, 2π] and cos θ is uniformly distributed in [−1, 1].

Uniformly distributed random configurations will not give enough samples for small ξ, for example, for ξ < 10 Å. Importance sampling with restricted distance and restricted nutation are used. The distance is restricted by a small maximum distance r_max. The cosine of the nutation angle θ is restricted to a uniform distribution in [(cos θ)_min, 1], for example, (cos θ)_min = 0.8 or (cos θ)_min = 0.95. Note that restricted Monte Carlo simulation gives correct relative ρ(ξ) only for those ξ that are small enough that they cannot be generated with nutation angle satisfying cos θ < (cos θ)_min or distance r > r_max. The restricted and unrestricted Monte Carlo simulation results are aligned at some common range of values of ξ which are valid for and have enough samples from each simulation.

In Fig. 5, each original density is valid for a certain region. These are aligned by vertical shifts and then smoothed to form a density for the full range.

FIGURE 5.

Monte Carlo simulations for the two-spheres problem give five original densities for differing ranges of distance and nutation angle. These are merged and smoothed to determine ρ(ξ). This curve is compared with straight lines corresponding to ρ(ξ) ∝ ξ² and ρ(ξ) ∝ ξ⁵.

The bias potential U_b(ξ) is shown in Fig. 6. When ξ is small, the bias force needs to overcome the strong entropy barrier caused by both translational and orientational restrictions. The relative movement of the spheres is like a particle moving in six-dimensional space with the reaction site being a radii 2 Å spherical surface in six-dimensional space. When ξ gets larger, the restriction from orientation vanishes, and the movement is similar to a three-dimensional free diffusion.

FIGURE 6.

The bias potential of the two-spheres problem with escape distance q = 360 Å.

Estimated cost of standard Brownian dynamics

We did not perform extensive numerical tests with the standard BD algorithm because of the time-consuming nature of these tests and because a good theoretical estimate is possible.

Recall Eq. 18 for the cost of an algorithm: it needs CPU seconds per integration step t_step, the average number of integration steps per trajectory 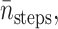VarB, and 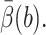The value of t_step is computed to be 4.49 × 10⁻⁶s for this test problem from computer timings. The value of 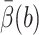is obtained from the biased BD result. Because the exit values of standard BD are either 1 or 0 depending on whether or not they react, EB² = EB and VarB = EB² − (EB)² = EB − (EB)² ≈ EB, which is obtained from the biased BD result for 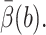Similar to the method used in Huber and Kim (1996), the average number of integration steps of one trajectory 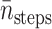is computed by

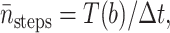where Δt = 2.38 ps is the maximum time step in the numerical integration scheme for Eq. 19, and T(r) is the mean first passage time (MFPT) for protein 1 starting at distance r away from protein 2 with exit boundary at q and reflecting boundary at a = a₁ + a₂ = 36 Å, the minimum-allowed distance between two proteins. Since the probability of reaction is so low, we neglect the possibility of exit at the reaction site. Thus, the MFPT is assumed to depend only on the distance between two proteins and not on their orientations. It can be shown (see Appendix) that T(r) satisfies the equation

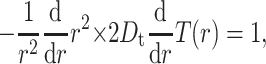with boundary conditions (d/dr)T(r)|_r=a = 0 and T(r)|_r=q = 0. The solution for the MFPT is

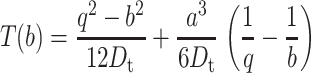Results for the model problem

The effect of using partly numerical instead of heuristic estimates of the reaction probability is shown in Table 3. For a heuristic density function we use Eq. 16 where d ln ρ(ξ)/d ln ξ = a(ξ) and a(ξ) is a step function that takes the value 5 for 2 < ξ < 30, the value 4 for 30 < ξ < 40, the value 3 for 40 < ξ < 50, and the value 2 for 50 < ξ < 600. Comparison to unbiased BD is given in Table 4. Column 5 of each table is an independent computation. The starred entries for unbiased BD denote the theoretical estimates. The per-step cost for biased BD is about twice as expensive as that of standard BD. Biased BD gains in both the average number of steps per trajectory and the variance. Overall, biased BD gives a factor of 2578 speedup with b = 45 Å and q = 360 Å and a factor of 3341 speedup with b = 80 Å and q = 360 Å.

TABLE 3.

Results for model protein with heuristic and partly numerical estimates of reaction probability

	Heuristic		Partly numerical
wt ctl?	No	Yes	No	Yes
tstep(s)	7.69 × 10−6	8.85 × 10−6	7.68 × 10−6	8.83 × 10−6
	1.94 × 105	1.48 × 105	1.37 × 105	1.33 × 105
Ntrials	200,000	200,000	200,000	200,000
CPU(h)	82.8	73.0	58.4	65.3
EB	4.95 × 10−6	8.66 × 10−6	5.48 × 10−6	8.52 × 10−6
VarB	6.41 × 10−8	4.06 × 10−9	4.92 × 10−8	3.40 × 10−9
k(M−1s−1)	1.05 × 105	1.83 × 105	1.16 × 105	1.80 × 105
Δk(M−1s−1)	2.35 × 104	5.91 × 103	2.06 × 104	5.41 × 103
tmethod(h)	1667.3	30.4	735.3	23.5

TABLE 4.

Model protein results for unbiased and full-featured biased Brownian dynamics

	Unbiased BD			Biased BD
b(Å)	45.0	80.0	45.0	80.0	140.0
q(Å)	360.0	360.0	360.0	360.0	1000.0
tstep(s)	4.49 × 10−6	4.49 × 10−6	8.73 × 10−6	8.68 × 10−6	8.59 × 10−6
	3.24 × 105*	3.15 × 105*	6.65 × 104	1.22 × 105	7.39 × 105
Ntrials			120,000	120,000	40,000
CPU(h)			19.4	35.3	70.6
EBest			1.72 × 10−5	8.56 × 10−6	5.42 × 10−6
VarB			1.67 × 10−8	3.28 × 10−9	1.33 × 10−9
k(M−1s−1)			1.82 × 105	1.81 × 105	1.81 × 105
Δk(M−1s−1)			7.74 × 103	6.85 × 103	1.20 × 104
tmethod(h)	36089.5*	70487.1*	14.0	20.2	122.5

APPENDIX: FEYNMAN-KAC FORMULA FOR ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS

Let

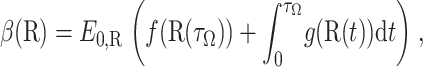(21)

where R(t) satisfies

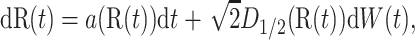with initial condition R(0) = R and where τ_Ω is the first exit time from domain Ω. The expectation β(R) is the solution of the elliptic boundary value problem

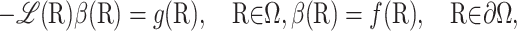(22)

with ℒ defined by

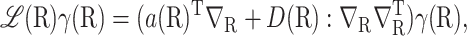where A:C means tr(A^TC) for two matrices A and C of the same dimensions, D = D_1/2D_1/2^T, and ∇_R∇_R^T operates only on γ(R).

To apply this to Eq. 5, note that ∇_R^TD(R)∇_R = (∇_R^TD(R))∇_R + D(R):∇_R∇_R^T.

To apply this to the calculation of the MFPT in last section, use Eq. 20 as the SDE, and let f ≡ 0, g ≡ 1 in Eq. 21. Then β(R) is the MFPT, and β(R) satisfies Eq. 22.