Simulations of Oligomeric Intermediates in Prion Diseases

Abstract

We extend our previous stochastic cellular automata-based model for two-dimensional (areal) aggregation of prion proteins on neuronal surfaces. The new anisotropic model allows us to simulate both strong β-sheet and weaker attachment bonds between proteins. Constraining binding directions allows us to generate aggregate structures with the hexagonal lattice symmetry found in recently observed in vitro experiments. We argue that these constraints on rules may correspond to underlying steric constraints on the aggregation process. We find that monomer-dominated growth of the areal aggregate is too slow to account for some observed doubling-time-to-incubation-time ratios inferred from data, and so consider aggregation dominated by relatively stable but noninfectious oligomeric intermediates. We compare a kinetic theory analysis of oligomeric aggregation to spatially explicit simulations of the process. We find that with suitable rules for misfolding of oligomers, possibly due to water exclusion by the surrounding aggregate, the resulting oligomeric aggregation model maps onto our previous monomer aggregation model. Therefore it can produce some of the same attractive features for the description of prion incubation time data. We propose experiments to test the oligomeric aggregation model.

INTRODUCTION

Prion diseases are a group of neurodegenerative diseases including bovine spongiform encephalopathy (BSE) in cattle, scrapie in sheep and goats, chronic wasting disease in deer and elk, and kuru and Creutzfeldt-Jakob disease (CJD) in humans. These diseases came to the forefront after BSE reached epidemic proportions in Great Britain in the early 1990s, and it was later shown that transmission of BSE to humans can lead to new variant CJD (vCJD) in humans (Bruce et al., 1997; Hill et al., 1997; Scott et al., 1999).

Prion diseases are unusual in that they appear to be caused by infection with some minimal infectious “seed” of misfolded prion protein, which alone may be able to cause disease by catalyzing further misfolding and, in many cases, aggregation of the prion protein. These aggregates are typically amyloidlike fibrils or amyloid plaques (Caughey, 2000). The infectious agent is unusually hard to eliminate by various methods including ultraviolet irradiation, suggesting it contains no nucleic acid and rather only protein, the so-called “protein-only” hypothesis in prion diseases (Weissmann et al., 2002).

In the case of CJD, a sporadic form of the diseases also exists, occurring more or less randomly worldwide with an incidence of about one in a million people per year. It has been suggested that this incidence is due to the very rare event of nucleating the minimal infectious seed by chance in a healthy individual (Come et al., 1993).

Developing an understanding of these diseases is important because, for one, they are invariably fatal. To date, no treatment exists. Additionally, it is not yet clear how large the vCJD epidemic in humans will be; an understanding of the disease process is important to be able to guide the search for treatment ideas.

In many cases, prion diseases result in large, up-to-micron-scale plaques in the brains of people and animals with these diseases. They also involve vacuolization or spongiform change in the brain due to death of neurons (Scott et al., 1996). Additionally, the normal form of the prion protein (known as PrP^C) has long been known to misfold and aggregate in vitro when catalyzed by the presence of a misfolded prion protein (PrP^Sc) seed (Come et al., 1993). Together, these observations have suggested to some that the aggregation process itself may be important in these diseases (Come et al., 1993; Masel et al., 1999). It has also been suggested that the rate-limiting step in aggregation is nucleation of an appropriate seed, thus the rapid aggregation in the seeded case described above (Come et al., 1993).

Another fact which may be important to this issue is that the prion protein is normally GPI-anchored to the cell surface. Aggregation in vitro as mentioned above is observed in solution rather than in the presence of the GPI anchor on a cell surface, leaving the possibility that the aggregation process in vivo is different.

Aggregation models developed to explore the aggregation process in prion disease include one-dimensional, fibrillar aggregation-and-fission models (Masel et al., 1999; Slepoy et al., 2001), since aggregates grown in vitro are typically seen to be fibrillar. Additionally, our earlier work suggested that an areal aggregation model could explain certain other properties of the diseases (Slepoy et al., 2001). By areal aggregation, we mean two-dimensional aggregation in a relatively regular array, probably on the cell surface due to GPI anchoring, in contrast to the one-dimensional, fibrillar aggregation observed in vitro, and also in contrast to two-dimensional plaques of crossing fibrils which can be observed in vivo. This earlier model is attractive in that it can provide a simple explanation for the long lag phase which is sometimes observed in growth of the amount of infectious material in the brain. This lag phase of little or no growth is followed by a doubling phase with a short characteristic doubling time. Additionally, our earlier model provides a possible explanation of some of the difference between infectious and sporadic forms of CJD (Slepoy et al., 2001). In later work, we used this model to explain and fit experimental dose incubation curves (Kulkarni et al., 2003).

However, there were drawbacks to the earlier aggregation model we proposed. First, no such areal aggregates had so far been observed. Second, the fissioning essential to the model would involve breaking of strong bonds between the proteins, probably bonds between β-sheets (Serag et al., 2002).

More recent experimental work found two-dimensional areal aggregates of prion protein produced during the purification process. These aggregates were examined under electron microscope and found to consist of trimeric or hexameric subunits. These subunits are linked together in a regular array, possibly by their N-terminal sugars or a weak protein-protein interaction (Wille et al., 2002).

This suggested we should modify our earlier model and attempt to reproduce this aggregate morphology. We thought of two basic schemes for growing aggregates of this sort:

1. Growing the aggregate outward, monomer by monomer, from an initial seed, or

2. Oligomeric intermediates (possibly very flexible and of unstable shape), which form on their own in solution and are only catalyzed into stably misfolding in the presence of an existing misfolded seed.

Some evidence in favor of case 2 has already been produced. Monomers of yeast prion can form intermediates if left to stand, which allows aggregation to proceed at an initial faster rate when catalyzed by addition of a seed (Serio et al., 2000). Additionally, the conformation-dependent immunoassay developed by Safar et al. (2002) detects both protease-sensitive and protease-resistant PrP^Sc. In hamster brains, sensitive PrP^Sc is observed earlier, followed by resistant PrP^Sc. This could correspond to case 2 above, where the sensitive PrP^Sc is the intermediates that are not yet stably misfolded and the resistant PrP^Sc is stably misfolded intermediates.

Work here has been done to further explore these two potential modifications of our earlier model to examine whether they retain the same features and if additional insight can be gained.

It is important to note that even if areal aggregation is not important to the time course of these diseases, the aggregates observed by Wille and co-workers have already provided insight into the structure of the misfolded prion protein (Wille et al., 2002). Theoretical modeling may be able to place further constraints on the protein or subunit structure necessary to reproduce these aggregates, and hence provide valuable information because these aggregates can form, even if they are not important to the disease progression.

BASICS OF OUR MODEL

Here we explore the two basic schemes suggested above for growing aggregates like those observed by Wille et al. (2002). To do so, we use a modification of our earlier model. Therefore a recap of common features of these models is useful.

These models are stochastic cellular automata models, meaning that they take place on a lattice with probabilistic interaction and diffusion rules governing the progression of the system. In this case, sites on the lattice are either occupied by individual prion proteins, or water (empty, in the simulation). The protein form at a site can also vary from PrP^C to PrP^Sc.

Rules vary depending on the model being explored, but the basic procedure is the same. For every simulation step, which represents a small amount of time, we allow proteins and any aggregates to diffuse a small amount on the lattice (each object has a probability 1/(size)^1/2 of moving one lattice site in a given step). Then we look at every protein in the lattice and update its state according to the rules. For example, in our original model, the conformation of an individual prion protein is determined solely by its number of neighboring prion proteins, and this can vary from step to step. After doing this, we add more normal prion monomers to replace any that converted to PrP^Sc. This is due to the assumption that this process would be taking place in a small area on a cell, and the normal prion monomers would be added by the cell or diffuse in from other locations on the cell surface to keep the monomer concentration relatively constant.

GROWTH VIA MONOMER ADDITION

First, case 1 from above was explored. Simple rules were developed (Fig. 1) which can reproduce aggregates similar to those observed by Wille et al. (2002). It is important to note that although the rules were designed to reproduce such aggregates, most modifications of these rules could not do so. This means that the rules provide some constraints on the protein-protein interactions necessary to reproduce such aggregates. Also, for the purposes of this model, we are assuming the subunits are hexameric, but the corresponding model for trimeric intermediates is actually much simpler than this model and will produce similar results. Details of the algorithm for this model are covered in Fig. 2.

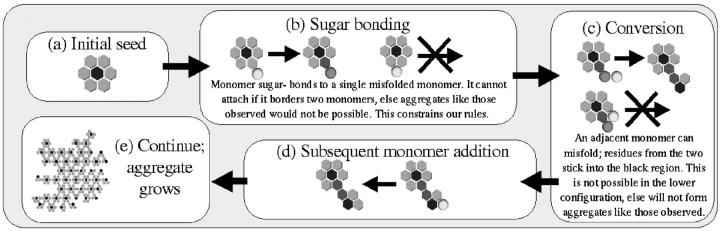
FIGURE 1.

Simple rules for monomer-by-monomer growth of aggregates like those observed. Some possible rules can be excluded, thus these rules give insight into how the proteins involved must be interacting with one another. (a) The initial seed consists of six misfolded monomers (light gray hexagons) surrounding a central region (black) which is occupied by some residues sticking into it from the adjacent six sites. (b) A healthy monomer (light gray sphere) can move adjacent to a misfolded one and attach via a sugar bond or other weak protein-protein interaction (proteins sugar-bonded are colored dark gray). This cannot happen if the monomer moves into the site between two misfolded proteins. (c) Subsequent monomers can move next to the attached one and misfold and begin to form a new hexamer. Residues from the two stick into the black region, preventing anything else from moving there. This cannot happen if the second monomer is adjacent to the existing hexamer; this would produce irregular aggregates unlike those observed by Wille and co-workers (Wille et al., 2002). (d) The forming hexamer can grow and finish via subsequent monomer addition. (e) Continue a–d for a long time, and an aggregate like the one shown can form.

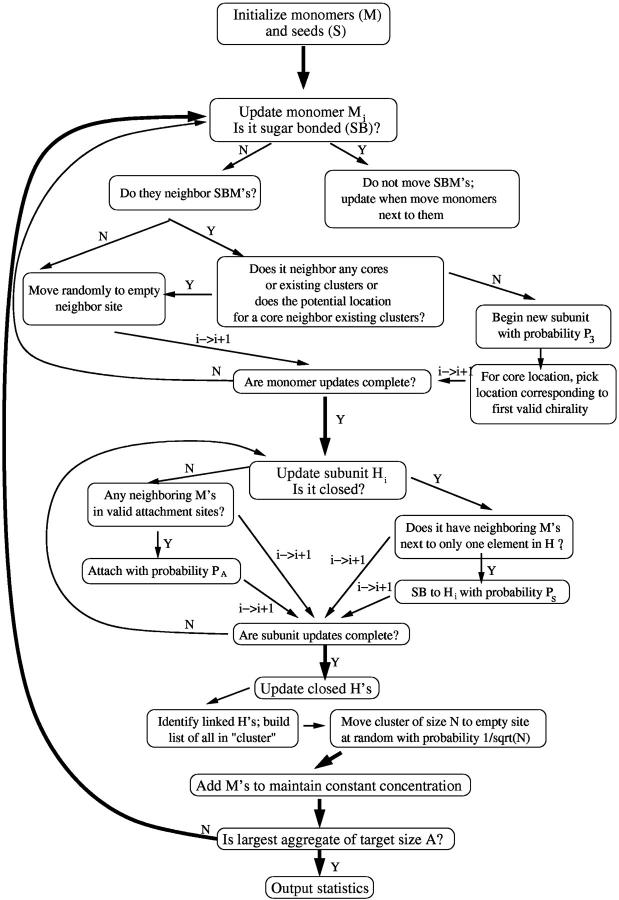
FIGURE 2.

Flow chart of simulation for monomer addition model. We typically use P₃ = 0.2; we tried a variety of different values for this and values near 0.2 seem to produce the most regular aggregates. We also typically use P_S = 0.9. This is not important and roughly sets the simulation timescale. Also, for our statistics, we typically average >1000 such runs as the one described here.

The rules are as follows. The simulation begins with a single hexagonal subunit consisting of six misfolded monomers (light gray hexagons in Fig. 1) which stick some of their residues into an adjacent site, excluding anything else from occupying that site (black). Healthy monomers (light gray spheres) can then attach via a sugar-bond or other weak protein-protein interaction to this subunit (dark gray spheres to dark gray hexagons) but only radially outward from a monomer in the initial hexamer. Additional monomers moving adjacent to the attached monomer can, together with it, misfold but only if the second monomer does not also neighbor the original hexamer. Then additional monomers can attach to this forming hexamer, allowing it to complete. Repeating this process many times can produce mostly regular aggregates with some holes, similar to those observed.

The rules are also probabilistic: above, “can” means that some fraction of the time the event occurs. These probabilities can be changed in the simulation and give different growth rates, but the same essential features and scaling as described below.

If this is in fact how these aggregates are forming, we find out about the orientation of monomers within a hexagonal subunit. We find, as mentioned in the discussion of the rules above, that the N-terminal sugars or attachment sites must stick radially outward from each monomer in a hexagonal subunit (Fig. 1 b). This is in agreement with the hexagonal structure proposed by Wille and co-workers (Wille et al., 2002). Additionally, we find that no such regular aggregates can be produced unless the monomer attaching to a previously attached monomer (Fig. 1 c) can only attach if it is not adjacent to an existing hexamer. This seems to indicate that the other spaces must be occupied by residues from the existing hexamer, preventing attachment in those sites.

This model can also reproduce gaps in aggregates as observed. In this model gaps are due to variations of the growth rate from average for part of the aggregate, causing several parts of the aggregate to grow apart and then rejoin after leaving a gap.

One reason for developing this model was to see if it would capture the same features of the disease as our original model. Our original model explained the difference between the lag phase and the doubling phase by suggesting that the doubling phase is initiated when aggregates begin to fission, then regrow to a certain fissioning size and break again. Key to this explanation is our result that aggregation speeds up, so that the time for an aggregate to double in size from half its fission size to its fission size is much less than the time for it to get from its initial size to its fissioning size.

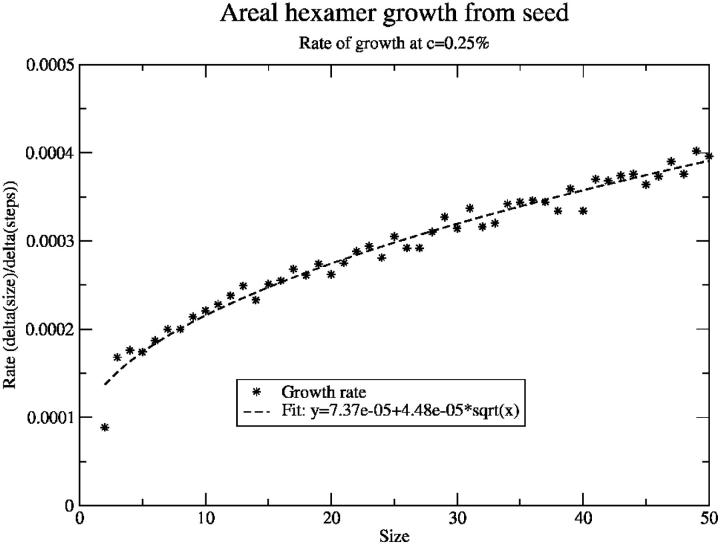
To see if this model could produce the same separation of lag and doubling phases, we examined the aggregate growth rate as a function of size in this model (Fig. 3) and found it speeds up only slowly. Naïvely, one would expect the growth rate to be roughly proportional to the square root of the size, as the growth rate is proportional to the circumference of the aggregate, which, assuming a circular aggregate, is 2πr. The size of the aggregate is proportional to the area, πr², so the radius is proportional to the square root of the size and thus the rate proportional to the square root of the size. To a good approximation, the growth rate observed here is well-fit by an offset plus a term proportional to (size)^1/2, as expected.

FIGURE 3.

Growth rate (change in aggregate size per step) as a function of size for seeded areal aggregation in the monomer growth model. Growth rate goes as the square root of the size with an offset, which was as expected for this model.

In this simple picture, one can calculate the ratio of the doubling time to the lag time. The lag time is the time to go from the initial size, say size 0 for simplicity, to size n; the doubling time from size n/2 to size n. Integrating the rate to get the times and taking the ratio we find 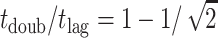or ∼0.293. This means that this model cannot produce such a large separation between lag and doubling times as our earlier model could, at least not without further modification.

This also indicates that if there is a lag phase and if the difference between it and the doubling phase is due to acceleration of aggregation, this picture is not sufficient and something more like case 2, growth from intermediates, may be a better representation of the disease process.

GROWTH VIA INTERMEDIATES

In this case, aggregation is assumed to be the assembly of independent hexameric intermediates into a larger areal aggregate. The intermediates themselves are not misfolded but only misfold, in this model, when they either aggregate with an existing misfolded seed, or come together in such a way that they can misfold and form a new stable seed. In this way, the model works essentially just like the model of Slepoy et al. (2001), except now hexameric intermediates are playing the role of monomers (Fig. 4). As mentioned above, there is some evidence that intermediates greatly increase aggregation rate in studies of yeast prions, so this emphasis on the importance of intermediates may be reasonable.

FIGURE 4.

(a) As in Slepoy's model (Slepoy et al., 2001), subunits were healthy monomers (light gray spheres) aggregating with misfolded monomers (dark gray hexagons); (b), subunits are hexagonal intermediates (light gray/dark gray) aggregating with misfolded hexagonal structures (medium gray/dark gray). In both cases, the aggregation process and kinetics ought to be, and indeed are, similar.

To be able to map this model back into our old model, though, we need to know how the intermediate concentration depends on monomer concentration. And this is not obvious. So a simulation was developed to explore how the concentration of hypothetical hexameric intermediates would depend on monomer concentration. Again, here we are assuming the intermediates are hexameric but we can easily modify the model to accommodate trimers.

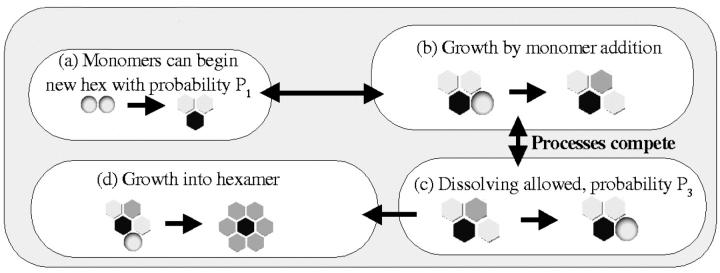
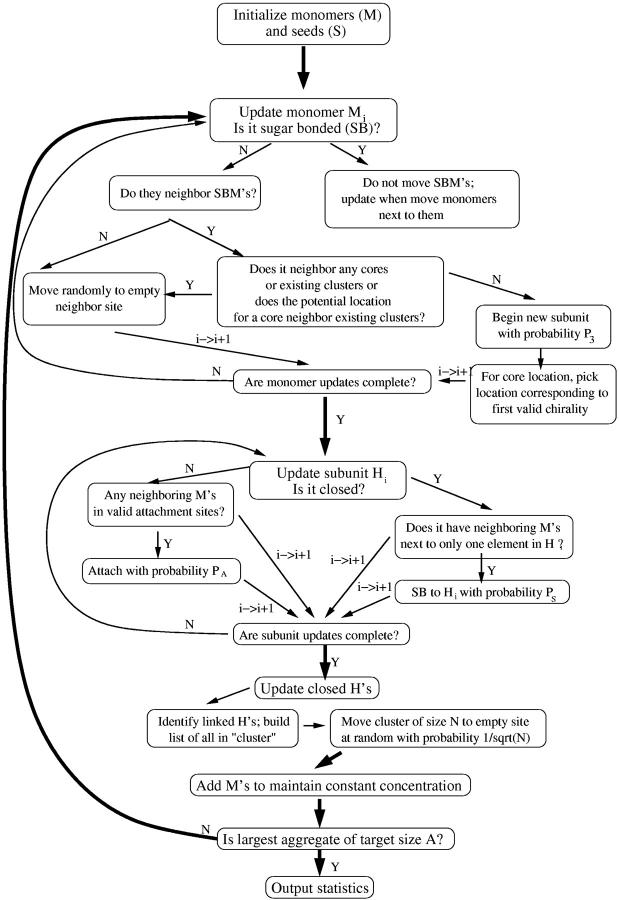
To get at the concentration of intermediates, it was assumed that two monomers have a probability P₁ of beginning a new hexameric subunit when they come into contact (see Fig. 5). This new subunit can grow by addition of monomers when they move into appropriate positions (changing this probability does not affect the outcome of the simulation, only the timescale, so it was set to 1). However, this growth process competes with a “dissolving” process by which a monomer that is part of an intermediate but only has one neighboring monomer can break off with a probability P₃. Thus the end destiny of any intermediate that begins is either to form a complete hexameric intermediate, in which case it can persist, or to dissolve completely. Details of the algorithm for this model are shown in Fig. 6.

FIGURE 5.

Rules for the formation of intermediates. Note that growth and dissolving compete, so that any intermediate eventually either becomes a complete, stable hexagon or dissolves back into monomers. (a) Two monomers have a probability P₁ of joining to begin a new intermediate, which is not yet stably misfolded. Black represents a region blocked by some of their residues. (b) This can grow by addition of monomers to either “end.” After attaching, the monomer sandwiched between the other two has two neighbors and is not allowed to break off, whereas the ones with only one neighbor can. (c) A monomer with only one neighboring monomer has a probability P₃ of breaking off in a given step. This competes with the growth process. (d) Continuing addition of monomers can result in a finished hexameric intermediate where every monomer has two neighbors and is safe from breaking off.

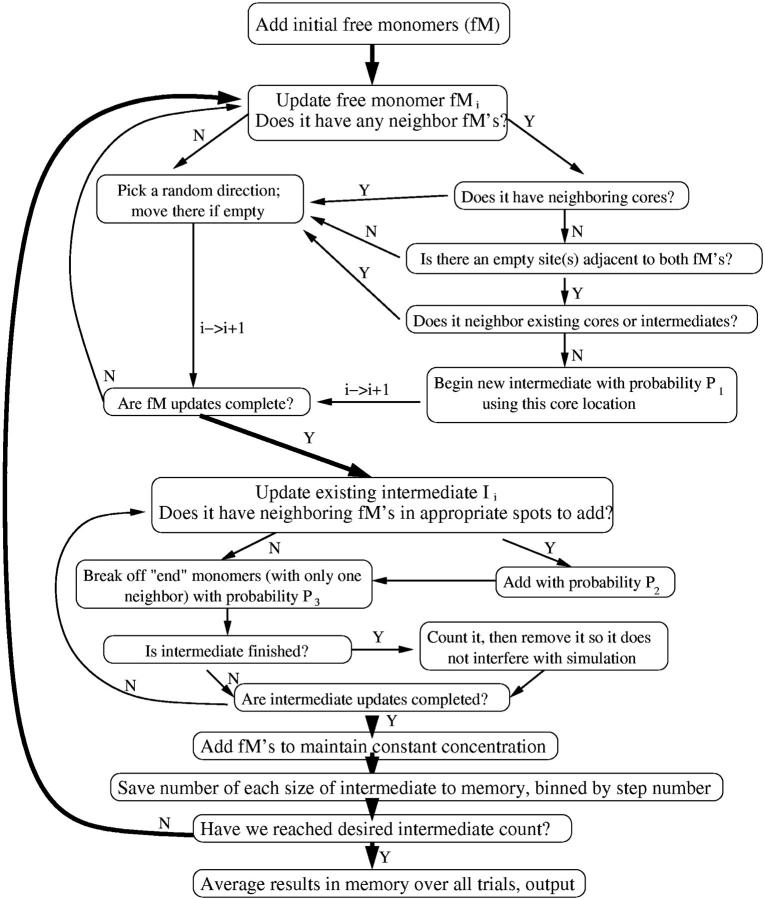
FIGURE 6.

Flow chart of simulation for the formation of intermediates. Note that P₁ we vary for different runs, P₂ we typically set to 1 (it sets the simulation timescale and is unimportant), and P₃ we also vary. Finished intermediates are removed so that we can run to a larger number of finished intermediates without the lattice getting clogged. Here, also, we typically average >1000 trials for good statistics.

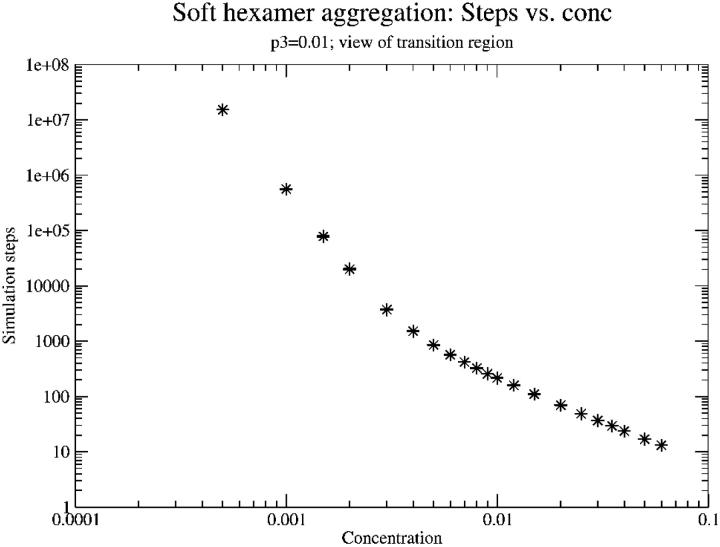
This dissolving, or reversibility, was included because it was not obvious that at low monomer concentrations, one would expect a reasonable formation rate of intermediates via this mechanism. It was initially thought that at concentrations below something on the order of P₃, breaking would dominate and the formation rate of intermediates would be almost zero. First, the simulation that was developed was used to examine the dependence of time for intermediate formation as a function of monomer concentration (Fig. 7). It was found that at high monomer concentration, the time to form an intermediate scales between 1/c and 1/c² (c is concentration). This is because the likelihood of starting an intermediate scales as the dimer concentration (1/c²), whereas the time to add monomers to it scales as 1/c. On the other hand, at very low monomer concentration, the time asymptotically approaches 1/c⁶. This is due to the fact that at these concentrations, dissolving dominates and it is only in the very rare event that six monomers are in the same place at almost the same time that an intermediate can finish. The probability of that scales as 1/c⁶.

FIGURE 7.

Simulation steps (time) to form a hexameric intermediate as a function of monomer concentration. Log-log scale. Note the broad transition to dissolving-dominated behavior at low concentration. The transition actually continues to even lower concentration than can be seen here. At very low concentration the time eventually scales as 1/c⁶. Standard deviations fall within the size of the data points on this plot.

It is interesting to note that the beginning of the transition between high concentration behavior, where most intermediates successfully become complete, and low concentration behavior, where only a lucky few do, begins at a concentration on the order of the breaking probability, P₃. This suggests that if the strength of bonds between intermediates could be weakened somehow, the biological number of intermediates could be drastically decreased by pushing biological monomer concentrations into the 1/c⁶ regime.

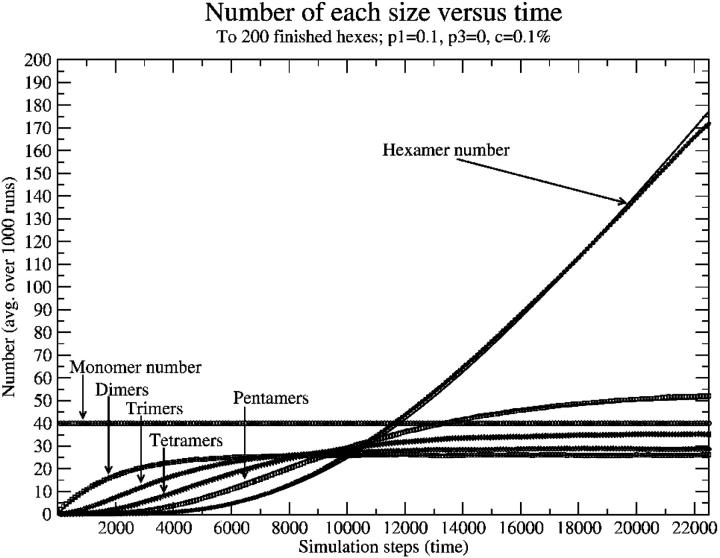
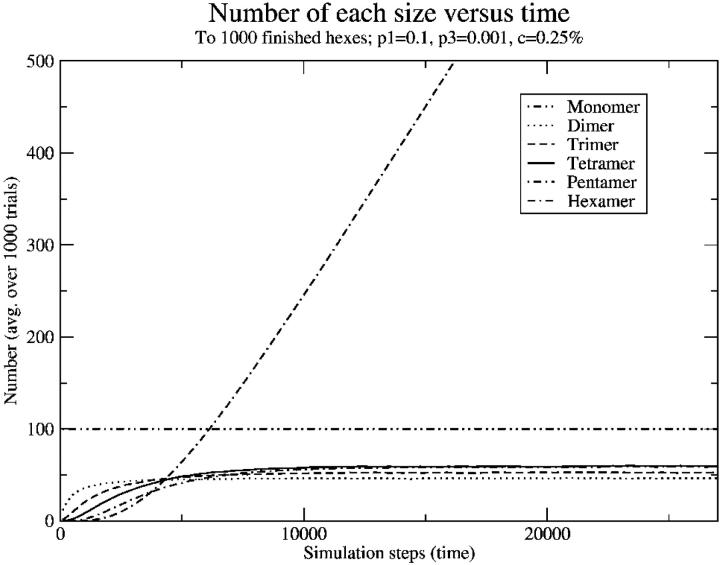
The goal, however, was to determine the dependence of the intermediate concentration on monomer concentration. This just provided a formation rate, and the functional form was uncertain. So another sort of result was examined, wherein we began examining behavior of the system as a function of time, and measured the number of different partial intermediates (two monomers, …five monomers, hexameric intermediates). We first examined the case with no breaking (P₃ = 0) to check our results, because it is relatively easy to work out kinetics in that case. A sample of one of these plots is shown in Fig. 8, with symbols as data points and solid lines as approximate kinetics fits. It is important to note that in this case, and in the case of nonzero breaking probability, the number of dimers, trimers, tetramers, and pentamers reaches equilibrium relatively quickly and then the hexamer number begins to grow linearly at a rate equal to the rate of dimer formation.

FIGURE 8.

Number of each size as a function of time (simulation steps), with zero breaking. Note that, at long times, intermediates reach equilibrium and the hexamer number begins growing linearly with time. Points are simulation data points; solid lines (mostly overlapping points) are approximate kinetics results.

Sample results with nonzero breaking are shown in Fig. 9. These results are qualitatively similar, except the number of pre-intermediates that persists is much lower. In the high-breaking limit, the very low level of intermediates demonstrates that either a potential intermediate gets “lucky” and quickly forms an intermediate, or it dissolves back to monomers, leaving few dimers, trimers, and so on.

FIGURE 9.

Number of each size as a function of time (simulation steps) with nonzero breaking. Compare to Fig. 6; note that the number of intermediates reaches equilibrium faster and at smaller numbers, but that the hexamer number still grows linearly at long times.

The kinetics equations we can write down to describe this simulation are relatively simple. With r_nm as the rate constant for forming m-mers from n-mers, and b_nm as the rate of breaking n-mers into m-mers plus monomers, we can write:

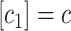(1)

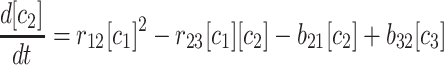(2)

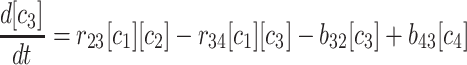(3)

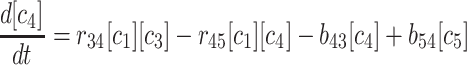(4)

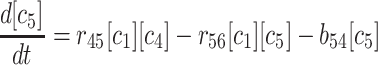(5)

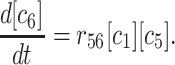(6)

Since we know that the hexamer number grows linearly at steady state and all of the other concentrations are unchanging, we can greatly simplify the above kinetics by looking at the steady state only. We can work backward from the steady-state behavior of the hexamers to find the dependence of the steady-state rate of hexamer formation on the different kinetic parameters and ultimately on the monomer concentration.

This straightforward kinetics analysis produces the equilibrium result

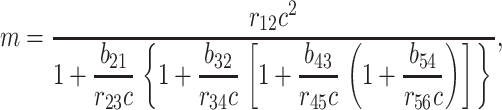(7)

where m is the slope at equilibrium of the hexamer formation rate.

The constants in our simple result for m, above, can be measured from our simulation. However, our simulation does not necessarily reproduce what these constants would be in a biological system. So it is difficult to say exactly what the rate of intermediate formation, m, would be in a real system. However, it is nevertheless useful to know the functional form of its dependence on the monomer concentration.

The result that the hexamer number begins growing linearly eventually is independent of monomer concentration. This is important because it means some hexamers can form given these simple rules even if breaking dominates. Given that result, it seems safe to assume that if hexameric intermediates are stable, some will form in biological systems.

In our model, the hexamer number grows linearly indefinitely, which is obviously unrealistic biologically. The reason for this is that we include no mechanism to remove finished hexamers. Realistically, they would be cleared from the body somehow. They could be endocytosed from the cell surface and degraded via the proteasome mechanism or some other pathway. Additionally, any hexamers being taken up into aggregates would reduce this number. Regardless, realistically the number should stabilize at some fixed value determined by the balance of the clearance rate and the formation rate.

With the result that some hexamers form even at low monomer concentrations (and more would form if they are trimers), a model was developed where now hexameric intermediates occupy a single cell on the lattice (equivalently, these could be trimeric intermediates). This model, described below, largely maintains the same attractive features of the original, showing that if areal aggregation is the explanation for these features, as we suggested, this aggregation could be of hexameric intermediates.

Part of our basis for this model is the observation that the intermediates are not yet stably misfolded since formation of intermediates in studies of yeast prions does not lead to a change in circular dichroism results; it is only when they aggregate with a seed that they stably misfold (Serio et al., 2000). This also is justified by observing that if intermediates were stably misfolded, they could act as seeds on their own, without the necessity of an external seed initiating the infection, and thus there would be no difference between sporadic and infectious CJD. Therefore, for aggregates consisting of misfolded oligomers like those observed by Wille et al. (2002), intermediate misfolding must be catalyzed by existing aggregates or few-hexamer misfolded oligomers. We hypothesize that the mechanism for this is intermediates forming bonds to an existing seed. When solvent is excluded locally around these oligomers and their neighbors include a misfolded oligomer or aggregate, they misfold. The important point is that it is solvent exclusion around an intermediate that can cause it to misfold, making this a very rare sporadic event. But a misfolded seed can help this process by providing a place where intermediates bond, helping the solvent-exclusion process. These rules make this model essentially identical in terms of kinetics to our original model. Details of the algorithm for this model and mapping are shown in Fig. 10.

FIGURE 10.

Flow chart for simulation mapping back into our original model. Here we basically have free monomers (fMs), attached monomers that are not yet stably misfolded (aM), and monomers that have stably misfolded and aggregated (H). We have some choice of a parameter, Q_bc = m. This model will capture the features of our original model for m between 3 and 6, and the simulation will proceed in exactly the same way. We compute N_bc, the bond coordination number, with N_bc = n_fM + n_aM + (m − 1) × n_H, where the n is the number of neighboring fMs, and so on. N_hc, the “hardening” or aggregating coordination number, is given by N_hc = n_fM + n_aM + n_H. We refer to Q_bc as the bonding critical coordination number and Q_hc as the “hardening” critical coordination number.

However, from our old model we estimated the sporadic form of the disease could have a peak at ∼1000 years, given a biological concentration of 10⁻³%. In our new model we find that it is very difficult to estimate this number as the scaling of the time as a function of monomer concentration is complicated. It was hoped that this model would give a result for the onset of sporadic disease that could be compared with the time for onset of the infectious form to see if the results were consistent with the roughly 1-in-10⁶ incidence of sporadic CJD that we earlier pointed out. Unfortunately, it is difficult for our model to give a concrete answer at this time as the answer depends too much on the value of the biological monomer concentration. We do find, however, that the power law used previously to scale the sporadic data, c⁻³, is a lower bound on the separation. That is, the actual exponent should be larger, meaning that we previously underestimated the separation of timescales. Thus although we cannot say exactly what the separation of timescales here will be, we can say that it will be greater than the two orders of magnitude that we previously estimated.

This work suggests that a model like our earlier one, modified to involve areal aggregation of hexameric or trimeric intermediates, could maintain the same attractive features of our earlier model in explaining certain aspects of the diseases. However, without precise knowledge of the biological monomer concentration and a way to measure relevant rate constants, it is difficult to make numerical predictions from this model.

DISCUSSION

Our work has shown that both in the case of monomer addition to a seed, and in the case of growth via intermediates, it is possible to produce aggregates like those observed by Wille et al. (2002). This leaves the question of how such aggregates actually grew. If areal aggregation is the cause, or part of the cause, of the difference between lag and doubling times, as suggested by Slepoy et al. (2001), then our work suggests that intermediates are already present in vivo before aggregation.

Our work has also shown that a model can be developed which, with suitable parameters, can reproduce areal aggregates like those actually observed while maintaining the same features of our original model.

Whether or not areal aggregation is actually important in these diseases, we can gain insight from this model. If the aggregates observed are growing via monomer addition, we gain some constraints on the structure simply from our rules. On the other hand, if intermediates are important to aggregation, then our results indicate the intermediate concentration can be quite important. At high intermediate concentrations, intermediates form relatively fast. However, at low intermediate concentrations, intermediate formation timescales as 1/c⁶. This result is exciting because it suggests the intermediates as a target to prevent aggregation. Simply reducing the monomer concentration by a factor of 2 would decrease the number of intermediates by a factor of 2⁶ or 64. Within our model, this would certainly increase the aggregation time, and thus slow down the disease, by at least the same factor. For a disease which can typically incubate for years, this obviously would be a great advantage.

In this case, the location of the transition between low concentration behavior and high concentration behavior is, roughly speaking, set by the probability of monomers breaking off from an intermediate before it becomes a stable hexamer. Thus if this probability could be increased slightly—that is, the bonds between monomers could be weakened slightly—it would have the result described above. This could provide an explanation for one experimental observation. Humans have a methionine/valine polymorphism at codon 129 of the gene for the prion protein. To date, everyone affected by vCJD has been methionine/methionine homozygous. This effect was also seen in the prion disease Kuru, where the methionine/methionine genotype was associated with increased susceptibility and the shortest incubation time (Goldfarb, 2002). If replacing methionine with valine weakened the monomer-monomer bonds within a forming intermediate and reduced intermediate concentration, this could have exactly the effect described above. This is, however, highly speculative, but as Wille et al. (2002) refine their model of the oligomer structures, it will be interesting to see if this residue falls in the region important to bonding between monomers.

In all, our work shows that our earlier model can be extended to produce aggregates like those observed in vitro while still maintaining its attractive features. Our work also suggests possible mechanisms for formation of these aggregates. If the aggregates form by monomer addition, it constrains protein structure. If they form by addition of intermediates, it highlights the importance of bonds within the intermediates as a target for possible treatment strategies. Our model suggests that an experiment to measure the biological intermediate concentration, if there is such a concentration, would be very useful. That would indicate whether such intermediates are present at a high enough concentration to be important biologically. Additionally, this work suggests that experimentalists should check and see whether reasonably-sized aggregates of prion protein can be found in vivo on the cell surface. This confinement to the cell surface conceivably could make the difference between the one-dimensional fibrillar aggregates typically observed in vitro and two-dimensional areal aggregates like those suggested by the model of Slepoy et al. (2001). Direct measurements, or detailed simulations, giving the strengths of β-bonds between monomers compared to bonds between subunits would be very useful.

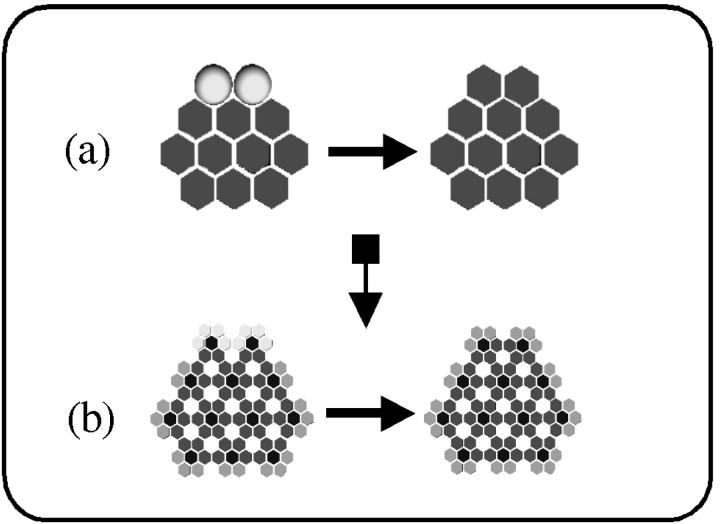
One simple way to experimentally discern between growth via monomers or intermediates may be to look at high resolution at the boundary of actual areal aggregates. If growth is by monomers, aggregates will form with monomer-scale roughness at their boundaries (Fig. 1 e) while if growth is by intermediates, there will be no such roughness (Fig. 4 b). Experimentally, the absence of such roughness would not prove the growth via intermediate hypothesis because incomplete oligomers at the edge of the aggregate could be removed in the purification process, possibly by proteinase K digestion. However, the presence of such roughness would certainly suggest that monomer growth is important.

A more general scheme for experimentally testing the possible role of intermediates and estimating their concentration is via spin labeling (Hubbell et al., 1998; Columbus and Hubbell, 2002). Briefly, a small molecule with a free spin can preferentially react and attach to cysteine residues in proteins. Frequently, these residues are moved around a protein via mutagenesis to then map out structures, but for these purposes a less refined approach is required. Since the PrP protein already possesses cysteine residues at the position of the disulfide bond, the spin labels can attach there (and will not disrupt the disulfide bond). Then the spin-spin interactions will produce a different characteristic spectrum for monomers, incomplete intermediates, and complete intermediates, in particular, with a progressive broadening upon moving from monomers to complete intermediates. Since the spins can have interactions with other spins within a 3-nm sphere, we do not doubt that the broadening will be observable. Of course, since the spin labels will react with any cysteines present, it is important to carry this out first by in vitro aggregation experiments with purified prion extracts. This will help to identify the conditions which can lead to areal aggregation as observed by Wille et al. (2000), and serve as an existence proof at least for significant oligomeric intermediate concentrations.