General Methods for Analysis of Sequential “n-step” Kinetic Mechanisms: Application to Single Turnover Kinetics of Helicase-Catalyzed DNA Unwinding

Abstract

Helicase-catalyzed DNA unwinding is often studied using “all or none” assays that detect only the final product of fully unwound DNA. Even using these assays, quantitative analysis of DNA unwinding time courses for DNA duplexes of different lengths, L, using “n-step” sequential mechanisms, can reveal information about the number of intermediates in the unwinding reaction and the “kinetic step size”, m, defined as the average number of basepairs unwound between two successive rate limiting steps in the unwinding cycle. Simultaneous nonlinear least-squares analysis using “n-step” sequential mechanisms has previously been limited by an inability to float the number of “unwinding steps”, n, and m, in the fitting algorithm. Here we discuss the behavior of single turnover DNA unwinding time courses and describe novel methods for nonlinear least-squares analysis that overcome these problems. Analytic expressions for the time courses, f_ss(t), when obtainable, can be written using gamma and incomplete gamma functions. When analytic expressions are not obtainable, the numerical solution of the inverse Laplace transform can be used to obtain f_ss(t). Both methods allow n and m to be continuous fitting parameters. These approaches are generally applicable to enzymes that translocate along a lattice or require repetition of a series of steps before product formation.

INTRODUCTION

The biological functions of many enzymes require the coupling of hydrolysis of nucleoside triphosphates (NTP or dNTP) to translocation of the enzyme along a linear protein or nucleic acid filament. Some of these so-called “motor proteins”, such as the kinesin family of proteins, move along microtubules (Howard et al., 1989; Block et al., 1990; Vale and Fletterick, 1997). Others, such as DNA and RNA polymerases (Kornberg and Baker, 1992), helicases (Matson and Kaiser-Rogers, 1990; Lohman and Bjornson, 1996; Soultanas and Wigley, 2000; Patel and Picha, 2000), some nucleases (Kovall and Matthews, 1997), and some restriction enzymes (Szczelkun, 2002) translocate along linear nucleic acid filaments. A complete understanding of the molecular mechanisms by which these motor proteins function requires quantitative kinetic information (rates and rate constants) on the intermediate steps involved in the translocation process. Single molecule approaches are beginning to allow the study of intermediate steps in some of these processes (Wuite et al., 2000; Visscher et al., 1999; Dohoney and Gelles, 2001; Ha et al., 2002; Bianco et al., 2001), although ensemble studies can also often be used to obtain such information (Roman and Kowalczykowski, 1989; Eggleston et al., 1996; Taylor and Smith, 1980; Cheng et al., 2001; Ali and Lohman, 1997; Lucius et al., 2002; Dillingham et al., 2002; Jankowsky et al., 2000; Raney and Benkovic, 1995).

This manuscript focuses on the use of ensemble approaches and the methods of analyses needed to examine the kinetic mechanisms by which a class of nucleic acid enzymes, called helicases (Matson and Kaiser-Rogers, 1990; Lohman and Bjornson, 1996; Soultanas and Wigley, 2000; Patel and Picha, 2000) unwind duplex nucleic acids and translocate along DNA. The assays that are most generally used to study the kinetic behavior of these enzymes are “all or none” assays, meaning that they directly detect only the final product or step of the reaction (i.e., completely unwound single-stranded DNA), although assays that directly detect partially unwound DNA intermediates have also been developed (Roman and Kowalczykowski, 1989; Eggleston et al., 1996; Taylor and Smith, 1980; Cheng et al., 2001). However, even when “all or none” assays are used, one can often still obtain mechanistic information about the number of steps and the rate constants for the intermediate steps through quantitative analysis of the time courses of single turnover reactions (Ali and Lohman, 1997; Jankowsky et al., 2000; Lucius et al., 2002). Systematic studies of the dependence of the single turnover time course of DNA unwinding on duplex DNA length can yield estimates of the unwinding rate and the kinetic “step size”, m, i.e., the average number of basepairs unwound between two successive rate limiting steps that are repeated during the unwinding cycle.

“All or none” assays for helicase-catalyzed DNA unwinding

“All or none” assays for studies of helicase-catalyzed unwinding of duplex nucleic acids involve the use of either radioactively labeled nucleic acid (Ali and Lohman, 1997; Ali et al., 1999; Jankowsky et al., 2000; Lucius et al., 2002) or fluorescently labeled nucleic acid to monitor complete unwinding of the DNA (Bjornson et al., 1994; Houston and Kodadek, 1994; Cheng et al., 2001; A. L. Lucius and T. M. Lohman, unpublished results). These approaches are described in detail in the papers cited above; however, Fig. 1 outlines these approaches and shows examples of time courses of unwinding of a 40 bp DNA duplex by Escherichia coli RecBCD helicase.

FIGURE 1.

Schematic representation of an all or none assay using either chemical quenched-flow techniques or fluorescence stopped-flow techniques. The combined circle, square, and triangle represent the RecBCD helicase prebound to a blunt-ended DNA substrate. Upon addition of ATP, x number of ATP molecules are hydrolyzed and multiple steps are taken to completely unwind the duplex region. (A) DNA substrate is radiolabeled with ³²P at the 5′ end. The radiolabeled DNA substrate is incubated with helicase and allowed to achieve binding equilibrium. The helicase-DNA complex is loaded into one syringe of the quenched-flow apparatus, and ATP and a large excess of unlabeled DNA, to serve as a protein trap, are loaded into the other syringe. The samples are then rapidly mixed together and allowed to incubate for various times, Δt, before mixing with quench and expelling into a tube. Each reaction is run on a gel to separate ssDNA from dsDNA (denoted as ss and ds, respectively, in the inset); these bands are then quantitated and plotted in the graph in the inset. As described, the quenched-flow assay is both an all or none assay and a discontinuous assay in that each time point is an individual reaction. (B) DNA substrate is labeled with donor and acceptor FRET pairs. Again, the DNA substrate is incubated in one syringe with helicase and the other syringe contains ATP and protein trap. The samples are rapidly mixed together and the fluorescence signals from the fluorophores are observed. At time zero, the donor and acceptor are in close proximity, thus energy transfer between the two fluorophores is very efficient. In principle, upon complete unwinding, the fluorescence from the donor increases and the fluorescence from the acceptor should exhibit an anticorrelated decrease. In the inset is the donor fluorescence as a function of time.

In both types of experiments, the helicase is prebound to a duplex DNA substrate at equilibrium. In a chemical quenched-flow experiment (Fig. 1 A), the prebound complex is rapidly mixed with ATP and a large excess of protein trap (typically unlabeled DNA or heparin) to ensure that rebinding of free protein to the DNA does not occur during the ensuing reaction. This ensures that each helicase is involved in only a single round of DNA unwinding (i.e., reactions are single turnover with respect to the DNA, although multiple rounds of ATP hydrolysis occur). The reaction is then allowed to proceed for a specified amount of time (Δt) before a quenching solution (typically an excess of EDTA to chelate the free Mg²⁺) is added to stop the reaction. The quenched sample is subsequently analyzed by nondenaturing gel electrophoresis to separate the product (fully unwound ssDNA) from the fully native dsDNA substrate. One such experiment yields only one point in the time course and thus must be repeated ∼20–25 times, varying Δt in each experiment, to obtain a full time course. Therefore, in addition to its “all or none” nature, the quenched-flow assay is also a discontinuous assay since each time point (see Fig. 1 A) is obtained from a separate experiment. In such experiments, the assumption is made that, at the time of quenching, all partially unwound DNA intermediates reanneal completely to re-form the native duplex DNA substrate, whereas any completely unwound ssDNA does not reanneal. Due to the length of time required to perform all of the experiments needed to describe an entire time course, this type of experiment is often performed at low DNA concentration (1 nM) so that no significant reannealing of the product DNA occurs during the course of the experiment. However, these experiments can be performed at high [DNA] by including a trap for ssDNA product (i.e., inclusion of a large excess of nonlabeled ssDNA that is complementary to one of the strands of the duplex DNA substrate) (Maluf et al., 2003).

In the fluorescence resonance energy transfer (FRET) analog of this experiment (Fig. 1 B), a DNA substrate is labeled with both a donor and an acceptor fluorophore. In the duplex DNA, the donor and acceptor fluorophores are in close proximity and thus the efficiency of FRET is high, whereas after complete unwinding of the DNA, the two complementary strands of ssDNA become separated, resulting in a complete loss of FRET. The resultant time course obtained from this experiment, in principle, will be identical to that determined in the quenched-flow experiment if the only change in fluorescence intensity of the donor and/or acceptor fluorophore is due to the change in FRET upon complete separation of the two fluorophores. Unlike the quenched-flow experiment, the FRET experiment can be performed as a continuous assay in a stopped-flow instrument. However, the assumption is still made that any partially unwound DNA intermediates from which the helicase dissociates before complete unwinding of the DNA will reanneal to re-form the duplex DNA substrate, resulting in no change in the FRET signal for that molecule.

The radioactive chemical quenched-flow assay is clearly more time consuming since each time point requires a separate experiment. This also sets a practical limit for the number of data points that are generally obtained for a single time course (typically 20–30). The fluorescence assay can be performed in a stopped-flow instrument, and thus one generally obtains 400–500 data points for a time course in a single experiment. The advantage of the chemical quenched-flow experiment is that one obtains a direct measure of the extent of DNA unwinding, whereas, in the FRET experiment, one must be able to correlate the extent of the fluorescence change with the known extent of DNA unwinding. Therefore, quantitative analysis of the fluorescence unwinding time course usually requires comparison with an otherwise identical experiment performed by chemical quenched-flow.

In the following sections, we first describe the general behavior of several “n-step” sequential mechanisms for helicase-catalyzed DNA unwinding, of increasing complexity. We then discuss the experimental approaches and analysis of a set of single turnover unwinding experiments needed to estimate the number of intermediate steps, n, required to unwind a duplex DNA of length, L, and the “kinetic step size”, m = L/n. Finally, we introduce novel methods to simultaneously (globally) analyze, by nonlinear least-squares (NLLS) methods, a series of time courses obtained for a set of DNA substrates varying in duplex DNA length, L. These methods allow for a noninteger number of steps as well as a noninteger kinetic step size, thus enabling one to float these parameters continuously in a NLLS analysis. These methods involve use of gamma and incomplete gamma functions when a closed form expression can be obtained for the time course of unwinding, f_ss(t), and Laplace transforms and numerical approaches to obtain the inverse Laplace transforms when a closed form expression for the time course is not obtainable. We note that many methods, including matrix methods and numerical methods, can be used if all that is sought is to simply simulate a kinetic time course for a given mechanism. Such methods are also suitable for NLLS analysis of reactions in which the number of steps in the pathway is defined and fixed. However, simultaneous NLLS analysis of a series of n-sequential step mechanisms in which the number of steps, n, is not fixed but changes for each substrate (DNA in our case) and is in fact an unknown parameter to be determined from the analysis, is much more suited to the method of Laplace transforms. These techniques have been applied recently to studies of RecBCD catalyzed DNA unwinding (Lucius et al., 2002), but are also applicable to the analysis of mechanistic studies of any enzyme-catalyzed reaction that requires repetition of a series of steps before product formation.

Single turnover kinetic time courses for helicase-catalyzed DNA unwinding determined from an “all or none” assay

Case 1 (Scheme 1): All unwinding steps the same, infinite processivity (P = 1)

The single turnover time courses for RecBCD helicase-catalyzed DNA unwinding obtained from either the “all or none” quenched-flow or FRET stopped-flow assays display clear lag phases for formation of fully unwound ssDNA product (see Fig. 1). Such a lag phase is expected if the helicase proceeds through multiple repeated steps to fully unwind the duplex DNA, and if the rate constants for each step are similar in magnitude (Gutfreund, 1995; Ali and Lohman, 1997). The simplest mechanism displaying this behavior is the “n-step” sequential mechanism shown in Scheme 1,

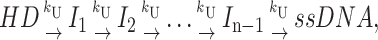(Scheme 1)

where the preformed helicase-DNA complex, HD, proceeds through a series of n repeated, irreversible steps (n − 1 intermediates, I_i) before yielding fully unwound ssDNA product. In Scheme 1, the rate constants for each step, k_U, are equal, and upon addition of ATP, the helicase unwinds m basepairs in each step. Previous treatments of n-step sequential mechanisms have only dealt with “n” irreversible steps with different rate constants for each step (Capellos and Bielski, 1972; Rodiguin and Rodiguina, 1964; Gutfreund, 1995). As written, Scheme 1 also assumes that once the helicase has initiated DNA unwinding, it does not dissociate until unwinding is completed (i.e., processivity, P = 1; see below).

We note that Scheme 1, and all of the schemes discussed in this manuscript, considers that all of the helicases initiate at time zero from the same point on the DNA, i.e., one end of the duplex, or a ss/ds-DNA junction. Thus, it is assumed that any helicase that unwinds a DNA molecule completely has proceeded through the same number of intermediates en route to product formation. This assumption needs to be kept in mind, since it is conceivable that some helicases may not initiate from the same point on the DNA substrate. For example, a helicase that requires a ssDNA flanking region (either 3′ or 5′ ssDNA) might initially be bound only to the ssDNA region, rather than the ss/ds-DNA junction. Upon addition of ATP, the helicase would then have to first translocate to the ss/ds-DNA junction before initiating DNA unwinding. If the ssDNA flanking region were long, then the steps required for translocation along the flanking ssDNA would also need to be considered in the analysis of the time course of DNA unwinding. Furthermore, since the ensemble population of helicases would be initially bound in some distribution (random?) along the ssDNA flanking region, all of these helicases would not reach the ss/ds-DNA junction synchronously. Although such a situation can be treated using the approaches described here, in this manuscript we only treat the case in which all of the helicases initiate DNA unwinding from the same start site.

There are several ways to obtain a general solution as a function of n for Scheme 1. The most direct method starts by solving the differential equations for a mechanism with one step (n = 1) to obtain an analytic solution for the time-dependent behavior of each species. One can then repeat the process for a two-step (n = 2) mechanism and so on until analytic solutions are obtained for n = 1, 2, 3, etc. These solutions can then be examined in an attempt to recognize a pattern and obtain a general analytic expression as a function of n. However, this is a tedious process even for the simplest mechanism.

We have used the method of Laplace transforms (see Appendix A) to solve the differential equations for the “n-step” sequential mechanisms described here. Any number of other methods, including matrix methods (Bujalowski and Jezewska, 2000; Arai et al., 1981) and numerical methods (Barshop et al., 1983), can be used if one is solely interested in simply simulating the time course of a defined mechanism in which the number of intermediates (steps) is known. However, these other methods are not well suited for NLLS analysis of an n-step sequential mechanism in which the number of steps, n, is to be determined from the analysis, or for simultaneous NLLS analysis of a series of substrates (in this case DNA) in which the number of steps, n, changes for each substrate. Matrix methods are not practical for global NLLS analysis of such systems because every change in the number of steps would require a new matrix of different dimensionality. However, a primary advantage of the Laplace transform method for the n-step sequential mechanisms discussed here is that it is relatively straightforward to obtain the Laplace transform for each intermediate species for a given “n”, and to easily recognize emerging patterns in the Laplace transform as the number of steps, n, is changed (See Appendix A). A further advantage is that the Laplace transform describing ssDNA formation as a function of the Laplace variable, s, can always be obtained in analytic form as a continuous function of n. This leads to the other major advantage that one can readily use the numerical solution to the inverse Laplace transform in a NLLS fitting routine and therefore treat the number of steps n as a continuous fitting parameter even when an analytic solution in the time domain is not available. In this article, we demonstrate that the methods discussed here enable global NLLS analyses of a series of time courses, such that the number of steps, n, and the step size, m, can be floated continuously in the analysis, which was not possible using previous approaches (Ali and Lohman, 1997; Jankowsky et al., 2000).

As shown in Appendix A for Scheme 1, the Laplace transform, F_ss(s), where s is the Laplace variable, of the fraction of ssDNA molecules formed in the time domain, f_ss(t), is given in Eq. 1 (see Eq. A24 in Appendix A).

(1)

The expression for the time dependence of the fraction of ssDNA molecules formed, f_ss(t), is then obtained by taking the inverse Laplace transform of Eq. 1, yielding Eq. 2,

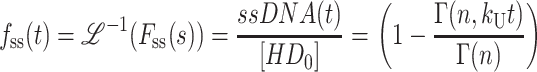(2)

(see Eq. A35 in Appendix A), where ℒ⁻¹ is the inverse Laplace transform operator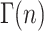, and and 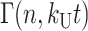are the gamma function and incomplete gamma function, respectively (NB: some mathematics texts define the ratio, Γ(n, k_U t)/Γ(n), as the incomplete gamma function, however, see Appendix A for the definition used here). Note that in the general solution for f_ss(t) given in Eq. 2, the number of steps, n, can be any positive value, including a noninteger. However, if n is an integer, then f_ss(t) can be expressed as the series given in Eq. 3:

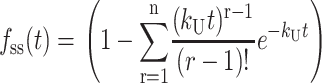(3)

Use of Eq. 2 has obvious advantages for NLLS analyses, since one can allow n to float continuously without restricting it to be an integer. Appendix A presents the derivations of these expressions as well as the expressions describing the time-dependent formation and disappearance of each intermediate species in Scheme 1.

In the following sections we also examine schemes that are more complex than Scheme 1. However, under some conditions, the solutions to these more complex schemes will have the same general form of Eqs. 1 and 2. In anticipation of this, we can write Eqs. 1 and 2 in the more general form given by Eq. 4, where k_U is replaced by an experimentally observed rate constant, k_obs, and n is replaced by an apparent number of steps, n_app. As we show below, each new scheme can then be described by Eq. 4 with a specific expression for k_obs and n_app applicable to that scheme.

(4)

Fig. 2 A shows a series of time courses for an “all or none” DNA unwinding assay simulated using Scheme 1 (Eq. 2) with values of n = 1–5. The time course for a single step reaction (n = 1) is a single exponential. However, the time courses for n ≥ 2 display clear lag phases that increase in duration as the number of intermediates in the reaction increase. Fig. 2 B shows the time courses of formation and decay of the DNA substrate (HD), product (ssDNA), and the partially unwound intermediates, I₁, I₂, I₃, and I₄, simulated using Scheme 1 with n = 5. This demonstrates that the lag phase results from the fact that each intermediate state is significantly populated during the unwinding time course. It is important to note that if any one of the five rate constants in Scheme 1 is significantly slower than the other four (e.g., k′_U ≪ k_U), then the observed time course of DNA unwinding will collapse to a single exponential with rate constant k′_U as given by Eq. 5:

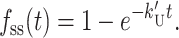(5)

Hence, the presence of a single slow step in the scheme yields a single exponential phase; the observation of a lag phase requires the presence of multiple steps with rate constants that are similar in magnitude.

FIGURE 2.

Simulated traces from Scheme 1 (Eq. 2). (A) Traces were simulated with an unwinding rate constant k_U = 30 s⁻¹ and a number of steps n = 1, 2, 3, 4, and 5 as denoted in the panel. The plot illustrates the increase in the lag phase as a function of increasing number of steps. (B) The time dependence of the concentration of the helicase-DNA complex, HD (red), Intermediate I₁ (green), I₂ (blue), I₃ (black), I₄ (red), and ssDNA (green) from Scheme 1 with k_U = 30 s⁻¹ and n = 5 steps.

Scheme 1 and the simulations in Fig. 2 indicate that in a single turnover helicase-catalyzed DNA unwinding reaction performed using an “all or none” assay, a lag phase will be observed if some rate-limiting step, with rate constant k_U, occurs repeatedly throughout the DNA unwinding reaction. Furthermore, the extent of this lag phase will increase as the number of bp, L, in the DNA duplex increases since the number of rate-limiting steps, n, will also increase in direct proportion to L. Therefore, if a series of experiments were performed as a function of duplex length, L, then analysis of the unwinding time courses can be used to estimate the number of steps required to unwind each DNA duplex and also the average number of basepairs unwound per rate limiting step, termed the kinetic step size, m = L/n (Ali and Lohman, 1997).

Case 2 (Scheme 2): All unwinding steps the same, finite processivity (0 < P < 1)

The next case we consider is Scheme 2,

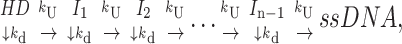(Scheme 2)

which differs from Scheme 1 in that the helicase can dissociate from the DNA substrate, with rate constant, k_d, at each step during the course of unwinding. Scheme 2 introduces the concept of a finite processivity for DNA unwinding. Processivity, P, of DNA unwinding is a measure of the number of basepairs that are unwound by the helicase per DNA binding event (i.e., before the helicase dissociates). It can be described, quantitatively, in either of two equivalent ways. First, processivity is the probability, P (0 ≤ P ≤ 1), that the helicase will proceed one step to unwind the next basepair (or m number of basepairs) rather than dissociate from the DNA. The processivity is also related to the average number of basepairs unwound (N) per binding event. As shown in Eq. 6 (McClure and Chow, 1980; Lohman and Bjornson, 1996; von Hippel and Delagoutte, 2001)

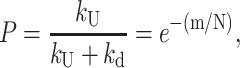(6)

where m is the DNA unwinding step size (bp unwound per step) (see Appendix B for a derivation of Eq. 6).

The differential equations that describe Scheme 2 can be solved following the same approaches detailed in Appendix A, yielding Eq. 7 for F_ss(s),

(7)

which is the Laplace transform of f_ss(t). The difference between the solutions for Scheme 2 (Eq. 7) versus Scheme 1 (Eq. 1) is that the rate constants k_d and k_U appear as a sum in the denominator in Eq. 7. This is always the case when dissociation can occur and thus we define an observed rate constant, k_obs, as in Eq. 8,

(8)

which leads to Eq. 9:

(9)

The inverse Laplace transform of Eq. 9 then yields Eq. 10 for f_ss(t):

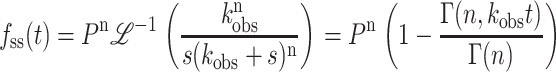(10)

Note that with the exception of the processivity term, Eqs. 9 and 10 have the same form as Eqs. 1 and 2. For integer values of n, f_ss(t) can also be expressed as in Eq. 11:

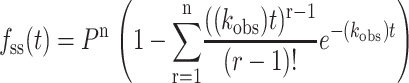(11)

In principle, an estimation of the processivity can be obtained if there is a detectable decrease in the total DNA unwinding amplitude with increasing duplex length, although there can also be other reasons for such decreases in amplitude.

Fig. 3 A shows a series of simulated time courses for Scheme 2, generated using Eq. 10 with k_U = 30 s⁻¹, k_d = 1 s⁻¹, (i.e., k_obs = 31 s⁻¹) and n = 1–5. These show the expected lag phase that increases with increasing n. However, due to the finite dissociation rate constant, k_d, the final amplitude of DNA unwinding also decreases with n. Fig. 3 B shows a plot of the total unwinding amplitude (f_ss(∞)) as a function of n, along with a fit of these amplitudes to f_ss(∞) = Pⁿ. In principle, one can estimate the processivity, P, from such data.

FIGURE 3.

Simulated traces from Scheme 2 (Eq. 10). (A) Traces were simulated with an unwinding rate constant k_U = 30 s⁻¹, a dissociation rate constant of k_d = 1 s⁻¹, and a number of steps n = 1, 2, 3, 4, and 5. (B) The total amplitude (A_T = f_ss(∞)) of each trace in A plotted as a function of the number of steps. Solid line is a nonlinear least-squares fit to A_T = Pⁿ, where A_T is the total unwinding amplitude, P is the processivity expressed in Eq. 6, and n is the number of steps. The fit predicts a processivity of 0.9677, which is equal to k_U/(k_U + k_d) or (30 s⁻¹)/(31 s⁻¹).

Case 3 (Scheme 3): All unwinding steps the same, finite processivity, biphasic time course

A number of DNA helicases that have been studied exhibit biphasic time courses in single turnover DNA unwinding studies (Lucius et al., 2002; Ali and Lohman, 1997), such that a second, slower phase occurs in addition to the expected “lag” phase. This behavior has been interpreted as reflecting the presence of two types of helicase complexes that are prebound to the DNA substrate before the addition of ATP, as depicted in Scheme 3. One is a productively bound complex, (HD)_P, that is poised to initiate DNA unwinding immediately. The other is a nonproductively bound complex, (HD)_NP, that must first isomerize to form a productive complex before initiating DNA unwinding.

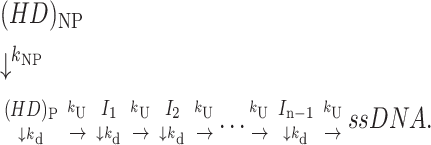(Scheme 3)

Scheme 3 was used to analyze the unwinding of DNA by E. coli UvrD helicase, using the approximate analytic solution shown in Eq. 12 (Ali and Lohman, 1997),

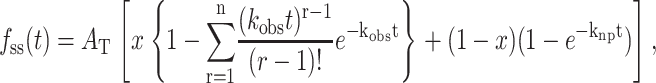(12)

where A_T is the total unwinding amplitude (Eq. 13), k_obs = (k_U + k_d), and x is the fraction of productively bound complexes as defined in Eq. 14.

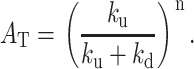(13)

(14)

The expression in Eq. 12 is an approximation that is strictly valid under conditions such that k_obs ≫ k_NP, and for small numbers of steps, n.

Equation 15 is the Laplace transform of f_ss(t) for Scheme 3, with no assumptions:

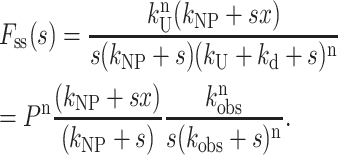(15)

The expression for f_ss(t) for Scheme 3 (with no assumptions) is obtained from the inverse Laplace transform of Eq. 15 and is given in Eq. 16. We now use Eq. 16 in place of Eq. 12 to analyze time courses based on Scheme 3 (Lucius et al., 2002):

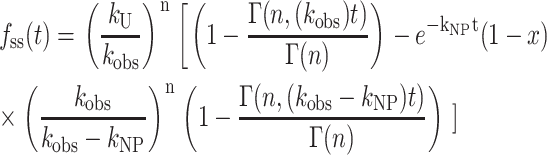(16)

Equation 16, unlike Eq. 12, has the advantage of being a continuous function of the number of steps, n, and therefore is easily implemented into NLLS routines. For comparison with previously published equations, we also show Eq. 17, which is the series representation of Eq. 16, valid only for integer values of n, and therefore not useful for a NLLS analysis to determine n:

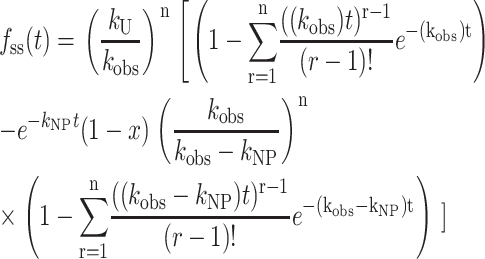(17)

Fig. 4 shows a series of time courses simulated using Scheme 3 (Eq. 16) for n = 1–5.

FIGURE 4.

Simulated traces from Scheme 3 (Eq. 16). Traces were simulated with an unwinding rate constant k_U = 30 s⁻¹, a dissociation rate constant k_d = 1 s⁻¹, a nonproductive rate constant k_NP = 5 s⁻¹, and a fraction of productively bound complexes x = 0.8, for n = 1, 2, 3, 4, and 5. These traces demonstrate a rapid lag phase followed by a slow second phase of unwinding.

Case 4: Additional steps in the mechanism, not involved directly in DNA unwinding (infinite processivity)

As discussed above, the simplest mechanism that can produce a lag in the time course of production of ssDNA is Scheme 1 in which one step is repeated n times, and the rate constants for each repeated step are identical or similar in magnitude. The next level of complexity is a mechanism that contains additional steps beyond those associated with DNA unwinding. An example of such a mechanism is shown in Scheme 4,

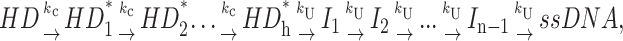(Scheme 4)

in which a series of steps, with rate constant, k_C, occurs before the actual unwinding steps, but the rate constants for these steps are not sufficiently slow as to eliminate the presence of the lag phase. In fact, the actual position of the steps with rate constants, k_C, within Scheme 4 does not affect the final expression for the time course of formation of the final ssDNA product. Hence, the steps with rate constant, k_C, could also occur after the unwinding steps, as depicted in Scheme 4a, or anywhere else within the sequential mechanism, if only the time course of the final ssDNA product is monitored.

For simplicity, we have not considered either dissociation of the helicase or the occurrence of any nonproductive complex in Scheme 4. The Laplace transform of the time dependence of ssDNA formation, f_ss(t), for Scheme 4 is given in Eq. 18:

(18)

We have been unable to obtain a general analytic expression as a function of h for f_ss(t), although one can obtain analytic expressions for specified integer values of h (i.e., h = 1, 2, or 3). However, even these analytic expressions are cumbersome; hence we do not include them here. On the other hand, as is generally true, one can obtain f_ss(t) by solving for the inverse Laplace transform numerically (see below and Appendix C). A series of time courses simulated using Scheme 4 are shown in Fig. 5 (k_U = 30 s⁻¹, k_C = 10 s⁻¹, n = 1, 2, 3, 4, and 5, and h = 2). Comparison of these simulations with those generated using the simpler Scheme 1 (Fig. 2), indicates that inclusion of the slow steps, with rate constant, k_C, results in significantly less separation between time courses for increasing values of n (or equivalently, duplex lengths). Of course, in the limit where k_C ≪ k_U, the time courses would become independent of n and display no dependence on duplex length. We note that for Scheme 4 (Fig. 5) when n = 1, a lag phase is still observed due to the presence of the two k_C steps, unlike for Scheme 1 (Fig. 2), where only a single exponential is observed for n = 1.

FIGURE 5.

Simulated traces from Scheme 4 (Eq. 18). (A) Traces were simulated with an unwinding rate constant k_U = 30 s⁻¹, k_c = 10 s⁻¹, n = 1 (red), 2 (green), 3 (blue), 4 (black), and 5 (red), and h = 2. The plot illustrates that inclusion of a slow step results in significantly less separation between time courses for increasing values of n when compared to Fig. 2 where there is no slow step.

As stated above, an interesting feature of Scheme 4 is that the final expressions for F_ss(s) and therefore f_ss(t) are independent of the actual positions of the different k_C steps within Scheme 4. As a result, one cannot determine where these steps occur within the Scheme based only on the time course of formation of the final ssDNA product. Independent information about the time course of the intermediate species is needed to determine this.

One can generalize Scheme 4 to the case in which a distribution of z different classes of steps exist, with each class of steps having rate constant k_i and each step within the class occurring n_i times, and with n₀ unwinding steps, each with unwinding rate constant, k_U. In this case, Eq. 18 can be generalized to Eq. 19:

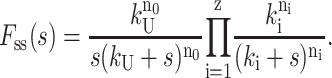(19)

For the case where a nonproductive binding mode occurs as in Scheme 3, then F_ss(s) is given by Eq. 20:

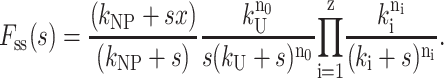(20)

Equations similar to Eqs. 19 and 20 have been described by Schnitzer and Block (1995). These authors also make the point that if a distribution of reaction rates occurs within a sequential scheme, then the Laplace transform, F_ss(s), is simply the product of the terms in the Laplace domain describing each step, as can be seen in Eqs. 19 and 20. We note that for the cases we consider here, the presence of the 1/s term in Eqs. 19 and 20 arises from the fact that our expressions describe the formation of only the final ssDNA product.

As pointed out above, no matter where in the mechanism the steps with rate constant k_C occur, the expression for f_ss(t) will be the same. However, all possible schemes will fall into three special cases. The first special case is when h is constant (independent of duplex length). The second special case is when n = h, i.e., each unwinding step is coupled to a different step (e.g., exhibiting a conformational change). The third special case is when both n and h are directly proportional to L, but with different proportionality constants, such that they occur with different frequencies during the unwinding scheme. These special cases are each considered below.

First special case: h is constant (independent of duplex length). The first special case can be described by either Scheme 4 or Scheme 4a and was used to analyze RecBCD-catalyzed DNA unwinding (Lucius et al., 2002):

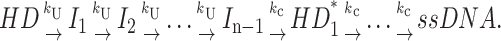(Scheme 4a)

The Laplace transform of f_ss(t) for either Scheme 4 or Scheme 4a is given by Eq. 18.

The steps with rate constant k_C can be resolved only if k_U ≥ k_C. In fact, in the limit as k_C approaches infinity, both Scheme 4 and Scheme 4a (Eq. 18) collapse to Scheme 1 (Eq. 1). This can be shown by examining Eq. 18 in this limit, which yields Eq. 21,

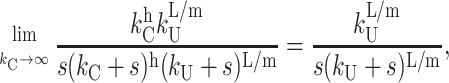(21)

which is equivalent to F_ss(s) for Scheme 1, with n = L/m. This makes sense, because if k_C is very fast relative to k_U, the step with rate constant k_C will not be observable, and Scheme 4 and Scheme 4a will collapse to Scheme 1.

However, if k_C = k_U, then the resulting time course can be described by Scheme 2 with n replaced by n_app = n + h = L/m + h. This can be illustrated by taking the limit of Eq. 18 as k_C approaches k_U, which yields Eq. 22:

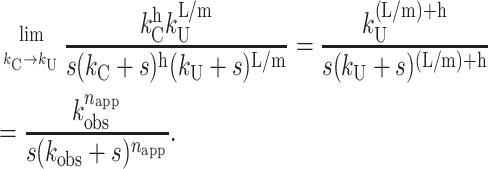(22)

The inverse Laplace transform of Eq. 22 yields Eq. 4, with n_app defined as in Eq. 23:

(23)

This predicts that if a second set of repeating steps occurs in addition to those involved in DNA unwinding, then a plot of n_app versus duplex length, L, will be linear, but exhibit a positive y-intercept, h. In this case, the values of n_app are obtained by performing a nonlinear least-squares fit of the set of time courses using Scheme 1 (Eq. 4), constraining k_obs to be a global parameter (i.e., the same for all duplex lengths), whereas n_app is treated as a local parameter (i.e., different for each duplex length).

Second special case: h = n (two repeating steps occur for every “m” basepairs unwound). Scheme 4b describes the case in which an additional step is linked to each unwinding step such that both steps are repeated an equal number of times during the unwinding time course.

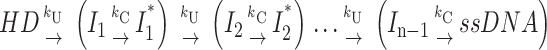(Scheme 4b)

This might describe a mechanism in which each unwinding step is accompanied by a conformational change occurring with rate constant k_C.

The Laplace transform of f_ss(t) for Scheme 4b is given by Eq. 24:

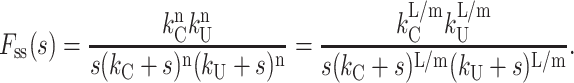(24)

For this case, it can be easily shown that by taking the limit as k_C approaches infinity, only the slowest step in each catalytic cycle will be observed (Eq. 24):

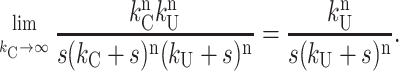(25)

This is an important result demonstrating that regardless of which repeating step occurs as the slowest step within each unwinding cycle, it will still report on the average number of basepairs unwound between two rate-limiting steps.

However, if k_U = k_C in Eq. 25, then a determination of the true step size becomes more difficult. This can be shown by taking the limit of Eq. 24 as k_U approaches k_C yielding Eq. 26, with n_app defined in Eq. 27:

(26)

(27)

Therefore, if one were to fit time courses to Scheme 1 (Eq. 4) that were actually generated by a mechanism that has two repeating steps with equal rate constants associated with the unwinding of m bp, this would result in a twofold underestimate of the true step size, even though the time courses would be well described by this model. One way to potentially uncover such a situation would be to perform a series of unwinding experiments under a variety of solution conditions in the hope that the two repeating rate constants would be affected differentially and eventually become resolvable. Since one does not know a priori that a situation such as Scheme 4b might exist, it is always advisable to perform additional experiments as a function of solution conditions, such as salt, temperature, pH, [ATP], etc., to determine whether the apparent step size is affected by solution conditions.

As we have discussed, even though multiple elementary kinetic steps will be associated with the unwinding of each “m” basepairs, the analysis of the time course will generally detect only the slowest step that is repeated in the unwinding cycle. Furthermore, one does not know a priori what physical process is associated with this repeated rate-limiting step. In fact, although we have used the designation k_U, for unwinding, to denote this repeated step, one needs to keep in mind that the step could reflect other processes such as ATP binding, hydrolysis, product release, or a protein conformational change, rather than the actual step associated with DNA unwinding.

Third special case: Both n and h are directly proportional to L, but with different proportionality constants. A separate translocation step is repeated with a different frequency than the unwinding steps. The third special case of Scheme 4 occurs if the two different steps are repeated during the course of DNA unwinding, but with different frequencies (e.g., two steps with different step sizes) as depicted in Scheme 4c:

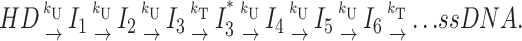(Scheme 4c)

In this case, one step with rate constant k_T (and step size m₂) occurs for every three steps with rate constant k_U (and step size m). The Laplace transform of f_ss(t) for Scheme 4c is given in Eq. 28, where n₂ = L/m₂:

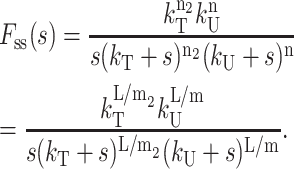(28)

This type of mechanism might reflect a case in which m basepairs are unwound for each of the n steps, followed by a translocation step with rate constant k_T, associated with a larger step size, m₂. The quantum inchworm model proposed for RecBC-catalyzed DNA unwinding (Bianco and Kowalczykowski, 2000) is an example of such a mechanism. The ability to detect either the smaller or the larger of the two step sizes depends strongly on both the difference between the two step sizes, m and m₂, and the relative magnitudes of the two rate constants, k_U and k_T. As pointed out above, unless the two rate constants are similar in magnitude, one will only be able to observe the slowest step in the repeating cycle. Therefore, if the translocation step is rate limiting, one will observe the step size associated with translocation and vice versa.

As a starting point, we can explore the behavior of n_app as a function of duplex length, L, when k_U = k_T. If k_U = k_T, then Eq. 28 reduces to Eq. 29, with n_app, defined by Eq. 30:

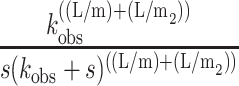(29)

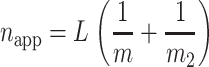(30)

If m₂ = m, then a twofold underestimate of the unwinding step size will be obtained as discussed above (see Eq. 27). However, if m₂ ≫ m, the time course will provide information only on m, the smaller of the two step sizes, as can be seen from Eq. 30. This analysis suggests that if k_U and k_T are equal, one will observe the smaller of the two step sizes; however, if one of the two rate constants is partially rate limiting, one will primarily observe the step size associated with the rate constant that is partially rate limiting. Again, since there is never a priori knowledge that a situation such as this might exist, it is advisable to examine whether n_app changes with solution conditions.

General Methods for Global Nonlinear Least-Squares Analysis of DNA Unwinding Time courses

Expressions for the time course of DNA unwinding that are continuous functions of n and m

To obtain the “best fit” values of the kinetic parameters, as well as n and m and their associated uncertainties, for a given kinetic mechanism it is necessary to use nonlinear least-squares methods to analyze the single turnover DNA unwinding time courses. It is certainly the case that numerical integration techniques can be used for NLLS fitting for complex kinetic models in which the number of steps is defined and fixed (Barshop et al., 1983). However, NLLS analysis of either a single DNA unwinding time course, or the simultaneous (global) analysis of a series of time courses obtained for a set of DNA substrates differing in duplex length, L, is not possible with the numerical integration packages that are currently available, since one is unable to float either the number of steps, n, or the kinetic step size, m = L/n. This limitation results from the fact that the currently available programs require one to include every intermediate explicitly in the “kinetic mechanism”, and thus these programs can only consider one particular scheme with a specified number of steps, n. Therefore, for the “n-step” sequential mechanisms considered here, n must be constrained to be an integer in those programs. However, n is one of the parameters to be determined from a quantitative analysis of the time course, and is thus not generally known a priori. This problem is compounded when attempting to analyze a set of time courses for DNA duplexes of different lengths, L, since n will differ for each length, L. Therefore, in previous approaches, one attempted to fit the time course to a series of schemes involving progressively increasing numbers of steps, n, rather than allowing the number of steps to be determined by the NLLS analysis (i.e., allowing n to “float”). This is why early analyses of DNA unwinding time courses (Ali and Lohman, 1997) were performed by a “bootstrapping” method in which n was constrained to be an integer, followed by a NLLS analysis for that value of n, then n was changed to another integer value, and the NLLS process was repeated. The results of analyses of a series of experiments performed with several duplex lengths were then compared to find a set of values of n, which was consistent for the different duplex lengths (i.e., for which a constant step size, m = L/n, was achieved). For these reasons, expressions for f_ss(t) that are continuous functions of n (and thus m) are required for rigorous NLLS analysis.

There are additional reasons for considering noninteger values of the number of steps, n, as well as the “step size”, m. First, it is conceivable that the number of basepairs unwound per step is not an absolute constant, but varies within some range. Thus, the average DNA unwinding step size determined from studies of a series of DNA duplexes might be expected to result in a noninteger value of m. A noninteger average step size could also arise if the DNA duplex lengths, L, used in the experimental determination of the kinetic step size are not all integer products of the step size (which of course is impossible to know a priori). Finally, an average noninteger step size is expected simply as a result of experimental uncertainty. Therefore, the ability to account for a noninteger number of steps simplifies any NLLS analysis, and allows one to consider more carefully the possible stochastic nature of the kinetic step size and its experimental uncertainties.

The analytic solutions for f_ss(t) discussed above and previously (Ali and Lohman, 1997; Lucius et al., 2002), which are expressed as a series multiplied by an exponential, are limited in use to integer values of n. However, as shown above and in Appendix A, the general form of the solution for f_ss(t) that is obtained using Laplace transform methods yields a ratio of gamma functions, which is a continuous function of n. For example, Eqs. 4, 10, and 16, which are the general solutions for Schemes 1, 2, and 3, respectively, are continuous functions of the number of steps, n, and therefore can be easily implemented for use in a NLLS fitting routine (Lucius et al., 2002).

As shown in Appendix A, it is relatively simple to obtain analytic expressions for the Laplace transform of f_ss(t) (i.e., F_ss(s)), even for Schemes for which an analytic solution for f_ss(t) is not obtainable. In fact, since one can obtain f_ss(t) by obtaining the numerical value for the inverse Laplace transform of F_ss(s), it is not even necessary to have the analytic solution for f_ss(t). One can directly perform NLLS analyses on a time course or a series of time courses using Eq. 31:

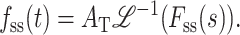(31)

In fact, by obtaining the inverse Laplace transform of F_ss(s) in numerical form, Lucius et al. (2002) were able to perform NLLS analysis using complex models such as Scheme 4 (Eqs. 18 and 31), even though an analytic solution in the time domain could not be obtained that was continuous in both n and h. Using numerical solutions to the inverse Laplace transform, one can float both n and h in a NLLS fitting algorithm for a set of time courses for duplexes of different lengths. This is currently the preferred method for analysis of experimental data in our laboratory.

Methods for determining the kinetic step size, m

Single-turnover studies of helicase-catalyzed DNA unwinding can be used to estimate the “kinetic step size”, m, i.e., the number of basepairs unwound between two successive rate limiting steps that are repeated in the unwinding cycle (Ali and Lohman, 1997; Jankowsky et al., 2000; Lucius et al., 2002). The expectation is that the number of “steps”, n, that are repeated during unwinding should be directly proportional to duplex length, L, such that n = L/m. However, one should not simply perform an unwinding experiment with a DNA substrate of one duplex length and estimate m by dividing the duplex length, L, by the number of apparent steps, n_app, required to fit the time course to a defined mechanism. One must consider whether all of the steps identified occur within each repeated cycle of unwinding or whether some steps might either be distinct from the unwinding cycle (e.g., slow initiation steps, etc.), or be coupled to each unwinding step, although not involved directly in DNA unwinding (e.g., conformational changes that occur after each unwinding step). As discussed above, the presence of such additional steps, not involved in unwinding, would yield an underestimate of the true step size. It is also not recommended to estimate m based on experiments performed with one duplex length since this would yield unacceptably high uncertainties. The reader is referred to a detailed analysis of single turnover DNA unwinding time courses catalyzed by the E. coli RecBCD helicase (Lucius et al., 2002) using the techniques described here, in which it was concluded that two additional steps occur in the mechanism that are not involved in DNA unwinding (see Scheme 4).

APPENDIX A: LAPLACE TRANSFORM METHODS FOR OBTAINING SOLUTIONS FOR THE TIME DEPENDENCE OF FORMATION OF FULLY UNWOUND DNA (F_SS(T)) FOR A SINGLE-TURNOVER HELICASE-CATALYZED DNA UNWINDING REACTION OCCURRING BY “N-STEP” SEQUENTIAL MECHANISMS

Here we present the details for deriving the expressions for the time dependence of formation of fully unwound single stranded DNA, f_ss(t), for single-turnover helicase-catalyzed DNA unwinding reactions. Since all of the “n-step” sequential mechanisms that we discuss in the text can be described by a series of linear, first order differential equations, we can use Laplace transform methods to solve for expressions for the time dependence of formation and dissipation of the various intermediates in each mechanism. In fact, this method can only be used for solutions of a series of linear first order differential equations. For more details, the reader can consult any general mathematics text (e.g., Kreyszig (1993)). Much of the mathematical manipulation presented here can be facilitated through use of any mathematical software package that allows symbolic manipulation of algebraic equations and matrices; however, we have generally used Mathematica (Wolfram Research, Champaign, IL) for this purpose.

One starts by writing the system of differential equations that describe the particular scheme under consideration. For example, the differential equations describing the time dependent formation and dissipation of the species in Scheme 1 are given by Eqs. A1–A6 for n number of steps:

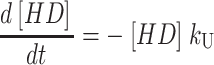(A1)

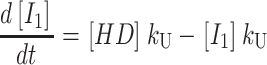(A2)

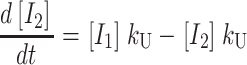(A3)

(A4)

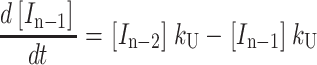(A5)

(A6)

Application of the Laplace transform to this series of coupled differential equations results in a series of coupled algebraic equations, which can then be handled much more readily. The Laplace transform, F(s), of a function, f(t), is defined in Eq. A7,

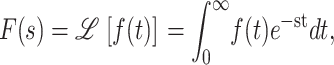(A7)

and the inverse Laplace transform of F(s) yields f(t), as defined in Eq. A8,

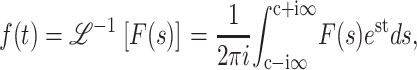(A8)

where 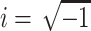, and c is chosen so that all of the singular points of F(s) lie to the left of the line Re{s} = c in the complex s plane. Eqs. A7 and A8 are the strict definitions of the Laplace and the inverse Laplace transform, respectively, however, as will become clear below, one does not typically perform these integrations to solve the problem. From Eq. A7 it follows that

(A9)

where is at 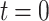. It also follows from Eq. A7 that the inverse Laplace transform of the product of two Laplace transforms, F(s) and G(s), is equal to the convolution of the corresponding time-dependent functions, 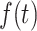and 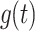, as shown in Eq. A10:

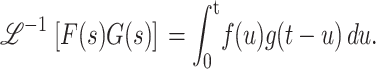(A10)

Taking the Laplace transforms of Eqs. A1–A6 yields Eqs. A11–A16:

(A11)

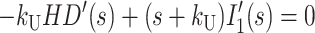(A12)

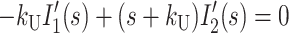(A13)

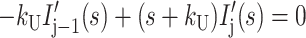(A14)

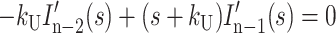(A15)

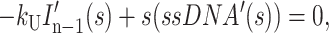(A16)

where HD′(s), I_j′(s), and ssDNA′(s) represent the concentrations of substrate-enzyme complex, intermediate j, and product, respectively, as functions of the complex variable s. HD₀ is the initial concentration of the HD complex at t = 0, and we have assumed that the initial concentrations of all intermediates and the final ssDNA product are zero.

Equations A11–A16 can be written in matrix form as in Eq. A17:

(A17)

Equation A17 can then be row reduced to yield Eq. A18, where each term in the last column is the Laplace transform for the concentration of each species in Scheme 1 (see Eqs. A19–A24):

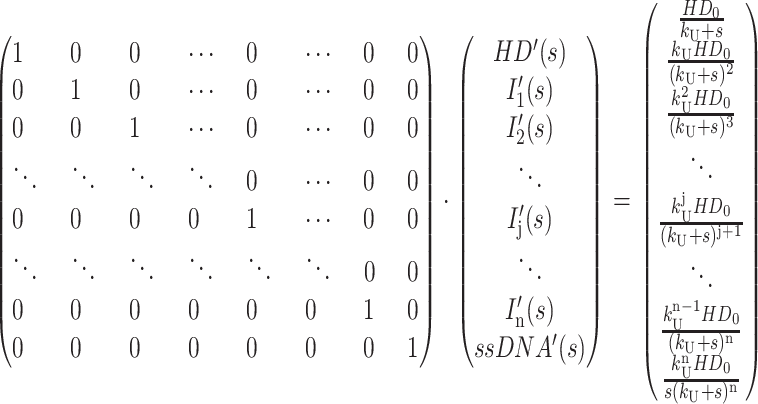(A18)

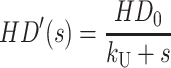(A19)

(A20)

(A21)

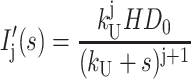(A22)

(A23)

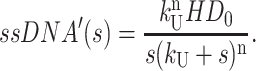(A24)

The time-dependent expressions for the concentrations of the initial enzyme-substrate complex, the final ssDNA product, and each intermediate are then obtained by taking the inverse Laplace transforms of Eqs. A19–A24. This can be accomplished using Eq. A8, or by consulting a table of known Laplace transforms or by using a mathematical software package such as Mathematica.

For example, Eq. A24 can be separated into two parts:

(A25)

The inverse Laplace transform of each part can be found in tables of Laplace transforms,

(A26)

where the gamma function, 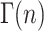, is defined in Eq. A27:

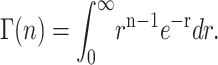(A27)

For integer values of n, the gamma function can be defined as in Eq. A28,

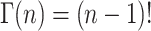(A28)

and

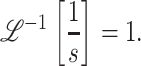(A29)

Through application of Eq. A10, we obtain Eq. A30:

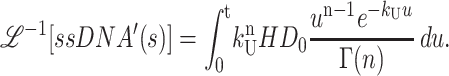(A30)

The integral in Eq. A30 can be rewritten as in Eq. A31,

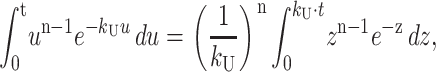(A31)

and then further simplified as in Eq. A32,

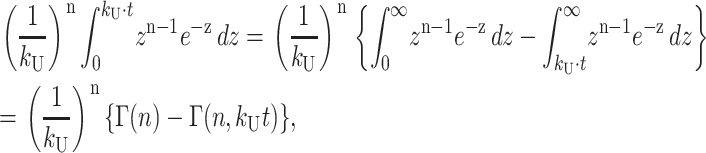(A32)

where Γ(n,z) is the incomplete gamma function, defined in Eq. A33:

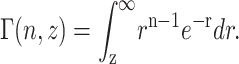(A33)

Thus, the final expression for [ssDNA(t)] is given in Eq. A34:

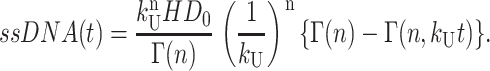(A34)

Upon rearranging, one obtains Eq. A35:

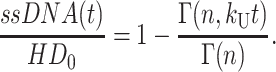(A35)

If n is an integer, the ratio of the gamma functions in Eq. A35 can be replaced with the series shown in Eq. A36,

(A36)

so that Eq. A35 can be rewritten as Eq. A37:

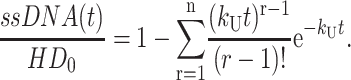(A37)

Using the same technique, the analytic solution for the time-dependent loss of the helicase-DNA complex and the formation and disappearance of the jth intermediate are given in Eqs. A38 and A39, respectively:

(A38)

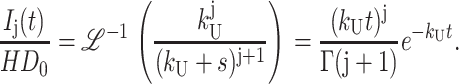(A39)

For Scheme 2, the Laplace transforms and inverse Laplace transforms for each species are given in Eqs. A40–A42:

(A40)

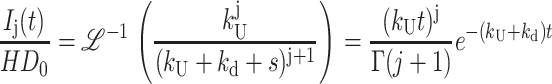(A41)

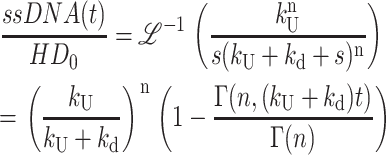(A42)

For Scheme 3, the time-dependent expressions for the concentrations of each species are given in Eqs. A43–A46:

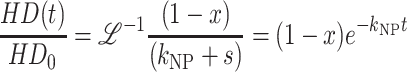(A43)

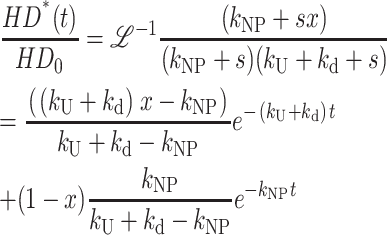(A44)

(A45)

(A46)

APPENDIX B: PROCESSIVITY OF DNA UNWINDING

The processivity, P, has been defined in terms of k_U, k_d (Eq. 6) as well as the average number of steps taken, N, (Eq. 6) (McClure and Chow, 1980). Derivations for these relationships have not been reported, thus we present them here.

The average value, 〈x〉, of any probability distribution function, f(x), is given by Eq. B1:

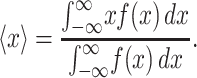(B1)

Therefore, the average number of steps taken, 〈N_stp〉, is defined by Eq. B2. The lower limit of integration in Eq. B2 is zero since we consider only forward motion Eq. B2:

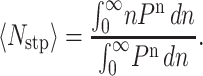(B2)

The integration of Eq. B2 results in Eq. B3,

(B3)

which upon rearrangement yields Eq. B4,

(B4)

Equation B4 can be expanded in a Taylor series to yield Eq. B5:

(B5)

In the limit of (〈N_stp〉) ≫ 1, this series can be approximated by only the first two terms

(B6)

To determine the average number of basepairs unwound, 〈N_bp〉, a similar integration can be performed by replacing n with L/m as in Eq. B7, if there are m basepairs unwound per step.

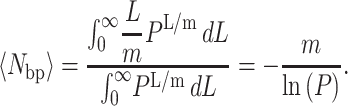(B7)

Rearranging Eq. B7 and expanding the result in a series yields Eq. B8,

(B8)

where again, the approximation is valid only when (〈N_bp〉) ≫ m.

APPENDIX C: NONLINEAR LEAST-SQUARES METHODS

We have used the program Conlin (Williams and Hall, 2000) for all NLLS analysis. The routine in Conlin used for the numerical inversion of the Laplace transform was purchased from Visual Numerics (Houston, TX) and is contained within the IMSL C Numerical Libraries. The routine is based on a modification of Weeks' method (Weeks, 1966) due to Garbow et al. (1988). To our knowledge, the only other commercially available package that implements the numerical inversion of the Laplace transform for the direct fitting of data is Scientist (MicroMath, St. Louis, MO). Mathematica can be used for determining the numerical inverse Laplace transforms; however, it does not contain a global NLLS analysis package. The gamma function representation of the analytic solution was implemented in Conlin using the routines for the gamma function and incomplete gamma function published in Numerical Recipes in C (Press, 1995).

The symbolic algebraic manipulations as well as the matrix manipulations described in Appendix A were performed using Mathematica. The time-dependent solutions were also found using the “InverseLaplaceTransform” command in Mathematica.

To determine if inversion of the Laplace transform by numerical methods could be used in our analysis, a set of data points were simulated using the analytic solution to Scheme 1 (Eq. 2). Data points were simulated for n = 5 steps, and k_U = 50 s⁻¹. The simulated data points were fit to both the analytic solution as well as the numerical inversion of the Laplace transform. In the case of the fit to the analytic solution, the number of steps was set to n = 5 and the series in Eq. 3 was expanded, so that the only fitting parameter was the unwinding rate constant k_U. In the case of the fit to the numerical inversion, both the rate constant k_U and the number of steps were floated as fitting parameters. The solid line in Fig. 6 is the result from the fitting of the data to the numerical inverse Laplace transform, which yields a rate constant of 50 s⁻¹ and a number of steps n = 5. The difference between the sum of the squared residuals for the fit to the analytic solution and the numerical inversion is 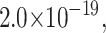leading us to conclude that the fit using the numerical routine is identical to the fit using the analytic solution. Furthermore, fitting of the data to the numerical inverse Laplace transform is significantly less cumbersome, given that finding the best model using the series solution results in having to fit the data several times to different expansions of the series until one finds the minimum in the sum of the squared residuals. Equally good agreement was obtained with the gamma function representations as expressed in Eq. 2.

FIGURE 6.

Simulation to determine if the numerical inversion of the Laplace transform can be used to perform nonlinear least-squares analysis. Data points (•) are simulated from Scheme 1 (Eq. 2) with n = 5 steps, and k_U = 50 s⁻¹. The solid line is a nonlinear least-squares fit using the numerical inverse Laplace transform of Eq. 1. The best fit to the simulated data points predicts an unwinding rate constant k_U = 50 s⁻¹, and the number of steps n = 5 by floating k_U and n as fitting parameters. The variance of the fit is , which results in a percent error in the fit to be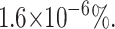

All fitting models implemented in Conlin will be made available for download at http://biochem.wustl.edu/∼lohman.