Optical Microwell Assay of Membrane Transport Kinetics

Abstract

In optical single transporter recording, membranes are firmly attached to flat solid substrates containing small wells or test compartments (TC). Transport of fluorescent molecules through TC-spanning membrane patches is induced by solution change and recorded by confocal microscopy. Previously, track-etched membrane filters were used to create solid substrates containing populations of randomly distributed TCs. In this study the possibilities offered by orderly TC arrays as created by laser microdrilling were explored. A theoretical framework was developed taking the convolution of membrane transport, solution change, and diffusion into account. The optical properties of orderly TC arrays were studied and the kinetics of solution change measured. Export and import through the nuclear pore complex (NPC) was analyzed in isolated envelopes of Xenopus oocyte nuclei. In accordance with previous reports nuclear transport receptor NTF2, which binds directly to NPC proteins, was found to be translocated much faster than “inert” molecules of similar size. Unexpectedly, NXT1, a homolog of NTF2 reportedly unable to bind to NPC proteins directly, was translocated as fast as NTF2. Thus, microstructured TC arrays were shown to provide optical single transporter recording with a new basis.

INTRODUCTION

Optical single transporter recording (OSTR; Tschödrich-Rotter and Peters, 1998) is a fluorescence microscopic method for the measurement of transport kinetics in membrane patches. In essence, a small chamber is employed that has a flat transparent bottom containing many microscopic wells or test compartments (TC). Membranes are transferred into the chamber and then firmly attached to the chamber bottom. Transport of fluorescent substrates across TC-spanning membrane patches is induced by changing the solution in the chamber and recorded by monitoring the concentration of the substrate within the TCs employing confocal microscopy. The TC diameter can be chosen in wide limits so that the membrane patches may contain single transporters or transporter populations of various sizes. Studies of nucleocytoplasmic transport (Keminer and Peters, 1999; Keminer et al., 1999; Siebrasse et al., 2002; Siebrasse and Peters, 2002) have outlined the basic properties of OSTR such as single-transporter resolution, transport substrate multiplexing, and parallel data acquisition (reviewed in Peters, 2003).

Previously, track-etched membrane filters that contain homogeneous populations of randomly distributed cylindrical pores were employed as bottom of the OSTR chamber. To generate TCs the filters were sealed on their external side by immersion oil. In this study orderly microwell arrays created by laser drilling were employed as chamber bottom thus making oil sealing unnecessary and largely increasing mechanical stability. In addition, a refined theoretical framework of OSTR was developed, which takes the convolution of membrane transport, solution change, and diffusion into account. By employing particularly large TCs the optical properties of microwells could be revealed and optimal conditions for the confocal recording of substrate concentrations defined. The kinetics of diffusion and solution change were measured and quantitatively modeled. The new theoretical and experimental methods were tested by measurements of nucleocytoplasmic transport, i.e., translocation through the nuclear pore complex (NPC; reviewed by Allen et al., 2000; Ryan and Wente, 2000; Fahrenkrog et al., 2001; Rout and Aitchison, 2001; Vasu and Forbes, 2001). The translocation kinetics of “inert” proteins (reviewed in Peters, 1986) such as green fluorescent protein (GFP) and α-lactalbumin (α-lact) were consistent with previous data (Paine et al., 1975; Keminer and Peters, 1999). Also, the translocation kinetics of NTF2 (Moore and Blobel, 1994; Paschal and Gerace, 1995), the nuclear transport receptor of RanGDP (Ribbeck et al., 1998; Smith et al., 1998; Stewart et al., 1998) whose translocation is facilitated by binding to phenylalanine glycine (FG)-repeats of nucleoporins (Bullock et al., 1996; Nehrbass and Blobel, 1996; Clarkson et al., 1997; Clarkson et al., 1997; Stewart et al., 1998; Chaillan-Huntington et al., 2000; Chaillan-Huntington et al., 2001; Ribbeck and Görlich, 2001; Bayliss et al., 2002; Braun et al., 2002), were consistent with previous data (Ribbeck and Görlich, 2001; Siebrasse and Peters, 2002). However, the translocation of NXT1 (Black et al., 1999), a homolog of NTF2 implicated in both protein (Black et al., 1999, 2001) and RNA export (Katahira et al., 1999; Ossareh-Nazari et al., 2000; Suyama et al., 2000; Guzik et al., 2001; Lévesque et al., 2001; Fribourg et al., 2001; Braun et al., 2001, 2002), turned out to be as fast as that of NTF2.

THEORY

Basic model of membrane transport kinetics

The OSTR specimen can be modeled as a two-compartment system consisting of a large compartment, the OSTR chamber, and a small compartment, the TC. The compartments are separated by a thin membrane, the nuclear envelope, containing discrete transporters, the NPCs. The transport substrate is instantaneously added to or removed from the chamber at zero time. The chamber shall be well stirred so that the transport substrate concentration in the chamber C_Ch is constant. The TC is so small that the transport substrate is rapidly dissipated by diffusion and the intra-TC concentration C_TC is a function of time only. For a purely passive, diffusional membrane transport process in which the substrate is not absorbed or produced anywhere in the system and its equilibration across the membrane is very fast (thin membrane approximation), the flux of substrate per unit membrane area (mol/μm²/s) is quasistationary at any time and can be expressed as:

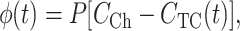(1)

where P is the permeability coefficient (μm/s). The total flux through a TC-spanning membrane patch is the sum of the unitary fluxes through individual NPCs, each having the average single-transporter permeability P_NPC (μm³/s). For a membrane patch of surface area S containing a large number n of NPCs at an average density σ (NPC/μm²)

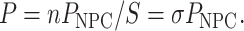(2)

For a constant concentration difference ΔC across the membrane (e.g., 1 μM), the flux and permeability described by Eq. 1 can be linked to the single-transporter permeability and expressed using Avogadro's number N_A as a unitary flux (molecules/s/NPC)

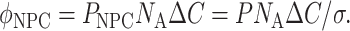(3)

OSTR chamber and TC shall have volumes V_Ch and V_TC, respectively, while the membrane patches covering the TCs shall have surface area S. The mean time of substrate diffusion inside the TC is proportional to (TC dimension)²/D where D is the diffusion coefficient of the substrate. If the TC has a size of a few micrometers only, the intra-TC diffusion time is very small, the TC can be considered as being well “stirred” and the concentration C_TC will be a function of time only. Then, the kinetics of substrate accumulation in the TC due to the flux through the membrane patch is given by (cf. Weiss, 1996)

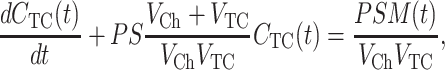(4)

where M(t) = V_Ch C_Ch(t) + V_TC C_TC(t) is the total amount of substrate. In the typical OSTR specimen the volume of the chamber is large (V_Ch ≫ V_TC) and the amount of substrate in the TC is negligible, so that Eq. 4 simplifies to

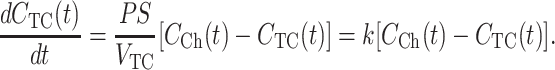(5)

For a constant concentration of the substrate in the chamber C_Ch(t) = C_max the solution of Eq. 5 is

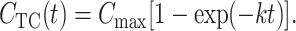(6)

The rate constant k is given by

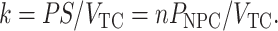(7)

For cylindrical TCs with length L and V_TC = SL the rate constant is

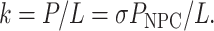(8)

From Eqs. 7 and 8 it can be seen that smaller ratios of membrane surface to TC volume (or larger length L of cylindrical TCs) can in principle slow down the observed kinetics at a given permeability P, only provided that the TC volume remains well stirred by fast diffusion as formulated above.

Accounting for solution exchange kinetics

In this study nuclear export was studied by attaching nuclear envelopes with their cytoplasmic sides to TC arrays. Then, a solution containing a transport substrate was injected into the OSTR chamber. Simultaneously, the appearance of substrate in the TCs was monitored by confocal microscopy. When the substrate had equilibrated between chamber and TCs, nuclear import was studied by injection of buffer into the chamber washing out the transport substrate. By these means the substrate concentration in the chamber could be changed within a few seconds. To evaluate the effect of solution exchange kinetics on measurements of fast membrane transport, we consider the case in which the substrate concentration in the chamber C_Ch(t) is homogeneous near the membrane but not constant, i.e., a function of time only. Then, Laplace transformation with parameter p can be applied to Eq. 5 leading to functions defined as

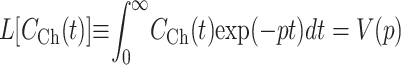and

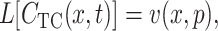so that in transformed form the solution of Eq. 5 is

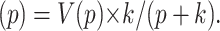(9)

This proves that the average concentration of substrate in the TC is a convolution of solution exchange and permeation kinetics, as inversion of the Laplace transform in Eq. 9 is:

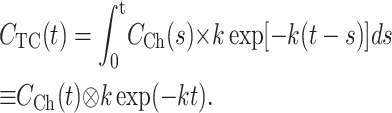(10)

The kinetics of the convolution process cannot be faster than the kinetics of slowest process contributing to convolution. Consequently, if the kinetics of solution exchange (first term in Eq. 10) is known, the rate constant of fast membrane transport can be recovered from recorded C_TC(t) by deconvolution, and the time resolution can be improved.

Accounting for diffusion inside the TCs

The formalism described by Eqs. 4–10 holds for the case in which the dissipation of substrate in the TC by diffusion is much faster than membrane transport, i.e., for small TCs or slow transport. In general, however, a large TC represents an “unstirred layer” where intra-TC diffusion delays substrate dissipation and thus further slows down apparent transport kinetics. To link observed kinetics to “true” membrane transport rates we model the TC as a cylindrical compartment extending from x = 0 to x = L (bottom). The substrate enters or leaves the TC by membrane transport at x = 0 and diffuses along the vertical axis giving rise to the concentration profile C(x,t) (index “TC” is omitted in the following). We neglect edge effects and reduce the problem to one-dimensional diffusion in a finite plane sheet described by equation:

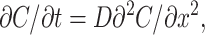(11)

where D is the diffusion coefficient of the substrate in the TC. As before, the chamber is regarded as well stirred, so that C_Ch is a function of time only. In an infinitesimal volume element at x → 0 the substrate concentration is increased or decreased by passive membrane transport flux according to Eq. 1. Simultaneously, the substrate concentration is decreased or increased by a diffusional flux which, according to Fick's first law, equals 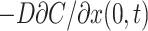. Because substrate does not accumulate in the volume element, the two fluxes have to be equal so that the condition for the boundary x = 0 is

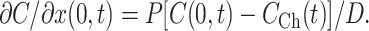(12)

Because the bottom of the TC is impermeable, the second boundary condition at x=L is

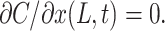(13)

The solution of Eq. 11 in Laplace coordinates with the boundary conditions given by Eqs. 12 and 13 is:

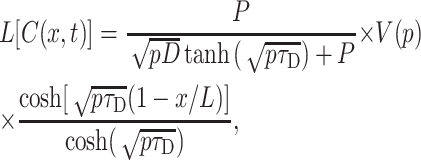(14)

where p is the transform parameter and τ_D = L²/D is the characteristic time of diffusion, e.g., for L = 50 μm and D = 80 μm²/s τ_D = 31.25 s.

For the analysis of Eq. 14 let us consider at first a complementary problem of diffusion into the TC without membrane (or with a membrane of infinitely large permeability) from an interface layer having prescribed substrate concentration C_Ch(t) at x = 0. The solution of this problem C_d(x,t), as given by Duhamel's theorem (Carslaw and Jaeger, 1959), is a convolution of solution change kinetics and diffusion and thus equals to the product of the two last terms of Eq. 14:

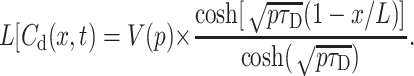(15)

Because the multiplication in Laplace coordinates is equivalent to a Laplace transform of convolution in time, the complete solution Eq. 14 represents an additional convolution of this complimentary solution defined by Eq. 15 with the first term, a function of permeability and diffusion F(P,D,L,t). After inversion of the Laplace transform, Eq. 14 should thus have the form

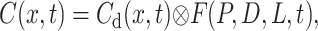(16)

where the Laplace transform of F(P,D,L,t) can be written as

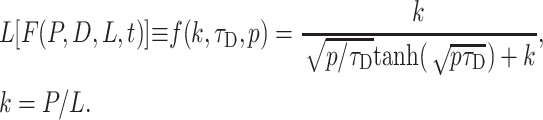(17)

In this form, the kinetics of intra-TC concentration appear close to a convolution with the same rate constant k as in Eqs. 5–10 if tanh[(pτ_D)^0.5](p/τ_D)^0.5 = p, as true for an infinitely small τ_D and consistent with the previous description. Equation 17 shows that two rate values P/L and D/L² for permeation and free diffusion control the kinetics of intra-TC concentration, which in general differs from exponential.

In this study, the pitch of the TCs was chosen such that substrate concentration could be measured simultaneously in nuclear envelope-covered and in free (control) TCs. Concentration changes recorded inside control TCs represent a convenient empirical estimate of the compound effect of solution change and diffusion, C_d(x,t) in Eq. 15. These data were taken as a basis for the analysis of the kinetics inside TCs covered by a membrane and for fitting the rate constants of permeation k in Eqs. 16 and 17. In this way we, in effect, deconvolved the contributions of solution change and intra-TC diffusion from permeation data. Approximate closed analytical forms for the functions C_d(x,t) and F(P,D,L,t) can be obtained (see Appendix).

The above equations were derived for the case in which the substrate concentration in the TCs was initially zero (export). Evidently, analog equations hold for efflux from the TC (import).

Recovery of the membrane permeability coefficient by deconvolution

Limits for the recovery of the permeability coefficient P by deconvolution were analyzed by model calculations (Fig. 1). In Fig. 1 A the time dependence of the substrate concentration at x = 30 μm in a TC of L = 50 μm is shown assuming instantaneous solution change at t = 0. The TC concentration increase purely due to permeation at P = 5 μm/s (and infinite D, dash-dotted curve marked P/L) is fastest. The concentration change due to pure diffusion at D = 80 μm/s² (and infinite P, dashed curve marked C_d) is somewhat slower, whereas the convolution of both processes is slowest (solid line marked C). The difference between curves C_d and C (Δ = C_d − C, dotted curve) is time dependent. We characterize the difference by the delay Δt (horizontal arrows), i.e., the difference in time required by curves C_d and C to reach half saturation (C/C_max = 0.5), and Δ_max, the maximum of Δ (vertical arrows).

FIGURE 1.

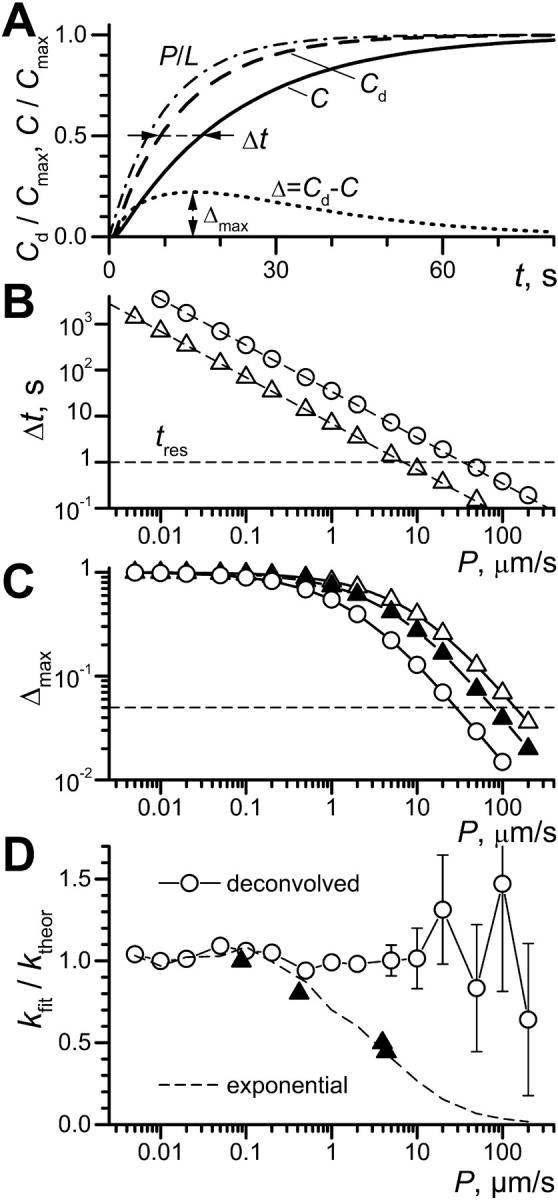
Refined theoretical description of OSTR experiments. (A) Example of calculated substrate concentration kinetics. Length of test compartment, L = 50 μm; observation at x = 30 μm; concentration in the chamber changed instantaneously from 0 to C_max at t = 0. Curve P/L (dash-dot line): pure permeation or membrane transport (D→∞, P = 5 μm/s; calculated according to Eq. 6 for k = P/L = 0.1 s⁻¹). Curve C_d (dashed line): pure diffusion (diffusion coefficient D = 80 μm²/s, permeability coefficient P→∞). Curve C (solid line): convolution of membrane transport and diffusion (D = 80 μm²/s, P = 5 μm/s). Horizontal arrows: difference between halftimes of permeation and diffusion Δt; vertical arrows: Δ_max, the maximum of the difference Δ = C − C_d (dotted line). (B) Dependence of Δt (see A) on P for TCs of 50-μm length (○) and 10-μm length (▵). Dashed lines represent function ln(2)L/P. Horizontal dashed line indicates an experimental time resolution t_res = 1 s. (C) Dependence of Δ_max (see A) on P for TCs of 50-μm length (○) and 10-μm length (▴, ▵). A level of 5% amplitude resolution is indicated by the dashed line. Solid triangles show data for diffusion and permeation curves in 10 μm TC both convolved with idealized exponential solution exchange 1–exp(−k_st), k_s = 1 s⁻¹. (D) From pairs of curves simulated with k_theor = P/L (see text) the membrane transport rate constants k_fit were recovered either by deconvolution (○) or by a simple exponential fit (dashed line). Experimentally obtained ratios of k-values for exponential and deconvolution fits are plotted for each transport substrate by solid triangles (data from Table 1).

With increasing permeability curve C approaches curve C_d. To determine the limits for a discrimination of C versus C_d, both Δt and Δ_max were calculated over a wide range of permeabilities for both large TCs with L = 50 μm as used in this study and small TCs with L = 10 μm as used previously (Tschödrich-Rotter and Peters, 1998). It can be seen that Δt (Fig. 1 B) decreases approximately linearly with increasing permeability for both large (open circles) and small (open triangles) TCs. Assuming somewhat deliberately that a time differences of 1 s can be picked up experimentally (t_res = 1 s, dashed line) the upper limit of resolvable permeability coefficients is 7 and 38 μm/s for 10-μm and 50-μm TCs, respectively.

In contrast, the amplitude discrimination on the basis of Δ_max (Fig. 1 C) is better in small (open triangles) than large (open circles) TCs. This is so because in large TCs diffusion is prolonged and thus permeation curves have shallower slopes. Assuming that amplitude differences >5% can be resolved experimentally (dashed line), the upper limits of detectable permeability coefficients are ∼140 and 28 μm/s for small and large TCs, respectively. However, this conclusion is misleading because an experimental time resolution of ∼100 ms would be required to realize that high limit of small TCs. Also, the kinetics of solution change play a significant role. As an example, Δ_max was calculated for 10-μm TCs assuming 1-s time constant of exponential solution exchange. This reduces the upper limit of P to ∼75 μm/s (closed triangles).

To test the quality of deconvolution fits, curves simulating experimental results were created and fitted by both the deconvolution procedure (cf. the Methods section) and the simple exponential (like permeation into small TCs, Eq. 6). Experimental curves were simulated assuming a TC length of 50 μm and a measuring position of 30 μm. The diffusion coefficient was set to D = 80 μm/s², and realistic kinetics of solution change, as measured in experiments described below, assumed. Then, curves were generated by convolving membrane transport for a wide range of permeability coefficients with diffusion and solution change, scaling permeation curve by 0.9 and adding random normally distributed noise with standard deviation of 5%. Fig. 1 D shows that the deconvolution procedure could retrieve from the pairs of curves the permeability coefficients up to 5–10 μm/s with <10% error, whereas exponential fitting in this range underestimated the values of P two to three times. Even for larger values of P = 20–50 μm/s, average results of fitting remained close to the preset values, although the fits became less precise and eventually unstable. In this range, exponential fits essentially converged to the kinetics of diffusion and did not yield correct permeability coefficients.

MATERIALS AND METHODS

Transport substrates and solutions

NXT1 was amplified from a human genomic DNA library and cloned in pGEX-2t (Pharmacia, Peapack, NJ). The resulting GST fusion protein was expressed in Escherichia coli BL21 and purified with glutathione-agarose beads following standard procedures. GST was removed by thrombin digest and NXT1 labeled with Alexa488 C5 maleimide (Molecular Probes, Leiden, The Netherlands). Free dye was removed by gel filtration on BioRad P6 column and the protein was stored in mock 3. Human Alexa488-labeled NTF2 and GFP were prepared as described (Siebrasse and Peters, 2002). Bovine α-Lact was obtained from Sigma (Taufkirchen, Germany) and labeled with Alexa488 C5 maleimide. Texas-Red-labeled 70 kDa dextran (TRD70) was from Molecular Probes. Transport solutions contained either Alexa488-NXT1 (2 μM), Alexa488-NTF2 (4 μM as monomer), GFP (4.0 μM) or Alexa488-α-Lact (9 μM) and 3–6 μM TRD70 and 100 mM sucrose in mock 3 buffer (90 mM KCl, 10 mM NaCl, 2 mM MgCl₂, 0.1 mM CaCl₂, 1.0 mM N-(2-hydroxyethyl)ethylene-diaminetriacetic acid, 10 mM HEPES, pH 7.3).

Microstructured TC arrays, OSTR chambers, initiation of transport, and image acquisition

Microstructured TC arrays were obtained from Bartels Mikrotechnik (Dortmund, Germany). The arrays were created by excimer laser irradiation of ∼200-μm thick polycarbonate foils through a metal masks. OSTR chambers of ∼15-μl volume were created as described (Siebrasse et al., 2002). Xenopus oocyte nuclei were isolated, purified, transferred into OSTR chambers and attached to TC arrays as described (Siebrasse et al., 2002). Confocal images were acquired using an inverted laser scanning microscope (Leica, Heidelberg, Germany) and a 16-fold, water immersion objective lens of 0.5 numerical aperture (NA) as described in the Results section. Export measurements were initiated by injection of 15 μl transport solution into the OSTR chamber using a very fine and flexible pipette tip (GeLoader tips of Eppendorf, Hamburg, Germany). The injected solution displaced the lighter buffer that was aspirated after injection using the same pipette. For import measurements an excess of plain buffer supplemented with 100 mM sucrose was injected into the OSTR chamber. For a second round of measurements the sucrose-containing buffer was replaced by plain buffer before adding sucrose-containing transport solution.

Evaluation of transport measurements

Confocal scans were evaluated by a specially written plug in for the image analysis program ImageJ (public domain Java version by W. Rasband, http://rsb.info.nih.gov/ij/). Using the plug in, average fluorescence intensities were determined, in the case of horizontal (xy) scans, for circular regions of interest (ROI) of ∼30 μm diameter. The readings of TC fluorescence were corrected for local background by measuring and subtracting the mean fluorescence of rings concentric with but slightly larger than the TCs. The circles were positioned concentrically on images of individual TCs so that the autofluorescent TC edges were not included (see Fig. 4 D). The results were averaged when several control or membrane-covered TCs were imaged simultaneously. Analogues procedures were applied to rectangular regions in vertical (xz) scans. For nuclear export (i.e., net transport from chamber into TCs) the initial dark TC fluorescence, measured before addition of the transport solution to the chamber, was subtracted from the data set, whereas for import all measurements were subtracted from the initial bright level, thus creating standardized curves rising with time from near-zero initial values. No normalization was applied. By calibration with solutions containing different substrate concentrations it was made sure that fluorescence was a linear function of concentration at the applied conditions. Because the substrate concentration in the bulk solution of the OSTR chamber was known, measured fluorescence intensities could be converted into concentrations using the fluorescence of control TCs as reference.

FIGURE 4.

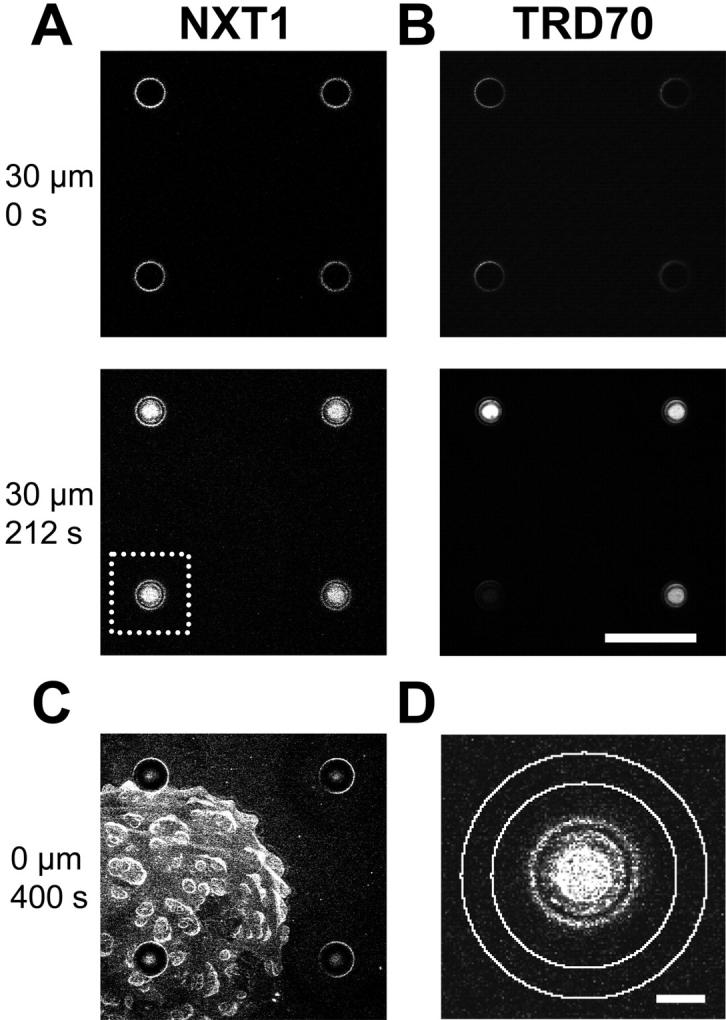
Measurement of NXT1 translocation through the NPC. In an OSTR chamber a Xenopus oocyte nuclear envelope was attached to a TC array. A region of the TC array was imaged containing one membrane-covered TC (measuring TC) and three noncovered TCs (reference TCs). (A,B) Transport was initiated by injecting a transport solution (2 μM Alexa488-NXT1, 3 μM TRD70, 100 mM sucrose) into the chamber at t = 0. A series of horizontal confocal scans, monitoring in parallel the green Alexa488-NXT1, A, and the red TRD70 fluorescence, B, was acquired at a depth of x = 30 μm below the array surface. NXT1 appeared quickly in both measuring and reference TCs, TRD70 only in reference TCs. Scale bar: 200 μm. (C) After completion of transport the focus was shifted to the array surface disclosing that NXT1 binds to the nuclear envelope. (D) Insert from A showing regions of interest selected for the measurements of TC fluorescence (inner circle) and background (ring between two outer circles). Scale bar: 30 μm.

For permeability measurements, the kinetics of substrate concentration changes recorded in control TCs and thus representing solution change and diffusion (C_d(x,t) in Eq. 15) were first fitted by a sum of two exponents with offset C₀:

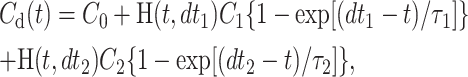(18)

where H(t,x) is a step function with H = 0 when t < x and H = 1 when t ≥ x. The values of amplitudes C_i, delays dt_i and time constants τ_i (i = 1,2) that yielded the best fit to the control TC data were than used in the second fitting of the kinetics in membrane-covered TCs. The Laplace transform of the fitting function C_d(t) Eq. 18 was multiplied by f(k,τ_D,p) × A (see Eq. 17), where the scaling parameter A accounted for the differences between final fluorescence amplitudes in measuring and control TCs. In thus obtained analytical expression, the Laplace transform was numerically inverted as described (Kiskin and Ogden, 2002). Then, the obtained numerical function of time was fitted to the experimental kinetics of fluorescence in covered TCs by variation of the parameters A and k, using τ_D values calculated from the values of L = 50 μm and D = 80 μm²/s for GFP, NTF2, NXT1, and 107 μm²/s for α-Lact (Adamson et al., 1988). Data fitting was performed in MathCad (version 6e, MathSoft, Cambridge, MA), which employs nonlinear Levenberg-Marquardt fitting routines using function derivatives, also expressed by numerical inversion. All rate constants reported in the Results section were obtained by fits using numerical inversion of Laplace transforms. In addition, an approximation to Eq. 17 derived in the Appendix was employed yielding all functions in analytical time-dependent form. All experimental data were also fitted by the approximation, and with τ_D unconstrained, with no substantial differences of the outcome to that of the chosen numerical approach.

RESULTS

Geometry and optics of microstructured TC arrays

Previously, TC arrays have been created from track-etched membrane filters having pores of 0.2–5.0 μm diameter (Tschödrich-Rotter and Peters, 1998). In this study OSTR was put on a new basis by applying orderly microstructured TC arrays created by laser drilling. Laser drilling permits to generate TCs > 1 μm. However, in this first application the size of the TCs was chosen to be particularly large. This had the decisive advantage that the optical properties of the TCs could be easily resolved, characterized and taken into account. The principles and procedures established with these large TCs also hold for much smaller TCs, although different rules apply for subwavelength, nanometer-sized TCs.

Microstructured TC arrays were used to create OSTR chambers of 3.5-mm diameter and 1.3-mm depth as shown in Fig. 2 A. To determine the TC geometry OSTR chambers were filled with immersion oil (n = 1.55) and observed through an oil immersion objective, thus largely reducing the refractive index mismatch between microarray (birefringent polycarbonate foil with n ∼ 1.63 and 1.58) and air (n ∼ 1) or buffer (n ∼ 1.35). The TC walls were found to display a distinct autofluorescence, probably caused by irradiation with a strong ultraviolet beam during laser drilling. In vertical confocal scans (Fig. 2 B, left) the TC appeared as a trough-like structure with an opening of 75-μm diameter, a bottom of 55-μm diameter, and a length L = 50 μm. At the bottom a sharp ring-like recess was also apparent. These dimensions were confirmed by horizontal confocal sections (Fig. 2 C, left).

FIGURE 2.

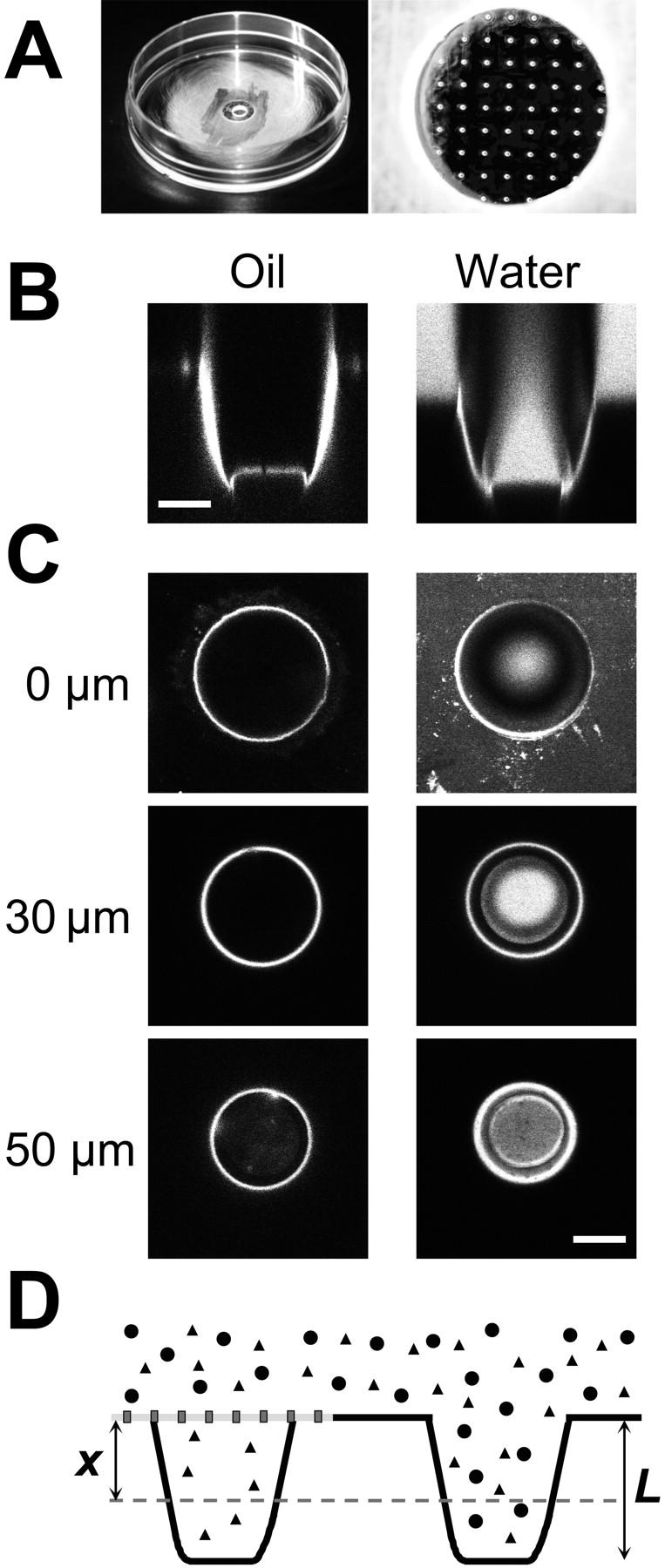
Optical properties of microstructured test compartments. (A) OSTR chamber with attached TC array. (B) Vertical confocal scan through TCs filled with immersion oil, 40-fold 1.0 NA objective (left) or a 4-μM aqueous solution of Alexa488-NTF2, 16-fold 0.5 NA objective (right). (C) Horizontal confocal scans of the TCs shown in B. Vertical positions of the scans as indicated. Scale bars: 30 μm. (D) Schematic drawing of arrangement in transport measurements (cf. Fig. 4). Two TCs are shown, one covered by a membrane (measuring TC), the other without membrane (reference TC). The transport substrate (triangles) is able to permeate the membrane and thus to fill both the measuring and the reference TC. The control substance (circles) cannot permeate the membrane and is therefore found only in the reference TC. The fluorescence is sampled (dashed line) at a depth of x = 30 μm (i.e., x/L = 0.6), which is optimal for measurements inside TCs.

When OSTR chambers were filled with the aqueous solution of a fluorescently labeled protein such as Alexa488-NTF2 vertical scans (Fig. 2 B, right) disclosed that the TC interior was properly imaged within a cone only, extending from the TC bottom to the TC entrance (the direction of illumination was from bottom to entrance). This effect as well as other optical phenomena apparent in Fig. 2 B (right) could be easily understood on a qualitative basis by application of a ray-tracing program (data not shown). The relatively planar TC bottom can be crossed from below by fluorescence-exciting rays within an imaging cone determined by the NA of the objective. The rays that encounter the polycarbonate/water interface near TC walls may be either refracted (focus shifts several micrometers down) or reflected, depending on the incidence angle. With low magnification objectives, the angle is mostly shallow. Thus, a loss of excitation due to wall reflections leads to dark areas outside the main imaging cone. A quantitative description of these optical phenomena is more involved and was not performed in the present study. The scan shown in Fig. 2 B (right) suggests measuring the fluorescence intensity in a central region of the TC where it is close to that of the solution in the chamber (horizontal scans Fig. 2 C). At present experimental conditions, the optimum was at x = 30 μm. Therefore, in all measurements described below the vertical position of the focal plane was adjusted to that value (x/L = 0.6). Finally, it may be recalled that in transport measurements, fluorescence intensities of measuring and reference TCs were recorded at identical axial position so that both were equally affected, if at all, by optical effects.

Kinetics of solution change in the OSTR chamber and diffusion inside test compartments

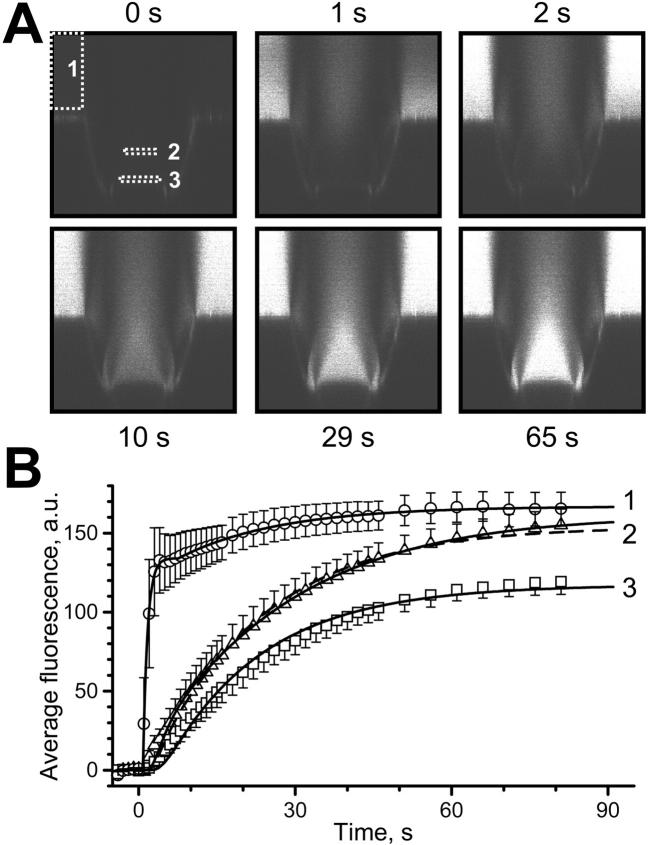
In the measurements described below, transport through the NPC was induced by rapidly changing the solution in the OSTR chamber. To study the kinetics of solution change, a TC filled with buffer was imaged by vertical confocal scans at a rate of one frame per second (Fig. 3 A). Then, a solution containing 4 μM GFP and 100 mM sucrose was injected into the OSTR chamber during scanning. The fluorescence in the OSTR chamber (measured in area 1 of Fig. 3 A) changed rapidly to reach a plateau a few seconds after injection. In contrast, the fluorescence change inside TCs (measured in areas 2 and 3 of Fig. 3 A) was delayed by 20–50 s by diffusion. From simultaneous records of fluorescence in the chamber and inside the TC we may quantify the speed of solution change and test an assumption that the convolution with diffusion C_d(x,t) (Eq. 15) can describe fluorescence kinetics inside the TC.

FIGURE 3.

Solution change kinetics and diffusion: experiment and theory. At t = 0, a solution containing 4 μM GFP and 100 mM sucrose was injected into a buffer-filled OSTR chamber. A series of vertical confocal 125 × 125 μm scans was acquired, employing the time lapse program of the microscope. (A) Examples of the image series at indicated times. White rectangles show regions where fluorescence was quantified. (B) Quantification and fit. Experimental data (symbols, average of six measurements, bars indicate SE) were derived from image series shown in A. Curve 1 represents best fit to solution change kinetics at the surface of the TC (box 1) yielding (in fluorescence units) C₀ = 0, C₁ = 134, C₂ = 32.9, τ₁ = 0.870 s, τ₂ = 19.4 s, dt₁ = 0.788 s, dt₂ = 7.59 s in Eq. 18. Curve 2 represents best fit to experimental concentration change in area 2 (x = 30 μm) at different conditions: solid line: unconstrained fit was obtained with τ_D = 53.4 s, x/L = 0.48, and ratio of amplitude to the amplitude of curve 1 equals 0.97; dashed line: fit with fixed x/L = 0.6 yielded τ_D = 39.6 s and amplitude ratio 0.92. Curve 3 shows fit to experimental concentration change at the TC bottom (x = 50 μm) giving τ_D = 34.1 s and amplitude ratio 0.70.

The quantification of six such experiments is given in Fig. 3 B. The mean fluorescence of areas 1, 2, and 3 was plotted versus time after injection (symbols). The fluorescence change in the chamber could be well fitted (Eq. 18) by two shifted rising exponents with time constants of 0.87 s and 19.4 s and amplitude ratio of 7.3:1 (curve 1). Treating that result as C_Ch(t), the fluorescence change measured at x = 30 μm was best fitted according to Eq. 15 by τ_D = 53.4 s (D = 46.8 μm²/s) and x/L = 0.48 (curve 2, solid line, unconstrained fit). When x/L was fixed at 0.6 as in all measurements, the best fit yielded τ_D = 39.6 s (curve 2, dashed line), corresponding to a diffusion coefficient D = 63.2 μm²/s. When the same procedure was applied to the fluorescence change at the TC bottom (x = L) τ_D amounted to 34.1 s (curve 3), corresponding to D = 73.2 μm²/s.

The diffusion coefficient of GFP has been previously determined by photobleaching to be D = 87 μm²/s in dilute buffer (Swaminathan et al., 1997). The value of D = 63–73 μm²/s estimated in these experiments agrees well with the value determined by photobleaching taking the viscosity of our transport medium (100 mM sucrose, ∼1.1 cPoise) and fit uncertainties into account. This suggests that the convolution approach adequately describes the experimental system.

Test measurements of translocation through the nuclear pore complex

To measure translocation through the nuclear envelope, an OSTR chamber (Fig. 2 A, right) was filled with mock 3 buffer. A manually isolated and purified Xenopus oocyte nucleus was deposited in that OSTR chamber. The nucleus was attached to the TC array by slight pressure and then opened with a fine needle. The nuclear contents were removed and the residual nuclear envelope purified by washing it three times with mock 3 buffer. The OSTR chamber was transferred on the stage of an inverted confocal laser scanning microscope and the nuclear envelope visualized in transmitted light using a water-immersion objective (16-fold, 0.5 NA). The nuclear envelope was positioned such (cf. Fig.2 D) that the scanned field contained at least one TC covered by the nuclear envelope (measuring TC) and one TC not covered by the nuclear envelope (reference TC). The focal plane was adjusted to a depth of 30 μm below the surface of the TC array. The time lapse program of the microscope system was started to acquire a series of horizontal confocal scans according to a preset schedule, and a transport solution was injected into the OSTR chamber during image acquisition. After completion of export and filling of TCs with transport substrate, import was studied by injecting an excess of mock 3 buffer into the OSTR chamber during scanning. In many cases a second round of export and import measurements was performed.

A representative measurement, in which a transport solution contained Alexa488-labeled recombinant human NXT1 (2 μM), TRD70 (3 μM), and sucrose (100 mM), is shown in Fig. 4. The scans show four TCs, one of which (lower left, white box) was covered by the nuclear envelope whereas three TCs were not covered. It can be recognized that at t = 0 s all TCs were void of fluorescence, both in the channel recording the green Alexa488 fluorescence (Fig. 4 A) and the channel recording the red TRD70 fluorescence (Fig. 4 B). The TC walls were visible from the beginning because of their autofluorescence. A few seconds after injection both NXT1 and TRD70 appeared in the reference TCs. In case of the membrane-covered TC, NXT1 appeared very shortly after injection indicating fast translocation through the NPC. However, TRD70 was excluded from the measuring TC for extended time periods, indicating tight sealing. Sometimes TRD70 leaked into the measuring TC; these experiments were discarded.

After completion of export the focal plane was shifted to the surface of the array and the nuclear envelope was imaged (Fig. 4 C). It became apparent that NXT1 bound to the nuclear envelope, very similarly to NTF2 as observed previously (Siebrasse and Peters, 2002). The binding of NXT1 to the nuclear envelope could be particularly well recognized on the protrusion typical of the Xenopus nuclear envelope. During attachment of the nuclear envelope to the TC array the protrusions collapsed forming onion-like structures. However, between collapsed protrusions large planar membrane areas occurred and it can be seen (Fig. 4 C) that the measuring TC was also covered by a planar membrane piece. Occasionally, TCs were covered by membrane protrusion, but such measurements were discarded.

The fluorescence of TCs was quantified by an image-processing program (cf. Methods section). In principles (Fig. 4 D), a circular region ROI was placed in the TC center. Another ring-shaped ROI surrounded the TC. The difference of the mean fluorescence of the two ROIs yielded a value of the background-corrected mean fluorescence F(t) of the solution in the TC.

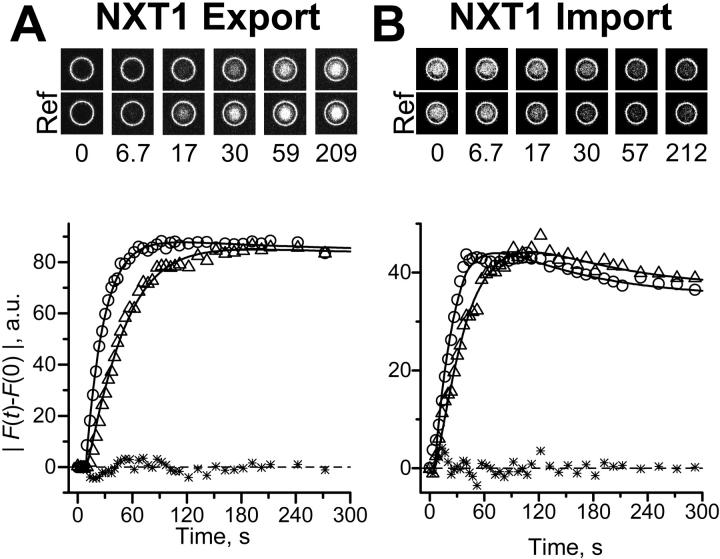
More details of the transport kinetics are given in Fig. 5. For an export experiment (Fig. 5 A) raw data are shown at the top by scans of a measuring and a reference TC (Ref) placed side by side. It can be recognized that the transport of NXT1 through the nuclear envelope was very fast; NXT1 appeared in the measuring TC only slightly later than in the reference TC. In the graph (bottom) the difference between F(t) and F(t = 0) was plotted as absolute value versus time (symbols) for both measuring (triangles) and the reference (circles) TC. The experimental data were fitted by Eqs. 15 and 18 (lines). An import experiment is illustrated in Fig. 5 B. Again it is obvious that the transport of NXT1 was very fast. Note that |F(t) − F(0)| rises with time in both import and export experiments.

FIGURE 5.

Export and import kinetics of NXT1. Translocation of NXT1 through the nuclear pore complex was measured as illustrated in Fig. 4. (A) Export. At the top, selected examples from a representative image series are given, placing a measuring TC and a reference TC (Ref) of channel 1 (Alexa488-NXT1 fluorescence) side by side (montage of parts of scans as shown in Fig. 4 A). At the bottom, the background-corrected change in fluorescence is given for the measuring TC (triangles) and the averaged reference TCs (circles). The fluorescence of reference TCs was fitted by Eq. 18 and that of the measuring TC by Eqs. 16 and 17 yielding k = 0.0446 s⁻¹ and an amplitude ratio of 0.981 (lines). Stars show the residues of this fit. (B) Import. Symbols and lines analogous to export. The best fit yielded k = 0.0595 s⁻¹ and an amplitude ratio of 1.05.

Average values of experiments with NXT1 on nine nuclei are collected in Table 1 and reveal three major facts: 1), export and import proceeded at rates not significantly different within measuring accuracy (p > 0.7, one-way ANOVA); 2), a comparison of the rate constants obtained by a simple exponential fit with that obtained by deconvolution shows that evaluation of the data improved the time resolution by a factor of ∼2; and 3), the transport rates, expressed in NXT1 molecules/s/NPC, were large.

TABLE 1.

Translocation of nuclear transport factors NXT1 and NTF2 and “inert” molecules of similar size through the nuclear pore complex of Xenopus oocytes

Substance	Molecular mass of monomer (kD)	Concentration in transport measurements μM of monomers	Import (I) Export (E)	Rate constant from exponential fit* (10−3 s−1)	Rate constant from deconvolution* (10−3 s−1)	Mean permeability P* (μm s−1)	Transport rate at actually used concentration† (molecules s−1 NPC−1)	Mean transport rate at ΔC = 1 μM† (molecules s−1 NPC−1)
NXT1	15	2.0	I	37.8 ± 3.43 (15)	90.2 ± 15.4 (12)	4.38 ± 0.470 (23)	108.6	52.8
			E	40.1 ± 3.53 (14)	84.8 ± 11.1 (11)		102.2
NTF2	15	4.0	I	30.1 ± 3.51 (9)	63.7 ± 14.1 (8)	3.93 ± 0.672 (14)	153.6	47.3
			E	47.4 ± 6.81 (10)	98.6 ± 24.2 (6)		237.2
α-Lact	14	9.0	I	6.71 ± 0.90 (8)	6.33 ± 1.48 (8)	0.418 ± 0.0758 (17)	34.3	5.03
			E	6.70 ± 0.80 (9)	10.2 ± 2.47 (9)		55.1
GFP	29	4.0	I	2.14 ± 0.40 (7)	1.91 ± 0.31 (6)	0.0881 ± 0.0119 (14)	4.6	1.06
			E	1.46 ± 0.42 (9)	1.65 ± 0.36 (8)		4.0

^*Mean ± SE of (n) measurements.

^†Calculated from deconvolved rate constant and σ = 50 NPC μm⁻².

In many experiments two complete rounds of export and import measurements were performed with one specimen. This involved five solution changes, two in which mock 3 buffer was replaced by transport solution and two in which transport solution was replaced by mock 3 buffer, with additional washout by mock 3 before the next export experiment. The whole sequence took at least 30 min, frequently substantially longer. It was found that the transport rates did not significantly depend on the number of preceding measurements. Thus, setting the rate constant determined in the first measurement as 1.00, the rate constant determined in the second, third, and fourth measurements amounted to 1.01 ± 0.30 (n = 7), 1.06 ± 0.07 (n = 4), and 1.16 ± 0.35 (n = 2) (mean ± SD of n measurements). This result implies that the fast translocation of NXT1 was probably not mediated by endogenous soluble factors.

We determined the translocation rate of NTF2 by the same methods employed in NXT1 experiments to permit a direct comparison. The data are illustrated in Fig. 6 A and collected in Table 1. In experiments on four nuclei we found that NFT2 was translocated at rates very similar to those of NXT1. Thus, the mean rate constants for NTF2 and NXT1 were in the range of (63.7–98.6) × 10⁻³ s⁻¹, without statistically significant difference (p > 0.5, one-way ANOVA). For NTF2, as for NXT1, export and import rate constants were not different (p > 0.2, one-way ANOVA). When the rate constants were used to derive initial transport rates according to Eq. 8 and using a density σ = 50 NPC/μm², the results were 108.6 and 102.2 molecules/s/NPC for the export and import of NXT1 and 153.6 and 237.2 molecules/s/NPC for the export and import of NTF2. Averaging of export and import rates and linear extrapolation to ΔC = 1.0 μM yielded 52.8 and 47.3 molecules/s/NPC for NXT1 and NTF2, respectively.

FIGURE 6.

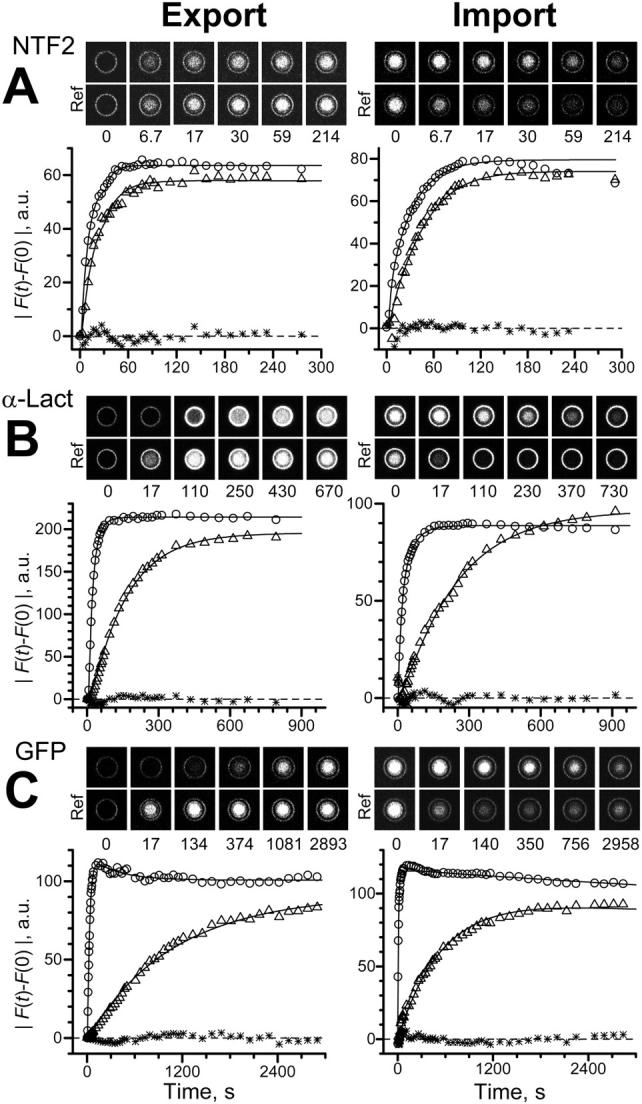
Export and import kinetics of NTF2, α-lact and GFP. Presentation as in Fig. 5. Best fits yielded (A) k = 0.117 s⁻¹, amplitude ratio A = 0.911 (NTF2 export), k = 0.0613 s⁻¹, A = 0.931 (NTF2 import); (B) k = 6.96 × 10⁻³ s⁻¹, A = 0.913 (α-lact export), k = 4.46 × 10⁻³ s⁻¹, A = 1.09 (α-lact import); (C) k = 8.79 × 10⁻⁴ s⁻¹, A = 0.911 (GFP export), k = 1.86 × 10⁻³ s⁻¹, A = 0.832 (GFP import). Note the different timescales.

The conclusion that the translocation of NTF2 through the NPC is facilitated was originally based (Ribbeck and Görlich, 2001) on the observation that the translocation rate of NTF2 was much larger than that of GFP. It was assumed that NTF2 forms stable dimers of 30 kDa, very similar in size to GFP (29 kDa). In the meantime, it has been shown that NTF2 exists in a monomer/dimer equilibrium with a dissociation constant of ∼1 μM (Chaillan-Huntington et al., 2001). For this reason and also because of uncertainties concerning the dimerization status of NXT1, we included α-lact, an “inert” 14 kDa molecule similar in size to NXT1/NTF2 monomers, and GFP in this study. The data are illustrated in Fig. 6, B and C, and collected in Table 1 for six and eight nuclei, respectively. It was found that the rate constant of α-lact, although fivefold larger than that of GFP, was still ∼10-fold smaller than that of NXT1 and NTF2. For each of the “inert” molecules export and import rates were not different (p > 0.2 and p > 0.6 for α-lact and GFP, one-way ANOVA). As expected, deconvolution was of no advantage in the case of this slow transport.

DISCUSSION

The impact of micro- and nanostructured TC arrays on OSTR has been discussed previously in more general terms (Peters, 2003). Here, we found several specific advantages of microstructured arrays in comparison to previously used track-etched filters: The experimental protocol was simplified and speeded up because bonding of filters by immersion oil was not required. The mechanical stability was largely increased permitting to change the solution in the OSTR chamber during scanning and to perform both export and import measurements. Very large TCs could be created, a fact facilitating optical studies and the direct observation of solution change kinetics, transport, and diffusion, and thus leading to the development of a refined theoretical framework taking the convolution of these processes into account.

The membrane patches created in this study had a diameter of 75 μm. Of course, to make use of the single-transporter option of OSTR much smaller patches are required. Electrophysiological studies have shown that single ion channels can be resolved in membrane patches of 2–25 μm² (Sakmann and Neher, 1995), corresponding to planar membrane patches of 1.6–5.6 μm diameter. In Xenopus oocyte nuclear envelopes the resolution of single NPCs requires membrane patches of ∼0.2 μm diameter (Keminer and Peters, 1999). Fortunately, many methods for the creation of micro- and nanometer-sized TCs are available (Madou, 2002) and thus the transition from large TCs as used in this study to small TCs yielding single-transporter resolution appears to be straight forward.

In OSTR experiments the membrane transport time depends on the TC length L (Peters, 2003). Here we found that a limiting parameter for the resolution of fast transport processes is the time required for the solution change by which transport is initiated. The solution change time was at least 1 s, although slower components were frequently present, as seen in Fig. 3 B and Fig. 6. The permeability coefficients of both NXT1 and NTF2 were large (∼4 μm/s). To properly resolve such large values of P at a solution change time of ∼1 s the permeation time L/P has to be >1 s, or L > 4 μm. However, increasing L increases the diffusion time τ_D, which is proportional to L², sharply. For instance, τ_D reaches 1 s at a L = 7–10 μm, assuming a diffusion coefficient D of ∼50–100 μm²/s. Therefore, when resolving large permeabilities by using long TCs it is crucial to deconvolve membrane transport and diffusion. It may be mentioned here that transport can be also initiated by photobleaching or photoactivation (Siebrasse and Peters, 2002) that yields an intrisically higher time resolution than solution change but has a more restricted scope of applicabilities.

The theoretical framework for the convolution of membrane transport, solution change, and diffusion made it possible to study complex kinetics in 50-μm long TCs at permeability coefficients up to 10–20 μm/s. The P values determined by deconvolution were well within the resolution limit of the method, improving the time resolution two- to threefold. However, any deconvolution procedure is model dependent and may be in error for the fastest components of the process. A central assumption of the procedure used in this study was that the solution change in the chamber, brought about by vigorous convection, did not disturb the diffusion process in the reference TCs. Experimental tests (see Fig. 3) suggested that this assumption was essentially correct, although the deviation between experimental data and fitted theoretical curves was usually slightly larger at t ≤ τ_D (Figs. 3, 5, and 6). The dependence of data evaluation on diffusion is larger at the beginning of the experiment. For these reasons it is necessary to extend data recording to longer periods, not relying on initial rates only. Another uncertainty of the deconvolution procedure may arise from local concentration differences in the chamber early after solution change. This effect could be monitored with TC arrays having a smaller pitch. Alternatively, the concentration in the chamber directly above the measuring TC could be monitored by vertical scans and taken into account in the deconvolution process which, however, would require explicit fitting of intra-TC diffusion.

The translocation of NTF2 and GFP through the NPC has been measured previously. In digitonin-permeabilized HeLa cells NTF2 or GFP were translocated at rates of 250 or 2 molecules/s/NPC, respectively, at ΔC = 1 μM (Ribbeck and Görlich, 2001). In isolated Xenopus oocyte nuclear envelopes the translocation rates for NTF2 or GFP were 91–123 or 3.8 molecules/s/NPC at ΔC = 1 μM, as measured by OSTR using TCs of 0.72-μm diameter and 10-μm length (Siebrasse and Peters, 2002). Conversion of the rate constants measured in this study into translocation rates (Table 1) yielded values of ∼50 or ∼1 molecules/s/NPC for NTF2 or GFP at ΔC = 1 μM. Thus, the present rates of both NTF2 and GFP were smaller than the rates determined previously by us (Siebrasse and Peters, 2002). The differences may be due to substantial uncertainties in estimating the number of functional NPCs per patch. In the previous study, NPCs touching the edge of the small TC were excluded (amounting to five from 20 NPCs assuming a NPC diameter of 65 nm), thus the rates may have been overestimated. Numbers in this study assume a uniform distribution of NPCs over the whole giant membrane patch area with the density σ = 50 NPC/μm². If some parts of the patch are void of NPCs, the NPC number is overestimated, and the unit rates are underestimated.

The translocation of NXT1 has not been measured previously. This study established that NXT1 is translocated as fast as NTF2, although it reportedly does not bind to FG repeats directly (Fribourg et al., 2001).

Translocation through the NPC probably proceeds via a channel (Rout et al., 2000) of ∼30–40-nm maximum diameter (Dworetzky et al., 1988; Panté and Kann, 2002) and ∼45-nm length (Keminer and Peters, 1999). The wall of the channel may be lined by flexible filaments containing FG-repeats (Grote et al., 1995; Stewart et al., 2001; Macara, 2001) leaving free, however, a central space of ∼10-nm diameter (Paine et al., 1975; Peters, 1984; Keminer and Peters, 1999). Translocation through such a fuzzy, binding site-containing channel has many implications. One interesting aspect is flux coupling. Binding transport substrates such as NTF2, which are small as compared to the channel diameter, should be able to pass through the channel on multiple parallel pathways without much interference thus yielding very high translocation rates (Ribbeck and Görlich, 2001; Siebrasse and Peters, 2002; this study). In contrast, larger objects such as karyopherin complexes, ribonucleoprotein particles or ribosomal subunits should interfere with each other during passage, yielding much smaller translocation rates (Keminer et al., 1999; Siebrasse et al., 2002). A limit is reached when the diameter of the transport substrate becomes larger than the channel radius. Then, the substrate molecules cannot pass each other and their translocation has to be coordinated resulting in single file diffusion. Flux coupling can be best characterized by the flux-ratio criterion (Ussing, 1949). With the help of two different tracers the rates of the unidirectional influx and efflux are determined simultaneously. If the flux ratio is equal to the electrochemical activity ratio across the membrane, the transport substrates move independently through the pore. A deviation from equality indicates flux coupling and provides a means for estimating channel properties such as the number of binding sites. OSTR permits the multiplexing of tracers. The present study provided the means for simultaneous import and export measurements. Thus, tools for characterizing translocation through the NPC by the flux-ratio criterion are now available.

APPENDIX

Approximate analytical forms of solutions for diffusion and permeation

For unobstructed diffusion in infinite planes from the surface x = 0 kept at constant concentration C_max, the solution of the diffusion equation in Laplace transformed form is

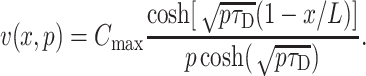Inversion of this transform leads to an infinite series that converges to the exact solution relatively slowly (Carslaw and Jaeger, 1959). For the concentration created by unobstructed diffusion at depth x the following approximate form may be found

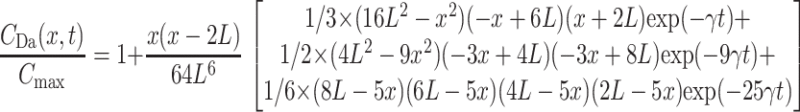from the truncated product representation of function cosh(x), where γ = π²D/(4L²) = 2.467/τ_D. Simulations show that this approximation becomes better as time increases and x decreases, whereas for large x and L delayed diffusion becomes difficult to fit.

The function describing kinetics of permeation in a TC of finite length, Eq. 17, can also be simplified. First, as described, approximation k/(k + p) leads after convolution to an exponent, which can be used for estimates of the time course of slow permeation. Second, using the Padé approximation for the function tanh(x)/x = (15 + x²)/(5 + 2x²)/3 + O(x⁶) (Kiskin and Ogden, 2002), Eq. 17 can be transformed:

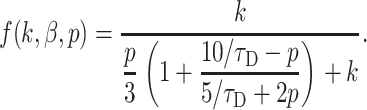(19)

Numerical inversion of the Laplace transform, Eq. 14, using this approximate form produces practically the same results as complete form in Eq. 17. The Laplace transform in obtained expression Eq. 19 can be inversed producing equivalent time-dependent expression

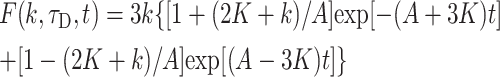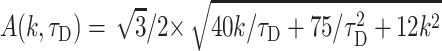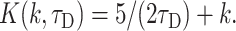To describe permeation, this function should be convolved with diffusion and with kinetics of solution change. Simulations show that an expression F(k,τ_D,t) ⊗ C_Da(x,t) gives good approximation to general solution of the permeation problem at instant solution change.

For alternative data analysis, the function F(k,τ_D,t) was convolved with Eq. 18, a fit to fluorescence in the control TC (already including diffusion and solution change), allowing fitting of k, τ_D and A as good as numerical form.