Comparison of the Effects of Surface Tension and Osmotic Pressure on the Interfacial Hydration of a Fluid Phospholipid Bilayer

Abstract

The effects of three so-called kosmotropic solutes, namely, betaine, sucrose, and choline chloride on 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine large unilamellar vesicles, were studied by measuring the generalized polarization (GP) for the fluorescence emission of the membrane partitioning probe Laurdan. The latter has been shown to be sensitive to the depth of water penetration into phospholipid bilayers. At equal osmotic pressures the three solutes produced different increments in GP, with a qualitative positive correlation. However, the increments in GP correlated also quantitatively with the increase of air-water surface tension caused by the three kosmotropes. Our findings suggest surface tension to determine the impact of these solutes on the lateral packing of the lipid bilayer. Based on the changes in area/lipid at different surface tensions, the equilibrium lateral pressure for a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine bilayer at 25°C was estimated to be ∼34 mN/m.

INTRODUCTION

Phospholipid bilayers constitute the principal structural element of all biomembranes. These surfaces are highly heterogenous in their lateral organization as well as vertical dynamics (Mouritsen and Kinnunen, 1996) and both types of dynamics modulate the function of membrane proteins (Mustonen et al., 1987; Burack and Biltonen, 1994; Janmey and Chaponnier, 1995; Goni and Alonso, 1999; Asturias et al., 1990). An inherent coupling among the organization, composition, physical state, and physiological functions of biomembranes has been postulated (Kinnunen, 1991; 1996a).

Biomembranes represent the paradigm for spontaneously assembling supramolecular structures, the main driving force being the hydrophobic effect arising from the lack of interactions of hydrocarbons with water and causing reduction in water entropy in the hydrocarbon/water interface. The forces determining the packing of a phospholipid bilayer are compiled in the lateral pressure profile (Seddon and Templer, 1995; Marsh, 1996; Cantor, 1997a). In brief, at equilibrium, steric repulsion between the phospholipid headgroups, and entropic repulsion between the acyl chains, balance the interfacial tension between water and the membrane hydrocarbon phase. Under these conditions there thus remains a significant exposure of hydrophobic surface (Marrink and Berendsen, 1994), resulting in interfacial tension and representing a direct expression of the hydrophobic effect (Tanford, 1980; Cevc and Marsh, 1987). The steric repulsion between the phospholipid headgroups is directly linked to the chemical potential of water. This is due to the fact that the effective size of the headgroup of phospholipids such as phosphatidylcholine involves a significant contribution by the headgroup hydration shell (Lehtonen and Kinnunen, 1994; 1995; Kinnunen, 1996b).

Penetration of water molecules into lipid bilayers is not homogeneous and although lipid headgroups are charged the organization of water molecules in their hydration shell has been proposed to be similar to an idealized clathrate structure of water around apolar solutes (Alper et al., 1993). Water associated with lipid headgroups and contacting the interfacial region has been postulated to be the main determinant of the dipole potential of lipid membranes (Gawrisch et al., 1992; Brockman, 1994). The number of water molecules in the hydration shell further depends on the phase state of lipids, the type of lipid headgroup (McIntosh, 1996), acyl chain composition, and the presence of cis-double bonds, and the presence of compounds such as sterols, with the headgroup hydration being augmented if the distance between adjacent headgroups is increased by the additives (Jendrasiak and Hasty, 1974; Jendrasiak and Mendible, 1976). The hydration of the hydrophilic headgroups plays an important role in the structure and function of phospholipid bilayers (Jendrasiak, 1996). Dehydration of phospholipid membranes has been shown to induce phase separation (Webb et al., 1993; Lehtonen and Kinnunen, 1995) and lamellar-to-hexagonal-II phase transition (Webb et al., 1993). Dehydration of phospholipid membranes is a prerequisite to the fusion of membranes (Wilschut and Hoekstra, 1986).

Water activity is lowered by the addition of any nonwater molecule into the system, and any region where water is excluded will be osmotically stressed (Parsegian et al., 2000; Rand et al., 2000). The exclusion of water from some regions may result from qualitatively different mechanisms. More specifically, when a solute is too large to enter into a particular region in the system, for example, into a cavity of a protein, the solute is sterically excluded. Preferential hydration means that the interface prefers to interact with water rather than with the solute (Parsegian et al., 2000; Rand et al., 2000). On the other hand, a solute may prefer to interact with water more strongly than with the interface. Both mechanisms can lead to the formation around a macromolecule of a depletion layer in which the concentration of the solute is lower than in the bulk phase. The above mechanisms can occur simultaneously in the same system, e.g., in addition to the preferential hydration-created depletion layer, the solute may also be too large to enter into some cavities, resulting in its steric exclusion. Dependence of the osmotic action on the solute size and chemical nature should be distinguished from the osmotic effect (Rand et al., 2000).

The introduction of different solutes in an aqueous medium also induces structural changes in water, and these compounds have been classified as “structure breakers” (chaotropes), or “structure makers” (kosmotropes), depending on their effect on the hydrogen-bonded networks of liquid water (Luu et al., 1990, and references therein; Collins, 1997). As kosmotropes increase the surface free energy, these compounds tend to decrease the interfacial area (increase interfacial tension), whereas chaotropes have the opposite effect, accumulating in the interface and decreasing surface tension. The magnitude of these changes depends on the degree of solute depletion (kosmotropes) or enrichment (chaotropes) at the interfaces, in comparison to the bulk phase (Koynova et al., 1997). Kosmotropes increase both the pretransition and main transition temperatures and decrease liquid-crystalline → H_II phase transition temperature of phospholipids (Koynova et al., 1997).

Taken together, any osmotically active solute could influence lipid lateral packing in membranes and thus the bilayer lateral pressure profile by two fundamental mechanisms, namely, by depleting osmotically water from the lipid hydration shell or by influencing the interfacial tension. In this study we compared these two mechanisms by using three kosmotropes, betaine, choline chloride, and sucrose. Liposome bilayers were made of the unsaturated 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and also incorporated the fluorescent probe Laurdan (molar fraction X = 0.01). The emission spectrum of this fluorophore has been shown to provide sensitive means to assess the hydration (Parasassi et al., 1998) and intermolecular distance (Bagatolli et al., 1998) in phospholipid surfaces.

MATERIAL AND METHODS

Materials

Choline chloride, EDTA, HEPES, POPC, and sucrose were from Sigma (St. Louis, MO). Betaine was from Cultor (Espoo, Finland), and Laurdan from Molecular Probes (Eugene, OR). Deionized water (18.2 MΩ) was Millipore-filtered (Millipore, Bedford, MA). Lipid stock solutions were made in chloroform. Concentration of POPC was determined gravimetrically using a high precision electrobalance (CAHN 2000, Cahn Instruments, Cerritos, CA). Concentration of Laurdan was determined spectrophotometrically using ɛ = 20,000 M⁻¹ at 364 nm (in CH₃OH).

Preparation of liposomes

POPC and Laurdan (X = 0.01) were mixed in chloroform whereafter the solvent was evaporated under a gentle stream of nitrogen. To remove residues of chloroform the lipids were further maintained under reduced pressure for at least 2 h. Notably, in multilamellar vesicles (MLV) the bilayers can be pushed into close proximity, which could influence the membrane dynamics. Also, in MLVs the access of osmolytes into the interlamellar space can be limited, thus causing osmotic gradients. In addition, MLVs in contact with excess solvent can spontaneously deplete small solute molecules from their interior by an entropy-driven mechanism (Diamant, 2002). To exclude the impact of the above factors large unilamellar vesicles (LUV) were used. MLVs were first obtained by hydrating the lipids with the indicated buffer for 30 min at room temperature. After hydration the MLV dispersions were freeze-thawed five times. These dispersions were subsequently processed to LUVs by extrusion through a Millipore (Bedford, MA) 100-nm-pore-size polycarbonate filters using a Liposofast-Pneumatic (Avestin, Ottawa, Canada), essentially as described by MacDonald et al. (1991). Whether the LUVs were freeze-thawed or not did not have any effect (data not shown).

Osmolarity and surface tension measurements

Freezing point depression method (Micro-Osmometer Model 3300, Advanced Instruments, Norwood, MA) was used to obtain osmotic pressure (Π) vs. osmolality curve for choline chloride. All measurements were done in duplicate. The difference between these duplicate assays was 0–16 mosm/kg, with an average difference of 6 mosm/kg. For betaine and sucrose the Π vs. osmolality data were retrieved from the homepage of the Laboratory of Physical & Structural Biology at the National Institutes of Health (http://dir.nichd.nih.gov/Lpsb/docs/OsmoticStress.html), measured by the vapor pressure method.

The effect of betaine, sucrose, and choline chloride on the surface tension of water was measured by a multichannel microtensiometer (MultiPi WS1, Kibron, Helsinki, Finland). Sample volume was 50 μl per well. The instrument uses the du Nouy technique with the wire probes attached to the microbalance sensor heads. All measurements were done at ambient temperature (∼22°C) and for each solute concentration at least six individual samples were measured. Surface tension recorded for pure water was 72.8 ± 0.1 mN/m, in keeping with the literature (Adamson, 1990).

Laurdan fluorescence measurements

Laurdan steady-state fluorescence measurements assessing the impact of the indicated solutes were carried out with a PerkinElmer LS50B spectrofluorometer (Perkin Elmer, Boston, MA) equipped with a magnetically stirred cuvette compartment thermostated at 25°C with a circulating waterbath (Haake F6/Haake C25, Karlsruhe, Germany). The data were analyzed by dedicated software from PerkinElmer. The temperature scans of Laurdan fluorescence were performed by a script-controlled Varian Cary Eclipse spectrofluorometer equipped with Peltier temperature control elements and a four-cell cuvette holder. The excitation wavelength was 350 nm and emission was monitored at 440 and 480 nm. The emission generalized polarization (GP) was calculated using the equation

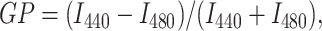(1)

where I₄₄₀ and I₄₈₀ are the emission intensities measured at 440 and 480 nm. In this context it is important to emphasize that these measurements do not relate to emission polarization but polarization of the fluorophore. In other words, GP does not relate to fluorescence emission polarization but instead to the electric polarization of the fluorophore due to the solvent environment, i.e., no optical polarizers are used in the measurement of GP.

RESULTS AND DISCUSSION

Increase of air-water interfacial tension by betaine, sucrose, and choline chloride

Several solutes such as NaCl (Adamson, 1990), polyols (Kaushik and Bhat, 1998), and many amino acid salts (Kita et al., 1994) have been reported to increase surface tension. Physically, a solute increasing surface tension of water will oppose an increase in the exposure of a hydrophobic surface to the aqueous phase. Yet, these solutes will also exert changes in any system responding to alterations in osmotic pressure. Accordingly, it was of interest to compare the effects of betaine, choline chloride, and sucrose on the surface tension (γ) of an aqueous buffer at equal osmotic pressures. These compounds are kosmotropes, which do not partition into the interface and because of the depletion layer increase surface tension (Landau and Lifshitz, 1980; Luzardo et al., 2000; Timasheff, 2002). The impact of these three solutes on the air/water interfacial tension measured at equal osmotic pressures, 0.5, 1.0, and 2.0 osm/kg are compiled in Table 1, and increased in the order of sucrose > betaine > choline chloride at all measured osmotic pressures. Largest increment was evident for sucrose, 2.78 mN/m at 2 osm/kg.

TABLE 1.

Increase in surface tension (Δγ) by betaine, choline chloride, and sucrose at increasing iso-osmolar concentrations; the respective molal concentrations are shown in brackets

Osmolyte	0.5 osm/kg	1.0 osm/kg	2.0 osm/kg
Betaine	0.17 ± 0.09 (0.47)	0.42 ± 0.15 (0.90)	0.80 ± 0.16 (1.65)
Choline chloride	0 ± 0.13 (0.29)	0.27 ± 0.20 (0.59)	0.64 ± 0.10 (1.22)
Sucrose	0.58 ± 0.13 (0.47)	1.34 ± 0.06 (0.91)	2.78 ± 0.18 (1.70)

Effects of betaine, sucrose, and choline chloride on Laurdan GP

Laurdan possesses a dipole moment due to the partial charge separation between 2-dimethylamino and the 6-carbonyl residues which further increases upon excitation (Weber and Farris, 1979; Parasassi et al., 1998). The extent of intramolecular charge separation in the excited state of Laurdan can be assessed by comparing the relative intensities of the emission bands at 440 nm and 480 nm. These data are conveniently expressed by the generalized emission polarization (GP) value. Laurdan is virtually insoluble to water, thus the GP value arises entirely from the probes located into the membrane (Parasassi et al., 1993). The solutes used in this study are highly water soluble. Accordingly, any direct interaction between these solutes and Laurdan is highly unlikely. In lipid membranes the fluorescent moiety of Laurdan resides at the level of glycerol backbone (Parasassi et al., 1998). While the emission maximum, λ_max of this probe is insensitive to phospholipid headgroup, charge, and pH, it depends on the phase state of the bilayer. Accordingly, λ_max is ∼440 nm in the gel phase and ∼490 nm in liquid crystalline phase phospholipid bilayers (Parasassi et al., 1998). The dipolar relaxation observed during phospholipid phase transition and in the fluid phase is not due to the probe itself or because of major changes in its orientation, but due to the water molecules penetrating to the glycerol backbone level (Parasassi et al., 1991; 1998). Yet, the position of Laurdan in the membrane is likely to change as the membrane hydration changes. Moreover, the width of the time-averaged distribution for a probe molecule may also be altered, both for its position and orientation. The extent of these effects with respect to this work and earlier work done with Laurdan is difficult and arduous to assess and could be involved in the mechanisms causing alterations in GP upon changing hydration. Laurdan fluorescence also correlates to membrane local bending fluctuations and membrane permeability (Lee et al., 2001a). Nevertheless, the value for GP assesses the relaxation of the water molecules surrounding the fluorescent moiety of Laurdan in phospholipid membranes and can be used to monitor water penetration into the bilayer: the higher the GP value, the lower the penetration (Parasassi et al., 1991; 1994; 1998).

Differences in GP for Laurdan incorporated in POPC LUVs induced by the three solutes present at concentrations yielding equal osmotic pressures are shown in Fig. 1. In brief, at equal osmotic pressures the GP values increased in the order of sucrose > betaine > choline chloride, and the increments correlated also with the increase in γ (Table 1). At 0.5 osm/kg choline chloride, a minor increment in GP was observed without a corresponding increase in surface tension. This is likely to be explained by the better sensitivity of fluorescence spectroscopic measurement. Instead, the change in surface tension at 0.5 osm/kg choline lies at detection limits of surface tension measurement. Importantly, when the values for GP were plotted against the change in Δγ a significant correlation became evident (Fig. 2).

FIGURE 1.

Effects of increasing concentrations of betaine (▪), choline chloride (▴), and sucrose (•) on the GP of Laurdan (X = 0.01) in POPC LUVs. Solutes were dissolved in buffer (5 mM HEPES and 0.1 mM EDTA, at pH 7.4) at concentrations corresponding to given increasing values of osmolarity Π, namely, 0.5, 1, and 2 osm/kg. Changes in fluorophore emission spectra were measured at 25°C. Total lipid concentration was 25 mM. Each data point represents the average of at least three separate measurements with the error bars indicating standard deviation.

FIGURE 2.

The GP values for each Π (0.5, 1, and 2 osm/kg) shown as a function of Δγ. The fitted curve starts from zero osmotic pressure (buffer). Data were taken from Fig. 1 and Table 1. The symbols for betaine, choline chloride, and sucrose are as in Fig. 1.

A similar phenomenon has been previously established for salts. Accordingly, the theory for the change in γ by Onsager and Samaris (Landau and Lifshitz, 1980) invokes the repulsive electrostatic image force seen by ions near an air/water interface. In this theory, all monovalent ions have the same repulsion, i.e., theory does not contain ion specificity and all monovalent ions should thus have the same effect on γ. This, however, is in disagreement with the experiments. The factors responsible for the failure of the Onsager-Samaris theory for even simple salts remain ambiguous. Boström et al. (2001) suggest that the specific ion effects could be partly explained by dispersion forces. Yet, these authors also point out the possible significance of other forces, particularly those involving water structure. Our data demonstrate for the first time this discrepancy for organic solutes. In other words, the observed solute-specific effects on surface tension show that depletion layer thickness varies for the solutes at equal osmotic pressure, implying that the general thermodynamic relation between surface tension and osmotic pressure (Parsegian et al., 2000) is not valid in this case (Table 1).

To conclude, if the osmotic pressure would be the dominant factor modulating hydration of the membrane interface, no differences would be expected between these solutes at equal osmotic pressures. However, at equal osmotic pressures different solutes clearly show different effects on GP, whereas GP values fall on single curve when plotted against Δγ. A possible connection between GP values and Δγ is likely to be provided by area changes per POPC molecule and consequent changes in bilayer hydration. Accordingly, if the area per POPC decreases, water penetration to the level of Laurdan decreases, and also the freedom of penetrating water molecules to orientate optimally around Laurdan decreases. Water penetration could additionally respond to changes in membrane tension and membrane stiffness, and consequent changes in thermal fluctuations of bilayers. Solutes influence γ, which in turn has an impact on water dynamics and structure at the interface, area/lipid, and energetics of area changes due to e.g., thermal fluctuations such as bilayer undulation. Increasing γ can be expected to affect bilayer rigidity, leading to diminished membrane fluctuations and attenuated lipid dynamics, evident as an increase in GP.

Surface tension for water decreases with temperature (Weast, 1979). As an independent test for the correlation between Laurdan GP and γ, we measured Laurdan GP values for POPC LUVs in the temperature range from 5 to 50°C in the absence of the kosmotropes. As expected, the values for GP decreased with increasing T. Subsequently, we plotted the Laurdan fluorescence as a function of Δγ, the latter increasing due to decreasing T and expressed GP values as ΔGP, representing the difference between GP at 25°C and at the given temperatures (Fig. 3). Measurement of GP is essentially ratiometric and we may therefore expect negligible influence due to thermal deactivation of the excited state of the fluorophore. The observed correlation suggests that the temperature-dependent changes in GP values for fluid, unsaturated POPC LUVs are likely to be explained by the temperature dependence of γ. Also shown in Fig. 3 are the data for ΔGP (difference between GP in the presence and absence of solutes) measured at 25°C and as a function of Δγ, the latter being increased by increasing concentrations of the three kosmotropes. These two sets of data coincide in keeping with a common mechanistic basis. The only exception is sucrose at 2 osm/kg, which does not overlay with the ΔGP vs. γ-curve (Fig. 3). It should be noted that this concentration sucrose is very viscous (∼4.8 mNs/m²), whereas the next highest viscosity is for betaine at 2 osm/kg (∼3.4 mNs/m²). Furthermore, sucrose at this high concentration may also directly interact with the phospholipid headgroups (Crowe et al., 1985; Strauss et al., 1986; Anchordoguy et al., 1987).

FIGURE 3.

The ΔGP values for POPC/Laurdan (99:1) LUVs as a function of Δγ varying due to temperature (○, open symbols) and due to the kosmotropes at 25°C (From Fig. 2, solid symbols). The temperatures were (from left to right) 50, 40, 30, 25, 20, 18, 15, 10, and 5°C. See text for details. The values for γ as a function of temperature were obtained from the literature (Weast, 1979).

Surface tension exerts its effect in the thin interfacial region accommodating the fluorescent moiety of Laurdan, i.e., at the level of phospholipid glycerol backbone within the dynamic interface between water and hydrocarbon phase. As γ increases, the number of interfacial water molecules is reduced due to augmented lipid lateral packing (i.e., decrease in the mean molecular area per lipid). In keeping with the membrane lateral pressure profile, this has to be compensated with increasing repulsion at headgroup and/or acyl chain level.

Based on changes in free energy as a function of the area of exposure of hydrocarbon to water (Tanford, 1979; 1980) we get an estimate of the involved energies. The interfacial free energy is G = γA. For small area changes the γ can be approximated to be independent of area, though in reality it will depend on the area per molecule becoming smaller as area per molecule decreases. From this approximation it follows . Furthermore, when the changes are small, we can also approximate 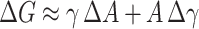. From our measurements with Laurdan we can calculate the intermolecular distance (ID) values for the different solutions and thus also obtain estimates for the mean molecular areas (Table 2). More specifically, Bagatolli et al. (1998) reported a linear correlation between ID and GP, the former defined as the distance between two neighboring acyl chain residues of adjacent phospholipids. ID was calculated by subtracting the diameters associated with the surface area circumscribed by the rotation of the lipid molecule (Bagatolli et al., 1998). Comparison of the Laurdan GP value for POPC LUVs at 25°C in the absence of kosmotropes to the data by Bagatolli et al. (1998) yields an intermolecular distance of ∼2.5 Å. Following this line of analysis we may further estimate the decrease in ID due to increasing γ, which reveals a linear reciprocal correlation (Fig. 4).

TABLE 2.

Results for the calculation of mean molecular area, free energy change per POPC molecule, and change in γ required to give ΔG = 0; see text for details

Solution	γair/water, mN/m	Δγair/water, mN/m	Area/POPC, nm2	ΔG, 10−21 J/POPC	ΔG, in kT at 298 K	Δγ, mN/m, required to give ΔG = 0
Water	72.8	0	0.653	0	0	0
Betaine 0.5 osm/kg	72.97	0.17	0.641	−0.62	−0.15	0.97
Betaine 1.0 osm/kg	73.22	0.42	0.632	−1.08	−0.26	1.71
Betaine 2.0 osm/kg	73.6	0.80	0.617	−1.86	−0.45	3.01
Sucrose 0.5 osm/kg	73.38	0.58	0.628	−1.31	−0.32	2.09
Sucrose 1.0 osm/kg	74.14	1.34	0.608	−2.34	−0.57	3.85
Sucrose 2.0 osm/kg	75.58	2.78	0.578	−3.93	−0.95	6.80
Choline 0.5 osm/kg	72.77	−0.03	0.647	−2.86	−0.07	0.44
Choline 1.0 osm/kg	73.07	0.27	0.643	−0.51	−0.12	0.79
Choline 2.0 osm/kg	73.44	0.64	0.630	−1.17	−0.29	1.86

FIGURE 4.

Intermolecular distance (ID) for POPC as a function of the increment in surface tension (Δγ) due to increasing concentration of the kosmotropic solutes. The symbols are as in Fig. 1.

We take the radius of a POPC molecule to be R = (r + ID/2), where r = 3.1 Å is the axial radius of gyration at level of carbonyl oxygens, calculated for diacylglycerol. (The value 3.1 Ų for r was obtained from molecular modeling of diacylglycerol. Gaussian 98W A.11 and GaussViewW, Gaussian Inc., Carnegie, PA, were used to optimize the geometry with ab initio calculations performed without any explicit or implicit solvent at the level HF/6-31G with AMD Athlon 1900+. Results were analyzed with MSI Cerius2, Molecular Simulations, San Diego, CA, operated at the Center for Scientific Computing, Espoo, Finland.) Subsequently, the mean molecular area for POPC was approximated by a hexagon constituted by six equilateral triangles, each with base 2 × x = 2 × R × tan(30°) = 2R/ and height R, giving A = 2 × × R² (Fig. 5). The derived value of 65.3 Ų for POPC in buffer agrees very well with the value 62 ± 1 Ų (at 50°C, 20–30% by weight in distilled water) obtained by x-ray scattering (Pabst et al., 2000), implying that the radius of gyration for diacylglycerol backbone together with ID values reported by Bagatolli et al. (1998) produce realistic molecular areas.

FIGURE 5.

Schematic representation of the geometries used in the calculation of molecular areas. See text for details.

Importantly, we may use the values for the changes in mean molecular areas ΔA and water-hexadecane interfacial tension (γ_{water/hexadecane} = 52.5 mN/m, Lee et al., 2001b) to estimate the decrease in free energy due to the decrease in interfacial area A. We further assume that because of the inertness of the solutes used, they will have no significant direct effect on the free energy of the bilayer, and that at the level of the bilayer the favorable free energy change, i.e., decrease in area/POPC, comes forth to balance the change due to increase in surface tension. Accordingly, ΔG = 0, and therefore γΔA = −AΔγ. This also includes the assumption that factors such as trans→gauche isomerization have only minor contribution to the surface free energy. We may now calculate the changes in γ needed to balance the area changes. The values obtained using γ_{water/hexadecane} = 52.5 mN/m for initial surface tension for the lipid-water interface are clearly too large (Table 2). However, assuming that the changes in surface tension are additive, i.e., Δγ_lipid/water = Δγ_air/water, we can obtain an estimate for the initial surface tension at the lipid/water interface. Rearranging AΔγ_lipid/water = −γ_lipid/waterΔA yields

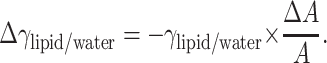Next, by varying initial γ_lipid/water we minimize the sum

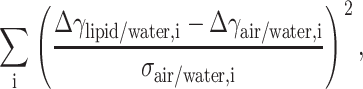where i represents the identification for the solution, and σ_air/water the error in measured γ_air/water. Due to the large deviation in GP values (and therefore ΔA values) for the 2 osm/kg sucrose solution, it was left out from the minimization procedure. The minimum for the weighed sum of squares is achieved with the value γ_lipid/water = 18.5 mN/m, which gives us the values for Δγ shown in Table 3. Subtracting the estimated γ_lipid/water = 18.5 mN/m from the γ_{water/hexadecane} = 52.5 mN/m results in π = γ_{water/hexadecane} − γ_lipid/water = 34.0 mN/m for the equilibrium lateral pressure in the bilayers, in excellent agreement with previous estimates (Marsh, 1996).

TABLE 3.

Changes in γ at the air-water interface for different osmolyte solutions

Solution	Δγair/water, mN/m	σair/water, mN/m	Δγlipid/water, mN/m
Betaine 0.5 osm/kg	0.17	0.09	0.34
Betaine 1.0 osm/kg	0.42	0.15	0.59
Betaine 2.0 osm/kg	0.80	0.165	1.01
Sucrose 0.5 osm/kg	0.58	0.13	0.71
Sucrose 1.0 osm/kg	1.34	0.06	1.27
Sucrose 2.0 osm/kg*	2.78	0.18	2.12
Choline 0.5 osm/kg	−0.03	0.13	0.15
Choline 1.0 osm/kg	0.27	0.2	0.27
Choline 2.0 osm/kg	0.64	0.1	0.63

σ_air/water indicates the standard deviations for the measurements of γ. Δγ_lipid/water is the calculated lipid-water interfacial tension. The large difference between Δγ_air/water and Δγ_lipid/water of sucrose at 2.0 osm/kg is not unexpected as for small area changes the γ can be roughly approximated to be independent of area, though in reality it will depend on the area per molecule, becoming smaller as area per molecule decreases. See text for details.

^*Not used in minimization due to large error in GP.

Any aqueous compartment (e.g., membrane surface) that is inaccessible to solute has its water activity controlled by the solute concentration, the activity being lowered by the addition of nonwater molecules (Parsegian and Rand, 1995). Under this osmotic pressure the components of the molecular assembly are pushed together (Parsegian and Rand, 1995). Although cells cannot control the chemical potential of pure water, they are able to change the water activity by accumulating different solutes (Rand et al., 2000). A change in water activity can have different responses on macromolecules. Isolated proteins undergo reversible transitions and get dehydrated, or kinetically find it more difficult to get to their more hydrated conformation (Parsegian and Rand, 1995). The osmotic work is observed as a change to a more dehydrated state (Parsegian and Rand, 1995). For single unilamellar liposome an analogous behavior can be expected. Lehtonen and Kinnunen (1994) used PEG to cause osmotic stress on LUVs. At equal osmotic pressures inside and outside LUVs PEG decreased membrane free volume and attenuated lipid dynamics. These effects were explained by decreased membrane hydration.

Although the depletion layers for air/water and bilayer/water interface could be considered to be similar it has been pointed out that comparison between these interfaces is not straightforward because the water structure associated with the phospholipids is different from bulk water (Feng et al., 1994), and also different from water structure at the air/water interface. Another example emphasizing the fundamental difference between the air/water and bilayer/water interfaces is provided by poly(ethylene-glycol) (PEG), which is excluded from phospholipid surfaces (Arnold et al., 1990). Yet, PEG as such is surface-active, accumulating at the air-water interface (Winterhalter et al., 1995). This comparison readily demonstrates the importance of steric exclusion for the former surface.

Exclusion of certain solutes (so-called compatible, or kosmotropic, solutes) from protein surface and resulting in increment in surface tension has been previously demonstrated to cause augmented molecular packing (Timasheff, 1993). The denaturation temperature of soluble proteins increases as γ is increased (Kaushik and Bhat, 1998). We have previously studied the effects of betaine on the structural dynamics of a soluble protein, Humicola lanuginosa lipase (Söderlund et al., 2002). In brief, betaine decreased the mean hydrodynamic volume of this protein and enhanced its molecular packing. On the basis of the results of our current study, we can conclude that for the three studied osmolytes (betaine, choline chloride, and sucrose), the main factor affecting the interfacial dynamics, water penetration into the phospholipid bilayers, and lateral packing of lipids is surface tension, whereas osmotic pressure had less effect. The impact of the increase in γ by betaine on the protein-water interface is thus essentially analogous to the augmented packing and decreased hydration of the lipid bilayer reported here. Changes in the lateral pressure profile have been proposed as a mechanism for membrane-mediated modulation of integral membrane proteins (Cantor, 1997a; 1997b). By necessity alterations in bilayer/water interfacial tension due to solutes must also influence the bilayer lateral pressure profile. As pointed out by Cantor (1997a), the magnitude of the lateral pressures prevailing in membranes is considerable, corresponding to bulk pressures of hundreds of atm. This is in keeping with the increment of the main transition temperature (T_m) of dimyristoylphosphocholine (DMPC) by betaine. More specifically, T_m for DMPC was increased progressively by this solute, reaching 5° at 5 M betaine (Söderlund et al., unpublished results). Similar increment in T_m for DMPC is observed at a hydrostatic pressure of ∼200 atm (Reyes Mateo et al., 1993).

Importantly, cells can and do control the concentration of these type of solutes. The effect of kosmotropes described here for lipid bilayers would thus provide a powerful means for the cell to modulate the physical state and functions of membranes (the activities of membrane proteins) via changes in water structure. However, this effect would not be limited to bilayer-mediated impact on integral membrane proteins only but would also apply to soluble proteins. To this end, it is of interest that the structurally closely related solute phosphorylcholine appears to be required for mitogenic signaling by growth factors and oncogenes (Cuadrado et al., 1993).