Adsorption of DNA to Mica Mediated by Divalent Counterions: A Theoretical and Experimental Study

Abstract

The adsorption of DNA molecules onto a flat mica surface is a necessary step to perform atomic force microscopy studies of DNA conformation and observe DNA-protein interactions in physiological environment. However, the phenomenon that pulls DNA molecules onto the surface is still not understood. This is a crucial issue because the DNA/surface interactions could affect the DNA biological functions. In this paper we develop a model that can explain the mechanism of the DNA adsorption onto mica. This model suggests that DNA attraction is due to the sharing of the DNA and mica counterions. The correlations between divalent counterions on both the negatively charged DNA and the mica surface can generate a net attraction force whereas the correlations between monovalent counterions are ineffective in the DNA attraction. DNA binding is then dependent on the fractional surface densities of the divalent and monovalent cations, which can compete for the mica surface and DNA neutralizations. In addition, the attraction can be enhanced when the mica has been pretreated by transition metal cations (Ni²⁺, Zn²⁺). Mica pretreatment simultaneously enhances the DNA attraction and reduces the repulsive contribution due to the electrical double-layer force. We also perform end-to-end distance measurement of DNA chains to study the binding strength. The DNA binding strength appears to be constant for a fixed fractional surface density of the divalent cations at low ionic strength (I < 0.1 M) as predicted by the model. However, at higher ionic strength, the binding is weakened by the screening effect of the ions. Then, some equations were derived to describe the binding of a polyelectrolyte onto a charged surface. The electrostatic attraction due to the sharing of counterions is particularly effective if the polyelectrolyte and the surface have nearly the same surface charge density. This characteristic of the attraction force can explain the success of mica for performing single DNA molecule observation by AFM. In addition, we explain how a reversible binding of the DNA molecules can be obtained with a pretreated mica surface.

INTRODUCTION

Atomic force microscopy (AFM) is a useful technique for imaging DNA and DNA-protein complexes on ultraflat surfaces (Allison et al., 1996; Cary et al., 1997; Guthold et al., 1994; van Noort et al., 1998). This microscope generates a three-dimensional (3D) image by probing the sample surface with a sharp tip attached to the end of a flexible cantilever. One of the most attractive features of AFM is that it can operate in liquid, making it possible to image DNA under biological conditions. The key element is to preserve the activity and integrity of the specimen. This requirement is not easy to reach because it implies that DNA molecules should be loosely attached to move freely above the surface. The most popular substrate in this respect is muscovite mica, a highly negatively charged surface. Those crystals exhibit a large degree of basal cleavage, allowing them to be split into atomically flat sheets. Weak electrostatic attachment of the DNA to the surface is obtained by using divalent cations (Mg²⁺, Ni²⁺, Ca²⁺…) in the buffer and either with a pretreated mica (Bezanilla et al., 1994; Thundat et al., 1992; Vesenka et al., 1992) or not (Han et al., 1997; Jiao et al., 2001; Thomson et al., 1996). Let us add that Mg²⁺ ion is generally preferred, for binding DNA to mica, to the transition metal cations that coordinate strongly to the DNA bases (Rouzina and Bloomfield, 1996b).

Based on this principle, mica has been successfully used in numberless studies especially for AFM imaging of moving double-stranded DNA and DNA-protein complexes in liquid (Guthold et al., 1994; Jiao et al., 2001; van Noort et al., 1998). The point is that the process allowing the adsorption of DNA on the mica surface is still unclear. Generally, authors refer to a “salt bridge” effect between the negatively charged mica surface and the negatively charged DNA that is mediated by the divalent or higher valence cations (Shao et al., 1996). Some AFM studies have been done to understand the process that binds DNA to mica (Bustamante and Rivetti, 1996; Hansma and Laney, 1996). However, several features of the DNA adsorption are still not understood, regarding the respective role of divalent and monovalent ions concentrations and the effect of mica pretreatment by various cations like Ni²⁺ (Bezanilla et al., 1994) or Al³⁺ (Weisenhorn et al., 1990). Obviously, the origin of the force that attracts DNA molecules onto the surface has not been established so far. It is important to know how the mica surface interacts with DNA while studying its biological function (Vainrub and Pettitt, 2000). The observation of DNA molecules by AFM could otherwise lead to misinterpretations. Indeed, the DNA molecules could be particularly sensitive to the surface influence because a major part of the DNA/protein interactions are electrostatic (Saecker and Record, 2002).

In this article, we study both theoretically and experimentally the forces involved in the negatively charged polyelectrolytes (DNA) binding to a flat negatively charged surface (mica). The theoretical study is carried out by using simple analytical models to qualitatively describe the DNA binding to mica surface. We suppose that only two forces play a major role on the DNA adsorption: the electrical double-layer repulsion between the counterion clouds of DNA and mica (Israelachvili, 1992; Lau and Pincus, 1999; Pashley, 1982), and the force due to the correlations between the counterion clouds (Arenzon et al., 1999; Kjellander and Marrelja, 1986; Levin, 1999; Ray and Manning, 1994; Rouzina and Bloomfield, 1996a,b). The electrical double-layer force can be well described by using the standard Poisson-Boltzmann (P-B) equation that encapsulates a mean-field approach to the many-body problem of mobile ions between two charged surfaces (Israelachvili, 1992; Lau and Pincus, 1999; Ni et al., 1999). To use this model, we assume that DNA can be treated as a charged surface (Rouzina and Bloomfield, 1996a,b).

For the study of the attraction force due to the counterion correlations, we select a simple model that determines the force induced by the correlations of the counterions in a mean-field theory by a very simple two-dimensional (2D) model involving two lines of negative charges (Arenzon et al., 1999). One line of charges represents the DNA and the other one represents the mica surface. We develop this model by adding the effect of thermal fluctuations that can lead to a lower binding strength, and the effect of the binding competition between divalent and monovalent cations. In addition, this model allows us to study the effect of mica pretreatment by divalent transition metal ions (Zn²⁺, Ni²⁺, Ca²⁺…). These ions remain generally strongly bound to the mica surface (Gier and Johns, 2000; Koppelman and Dillard, 1977; Pashley and Israelachvili, 1984), which improves the DNA binding during AFM experiments in liquid (Bezanilla et al., 1994; Piétrement et al., 2003).

We also investigate the effect of the competition between monovalent/divalent cations on the DNA binding strength by AFM. This experimental study can indicate if the DNA adsorption is due to the counterion correlations. However, the DNA/mica binding strength cannot be easily reached by AFM. We choose to measure end-to-end distances of the DNA molecules: large end-to-end distances indicate that the DNA molecules are loosely bound to the surface whereas shorter end-to-end distances reflect the strong adsorption of the molecules.

In the last section of this article, we study the short-range and long-range limits of the attractive and repulsive forces. A possible explanation of the reversible binding of DNA previously obtained on pretreated mica (Piétrement et al., 2003) is advanced. In addition, we describe the effect of the surface charge density on the DNA adsorption that can explain the ability of mica to adsorb DNA molecules.

THEORY

The adsorption of polyelectrolytes onto oppositely charged surfaces has been the aim of several works. Either numerical or analytical approaches have been developed to describe the force involved in the polyelectrolytes adsorption (Beltràn et al., 1991; Netz and Joanny, 1999; van der Schee and Lyklema, 1984). If the polyelectrolytes and the surface are liked charged, the interaction between them is generally repulsive. The so-called electrical double-layer force (Israelachvili, 1992) repels the two surfaces. This force is in fact the sum of the electrostatic repulsion between the counterion clouds and the thermal pressure, and is well described by solving the P-B equation. Because AFM experiments have brought experimental evidence that DNA can be strongly adsorbed onto the mica surface, an attraction force should occur to pull the negatively charged DNA backbone onto the negatively charged mica surface. The attractive hydrophobic force (Craig et al., 1998; Israelachvili, 1992) between the mica surface and DNA polyelectrolyte could be involved in this binding. Nevertheless, this force should not play a key role in the DNA adsorption because the attraction of the DNA molecules to the surface is strongly dependent on the presence of divalent cations that neutralize both the mica surface and the DNA backbone, which suggests that the attraction force has an electrostatic origin. The electrostatic attraction between like charged particles has been already observed for polyelectrolytes and has been the aim of several theoretical studies (Arenzon et al., 1999; Kjellander and Marrelja, 1986; Kornyshev and Leikin, 1999; Levin, 1999; Ray and Manning, 1994; Rouzina and Bloomfield, 1996a,b; Sitko et al., 2003). This force comes from the correlations of the counterions between two like-charged polyelectrolytes and, for example, is involved in the DNA condensation mediated by multivalent cations. The main characteristic of this mechanism is its short range and its strong dependence on the surface competition between the divalent and the monovalent counterions.

In this section we use a simple model to assess the influences of the double electrical layer force and the force due to the counterion correlations acting between DNA and mica.

Double-layer electrical forces between mica and DNA

To perform this study we assume that only the divalent counterions neutralize the DNA molecules and the mica surface. Highly charged polyions like DNA can be treated as a charged plane surface provided that the ionic strength is higher than 0.1 M and is lower than 1 M (Rouzina and Bloomfield, 1996a,b). For ionic strength between 0.01 and 0.1 M, the cylindrical geometry of the DNA molecules should be taken into account but planar approximation can provide interesting information for a qualitative description of the electrostatic forces acting on DNA and mica. At such ionic strength and for diluted DNA solution (we use a concentration of DNA lower than 1 μg/ml), the counterions form a thin condensed layer on DNA (Manning, 1978). Its thickness λ_z depends only on the valence of the counterions and on the surface charge density, but does not depend on the bulk salt concentration (Rouzina and Bloomfield, 1996b):

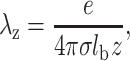(1)

where e is the electron charge, z the ion valence, σ the surface charge, and l_b the Bjerrum length equals:

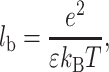(2)

where ɛ is the dielectric constant, k_B the Boltzmann constant, and T the temperature.

The relation in Eq. 1 is valid for the DNA surface (λ_z = 0.0595 nm for z = 2) and the mica surface (λ_z = 0.0297 nm for z = 2). As we assume that DNA can be considered as a charged plane, we can obtain an analytical expression of the electrical double-layer force. Indeed, the problem is then reduced to the simple calculation of the pressure acting on two planes in the presence of divalent counterions. The two planes correspond to the mica and DNA surfaces with surface charge density σ_a and σ_b, respectively. This approximation is suitable if the distance between DNA and mica is lower than R the radius of the DNA molecule (R ≈ 1 nm). However this approximation is used for larger distance as well as to obtain qualitative information. Due to translational invariance, the P-B equation for this problem is one-dimensional and thus the normalized electrostatic potential ϕ(x) and the external charge density n(x) due to the two charged surfaces depend only on the axis (x) perpendicular to the charged planes. The P-B equation for a single plane can be written as (Lau and Pincus, 1999):

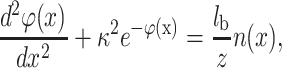(3)

where κ is a constant depending only on boundary conditions. Note also that we use the normalized electrostatic potential ϕ(x) = eψ(x)/k_BT. The boundary conditions for two charged planes with a surface charge density σ_a at x = 0 and σ_b at x = d can be written:

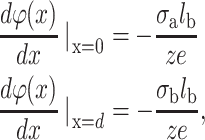(4)

where d is the distance between the two surfaces.

This approach has already been used to describe the electrical double-layer force acting on the mica surface to interpret surface force experiments (Pashley, 1982). It is assumed that the adsorbed ions determine the net surface charge of the two surfaces. The net surface charge density (σ_a for mica; σ_b for DNA) is given by the sum of the adsorbed ion density and the known surface charge density (σ_mica ≈ −2.10¹⁸ e.m⁻² for the mica and σ_DNA ≈ −10¹⁸ e.m⁻² for DNA, with e the electron charge). The double-layer potential is supposed to be situated at a plane just outside the adsorbed ion layer. As the net surface charge density of the mica depends on the mica pretreatment, we study the pressure acting between the two surfaces for different ratios σ_a/σ_b. Furthermore we assume that the net surface charge density of the DNA is constant and is ∼15% of its surface charge. This value is obtained by considering that the adsorbed divalent cations are those for which the electrostatic attraction to DNA is larger than the thermal energy k_BT.

The pressure P(d) between the two planes is given by the following equation (Lau, 2000):

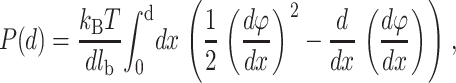(5)

where d is the distance of separation between the absorbed ion layers.

The first term of the integral represents the thermal pressure of the counterions whereas the second one is the electrostatic stress of the counterion clouds. The thermal pressure can give a repulsive force in the short range even if the two planes are oppositely charged. From Eqs. 4 and 5, the pressure can be obtained by solving numerically the following system of transcendental equations (Lau, 2000):

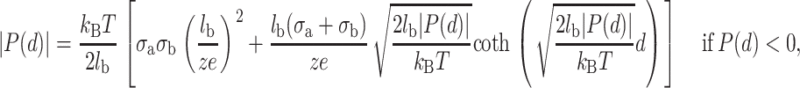(6)

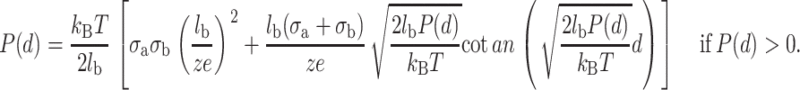(7)

P(d) is positive if the force is repulsive and negative if the force is attractive. Let us note that the pressure between the two planes does not depend on the bulk divalent concentration, which seems obvious because the electrical double-layer density profile is not influenced by the bulk salt concentration. In fact, it depends only on the valence of the counterions and on the surface charge density of the two planes.

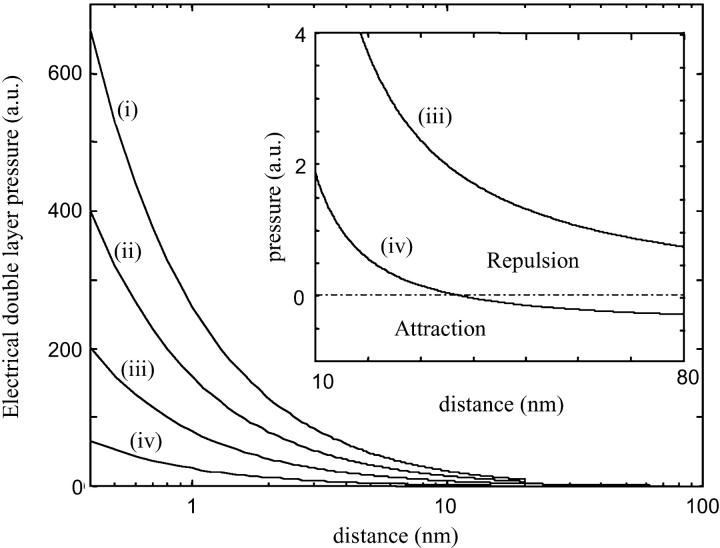
Fig. 1 represents the pressure between the mica surface and the DNA surface versus the distance d for different mica surface charges. We notice that the repulsion is considerably smaller for a lower mica surface charge. Therefore, we can expect that NiCl₂ pretreatment enhances DNA binding onto mica. Let us remind that Ni²⁺ ions (and transition metal ions) can form a large range of complexes with the mica surface compared to Mg²⁺ ions (Hansma and Laney, 1996). In particular, Ni²⁺ ions are able to form (Ni-OH)⁺ hydroxyl complexes (Gier and Johns, 2000; Koppelman and Dillard, 1977) thanks to their high ionic potential. The strong adsorption of Ni²⁺ ions during pretreatment neutralizes the mica surface if the major part of the potassium ions is exchanged with the Ni²⁺ ions. We can also expect a charge inversion. However, the force between the surfaces is generally still repulsive for the short range (Lau and Pincus, 1999). The reason is that the repulsive thermal force, due to the entropy loss of the counterion clouds, is stronger near the surface even if the mica surface charge is partially reversed by pretreatment. The pressure between the two oppositely charged surfaces becomes attractive for the large distances (see Fig.1). More precisely the electrostatic attraction overcomes the thermal repulsion if 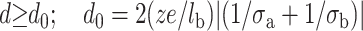(the distance d₀ is obtained by solving P(d₀) = 0).

FIGURE 1.

Electrical double-layer pressure acting between the mica and the DNA surface for several σ_a/σ_b ratios, with σ_a and σ_b the net surface charge densities of the mica and DNA surfaces, respectively: (i) σ_a/σ_b = 4 with σ_b = 0.15 e.nm⁻² (net surface charge of DNA); (ii) σ_a/σ_b = 2; (iii) σ_a/σ_b = 0.5, (iv) σ_a/σ_b = −0.5. The repulsive pressure is weaker if the mica surface is less charged. Lower surface charge can be obtained through mica pretreatment by divalent cations. If the DNA and the mica surface are oppositely charged (σ_a/σ_b = −0.5), the electrical double force can become attractive for a distance of separation larger than d₀ (see the inset and the text for the d₀ value).

The pretreatment by transition metal cations helps to adsorb DNA on mica because it neutralizes the mica surface charge and then weakens the repulsive pressure. However, another kind of electrostatic force is required to explain the DNA adsorption. Indeed, to generate a strong attraction between the DNA and the mica, the two bodies should attract each other via a short-ranged force.

Attraction between two oppositely charged bodies

Highly charged surfaces in solution containing multivalent electrolytes can attract each other electrostatically through correlations in their shared counterion environments. To study the mechanism of this phenomenon, we use a simple model, which considers that DNA and mica surfaces are represented by two parallel lines of charges (Arenzon et al., 1999). Even if it is a rough approximation, it is particularly suitable to obtain qualitative information. We also assume that the only effect of the counterion association is a local renormalization of the surface charge and that the counterions are considered as point-like charges (Rouzina and Bloomfield, 1996b). The Hamiltonian H for the unscreened electrostatic interactions between the DNA line of charges and the mica line of charges takes a particularly simple form (Arenzon et al., 1999):

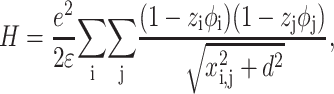(8)

where i is the label of the mica sites and j is the label of the DNA sites. It is important to note that d is the distance between the DNA/mica counterion layers. z_j is the valence of the j^th ion and 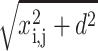is the distance between the j^th DNA site and i^th mica site. φ_j or φ_i are the occupation variables of the sites. φ_j = 0 if the j^th site is unoccupied whereas φ_j = 1 if the j^th site is occupied. The charge sites onto the line are supposed to be spaced uniformly. For DNA, the mean distance between two charges is b ≅ 1 nm, which is obtained by considering the DNA surface charge σ_DNA = 1 e.nm⁻² (Rouzina and Bloomfield, 1996b). For the mica, the distance between two charges is about 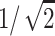nm (Pashley, 1982).

The force generated by the counterion correlations on the DNA line and the mica surface is then (Arenzon et al., 1999):

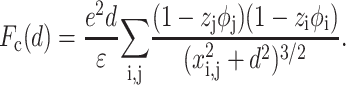(9)

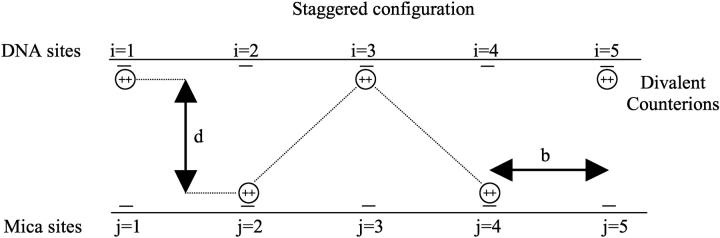
The optimum occupation variables of the sites are determined through the minimization of the free energy which, in turn, involves that the counterions of the DNA line with respect to the surface adopt a staggered configuration (Arenzon et al., 1999). It seems logical that the staggered configuration minimizes the free energy because if the site of one line is occupied and the parallel site of the second line remains vacant, the electrostatic repulsion between the two lines is weaker (see Fig. 2).

FIGURE 2.

Position of the counterions in the staggered configuration. The labels i and j define the charged site position on the DNA and mica surfaces, respectively.

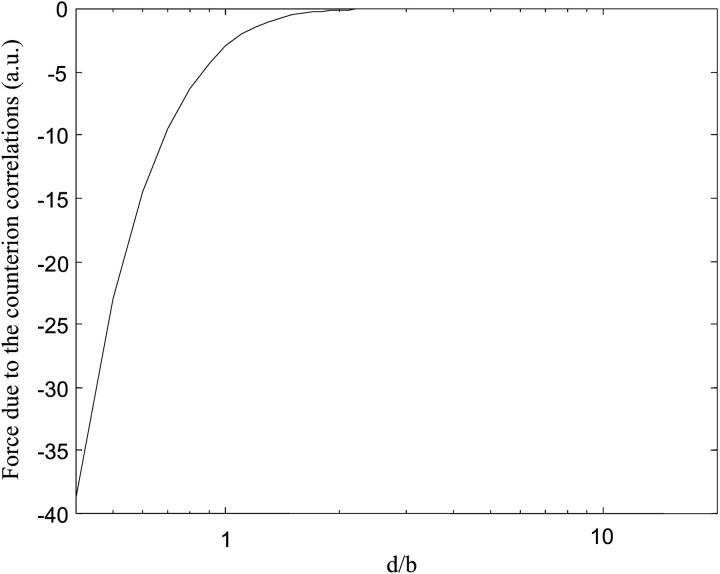
To simplify the calculations, we assume that only divalent counterions participate in the two lines' neutralization and we take b′ ≅ b = 1 nm. Fig. 3 is the plot of F_c(d) for a perfect staggered configuration. It can be observed that the force is attractive and intervenes for the short distances d < b. As the range of the attraction is given by b, the separation between two sites along the lines, a short range is expected for highly charged bodies like DNA and mica. The curve on Fig. 3 represents the force obtained by neglecting the influences of the thermal motion and the competition between the monovalent/divalent cations, which can strongly influence the attraction mechanism.

FIGURE 3.

Attraction force generated by the counterions shared between the DNA and the mica. We assume that only the divalent counterions can participate in the surface neutralization and we neglect the effect of thermal motion (T = 0 K). b is the distance of separation between the counterion sites and d represents the distance between the DNA and mica counterion layers. The calculations are performed for a 1444-bp DNA.

Effect of the ionic strength on the thermal motion

We have assumed that the two lines of charges adopt a perfect staggered configuration, which in fact happens only for T = 0 K. Thermal motion at ambient temperature can perturb the counterion distribution and thus can weaken the attraction force. The ionic strength plays a key role in this mechanism because the cations are more likely to move if the electrostatic interactions are screened. To study the influence of the ionic strength on the attraction force, we discuss qualitatively its effect through the probability for one counterion to be placed in a nonstaggered position under ambient temperature:

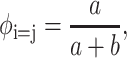(10)

with:

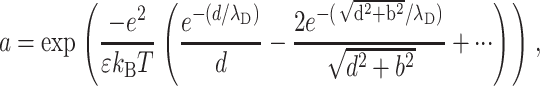(11a)

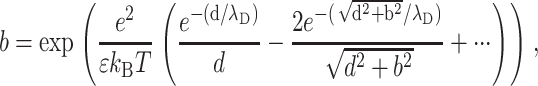(11b)

whereas the probability for a staggered position is:

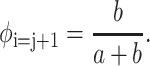(12)

These probabilities are based on the interaction of one counterion with the nearest counterions of the other line assuming that the distance between two sites on the same line is b and the nearest counterions adopt a staggered configuration. λ_D is the Debye length that defines the screening length of the electrostatic potential in water and is expressed in nanometers as:

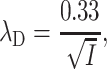(13)

with I the ionic strength of the solution (summing over all ions species i):

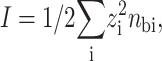(14)

where z_i and n_bi are the valence and the bulk concentration of each species, respectively.

Let us separate the short distances of separation from the intermediate distances:

• For the short distances of separation (d ≪ l_b), the probability of nonstaggered position is very small because the average electrostatic energy between two counterions, that is proportional to e²/ɛd, is larger than the thermal energy k_BT. (Let us recall that the Bjerrum length l_b, ∼ 0.7 nm in water, is the distance for which the electrostatic potential of two charges equals their thermal energy).

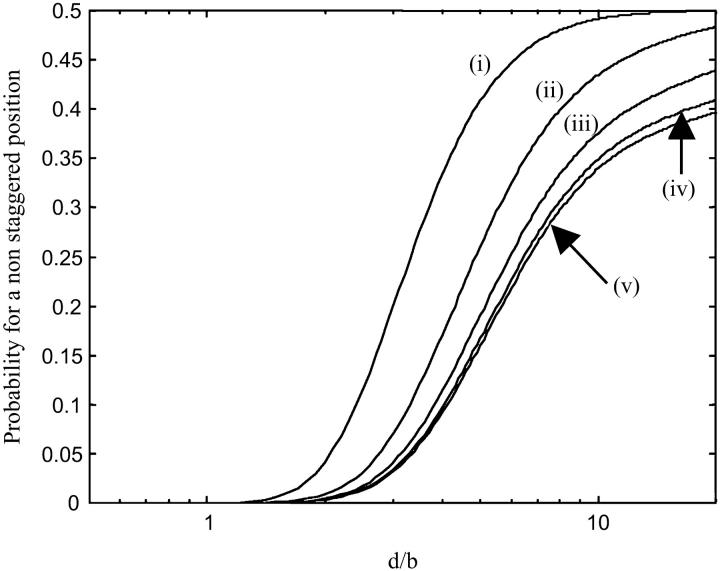
• For the intermediate distances l_b/10 < d < b; we distinguish the high ionic strength (I ≥ 0.1 M) and the low ionic strength environment (I < 0.1 M). Fig. 4 represents the probability for a nonstaggered position of the counterions versus the distance between the two lines for different ionic strengths.

  • At low ionic strength (I < 0.1 M), the Debye length is larger than the Bjerrum length. The electrostatic interactions between counterions can then maintain a pretty stable staggered configuration provided that b is not significantly larger than l_b. This condition is satisfied for highly charged bodies like DNA and mica. We can see in Fig. 4 that the probability for a nonstaggered position is lower than 0.35 if d < b and just slightly depends on the ionic strength. Thus, the DNA attraction to mica is not ionic strength dependent for I < 0.1 M and the thermal motion perturbs weakly the DNA attraction.
  • Concerning higher ionic strength (I ≥ 0.1 M), we observe in Fig. 4 that ionic strength strongly enhances the probability that a counterion occupies a nonstaggered position if I ≥ 0.1 M. As a consequence, the DNA can become loosely attached to the surface. More generally, the force due to the correlations between the counterions is significantly screened provided that λ_D < b (for DNA, it comes I ≥ 0.1 M). Therefore, the thermal motion can inhibit the correlation between the counterions.

FIGURE 4.

Plot of the occupation probability φ_i=j of a counterion in a nonstaggered configuration for (i) I = 1 M; (ii) I = 0.1 M; (iii) I = 10 mM; (iv) I = 1 mM; (v) I = 0.1 mM. If φ_i=j = 0.5, the counterions are randomly distributed in the different sites: no adsorption due to the counterion correlation is attempted. We can see that the probability of a nonstaggered position is enhanced at higher ionic strength (I ≥ 0.1 M) due to the screening effect of the ions.

We shall also distinguish whether the mica has been pretreated or not. On untreated mica, the Mg²⁺ counterions that are generally added to the buffer for DNA binding to mica do not have a great affinity with the mica surface. The correlations of the Mg²⁺ counterions can therefore be perturbed by thermal agitation. On the other hand, Ni²⁺ ions (or other divalent transition metal cations) adsorbed at the mica surface after pretreatment are strongly bound to the mica surface (Gier and Johns, 2000) and can be considered fixed. As a consequence, adsorbed Ni²⁺ counterions can hardly be removed by thermal motion. This effect can partly explain why the divalent ions (Gier and Johns, 2000) pretreatment can enhance the DNA adsorption. Let us add that a strong attraction between two mica surfaces, in the presence of strongly bound divalent cations, has already been observed during surface force experiments in liquid (Pashley, 1982).

Effect of the competition between monovalent and divalent cations

One of the major features of the attraction force is its dependence upon the valence of the counterions. This force is attractive provided that the cations are divalent or of higher valence. The correlations of the monovalent cations do not contribute to the attraction force due to the (1 − z_jφ_j) terms in Eq. 9. Therefore, the adsorption is monitored by the binding competition between monovalent and divalent cations on the two surfaces. High surface density of monovalent cations can inhibit DNA attraction to the mica surface. Let us calculate the fractional DNA surface density of the divalent cation n_s2, which is the ratio of the divalent counterion surface density to the total surface density of the counterions. We can use a simple model to study the competitive electrostatic binding of monovalent and divalent counterions to mica. This model can be applied to DNA as well (Rouzina and Bloomfield, 1996b). With the P-B equation, it comes:

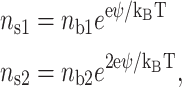(15)

where n_b1 is the monovalent salt bulk concentration and n_b2 is the divalent salt bulk concentration. n_s1 is the fractional surface density of the monovalent cation. For this approach the effect of ion size and the specific surface/cation interactions are not taken into account, however, some improvements can be performed to adjust this model (Rouzina and Bloomfield, 1996a). The fractional surface density of the divalent cations versus the bulk concentration of the monovalent and divalent cations is obtained by solving this simple equation (Rouzina and Bloomfield, 1996b):

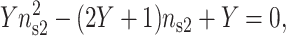(16)

with:

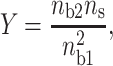(17)

where n_s is the surface concentration of the counterions (n_s ≅ 6.6 M for DNA; n_s′ ≅ 16 M for mica). We remark that the fractional values of the divalent surface densities are constant for a given ratio 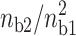, this characteristic implies that the force due to the counterion sharing is constant provided that I < 0.1 M.

To study the effect of divalent/monovalent salt competition, we plot the correlation force due to the counterion correlations for different n_s2 values that correspond to a given 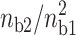ratio. The theoretical curves have been obtained by randomly filling the different sites of the two lines with divalent cations or monovalent cations so that the fractional counterion densities (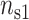, 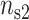) for DNA and (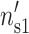, 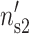) for the mica are equal to the theoretical values calculated above. We assume in this section that the divalent counterions adopt a perfect staggered configuration and that the effect of the thermal motion can be neglected.

Fig. 5. A represents the force due to the counterion correlations for different n_s2 values on the DNA surface for untreated mica, which means that the monovalent cations can compete for both the DNA and mica sites. We can see that the attraction force is greatly sensitive to the n_s2 value. This effect is a constraint for the experimentalist, which cannot raise the monovalent salt concentration up to the physiological conditions without releasing DNA molecules from the surface.

FIGURE 5.

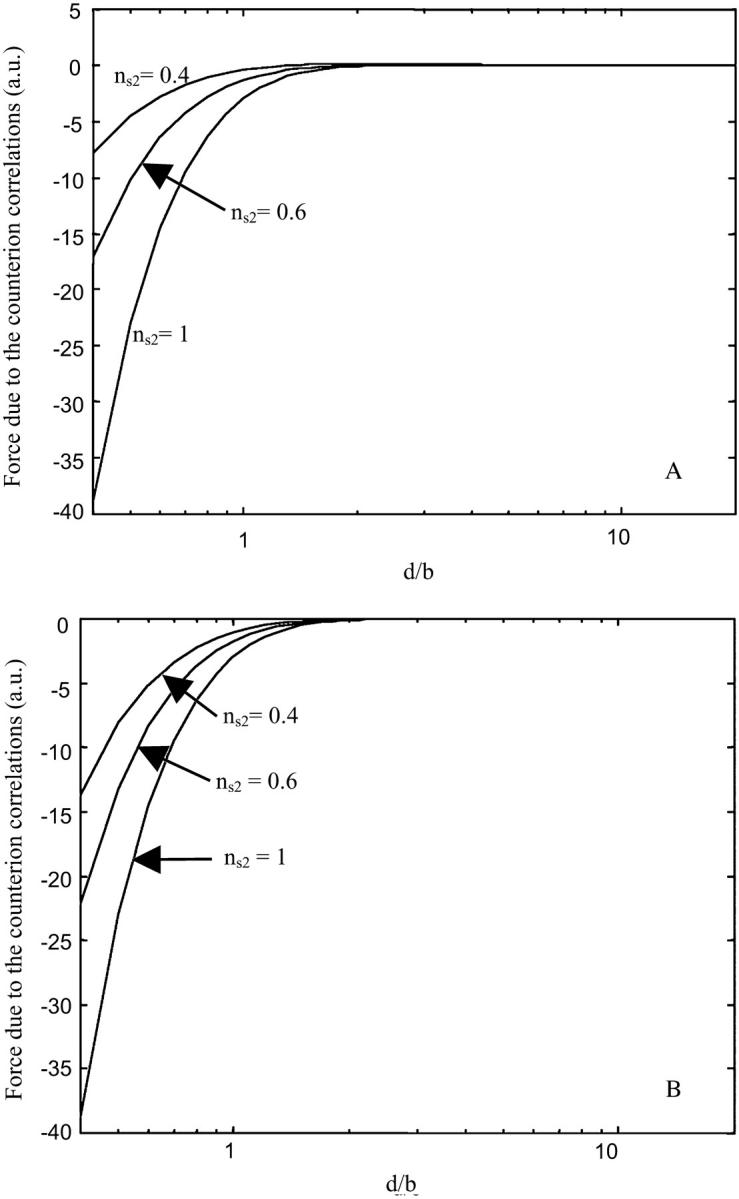
Effect of the competitive binding between monovalent and divalent cations on the attraction force due the correlations of the counterions where n_s2 is the fractional divalent surface density of DNA. (A) For untreated mica, it should be remarked that the attraction force is weaker if the surface concentration of the divalent cation is lower. (B) For NiCl₂ pretreated mica, we can see that the mica pretreatment allows a higher binding strength compared to an untreated surface. It is assumed that the monovalent cations can compete with the divalent cations for the DNA neutralization but not for the mica neutralization if the mica has been pretreated.

Fig. 5 B represents the attractive force that pulls DNA on mica while mica has been pretreated by divalent transition metal cations. We assume that the divalent cations adsorbed during pretreatment cannot be removed due to their high binding affinity. Thus, the competition between monovalent and divalent cations acts only on the DNA sites and does not act on the mica sites. We can see in Fig. 5 B that the attraction force is stronger than the attraction force acting on untreated mica for the low n_s2 values. In that respect, strongly adsorbed cations are more efficient to bind DNA via counterion correlations, which is in full agreement with experimental evidence on the strong adsorption of DNA on pretreated mica (Bezanilla et al., 1994; Piétrement et al., 2003; Thundat et al., 1992; Weisenhorn et al., 1990).

Hydration forces between the surfaces

The hydration forces arise when hydrated counterions are prevented from desorption as the two interacting surfaces approach (Israelachvili, 1992; Pashley, 1982). Dehydration of the cations leads to a strong repulsive hydration force. This repulsive force can be characterized by an exponential decaying force that overcomes the attractive force if the distance between the surfaces is shorter than the hydrated diameter of the counterions. For Mg²⁺ ions, the hydrated radius is 4.3 Å whereas for Na⁺ ions the hydrated radius is 3.6 Å (Israelachvili, 1992). It can be remarked that the hydrated radius of these ions is relatively small and the hydration forces should intervene at a shorter distance compared to the attraction force allowing the DNA adsorption. However, the adsorption of the DNA molecules can be inhibited by counterions with larger hydrated radius.

EXPERIMENTAL STUDY

Materials and methods

Atomic force microscope

These experiments were carried out using a Nanoscope IIIa atomic force microscope (Digital Instruments, Veeco, Santa Barbara, CA). We used Olympus (Hamburg, Germany) silicon cantilevers AC160TS with resonant frequencies contained between 250 and 350 kHz. The scan frequency was typically 1 Hz per line and the modulation amplitude was about a few nanometers.

DNA samples

Twenty microliters of a 10 mM NiCl₂ solution was deposited onto the surface of a freshly cleaved mica (muscovite) for 1 min. Then, the mica was thoroughly rinsed with pure water (Molsheim, France) and dried. DNA fragments of 1444 bp were obtained from pBR322 plasmid (position 2576-4020) by polymerase chain reaction (PCR) amplification. PCR product is purified on an anion exchange monoQ column (Amersham Biosciences, Uppsala, Sweden) with a SMART system (Amersham Biosciences), ethanol precipitated and suspended in TE buffer (Tris 10 mM, EDTA 1mM). DNA length and the quality of the preparation were analyzed by 1% agarose gel and by electron microscopy (Beloin et al., 2003).

DNA molecules were diluted to a concentration of 0.2 μg/ml in a buffer solution containing 10 mM Tris and different MgCl₂ and NaCl concentrations (see below). A 5-μl droplet of DNA solution is deposited onto the NiCl₂-treated mica for 1 min. Then, the sample is thoroughly rinsed with the imaging solution. The drying step is performed after using a 0.02% diluted uranyl acetate solution for fixing the DNA molecules in their conformations (Revet and Fourcade, 1998).

RESULTS

Several experimental facts tend to indicate that the mica surface attracts DNA through counterion correlations because this force is strongly influenced by the relative bulk concentration of monovalent and divalent salts. Indeed, the addition of monovalent salt to the deposition buffer in the AFM cell can lead to release of the DNA molecules from the surface. High fractional bulk concentration of divalent salt favors the DNA binding and is generally used for imaging DNA by AFM (Allison et al., 1996; Bustamante and Rivetti, 1996; Cary et al., 1997; Guthold et al., 1994; Jiao et al., 2001; Thomson et al., 1996; Thundat et al., 1992; van Noort et al., 1998; Vesenka et al., 1992). These observations are consistent with the fact that the attraction force is monitored by the competition between monovalent ions and divalent ions, but more precise results are needed for this study.

We show previously that attraction force due to the counterion sharing is constant for a given [Mg²⁺]/[Na⁺]² ratio. This law can be very useful to the experimentalists and can provide a direct demonstration that the attraction is due to the counterion sharing. By varying the [Mg²⁺]/[Na⁺]² ratio, we can see if the binding strength of the DNA molecules is monitored by the divalent/monovalent cation competition binding. In addition the effect of the ionic strength on the DNA binding strength can be studied by keeping n_s2 constant for different MgCl₂ and NaCl concentrations.

Before processing AFM experiments, it is first required to find a way to study the DNA binding strength. It has been demonstrated that loosely bound molecules are able to equilibrate in a 2D conformation leading to the mean square of the end-to-end distance value h (Rivetti et al., 1996):

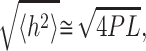(18)

where P is the persistence length and L is the length of the DNA molecules.

If the molecules are strongly bound to the surface, the three-dimensional molecules could be projected onto the surface because the force that attracts the molecule is stronger and accelerates the molecule adsorption. The mean square of the end-to-end distance for a 3D/2D projection becomes (Rivetti et al., 1996):

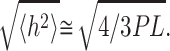(19)

Thus, the DNA end-to-end distance is lower for a direct projection, which means that the end-to-end distance can be a very suitable parameter to study the DNA binding strength. The shorter the end-to-end distance is, the stronger the binding is. To measure the end-to-end distances we choose to work on treated mica because NiCl₂ pretreatment contributes to a better uniformity of the mica surface potential and allows us to bind DNA with a lower n_s2 value. All the measurements are performed at least on 200 molecules and in air. All molecules with suspicious path and/or length were excluded from the analysis. The DNA lengths and end-to-end distances were measured with Scion Imaging software (Scion Corp., Frederick, MD).

These studies cannot be performed in liquid because moving DNA molecules are very difficult to image by AFM. Furthermore, for a n_s2 value lower than 0.85 it appears that the atomic force microscope tip removes the DNA molecules from the surface and the images become very fuzzy. After the deposition of the diluted DNA solution onto the mica, the mica is rinsed with the deposition buffer, to remove DNA molecules in excess in the solution. Then, we fix the adsorbed DNA molecules in their conformations thanks to uranyl acetate and we dry the sample using filter paper.

We choose Tris buffer to maintain a stable pH (pH = 7.5) because Tris molecules carry a single positive charge in solution, which slightly perturbs the measurements contrarily to Hepes buffer that enhances the DNA attraction onto the mica surface due to its two positive charges (Bezanilla et al., 1995). Let us also remark that Tris ions can compete with Mg²⁺ ions for the DNA neutralization at very low ionic strength (I < 0.03 M) and can slightly reduce the relative Mg²⁺ surface concentration.

The end-to-end distance is measured for n_s2 ≈ 0.95 and n_s2 ≈ 0.65, and for five different concentrations of MgCl₂ and NaCl:

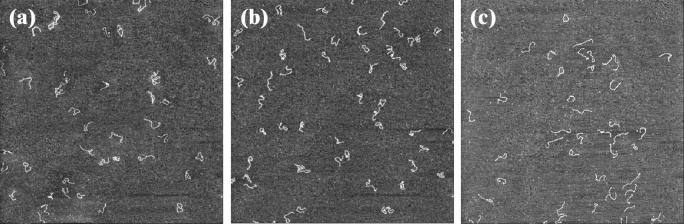
Figs. 6 and 7 present experimental results with AFM. Concerning n_s2 = 0.95, this relatively high fractional surface concentration of Mg²⁺ ions should correspond to a strong DNA binding onto the mica. Fig. 6 shows a set of AFM images of DNA molecules for n_s2 = 0.95. We observe that the molecules are trapped onto the surface and several crossovers indicate that the molecules have been projected. The molecules conformation is nearly the same for the different buffers whereas the ionic strength varies over several orders of magnitude. However, the end-to-end distance on Fig. 8 is larger at high ionic strength (I > 0.1 M), which indicates that DNA binding is weaker.

FIGURE 6.

AFM images of the 1444-bp DNA fragments deposited onto mica for a n_s2 value equal to 0.96 and with three different concentrations of MgCl₂ and NaCl: (a) [MgCl₂] = 6 mM and [NaCl] = 9 mM; (b) [MgCl₂] = 20 mM and [NaCl] = 15 mM; (c) [MgCl₂] = 60 mM and [NaCl] = 30 mM. Scan area, 4 × 4 μm²; z range, 3 nm; scan frequency, 1 Hz.

FIGURE 7.

AFM images of the 1444-bp DNA fragments deposited onto mica for a n_s2 value equal to 0.65 and with three different concentrations of MgCl₂ and NaCl: (a) [MgCl₂] = 6 mM and [NaCl] = 90 mM; (b) [MgCl₂] = 20 mM and [NaCl] = 150 mM; (c) [MgCl₂] = 60 mM and [NaCl] = 300 mM. Compared with Fig. 6, we can observe that DNA molecules have a more released shape, whereas they appear more condensed with a lot of crossovers for n_s2 = 0.95. Scan area, 4 × 4 μm²; z range, 3 nm; scan frequency, 1 Hz.

FIGURE 8.

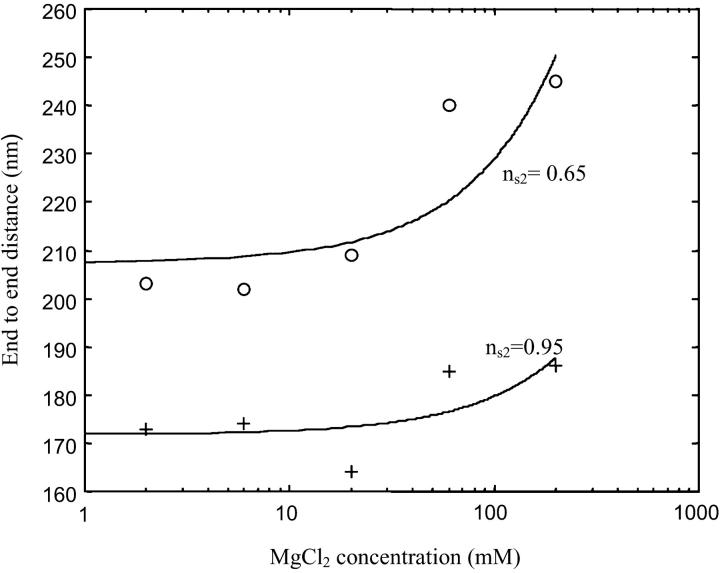
End-to-end distances for different buffers versus Mg²⁺ ions concentration: (top trace) n_s2 ≅ 0.95 obtained for six different buffers: [MgCl₂] = 2 mM and [NaCl] = 5 mM; [MgCl₂] = 6 mM and [NaCl] = 9 mM; [MgCl₂] = 20 mM and [NaCl]= 15 mM; [MgCl₂] = 60 mM and [NaCl] = 30 mM; [MgCl₂] = 200 mM and [NaCl] = 50 mM. (Bottom trace) n_s2 ≅ 0.65 obtained for six different buffers: [MgCl₂] = 2 mM and [NaCl] = 50 mM; [MgCl₂] = 6 mM and [NaCl] = 90 mM; [MgCl₂] = 20 mM and [NaCl] = 150 mM; [MgCl₂] = 60 mM and [NaCl] = 300 mM; [MgCl₂] = 200 mM and [NaCl] = 500 mM. The error bar of the end-to-end measurements is about ± 30 nm and can hardly be improved by increasing the number of observed molecules. The experimental values of the end-to-end distances have been fitted by a polynomial function to observe the evolution of the end-to-end distances. We observe that the end-to-end distances appear to be nearly constant at low ionic strength for a given value of n_s2. However, for the high ionic strength (I ≥ 0.1 M), the end-to-end distances are slightly larger for both n_s2 = 0.95 and n_s2 = 0.65.

The same experiments are also performed for n_s2 equal to 0.65. For low n_s2 value, the DNA molecules are loosely attached on the mica surface and cannot be observed by AFM in liquid. Fig. 7 shows a set of AFM images of DNA molecules for n_s2 = 0.65. We can see that just a few crossovers are observed: the molecules can equilibrate onto the surface. So the end-to-end distances (see Fig. 7) are larger than for n_s2 = 0.95: lowering n_s2 weakens the binding strength. Let us note that the binding strength is larger for [MgCl₂] = 2 mM and [NaCl] = 50 mM solution (n_s2 = 0.95) than for [MgCl₂] = 200 mM and [NaCl] = 50 mM solution (n_s2 = 0.65), which emphasizes that the binding is not only governed by the ionic strength.

We can also remark that the end-to-end distances are generally greater if the ionic strength is raised up to 0.1 M, whatever the fixed n_s2 value is. At such a high ionic strength, the molecules are certainly more loosely attached to the surface because the Debye length is lower than b ≅ 1 nm, which is nearly equal to the range of the attraction force due to the counterion sharing. Therefore, the counterion distribution is perturbed by the thermal motion. It is remarkable to note in Fig. 8 that the ionic strength effect becomes significant at around 0.1 M, as predicted theoretically.

DISCUSSION

Attraction force due to the correlations of the counterions seems to be involved in the electrostatic adsorption of DNA. However, there is one point still to elucidate: is the attraction force larger than the electrical double-layer repulsion force and which parameters can define whether DNA is adsorbed on the surface or not? To answer these questions we study the asymptotic values of the DNA/surface forces in the short- and long-range limits.

Let us first consider the force acting on the polyelectrolyte in the large distance limit. From Eq. 7, if the two surfaces are like-charged, the limiting value of the electrical double-layer pressure is:

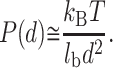(20)

Concerning the attraction mediated by counterion sharing, this force is sharply reduced in the long range because of the thermal effect on the counterion distribution. Thus, the electrical double-layer force generally overcomes the attraction force for the long distance limit (d ≫ l_b). The force is therefore not attractive if the surface and the polyelectrolyte are both negatively charged (or positively charged).

The long-range force can be attractive if the surface and the polyelectrolyte are oppositely charged. For mica, the net surface charge density can be reversed after pretreatment by transition metal cations. The long-range force can become attractive (see Fig. 1) and a reversible binding of the polyelectrolytes can be obtained (Piétrement et al., 2003). Indeed, if the n_s2 value is decreased by adding monovalent salt to a divalent salt solution the binding strength becomes weaker but the long-range attractive force can prevent the DNA from being released in the solution. If n_s2 is raised up, the molecule can bind tightly to the mica surface again.

For the short-range limit d ≪ l_b, the double electrical layer pressure can be written (σ_a ≅ σ_mica, σ_b ≅ σ_DNA in the short range):

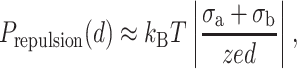(21)

whereas the pressure limit of the attraction force is:

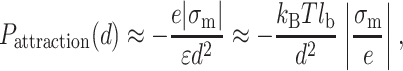(22)

where σ_m = min(σ_a, σ_b). 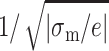is proportional to the distance between two counterions on the lower-charged surface. The divalent counterions of this surface experience a coulombic force with an unoccupied site on the higher-charged surface.

The attraction force can bind tightly DNA to the surface in the short range because the repulsive pressure of the electrical double-layer scales like 1/d whereas the pressure of the attraction force scales like 1/d². We can consider the distance d^* that defines the limit where the attraction overcomes the repulsion:

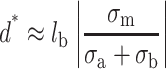(23)

Therefore d^* is proportional to 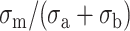, which indicates that the attraction overcomes the repulsion at the largest distance d^* if σ_a (surface) ≅ σ_b (polyelectrolyte). Only a highly charged surface can attract the highly charged DNA molecules. Because the surface charge densities of the mica and DNA are nearly the same, this equation provides a direct demonstration of the mica ability to adsorb DNA compared to other less-charged surfaces. Silica is a slightly negatively charged surface compared to DNA and DNA molecules cannot be adsorbed on this surface by adding only divalent cations.

CONCLUSION

Attraction force due to the correlations of the shared counterions between the DNA molecules and the mica can generate a strong adsorption of the DNA molecules in the presence of divalent cations or higher valence cations. Mica and DNA have nearly the same surface charge. In this case, the theoretical results indicate that this configuration is suitable for the DNA binding: bodies that have a surface charge concentration of the same order of magnitude can attract each other through correlation of their counterion clouds.

In addition, we have demonstrated that the adsorption strength can be monitored by adding monovalent cations that can compete with divalent cations for the DNA and mica neutralization. Low surface concentration of divalent cations leads to a very loose attachment of the DNA to the surface. Concerning the effect of the ionic strength, it appears that the binding of the DNA molecules is affected by the screening effect of the ions if λ_D < b.

To enhance the binding, pretreatment with divalent metal cations or higher valence cations can be performed. Pretreatment lowers the net surface charge of the mica and then reduces the repulsive pressure due to the interpenetrating counterion clouds. Moreover, strongly adsorbed transition metal cations are hardly exchanged with monovalent cations and do not experience thermal fluctuation, which strengthens the binding.