Abstract
During electrophoretic separations of DNA in a sieving medium, DNA molecules stretch from a compact coil into elongated conformations when encountering an obstacle and relax back to a coil upon release from the obstacle. These stretching dynamics are thought to play an important role in the separation mechanism. In this article we describe a silicon microfabricated device to measure the stretching of tethered DNA in electric fields. Upon application of an electric field, electro-osmosis generates bulk fluid flow in the device, and a protocol for eliminating this flow by attaching a polymer brush to all silicon oxide surfaces is shown to be effective. Data on the steady stretching of DNA in constant electric fields is presented. The data corroborate the approximate theory of hydrodynamic equivalence, indicating that DNA is not free-draining in the presence of both electric and nonelectric forces. Finally, these data provide the first quantitative test of a Stigter and Bustamante's detailed theory of electrophoretic stretching of DNA without adjustable parameters. The agreement between theory and experiment is good.
INTRODUCTION
Gel electrophoresis is a powerful and ubiquitous technique for separation of biopolymers, particularly DNA. However, the mechanisms involved in electrophoretic separations are not fully understood (Viovy, 2000; Zimm and Levene, 1992). Because conventional gel electrophoresis is slow and typically limited to DNA lengths <20 kbp, considerable effort has been applied to the development of new electrophoresis techniques. There have been a number of significant advances, most notably capillary electrophoresis, which decreased the necessary separation time by orders of magnitude (Drossman et al., 1990; Jorgenson and Lukacs, 1983), and pulsed field techniques, which extended the separable size to the mega-basepair range (Carle et al., 1986; Clark et al., 1988). However, theories presented to explain the separation mechanism in gel electrophoresis have lagged behind experimental advances, and often relied on incorrect descriptions of the underlying physics to match data. Epifluorescence video microscopy has become a powerful tool for verifying models of electrophoresis, as it permits direct observation of DNA molecules during electrophoretic separations. Videomicroscopy data have shown that during electrophoresis in a sieving medium, DNA molecules cycle through extended conformations when they encounter an obstacle, and assume compact conformations when they release from the obstacle (Smith et al., 1989; Song and Maestre, 1991). These large-scale conformational changes have not been well-studied and are not included in most models of gel electrophoresis.
In recent years, observations of single molecules of DNA have improved our understanding of polymer physics at the molecular scale. The pioneering experiments of Smith et al. (1992) on the elasticity of single DNA molecules demonstrated that DNA does not behave as a freely jointed chain (FJC), but no theory then available could describe their data. As a result, the theoretical foundation of the Kratky-Porod model for stiff chains (the wormlike chain model, or WLC) was extended by Marko and Siggia (1995) to describe the elasticity of DNA. Their force-extension relationship has since been used extensively to determine the stiffness, or persistence length, of both natural and synthetic polymers (Hugel et al., 2000; Rief et al., 1997). Single molecules of fluorescently labeled DNA have also been used to further test and develop the theories of polymer physics. By tethering a single DNA molecule to a latex sphere and dragging it through a concentrated DNA solution, it was demonstrated that an entangled polymer indeed behaves as if it were confined to a tube along its contour length. This was the first direct observation of reptation, a model that has been applied to the movement of polymer melts, as well as to DNA electrophoresis (Perkins et al., 1994; Viovy, 2000) Isolated DNA molecules have also been observed in extensional flow, steady shear flow, and uniform flow (Perkins et al., 1997, 1995; Smith et al., 1999; Smith and Chu, 1998). These data have shown that the dynamics of DNA in flow are highly dependent on the initial conformation of the molecule and have highlighted the importance of hydrodynamic interactions between segments of DNA. In addition, the Brownian dynamics simulation technique has been validated as a quantitative model for DNA by predicting many of the conformational states and their statistical distributions in these flow regimes (Larson and Hu, 1999). Its success in describing DNA dynamics has led other researchers to apply this technique to DNA electrophoretic separations (Patel and Shaqfeh, 2003).
The observation of single molecules of DNA using fluorescence microscopy has also provided new information on biological processes. For example, several groups have investigated the structure of chromatin fibers, a packaging structure in eukaryotes made up of DNA wound tightly around an octamer of histone proteins. Ladoux et al. (2000) used fluorescence video microscopy to follow the formation of chromatin fibers from stretched DNA and free histones. A complete chromatin fiber was formed in under a minute, much more rapidly than predicted by biochemical methods. The authors were able fit a three-stage model for DNA compaction to their data and extract kinetic parameters for the sequential events.
In the present work, we apply single molecule observations of tethered DNA during electrophoresis to further elucidate and quantify the mechanisms involved in gel electrophoresis. Because the dynamics of DNA stretching and relaxation play an important role in the separation of DNA in electrophoresis, we observe these processes at the single-molecule level for various experimental conditions. The effects of variables such as field strength, buffer composition, and DNA length on the dynamics of DNA stretching during electrophoresis are not well known and must all be addressed to quantitatively model gel electrophoretic separations of DNA.
We describe the microfabrication and characterization of a device to measure the deformation of single tethered molecules of DNA in an electric field. We present data on the steady stretching of DNA molecules of varying lengths in a constant electric field. Our data support the theory of hydrodynamic equivalence proposed by Long and Viovy (Long et al., 1996a,b), which purports that DNA in an electric field will stretch in the same manner as if it were deformed by hydrodynamic flow with velocity μE where μ is the electrophoretic mobility.
MATERIALS AND METHODS
Microfabrication procedures
Electrophoresis microcell
P-type silicon wafers were cleaned in a piranha bath (5:1 H2SO4:H2O2) for 10 min and then rinsed with de-ionized water until the resistivity of the rinse tank rose >13 MΩ. Positive photoresist (PR) was then patterned onto the wafer in 2 μm × 4 μm islands by contact lithography. After reactive ion etching, the wafers were again cleaned, and a 1.5-μm-thick layer of silicon oxide was grown by wet thermal oxidation at 1000°C. Next, another layer of PR was applied to the oxidized wafers with the negative image of the previous layer, leaving PR covering the entire surface except the tops of the etched posts. A 50-nm layer of gold was applied by thermal evaporation, using a 7-nm film of chrome to facilitate adhesion. The wafers were then soaked in acetone to dissolve the PR and remove the Cr/Au from the wafer everywhere except for the tops of the posts (liftoff).
Microfluidic channels
A separate microfluidic channel was fabricated for particle image velocimetry experiments. Wafers were cleaned and etched as described above to generate a straight channel 200-μm wide and 65-μm deep (∼3:1 aspect ratio). Glass covers were bonded over the microchannels using anodic bonding. Inlet and outlet ports were drilled into the covers for fluid transfer.
Coating procedures
Before use, the microcells and glass coverslips were cleaned with piranha then rinsed thoroughly in de-ionized water. All surfaces were then coated with a self-assembled monolayer (SAM) of methacryloxypropyltrimethoxysilane (MPTS, Sigma, St. Louis, MO) by immersing in a 2% solution of MPTS in 95% ethanol (0.3% acetic acid) for 10 min, rinsing with ethanol, and curing at 110°C for 5 min. A polyacrylamide brush was then polymerized from the surface by soaking overnight in an 8% solution of acrylamide (Bio-Rad Laboratories, Hercules, CA) in 0.5× TBE buffer, pH 8.0 (45 mM tris, 45 mM borate, 1 mM EDTA, all Sigma) using ammonium persulfate as a free-radical generator and n,n,n′,n′-tetramethylenediamine (TEMED, Sigma) as a stabilizer. The unbound polymer was then removed by rinsing with TBE.
DNA functionalization and immobilization
Lambda bacteriophage DNA (λ, New England Biolabs, Beverly, MA) was functionalized at one end by ligation of a 12 bp 3′-biotin conjugated oligonucleotide (Genemed Synthesis, San Francisco, CA) and the functionalized molecules purified by ultrafiltration (Microcon 50, Amicon, Beverly, MA). Since the polymer brush on the electrophoresis microcell only covers the SiO2 surfaces, the gold posts could be used as binding points for the DNA. The biotinylated DNA molecules were immobilized on the gold using the protocol developed by Zimmermann and Cox (1994). Briefly, an SAM of thiolated biotin (biotin-HPDP, Pierce Endogen, Rockford, IL) was formed on the gold. Next, the protein neutravidin (Pierce Endogen) was bound to the SAM and the biotinylated DNA subsequently immobilized. With this technique DNA was immobilized only at the very top surface of the posts that were etched into the silicon wafer. The tether point of the DNA molecules relative to the solid, bounding surface was known exactly. Multimers of λ were made by incubating a solution of λ-monomers for several hours at room temperature with T4 DNA ligase (New England Biolabs).
Fluorescence microscopy
Characterization of electro-osmotic flow (EOF) in a microfluidic channel
Straight microfluidic channels, 200-μm wide and 65-μm deep (∼3:1 aspect ratio), were fabricated and coated as above. The channel was filled with a solution of 0.3-μm fluorescently labeled latex particles (Bangs Labs, Fishers, IN) that had been sonicated for 5 min to reduce aggregation, and platinum electrodes were inserted at each end of the channel. The particles were illuminated with a xenon arc lamp through a standard FITC filter set (450 < ex < 490, em > 510), on a Zeiss upright epifluorescence microscope (25×, NA = 0.45). The images were captured with a CCD camera and analyzed with the freeware FlowVIs (Crenshaw et al., 1998).
Electrophoretic stretching of DNA
DNA was fluorescently labeled with YOYO-1 (Molecular Probes, Eugene, OR) at a 8:1 bp:dye ratio. The silicon electrophoresis device and the coverslip were separated by 30-μm-thick Kapton tape (3M, Minneapolis, MN), and sealed with nail polish. The electrophoresis experiments were performed in 0.5× TBE buffer with 3% 2-mercaptoethanol, 50 μg/ml glucose oxidase, 15 μg/ml catalase, and 0.1% glucose (all Sigma) added to reduce photobleaching and photoscission. The DNA was illuminated and imaged as above with a 100× oil immersion objective (NA = 1.3), intensified and recorded to a computer hard drive using a low light vidicon camera.
RESULTS
Electro-osmotic flow
The literature contains limited data on the electrophoretic stretching of DNA as studied by fluorescence microscopy, but very few of these data appear to be obtained in the absence of effects that obscure their interpretation. Smith and Bendich (1990) reported the stretching of single plasmid DNA molecules that had been permanently hooked on gel fibers. They reported only the data for which molecules appeared to be immobilized very near to the glass coverslip, and therefore not hindered by a tortuous path through the gel. Their data are scattered, probably due to electro-osmotic flow (EOF) generated by the glass coverslip, or possibly due to DNA-gel interactions. Song and Maestre (1991) reported on the unhooking of single U-shaped T4 DNA molecules during gel electrophoresis. If their data are extrapolated to the point where the arms of the “U” are of equal length, then this length would correspond to the steady stretching of DNA in an electric field. Their data also show a large scatter, again possibly due to EOF, gel interactions, or because the molecules had not reached an equilibrium length before unhooking. Bakajin et al. (1998) studied the stretching of single molecules wrapped around microfabricated posts in thin slits of different depths. While the authors reported that EOF was negligible, no precautions were taken to reduce this flow. Since their experiments were performed on a silicon surface, which readily develops a surface charge in water, EOF would certainly be present at the ionic strengths used in their experiments (0.5× TBE), and interfere with the interpretation of their data.
From the above examples, it is apparent that to accurately measure the stretching of DNA in an electric field, electro-osmotic flow must be eliminated. To determine the extent of the EOF present in our experimental system, we performed particle image velocimetry (PIV) on fluorescently labeled latex microspheres in a separate microfluidic channel. In an infinite or open rectangular channel filled with an electrolyte solution at high ionic strength, a constant electric field will generate plug flow with a velocity described by the Helmholtz-Smoluchowski equation (Probstein, 1994). However, if the channel is bounded, as is the case with the experiments reported here, there can be no net flow, so a resulting pressure gradient is established in the opposite direction. This pressure gradient will generate a parabolic flow opposite to the EOF, so that the net flow at any cross section is zero. We can therefore discern whether EOF is present in a channel by observing the movement of the fluorescent particles when a field is applied. If EOF is present, then the flow profile will be parabolic. If there is no EOF, then the particles will move at their electrophoretic velocity (since the particles themselves are charged) and the observed profile will be flat.
Fig. 1 A shows a still frame of videomicroscopy of the fluorescent particles in a 200-μm-wide channel through a 25× objective. Because the depth of focus in these experiments was ∼2 μm, particles from several different planes are captured in the images. In pressure-driven flow the beads in different focal planes will be moving at different speeds, so the absolute values of the velocity profiles can be altered by tracking particles in different planes. However, we are primarily concerned with shapes of the velocity profiles, not with the absolute values of the tracer velocities, so the relatively large depth of field should not affect our conclusion. Segments of video were analyzed using the freeware FlowVIS DPIV (Crenshaw et al., 1998). Over 20 separate frames captured at 10 fps with an electric field of 8 V/cm were averaged to obtain velocity profiles. In Fig. 1 A, some bead clumping is still evident, but by averaging over many frames, the effect of bead aggregation on the PIV analysis can be minimized. The velocity profiles are plotted in Fig. 1 B for both coated and uncoated channels. For the uncoated channel, the profile is not flat, as would be expected if no EOF were present, but shows unidirectional flow, which is not expected in this system. However, the movement of the particles is not caused strictly by EOF, but also by electrophoresis of the fluorescent particles. We are not able to visualize the flow in the opposite direction near to the surfaces because the electrophoretic velocity of the beads is approximately equal to the EOF velocity. The uncoated velocity profile is also not parabolic, as the dotted line fit to the data shows. The deviation from the parabolic profile was thought to be due to the small aspect ratio of the channel. This was confirmed by solving the Navier-Stokes equations for a three-dimensional finite-element model with the same aspect ratio as our experiments. The solid line on Fig. 1 B shows this solution, indicating a very good fit to the data and confirming the presence of EOF in the system.
FIGURE 1.
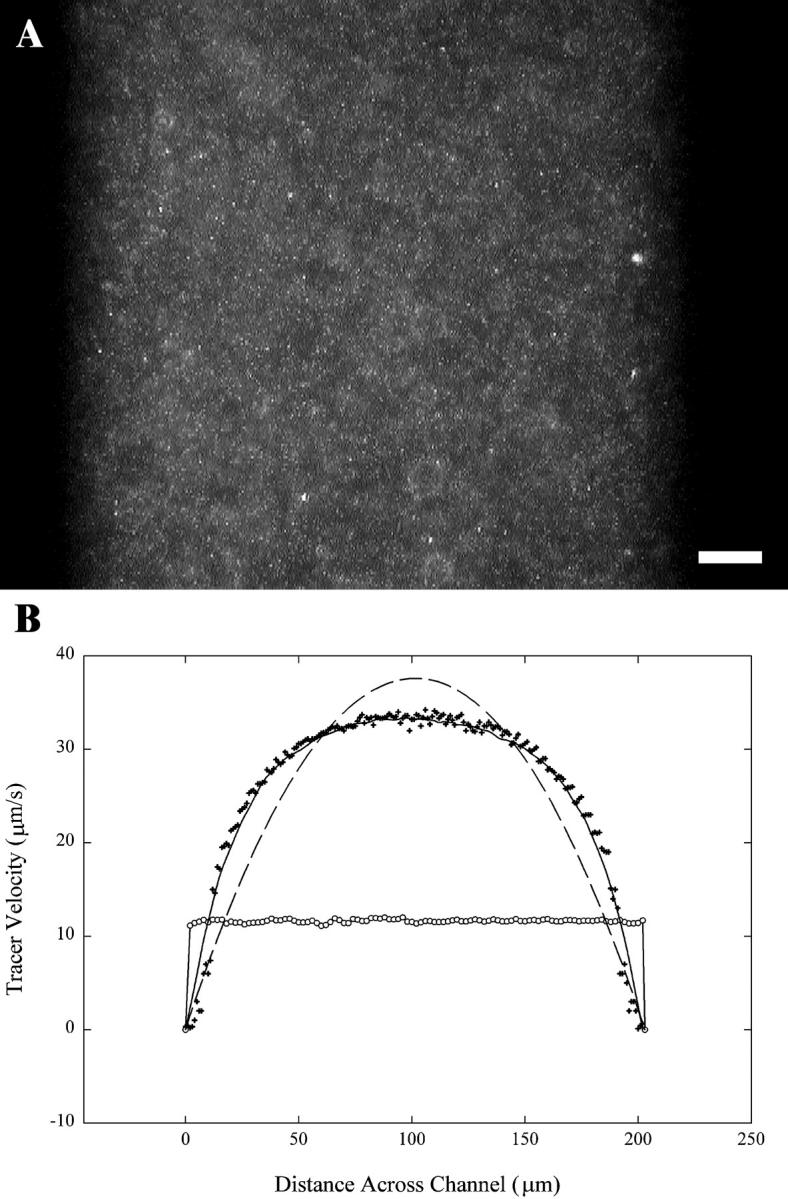
(A) Epifluorescent image of a typical PIV experiment. 0.3-μm fluorescently labeled particles undergoing electro-osmosis and electrophoresis are traced through a 200-μm-wide channel at 8 V/cm. The scale bar is equal to 20 μm. (B) Velocity profiles of the tracer beads in an uncoated channel (+) and coated channel (○). The dashed line is a parabolic fit to the PIV data in an uncoated channel, and the solid line is the result of a finite element model for pressure flow in a rectangular channel.
Many techniques have been developed to dampen EOF in capillary electrophoresis. We adopted the technique developed by Hjerten (1985), employing a polymer brush at the SiO2 surface, which effectively retards the movement of the ions in the double layer. This approach has been shown to eliminate EOF in capillary electrophoresis (Chiari et al., 1994; Hjerten, 1985; Stellwagen et al., 1997). Fig. 1 B also shows the flow profile obtained in a coated channel. As predicted, the profile is flat across the channel, showing that no EOF is present.
Electrophoretic stretching of DNA
Characterization of the microcell
The posts to which the DNA was tethered are ellipses with a long axis of 4 μm, a short axis of 2 μm as shown in Fig. 2. Bakajin et al. (1998) showed that as the DNA approaches a surface, the hydrodynamic interactions between segments (arising from the EOF generated along the charged backbone of DNA) become screened by the surface. Since the hydrodynamic interactions decrease the force on the molecule, the screening results in a larger deformation of the molecules and complicates the analysis. To test the behavior of DNA stretching in free solution the bounding surfaces of the electrophoresis cell must be far enough away so as not to screen any of the hydrodynamic interactions along the backbone of DNA. We measured the electrokinetic stretch of λ-DNA monomers for post heights ranging from 50 nm to 7.5 μm. As expected, the extension of the molecules increased as the post height decreased (data not shown). Wall effects were negligible when DNA was bound to the tops of posts with heights above 5 μm, so we chose to perform all experiments with DNA tethered to 7.5-μm-tall posts.
FIGURE 2.

Scanning electron microscopy image of an array of posts etched into a silicon wafer. The scale bar is equal to 20 μm.
Since the solid post to which the DNA is tethered acts as an insulator, the electric field is not constant throughout the microcell. To determine the extent of this perturbation on the field, Laplace's equation was solved on a finite element grid for the full three-dimensional model of the microcell, obtaining the electric field at each point. To quantify how this difference in the electric field would affect the stretching of the DNA, we performed a series of Monte Carlo (MC) simulations in three dimensions. Following previous MC simulations of DNA (Tessier et al., 2002), we employed the bond-fluctuation algorithm for the chain, described in detail elsewhere (Carmesin and Kremer, 1988; Deutsch and Binder, 1991). In this algorithm the chain is freely jointed (FJC), unlike DNA which has been shown to behave as a wormlike chain (WLC) due to its intrinsic stiffness. Both experiment and theory have shown that an FJC will deform much more easily under an external force than a WLC (Marko and Siggia, 1995; Schurr and Smith, 1990; Smith et al., 1992). Thus the MC simulation will overestimate the extent of the deformation. The Metropolis weight associated with the move of a segment one lattice site is exp(−qΔV/kBT), where q is the charge on the segment and ΔV is the voltage difference between the two sites. In this way, if a move is in the direction of a voltage drop, then it is automatically accepted. If the move is in the direction of a voltage increase, then it is accepted only if the Metropolis weight is greater than a random number between 0 and 1.
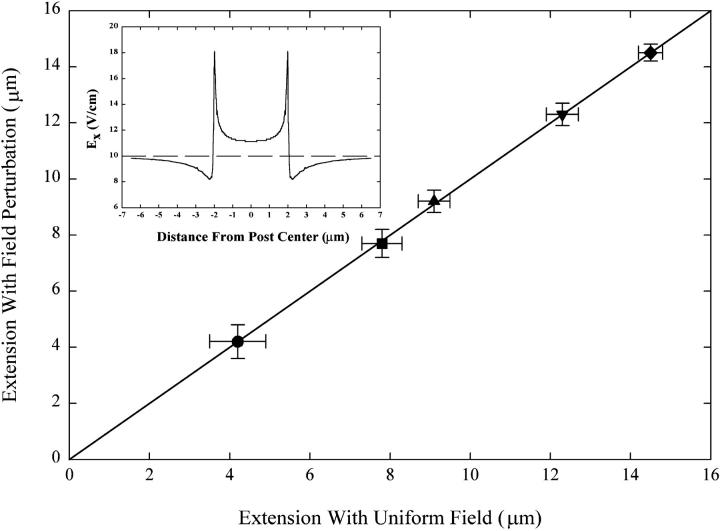
To compare our simulations as closely as possible to experiment, we chose the charge density of our simulated chain at each electric field to match the extension of a λ-monomer in our experiments at that particular electric field. Because the algorithm employs a variable bond length to speed dynamics, the lattice site size, a, and number of segments, N, depends on the probability of finding a particular bond vector. The algorithm at equilibrium has an average bond length of 2.8a (Deutsch and Binder, 1991). We chose the lattice size to make the average bond length equal to the persistence length (∼50 nm). Therefore, the simulated chain consisted of 332 segments (corresponding to a lattice site size a = 20 nm) to fit the contour length of the DNA found in our experiments. A parity plot of the equilibrium extension of the DNA averaged over several simulations fits a straight line through the origin with slope 1 (Fig. 3). The close agreement between the two cases for an FJC implies that we can assume a constant electric field in the analysis of our DNA stretching experiments.
FIGURE 3.
A parity plot of the extension of a polyelectrolyte found from MC simulations of an FJC in a constant electric field versus the extension in the field found from the full solution of Laplace's equation around an elliptical post. The straight line through the origin has a slope of 1, demonstrating that the perturbation of the field by the post has no effect on the total stretching of the chain. The data points are for 1 V/cm (•), 2.5 V/cm (▪), 5 V/cm (▴), 10 V/cm (▾), and 20 V/cm (♦). The inset plots the x-component of the electric field around the post for a bulk electric field of 10 V/cm.
Electrophoretic stretching
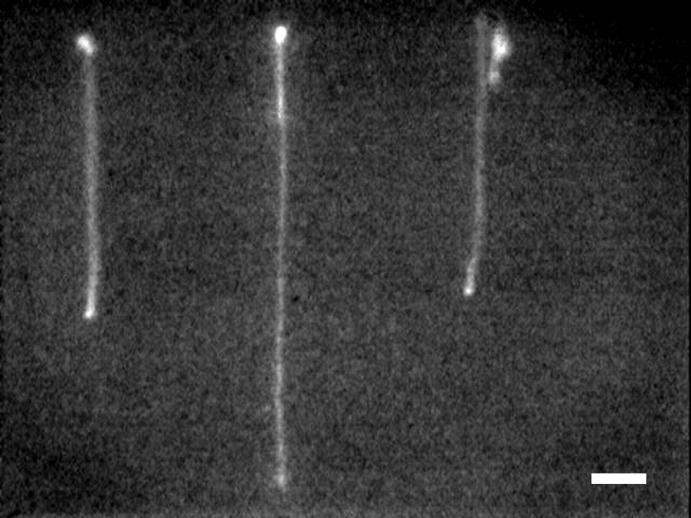
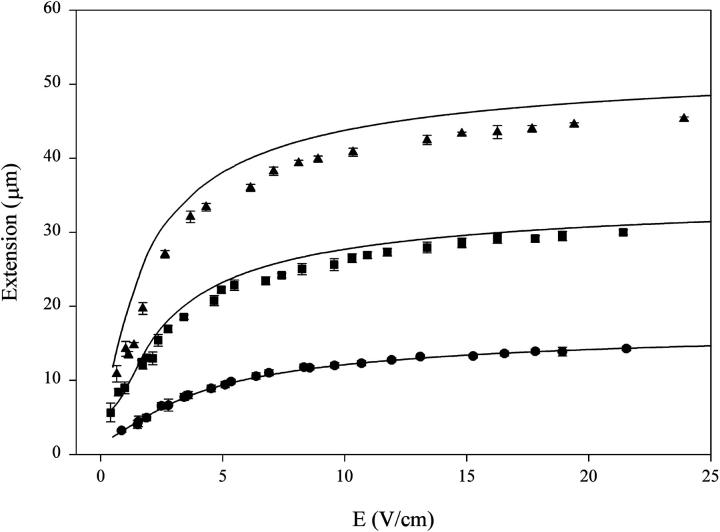
Fig. 4 shows a representative image of DNA concatamers stretching under the influence of an electric field. The regular spacing of the chains along the transverse direction of the image confirms that the DNA immobilization occurs only on the functionalized gold posts. Often multiple molecules will bind to the same post, as can be seen on the middle post in Fig. 4, or the binding point may not be obvious, as for the leftmost post. These effects can lead to errors in the data, so we chose to collect data only on molecules that were singly bound to the posts and where the binding point could be clearly seen. The deformation of λ-DNA monomers, dimers, and trimers was determined for electric fields varying from <1 V/cm up to 25 V/cm (Fig. 5). To find the contour length of the molecules, we used the theoretical prediction of Marko and Siggia (1995), which assumes a molecule of DNA stretching in an electric field will show the same functional behavior as under any other force F (in the high force limit). This is the characteristic 1/F2 dependence predicted by the wormlike chain model. Perkins et al. (1995) demonstrated that a molecule of DNA tethered in a uniform flow behaves as if it were being stretched by forces applied at the two extremities, and we have found that our data also follows this functional behavior. Our data can be fit to the dominant term of the WLC model for entropic elasticity (the first term on the right side of Eq. 1):
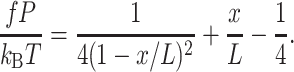 |
(1) |
Here, f is the force being applied to the ends of the chain, P is the persistence length, kB is Boltzmann's constant, T is the temperature, x is the end-to-end separation, and L is the contour length. The contour lengths determined from Eq. 1 for the three chains are 18.4 μm, 36.8 μm, and 55.3 μm, for the λ-monomers, dimers, and trimers respectively. The native contour length of the λ-genome is 16.3 μm; however, it has been found that the length of a λ-monomer increases to 22.4 μm when stained with the intercalating dye YOYO-1 at a saturating concentration (Perkins et al., 1995). It has been shown from crystallographic data that the DNA helix is extended by ∼4 Å per bis-intercalated YOYO molecule (Johansen and Jacobsen, 1998). At the dye concentration employed here, this leads to a contour length of 18.7 μm for a λ-monomer, very close to the value found by fitting the WLC.
FIGURE 4.
Representative epifluorescent image of DNA concatamers immobilized on the gold-topped posts and stretching in an electric field. The scale bar is equal to 7 μm.
FIGURE 5.
Average extension of λ-DNA monomers (•), dimers (▪), and trimers (▴) as a function of electric field in 0.5× TBE buffer. The solid lines are from the theory of Stigter (Stigter, 2002; Stigter and Bustamante, 1998).
DISCUSSION
The velocity of a DNA molecule in free electrophoresis has little dependence on length for molecules >100 bp (Stellwagen et al., 1997). When an electric field is applied across an electrolyte solution containing DNA, the counterion cloud (electric double layer) around the molecule experiences a force in the opposite direction to that of the DNA. At a very small length scale, this EOF balances the flow perturbation that is generated by the DNA moving through the quiescent solution and there are no long-ranged hydrodynamic interactions. Hence, DNA is free-draining during free electrophoresis. Every segment feels the same friction from the fluid, so molecules of varying sizes will have the same mobility. However, when DNA is tethered, the effect of the EOF generated by the flow of counterions past the DNA backbone is different. This EOF will not be balanced out by the hydrodynamics of the DNA moving through solution. Instead, it will build up collectively, leading to long-range hydrodynamic interactions so that DNA will not be free-draining. This observation was made by Long et al. (1996a,b), and led to their hypothesis that tethered DNA in an electric field will deform in the same way as DNA in a uniform flow field with velocity of μE, where μ is the free electrophoretic mobility of DNA.
If this hypothesis is correct, then we should be able to compare our data directly to the data of DNA stretching in uniform flow by measuring the free electrophoretic mobility of our DNA molecules. We measured the electrophoretic mobility of λ-monomers and multimers at the start of every experiment by averaging the velocity of hundreds of molecules using FlowVIS DPIV. (Not only is this a useful quantity for data analysis, but it is also a good test for the presence of EOF. If the electrophoretic mobility is constant between experiments and at different electric field strengths, then we have successfully eliminated the EOF.) We found the mobility of the DNA to be (3.2 ± 0.1) × 10−4 cm2V−1s−1, consistent with the prediction of Stigter (2002).
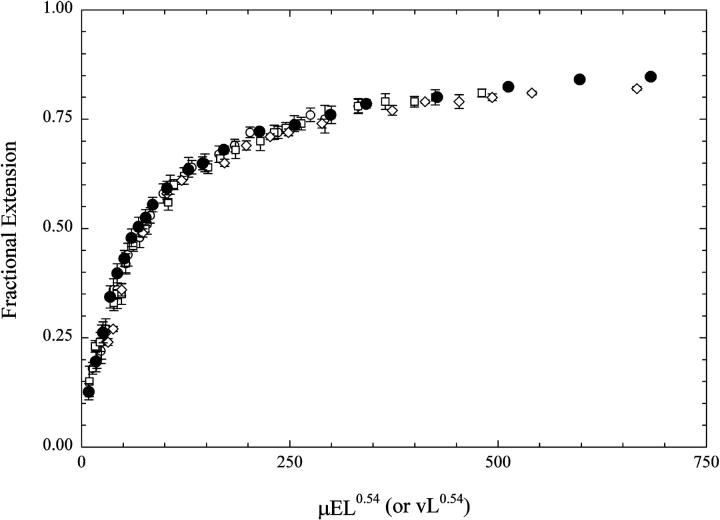
In a uniform flow field, the fractional extension for different length molecules of DNA was found to collapse onto a universal curve when it is plotted as a function of vLν, where v is the fluid velocity, L is the contour length of the molecule, and ν is the scaling exponent (Perkins et al., 1995). For a free-draining polymer, the scaling exponent should be 1, but for DNA lengths up to 80 μm it was found to be 0.54, showing that, even for very high extensions (>80%) in uniform flow, DNA cannot be considered free-draining. It has also been found that this exponent is scale-dependent (Larson et al., 1997), that is, for molecules longer than 80 μm the exponent shifts to a value of 0.75. If the hydrodynamic equivalence hypothesis of Long et al. (1996a,b) is correct, then the present data should scale exactly with the data of Perkins et al. (1995). Fig. 6 compares our data plotted with a scaling exponent of 0.54 (appropriate for DNA of this length), along with the data of Perkins and co-workers (Perkins et al., 1995). Although there are some systematic differences, the agreement between the two data sets is good, corroborating the approximate theory of hydrodynamic equivalence.
FIGURE 6.
The fractional extension of λ-DNA monomers (○), dimers (□), and trimers (⋄) plotted vs. μEL0.54, where μ is the electrophoretic velocity. Also plotted are the data of Perkins et al. (1995), (•) plotted versus. vL0.54, where v is the bulk fluid velocity.
Several models have been developed to quantitatively describe the steady stretching of DNA in a constant electric field. Schurr and Smith (1990) developed a FJC model for a polyelectrolyte in an external field, while Marko and Siggia (1995) applied the WLC model for the same case. Both theories use the linear charge density of DNA as an adjustable parameter, lumping all of the double layer effects, such as charge screening and electro-osmotic friction, into this parameter. In addition, the DNA is modeled to be free-draining—omitting hydrodynamic interactions between segments. To properly fit either model to our data, a different charge density must be used for each length of DNA. In light of the present results, it is obvious that an effective charge density is not physically realistic for describing the free solution stretching of tethered DNA in electric fields.
Consequently, we applied a numerical model developed by Stigter and Bustamante (Stigter, 2002; Stigter and Bustamante, 1998) for the electrophoretic stretch of DNA that includes the effects of electro-osmotic friction and hydrodynamic interactions. The model treats DNA as a chain of freely jointed ellipsoidal segments equal in size to the Kuhn length of DNA. The double layer effects are not taken into account explicitly, but instead an indirect method is used to calculate the force on each segment of the DNA. First, the free electrophoretic velocity is found from Gouy-Chapman theory for each segment based upon its orientation with respect to the electric field:
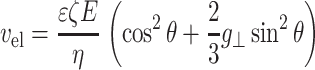 |
(2) |
In Eq. 2, vel is the electrophoretic velocity of the segment projected in the direction of the potential drop, ɛ is the permittivity of the medium, ζ is the zeta potential of the DNA, E is the electric field, η is the viscosity, θ is the angle of orientation with respect to the electric field, and 2/3g⊥ is a numerical factor accounting for the perturbation of the electric field by the DNA and for the relaxation of the double layer. The electrophoretic force on the segment is calculated from the hydrodynamic drag necessary to exactly compensate for the free electrophoresis. The hydrodynamic perturbation for each segment is then calculated from low Reynolds number transport theory and the total force on each segment found by summing the flow perturbation created by all other segments and adding this to the electrophoretic force, as in Eq. 3:
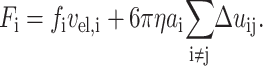 |
(3) |
Here, fi is the friction factor of segment i (which depends on its orientation to the field), ai is the equivalent Stokes radius of the segment, and Δuij is the hydrodynamic perturbation at segment i due to segment j.
Since the DNA is tethered at only one end, the tension in the chain will increase from zero at the free end to a maximum at the tethering point. If segment 1 is at the tethering point of a chain with N segments, then the tension at segment i is the sum of the forces on all segments with index greater than i, as in Eq. 4:
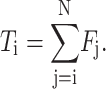 |
(4) |
A WLC entropic elasticity formula is then used to find the orientation of the segment relative to the field from the tension on the segment. The orientation of each segment is therefore coupled to the conformation of the full chain through the hydrodynamics. The model requires an iterative calculation procedure, cycling between the tension and orientation until self-consistency is found.
To apply the theory, we require the ζ-potential of the DNA-YOYO complex, as well as the persistence length and hydrodynamic radius of the DNA. We employed a value of 50 nm for the persistence length (a value that is somewhat uncertain, but generally accepted) and a value of 2.28 nm for the hydrodynamic radius found from atomistic modeling (Fernandes et al., 2002). Based upon our dye:bp ratio and the data reported by Stigter (Stigter, 2002; Stigter and Bustamante, 1998) for DNAs of various charges, we interpolated the ζ-potential of the DNA in our experiments to be 0.079 V. The results of the theory are shown as the solid lines in Fig. 5.
Recently, Stigter has extended his theory to include the screening of hydrodynamic interactions by nearby surfaces (Stigter, 2002). The model approximates no-slip at the bounding surfaces by the method of images (Happel and Brenner, 1965). The model corroborates our observation that DNA molecules of the length used here will stretch the same as in free solution if tethered 7.5 μm from the surface (data not shown).
CONCLUSIONS
The hydrodynamic equivalence model does have some limitations. Its development depends on the linearization of the coupled electro-hydrodynamic governing equations, which is not strictly valid except at low fields. On a small length scale, DNA behaves as a rigid rod, which will have a different electrophoretic mobility when it is aligned parallel to the field than when it is aligned perpendicular to the field. When the DNA is at low extensions, most of the chain will be oriented randomly and the linearization of the electrohydrodynamic equations will be valid. As the field strength increases, the DNA will be preferentially oriented parallel to the field, an orientation that has a larger electrophoretic mobility (Stigter and Bustamante, 1998). The proportionality constant therefore has a weak dependence on the orientation, and hence on the field strength. The systematic differences between the data of Fig. 6 are therefore not surprising.
Since the theory of Stigter (Stigter, 2002; Stigter and Bustamante, 1998) explicitly includes the variation in the electrophoretic velocity with orientation and also includes intersegment hydrodynamic interactions, there is no need to use adjustable parameters to fit the stretching data for DNA molecules of different length. However, the model still does not exactly predict the observed stretching of DNA and deviates more from the data as the length of the molecule increases. There are several aspects to the theory that may explain this deviation. First, it may be due to an incorrect estimate for one of the parameters in the model. Stigter addresses the sensitivity of the electrophoretic velocity on the hydrodynamic radius of the DNA (Stigter, 2002; Stigter and Bustamante, 1998), and we do not have an absolute value for the ζ-potential or the persistence length of the stained DNA. Accurate measurements of these parameters could lead to a better fit of the theory to experiment. However, if the fit of the theory with our data is compared to the fit of the accompanying hydrodynamic theory to the data of Perkins et al. (1995), the same deviation is seen. The theory closely predicts the extension of the shorter DNA, but at longer lengths, the model begins to overpredict the extension. This systematic inconsistency also occurs when the FJC model of Schurr and Smith (1990) is applied to our data. It is possible, then, that treating the segments of DNA as freely jointed overestimates the stretching in electric fields.
In this work we have shown that electro-osmotic flow must be considered when performing single molecule experiments in silicon or glass microfluidic devices, but that the EOF can be eliminated by applying a polymer brush to all silicon surfaces. The present study of the deformation of single molecules of DNA in electric fields has corroborated the hydrodynamic equivalence model and provides a framework for developing a physical model of electrophoretic stretching.
Acknowledgments
We thank Dr. Dirk Stigter for many helpful discussions and suggestions, and Dr. Thomas T. Perkins for the data on hydrodynamic stretching in Fig. 6. All microfabrication was performed at the University of California, Berkeley, Microfabrication Facility. Electron microscopy images were obtained at the Berkeley Electron Microscopy Laboratory.
This work was supported by the United States Department of Energy under grant FG03-94ER-14456.
References
- Bakajin, O. B., T. A. J. Duke, C. F. Chou, S. S. Chan, R. H. Austin, and E. C. Cox. 1998. Electrohydrodynamic stretching of DNA in confined environments. Phys. Rev. Lett. 80:2737–2740. [Google Scholar]
- Carle, G. F., M. Frank, and M. V. Olson. 1986. Electrophoretic separations of large DNA molecules by periodic inversion of the electric field. Science. 232:65–67. [DOI] [PubMed] [Google Scholar]
- Carmesin, I., and K. Kremer. 1988. The bond fluctuation method: a new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules. 21:2819–2823. [Google Scholar]
- Chiari, M., M. Nesi, and P. G. Righetti. 1994. Capillary zone electrophoresis of DNA fragments in a novel polymer network: poly(n-acryloylaminoethoxyethanol). Electrophoresis. 15:616–622. [DOI] [PubMed] [Google Scholar]
- Clark, S. M., E. Lai, B. W. Birren, and L. Hood. 1988. A novel instrument for separating large DNA molecules with pulsed homogeneous electric fields. Science. 241:1203–1205. [DOI] [PubMed] [Google Scholar]
- Crenshaw, H. C., S. Tennakoon, and S. L. Katz. 1998. FlowVIs: flow visualization software (Freeware).
- Deutsch, H. P., and K. Binder. 1991. Interdiffusion and self-diffusion in polymer mixtures: a Monte Carlo study. J. Chem. Phys. 94:2294–2304. [Google Scholar]
- Drossman, H., J. A. Luckey, A. J. Kostichikow, J. D'Cunha, and L. M. Smit. 1990. High speed separation of DNA sequencing reactions by capillary electrophoresis. Anal. Chem. 62:900–903. [DOI] [PubMed] [Google Scholar]
- M. X. Fernandes, A. Ortega, M. C. Lopez Martinez, and J. Garcia de la Torre. 2002. Calculation of hydrodynamic properties of small nucleic acids from their atomic structure. Nucl. Acids Res. 30:1782–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happel, J., and H. Brenner. 1965. Low Reynolds Number Hydrodynamics. Prentice Hall, Englewood Cliffs, NJ.
- Hjerten, S. 1985. High-performance electrophoresis: elimination of electroendosmosis and solute adsorption. J. Chromatogr. 347:191–198. [Google Scholar]
- Hugel, T., M. Grosholz, H. Clausen-Schaumann, A. Pfau, H. Gaub, and M. Seitz. 2000. Elasticity of single polyelectrolyte chains and their desorption from solid supports by AFM-based single molecule force spectroscopy. Macromolecules. 34:1039–1047. [Google Scholar]
- Johansen, F., and J. P. Jacobsen. 1998. 1H NMR studies of the bis-intercalation of a homodimeric oxazole yellow dye in DNA oligonucleotides. J. Biomol. Struct. Dyn. 16:205–222. [DOI] [PubMed] [Google Scholar]
- Jorgenson, J. W., and K. P. Lukacs. 1983. Capillary zone electrophoresis. Science. 222:266–272. [DOI] [PubMed] [Google Scholar]
- Ladoux, B., J.-P. Quivy, P. S. Doyle, O. de Roure, G. Almonouzni, and J. Viovy. 2000. Fast kinetics of chromatin assembly revealed by single-molecule videomicroscopy and scanning force microscopy. Proc. Natl. Acad. Sci. USA. 97:14251–14256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson, R. G., and H. Hu. 1999. Brownian dynamics simulations of a DNA molecule in an extensional flow field. J. Rheol. 43:267–304. [Google Scholar]
- Larson, R. G., T. T. Perkins, D. E. Smith, and S. Chu. 1997. Hydrodynamics of a DNA molecule in a flow field. Phys. Rev. E. 55:1794–1797. [Google Scholar]
- Long, D., J. Viovy, and A. Ajdari. 1996a. Simultaneous action of electric fields and nonelectric forces on a polyelectrolyte: motion and deformation. Phys. Rev. Lett. 76:3858–3861. [DOI] [PubMed] [Google Scholar]
- Long, D., J. Viovy, and A. Ajdari. 1996b. Stretching DNA with electric fields revisited. Biopolymers. 39:755–759. [Google Scholar]
- Marko, J. F., and E. D. Siggia. 1995. Stretching DNA. Macromolecules. 28:8759–8770.
- Patel, P. D., and E. S. G. Shaqfeh. 2003. A computational study of DNA separations in sparse disordered and periodic arrays of posts. J. Chem. Phys. 118:2941–2951. [Google Scholar]
- Perkins, T. T., D. E. Smith, and S. Chu. 1994. Direct observation of tube-like motion of a single polymer chain. Science. 264:819–822. [DOI] [PubMed] [Google Scholar]
- Perkins, T. T., D. E. Smith, and S. Chu. 1997. Single-polymer dynamics in an elongational flow. Science. 276:2016–2021. [DOI] [PubMed] [Google Scholar]
- Perkins, T. T., D. E. Smith, R. G. Larson, and S. Chu. 1995. Stretching of a single tethered polymer in a uniform flow. Science. 268:83–87. [DOI] [PubMed] [Google Scholar]
- Probstein, R. F. 1994. Physicochemical Hydrodynamics. John Wiley & Sons, Inc., New York City.
- Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
- Schurr, J. M., and S. B. Smith. 1990. Theory for the extension of a linear polyelectrolyte attached at one end in an electric field. Biopolymers. 29:1161–1165. [Google Scholar]
- Smith, D. E., H. P. Babcock, and S. Chu. 1999. Single-polymer dynamics in steady shear flow. Science. 283:1724–1727. [DOI] [PubMed] [Google Scholar]
- Smith, D. E., and S. Chu. 1998. Response of flexible polymers to a sudden elongational flow. Science. 281:1335–1340. [DOI] [PubMed] [Google Scholar]
- Smith, S. B., P. K. Aldridge, and J. B. Callis. 1989. Observation of individual DNA molecules undergoing gel electrophoresis. Science. 243:203–243. [DOI] [PubMed] [Google Scholar]
- Smith, S. B., and A. J. Bendich. 1990. Electrophoretic charge density and persistence length of DNA as measured by fluorescence microscopy. Biopolymers. 29:1167–1173. [DOI] [PubMed] [Google Scholar]
- Smith, S. B., L. Finzi, and C. Bustamante. 1992. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 258:1122–1126. [DOI] [PubMed] [Google Scholar]
- Song, L., and M. F. Maestre. 1991. Unhooking dynamics of U-shaped DNA molecule undergoing gel electrophoresis. J. Biomol. Struct. Dyn. 9:87–99. [DOI] [PubMed] [Google Scholar]
- Stellwagen, N. C., C. Glefi, and P. G. Righetti. 1997. The free solution mobility of DNA. Biopolymers. 42:687–703. [DOI] [PubMed] [Google Scholar]
- Stigter, D. 2002. Wall effects on DNA stretch and relaxation. Biophys. Chem. 101–102:447–459. [DOI] [PubMed] [Google Scholar]
- Stigter, D., and C. Bustamante. 1998. Theory for the hydrodynamic and electrophoretic stretch of tethered B-DNA. Biophys. J. 75:1197–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tessier, F., J. Labrie, and G. W. Slater. 2002. Electrophoretic separation of long polyelectrolytes in submolecular-size constrictions: a Monte Carlo study. Macromolecules. 35:4791–4800. [Google Scholar]
- Viovy, J. 2000. Electrophoresis of DNA and other polyelectrolytes: physical mechanisms. Rev. Mod. Phys. 72:813–872. [Google Scholar]
- Zimm, B. H., and S. D. Levene. 1992. Problems and prospects in the theory of gel electrophoresis of DNA. Quart. Rev. Biophys. 25:171–204. [DOI] [PubMed] [Google Scholar]
- Zimmerman, R. M., and E. C. Cox. 1994. DNA stretching on functionalized gold surfaces. Nucleic Acids Res. 22:492–497. [DOI] [PMC free article] [PubMed] [Google Scholar]