Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Oct;85(4):2599–2605. doi: 10.1016/s0006-3495(03)74682-7

Computational Study on the Function of Water within a β-Helix Antifreeze Protein Dimer and in the Process of Ice-Protein Binding

Zuoyin Yang *, Yanxia Zhou *, Kai Liu *, Yuhua Cheng *, Ruozhuang Liu *, Guangju Chen *, Zongchao Jia †
PMCID: PMC1303483  PMID: 14507722

Abstract

Antifreeze proteins (AFPs) help many organisms protect themselves from freezing in subzero temperatures. The most active AFPs found to date are those from insects, which possess exceptionally regular β-helical structures. On the ice-binding surface of these proteins, regularly arrayed water molecules are observed within the repeating Thr-Xxx-Thr motif, but the exact role of these water molecules remains unknown. In this work, we have employed a number of computational methods to examine the role of these water molecules in an AFP from Tenebrio molitor (TmAFP). Our investigation involved a combination of molecular and quantum mechanical approaches. Properties such as stability, interaction energy, orbital overlap, and conformational analysis of various systems, including TmAFP-water, TmAFP-water-ice, and TmAFP-ice, were systematically evaluated and compared. The regularly arrayed water molecules were found to remain associated with TmAFP before ice binding, demonstrating that they are an intrinsic part of the protein. These water molecules may assist TmAFP in the process of ice recognition and binding. However, after facilitating the initial stages of ice recognition and binding, these water molecules are excluded in the final formation of the AFP-ice complex. The departure of these water molecules enables a better two-dimensional match between TmAFP and ice. These results agree with experimental observations showing that although these water molecules are aligned with the ice-binding hydroxyl groups of Thr residues in one dimension, they are in fact positioned slightly off in the second dimension, making a good two-dimensional match impossible.

INTRODUCTION

Antifreeze proteins (AFPs) and glycoproteins, also known as thermal hysteresis proteins and glycoproteins, play an important biochemical role in many cold-tolerant animals (Devries, 1971), insects (Baust et al., 1985; Knight and Duman, 1986; Graether et al., 2000), and plants (Urrutia et al., 1992). AFPs and antifreeze glycoproteins lower the freezing point of a solution without affecting the melting point and osmotic pressure of that solution (Knight et al., 1984). These proteins do not prevent the formation of ice, but instead function by modifying the ice morphology to inhibit further ice growth (Madura et al., 2000). Insect AFPs are much more effective than fish AFPs at depressing solution freezing points and are, in fact, the most active AFPs discovered to date (Tyshenko et al., 1997; Graether et al., 2000).

Because of the inability to observe directly interactions between AFPs and ice at the molecular level, computational studies and molecular modeling have been used to obtain a representation of AFP-ice associations and to investigate the molecular mechanism of AFP ice growth inhibition (Madura et al., 2000). The rapid advancement of computing power, combined with traditional molecular mechanical (MM) and molecular dynamical (MD) methods, has been very useful in such studies. Recently, the quantum mechanical method (QM) has been employed because it allows for the derivation of properties that depend upon the electronic distribution within assemblies of molecules and, in particular, it allows for the investigation of essential interactions between molecules (Cheng et al., 2002).

Structure-function studies, ice etching experiments, x-ray structures, and computer modeling have been employed to make various hypotheses about ice growth inhibition by AFPs. However, compared with the macromolecular mechanism, a definitive molecular mechanism of action has not emerged and remains a source of debate (Madura et al., 2000). In general, our current understanding is that AFPs adsorb to ice via hydrogen bonds, van der Waals forces, and even hydrophobic forces. This interaction network is provided through surface-accessible polar groups that are arranged in such a way as to promote optimum overall interactions (Jia and Davies, 2002).

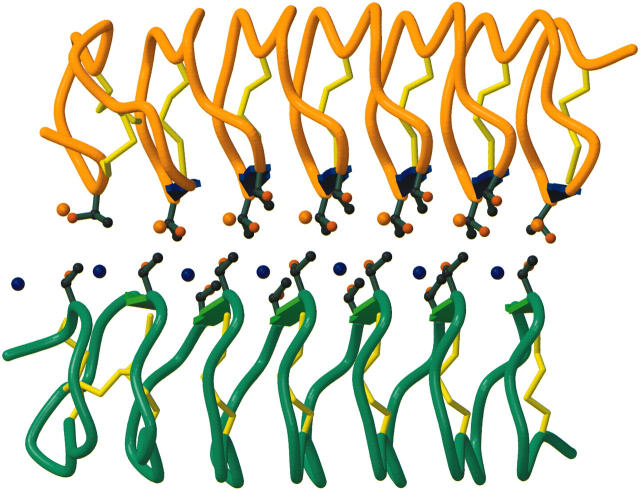
The high resolution (1.4 Å) x-ray structure of an insect antifreeze protein dimer from Tenebrio molitor (TmAFP) has been determined (Liou et al., 2000). TmAFP consists of seven loops, each composed of tandem 12-residue repeats (TCTxSxxCxxAx) arranged into an exceptionally regular β-helix with regularly spaced surface hydroxyls and accompanying water molecules. This structure is perhaps the most regular protein structure observed to date. Despite having no overall sequence homology, interestingly the highly regular β-helical structure and associated water molecules in the ice-binding site are also found in the AFP from spruce budworm AFP (Leinala et al., 2002a,b). Although the exact locations of the water molecules are not identical, in both cases they are regularly positioned in a trough encircled by two ranks of Thr residues. Presumably, convergent evolution has brought both TmAFP and spruce budworm AFP to the same β-helix fold. Conserved motifs formed by Thr-Cys-Thr residues on one side of the TmAFP are arrayed to form a flat β-sheet that makes up the ice-binding surface, with the OH groups of the Thr residues making a near perfect match to the prism plane of the ice lattice. In the crystal structure, a dimer is formed along the surfaces of parallel β-sheets. The two monomers do not interact directly with each other; instead, two ranks of seven water molecules mediate the interaction. In light of the bound coplanar external water molecules and the spacing between OH groups of the Thr residues (Fig. 1), it was predicted that in one monomer the three ranks of oxygen atoms (two ranks from the –OH groups of ordered Thr residues plus one rank from the regularly arrayed water molecules) would form a two-dimensional array with an orientation similar to that of oxygen atoms found on both the primary prism plane and, to less extent, the basal plane of ice (Liou et al., 2000). Another monomer would bind to this ice-like lattice via the same motif. This is considered to be the first glimpse of an AFP in an ice-bound state. This mimicry of an ice structure and a near perfect two-dimensional ice lattice match readily explains the hyperactivity of TmAFP. An intriguing problem is therefore to evaluate whether the regularly arrayed water molecules observed in the crystal dimer play any role in TmAFP-ice binding.

FIGURE 1.

FIGURE 1

Open in a new tab

Dimer of TmAFP and the regularly spaced water molecules (single dark blue and orange spheres) trapped in between the two TmAFP monomers (dark green and orange ribbons). Yellow bonds represent disulfide bridges within the β-helix cylinder. Regularly arrayed Thr residues are also displayed.

In this article, we investigate the potential role of these water molecules. The methods of MM, MD, QM, and mixed MM/QM are first used to examine the interactions between these water molecules and the TmAFP dimer. Monomeric TmAFP is then explored on its own and in conjunction with its associated rank of water molecules. Based on the monomer structure, the course of TmAFP adsorption on to the primary prism ice plane is also investigated using MM and MD methods. Finally, the interaction energies between ice and the protein, with or without the regularly arrayed water molecules, are calculated by two independent computational methods (MM and QM).

PROCEDURES AND COMPUTATION METHODS

Calculations of the dimer

Based on the high-resolution x-ray structure of the TmAFP dimer, hydrogen atoms were added to two TmAFP monomers and two ranks of water molecules. The model was then energy minimized or optimized using MM with the AMBER force field (Cornell et al., 1995), keeping nonhydrogen atoms fixed. MM and semiempirical quantum mechanical (QM/AM1) methods (Dewar et al., 1985) were used to calculate the interaction energy between water molecules and the two monomers. Another computational method, known as ONIOM, or the “hybrid approach” (Field et al., 1990; Svensson et al., 1996), was also employed to best evaluate the interaction between the proteins and the two ranks of water molecules. We chose this strategy mainly based on the compromise between available computing power and an attempt to study the system as thoroughly as possible. In this process, all atoms in the dimer were divided into three layers according to their distance from a fictitious plane in the middle of the dimer and parallel to the long axis of the TmAFPs. Atoms within 3.0 Å of the plane were placed in the first layer in which stronger interactions are found, containing 131 atoms. Atoms between 3.0 Å and 5.0 Å of the plane were included in the second layer that possesses weaker but still significant interactions, containing 205 atoms. The rest were placed in the third layer representing all long-range interactions. For the ONIOM approach, to make the method computationally feasible we performed single-point energy calculations for the first layer only using the higher-level quantum method-density functional method (B3LYP) (Becke, 1993; Lee et al., 1988) with a larger basis set 6-31G*. Specifically, the calculation was applied to the dimerization region, which was composed of the two ranks of water molecules together with the nearby protein residues. Given the much increased number of atoms in the second layer and the need to still use method(s) of best possible level within our available computing power, the QM/AM1 method was used for the second layer. Last, we employed the MM method for the third layer. Single-point energy computations were carried out using the Gaussian 98 package (Gaussian, Carnegie, PA) (Frisch et al., 1998).

MM and MD computations

A half of the dimer, which contains a monomer and a single rank of the regularly arrayed water molecules, was considered as the solute in our calculations. The solute was dipped in aqueous solvent using a periodic box with dimensions of 34.1 Å × 29.1 Å × 50.1 Å as implemented in the HyperChem software package (HyperChem, version 5.01, HyperCube, Gainesville, FL), and the solvent water molecules were added with TIP3P models (Jorgensen et al., 1983). After an energy minimization step, the solvated system was subjected to 400 ps of dynamics simulation with a step size of 1 fs and at the constant temperature of 273 K. After the MD process finished, another round of energy minimization was performed. In these steps, no constraints were imposed on the system, and all atoms were allowed to move freely.

Next, the solute was picked out from the solvated system and manually docked on to the primary prism ice plane using the β-surface of the protein. In a process similar to the method described above, the solute and ice were dipped in aqueous solvent using TIP3P models, in which the periodic box was of the dimensions of 40.0 Å × 35.1 Å × 50.1 Å. After structure optimization, MD was employed for 210 ps at 273 K. Unlike in the MD employed for the solute-solvent system above, the oxygen atoms in the ice were fixed in place so that the original form of the ice lattice could be retained during the MM and MD computations. For more details, see our previous report (Chen and Jia, 1999).

Calculations of the interaction energies between protein and ice

In this section, two models were built based on the energy-minimized TmAFP structure. Both of them contained the protein monomer docked to the primary prism plane of ice with the same orientation as described above. Model A contained the protein docked to the ice plane only, whereas model B also included a rank of regularly arrayed water molecules in the TmAFP monomer. Before energy evaluation using QM/AM1, it was necessary to optimize both models using MM. During the energy minimization process, all atoms in the models were allowed to move freely, with the exception of the oxygen atoms in the ice. Both structural optimizations were terminated with the same convergence criterion of rms gradient ≤0.00001 kcal/mol. Finally, both models were subjected to 500 ps of simulation in a vacuum at 273 K, with the ice oxygen atoms remaining fixed. Unlike the MD procedure above, the oxygen atoms of the TmAFP-associated water molecules in the second model were also fixed to investigate the conformational changes in TmAFP.

RESULTS AND DISCUSSION

The bridge-linked interaction of water with the TmAFPs

For ease of presentation, the dimer composed of two protein monomers and two ranks of water molecules are labeled P1, P2, W1, and W2, in which P1 and P2 represent individual TmAFP monomers, and W1 and W2 represent the two ranks of water molecules. P1 and W1 are closer together and form the first half of the dimer, while P2 and W2 are similarly arranged and form the second half of the dimer. Although the distance between the two backbones of the TmAFP monomers is at least 8 Å (Liou et al., 2000), many side-chain atoms, such as the –OH and –CH3 groups of the Thr residues, are much closer, measuring no more than 3 Å apart (according to the structure optimized by MM). Hence it should be expected that there will be some interactions between all adjacent components in the four-component (P1W1W2P2) system. To investigate the bridge-linked interactions between the water molecules in the dimer, we first considered (W1W2) and (P1P2) to be two independent entities. The interaction energy (E) between the two ranks of water molecules and the TmAFPs can be expressed as follows:

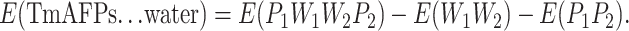graphic file with name M1.gif (1)

Similarly, we could take the three-component part (P1W1P2) or (P1W2P2) as a single entity. Using this, the interaction energy between the two ranks of water molecules can then be calculated according to Eq. 2:

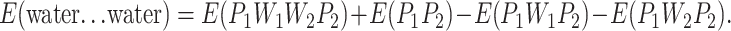graphic file with name M2.gif (2)

The total bridging interaction energy can therefore be obtained from the following expression:

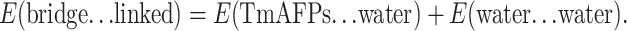graphic file with name M3.gif (3)

The results derived from the calculations of the MM, QM/AM1, and ONIOM—which includes B3LYP/6-31G*, AM1, and AMBER—methods are listed in Table 1. Corresponding interaction energies, such as E(bridge…linked), vary somewhat depending on the method used. This variation is expected because of differences in the algorithms used among the various methods. The most important observation is that the ratio of E(TmAFPs…water) to E(bridge…linked) resulting from any two different calculations is almost the same, proving that water molecules indeed mediate the association within the TmAFP dimer by offering bridging interactions between the two monomers. On the other hand, the ratio of E(TmAFPs…water) to E(bridge…linked) is approximately nine times that of E(water…water) to E(bridge-linked). This implies that the interactions between the two halves (P1W1 and W2P2) of the dimer are much stronger than between the two ranks of water molecules alone (W1 and W2). Dimer association is therefore a result of the overall contribution of both protein and water. Since the interaction between the two equivalent parts (P1 and W1, P2 and W2) contributes equally to E(TmAFPs…water), the E(TmAFPs…water) values, and particularly the one derived from ONIOM using density function calculations, indicate that there is a strong nonbonding interaction between one monomer and its own rank of water molecules.

TABLE 1.

Interaction energies (kcal/mol) calculated with various methods

Interaction energy MM AM1 ONIOM (B3LYP/6-31G*:AM1:AMBER)
E(TmAFPs…water) −36.3001 −22.5978 −54.6561
E(water…water) −4.7399 −2.1177 −5.7750
E(bridge-linked) −41.04 −24.7155 −60.4311
Open in a new tab

Regular water in the aqueous TmAFP-water system

Although there are strong interactions between the TmAFP monomer and its own rank of water molecules in the dimer crystal, it is necessary to investigate the behavior of these water molecules with TmAFP in solution. The first simulation of TmAFP-water in aqueous solution was undertaken to investigate whether bound water molecules would retain their relative positions observed in the dimer. After the simulations, the RMSD of the resulting TmAFP from the starting structure is only 1.10 Å, demonstrating that the overall structure of the TmAFP in solution is stable and rigid. In addition, to further assess the stability we carried out statistical analysis of energy and temperature from 200 ps to 400 ps in the course of 400 ps simulation. The results show that the standard derivations of the total energy, potential energy, kinetic energy, and temperature were only 12.90, 31.23, 25.17 kcal/mol, and 2.14 K. The system was therefore deemed stable.

It is important to track the movements of the oxygen atoms in the associated rank of water molecules and their distance variation with respect to the planes formed by the oxygen atoms of Thr residues in adjacent loops. As an example, Fig. 2 shows the course of a 400-ps simulation. According to the definition of torsion angle, positive and negative values indicate the reverse position of the fourth atom relative to the plane formed by three previous atoms. Therefore, if the oxygen atom of a water molecule is chosen as the fourth atom and those from –OH groups of three adjacent Thr on the β-surface are taken as a reference plane, then the signs and values of torsion angle could demonstrate the deviation of water from the reference plane. A positive sign indicates that water is positioned outside of the plane in this study. In Fig. 2, Panel 1, it can be seen that the torsion angles of water molecules oscillate in the range of −19.96° to 27.23°, with an average torsion angle of 6.61° during the course of simulation. These results show that observed water molecules are located outside the reference plane and toward solvent according to the orientation selected in this study. Most significant, these water molecules were unable to break loose from TmAFP. The distance between two oxygen atoms from adjacent water molecules fluctuated between 3.12 Å and 6.11 Å with an average value of 4.49 Å (Fig. 2, Panel 2). This is similar to the changes between –OH groups in neighboring loops on the β-surface of TmAFP (Fig. 2, Panel 3), though the variation is smaller (only ∼1.7 Å). As for the –OH groups of the same loop, the spacing of two oxygen atoms varies to approximately the same extent as that in different loops and has a larger average value of 7.63 Å (Fig. 2, Panel 4). From these observations, we drew three conclusions. First, the water molecules bound in the TmAFP crystal dimer maintain their relative position to the β-sheet of the TmAFP monomer when in aqueous solution. The water molecules are neither replaced by solvent molecules nor moved from their original positions. Second, the coplanar feature of the oxygen atoms of the water molecules and the –OH groups of Thr is less optimal when compared with that of the crystal, but the deviation is not significant, despite the fact that the water array shifts slightly toward the outside of the β-surface. This observation implies that, before ice binding, certain flexibility of the planar β-surface is desirable in initializing the process of recognition and binding to ice because of the dynamic nature of ice growth fronts. Once the AFP-ice complex is formed, planarity would provide best possible match to ice lattice. Third, as a whole, these water molecules would move along with any TmAFP shift simultaneously. Therefore, when investigating the interaction between TmAFP monomers and ice, regularly bound water molecules should be included.

FIGURE 2.

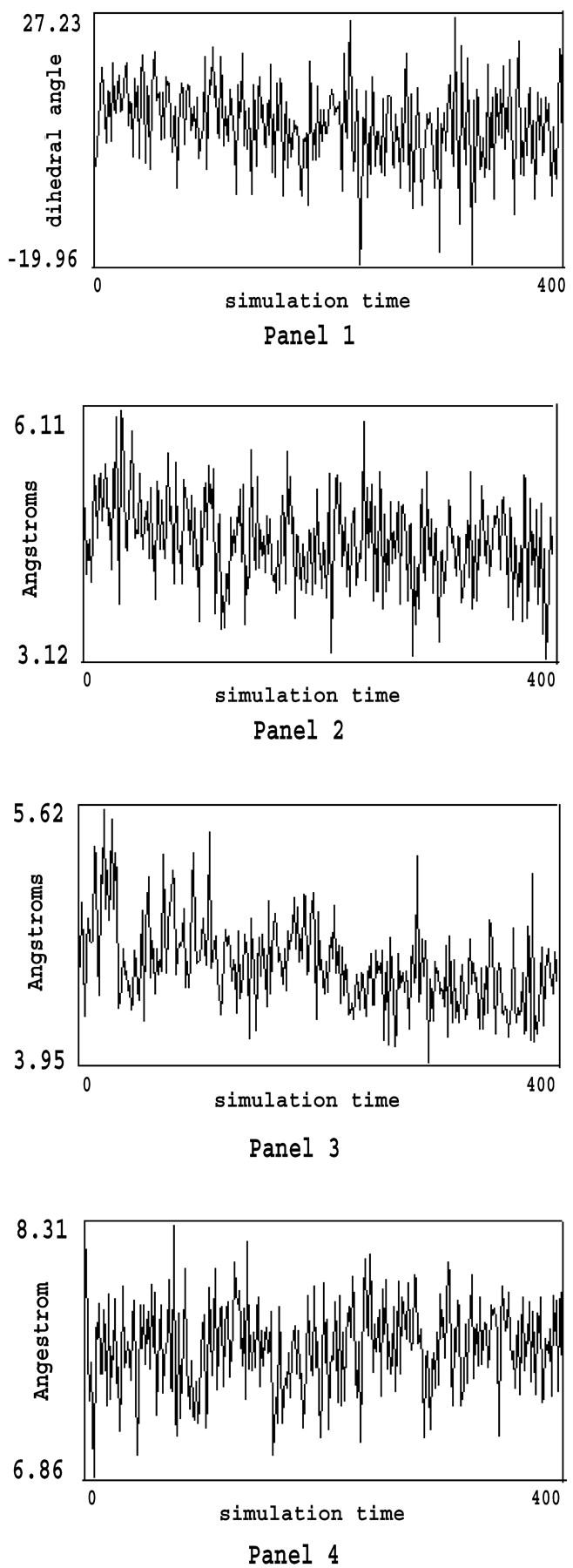
FIGURE 2

Open in a new tab

These graphs show an example of the geometry changes during the simulation of aqueous TmAFP. Panel 1 shows the changes in torsion angle (°) formed by the four closest oxygen atoms (three from hydroxyls in the β-sheet of the fourth and the fifth loop and one from the water imbedded in these two loops). The other panels show O–O bond distance variation (Å): Panel 2 is of adjacent waters that are close to the fourth loop; Panel 3 is of hydroxyls in the β-sheet on the fourth and the fifth loop; Panel 4 is of hydroxyls on the fourth loop.

Modeling the complex of TmAFP-water and ice in solution

To investigate the mechanism by which the β-surface of TmAFP docks to an ice plane, the effect of bound water molecules must be considered. As described above, the protein monomer and its associated rank of water molecules were docked as a single structure to the primary prism plane of ice. The movement of the water molecules was tracked during the course of the simulation.

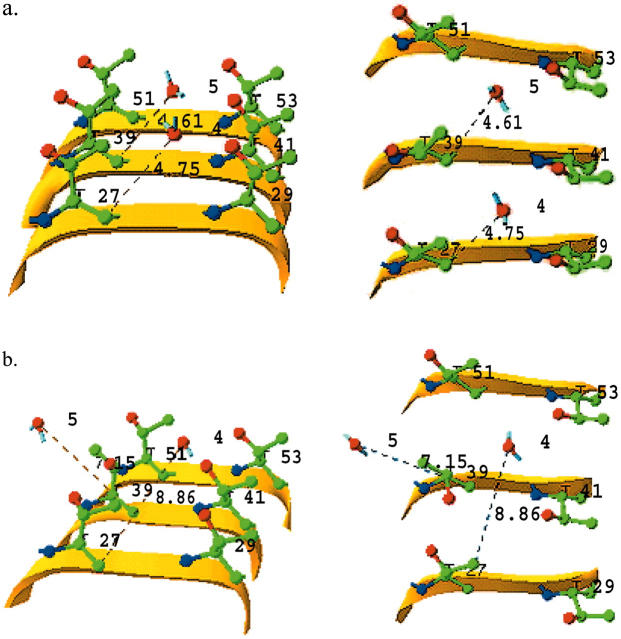
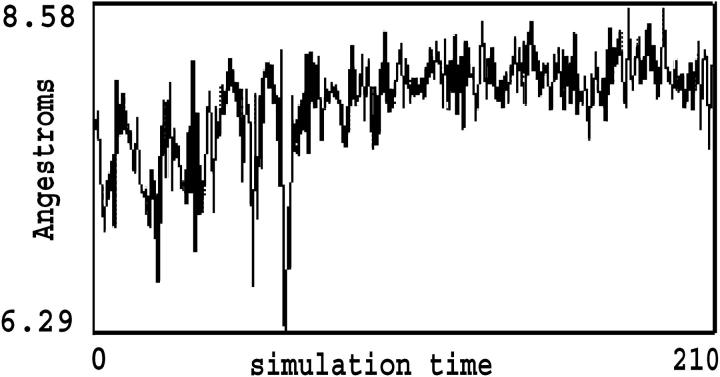
At the beginning of the simulation, the oxygen atom in water molecule 4, surrounded by four Thr residues numbered 27, 29, 39, and 41, is 4.75 Å away from the backbone carbon atom of Thr-27, while the oxygen atom in water molecule 5, located in another cage formed by Thr residues 39, 41, 51, and 53, is 4.61 Å from the Thr-39 backbone carbon atom (Fig. 3 a). Since the regular water molecules move together with the TmAFP monomer before ice recognition and initial interaction, they form part of the overall ice-binding substructure of AFP responsible for initial recognition and interaction. The increased number (by ∼30%) of regular structural elements as a result of including regular water molecules would render ice recognition much easier. This is not surprising since an increase of regular structural elements in a given area (β-surface) would facilitate the initial two-dimensional match to the ice lattice. After ∼30 ps of simulation, water molecule 4 gradually moves away from Thr-27 and forces water molecule 5 to break free from its surrounding Thr residues (Fig. 3 b). In other words, these water molecules are unable to retain their original positions while TmAFP interacts with ice. In fact, by the end of the simulation, five water molecules left the β-surface of TmAFP and merged with the surrounding solvent molecules. In the meantime, as the regular water molecules were departing from the β-surface of TmAFP, the spacing between adjacent oxygen atoms from the –OH groups in Thr residues, such as 39 and 41, changed substantially (Fig. 4). Distance variation is larger than 2.0 Å during the first 70 ps of the simulation but decreases to ∼1.1 Å for the remainder of the simulation. The standard deviation in the first 70 ps is 0.419 Å, about twice that of the remainder of the simulation, indicating that the distance variation between O atoms of Thr residues was the largest during water release. On the other hand, the potential energies of the whole system changed very little. The favorable increase in entropy, resulting from the water released, may be balanced by the decreased motion of the –OH groups of Thr residues. The general observation is that positional variation of Thr resides became gradually reduced as water releasing and ice interacting proceed. The markedly reduced distance variation in the TmAFP-ice system after 70 ps of simulation (Fig. 4) implies that the oxygen atoms in the –OH groups might be confined by O atoms in the ice lattice via nonbonded interactions.

FIGURE 3.

FIGURE 3

Open in a new tab

Example of water molecules leaving the trough formed by Thr residues during the simulation of TmAFP-water-ice solution. (a) Before simulation (0 ps); (b) 30 ps. Yellow ribbons represent the local backbone. Thr side chains and water molecules are also displayed: oxygen, nitrogen, and carbon atoms are represented in red, blue, and green, respectively. Left and right panels show the same substructure tilted vertically for a better three-dimensional appreciation.

FIGURE 4.

FIGURE 4

Open in a new tab

O–O distance variation of the hydroxyl between Thr-39 and Thr-41 during the simulation of the aqueous TmAFP-water-ice system. Distance variation is decreased by ∼1.1 Å after 70 ps of simulation. The standard deviations are ∼0.419 Å for the first 70 ps, and 0.210 Å for the remainder of the simulation.

Interaction energy between TmAFP and ice

In contrast to the aqueous TmAFP system, the rank of bound water molecules prefers to break away from the protein when TmAFP is docked to ice. To evaluate the effect of these water molecules on the TmAFP-ice interaction energies, we have evaluated the interaction energy in two models which were optimized using MM. The interaction energies for model A and model B are listed in Table 2. In addition, molecular orbital analysis by QM/AM1 was employed using an approach previously reported (Cheng et al., 2002).

TABLE 2.

Interaction energies (Einter) in models A and B (kcal/mol), derived from MM and QM/AM1 calculations. In the case of QM/AM1, n represents the number of interacting orbitals. The ratio of interacting orbitals to the total number of molecular orbitals of the system is given as a percentage

MM
QM/AM1
Model Einter Einter n Percentage
A (TmAFP…ice) −50.2979 −117.4887 32 0.92
B (TmAFP+water…ice) −44.5842 −51.3761 28 0.80
B (TmAFP…ice) −39.5944 −36.6453 25 0.71
Open in a new tab

Model B is a complex consisting of TmAFP, water, and ice, in which the ice is able to interact with both TmAFP and the water molecules. In addition to the interaction energy between ice and TmAFP-water [E(TmAFP + water…ice)], the interaction energy between TmAFP and ice [E(TmAFP…ice)] also was analyzed so that direct comparisons could be made with model A. As can be seen in Table 2, the nonbonding interaction between the protein and ice in model A is significantly greater than that in model B (more than three times). Even when the TmAFP and the water molecules in model B are taken as a single entity, their interaction with ice is still weaker than that in model A from both MM and QM calculations.

Why does model A have stronger interaction energy than that of model B? We can better understand this by further analyzing the orbital interactions between AFP and water molecules in ice. In model A, there are 32 interaction orbitals, which represent 0.92% of the total number of molecular orbitals (Table 2). For model B, there are two scenarios. When TmAFP, ice, and water are considered, there are 28 interaction orbitals. There are 25 orbitals when TmAFP and ice only are considered. In both cases, the percentage of the interaction orbitals in model B is less than that in model A. More interacting orbitals correspond to more electron density in the vicinity of interaction, which results in higher interaction energy. Obviously, the existence of the regular water weakens the interaction between TmAFP and ice, demonstrating that model A is a better system than model B.

Since it is difficult to overcome the potential barrier for large-scale change such as rotation of a whole molecule using optimization alone, the two models were subjected to 500-ps simulations in vacuum at a constant temperature of 273 K. At the end of these simulations, model A had almost no positional change (Fig. 5, a and a′). In contrast, when the oxygen atoms of the water molecules were fixed, the TmAFP in model B not only rotated by at least 20° but also shifted, and the rank of water molecules was almost completely expelled (Fig. 5, b and b′). These observations indicate that the rank of water molecules would interfere with the β-sheet of TmAFP during docking, preventing a better fit with the ice lattice. TmAFP appears to prefer adsorbing directly to the ice plane without the extra rank of water, forming a strong, near-perfect two-dimensional match (7.6 Å × 4.5 Å) with the ice lattice.

FIGURE 5.

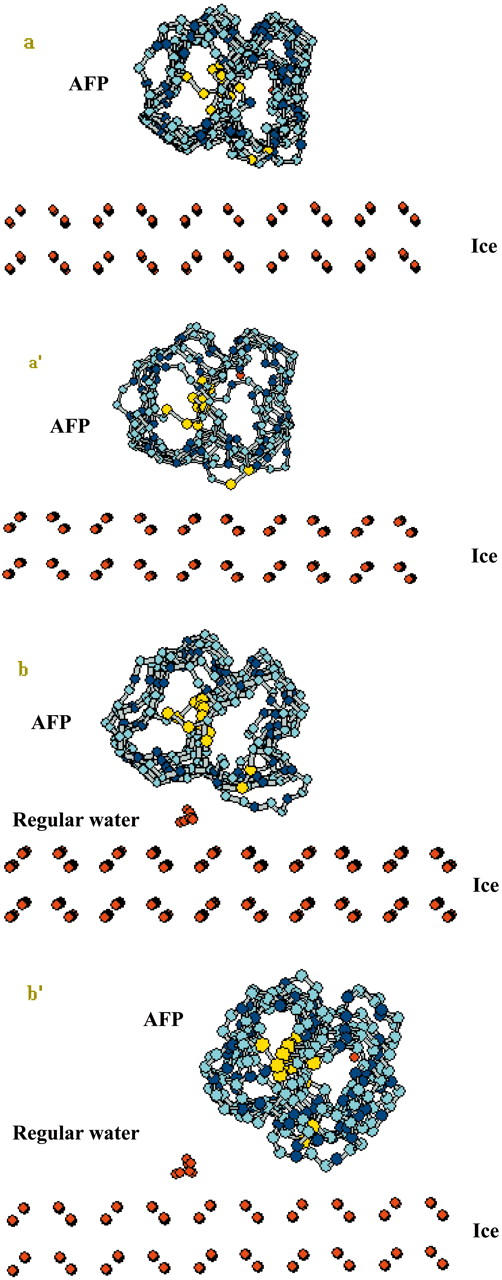
FIGURE 5

Open in a new tab

Adsorption models for TmAFP on ice (its oxygen atoms shown in red). Panels a and a′ represent the structure of model A at the beginning and the end of the 500-ps simulation, respectively; panels b and b′ represent the analogous information for model B.

CONCLUDING REMARKS

In this article, we have employed a computational approach to investigate the role of the rank of regularly arrayed water molecules observed in the crystal structure of TmAFP and attempted to better understand the mechanism by which TmAFP binds to ice. These water molecules, confined by a trough of Thr residues, participate in strong nonbonded interactions with TmAFP and stick to the protein monomer as a single structure in solution. These water molecules are therefore expected to move with the TmAFP monomer as it comes into contact with the ice plane at the beginning of the recognition and adsorption process. It is likely that by increasing the number of “lattice” points (i.e., the number of regularly arrayed O atoms) or “density” on the ice-binding site, TmAFP would have a better chance to initiate the recognition and binding process, even though the O-atom lattice containing the water molecules is less ideal than without these water molecules. Although the spacing of these water molecules fits the ice lattice at the one-dimensional level, TmAFP appears to force them out of the protein because of their weaker co-plane orientation with respect to the side chains of the β-sheet once the protein becomes properly aligned with the ice lattice. The β-surface of the TmAFP docked to the ice plane alone is predicted to provide better electron overlap and achieve greater interaction energy without its rank of associated water molecules. Although the water molecules themselves are not adsorbed on the ice as a part of protein docking, the process of their release provided a unique probe for us to investigate the AFP-ice recognition and binding mechanism.

Acknowledgments

We are grateful to Brent Wathen for his critical reading of the manuscript.

This work was funded by the Science Foundation of the National Natural Science Foundation of China (NSFC) (grants 20271009, 20231010, 30228006, and 29992590-1), the Major State Basic Research Development Programs (grant G2000078100), and the Foundation for University Key Teacher, Key Projection and Scientific Research Foundation, China, for the Returned Overseas Chinese Scholars Fund, China, by the Ministry of Education, China (G.C.); and Canadian Institutes of Health Research (Z.J.). Z.J. is a Canada Research Chair in Structural Biology.

References

  1. Baust, J. G., R. R. Rojas, and M. D. Hamilton. 1985. Life at low temperatures: representative insect adaptations. Cryo. Letters. 6:199–210. [Google Scholar]
  2. Becke, A. D. 1993. Density-functional thermochemistry. III. The role of exact exchange. J. Phys. Chem. 98:5648–5652. [Google Scholar]
  3. Chen, G. J., and Z. Jia. 1999. Ice-binding surface of fish type III antifreeze. Biophys. J. 77:1602–1608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cheng, Y. H., Z. Y. Yang, H. W. Tan, R. Z. Liu, G. J. Chen, and Z. Jia. 2002. Analysis of ice-binding sites in fish type II antifreeze protein by quantum mechanics. Biophys. J. 83:2202–2210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cornell, W. D., P. Cleplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  6. Devries, A. L. 1971. Glycoproteins as biological antifreeze agents in Antarctic fishes. Science. 172:1152–1155. [DOI] [PubMed] [Google Scholar]
  7. Dewar, M. J. S., E. G. Zoebisch, E. F. Healy, and J. J. P. Stewart. 1985. AM1: a new general purpose quantum mechanical model. J. Am. Chem. Soc. 107:3902–3909. [Google Scholar]
  8. Field, M. J. M., P. A. Bash, and M. A. Kauplus. 1990. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulation. J. Comput. Chem. 11:700–733. [Google Scholar]
  9. Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle, and J. A. Pople. 1998. Gaussian 98. Gaussian, Inc., Pittsburgh, PA.
  10. Graether, S. P., M. J. Kuiper, S. M. Gagné, V. K. Walker, Z. Jia, and P. L. Davies. 2000. β-helix structure and ice-binding properties of a hyperactive antifreeze protein from an insect. Nature. 325:325–328. [DOI] [PubMed] [Google Scholar]
  11. Jia, Z., and P. L. Davies. 2002. Antifreeze proteins: an unusual receptor-ligand interaction. Trends Biochem. Sci. 27:101–106. [DOI] [PubMed] [Google Scholar]
  12. Jorgensen, W. L., J. Chandrasekhar, and J. D. Madura. 1983. Comparison of simple potential functions of simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  13. Knight, C. A., A. L. Devries, and L. D. Oolman. 1984. Fish antifreeze protein and the freezing and recrystallization of ice. Nature. 308:295–296. [DOI] [PubMed] [Google Scholar]
  14. Knight, C. A., and J. G. Duman. 1986. Inhibition of recrystallization of ice by insect thermal hysteresis proteins: a possible cryoprotective role. Cryobiology. 23:256–262. [Google Scholar]
  15. Lee, C., W. Yang, and R. G. Parr. 1988. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 37:785–789. [DOI] [PubMed] [Google Scholar]
  16. Leinala, E. K., P. L. Davies, D. Doucet, M. G. Tyshenko, V. Walker, and Z. Jia. 2002a. A β-helical antifreeze protein isoform with increased activity: structural and functional insights. J. Biol. Chem. 277:33349–33352. [DOI] [PubMed] [Google Scholar]
  17. Leinala, E. K., P. L. Davies, and Z. Jia. 2002b. Crystal structure of β-helical antifreeze protein points to a general ice binding model. Structure. 10:619–627. [DOI] [PubMed] [Google Scholar]
  18. Liou, Y. C., A. Tocilj, P. L. Davies, and Z. Jia. 2000. Mimicry of ice structure by surface hydroxyls and water of β-helix antifreeze protein. Nature. 406:322–324. [DOI] [PubMed] [Google Scholar]
  19. Madura, J. D., K. Baran, and A. Wierzbicki. 2000. Molecular recognition and binding of thermal hysteresis proteins to ice. J. Mol. Recognit. 13:101–113. [DOI] [PubMed] [Google Scholar]
  20. Svensson, M., S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber, and K. Morokums. 1996. Oniom: a multilayered integrated MO+MM method for geometry optimizations and single point energy predictions. A test for Diels-Alder reactions and Pt(P(t−Bu)3)2+H2 oxidative addition. J. Phys. Chem. 100:19357–19363. [Google Scholar]
  21. Tyshenko, M. G., D. Doucet, P. L. Davies, and V. K. Walker. 1997. The antifreeze potential of the spruce budworm thermal hysteresis protein. Nat. Biotechnol. 15:887–890. [DOI] [PubMed] [Google Scholar]
  22. Urrutia, M. E., J. G. Duman, and C. A. Knight. 1992. Plant thermal hysteresis proteins. Biochim. Biophys. Acta. 1121:199–206. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES