Abstract
Voltage-sensitive fluorescent dyes are commonly used to measure cardiac electrical activity. Recent studies indicate, however, that optical action potentials (OAPs) recorded from the myocardial surface originate from a widely distributed volume beneath the surface and may contain useful information regarding intramural activation. The first step toward obtaining this information is to predict OAPs from known patterns of three-dimensional (3-D) electrical activity. To achieve this goal, we developed a two-stage model in which the output of a 3-D ionic model of electrical excitation serves as the input to an optical model of light scattering and absorption inside heart tissue. The two-stage model permits unique optical signatures to be obtained for given 3-D patterns of electrical activity for direct comparison with experimental data, thus yielding information about intramural electrical activity. To illustrate applications of the model, we simulated surface fluorescence signals produced by 3-D electrical activity during epicardial and endocardial pacing. We discovered that OAP upstroke morphology was highly sensitive to the transmural component of wave front velocity and could be used to predict wave front orientation with respect to the surface. These findings demonstrate the potential of the model for obtaining useful 3-D information about intramural propagation.
INTRODUCTION
Voltage-sensitive fluorescent dyes have proven to be invaluable research tools in the field of electrobiology (Fromherz and Lambacher, 1991; Gross et al., 1986; Loew et al., 1992; Tominaga et al., 2000), including cardiac electrophysiology (for a review see Rosenbaum and Jalife, 2001). The voltage-sensitive dyes most commonly used in the study of cardiac electrical activity are the styryl dyes (e.g., di-4-ANEPPS, di-8-ANEPPS, RH-237). The advantage of these dyes is that their fluorescence accurately follows the rapid changes in the transmembrane potential of cardiomyocytes, including the action potential upstroke. Until recently it was assumed that fluorescence signals recorded from the heart surface represent only activation of the uppermost layers of myocardial cells (<300-μm depth). Recent experimental observations suggest, however, that due to the relatively weak absorption but strong scattering of photons inside heart tissue, optical signals originate from a significantly larger volume of tissue located >1 mm beneath the surface (Baxter et al., 2001; Welch and van Gemert, 1995). This volume includes not only cells located directly under the surface recording site (Baxter et al., 2001), but also cells from widely distributed regions around it (Ding et al., 2001; Popp et al., 2001). This fact must be taken into account when interpreting optical mapping data from thick heart preparations. For example, cardiomyocytes widely separated from one another may be at different phases of excitation. As a result, the optical action potential (OAP), which represents a weighted sum of single-cell transmembrane potentials within a certain volume, may differ considerably from the real transmembrane potential (Baxter et al., 2001; Choi and Salama, 1998; Efimov and Mazgalev, 1998; Efimov et al., 1999; Gray, 1999). The goal of this study, therefore, was to quantify the effects of the summation of subsurface optical signals and to determine the main factors affecting the shape of OAP in three-dimensional (3-D) myocardium.
In this study, we obtained a solution for the so-called “forward problem,” in which the voltage-dependent signal on the myocardial surface, that we term “optical action potential,” was synthesized for a given 3-D transmembrane potential distribution. The computational model we present in this study consists of two parts: a 3-D model of electrical activity (Fenton and Karma, 1998) and a multiple-scattering photon transport model (Popp et al., 2001; Welch and van Gemert, 1995). The two models are then coupled to produce simulated optical mapping data. The photon transport model describes both the penetration of incident excitation light into, and the escape of fluorescent light from, heart tissue. The photon transport model also fully takes into account lateral photon scattering, which plays a major role in generating OAPs in 3-D myocardium. Therefore, our two-stage model represents a significant improvement over previous depth-averaging models (Baxter et al., 2001; Janks and Roth, 2002) that consider summation exclusively under the recording site.
The present work focuses on the case of uniform illumination, the most common configuration used in cardiac optical mapping to excite voltage-sensitive dye fluorescence. In all computer simulations, we used the optical characteristics of heart tissue (adult pig right ventricle) measured at the excitation and emission wavelength of di-4-ANEPPS. For this case, we analyze several basic examples to illustrate the predictive ability of our model. Specifically, we demonstrate that, in agreement with experimental observations, the OAP upstroke is significantly prolonged when compared with single-cell action potential upstrokes (Gray, 1999). More importantly, we have discovered that the OAP upstroke morphology can provide information on the orientation of the propagating wave front with respect to the heart surface. As we will show, this finding may have important implications for measurements of conduction velocity in intact myocardium.
Although we have tested the two-stage model only for simple patterns of activation (i.e., point and plane wave stimulation), we briefly discuss other potential applications of the model, including quantitative interpretation of dual-humped optical action potentials recorded using conventional optical mapping and attributed to intramural reentry (Efimov et al., 1999), as well as interpretation of virtual electrode effects produced by strong electrical shocks (Fast et al., 2002; Lin et al., 1999).
GENERAL THEORY
Simulations of photon transport in the tissue
Recent experimental data indicate that fluorescent photons, particularly those photons arising from depths >0.5 mm beneath the surface of tissues such as the heart, undergo multiple scattering events before reaching the surface (Ding et al., 2001; Jacques, 1998; Popp et al., 2001; Welch and van Gemert, 1995). Therefore, to calculate the voltage-dependent (and therefore time-dependent) fluorescent signal we used the photon diffusion equation for highly scattering media:
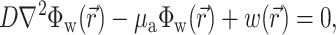 |
(1) |
where Φw is the fluorescent photon density (photons/mm3) within the tissue due to a distributed source of voltage-sensitive fluorescence 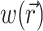 ,
, 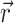 is the position vector, D is the photon diffusivity (assumed constant), and μa is the photon absorption coefficient. Equation 1 is quasi-static due to the large value for the speed of photons (light) in tissue. Because of this, the photon density reaches equilibrium nearly instantaneously when compared with the timescale of other events, such as electrical wave front propagation in the heart tissue. Accordingly, Eq. 1 omits the explicit time derivative ∂Φw/∂t. The geometry of our preparation is an infinite parallel slab of thickness L. The boundary conditions are Φw = 0 at the tissue slab surfaces (i.e., epi- and endocardium).
is the position vector, D is the photon diffusivity (assumed constant), and μa is the photon absorption coefficient. Equation 1 is quasi-static due to the large value for the speed of photons (light) in tissue. Because of this, the photon density reaches equilibrium nearly instantaneously when compared with the timescale of other events, such as electrical wave front propagation in the heart tissue. Accordingly, Eq. 1 omits the explicit time derivative ∂Φw/∂t. The geometry of our preparation is an infinite parallel slab of thickness L. The boundary conditions are Φw = 0 at the tissue slab surfaces (i.e., epi- and endocardium).
The solution of Eq. 1 can be found by performing a convolution over the tissue volume, Ω′, of the Green's function, 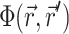 , with the distributed source of voltage-sensitive fluorescence
, with the distributed source of voltage-sensitive fluorescence 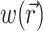 function:
function:
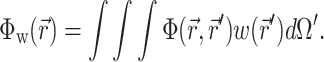 |
(2) |
Green's function
The Green's function 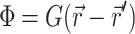 was determined using the steady-state diffusion-absorption equation:
was determined using the steady-state diffusion-absorption equation:
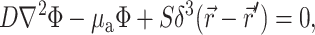 |
(3) |
where S (photons/s) is the strength of a point source of light at a location 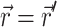 in the tissue and δ3 is the three-dimensional delta function.
in the tissue and δ3 is the three-dimensional delta function.
For an infinite parallel slab or even a finite cylindrical slab of thickness L with zero photon density at both surfaces, an explicit analytical solution of Eq. 3 can be readily obtained. Let the observation point and the source be located at a depth z and z′ from the surface, respectively; let R be, in magnitude, the surface projection of 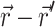 . We then have the explicit solution for the photon concentration, Φ, in cylindrical coordinates
. We then have the explicit solution for the photon concentration, Φ, in cylindrical coordinates 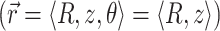 :
:
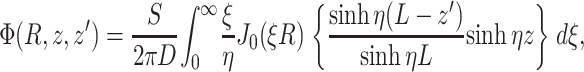 |
(4) |
where J0 is the 0th order Bessel function, and where
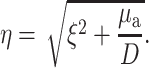 |
(5) |
Note that, due to radial symmetry, Φ does not depend on θ. In Eqs. 4 and 5, the parameter ξ is a dummy integration variable. Note that μa and D do not occur as independent parameters but only in the combination μa/D (in mm−2).
In a cylinder, a series of Bessel functions is unavoidable. The integral in Eq. 4 is its infinite-slab version.
Source function
To define the source function, 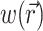 , we assume that the fluorescence emission at a given point in the heart tissue is proportional to the intensity of the excitation light reaching the point and depends linearly on the transmembrane potential at that point. Therefore, we are concerned with a distributed source function
, we assume that the fluorescence emission at a given point in the heart tissue is proportional to the intensity of the excitation light reaching the point and depends linearly on the transmembrane potential at that point. Therefore, we are concerned with a distributed source function 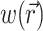 that is simply a product of the transmembrane voltage
that is simply a product of the transmembrane voltage 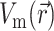 at a given moment of time and the intensity of the excitation light
at a given moment of time and the intensity of the excitation light 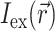 :
:
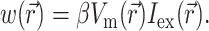 |
(6) |
The parameter β is a proportionality factor that takes into account the quantum yield of the dye and the fractional change in fluorescence in response to voltage changes. For simplicity, the spatial distribution and properties of the dye are assumed to be uniform throughout the tissue and therefore the parameter β is constant. For simplicity we also assume 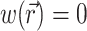 at Vm = 0, which means that background voltage-independent fluorescence is always considered subtracted from the optical signal.
at Vm = 0, which means that background voltage-independent fluorescence is always considered subtracted from the optical signal.
The specific form of 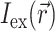 is determined by the type of illumination and can vary depending on the type of optical mapping techniques employed. The two most common techniques used in optical mapping of the heart surface are laser scanning (Knisley, 1995; Morad et al., 1986) and uniform illumination combined with high frame rate CCD cameras or photodiode arrays (Choi and Salama, 2000; Efimov and Mazgalev, 1998; Wang et al., 2001; Zaitsev et al., 2000). In this study we examine only the uniform illumination technique.
is determined by the type of illumination and can vary depending on the type of optical mapping techniques employed. The two most common techniques used in optical mapping of the heart surface are laser scanning (Knisley, 1995; Morad et al., 1986) and uniform illumination combined with high frame rate CCD cameras or photodiode arrays (Choi and Salama, 2000; Efimov and Mazgalev, 1998; Wang et al., 2001; Zaitsev et al., 2000). In this study we examine only the uniform illumination technique.
A reasonable approximation for 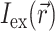 in case of uniform illumination is a simple exponential function (see Discussion for more detail):
in case of uniform illumination is a simple exponential function (see Discussion for more detail):
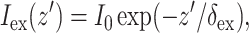 |
(7) |
where z′ is the depth beneath the surface, δex is the attenuation length at the excitation wavelength, and I0 is the intensity of the excitation light at the surface. This gives rise to the following expression for 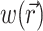 :
:
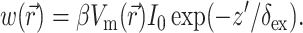 |
(8) |
Electrical propagation model
Next, we substitute into Eq. 8 the 3-D distribution of the transmembrane potential 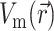 . To generate
. To generate 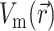 , one can use a model of electrical propagation of any level of complexity. To provide realistic cardiac action potentials, while avoiding the computational complexity associated with more comprehensive ionic models of the heart, we chose the three-state Fenton-Karma (FK) ionic model with Luo-Rudy-1 type restitution properties (Fenton and Karma, 1998). In certain cases, we also performed simulations using the original Luo-Rudy-1 (LR-1) ionic model (Luo and Rudy, 1991) for direct comparison with the FK model. We simulated a 3.2 cm × 3.2 cm × 0.8 cm slab of tissue, which is roughly the size of isolated swine right ventricle preparations used in optical mapping experiments (Baxter et al., 2001).
, one can use a model of electrical propagation of any level of complexity. To provide realistic cardiac action potentials, while avoiding the computational complexity associated with more comprehensive ionic models of the heart, we chose the three-state Fenton-Karma (FK) ionic model with Luo-Rudy-1 type restitution properties (Fenton and Karma, 1998). In certain cases, we also performed simulations using the original Luo-Rudy-1 (LR-1) ionic model (Luo and Rudy, 1991) for direct comparison with the FK model. We simulated a 3.2 cm × 3.2 cm × 0.8 cm slab of tissue, which is roughly the size of isolated swine right ventricle preparations used in optical mapping experiments (Baxter et al., 2001).
The equation used to describe electrical activity is
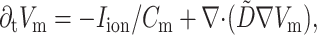 |
(9) |
where Vm is the transmembrane potential, Cm is the membrane capacitance, and Iion is the total ionic current density of the membrane. 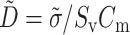 is the diffusivity tensor, where
is the diffusivity tensor, where 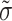 is the conductivity tensor, and Sv is the surface-to-volume ratio of the cell. The diffusivity tensor,
is the conductivity tensor, and Sv is the surface-to-volume ratio of the cell. The diffusivity tensor, 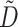 , was defined as in Berenfeld and Pertsov (1999). In all simulations, the diffusivity in the longitudinal direction, DL, was 1 cm2/s and in the transverse direction, DT, was 1/9 cm2/s. In the majority of experiments, unless stated otherwise, the transmural diffusivity, DZ was set at 1/9 cm2/s (DZ = DL). At these diffusivity values, the conduction velocity of planar waves in the longitudinal and transverse directions was 56.1 cm/s and 16.7 cm/s respectively (∼3:1). Note that the diffusivity tensor, D̃, as well as its components (DL, DT, DZ), should not be confused with D, the photon diffusion coefficient introduced earlier.
, was defined as in Berenfeld and Pertsov (1999). In all simulations, the diffusivity in the longitudinal direction, DL, was 1 cm2/s and in the transverse direction, DT, was 1/9 cm2/s. In the majority of experiments, unless stated otherwise, the transmural diffusivity, DZ was set at 1/9 cm2/s (DZ = DL). At these diffusivity values, the conduction velocity of planar waves in the longitudinal and transverse directions was 56.1 cm/s and 16.7 cm/s respectively (∼3:1). Note that the diffusivity tensor, D̃, as well as its components (DL, DT, DZ), should not be confused with D, the photon diffusion coefficient introduced earlier.
The spatial derivatives were solved using central finite differences and the first-order time derivatives were solved using an explicit forward Euler method. The internode spacing was 175 μm. The time step was set at Δt = 0.08 ms. Further refinement of the time or space steps had an insignificant effect on conduction velocity or upstroke rise times. Neumann no-flux boundary conditions were imposed at all tissue boundaries, that is, 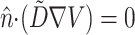 , where
, where 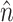 is the unit vector normal to the boundary (Berenfeld and Pertsov, 1999; Fenton and Karma, 1998).
is the unit vector normal to the boundary (Berenfeld and Pertsov, 1999; Fenton and Karma, 1998).
Transmural fiber rotation was introduced into the model where noted and the rotation angle was a linear function of depth. The rotation angle was given by 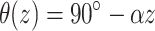 , where α gives the rate of rotation as a function of depth (i.e., α = 22.5°/mm). Thus, on the epicardium the longitudinal fiber direction was parallel to the y-axis. The rotation rate and total transmural fiber rotation (total of 180°, +90° to –90°, epi- to endocardium) was based on measurements performed on the heart right ventricle (Armour and Randall, 1970; Muzikant and Henriquez, 1997).
, where α gives the rate of rotation as a function of depth (i.e., α = 22.5°/mm). Thus, on the epicardium the longitudinal fiber direction was parallel to the y-axis. The rotation rate and total transmural fiber rotation (total of 180°, +90° to –90°, epi- to endocardium) was based on measurements performed on the heart right ventricle (Armour and Randall, 1970; Muzikant and Henriquez, 1997).
Calculating the surface distribution of voltage-dependent fluorescence
After we obtain the fluorescent photon density within the 3-D myocardial slab, Φw (see Eq. 2), we may then calculate the distribution of voltage-dependent fluorescence on the surface of the slab 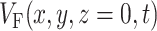 . We calculate the voltage-dependent surface fluorescence (i.e., optical action potential) at any location on the surface
. We calculate the voltage-dependent surface fluorescence (i.e., optical action potential) at any location on the surface 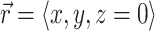 using Fick's law,
using Fick's law,
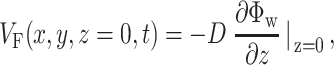 |
(10) |
where z is the coordinate normal to the surface and D is the photon diffusivity as described previously. The value of VF calculated using this formula represents a signal that would be recorded from an ideal sensor array (i.e., with infinitely small pixel size) placed directly onto the myocardial surface. In reality, similar signals can be obtained using an optical system that has a large depth of field (i.e., comparable with the myocardial tissue thickness from which all the voltage-sensitive fluorescence arises). Optical mapping systems used for imaging cardiac preparations at a macroscopic scale of several centimeters often meet this requirement.
SPECIFIC EXAMPLES
Our next step will be to apply the theory described above to simulate typical epifluorescence measurements in heart tissue. It should be noted that optical characteristics of our model are dye and tissue-specific. The numerical values of optical parameters (see below) were derived for Tyrode-perfused swine RV tissue stained with voltage-sensitive dye di-4-ANEPPS. The value we used for δex was 0.8 mm, based on our measurements at 514 nm, which is close to excitation wavelength of this particular dye. Calculations of the Green's function (Eq. 6) require values for μa and D that are measured at the emission wavelength of di-4-ANEPPS (∼630 nm). The values for μa and D (μa = 0.12 mm−1, D = 0.22 mm) were chosen based on data by Popp et al. (2001). (Note: a factor common to all terms, the speed of light—in mm/s—has been removed from Eq. 1, thus resulting in the units given above.) The values result in an emission attenuation length of δem = 1.36 mm (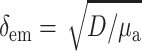 , see Jacques, 1998), which is consistent with δem = 1.34 mm found by Baxter and co-workers using a different experimental approach (Baxter et al., 2001).
, see Jacques, 1998), which is consistent with δem = 1.34 mm found by Baxter and co-workers using a different experimental approach (Baxter et al., 2001).
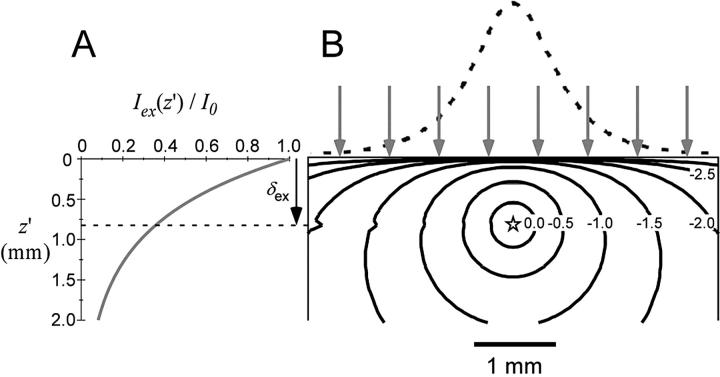
Fig. 1 summarizes the optical properties of the tissue as described by the photon diffusion theory above. Fig. 1 A illustrates the intramural exponential decay of green excitation light intensity in the case of uniform illumination of the heart surface. Fig. 1 B depicts both the intramural photon concentration, Φ (photons/mm3), and photon irradiance (photons·mm−2s−1) due to a point source of unity strength (S = 1) of red emission located at depth 0.8 mm beneath the surface. Note that the contours of equal photon concentration, Φ(R,z,z′), are asymmetric within the heart wall due to the boundary conditions at the heart surface, which require that Φ = 0 at z = 0. Note also the rapid decrease (logarithmic scale) in photon concentration, Φ, with distance from the point source.
FIGURE 1.
Optical characteristics of cardiac tissue. (A) Intramural exponential decay of excitation light in the case of uniform green (520 nm) illumination. (B) Contours of equal photon concentration, Φ (solid lines), determined using Eq. 6 (logarithmic scale, value on contours indicate power of 10), due to a point source (emission, 630 nm) of unity strength located at a depth of 0.8 mm. Also shown is the emitted light intensity profile at the heart surface due to the point source (dashed line). The arrows indicate uniform illumination of the heart surface.
Simulating the optical signal at the heart surface: spatial dependence
To demonstrate the two-stage model, we begin with a simulation of the optical signal intensity on the heart surface (i.e., Vf(x,y)) due to a simple excitation wave front propagating in 3-D ventricular myocardium. The wave front was initiated by a point stimulus applied to the heart surface (epicardium). To reconstruct the fluorescence image, we first inserted the instantaneous 3-D distribution of the transmembrane potential Vm(x,y,z) (from Eq. 9) into the source function, 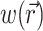 (Eq. 8). Then we substituted
(Eq. 8). Then we substituted 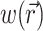 into the convolution equation (Eq. 2) and solved for the photon density, Φw. Lastly, we inserted the solution for Φw into Eq. 10 and solved for Vf(x,y) at the heart surface (Fig. 2 A, top left). In Fig. 2 A, bottom left, the corresponding distribution of the surface transmembrane potential, Vm(x,y), at t = 19.5 ms, is shown.
into the convolution equation (Eq. 2) and solved for the photon density, Φw. Lastly, we inserted the solution for Φw into Eq. 10 and solved for Vf(x,y) at the heart surface (Fig. 2 A, top left). In Fig. 2 A, bottom left, the corresponding distribution of the surface transmembrane potential, Vm(x,y), at t = 19.5 ms, is shown.
FIGURE 2.
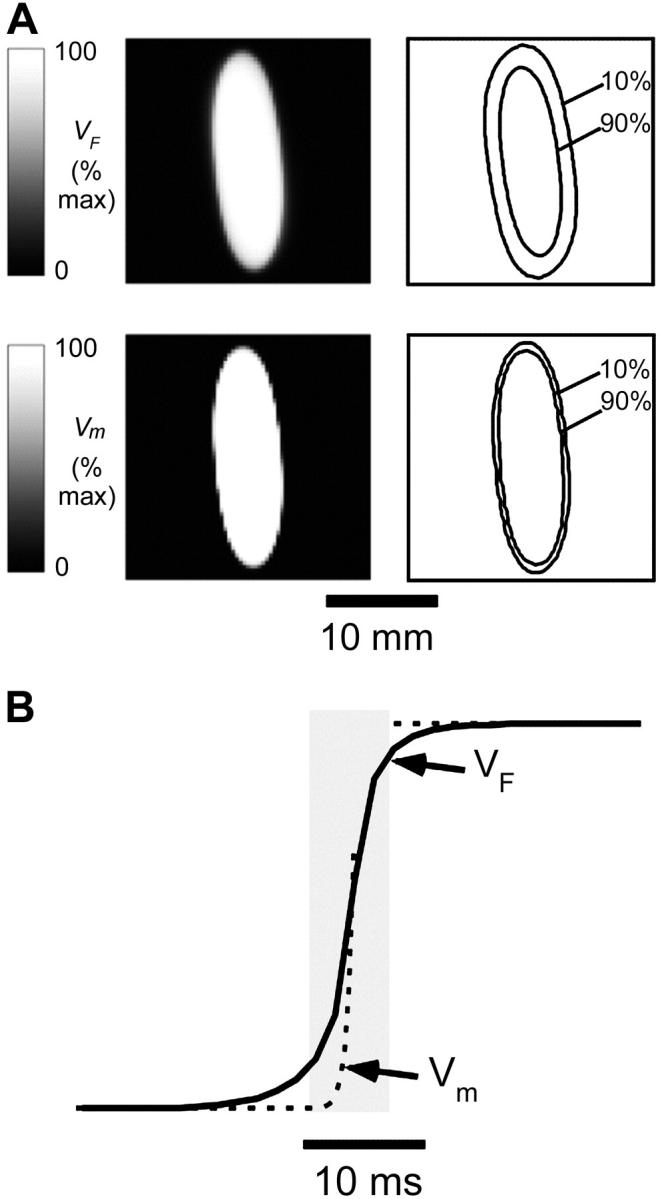
Simulated optical recordings of electrical activity after epicardial point stimulation (t = 19 ms). (A) Top left, Snapshot of voltage-dependent fluorescence VF; top right, corresponding map showing 10% and 90% (of maximum) fluorescence contours. Bottom left, snapshot of the surface distribution of the transmembrane potential Vm; bottom right, corresponding map showing 10% and 90% (of maximum) isopotential lines. (B) Upstrokes of the optical (solid) and electrical (dashed) action potentials obtained from the same epicardial site.
Both the optical and the electrical fronts show similar elliptical shapes due to anisotropy of myocardial propagation. However, the image of simulated VF fluorescence on the epicardium shows significantly more blurring than the corresponding epicardial map of Vm (compare images in Fig. 2 A, top left and bottom left). The effect becomes more obvious if we compare the separation between isopotential lines at 10% and 90% maximum depolarization for both cases shown on the right of the respective panels. The width of the optical front is ∼3× wider than the electrical front, which is consistent with the assumption that OAPs result from the summation of fluorescence from many cardiomyocytes widely distributed beneath the surface. A pronounced deviation of the 10% isoline in Fig. 2 A from an elliptical shape and the rotation of its main axis is due to the combined effect of significant subsurface contributions to the optical signal and transmural fiber rotation.
It should be noted that the degree of blurring of the optical fronts due to 3-D summation is an important parameter that has major practical implications for designing optical mapping systems and processing optical mapping data. It determines the theoretical limits for the spatial resolution of optical mapping systems and the appropriate use of spatial filters (see Discussion).
Simulating the optical signal at the heart surface: temporal dependence
To reconstruct the time dependence of VF, we simulated sequential optical images of the excitation front as described in the previous section. From a set of such images taken with sufficiently short time intervals (1.6 ms/frame) we could then extract the time dependence of the fluorescence signal for any location. In this study we focused primarily on the optical upstroke, which is the most sensitive component of the OAP to subsurface integration of optical signals. Calculation of only the upstroke also requires only a relatively small number of frames and thus reduces the computational load.
Fig. 2 B compares simulated VF and Vm upstrokes obtained from the same site on the slab surface, using the Fenton-Karma ionic model. We determined the upstroke duration as the difference in time during a change in the signal from 10% to 90% of its maximum amplitude. The VF upstroke was almost 5× longer: the VF upstroke duration, which we hereafter denote as TF, was ∼6.6 ms whereas the electrical upstroke duration, which we hereafter denote as Tm, was only ∼1.3 ms. Over the entire 2.2 × 2.2 cm mapped surface, the average TF was 6.1 ± 0.8 ms, whereas the average Tm was 1.3 ± 0.2 ms. Similar to spatial blurring described in the previous section, the significantly longer duration of the optical upstroke is also a result of spatial summation of optical signals. It should not be confused with device-dependent blurring (Girouard et al., 1996). It is important at this time to restate that VF represents the signal obtained using an ideal sensor array, that is, one with infinitely small pixel size (i.e., infinite spatial resolution) and placed directly onto the myocardial surface.
The duration of optical upstroke, TF, is an important parameter that determines the required frame rate of optical mapping systems. Therefore it is important to determine the main factors affecting TF and its range for different activation patterns. Our model demonstrates that conduction velocity (CV) of the excitation front is one of the principal determinants of TF. Fig. 3 A compares TF and Tm (dashed line) at different lateral and transmural CV values. Reductions in CV in the lateral and transmural directions were produced by reducing DT and DZ, respectively. Note that a reduction in the diffusivities DT and DZ does not affect Tm, which is fully consistent with cable theory; altering the diffusivity, a space-dependent characteristic of the tissue, does not affect time-dependent parameters. Whereas Tm remained essentially unchanged, reducing the CV caused a significant increase in TF.
FIGURE 3.
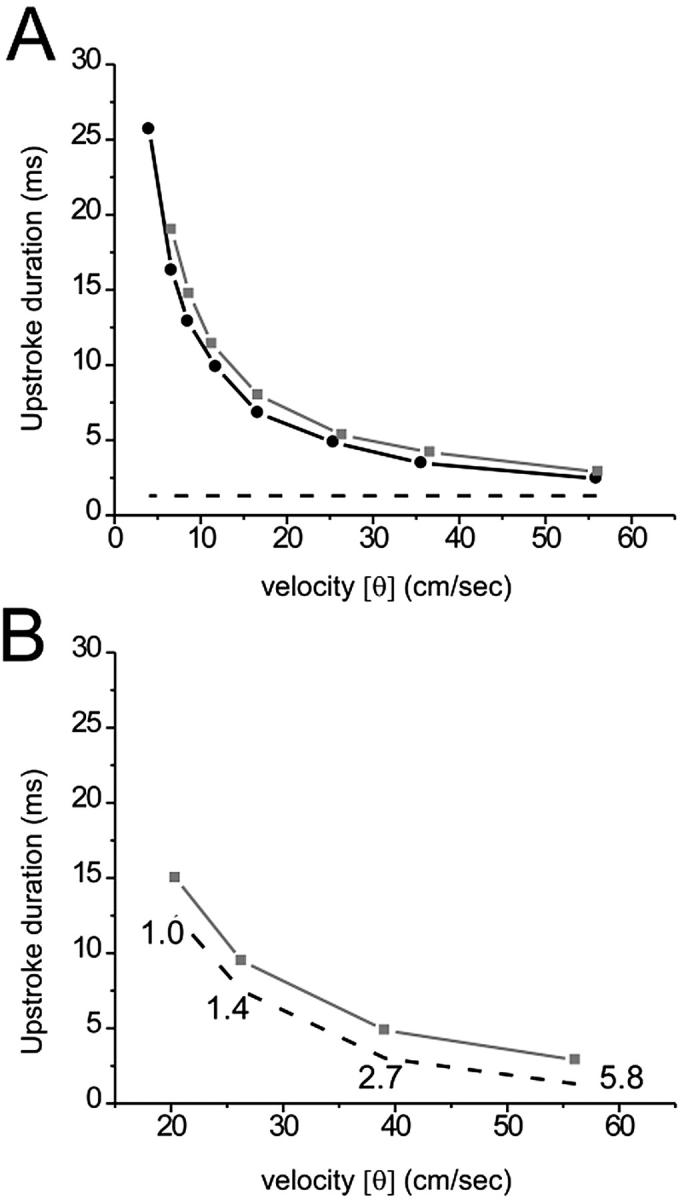
Optical and electrical upstroke duration as a function of plane wave conduction velocity (CV). (A) Here, CV was set by varying the electrical coupling in the direction of propagation. The plot depicts OAP upstroke duration for plane wave propagation in the transmural direction (black line, solid circle), away from the mapped surface, and lateral direction (gray line, solid box), perpendicular to the mapped surface. Electrical upstroke duration was the same for both cases (dashed line). (B) Here, plane wave CV was set by varying the fast inward current. The plot depicts OAP (gray line, solid box) and electrical (dashed line) upstroke duration for plane wave propagation in the lateral direction only. Fast inward channel conductance (mmho/cm2) is indicated near each corresponding data point.
The increase in TF described above has a simple qualitative explanation. The increase in TF is a result of increased spatial blurring caused by reduced CV. Indeed, the degree of spatial blurring is roughly inversely proportional to the width of the propagating front (W): the narrower the front, the more it is blurred. The same relation applies to TF (TF ∼ 1/W). Due to the fact that W = Tm CV, and that Tm, in our model, was not affected by changes in the diffusivity, this relation can be transformed into: TF ∼ 1/CV. This is fully consistent with our observations; both plots in Fig. 3 A are hyperbolic.
We also reduced CV by decreasing the fast inward current, while intercellular electrical coupling was held constant. We again observed an increase in TF (see Fig. 3 B). In this case, however, the effect of optical summation on TF was relatively small; the increase in TF was due primarily to an increase in Tm (dashed line). This is consistent with the fact that changes in the fast inward current have little effect on W; the decrease in CV is compensated by an increase in Tm (Pertsov,1997). The difference between TF and Tm remained approximately the same for all values of the inward current tested.
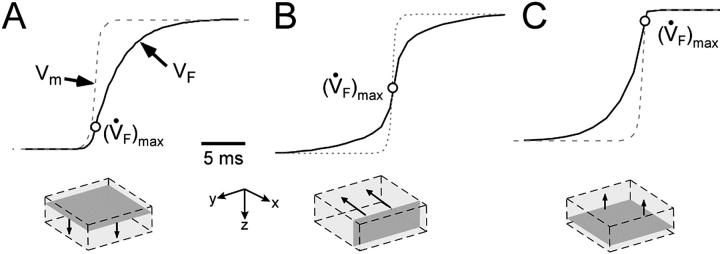
OAP upstroke morphology and transmural propagation
While the upstroke blurring due to light scattering was expected, the surprising finding was that the model predicted unique OAP upstroke morphologies for wave fronts propagating toward, perpendicular to, or away from the mapped surface (see Fig. 4, A, B, and C, respectively). Specifically, for plane wave fronts propagating away from the mapped surface (i.e., from epi- to endocardium), the model predicted a maximal rate of change in the voltage-dependent fluorescence signal (i.e., dVF/dtmax or (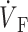 )max) at the foot of the OAP upstroke (Fig. 4 A). Conversely, when simulated plane wave fronts propagate toward the surface, the model predicts (
)max) at the foot of the OAP upstroke (Fig. 4 A). Conversely, when simulated plane wave fronts propagate toward the surface, the model predicts (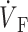 )max near the apex of the OAP (Fig. 4 C). The intermediate case occurs for plane waves propagating perpendicular to the mapped surface (lateral plane waves). In this case, the OAP upstroke morphology will be sigmoidal (Fig. 4 B).
)max near the apex of the OAP (Fig. 4 C). The intermediate case occurs for plane waves propagating perpendicular to the mapped surface (lateral plane waves). In this case, the OAP upstroke morphology will be sigmoidal (Fig. 4 B).
FIGURE 4.
OAP upstroke morphology as a function of the direction of transmural propagation (see diagrams below each plot). (A) Propagation away from the recording surface; (B) propagation perpendicular to the recording surface; and (C) propagation toward the recording surface. Open circles on the OAP upstrokes indicate (the Fenton-Karma ionic model) locations of (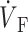 )max. Electrical upstrokes are indicated by dashed lines.
)max. Electrical upstrokes are indicated by dashed lines.
These unique OAP upstroke morphologies result directly from the summation of optical signals from subsurface tissue. In Fig. 4 A, the sharp foot represents the early activation of the uppermost layers, which contribute the strongest signal, while the rounded apex represents the delayed activation of subsurface tissue, from which weaker optical signals arise. On the other hand, in Fig. 4 C, the slow foot represents the earlier activation of subsurface tissue (where the optical signal reaching the surface is relatively weak), whereas the sharp apex represents the later activation of surface tissue (where the optical signal is strongest). Unlike the previous two cases, the pronounced prolongation of the OAP upstroke observed in Fig. 4 B occurs due to lateral scattering of fluorescence light. In the case of Fig. 4 B, if only integration of optical signals with depth is assumed (no photon scattering, as with the model of Baxter et al. (2001), there would be neither an increase in OAP upstroke duration nor a change in OAP upstroke morphology when compared with the electrical upstroke. Conversely, in the previous two cases (Fig. 4, A and C), the only contributing factor to the increased OAP upstroke duration was the depth from which the optical signal originated, i.e., lateral scattering of fluorescent light in the tissue did not contribute to prolongation of the OAP upstroke.
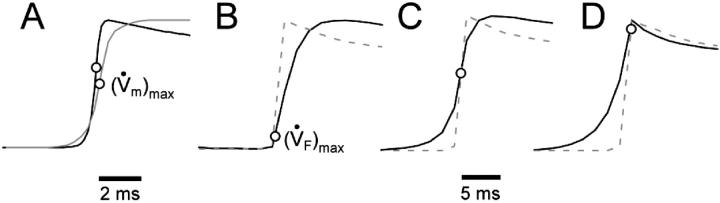
We obtained very similar results when we used the LR-1 ionic model despite the fact that LR-1 has significantly different electrical upstroke morphology. Fig. 5 A shows electrical upstrokes for both the FK and LR-1 ionic models. The electrical upstroke for the FK model is sigmoidal and symmetric, has a duration of 1.3 ms, and (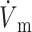 )max is located at the 50% depolarization level. In contrast, the electrical upstroke for LR-1 is asymmetric, with a sharper apex than foot, and Vm decreases significantly immediately after the apex. Furthermore, the electrical upstroke duration for LR-1 is only 0.65 ms (vs. 1.3 ms), and (
)max is located at the 50% depolarization level. In contrast, the electrical upstroke for LR-1 is asymmetric, with a sharper apex than foot, and Vm decreases significantly immediately after the apex. Furthermore, the electrical upstroke duration for LR-1 is only 0.65 ms (vs. 1.3 ms), and (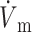 )max is located at the 62% depolarization level rather than at the 50% level. Despite the differences in electrical upstroke morphology, changes in OAP upstroke morphology due to subsurface wave front orientation remained qualitatively the same as in the FK model (compare Fig. 5, B–D, with Fig. 4, A–C). The minor differences in the simulated OAP upstrokes for the two ionic models occurred mainly for lateral plane waves (Fig. 5 C) or plane waves directed toward the mapped surface (Fig. 5 D). For lateral plane waves (Fig. 5 C), the simulated OAP upstroke for the LR-1 ionic model was again somewhat asymmetric when compared with the FK ionic model. The difference here, however, was less pronounced in the OAP upstroke than the electrical upstroke. The location of (
)max is located at the 62% depolarization level rather than at the 50% level. Despite the differences in electrical upstroke morphology, changes in OAP upstroke morphology due to subsurface wave front orientation remained qualitatively the same as in the FK model (compare Fig. 5, B–D, with Fig. 4, A–C). The minor differences in the simulated OAP upstrokes for the two ionic models occurred mainly for lateral plane waves (Fig. 5 C) or plane waves directed toward the mapped surface (Fig. 5 D). For lateral plane waves (Fig. 5 C), the simulated OAP upstroke for the LR-1 ionic model was again somewhat asymmetric when compared with the FK ionic model. The difference here, however, was less pronounced in the OAP upstroke than the electrical upstroke. The location of (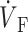 )max on the OAP upstroke was also slightly higher for the LR-1 than the FK ionic model (54% vs. 50% level). Here again, however, the difference was less significant for the OAP upstroke than the electrical upstroke. For plane wave fronts directed toward the mapped surface (Fig. 5 D), the OAP for the LR-1 ionic model actually had a more rapid decrease in signal immediately after the peak of the upstroke than the electrical AP. In contrast, for the FK ionic model, immediately after the upstroke peak, the optical and electrical AP morphologies were the same.
)max on the OAP upstroke was also slightly higher for the LR-1 than the FK ionic model (54% vs. 50% level). Here again, however, the difference was less significant for the OAP upstroke than the electrical upstroke. For plane wave fronts directed toward the mapped surface (Fig. 5 D), the OAP for the LR-1 ionic model actually had a more rapid decrease in signal immediately after the peak of the upstroke than the electrical AP. In contrast, for the FK ionic model, immediately after the upstroke peak, the optical and electrical AP morphologies were the same.
FIGURE 5.
OAP upstroke morphology as a function of the direction of transmural propagation (using the LR-1 ionic model). (A) Comparison of the electrical upstrokes for the Fenton-Karma (gray) and LR-1 (black) ionic models. Open circles on the electrical upstrokes indicate approximate locations of (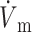 )max. (B) Plane waves directed away from the recording surface; (C), propagation perpendicular to the recording surface; and (D), propagation toward the recording surface. Open circles on the OAP upstrokes indicate locations of (
)max. (B) Plane waves directed away from the recording surface; (C), propagation perpendicular to the recording surface; and (D), propagation toward the recording surface. Open circles on the OAP upstrokes indicate locations of (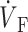 )max. Electrical upstrokes are shown by dashed lines.
)max. Electrical upstrokes are shown by dashed lines.
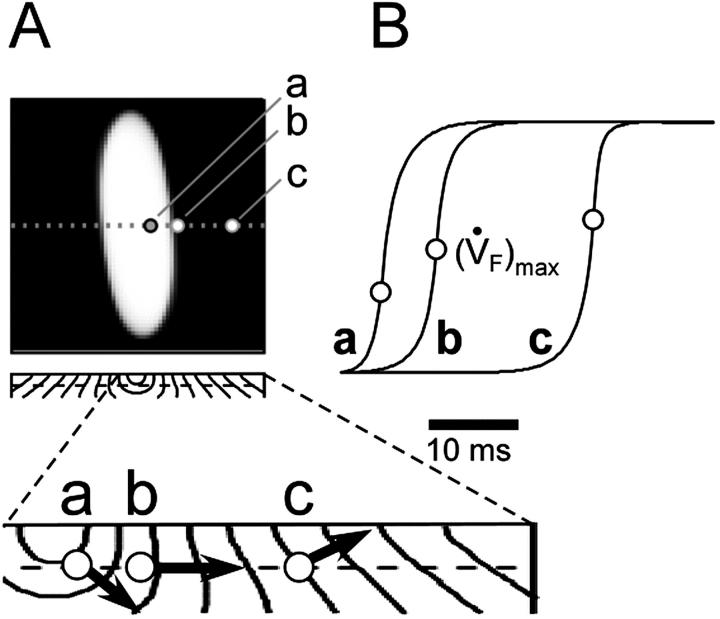
It is noteworthy that all three unique OAP upstroke morphologies described above were observed after simulated epicardial point stimulation (Fig. 6). At consecutive sites transverse to the surface fiber direction, the OAP upstroke morphology changes from having a fast foot and slow apex (site a), to having a roughly sigmoidal shape (site b), and then finally to having a slow foot and fast apex (site c) (see Fig. 6, A and B, traces a, b, and c, respectively). Examination of the isochrone map of a transmural slice along the transverse axis (Fig. 6 A, bottom) shows that indeed the changes in upstroke shape correlate with the orientation of the transmural component of CV with respect to epicardial surface. At site a, the net direction of the wave front in the first millimeter (from which most of the optical signals originates) is away from the mapped surface, at site b the wave front is roughly perpendicular to the mapped surface, and at site c the net direction of the wave front is toward the mapped surface in full agreement with the OAP morphologies.
FIGURE 6.
Spatial variation in epicardial OAP upstroke morphology after point stimulation; (A) Epicardial snapshot of voltage-dependent fluorescence VF (top, snapshot dimension: 22 × 22 mm). Transmural (middle) and zoomed transmural (bottom) isochrone maps (5-ms intervals; map dimensions: 22 × 2 mm). The position of the transmural slice is indicated by dotted line in epicardial snapshot. Dashed line in transmural map is located 1 mm beneath the epicardium and represents the depth from which most of the optical signal originates. Sites a, b, and c are indicated (top), and the approximate net transmural wave front direction at each of these sites is shown by an arrow in the zoomed version of the transmural slice isochrone map (bottom). (B) The corresponding OAP upstroke morphology at sites a, b. and c. Open circles on the OAP upstrokes indicate locations of (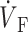 )max.
)max.
DISCUSSION
Recent experimental observations suggest that voltage-dependent fluorescence signals recorded from the myocardial surface may contain useful 3-D information about intramural electrical activity (Baxter et al., 2001; Choi and Salama, 1998; Efimov and Mazgalev, 1998; Efimov et al., 1999; Nikolski and Efimov, 2001). An important step toward extracting such 3-D information is the solution of the so-called “forward problem” which enables synthesis of the voltage-sensitive fluorescence signal (i.e., the optical action potential) on the surface of the heart from an arbitrary 3-D distribution of the transmembrane potential inside the heart wall. In the present study, we have proposed a two-stage computational model for solving the forward problem. The first stage was a photon transport model, based on multiple-scattering (diffusion) theory for photons, and the second stage was a standard 3-D model of cardiac electrical activity. Mathematical convolution of the optical data with the electrical data allowed simulation of optical action potentials.
The two-stage model was used to predict both 2-D fluorescence patterns and time-dependent fluorescence signals, i.e., optical action potentials, as recorded from the myocardial surface. Although in this study we have not attempted three-dimensional reconstruction (this will require multiple projections, whereas we assume that only one projection is available), we demonstrate that even a single surface projection can provide useful three-dimensional information. Using our model, we were able to estimate the degree of intrinsic spatial blurring of optically recorded electrical wave fronts and the intrinsic temporal blurring of the optical upstroke, which is important for establishing theoretical limits for the spatial and temporal resolution of optical mapping systems. We also discovered that the upstroke of the optical action potential contains specific 3-D signatures that can be used to distinguish between intramural excitation fronts with various orientations with respect to the surface, which may find important application in accurate measurements of conduction velocity.
Theoretical limits for the spatial and temporal resolution of optical mapping systems
The fact that our model provides estimates of the intrinsic blurring will have important practical implications; these estimates can be used to establish the theoretical limits for the spatial and temporal resolution of optical mapping systems, as well as providing the criteria for choosing parameters of digital filters used for processing of the optical data. The spatial resolution of the imaging device need only be fine enough to resolve the spatial width of the wave front in voltage-sensitive fluorescence. The width of the front in fluorescence is simply WF = TF CV. For conservative values of TF = 5 ms and CV = 25 cm/s (the conduction velocity perpendicular to myocardial fibers), we have WF = 0.125 cm. Ideally, at least three consecutive evenly-spaced recording sites should span the front for proper resolution, which leads to a spatial criterion of ∼0.625 mm between recording sites. This criterion can be used when choosing the appropriate sensor array and overall magnification for a given application. For example, when imaging a 22 × 22 mm region using a photodiode array system with 16 × 16 imaging elements, there is ∼1.4 mm between recording sites. This is insufficient for resolving the width of the front described above. In contrast, when imaging a 22 × 22 mm region using a fast CCD camera system with 64 × 64 imaging elements, there is ∼0.35 mm between recording sites, which is adequate for resolving the front.
The spatial criterion is relaxed for larger values of TF and CV. For example, it should be less stringent for longitudinally propagating fronts as well as for fronts recorded during ventricular fibrillation, which is characterized by slower action potential upstrokes. The temporal resolution of the imaging device has only to adequately resolve the OAP upstroke. For an OAP upstroke duration of 5 ms, for example, a recording rate of ∼400 frames (or samples) per second would then be the minimum requirement. The typical frame rates used in photodiode and CCD optical mapping systems are usually higher (Baxter et al., 1997; Choi and Salama, 1998; Girouard et al., 1996; Valderrábano et al., 2001; Zaitsev et al., 2000).
It should be noted that estimates provided above apply only to thick (>1 mm) tissue preparations. In thin excitable tissues, intrinsic blurring will be become less pronounced and, in fact, may be less significant than the device-dependent temporal blurring due to the finite pixel size and frame rate of the imaging device (Girouard et al., 1996). In thick heart preparations, however, OAP upstroke blurring and changes in OAP upstroke morphology are largely due to intrinsic (i.e., tissue-dependent) effects that cannot be reduced or otherwise affected by the spatial resolution of the imaging system or the choice of optics.
OAP and measurements of conduction velocity
Using the two-stage model, we discovered that the morphology of the OAP upstroke could predict the direction of transmural propagation. This criterion should significantly improve the accuracy of measurements of conduction velocity on the surface of 3-D myocardium. The major problem of such measurements has been that the excitation wave does not always propagate parallel to the surface. The wave front will often propagate toward or away from the surface from inside the myocardial wall at some angle. In such cases, the apparent surface CV can often differ significantly from the actual CV of the wave front. Until recently there were no reliable criteria that would allow recognition of such cases. If confirmed experimentally, our finding should provide such a criterion—wave fronts propagating perpendicular to the surface should produce upstrokes with a symmetric sigmoidal shape and such wave fronts will not have a transmural or z-component to the conduction velocity. In contrast, wave fronts propagating at an angle with respect to the surface will have an asymmetric upstroke and these wave fronts will typically have a nonzero transmural component to the conduction velocity. Surface regions exhibiting these types of OAPs are unreliable for measurements of the characteristic CV of the preparation.
Relation to previous models
The two-stage model for calculating OAP represents a significant improvement over the previous model proposed by Baxter et al. (2001). Although this previous model incorporated light absorption by the tissue, and yielded reasonable values for the excitation and emission light attenuation lengths, it did not take into account photon scattering in the tissue. As a consequence, it only provided accurate results in a very few extraordinarily rare cases when photon scattering effects could be neglected, such as, for example, plane waves propagating away from or toward the surface. With the model of Baxter and co-workers, plane wave fronts propagating perpendicular to the surface would not exhibit any blurring of the OAP upstroke whatsoever, regardless of the conduction velocity (see Fig. 4 A). This limitation, however, does not apply to our two-stage model, which provides accurate results for any wave front shape and any direction of wave front propagation with respect to the surface.
In our simulations we elected to use a monoexponential function to describe the excitation light intensity with depth rather than the biexponential function as described by Baxter et al. (2001). The size of the subsurface hump in excitation light intensity in that study may have been exaggerated due to the methods used. As Jacques has described (Jacques, 1998), for a broad collimated source of incident light, there is indeed often a deviation from a pure exponential near the surface, appearing as either a plateau or even a small subsurface hump in excitation intensity, but in cardiac tissue we now believe this subsurface hump may not be as large as measured in our previous study. We therefore chose to conservatively estimate the excitation intensity profile as a simple monoexponential. Deviations from a monoexponential, as mentioned above, only accentuate subsurface contributions to the optical action potential. We did, however, perform simulations using the original biexponential function, but our results were qualitatively identical, the only important difference being the upstroke duration was slightly increased (+1.2 ms) when the biexponential was used.
Study limitations
In our simulations we used a monodomain model of electrical propagation. This did not allow us to investigate 3-D virtual electrode effects (Knisley et al., 1994; Roth, 1997) occurring in the vicinity of the stimulating electrode. This limitation, however, will likely have little or no effect on any of the conclusions and main results described above. It should be noted that in future studies, this limitation could be readily overcome. Indeed, our main formula (Eq. 3) does not introduce any restriction on the distribution of the transmembrane potential. It can be applied to any model of electrical propagation with any level of additional detail, including mono- and bidomain models with various formulations of ionic currents and/or fiber organization.
We should note that in all of our computer simulations, the values we used for the tissue optical characteristics (e.g., μ, D, and δex) were measured in Tyrode-perfused swine right ventricular wall preparations at distinct wavelengths near the peak excitation and emission wavelengths of di-4-ANEPPS (i.e., using laser wavelengths of 514 nm and 630 nm, respectively). However, in optical mapping experiments, we used quartz-tungsten halogen light source with band-pass excitation and emission filters. This may influence the effective values of μ, D, and δex. We also did not take into account intrinsic re-excitation of fluorescence, i.e., re-absorption and re-emission of di-4-ANEPPS due to fluorescent photons on the blue tail of the emission spectrum. Both factors, however, should be relatively small and it is unlikely that they will affect significantly the predictions of the model.
Our two-stage model did not take into account such factors as photobleaching, tissue (i.e., optical) heterogeneities of real myocardium (e.g., fatty and connective tissue), or heterogeneous staining of the voltage-sensitive dye. An assessment of these factors, however, should be evaluated on a case-by-case basis, because such factors will be highly dependent on the type of heart preparation and optical mapping setup used. Photobleaching, for example, in our laboratory has been found to be negligible for our swine right ventricular preparations and optical mapping setup. In contrast, photobleaching in thinner heart preparations (e.g., guinea pig, rat, mouse) may be more significant, due to the fact that these thinner tissues often require higher excitation light intensities to obtain an adequate signal. Once an assessment of such factors for a particular heart preparation and experimental setup are made, however, these factors can easily be incorporated into the model by allowing parameter β in Eq. 2 to be space- and/or time-dependent (i.e., 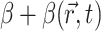 ).
).
Finally, although we have provided an estimate of the theoretical limits for the spatial and temporal resolution of optical mapping systems, we did not attempt an in-depth assessment of the impact of the imaging system on the optical action potential. The extrinsic effects of optical systems (e.g., depth of field, magnification) on fluorescence imaging of biological preparations, however, have been studied extensively elsewhere (Cinelli, 2000; Ebner and Chen, 1995; Girouard et al., 1996; Heintzmann et al., 2002; Yae et al., 1992).
Experimental verification
All predictions of the model described above can be tested experimentally using existing optical imaging techniques. Moreover, experimental verification of our model results was anticipated when we measured the optical characteristics of heart tissue. All optical measurements were conducted in the swine right ventricular preparations commonly used in our optical mapping experiments (Baxter et al., 2001; Popp et al., 2001). The wavelengths were chosen to match those of the excitation and emission wavelength of di-4-ANEPPS, the most widely used voltage-sensitive fluorescent dye in cardiac electrophysiology. Although the existing literature does not contain enough information to validate all theoretical predictions of our model, we have found some support for our predictions. Specifically, some experimental data has suggested that the duration of the OAP upstroke is usually significantly longer than the electrically-recorded action potential upstroke, and the prolongation could not be attributed to an inadequate spatial resolution or sampling rate of the recording device (Gray, 1999).
Future applications
One potential application of our two-stage model is in the analysis of intramural re-entry. In particular, it can be used to validate the hypothesis of subsurface ribbonlike scroll waves produced by strong electrical shocks (Efimov et al., 1999). Our model provides a tool for simulating OAPs produced by such scroll waves that can be directly compared with the experimental data. Specifically, one can determine whether such scroll waves produce characteristic “dual-humped” optical action potentials. Another potentially useful application of the two-stage model is in the interpretation of optical mapping data from studies of electrical defibrillation in 3-D tissue preparations (Clark et al., 1999; Efimov et al., 1999; Entcheva et al., 1998; Fast et al., 2002; Wang et al., 2001). In particular, our model should provide a tool for testing the hypothesis that light scattering may be responsible for masking virtual electrode effects in such preparations.
It should be noted that our two-stage model only applies to a specific, but quite common, optical mapping scenario. In this study, we assumed a di-4-ANEPPS stained thick heart preparation, with fluorescence excitation and emission occurring in specific wavelength bands, namely, green excitation (∼514 nm) and red emission (∼630 nm). To apply the two-stage model to other species and voltage-sensitive dyes, some adjustment of the model parameters will be required, particularly in regards to the measurement of δex and δem (see Methods). It is also important to note that our two-stage model for calculating OAPs applies only to systems using uniform illumination (excitation) of the preparation. An important next step would be extending the model for solving the forward problem for the case of laser scanning optical mapping systems (Dillon et al., 1998; Ding et al., 2001; Knisley, 1998).
CONCLUSION
Our two-stage model, consisting of a model of cardiac electrical activity combined with an optical model of voltage-sensitive fluorescence excitation and photon transport in heart tissue, has shown that optical mapping may provide useful information on three-dimensional wave front propagation. Future improvements in our model may provide a useful means of interpreting three-dimensional effects in optical mapping experiments of intact tissue, during both normal and arrhythmic conduction.
Acknowledgments
We thank Stephen Simons for assistance in preparation of the manuscript.
This research was supported, in part, by grants 1RO1-HL071635-01 and 2POI-HL39707, and by grant RO1-HL60843 from the Heart, Lung and Blood Institute of the National Institutes of Health.
References
- Armour, J. A., and W. C. Randall. 1970. Structural basis for cardiac function. Am. J. Physiol. 218:1517–1523. [DOI] [PubMed] [Google Scholar]
- Baxter, W. T., J. M. Davidenko, L. M. Loew, J. P. Wuskell, and J. Jalife. 1997. Technical features of a CCD video camera system to record cardiac fluorescence data. Ann. Biomed. Eng. 25:713–725. [DOI] [PubMed] [Google Scholar]
- Baxter, W. T., S. F. Mironov, A. V. Zaitsev, J. Jalife, and A. M. Pertsov. 2001. Visualizing excitation waves inside cardiac muscle using transillumination. Biophys. J. 80:516–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berenfeld, O., and A. M. Pertsov. 1999. Dynamics of intramural scroll waves in three-dimensional continuous myocardium with rotational anisotropy. J. Theor. Biol. 199:383–394. [DOI] [PubMed] [Google Scholar]
- Choi, B. R., and G. Salama. 1998. Optical mapping of atrioventricular node reveals a conduction barrier between atrial and nodal cells. Am. J. Physiol. 274:H829–H845. [DOI] [PubMed] [Google Scholar]
- Choi, B. R., and G. Salama. 2000. Simultaneous maps of optical action potentials and calcium transients in guinea-pig hearts: mechanisms underlying concordant alternans. J. Physiol. 529:171–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cinelli, A. R. 2000. High-definition mapping of neural activity using voltage-sensitive dyes. Methods. 21:349–372. [DOI] [PubMed] [Google Scholar]
- Clark, D. M., A. E. Pollard, R. E. Ideker, and S. B. Knisley. 1999. Optical transmembrane potential recordings during intracardiac defibrillation-strength shocks. J. Interv. Card. Electrophys. 3:109–120. [DOI] [PubMed] [Google Scholar]
- Dillon, S. M., T. E. Kerner, J. Hoffman, V. Menz, K. S. Li, and J. J. Michele. 1998. A system for in-vivo cardiac optical mapping. IEEE Eng. Med. Biol. Mag. 17:95–108. [DOI] [PubMed] [Google Scholar]
- Ding, L., R. Splinter, and S. B. Knisley. 2001. Quantifying spatial localization of optical mapping using Monte Carlo simulations. IEEE Trans. Biomed. Eng. 48:1098–1107. [DOI] [PubMed] [Google Scholar]
- Ebner, T. J., and G. Chen. 1995. Use of voltage-sensitive dyes and optical recordings in the central nervous system. Prog. Neurobiol. 46:463–506. [DOI] [PubMed] [Google Scholar]
- Efimov, I. R., and T. N. Mazgalev. 1998. High-resolution, three-dimensional fluorescent imaging reveals multilayer conduction pattern in the atrioventricular node. Circulation. 98:54–57. [DOI] [PubMed] [Google Scholar]
- Efimov, I. R., V. Sidorov, Y. Cheng, and B. Wollenzier. 1999. Evidence of three-dimensional scroll waves with ribbon-shaped filament as a mechanism of ventricular tachycardia in the isolated rabbit heart. J. Cardiovasc. Electrophys. 10:1452–1462. [DOI] [PubMed] [Google Scholar]
- Entcheva, E., J. Eason, I. R. Efimov, Y. Cheng, R. Malkin, and F. Claydon. 1998. Virtual electrode effects in transvenous defibrillation-modulation by structure and interface: evidence from bi-domain simulations and optical mapping. J. Cardiovasc. Electrophys. 9:949–961. [DOI] [PubMed] [Google Scholar]
- Fast, V. G., O. F. Sharifov, E. R. Cheek, J. C. Newton, and R. E. Ideker. 2002. Intramural virtual electrodes during defibrillation shocks in left ventricular wall assessed by optical mapping of membrane potential. Circulation. 106:1007–1014. [DOI] [PubMed] [Google Scholar]
- Fenton, F., and A. Karma. 1998. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos. 8:20–47. [DOI] [PubMed] [Google Scholar]
- Fromherz, P., and A. Lambacher. 1991. Spectra of voltage-sensitive fluorescence of styryl-dye in neuron membrane. Biochim. Biophys. Acta. 1068:149–156. [DOI] [PubMed] [Google Scholar]
- Girouard, S. D., K. R. Laurita, and D. S. Rosenbaum. 1996. Unique properties of cardiac action potentials recorded with voltage-sensitive dyes. J. Cardiovasc. Electrophys. 7:1024–1038. [DOI] [PubMed] [Google Scholar]
- Gray, R. A. 1999. What exactly are optically recorded “action potentials”? J. Cardiovasc. Electrophys. 10:1463–1466. [DOI] [PubMed] [Google Scholar]
- Gross, D., L. M. Loew, and W. W. Webb. 1986. Optical imaging of cell membrane potential changes induced by applied electric fields. Biophys. J. 50:339–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heintzmann, R., T. M. Jovin, and C. Cremer. 2002. Saturated patterned excitation microscopy—a concept for optical resolution improvement. J. Opt. Soc. Am. A. 19:1599–1609. [DOI] [PubMed] [Google Scholar]
- Jacques, S. L. 1998. Light distributions form point, line and plane sources for photochemical reactions and fluorescence in turbid biological tissues. Photochem. Photobiol. 67:23–32. [PubMed] [Google Scholar]
- Janks, D. L., and B. J. Roth. 2002. Averaging over depth during optical mapping of unipolar stimulation. IEEE Trans. Biomed. Eng. 49:1051–1054. [DOI] [PubMed] [Google Scholar]
- Knisley, S. B. 1995. Transmembrane voltage changes during unipolar stimulation of rabbit ventricle. Circ. Res. 77:1229–1239. [DOI] [PubMed] [Google Scholar]
- Knisley, S. B. 1998. Optical mapping of cardiac electrical stimulation. J. Electrocardiol. 30:11–18 (Suppl.). [DOI] [PubMed] [Google Scholar]
- Knisley, S. B., B. C. Hill, and R. E. Ideker. 1994. Virtual electrode effects in myocardial fibers. Biophys. J. 66:719–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, S. F., B. J. Roth, and J. P. Wikswo, Jr. 1999. Quatrefoil reentry in myocardium: an optical imaging study of the induction mechanism. J. Cardiovasc. Electrophys. 10:574–586. [DOI] [PubMed] [Google Scholar]
- Loew, L. M., L. B. Cohen, J. Dix, E. N. Fluhler, V. Montana, G. Salama, and J. Y. Wu. 1992. A naphthyl analog of the aminostyryl pyridinium class of potentiometric membrane dyes shows consistent sensitivity in a variety of tissue, cell, and model membrane preparations. J. Membr. Biol. 130:1–10. [DOI] [PubMed] [Google Scholar]
- Luo, C. H., and Y. Rudy. 1991. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 68:1501–1526. [DOI] [PubMed] [Google Scholar]
- Morad, M., S. Dillon, and J. Weiss. 1986. An acousto-optically steered laser scanning system for measurement of action potential spread in intact heart. Soc. Gen. Physiol. Ser. 40:211–226. [PubMed] [Google Scholar]
- Muzikant, A. L., and C. S. Henriquez. 1997. Paced activation mapping reveals organization of myocardial fibers: a simulation study. J. Cardiovasc. Electrophys. 8:281–294. [DOI] [PubMed] [Google Scholar]
- Nikolski, V., and I. Efimov. 2001. Fluorescent imaging of a dual-pathway atrioventricular-nodal conduction system. Circ. Res. 88:E23–E30. [DOI] [PubMed] [Google Scholar]
- Pertsov, A. M. 1997. Scale of geometric structures responsible for discontinuous propagation in myocardial tissue. In Discontinuous Conduction in the Heart. P.M. Spooner, R.W. Joyner, and J. Jalife, editors. Futura Press, Armonk, NY. pp.273–293.
- Popp, A. K., A. M. Pertsov, and D. A. Weitz. 2001. Internal point spread imaging of cardiac tissue to provide depth resolution for bulk tissue imaging experiments. Proc. SPIE. 4431:141–152. [Google Scholar]
- Rosenbaum, D. S., and J. Jalife. 2001. Optical Mapping of Cardiac Excitation and Arrhythmias. Futura Press, Armonk, NY.
- Roth, B. J. 1997. Nonsustained reentry following successive stimulation of cardiac tissue through a unipolar electrode. J. Cardiovasc. Electrophys. 8:768–778. [DOI] [PubMed] [Google Scholar]
- Tominaga, T., Y. Tominaga, H. Yamada, G. Matsumoto, and M. Ichikawa. 2000. Quantification of optical signals with electrophysiological signals in neural activities of Di-4-ANEPPS stained rat hippocampal slices. J. Neurosci. Meth. 102:11–23. [DOI] [PubMed] [Google Scholar]
- Valderrábano, M., M. H. Lee, T. Ohara, A. C. Lai, M. C. Fishbein, S. F. Lin, H. S. Karagueuzian, and P. S. Chen. 2001. Dynamics of intramural and transmural reentry during ventricular fibrillation in isolated swine ventricles. Circ. Res. 88:839–848. [DOI] [PubMed] [Google Scholar]
- Wang, N. C., M. H. Lee, T. Ohara, Y. Okuyama, G. A. Fishbein, S. F. Lin, H. S. Karagueuzian, and P. S. Chen. 2001. Optical mapping of ventricular defibrillation in isolated swine right ventricles: demonstration of a postshock isoelectric window after near-threshold defibrillation shocks. Circulation. 104:227–233. [DOI] [PubMed] [Google Scholar]
- Welch, A. J., and M. J. C. van Gemert. 1995. Optical-Thermal Response of Laser-Irradiated Tissue. Plenum Press, New York.
- Yae, H., S. A. Elias, and T. J. Ebner. 1992. Deblurring of 3-dimensional patterns of evoked rat cerebellar cortical activity: a study using voltage-sensitive dyes and optical sectioning. J. Neurosci. Meth. 42:195–209. [DOI] [PubMed] [Google Scholar]
- Zaitsev, A. V., O. Berenfeld, S. F. Mironov, J. Jalife, and A. M. Pertsov. 2000. Distribution of excitation frequencies on the epicardial and endocardial surfaces of fibrillating ventricular wall of the sheep heart. Circ. Res. 86:408–417. [DOI] [PubMed] [Google Scholar]