Microfabricated Teflon Membranes for Low-Noise Recordings of Ion Channels in Planar Lipid Bilayers

Abstract

We present a straightforward, accessible method for the fabrication of micropores with diameters from 2 to 800 μm in films of amorphous Teflon (Teflon AF). Pores with diameters ≤40 μm made it possible to record ion fluxes through ion channels in planar bilayers with excellent signal characteristics. These pores afforded: i), stable measurements at transmembrane voltages up to 460 mV; ii), recordings at low noise levels (0.4 pA rms at 4.3 kHz bandwidth); iii), recordings at high effective bandwidth (10.7 kHz); and iv), formation of multiple planar lipid bilayers in parallel. Microfabricated pores in films of Teflon AF made it possible to examine, experimentally and theoretically, the influence of the pore diameter on the current noise in planar bilayer recordings. Reducing the pore diameter below 40 μm mainly increased the stability of the planar bilayers, but had only a small effect on the level of the current noise. The low-noise properties of bilayer recordings on micropores in Teflon AF films were exploited to record the smallest conductance state of alamethicin (24 pS) at an unprecedentedly high bandwidth of 10.7 kHz.

INTRODUCTION

Both planar lipid bilayer and patch clamp experiments allow studies of the function of single ion channel proteins. Recordings of planar bilayers and patch clamp preparations provide the most detailed information now available concerning the biophysics of ion channels: they enable the study of single-channel conductance, opening and closing lifetimes, and opening and closing probabilities. Despite the importance of both techniques, the signal and time resolution of patch clamp and, in particular, planar bilayer recordings are limited by electrical current noise. To resolve the gating events of ion channels with small single-channel conductance and fast gating dynamics, it is important to minimize the noise of electrophysiological recordings. Here we present a method to achieve low-noise recordings with planar lipid bilayers.

Planar bilayer experiments have four advantages over patch clamp experiments: i), The composition of the lipid membrane and the surrounding electrolyte can be defined precisely (that compositional definition includes the ability to form asymmetric bilayers). ii), Planar lipid bilayers make it possible to perform electrophysiological studies on ion channels that are difficult to access with patch clamp pipettes, e.g., ion channels in lipid membranes of organelles or bacteria. iii), Both sides of the bilayer can be accessed easily. iv), The technique is relatively easy to use. Planar bilayer experiments also have limitations: i), Their noise level is usually higher than that in patch clamp recordings. This noise is mainly due to the large capacitance (≫100 pF) of most planar bilayers. ii), Planar bilayer experiments are done with artificial lipid membranes in buffer solutions and are thus carried out under nonphysiological conditions. iii), To study ion channels in planar lipid bilayers, the channels have to be reconstituted into the bilayer (Miller, 1986).

Planar lipid bilayer experiments are usually performed with the bilayer supported using polymer sheets with a single pore (Schlue and Hanke, 1993; Wonderlin et al., 1990). Teflon is a well-suited polymer for this application because it is chemically stable, it has good electrical properties (high resistivity, low dielectric constant, and low dielectric loss (Penner, 1995)), and it supports planar lipid bilayers that are stable for several hours (Schlue and Hanke, 1993; Wonderlin et al., 1990). Standard methods to make pores include simple mechanical punching, drilling, or indentation, combined with shaving away material from the opposite side of the sheet until the indentation is intersected (Wonderlin et al., 1990). Pores are also prepared using a high voltage pulse to “burn” holes through thin polymer sheets (Schlue and Hanke, 1993; Wonderlin et al., 1990). It is difficult to generate pores with diameters below 15 μm with these methods (Wonderlin et al., 1990); they also are not easily applied to positioning the pores relative to the supporting membrane, or to generating regular arrays of pores (Pantoja et al., 2001; Peterman et al., 2002). Pore diameters smaller than 15 μm would be desirable to reduce the capacitance across the bilayers, and to enable low-noise recordings. Micrometer-scale control of the position of the pore is required to perform planar lipid bilayer experiments in parallel. Only precisely positioned pores will make it possible to record from multiple bilayers simultaneously and to combine electrical with optical single-molecule detection in an array format (Borisenko et al., 2003; Ide and Yanagida, 1999; Schmidt et al., 2000).

Silicon microfabrication technology has been used to microfabricate single pores in silicon nitrite and silicon dioxide (Fertig et al., 2000; McGeoch et al., 2000; Pantoja et al., 2001; Peterman et al., 2002; Schmidt et al., 2000). Although these septa can be produced with high precision, widespread use of these methods will be limited by the requirement for access to microfabrication facilities to produce them.

Here we present new, simple methods for the fabrication of micropores based on soft-lithographic methods (micro- molding and casting) (Whitesides et al., 2001; Xia and Whitesides, 1998). Using these methods, fabrication of pores with diameters in the range 2–800 μm can be carried out in a time as short as 4 h, and does not require access to clean rooms or microfabrication facilities. We used amorphous Teflon (Teflon AF) as the material for the septum. This material is comparable to standard Teflon in its chemical robustness, and superior to it in its electrical and optical properties (Makohliso et al., 1998; Resnick and Buck, 1999). We demonstrate the use of micropores in Teflon AF sheets for planar lipid bilayer experiments, and show low-noise, single-channel recordings of ion channels formed by the antibiotic peptide alamethicin (Boheim, 1974; Sakmann and Boheim, 1979). We characterize the stability, electrical resistance, capacitance, and current noise of the bilayers and the supporting Teflon AF septa, and examine experimentally the breakdown voltage and noise of planar lipid bilayers as a function of the pore diameter.

MATERIALS AND METHODS

Fabrication of micropores in films of Teflon AF

Fig. 1 summarizes the fabrication of micropores in sheets of Teflon AF (type 1601, 6% in Fluorinert FC-75, DuPont Fluoroproducts, Wilmington, DE) by molding a solution of Teflon AF around a probe with a sharp tip, positioned to be in contact with a silicon wafer or a hydrogel slab. After evaporation of the Fluorinert solvent, the resulting Teflon AF film has a hole at the point of contact between the tip and the wafer or hydrogel. We used commercially available probes from Lucas Signatone (Gliroy, CA) with nominal tip diameters from 0.20 to 125 μm (Lucas Signatone defines the tip diameter as the diameter of the cone at the point where the profile of the cone changes from a steep (cone angle 6°) to a shallow angle (≫6°)). We used the following probe tips: 125 μm (beryllium copper), 25 μm (tungsten), 10 μm (gold-plated tungsten), 5 μm (tungsten), 3.5 μm (tungsten), 1 μm (tungsten cat whisker), and 0.20 μm (tungsten cat whisker). Before use, we usually immersed the gold-plated tungsten tips (tip diameter 10 μm) in a fresh solution of ∼5 mM 1-hexadecanethiol in ethanol over night followed by rinsing with ethanol. This treatment decreased the adhesion of Teflon AF to the tip and resulted in well-defined conical pores. Depending on the mechanical stability of the probe tips, we formed Teflon sheets either on a silicon wafer (Silicon Sense, Nashua, NH) or on an agarose (OmniPur, Merck KGaA, Darmstadt, Germany) gel slab. The silicon wafer was oxidized in an air-plasma, and silanized with tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane (United Chemical Technologies, Bristol, PA), under vacuum (∼60 mm Hg). This pretreatment facilitated peeling the Teflon sheets off the wafer after fabrication, and resulted in films with a smoother surface than films made on other substrates (e.g., glass).

FIGURE 1.

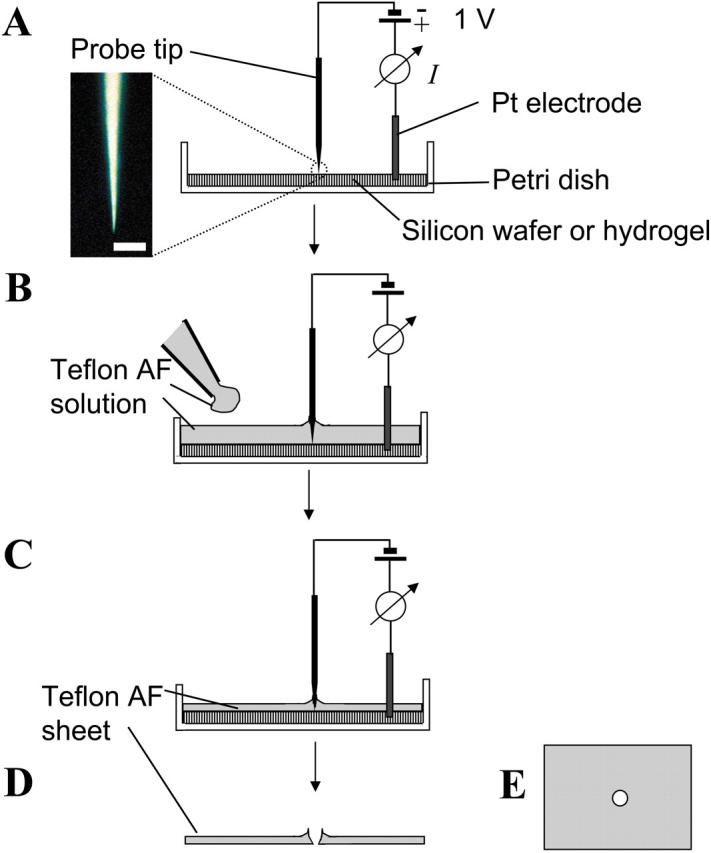
Microfabrication of pores in Teflon AF sheets. (A) A tip of a sharp probe (e.g., a probe tip) is placed in mechanical or electrical contact with, and oriented perpendicular, to a substrate. Mechanically robust probe tips (tip diameter, d_t ≥ 5 μm) are lowered onto a silicon wafer by their own weight. Fragile tips (d_t < 5 μm) are lowered onto an agarose gel (1% in 1 M KCl) with a micromanipulator. In the case of fragile tips, contact between the tip and the gel is verified by monitoring the electrical current flowing between the probe tip and a platinum electrode in the hydrogel at a potential of 1 V DC. The optical micrograph shows a probe tip with a nominal diameter of 200 nm (scale bar, 10 μm). (B) A solution of 6% Teflon AF in Fluorinert FC-75 is added and allowed to mold around the tip. (C) Most of the solvent evaporates within 4 h at room temperature and leaves a sheet of amorphous Teflon behind. (D and E) The resulting Teflon AF sheet (thickness ∼60 μm) has a pore at the position of the tip. The opening diameter of the pore is determined by the diameter of the tip and, in the case of preparations using hydrogels as substrates, by its depth of immersion in the hydrogel.

In making pores using mechanically robust tips (tip diameter ≥5 μm), we used a silicon wafer as substrate, because it is flat and hard (we wanted to avoid indentation of the substrate by the probe tips). For probe tips with nominal tip diameters below 5 μm, we used hydrogel substrates, because these fragile tips bent on contact with a silicon wafer. To obtain small pore diameters (<5 μm) on hydrogel substrates, it was important that the conical tips contacted the gel without deeply penetrating it. We controlled the depth by lowering the probe tips just enough to allow detectable current to flow between the probe tip and a Pt electrode embedded in the hydrogel. Upon contact, the current typically jumped from 0 to >5 nA (1 V applied potential). Tips with diameters above 5 μm could be lowered gently onto silicon wafers. They did not require electrical verification of contact.

Fig. 2 summarizes an alternative procedure to make micropores with a wide range of diameters (30–800 μm) in Teflon AF; this procedure also generates arrays of pores. The first fabrication step uses conventional photolithography (Qin et al., 1996) to prepare a master with posts of SU-8 photoresist (Microlithography Chemical, Newton, MA). Using this master, an unlimited number of poly(dimethylsiloxane) (PDMS) membranes could be made by spin-coating. The actual fabrication of the micropores in Teflon AF was carried out on the benchtop, and did not require access to microfabrication facilities. We supported the polydimethylsiloxane (PDMS) membranes containing pores on a glass substrate and spin-coated a Teflon AF solution onto the PDMS. After evaporation of the solvent (for > 24 h at room temperature), we peeled the resulting Teflon AF sheets from the supporting PDMS film; this sheet had pores at the position of the holes in the PDMS films. The PDMS films could be reused after placing them onto a fresh glass slide.

FIGURE 2.

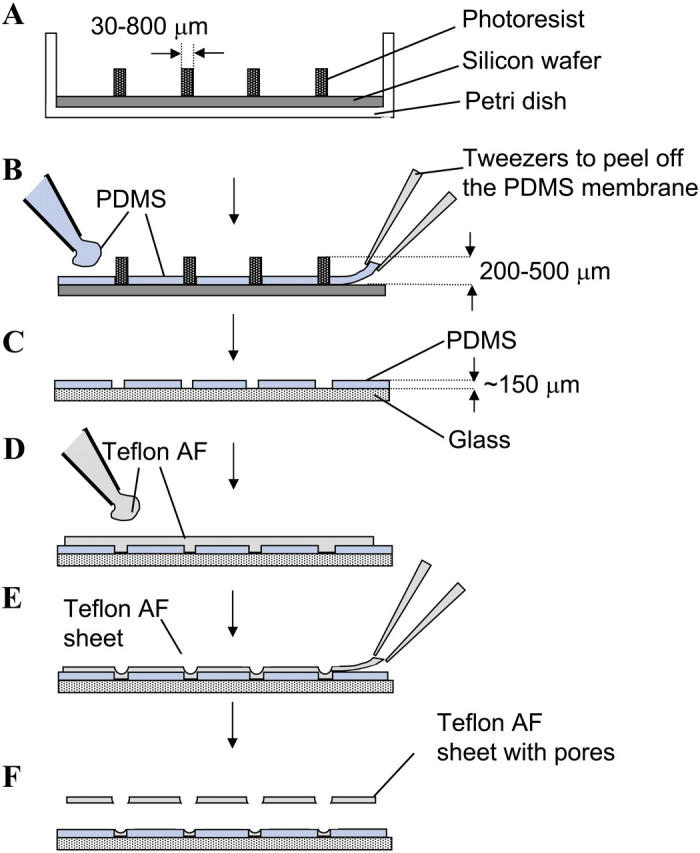
Microfabrication of single pores or arrays of pores in Teflon AF films by spin-coating. (A) The first step involves the fabrication of a master with posts of SU-8 photoresist. Using soft lithography, the diameter of the posts can be varied from 30 to 800 μm. The height of the posts was 200–500 μm. (B) After spin-coating (2000 rpm, 30 s) and curing the PDMS prepolymer on the master, a PDMS membrane with pores is obtained. This membrane is peeled off and (C) placed onto a glass slide. (D) A solution of 9% Teflon AF in a 1:1 mixture of Fluorinert FC-75 and FC-40 (Sigma-Aldrich, St. Louis, MO) is added on top of the supported PDMS membrane and spin-coated at 400 rpm for 30 s. (E) The solvents in the Teflon AF solution are allowed to evaporate at room temperature. (F) Due to its strong adhesion to glass, the Teflon AF in the PDMS wells remains attached to the glass when the Teflon AF film is peeled from the PDMS master; this adhesion results in a membrane with a single pore or with arrays of pores.

The access resistance of the pores was determined with the experimental system shown in Fig. 3. Access resistance is defined as the sum of several resistances in series, including the resistance of i), the electrolyte in the pore R_p, ii), the electrolyte converging to the pore (convergence resistance) R_c, iii), the bulk of the electrolyte R_e, iv), the electrolyte/electrode interfaces R_i, and, if employed, v), salt bridges (Wonderlin et al., 1990). We measured the sum of R_e and R_i in 1 M KCl using the Teflon chamber without a Teflon AF sheet: R_e + R_i = 145 Ω.

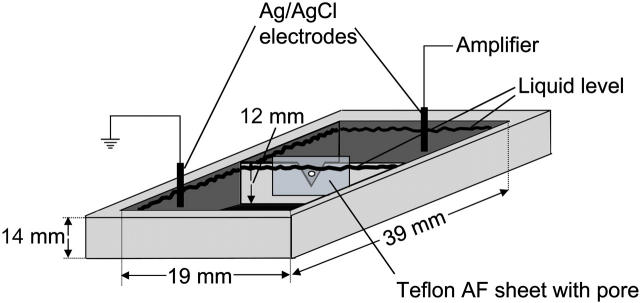
FIGURE 3.

Planar bilayer setup used for folding lipid monolayers over micropores in Teflon AF sheets to form solvent-free lipid bilayers. The Teflon AF sheets were attached to the chamber with high-vacuum grease (Dow Corning, Midland, MI). After spreading the lipid mixture on the air electrolyte interface, the liquid levels were repeatedly raised above and lowered below the pore until a stable bilayer was obtained.

Formation of planar lipid bilayers

Before using the Teflon AF sheets for planar lipid bilayer experiments, we pretreated (Schlue and Hanke, 1993) the area around the pores by sweeping it about five times with the tip of a tissue paper that had been dipped in a solution of 3–5% squalene (Sigma, St. Louis, MO) in pentane (Sigma-Aldrich, St. Louis, MO) (Tosteson and Chow, 1997). We formed all bilayers from apposition of two monolayers of a 1:1 mixture of L-α-phosphatidylserine from brain and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (both from Avanti Polar Lipids, Alabaster, AL) using the method described by Montal and Mueller (1972). Briefly, we mounted a Teflon AF sheet in a Teflon chamber (Fig. 3) separating two buffer compartments (Alvarez, 1986), each with a volume of 3.5 mL. The lipid mixture (2–10 μL with a concentration of ∼12 mg mL⁻¹ of each lipid) was spread from a solution in pentane onto the surface of the electrolyte solutions (1 M KCl). We formed the bilayers by consecutively raising the liquid level in each compartment until the pore was completely covered by electrolyte. If at this point the pore was not closed by a lipid bilayer, that is, if the seal resistance was ≪1 GΩ, then the liquid level in one or both compartments was lowered below the pore by aspirating electrolyte into a 3 mL syringe. Subsequently, the liquid levels were again raised. This cycle was repeated until a high resistance seal (>10 GΩ) was achieved.

The method described above was used for pores that had been prepared by the spin-coating method (Fig. 2). To form lipid bilayers over pores that had been fabricated with the probe-tip method (Fig. 1), we made two modifications. i), After spreading the lipids at the air-electrolyte interface, we raised the liquid levels above the pore on both sides of the Teflon AF film and placed the chamber in a vacuum (∼60 mm Hg) for 5 min (while stirring each compartment) to remove air bubbles that might be trapped in the pores. ii), We lowered and raised the liquid level only in the compartment of the Teflon chamber that faced the flat side of the Teflon AF film (the side that faced the wafer or hydrogel during fabrication). By preparing the bilayer from this side, we were sure that it was formed at the position where the cone-shaped pore had its smallest diameter.

To explore if planar lipid bilayers could also be formed on films of Teflon AF by the “painting technique” (Mueller et al., 1962), we pretreated the area around the pore with 1 μl of a solution of 5 mg mL⁻¹ asolectin (Fluka) in pentane before mounting the film into the chamber (Fig. 3). After filling both compartments with 3.5 mL of 1 M KCl, we applied a solution of 30 mg mL⁻¹ asolectin in n-decane (Fluka) with a paintbrush.

Electrophysiological recordings, filter settings, and noise bandwidth

All recordings were performed in the capacitive feedback configuration of the Axopatch 200B amplifier (Axon Instruments, Union City, CA) and the data were filtered with the built-in four-pole Bessel filter with a cutoff frequency (−3 dB frequency) of f_c1 = 10 kHz. The sampling rate of the data acquisition system (Digidata 1322A, Axon Instruments) was 50 or 100 kHz (according to sampling theory, the sampling rate should be at least four times higher than the cutoff frequency of the filter). When no additional filter was used, the overall cutoff frequency f_c′ was equal to f_c1; most data were, however, also filtered digitally with the Gaussian filter of the pClamp software (Axon Instruments). The overall cutoff frequency f_c′ for filter combinations was estimated using Eq. 1 (Benndorf, 1995; Sherman-Gold, 1993):

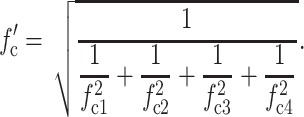(1)

We first filtered with a cutoff frequency f_c2 = 10 kHz; this filter combination resulted in an overall cutoff frequency f_c′ = 7071 Hz. If we wanted to reduce the noise levels further, we filtered the data further with a cutoff frequency of f_c3 = 5 kHz (resulting in an overall cutoff frequency f_c′ = 4082 Hz) and f_c4 = 1 kHz (overall cutoff frequency f_c′ = 971 Hz). To compare the values of the experimentally determined current noise with theoretically estimated noise levels, we converted the overall cutoff frequency f_c′ of the employed filter combinations to the overall theoretical bandwidth of the current noise B_th. A precise conversion is, however, complicated for filter combinations. Here we approximated B_th by applying the conversion factor for a Gaussian filter (Blinchikoff and Zverev, 1976) to the overall cutoff frequency: B_th = 1.065 × f_c′. This estimation yielded the following values for the overall theoretical bandwidth of the noise of the four filter combinations used in this work: B_th1 = 10650 Hz, B_th2 = 7531 Hz, B_th3 = 4347 Hz, and B_th4 = 1034 Hz. Since the overall theoretical noise bandwidth B_th was used as a fitting parameter in this work, we also used an experimental method to estimate B_th for all four filter combinations. We recorded the current noise with a cutoff frequency of 100 kHz of the four-pole Bessel filter of the amplifier (sampling rate 500 kHz) and used the pClamp software to obtain the power spectrum of the noise trace. We then recorded the current noise under the same conditions but with a cutoff frequency of the four-pole Bessel filter of f_c1 = 10 kHz and computed the power spectrum from this trace. Power spectra were also computed for the same noise trace after filtering it with the other filter combinations (f_c2–f_c4) used in this work. Each power spectrum that was obtained for the cutoff frequencies f_c1–f_c4 was then divided by the power spectrum that was obtained for the cutoff frequency of 100 kHz. The integrals under the resulting four functions yielded an estimate of the noise bandwidth B_th of the filter combinations used in this work. We obtained the following values for B_th: 10785, 7404, 4459, and 1047. These values are close to the theoretically estimated values B_th1–B_th4 described above (deviation ≤2.6%). Throughout this work we used the values for B_th1–B_th4 for the analysis of the current noise.

RESULTS AND DISCUSSION

Microfabrication and access resistance of pores in Teflon AF

Fig. 4 shows pores with various diameters in sheets of Teflon AF. The “probe-tip method” resulted in Teflon sheets with a thickness of ∼60 μm when their fabrication was carried out using wafers, and ∼30 μm using hydrogels. The pores had diameters from 2 to 230 μm, and had a conical shape replicating the taper of the tips. Conical pores are well suited for bilayer experiments because they make it possible to fabricate small opening diameters in relatively thick sheets without the disadvantage of a high electrical access resistance R_a of the pores (Wonderlin et al., 1990). Thick sheets (>20 μm) are desirable because they contribute a smaller capacitance than thinner films, and because they are mechanically robust. Small pore opening diameters are good because they facilitate the formation of planar bilayers with the folding technique, and because they minimize bilayer capacitance. The advantage of a small access resistance is reduced electrical current noise (Wonderlin et al., 1990).

FIGURE 4.

Micrographs of pores in Teflon AF films. (A) SEM image of a pore, fabricated with the probe tip method described in Fig. 1 using an agarose gel as substrate and a probe tip (tungsten cat whisker) with a nominal diameter of 200 nm. (B) A micropore fabricated on a silicon wafer with a gold-plated tungsten probe tip with a nominal diameter of 10 μm. The dark region is caused by the tapered shape of the pore. The actual opening diameter of the pore can be seen in the center of the dark region. (C–E) Micropores fabricated by spin-coating a Teflon AF solution over a supported PDMS film with pores as described in Fig. 2. The following pore diameters in the PDMS film were used: (C) 50 μm, (D) 110 μm, and (E) 220 μm. (F) Array of micropores fabricated with the method described in Fig. 2. The diameter of the pores in PDMS was 150 μm.

The access resistance R_a of the conical pores fabricated with the probe-tip method could be described well (r² = 0.98, n = 10) using Eq. 2. We derived this equation by integrating the resistance of the electrolyte over the length of a conical pore (Sakmann and Neher, 1995).

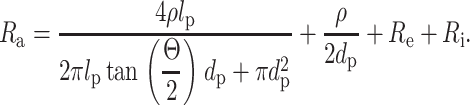(2)

Here, ρ = 0.1134 Ωm represents the specific resistance of the 1 M KCl solution, l_p (m) the length of the pore, Θ the cone angle of the tip, d_p (m) the opening diameter of the pore, R_e the resistance of the bulk of the electrolyte solution, and R_i the resistance of the electrolyte/electrode interfaces (R_e + R_i = 145 Ω in 1 M KCl). The second term in Eq. 2 accounts for the convergence resistance to the pore—that is the resistance of the electrolyte converging from the bulk of the solution to the entrance of the pore at the flat side of the film (Wonderlin et al., 1990).

As indicated schematically in Fig. 1, the Teflon AF solution formed a meniscus around the probe tips, which, after evaporation of the solvent, resulted in a rim (height 40–500 μm) of Teflon around the pore on the side of the Teflon AF sheet, opposite to the wafer or hydrogel. Because of the conical shape of the pore, this rim did not significantly increase the access resistance, and we did not notice an effect from it on the noise levels of experiments carried out with planar bilayers.

The opening diameter of the pores in Teflon AF depended on the diameter of the probe tips that were used for the fabrication. For fabrication on a hard substrate (a wafer), the diameter of the pore was typically a factor of 1.3–2.5 larger than the diameter of the probe tips; e.g., in the case of probe tips with a diameter of 10 μm, the pores had a diameter of 18 ± 3 μm (n = 5). Fabrication on hydrogel substrates typically resulted in pores with diameters from 2 to 8 μm when a probe tip with a diameter of 200 nm was used.

Fig. 4 also shows pores in Teflon AF sheets, which were fabricated by the spin-coating method outlined in Fig. 2. This method was particularly useful for the fabrication of arrays of pores in Teflon AF. Since the position, shape, and diameter of the pores in Teflon AF were determined by the microfabricated PDMS membrane that was used for their fabrication, the spin-coating method made it possible to fabricate pores, and arrays of pores, of any desired geometry and diameter. The thickness of the Teflon sheets depended on the angular velocity of the spinner used in spin-coating: with 9% Teflon AF solutions and 30 s spin time, the thickness of the dry Teflon sheets was 38 μm for 300 rpm, 32 μm for 400 rpm, 26 μm for 500 rpm, and 15 μm for 1000 rpm spin speed. The area around the pore was somewhat tapered and therefore thinner than the rest of the sheet.

The spin-coating method resulted in pores with diameters that were 1.0–1.2 that of the diameter of the hole in the PDMS film. For pore diameters from 43 to 615 μm, the access resistance R_a of these pores was described well (r² = 0.96, n = 7) by the convergence resistance at both sides of the pore and the sum of R_e and R_i:

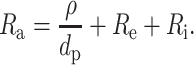(3)

Properties of planar bilayers as a function of their diameter

We tested Teflon AF sheets containing pores that were made by the probe-tip method and by the spin-coating method for use for planar bilayer experiments. Bilayers formed readily when the Teflon AF membranes were pretreated with squalene: After spreading the lipids on the air-electrolyte interface, we usually obtained stable bilayers within the first two to five cycles of raising and lowering the liquid levels. It was more difficult, but nonetheless possible, to obtain bilayers when the membranes were pretreated with hexadecane or decane instead of squalene.

We were also successful in forming bilayers on films of Teflon AF by the painting technique (Mueller et al., 1962; White, 1986). The typical thinning of the decane/lipid droplet to a bilayer with high resistance was, however, only observed with pore diameters ≥70 μm. Throughout this work we used the folding technique (Fig. 3) for the formation of planar lipid bilayers.

The seal resistance of the bilayers increased with decreasing pore diameter: with pore sizes from 2 to 130 μm, the resistance ranged from 49 to ∼660 GΩ (mean: 258 GΩ, n = 25) and with pore sizes from 230 to 800 μm, the resistance was 24–141 GΩ (mean: 62 GΩ, n = 11). We evaluated the resistance of Teflon AF sheets without holes, and found a value of >10¹² Ω for a thickness of ∼60 μm. The Teflon AF sheets were therefore considered insulating in the context of this work.

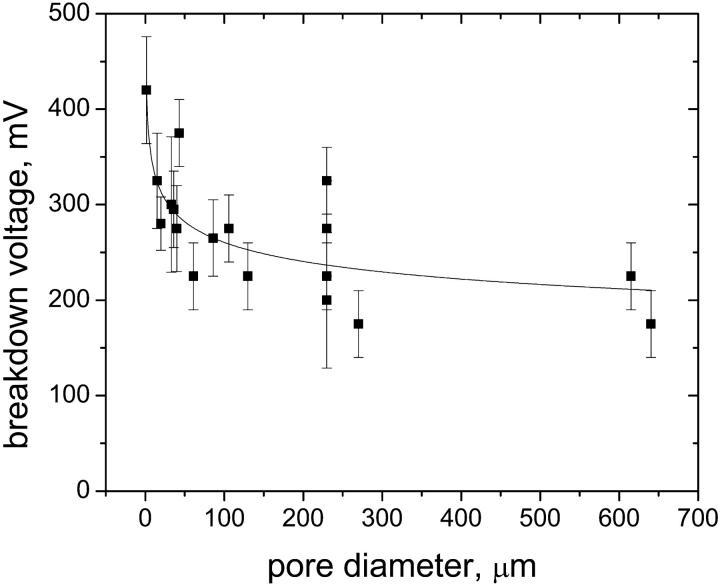
Most bilayers were stable for at least 1 h at voltages of ±150 mV. Bilayers that were left undisturbed at potentials ≤|100 mV| frequently lasted for more than 5 h before breakdown. Fig. 5 shows the dependence of the breakdown voltage of the bilayers on the pore diameter. With the 2 μm diameter pore, we were able to perform alamethicin recordings at up to 460 mV. Breakdown voltages higher than 300 mV were observed frequently (>50%) for pore diameters below 50 μm. High breakdown voltages are clearly beneficial for studying ion channels with small single-channel conductance (Peterman et al., 2002). Using comparable pore diameters, we found no difference in the stability of the pores made by the probe-tip and the spin-coating methods. For comparison, we also determined the breakdown voltage of a 60 μm pore that had been burned into a standard PTFE Teflon foil with a high voltage pulse (Tosteson and Chow, 1997) and found that the bilayers broke down electrically at potentials between 200 and 250 mV; the corresponding value for pores in Teflon AF was 250–300 mV.

FIGURE 5.

Breakdown voltage of planar bilayers on Teflon AF membranes as a function of the pore diameter. Breakdown voltage was defined as the minimum voltage (applied for ≥5 min) required to break a bilayer irreversibly or disturb it such that an abrupt increase in current noise was observed. The error bars represent the standard deviation of the breakdown voltages of at least three repetitions. The line represents the best fit: y = 422 × x^−0.115.

The increase in membrane capacitance C_m (F) with pore diameter d_p of bilayers formed after squalene pretreatment is described by Eq. 4:

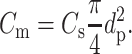(4)

Here C_s is the specific capacitance (Reyes and Latorre, 1979; Waldbillig and Szabo, 1979; White and Thompson, 1973). Our experimental data were fitted best (r² = 0.92, n = 13) with C_s = 9.63 × 10⁻³ F m⁻² (0.963 μF cm⁻²). The total capacitance C_t (F) is given by Eq. 5,

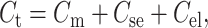(5)

where C_se = 9 × 10⁻¹² F was the capacitive contribution of the Teflon AF sheets, and C_el = 10 × 10⁻¹² F was the capacitance of the immersed electrodes.

Preparation of planar lipid bilayers over multiple pores

The procedure outlined in Fig. 2 makes it possible to prepare Teflon AF films with multiple pores. We used a Teflon film with three pores of equal diameter (120 μm) to test the possibility of forming multiple planar bilayers in parallel. The Teflon AF film was mounted into the experimental system (Fig. 3) such that the three pores were oriented in a vertical line. Employing the same protocol as used for single pores, we were able to form three bilayers in parallel. The capacitance increased stepwise while the liquid level of the electrolyte was raised over one, two, and three pores. The total capacitance was 328 pF, corresponding well to the theoretical capacitance (Eq. 4) of 327 pF of three planar bilayers with a diameter of 120 μm. The bilayers were stable for at least 1 h.

Analysis of the current noise as a function of the pore diameter

The electrical current noise is an important aspect of planar bilayer experiments. Noise can be characterized by its power spectral density or by its variance (which is the integral of the spectral density over the frequency range f = 0–B, where B represents the bandwidth). The spectral density of the noise (S² in A² Hz⁻¹) and the noise variance (i² in A²) in planar bilayer recordings have contributions from four sources of noise. The first is the noise resulting from the interaction of the headstage input voltage noise and the input capacitance, described by Eqs. 6 (power spectral density) and 7 (noise variance) (Wonderlin et al., 1990) (“headstage” refers to the amplifier, which is placed as close as possible to the recording electrodes. It amplifies small currents into values sufficient for the main amplifier to accept):

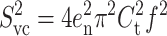(6)

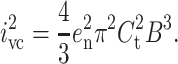(7)

Here e_n is the root mean-square (rms) noise voltage in the headstage input. We used a value of e_n = 2.3 × 10⁻⁹ V Hz^−0.5 (Rae and Levis, 1984; Sherman-Gold, 1993). C_t is the total input capacitance, f (Hz) is the frequency, and B (Hz) is the bandwidth. The second contribution to noise is the thermal voltage noise of the access resistance R_a in series with the bilayer capacitance C_m (Eqs. 8 and 9) (Wonderlin et al., 1990),

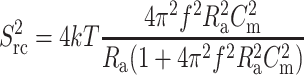(8)

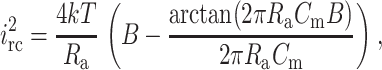(9)

where k is the Boltzmann constant (k = 1.38 × 10⁻²³ J K⁻¹) and T is the absolute temperature (K). The third noise source in planar bilayer experiments is the dielectric noise. It results from thermal fluctuations in lossy dielectric materials with a capacitance C_t (Eqs. 10 and 11) (Levis and Rae, 1998).

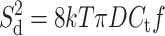(10)

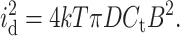(11)

Here the dielectric loss factor (also called dissipation factor) D (unitless) is composed of the loss factors of all dielectric materials that contribute to the capacitance C_t. Not all materials that contribute to C_t contribute to D to the same extent. It is thus complicated to evaluate the precise value of the overall D. The biggest contribution is, however, expected from the septum (K. Benndorf, personal communication); the contribution from the lipid bilayer is predicted to be small (Lauger, 1979). D can be considered constant in the important bandwidth range between 1 and 100 kHz (Sherman-Gold, 1993). The dielectric loss factor of Teflon AF is very low, D = 8.0 × 10⁻⁵ − 2.0 × 10⁻⁴, and Teflon AF has the lowest known dielectric constant of any solid, uniform plastic material (ɛ = 1.89–1.93) (Resnick and Buck, 1997, 1999); both properties minimize the dielectric noise.

In the context of planar bilayer recordings, noise sources such as shot noise, Johnson noise and 1/f noise are small compared to the three noise sources discussed above (Wonderlin et al., 1990). We summarized all noise sources apart from the ones described by Eqs. 6–11 as “excess noise” i_e. Due to the random nature of the individual noise sources, the total root mean-square value of the current noise can be calculated using Eq. 12 (Sherman-Gold, 1993):

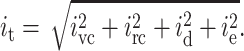(12)

The total rms current noise can be determined experimentally. It is defined as the standard deviation of the current from its mean value.

Equations 5–12 indicate that the noise in planar bilayer experiments depends on the recording bandwidth, the bilayer capacitance, and the access resistance of the pore.

Since the recording bandwidth has to be adjusted to the single-channel conductance and kinetics of the ion channel under investigation, it can only be minimized to a certain degree. If high bandwidth is required, the most accessible experimental parameters that can be optimized to achieve low noise are the access resistance and the total capacitance. Both parameters depend on the pore diameter. The fabrication methods presented here allow the preparation of micropores with a wide range of diameters; this capability, in principle, makes it possible to optimize the pore diameter for specific applications.

We examined the rms current noise as a function of the pore diameter. Fig. 6 shows the rms current noise as a function of the pore diameter measured with lipid bilayers on Teflon AF membranes that had been prepared by the spin-coating method. The data were fitted with Eq. 13—a modified form of Eq. 12, containing factors that account for the nonideal behavior of low-pass filters (Benndorf, 1995; Levis and Rae, 1998). Since we do not know the precise correction factors for the digital Gaussian filter, we used the correction factors for an eight-pole Bessel filter (the characteristics of Bessel filters with increasing numbers of poles approach the characteristics of Gaussian filters (Lindquist, 1977)). The correction factors are determined by the frequency dependence of the spectral density of the noise: for flat noise the factor is ∼1.04, for f-noise it is ∼1.3, and for f ²-noise it is ∼2.0 (Benndorf, 1995; Levis and Rae, 1998). The corrected version of Eq. 12 is therefore:

(13)

The correction factor of 1.3 for the noise variance of the excess current noise i_e was inferred from the curve fits in Fig. 6. We observed that i_e was proportional to the bandwidth (Table 1); the spectral density of the excess noise 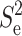was therefore linearly dependent on f. Thus in the range of bandwidth examined here (1034–7531 Hz), the excess current noise was of the f-noise type.

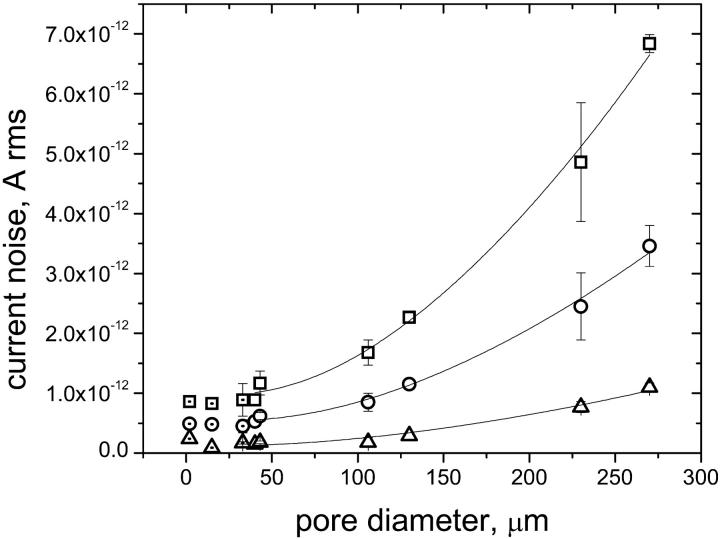
FIGURE 6.

Total rms current noise as a function of the pore diameter. The noise levels were recorded at three different values of the overall bandwidth of the noise B_th: 7531 Hz (□), 4347 Hz (○), and 1034 Hz (Δ). The lines represent the best curve fits using Eqs. 3–13 and a dielectric loss factor of D = 2 × 10⁻⁴. Error bars represent the standard deviation of the noise levels recorded with different Teflon AF films, which had approximately the same pore diameters. The results of the curve fits are summarized in Table 1. Data with a dot in the symbol were obtained with pores that had been fabricated with the probe-tip method. These data were not included in the curve fits.

TABLE 1.

Fitting parameters (B, i_e, and r²) obtained from best curve fits of the measured total rms current noise at three different values of the noise bandwidth B_th

Bth (Hz)	B (Hz)	ie (A rms)	r2
1034	2187	9.8 × 10−14	0.98
4347	4769	4.5 × 10−13	0.99
7531	7554	8.1 × 10−13	0.99

We used Eqs. 3–13 and a value of D = 2 × 10⁻⁴ for the curve fits.

In Fig. 6, we plotted the total rms current noise that was obtained at three different values of the overall theoretical bandwidth of the noise B_th as a function of the pore diameter. Only noise values that were measured with pores made by the spin-coating method were included in this analysis. Fig. 6 shows the best fits of the data by curves calculated using Eq. 13; these curves were obtained by assuming a dielectric loss factor of D = 2 × 10⁻⁴ for Teflon AF. The fitting parameters were the excess current noise i_e, which was assumed to be independent of the pore diameter, and the bandwidth B. Table 1 summarizes the fitting parameters.

Fig. 6 and the values for r² in Table 1 establish that the experimental current noise can be described well with Eq. 13. The bandwidths determined from the curve fits are also close to the values of the theoretically estimated bandwidth of the noise B_th. We found, however, a deviation at the lowest bandwidth: the data were fitted best with B = 2187 Hz, although the estimated value of B_th was 1034 Hz. It seems that at lower frequencies, additional sources of noise, which are dependent on the pore diameter, become important for the overall noise. Since these additional sources appeared to be less important at B_th values ≥4347 Hz, we used only the data recorded at B_th = 4347 and 7531 Hz for further analyses.

To estimate the dielectric loss factor D, we fitted the experimental data in Fig. 6 with Eq. 13 by setting the bandwidth fixed to B_th and by varying D. The results of the best curve fits are summarized in Table 2. As expected, the curve fit for the data recorded at B_th = 1034 Hz was poor. For the higher values of B_th, however, the fits were good; this agreement indicates that the overall dielectric loss factor was in between the value for Teflon AF (D = 2 × 10⁻⁴) and D ∼ 3 × 10⁻³.

TABLE 2.

Fitting parameters obtained from best curve fits of the measured total rms current noise with Eqs. 3–13 and B = B_th

Bth (Hz)	B (Hz)	D	ie (A rms)	r2
1034	1034	1.8 × 10−2	1.1 × 10−19	0.88
4347	4347	3.3 × 10−3	3.1 × 10−13	0.99
7531	7531	2.4 × 10−4	8.2 × 10−13	0.99

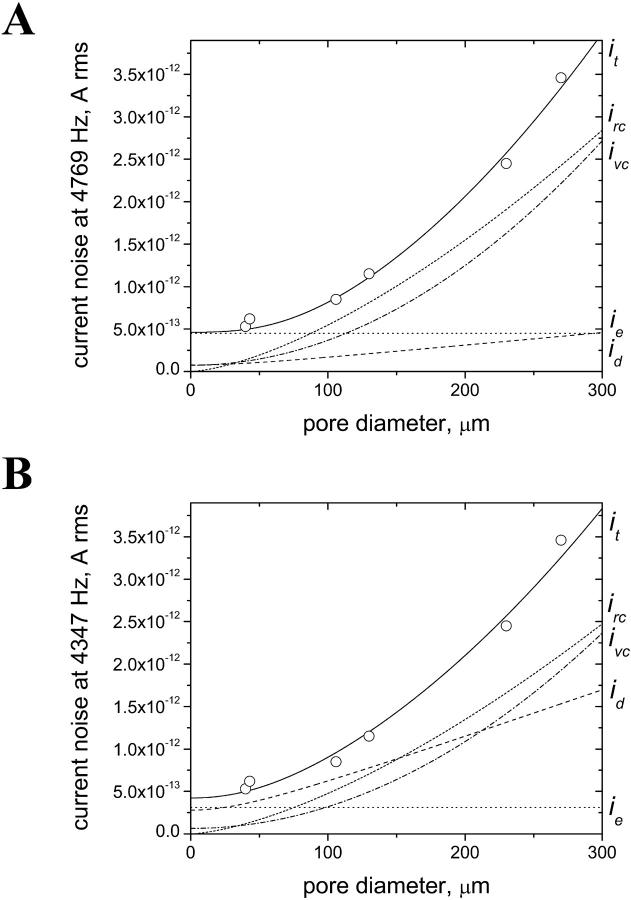
To minimize the overall noise in planar bilayer experiments, it is helpful to examine the importance of the individual noise sources. Before discussing the data, however, we point out that since the individual noise sources add in an rms fashion (Eq. 13), the largest individual source of noise tends to dominate the total noise (Levis and Rae, 1998). Fig. 7 A shows the contribution of each source of noise to the experimentally measured total rms current noise as a function of the pore diameter. The curve was calculated with a bandwidth of 4347 Hz and a dielectric loss factor of D = 2 × 10⁻⁴. Up to a pore diameter of ∼25 μm, the overall rms current noise i_t is dominated by the excess noise i_e. As mentioned earlier, in the approach taken here, i_e includes the shot noise, Johnson noise, and 1/f noise. At ∼100 μm pore diameter, i_e, i_vc, and i_rc contribute about equally to the overall rms current noise. With further increasing pore diameters, the contributions of i_rc and i_vc become more and more important and dominate the overall current noise. In the example represented in Fig. 7 A, the contribution of the dielectric noise i_d to the overall current noise was small (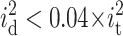, for all diameters).

FIGURE 7.

Individual sources of noise as obtained by the best curve fits of the total rms current noise i_t for different values of the bandwidth B and the dielectric loss factor D. (A) Individual noise sources i_rc, i_vc, i_e, i_d, and total rms current noise i_t obtained by the best curve fit to the noise measured with B_th = 4347 Hz. The fitting parameters were the bandwidth B and the excess current noise i_e; the dielectric loss factor was assumed to be D = 2 × 10⁻⁴. The best curve fit was obtained with B = 4769 Hz and i_e = 0.45 pA rms. (B) Individual noise sources and total rms current noise obtained by the best curve fit with the dielectric loss factor D as the fitting parameter and setting the bandwidth B to B_th = 4347 Hz. The best curve fit was obtained with D = 3.3 × 10⁻³ and i_e = 0.31 pA rms.

The importance of the dielectric noise increases, however, with an increasing dielectric loss factor D. As mentioned before, the septum contributes to the overall dielectric loss factor, but so do other materials in the vicinity of the headstage. Table 2 lists the estimated overall values of D as obtained from the best curve fits of the total rms current noise to the current noise recorded at three values of B_th. The highest value of D = 1.8 × 10⁻² is unlikely since it is impossible to obtain good curve fits for the data recorded at a higher cutoff frequency than B_th = 1034 Hz. Fig. 7 B shows the best fit of the total rms current noise at 4347 Hz assuming an overall loss factor of D = 3.3 × 10⁻³. Under these conditions, the dielectric noise represents the largest contribution to the total noise for pore diameters between 25 and 160 μm. Wonderlin et al. (1990) reported that the rms current noise increased by a factor of 1.5 when nylon instead of Teflon was used for bilayer experiments. The dielectric loss of nylon is ∼1.5 × 10⁻² (Pflueger, 1989), compared to ≤2 × 10⁻⁴ for Teflon AF. Due to its low dielectric loss factor, Teflon AF is an excellent material to use in minimizing the dielectric noise.

Fig. 7 illustrates that with our experimental setup and protocol, the rms current noise is dominated by the excess noise i_e, when the pore diameter is smaller than 25 μm. A reduction of the pore diameter below 25 μm will therefore not result in a significant reduction of the overall noise. This result is in agreement with the work from Fertig et al. (2001), in which a glass chip with a small pore (d_p = 2 μm) was used for planar bilayer recordings. The authors report an overall rms current noise of 0.32 pA rms at a bandwidth of ∼3 kHz and ∼0.1 pA rms at ∼1 kHz; these values compare well to our noise of 0.46 pA rms at 4.35 kHz, and 0.09 pA rms at 1.03 kHz. It follows that a further reduction in the noise of planar bilayer recordings can only be achieved if the excess noise is minimized. From patch clamp experiments, it is known that noise levels as low as 0.083 pA rms at a bandwidth of 5 kHz can be achieved (Rae and Levis, 1992).

To understand better why the excess noise in planar bilayer experiments is higher than in patch clamp experiments, we measured the noise of the amplifier under different experimental conditions. The noise of the shielded headstage was 0.044 pA rms (B ≅ 5.1 kHz). Connecting Ag/AgCl wire electrodes to the headstage and ground, but leaving both electrodes in air, yielded a noise of 0.07 pA rms (B_th = 4347 Hz). When both electrodes were immersed in 1 M KCl in separate glass vials with an air gap between the vials, the noise was 0.43 pA rms (B_th = 4347 Hz). Finally, with both electrodes in 1 M KCl in the planar bilayer setup and a spin-coated Teflon AF membrane without a hole between the compartments, the noise was 0.44 ± 0.08 pA rms (B_th = 4347 Hz). The total noise i_t recorded with the setup used in this work (Fig. 3) was dependent on the input capacitance C_t. At a bandwidth of 4082 Hz, we found a linear relationship between the rms current noise and the capacitance in the range of 10–28 pF. The slope was 0.012 pA rms/pF and the y-intercept was 0.15 pA rms (r = 0.99, n = 5). The y-intercept can be used as an approximation of the minimum noise that could be achieved with the experimental setup and protocol used here, if the input capacitance could be reduced to <1 pF. An rms current noise of 150 fA is about twice the value that can be achieved with the best low-noise patch clamp setups. To reach such low noise levels, the capacitance of the setup would have to be reduced to <1 pF (in our case, the electrodes in electrolyte contribute 10 pF and the Teflon AF septa contribute ∼9 pF) and the complete setup would have to be rigorously optimized for low-noise characteristics. The pores would have to be ≤10 μm in diameter; these sizes would result in a membrane capacitance of C_m≤0.75 pF. Further optimization might involve improved grounding, shielding, and vibration damping, as well as frequent formation of fresh silver chloride on the Ag/AgCl electrodes.

Although our minimum noise levels of ∼0.4 pA rms at 4.35 kHz bandwidth are high compared to patch clamp experiments, they are very low compared to most bilayer experiments. To test the performance of the Teflon AF septa, and to make use of the low-noise characteristics, we recorded single-channel current traces of alamethicin ion channels.

Low-noise single-channel recordings of alamethicin pores

Alamethicin, an antibiotic peptide containing 20 amino acids, self-integrates into bilayers and forms voltage-gated ion channels of defined conductance by oligomerization (Boheim et al., 1983; Fox and Richards, 1982). We added alamethicin to both chambers to a final concentration of 10 ng mL⁻¹. After ∼10 min, we recorded typical voltage-gated activation of alamethicin channels: at potentials <|60 mV|, no events were observed. At higher voltages, we saw single-channel events with current amplitudes that increased with increasing potential. Fig. 8 shows single-channel alamethicin events recorded at −202 mV, and the point-amplitude histogram derived from the single-channel current. The single-channel conductance values of open states O₁–O₆ were: 24, 395, 1375, 2662, 3989, and 5430 pS. These values compare well to previously reported conductance values of 19, 280, 1300, 2700, 4400, and 6200 pS in 1 M KCl (Hanke and Boheim, 1980). Fig. 8 C and the corresponding point-amplitude histogram show the lowest conductance state O₁ of alamethicin. We were able to resolve O₁ at an unprecedentedly high bandwidth of B_th = 10,650 Hz. This result demonstrates that the microfabricated Teflon AF septa employed in this work make it possible to resolve small ion channel events at high bandwidth.

FIGURE 8.

Single channel recording of alamethicin events at high effective bandwidth (10.7 kHz) and corresponding point-amplitude histograms of the current trace. (A) Alamethicin channel events recorded at −202 mV. The dotted lines indicate a current I = 0 pA, and the open state current amplitudes O₂–O₆ as revealed by the peak maxima of the histogram. (B) Point-amplitude histogram of the current trace shown in A. (C) Magnified area from the trace shown in (A, dotted square). The recording shows the baseline current, C, in the closed state of the alamethicin channel. (D) Corresponding point-amplitude histogram, revealing the open state O₁. The single-channel conductance values of open states O₁–O₆ are: 24, 395, 1375, 2662, 3989, and 5430 pS. Alamethicin concentration: 10 ng mL⁻¹ in both chambers; buffer: 1 M KCl. A Teflon AF sheet with a pore diameter of 15 μm was used and the total capacitance C_t was 36 pF. The filter frequency was 10 kHz (B_th = 10650 Hz) and the sampling frequency was 50 kHz.

Fig. 8 C also illustrates that the transition of alamethicin channels from one conductance state to the next higher or lower state is very rapid. We made use of this characteristic to evaluate the effective cutoff frequency f_c″ of our recordings under “real” recording conditions. Using only the built-in four-pole Bessel filter with a cutoff frequency of 10 kHz, we found that it took 28.5 μs for alamethicin channels to change from one conductance state to the next (more precisely to switch from 10% to 90% of the total change in current). With this 10–90% step rise time t_10–90, the effective cutoff frequency f_c″ of all filter combinations can be estimated with Eq. 14 (Colquhoun and Sigworth, 1995):

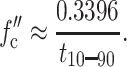(14)

The result of this calculation for all filter combinations used in this work is listed in Table 3. The effective cutoff frequency f_c″ calculated with the step rise time was close to the values of f_c′ and B_th at a given filter setting. Alamethicin events can therefore be used to explore the effective bandwidth of a planar bilayer setup up to a bandwidth of at least 10 kHz. Wonderlin et al. (1990) reported that the access resistance R_a and the capacitance at the headstage input C_t limited the maximum recording bandwidth achievable in planar bilayer experiments. In the absence of series resistance compensation, the maximum bandwidth can be estimated with Eq. 15 (Levis and Rae, 1998):

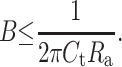(15)

The access resistance of the Teflon AF septa that had been fabricated using the probe-tip or spin-coating method was very low (Eqs. 2 and 3, respectively); as a result, even without series resistance compensation, the maximum bandwidth as calculated with Eq. 15 was at least 30 kHz. Therefore, in the work presented here, the effective recording bandwidth was never limited by the product C_t × R_a but by the filter settings of the low-pass filter that were chosen for the recording.

TABLE 3.

Ten–90% step rise time analysis of alamethicin events obtained with different overall cutoff frequencies f_c′

fc′ (Hz)	Bth (Hz)	t10–90 (μs)	fc″ (Hz)
971	1034	335.2	1013
4082	4347	76.2	4457
7071	7531	44.5	7631
10000	10650	28.5	11916

We listed the effective cutoff frequency f_c″ that was calculated with Eq. 14.

Table 3 also shows that it does not take longer than 28.5 μs for alamethicin to switch from one conductance state to the next; the real transition time is, however, presumably considerably shorter.

CONCLUSION

By preparing planar lipid bilayers over pores with varying diameters, we found that above pore diameters of 40 μm, the current noise increased strongly with increasing pore diameter and bandwidth as predicted by theory. The main sources of noise were i), the thermal voltage noise of the access resistance in series with the bilayer capacitance, i_rc; ii), the noise resulting from the interaction of the headstage input voltage noise and the input capacitance, i_vc; and iii), in the case of septa made of Teflon AF, to a smaller extent the dielectric noise, i_d. The noise recorded with bilayers on pores with a diameter smaller than 40 μm, however, was dominated by additional sources of noise, which were summarized as excess noise, i_e. Possible contributions to i_e are shot noise, seal noise, flicker noise (1/f noise), electrode noise, and noise from external sources (Sherman-Gold, 1993). The excess noise i_e was proportional to the total input capacitance C_t. For small pore diameters (<15 μm), C_t was dominated by the capacitance of the Teflon film and the electrodes; consequently, a further reduction of the pore diameter would have only a small effect on the current noise. To approach the low-noise characteristics of patch clamp recordings with planar lipid bilayer experiments, the capacitance of the bilayer setup (electrodes, electrode holder, Teflon film) would have to be reduced to a total value of ≤2 pF.

Although the noise levels obtained with Teflon AF films were higher than the levels of patch clamp experiments, they were extremely low in the context of planar bilayer experiments. Pores with diameters ≤40 μm allowed planar bilayer recordings with a current noise ≤0.4 pA rms at a bandwidth of 4.3 kHz and supported bilayers that were stable at voltages up to 460 mV. The low access resistance of the tapered pores afforded recordings with fast time resolution (effective bandwidth ≥10.7 kHz).

Recently the interest in employing electrophysiological techniques for high-throughput screening is increasing (Denyer et al., 1998; Fertig et al., 2002; Schmidt et al., 2000; Xu et al., 2001). Performing recordings from multiple planar lipid bilayers in parallel would be an attractive approach. In a first step toward this goal, we showed here that Teflon AF films with multiple microfabricated pores could be used for the stable formation of multiple lipid bilayers at defined locations in the supporting film.