Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Nov;85(5):2801–2807. doi: 10.1016/S0006-3495(03)74703-1

A Molecular Dynamics Method for Calculating Molecular Volume Changes Appropriate for Biomolecular Simulation

Russell DeVane *, Christina Ridley *, Randy W Larsen *, Brian Space *, Preston B Moore †, Sunney I Chan ‡
PMCID: PMC1303561  PMID: 14581185

Abstract

Photothermal methods permit measurement of molecular volume changes of solvated molecules over nanosecond timescales. Such experiments are an important tool in investigating complex biophysical phenomena including identifying transient species in solution. Developing a microscopic understanding of the origin of volume changes in the condensed phase is needed to complement the experimental measurements. A molecular dynamics (MD) method exploiting available simulation methodology is demonstrated here that both mimics experimental measurements and provides microscopic resolution to the thermodynamic measurements. To calculate thermodynamic volume changes over time, isothermal-isobaric (NPT) MD is performed on a solution for a chosen length of time and the volume of the system is thus established. A further simulation is then performed by “plucking” out a solute molecule of interest to determine the volume of the system in its absence. The difference between these volumes is the thermodynamic volume of the solute molecule. NPT MD allows the volume of the system to fluctuate over time and this results in a statistical uncertainty in volumes that are calculated. It is found in the systems investigated here that simulations lasting a few nanoseconds can discern volume changes of ∼1.0 ml/mole. This precision is comparable to that achieved empirically, making the experimental and theoretical techniques synergistic. The technique is demonstrated here on model systems including neat water, both charged and neutral aqueous methane, and an aqueous β-sheet peptide.

BACKGROUND

A novel molecular dynamics (MD) method to determine both thermodynamic volumes of solvated molecules and time-dependent volume changes in the condensed phase, the “pluck” method, is presented here. The method utilizes contemporary MD methods (Martyna et al., 1996; Tuckerman and Martyna, 2000)—specifically, extended system, isothermal-isobaric (NPT) MD to determine the volume of a system while simultaneously exploring the dynamics of the system.

The thermodynamic volume of a solution is obtained directly from the volume coordinate in NPT MD. Consider, e.g., a single solute in a solvent. Solute volumes can be calculated by “plucking” the solvated species from the system, i.e., simulating the remaining system in the absence of solute-solvent forces. After re-equilibration, the volume of the remaining system, in this case pure solvent, is determined using NPT MD. The difference between the solution and solvent volumes determines the solute molecular volume. “Plucking” the molecule from an otherwise equilibrated system often produces an initial condition for a system configurationally near the new equilibrium and thus aids in equilibration; this is especially important in simulating complex systems. Also, in simple solutions consisting of a single yet variable solute, the volume of the neat solvent need only be determined once, simplifying the computation. The method is, however, not limited to simple solutions and can be used in very complex biological simulations to determine molecular volumes of any of the components of an assembly of biomolecules and solvents.

NPT dynamics produces a fluctuating volume coordinate and the thermodynamic volume is the average value over time. This leads to an uncertainty in the thermodynamic volume calculation that must be assessed. It is demonstrated in Results from a Simple Model System that the volume fluctuations are Gaussian and thus the standard deviation of the volume fluctuation is a useful measure of the uncertainty. However, as a consequence of the dynamical nature of the MD, successive volume values are not statistically independent. Following earlier work, the correlation time of the volume coordinate is calculated and only uncorrelated values are sampled. (Allen and Tildesley, 1989; Friedberg and Cameron, 1970; Jacucci and Rahman, 1984) This is equivalent to sampling more frequently and correcting for the correlation between volumes. For the aqueous systems investigated here solute volume uncertainties of ∼1.0 ml/mole are obtained from a few nanoseconds of dynamics and all the volume values in the article are given with respect to the change in solute volume.

It should be noted that NPT MD algorithms are not strictly equivalent to microcanonical dynamics, although the method employed here samples the NPT ensemble exactly (Martyna et al., 1996). These methods couple the real system variables to fictitious variables that regulate the thermodynamic properties of interest (e.g., thermostat, the temperature; and barostat, the pressure) such that they fluctuate around the desired, preset average values. The methods for calculating thermodynamic volumes is therefore exact for a given MD potential energy model, and the only issue is whether dynamical events observed are physically relevant. NPT dynamics does closely mimic true microcanonical (NVE) dynamics (e.g., the perturbation of the dynamics is order 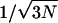Inline graphic, where N is the number of atoms in the system), and has even been suggested as the method of choice for biophysical systems. (Hansson et al., 2002)

The motivation in using NPT dynamics to calculate volume changes via this approach is to mimic photothermal experiments on biological systems that also determine molecular volume changes on nanosecond timescales with similar precision (Hansen et al., 2000; Larsen and Langley, 1999; Larsen et al., 1998). For example, photothermal experiments can identify protein/peptide intermediates with characteristic volumes that have lifetimes of several nanoseconds. The present theoretical methods can be employed in the same fashion. Transient species with characteristic volumes can be identified by statistically significant changes in the volume coordinate over time, indicative of metastable equilibrium between the solute and solvent. MD can then provide microscopic resolution to the observation by identifying the structures of any intermediates. Further, while the NPT MD is not dynamically exact, it is always possible to verify configurational events by repeating simulations microcanonically to verify the veracity of the dynamics. The dynamic interpretation of the proposed methods is therefore a computational convenience. Computational efficiency is, however, clearly desirable given the inherent challenge of simulating interesting biological systems for hundreds of nanoseconds, a relatively short timescale over which to look for large conformational changes in biopolymers. To access longer timescales and to sample volume efficiently, multiple timescale integration techniques are employed and permit the use of larger MD time steps (Tuckerman and Martyna, 2000). It is notable that photothermal methods can also map out enthalpy profiles over similar timescales, and MD directly complements these measurements by providing a molecular interpretation of the energetics.

Other effective methods exist to calculate molecular volumes and related excess compressibilities (Matubayasi and Levy, 2000; Lockwood and Rossky, 1999; Lockwood et al., 2000; Dadarlat and Post, 2001), but the “pluck” method is ideally suited to modeling biological systems and their time evolution. The flexibility in dissecting the physical origin of volume changes using the “pluck” method will also be demonstrated by the examples that will be presented. For example, by varying potential energy interactions between a solute and solvent the volume can be dissected into different contributions in a thermodynamically consistent manner (Imai et al., 2001). It is important to note that the precision of measuring volume changes will be affected by the duration of the simulation that is (computationally) possible for larger systems. For example, when modeling large solvated proteins (e.g., >100 residues), simulations are currently limited to durations on the order of 100 ns. It is demonstrated below that 10 ns of MD would permit the determination of the volume to within ∼4.0 ml/mole. Also, the protein volume is larger in this case and the relative error in the volume measurement is reduced. Further, volume changes associated with folding may be greater, on a per-residue basis, for larger proteins (Foygel et al., 1995).

In Methods and Applications to a Model System, the molecular volume of a β-sheet peptide, which has been investigated experimentally using photothermal methods (Hansen et al., 2000), is calculated to demonstrate the analysis involved in the “pluck” method. The technique is then applied on model systems including neat water, both neutral and (fictitious) charged aqueous methane in Results from a Simple Model System. A series of molecules was chosen to highlight the methods ability to probe the relative volume changes associated with electrostriction and ionic solvation. The present methods can also be extended to calculate excess compressibilities by simulating at different pressures and calculating the compressibility via finite difference (Lockwood and Rossky, 1999; Lockwood et al., 2000; Dadarlat and Post, 2001).

METHODS AND APPLICATIONS TO A MODEL SYSTEM

Fig. 1 presents a snapshot of a solvated β-sheet peptide including a panel with the solvent removed for better visualization. The peptide was chosen because it is currently the subject of experimental investigation using photothermal methods (Hansen et al., 2000). Chan and co-workers synthesized a “caged” unfolded version of the peptide that can be photolysed in neat water solution to initiate peptide folding (Hansen et al., 2000; Chen et al., 2001). Using photothermal methods it is then possible to map out volume and enthalpy profiles during the roughly 1.0-μs folding process. The folded structure was created based on an NMR structure (Chen et al., 2001), and two separate folded systems were prepared and their equilibrium structures were compared and found to be essentially indistinguishable. To demonstrate the “pluck” method, Fig. 2 shows a time trace of the solvated peptide volume coordinate. For comparison, the relaxation of the system volume after the peptide is “plucked” from solutions is also shown. The inset of Fig. 2 shows the short time dynamics of the system to highlight the transient volume change. The system quickly approaches a new equilibrium and has a system volume characteristic of pure water 50.0 ps after removal of the peptide. Equilibrium volume fluctuations are then followed for several nanoseconds to determine the volume of the systems to a desired precision; 2.0 ns of the dynamics are shown in Fig. 2.

FIGURE 1.

FIGURE 1

Open in a new tab

A snapshot of the β-sheet peptide is shown (right) with solvent and (left) with water removed for better visualization and in a different orientation to better display the three-dimensional structure of the peptide. The colors represent the atom types as follows: C, green; O, red; N, blue; and H, white.

FIGURE 2.

FIGURE 2

Open in a new tab

The curve with the larger average value shows a time trace of the volume fluctuations for the folded aqueous β-sheet peptide. The lower curve displays the relaxation of the neat water system volume to its equilibrium value after the peptide is “plucked” from solution. The inset presents the short time volume fluctuations to highlight the relaxation to equilibrium. Note that the volume of the “plucked” system transiently spikes to a value greater than the previous equilibrium fluctuations after the peptide is removed. The horizontal lines represent the average system volume.

Fluctuations of observable quantities from their means, obtained from MD simulations, are typically Gaussian. They can thus be characterized by their standard deviation, σ. The inset of Fig. 3 presents a histogram of the volume fluctuations of the solvated peptide system. Clearly the distribution is well-described as Gaussian. If the successive values of the volume were uncorrelated, one could calculate the uncertainty of the volume simply as

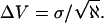graphic file with name M2.gif (1)

In Eq. 1, ℵ is the total number of samples. However, closely spaced values of an observable quantity (in this case the volume is of interest) are not statistically independent because they are connected to each other implicitly by the dynamical equations of motion. It is possible to define a correlation time, tc = s Δt, during which the volumes are not independent, and s is the statistical inefficiency or number of correlated data measurements (Allen and Tildesley, 1989; Jacucci and Rahman, 1984). Multiplying s by Δt, the time length between successive measurements, gives the correlation time, tc. The s-value is calculated by performing volume averages over blocks of time of successively longer lengths ending with the entire length of the MD run. The parameter s is formally defined by Friedberg and Cameron (1970) as

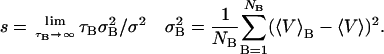graphic file with name M3.gif (2)

In Eq. 2, NB is the number of blocks of length τB such that the product, NB τB = ℵ, is the total number of samples. The inherent correlations then modify the uncertainty in the volume as Inline graphic. This modified formula reduces to Eq. 1 if the time between successive volume samples is longer than tc, and in that case s = 1. For long MD runs it is computationally convenient to save a minimal amount of data and therefore choose a sampling time slightly greater than tc, and this approach was adopted; s and tc are determined initially via trial MD runs.

FIGURE 3.

FIGURE 3

Open in a new tab

The uncertainty in the volume of the β-sheet peptide system as a function of the length of the MD simulation. Volume uncertainties for specific times of interest are also identified. The inset displays a histogram of the system volume fluctuations and a superimposed Gaussian function with a standard deviation calculated from the volume fluctuations.

Fig. 3 also displays a curve demonstrating how the ΔV values decrease over time for the solvated β-sheet peptide. The graph demonstrates that 50.0 ns of dynamics results in an uncertainty of 0.68 ml/mole. This several-ns timescale corresponds to a typical photothermal experimental time resolution for identifying dynamical intermediates. The volume resolution over this timescale is sufficient to identify relatively modest conformational changes in a peptide/protein or other biomolecule. In fact, one study estimated that volume changes of ∼3.0 ml/mole/residue are to be expected for a helix-to-coil transition in a protein (Imai et al., 2001). Because the uncertainty in the volume diminishes only as the square root of the number of volume measurements, 50-ns timescales are needed to reduce the error to the 0.68-ml/mole level. However, it is encouraging that meaningful volume differences were obtained from only a nanosecond of dynamics where the error is 4.2 ml/mole. The figure also gives a volume of 1668.0 ± 2.4 ml/mole for the folded peptide from the 7.5 ns of dynamics that were performed in this study. The molar volume of the neat water system was determined once with sufficient precision to not effect the net volume uncertainty, and this will be discussed further in Results from a Simple Model System. For the folded peptide, the value of the statistical correlation time was found to be tc = 2.4 ps.

Preliminary investigations involving 5.8 ns of MD for an unfolded configuration of the peptide resulted in a volume of 1672.0 ± 3.1 ml/mole. It is interesting that the folded and unfolded state, to within the present statistical certainty, have the same volume. This is somewhat surprising due to the difference in solvation structure associated with each state. Longer MD simulations are required to distinguish between the volumes of these two distinct conformational states. Further, this result does not necessarily imply that dynamical intermediates with significantly different volumes are not present during folding. Further experimental and theoretical investigations are required to determine the volume changes during folding. The determination and structural and dynamical origin (Dadarlat and Post, 2001) of any volume change upon folding is the subject of ongoing investigation. It is notable that larger proteins may exhibit larger (per-residue) volume changes making them amenable to investigation using the present technique (Foygel et al., 1995).

The simulations were performed using a code originally developed by the Klein group at the Center for Molecular Modeling at the University of Pennsylvania, and the Space group is currently a co-developer and user of the code. It is a fast code that includes parallel execution, extended system, particle mesh Ewald, and multiple timescale integration algorithms. The code has been employed in a number of biological MD simulations (Moore et al., 2001, 1998; Zhong et al., 1998; Tarek et al., 1999). The extended system MD methods employed require a coupling between the real system and extended system variables and this could alter the effectiveness of the volume sampling. A variety of coupling constants (representing the coupling of the barostat to the system) between the volume coordinate and the molecular coordinates were tried in preliminary simulations. Physically acceptable values of the “barostat” mass (Martyna et al., 1996; Tuckerman and Martyna, 2000) led to only a weak dependence on the sampling efficiency for the solvated peptide system.

In the simulations, the water model was a flexible SPC model described elsewhere (Moore et al., 2002; Ahlborn et al., 1999, 2000). The force field includes partial charges on the hydrogen and oxygen atoms representing the condensed phase permanent dipole. The protein force field was AMBER ff99. All the aqueous methane systems employed 62 water molecules. The peptide (Chen et al., 2001) had no net charge and was solvated with 810 water molecules using cubic periodic boundary conditions. An all-atom methane model was used, including a flexible force-field fit, to reproduce experimental infrared frequencies with harmonic C-H bonds (Herzberg, 1946). Lennard-Jones interactions were introduced only between the methane carbon and water oxygen with σ = 3.33 Å and ɛ = 51.0 K. The equilibrium bond length for the C-H interaction is 1.09 Å, and its geometry is tetrahedral. When simulating ionic systems the net charge on the system is canceled by employing a neutralizing background in the standard fashion (Allen and Tildesley, 1989). In all cases, the temperature was 298 K and the pressure was 1.0 atmosphere. The multiple timescale integration methods allowed the stable use of 4.0 fs time steps performing NPT dynamics and 8.0 fs time steps when simulating at constant NVE.

This system serves to introduce the method and its properties. Using NPT MD in this fashion permits both the calculation of equilibrium molar volume changes and identification of metastable dynamic intermediate species exhibiting distinct molar volumes. The method will also be ideally suited to decomposing volume changes into differing physical origins such as attributing a volume change to peptide or solvent rearrangements and assessing the role of, e.g., sterics and electrostatics; this will be discussed further in the next section.

RESULTS FROM A SIMPLE MODEL SYSTEM

To test the approach and demonstrate its flexibility, molar volumes were calculated for neat water and a solvated methane model. These systems were the subject of earlier investigations, although somewhat different potentials were used in that work (Lockwood and Rossky, 1999). First, the volume of the flexible SPC water was calculated to high precision to minimize the error in calculating volumes of aqueous solvated species, and was found to be 18.0 ± 0.0057 ml/mole. The state point considered in all these studies is a pressure of 1.0 atmosphere and a temperature of 298 K.

To assess the effects of electrostatic forces in solvation, aqueous methane was simulated for a variety of models with differing partial charges on the CH4 atoms and for an uncharged model. When there are no partial charges on the hydrogens, the methane-water potential energy interaction becomes equivalent to an united atom description of methane. The partial charges in the first model were fit to the electrostatic potential surface calculated via ab initio electronic structure methods that reproduce the octupole moment of gas phase methane (the resulting charges are −0.52 e− on C and +0.13 e− on H; see Sigfridsson, 1998). With these partial charges, the methane volume is 31.54 ± 0.41 ml/mole; and without them, it is 31.74 ± 0.41 ml/mole. The volume correlation time was found to be tc = 1.6 ps for these systems. The volume of a methane is calculated as the difference between the system volume of the aqueous methane and a neat water system with the same number of H2O molecules as the solvated methane, i.e., the volume of the original aqueous system after the methane is “plucked” out. These uncertainties were obtained from 10.0 ns of dynamics. The slight volume change obtained is not statistically significant; the electrostriction effects associated with the solvated highly symmetric methane, which lacks a permanent dipole and quadrupole moment but has an octupole moment, are expected to be small.

Fig. 4 shows the time evolution of the solvated uncharged methane system volume. Fig. 5 shows the time-dependent error estimates for the uncharged methane model, and the quadrupolar methane error estimate curve is very similar. These volume uncertainties are similar to that obtained in the case of the solvated β-sheet peptide, suggesting that the observed behavior would be similar in other aqueous systems. Fig. 5 also demonstrates that slightly over 100 ns of dynamics would be required to resolve any difference between these methane models. The inset of Fig. 5 demonstrates the Gaussian nature of the system volume fluctuations.

FIGURE 4.

FIGURE 4

Open in a new tab

The curve shows a time trace of the volume fluctuations for the aqueous uncharged methane system. The average system volume value and its uncertainty are also represented in the figure.

FIGURE 5.

FIGURE 5

Open in a new tab

The uncertainty in the uncharged aqueous methane system as a function of the length of the MD simulation is shown. Volume uncertainties for specific times of interest are also identified. The inset displays a histogram of the system volume fluctuations and a superimposed Gaussian function with a standard deviation calculated from the volume fluctuations.

To further test the effects of electrostatic moments on solvation and to assess the associated volume changes, both fictitious monopolar (charged) and dipolar methane was simulated. The dipolar methane consisted of again placing a partial charge of −0.52 e− on C and a +0.52 e− on only one of the hydrogens, whereas the other three were uncharged. These charges result in a permanent dipole of 2.7 Debye, comparable to that of liquid water that has an average dipole of 2.4 Debye for the model used here. The permanent dipolar methane exhibits a molecular volume change from the uncharged methane via electrostriction with net volume decrease of 1.73 ± 1.02 ml/mole compared to the uncharged methane model. The relatively small volume change associated with dipolar solvation is consistent with the lack of volume change observed upon solvation of the octupolar model.

Next, a charge of +e− and −e− was placed on the methane carbon and the hydrogens were left uncharged. In both cases the aqueous-charged models produced dramatic electrostriction effects, and the solvated anion had the largest volume change. The volume change was −40.13 ± 0.48 ml/mole for anionic solvation and −20.96 ± 0.39 ml/mole for cationic solvation. The errors are the result of 10.0 ns and 12.0 ns of dynamics, respectively. Notice that this implies a negative solution volume for the anion. The larger anionic electrostriction effect is due to the nature of its solvation. This result highlights the importance of properly accounting for electrostatic interactions in calculating molecular volumes, and this effect may well be important in volume changes associated with the dynamics of biomolecules.

Fig. 6 shows the radial distribution function between the methane carbon atom and (Fig. 6 A) the water oxygen atoms and (Fig. 6 B) the water hydrogen atoms. The radial distribution functions are presented for both solvated ion systems along with the uncharged methane system. It is clear that the solvated anion permits the water hydrogen to penetrate effectively into the carbon van der Waals sphere, thus maximizing the interaction between the positive partial charge on the hydrogen and the negative ionic charge. The cation is also tightly solvated compared to the neutral, and both ions display a far more structured solvation shell than the neutral. The cation hydrogen first-neighbor peak is in approximately the same location as the neutral but is sharper, indicative of more ordering; the anion second-neighbor peak is shifted slightly inward from the neutral's first peak. Electrostriction effects are essentially screened out by ∼5.5 Å. The radial distribution functions in Fig. 6 are clearly consistent with the observed volume changes and demonstrate the physical mechanism giving rise to electrostriction. Solvating the cation draws the oxygen atoms in more tightly to the methane and causes some solvent ordering, but does not dramatically disrupt the solvent structure. Solvating the anion causes the water to preferentially point a hydrogen in toward the negative charge, creating a new species of coordinated hydrogen atoms appearing between 1.5 and 2.2 Å in Fig. 6 B.

FIGURE 6.

FIGURE 6

FIGURE 6

Open in a new tab

(A) The radial distribution function between the methane carbon atom and the water oxygen atoms is shown. (B) The radial distribution function between the methane carbon atom and the water hydrogen atoms is displayed. The solid line represents the anion, the dashed line is the cation, and the dotted line is the uncharged molecule.

A strength of MD is in providing detailed molecular mechanisms for observed structure and dynamics. Fig. 7 shows a snapshot of both the solvated anion and cation. Fig. 7 A shows the anion solvated such that the water aligns itself with one of the hydrogens effectively penetrating in toward the negative carbon atom whereas the second hydrogen is held at a distance. This is consistent with Fig. 6 B where we see high ordering with the first sharp hydrogen peak representing the hydrogen that effectively penetrates and a second sharp peak representing the second hydrogen being held at a distance from the negative carbon. Fig. 7 B also demonstrates that the water solvates the cation, with the oxygen approaching close to the methane molecule and the hydrogens pushed back; however, the bulkier oxygen cannot penetrate as effectively.

FIGURE 7.

FIGURE 7

FIGURE 7

Open in a new tab

Representative snapshots of solvated methane are shown: (A) the anion; (B) the cation.

The MD models employed here serve to demonstrate the power of the methods presented to assess molar volume changes associated with solvation in the presence of different electrostatic fields. To make the approach more realistic it would be necessary to more carefully simulate a system of interest, including possibly simulating larger systems and including effects such as polarization forces. Nonetheless the observation that anionic solvation leads to larger molar volume changes than cationic solvation is in agreement with experimentally measured trends and the observed volume changes are on the same order of magnitude (van Eldik, 1989).

In summary, we have presented an approach to calculating molar volume changes that is especially useful for comparing with photothermal experimental results. Both the experimental and theoretical methods permit the determination of time-dependent molar volume changes, and the identification of metastable intermediate species with lifetimes lasting tens of nanoseconds. The method is also useful in accounting for the molecularly detailed origin of observed molar volume changes, including dissecting such changes into physically meaningful partial contributions from different potential energy interactions.

Acknowledgments

Brian Space and Preston Moore thank Professor M. L. Klein for continuing encouragement in their collaboration.

The research was supported by National Science Foundation grants (CHE-0312834 to B.S., 9904713 to R.W.L), and the Petroleum Research Foundation to B.S. and the American Heart Association to R.W.L. The authors gratefully acknowledge the University of South Florida Research Oriented Computing Center for a generous allocation of computer time on the University of South Florida Beowulf Cluster.

References

  1. Ahlborn, H., X. Ji, B. Space, and P. B. Moore. 1999. A combined instantaneous normal mode and time correlation function description of the infrared vibrational spectrum of water. J. Chem. Phys. 111:10622–10632. [Google Scholar]
  2. Ahlborn, H., X. Ji, B. Space, and P. B. Moore. 2000. The effect of molecular geometry and detailed balance on the infrared spectroscopy of water (H2O and D2O): a combined time correlation function and instantaneous normal mode analysis. J. Chem. Phys. 112:8083. [Google Scholar]
  3. Allen, M. P., and D. J. Tildesley. 1989. Computer Simulation of Liquids. Clarendon Press, Oxford, UK.
  4. Chen, P., C. Lin, H. Jan, and S. I. Chan. 2001. Effects of turn residues in directing the formation of the β-sheet and in the stability of the β-sheet. Prot. Sci. 10:1794–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Dadarlat, V. M., and C. B. Post. 2001. Insights into protein compressibility from molecular dynamics simulations. J. Chem. Phys. B. 105:715–724. [Google Scholar]
  6. Foygel, K., S. Spector, S. Chatterjee, and P. C. Kahn. 1995. Volume changes of the molten globule transition of horse heart ferricytochrome c: a thermodynamic cycle. Prot. Sci. 4:1426–1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Friedberg, R., and J. E. Cameron. 1970. Test of the Monte Carlo method: fast simulation of a small Ising lattice. J. Chem. Phys. 52:6049–6058. [Google Scholar]
  8. Hansen, K. C., R. S. Rock, R. W. Larsen, and S. I. Chan. 2000. A method for photo-initiating protein folding in a non-denaturing environment. J. Am. Chem. Soc. 122:11567–11568. [Google Scholar]
  9. Hansson, T., C. Oostenbrink, and W. F. van Gunsteren. 2002. Molecular dynamics simulations. Curr. Op. Struct. Biol. 12:190–196. [DOI] [PubMed] [Google Scholar]
  10. Herzberg, G. 1946. Infrared and Raman Spectra of Polyatomic Molecules. D. Van Nostrand Company, Inc., New York, NY.
  11. Imai, T., Y. Harano, A. Kovalenko, and F. Hirata. 2001. Theoretical study for volume changes associated with the helix coil transition of peptides. Biopolymers. 59:512–519. [DOI] [PubMed] [Google Scholar]
  12. Jacucci, G., and A. Rahman. 1984. Comparing the efficiency of metropolis Monte Carlo and molecular dynamics methods for configuration space sampling. Nuovo Cimento. D4:341–356. [Google Scholar]
  13. Larsen, R. W., and T. Langley. 1999. Volume changes associated with CO photolysis from fully reduced bovine heart Cyt·aa3. J. Am. Chem. Soc. 121:4495–4499. [Google Scholar]
  14. Larsen, R. W., J. Osborne, T. Langley, and R. B. Gennis. 1998. Volume changes associated with CO photodissociation from fully reduced cytochrome. J. Am. Chem. Soc. 120:8887–8888. [Google Scholar]
  15. Lockwood, L. M., and P. J. Rossky. 1999. Evaluation of functional group contributions to excess volumetric properties of solvated molecules. J. Phys. Chem. B. 103:1982–1990. [Google Scholar]
  16. Lockwood, L. M., P. J. Rossky, and R. M. Levy. 2000. Functional group contributions to partial molar compressibilities of alcohols in water. J. Phys. Chem. B. 104:4210–4217. [Google Scholar]
  17. Martyna, G. J., M. E. Tuckerman, D. J. Tobias, and M. L. Klein. 1996. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 87:1117. [Google Scholar]
  18. Matubayasi, N., and R. M. Levy. 2000. Thermodynamics of the hydration shell. 2. Excess volume and compressibility of a hydrophobic solute. J. Phys. Chem. B. 104:4210–4217. [Google Scholar]
  19. Moore, P. B., Q. Zhong, T. Husslein, and M. L. Klein. 1998. Simulation of the HIV-1 VPU transmembrane domain as a pentameric bundle. FEBS Lett. 431:143–148. [DOI] [PubMed] [Google Scholar]
  20. Moore, P. B., C. F. Lopez, and M. L. Klein. 2001. Dynamical properties of a dimiristoylphosphatidylcholine fully hydrated bilayer from a multinanosecond molecular dynamics simulation. Biophys. J. 81:2484–2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Moore, P., H. Ahlborn, and B. Space. 2002. A combined time correlation function and instantaneous normal mode investigation of liquid state vibrational spectroscopy. In Liquid Dynamics Experiment, Simulation and Theory. M. D. Fayer., and John T. Fourkas, editors. ACS Symposium Series, New York.
  22. Sigfridsson, E. 1998. A comparison of methods for deriving atomic charges from the electrostatic potential and its moments. J. Comp. Chem. 19:377–395. [Google Scholar]
  23. Tarek, M., K. Tu, M. L. Klein, and D. J. Tobias. 1999. Molecular dynamics simulations of supported phospholipid/alkanethiol bilayers on a gold(111) surface. Biophys. J. 77:964–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Tuckerman, M. E., and G. J. Martyna. 2000. Understanding modern molecular dynamics: techniques and applications. J. Phys. Chem. B. 104:159–178. [Google Scholar]
  25. van Eldik, R. 1989. Activation and reaction volumes in solution II. Chem. Rev. 89:549. [DOI] [PubMed] [Google Scholar]
  26. Zhong, Q., P. B. Moore, and M. L. Klein. 1998. Molecular dynamics study of the LS3 voltage-gated ion channel. FEBS Lett. 427:267–274. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES