Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Nov;85(5):2845–2853. doi: 10.1016/S0006-3495(03)74707-9

Conferring Thermostability to Mesophilic Proteins through Optimized Electrostatic Surfaces

Michael Torrez 1, Michael Schultehenrich 1, Dennis R Livesay 1
PMCID: PMC1303565  PMID: 14581189

Abstract

Recently, there have been several experimental reports of proteins displaying appreciable stability gains through mutation of one or two amino acid residues. Here, we employ a simple theoretical model to quickly screen mutant structures for increased thermostability through optimization of the protein's electrostatic surface. Our results are able to reproduce the experimental observation that elimination of like-charge repulsions and creation of opposite-charge attractions on the protein surface is an efficient method to confer thermostability to a mesophilic protein. Using Poisson-Boltzmann electrostatics, we calculate relative protein stabilities for the exhaustive surface mutagenesis of the cold shock, RNase T1, and CheY proteins. Comparison with 25 experimentally characterized cold shock protein mutants reveals an average correlation of 0.86. The model is also quantitatively accurate when reproducing the experimental D49A and D49H mutant stabilities of RNase T1. This work represents the first comprehensive in silico screening of mutant candidates likely to confer thermostability to mesophilic proteins through optimization of surface electrostatics. Systematic single mutant, followed by double mutant, screening yields a limited number of mutant structures displaying significant stability gains suitable for subsequent experimental characterization.

INTRODUCTION

Several organisms, mainly from archaea, thrive under extreme environmental conditions, e.g. high pressure, high salt concentrations, extremely high and low temperatures, and extreme pH. Enzymes that function optimally in these adverse conditions mediate the metabolic and biological functions of these organisms. There has been a growing interest in understanding the stabilization of proteins from these organisms, especially those from thermophilic bacteria. Thermophilic proteins represent ideal structural targets to advance our theoretical understanding of protein stability and potential high temperature catalysts for a myriad of biotechnology applications. The role of electrostatics in stabilizing thermophilic (Tm = 70–100°C) proteins is exemplified by the observation that increased stability often results from increased numbers of electrostatic interactions (i.e., hydrogen bonds and salt bridges) (Kumar et al., 2000; Xiao and Honig, 1999).

Several efforts have attempted to identify the most efficient method of conferring enhanced thermostability to a mesophilic protein structure. Earlier efforts in this direction have concentrated on repacking of hydrophobic cores, engineering disulfide bridges, adding extra hydrogen bonds or salt bridges, and improving side chain-helix dipole interactions (Bryson et al., 1995; Cordes et al., 1996; Matthews, 1995; Pace, 1995; Perry et al., 1989; Scholtz and Baldwin, 1992; Serrano et al., 1992). All of these methods optimize short-range interactions within the protein structure. This approach is well justified because it is becoming increasingly clear that protein folding is a hierarchical process and thus is mostly driven by local interactions (Baldwin and Rose, 1999a,b). However, recent results reveal that surface properties of the protein also contribute significantly to thermostability. Several recent studies have successfully increased mesophilic (Tm ≈ 40°C) protein stability by mutagenesis of a single solvent-exposed residue, presumably through optimization of the protein's electrostatic surface (Grimsley et al., 1999; Loladze et al., 1999; Loladze and Makhatadze, 2002; Martin et al., 2001; Pedone et al., 2001; Perl et al., 2000; Perl and Schmid, 2001; Spector et al., 2000; Strop and Mayo, 2000). From these experimental results, it is apparent that surface electrostatics are intimately related to protein stability, and, in some instances, mutation of only a few solvent-exposed residues is sufficient for conferring thermostability to mesophilic proteins.

The observed stability gains often fail to reach those predicted by simple Coulombic interactions, and can, at times, lead to the opposite of the predicted effect. For example, the stability of T4 lysozyme is generally decreased, despite a projected increase, by charge changing mutations on the protein surface (Dao-pin et al., 1991). This result is attributed to complex long-range electrostatic interactions. Pace et al. (2000) correctly point out that favorable charge-charge interactions are equally important to determining the denatured state ensemble conformations as the native protein structure. Thus, the observed destabilization in T4 lysozyme might be attributed to decreasing the free energy of the denatured state, versus increasing the free energy of the native state. Put simply, it is possible to stabilize the denatured ensemble more than the native fold, thus destabilizing the protein. Conversely, the stability of a thermophilic cold shock protein has been shown to be partly dependent on electrostatic destabilization of its denatured state (Zhou and Dong, 2003).

Here, we employ a fast and accurate computational model for determining which mutations on the protein surface are likely to lead to increased or decreased structural stability. Our method is based on electrostatic free energy comparisons, calculated from finite difference solutions of Poisson-Boltzmann continuum electrostatic theory (Antosiewicz et al., 1994; Gilson, 1993). To gauge protein stabilities, changes in the denaturation electrostatic free energy (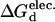Inline graphic) are calculated and compared for each wild-type and mutant protein. The denatured state is represented using the model of Elcock (1999), which provides more realistic local electrostatic environments than fully extended conformations. Although superior to fully extended models, this model is still crude. Several techniques, i.e., hydrogen/deuterium exchange (Houry and Scheraga, 1996; Maier et al., 1999), circular dichroism (Houry et al., 1996; Sehorn et al., 2002), and high-temperature molecular dynamics simulations (Brooks, 2002; Daggett, 2002), clearly indicate that some features of the natively folded protein (e.g., secondary structure) can be present in the denatured ensemble. The Elcock model employed here results in total loss of secondary structure and (nearly) all intramolecular contacts. Despite the apparent shortcomings, the model's credibility is established through reliable reproduction of experimental stability results (Elcock, 1999).

Our comprehensive in silico screening on three unique protein structures identifies surface mutant candidates likely to confer thermostability to mesophilic proteins. We test the validity of our method through comparisons with 25 experimental cold shock protein (CSP) mutants (Perl and Schmid, 2001). Our results parallel the relative experimental stability trends reported. Exhaustive mutant screening of the globular RNase T1 and CheY proteins demonstrates the predictive ability of our approach. Mutant structures displaying appreciable stability gains populate a list of candidates for subsequent experimental characterization. Our results on these three molecular exemplars further the suggestion that optimization of protein surface electrostatics is a robust and efficient mechanism for conferring thermostability to mesophilic proteins. Additionally, as the amount of sequence and structure data continues to increase at overwhelming rates, our method provides a practical approach to quickly identify surface mutants likely to result in appreciable stability gains before experimental characterization.

THEORETICAL METHODS

Protein structures

Protein structures used here are modified versions of the coordinates retrieved from the Protein Databank (PDB). The continuum electrostatics method implemented in the University of Houston Brownian Dynamics (UHBD) suite of programs requires explicit polar hydrogen atoms. Polar hydrogens are added using the Molecular Operating Environment (MOE) software package. (MOE is a commercial implementation of many algorithms used in computational biology (http://www.chemcomp.com/).) Proteins and PDB identification codes for the wild-type protein structures used are: the mesophilic cold shock protein from Bacillus subilis (1CSP) (Schindelin et al., 1993), the thermophilic cold shock protein from Bacillus calodyticus (1C9O) (Mueller et al., 2000), the mesophilic CheY protein from Escherichia coli (3CHY) (Volz and Matsumura, 1991), and the mesophilic RNase T1 from (9RNT) (Martinez-Oyanedel et al., 1991). CheY mutant sites are determined from the pairwise sequence alignment of the thermophilic, from Thermotoga maritima (1TMY) (Usher et al., 1998), and mesophilic sequences. All solvent-exposed positions not conserved in sequence are targeted for mutation.

The 25 cold shock protein mutants studied here are taken from Perl et al. (Perl and Schmid, 2001). Positions implicated as being critically related to the electrostatic surface stability from experimental studies are systematically mutated to the following residues: Ala, Val, Leu, Ile, Phe, Tyr, Ser, Thr, Cys, Asn, Gln, Asp, Glu, Arg, and Lys. In the RNase T1 and CheY protein single-mutant screenings, all targeted residues are mutated to: Ala, Val, Asp, Glu, Asn, Gln, Ser, Thr, Arg, and Lys. In RNase T1, all solvent-exposed residues are selected for single-mutant screening, whereas with CheY mutant positions are identified as discussed above. Especially stabilizing and destabilizing single mutants are selected for double-mutant screening. All of the above mutant structures are generated using the Mutate Residue functionality within MOE, which is an implementation of the method presented in Bower et al. (1997). Mutant side chain conformations are determined from a systematic rotamer search. This method results in acceptable side chain structures based on the local environment, and eliminates the need to further minimize the protein, which is an important consideration in such a comprehensive analysis.

Denatured structures (Fig. 1 B) are generated using the molecular mechanics protocol of Elcock (1999). The method is based on the premise that the denatured state is similar to the native structure (Gillespie and Shortle, 1997), and thus can be generated from the native structure. The method works by systematically increasing (up to 6 Å in 1-Å increments) the location of the energy minima within the Lennard-Jones portion of the CHARMM (Brooks et al., 1983) force field. The resulting “exploded” structure lacks any realistic contacts that would still be present in the denatured ensemble. Although seemingly arbitrary, the model is more accurate than fully extended representations because it approximates the average electrostatic profile of the denatured ensemble. As noted by Elcock (1999), using a single structure to represent the exceedingly large denatured ensemble is clearly a considerable approximation. However, the method's rationale is confirmed through favorable comparisons with experimental stability values. All of the above PDB manipulations and computation are designed to be as minimal as possible to enable comprehensive mutant screening.

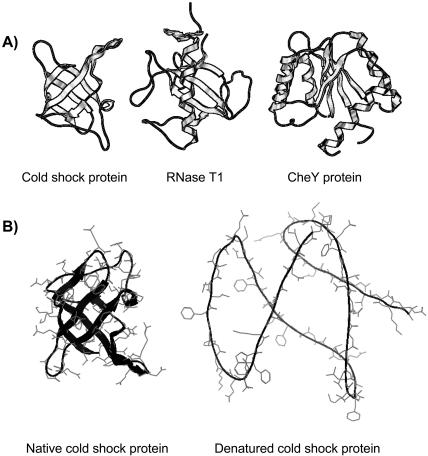
FIGURE 1.

FIGURE 1

Open in a new tab

(A) Structures of the three proteins investigated here: cold shock protein, RNase T1, and CheY protein. (B) Denatured structures are generated using the molecular mechanics protocol reported in Elcock (1999). Although lacking any realistic structural organization of the denatured ensemble, this model does provide an improved representation, versus fully extended conformations, of the local electrostatic environment. Calculated structural stabilities using this model are in line with experimental values, especially when comparing relative mutant stabilities.

Continuum electrostatic calculations

Electrostatic free energies are calculated using the University of Houston Brownian Dynamics suite of programs (Madura et al., 1995). UHBD calculates electrostatic free energies using the single-site titration method described in Gilson (1993) and Antosiewicz et al. (1994). The protonation state of acids and bases is calculated versus pH, allowing calculation of the ideal charge state at a particular pH. All reported energy values correspond to neutral pH, and the appropriate protonation state, as determined by the single-site titration procedure. The linearized Poisson-Boltzmann equation (LPBE) is solved using the Choleski preconditioned conjugate gradient method. The protein is centered on a 65 × 65 × 65 grid with each grid unit equaling 1.5 Å. Using our standard procedure, focusing is used around each titrating site with the grid spacing becoming 1.2, 0.75, and 0.25 Å (Gibas and Subramaniam, 1996; Gibas et al., 1997; Livesay et al., 1999, 2003). We also provide the relative stabilities (Inline graphic) calculated from only the first three focusing levels to provide an estimate of the uncertainty in the calculated values (supplemental data). The values are generally similar, especially for RNase T1 and, to a lesser extent, CSP. However, some variation in the values should be expected as the grid spacing difference between the third and fourth focusing levels is fairly large (0.5 Å). A solvent dielectric constant of 80 and a protein dielectric constant of 20 are used for all stability calculations. Using an interior protein dielectric of 20 has been shown to reproduce experimental pKa results much better than lower values (Antosiewicz et al., 1996; Gibas and Subramaniam, 1996). Protein partial charges are taken from the CHARMM parameter set (Brooks et al., 1983) and radii from the optimized potentials for liquid systems (Jorgensen and Tirado-Rives, 1988). The temperature is 298 K, and the ionic strength equals 0.15 M in all cases, except with cold shock protein, where in keeping with experimental conditions, ionic strengths of 0.0 and 2.0 M are used.

Electrostatic potential maps

Electrostatic potential maps are calculated using the Poisson-Boltzmann equation solver within MOE. MOE only provides the full nonlinear Poisson-Boltzmann equation solver, while all reported electrostatic free energies are calculated using the truncated linearized Poisson-Boltzmann equation. Despite subtle differences, the electrostatic potential maps generated within MOE allow qualitative comparisons between mutants, which compare favorably with quantitative differences between electrostatic free energies calculated by UHBD. The protein is centered on a 65 × 65 × 65 cubic grid. A solvent dielectric constant of 80 and a protein dielectric constant of 4, which are standard values in electrostatic potential map calculations (Sharp and Honig, 1990), are used in all electrostatic potential map calculations. Protein partial charges are taken from the CHARMM parameter set (Brooks et al., 1983). The temperature is 300 K, the counter ion radii equals 1.4 Å, the ionic strength equals 0.15 M, and the protein concentration equals 0.001 M. Electrostatic potentials are rendered in blue and red at ±3.0 kcal/mol/e, respectively.

RESULTS AND DISCUSSION

Cold shock protein

The ability of our model to accurately evaluate surface mutants leading to increased or decreased thermostability is largely determined through comparisons with experimental results on cold shock protein (Martin et al., 2001; Perl et al., 2000; Perl and Schmid, 2001). Perl et al. have experimentally determined the stability of 30 cold shock protein mutants, 24 on the thermophilic CSP from Bacillus caldolyticus and 6 on its mesophilic ortholog from Bacillus subtilis. The sequences of the two proteins vary at only 12 positions, yet only two positions are largely responsible for the observed difference in Gibbs free energy of denaturation (15.8 kJ/mol). These two positions (E3R and E66L, meso to thermo) are far apart in sequence space (total protein length is 75 residues), but are structurally local. Double and triple mutant stabilities reveal that the added stability of the thermophilic protein arises largely from improved hydrophobic packing of Arg's side chain, elimination of charge-charge repulsion, and a general electrostatic stabilization due to the cationic Arg, which is not due to any specific ion pair. All of the factors indicated above can be (at least in part) modeled using continuum methods.

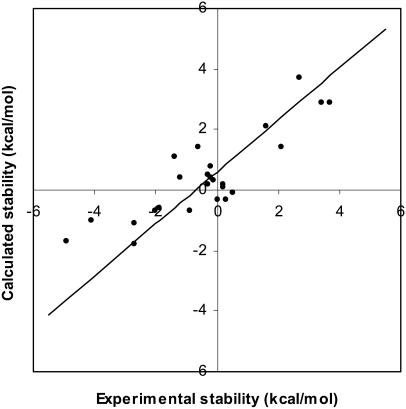
Our calculated results (Table 1) on the mesophilic and thermophilic CSP compare favorably with those of Perl and Schmid (2001). The correlation coefficient between the experimental and calculated ΔΔGd results presented in Table 1 equals 0.86 (Fig. 2). The demonstrated correlation is not absolute, yet it is significant. Actually, Perl and Schmid (2001) report experimental stabilities at ionic strengths of 0.0 and 2.0 M. The results presented above describe the correlation between the zero ionic strength results. There is no demonstrated correlation (correlation coefficient = 0.16) at the higher ionic strength between the experimental and calculated results for the thermophilic Bacillus caldolyticus structure. It has been reported that the direct relationship between Poisson-Boltzmann calculated electrostatic free energies and ionic strength degrades at large ionic strength values (Boschitsch et al., 2002). In addition, continuum models have been used to investigate the origins of thermostability in the CSP family, especially as related to ionic strength (Dominy et al., 2002). These results clearly indicate that thermophilic protein stability decreases with increasing ionic strength. The lack of correlation between calculated and experimental thermophilic mutant stabilities at high ionic strength is related to shielding of the many stabilizing electrostatic interactions on the thermophilic protein's surface, making calculated electrostatic energies less able to approximate overall free energies. All subsequent calculations are performed at physiological (0.15 M) ionic strength, making concerns about the model's performance at high ionic strength moot.

TABLE 1.

Calculated and experimental stability results for cold shock protein mutants

Experimental (kcal/mol) Calculated (kcal/mol)
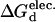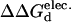ΔGd ΔΔGd Inline graphic Inline graphic
1CSP
 Wild-type −2.7 −0.9
 E3R −0.1 2.7 2.8 3.7
 E3L −1.1 1.6 1.2 2.1
 A46E −3.3 −0.6 0.5 1.4
 E66L −0.6 2.1 0.5 1.4
 E3R/E66L 0.7 3.4 2.0 2.9
 E3R/T64V/E66L 1.0 3.7 2.0 2.9
1C90
 Wild-type 1.1 2.1
 Q2L 1.6 0.5 2.0 −0.1
 R3E −1.7 −2.7 0.3 −1.8
 R3E/E21A −1.6 −2.7 1.0 −1.1
 R3E/E46A −0.9 −2.0 1.4 −0.7
 R3E/L66E −3.9 −4.9 0.4 −1.7
 R3E/E46A/L66E −3.0 −4.1 1.1 −1.0
 R3L 0.1 −0.9 1.4 −0.7
 R3K 0.9 −0.2 2.9 0.8
 R3A −0.9 −1.9 1.5 −0.6
 N11S 1.4 0.3 1.8 −0.3
 Y15F 1.0 0.0 1.8 −0.3
 E21A 0.8 −0.3 2.6 0.5
 G23Q 0.8 3.5 – –*
 G23Q/S24D 1.0 3.7 – –*
 S24D 1.3 0.2 2.2 0.1
 T31S 1.2 0.2 2.3 0.2
 E46A 0.9 −0.2 2.5 0.4
 E46A/L66E −0.3 −1.4 3.2 1.1
 E46A/L66E/67A 0.8 3.5 – –*
 Q53E 1.0 −0.1 2.4 0.3
 V64T 0.8 −0.3 2.3 0.2
 V64T/L66E/67A −0.6 2.1 – –*
 L66E −0.2 −1.2 2.5 0.4
 67A 1.1 3.8 – –*
Open in a new tab

Experimental results taken from Perl and Schmid (2001). Positive ΔΔGd represent a stability increase. The overall correlation between the experimental and calculated ΔΔGd results (columns 3 and 5) is 0.86. Mutants without acceptable rotamer structures are not included in the correlation calculation. Keeping with experimental conditions, the ionic strength used in the above calculations is 0.0 M.

*

All PDB manipulations and computation are designed to be as minimal as possible to enable comprehensive mutant screening. As such, mutants without acceptable rotamer structures or any mutation that results in changes in the backbone structure is excluded.

FIGURE 2.

FIGURE 2

Open in a new tab

Calculated versus experimental cold shock protein mutant stabilities. The correlation between the experimental and calculated ΔΔGd values (presented in Table 1) equals 0.86. The intercept value equals 0.61 and the p-value is 4.5 × 10−4.

Recently, a similar study using Poisson-Boltzmann electrostatic theory to reproduce the experimental results of Perl and Schmid (2001) has been published. Zhou and Dong (2003) are able to reproduce the experimental results with high precision. Using a more sophisticated representation of the protein denatured state, based on a Gaussian chain (Zhou, 2002a), Zhou achieves a correlation of 0.98 with the experimental CSP mutants, compared to our 0.86. A Gaussian chain representation of the protein denatured state allows sampling over all conformations, and thus provides more quantitatively accurate results when the denatured state is predominantly composed of nonspecific electrostatic interactions. The likelihood of interactions decreases with sequence separation in the Gaussian chain model. Thus, the model will fail in denatured states with large numbers of nonlocal charge-charge interactions (Zhou, 2002b). However, it is clear that the unfolding/refolding transition states are “native-like” and possess many of the nonlocal interactions found in the natively folded protein (Daggett, 2002). The Elcock model is based on this observation and is designed to conserve the explicit interactions not local in sequence.

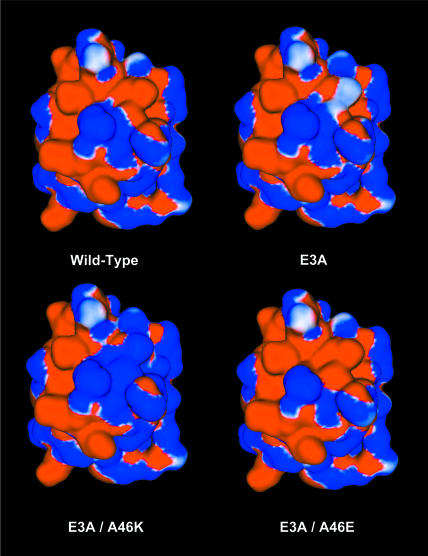
Further mutant screening of the mesophilic CSP at positions Glu3 and Ala46 provides a list of mutants that are likely to be even more resistant to thermal denaturation. The E3R and E3K mutants are the most stabilizing single mutants screened (Table 2). Very few of the mutations at Ala46 are appreciably stabilizing, and several are substantially destabilizing. The E3A/A46X double mutants reveal that, at least in this case, positions with little stability improvements in a single mutant screening can have marked improvement when paired with a second mutation. The E3A/A46K mutant is the second most stabilizing CSP mutation screened here, while the A46K single mutant is the most destabilizing. These results highlight the importance of all pairwise electrostatic interactions toward the total free energy (Fig. 3). The calculated added stability (1.9 kcal/mol) of the E3A mutant largely results from elimination of the destabilizing E3:E66 repulsion (Table 3). Table 3 quantifies the electrostatic interaction between each residue pair. Reported here are the pair energetic differences between the natively folded A3E and A3E/A46E and A3E and A3E/A46K mutant structures. These results quantify the conclusions made from the qualitative visual comparisons of the electrostatic potential maps (Fig. 3). (Note: positive values represent stability decreases, whereas negative values represent stability gains.) The added stability of the E3A/A46K mutant (4.3 kcal/mol) results from the same as above, plus the additional favorable K46:E66 and K46:CT surface ion pairs.

TABLE 2.

Mutant screening of mesophilic cold shock protein

E3X A46X E3A/A46X
Ala 1.9 – –
Val 1.7 −0.2 1.6
Leu 2.5 −0.3 1.7
Ile 1.7 −0.3 1.4
Phe 1.9 1.2 1.5
Tyr 1.5 0.7 1.0
Ser 1.9 0.1 1.9
Thr 1.9 0.1 2.1
Cys 1.8 0.1 1.8
Asn 2.1 −0.3 1.5
Gln 2.5 −0.3 1.2
Asp 1.8 0.1 1.8
Glu – −0.8 −0.2
Arg 4.0 0.5 3.0
Lys 4.9 −1.8 4.3
Open in a new tab

Reported values (kcal/mol) are calculated 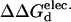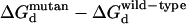Inline graphic (Inline graphic). Positive values indicate a stability increase, whereas negative values indicate a stability decrease.

FIGURE 3.

FIGURE 3

Open in a new tab

Insights into the relative mutant stabilities can be explained by scrutinizing electrostatic potentials. The E3A mutant is stabilized (versus the wild-type) through elimination of the destabilizing E3:E66 charge repulsion. The E3A/A46E mutant is destabilized, largely due to the E46:E66 and E46:CT repulsions. The E3A/A46K mutant is one of the most stable CSP mutants investigated here. The stability gained from the E3A mutation is complemented by favorable K46:E66 and K46:CT ion pairs on the protein surface. Electrostatic potentials are rendered in blue and red at ±3.0 kcal/mol/e, respectively. The above results are quantified using UHBD calculated electrostatic energies (Table 3).

TABLE 3.

Cold shock protein electrostatic energy interaction differences

A3E − A3E/A46E A3E − A3E/A46K
Glu46 to X Lys46 to X
NT −0.1 0.2
Lys5 −0.8 0.4
Lys7 −0.1 0.0
Glu12 0.0 0.0
Lys13 0.0 0.0
Glu19 0.3 −0.1
Asp24 0.0 0.0
Asp35 0.1 −0.1
His29 0.0 0.0
Lys39 0.0 0.0
Glu42 0.1 −0.1
Glu43 0.1 −0.1
Glu50 0.1 −0.1
Glu53 0.0 0.0
Arg56 0.0 0.0
Lys65 −0.1 0.1
Glu66 1.1 −3.7
CT 0.8 −0.8
SUM +1.5 −4.3
Open in a new tab

Individual electrostatic interaction energies assess the quantitative contribution of each amino acid pair to the overall electrostatic potential map. Reported here are the pair energetic differences between the natively folded A3E and A3E/A46E and A3E and A3E/A46K mutant structures. These results confirm the conclusions described above concerning the stability changes in the A3E/A46E and A3E/A46E mutants. All other differences are equal to zero. Positive values represent stability decreases, whereas negative values represent stability gains.

RNase T1

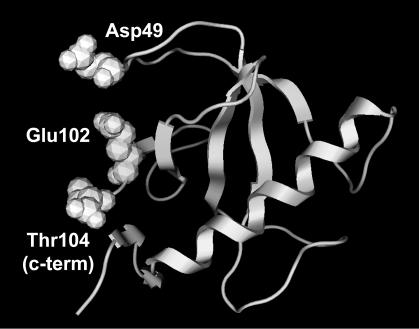
RNase T1 is moderately larger than CSP (104 vs. 76 residues). The globular RNase T1 structure is composed of a single helix packed against an antiparallel sheet (Martinez-Oyanedel et al., 1991). Grimsley et al. (1999) report that mutation of the completely solvent-exposed Asp49, which lacks any specific Coulombic interactions, to Ala results in a stability gain of 0.5 kcal/mol. The experimental stability gain is attributed to lessening the heavy anionic concentration on the wild-type protein surface. The experimental stability of the D49H mutant is 1.1 kcal/mol greater than the wild-type protein, which is due to the generation of nonspecific opposite-charge attractions on the protein surface. However, a simple Coulombic model for estimating the stability gains for the D49H mutation overestimates the observed stability by 1.9 kcal/mol (Grimsley et al., 1999).

We systematically mutate every solvent-exposed residue as described above, which includes D49, resulting in 251 screened single-mutant structures. As an additional test of our model, we compare the calculated D49A and D49H results to reported experimental values. Due to time constraints, normally His residues are not included in our screening procedure. However, because of the available experimental results, the D49H mutation is added to the 251 above. Based on the similarity between the calculated pKa (7.2) and pH investigated, the solvent exposed His49 is protonated only marginally more than deprotonated; the UHBD calculated charge on the residue is 0.589e. We are surprised to report that not only does our model qualitatively reproduce the relative experimental values, but it also generates quantitatively similar values (0.6 and 1.1 kcal/mol, respectively). We hesitate from making drastic claims concerning the quantitative similarity of these results. Due to the inherent approximations within our model, it is possible that the quantitative similarity is fortuitous. On the other hand, the fact that relative trends between mutants are once again consistent further supports the model's legitimacy.

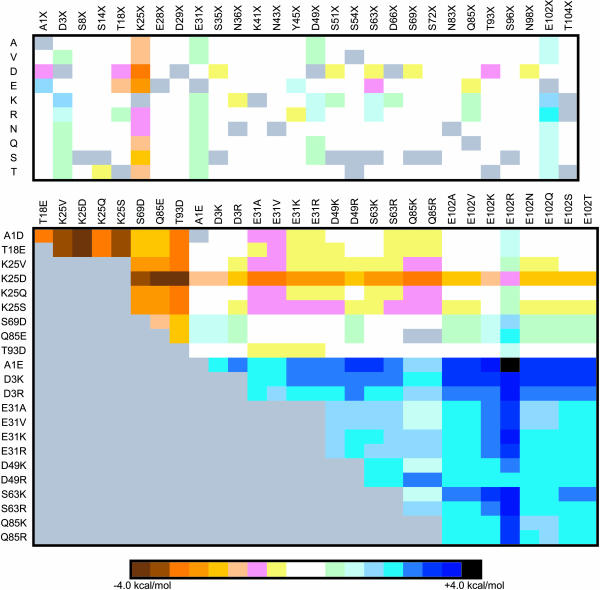
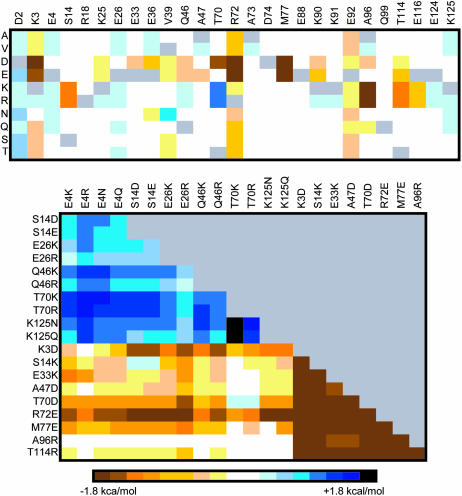
Of the 251 screened single-mutant structures, 17 mutants display appreciable (>0.75 kcal/mol) stability gains (Fig. 4). Most of these mutations are to an Arg or Lys residue, which is consistent with the experimental anionic charge density conclusions discussed above. Similarly, mutation of Glu102 to any residue (other than Asp) results in significant stability gains (>1.3 kcal/mol). In fact, the two most stabilizing mutations (E102KorR) both result in stability gains >2.0 kcal/mol. From the single-mutant results, 21 stabilizing and 9 destabilizing mutants are chosen for double-mutant screening. Unlike CSP, double mutants are almost always the sum of the two constituent single mutants, unless they are structurally local. The most stabilizing double mutant (A1E/E102R) displays a stability gain equal to 4.5 kcal/mol (a 67% change), which is exactly equal to the sum of the stability gains from the two corresponding single mutants. The A1E/E102K mutant is only marginally less stable than its Arg equivalent. The next most stable “set” of double mutants is D3KorR/E102KorR. Stabilizing single and double mutants nearly always results in decreases within the anionic charge density on the protein's surface, or formation of positive charges interspersed within the anionic distribution, or both (Fig. 5).

FIGURE 4.

FIGURE 4

Open in a new tab

Mutant stability screening matrix of RNase T1 single and double mutants. Each solvent-exposed position is systematically mutated to ten different amino acid identities. The list of double mutants screened is generated from 21 potentially stabilizing and 8 destabilizing single-mutant structures. In each cell, the color hue represents the 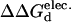Inline graphic (kcal/mol). Inline graphic values between ±0.5 kcal/mol are colored white, each subsequent darker color represents 0.5-kcal/mol increments. Positive values indicate a stability increase; negative values indicate a stability decrease.

FIGURE 5.

FIGURE 5

Open in a new tab

RNase T1 stability largely results from decreasing the anionic charge density on the protein's surface. Asp49, Glu102, and the C terminus constitute a destabilizing anionic triad. Mutations at positions 49 and 102 result in some of the most stabilizing mutant structures screened.

Structurally similar single-mutant pairs are constructed, inasmuch as possible, to corroborate the effect of electrostatic interactions. Nearly all chemically similar mutant pairs (i.e., Arg/Lys, Asp/Glu, Ser/Thr, etc.) have similar stability changes. Thus, it is puzzling that the A1E single mutant is stabilizing, whereas the A1D mutant is destabilizing. This is the most striking instance where such contradictory results are observed. Careful analysis of the mutant structures reveals the origin of the apparently contradictory results. No significant differences are observed in the A1D and A1E denatured structures. However, the added methylene group of Glu provides enough conformational flexibility that the rotamer search predicts that the side chain carboxylate forms an ionic interaction with the N-terminal group. The shorter Asp side chain is unable to form such an interaction, leading to the stability difference. Similar arguments resolve the apparent discrepancies with the CheY (see next section) E31D, E33D, A47DvsE, T70DvsE, E92D, and A96DvsE mutants.

CheY protein

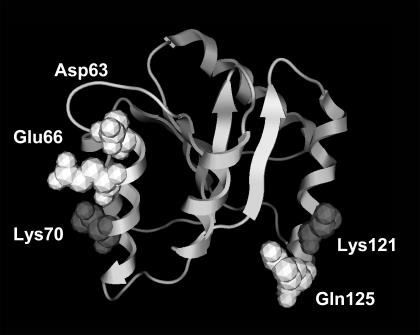
CheY, a response regulator (Matsumura et al., 1984) from the bacterial chemotaxis pathway, is the third protein investigated here. There are no experimental surface mutants for CheY (that we are aware of) leading to thermostability. However, the protein is well suited to our model (intermediate size and globular) and has high-quality structures for both mesophilic (Bacillus subtilis) (Volz and Matsumura, 1991) and thermophilic (Thermotoga maritima) (Usher et al., 1998) organisms. Twenty-seven solvent-exposed positions vary between the mesophilic and thermophilic proteins. Each of these positions is systematically mutated as described above, resulting in 244 single-mutant structures. Of those, 14 potentially stabilizing and 9 destabilizing mutants are selected for double mutant screening, resulting in 238 more mutant structures (Fig. 6) screened for increased stability. The T70K and T70R single mutants display the largest stability gains (1.4 kcal/mol for both), whereas the K3DorE, R72DorE, M77DorE, and A96KorR mutations are the most destabilizing. As expected, the most stabilizing double mutants also incorporate the T70KorR mutations. The T70KorR/K125NorQ double mutants display the largest stability gains (ranges from 1.6 to 2.0 kcal/mol), which is approximately the sum of the two corresponding single mutants. (Note: CheY stabilization of 2.0 kcal/mol represents a 72% change.) The stability gains largely result from formations of stabilizing or elimination of destabilizing surface interactions. For example, the T70KorR mutations result in the generation of favorable ion pairs between the new basic residue and a pair of acid residues (Asp63 and Glu66), whereas the stability gains from the K125NorQ mutants is mostly a result of eliminating unfavorable charge repulsion between the Lys125 and Lys121 (Fig. 7). As expected, analysis of nearly all single mutants in the RNase T1 and CheY systems reveal this to be a consistent theme. Like the RNase T1, CheY double-mutant stability changes are nearly always the approximate sum of the corresponding single mutants. Additionally, when deviations do occur, it is when the two mutant positions are local in structure space.

FIGURE 6.

FIGURE 6

Open in a new tab

Mutant stability screening matrix of CheY single and double mutants. Each solvent-exposed position varying between the mesophilic and thermophilic CheY sequences are systematically mutated to ten different amino acid identities. The list of double mutants screened is generated from 14 potentially stabilizing and 9 destabilizing single mutant structures. In each cell, the color hue represents the 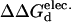Inline graphic (kcal/mol). 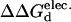Inline graphic values between +0.3 and −0.3 kcal/mol are colored white, each subsequent darker color represents 0.3-kcal/mol increments. Positive values indicate a stability increase, negative values indicate a stability decrease.

FIGURE 7.

FIGURE 7

Open in a new tab

The T70K/K125Q mutant is the most stabilizing (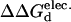Inline graphic =2.0 kcal/mol). Stability gains result from local interactions, and are generally additive. The T70K mutation results in the formation of the favorable ionic pairs between Lys70 and Glu66 and Asp63. Whereas the K125Q mutation results in the elimination of unfavorable charge repulsion between Lys121 and Lys125 (Gln125 is shown).

CONCLUSIONS

We employ a fast and accurate electrostatic model for evaluating protein structures with increased or decreased stabilities based on surface charge-charge interactions. This work represents the first comprehensive in silico screening of mutant candidates likely to confer thermostability to mesophilic proteins through optimization of the surface electrostatics. Protein stabilities are calculated using Poisson-Boltzmann continuum electrostatic theory, which is able to reproduce experimental relative mutant stabilities and, in some cases, is quantitatively accurate. In the case of CSP, single-mutant results cannot be used to predict double-mutant trends. This is largely due to the protein's small structure making nearly all possible double mutants structurally local, and possibly due to complicated electrostatic interactions occurring within the unfolded protein. On the other hand, for the larger RNase T1 and CheY proteins, double-mutant results reveal most single-mutant stabilities to be additive. Systematic single-, followed by double-mutant, screening yields very stable mutants, which are good candidates for further experimental screening. In the latter examples, generally the most stabilizing mutants are those with the consequence of charge reversal. Our results on the three unique molecular examples presented here advance the suggestion that optimization of the protein's electrostatic surface is an efficient and robust mechanism to confer thermostability to mesophilic proteins.

Supplementary Material

[Supplemental Material]
biophysj_85_5_2845__index.html (830B, html)

Acknowledgments

We thank Dr. Shankar Subramaniam for his helpful discussions pertaining to this work and Dr. Patrick Mobley for carefully reading early versions of this manuscript and providing key suggestions.

This work was supported by an National Institutes of Health Score grant (S06 GM53933), an American Chemical Society, Petroleum Research Fund Type G grant (36848-GB4), and a supercomputer allocation from the National Center for Supercomputing Applications to DRL.

References

  1. Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1994. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 238:415–436. [DOI] [PubMed] [Google Scholar]
  2. Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1996. The determinants of pKas in proteins. Biochemistry. 35:7819–7833. [DOI] [PubMed] [Google Scholar]
  3. Baldwin, R. L., and G. D. Rose. 1999a. Is protein folding hierarchic? I. Local structure and peptide folding. Trends Biochem. Sci. 24:26–33. [DOI] [PubMed] [Google Scholar]
  4. Baldwin, R. L., and G. D. Rose. 1999b. Is protein folding hierarchic? II. Folding intermediates and transition states. Trends Biochem. Sci. 24:77–83. [DOI] [PubMed] [Google Scholar]
  5. Boschitsch, A. H., M. O. Fenley, and H.-X. Zhou. 2002. Fast boundary element method for the linear Poisson-Boltzmann equation. J. Phys. Chem. B. 106:2741–2754. [Google Scholar]
  6. Bower, M. J., F. E. Cohen, and R. L. Dunbrack, Jr. 1997. Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: a new homology modeling tool. J. Mol. Biol. 267:1268–1282. [DOI] [PubMed] [Google Scholar]
  7. Brooks, B. R., R. E. Ruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM, A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
  8. Brooks, III, C. L. 2002. Protein and peptide folding explored with molecular simulations. Acc. Chem. Res. 35:447–454. [DOI] [PubMed] [Google Scholar]
  9. Bryson, J. W., S. F. Betz, H. S. Lu, D. J. Suich, H. X. Zhou, K. T. O'Neil, and W. F. DeGrado. 1995. Protein design: a hierarchic approach. Science. 270:935–941. [DOI] [PubMed] [Google Scholar]
  10. Cordes, M. H., A. R. Davidson, and R. T. Sauer. 1996. Sequence space, folding and protein design. Curr. Opin. Struct. Biol. 6:3–10. [DOI] [PubMed] [Google Scholar]
  11. Daggett, V. 2002. Molecular dynamics simulations of the protein unfolding/folding reaction. Acc. Chem. Res. 35:422–429. [DOI] [PubMed] [Google Scholar]
  12. Dao-pin, S., D. E. Anderson, W. A. Baase, F. W. Dahlquist, and B. W. Matthews. 1991. Structural and thermodynamic consequences of burying a charged residue within the hydrophobic core of T4 lysozyme. Biochemistry. 30:11521–11529. [DOI] [PubMed] [Google Scholar]
  13. Dominy, B. N., D. Perl, F. X. Schmid, and C. L. Brooks, III. 2002. The effects of ionic strength on protein stability: the cold shock protein family. J. Mol. Biol. 319:541–554. [DOI] [PubMed] [Google Scholar]
  14. Elcock, A. H. 1999. Realistic modeling of the denatured states of proteins allows accurate calculations of the pH dependence of protein stability. J. Mol. Biol. 294:1051–1062. [DOI] [PubMed] [Google Scholar]
  15. Gibas, C. J., and S. Subramaniam. 1996. Explicit solvent models in protein pKa calculations. Biophys. J. 71:138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gibas, C. J., S. Subramaniam, J. A. McCammon, B. C. Braden, and R. J. Poljak. 1997. pH dependence of antibody/lysozyme complexation. Biochemistry. 36:15599–15614. [DOI] [PubMed] [Google Scholar]
  17. Gillespie, J. R., and D. Shortle. 1997. Characterization of long-range structure in the denatured state of staphylococcal nuclease. II. Distance restraints from paramagnetic relaxation and calculation of an ensemble of structures. J. Mol. Biol. 268:170–184. [DOI] [PubMed] [Google Scholar]
  18. Gilson, M. K. 1993. Multiple-site titration and molecular modeling: two rapid methods for computing energies and forces for ionizable groups in proteins. Proteins. 15:266–282. [DOI] [PubMed] [Google Scholar]
  19. Grimsley, G. R., K. L. Shaw, L. R. Fee, R. W. Alston, B. M. Huyghues-Despointes, R. L. Thurlkill, J. M. Scholtz, and C. N. Pace. 1999. Increasing protein stability by altering long-range coulombic interactions. Protein Sci. 8:1843–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Houry, W. A., D. M. Rothwarf, and H. A. Scheraga. 1996. Circular dichroism evidence for the presence of burst-phase intermediates on the conformational folding pathway of ribonuclease A. Biochemistry. 35:10125–10133. [DOI] [PubMed] [Google Scholar]
  21. Houry, W. A., and H. A. Scheraga. 1996. Structure of a hydrophobically collapsed intermediate on the conformational folding pathway of ribonuclease A probed by hydrogen-deuterium exchange. Biochemistry. 35:11734–11746. [DOI] [PubMed] [Google Scholar]
  22. Jorgensen, W. L., and J. Tirado-Rives. 1988. The OPLS potential function for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 110:1657–1666. [DOI] [PubMed] [Google Scholar]
  23. Kumar, S., C. J. Tsai, and R. Nussinov. 2000. Factors enhancing protein thermostability. Protein Eng. 13:179–191. [DOI] [PubMed] [Google Scholar]
  24. Livesay, D., S. Linthicum, and S. Subramaniam. 1999. pH dependence of antibody: hapten association. Mol. Immunol. 36:397–410. [DOI] [PubMed] [Google Scholar]
  25. Livesay, D. R., P. Jambeck, A. Rojnuckarin, and S. Subramaniam. 2003. Conservation of electrostatic properties within enzyme families and superfamilies. Biochemistry. 42:3464–3473. [DOI] [PubMed] [Google Scholar]
  26. Loladze, V. V., B. Ibarra-Molero, J. M. Sanchez-Ruiz, and G. I. Makhatadze. 1999. Engineering a thermostable protein via optimization of charge-charge interactions on the protein surface. Biochemistry. 38:16419–16423. [DOI] [PubMed] [Google Scholar]
  27. Loladze, V. V., and G. I. Makhatadze. 2002. Removal of surface charge-charge interactions from ubiquitin leaves the protein folded and very stable. Protein Sci. 11:174–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Madura, J. D., J. M. Briggs, R. C. Wade, M. E. Davis, B. A. Lutty, A. Ilin, J. Antosiewicz, M. K. Gilson, B. Gagheri, L. R. Scott, and J. A. McCammon. 1995. Electrostatics and diffusion of molecules in solution, simulations with the University of Houston Brownian dynamics program. Comput. Phys. Comm. 91:57–95. [Google Scholar]
  29. Maier, C. S., M. I. Schimerlik, and M. L. Deinzer. 1999. Thermal denaturation of Escherichia coli thioredoxin studied by hydrogen/deuterium exchange and electrospray ionization mass spectrometry: monitoring a two-state protein unfolding transition. Biochemistry. 38:1136–1143. [DOI] [PubMed] [Google Scholar]
  30. Martin, A., V. Sieber, and F. X. Schmid. 2001. In-vitro selection of highly stabilized protein variants with optimized surface. J. Mol. Biol. 309:717–726. [DOI] [PubMed] [Google Scholar]
  31. Martinez-Oyanedel, J., H. W. Choe, U. Heinemann, and W. Saenger. 1991. Ribonuclease T1 with free recognition and catalytic site: crystal structure analysis at 1.5 Å resolution. J. Mol. Biol. 222:335–352. [DOI] [PubMed] [Google Scholar]
  32. Matsumura, P., J. J. Rydel, R. Linzmeier, and D. Vacante. 1984. Overexpression and sequence of the Escherichia coli cheY gene and biochemical activities of the CheY protein. J. Bacteriol. 160:36–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Matthews, B. W. 1995. Studies on protein stability with T4 lysozyme. Adv. Protein Chem. 46:249–278. [DOI] [PubMed] [Google Scholar]
  34. Mueller, U., D. Perl, F. X. Schmid, and U. Heinemann. 2000. Thermal stability and atomic-resolution crystal structure of the Bacillus caldolyticus cold shock protein. J. Mol. Biol. 297:975–988. [DOI] [PubMed] [Google Scholar]
  35. Pace, C. N. 1995. Evaluating contribution of hydrogen bonding and hydrophobic bonding to protein folding. Methods Enzymol. 259:538–554. [DOI] [PubMed] [Google Scholar]
  36. Pace, C. N., R. W. Alston, and K. L. Shaw. 2000. Charge-charge interactions influence the denatured state ensemble and contribute to protein stability. Protein Sci. 9:1395–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Pedone, E., M. Saviano, M. Rossi, and S. Bartolucci. 2001. A single point mutation (Glu85Arg) increases the stability of the thioredoxin from Escherichia coli. Protein Eng. 14:255–260. [DOI] [PubMed] [Google Scholar]
  38. Perl, D., U. Mueller, U. Heinemann, and F. X. Schmid. 2000. Two exposed amino acid residues confer thermostability on a cold shock protein. Nat. Struct. Biol. 7:380–383. [DOI] [PubMed] [Google Scholar]
  39. Perl, D., and F. X. Schmid. 2001. Electrostatic stabilization of a thermophilic cold shock protein. J. Mol. Biol. 313:343–357. [DOI] [PubMed] [Google Scholar]
  40. Perry, K. M., J. J. Onuffer, M. S. Gittelman, L. Barmat, and C. R. Matthews. 1989. Long-range electrostatic interactions can influence the folding, stability, and cooperativity of dihydrofolate reductase. Biochemistry. 28:7961–7968. [DOI] [PubMed] [Google Scholar]
  41. Schindelin, H., M. A. Marahiel, and U. Heinemann. 1993. Universal nucleic acid-binding domain revealed by crystal structure of the B. subtilis major cold-shock protein. Nature. 364:164–168. [DOI] [PubMed] [Google Scholar]
  42. Scholtz, J. M., and R. L. Baldwin. 1992. The mechanism of alpha-helix formation by peptides. Annu. Rev. Biophys. Biomol. Struct. 21:95–118. [DOI] [PubMed] [Google Scholar]
  43. Sehorn, M. G., S. V. Slepenkov, and S. N. Witt. 2002. Characterization of two partially unfolded intermediates of the molecular chaperone DnaK at low pH. Biochemistry. 41:8499–8507. [DOI] [PubMed] [Google Scholar]
  44. Serrano, L., J. T. Kellis, Jr., P. Cann, A. Matouschek, and A. R. Fersht. 1992. The folding of an enzyme. II. Substructure of barnase and the contribution of different interactions to protein stability. J. Mol. Biol. 224:783–804. [DOI] [PubMed] [Google Scholar]
  45. Sharp, K. A., and B. Honig. 1990. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19:301–332. [DOI] [PubMed] [Google Scholar]
  46. Spector, S., M. Wang, S. A. Carp, J. Robblee, Z. S. Hendsch, R. Fairman, B. Tidor, and D. P. Raleigh. 2000. Rational modification of protein stability by the mutation of charged surface residues. Biochemistry. 39:872–879. [DOI] [PubMed] [Google Scholar]
  47. Strop, P., and S. L. Mayo. 2000. Contribution of surface salt bridges to protein stability. Biochemistry. 39:1251–1255. [DOI] [PubMed] [Google Scholar]
  48. Usher, K. C., A. F. de la Cruz, F. W. Dahlquist, R. V. Swanson, M. I. Simon, and S. J. Remington. 1998. Crystal structures of CheY from Thermotoga maritima do not support conventional explanations for the structural basis of enhanced thermostability. Protein Sci. 7:403–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Volz, K., and P. Matsumura. 1991. Crystal structure of Escherichia coli CheY refined at 1.7-Å resolution. J. Biol. Chem. 266:15511–15519. [DOI] [PubMed] [Google Scholar]
  50. Xiao, L., and B. Honig. 1999. Electrostatic contributions to the stability of hyperthermophilic proteins. J. Mol. Biol. 289:1435–1444. [DOI] [PubMed] [Google Scholar]
  51. Zhou, H. X. 2002a. A Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. Proc. Natl. Acad. Sci. USA. 99:3569–3574. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhou, H. X. 2002b. Residual electrostatic effects in the unfolded state of the N-terminal domain of L9 can be attributed to nonspecific nonlocal charge-charge interactions. Biochemistry. 41:6533–6538. [DOI] [PubMed] [Google Scholar]
  53. Zhou, H. X., and F. Dong. 2003. Electrostatic contributions to the stability of a thermophilic cold shock protein. Biophys. J. 84:2216–2222. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental Material]
biophysj_85_5_2845__index.html (830B, html)
biophysj_85_5_2845__Supplemental_Information.xls (97.5KB, xls)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES