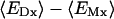An Implicit Membrane Generalized Born Theory for the Study of Structure, Stability, and Interactions of Membrane Proteins

Abstract

Exploiting recent developments in generalized Born (GB) electrostatics theory, we have reformulated the calculation of the self-electrostatic solvation energy to account for the influence of biological membranes. Consistent with continuum Poisson-Boltzmann (PB) electrostatics, the membrane is approximated as an solvent-inaccessible infinite planar low-dielectric slab. The present membrane GB model closely reproduces the PB electrostatic solvation energy profile across the membrane. The nonpolar contribution to the solvation energy is taken to be proportional to the solvent-exposed surface area (SA) with a phenomenological surface tension coefficient. The proposed membrane GB/SA model requires minor modifications of the pre-existing GB model and appears to be quite efficient. By combining this implicit model for the solvent/bilayer environment with advanced computational sampling methods, like replica-exchange molecular dynamics, we are able to fold and assemble helical membrane peptides. We examine the reliability of this model and approach by applications to three membrane peptides: melittin from bee venom, the transmembrane domain of the M2 protein from Influenza A (M2-TMP), and the transmembrane domain of glycophorin A (GpA). In the context of these proteins, we explore the role of biological membranes (represented as a low-dielectric medium) in affecting the conformational changes in melittin, the tilt of transmembrane peptides with respect to the membrane normal (M2-TMP), helix-to-helix interactions in membranes (GpA), and the prediction of the configuration of transmembrane helical bundles (GpA). The present method is found to perform well in each of these cases and is anticipated to be useful in the study of folding and assembly of membrane proteins as well as in structure refinement and modeling of membrane proteins where a limited number of experimental observables are available.

INTRODUCTION

Membrane protein folding and stability are directly governed by the unique hydrophilic and hydrophobic environment provided by biological membranes (Popot and Engelman, 2000). Modeling of this heterogeneous environment has been both an obstacle and an essential requisite to experimental and computational studies on the structure and function of membrane proteins (von Heijine, 1999). For example, detergents have been introduced into crystallization mixes in x-ray crystallography to model the hydrophobic region of membranes for the determination of the structure of relatively large membrane proteins (Cowan et al., 1992; Doyle et al., 1998; Toyoshima et al., 2000; Jiang et al., 2002). Structural studies of membrane proteins by solid-state or solution nuclear magnetic resonance (NMR) techniques have also utilized membrane mimics. Lipid bilayers, as used in the former approach, are probably the best representation of biological membranes (Wang et al., 2001; Smith et al., 2001). Depending on experimental difficulties and limitations, however, the environment provided by the biological membrane is often mimicked in solution NMR studies with a mixture of organic solvents (Rastogi and Girvin, 1999; Lamberth et al., 2000) or detergent micelles (Almeida and Opella, 1997; MacKenzie et al., 1997).

Similarly, membrane/protein complex systems have been modeled in computational studies using explicit lipid bilayers (Petrache et al., 2000; Roux, 2002; Im and Roux, 2002b; Murray and Honig, 2002; Fischer and Sansom, 2002) or implicit membranes (Roux et al., 2000; Im and Roux, 2002a; Spassov et al., 2002). The best representation of a biological membrane in computational studies may depend upon the specific questions to be addressed, and the limitations of available computational resources. Arguably, molecular simulations, in which all solvent/lipid molecules are treated explicitly, yield the most detailed approach to molecular modeling, protein folding, and dynamics of integral membrane proteins (Brooks III et al., 1988; Roux, 2002). However, mainly due to the increasing time requirements as the system size increases, considerable effort has been expended to develop implicit solvent models which treat the average influence of solvent, membranes, or both on a solute in an approximate manner (Gabdoulline and Wade, 1996; Roux and Simonson, 1999; Lazaridis and Karplus, 1999, 2000; Roux et al., 2000; Hassan et al., 2000). In general, continuum electrostatics can be used to define the electrostatic potential and the electrostatic solvation energy of a solute with arbitrary shape by solving the Poisson-Boltzmann (PB) equation using finite-difference methods (Warwicker and Watson, 1982; Klapper et al., 1986; Nicholls and Honig, 1991). In this context, the environment of biological membranes has been successfully modeled by either explicit lipid molecules (Murray and Honig, 2002) or as a continuum low-dielectric slab (Roux et al., 2000). In both situations, the computational cost of solving the PB equation is still a bottleneck to the application of PB theory to protein folding and dynamics of biomolecules, particularly with membranes (David et al., 2000; Luo et al., 2002).

Alternatively, inspired by the Born equation for solvation energies of ions (Born, 1920), the generalized Born (GB) model has been used quite successfully to estimate the electrostatic solvation energy, ΔG_elec, for molecules in aqueous solution (Still et al., 1990; Qiu et al., 1997; Scarsi et al., 1997; Ghosh et al., 1998; Dominy and Brooks III, 1999; Onufriev et al., 2000; Lee et al., 2002; Im et al., 2003). The most reliable GB formula was first proposed by Still et al. (1990),

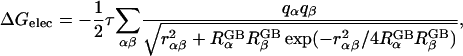(1)

where 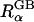is the “effective Born radius” of atom α and τ = 1/ɛ_p − 1/ɛ_s; ɛ_p is the dielectric constant in the interior of the solute and is normally taken as values between 1 and 20, and ɛ_s describes the high dielectric solvent region. ΔG_elec in Eq. 1 corresponds to the electrostatic free energy of transferring a solute in a medium of dielectric ɛ_p to a medium of dielectric ɛ_s. The dielectric constant ɛ_p is often set to one to be consistent with the molecular mechanics force field. The “exact” effective Born radii can be calculated by performing PB calculations for one atom at a time while setting all other charges to zero, and then by inserting the calculated self- (or atomic) electrostatic solvation energy into the Born equation. This process provides a physical interpretation of the inverse of the Born self-energy as the distance between a particular atom and an “effective” spherical dielectric boundary. Substitution of these radii into Eq. 1 thus provides an “exact” expression for the electrostatic self-energy (α = β), and the key assumption in the GB model is that the solvent-shielded charge-to-charge interactions in PB can be reproduced by the cross terms in Eq. 1, with the same effective Born radii. Indeed, Eq. 1 has been shown to excellently reproduce the corresponding PB ΔG_elec, provided that the effective Born radii are accurate (Lee et al., 2002, 2003; Onufriev et al., 2002; Im et al., 2003). Thus, improvements and extensions of the GB theory have focused on the efficient and accurate evaluation of the Born radii, based on numerical surface/volume integration methods (Still et al., 1990; Scarsi et al., 1997; Ghosh et al., 1998; Lee et al., 2002, 2003; Im et al., 2003), which are more rigorous than conventional pairwise summation approximations (Hawkins et al., 1996; Qiu et al., 1997; Dominy and Brooks III, 1999).

In the present study, we are interested in the extension of the GB theory to include a heterogeneous dielectric environment representation of biological membranes. For the sake of simplicity and computational efficiency, we describe the influence of the biological membrane by a solvent-inaccessible low-dielectric slab, and not by explicit lipid molecules. In this context, one must reformulate the calculation of the self-electrostatic solvation energy in GB, i.e., the effective Born radius, to include the influence of this low-dielectric slab. For example, electrostatic solvation energies of a monovalent spherical ion of 2 Å radius are −82 kcal/mol in aqueous solution (ɛ_s = 80) and −8 kcal/mol in the center of a 30 Å-thick low-dielectric slab assigned by a dielectric constant of one, which corresponds to effective Born radii of 2 Å and 20.5 Å, respectively. Recently, Spassov et al. (2002) proposed an empirical approach to model the solvent effects in protein-membrane complexes within the context of a pairwise additive GB model. They separated the integral for the self-electrostatic solvation energy into two parts. One yielded the contribution from the membrane, which was approximated by an empirical function, and the other was that from solvent, which was calculated using conventional pairwise summation approximations (Spassov et al., 2002). This solvation model, while reasonable, involved the ad hoc membrane self-energy term and utilized the less accurate pairwise summation approximation for the GB radii.

We propose another route to the calculation of the self-electrostatic solvation energy within GB theory where a low-dielectric planar membrane is to be included. The proposed approach is rigorous within the framework of GB theory and its implementation is straightforward in the context of the numerical volume integration method (Lee et al., 2002; Im et al., 2003). In fact, the present work was motivated through the recognition of the fact that the volume function used in the volume integration method represents the solvent inaccessibility, i.e., it is one in the interior of a solute and zero in the solvent region. Thus, the influence of the low-dielectric slab can be captured by setting the volume function to one inside the solvent-inaccessible planar membrane. In the next section the background and theoretical development are given in detail. Then, tests of the accuracy of our membrane GB theory compared with an equivalent representation of the membrane in PB are presented, and the potential utility of the present model is illustrated by applications to three membrane peptides; melittin from bee venom, the transmembrane domain of the M2 protein from Influenza A (M2-TMP), and the transmembrane domain of glycophorin A (GpA). The article concludes with a brief summary of our main finding.

THEORETICAL DEVELOPMENT

The solvation free energy is generally expressed as the sum of nonpolar (np) and electrostatic (elec) contributions, i.e., ΔG_solv = ΔG_elec + ΔG_np (Roux and Simonson, 1999). The nonpolar solvation energy, ΔG_np, includes the free energy cost of a cavity formation in the solvent as well as the solvent-solute dispersion interactions. This term is often expressed as the product of (solvent-accessible) surface area, S, of the solute and a phenomenological surface tension coefficient γ (Hermann, 1972; Gilson et al., 1993; Simonson and Brunger, 1994),

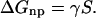(2)

The electrostatic solvation energy, ΔG_elec, is the work required to assemble the charges, {q_α}, of the solute in the solvent. It may be expressed in terms of the reaction field potential φ_rf(r), i.e., 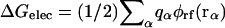(Warwicker and Watson, 1982; Klapper et al., 1986; Sharp and Honig, 1990). Based on continuum electrostatics, in which the solvent is represented as a featureless high dielectric medium, the reaction field potential, φ_rf(r), can be computed by solving the PB equation numerically using finite-difference methods (Warwicker and Watson, 1982; Klapper et al., 1986; Nicholls and Honig, 1991; Im et al., 1998; Luo et al., 2002),

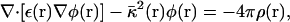(3)

where ε(r), 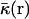, and ρ(r) are the dielectric constant, the modified Debye-Hückel screening factor, and the fixed charge density of the solute, respectively. To model membranes with a low-dielectric slab in the context of PB theory, ɛ(r) is often set to a dielectric constant ɛ_m for the membrane hydrophobic region and finite-difference numerical solutions of Eq. 3 are developed. However, solving the PB equation is computationally too expensive to facilitate long molecular dynamics (MD) simulations of biomolecules, particularly when membranes are present. An alternative and efficient GB theory based on Eq. 1 is developed below to approximate the influence of the solvent/membrane on the solute in the context of continuum electrostatics.

Effective Born radii evaluation with membranes

Since the GB model is intrinsically based on the same underlying continuum approximation as used in PB theory, its accuracy is most naturally assessed by comparison with PB results. The quantitative agreement between ΔG_elec from PB calculations and ΔG_elec from the GB model strongly depends on the effective Born radii 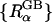in the GB theory (Lee et al., 2002; Onufriev et al., 2002; Im et al., 2003). From the Born equation (Born, 1920), one can extract the exact Born radius 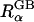of atom α in a solute by calculating its self-electrostatic free energy, ΔG_elec,α, using Eq. 3 by setting all other charges to zero,

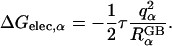(4)

Thus, ΔG_elec,α or 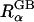calculated by solving Eq. 3 can serve as a benchmark to assess the quality of the effective Born radii calculated by various approximations in GB.

In continuum electrostatics, the self-electrostatic solvation energy can be expressed rigorously in terms of an integral of a space-dependent electrostatic field density (Scarsi et al., 1997; Ghosh et al., 1998). Most GB models have approximated the electrostatic field as the Coulomb field, neglecting the reaction field which is generated by the charge density arising from solvent polarization at the dielectric boundary; this is the so-called “Coulomb field approximation”. Based on this approximation (Still et al., 1990; Scarsi et al., 1997; Onufriev et al., 2000), one can express the self-electrostatic solvation energy, ΔG_elec,α, as a volume integration,

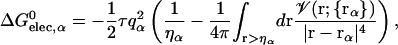(5)

where η_α is an arbitrarily defined integration starting point necessary to avoid the singularity at |r − r_α| = 0, and 𝒱(r) is a solute volume function which is one in the interior of a solute and zero in the solvent region. Thus, 𝒱(r) represents the solvent inaccessibility at a position r. Since the Coulomb field approximation neglects the reaction field, it is well-known that this approximation underestimates the self-electrostatic solvation energy, and thus overestimates the effective atomic Born radii compared to the exact ones calculated from numerical solutions of Eq. 3 (Lee et al., 2002). In principle, one can express the exact self-solvation energy, ΔG_elec,α, as the sum of a series of correction terms beyond the Coulomb field approximation. Recently, Lee et al. (2002) introduced an additional correction, 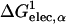, to the Coulomb field, 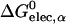, which showed a great improvement over the Coulomb field approximation for the calculated effective Born radii. Using this correction term (Lee et al., 2002, 2003; Im et al., 2003), one can approximate ΔG_elec,α as

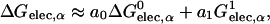(6)

where a₀ and a₁ are the empirical coefficients, and 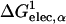is defined as

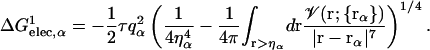(7)

It should be noted that the functional form of 𝒱(r) in Eqs. 5 and 7 depends on the definition of the dielectric boundary used in the reference PB calculations. Furthermore, both PB and GB theories have to use a continuous and smooth dielectric boundary, which is related to the volume function 𝒱(r), because a discontinuous dielectric boundary leads to numerical instability in calculations of solvation forces (Gilson et al., 1993; Im et al., 1998, 2003). Recently, Im et al. (2003) reformulated the calculation of the self-electrostatic solvation energy to utilize a simple smoothing function for the volume function in Eqs. 5 and 7. The smoothed dielectric boundary is closely related with the van der Waals surface representation and it is more efficient at the same level of accuracy than the molecular surface representation used in the implementation by Lee et al. (2002, 2003). The proposed GB model is fully consistent with the PB theory previously developed to obtain numerically stable electrostatic solvation forces using the finite-difference method (Im et al., 1998). Briefly, the space-dependent dielectric constant ɛ(r) in the framework of Eq. 3 can be defined as a (smooth) volume exclusion function, ℋ(r), which changes from zero in the interior of the solute to one in the solvent region,

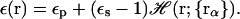(8)

ℋ(r) is a function of all atomic positions, {r_α}, in the system, and can be expressed as a product of a simple polynomial atomic volume exclusion function H_α(r),

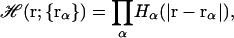(9)

where

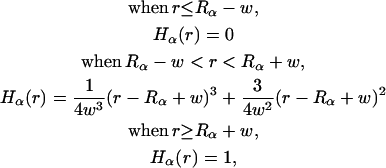(10)

where r is the distance between a spatial point and atom α, 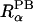is the atomic radius to define a dielectric boundary in the PB calculation, and 2w is a smoothing length that confines the region where the smoothing function is applied (Im et al., 1998). The first derivative of the smoothing function is zero at − w and 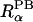+ w. It is straightforward to link the volume exclusion function, ℋ(r), in PB theory to the volume function, 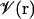, in the GB models, i.e.,

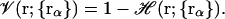(11)

In the present study, the formalism for the volume function, 𝒱(r), is modified to approximately take into account the heterogeneous environment of biological membranes represented as a low-dielectric slab,

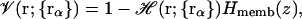(12)

where H_memb(z) is a membrane volume exclusion function going from zero inside the membrane hydrophobic region to one in the solvent region. By construction, we write the planar membrane as a slab perpendicular to the z axis and centered at z = 0. For simplicity, we use the same polynomial function for the smoothing region of H_memb(z) as used in H_α(r) in Eq. 10, i.e.,

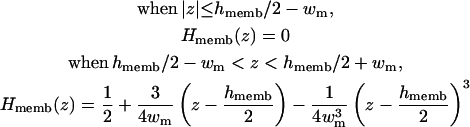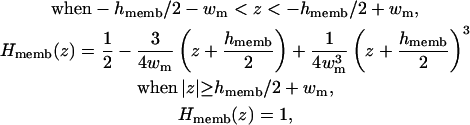(13)

where 2w_m is a membrane smoothing length and h_memb is the thickness of the membrane hydrophobic region. Therefore, the existence of a low-dielectric semi-infinite slab can be captured in the volume function in Eq. 12, and thus effects the calculation of the self-electrostatic solvation energy via Eqs. 5 and 7. Furthermore, following recent developments of Im et al. (1998, 2003), it is also possible to calculate the solvent-exposed surface area (SA) approximately by taking the presence of a low-dielectric slab into account,

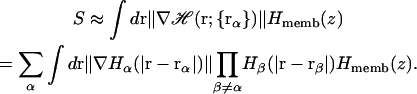(14)

In this context, it is implicitly assumed that protein-to-lipid nonpolar interactions are uniform because the surface area becomes zero inside the membrane, i.e., attraction of nonpolar residues into the hydrophobic core is active only in the membrane interface.

As seen from Eq. 12, the implementation of a modified volume function, 𝒱(r), to represent membranes in GB requires only minor changes to the previously developed methodology (or any approach using the volume integration method). Consequently, we will skip the description of the detailed numerical implementation of the present development. For detailed information the reader is referred to Im et al. (2003), where expressions for the numerical integration of Eqs. 5, 7, 14, and the calculations of the forces for each component without H_memb(z), are well-documented. We also note that the introduction of the volume exclusion function, as discussed above in the context of membranes, is quite general and relatively arbitrary “shapes” may be incorporated with little trouble.

Computational methods

The performance of the present GB model depends on several parameters. First, two coefficients, a₀ for the Coulomb field term and a₁ for the correction term in Eq. 6, are key for accurate estimates of ΔG_elec in the GB theory. We assume that these parameters do not depend on the physical environment, and the previously optimized values were used without modification (see Table 1 in Im et al., 2003). We note that optimization with respect to these parameters could improve the accuracy of our model; however, at this stage of development such optimization is not warranted.

TABLE 1.

Various average properties from the melittin simulations

			Energy, kcal/mol‡
	Zcom,* Å	Kink angle,† degree	𝒲	Uint	Uext	ΔGelec	ΔGnp
S1	12.4 ± 1.2	154.9 ± 10.4	−377.7 ± 15.2	445.6 ± 15.8	−306.1 ± 36.7	−565.3 ± 41.3	48.0 ± 6.7
S2	13.4 ± 0.8	155.3 ± 10.7	−395.3 ± 15.3	449.0 ± 15.8	−373.6 ± 38.6	−522.4 ± 38.2	51.6 ± 4.0
S3	12.9 ± 0.9	154.2 ± 10.3	−385.4 ± 15.9	443.1 ± 15.6	−282.4 ± 35.8	−596.3 ± 40.4	50.2 ± 5.0
S4	15.3 ± 1.3	47.4 ± 19.8	−381.5 ± 16.1	445.4 ± 16.0	−288.7 ± 35.9	−602.7 ± 42.7	64.3 ± 6.6
S5	12.6 ± 1.1	162.1 ± 9.2	−380.6 ± 15.2	445.9 ± 15.6	−292.5 ± 28.0	−581.2 ± 27.4	47.2 ± 5.9
S6	5.8 ± 0.5	122.0 ± 11.4	−380.1 ± 14.7	441.3 ± 15.3	−311.1 ± 41.4	−548.2 ± 40.6	37.9 ± 2.6

The average and fluctuations of the melittin simulations were taken from 2500 snapshots after 1.0 ns.

^*Z_com is the center of mass of melittin along the z axis.

^†Kink angle represents an angle between the two helical segments, defined by the two vectors connecting Val5 C_α to Gly12 C_α and Leu16 C_α to Lys23 C_α (Bernèche et al., 1998).

^‡The free energy, 𝒲, in solvent/membrane environment is defined as the sum of the internal (bond, angle, dihedral, etc.) molecular mechanics energy, U_int; the external (van der Waals, U_vdW, and Coulomb, U_Coul) molecular mechanics, energy U_ext; the electrostatic solvation energy, ΔG_elec; and the nonpolar solvation energy, ΔG_np.

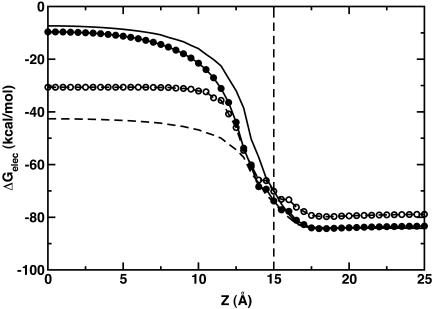
We have used numerical quadrature techniques in the integration of Eqs. 5 and 7 for each atom (Im et al., 2003); the integration points and weights for the radial component are generated by the Gaussian-Legendre quadrature (Press et al., 1989) and those for the angular component by the Lebedev quadrature (Lebedev and Laikov, 1999). It was shown that 24 radial integration points up to 20 Å (5 points between 0.5 Å and 1 Å, and 19 points between 1 Å and 20 Å) and 38 angular integration points were sufficient and optimal for GB calculations in solution (Im et al., 2003). However, in contrast to calculations of ΔG_elec in solution, the GB solvation energies with membranes appear to be more sensitive to the number of integration points. For instance, Fig. 1 illustrates a rather extreme case in which ΔG_elec shows a significant difference (21 kcal/mol) in the center of the membrane and a moderate difference (4.5 kcal/mol) in bulk solution, depending on only the number of radial integration points. Because ɛ_p = 1 is used in Eq. 1, ΔG_elec from the GB model should reproduce ΔG_elec from PB with ɛ_m = 1. Indeed, as shown in Fig. 1, ΔG_elec with 50 radial integration points does so. With 50 radial integration points, it should be noted that the calculation of ΔG_elec is fully converged; e.g., the same calculation with 100 integration points yields nearly identical results (data not shown). However, it is also clear that ΔG_elec does not reach convergence and shows significant differences inside the membrane when 24 radial integration points are used. A close examination reveals that when 24 radial integration points are used, 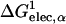in Eq. 7 is always underestimated inside the membrane region, whereas 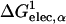in Eq. 5 is fully converged compared to the corresponding values calculated with 50 radial integration points (data not shown). Consequently, ΔG_elec is systematically underestimated but appears (empirically) to be close to the PB results calculated with ɛ_m = 2 (see also next section). The use of ɛ_m >1 (typically 2) is common in representing the low-dielectric region of the membrane in PB calculations (Roux et al., 2000; Im and Roux, 2002a). Since the computational time of the GB calculations increases as the number of integration points increases, and because the differences we observe are systematic, we use 24 radial integration points in the present study. Clearly, calculations with a larger number of radial integration points can be employed if found to be necessary to reproduce the essential physical effects of the membrane environment.

FIGURE 1.

Electrostatic solvation energy of a monovalent spherical ion of 2 Å radius in the presence of a semi-infinite planar membrane with 30 Å thickness (dashed thin line) as a function of ion's position along the z direction. The planar membrane is centered at z = 0. Both PB and GB calculations were done with a smoothing length of 0.6 Å (w = 0.3 Å). All PB calculations were performed with a grid spacing of 0.21 Å, ɛ_p = 1, ɛ_s = 80, and ɛ_m = 1 (solid line) or ɛ_m = 2 (dashed line) using the PBEQ module (Roux, 1997; Im et al., 1998, 2001) of the biomolecular simulation package CHARMM (Brooks et al., 1983). All GB calculations were done with ɛ_p = 1, ɛ_s = 80, 38 angular integration points, and 50 (solid line with filled circles) or 24 (dashed line with open circles) radial integration points up to 20 Å.

ΔG_elec from both PB and GB calculations also depends on the atomic radii and the definition of dielectric boundary. In the present study we used the optimized PB atomic radii for proteins, previously developed by Nina et al. (1997). However, the present smoothed dielectric boundary does not correspond to the “exact” van der Waals surface (overlapping atomic spheres). To take the influence of the smoothed boundary on the PB energy into account, and to closely reproduce the PB energy with the van der Waals surface for the 20 standard amino acids, Nina et al. (1999) empirically modified the optimal protein PB radii 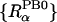for the smoothed dielectric boundary using

(15)

where s is a scaling factor with a value close to 1. We utilized the values in Table 2 of the work from Nina et al. (1999).

TABLE 2.

Various average properties of the M2-TMP simulations

						Energy changes, kcal/ mol§
	hmemb, Å	γ, kcal/(mol · Å2)	H-bond,* %	RMSD,† Å	Tilt angle,‡ degree	Δ𝒲	ΔUint	ΔUvdw	Δ𝒲eelac	ΔΔGnp
S1	25.0	0.04	89 ± 10	0.29	43.1 ± 3.3	−26.2	−1.6	−0.2	−8.7	−15.7
S2	27.0	0.04	91 ± 6	0.24	36.3 ± 3.8	−24.4	−1.0	−0.6	−10.4	−12.4
S3	29.0	0.04	92 ± 7	0.29	28.5 ± 5.1	−23.3	−0.8	+1.5	−16.3	−7.5
S4	31.0	0.04	89 ± 9	0.30	22.5 ± 4.9	−25.0	−2.5	−2.2	−15.4	−4.8
S5	25.0	0.03	89 ± 13	0.31	34.8 ± 5.5	−17.8	−1.4	+0.1	−7.8	−8.7

^*The average was taken from residue i = 24 to i = 42 in Fig. 5 B.

^†The root mean-square deviation (RMSD) of the backbone atoms of the transmembrane domain (Leu26–Leu43) relative to the NMR average structure (PDB code: 1MP6). The MD average structures were calculated from 2.4-ns trajectories (after 1.1 ns) for each run.

^‡The average was taken after 1.1 ns (see Fig. 5 D).

^§The energy change of each term was calculated by subtracting averages in equilibration runs with restraints (0.3 ns) from averages in production runs without restraints (3.2 ns). All the energy terms are defined in Table 1 except 𝒲_elec, which is the sum of U_Coul and ΔG_elec.

All calculations were performed using the CHARMM biomolecular simulation program (Brooks et al., 1983). The present GB model has been implemented into the GBSW module in CHARMM (c30a1). The all-atom parameter set PARAM22 for proteins was used (MacKerell Jr. et al., 1998). Recently, Feig et al. (2003) demonstrated that the CHARMM empirical force field rapidly converts from an initial α-helical conformation, (i, i + 4) hydrogen bonding, to π-helical conformation, (i, i + 5) hydrogen bonding in solution, which does not agree with experimental data where π-helices are rarely observed. Based on the backbone dihedral φ-ψ potential map in vacuum, which is matched to high-level quantum mechanical data for an alanine dipeptide model system, they have developed a newly extended PARAM22/CMAP force field which significantly diminishes the population of π-helices. Thus, we used the PARAM22/CMAP force field for all the simulations. No cutoff was used for nonbonded interactions and the GB terms in Eq. 1. Unless specified explicitly, we used a smoothing length of 0.6 Å (w = 0.3 Å) in both the PB and GB calculations, for which a₀ = −0.081, a₁ = 1.6, and s = 0.952. Since it was shown previously that ΔG_elec from PB was reproduced with <1% error on average for a variety of proteins with w = 0.3 Å (Im et al., 2003), we continue to use this value here. Although one can use different smoothing lengths for the membrane exclusion function in Eq. 13, we simply set w_m = w in the present study. The planar membrane is perpendicular to the z axis and centered at z = 0. As discussed above, 24 radial integration points up to 20 Å and 38 angular integration points were used for integration of Eqs. 5 and 7. All PB calculations were performed with a grid spacing of 0.21 Å using the PBEQ module (Nina et al., 1997; Roux, 1997; Im et al., 1998, 2001) of CHARMM (Brooks et al., 1983). In the present study, the surface tension coefficient γ in Eq. 2 was considered as an empirical parameter because its value in the context of the implicit membrane model is not known. We used two values, 0.03 and 0.04 kcal/(mol · Ų), which are believed to be reasonable in the calculation of the nonpolar contribution in soluble proteins. All MD simulations were performed at 300 K with a time-step of 2 fs. In addition, to increase sampling efficiency in conformational space, the replica exchange method was used with different numbers of replica systems and different temperature ranges depending on the system being studied (Hansmann, 1997; Sugita and Okamoto, 1999; Zhou et al., 2002; Sanbonmatsu and Garcia, 2002). The MMTSB Tool Set, which is available at the web site http://mmtsb.scripps.edu, was used to control the replica exchange simulations (Feig et al., 2003).

COMPUTATIONAL ILLUSTRATIONS

Melittin

Melittin is the membrane-lytic amphipathic α-helical peptide of 26 amino acids with the sequence Gly₁-Ile₂-Gly₃-Ala₄-Val₅-Leu₆-Lys₇-Val₈-Leu₉-Thr₁₀-Thr₁₁-Gly₁₂-Leu₁₃-Pro₁₄-Ala₁₅-Leu₁₆-Ile₁₇-Ser₁₈-Trp₁₉-Ile₂₀-Lys₂₁-Arg₂₂-Lys₂₃-Arg₂₄-Gln₂₅-Gln₂₆ (Habermann, 1972). Its x-ray structure shows two α-helical segments that are kinked due to Pro14, as shown in Fig. 2 A (Terwilliger and Eisenberg, 1982b). In this section the accuracy and reliability of the present membrane GB/SA model is assessed by studying the energetics and stability of melittin at the membrane interface in comparison with previous MD simulations of melittin embedded in explicit lipid molecules (Bernèche et al., 1998; Bachar and Becker, 2000). The atomic model of melittin at the membrane interface was graciously provided by S. Bernèche and B. Roux (Bernèche et al., 1998): an amphipathic α-helix roughly parallel to the membrane interface with the unprotonated N-terminus buried in the hydrophobic core (see Fig. 2 A).

FIGURE 2.

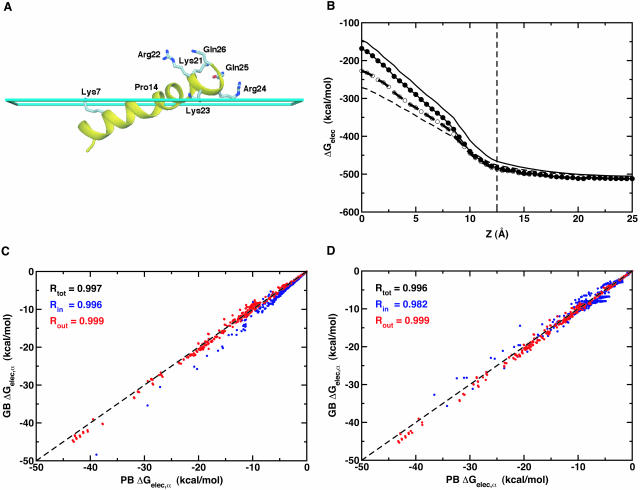
(A) Conformation of melittin at the membrane interface (cyan slab at z = 12.5 Å), which was graciously provided by S. Bernèche and B. Roux (Bernèche et al., 1998). Some hydrophilic residues are shown as labeled ball-and-stick models. The figure was produced with DINO (Philippsen, 2001). (B) Electrostatic solvation energy of melittin in the presence of a planar membrane with 25 Å thickness (dashed thin line at z = 12.5 Å) as a function of the position of its center of mass along the z direction. The planar membrane is centered at z = 0. The line types are the same as used in Fig. 1. For C and D, Comparison of PB and GB self-electrostatic free energy, ΔG_{elec, α}, in melittin for six different locations of its center of mass along the z-direction: z = 0, 5, 10, 15, 20, and 25 Å. GB results with 50 radial integration points are compared with PB results calculated using ɛ_m = 1 in C, where ΔG_elec,α is colored differently with the correlation coefficients R, depending on atomic positions; atoms inside the membrane are blue and atoms outside the membrane are red. In D, GB results with 24 radial integration points are compared with PB results calculated using ɛ_m = 2 with the same color scheme as used in C.

We first examined the accuracy of the proposed GB model by performing the same comparison as described in Fig. 1. The thickness of the planar membrane was set to 25 Å to represent the hydrophobic region of a DMPC lipid bilayer (Bernèche et al., 1998). Fig. 2 B shows the electrostatic solvation energy of melittin as a function of the position of its center of mass along the z direction. Clearly, the statement made in the previous section holds for melittin (certainly for other proteins too), i.e., the GB results with 50 radial integration points are close to the PB results calculated with ε_m = 1, whereas the GB results with 24 radial integration points are more similar to the PB results with ε_m = 2. This fact is further supported by the comparison of PB and GB self-electrostatic free energy, ΔG_elec,α, in melittin, as shown in Fig. 2, C and D. It should be noted that ΔG_elec as well as ΔG_elec,α from GB reproduce the corresponding PB results excellently no matter where the atoms are located (inside or outside membrane).

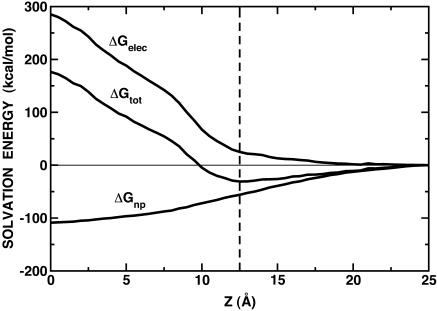
The stability of melittin in the membrane interface was examined by calculating the (relative) solvation free energy surface using GB. Fig. 3 shows a free energy minimum at the interface region, i.e., z = 12.5 Å, where melittin is stabilized by ∼−31 kcal/mol. Bernèche et al. (1998) reported the stabilization energy of ∼−18 kcal/mol at ∼12–13 Å along the z axis, based on PB calculations. The discrepancy is about the same as the difference between PB and GB ΔG_elec estimated from Fig. 2 B, i.e., ∼11 kcal/mol at z = 12.5 Å. As shown in Fig. 3, the electrostatic contribution, ΔG_elec, is always unfavorable in the membrane environment. However, the nonpolar contribution, ΔG_np, compensates this penalty and even further stabilizes the peptide near the membrane interface. This stabilization can be attributed to the amphipathic helical conformation of melittin, i.e., the hydrophobic residues are in the low dielectric region, whereas the hydrophilic residues are in the high dielectric region (see Fig. 2 A).

FIGURE 3.

Relative solvation energy of melittin in the presence of a planar membrane with 25 Å thickness (dashed thin line at z = 12.5 Å) as a function of the position of its center of mass along the z direction; ΔG_tot = ΔG_elec + ΔG_np. ΔG_elec is calculated with 24 radial integration points. The planar membrane is centered at z = 0. The surface tension coefficient γ for ΔG_np is set to 0.04 kcal/(mol · Ų).

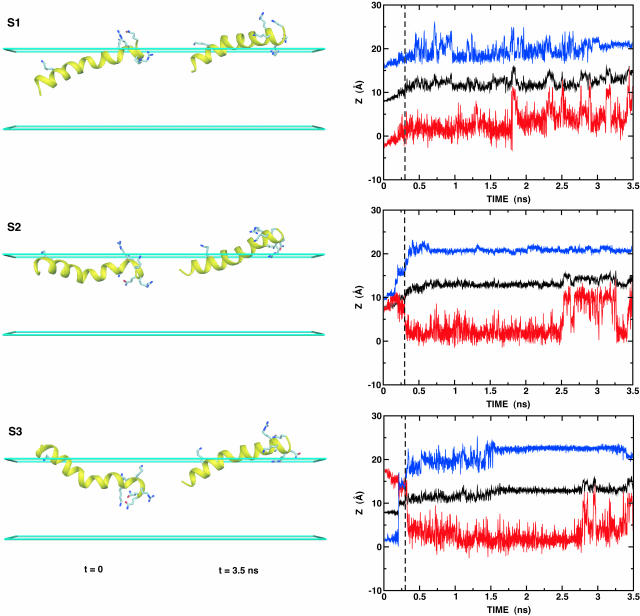
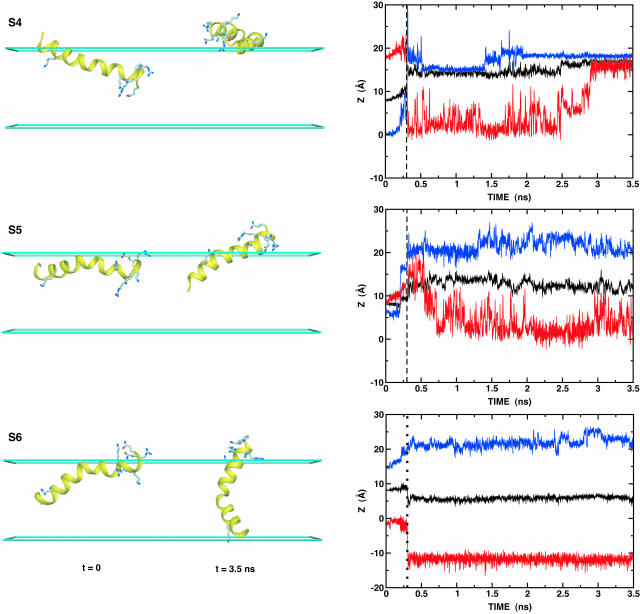
The dynamics of this peptide at the membrane interface was not taken into account in any previous calculations. It is therefore interesting to investigate the conformational changes of melittin at the membrane interface, starting from a number of random orientations relative to the membrane. To explore how melittin (and our model) respond to perturbations away from the “equilibrium” conformation with melittin tilted at the interface, six starting configurations (S1–S6) were generated by rigid body rotations and translations; the initial structure in Fig. 2 A was rotated by 60° intervals around an axis going through its center of mass and parallel to the x-axis, and the rotated structures were then translated such that their centers of mass were positioned at z = 8 Å (see Fig. 4). Each configuration was then subjected to 3.5 ns of constant-temperature molecular dynamics at 300 K, including a 300-ps equilibration during which harmonic restraints on the peptides were gradually reduced. As expected, and deduced from Fig. 4, the hydrophilic residues embedded initially in the low dielectric region move quickly into the high dielectric region during equilibration, and at the same time the unprotonated N-terminus moves into the hydrophobic core. Based on the inspection of Fig. 4 and the average kink angle between the two helical segments shown in Table 1 , three different configurations were identified; a parallel orientation to the membrane interface with a large kink angle of ∼155° (S1, S2, S3, and S5), a parallel orientation with a small kink angle of ∼48° (S4), and a perpendicular orientation with a kink angle of ∼122° (S6). Experimental measurements show large variation in the kink angle, depending on surrounding environment; 120° in the x-ray structure (Terwilliger and Eisenberg, 1982a), 160° or 140° in the lipid bilayer (Naito et al., 2000), 120° in methanol, and 160° in water (Bazzo et al., 1988). It should be noted that all the simulations yield the average kink angles within these various experiments, except for the case of S4.

FIGURE 4.

Six starting (t = 0) and final (t = 3.5 ns) configurations (S1–S6) with the time series of the z component of center of mass of melittin (black on right plot); the z coordinates of C_α atoms of Gly1 (red) and Gln26 (blue). Some hydrophilic residues are shown as labeled ball-and-stick models, as shown in Fig. 2 A. The figure was produced with DINO (Philippsen, 2001).

To the best of our knowledge there are no experimental findings to support the existence of the S4-like structure. Thus, one may consider this structure an artifact resulting from the initial structure, which has the hydrophilic groups deeply embedded in the low-dielectric slab. Nonetheless, it is also feasible to consider this structure as one of the early stages of the membrane-bound conformation before the unprotonated N-terminus becomes buried in the hydrophobic core (S1, S2, S3, and S5). The reason for this conjecture is that the free energy, 𝒲, of this conformation, defined in Table 1, is quite similar to the others and the structure is still bound to the membrane.

To make sure that each structure in the six simulations is converged and accessible at 300 K, we used the replica exchange method in which six replicas were distributed over an exponentially-spaced temperature range between 300 and 400 K, and each replica was subjected to a 10-ns MD simulation starting from the final structures of each MD simulation. The replica exchange method can be used to rank different configurations according to their free energies. A replica exchange was attempted every 2 ps and the pairwise exchange ratio was ∼30%. Each of the replicas remained close to their starting configuration without conformational change between them. Their populations, averaged over the last 5 ns at 300 K, were 21.4 (S1), 27.8 (S2), 5.5 (S3), 12.6 (S4), 2.3 (S5), and 0.4% (S6). As expected, all the replicas are accessible to the lowest temperature, even though their occupancies are quite different.

The present results suggest that the membrane GB/SA model can be used to generate initial configurations of small membrane proteins for detailed MD simulations. As shown in Fig. 4 and Table 1, the structures of S1, S2, S3, and S5 are similar to that in Fig. 2 A, one snapshot from a previous MD simulation (Bernèche et al., 1998); S6 is also similar to the structures observed in other MD simulations (Bachar and Becker, 2000; Lin and Baumgaertner, 2000). It should be noted that it is generally not feasible to observe configurational changes of the magnitude seen with our implicit membrane model in detailed MD simulations, because of the low conformational exchange rate of peptides in such simulations.

Transmembrane domain of the M2 protein H⁺ channel

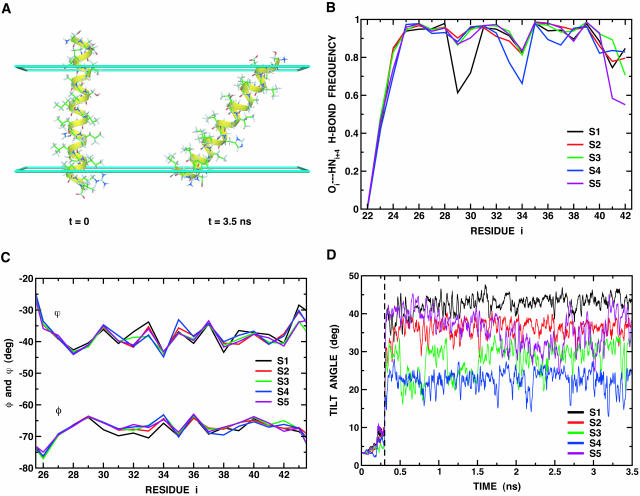
The M2 protein from Influenza A virus is comprised of 97 amino acids and forms a tetrameric H⁺ channel in the viral membrane which is activated in the low pH environment of the endosome (Lamb et al., 1994). The structure of a membrane-spanning 25-residue peptide called M2-TMP, showing an ideal α-helix and a helical tilt of 38 ± 3° with respect to the membrane normal, was recently determined in a DMPC bilayer using solid-state NMR techniques (Wang et al., 2001). We examine this sequence, which comprises a single transmembrane domain and few hydrophilic residues on either end: Ser₂₂-Ser₂₃-Asp₂₄-Pro₂₅-Leu₂₆-Val₂₇-Val₂₈-Ala₂₉-Ala₃₀-Ser₃₁-Ile₃₂-Ile₃₃-Gly₃₄-Ile₃₅-Leu₃₆-His₃₇-Leu₃₈-Ile₃₉-Leu₄₀-Trp₄₁-Ile₄₂-Leu₄₃-Asp₄₄-Arg₄₅-Leu₄₆. Our primary focus is on the influence of the membrane thickness, h_memb, and the surface tension coefficient, γ, on the dynamics of the peptide in our planar membrane model, i.e., the stability of the α-helical conformation as well as the helical tilt angle. Five different constant-temperature MD simulations (S1–S5) of the M2-TMP monomer were performed at 300 K for 3.5 ns with the membrane GB/SA model, starting from the NMR structure (PDB code: 1MP6) which was oriented perpendicular to the membrane interface (see Fig. 5 A and Table 2).

FIGURE 5.

(A) Configurational change of M2-TMP at the membrane interface (cyan slabs at z = ±12.5 Å represent the upper and lower membrane interface). All atoms are shown as ball-and-stick models. The figure was produced with DINO (Philippsen, 2001). (B) Hydrogen bonds of backbone atoms are defined by d_Oi··HNi+4 ≤ 2.6 Å and 120° ≥ θ_O…H…N ≤ 180°, where d_Oi··HNi+4 is the distance between the carbonyl oxygen of residue i, O_i; and the amide hydrogen of residue i + 4, HN_i+4; and θ_O…H…N is the angle between O_i, HN_i+4, and N_i+4. The H-bond frequency is calculated from 2.4-ns trajectories (after 1.1 ns) for each run. (C) The φ and ψ backbone dihedral angles from Leu26 to Leu43, calculated from 2.4 ns trajectories (after 1.1 ns) for each run. For simplicity, the fluctuation of each angle, which is ∼± 7–10°, is omitted. (D) The tilt angle is defined by the angle between the membrane interface and the principal axis of the backbone heavy atoms of Leu26 to Leu43.

Analysis of both hydrogen-bond frequency and φ-ψ backbone dihedral angles, as shown in Table 2 and Fig. 5, B and C, reveals little deviation from a regular α-helix (φ = −65° and ψ = −40°) upon the change of h_memb and γ. This is further supported by the fact that the calculated root mean-square deviation (RMSD) of the backbone atoms of the transmembrane domain (Leu26–Leu43) relative to the NMR average structure is ∼0.3 Å, as shown in Table 2. In general, Gly34 has slightly lower backbone hydrogen-bond frequency, probably due to the flexibility of its backbone, but it still forms the continuous α-helix due to the strong backbone hydrogen-bonding inside the low dielectric region (Popot and Engelman, 2000). Similarly, the hydroxyl group of Ser31, which is embedded inside the membrane, makes hydrogen bonds with the carbonyl oxygen of Val27 to stabilize the polar group inside the low dielectric region.

Fig. 5 D shows the time series of the tilt angle of M2-TMP relative to the membrane interface; average values are given in Table 2. The calculated tilt angles are clearly dependent on both h_memb and γ; the tilt angle is decreased as h_memb is increased or γ is decreased. Based on the “hydrophobic mismatch” concept, one might envision that transmembrane proteins or peptides could tilt or kink when their transmembrane hydrophobic length is too long to match the bilayer to overcome the energetically unfavorable mismatch (de Planque et al., 1998). To better understand the microscopic origin for the tilt, average energy changes after the tilt were decomposed into various contributions and the results are illustrated in Table 2. Electrostatic and nonpolar solvation terms appear to be dominant, but they are anticorrelated upon the change of h_memb. In general, the electrostatic contribution increases and the nonpolar one decreases, as h_memb is increased. As might be expected, decreasing γ confers more motional freedom upon the nonpolar residues in the membrane interface, resulting in a smaller tilt and larger fluctuations. Thus, h_memb and γ can be considered as empirical parameters in the present membrane GB/SA model. Interestingly, Kovacs et al. (2000) showed that M2-TMP has a tilt of 37 ± 3° in DMPC and 33 ± 3° in DOPC, based on the solid-state NMR experiments. Here, DMPC might correspond to h_memb = 25 Å and DOPC to h_memb = 29 Å. In contrast to the experiments, the tilt of M2-TMP shows significant differences between S1 (43 ± 3°) and S4 (29 ± 5°). However, it should be stressed that M2-TMP is believed to exist in a tetrameric form in the NMR experiments (Kovacs et al., 2000; Wang et al., 2001), whereas the present simulations were all done with a monomer. We anticipate that the dependence of the tilt angle on the membrane thickness might be less sensitive in a tetrameric form of M2-TMP (in the NMR experiments) than in its monomeric form (Kovacs et al., 2000) (see also next section). Unfortunately, we are not presently at the stage where the full tetrameric form can be simulated or modeled by including the influence of the solvent-accessible pore region, and thus we leave the matter as a future study.

As a preliminary study of membrane protein folding, it is of interest to examine if one can fold this (simple) single transmembrane peptide from an extended conformation. For efficient sampling, we used the replica exchange method in which eight replicas were distributed over an exponentially-spaced temperature range of 300–500 K, and each replica was subject to a 20-ns MD simulation with h_memb = 25 Å and γ = 0.04 kcal/(mol · Ų), starting from an extended conformation (see Fig. 6 C). A replica exchange was attempted every 2 ps and the pairwise exchange ratio was ∼20%. Fig. 6 A shows RMSD changes of all eight replicas as a function of time. It is observed that, after ∼13 ns, all of the replicas fold into a continuous α-helical structure which is almost identical to the average NMR structure, and the efficiency of each replica to adopt a helical conformation appears to depend on how it travels the temperature range. As shown in Fig. 6 B, there is a clear correlation between RMSD and the tilt angle, i.e., the correct tilt angle is only obtained once the structure folds correctly. Fig. 6 C shows a few snapshots of the replica in Fig. 6 B, suggesting that forming a helix in the membrane interface appears to be the rate-limiting step.

FIGURE 6.

(A) RMSD of the backbone atoms of the transmembrane domain (Leu26–Leu43) relative to the NMR average structure as a function of time for all eight replicas. (B) Correlation between the tilt angle (black) and RMSD (red) of one replica (black in A). The definition of the tilt angle is the same as used in Fig. 5 D. A tilt of 43.1 ± 3.3° was obtained after 3.5 ns simulations with h_memb = 25 Å and γ = 0.04 kcal/(mol · Ų), as shown in Table 2. The conformational and configurational change of the replica as time evolves is shown in C. The figure was produced with DINO (Philippsen, 2001).

We note that our model of the membrane in these calculations mimics only the continuum aspects of such systems, i.e., a static, semi-infinite, low-dielectric, and hydrophobic slab “embedded” in an aqueous environment with a continuum representation of water above and below the membrane. Unlike true biological membranes, our model does not capture temperature-dependent transitions, i.e., it does not “melt” at elevated temperature. As a result of this shortcoming of the continuum model, peptides which fold in the low dielectric environment of the membrane are expected to show much-shifted (to higher temperatures) folding/unfolding transitions; as we observe here. We also note that physical membranes are anticipated to “dissolve” at temperatures below, or near, those expected to unfold helical peptides. That the observed high temperature of folding/unfolding transitions in our peptides are related to the static nature of the membrane model is reinforced by the fact that similar helical peptides undergo helix-to-coil transitions at much lower temperatures when the same GB model is employed but the membrane region is eliminated. Thus, we believe the key physical characteristics of biological membranes in biologically relevant temperature ranges (near 300 K) are reproduced by our model. Although it is limited for studies at temperatures where the membrane integrity is violated, our model reproduces the conformational characteristics of helical peptides in membranes near physiological temperatures. Therefore, the present result is quite promising, suggesting that the membrane GB/SA model can be used for the study of membrane protein folding.

Transmembrane domain of glycophorin A

Glycophorin A (GpA) forms a dimer due to specific interactions of its transmembrane α-helices, and it is the most well-characterized model system in the study of helix-to-helix interactions in membranes (Popot and Engelman, 2000; Arkin, 2002). The structure of the transmembrane domain of the dimer was determined by both solution NMR in micelles (MacKenzie et al., 1997) and solid-state NMR in lipid bilayers (Smith et al., 2001). Except for some minor differences, the structures have the same fold; a right-handed helical dimer with the dimerization motif of LIxxG⁷⁹VxxG⁸³VxxT. In our study, we used the following sequence, which has a single transmembrane domain and few hydrophilic residues on either end: Pro₇₁-Glu₇₂-Ile₇₃-Thr₇₄-Leu₇₅-Ile₇₆-Ile₇₇-Phe₇₈-Gly₇₉-Val₈₀-Met₈₁-Ala₈₂-Gly₈₃-Val₈₄-Ile₈₅-Gly₈₆-Thr₈₇-Ile₈₈-Leu₈₉-Leu₉₀-Ile₉₁-Ser₉₂-Tyr₉₃-Gly₉₄-Ile₉₅. We note that several basic residues at the C-terminus (Arg₉₆-Arg₉₇-Leu₉₈-Ile₉₉-Lys₁₀₀-Lys₁₀₁) are ignored in our calculations and this may influence stabilization of the helical interface.

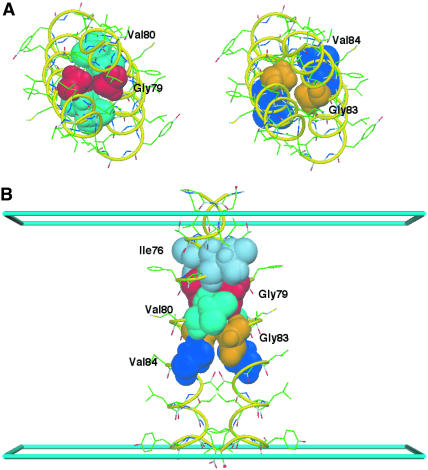
To investigate the influence of the membrane thickness, h_memb, and the surface tension coefficient, γ, on the stability of the GpA dimer in a planar membrane, eight different constant-temperature MD simulations were performed at 300 K for 3.2 ns including 0.2-ns equilibration; four simulations (D1, D2, D3, and D4) starting from one of the solution NMR dimeric structures; and four simulations (M1, M2, M3, and M4) starting from one helix, which is one-half of the dimeric structure, oriented to be perpendicular to the membrane interface. Various average properties from the simulations are summarized in Table 3. The continuous regular α-helical conformation remained in all simulations except M1, in which a π-helical conformation, (i, i + 5) hydrogen bonding, was dominantly found from Ile76 to Val81 (data not shown). This is the reason that the hydrogen bond frequency is relatively low for M1 in Table 3. Together with its larger tilt angle, the deformation of the α-helix in M1 is attributed to the stress by the shorter length of transmembrane hydrophobic core, i.e., the hydrophobic mismatch. As proposed in the previous section, the dependence of the tilt angle on the membrane thickness is much less sensitive in the dimer than the monomer (see D1 and M1 in Table 3). Regardless of h_memb and γ, the trajectories of the dimer remained at similar interhelical crossing angles (or tilt angles) relative to the solution NMR structure (40°) (MacKenzie et al., 1997) and the solid-state NMR structure (35°) (Smith et al., 2001). The RMSDs of the backbone atoms of the transmembrane domain (Leu75–Ile91) relative to the starting NMR structure remained ∼1 Å, except in the case of M1. As shown in Table 4, the interhelical distances calculated from the MD trajectories appear to be closer to those measured by solid-state NMR (Smith et al., 2001) than those by solution NMR (MacKenzie et al., 1997), although all the simulations started from the solution NMR structure. The close packing between glycine residues at positions 79 and 83 was found in all simulations, as shown in Fig. 7. However, Thr87, which appeared to hydrogen-bond across the dimer interface in the solid-state NMR data, forms a hydrogen bond to the backbone of Gly83 in the same helix. As shown in Table 3, the decomposition of the helix-to-helix interaction energies shows that interhelical van der Waals interactions exclusively contribute to the dimer formation.

TABLE 3.

Various average properties from the GpA simulations

							Helix-to-helix interaction energies, kcal/mol¶
	hmemb Å	γ, kcal/(mol · Å2)	H-bond,* %	Tilt angle,† degree	Crossing angle,‡ degree	RMSD,§ Å	𝒲	Uvdw	𝒲elec	ΔGnp
Dimer
D1	25	0.04	94 ± 5	25.9 ± 5.0	−48.3 ± 3.4	1.18	−56.4 ± 5.0	−49.1 ± 3.3	−3.0 ± 2.7	−4.2 ± 1.1
			93 ± 7	24.2 ± 5.0
D2	29	0.04	92 ± 8	21.8 ± 3.7	−42.5 ± 2.5	1.09	−56.9 ± 3.4	−52.1 ± 3.1	−2.6 ± 1.3	−2.2 ± 0.6
			90 ± 9	21.6 ± 3.9
D3	29	0.03	92 ± 7	22.8 ± 3.4	−41.6 ± 2.6	1.09	−56.0 ± 3.5	−51.8 ± 3.1	−2.6 ± 1.0	−1.5 ± 0.4
			89 ± 14	19.6 ± 3.3
D4	31	0.04	92 ± 6	20.7 ± 3.1	−40.0 ± 2.5	0.99	−55.0 ± 3.5	−51.3 ± 3.2	−2.3 ± 1.2	−1.3 ± 0.5
			89 ± 11	20.2 ± 3.2
Monomer
M1	25	0.04	59 ± 38	30.9 ± 4.0	–	2.31	–	–	–	–
M2	29	0.04	86 ± 9	18.8 ± 5.5	–	0.92	–	–	–	–
M3	29	0.03	90 ± 9	14.8 ± 6.1	–	0.92	–	–	–	–
M4	31	0.04	90 ± 10	11.3 ± 5.0	–	0.96	–	–	–	–

The average and fluctuations of the GpA simulations were calculated from 2.6-ns trajectories (after 0.6 ns) for each run.

^*The average hydrogen-bond frequency was taken from residues i = 74 to i = 90. The definition of a H-bond is the same as used in Fig. 5 B. In the case of the dimer simulations, the values are given separately for each monomer.

^†The tilt angle is defined by the angle between the membrane interface and the principal axis of the backbone heavy atoms of Leu75 to Ile91. In the case of the dimer simulations, the values are given separately for each monomer.

^‡The crossing angle is measured by the angle between two principal axes defined by the backbone heavy atoms of each monomer from Leu75 to Ile91. The negative sign means that it forms a right-handed dimer.

^§The root mean-square deviation (RMSD) of the backbone atoms of the transmembrane domain (Leu75–Ile91) relative to one of the solution NMR structures (PDB code: 1AFO).

^¶The helix-to-helix interaction energies were calculated by where x is 1, 2, 3, and 4. All the energy terms are defined as in Tables 1 and 2.

TABLE 4.

Interhelical distances (Å) from experiments and simulations of the GpA transmembrane dimer

		Solid-state NMR*	Solution NMR†	MD simulation‡
Gly79 C	Gly79 Cα	4.1	5.3	4.0 ± 0.2
Gly79 Cα	Ile76 C	4.8	5.4	4.5 ± 0.3
Gly83 C	Gly83 Cα	4.3	4.9	4.4 ± 0.4
Gly83 Cα	Val80 C	4.2	4.6	4.9 ± 0.3
Gly79 C	Val80 Cγ	4.0	2.8	4.2 ± 0.3
Gly83 C	Val84 Cγ	4.0	3.4	4.5 ± 0.5

^*Taken from the solid-state NMR data (Smith et al., 2001).

^†Taken from the starting solution NMR structure (PDB code: 1AFO) (MacKenzie et al., 1997).

^‡The average distance and fluctuations were calculated from 2.6-ns trajectories (after 0.6 ns) of D3 in Table 3. The results from D1, D2, and D4 are similar (data not shown).

FIGURE 7.

Average structure of the GpA dimer from a 3.2-ns MD simulation (D2) with h_memb = 29 Å (cyan slabs at z = ± 14.5 Å represent the membrane boundaries along z) and γ = 0.04 kcal/(mol · Ų). Some key residues are shown as labeled CPK models and the rest as ball-and-stick models. (A) View down the dimer axis: glycine-to-glycine close packing at positions 79 and 83. (B) View along the dimer interface: the dimerization motif of LIxxG⁷⁹VxxG⁸³VxxT. In fact, A and B have the same orientation as Figs. 5 and 6 of Smith et al. (2001). The figure was produced with DINO (Philippsen, 2001).

It is important to model the transmembrane helix-to-helix interactions reasonably well if one wishes to predict the correct assembly of membrane proteins. Various computational approaches have been employed to predict the conformation of homo-oligomeric helical bundles (Adams and Brunnger, 2001; Fleming and Engelman, 2001; Torres et al., 2002; Arkin, 2002) or tightly packed transmembrane α-helices (Fleishman and Ben-Tai, 2002; Vaidehi et al., 2002). In general, the candidate models are generated by exploring a quite limited configuration space, and the correct structure is identified based on an energy (or scoring) function, or on experimental observations. Despite its success, the heterogeneous membrane/solvent environment is often neglected in these approaches. It was shown in the previous section that the folding of a simple transmembrane domain is relatively straightforward with the present membrane GB/SA model. Here, as a next step in modeling and folding studies of membrane proteins, we examined the reliability of our model by recapitulating the transmembrane helix-to-helix interactions with the GpA dimer. For efficient sampling, the replica exchange method was employed with 16 replicas distributed over an exponentially-spaced temperature range between 300 K and 600 K. Starting from two helices which are perpendicular to the membrane interface and separated by 20 Å, each replica was subjected to a 20-ns MD simulation with h_memb = 29 Å and γ = 0.04 kcal/(mol · Ų). A replica exchange was attempted every 2 ps and the pairwise exchange ratio was ∼26%.

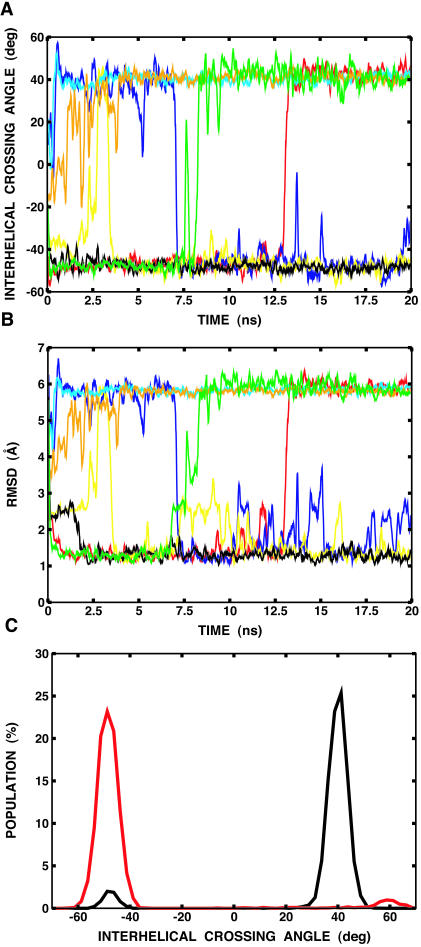
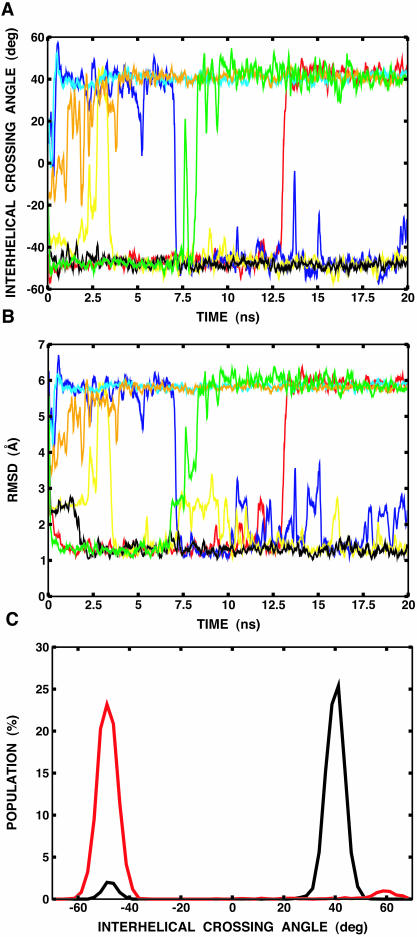
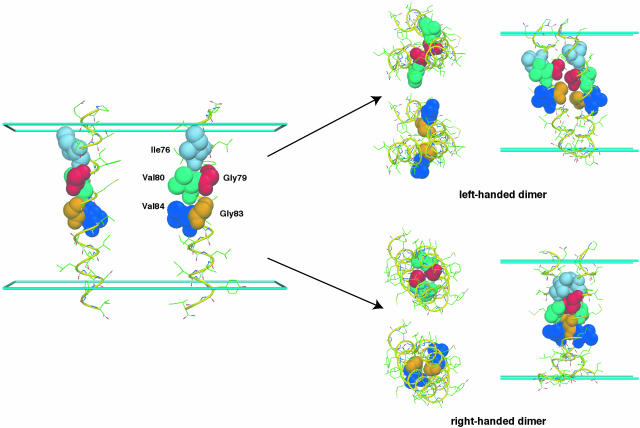
Fig. 8 A shows the interhelical crossing angle as a function of time for a few selected replicas. After ∼0.5-ns simulation, the initially separated helices rapidly formed a dimer and clustered into two distinct families of conformations: a right-handed dimer (at ∼−50°), and a left-handed dimer (at ∼+40°). Interestingly, a few transitions between the two configurations occurred at the highest temperature. The interhelical crossing angle is well-correlated with the RMSD values of the backbone atoms of the transmembrane domain (Leu75–Ile91) relative to the NMR structure, as shown in Fig. 8 B. The right-handed dimer yields an RMSD value of ∼1.2 Å, whereas the left-handed one shows an RMSD value of ∼5.8 Å. Fig. 8 C shows the population of right- and left-handed dimers at the lowest temperature, 300 K, as a function of the interhelical crossing angle. The left-handed configuration shows 94% occupancy, whereas the right-handed one only occurs 4% of the time. This corresponds to the free energy difference of ∼1.6 kcal/mol between the two configurations. The representative structures of both right- and left-handed dimers, including the starting structure, are shown in Fig. 9 .

FIGURE 8.

(A) Interhelical crossing angle as a function of time. For clarity, trajectories of only seven replicas (out of 16) are shown. The rest were also clustered into the right-handed dimer (at ∼−50°) or the left-handed dimer (at ∼+40°). (B) RMSD of the backbone atoms of the transmembrane domain (Leu75–Ile91) relative to the NMR structure as a function of time for the same replicas used in A. It can be shown that the calculated RMSD is well-correlated with the interhelical crossing angle. (C) Population of right-handed and left-handed dimers at the lowest temperature, 300 K, from a 20-ns replica-exchange simulation of two explicit helices (black) and an 11-ns replica-exchange simulation of one helix with the imposition of twofold symmetry (red), as a function of the interhelical crossing angle. The same simulation protocol was used when the twofold symmetry was imposed using the IMAGE facility in CHARMM (Brooks et al., 1983). The helices are considered as a dimer when their interhelical distance is <7 Å.

FIGURE 9.

Molecular graphics representation of GpA dimerization starting from 20 Å-separated helices (left). The dimers have the same orientations as used in Fig. 7.

Although the membrane GB/SA model with the replica exchange method is able to efficiently generate the correct configuration starting from 20 Å-separated helices, it might be worthwhile to investigate the origin of the high occupancy of the left-handed configuration, which is not observed in experiment. For this purpose, an additional MD simulation was performed starting from one of the left-handed structures. Various average properties for the right- and left-handed GpA dimers are summarized in Table 5. The buried surface area of the left-handed configuration is slightly larger than that of the right-handed one. This is an unexpected result because the right-handed configuration was thought to provide the closest packing in the GpA dimerization (MacKenzie et al., 1997; Smith et al., 2001). In fact, the close packing of the left-handed dimer is attributed to a break of the twofold symmetry. As shown in Fig. 9, Gly83 in one monomer of the left-handed dimer becomes interlocked between Gly79 and Gly83 in the other monomer, whereas in the right-handed dimer the close packing occurs between the glycine residues at both positions 79 and 83. This interdigitation of the left-handed dimer results in the fact that one of its monomers has a larger tilt angle and, consequently, the dimer also has a significant tilt, as shown in Table 5. Similarly, the influence of breaking twofold symmetry is also distributed over the various energy contributions, and results in an ∼11 kcal/mol energy (solvent renormalized free energy) difference between right- and left-handed dimers. This energy difference is significantly larger than the free energy difference estimated from the population at 300 K in the replica exchange method. The large fluctuation in the MD free energy made the exchange of the two configurations possible at 300 K, despite the 11 kcal/mol energy difference. To explore whether symmetry-breaking is the origin of the high population of the left-handed dimer, we imposed twofold symmetry, using the IMAGE facility in CHARMM (Brooks et al., 1983), on one of the monomers during the course of replica exchange simulations analogous to those carried out on the full dimer structures. As shown in Fig. 8 C, twofold symmetry greatly stabilizes the correct right-handed dimer, shifting the populations of right-handed and left-handed dimers to 95:5.

TABLE 5.

Various average properties of right- and left-handed GpA dimers

			Energy, kcal/mol‡
	Buried area,* Å2	Tilt angle,† degree	𝒲	Uint	Uvdw	𝒲elec	ΔGnp
Right-handed configuration
dimer	186.5 ± 30.7	5.7 ± 2.7	332.4 ≥ 19.8	758.2 ± 20.5	−128.8 ± 10.2	−335.3 ± 10.5	38.3 ± 1.8
monomer1	–	21.8 ± 3.7	194.7 ± 13.9	379.0 ± 14.2	−38.6 ± 6.9	−166.1 ± 7.5	20.3 ± 1.9
monomer2	–	21.6 ± 3.9	194.6 ± 13.8	379.2 ± 14.2	−38.1 ± 7.1	−166.7 ± 7.7	20.2 ± 1.8
Left-handed configuration
dimer	188.0 ± 82.1	19.7 ± 4.1	321.7 ± 20.0	765.9 ± 20.4	−137.1 ± 9.9	−341.2 × 10.3	34.3 ± 1.7
monomer1	–	26.5 ± 3.5	188.1 ± 13.9	382.1 ± 14.2	−44.0 ± 6.7	−166.7 ± 6.8	16.6 ± 1.4
monomer2	–	18.8 ± 0.5	196.4 ± 14.2	383.8 ± 14.7	−38.5 ± 7.0	−169.1 ± 7.4	20.2 ± 1.4

The average and fluctuations of right- and left-handed GpA dimers were calculated from 2.6-ns trajectories (after 0.6 ns) for each run. The trajectory for the D2 simulation in Table 3 was used for the right-handed configuration.

^*The buried surface area was calculated using the contact surface defined by the van der Waals radii.

^†The tilt angle is defined the same as in Table 3.

^‡All the energy terms are defined as in Tables 1 and 2.

CONCLUDING DISCUSSION

Based on the volume integration approach in generalized Born (GB) electrostatics theory (Lee et al., 2002, 2003; Im et al., 2003), we reformulated the calculation of the self-electrostatic solvation energy to take into account the influence of a model of the biological membrane. Consistent with continuum PB theory, the membrane is represented approximately as a semi-infinite planar low-dielectric slab. The present membrane GB model closely reproduces the PB electrostatic solvation energy profile across the membrane. The nonpolar contribution to the solvation energy is approximated by the product of solvent-exposed surface area and a phenomenological surface tension coefficient. In this context, it is implicitly assumed that protein-to-lipid nonpolar interactions are uniform because the surface area becomes zero inside the membrane. Despite these simplifications of the detailed microscopic protein-to-lipid interactions, the present membrane model appears to capture the essential features of biological membranes, i.e., their unique hydrophilic and hydrophobic heterogeneous environment.

To illustrate reliability and potential applications of the present membrane GB/SA theory, three membrane proteins were chosen for study. These included melittin from bee venom, the transmembrane domain of the M2 protein from Influenza A (M2-TMP), and the transmembrane domain of glycophorin A (GpA). The key role of biological membranes as low-dielectric media providing driving forces for hydrophobic and hydrophilic group segregation was illustrated with melittin, in which the charged groups initially buried inside the membrane were quickly translocated into the high dielectric solvent region. The results suggest that the method can be used to generate initial structures for detailed MD simulations when there is no detailed structural information about the membrane-bound state. Interestingly, three membrane-bound states were observed; an early stage membrane-bound state on the surface of the membrane, a membrane-anchored state with the N-terminus inside the membrane, and a transmembrane-spanning state. Detailed energy analysis and simulations with the replica exchange method showed that all these states are accessible at 300 K.

The extent of tilt of M2-TMP relative to the membrane surface was examined as a function of the thickness of the hydrophobic core, h_memb. In general, the tilt is increased as the thickness decreases. For example, the tilt of M2TMP was changed from 43° when h_memb = 25 Å to 28° when h_memb = 29 Å. This result is consistent with the “hydrophobic mismatch” concept that transmembrane proteins or peptides should tilt or kink when their transmembrane hydrophobic length is too long to match the bilayer to overcome an energetically unfavorable mismatch (de Planque et al., 1998). However, our results appear to be inconsistent with the solid-state NMR experiments, which suggest M2-TMP has a tilt of 37 ± 3° in DMPC (h_memb = ∼25 Å) and 33 ± 3° in DOPC (h_memb = ∼29 Å) (Kovacs et al., 2000). Since M2-TMP probably exists in a tetrameric form in the NMR experiments (Kovacs et al., 2000), the present results suggest that the dependence of the tilt angle on the membrane thickness may be less sensitive in a tetrameric form of M2-TMP (oligomerization) than in its monomeric form. This idea was demonstrated in the case of the GpA dimer. It was also shown that the present membrane model with the replica exchange method is able to correctly fold a single transmembrane domain of a membrane protein from a fully extended conformation.

As a final illustration of our method, the dimerization motif of the GpA transmembrane domain and its attendant helix-to-helix interactions were examined. MD simulations starting from one of the solution NMR structures of MacKenzie et al. (1997) showed that the important dimerization motif remained stable and the dimer was stabilized mostly by van der Waals interactions. The comparison with NMR interhelical distance data reveals that the close packing between glycine residues at positions 79 and 83 is quite similar to the solid-state NMR data of Smith et al. (2001). Modeling of transmembrane helix-to-helix interactions is of great importance in prediction of transmembrane helical bundles or oligomerization, but it is still a difficult problem despite the progress in computational methodologies. Here, the present membrane model with the replica exchange method was able to efficiently generate the correct right-handed dimer configuration with an RMSD of ∼1.2 Å, starting from 20 Å-separated helices, although a left-handed dimer, which is not observed in experiments, was also observed at the lowest temperature.

The main applications of the present method are the study of folding and assembly of membrane proteins. Furthermore, it might be very desirable to use the method in structure refinement and modeling of membrane proteins for which a limited number of experimental observables are available. Efforts in these directions are currently in progress. At the same time, it is an ongoing project to improve the present membrane model and its accuracy.