Thermodynamics of Heat Activation of Single Capsaicin Ion Channels VR1

Abstract

Temperature affects functions of all ion channels, but few of them can be gated directly. The vanilloid receptor VR1 provides one exception. As a pain receptor, it is activated by heat >42°C in addition to other noxious stimuli, e.g. acids and vanilloids. Although it is understood how ligand- and voltage-gated channels might detect their stimuli, little is known on how heat could be sensed and activate a channel. In this study, we characterized the heat-induced single-channel activity of VR1, in an attempt to localize the temperature-dependent components involved in the activation of the channel. At <42°C, openings were few and brief. Raising the ambient temperature rapidly increased the frequency of openings. Despite the large temperature coefficient of the apparent activity (Q₁₀ ≈ 27), the unitary current, the open dwell-times, and the intraburst closures were all only weakly temperature dependent (Q₁₀ < 2). Instead, heat had a localized effect on the reduction of long closures between bursts (Q₁₀ ≈ 7) and the elongation of burst durations (Q₁₀ ≈ 32). Both membrane lipids and solution ionic strength affected the temperature threshold of the activation, but neither diminished the response. The thermodynamic basis of heat activation is discussed, to elucidate what makes a thermal-sensitive channel unique.

INTRODUCTION

The burning sensation felt by the consumption of hot peppers is caused by the active ingredient capsaicin (Jancso et al., 1967). A similar response is also evoked by tissue damage, believed to be caused by the acidification of the extracellular matrix and exacerbated by high temperatures and proinflammatory agents released from damaged cells (Szallasi and Blumberg, 1999). The similarity and cross-sensitization between heat-, capsaicin-, and acid-induced responses led the way to the discovery of convergent transduction mechanisms for peripheral pain sensation (Cesare and McNaughton, 1996; Caterina et al., 1997).

In search of proteins involved in capsaicin-related pain sensations, several homologous ion channels have been cloned. The predicted membrane topology of these channels places them in the superfamily of channels with six transmembrane domains, which includes the transient receptor potential (TRP), voltage, and cyclic-nucleotide-gated channels. Sequence homology suggests that they are closest to the family of TRP channels, and because the first clone (VR1) was activated by the vanilloid capsaicin, they were subgrouped as TRPV or vanilloid receptor (VR; Gunthorpe et al., 2002; Montell et al., 2002). However, only VR1 in the family is known to have the vanilloid sensitivity. The channels that respond to temperatures are more diverse, including VR-OAC/TRPV4, which is activated at moderate temperatures >27°C (Guler et al., 2002), VRL3 (TRPV3), and VR1 (TRPV1), which have higher thresholds at ≥39 and 42°C, respectively (Smith et al., 2002; Xu et al., 2002; Peier et al., 2002b; Caterina et al., 1997), and VRL1 (TRPV2), which responds only to extremely high temperatures (>50°C; Caterina et al., 1999). There are also ion channel receptors that respond to temperatures but do not belong to the TRPV group, such as the menthol/cool receptor (CMR/TRPM8; McKemy et al., 2002; Peier et al., 2002a) and the cold receptor (ANKTM1; Story et al., 2003), which are activated by cool temperatures in the range of 23–28°C and the noxious cold at <10°C, respectively. The presence of these receptors with different activation thresholds has been suggested to provide the ability to distinguish between the slightest temperature gradients (Julius and Basbaum, 2001).

Temperature affects all biological processes, including the gating of ion channels. Generally, a reaction with Q₁₀ > 2 is suggestive of a significant temperature-dependent event. The Q₁₀ for the gating of most ion channels is ∼2–3 (Hille, 2001), but some have been shown to be as high as 5–10 or even above (DeCoursey and Cherny, 1998; Lee and Deutsch, 1990; Murrell-Lagnado and Aldrich, 1993; Nobile et al., 1997; Beam and Donaldson, 1983; Boheim and Benz, 1978; Kirsch and Sykes, 1987; Pusch et al., 1997; Chiu et al., 1979). Yet, even the channels with a high temperature-dependence cannot be directly activated by temperature alone. To this extent, VR1 is quite remarkable. Previous whole-cell studies have shown that the channel has a Q₁₀ > 20 in response to a temperature ramp in the absence of any extrinsic activator (Welch et al., 2000; Vlachova et al., 2003, 2001; Vyklicky et al., 1999; Nagy and Rang, 1999). As a result, it has been suggested to function as a physiological noxious heat sensor (Caterina et al., 1997).

Several recent studies have examined the molecular determinants in VR1 activation. Chimeras with the chick isoform and VRL1, both capsaicin-insensitive, revealed the ligand-binding domain to involve the intracellular linker between TM2 and TM3 (Jordt and Julius, 2002). Resinferatoxin was further shown to require part of TM2. A subsequent study showed that ligand-dependent activation also requires at least the first 70 residues proximal to TM6 (Jung et al., 2002) as well as a triplet of residues in TM6 (Kuzhikandathil et al., 2001). In addition, mutagenesis studies suggested that proton activation and potentiation involves separate acidic residues in the extracellular pore loop between TM5 and TM6 (Jordt et al., 2000; Welch et al., 2000; Garcia-Martinez et al., 2000). PKC-dependent potentiation was also shown to involve residues in the C-terminal and TM2–TM3 loop (Numazaki et al., 2002). Lastly, two Walker motifs, one at each terminal, were identified as being involved in ATP-dependent potentiation of capsaicin activity (Kwak et al., 2000). It appears that at least four main regions are required for the activation/function of VR1: the TM2–TM3 linker including parts of TM2, TM6, and the proximal portions of the C-terminal, the N-terminal, and the extracellular pore loop.

Much less is known about the mechanism of the activation of VR1 by heat. The existing studies have been mostly based on nonstationary whole-cell recordings (Cesare and McNaughton, 1996; Tominaga et al., 1998; Vyklicky et al., 1999), which are unfortunately complicated by the fact that they measured a conglomeration of multiple events, yielding little information on the origin of the heat sensitivity. The purpose of this study was to localize the specific effects of temperature on the activation of the channel. In particular, we examined the unitary conductance, the activation kinetics, and the contributions of lipids and ionic strength. We determined the kinetics of activation by deducing a minimal number of closed and open components from maximal likelihood fits of the dwell-time sequence. By resolving these components, it was found that the heat sensitivity of the channel resides mostly on its initial activation phase. The subsequent gating, along with the unitary current amplitudes, has a temperature dependence typical of those of other ion channels. Membrane lipids and ionic strength both have an effect on the temperature threshold of the activation, but neither diminishes the response. We discuss the thermodynamic basis of how temperature might activate a channel and the structural implications.

METHODS AND MATERIALS

Channel expressions

Experiments were done on two expression systems. The oocyte expression system was used for single-channel recordings. Rat VR1 from dorsal root ganglia cloned in pFROG vector, generously provided by Dr. David Julius (Jordt et al., 2000; Caterina et al., 1997), was linearized by MluI digest. In vitro transcription was performed using T7 RNA polymerase via the mMessage mMachine kit (Ambion, Austin, TX). The final cRNA was resuspended in RNAse free water to approximately 1 ng/nl, and kept at −80°C. Xenopus laevis oocytes were surgically removed and enzymatically separated using collagenase as described previously (Hui et al., 2003). Oocytes were microinjected with 0.5–50 ng of the cRNA 1 day after and incubated in Ringer's solution at 15°C until use. Patch-clamp recordings usually took place 2–8 days after, which gave a high success rate of capturing single channels.

Whole-cell experiments were conducted on the human embryonic kidney cell line (HEK 293; American Type Culture Collection, Rockville, MD). Cells were maintained in DMEM plus 10% fetal bovine serum (Hyclone Laboratories, Logan, UT) with 1% penicillin/streptomycin. Transfection took place usually at a confluency of 80% using the standard calcium phosphate precipitation method. VR1 in pFROG (0.5–10 μg/0.2 ml) was cotransfected with either GFP or CD8 (0.5 μg/0.2 ml). Electrophysiological recordings were made 10–28 h after. For cells that were cotransfected with CD8, they were incubated briefly before experiments with Dynabeads M450 conjugated with antibody to CD8 (0.5 μl/ml; Dynal, Lake Success, NY). Cells that expressed CD8 became coated with beads, which served as a visual marker for identifying transfected cells (Jurman et al., 1994).

Electrophysiology

Patch pipettes were fabricated from borosilicate glass (Sutter Instrument, Novato, CA), coated with Sylgard (Dow Corning, Midland, MI), and fire-polished. Series resistance ranged from 0.5 to 2.5 MΩ for whole-cell recordings and from 6 to 10 MΩ for single-channel recordings in their respective bath solutions. Currents were recorded using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA). The data were low-pass filtered to 10 kHz, digitized at 25 kHz through a BNC-2090/MIO acquisition system (National Instruments, Austin, TX), and recorded with a custom-designed software using Labview 5.1 (National Instruments). Whole-cell recordings were made at a holding potential of −60 mV. Single-channel currents were recorded from excised patches at a membrane potential of +60 mV (intracellular positive). The presence of single VR1 channels in the patch was confirmed by application of high capsaicin (>1 μM) and block by capsazepine. Only patches with one channel were used for single-channel analysis.

For whole-cell recordings from HEK 293 cells, the standard bath solution contained (mM): 150 NaCl, 10 EGTA, and 10 HEPES, at pH 7.4 (adjusted with NaOH). The internal pipette solution contained (mM): 150 KCl, 5 EGTA, and 10 HEPES, at pH 7.4 (adjusted with KOH). For single-channel recordings from oocytes, the bath and pipette solutions were symmetrical and contained 100 mM NaGluconate and 10 mM NaCl instead of 140 mM NaCl, and other components were the same as for HEK 293 cells. Capsaicin and capsazepine were dissolved to a concentration of 0.1–10 μM and 10 μM, respectively, in the corresponding recording solutions from a 1 mM ethanol-dissolved stock (0.001–0.1% final ethanol). Drug delivery was controlled by a gravity-driven local perfusion system (ALA Scientific Instruments, Westbury, NY). The perfusion solutions were the same as the bath solutions except for appropriate agonist or antagonist. Unless stated, all reagents were purchased from Sigma (St. Louis, MO). Capsaicin, with purity ≥98%, was from Fluka through Sigma, and capsazepine from Precision Biochemicals (Vancouver, BC, Canada).

Temperature control

The temperature was controlled by constant perfusion of recording solution through an inline SH-27B heater powered by a TC-324B temperature controller (Warner Instruments, Hamden, CT). In some experiments, a Peltier device was mounted on the metal plate around the recording chamber to raise the base temperature and reduce the time required for heating. A custom-made two-bath chamber was used, where the recording was made in the small chamber, which is narrow and has a rectangular shape, to minimize heat dissipation and local temperature fluctuations. The oocyte was maintained in the large bath at ambient temperatures. Upon excision from cell, the patch was steadily moved to the recording bath. Heat stimulus was applied by exchanging the entire contents of the recording bath. The patch pipette was placed at a relatively fixed position, ∼5 mm from the outlet of the inline heater. There was a temperature drop of ∼3–5°C between the internal temperature of the heater and the bath temperature at the pipette tip. Before experiments, this temperature drop was carefully measured to calibrate the heater temperature (by adding the drop to the desired temperature of the patch). The actual temperature of the patch during an experiment was monitored with a miniature thermocouple (Warner Instruments) placed ∼1 mm from the pipette tip. The temperature drop between the tip and the thermocouple is <0.5°C throughout the entire tested temperature range (40–50°C). Since the analysis was done with a resolution on the order of 1°, this temperature drop was considered insignificant, and the reported temperatures correspond to the readouts of the thermocouple without corrections.

Constant temperature stimuli were used for single-channel measurements. The duration of each stimulus was variable, ranging from seconds to minutes. At lower temperatures, the channel opened less frequently and the recording usually lasted longer so as to accumulate a reasonable number of events. An individual patch could sustain up to 3–4 temperature changes. The temperature was jumped usually in an ascending order, without explicitly cooling the solution to the ambient temperature. The interstimulus period was variable, on the order of 10–30 s, depending on the response time of the heater. Data collection began a few s after the temperature reached its steady state. During analysis, the unitary amplitude was carefully examined to ensure constant stimuli. The data within the first few s of the recording was usually discarded to ensure that only the data at equilibrium was analyzed.

One technical problem we encountered in single-channel recording at high temperatures (>45°C) was the occurrence of large electrical spikes, which appeared to be generated from the condensation of evaporated solutions into small water droplets near the pipette tip and fusion of such small droplets into large ones. The problem was overcome by application of a thin layer of mineral oil onto the bath above the pipette tip to minimize the evaporation of the solution.

Cholesterol enrichment and depletion

The cellular cholesterol content was manipulated by incubating cells with methyl-β-cyclodextrin (MβCD) either loaded with or without cholesterol. This cyclic oligosaccharide has a hydrophilic surface and a hydrophobic cavity that binds cholesterol with a high affinity and has been widely used as an effective tool to transport cholesterol into and out of cell surfaces. To increase the cholesterol level in the membrane, cholesterol-enriched MβCD-cholesterol complex was supplemented into serum-free DMEM, resulting in a concentration of 2.5 mM MβCD and 0.21 mM cholesterol. Cells were then incubated in a humidified CO₂ incubator at 37°C. To decrease the cholesterol content, cells were treated similarly except that they were incubated with MβCD containing no cholesterol. The incubation times were ∼2.5–3.5 h for cholesterol enrichment and ∼2 h for depletion. Prolonged incubation times were attempted, but appeared to be toxic to cells. Before experiments, MβCD and free cholesterol were washed off either with DMEM or recording solution. MβCD-cholesterol complexes were prepared following the procedure described by Christian et al. (1997). Both MβCD and cholesterol were purchased from Sigma.

Data analysis

Before analysis, data were usually corrected for slow and nonperiodic baseline drifts using manually specified piece-wise linear functions. Bursts of openings were identified using a fixed closed criterion, τ_crit = 50 ms, with little open activity (P_o < 0.01%). The value of τ_crit was chosen so that it could sufficiently distinguish the longest closures (interburst gaps) from the others that were concentration-independent, as verified by the duration histograms. Gaps (long closures) that separate the bursts were detected similarly.

Single-channel currents were idealized using a segmental k-means method based on hidden Markov modeling (HMM) (Rabiner et al., 1986). The data was modeled as a discrete Markov chain embedded in white background noise. Starting from a set of initial model parameters including current amplitudes, noise variances, and transition probabilities, a most likely dwell-time sequence was detected via the Viterbi algorithm (Forney, 1973). From the resultant idealization, the model parameters were refined, and the entire process was repeated until the likelihood of the idealized dwell-time sequence reached its maximum. Upon convergence, the mean lifetimes and occupancy probabilities of the channel were calculated. An amplitude probability density was then constructed from the amplitude and noise variance estimates, and was superimposed with the all-points amplitude histogram for validation of results. The idealized dwell-time sequence was also carefully compared with the raw data for assessment of the detection accuracy. Compared with the half-amplitude threshold detection, the approach requires less filtering and therefore permits reliable detections of events at a relatively high bandwidth (10 kHz). Although the approach initially requires a kinetic model, the results are insensitive to the details of the model. Normally, a model with one open and two closed states was sufficient for satisfactory idealization.

The idealized dwell-time sequences were analyzed using a full-maximum-likelihood approach (Qin et al., 1996, 1997). Iterations of the algorithm were terminated when the gradients of all parameters were sufficiently small. Precautions were always taken for possible local maximums by starting the algorithm with different initial values of rate constants. The effect of missed events was corrected by imposition of a fixed dead-time of 40 μs, which corresponds to the sampling duration and is approximately equal to the rise-time of the low-pass Gaussian filter applied (33 μs). Because no kinetic scheme is available for VR1, a fully connected but uncoupled model (Hui et al., 2003) was employed. Models of such a topology have a generality to ensure the complete use of all information in the data and the analysis results are essentially independent of particular models. For each fitting, the open and closed dwell-time distributions were calculated and superimposed with the experimental histograms for visual validation of the goodness of fit. The number of kinetic components was determined by gradually increasing the complexity of the model until little improvement in the final likelihood values as well as a tight superimposition between the predicted distributions and the histograms. At the end of fitting, various properties of the model such as the time constants and areas of individual closed and open components were determined. The couplings between closed and open components were evaluated from the two-dimensional (2D) dwell-time distribution by calculating the relative volume of each 2D component in the distribution.

RESULTS

Single-channel activity

The heat activity of VR1 arises from a membrane-bound mechanism. It was observed from both outside-out and inside-out patches. However, the amount of activity appeared somewhat dependent on the patch configuration. In general, the inside-out patches exhibited more robust responses particularly to high temperatures. The outside-out patches sometimes showed only marginal increases or even “disappeared,” possibly due to rundown of the channel, at high temperatures. The underlying mechanism for this difference is unclear. To minimize the heterogeneity, we have limited our analysis to the data recorded from inside-out patches.

The single-channel activity of the channel occurred at about the same temperature threshold as the whole-cell currents, ∼40–42°C. Fig. 1 illustrates an example of the activity from a representative patch. Below the threshold, openings were few and brief, sometimes clustered into short bursts. As the temperature was elevated, more openings occurred and bursts became prolonged. On the other hand, the long closures (gaps) decreased in their durations. This combination of increased openings, longer bursts, and shorter gaps led to a sharp increase in overall activity, and appeared to be a general mechanism for the activation to the channel, as it was also observed in the currents evoked by other types of stimuli.

FIGURE 1.

Heat-evoked single-channel activity in oocytes expressing VR1. The temperature was elevated from 25 to 50°C, activating the channel at ∼42°C. Both channel opening and unitary current amplitude increased with temperature. Data were acquired from an inside-out patch at a holding potential of −60 mV, and low-pass filtered at 1 kHz for display.

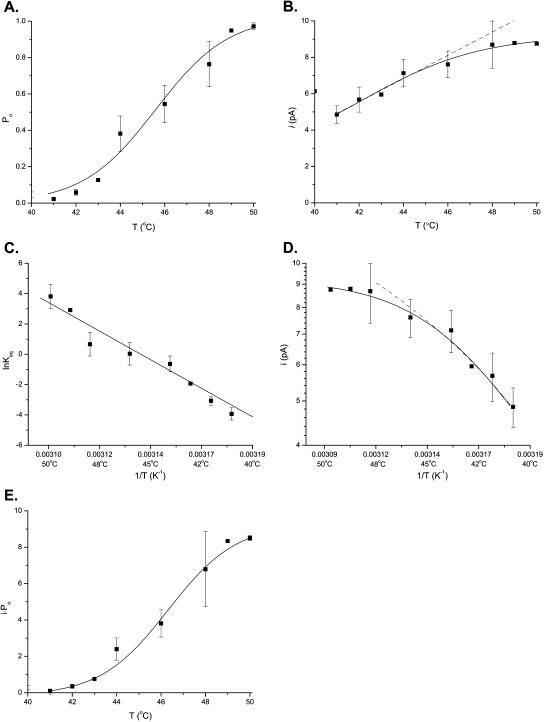
Fig. 2 A shows the dose-response curve of the single-channel P_o averaged from 21 experiments. Similar to ligand or voltage-gated channels, the increase of P_o was sigmoidal with a steep slope and negligible activity below the activation point. At 50°C the activity did not saturate, but the trend appeared to approach unity, suggesting that heat alone may fully open the channel. The temperature coefficient of the single-channel activity was estimated to be Q₁₀ = 26.9 ± 8.4 over the range of 41–50°C. This value is comparable to the lower estimates from whole-cell currents (Welch et al., 2000; Vlachova et al., 2003, 2001; Vyklicky et al., 1999; Nagy and Rang, 1999), indicating that the kinetics is the major contributor to the temperature-sensitivity of the channel.

FIGURE 2.

Temperature dependence of single-channel P_o and unitary current amplitude of VR1 from inside-out patches. (A) The single-channel P_o exhibited a sigmoidal increase with temperature. The response initiated at ∼42°C with a half-activation threshold at 45.6 ± 0.4°C, and appeared to saturate after 50°C. (B) The unitary current amplitude was temperature dependent also, albeit to a lesser degree. (C) The van't Hoff plot of the equilibrium constant, K_eq, determined from the open channel probability (P_o). The plot could be approximately regressed by a linear line, corresponding to an enthalpy ΔH = 150 ± 13 kcal/mol and entropy ΔS = 470 ± 40 cal/mol · K, respectively. The equation used for fitting is described in the text. (D) The van't Hoff plot of the unitary current of VR1. The plot was approximately linear in the lower temperature ranges (41–45°C; right part of the curve) but became saturated at high temperatures (>45°C; left part). A linear regression of the values at the low temperature range (41–45°C) resulted in an activation energy of ΔH = 33 ± 4 kcal/mol. (E) Expected temperature dependence of whole-cell currents as determined from the unitary current amplitude and single-channel P_o. Similar to single-channel P_o, the product activates at ∼42°C and saturates at >50°C. In contrast, however, it is more strongly dependent on temperature, with a Q₁₀ = 40.5 ± 14.4. Recordings were made at the holding potential of −60 mV. Each point represents 11 experiments for P_o and the unitary current amplitude.

The unitary current amplitude of the channel increased with temperature too, but the dependence is much weaker than that of its kinetics (Fig. 2 B). The temperature coefficient of the current amplitude was estimated ∼Q₁₀ = 1.42 ± 0.12 between 41 and 50°C. The Arrhenius plot of the amplitudes yielded an activation energy of ∼7 kcal/mol, assuming the conduction could be treated as a simple rate process. This value is higher than the activation energy of electrolyte conductivity (3.58 kcal/mol; Conway, 1981), but comparable to that of other ion channels (Hille, 2001). The Arrhenius plot is approximately linear at the lower temperature part, but deviates at high temperatures. Similar nonlinearity has also been reported for other types of ion channels (Anderson et al., 1977; Quartararo and Barry, 1988; Urry et al., 1984; Milburn et al., 1995). The violation of the linearity may suggest that the permeation of the ions involves a more complicated energy profile, or that the structure of the pore is not static with temperature.

The temperature dependence of the single-channel P_o allows estimation of some thermodynamic properties of the channel, in particular, the enthalpy and entropy between closed and open conformations. The free energy difference between the two conformations

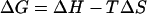can be related to the single-channel P_o by

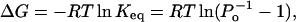which leads to the van't Hoff equation

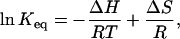where K_eq is the equilibrium rate constant, R is the molar gas constant, and T is the absolute temperature. Fig. 2 C shows the van't Hoff plot of lnK_eq using the same data in the dose-response curve. The plot follows a general linear trend, suggesting that ΔH and ΔS could be considered to be independent of temperature. A linear regression of the data gave an estimate of enthalpy ΔH = 150 ± 13 kcal/mol and entropy ΔS = 470 ± 40 cal/mol · K, respectively. These values are quite large, with the enthalpy on the order of ≥30 hydrogen bonds (ΔH = 2–5 kcal/mol), suggesting that the activation of the channel is accompanied with an enormous energetic increase, which is indicative of a highly cooperative process involving large conformational changes.

Despite the large increase in enthalpy and entropy, the free energy difference between the closed and open conformations is relatively small. With P_o = 0.04 at 40°C and 0.98 at 50°C, ΔΔG lies between 2 and −2 kcal/mol over the temperature range. This is close to the thermal energy RT = 0.622 kcal/mol at 40°C. In contrast to enthalpy and entropy, an increase of temperature lowers the free energy of the open conformation as opposed to the closed one. The zero-crossing point of ΔΔG is at ∼T_c = 46°C, above which the open conformation becomes more stable. The small free energy difference is made possible due to the simultaneous increase of enthalpy and entropy. The large increase in enthalpy is almost completely compensated by a large increase in entropy. At 50°C, the entropic energy amounts to TΔS = 152 kcal/mol, indicating that the entropy of the channel plays an essential role as a driving force to open the channel.

Given that both the conductance and the kinetics of the channel vary with temperature, we examined whether the combination of the two has a temperature dependence similar to that of whole-cell currents, in part to verify our single-channel analysis. Fig. 2 E shows the product of the two, i × P_o, plotted as a function of temperature. It exhibits a more rapid increase than the single-channel P_o, with a temperature coefficient estimated ∼Q₁₀ = 40.5 ± 14.4 between 41 and 50°C. This value is comparable to the higher estimates from whole-cell measurements (Vyklicky et al., 1999; Vlachova et al., 2001). It should be noted, however, that the whole-cell currents were typically measured at nonequilibrium using a temperature ramp, which is fundamentally different from the stimulus used in our experiments. Therefore, the difference of the Q₁₀ values may also reflect the use of different stimulus protocols.

Burst and gap durations are highly temperature dependent

Our previous study of capsaicin responses of VR1 suggests that the channel activation involves short openings occurring in brief bursts separated by long closures (gaps). Increasing ligand concentration has dual effects of shortening the gaps while prolonging the bursts. Inspection of the heat-activated single-channel currents suggests that it follows a similar pattern. Therefore, as a first effort to localize the specific steps in heat activation, we studied the temperature dependences of burst and gap durations.

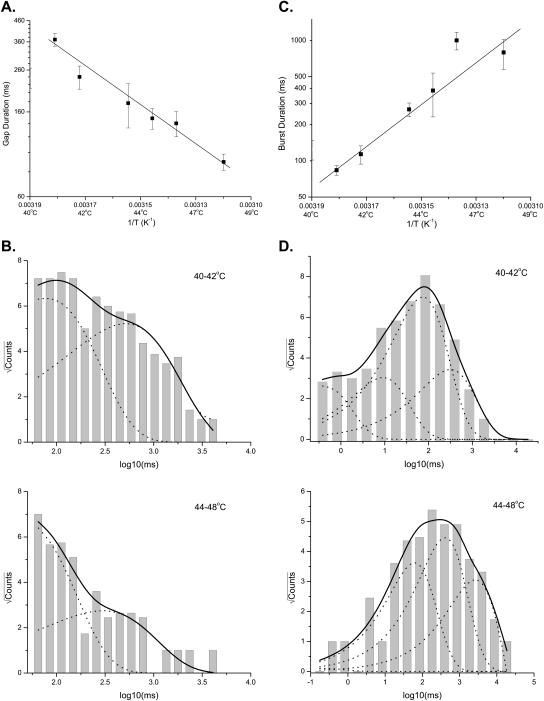
Fig. 3 A shows the mean gap duration at different temperatures. It exhibited a consistent reduction as temperature was increased. The change was significant; a linear regression of the data gave a Q₁₀ ≈ 7 at 40°C, which is considerably larger than the temperature coefficient of the gating of most ion channels reported in the literature. The actual temperature dependence of these gap durations is likely to be even higher since they tend to be underestimated at high temperatures because a significant portion of them may become shorter than the threshold and therefore go undetected. The strong temperature dependence of these long closures suggests that they may play an essential role as one of the temperature-sensitive steps in channel opening.

FIGURE 3.

Temperature dependence of gap and burst durations. (A) The mean gap duration showed a significant temperature dependence, with Q₁₀ ≈ 7 at 40°C. Increasing temperature reduced the gap duration. Assuming the gap duration reflects an opening rate of the channel, a linear regression of the Arrhenius plot yielded an activation enthalpy of ΔH ≈ 39.5 kcal/mol and an entropy of 100 cal/mol · K, respectively. (B) Distributions of the individual gap durations at two temperature ranges. Superimposed on the histograms are the best exponential fits, where the dotted lines represent the individual components and the solid lines correspond to the sums. A best fitting required at least two exponentials. The time constants of the fits were ∼80 and 524 ms for 40–42°C, and 45 and 303 ms for 44–48°C, respectively. (C) Temperature dependence of burst durations. Increasing temperature prolonged bursts. The bursts had a temperature dependence Q₁₀ ≈ 32. The line through the data points represents an Arrhenius fit of the durations, assuming that they are determined by a closing rate of the channel. The fit gave a deactivation enthalpy of ΔH ≈ −70 kcal/mol and an entropy of ΔS ≈ −123 cal/mol · K. (D) Distributions of individual burst durations. Fitting of the distributions resolved four exponential components with time constants (ms): 0.5, 10, 83, and 350 for 40–42°C, and 0.3, 69, 458, and 2922 for 44–48°C, respectively. The individual components are shown as the dotted lines whereas the sums are shown as the solid lines.

To determine the kinetic composition of the long closures, we examined their duration distribution. Unfortunately, the analysis was somewhat hindered by the scarcity of events, which arose partly due to their relatively infrequent occurrences and partly due to the difficulty of maintaining tight seals at high temperatures for long periods. As a compromise, we combined gaps from different temperatures to form two groups: those between 40 and 42°C and those >42°C, as shown in Fig. 3 B. As evident from the figure, each distribution could hardly be fitted with a single exponential. Instead, a visually adequate fit required at least two components. Because of its temperature dependence, the merging of the data over multiple temperatures could complicate the distributions and therefore biased the estimates of the components. Nevertheless, the presence of two components in the distributions suggests that the apparent long closures have a complex composition involving multiple kinetically distinct steps; otherwise, the short closed component at lower temperatures would necessarily be longer than the long component at higher temperatures.

The occurrences of the long closures probably precede the activation of the channel, since they are observed more frequently at low temperatures. Given their temperature dependence, we estimated the corresponding activation energy barrier that the channel has to surmount. Based on transition state theory, the temperature dependence of a rate constant is given by

where R is the molar gas constant and ν^† the prefactor of the rate (Hille, 2001). As a first-order approximation, we assumed that the rate is inversely proportional to the gap duration. From the linear regression of the temperature dependence of gap durations in Fig. 3 A, we estimated an activation enthalpy ΔH^‡ ≈ 40 kcal/mol (63RT) and an entropy ΔS^‡ ≈ 128 − R × lnν^† cal/mol · K. An exact value of the entropy requires the knowledge of the prefactor ν^†. For gas phase reactions of small molecules, the prefactor is ν^† = k_BT/h ≈ 5 × 10¹²/s, where k_B is the Boltzmann constant and h the Planck constant. But for large molecules in condensed phase such as aqueous solutions, it is largely unknown and depends on the specific conditions and the molecules involved. Recent measurements have put the value on the order of μs for protein folding (Yang and Gruebele, 2003; Portman et al., 2001; Hagen et al., 1997). Taking ν^† = 10⁶/s resulted in an activation entropy ΔS^‡ ≈ 100 cal/mol · K. The actual prefactor value is likely different, but the corresponding entropy is expected to remain close to the range of this estimate, given its logarithmic dependence on ν^†. For example, a 10-fold change in the prefactor results in a variation of only ∼2 cal/mol · K in ΔS^‡ (<2%). With the estimated enthalpy and entropy values, the height of the free energy barrier could be determined as ΔG^‡ = 8.2 kcal/mol (13 RT) at 40°C and 7.2 kcal/mol (11 RT) at 50°C, respectively. Activation involves only a small reduction (<2 RT) in the barrier height. It should be stressed that this small free energy change does not necessarily mean that the underlying conformational changes of the channel are small. To the contrary, the large enthalpy and entropy values suggest that the actual structural changes are large. The activation entropy is much less than the entropy change between closed and open states estimated from the equilibrium constant. This suggests that the transition state has a conformation closer to the closed channel than to the open one, and that there are additional large conformational changes occurring after the transition state.

Although the long closures are highly temperature-dependent, they cannot account for all the temperature dependence of the channel. The single-channel P_o has a Q₁₀ (27) much greater than that of the long closures, suggesting the existence of other temperature-sensitive elements. One such candidate is the burst duration, as shown in Fig. 3 C. The bursts became longer as the temperature was elevated, and the increase in duration had a Q₁₀ as high as 32. Assuming the burst duration reflects a closing rate of the channel, such a high Q₁₀ would imply a transitional (deactivation) enthalpy ΔH ≈ −70 kcal/mol · K and entropy ΔS ≈ −123 cal/mol · K, as determined from the linear regression fit in Fig. 3 C. These values were even higher than those of the opening rate of the channel as measured by the gap durations. For the same reason that led to underestimates of the gap durations, the absolute values of the burst durations could be overestimated, especially at high temperatures. However, the strong temperature dependence is evident, and contributes significantly to the overall temperature-sensitivity.

There are two possible mechanisms that may cause apparent increases of burst durations. One is that the closing rate of the channel is highly temperature dependent, and the other is that there are multiple types of bursts with different durations, and increasing temperature does not alter the burst durations, but shifts the equilibrium from short bursts to long ones, thereby leading to an apparent prolongation. We attempted to resolve the issue by examining the burst duration distributions, as shown in Fig. 3 D. Fitting of the distributions with sums of exponentials revealed four components in both low and high temperature ranges. The two most populated components exhibited similar time constants irrespective of temperature changes, which were ∼70–80 ms and ∼400 ms, respectively. They differed mainly in their relative populations. The shortest components of the two distributions also had a comparable time constant, <1 ms, corresponding probably to isolated openings. The distribution at the high temperature range showed an additional long component with a time constant ∼3 s. It was absent in low temperatures, presumably due to its low occurrence under such conditions. These results suggest that the apparent prolongation of the bursts can be attributed to the redistribution of multiple components in favor of long ones at high temperatures. The conclusion is also consistent with the findings on capsaicin activation, where a low level of stimulus evokes mostly short bursts, while a high level of stimulus favors the long ones (Hui et al., 2003).

Gating is weakly temperature dependent

The activation of VR1 involves multiple closed and open conformations. The long closures examined above represent only one of the many components in this complicated process. To obtain a more complete picture on the heat sensitivity of the channel, we further determined the temperature dependences of these components. In this part of analysis, the long closures were excluded, so that we could focus on the intraburst activity, where the channel openings and closings have a relatively homogeneous time span.

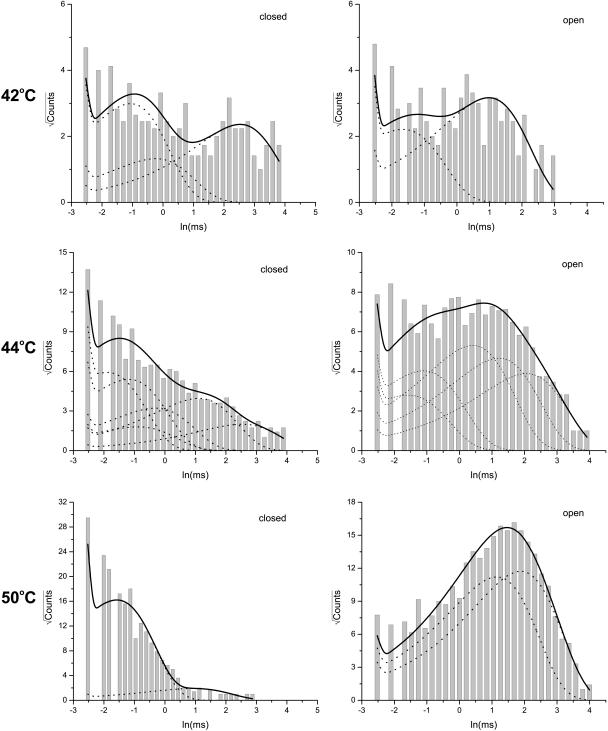
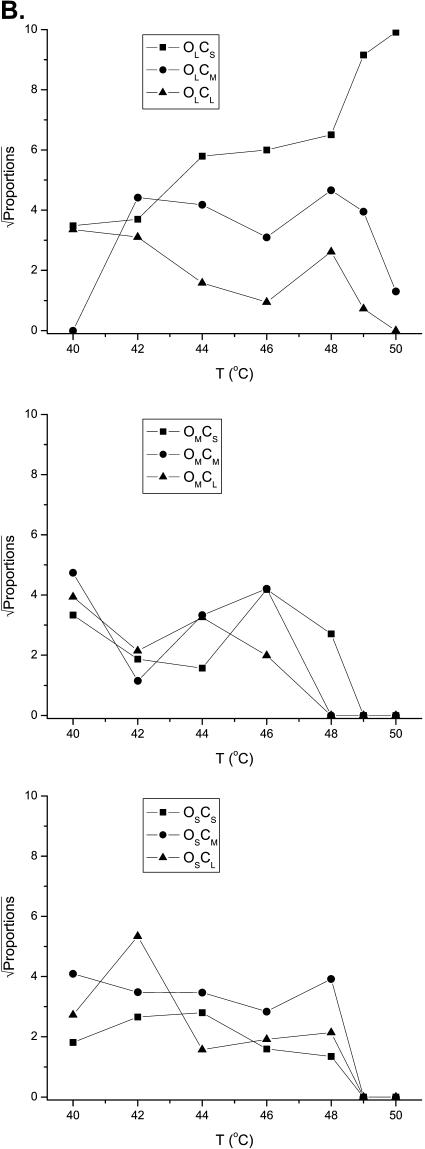
The kinetic components of the closures and openings were identified from the idealized dwell-time sequence by fitting them with uncoupled and fully connected models. Fig. 4 illustrates an example of the analysis results for the single-channel activity shown in Fig. 1. Multiple components were apparent from the dwell-time distributions for both closures and openings at each individual temperature. As temperature increased, the closed distributions left-shifted in favor of the short closures, whereas the open distributions right-shifted in favor of the long openings. The maximum likelihood fitting of the dwell-times revealed 2–6 closed and 2–5 open components across the temperature. The time constants and the relative proportions of these components are depicted in Table 1. The distributions in the intermediate temperature showed a more complex composition than at low and high temperatures, presumably because some of these components were not abundant at the extreme temperatures. At 50°C, the channel was mostly open, predominantly involving only the short closures and long openings.

FIGURE 4.

Dwell-time histograms for the experiment shown in Fig. 1. The data were analyzed at 10 kHz and idealized using the segmental k-means method. Only the intraburst activity was analyzed. The long closures with durations >50 ms were excluded. The resultant dwell-time sequences were subject to a dead-time of 40 μs. Superimposed with the histograms are the distributions predicted from the results of maximum likelihood fitting. The dotted lines show the contributions of individual components. For this particular experiment, 2–6 closed and 2–5 open states were necessary for an adequate fit across all temperatures. The time constants and proportions of the components are listed in Table 1.

TABLE 1.

Time constants (in ms) and relative proportions of the closed and open components determined from the maximum likelihood fits for the data shown in Fig. 4

Closed components
42°C	0.31 (52%)	0.71 (11%)	11.39 (37%)
44°C	0.14 (31%)	0.28 (30%)	0.37 (4%)	0.66 (12%)	2.73 (19%)	11.32 (5%)
50°C	0.19 (98%)	2.30 (2%)
Open components
42°C	0.18 (28%)	2.45 (72%)
44°C	0.19 (8%)	0.30 (17%)	1.37 (32%)	3.04 (26%)	7.10 (18%)
50°C	2.86 (48%)	5.94 (52%)

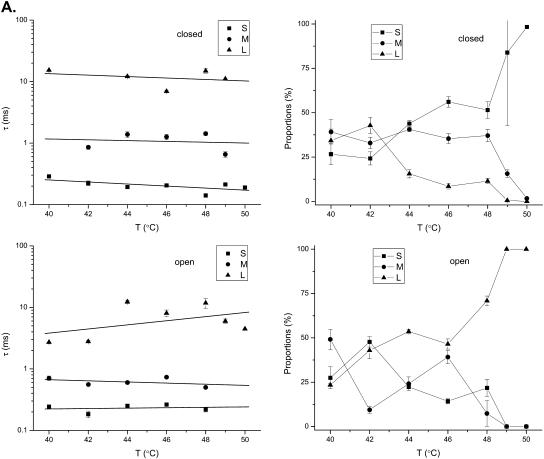
As explained in Methods, fitting a dwell-time sequence with an uncoupled and fully connected model allows a complete use of all kinetic information in the data. Such a fitting appeared to be more sensitive than the standard one-dimensional exponential fitting, and often resulted in more components. Some of the components had very similar time constants, as could be seen from the example shown above. It was also observed that the number of necessary components varied across temperatures and experiments. For the purpose of comparison, we took a strategy of grouping the components that had similar time constants. The mean time constant for each group was then calculated as the average of the individuals in the group with their proportions as the weighting factors. By doing so, both closed and open components fell into three groups, designated as S, M, and L for short, medium, and long, respectively. The ranges of the time constants of these groups are, in ms, 0–0.4, 0.4–5, and >5 for the closures; and 0–0.4, 0.4–1, and >1 for the openings.

Fig. 5 A shows the temperature dependences of the resultant components averaged from 21 experiments. Surprisingly, the time constants of all components exhibited only a low to moderate temperature dependence, with Q₁₀ < 3, as determined from linear fits of the pseudo rate-constants on semilog plots (Table 2). Among all components, the long openings showed the most significant increase with temperature. However, such a prolongation was also observed in pH-potentiated capsaicin activation (Ryu et al., 2003), raising the possibility that the increase may not be specific to temperature. In contrast to the rate constants, the relative proportions of the components were profoundly variable to temperature. At ∼40°C, the long closures were as frequent as the short ones. When the temperature was increased, the short closures became increasingly dominant, and by 50°C they became almost exclusive in the distribution. Conversely, the long openings, which were relatively rare at low temperatures, became favored at high temperatures, whereas the short openings, which were rich at low temperatures, were suppressed at high temperatures. Therefore, it appears that temperature mostly affected the equilibrium distributions among the different components, and only weakly their transition rates. This is reminiscent of the effect of capsaicin on the gating of the channel, suggesting a mechanism in which channel openings and closings may be accessible from either partial or full activation, and the stimulus acts to alter the level of activation and thereby the equilibrium distribution among the components, but has little effect on their time constants (Hui et al., 2003). It is also noted that although the time constants of the components are not very temperature-sensitive, the combination of the changes in their populations are likely to contribute to some extent to the observed temperature dependence of the P_o, since the increase of the occupancy of long openings and short closures are both in favor of channel openings.

FIGURE 5.

Temperature dependence of dwell-time components. (A) Time constants and relative proportions of the closed and open components plotted against temperature. Results were averaged from 11 experiments. The numbers of the resolved closed and open components were not all consistent across experiments and temperatures. However, they generally fell into three categories for both closures and openings, as evident from their time constant distributions. As such, they were grouped into three ranges: 0–0.4, 0.4–5, and >5 ms for the closures; and 0–0.4, 0.4–1, and >1 ms for the openings, which were named short (S), medium (M), and long (L), respectively. Degenerate components that belonged to the same group within an experiment were averaged with their relative proportions as the weighting factor. The resultant components exhibited a weak temperature dependence on their time constants. Increasing temperature had a more profound effect on their relative proportions. The solid lines through the data points on the time constant plots correspond to the best linear regressions. (B) Coupling between closed and open components, as determined from the relative volumes of the 2D exponentials in the 2D dwell-time distributions. The most significant coupling occurred between short closures and long openings. Increasing temperature further enhanced their occurrences. The couplings between other types of components were significant at low to medium temperature ranges, but tended to vanish at high temperatures.

TABLE 2.

Temperature coefficient and transitional enthalpy and entropy of the closed and open components averaged across experiments; the values were obtained from the linear regressions shown on the time constant plots in Fig. 5

Component	Q10 (40°C)	ΔH (kcal/mol)	ΔS (cal/mol · K)
CS	0.68	7.77	13.83
CM	1.34	−5.85	−32.24
CL	0.76	5.54	−1.20
OS	1.08	−1.50	−15.55
OM	0.81	4.20	0.48
OL	2.19	−15.73	−66.59

The correlations between the closed and open components were analyzed using the 2D dwell-time distributions. Fig. 5 B shows the coupling between adjacent closed and open dwell-times, as determined from the relative volumes of the individual 2D exponentials in the 2D dwell-time distributions. From the figure, it is evident that the short closures and the long openings were most significantly coupled, especially at high temperatures. This explains why the occupancies of these two components both increased with temperature, and suggests that they may be mechanistically correlated. Besides the short closures and long openings, no clear pattern was observed that might be suggestive of specific couplings between other states. Instead, it appears that all other closed and open components were coupled to each other nonexclusively, suggesting that the different types of openings may be accessible from any type of closures. This was also observed in the activation of the channel by other stimuli, alluding to the possibility that it may be a general mechanism involved in opening of the channel.

Effect of cholesterol on heat sensitivity

The activation temperature of VR1 coincides strikingly well with the phase transition point of lipid bilayers, both of which occur at ∼42°C (Yeagle, 1985). Eukaryotic cell membranes usually have a heterogeneous composition, which prevents phase transitions from occurring; but nonetheless, many of the temperature effects observed on the physical properties of pure lipids may be extended to biological membranes. This prompted us to investigate whether the heat sensitivity of VR1 is intrinsic to the lipid bilayer rather than to the channel protein itself. To address the issue, we examined the channel activity by altering the amount of cholesterol in the membrane, which is known to have a significant effect on the fluidity of the membrane. If the membrane fluidity is essential to VR1 activation, one might expect that the enrichment of cholesterol may be able to abolish channel activity.

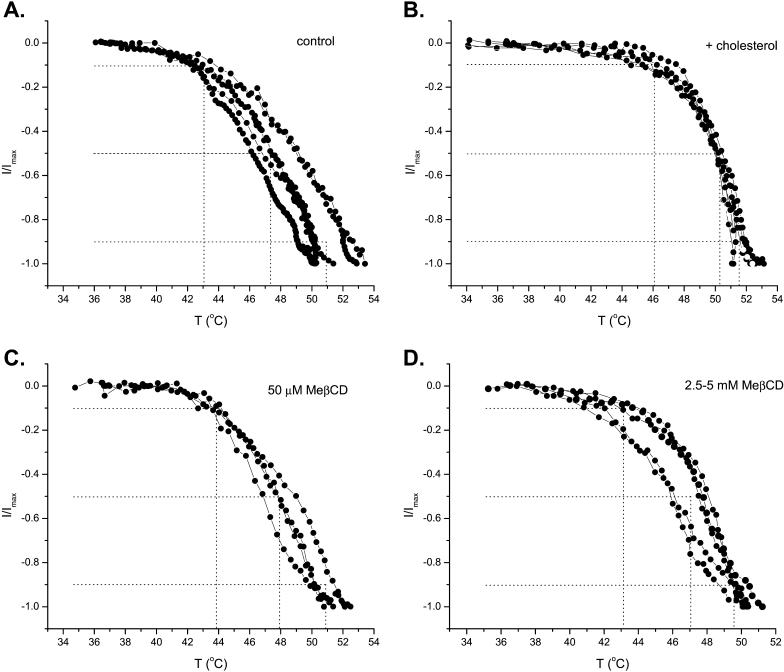
Both cholesterol enrichment and depletion were attempted. Fig. 6, A and B, shows the whole-cell currents recorded from VR1-transfected HEK293 cells with and without cholesterol supplement. The control cells exhibited a temperature response similar to those previously reported, with a threshold of ∼42°C and a half-activation at ∼47°C, and unsaturated by 50°C. After 2 h of incubation with cholesterol micelles, the cells were noticeably stiffer and more difficult to patch. For those cells that were patched, the activation temperature was significantly increased, with the 10% activation point shifted to ∼46°C and the half-activation point to ∼50°C. However, once above the temperature threshold, the activity increased rapidly with temperature, similar to that from untreated cells. There appeared to be quantitative differences in the slope of the temperature dependence of the activity. While the initial rise of the activity from its 10% to 50% level exhibited a similar rate (4°C), the second phase of the response (50–90%) became noticeably steeper after cholesterol enrichment. The overall temperature span of the activation from 10% to 90% was ∼6°C after enrichment as compared to 8°C for controls, indicating a considerable change in the slope of the temperature dependence (Student's t-test, p < 0.1, n = 5). Nevertheless, raising cholesterol amount in the membrane did not abolish the heat sensitivity of the channel, despite profound changes in the activation threshold.

FIGURE 6.

Effect of cholesterol enrichment and depletion on the heat response of VR1. The currents were recorded from VR1-expressing HEK 293 cells in whole-cell configuration using a ramp protocol stimulus (25–50°C in 40 s). The instantaneous currents at different temperatures were plotted. (A) Cells at the normal condition without any treatment exhibited an averaged response with the 10% and the half-activation at ∼43 and 47°C, respectively. (B) Incubation of cells in a high cholesterol solution right-shifted the activation temperature by 3–4°C. The depletion of cellular cholesterol with β-methyl cyclodextrin, either at 50 μM (C) or 2.5/5 mM (D), resulted in little change in the heat response. The half-activation of the currents remained at 47–48°C. Each trace in the figure represents a recording from a single cell.

In contrast to the enrichment experiment, cholesterol depletion was found to have little effect on the heat response of the channel (Fig. 6 C). After 2 h of treatment with 50 μM methyl-β-cyclodextrin, the cells became noticeably fragile, suggesting that the cholesterol content of the membrane had been significantly reduced. However, the whole-cell currents from these cells had approximately the same appearance as controls, with 10% activation occurring at 43–44°C and half-activation at 48°C. No significant changes were observed in either the activation temperature or the sensitivity.

Given the effect of cholesterol enrichment on channel activation, it is surprising that the depletion of cholesterol from the membrane produced no significant effect. To assert that the membrane cholesterol was successfully removed, we repeated the experiments with high concentrations of cyclodextrin at 2.5 and 5 mM. Again, no major changes were observed, as shown in Fig. 6 D. This suggests that the insensitivity to the cholesterol depletion in the previous experiment was not due to a low concentration of cyclodextrin. Cholesterol apparently only exerts its effect on channel activation when its concentration is high. The amount of cholesterol in the native membrane may be too low, so that its removal will not produce a noticeable effect.

Effect of ionic strength on heat sensitivity

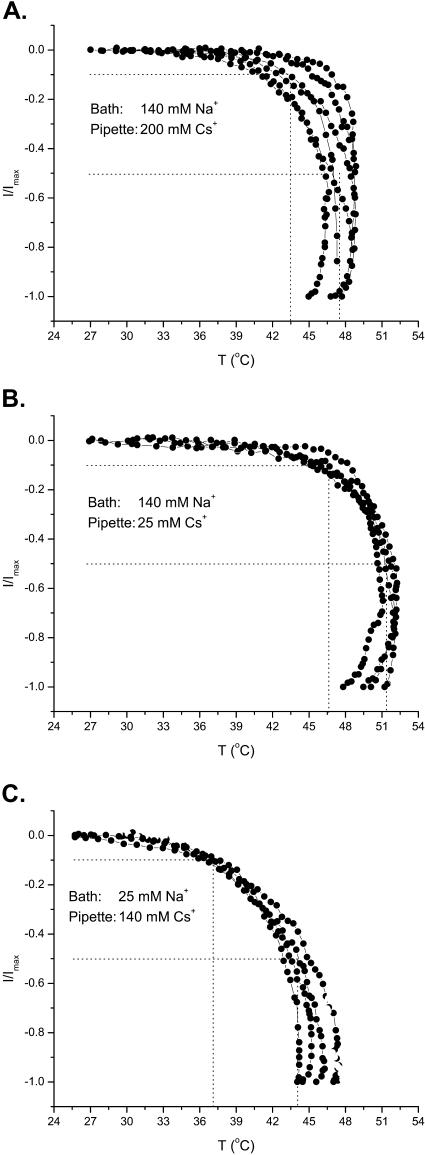
Besides the membrane, temperature affects physical properties of local aqueous environments of the channel. To evaluate whether this aqueous phase is critical, we examined the effect of ionic strength of both intracellular and extracellular solutions. Four conditions were considered: high (200 mM) and low (25 mM) on either side. For unknown reasons, the use of high ionic strength extracellular solution resulted in difficulty in maintaining seals at high temperatures. Therefore, only the results from the other three conditions are reported below.

As shown in Fig. 7 A, the whole-cell currents obtained at the high intracellular ionic concentration exhibited considerable variations in both activation temperature and response sharpness between experiments. On average, however, the currents reached the 10% activation at ∼43°C and the half-activation at ∼47–48°C, both of which resembled those at control conditions. On the other hand, lowering the intracellular ionic concentration produced a more consistent effect (Fig. 7 B), with 10% activation occurring at 46–47°C and half-activation at 51–52°C. The current responses were right-shifted by ∼3–4°C, as compared to those at control ionic concentrations. The channel became more difficult to activate.

FIGURE 7.

Effect of ionic strength on the heat response of VR1. Three conditions are shown. (A) High concentration (200 mM Cs⁺) in pipette. (B) Low concentration (25 mM Cs⁺) in pipette. (C) Low concentration (25 mM Na⁺) in bath. Increasing the intracellular ionic strength had little effect on the activation temperature of the channel, with the 10% activation at 43–44°C and the half-activation at 47–48°C, both of which were similar to those at the control condition (140 mM Cs⁺ in pipette and 140 mM Na⁺ in bath). In contrast, lowering the intracellular ionic strength increased the activation temperature by ∼4°C, with the 10% activation shifted to 46–47°C and the half-activation to 51°C. Lowering the extracellular ionic strength, on the other hand, yielded the opposite effect. The activation temperature was reduced by ∼4°C, with 10% activation occurring at ∼37°C and half-activation at ∼44°C. The protocol of the stimulus used in these experiments was slightly different from that in the cholesterol experiments, consisting of a heating to the maximal temperature first, followed by a cooling to the room temperature. The heating followed a ramp protocol as described. The currents plotted were the instantaneous recordings. Only the currents during the heating phase are shown.

The change of the extracellular ionic strength produced the opposite effect. Lowering the extracellular ionic concentration to 25 mM resulted in a leftward shift in the response (Fig. 7 C). The activation temperature was reduced to 37–38°C for 10% activation and 43–44°C for half-activation, which was ∼6°C less than at the control condition. This is a considerable change, considering that the channel normally reached the half-activation in <5°C. The extracellular ionic strength also altered the steepness of the activation curves. Normally, the temperature range between the 10% and the half-activation was ∼4°C, but with 25 mM extracellular ionic concentration, it increased to ∼6°C. Taken together, these results suggest that both internal and external ionic strength modulates the temperature response of the channel. Similar to the cholesterol effects, however, the changes of the ionic strength did not suffice to eliminate the response, suggesting that the sensitivity of the channel is not critically dependent on the aqueous ionic conditions.

DISCUSSION

VR1 represents a novel family of ion channels that are gated by temperature. In the present study, we conducted an extensive single-channel analysis to reveal the mechanisms underlying this novel property. The temperature-sensitivity of the receptor arises primarily from its initial activation, with little contribution from ion permeation and subsequent gating. The activation involves a large transitional enthalpy and entropy as determined from the van't Hoff analysis at equilibrium. At the single-channel level, the activity appears in bursts, and heat promotes channel openings by shortening the long closures while prolonging the bursts. Within bursts, the activity is complex, involving at least three closed and three open states. Remarkably, none of them appears to be significantly temperature dependent, as compared to the gap and burst durations. The activity evoked by heat is somewhat dependent on the physical properties of lipids and aqueous solutions, particularly with respect to the temperature threshold of the activation, but neither suffices to abolish the response. Together, these results provide an important basis for understanding the mechanism of the thermal activation of the channel.

The evaluation of enthalpy and entropy in our analysis is based on the assumption that they are independent of temperature. The assumption is hypothetical, but there is some justification. Scanning calorimetric experiments show that proteins do have a heat capacity. It is much smaller than that of water, but nonetheless significant (0.3 cal/K · g) (Privalov, 1979). This heat capacity comprises several components. The most significant one increases linearly with temperature. However, this component is a generic property of the protein, i.e., it depends on protein composition and not on conformation. As a result, it cancels out in the transitional enthalpy between two conformations. The component that depends on conformation is mostly contributed by solvation of nonpolar residues. This component, however, is small. In an extreme case when a globular protein is denaturated, it increases by ∼0.1 cal/K · g, and in general it is ∼12 cal/K · mol per pair of nonpolar interactions (Privalov, 1979). For 10 interactions with a 10°C temperature increase, this heat capacity contributes <5% to the total enthalpy change. Ion channels are certainly different from globular proteins. Unfortunately, there has been little data in the literature on the direct physical measurement of thermodynamic properties of membrane proteins. Nevertheless, many arguments that are made on the globular proteins are expected to be applicable to membrane proteins as well. Therefore, the results obtained under the assumption provide reasonable approximations.

Energetic perspectives of thermal activation

With an apparent Q₁₀ of 27 on single-channel P_o, the temperature dependence of VR1 is exceptionally high. Ion channels that have been reported to have abnormally high temperature dependences usually have a Q₁₀ between 5 and 10. These include, for example, the gating of voltage-activated H⁺ channels (DeCoursey and Cherny, 1998), the deactivation and inactivation recovery of K_v channels from human T-cells (Lee and Deutsch, 1990), and the inactivation of K⁺ channels (Murrell-Lagnado and Aldrich, 1993; Nobile et al., 1997). Some ion channels exhibit high dependences at low temperature ranges, such as the activation and deactivation of K_v channels from rat muscle (Beam and Donaldson, 1983), the alamethicin pore formation (Boheim and Benz, 1978), and the inactivation of Na⁺ channels from frog and rabbit muscles (Kirsch and Sykes, 1987). It is relatively rare that channels have a Q₁₀ > 10, except for a few occasions, e.g., the gating of Cl⁻ channels (Pusch et al., 1997) and inactivation of rabbit neuronal Na⁺ channels (Chiu et al., 1979), which have a Q₁₀ as high as 40 and 33, respectively.

Even with these highly temperature-dependent channels, they do not have the capability to be gated by temperature directly. In this regard, VR1 and its family members are particularly unique, alluding to the speculation that specialized apparatus might be necessary not only able to sense high temperatures but also couple the thermal energy to the gating of the channel. Indeed, ion channels, whether gated by ligand, voltage, or force, all possess specialized molecular sensors for detection of their stimuli. Ligand-gated channels have receptor sites and transmit the energy released from binding to open the channel. Similarly, voltage-gated channels have charged segments that can be influenced by the membrane electrical field, and mechanosensitive channels have “springlike” links that can respond to displacements. Common to all these channels is that a stimulus produces only a local effect on specific sites of the channel. Heat, however, is a global factor. Furthermore, it tends to have a destructive effect as high temperatures can cause protein denaturation. It seems to be paradoxical that such a global stimulus can be detected at specific sites without adverse effects on the integrity of the receptor.

Although the molecular basis of heat sensing is unknown, some aspects of its energetics may be speculated as to whether thermal activation is possible in principle and how it might be different from other types of activations. The temperature-sensitivity of a rate arises predominantly from the transitional enthalpy,

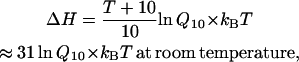where k_B is Boltzmann's constant and T is the absolute temperature. The gating of a channel typically has a temperature coefficient Q₁₀ ≈ 3, which corresponds to an enthalpy change of approximately ΔH = 20 kcal/mol or 33 k_BT per channel. However, this energy is well above the limit of thermal fluctuations, which is only on the order of k_BT. The transitions would be prohibited if there were no entropy compensation. To bring down the energy barrier to a level that can be reached by thermal fluctuations, a large entropy change is required, and the energy it contributes must be comparable to that of the enthalpy, so that the net free energy ΔG = ΔH − TΔS remains small. Therefore, a highly temperature-dependent transition is possible only if enthalpy and entropy are both large and can compensate each other. This property is unnecessary for other types of channels since the free energy of the activation of those channels can be offset through specific interactions involving the stimulus without the need to significantly alter the enthalpy and entropy.

Although a high temperature sensitivity can be achieved by increasing enthalpy and entropy, there may be a practical limit on how high it could be. Major enthalpic factors that affect protein stability include hydrogen bonds and hydrophobic interactions. The hydrogen bonds are strong (2–10 kcal/mol), but their breakage is often accompanied with formation of new ones either with water or within the protein, yielding little net change. The hydrophobic interactions play a more significant role, but they are nevertheless small. An analysis of Rnase T1, a globular protein of 104 residues, puts the total interaction of all buried hydrophobic groups on the order of 94 kcal/mol (Pace et al., 1996), which is less than the hydration energy of a small ion. The thermal denaturation of a tightly packed globular protein like lysozyme results in an enthalpy change at ∼41 kcal/mol and an entropy change at ∼112 cal/mol × K (Privalov, 1979). Notably, the energy arising from this entropy change, which is ∼37 kcal/mol at the melting temperature, matches the enthalpy change quite closely, paralleling our observation on the simultaneous increases in enthalpy and entropy. An enthalpy change of 41 kcal/mol gives a Q₁₀ ≈ 9 at room temperature. Interestingly, this is about the upper limit of the temperature dependence of the gating of ion channels. Considering that it arises from a structural change from a compact protein to a nearly random coil, it is remarkable how large the conformational changes involved in channel gating may be. On the other hand, it also underscores the potential limit on the temperature dependence of a thermal transition; large structural changes are necessary to achieve a high Q₁₀.

With a limited attainable temperature dependence, how can temperature then activate a channel? Our analysis of VR1 provides some intriguing clues. The sharp activation of the channel entails an apparent van't Hoff enthalpy of 150 kcal/mol and entropy of 470 cal/mol × K, which may be inaccessibly large. This temperature dependence appears to arrive from two distinct but complementary mechanisms: one is the shortening of gaps and the other the elongation of bursts. The channel may have multiple heat-sensitive sites distributed over multiple subunits. The activation of each site is able to open the channel, but only for a brief duration, which is observed as short bursts. As the temperature increases, more heat-sensitive sites become active, which result in more stabilized bursts. In other words, the elongation of bursts is not a direct effect of temperature, but a result of allosteric interactions between subunits. This is consistent with the activation of the channel by capsaicin, where both partially and fully liganded channels are found to be able to open and a high level of ligand bindings give rise to elongated bursts (Hui et al., 2003). Therefore, the elemental process that temperature has a direct effect on may not have a temperature dependence as large as the apparent P_o suggests; allosteric cooperativity within the protein can play a compensatory role. To this end, it is noteworthy that the gap duration has a Q₁₀ ≈ 7, which is thermodynamically accessible and in the range of the temperature dependence of the gating of ion channels.

Does a heat-activated channel necessarily involve unusual conformational changes? Given that the gating of most channels has a Q₁₀ ≈ 3, it seems to be conceivable that an abnormally high temperature dependence may signal something special about the process. Indeed, many channels that have been reported with a very high Q₁₀ are believed to involve large-scale structural rearrangements. For example, the inactivation of the K⁺ channels (Q₁₀ ≈ 5) involves interaction between two peptide units, with at least one of them having a low probability to adopt the correct conformation for docking at low temperatures (Murrell-Lagnado and Aldrich, 1993). The formation of the alamethicin channel (Q₁₀ ≈ 9) involves self-assembling of 6–10 molecules in the membrane in a helix-bent-helix arrangement (Boheim and Benz, 1978). The gating of the voltage-activated H⁺ channel (Q₁₀ ≈ 6–9) is accompanied with assembling of several channel protomers in the membrane to form a functional channel (DeCoursey and Cherny, 1998). The activation of the Cl⁻ channel (Q₁₀ ≈ 40) requires its permeant ion, which is believed to affect channel subunit interaction (Pusch et al., 1997). These examples appear to support the notion that an abnormally strong temperature dependence is correlated with some unusual and large conformational changes.

Origins of heat sensitivity

The heat sensitivity of VR1 is compounded by its heterogeneous environments. We examined the possible contributions from the lipid and aqueous phases. Incorporating cholesterol into membrane shifted the activation temperature, making the channel more difficult to open, an effect similar to a reduction of intracellular ionic strength. However, neither eliminated the temperature response. The sharp none-to-all activation persisted, suggesting that the heat sensitivity of the channel does not arise solely from its environment. Energetically, the increase of the activation temperature can be accounted for by only small changes in enthalpy and entropy. Assuming that the activation temperature increased from 42°C to 46°C and that the same Q₁₀ is retained, the transitional enthalpy would only need to increase by 2%. An additional change in entropy would further alter the temperature coefficient of the activation as well.

The mechanisms of the observed effects of cholesterol and solution ionic strength are not clear, due to their nonspecific interactions. The ionic strength usually has an effect on local dielectrics, suggesting that possible long-range electrostatic interactions might be involved in heat activation of the channel. Given that lowering solution ionic strength tends to increase the electrostatic interactions, our results would imply that the intracellular electrostatic interactions make the channel more difficult to open while the extracellular interactions facilitate opening. The altered channel responses may also arise from other effects of ionic solutions, e.g., the screening of membrane charges. VR1 is highly rectified in both kinetics and conductance. While possible, this mechanism has the difficulty of explain why lowering the intracellular and extracellular ionic strength produced an opposite effect. Other mechanisms—for example, the perturbation of local water structure around residues, hydrophobic residues in particular—may also play a role.

Cholesterol can affect physical properties of lipid bilayers (McMullen and McElhaney, 1996). When present at high concentrations, cholesterol enhances mechanical strength of the membrane, reduces its permeability, and broadens or even eliminates the phase transition. Assuming that the effect we observed resulted from modifications of the membrane, it would suggest that the membrane fluidity modulates channel activation. It is possible that the opening of the channel involves large conformational changes in which some lipid molecules have to be displaced, or in which some moieties of the channel protein have to move into the membrane. In either case, a decrease in the fluidity of the membrane would reduce its mobility, thereby making the channel more difficult to open. This is also consistent with the notion that the activation of the channel involves a large entropy change as necessitated by its high temperature dependence. Some of the changes may originate from the membrane, making the activation partly dependent on its physical properties.

Cholesterol has been reported to play an important modulatory role in several ion channels, including acetylcholine receptor channels (AChR; Santiago et al., 2001), volume-activated anion channels (VAAC; Levitan et al., 2000), calcium-activated potassium channels (BK; Bolotina et al., 1989; Chang et al., 1995), and several types of calcium channels (Sen et al., 1992; Gleason et al., 1991; Lundbaek et al., 1996). Despite extensive studies, the mechanism involved remains obscure. In some cases the channel functions are believed to depend on some physical property of bulk lipid bilayer such as fluidity, whereas in others, specific binding sites for cholesterol on the protein, either in the lipid-protein interface or within the protein itself, have been suggested. In many ion channels studied, cholesterol is found to have an inhibitory effect as observed with VR1. Single-channel studies in AChR, VAAC, BK, and N-type Ca²⁺ channels show that cholesterol supplement results in a large reduction in the open channel lifetime, often accompanied with a small reduction in the conductance. One proposed interpretation is that the stiffness in the membrane destabilizes the open channel conformation, leading to an increase in the open-to-closed transition rate. If a similar mechanism existed for VR1, then cholesterol would not be directly involved in the activation process of the channel, since the temperature acts mostly on the long closures before opening. However, if cholesterol inhibited the closed-to-open transition, thereby increasing the closed dwell-times, then it may be directly involved in the VR1 activation. Single-channel measurements will be necessary to resolve the issue in future experiments.

Relation to activations by capsaicin and low pH

Besides heat, VR1 is activated by other stimuli such as capsaicin and low pH. At the single-channel level, the activity evoked by these stimuli shares many common characteristics. With a low level of stimulus, the openings appear in brief bursts separated by long closures. As the level of stimulus increases, the long closures are shortened while the bursts become prolonged. Importantly, the closures that are evoked by one stimulus appear to be sensitive to another. For example, the long closures occurring at low capsaicin concentrations can be shortened and eventually eliminated by lowering extracellular pH (Ryu et al., 2003). It is also observed that capsaicin has a similar effect on heat activation (data not shown). Furthermore, a full reduction of the durations of the long closures does not seem to require a simultaneous application of multiple stimuli. Capsaicin alone, for example, suffices to shorten their durations at high concentrations to a virtually undetectable range, indicating no significant rate-limiting step along its activation pathway. These results strongly suggest that the closures that are sensitive to different stimuli arise from common mechanisms. It is evident that these stimuli probably do not act on the same site on the channel, since pH works only from the outside of the cell whereas capsaicin appears to bind the intracellular side (Jung et al., 1999). Therefore, different stimuli are likely to interact in an allosteric manner.

The activity evoked by different stimuli also exhibits similar characteristics on the gating (conformational changes after ligand binding) of the channel. With capsaicin alone, there are about three closed and three open states that are invariant to capsaicin in their time constants and remain abundant in their populations even at saturating concentrations (Hui et al., 2003). These components are observed with pH-potentiated capsaicin activation too, though there is some complication on the elongation of one open state as well as less significant populations of short openings and long closures when high capsaicin and low pH are both applied (Ryu et al., 2003). The present study reveals again similar components involved in heat activation of the channel. Taken together, these results suggest that common gating machinery may be involved in the activation pathways induced by different stimuli.

On the other hand, there is also compelling evidence suggesting the divergence among different activation pathways. Mutations of some residues around the pore of the channel result in discriminative effects on the dose-responses of capsaicin and pH (Welch et al., 2000). Mutations in the region of TM6 abolish the capsaicin but not the pH response (Kuzhikandathil et al., 2001). As mentioned above, we also observed that very low pH prolongs channel openings, indicating that pH has additional effects besides activating the channel and potentiating capsaicin responses. Future work that combines single-channel analysis with this mutagenesis may help us understand, in more detail, the mechanistic nature of the activation pathways evoked by different stimuli and its molecular and structural basis.