Kinetic Diversity of Single-Channel Burst Openings Underlying Persistent Na⁺ Current in Entorhinal Cortex Neurons

Abstract

The kinetic diversity of burst openings responsible for the persistent Na⁺ current (I_NaP) in entorhinal cortex neurons was examined by separately analyzing single bursts. Although remarkable kinetic variability was observed among bursts in terms of intraburst opening probability and mean open and closed times, the values of time constants describing intraburst open times (τ_o(b)s) and closed times (τ_c(b)s) were distributed around well-defined peaks. At −40 mV, τ_o(b) peaks were found at ∼0.34 (τ_o(b)1) and 0.77 (τ_o(b)2) ms, and major τ_c(b) peaks were found at ∼0.24 (τ_c(b)1) and 0.54 (τ_c(b)2) ms. In ∼80% of the bursts two preferential gating modes were found that consisted of a combination of either τ_o(b)1 and τ_c(b)2 (“intraburst mode 1”), or τ_o(b)2 and τ_c(b)1 (“intraburst mode 2”). Individual channels could switch between different gating modalities, but normally tended to maintain a specific gating mode for long periods. Mean burst duration also displayed considerable variability. At least three time constants were found to describe burst duration, and the frequencies at which each of the corresponding “bursting states” occurred varied in different channels. Short-lasting bursting states were preferentially associated with intraburst mode 1, whereas very-long-lasting bursts tended to gate according to mode 2 only or other modes that included considerably longer mean open times. These results show that I_NaP channels can generate multiple intraburst open and closed states and bursting states, but these different kinetic states tend to combine in definite ways to produce a limited number of prevalent, well-defined gating modalities. Modulation of distinct gating modalities in individual Na⁺ channels may be a powerful form of plasticity to influence neuronal excitability and function.

INTRODUCTION

The persistent Na⁺ current (I_NaP) is expressed by a variety of neuronal (Stafstrom et al., 1985; French and Gage, 1985; Uteshev et al., 1995; Chao and Alzheimer, 1995; Baker and Bostock, 1997; Kay et al., 1998; Magistretti and Alonso, 1999) and non-neuronal (Gage et al., 1989; Saint et al., 1992; Sakmann et al., 2000) excitable cell types. In central neurons, I_NaP can significantly influence membrane electroresponsiveness and excitability, especially in a sub- and near-threshold range of potentials (e.g., Alonso and Llinás, 1989; Schwindt and Crill, 1995; Azouz et al., 1996; Lipowsky et al., 1996; Takakusaki and Kitai, 1997; Pape and Driesang, 1998; Sandler et al., 1998; Bevan and Wilson, 1999; Bennett et al., 2000; Taddese and Bean, 2002). Although the biophysical and functional properties of the macroscopic I_NaP are well-characterized in a number of cell systems, so far only a limited number of studies have addressed the issue of the single-channel correlates of this current in native neurons (Alzheimer et al., 1993; Ju et al., 1994; Uteshev et al., 1995; Segal and Douglas, 1997; Magistretti et al., 1999a,b; Agrawal et al., 2001; Magistretti and Alonso, 2002). In neurons of entorhinal cortex layer II (Magistretti et al., 1999a) and V (Agrawal et al., 2001), I_NaP is generated by a Na⁺-channel activity characterized by prolonged burst openings and a conductance of ∼20 pS under standard ionic conditions. Also in skeletal muscle fibers (Patlak and Ortiz, 1986) and myocardial cells (Ju et al., 1994) prolonged burst openings generated by Na⁺ channels have been reported to occasionally occur. These bursts display a remarkable kinetic diversity that has been proposed to derive from an intrinsic variability of the underlying gating mechanisms (Patlak and Ortiz, 1989).

In a previous study we carried out a kinetic characterization of burst openings responsible for I_NaP generation in entorhinal cortex layer-II neurons (Magistretti and Alonso, 2002). In that study we analyzed the kinetics of opening and closing events occurring within bursts by pooling data from individual bursts and patches. Burst duration was also analyzed by pooling data from different patches. This allowed us to provide a description of the “average” kinetic behavior of “persistent” Na⁺ channels at various membrane potentials, thereby unveiling the single-channel bases of the macroscopic I_NaP's voltage-dependence and kinetics. However, such an approach is not able to preserve information that may be contained in the original data about possible differences in the kinetic behavior of individual bursts and/or channels. The issue of the possible kinetic diversity of channels responsible for I_NaP generation may be important. Indeed, it is not known yet whether different Na⁺-channel subsets combine to produce the macroscopic I_NaP; nor is it known whether channels of a single, homogeneous pool can undergo gating modifications able to influence I_NaP amplitude, kinetics, or voltage-dependence.

To address the above issue, in this study we undertook a more detailed kinetic characterization of channels responsible for I_NaP generation in entorhinal cortex layer-II neurons by separately analyzing the kinetic properties of single bursts. Our data revealed the existence of a prominent variability in intraburst opening and closing kinetics as well as in mean burst duration. However, our results also allowed us to conclude that I_NaP channels tend to operate according to a few, prevalent gating modalities, and that each of them tends to persist in one of these gating modalities at least for prolonged periods of time.

METHODS

Cell preparation and patch-clamp recordings

Acutely isolated neurons were prepared from layer II of entorhinal cortex from young-adult Long-Evans rats (P25-P35). The details on the dissection procedure followed and the enzymatic and mechanical dissociation method applied are described elsewhere (Magistretti and de Curtis, 1998; Magistretti et al., 1999a; Magistretti and Alonso, 2002). After isolation, cells were seeded on a recording chamber mounted on the stage of an inverted microscope (Axiovert 100, Zeiss), and observed at ×400 magnification. Cells were initially perfused with a standard HEPES buffer containing (in mmol/l) 140 NaCl, 5 KCl, 10 N-[2-hydroxyethyl]piperazine-N′-[2-ethanesulphonic acid] (HEPES, free acid), 2 CaCl₂, 2 MgCl₂, and 25 glucose, at pH 7.4 with NaOH, bubbled with pure O₂. Single-channel patch pipettes were prepared from thick-wall glass capillaries, coated with the product Sylgard (Dow Corning, Midland, MI), and filled with a solution containing (in mmol/l) 130 NaCl, 35 tetraethylammonium (TEA)-Cl, 10 HEPES-Na, 2 CaCl₂, 2 MgCl₂, and 5 4-aminopyridine, at pH 7.4 with HCl. Patch pipettes had resistances ranging from 10 to 35 MΩ when filled with the above solution. After obtaining the cell-attached configuration, the extracellular perfusion was switched to a high-potassium solution containing 140 K-acetate, 5 NaCl, 10 HEPES (free acid), 4 MgCl₂, 0.2 CdCl₂, and 25 glucose, at pH 7.4 with KOH, so as to hold the neuron resting membrane potential at near 0 mV. Recordings were performed at room temperature using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA). Capacitive transients and linear current leakage were minimized on-line by acting on the respective built-in compensation sections of the amplifier. To elicit voltage-gated Na⁺-channel currents, 500-ms depolarizing voltage steps were delivered one every 5.6 s. The holding potential was −100 mV.

Data acquisition and analysis

Voltage protocols were commanded and current signals were acquired with a Pentium PC interfaced to an Axon TL1 interface, using the Clampex program of the pClamp 6.0.2 software package (Axon Instruments). Current signals were filtered on-line using the amplifier's built-in low-pass filter (4-pole low-pass Bessel filter, with an attenuation above the −3-dB frequency, of 24-dB/octave) at 2 kHz, and were digitized at 10 kHz.

Single-channel recordings were analyzed using Fetchan, pStat, and Clampfit (from the pClamp 6.0.5 software package, Axon Instruments). Residual capacitive transients were nullified by off-line subtracting fits of average blank traces. Residual leakage currents were carefully measured in trace regions devoid of any channel openings, and digitally subtracted.

For the analysis here presented, bursts of at least 10 ms in duration were selected. As a rule, a burst was considered as terminated when it was separated from another burst by a closing interval of at least 10 ms: this criterion was adopted due to the known kinetic properties of interburst closed states (Magistretti and Alonso, 2002). Unless otherwise stated, bursts that showed signs of multiple, superimposed openings were excluded from the analysis.

Channel dwell times were determined by applying a standard half-amplitude crossing protocol using Fetchan. No minimum-duration threshold for detection of state transitions was imposed. With the low-pass filtering cutoff frequency used (2 kHz), and assuming that the filter output approaches that of a Gaussian filter, a theoretical “dead-time” for event detection of 90 μs is predicted (Colquhoun and Sigworth, 1995). To analyze channel open and closed times, logarithmic frequency-distribution graphs of the same quantities were constructed (see Blatz and Magleby, 1986; Sigworth and Sine, 1987; McManus et al., 1987; Magistretti and Alonso, 2002). To do this, lower and upper bin limits were first set according to a logarithmic scale that yielded 11.4 bins/decade. To avoid arbitrary over- or underestimations of the calculated numbers of events per ms, the upper-limit value of each bin was approximated to the nearest 10^th of ms above, so as to make each bin width equal an integer multiple of the sampling interval routinely used (100 μs). After data binning, the natural logarithm of the number of observations per time unit was calculated for each bin. The values thus obtained were plotted as a function of x = ln t to construct log-log frequency-distribution graphs (see Fig. 3, A2 and B2, insets). Due to the dead-time value holding under our experimental and analytical conditions (90 μs, see above), which did not warrant for consistent detection of transitions lasting ∼100 μs, events consisting of only one 100-μs sample (or, occasionally, two samples) were excluded from histograms and were not considered for fitting. Exponential fitting of log-log histograms was carried out by applying the following double logarithmic transform of a sum of exponential functions (see Magistretti and Alonso, 2002):

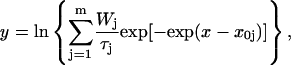(1)

where x_0j = ln τ_j, and W_j and τ_j are the weight coefficient and time constant, respectively, of each exponential component. Logarithmically binned histograms constructed as described above were also displayed on a linear timescale to obtain log-linear graphs (see Fig. 3, A2 and B2, main panels), which allowed for a better visualization of single exponential components as straight lines. Theoretical mean open times within bursts (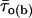s) were derived from the exponential fitting functions obtained from open-time histograms according to the relationship

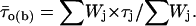(2)

Burst duration was analyzed using logarithmic frequency-distribution graphs in the same way as described for intraburst dwell times. In this case, the logarithmic scale employed for data binning yielded 11.8 bins/decade.

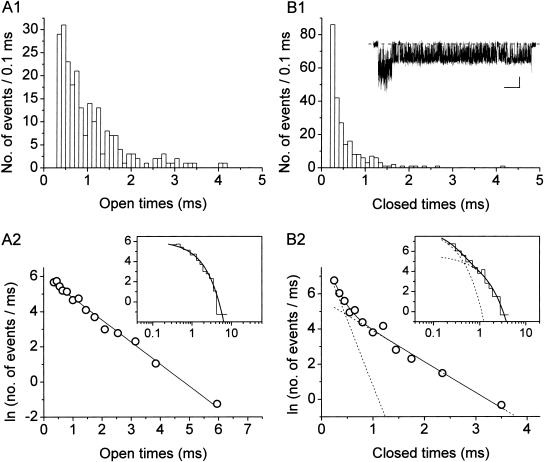
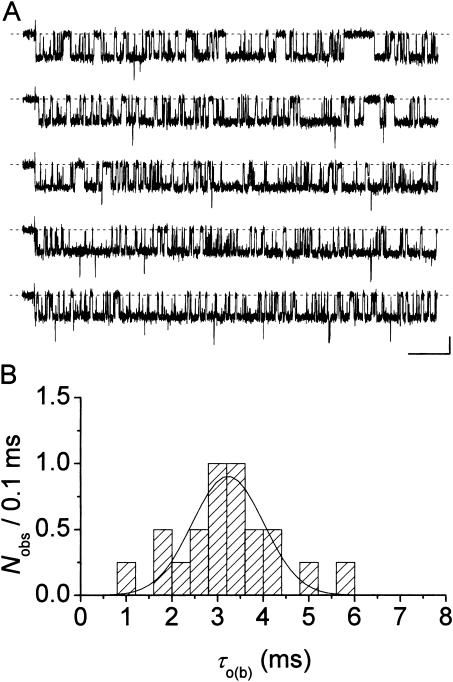
FIGURE 3.

Display and analysis of intraburst open- and closed-time data from single bursts. (A) Frequency-distribution diagrams of intraburst open times for a single, exemplary burst recorded at −40 mV. (B) Frequency-distribution diagrams of intraburst closed times for the same burst. The burst from which the analysis here presented was derived is depicted in B1, inset (calibration bars are 1 pA, 50 ms). A1 and B1 show histograms constructed after linear binning of original data and displayed on a double-linear scale (bin width is 0.1 ms in both cases). A2 and B2 are logarithmic histograms. Data were binned logarithmically (11.4 bins/decade), and the natural logarithm of the numbers of observations per ms, i.e., ln(n/ms), was plotted as a function of time in a logarithmic (insets) or linear (main panels) scale. In log-linear histograms, the x-value of each point is the logarithmic midpoint of the corresponding bin. Smooth, enhanced lines are first-order (A2) or second-order (B2) exponential functions obtained by applying the fitting function of Eq. 1 (Methods) to log-log histograms. Smooth, dotted lines in B2 are the single exponential components shown separately. Fitting parameters are W = 336.5, τ_o(b) = 795.2 μs (A2); and W₁ = 537.0, τ_c(b)1 = 133.0 μs, W₂ = 164.6, τ_c(b)2 = 567.3 μs (B2). In log-linear histograms (main panels), single exponential fitting components appear as straight lines.

Time constants describing open times (τ_o(b)s) and closed times (τ_c(b)s) within single bursts, and burst duration (τ_bs) in single patches, were further analyzed by constructing frequency-distribution diagrams of the same quantities. The bin widths used for data binning were either constant or variable (see Results). The histograms thus obtained were fitted with single Gaussian functions or the sum of 2–4 Gaussian functions. All fittings were performed using the fitting routine of Origin 6.0 (MicroCal Software, Northampton, MA), based on a minimum-χ² method.

To assess the effect of random sampling as a variability generator in the evaluation of time constants, “artificial” dwell-time values distributed exponentially according to a given time constant, τ, were randomly generated. Sets of random decimal numbers (0–1) were created using Origin 6.0, then these numbers were used to calculate random dwell-time values as t_i = −τ × ln(n_i), where n_i is each random number.

Average values are expressed as mean ± standard error (SE). Statistical significance was evaluated by means of the two-tailed Student's t-test for unpaired data.

RESULTS

Channel openings responsible for persistent-Na⁺-current generation in entorhinal cortex layer-II neurons occur in bursts (Magistretti and Alonso, 2002). In this study we examined in detail the possibility that different kinetic behaviors of intraburst openings and closings can be expressed by different burst events, and/or that different channels can generate bursts of different average duration.

Kinetic diversity of intraburst openings and closings

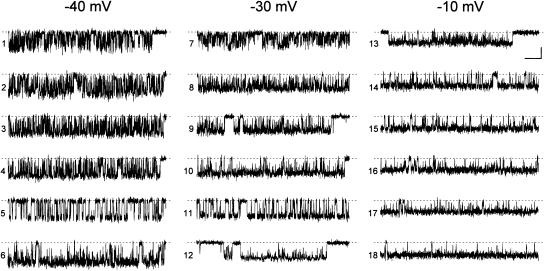
We first noticed that single bursts could appear remarkably different as far as the average duration of intraburst openings and closings is concerned. Fig. 1 shows exemplary burst openings recorded at three membrane potentials (V_m) in six different patches (each trace is a detail of a single burst). A simple visual inspection clearly reveals that at each V_m the average duration of intraburst openings and/or closings, as well as the overall fraction of time spent in an open state, could vary considerably from one burst to another. For instance, the fractional open time of the lowermost burst in the middle column of Fig. 1 was 0.877, whereas that of the uppermost burst in the same column was only 0.352.

FIGURE 1.

Different “persistent” Na⁺-channel burst openings can display major differences in open- and closed-time duration. The figure shows exemplary burst openings chosen from those recorded in six different patches to illustrate the kinetic diversity typically observed in such events at the same membrane potential (V_m). Each trace is a detail of a single burst. Burst openings were elicited with 500-ms step depolarizations at three different V_m measurements (−40 mV, −30 mV, and −10 mV). Bursts 1–3, 7, 10, 14–16, and 18 are from patch C8708; bursts 8, 9, and 17 from patch B8708; bursts 4 and 13 from patch F8711; bursts 5 and 11 from patch A8721; burst 6 from patch A8618; and burst 12 from patch D8708. Calibration bars are 1 pA, 25 ms.

The kinetic diversity of intraburst opening and closing events that was revealed by the comparison of different bursts could not be attributed to the possible existence of subtle differences in some experimental condition(s) or variable(s) (e.g., temperature, composition of the intracellular milieu, etc.) in different recordings. Indeed, bursts displaying very dissimilar kinetic behaviors could be observed in single patches and sometimes in the same sweep. This is exemplified in Fig. 2, which shows six consecutive sweeps recorded at −30 mV in a patch in which two distinct channels displaying dramatically different patterns of intraburst open and closed times were active. One of these channels generated bursts characterized by an intense “flickering” behavior, with very short openings separated by short or medium-duration closings (traces 1 and 2 in Fig. 2), whereas the other channel produced bursts consisting of much more prolonged, or “stable,” openings and closings (traces 5 and 6 in Fig. 2). In some sweeps the two types of openings occurred simultaneously and appeared superimposed (traces 3 and 4 in Fig. 2).

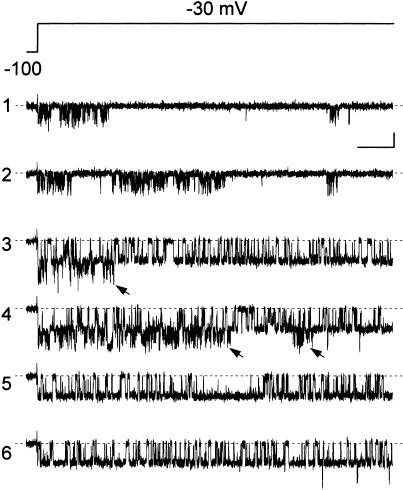
FIGURE 2.

Prominent differences in burst gating properties can be observed in single patches. The figure shows six consecutive sweeps from a patch (A8721) displaying the activity of two channels characterized by prominent differences in intraburst open- and closed-time behaviors. The voltage protocol applied is illustrated in the upper panel. In traces 1 and 2, burst openings characterized by an intense “flickering” behavior are seen. The bursts observed in traces 5 and 6 show much more “stable” opening and closing events. In traces 3 and 4, burst openings characterized by the two different gating modalities occurred simultaneously and appear superimposed (arrows). Calibration bars are 1 pA, 50 ms.

A quantitative description of the above-illustrated diversity of intraburst-gating kinetics requires a detailed analysis of open and closed times. In a previous study (Magistretti and Alonso, 2002) intraburst open and closed times were analyzed by pooling data from several patches (and, consequently, from a number of different bursts) and generating a lumped histogram for each V_m. This analysis revealed the existence of three time constants for open states and two time constants for intraburst closed states. However, as pointed out by Patlak and Ortiz (1989), it is not necessarily clear how the time constants derived in this way relate to those actually describing open-closed state transitions in individual bursts. The kinetic diversity of intraburst openings and closings was therefore characterized by analyzing open and closed times in single bursts. The analytical procedure adopted for this purpose is illustrated in Fig. 3. Dwell-time event lists were derived for each single burst as explained in the Methods, and only bursts in which at least 40 state transitions were detected were considered for further analysis. Frequency-distribution diagrams were then constructed as log-log (Fig. 3, A2 and B2, insets) and log-linear (Fig. 3, A2 and B2, main panels) plots.

Analysis of open times

In most bursts, the frequency distribution of open times was properly described by a single exponential function (Fig. 3 A2). At V_m = −40 mV, a single time constant was revealed by the open-time analysis in 52 bursts out of 67, whereas in the remaining 15 bursts two time constants were required for appropriate fitting. The time constants describing intraburst open times (τ_o(b)s) showed considerable variability: at −40 mV, τ_o(b) values ranged from 0.105 to 3.57 ms. (Note: Events shorter than 100 μs (the sampling interval of the depolarizing protocols here applied) were missed in our dwell-time analysis. In addition, due to the dead-time for event detection holding under our conditions (90 μs: see Methods), transitions of ∼100 μs or somewhat longer could have been incompletely detected. These limitations could affect our estimations of mean open and closed times. The algorithms that can be employed to correct such errors (e.g., Colquhoun and Sigworth, 1995), could not be applied here, since the fastest time constants observed were not long enough as compared to the limit of resolution of the measurements, which is one of the basic requirements for these corrections being applicable. Therefore, the time constants we report are uncorrected, and should be interpreted as upper limits for the exact, real values.)

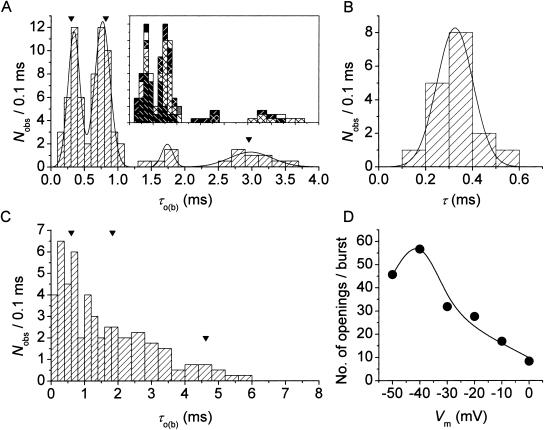
To quantitatively describe τ_o(b) variability, the frequency distribution of the τ_o(b) values obtained as described above was then analyzed in detail. An overall τ_o(b) histogram was constructed for each V_m (Fig. 4, A and C). At −40 mV, the histogram revealed two distinct and prominent τ_o(b) peaks at ∼350 and ∼750 μs, plus another clear, although less pronounced, peak at ∼3.0 ms, and probably an additional peak at ∼1.75 ms (Fig. 4 A). Data derived from several patches, and therefore from many different channels, contributed to each of the major peaks (Fig. 4 A, inset). The histogram could be fitted with the sum of four Gaussian functions, which returned mean (μ) values of 0.343, 0.769, 1.74, and 2.982 ms. The arrowheads in Fig. 4 A indicate the τ_o(b) values, reported elsewhere (Magistretti and Alonso, 2002), that were returned by the analysis of data from different patches pooled. It can be clearly seen that these time constants are very close to the μ-values of the three main peaks observed in the τ_o(b) histogram here analyzed.

FIGURE 4.

Diversity of open times. (A) Frequency distribution of time constants describing intraburst open times (τ_o(b)s) at −40 mV. The τ_o(b)-values used to construct the histogram were derived from individual bursts (n = 67) recorded in nine different patches. Note the two different bin widths (0.1 ms for τ_o(b) < 1.1 ms and 0.2 ms for τ_o(b) ≥ 1.1 ms). The inset shows the same histogram constructed as a stack-column diagram, with each column pattern corresponding to data from a single patch. The histogram was best fitted with the sum of four Gaussian functions (smooth line), which returned the fitting parameters A₁ = 26.33, μ₁ = 0.343 ms, σ₁ = 0.181 ms; A₂ = 35.93, μ₂ = 0.769 ms, σ₂ = 0.229 ms; A₃ = 4.11, μ₃ = 1.74 ms, σ₃ = 0.167 ms; and A₄ = 10.15, μ₄ = 2.982 ms, σ₄ = 0.635 ms. The arrowheads indicate the previously-reported τ_o(b)-values obtained by pooling data from different patches (Magistretti and Alonso, 2002). (B) Frequency distribution of τ_o(b)s for randomly-generated open times. Seventeen groups of numeric values distributed exponentially according to a time constant of 0.343 ms (a value which coincides with the μ₁ returned by the Gaussian fitting illustrated above) were generated randomly. Each group consisted of 49–255 values (see the text), which were binned logarithmically, as explained in the legend for Fig. 3, to construct a “simulated” open-time frequency distribution. Each of the histograms thus obtained was best-fitted with a single exponential function, and the time-constant values returned by fittings (“simulated” τ_o(b)s) were in turn binned to construct a “simulated”-τ_o(b) histogram, shown here. The smooth line is the best fitting obtained applying a single Gaussian function; fitting parameters were A = 16.04, μ = 0.325 ms, and σ = 0.154 ms. (C) Frequency distribution of τ_o(b) at −30 mV. τ_o(b)-values were derived from individual bursts (n = 87) recorded in 11 different patches. Note the two different bin widths (0.2 ms for τ_o(b) < 2 ms and 0.4 ms for τ_o(b) ≥ 2 ms). Arrowheads are as in A. (D) Plot of the average number of openings per burst as a function of V_m. Data were obtained by dividing the average burst duration (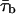) by the sum 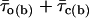(where 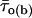is the mean open time and 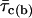is the mean closed time) for each V_m. 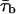-, -, 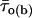and 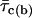-values were derived from Magistretti and Alonso (2002).

The above data show that, despite the wide variability found in τ_o(b)-values, a few, major time constants appear to account for the distribution of intraburst open times in I_NaP channels. We next sought to establish whether the variability displayed by τ_o(b)-values around each τ_o(b) peak is indeed compatible with the statistical variations inherent in the measurements we carried out. In our case, τ_o(b) variability can be properly expressed as the coefficient of variation, CV (with CV = σ/μ, where σ is standard deviation), of each Gaussian component. The highest CV-value was observed in the first Gaussian component, and equaled 0.528. In the other Gaussian components, CV ranged from 0.096 to 0.298. To compare such variability levels with those expected on a statistical basis, we applied the same open-time analysis described above to synthetic data. Seventeen groups of numeric values distributed exponentially according to a time constant of 0.343 ms (a value that coincides with the mean of the first Gaussian component revealed by our analysis; see above) were generated randomly as explained in Methods. Each group of randomly-generated open times consisted of a number of values (49–255) equal to the number of events detected in one specific burst of a group of 17 experimental bursts (which were randomly selected from the 29 bursts, the analysis of which returned τ_o(b)-values included in the first peak of Fig. 1 A's histogram; in this way, the correspondence between experimental data and “synthetic” data was optimized). The open-time values thus generated within each group were binned logarithmically as done for experimental data (see Methods) to construct a “simulated” open-time frequency distribution. Each of the histograms thus obtained was best-fitted with a single exponential function, and the time-constant values returned by fittings (“simulated” τ_o(b)s) were in turn binned to construct a “simulated”-τ_o(b) histogram which is shown in Fig. 4 B. This histogram was best-fitted with a single Gaussian function, which returned μ = 0.325 ms and CV = 0.475. The CV-value thus obtained was only slightly smaller than that found for the first Gaussian component of Fig. 1 A's histogram. Hence, the variability displayed by the experimentally determined τ_o(b)-values is comparable with that expected on a simple statistical basis. The slight, extra variability found in experimental data can be easily explained as the consequence of experimental and/or measurement errors.

The same open-time analysis described above was also carried out for other membrane potential levels. For example, 87 bursts recorded at −30 mV were analyzed, τ_o(b)-values were derived from fittings of open-time frequency distributions, and a τ_o(b) histogram was constructed (Fig. 4 C). Also in this case τ_o(b)s turned out to vary in a wide range of values. However, τ_o(b) peaks appeared much less distinct and separated from each other than was observed at −40 mV. The correspondence between τ_o(b) peaks and the τ_o(b)s returned by the analysis of data from different patches pooled (Fig. 4 C, arrowheads) was also less clear. These phenomena appeared even more pronounced at more positive membrane potentials. We interpret this finding to mean that only at −40 mV could the open-time analysis we applied be accurate enough to allow for recognition of distinct τ_o(b) peaks. This is likely due to the fact that the number of open-closed state transitions per burst is much higher at −40 mV than at more positive (or negative) potentials, because of the pronounced voltage-dependence of I_NaP channels' mean open time (Magistretti and Alonso, 2002). Indeed, the estimated, average number of openings per burst (Fig. 4 D) showed a maximum at −40 mV and a sharp decline at more positive voltages. Consistently with these data, in the bursts we used for open-time analysis the number of events per burst was on average 158.9 ± 12.0 at −40 mV (n = 67) and 94.5 ± 6.1 at −30 mV (n = 87). Clearly, a smaller number of events per burst would make the corresponding open-time histogram less proximate to the real distribution and, consequently, the τ_o(b) estimation obtained from data fitting less accurate.

Single channels can open according to multiple gating modalities

So far our analysis has shown that the channel open times observed within bursts distribute according to at least four major time constants, which, according to the accepted theories on channel gating, can be assumed to reflect four different open states, or gating modalities. The question could then be raised whether individual channels can generate multiple open states (or gating modalities), or, rather, whether distinct channel subsets are responsible for these different kinetic states. Our results indicate that single channels can indeed open according to more than one gating modality. First of all, in a minority of cases, open times from single bursts clearly distributed according to a double exponential function (see Fig. 5, A2 and B2, Fig. 6 A2). Moreover, we found that, occasionally, sudden, frequently transient switches from a more “flickering” opening modality to a more “stable” one, or vice versa, were unequivocally recognizable within individual burst events. Examples of such gating transitions observed in three different bursts are shown in Fig. 5, A1, B1, and C.

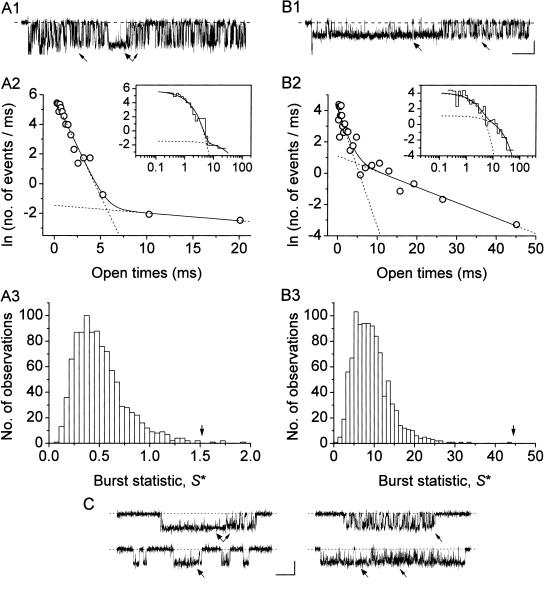
FIGURE 5.

Single channels can generate multiple τ_o(b)s and gating modes. (A, B) Open-time analysis of two long-lasting burst openings (patch C8708 in A, A8716 in B; V_m = −50 mV in A, −10 mV in B). A1 and B1 show the original bursts; note that, in both, a relatively “stable” gating modality (wide arrowheads) was preceded and/or followed by a more “flickering” one (thin arrowheads). Calibration bars are 1 pA, 50 ms. A2 and B2 show the frequency distributions of open times within the same bursts. Data were binned logarithmically and in the main subpanels are shown in a log-linear plot. In the insets, the same data are shown as log-log histograms. Two exponential components are clearly recognizable in both cases. In all subpanels, the smooth, continuous line is the best second-order exponential fitting obtained applying Eq. 1 to the log-log plot. Dotted lines are the single exponential components of the fitting functions shown separately. Fitting parameters are W₁ = 232.72, τ_o(b)1 = 0.765 ms; W₂ = 4.49, τ_o(b)2 = 19.283 ms (A2); W₁ = 76.45, τ_o(b)1 = 1.345 ms; and W₂ = 30.46, τ_o(b)2 = 10.093 ms (B2). A3 and B3 show the distributions of the null statistic, S^*, for the same bursts (see the text for details). The variability statistic, S, was calculated by dividing each burst into six subsections, each with an approximately equal number of openings. S-values (1.517 in A3 and 44.48 in B3) are indicated by the arrows. Each set of individual bars is a histogram of 1000 values of S^*, obtained by repeatedly scrambling the order of the burst's open times and recalculating the variability statistic. Note that S is >S^* for 996 out of 1000 of the observed S^*-values in A3, and for all S^*-values in B3, indicating that the open-time variability along these bursts is greater than expected from a random occurrence of open times. (C) Another example of burst opening showing distinct gating modalities (patch F8711; V_m = −10 mV). Both stable and flickering gating modalities (wide and thin arrowheads, respectively) were observed in bursts from the same patch, and occasionally occurred in sequence within a single burst (double arrow). Calibration bars are 1 pA, 25 ms.

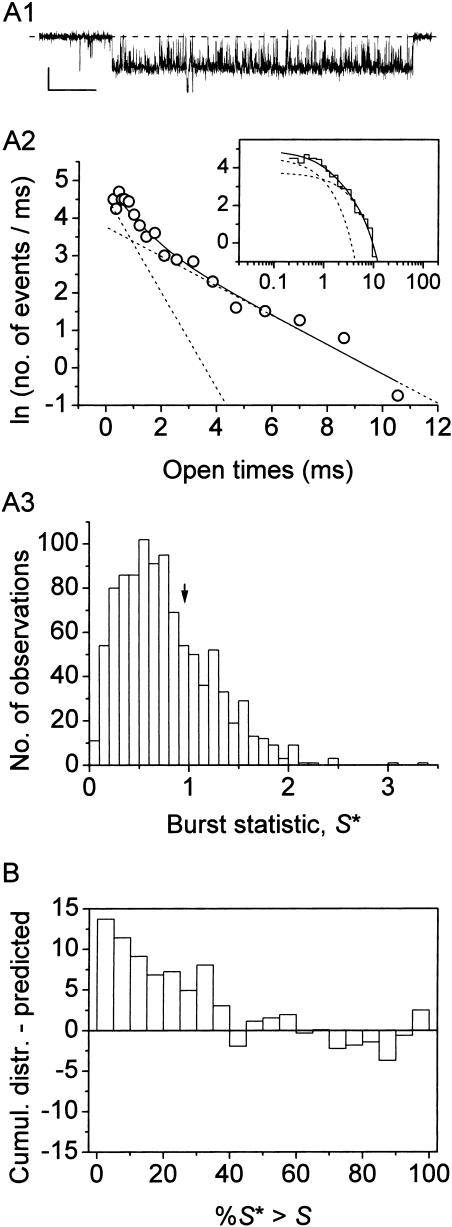
FIGURE 6.

Statistical analysis of open-time variability within bursts. (A) The burst shown in A1 (from B8708; V_m = −30 mV; calibration bars are 1 pA, 50 ms) showed a biexponential distribution of open times, as illustrated in A2. Open-time data were binned logarithmically and in the main subpanel are shown in a log-linear plot. In the inset, the same data are shown as a log-log histogram. Two exponential components are clearly recognizable. In both subpanels, the smooth, continuous line is the best second-order exponential fitting obtained applying Eq. 1 to the log-log plot. Dotted lines are the single exponential components of the fitting function shown separately. Fitting parameters are W₁ = 75.33, τ_o(b)1 = 0.784 ms; and W₂ = 109.22, τ_o(b)2 = 2.552 ms. A3 compares the distribution of the null statistic, S^*, with the variability statistic, S, for the same burst (see the text and Fig. 5, legend, for details). The value of S (0.955) is indicated by the arrow. Note that S is well within the random S^* distribution, indicating that the open-time variability along this burst is consistent with a random occurrence of open times. (B) The cumulative frequency distribution of %S^* > S was determined for 37 bursts recorded at −40 or −30 mV, values in all bins were normalized for the total number of observations, and the percentages thus obtained were subtracted from the “theoretical” percentages predicted on the basis of the null hypothesis. Note the prominent excess of positive values (indicative of a more frequent occurrence than expected on the basis of chance) in the leftmost portion of the plot, i.e., for low values of %S^* > S.

To more quantitatively address the issue of the possible occurrence of multiple gating modes within individual burst, we adopted the nonparametric test introduced by Patlak et al. (1986). Thirty-nine bursts were selected according to two criteria: 1), occurrence of at least 60 intraburst state transitions; and 2), presence of more than one time constant in fittings of open-time distribution. Each burst was then artificially divided into six subsections, each with approximately the same number of open times. The arithmetic mean of open times in each of the six subsections (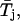 with j = 1, 2, …, 6) as well as the grand mean of open times in the whole burst (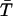) were determined, and the quantity

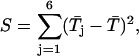which represents an estimate of the variability of 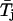within a burst, was calculated. If open-time duration is unevenly distributed along a single burst, then the mean open time in each subsection may be significantly different from that of others, and in this case the values of the statistic S may be larger than expected on the basis of a random occurrence of open times. An estimate of the expected value of S under the null hypothesis was obtained by scrambling the order of the n open times of a burst and recalculating S. Data scrambling randomizes the order of the original open times and creates an artificial data set. This was done 1000 times to generate 1000 scrambled data sets per burst. For each we calculated the value of the above statistic, denoted S_i^* (with i = 1, 2, …, 1000). The empirical distribution of S_i^* was compared with the original value of S obtained from the ordered data to see if the latter is unusually large.

In those bursts in which mode switches were already evident at a visual inspection, the above test clearly excluded the null hypothesis, since in these cases the percent of S^*-values that exceeded S (%S^* > S) was <1% (see Fig. 5, A3 and B3). However, in most bursts in which open times showed a biexponential distribution, the null hypothesis could not be rejected on the basis of this analysis. A typical example is shown in Fig. 6 A. In 31 bursts out of 39, %S^* > S was >5%, and in 35 out of 39 it was >1%. This suggests that, in such cases, switches between different open states and/or gating modes were not stable and occurred in a rather uniform manner throughout a single burst. Nevertheless, the above negative finding could also be the consequence, at least in some cases, of the sensitivity limits inherent in the analysis here adopted. In particular, the subdivision of bursts in subsections was completely arbitrary, and, in general, the boundaries between subsections will be unrelated with hypothetical switches between gating modes: this could markedly affect estimations of S, especially if multiple mode switches occur in a single burst. A further analysis was therefore carried out to determine whether the quantity %S^* > S tended to cluster around low values in a higher percentage of cases than expected on the basis of chance. The cumulative frequency distribution of %S^* > S was determined for 37 bursts recorded at −40 or −30 mV, and values in all bins were normalized for the total number of observations (n = 37). The percentages thus obtained were then subtracted from the “theoretical” percentages predicted on the basis of the null hypothesis, which coincide with the midpoint of each bin. Under the hypothesis of a random distribution, the quantities returned by this analysis should evenly fluctuate around zero over the entire x-axis. A column diagram of the values actually obtained is shown in Fig. 6 B: a prominent excess of positive values (indicative of a more frequent occurrence than expected on the basis of chance) could be clearly identified in the leftmost portion of the plot, i.e., for low values of %S^* > S. Hence, the percentage %S^* > S was characterized by relatively low values more frequently than expected on the basis of chance. These observations strongly suggest that in a significant fraction of cases, the alternation of multiple open states within a burst tends to organize accordingly to true, relatively stable switches between different gating modes.

Analysis of intraburst closed times

The frequency distribution of intraburst closed times was best described by a double exponential function in the majority of bursts (Fig. 3 B2). At V_m = −40 mV, two time constants were revealed by the analysis of closed times in 39 bursts out of 67, whereas in the remaining 28 bursts only one exponential component was apparent. The time constants describing intraburst closed times (τ_c(b)s) also showed wide variability, with values that, at −40 mV, ranged from 97.4 μs to 3.69 ms.

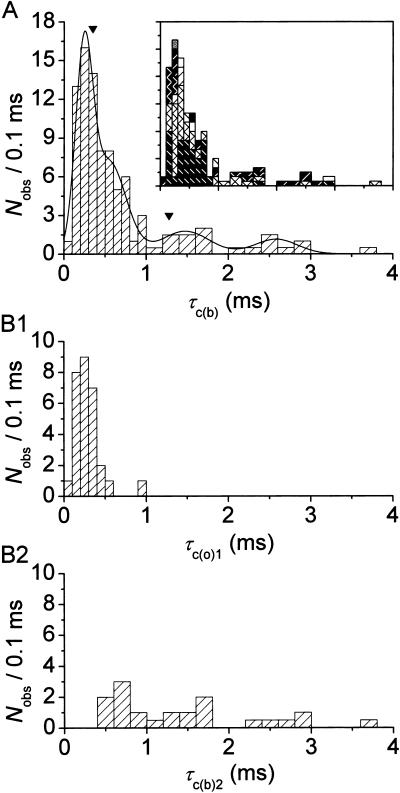
τ_c(b) histograms were then constructed as done for τ_o(b). The histogram obtained for V_m = −40 mV is shown in Fig. 7 A. Gaussian fitting revealed four distinct components, the first two of which (characterized by μ-values of 0.241 and 0.543 ms) were more prominent, with the other two (μ = 1.475 and 2.581 ms) less represented. Since the mean values of the first two Gaussian components were pretty close to each other, and the two corresponding peaks of the τ_c(b) histogram did not appear clearly separated, it could be wondered whether the distinction between these two components is real or instead, simply the artifactual consequence of a wide variability intrinsic in a single component. The analysis of τ_c(b)s limited to those bursts in which closed times were distributed according to a double exponential function showed that the latter possibility can be excluded. In these cases, indeed, single bursts could simultaneously display pairs of τ_c(b)s, the faster and the slower of which (τ_c(b)1 and τ_c(b)2, respectively) fell well within the first and the second Gaussian components, respectively, revealed by the general analysis of τ_c(b)s (Fig. 7, B1 and B2).

FIGURE 7.

Diversity of closed times. (A) Frequency distribution of time constants describing intraburst open times (τ_c(b)s) at −40 mV. The τ_c(b)-values used to construct the histogram were derived from individual bursts (n = 67) recorded in nine different patches. Note the two different bin widths (0.1 ms for τ_o(b) < 1.0 ms and 0.2 ms for τ_o(b) ≥ 1.0 ms). The inset shows the same histogram constructed as a stack-column diagram, with each column pattern corresponding to data from a single patch. The histogram was best-fitted with the sum of four Gaussian functions (smooth line), which returned the following fitting parameters: A₁ = 38.07, μ₁ = 0.241 ms, σ₁ = 0.207 ms; A₂ = 37.61, μ₂ = 0.543 ms, σ₂ = 0.419 ms; A₃ = 13.06, μ₃ = 1.475 ms, σ₃ = 0.589 ms; and A₄ = 7.48, μ₄ = 2.581 ms, σ₄ = 0.521 ms. The arrowheads indicate the previously-reported τ_c(b)-values obtained by pooling data from different patches (Magistretti and Alonso, 2002). (B) Histograms of “fast” τ_c(b) (τ_c(b)1: B1) and “slow” τ_c(b) (τ_c(b)2: B2) for bursts in which closed times were distributed according to a double exponential function.

Correlation between intraburst open and closed times

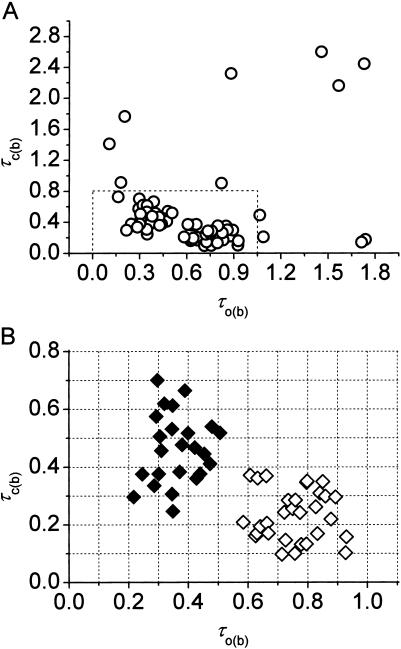
We then examined the possible existence of a correlation between intraburst open and closed times by plotting τ_c(b) versus τ_o(b) for each burst. When the analysis of a single burst revealed two τ_c(b)s and/or τ_o(b)s, the prevalent τ_c(b) or τ_o(b) was used for this plot. This could be done because when two τ_c(b)s and/or τ_o(b)s were present in a single burst, one of the two (most frequently the faster one) was much more represented (in terms of weight coefficient, W_j) than the other: at −40 mV, the relative weight coefficient, 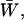of the prevalent component was always >0.71 for open times ( 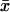= 0.909 ± 0.025, n = 15) and 0.63 for closed times ( 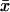= 0.871 ± 0.018, n = 39). (These values were calculated only for those cases in which two exponential components were observed, thus excluding the cases in which the relative weight of the “prevalent” component was 1.) As a whole, the plot of τ_c(b) as a function of τ_o(b) (for V_m = −40 mV; see Fig. 8 A) did not show any systematic correlation between the two variables. However, a closer inspection of a restricted region of the graph (τ_o(b) < 1.0 ms and τ_c(b) < 0.8 ms), in which 55 out of 67 pairs of values were concentrated, clearly revealed that data points tended to group in two major, distinct clusters (Fig. 8 B). In one of these clusters (solid diamonds), τ_o(b) and τ_c(b) averaged 0.362 ± 0.016 ms and 0.462 ± 0.025 ms, respectively (with τ_o(b) always <0.55; n = 24); in the other (unfilled diamonds), τ_o(b) and τ_c(b) averaged 0.755 ± 0.018 ms and 0.233 ± 0.016 ms, respectively (with τ_o(b) always >0.55; n = 30). Note that these values are very close to those characterizing the most prominent peaks of both τ_o(b) and τ_c(b) frequency distribution (see above). Hence, our data demonstrate that, at −40 mV, >80% of the burst openings generated by I_NaP channels occur according to either one of two predominant gating modalities, one of which includes mean open and closed times of ∼0.36 ms and ∼0.46 ms, respectively, and the other higher mean open times (∼0.76 ms) and lower mean closed times (∼0.23 ms).

FIGURE 8.

Correlation between τ_o(b) and τ_c(b). (A) Scatter plot of τ_c(b) as a function of τ_o(b) for single bursts. In the cases of bursts in which open and/or closed times were distributed according to a double exponential component, the prevalent τ_o(b) and/or τ_c(b) (in terms of the corresponding weight coefficient) were considered. (B) Detail of the region of the τ_c(b)(τ_o(b)) plot delimited by the dotted-line box in A. Two clusters of points are evident (solid and open symbols).

Single channels preferentially maintain a single gating modality for prolonged periods

Although single I_NaP channels proved able to generate multiple open states and gating modalities, the examination of prolonged sequences of consecutive sweeps displaying high-opening-probability, long-lasting bursts, most probably due to the activity of one single channel, made it clear that each channel preferentially operates, at least for prolonged periods, according to a single, specific gating mode. This is exemplified in Fig. 9 A, which shows five consecutive sweeps recorded in a patch in which a single channel continued to generate long-lasting burst openings for prolonged periods. In particular, bursts lasting >250 ms occurred, in a first phase of the recording (∼3.75 min), in 27 out of 40 consecutive 500-ms sweeps, and in a later phase (of ∼2.5 min) in 23 out of 26 sweeps. These bursts displayed a very characteristic and constant pattern of gating, with relatively prolonged and stable openings and closings. Superimposition of two (or more) burst openings both showing such particular gating modality were never observed in this patch. The analysis of open times of 22 such bursts from 26 consecutive sweeps recorded at the step potential of −30 mV revealed a fairly uniform distribution of τ_o(b) around a single peak (Fig. 9 B). Gaussian fitting returned a mean value of 3.227 ms and a reasonably small CV coefficient (0.484), compatible with the statistical variability inherent in the measurements of the events generated by a single open state. Also the analysis of closed times indicated the presence, within these burst events, of one prevalent, well-defined closed state (μ = 1.164 ms, CV = 0.46). A similar consistency of intraburst open and closed states was observed in four other patches in which prolonged sequences of burst openings could be unequivocally attributed to the activity of one single channel.

FIGURE 9.

Single channels preferentially operate according to a specific gating modality. (A) Consecutive sweeps recorded at the step potential of −30 mV in a patch (A8721) in which a single channel continued to generate long-lasting burst openings for prolonged periods. The characteristic and homogeneous pattern of gating of these bursts, with relatively prolonged and stable openings and closings, clearly appears at a simple visual inspection. Calibration bars are 1 pA, 50 ms. (B) Frequency distribution of τ_o(b) for 22 bursts recorded at −30 mV in the same patch of A. The histogram was best-fitted with a single Gaussian function (continuous line), which returned the fitting parameters of A = 17.72, μ = 3.227 ms, and σ = 1.562 ms.

Analysis of burst duration

The kinetic variability that characterized burst openings generated by I_NaP channels not only involved intraburst openings and closings, but also burst duration. The analysis of the diversity of mean burst duration in different channels was hindered by the fact that most of the patches recorded were multichannel patches, which prevented us from attributing the results obtained in a particular patch to one, and only one, channel. Nonetheless, on the basis of the obvious consideration that the channel activities observed in different patches must be due to different channels, we approached the issue of burst-duration diversity by separately analyzing the same parameter in each single patch studied.

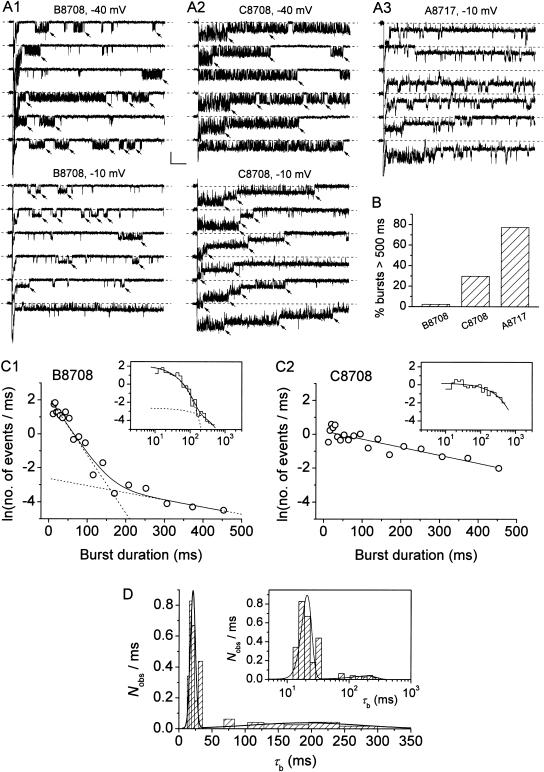
The existence of a kinetic diversity in burst duration is clearly exemplified in Fig. 10, in which traces recorded in three representative patches are shown. In the patch illustrated in Fig. 10 A1, most bursts were of relatively short duration, with only a few, occasional bursts showing a more “persistent” behavior (fourth trace from top at −40 mV; last trace at −10 mV; see also Fig. 10 B). In the patch of Fig. 10 A2, burst openings were typically much more prolonged, although only a minority of them (∼30%) exceeded in duration the 500-ms depolarizing pulses applied (Fig. 10 B). In the patch of Fig. 10 A3 a vast majority of bursts (∼80%) extended over the whole 500-ms depolarizing pulse (Fig. 10 B). To quantify this diversity, burst-duration histograms were constructed for each patch as explained in the Methods. It has been reported elsewhere (Magistretti and Alonso, 2002) that I_NaP channels' burst duration is basically voltage-independent over a wide window of membrane potentials (see also Fig. 10, A1 and A2). Therefore, to increase the number of observations per histogram, the measurements obtained from each patch at all membrane voltages were pooled. The histograms derived from the patches of Fig. 10, A1 and A2, are shown in Fig. 10, C1 and C2, respectively (patches like that of Fig. 10 A3 could not be further analyzed due to the small number of bursts of defined duration). Exponential fittings of such histograms returned one or two burst-duration time constants (τ_bs) per patch. To further analyze τ_b variability, the τ_b-values thus obtained from all patches (listed in Table 1) were used to construct an overall τ_b frequency-distribution diagram (Fig. 10 D). This histogram showed a clear peak between 17 and 32 ms, plus a more dispersed peak for τ_b-values >80 ms. Displaying the histogram on a logarithmic x-axis made the two peaks more clearly recognizable (Fig. 10 D, inset). Gaussian fitting of the histogram returned μ-values of 20.8 and 211.1 ms. The above data suggest that I_NaP channels can operate according to at least three “bursting states,” two of which generate bursts of mean duration equal to ∼20 ms and ∼200 ms, and the third of which produces much more prolonged bursts, normally exceeding 500 ms in duration. It is also worth noting that: 1), the mean τ_b-values presented here are very close to those obtained by pooling data from different patches at each test potential, as reported elsewhere (Magistretti and Alonso, 2002); and 2), although burst openings distributing according to a “slow” time constant (τ_b2 in Table 1) occurred occasionally in some patches and systematically in others, the values of this slow time constant were very similar in both cases (see Fig. 10, C1 and C2).

FIGURE 10.

Diversity of burst duration. (A) Exemplary traces recorded at −40 mV or −10 mV in three different patches that displayed prevalence of medium-duration (A1), long (A2), and very long (A3) bursts. The arrows point to exemplary bursts selected for burst-duration analysis. When superimposed bursts were recorded, only those ones the starting point and the end of which could be clearly identified (i.e., when the burst's starting point coincided with the depolarizing pulse's onset; see A2) were considered for burst-duration analysis. Note in A3, third trace from top, two very-long-lasting openings superimposed. Calibration bars are 2 pA, 50 ms. (B) Bar diagram of the percent of bursts that exceeded in duration the 500 ms of the depolarizing pulses applied in the three above patches. (C) Frequency distribution of burst duration in the two patches illustrated in A1 and A2. Data were binned logarithmically as explained in Methods, and in the main subpanels are shown in a log-linear plot. In the insets, the same data are shown as a log-log histogram. In all subpanels, the smooth, continuous line is the best second-order (C1) or first-order (C2) exponential fitting obtained applying Eq. 1 to the log-log plot. Dotted lines in C1 are the single exponential components of the fitting function shown separately. Fitting parameters are W₁ = 252.9, τ_b1 = 29.33 ms; W₂ = 17.25, τ_b2 = 239.9 ms (C1); and W = 254.1, τ_b = 209.6 ms (C2). Note that the two plots are shown on the same x- and y-scales. (D) Frequency distribution of time constants describing burst duration (τ_bs). The τ_b histogram was constructed after binning data according to a logarithmic scale that yielded 10.8 bin/decade, and is shown on a linear x-scale in the main panel, and a logarithmic x-scale in the inset. The smooth line in both subpanels is the fitting obtained applying a double Gaussian function. Fitting parameters are A₁ = 8.637, μ₁ = 20.75 ms, σ₁ = 7.73 ms; and A₂ = 8.174, μ₂ = 191.26 ms, σ₂ = 168.48 ms.

TABLE 1.

Kinetic parameters obtained from the analysis of frequency-distribution diagrams of burst duration in 15 patches

Patch no.	τb1 (ms)	τb2 (ms)		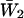% bursts > 500 ms	nT
A8618	14.64	74.4	0.257	2.7	74
B8723	17.65	–	0	0	38
D8716	18.41	255.68	0.044	0	147
F8711	18.49	139.7	0.123	0	95
B8709	20.77	–	0	8.1	62
D8711	21.16	–	0	0	58
A8716	21.56	168.72	0.125	1.4	71
B8714	27.98	–	0	0	149
C8703	29.26	–	0	0	86
B8708	29.33	239.89	0.063	2.3	218
D8708	32.92	–	0	0.65	154
A8721 (1)	–	97.7	1	0	57
C8708	–	209.61	1	29.7	317
A8717	–	–	–	77.27	82
A8721 (2)	–	–	–	84.62	54

Burst-duration histograms were fitted with single or double exponential functions (see Eq. 1 in Methods). τ_b-values are the time constants returned by fittings; 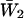is the relative weight coefficient of the slow exponential component, calculated as 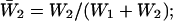and n_T is the total number of bursts analyzed per patch. The fifth column specifies the percentage of bursts that in each patch exceeded in duration the 500-ms depolarizing pulses applied. Patch A8721 displayed two types of clearly distinguishable channel activity (see Fig. 2), that were most probably due to distinct channels, and were treated separately—A8721 (1) and A8721 (2).

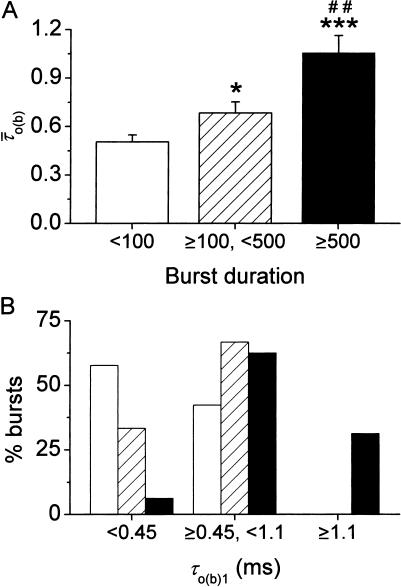
Finally, we examined the possible correlation between burst duration and intraburst gating modes. The bursts recorded at −40 mV in all patches were divided in three groups according to their duration, Δt_b (group 1, Δt_b < 100 ms; group 2, 100 ms ≤ Δt_b < 500 ms; and group 3, Δt_b ≥ 500 ms). In each group the mean intraburst open time, 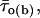was calculated as explained in Methods (Eq. 2) for each burst. 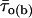turned out to clearly correlate with burst duration, in that average 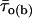was significantly higher in group-2 than in group-1 bursts, and even more so in group-3 than in group-1 bursts (Fig. 11 A). We further extended this analysis by determining, within each of the three burst groups, the percent of bursts in which the predominant τ_o(b) was: 1), <0.45 ms (thus falling within the first peak in the τ_o(b) distribution, see Fig. 4 A); 2), ≥0.45 and <1.1 ms (thus falling within the second peak in the τ_o(b) distribution); and 3), ≥1.1 ms. The results of this analysis, illustrated in Fig. 11 B, clearly showed that the shorter the burst, the higher the probability for the channel to gate in a short-lived open-state modality; and the longer the burst, the higher the probability for the channel to choose a long-lived open-state modality. The probability of very-long-lasting bursts to generate openings distributed according to a τ_o(b) < 0.45 ms was minimal (<0.07).

FIGURE 11.

Correlation between intraburst mean open times and burst duration. The bursts recorded at −40 mV in all patches were divided in three groups according to their duration, Δt_b: group 1 (open bars), Δt_b < 100 ms; group 2 (hatched bars), 100 ms ≤ Δt_b < 500 ms; group 3 (filled bars), Δt_b ≥ 500 ms. (A) Bar diagram of the mean intraburst open time, 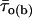. The bars are average 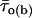-values calculated for each burst group: n = 26 (group 1), 24 (group 2), and 16 (group 3). Key: ^* is p < 0.05 and ^*** is p <0.001 with respect to group 1; ^## is p < 0.01 with respect to group 2. (B) Bar diagram of the burst percentage, within each of the above burst groups, in which the predominant τ_o(b) was i) <0.45 ms; ii) ≥0.45 and <1.1; and iii) ≥1.1 ms.

DISCUSSION

The present study provides a detailed description of the kinetic diversity of Na⁺-channel burst openings responsible for I_NaP generation in entorhinal cortex neurons. Our main findings can be summarized as follows: 1), I_NaP channels display a remarkably wide range of kinetic variability as far as both intraburst state transitions and mean burst duration are concerned; 2), nevertheless, a few, predominant, specific patterns of combination of mean open time, mean closed time, and mean burst duration can be distinguished, and these probably correspond to a limited number of “gating modalities” that I_NaP channels can generate; and 3), individual I_NaP channels are able to transit through multiple ones of these states although, normally, each channel tends to operate for prolonged periods according to only one of these gating modalities.

Analysis of single bursts revealed a rather striking variability of intraburst fractional open time, mean open time, mean closed time, and combinations of the two latter parameters, that produced a clear diversity of gating patterns in different bursts (Figs. 1 and 2). A similar kinetic variability has also been described in long-lasting Na⁺-channel bursts that are occasionally observed in membrane patches from skeletal muscle fibers (Patlak and Ortiz, 1989). Such a diversity in intraburst-gating processes could generate the impression that state-transition kinetics within bursts show no well-defined and constant patterns. Indeed, to avoid the necessity of postulating an unreasonably high number of open and closed states to account for the wide variability and the seemingly continuous distribution of intraburst kinetic parameters, Patlak and Ortiz (1989) proposed that the Markovian assumption of fixed rate constants in state transitions could be relaxed somewhat, and that these rate constants could be endowed with intrinsic variability, other factors being equal.

Our analysis, however, clearly demonstrates that the variability displayed by intraburst kinetic processes, although wide, is neither anarchic nor compatible with a “continuous” dispersion of the kinetic parameters that define state transitions. Indeed, at −40 mV the time constants describing intraburst open and closed times (τ_o(b)s and τ_c(b)s, respectively) turned out to be distributed around a limited number of well-defined peaks. This indicates the existence of (at least) four open states and (at least) four closed states in channels engaged in bursting activity. Our ability to recognize these distinct kinetic states depended on the fulfillment of the following requirements: 1), the availability of a high number of bursts to be analyzed, which was achieved, in our experimental model, due to the relatively high frequency of occurrence of persistent Na⁺-channel activity in the neurons under study; 2), a high number of openings per burst; and 3), the construction of logarithmic histograms of τ_o(b)s and τ_c(b)s and the application of appropriate logarithmic transforms of exponential fitting functions, which made the analysis of frequency distributions much more sensitive. Requirement 2 was met by concentrating the analysis on bursts recorded at −40 mV, because, due to the voltage-dependent properties of I_NaP channels (Magistretti and Alonso, 2002), at this membrane potential the average number of open-closed state transitions within bursts was maximal.

Individual channels proved able to explore multiple intraburst open and closed states, and to undergo transient switches between different gating modalities during single burst openings. This suggests that a single population of channels could generate the whole spectrum of kinetic behaviors observed in different bursts. Nonetheless, prolonged sequences of burst openings that could be attributed to the activity of a single channel revealed that individual channels tend to maintain a specific gating modality for long periods. Moreover, a few well-defined combinations of specific open and closed states were prevalent over others during burst activity. At −40 mV, >80% of bursts consisted of openings and closings distributed according to time constants of ∼0.36 ms and ∼0.46 ms, respectively (“intraburst mode 1”), or ∼0.76 ms and ∼0.23 ms, respectively (“intraburst mode 2”).

It is also possible that intraburst closings may actually reflect block of open channels by some extracellular component (e.g., divalent cations such as Ca²⁺ or Mg²⁺), rather than transitions to true closed states, as it is known to be the case in other ion channels (for example, see Lansman et al., 1986; Stuenkel et al., 1990; Nakazawa and Hess, 1993). Further experiments will be needed to ascertain this possibility. However, our conclusion that multiple open states must exist would not be invalidated, since in such a case different τ_o(b)s and τ_c(b)s would reflect different blocker affinities, and therefore the existence of different “targets”, or channel states.

Mean burst duration was also variable from channel to channel. Our data indicate the existence of at least three distinct time constants describing burst duration, which are likely to correspond to as many “bursting states” (see Magistretti and Alonso, 2002). We found a clear correlation between burst duration and intraburst-gating events. Indeed, bursts of relatively short duration had the highest probability to gate in intraburst mode 1, whereas bursts of longer duration were more likely to gate in intraburst mode 2, although mode 1 was also represented. Very-long-lasting bursts tended to gate according to mode 2 only or other modes that included considerably longer mean open times, with almost complete exclusion of mode 1.

The issue of whether a homogeneous population of voltage-gated Na⁺ channels can generate both the classic transient Na⁺ current and I_NaP via a simple mechanism of modal gating, or whether more specialized mechanisms of modification of Na⁺-channel function are implicated in I_NaP expression, has yet to be fully elucidated (see Alzheimer et al., 1993; Magistretti et al., 1999a; Taddese and Bean, 2002; Magistretti and Alonso, 2002). Regardless of the importance of modal gating of regular, “fast” Na⁺ channels in I_NaP generation, the data discussed above clearly show that Na⁺ channels engaged in “persistent” activity can operate according to multiple, well-defined gating modalities. The phenomenon of modal gating has been observed in several types of ionic channels (e.g., Plummer and Hess, 1991; Delcour et al., 1993; Marrion, 1993; Zahradnikova and Zahradnikov, 1995; Shirokov et al., 1998; Singer-Lahat et al., 1999), and could turn out to be a general mechanism of modification and control of ion-channel function.

Our results show that different channels can produce long-lasting burst openings with very different frequencies. In some patches, indeed, such openings were observed occasionally, whereas in others their occurrence was systematic. Nonetheless, in both cases the duration of these prolonged bursts appeared to distribute according to very similar time constants. Therefore, it seems likely that channels of the same type can behave differently as to the probability of producing prolonged burst openings. It is tempting to hypothesize that switches of I_NaP channels from a gating modality in which relatively short burst openings are most frequent, to another one characterized by prevalent or exclusive long-duration bursts, or vice versa, represents a physiological mechanism to modulate the function of the same channels, and, consequently, to modify I_NaP amplitude. Such an effect on I_NaP amplitude would be further potentiated by the fact that, as discussed above, long-lasting bursting states preferentially associate with intraburst-gating modalities characterized by long open times and high opening probabilities, whereas shorter bursts more often include short open times and lower opening probabilities. Indeed, I_NaP has been shown to be the target of modulatory processes that may involve neurotransmitter receptors (Cepeda et al., 1995; Cantrell et al., 1996; Mittmann and Alzheimer, 1998; Gorelova and Yang, 2000), G proteins (Ma et al., 1997), and phosphorylations (Cantrell et al., 1996; Astman et al., 1998; Franceschetti et al., 2000). Stable molecular modifications of I_NaP channels, such as phosphorylations/dephosphorylations and/or other covalent modifications, would be suitable to account for the prolonged periods of either short- or long-duration burst activity typically observed in our recordings. The issue of the possible effects of these modulatory pathways on the elementary properties of persistent Na⁺-channel activity will deserve further investigation.