Characterization of DNA/Lipid Complexes by Fluorescence Resonance Energy Transfer

Abstract

Fluorescence resonance energy transfer (FRET) is a potential method for the characterization of DNA-cationic lipid complexes (lipoplexes). In this work, we used FRET models assuming a multilamellar lipoplex arrangement. The application of these models allows the determination of the distance between the fluorescent intercalator on the DNA and a membrane dye on the lipid, and/or the evaluation of encapsulation efficiencies of this liposomal vehicle. The experiments were carried out in 1,2-dioleoyl-3-trimethylammonium-propane/pUC19 complexes with different charge ratios. We used 2-(3-(diphenylhexatrienyl)propanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (DPH-PC) and 2-(4,4-difluoro-5-octyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (BODIPY-PC) as membrane dyes, and ethidium bromide (EtBr) and BOBO-1 as DNA intercalators. In cationic complexes (charge ratios (+/−) ≥ 2), we verified that BOBO-1 remains bound to DNA, and FRET occurs to the membrane dye. This was also confirmed by anisotropy and lifetime measurements. In complexes with all DNA bound to the lipid (charge ratio (+/−) = 4), we determined 27 Å as the distance between the donor and acceptor planes (half the repeat distance for a multilamellar arrangement). In complexes with DNA unbound to the lipids (charge ratio (+/−) = 0.5 and 2), we calculated the encapsulation efficiencies. The presented FRET methodology is, to our knowledge, the first procedure allowing quantification of lipid-DNA contact.

INTRODUCTION

Gene therapy offers promise for the treatment of disease through the use of DNA-based vectors that allow targeting, delivery of DNA to cells, and expression of the gene. Among the nonviral vectors, cationic liposomes seem to be the most widely used DNA delivery system (Huang et al., 1999). Despite low transfection efficiencies, they show nonimmunogenicity, low toxicity, and possibility of large-scale production. Many efforts have been made to fully characterize cationic liposome-DNA complexes (lipoplexes), because it is the only way to understand, improve, and control the transfection efficiency of these nonviral-based vectors. In 1987, it was reported for the first time that plasmid DNA and cationic liposomes aggregate due to electrostatic attractive forces and origin small complexes able to transfer DNA to the cells (Felgner et al., 1987). Since then, most of the published data regard the optimization of lipid formulations and measurement of the transfection efficiency as a function of DNA/lipid charge ratio (Zhou and Huang, 1994; Farhood et al., 1995; Lee et al., 1996; Templeton et al., 1997; Hong et al., 1997; Thierry et al., 1997; Ross and Hui, 1999; Simões et al., 2000; Smisterová et al., 2001). The ability of DNA and oligonucleotides to induce lipid mixing (Xu et al., 1999; Jaaskelainen et al., 1994; Eastman et al., 1997; Gershon et al., 1993; Wasan et al., 1999), the electrostatic properties of the lipoplexes during and after their formation (Zuidam and Barenholz, 1997; Hirsh-Lerner and Barenholz, 1998; Zuidam et al., 1999), the DNA accessibility to DNase I after complexation with lipids (Zhang et al., 1997; Ferrari et al., 2001; Crook et al., 1996), the size and zeta potential of the lipoplexes (Perrie and Gregoriadis, 2000; Son et al., 2000; Kennedy et al., 2000; Kreiss et al., 1999) and the encapsulation efficiency (Gregoriadis et al., 1996; Ferrari et al., 2001) of the lipid vector are some of the considered parameters to characterize lipoplexes. In parallel with the studies referred above, several other techniques were used to visualize the lipoplexes structure, such as atomic force microscopy (Oberle et al., 2000), electron microscopy (Gershon et al., 1993; Gustafsson et al., 1995; Simberg et al., 2001; Sternberg et al., 1994; Lasic et al., 1997; Battersby et al., 1998; Huebner et al., 1999; Radler et al., 1997), and x-ray diffraction (Caracciolo et al., 2002; Lasic et al., 1997; Radler et al., 1997; Kreiss et al., 1999). Electron microscopy and x-ray diffraction used in parallel revealed a multilamellar structure of lipid bilayers with sandwiched DNA, with a constant interlayer spacing invariant with the charge ratio, and depending on cationic liposomes formulations (Lasic et al., 1997; Radler et al., 1997). Kreiss and co-workers verified, using small-angle x-ray scattering, that the cationic lipid determines the spacing of the structure, and lipoplexes with the same lipidic formulation but different plasmid sizes have the same interlayer spacing (Kreiss et al., 1999). In a recent publication, Caracciolo et al. (2002) studied the structure of DOTAP/DNA lipoplexes by energy dispersive x-ray diffraction technique and also observed an ordered multilamellar structure with a periodicity d = 61.2 ± 2 Å, invariant with the lipid/DNA ratio.

In this work, the methodology of fluorescence resonance energy transfer (FRET) is presented as a promising tool in the scope of biophysical and structural characterization of the lipoplexes. Recently, the interaction of complexes of DNA labeled with a dimeric cyanine dye (YOYO-1) and cetyltrimethylammonium liposomes containing 2-(3-(diphenylhexatrienyl)propanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (DPH-PC) was monitored by FRET (Clamme et al., 2000). However, these authors try to analyze their results calculating a single donor-acceptor distance for an intermolecular FRET geometry, which is incorrect. Using the same DNA intercalator and FRET methodology, Wong and co-workers also verified that YOYO-1 remains intercalated after addition of excess cationic lipid, suggesting YOYO-1 as a qualitative DNA marker in intracellular delivery studies (Wong et al., 2001). Although these studies have revealed the usefulness of FRET in this field, full advantage of the peculiar sensitivity of this technique to distance in the nanometer range was not taken. Using the actual FRET kinetics for these systems (Theory of FRET in Lipoplexes, below), we show that structural details can be obtained, as well as the quantification of the amount of unbound DNA.

THEORY OF FRET IN LIPOPLEXES

To use FRET in a quantitative way it is essential to model the topological distribution of the probes on the DNA and on the lipid. For this purpose, we will consider a multilamellar model (with DNA sandwiched between adjacent lipid bilayers, see Fig. 1) for lipoplexes as suggested from recent works (see Introduction). In this specific geometry we have transfer from one donor molecule (restricted to a plane) to acceptor molecules randomly distributed in two adjacent parallel planes. Two distinct possibilities are shown schematically in Fig. 1: either the donor is a labeled phospholipid and the acceptor is a DNA-intercalating probe (Fig. 1 A) or the other way round (Fig. 1 B). As will be described and explained in Results, the arrangement of Fig. 1 A was used solely for DOTAP/pUC19 charge ratio (+/−) < 1, whereas the arrangement of Fig. 1 B was used both for DOTAP/pUC19 charge ratio (+/−) < 1 and for DOTAP/pUC19 charge ratio (+/−) > 1. Strictly, for each bilayer, there should be two planes of acceptor molecules (one for each bilayer leaflet), and the distances between those planes and that of the donors should not coincide, because the fluorophores in the labeled phospholipids are not expected to be located at the exact center of the bilayer (that is, strictly, we should have d₁ ≠ d₂ in Fig. 1). However, for the used lipid probes (see structures in Fig. 2), the difference in transverse location for chromophores belonging to labeled lipid molecules in opposing leaflets of the same bilayer is small for FRET purposes (≪R₀) and will from this point on be neglected (that is, we can take d ≈ d₁ ≈ d₂ ≈ one-half the multilamellar repeat distance in Fig. 1). We will only consider FRET from each donor to the two closest acceptor planes. For a multibilayer structure, a second set of two acceptor planes would be located at ≈3d. However, the contribution of FRET to this plane (and further planes) of acceptors would be much smaller and effectively masked by FRET to acceptors located at ≈d.

FIGURE 1.

Schematic representation of the lipoplexes multilamellar structure with the fluorescent probes within the DNA and the lipid. (A) Acceptor (a) on the DNA (EtBr) and donor (d) on the lipid (DPH-PC and BODIPY-PC). This arrangement was used for DOTAP/pUC19 charge ratio (+/−) = 0.5. (B) Acceptor on the lipid (BODIPY-PC) and donor on the DNA (BOBO-1). This arrangement was used for DOTAP/pUC19 charge ratio (+/−) = 0.5, 2, and 4.

FIGURE 2.

Chemical structures of fluorescently labeled lipids (DPH-PC and BODIPY-PC) and cationic lipid (DOTAP) used in this study.

The basic equation for the decay of the donor to a plane of acceptors, which assumes low density of excited acceptors, no energy migration among donors, no translational diffusion of probes during the donor excited state lifetime, uniform distribution of acceptors, a single Förster distance R₀ (defined in Eq. 10) value for all donor-acceptor pairs, and probe dimensions ≪R₀ is given by (Davenport et al., 1985) as

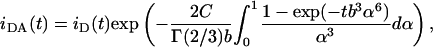(1)

where

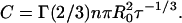(2)

In these equations, τ is the donor lifetime in the absence of acceptor, i_D(t) = exp(−t/τ) is the donor decay in the absence of acceptor, n is the acceptor surface density (number of molecules/unit area), Γ is the complete gamma function, R₀ is the Förster distance (defined in Eq. 10), and b = (R₀/d)²τ^−1/3. For donors with nonexponential decay (as often is the case), i_D(t) should be the experimental decay law (sum of exponentials) and τ should be replaced by the average lifetime in the definition of b (e.g., Loura et al., 2001).

For the purpose of theoretical computation of the decay, n is easily calculated using

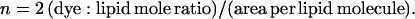(3)

The factor 2 reflects the fact that, in a multibilayer geometry, the available surface area is only half of the product of the number of total lipid molecules times the area per lipid. For the DOTAP area in the plane of the bilayer, a value of 65 Ų was considered (Zuidam and Barenholz, 1997). Eqs. 1–3 are also valid for FRET to two opposing equivalent acceptor planes, as in Fig. 1, but, in this case, the acceptor surface density should be further doubled.

Eq. 1, as it stands, is only valid for significant excess of cationic lipid, leading to essentially no unbound DNA (as verified from the agarose gel electrophoresis results, see below). In these conditions, for the arrangement depicted in Fig. 1 B, all DNA-located donors have acceptors in their vicinity and are available for energy transfer. We verified that for the charge ratio (+/−) DOTAP/DNA = 2, there is already a small but significant fraction of unbound DNA (see agarose gel electrophoresis results below), which implies the existence of donor molecules isolated from acceptors. To take this into account, the donor time-resolved fluorescence law should allow for a fraction γ of molecules, the decay of which is unaffected by the acceptors. If the decay of donors intercalated in lipid-bound DNA in the absence of acceptors (i_D(t)) differs from that of donors in unbound DNA (i_D0(t)), then Eq. 1 should be rewritten as

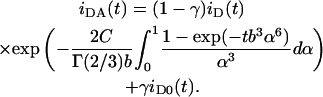(4)

For the charge ratio (+/−) DOTAP/DNA = 0.5, whereas Eq. 4 is valid for the arrangement of Fig. 1 B, there is a major difference in FRET geometry for the arrangement of Fig. 1 A: donors (labeled phospholipids) are located close to the center of the bilayer, and acceptors (DNA-intercalated probes) are inside the DNA helix. Because of the excess of DNA in this system, a significant amount of DNA molecules are not involved in the complexes, and only a fraction f of acceptors will be available for transfer. The decay law (neglecting isolated donors—it is assumed that all bilayer-located donors have DNA in their vicinity, i.e., there are no lipid molecules outside lipoplexes) is now

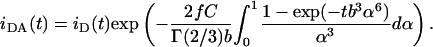(5)

In all cases, the experimental FRET efficiency (see Experimental section and Fluorescence Measurements subsection) can be compared with the theoretical expectation, which is computed numerically from

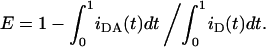(6)

EXPERIMENTAL

Materials

The plasmid pUC19 (2690 bp) was purchased from Promega (Madison, WI). The cationic lipid 1,2-dioleoyl-3-trimethylammonium-propane (DOTAP; structure depicted in Fig. 2) was obtained from Avanti Polar Lipids (Alabaster, AL). The membrane dyes 2-(3-(diphenylhexatrienyl)propanoyl)-1-hexadecanoyl-sn-glycero-3-phosphacoline (DPH-PC) and 2-(4,4-difluoro-5-octyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocoline (BODIPY-PC; structures depicted in Fig. 2), as well as the DNA intercalating dyes ethidium bromide (EtBr) and BOBO-1 iodide, were obtained from Molecular Probes (Eugene, OR). 3-(2-benzothiazoyl)-7-n,n-diethylaminocoumarin (coumarin 6), purchased from Aldrich (Milwaukee, WI) was used for BOBO-1 quantum yield measurements. The liposomes and lipoplexes were prepared in 30 mM Tris(hydroxymethyl)-aminomethan (Tris) buffer, pH 7.4 adjusted with hydrochloric acid, both obtained from Merck (Darmstadt, Germany). All other chemicals were purchased from Sigma (St. Louis, MO).

Plasmid DNA and dye/DNA complexes

pUC19 was replicated in Escherichia coli (DH5α) and purified employing a Qiagen (Valencia, CA) Plasmid Midi Kit procedure. DNA concentration was measured spectrophotometrically (50 μg/mL of double-stranded DNA has an absorbance of 1 at 260 nm) (Sambrook et al., 1989). Its purity and integrity was assessed using agarose gel electrophoresis. All plasmid preparations showed a major amount of supercoiled plasmid and a minor amount of relaxed plasmid (see Fig. 3, lane 1). Working solutions of BOBO-1 were prepared immediately before use by diluting the dimethylsulphoxide stock solution into 30 mM Tris/HCl buffer at pH 7.4. The dye/DNA solutions were always prepared by adding an adequate amount of DNA to a larger volume of dye in the working solution, to yield the desired dye:DNA ratio (dye molecule/DNA base) (Rye et al., 1992). In case that dye is added to DNA solution, identical photophysical data were obtained. The mixing ratio, dye:DNA base (d/b), is defined as the concentration ratio between dye molecule and DNA base. The dye/DNA complex was allowed to equilibrate for at least 30 min, at 20°C, before adding DOTAP or carrying out any measurements. All solutions containing membrane or intercalator dyes were protected from light between preparation and measurements.

FIGURE 3.

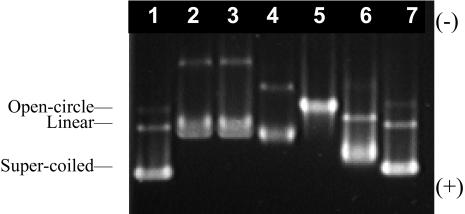
Electrophoretic profile of BOBO-1/pUC19 complexes (30 mM Tris/HCl, pH 7.4) at dye:DNA base (d/b) values: 0 (lane 1), 0.2 (lane 2), 0.167 (lane 3), 0.09 (lane 4), 0.06 (lane 5), 0.03 (lane 6), and 0.01 (lane 7), after 30 min incubation at room temperature. [DNA] = 0.03 μM.

Liposome and lipoplex preparation

Cationic liposomes were prepared at concentrations between 0.5 and 6 mM. The appropriate amount of lipid was diluted in chloroform solution. The solvent was evaporated under a nitrogen stream to obtain a thin lipid film. Residual solvent was removed under vacuum overnight. The lipid films were solubilized in Tris/HCl solution (30 mM, pH 7.4). To obtain large unilamellar vesicles (diameter of ∼100 nm) the hydrated lipid dispersions were extruded, 5× through 0.4-μm and 10× through 0.1-μm pore diameter polycarbonate filters (Whatman, Clifton, NJ), successively. The liposomes were then stored at 4°C. Fluorescently labeled liposomes were obtained by adding the proper amount of probe (DPH-PC or BODIPY-PC) to the chloroform solution. The exact probe concentration is indicated where appropriate. The lipoplexes (cationic liposomes-DNA complexes) were obtained by direct and rapid addition of appropriate amount of the cationic lipid dispersion to the pUC19 plasmid solution (30 mM Tris/HCl, pH 7.4) at various charge ratios (DOTAP/DNA between 0.001 and 10). The complexes were incubated at room temperature for 10 min, minimum, before use.

Agarose gel electrophoresis

Characterization of all plasmid batches and dye/plasmid complexes was carried out by loading samples (20 μL) in a 0.8% agarose gel, under a constant electric field of 2.0 V/cm with 40 mM Tris-acetate, 1 mM EDTA as electrophoresis buffer. Lipoplexes samples, 40 μL, were also analyzed by electrophoresis using the same procedure. All the gels were poststained in EtBr (0.5 μg/mL) for 30 min and then visualized, integrated, and photographed on ultraviolet transillumination equipment (Eagle Eye II, vers.1.1, Stratagene, Cedar Creek, TX) with a charge-coupled device camera system.

Dynamic light scattering

Plasmid DNA, dye/DNA complexes, liposomes, and lipoplexes' size measurements were carried out using a Brookhaven Instrument (Brookhaven, NY) device for dynamic light scattering with a multi-angle sizing option on the Zeta Plus (BI-MAS) using a 15-mW argon ion laser at 635 nm.

Fluorescence measurements

Steady-state fluorescence measurements were carried out with a SPEX F112 A Fluorog spectrofluorometer (Jobin Yvon, Edison, NJ) in a right-angle geometry. Correction of excitation and emission spectra was performed using a Rhodamine B quantum counter solution and a standard lamp, respectively (Lakowicz, 1999). Fluorescence intensities were measured at λ_exc = 465 nm and λ_em = 490 nm for BOBO and at λ_exc = 505 nm and λ_em = 595 nm for EtBr, with spectral bandwidths of 4.5 nm.

The steady-state anisotropy, 〈r〉, was calculated from

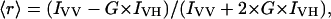(7)

where the different intensities are the steady-state vertical and horizontal components of the fluorescence emission with excitation vertical (I_VV and I_VH, respectively) and horizontal (I_HV and I_HH, respectively) to the emission axis. The latter pair of components is used to calculate the correction factor G = I_HV/I_HH (Chen and Bowman, 1965). Fluorescence quantum yields of BOBO-1, free in solution, with DNA and within lipoplexes (DOTAP/DNA charge ratio = 2) were determined. For this purpose, solutions were prepared with absorbance <0.05 to avoid fluorescence self-absorption. The fluorescence spectra of coumarin 6 (Fery-Forgues and Lavabre, 1999), with absorption at the excitation wavelength close to that of the dye at the same wavelength, was also measured with the same instrumental parameters used for the dye solutions. All emission spectra, recorded with λ_exc = 430 nm, were corrected, integrated, and the ratio of the areas for the dye solutions and the standard was determined, after subtraction of the solvent signal and spectra correction (as described above). Absorption spectra were carried out in a Jasco (Easton, MD) V-560 spectrophotometer. When necessary, corrections for turbidity were carried out according to Castanho et al. (1997). Considering the coumarin 6 quantum yield of 0.78 (Φ_C), the ethanol refractive index of 1.36 (n_C) (Fery-Forgues and Lavabre, 1999) and the buffer refractive index of 1.33 (n_B), it is possible to calculate the BOBO-1 quantum yield (Φ_C) from

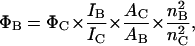(8)

where Φ_i is the quantum yield, I_i represents the integrated intensity, and A_i is the absorbance value at the excitation wavelength for BOBO (i = B) and coumarin (i = C).

Fluorescent decay measurements were carried out with a time-correlated single-photon counting system. For excitation of BOBO-1 at 284 nm, a frequency-doubled, cavity-dumped, dye laser of Rhodamine 6G (Coherent 701-2), synchronously pumped by a mode-locked Ar⁺ laser (514.5 nm, Coherent Innova 400-10) was used (Coherent, Santa Clara, CA). Filters were added to a Jobin Yvon HR320 monochromator, to respectively further screen-scattered excitation light, and isolate donor fluorescence from that of acceptor. For the detection, a Hamamatsu (Bridgewater, NJ) R-2809 MCP photomultiplier was used, and the instrumental response functions (50 ps full-width at half-maximum) for deconvolution were generated from a scatter dispersion (Silica, colloidal water suspension, Aldrich, Milwaukee, WI). Emission (at 485 nm) was detected at the magic angle relative to the vertically polarized excitation beam. The number of counts on the peak channel was ≈20,000, and the number of channels per curve used for analysis was ≈1000. Data analysis was carried out using a nonlinear, least-squares iterative convolution method based on the Marquardt algorithm (Marquardt, 1963). The goodness of the fits was judged from the chi-square values (χ²). Lifetime-weighted quantum yields, 〈τ〉, were calculated from (Lakowicz, 1999)

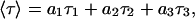(9)

where τ_i are the decay lifetime components and a_i are their respective normalized amplitudes.

Critical distances for energy transfer, R₀, were calculated from (Berberan-Santos and Prieto, 1987)

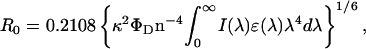(10)

where Φ_D is the donor quantum yield, ɛ(λ) is the acceptor molar absorption coefficient (regarding the acceptors in this work, we used 86,000 M⁻¹cm⁻¹—Haugland, 1996—and 5680 M⁻¹cm⁻¹—Graves et al., 1981—as the ɛ-values at the absorption maximum for BODIPY-PC and EtBr, respectively), κ² is the orientation factor (we used the dynamic isotropic limit, κ² = 2/3; for a discussion on this parameter, see van der Meer et al., 1994), n is the refractive index (1.33), and λ is the wavelength. If the λ-units used in Eq. 10 are nm, the calculated R₀ has Å units. Experimental FRET efficiencies were obtained from steady-state measurements using

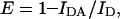(11)

where I_DA and I_D are the measured donor fluorescence intensities in absence and in presence of acceptor, respectively.

RESULTS

Interaction of BOBO-1 with dsDNA

Fig. 3 shows the band pattern obtained for BOBO-1/pUC19 complexes at different dye/DNA base ratios (dye molecule/base of pUC19), after 30 min incubation at room temperature. In the unlabeled DNA (lane 1) we can observe the supercoiled (faster and larger band), open-circle, and linear forms of the plasmid. The band pattern of the complex with the lowest mixing ratio d/b = 0.01 (lane 7) is very similar to the unlabeled plasmid DNA pattern. With the increase of BOBO-1 relative concentration (lane 6) the three plasmid forms show slower migration. At d/b = 0.06, only one band is observed. With the increase of the DNA concentration (0.3 μM), 2 h at room temperature were necessary to achieve the same band pattern of the BOBO/DNA complex d/b = 0.06 (data not shown). When we increase even further the dye quantity, d/b = 0.09, 0.167, and 0.2 (lanes 4, 3, and 2, respectively), the merging of open-circle and linear forms of the plasmid is observed and, as it also happens with the supercoiled form, they too migrate slower due to the binding of extra dye molecules. The same band pattern was obtained for incubation times of 10, 60, and 90 min for all complexes, using 0.03 μM of plasmid DNA.

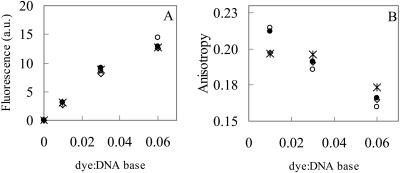
In Fig. 4, fluorescence intensity and anisotropy of BOBO-1/pUC19 complexes are shown. The measured signal originates solely from bound dyes since the fluorescence arising from free BOBO-1 was found to be negligible. It is observed that the fluorescence intensity and anisotropy values of these dye/DNA complexes do not depend on the incubation time of BOBO-1 with pUC19, when 0.006 μM of plasmid is used (Fig. 4, A and B). On the other hand, for complexes with a DNA concentration 10× higher, the anisotropy values vary with the incubation time (results not shown). This fact corroborates the electrophoresis results, in which complexes with higher DNA and BOBO concentrations, at higher mixing ratios (d/b = 0.06), take longer to reach the equilibrium. The fluorescence intensities of these complexes, with higher DNA concentration, do not vary with the incubation time (results not shown) and have the same profile obtained for complexes with lower DNA concentration that are shown on Fig. 4 A.

FIGURE 4.

Steady-state fluorescence intensity (A) and fluorescence anisotropy (B) of BOBO-1/pUC19 complexes (30 mM Tris/HCl, pH 7.4) with different dye/base ratios, at several incubation times: 10 min (⋄), 30 min (○); 60 min (*); and 90 min (•). [DNA] = 0.006 μM.

Titration of BOBO-1/pUC19 complexes with cationic liposomes

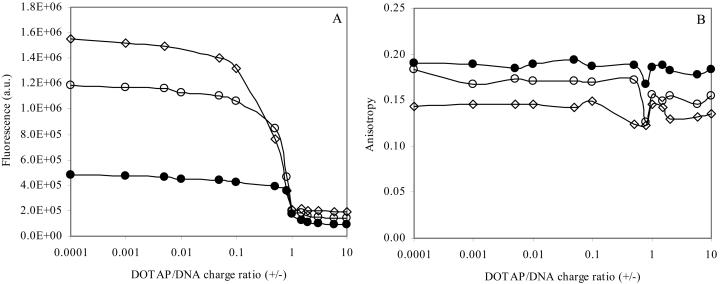
To verify the binding of DNA probes to plasmid DNA in the presence of cationic liposomes, titrations of dye/DNA complexes (for different dye/base mixing ratios) with DOTAP were carried out, in which the fluorescence intensity and anisotropy of the dyes in several lipoplexes were measured. The fluorescence curves obtained for BOBO (Fig. 5 A) were observed to have a similar profile with those obtained for EtBr, previously published by other authors (and verified by ourselves; result not shown). EtBr is commonly used as a DNA intercalator in structural and biophysical characterization (Gershon et al., 1993; Xu et al., 1999; Eastman et al., 1997), and transfection mechanisms (Xu and Szoka, Jr, 1996) of lipoplexes, among other studies. However, when compared with dimeric cyanine dyes, such as BOBO-1, EtBr has lower sensitivity and binding affinity constants (Benson et al., 1993). In general, depending on EtBr concentration, an increase of the charge ratio (+/−) of the lipoplexes (cationic liposome/DNA complexes) corresponds to a decrease of the EtBr fluorescence, indicating that less DNA is accessible to the dye (Eastman et al., 1997). The exclusion of EtBr from the dye/DNA complexes was also verified by the quenching of fluorescence intensity at high lipid/DNA charge ratio, to a value similar to that measured in buffer (data not shown). In this study, we verified that when using BOBO-1/DNA complexes, the decrease in fluorescence accompanying the increase of lipoplexes charge ratio has a sigmoidal profile for the mixing dye/base ratios of 0.06, 0.03, and 0.01 (Fig. 5 A).

FIGURE 5.

Titration of BOBO/pUC19 complexes: d/b = 0.06 (⋄); d/b = 0.03 (○); and d/b = 0.01 (•) with cationic liposomes (DOTAP). BOBO-1 complexes: λ_exc = 490 nm, and λ_em = 465 nm. [DNA] = 0.006 μM. (A), fluorescence intensity; (B), anisotropy.

Whereas the fluorescence intensity of this probe in lipoplexes with charge ratio (+/−) > 1 is much diminished relative to the value for lipoplexes with charge ratio (+/−) < 1, it does not fall to the essentially zero value measured in water. Moreover, the anisotropy profile of BOBO-1 within the lipoplexes (Fig. 5 B) has a subtle perturbation in the electroneutrality region (charge ratio (+/−) ≈ 1), but does not decrease at higher charge ratios. Within lipoplexes, the anisotropy values of BOBO-1 intercalated in pUC19 increase with decreasing BOBO-1 concentration, similarly to the complexes without cationic liposomes (Fig. 4 B). These observations suggest that BOBO-1 is not excluded from the lipoplexes at higher charge ratios (+/−), which allows further characterization of these cationic liposome/DNA complexes using this probe. Taking into account the photophysical data described above, the subsequent studies were carried out with plasmid DNA labeled with BOBO-1 at a dye/DNA base ratio of 0.01.

Fluorescence decays of BOBO-1 within lipoplexes were measured to get further information (Table 1). The decays are complex even in the absence of DOTAP, and three exponentials are needed to describe them satisfactorily. Addition of DOTAP leads to a decrease in lifetime-weighted quantum yield, most notably for DOTAP/DNA charge ratio (+/−) > 1, similarly to the steady-state intensity variation shown in Fig. 5 A.

TABLE 1.

Decay parameters of BOBO-1 in pUC19 in the presence and absence of DOTAP; BOBO-1/DNA: dye/base = 0.01

	DOTAP/DNA charge ratio (+/−)
	0	0.5	2	4
τ1 (ns)	0.38 (27%)	0.43 (35%)	0.25 (50%)	0.20 (52%)
τ2 (ns)	1.54 (44%)	1.65 (51%)	0.96 (38%)	0.89 (36%)
τ3 (ns)	3.33 (29%)	3.72 (14%)	2.95 (12%)	3.73 (12%)
〈τ〉 (ns)	1.75	1.52	0.85	0.88
χ2	1.03	1.10	1.15	1.27

Lipoplexes agarose gel electrophoresis

Lipoplexes with different charge ratios were loaded on agarose gel. Formed lipoplexes, due to size exclusion, remain at the site of application (Eastman et al., 1997). Free DNA (unbound to the lipid) migrates toward the cathode and Fig. 6 shows its gel mobility characteristics. When DOTAP concentration is raised (from lane 2 to 8), less unbound DNA migrates on the gel. For this lipoplex system, under these conditions, for lipid/DNA ratio ≥3, no free DNA is observed, suggesting that all DNA is bound to liposomes.

FIGURE 6.

Electrophoresis of lipoplexes (DOTAP/pUC19) at several charge ratios (+/−) on agarose gel in 30 mM Tris/HCl, pH 7.4. Lipoplexes with charge ratios (+/−): 0 (lane 1), 0.01 (lane 2), 0.1 (lane 3), 0.5 (lane 4), 0.8 (lane 5), 1 (lane 6), 1.5 (lane 7), 2 (lane 8), 3 (lane 9), 6 (lane 10), and 10 (lane 11). [DNA] = 0.02 μM.

Size of lipoplexes

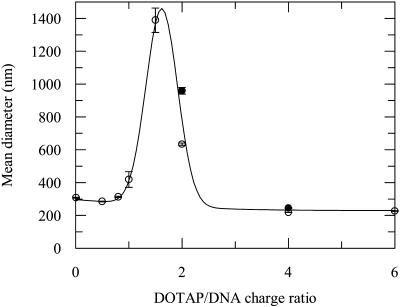
The mean diameters of lipoplexes with several charge ratios are shown in Fig. 7. Whereas lipoplexes with charge ratios close to neutrality (1–2) are colloidally more unstable and show an increased size, lipoplexes with charge ratios <1 and >2 have approximately the same mean diameter of 300 nm. This dependence of lipoplex size on charge ratio was also observed by other researchers in different systems (Xu et al., 1999; Kreiss et al., 1999; Radler et al., 1998). In this study, we compare the size of lipoplexes with and without BOBO-1 intercalated on DNA, for DOTAP/DNA charge ratio of 2 and 4. For the latter system, the lipoplex size is the same in presence and absence of intercalated BOBO-1. The larger difference in the values for charge ratio (+/−) 2 is due to the steeper variation of size in this charge ratio range, which is probably related to the decreased stability of these complexes.

FIGURE 7.

Mean diameter of pUC19 without (○), and with (•), BOBO-1 at d/b = 0.01, with cationic liposomes (DOTAP) at several charge ratio (+/−). [DNA] = 0.007 μM. The line is a mere guide to the eye.

FRET measurements

For these experiments, the choice of the donor-acceptor pairs was partially based on the results shown in Fig. 5. EtBr remains intercalated in the DNA in lipoplexes with charge ratios (+/−) < 1. In this case, DPH-PC or BODIPY-PC can be chosen as donors to EtBr because their emission spectra strongly overlap the EtBr absorption spectrum (Fig. 8, B and C), which is an essential FRET requirement. For higher lipoplexes charge ratios (2 and 4), EtBr was discarded because it is displaced by DOTAP (see previous subsection). For these samples, BOBO-1 was used as the DNA probe, and it was the FRET donor. As acceptor, BODIPY-PC was used due to its excellent spectral overlap with BOBO-1 emission for FRET purposes (Fig. 8 A). This same pair was also used in the charge ratio (+/−) = 0.5 system, for comparison.

FIGURE 8.

Absorption spectra (thin line) of BODIPY-PC (A) and EtBr (B and C) and emission spectra (thick line) of BOBO (A), DPH-PC (B), and BODIPY-PC (C).

Table 2 summarizes the different FRET settings (DOTAP/DNA charge ratio, FRET pair) used, and shows, for each case, the measured donor quantum yields and the R₀ values calculated with Eq. 10 (using these quantum yield values and the molar absorption coefficients given in the Experimental section and the spectra of Fig. 8).

TABLE 2.

Donor dye quantum yields and R₀ values calculated for the donor-acceptor pairs used in this study

DOTAP/DNA charge ratio	Donor dye	Acceptor dye	Donor quantum yield	R0 (Å)
4	BOBO-1	BODIPY-PC	0.13 (inside lipoplexes)	41.0
2	BOBO-1	BODIPY-PC
0.5	BOBO-1	BODIPY-PC
0.5	DPH-PC	EtBr	0.36	31.3
0.5	BODIPY-PC	EtBr	0.90	39.4

Fig. 9 shows a series of experiments with the FRET pair BOBO-1/BODIPY-PC, in lipoplexes with charge ratio (+/−) of 4, 2, and 0.5. For each charge ratio value, the FRET efficiency increases as the acceptor concentration increases, as expected. The experimental results illustrate the overall decrease of FRET efficiency with decreasing charge ratio. These results are compared with the theoretical curves obtained with Eqs. 2–4 and 6 (see Theory of FRET in Lipoplexes). After the agarose gel electrophoresis study (see Fig. 6), the data for charge ratio (+/−) = 4 was analyzed assuming no isolated donors (under these conditions, there is no free DNA, and all BOBO-1 donor molecules would be available for transfer), that is, γ in Eq. 4 was taken as zero. Having fixed the value of this parameter, the sole fitting variable in Eq. 4 is b, or alternatively the donor-acceptor interplanar distance d = R₀〈τ〉^−1/6b^−1/2. From this procedure, d = 27 Å is obtained. The larger plot in Fig. 9 A is a zoom of the inset figure. In addition to the best fit value, the curves for two other fitting values for d (a lower value, 22 Å, and a higher value, 32 Å) are also shown. This best fit value, d = 27 Å, was in turn fixed in the analyses of the data for charge ratios (+/−) = 2 and 0.5. For these, the sole fitting parameter was now γ, the fraction of isolated donors. The values γ = 0.20 and 0.50 were recovered as best fit values for DOTAP/DNA charge ratios 2 and 0.5, respectively. In Fig. 9, B and C, curves obtained for other γ values (which give rise to significantly worse fits) are also shown for the sake of comparison. Assuming that the DNA-intercalated probe is uniformly distributed in the plasmid, this fraction corresponds to that of DNA not surrounded by lipid, and an encapsulation efficiency may be calculated as (1-γ) × 100% = 80% and 50% for DOTAP/DNA charge ratios 2 and 0.5, respectively.

FIGURE 9.

FRET quenching ratios, I_DA/I_D = 1−E, for BOBO-1/BODIPY pairs in DOTAP/DNA complexes with charge ratios (+/−) of 4 (A; larger figure is a zoom of the inset), 2 (B), and 0.5 (C). Experimental data (•); Fitting curves using Eqs. 2–4 and 6. The assumed fitting parameters were: (A) γ = 0 (fixed); d = 32 Å (- - -); d = 27 Å (- - -); and d = 22 Å (·····). (B) d = 27 Å (fixed); γ = 0.20 (—); γ = 0.30 (- - -); and γ = 0.10 (·····). (C) d = 27 Å (fixed); γ = 0.50 (—); γ = 0.60 (- - -); and γ = 0.40 (·····).

FRET studies with the DPH-PC/EtBr and BODIPY-PC/EtBr pairs in lipoplexes with charge ratio (+/−) of 0.5, are plotted in Fig. 10. For these systems, the phospholipid probe is the donor, whereas the DNA intercalator is the acceptor, hence Eq. 5 should be used instead of Eq. 4 for data analysis (see Theory of FRET in Lipoplexes). Again, the distance d = 27 Å was used, and a good fit to the experimental results was obtained considering f = 0.88 and f = 0.90 (see Eq. 5), using DPH-PC and BODIPY-PC, respectively, as donors. This represents the fraction of acceptors not available for FRET. Because the acceptor is now the DNA probe, this has the same meaning as γ for the BOBO-1/BODIPY-PC pair, and encapsulation efficiencies of 12% and 10% are calculated (from the DPH-PC/EtBr and BODIPY-PC/EtBr data, respectively). Whereas these values show good internal agreement (as expected, because the only difference in these systems is the donor probe used), they are perhaps unexpectedly low, and significantly smaller than the value recovered from the BOBO-1/BODIPY-PC experiment (see above) for the same lipoplex composition (50%). Table 3 summarizes the experimental settings and recovered parameters for all FRET experiments.

FIGURE 10.

FRET quenching ratios, I_DA/I_D, for DPH/EtBr (A) and BODIPY/EtBr (B) pairs in DOTAP/DNA complexes with charge ratios (+/−) of 0.5. Experimental data (•); Fitting curves using Eqs. 2, 3, 5, and 6. The assumed fitting parameters were: (A) d = 27 Å (fixed); f = 0.88 (—); f = 0.82 (·····); and f = 0.91 (- - - - -). (B) d = 27 Å (fixed); f = 0.90 (—); f = 0.85 (·····); and f = 0.93 (- - - - -).

TABLE 3.

Encapsulation efficiencies, considering the model equation used to fit the experimental results and constituents quantities

DOTAP/DNA charge ratio	Donor/Acceptor pair	[DNA] (μM)	[Donor] (μM)	[DOTAP] (M)	Equation for iDA(t)	Encapsulation efficiency (%)*
4	BOBO-1/BODIPY-PC	0.020	1.10	3.2 × 10−4	4	100
2	BOBO-1/BODIPY-PC	0.020	1.70	2.4 × 10−4	4	80
0.5	BOBO-1/BODIPY-PC	0.020	1.70	6.1 × 10−5	4	50
0.5	DPH-PC/EtBr	0.003	0.08	7.6 × 10−6	5	12
0.5	BODIPY-PC/EtBr	0.020	0.08	6.1 × 10−5	5	10

^*Fixed for the first experiment (from which d = 27 Å was recovered), and optimized for all others (assuming d = 27 Å, fixed).

DISCUSSION

Fluorescence spectroscopy has received increasing attention as a tool for characterization of lipoplexes, and in recent reports DNA probes (Ferrari et al., 2001; Eastman et al., 1997; Even-Chen and Barenholz, 2000), lipid probes (Gershon et al., 1993; Xu et al., 1999; Kennedy et al., 2000; Harvie et al., 1998; Huang et al., 1999; Zuidam et al., 1999), or both types of probes simultaneously (Clamme et al., 2000; Wong et al., 2001) have been used. Frequently, encapsulation efficiencies of cationic liposomes are evaluated using DNA fluorescent intercalators measuring, for example, the degree of DNA accessibility to TO-PRO-1 (Ferrari et al., 2001; Zhang et al., 1997) or to PicoGreen (Ferrari et al., 2001), the internalized DNA, after methanol/chloroform extraction, using Hoescht dye 33258 (Xu et al., 1999) or EtBr (Gershon et al., 1993) or free DNA by electrophoresis agarose gel stained with SYBR Green I (Even-Chen and Barenholz, 2000). With the exception of the latter, all methods provide an indirect estimate of the encapsulation efficiency of the lipoplex.

Essentially, we used an established fluorescence spectroscopy technique, FRET, as a novel tool to quantitate directly the encapsulation efficiency of a given lipoplex system. For this purpose, and to take full advantage of the FRET sensitivity to distance/concentration, we used formalisms for FRET kinetics identical to those previously applied in membrane studies (for a review see Loura et al., 2001). The most informative experiment involves the use of a DNA intercalating probe as donor and a labeled lipid as acceptor, or the other way round. As explained in detail in the Theory of FRET in Lipoplexes, the FRET observable (donor decay in the presence of acceptor, FRET efficiency) in this experiment contains information on the lipoplex components' molecular arrangement. In the multilamellar model used, the unknown parameters are essentially the lamellar repeat distance and the fraction of unbound DNA (which is complementary to the encapsulation efficiency). With this study we aimed to use FRET to 1), verify the values of lamellar repeat distance obtained by totally independent methods such as diffraction methods (Salditt et al., 1998; Caracciolo et al., 2002); and 2), evaluate the encapsulation efficiency for different lipid/DNA formulations.

Of course, a requirement for the use of fluorescent probes is that they do not cause significant perturbation to their environment. The BOBO-1/DNA electrophoresis profile and steady state fluorescence and anisotropy measurements aimed to study the effect of BOBO-1 (relative concentration and incubation times) on the DNA conformation. The binding of dimeric cyanine dyes has been shown to strongly modify the conformation of DNA, depending on the dye/DNA ratio (Rye et al., 1992, 1993; Larsson et al., 1994), and equilibrium between DNA and some of these dyes (YOYO-1 and TOTO-1) has been shown to be reached after several hours (Carlsson et al., 1995). As shown in Fig. 3, with the increase of BOBO-1 relative concentration the supercoiled, open-circle, and linear forms show slower migration in the agarose gel due to the binding of the dye, and at d/b = 0.06 (lane 5) only one band can be observed. Carlsson et al. (1995) observed the same band pattern using YOYO-1 for a specific dye/DNA ratio of 0.167, which they rationalized assuming a two-step equilibration process. For this high probe concentration, the DNA conformation is clearly altered, as seen from the change in band profile. On the other hand, BOBO-1/DNA complexes with the lower d/b ratio 0.01 have a very similar profile when compared with unlabeled pUC19. This profile is maintained after 90 min of incubation at room temperature, using either 0.03 μM or 0.3 μM of DNA, and agrees with the results of Wong et al. (2001), who report no change in DNA conformation for the same d/b ratio with a similar dimeric cyanine dye, YOYO-1. In the FRET methodology used in this work, it is important to assure that both DNA conformation and integrity are not modified and that there is no self-absorption of fluorescence or energy migration (which could bias the results), because BOBO-1 absorption and emission spectra have a reasonable overlap. These photophysical artifacts are also best avoided using low probe concentration. In Fig. 4 A, we can verify that complexes with dye/base = 0.06 have higher fluorescence intensities, revealing that the dye is still bound to DNA, but has lower anisotropy values (Fig. 4 B), which could be due to faster rotational diffusion, or would also result from depolarization of the emission due to energy migration among BOBO-1 molecules. This could happen due to the overlap of the BOBO-1 absorption and emission spectra. At low mixing ratios, interchromophore distances in the BOBO-1-DNA complexes are too large to give any appreciable energy transfer, and the depolarization is thus small (higher anisotropy value). When the mixing ratio is increased, the energy migration becomes more efficient and, therefore, a decrease in the anisotropy is observed. This study showed that the mixing ratio d/b = 0.01 was adequate for FRET studies using BOBO-1 as donor. However, it remained to be seen whether BOBO-1 would remain an adequate DNA probe after the addition of cationic lipid. Fig. 7 shows that the lipoplex size is not significantly affected by the presence of BOBO-1 in this low concentration. It is known that EtBr is displaced from DNA as a result of cationic lipid addition (Eastman et al., 1997; Gershon et al., 1993; Xu et al., 1999). For excess of cationic lipid, EtBr fluorescence intensity (Xu et al., 1999); also verified by us) and fluorescence lifetime (Clamme et al., 2000) drop to the levels in buffer. When DOTAP is added to BOBO-1/DNA complexes, the fluorescence intensity of the dye also decreases abruptly at DOTAP/DNA charge ratio ≈1 (Fig. 5 A), suggesting that a significant amount of dye is displaced from the DNA. However, unlike EtBr, the fluorescence does not decrease to the values in buffer (essentially zero for this probe), and the invariance of anisotropy values (Fig. 5 B) also suggests that there still is dye on the DNA, inside the lipoplexes. If most of the dye were displaced into the buffer, the polarized fluorescent signal would probably be too weak to be measured, and even if anisotropies could be calculated, their values would possibly be lowered as a result of unrestricted molecular rotation. The significant drop in fluorescence intensity is partly explained by the decay data (Table 1), although displacement of some of the probe into the buffer cannot be excluded (these molecules would have a very short fluorescence lifetime in buffer, out of the measurable range of the instrument). A ≈50% drop in lifetime-weighted quantum yield is observed for DOTAP/DNA ratios >1, indicating that BOBO-1 is intrinsically half as fluorescent in cationic lipoplexes, and the fivefold fluorescence intensity decrease seen in Fig. 5 A for d/b = 0.01 would denote a 2.5-fold concentration decrease, that is, ∼40% of the probe would remain in the lipoplexes. This value must be seen as a minimal limit, as there is the possibility of static self-quenching due to BOBO-1 aggregation upon the formation of cationic lipoplexes, which would not affect the lifetime-weighted quantum yield values, but would reduce the steady-state intensities for charge ratios >1 in Fig. 5 A. Other cyanine dyes show significant quenching as a result of lipoplex formation. Wong et al. (2001) reported that YOYO-1 fluorescence is quenched to approximately one-third in DNA/(n-n-Dioleyl-n,n-dimethylammonium chloride (DODAC)/1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) 1:1) lipoplexes for charge ratio (+/−) 2. Even-Chen and Barenholz (2000) reported partial quenching of asymmetrical cyanine dye SYBR Green 1, which they interpreted as probably related to self-quenching as a result of increase in fluorophore local concentration upon DNA condensation. Note that, using BOBO-1 as the FRET donor in the experiments using this dye, the possibility of displacement of BOBO-1 into the buffer would not affect the FRET results, because the BOBO-1 molecules in buffer do not fluoresce and would be “silent” in these experiments. Additionally, using each data series obtained for constant DOTAP/DNA charge ratio (the sole variable is the amount of acceptor probe, BODIPY-PC), their proportion would be the same for all points. The fact that FRET does occur between BOBO-1 and BODIPY-PC is another proof that a significant amount of BOBO-1 “senses” the lipids, and must therefore still be located in the DNA (we verified that BOBO-1 does not partition into the positively charged liposomes, as expected given its charge, which is +4; results not shown). Interestingly, the factor of reduction of BOBO-1 fluorescence intensity is larger for d/b ratios 0.03 and 0.06 (approximately eightfold rather than fivefold for d/b ratio 0.01), indicating that less dye remains bound to lipoplexes for these larger dye concentrations than for d/b ratio 0.01 (the conditions chosen for the FRET experiments).

For these lipoplex systems, using pUC19 (2690bp) and DOTAP, for several charge ratios, in 30 mM Tris/HCl, pH 7.4, we verified that for charge ratios ≤2 there is free or unbound DNA (Fig. 6), and lipoplexes with charge ratios >3, no free DNA is observed. This agrees with encapsulation efficiencies calculated for several DOTAP-based liposomal vehicles (Even-Chen and Barenholz, 2000; Xu et al., 1999) and was important for the analysis of the FRET data, in that it allowed us to force γ = 0 (no unbound DNA) in Eq. 4 for the higher DOTAP/DNA charge ratio (4).

It could be argued that DNA is being actively released from the lipoplexes by electrophoresis in Fig. 6, which would account for the fact that an abrupt transition is not seen for charge ratio 1, at variance with the data in Fig. 5 A. Firstly, whereas from the electrophoresis data of Fig. 6 we are able to detect the free DNA, not associated with liposomes, in the titration curve the BOBO-1 fluorescence is the measured observable. BOBO-1 fluorescence is influenced by several factors: the amount of free DNA, the distribution equilibria of the dye among all possible environments (even excluding the liposomes, these include lipoplexes, free DNA, and possibly buffer) and the quantum yield values in each environment. Thus, the profile of decrease of dye fluorescence is not directly comparable to that of free DNA in the electrophoresis experiment. Secondly, an active release of DNA from the lipoplexes by electrophoresis is not probable, at least in large extension. Even if some release of DNA happens, this technique has too low a sensitivity to detect that occurrence. The effect of such phenomenon would be the appearance of free DNA for ratios where it would not be expected. However, even in such a case, the lack of a free DNA band, as observed for the charge ratio (+/−) ≥ 4, would still mean that no free DNA exists for that system in particular, and it could be used for the subsequent FRET experiment, having no effect on the conclusions.

From the analysis of FRET results charge ratio (+/−) 4 we were able to recover d = 27 Å for the donor-acceptor interplanar system, in fair agreement with the values obtained using diffraction and microscopy techniques (Salditt et al., 1998; Radler et al., 1997; Caracciolo et al., 2002). The fact that this value is slightly lower than expected from these authors' results (≈30 Å) is justified because the recovered distance is, in fact, an average of d₁ and d₂ (see Fig. 1). Because of the nonlinear dependence of FRET with distance, it is expected that this average should be closer to the smaller value d₁ (the distance to the acceptor planes responsible for most of the quenching) and thus smaller than the actual d-value. Moreover, eventual small inaccuracies in the values of DOTAP and BODIPY-PC concentration may influence the acceptor surface concentration and thus the FRET efficiency. The value used for κ² always brings some additional uncertainty, although in this case the use of the dynamical isotropic limit value (2/3) is justified, given that the DOTAP bilayers should be in the fluid phase (and hence the lipid-bound fluorophores will likely have a considerable amount of rotational freedom) and the relatively low fluorescence anisotropy of BOBO-1 (<0.2, as seen from Fig. 5 B) denotes a reasonably high degree of orientation randomization during the excited state lifetime. The small deviation in d (≤3 Å) probably stems from these cumulated uncertainties. Being that this value is independent of the DOTAP/DNA charge ratio (Kreiss et al., 1999), it was subsequently fixed for the analysis of the data for charge ratios (+/−) 2 and 0.5, allowing us to estimate γ for these systems, as the sole fitting parameter.

Whereas for the system with charge ratio (+/−) 2 only one experiment was carried out (with the BOBO-1/BODIPY-PC pair, encapsulation efficiency ≈80% being recovered), for the charge ratio (+/−) 0.5 we must compare the three encapsulation efficiency estimates obtained using the three FRET pairs (BOBO-1/BODIPY-PC is ≈ 50%; DPH-PC/EtBr is ≈ 12%; and BODIPY-PC/EtBr is ≈ 10%). Clearly, there is good agreement between the values obtained with the pairs that have EtBr as acceptor, but these are much lower than that obtained with BOBO-1 as DNA probe. The most probable explanation, given the complete displacement of EtBr from DNA for DNA/DOTAP charge ratios >1, is that when there is excess DNA, EtBr intercalates inside free DNA, whereas lipid-complexed DNA is depleted of EtBr. This would result in a much lower fraction f of EtBr acceptors sensed by the labeled-lipid probes, most probably coming from regions of DNA adjacent to (but not complexed by) DOTAP. Regarding BOBO-1/BODIPY-PC, the recovered γ parameter reports the fraction of BOBO-1 that is intercalated inside free DNA. This fraction will represent that of free DNA, if the BOBO-1 labeling ratio is the same for free DNA as that bound to the lipoplexes. Because BOBO-1 is not completely (if at all) displaced by DOTAP, we will assume this approximation to hold. Of course, it is reasonable to think that, if BOBO-1 is significantly displaced by DOTAP, then the labeling ratio will be higher for free DNA. In this situation, the calculated encapsulation efficiency would be lower than the true efficiency (because the amount of free DNA would be overestimated), but will be a better estimate than those coming from the DPH-PC/EtBr and BODIPY-PC/EtBr pairs. In any case, our estimates obtained with the BOBO-1/BODIPY-PC pair are similar to results obtained by different methods, in systems containing DOTAP as cationic lipid (plus helper lipids; Even-Chen and Barenholz, 2000; Xu et al., 1999), which indicates that this shortcoming is probably not critical. The dispersion of experimental data obtained for lipoplex with charge ratio of 2 (Fig. 9 B) may be related with the instability of the lipoplex near the neutrality charge ratio. This instability is normally assessed by lipoplex size measurements. We verified that lipoplexes with this charge ratio have mean diameter ≈1000 nm, whereas lipoplexes with charge ratios of 0.5 and 4 have mean diameter ≈300 nm (Fig. 7). Similar results were obtained by other groups (Xu et al., 1999; Radler et al., 1998; Kreiss et al., 1999).

We now turn our attention to specific issues related to our FRET methodology. The first point is the relative mathematical complexity associated with this methodology. This is a necessity if one wishes to extract quantitative structural information from the FRET experiment. A less careful analysis of the FRET geometry might result in an incorrect modelation, from which the recovered “information” is essentially meaningless (Clamme et al., 2000; Lleres et al., 2001). In our procedure, the estimation of the encapsulation efficiency relies on a double numerical integration procedure: for a given time t, the probability of donor excitation in presence of acceptor, i_DA(t), must be computed using one of Eqs. 1, 4, or 5, which all involve numerical integration. After calculation of this function for a large number of t-values, the theoretical FRET efficiency E (which is directly comparable with the experimental observable) is obtained through integration over time (Eq. 6). This should in turn be repeated for a number of acceptor concentrations, to obtain theoretical E vs. acceptor concentration curves such as those plotted in Figs. 9 and 10. We are currently deriving approximate solutions based on simpler functions, which could be used in a more immediate manner. In any case, in our opinion, the whole exact (in the frame of the assumptions mentioned in the Theory of FRET in Lipoplexes) analysis is not difficult, and can be achieved in a (admittedly large) spreadsheet. This spreadsheet, if well designed, is easy to adapt for different experiments. If the lipid formulation, DNA type, and donor/acceptor pair are kept the same, the only cells which need changing for analysis of two different experiments are those of the experimental points and the fraction of uncovered DNA (the fitting parameter). The second point is the meaning of “free DNA” and “encapsulation efficiency.” It is well-established that lipoplexes have a multilamellar structure with alternating DNA and cationic lipid bilayers. In this way the older picture of DNA encapsulated inside a liposome is now ruled out. For FRET purposes, “free DNA” includes all DNA regions that are not in direct contact (<2R₀) with lipids. If parts of a DNA helix are not covered by lipid, or “stick out” (see Fig. 1) of the multilamellar structure, they will be included in our determined free DNA fraction, even though they might not be so in a gel electrophoresis experiment. In terms of transfection it was verified by other groups that lipoplexes with unprotected (free) DNA show lower transfection activity than lipoplexes with higher (+/−) charge ratios (1–8) (Xu et al., 1999) and have the same transfection efficiency of lipoplexes pretreated with nucleases (Crook et al., 1996). These findings suggest that in clinical trials, the free DNA of lipoplexes is susceptible to nuclease degradation. Therefore, the estimate provided by the present methodology, which reflects the “uncovered” DNA fraction, is probably the most relevant predicting observable regarding transfection efficiency. It should be stressed that, to our knowledge, FRET is the only methodology that allows quantification of lipid-DNA contact. X-ray diffraction techniques, which were instrumental in the establishment of the multibilayer model, are not sensitive to the DNA fraction that is not in contact with the cationic lipid.

The design of FRET experiments using different experimental settings is already underway in our laboratory. They will hopefully provide a fresh contribution to the understanding of the mechanisms governing the efficiency of DNA encapsulation (and possibly in vivo transfection).