Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Nov;85(5):3154–3161. doi: 10.1016/S0006-3495(03)74733-X

Hyper-Mobile Water Is Induced around Actin Filaments

Syed Rashel Kabir *, Keiichi Yokoyama *, Koshin Mihashi †, Takao Kodama ‡, Makoto Suzuki *
PMCID: PMC1303591  PMID: 14581215

Abstract

When introduced into water, some molecules and ions (solutes) enforce the hydrogen-bonded network of neighboring water molecules that are thus restrained from thermal motions and are less mobile than those in the bulk phase (structure-making or positive hydration effect), and other solutes cause the opposite effect (structure-breaking or negative hydration effect). Using a method of microwave dielectric spectroscopy recently developed to measure the rotational mobility (dielectric relaxation frequency) of water hydrating proteins and the volume of hydration shells, the hydration of actin filament (F-actin) has been studied. The results indicate that F-actin exhibits both the structure-making and structure-breaking effects. Thus, apart from the water molecules with lowered rotational mobility that make up a typical hydration shell, there are other water molecules around the F-actin which have a much higher mobility than that of bulk water. No such dual hydration has been observed for myoglobin studied as the representative example of globular proteins which all showed qualitatively similar dielectric spectra. The volume fraction of the mobilized (hyper-mobile) water is roughly equal to that of the restrained water, which is two-thirds of the molecular volume of G-actin in size. The dielectric spectra of aqueous solutions of urea and potassium-halide salts have also been studied. The results suggest that urea and I− induce the hyper-mobile states of water, which is consistent with their well-known structure-breaking effect. The molecular surface of actin is rich in negative charges, which along with its filamentous structure provides a structural basis for the induction of a hyper-mobile state of water. A possible implication of the findings of the present study is discussed in relation to the chemomechanical energy transduction through interaction with myosin in the presence of ATP.

INTRODUCTION

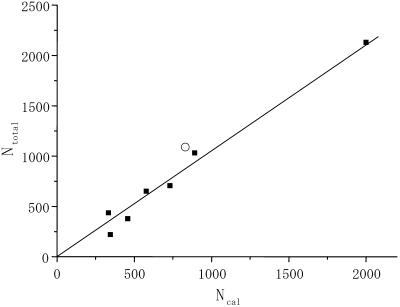
Protein-water interactions are key to biological functions (Mattos, 2002), among which those at the protein surface have the greatest relevance to stability, dynamics, and functions of proteins and hence have been extensively studied by a multitude of physico-chemical methods (Bellissent-Funel, 1999; Bryant, 1996; Gregory, 1995). Microwave dielectric spectroscopy is a powerful technique to investigate liquids, of which the structure and dynamics are dominated by intermolecular hydrogen bonds (for a review see Ellison et al., 1996). We have recently developed a method to measure the total volume of water molecules interacting with (hydrating) proteins in solution (dielectric exclusion volume or hydration-shell volume) as well as their rotational mobility (dielectric relaxation frequency, fc) (Suzuki et al., 1996, 1997a; Yokoyama et al., 2001). For the globular proteins examined so far, the fc values of hydrating water are in the range between 4 and 8 gigahertz (GHz) or lower, which is compared to the reported value of fc for bulk water of 17 GHz at 20°C (Buchner et al., 1999). Those fc values are equivalent to the dielectric relaxation times (τdiel) ≥20–40 ps (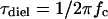Inline graphic). In theory, τdiel = 3 τc (Bloomfield, 2002; Fabelinskiĭ, 1997a), where τc is the orientational correlation time (residence time, the average time that a water molecule spends bound at a protein site) for water molecules hydrating protein surfaces estimated by nuclear-magnetic resonance-related methods (Bellissent-Funel, 1999; Halle and Denisov, 2001; Wüthrich, 2001). In addition, the number of hydrating water molecules per protein molecule (Ntotal) calculated from the dielectric exclusion volume agrees well with the solvent-accessible surface area-based estimate (Ncal) (Fig. 1). The data also gave an averaged value of the weight-based hydration (0.38 g/g protein), which falls within a range of values for various proteins estimated by other methods (Gregory, 1995; Zhou, 2001). Taken together, our dielectric method can provide the overall characteristics of the first hydration layer of proteins and the values are consistent with those obtained by other methods.

FIGURE 1.

FIGURE 1

Open in a new tab

Hydration numbers of proteins estimated using dielectric spectroscopy. The ordinate (Ntotal) is the number of hydrating water molecules per protein molecule calculated from the dielectric exclusion volume, and the abscissa (Ncal) is the solvent-accessible surface areas (ASA)-based estimate. Data were from Yokoyama et al. (2001) and Suzuki et al. (1997b), for which the line was drawn by a linear regression analysis excluding the unfilled circle denoting a value for F-actin on the basis of its monomer unit estimated in this study (see Table 1).

Using this dielectric method, the hydration of the myosin motor domain (S1) and its dynamic change during the ATP hydrolysis has been examined (Suzuki et al., 1997b). The result indicated that although S1 is not greatly different from other proteins in the total hydration level (see Fig. 1), the change of bound nucleotide ADP to ADP + Pi (ADP release followed by ATP binding and cleavage on addition of ATP) is accompanied by a small but substantial decrease (∼5%) in the number of S-1 hydrating water molecules. It was then suggested that hydration and its dynamic change in motor proteins may play an important role in the underlying mechanism of muscle contraction. At the time, however, little information was available on the hydration properties of actin. Such information is essential to argue the mechanism of chemomechanical energy transduction in terms of water dynamics in S1-actin interaction (Highsmith et al., 1996).

In this study, we have extended the use of our dielectric method to actin solution. To achieve this, several difficulties had to be overcome in the recording of dielectric spectra, and the method of data analysis was elaborated. The results obtained indicate that the dielectric spectra of hydrated actin are distinct from those of proteins examined so far. In fact, it is virtually impossible to interpret the spectra without assuming that besides the lowered mobility of ordinary hydrating water, a component with much higher rotational mobility (fc ∼ 40 GHz) around the actin filaments (F-actin) exist. The dielectric exclusion volume is approximated to two-thirds of the molecular volume of globular monomer unit of F-actin (G-actin: Mr, 42.3 K). To check the validity of this finding, the dielectric spectra of solutions of urea and potassium-halides, KF, KCl, and KI were also measured. The hyper-mobile states of water are indeed induced in these solutions, which is consistent with well-known water-structure breaking effect of those solutes (Robinson et al., 1996).

Experimental and theoretical studies (Hribar et al., 2002; Tovchigrechko et al., 1999) suggest that the charge density of solute and the balance of strength between water-solute interaction and water-water hydrogen bond are major factors affecting structure of water around solute ions and molecules. Taking this into account, we have offered an explanation for how F-actin may enhance the mobility of the surrounding water molecules on the basis of its characteristic double-helix structure consisting of G-actin subunits with a negative charge-rich molecular surface. The rotational mobility of water molecules around solute molecules is directly related to their diffusibility and this is critical to translational motion of proteins (Bloomfield, 2002). Thus, a possible implication of the finding of the present study is also discussed in relation to chemomechanical energy transduction through interaction with myosin in the presence of ATP.

MATERIALS AND METHODS

Proteins and buffers

Actin was prepared from chicken pectoral and leg muscle (Spudich and Watt, 1971) and concentrated with Aquacide II (Calbiochem, San Diego, CA), which did not affect the polymerization capacity of actin. The protein concentration was determined from absorption at 290 nm with 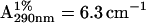Inline graphic (Sheterline et al., 1998). Myoglobin was purchased from Sigma (St. Louis, MO). The low-salt buffer contained 2 mM HEPES (pH 7.2), 0.2 mM ATP, and 0.1 mM CaCl2. This buffer was supplemented with KCl and MgCl2 to make the high-salt buffer (2 mM HEPES, 0.2 mM ATP, 0.1 mM CaCl2, 50 mM KCl, and 2 mM MgCl2, at pH 7.2). The ratio of G- and F-actins was determined by fluorimetry using n-(1-pyrenyl)iodoacetamide (Kouyama and Mihashi, 1981). The partial specific volume (sv) of proteins was calculated from the density of their solutions measured with an Anton-Paar (Graz, Austria) DMA-58 density meter.

Dielectric spectroscopy and data analysis

All measurements were made in a conically shaped glass cell (total volume, 3.2 ml) connected to a microwave network analyzer at 20.0 ± 0.01°C (Agilent, Palo Alto, CA, 8720C-85070A). The frequency-dependent signals were converted into complex dielectric spectrum consisting of real and imaginary parts, ɛ* = ɛ′ – iɛ″ (Fig. 2). Noises inherent to the measuring system such as mismatching of cable-connectors as well as those from other sources and systematic interfering components were superimposed on the dielectric spectra. Thus, to overcome these noises the actual measurement and data processing were performed using the following three procedures. First, the spectra of the buffer 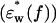Inline graphic and protein solution 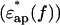Inline graphic were measured in pairs ∼8–10× at a given protein concentration. The difference was taken for each pair (difference spectrum, protein solution vs. solvent buffer). The difference spectra obtained were then averaged and subjected to mathematical “smoothing” using fifth or higher order polynomial functions of log10f. This gave the difference dielectric spectrum of the protein solution consisting of real and imaginary parts (Δɛ*(f) = Δɛ′(f) – iΔɛ″(f)) with greatly reduced noise level (Fig. 3 a). Secondly, there is a small inevitable difference in the free concentrations of ions between buffer and protein solution due to the binding of ions to proteins. This affects the imaginary part of the spectrum (Δɛ″(f)) as an ionic conduction effect. This was corrected by subtracting Δσ/(2πɛ0f) (Δσ, the ionic conduction difference) from Δɛ″ (Fig. 3 a). The value of Ds was empirically determined to bring the absolute value of Δɛ″ at 0.2GHz within the range between 0 and 1.0 in the present work. This correction gave little influence on the values of Δɛ′ and Δɛ≈ in the frequency range between 2 and 20 GHz. Finally, the spectrum of the sample protein solution 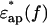Inline graphic was calculated by adding the difference spectrum (Δɛ*(f)) as estimated to the buffer spectrum 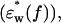Inline graphic which had also been processed using the averaging and smoothing techniques described.

FIGURE 2.

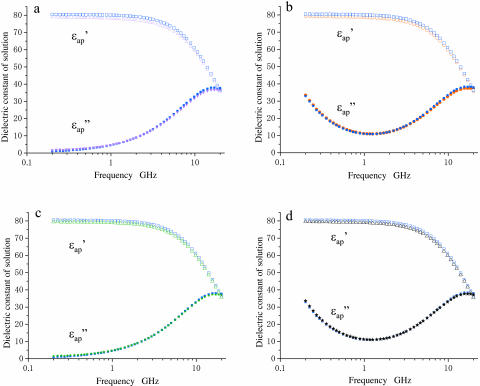
FIGURE 2

Open in a new tab

Dielectric spectra of actin and myoglobin solutions. Unfilled and solid symbols refer to the real and imaginary parts of dielectric spectra, respectively; blue symbols refer to buffers. (a) Spectra of actin (magenta triangles, 21.0 mg/ml) in the low-salt buffer (2 mM HEPES, 0.2 mM ATP, and 0.1 mM CaCl2, at pH7.2). (b) Spectra of actin (red circles, 13.8 mg/ml) in the high-salt buffer (2 mM HEPES, 0.2 mM ATP, 0.1 mM CaCl2, 50 mM KCl, and 2 mM MgCl2, at pH 7.2). (c) Spectra of myoglobin (green triangles/stars, 14.0 mg/ml) in the low-salt buffer. (d) Spectra of myoglobin (black triangles/stars, 13.8 mg/ml) in the high-salt buffer.

FIGURE 3.

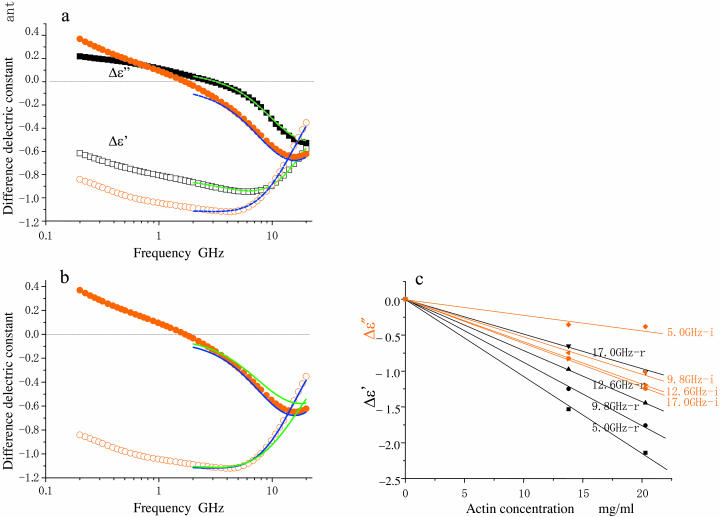
FIGURE 3

Open in a new tab

Difference dielectric spectra of F-actin (red circles) and myoglobin (black squares) solutions. Data were obtained from eight independent measurements for both proteins, averaged as described in Materials and Methods, and normalized to a protein concentration of 10 mg/ml. The size of the spectral symbols are roughly equal to the error widths. Unfilled and solid symbols refer to the real and imaginary parts of dielectric spectra as in Fig. 2. (a) Difference spectra (Δɛ′ (f), Δɛ″(f)) to show that actin and myoglobin are distinct. The theoretical curves for myoglobin were calculated according to Yokoyama et al. (2001) and those for F-actin by analysis using the model shown in Fig. 5. (b) Comparison of fit of theoretical curves: the single-shelled model, green solid lines; the double-shelled model, blue solid lines. (c) Protein concentration-dependence of Δɛ′ (black) and Δɛ″ (red) of F-actin at the frequencies indicated.

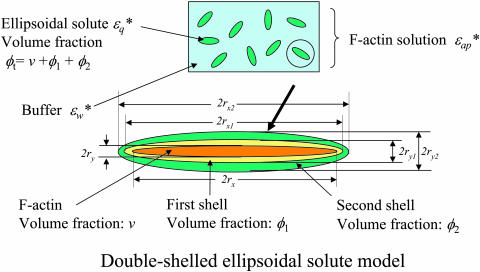
This “back-synthesized” spectrum 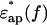Inline graphic was analyzed as previously described (Yokoyama et al., 2001), with the exception that instead of using a spherical-solute model, a randomly oriented ellipsoidal-solute model was used as shown in Fig. 5 (Asami et al., 1980). The ellipsoid was assumed to have the major axis (x-axis) of 2rx and the minor axis (y-axis) of 2ry = 2rz with a rotational symmetry around the major axis and double shells which cover the core ellipsoid coaxially. The major and minor axes of the shells are 2rxk and 2ryk, where k is 1 or 2 corresponding to the first and second shell, respectively (Fig. 5). A constant axial ratio was adopted here as q0 = rx / ry = rx1 / ry1 = rx2 / ry2 · q0 was assumed to be 30 for F-actin and 1.001 (quasi-unity, practically equivalent to a spherical model) for myoglobin. The complex dielectric constants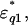 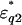Inline graphic Inline graphic of the first and second shells were set by assuming a Debye-type relaxation function with relaxation frequencies fck and amplitudes δk as described in the following equations:

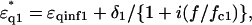graphic file with name M10.gif (1)
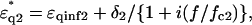graphic file with name M11.gif (2)

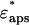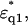
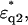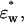where the dielectric constants of the shells at the high frequency limit ɛqinf1, ɛqinf2 were set to 5.6 assuming that the values are close to that of free water (Kaatze, 1990). The dielectric constant of the model solution containing double-shelled ellipsoidal solutes Inline graphic was then calculated using Inline graphic Inline graphic and Inline graphic and the volume fraction of the double-shelled solute, φt, by the following equations derived from the method by Asami et al. (1980):

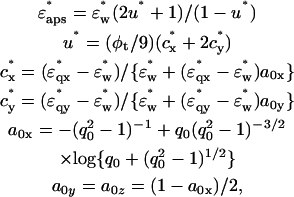graphic file with name M16.gif (3)

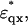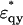where Inline graphic and Inline graphic are given by

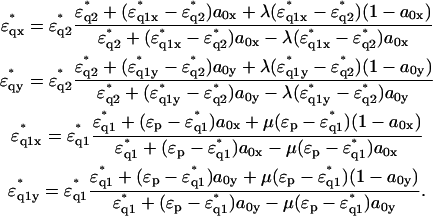graphic file with name M19.gif (4)

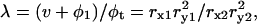
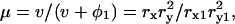where Inline graphic Inline graphic φ1 is the volume fraction of the first shell in the solution, and v is the volume fraction of the core ellipsoid. The values of fc1, δ1, and φ1 were determined as adjustable parameters by least-square fitting to the real part Δɛ′ in the frequency range between 2 and 10 GHz. Using this parameter set of the first Debye component, the second set of adjustable parameters, fc2, δ2, and φ2 was determined by least-square fitting taking into account the φ2-effect on Δɛ′ for ∼10–14 GHz, and the fc2-effect on Δɛ″ for ∼12–20 GHz. The entire set of parameters (fc1, δ1, φ1; fc2, δ2, φ2) thus obtained was used as the initial estimates for the second stage of fitting, which was repeated until no further improvement resulted. Thus, the total volume fraction of the hydrated solute φt (= v + φ1 + φ2) could be determined. 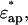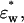Finally, assuming that F-actin solution is a one-solute/one-solvent system, the apparent dielectric constant of the double-shelled ellipsoid, Inline graphic was calculated from the experimental values of Inline graphic Inline graphic and the value of φt by the following equations:

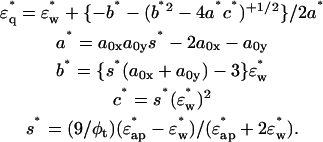graphic file with name M25.gif (5)

FIGURE 5.

FIGURE 5

Open in a new tab

Double-shelled ellipsoidal solute model. This model (Asami et al., 1980) was used to analyze the dielectric spectrum of F-actin solution as outlined in Materials and Methods. The expressions 2rx and 2ry refer to the lengths of major and minor axes of the ellipsoidal shells, respectively. Theoretical spectral curves obtained were superimposed on the observed values for Δɛ′(f) and Δɛ″(f) (blue-colored solid lines in Fig. 3 a). Note that when applied to the spectrum of the myoglobin solution with the protein axial ratio of 1.001, a curve essentially the same as estimated by the previous method was obtained (Yokoyama et al., 2001).

RESULTS AND DISCUSSION

Dielectric spectra of actin solutions

Dielectric spectra of the actin solution (the real part, 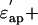Inline graphic the imaginary part, 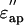Inline graphic) in the low-salt buffer recorded after being introduced into the measuring cell (Fig. 2 a) were very similar to those of other globular proteins (Yokoyama et al., 2001), among which myoglobin was chosen as a reference protein in the present study (Fig. 2 c). When the concentration of actin exceeds ∼4 mg/ml, the extra actins assemble into filaments even at low ionic strengths (Sheterline et al., 1998). Using a fluorimetry technique, it was determined that a mol fraction of F-actin exceeded 45% in the low-salt buffer at actin concentrations >10 mg/ml, which was a prerequisite for successful dielectric measurements. Hence, after introducing the actin into the measuring cell, the actin was completely polymerized by adding KCl + MgCl2. Measurements were then made using the high-salt buffer as the reference (Fig. 2 b). In the low frequency region (<2 GHz) the ionic conduction effect could be observed on the imaginary part 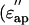Inline graphic). The spectra were not substantially different from those recorded in the low-salt buffer. These observations also apply to the myoglobin spectra (Fig. 2 d).

A small but systematic difference between the dielectric spectra of the protein solution and the buffer seen over the frequency range investigated (Fig. 2) is a reflection of the difference in polarizability between the hydrated protein and the solvent. This is clearly shown in the difference spectra (Fig. 3 a: Δɛ*(f)). The description from here onward is based on the analysis of the dielectric spectra, which was limited in the frequency range above 2 GHz for two reasons. First, the effect of ionic conduction difference between protein and buffer solutions could not be completely removed from the spectra in the lower frequency range. Second, some relaxation phenomena such as subdomain fluctuation of a large protein (Hayashi et al., 2000) or orientation relaxation of molecular dipoles of amino acids (Suzuki et al., 1997a) were observed in the range <1 GHz. The effects of these relaxation irrelevant to the rotational mobility of water can be minimized, if not totally excluded, by the analysis in the frequency range >2 GHz.

As for the real-part spectrum, Δɛ′(f), in the frequency range >2 GHz, actin stays below that of myoglobin up to 9 GHz, but then rises more steeply thereafter. Corresponding to this, the pattern of the actin imaginary part, Δɛ″(f), is clearly distinct from that of myoglobin. It should be noted that both the Δɛ′ and Δɛ″ values calculated at the different frequencies are proportional to the actin concentration (Fig. 3 c). The magnitudes of standard errors of both Δɛ′ and Δɛ″ were in a range between 0.010 and 0.027.

Dielectric characterization of hydrated actin

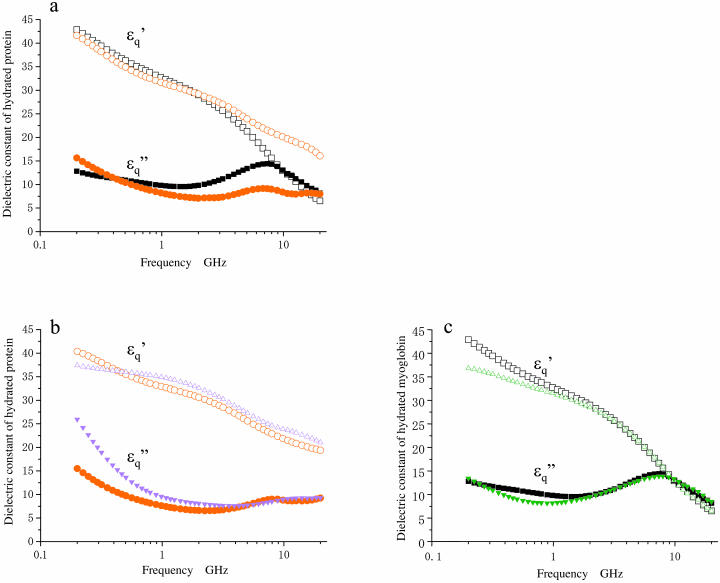
In the spectrum of the hydrated solutes at frequencies >2 GHz (Fig. 4 a), the real-part 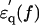Inline graphic of the actin spectrum (circles) decreased gradually. Accompanying this change was a slow increase of the imaginary-part 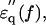Inline graphic whereas myoglobin (squares) 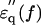Inline graphic showed a broad but clear peak at 7 GHz. The actin spectra in the low (triangles) and high-salt (circles) buffers are similar (Fig. 4 b) but different from the myoglobin spectra (Fig. 4 c). Among the proteins other than actin examined so far (Yokoyama et al., 2001), bovine serum albumin and ovalbumin showed the myoglobin-type spectra irrespective of the buffer used, i.e., low- or high-salt (data not shown). Thus, the dielectric characteristics of actin solution are genuine, and cannot be ascribed to an effect of ionic strength.

FIGURE 4.

FIGURE 4

Open in a new tab

Dielectric spectra 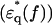Inline graphic of hydrated F-actin and myoglobin. Unfilled and solid symbols refer to the real and imaginary parts of dielectric spectra as in Fig. 2. (a) Comparison of actin (red circles) and myoglobin (black squares) in the high-salt buffer. (b) Comparison of actin in the low-salt buffer (magenta triangles) and the high-salt buffer (red circles). (c) Comparison of myoglobin in the low-salt buffer (green triangles) and the high-salt buffer (black squares).

Double-shelled model for analysis of actin spectra

A single-shelled sphere model describes well the dielectric spectra for non-actin globular proteins (Yokoyama et al., 2001), as illustrated by the theoretical curve (green solid lines) obtained for myoglobin (Fig. 3 a). In contrast, it was not possible to obtain any satisfactory theoretical spectra of actin no matter what dielectric parameters were chosen, which was clearly shown by systematic deviations of the best fitted theoretical curves (green solid lines in Fig. 3 b) from the observed spectra between 2 GHz and 10 GHz. Hence, a more complex analysis was attempted using the concept of a double-shelled ellipsoidal solute consisting of an actin filament surrounded by two layers of hydrating water, each of which had characteristic dielectric properties (Fig. 5). This analysis provided satisfactory fitting curves (blue solid lines) for the observed difference spectrum of actin (Fig. 3, a and b).

Thus, a unique feature of actin hydration has emerged (Table 1). The number of water molecules for every G-actin unit in the first hydration shell (N1) is slightly excess to make the mono-layer covering the three-dimensional structure model of G-actin unit in F-actin (Lorenz et al., 1993). The volume fraction of the second shell with a high fc is approximately two-thirds of the molecular volume of G-actin. Judging from its dielectric parameters, it seems almost impossible to postulate that any substance other than water could constitute this second shell. In this context, it seems appropriate to give a rough sketch of the hydration profile of F-actin. Assuming a filament as a straight cylinder with smooth surface, its radius would be 2.6 nm or 3.3 nm inclusive of the first hydration shell (see above). If the hyper-mobile water molecules were evenly distributed on the surface of cylinder, the overall radius could be 3.9 nm. However, such even distribution, which is most likely for the restrained water constituting the first hydration shell as judged from the linear relationship between Ntotal and Ncal (Fig. 1), is by no means realistic for the hyper-mobile water, because the molecular shape and chemical nature of the protein surface are very complex. In addition, it is not known yet where water molecules are hyper-mobilized on the actin surface (see below) or how they exchange with those of lower mobilities.

TABLE 1.

Dielectric parameters for hydration of F-actin and myoglobin

Relaxation component 1st 2nd
Protein fc1 (GHz) δ1 φ1/c* N1 fc2 (GHz) δ2 φ2/c*
F-actin† 6.5 45 0.506 1190 40 75 0.600
Myoglobin 6.2 79 0.588 581‡ – – –
Open in a new tab
*

N1 = φ1Mw/18c, where Mw is mass weight of protein. See text for other details. c is the protein concentration (g/ml). The values of the partial specific volume sv (F-actin, 0.743 ml/g; myoglobin, 0.74 ml/g) were measured with a density meter (Anton Paar DMA-58). φ1/c and φ2/c are the volume fractions of the hydration shells per unit protein concentration.

†

The values were calculated from the averaged and smoothed spectrum as described in Materials and Methods. The individual spectra (not averaged but smoothed) were also analyzed to estimate the errors accompanying the best-fit values given here to show the precision of eight independent measurements. The means were almost identical to the values obtained for the averaged spectrum, and the relative standard errors of the means for fc1, δ1, and φ1 were 3.0%, 4.0%, and 3.0%, respectively, and those for fc2, δ2, and φ2 were 4.6%, 4.8%, and 7.0%, respectively.

‡

This value was much larger than the one reported previously (∼380). This discrepancy is most likely due to the difference in the frequency range employed, 2–20 GHz in the present work compared to the earlier of 2–10 GHz. Increasing the frequency range may be equivalent to taking into account the hydrating water with a higher mobility. Taking into consideration weakly and strongly restrained water (Suzuki et al., 1996; Yokoyama et al., 2001), these values are roughly consistent with those estimated by MD calculations (Makarov et al., 2000).

Hyper-mobile water around solute molecules

A state where water has a mobility higher than that of the bulk water (here we refer to as hyper-mobile water) was first hypothesized to explain hydration anomalies of some ions such as I− and Cs+. This effect has been referred to as water-structure breaking (Frank and Wen, 1957) or negative hydration (Samoilov, 1957). For diluted solution of urea (Tovchigrechko et al., 1999) and solutions of alkali-halide salts (Collins, 1997; Hribar et al., 2002; Imai et al. 2002), experimental and theoretical (computational) studies indicated that this effect was attributable to the charge density of the solute and the balance of strength between water-solute interaction and water-water hydrogen bond. We measured the dielectric spectrum of a urea solution (Fig. 6 a), which could only be explained assuming a dipole with an fc value of 30 GHz in addition to the low frequency component (fc = 6.5 GHz, probably the urea dipole itself and weakly restrained water together). Dielectric measurements and analysis were also made for solutions of potassium halide-salts, KF, KCl, and KI. The results were similar to those obtained for urea. Thus, I− and Cl− but not F− seemed to induce some high frequency component(s) and I− showed a much stronger effect (Fig. 6 b). Adopting the criterion that if the peak frequency of 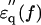Inline graphic is higher than 17 GHz, the solute is regarded as a water-structure breaker, the result is consistent with the order of strength of the structure-breaking effect obtained using other techniques (Robinson et al., 1996). These results strongly support our dielectric method which has enabled us to reveal this unique hydration property of actin.

FIGURE 6.

FIGURE 6

Open in a new tab

Dielectric spectra of hydrated solutes in urea and potassium halides solutions. (a) Experimental values for urea (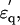Inline graphic squares; 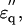Inline graphic circles) measured in 2% (w/v) solution are superimposed with theoretical curves (red and blue) simulated with the two components combined together: one with fc1 = 6.5 GHz, δ1 = 110, and N1 = 2.4; and the other with fc2 = 30GHz, δ2 = 88, and N2 = 2.4 using Eqs. 1–5 and N1,2 = φ1,2Mw/18c. The magenta-colored curve is the spectrum (imaginary part) of the component with fc1 = 6.5 GHz. (b) Spectra of potassium halide salts, KF (black), KCl (red), and KI (blue) measured in 0.2 M solutions. The curves were calculated using Eq. 5 with a constant φt = 0.117, which was the largest among those of KF, KCl, and KI. The peak in 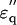Inline graphic spectra are at 18 GHz for KF, whereas the simulation indicates peaks at fc2 = 22 GHz and 25 GHz for KCl and KI, respectively.

In the first hydration shell of a protein, the mobility of water is generally lowered due to the interaction with residues on the protein surface (Bellissent-Funel, 1999; Halle and Denisov, 2001; Makarov et al., 2000; Mattos, 2002). In this respect, actin is not different from other proteins as outlined above. How then is the hyper-mobile state of water induced in actin? The surface of G-actin is rich in negative charges (Sheterline et al., 1998; Janmey et al., 2001), which could be responsible for inducing a hyper-mobility of water molecules that interact with such charges. This possibility, however, cannot be tested by the present dielectric spectroscopic techniques, because the dielectric spectrum of G-actin alone is practically immeasurable as noted above. An alternative view is that the induction of hyper-mobile water may be inherent to the F-actin structure. Using an x-ray structure-based three-dimensional model (Lorenz et al., 1993), the electrostatic potential for F-actin was predicted by recent simulations (Ouporov et al., 1999). This indicates that F-actin can be seen as a double helix of bulbs of negative potential extending into the solvent. Thus, F-actin may be likened to a charged cylinder (Oosawa, 1971). The strength of its electric field would decay much less abruptly than that of a charged sphere. Hence, there may be a region in the vicinity of the cylinder surface where the strength of the electric field is comparable to that formed by large halide ions such as I−. This may be the site where the hydrogen-bonded network of water is modulated. This would result in some of the bonds being short-lived and thereby enabling water molecules to become more mobile. To the best of our knowledge, the present work is the first to describe the presence of hyper-mobile water around a protein. Thus, it is important to examine whether or not this hypothesis is feasible using molecular dynamics and other related methods. If not, then the great challenge is to predict the structure of the actin molecule surface and/or the shape responsible for induction of such a large mass of hyper-mobile water.

Implication of hyper-mobile water in chemomechanical coupling

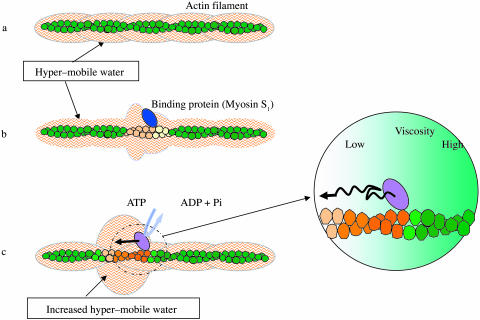
The diffusion coefficient of solute particles in water is inversely proportional to the viscosity of water, which is in a reciprocal relation with the rotational mobility of water molecules (Bloomfield, 2002; Fabelinskiĭ, 1997). Thus, our results suggest that a unique hydration shell containing water components with high and low viscosity is formed around F-actin (Fig. 7 a). Since the effect is undoubtedly structure-dependent, it would most likely undergo compositional fluctuations upon interaction with a specific binding protein. The binding proteins would induce characteristic conformational changes in the G-actin unit (Sheterline et al., 1998; Janmey et al., 2001) and some such changes would be cooperatively propagated through a filament (Oosawa et al., 1973; Orlova and Egelman, 1997). Thus, it is conceivable that upon interaction with actin, certain binding proteins bring themselves in solvent space asymmetric in viscosity along the filament axis (Fig. 7 b). We propose that in muscle contraction, the energy resulting from ATP hydrolysis is ultimately converted into the viscosity anisotropy around each myosin interacting with the actin filament, which would facilitate the directional movement of myosin along the filament (Fig. 7 c). This offers an explanation for the key issue of the chemomechanical energy transduction: how the molecular motors work efficiently by breaking the symmetry of thermal motions of molecules even though the energy input only marginally exceeds the thermal energy.

FIGURE 7.

FIGURE 7

Open in a new tab

A diagrammatic representation of the idea underlying the hypothesis of unidirectional sliding of myosin along F-actin. (a) The surface of F-actin is covered by a layer of hyper-mobile water (for simplicity's sake, the ordinary restrained water is not shown). (b) Upon interaction with a specific binding protein, actin changes its conformation, which is in turn propagated directionally to adjacent monomers to generate solvent space of axially skewed viscosity. (c) During an ATP hydrolyzing cycle, myosin undergoes conformational changes in coupling with alternating strong and weak affinities for actin. The conformational changes are transmitted to actin and propagated as in b. Thus, the asymmetric space for diffusion is dynamically generated, where myosin moves toward the direction of lower viscosity.

Acknowledgments

We thank K. Asami, K. Sekine, F. Hirata, M. Irisa, T. Miyazaki, H. Takata, T. Yasunaga, S. Nishikawa, H. Higuchi, Y. Osada, and Y. Harada for discussions and support, and J. West for reading the manuscript.

This work was supported by Grant in Aid #11167203 from the Ministry of Education, Culture, Sports, Science and Technology of Japan.

References

  1. Asami, K., T. Hanai, and N. Koizumi. 1980. Dielectric analysis of Escherichia coli suspensions in the light of the theory of interfacial polarization. Biophys. J. 31:215–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bellissent-Funel, M.-C. 1999. Hydration Process in Biology, NATO Science Series, Series A, Vol. 305. IOS Press, Amsterdam, The Netherlands.
  3. Bloomfield, V. 2002. Survey of biomolecular hydrodynamics. In Separations, and Hydrodynamics. J. Correia, editor. Biophysical Society, Bethesda, MD. http://www.biophysics.org/btol/separat.html.
  4. Bryant, R. G. 1996. The dynamics of water-protein interactions. Annu. Rev. Biophys. Biomol. Struct. 25:29–53. [DOI] [PubMed] [Google Scholar]
  5. Buchner, R., J. Barthel, and J. Stauber. 1999. The dielectric relaxation of water between 0°C, and 35°C. Chem. Phys. Lett. 306:57–63. [Google Scholar]
  6. Collins, K. D. 1997. Charge density-dependent strength of hydration and biological structure. Biophys. J. 72:65–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ellison, W. J., K. Lamkaouchi, and J. M. Moreau. 1996. Water: a dielectric reference. J. Mol. Liq. 68:171–279. [Google Scholar]
  8. Fabelinskiĭ, I. L. 1997. Macroscopic and molecular shear viscosity. Physics-Usppekhi. 40:689–700. [Google Scholar]
  9. Frank, H. S., and W. Y. Wen. 1957. Structural aspects of ion-solvent interaction in aqueous solutions: a suggested picture of water structure. Disc. Faraday Soc. 24:133–140. [Google Scholar]
  10. Gregory, R. B. 1995. Protein-Solvent Interactions. Marcel Dekker, New York.
  11. Halle, B., and V. P. Denisov. 2001. Magnetic relaxation dispersion studies of biomolecular solutions. Meth. Enzymol. 338:178–201. [DOI] [PubMed] [Google Scholar]
  12. Hayashi, Y., N. Miura, J. Isobe, N. Shinyashiki, and S. Yagihara. 2000. Molecular dynamics of hinge-bending motion of IgG vanishing with hydrolysis by papain. Biophys. J. 79:1023–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Highsmith, S., K. Duignan, R. Cooke, and J. Cohen. 1996. Osmotic pressure probe of actin-myosin hydration changes during ATP hydrolysis. Biophys. J. 70:2830–2837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hribar, B., T. N. Southall, V. Vlachy, and K. A. Dill. 2002. How ions affect the structure of water. J. Am. Chem. Soc. 124:12302–12311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Imai, T., H. Nomura, M. Kinoshita, and F. Hirata. 2002. Partial molar volume and compressibility of alkali-halide ions in aqueous solution: hydration shell analysis with an integral equation theory of molecular liquids. J. Phys. Chem. B. 106:7308–7314. [Google Scholar]
  16. Janmey, P. A., J. X. Tang, and C. F. Schmidt. 2001. Actin filaments. In Supramolecular Assemblies, Chapter 5. V. Bloomfield, editor. Biophysical Society, Bethesda, MD. http://www.biophysics.org/btol/supramol.html.
  17. Kaatze, U. 1990. On the existence of bound water in biological systems as probed by dielectric spectroscopy. Phys. Med. Biol. 35:1663–1681. [DOI] [PubMed] [Google Scholar]
  18. Kouyama, T., and K. Mihashi. 1981. Fluorimetry study of n-(1-pyrenyl) iodoacetamide-labelled F-actin. Local structural change of actin protomer both on polymerization and on binding of heavy meromyosin. Eur. J. Biochem. 114:33–38. [PubMed] [Google Scholar]
  19. Lorenz, M., D. Popp, and K. C. Holmes. 1993. Refinement of the F-actin model against x-ray fiber diffraction data by the use of a directed mutation algorithm. J. Mol. Biol. 234:826–836. [DOI] [PubMed] [Google Scholar]
  20. Makarov, V. A., B. K. Andrews, P. E. Smith, and B. M. Pettitt. 2000. Residence times of water molecules in the hydration sites of myoglobin. Biophys. J. 79:2966–2974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Mattos, C. 2002. Protein-water interactions in a dynamic world. Trends Biochem. Sci. 27:203–208. [DOI] [PubMed] [Google Scholar]
  22. Oosawa, F. 1971. Polyelectrolytes. Marcel Dekker, New York.
  23. Oosawa, F., S. Fujime, S. Ishiwata, and K. Mihashi. 1973. Dynamic property of F-actin and thin filament. Cold Spring Harb. Symp. Quant. Biol. 37:277–285. [Google Scholar]
  24. Orlova, A., and E. H. Egelman. 1997. Cooperative rigor binding of myosin to actin is a function of F-actin structure. J. Mol. Biol. 265:469–474. [DOI] [PubMed] [Google Scholar]
  25. Ouporov, I. V., H. R. Knull, and K. A. Thomasson. 1999. Brownian dynamics simulations of interactions between aldolase and G- or F-Actin. Biophys. J. 76:17–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Robinson, G. W., S. B. Zhu, S. Singh, and M. W. Evans. 1996. Water in Biology, World Scientific Series in Contemporary Chemical Physics, Vol. 9. World Scientific, Singapore.
  27. Samoilov, O. Y. 1957. A new approach to the study of hydration of ions in aqueous solutions. Disc. Faraday Soc. 24:141–146. [Google Scholar]
  28. Sheterline, P., J. Clayton, and J. C. Sparrow. 1998. Actin, 4th Ed. Oxford University, Oxford, UK.
  29. Spudich, J. A., and S. Watt. 1971. The regulation of rabbit skeletal muscle contraction. 1. Biochemical studies of the interaction of the tropomyosin-troponin complex with actin and the proteolytic fragments of myosin. J. Biol. Chem. 246:4866–4871. [PubMed] [Google Scholar]
  30. Suzuki, M., J. Shigematsu, and T. Kodama. 1996. Hydration study of proteins in solution by microwave dielectric analysis. J. Phys. Chem. 100:7279–7282. [Google Scholar]
  31. Suzuki, M., J. Shigematsu, Y. Fukunishi, and T. Kodama. 1997a. Hydrophobic hydration analysis on amino acid solution by the microwave dielectric method. J. Phys. Chem. B. 101:3839–3845. [Google Scholar]
  32. Suzuki, M., J. Shigematsu, Y. Fukunishi, Y. Harada, T. Yanagida, and T. Kodama. 1997b. Coupling of protein surface hydrophobicity change to ATP hydrolysis by myosin motor domain. Biophys. J. 72:18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tovchigrechko, A. D., M. N. Rodnikova, and J. Barthel. 1999. Comparative study of urea and tetramethylurea in water by molecular dynamics simulation. J. Mol. Liq. 79:187–201. [Google Scholar]
  34. Wüthrich, K. 2001. The way to NMR structures of proteins. Nature (Struct. Biol.) 8:923–925. [DOI] [PubMed] [Google Scholar]
  35. Yokoyama, K., T. Kamei, H. Minami, and M. Suzuki. 2001. Hydration study of globular proteins by microwave dielectric spectroscopy. J. Phys. Chem. B. 105:12622–12627. [Google Scholar]
  36. Zhou, H. X. 2001. A unified picture of protein hydration: prediction of hydrodynamic properties from known structures. Biophys. Chem. 93:171–179. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES