Exciton Theory for Supramolecular Chlorosomal Aggregates: 1. Aggregate Size Dependence of the Linear Spectra

Abstract

The interior of chlorosomes of green bacteria forms an unusual antenna system organized without proteins. The steady-spectra (absorption, circular dichroism, and linear dichroism) have been modeled using the Frenkel Hamiltonian for the large tubular aggregates of bacteriochlorophylls with geometries corresponding to those proposed for Chloroflexus aurantiacus and Chlorobium tepidum chlorosomes. For the Cf. aurantiacus aggregates we apply a structure used previously (V. I. Prokhorenko., D. B. Steensgaard, and A. R. Holzwarth, Biophys. J. 2000, 79:2105–2120), whereas for the Cb. tepidum aggregates a new extended model of double-tube aggregates, based on recently published solid-state nuclear magnetic resonance studies (B.-J. van Rossum, B. Y. van Duhl, D. B. Steensgaard, T. S. Balaban, A. R. Holzwarth, K. Schaffner, and H. J. M. de Groot, Biochemistry 2001, 40:1587–1595), is developed. We find that the circular dichroism spectra depend strongly on the aggregate length for both types of chlorosomes. Their shape changes from “type-II” (negative at short wavelengths to positive at long wavelengths) to the “mixed-type” (negative-positive-negative) in the nomenclature proposed in K. Griebenow, A. R. Holzwarth, F. van Mourik, and R. van Grondelle, Biochim. Biophys. Acta 1991, 1058:194–202, for an aggregate length of 30–40 bacteriochlorophyll molecules per stack. This “size effect” on the circular dichroism spectra is caused by appearance of macroscopic chirality due to circular distribution of the transition dipole moment of the monomers. We visualize these distributions, and also the corresponding Frenkel excitons, using a novel presentation technique. The observed size effects provide a key to explain many previously puzzling and seemingly contradictory experimental data in the literature on the circular and linear dichroism spectra of seemingly identical types of chlorosomes.

INTRODUCTION

Chlorosomes occurring in green bacteria represent a very special case of pigment organization among the photosynthetic antenna complexes. They contain several tens of thousands of bacteriochlorophylls (BChl) arranged into rodlike aggregates (∼10–30 rods per chlorosome) which are tightly packed in an organelle surrounded by a lipid monolayer (Staehelin et al., 1978, 1980; Olson, 1998; Blankenship et al., 1995). In contrast to all other antenna complexes the chlorosomes, and in particular their rod aggregates, do not contain a protein as a major structure-determining element. Rather, the BChl-molecules form stacked structures, which are self-assembled in a supramolecular hydrogen-bonding network that is wrapped into cylinders with a diameter of 5–10 nm (Staehelin et al., 1978). The mechanism of self-assembly of these special BChls contained in chlorosomes is now quite well-established (Schaffner and Holzwarth, 1997; Balaban et al., 2000; D. B. Steensgaard, T. S. Balaban, K. Schaffner, and A. R. Holzwarth, unpublished results). The structural arrangement is supported by numerous spectroscopic data (Holzwarth et al., 1990; Hildebrandt et al., 1991; Chiefari et al., 1995; Tamiaki et al., 1996; Prokhorenko et al., 2000a), and a detailed structural model has been developed using molecular modeling techniques (Holzwarth and Schaffner, 1994) taking into account these spectroscopic data. This structural model was further confirmed and detailed experimentally by solid-state nuclear magnetic resonance (NMR) (Balaban et al., 1995b; Mizoguchi et al., 1998; van Rossum et al., 1998a,b, 2001). Earlier exciton calculations have been performed by Alden et al. (1992) for various smaller pigment arrangements before detailed structural information had been available.

The optical properties of these aggregates are dominated by the strong excitonic coupling of the pigments which are nearly at van der Waals distance to each other. For characterization of the spectral properties of such systems, circular dichroism (CD) spectroscopy is the method of choice. In some cases, especially for simple systems like dimers, the shape of the CD-spectrum straightforwardly provides information about the spatial arrangement of the transition dipole vectors of the interacting molecules (see, for example, Pearlstein, 1991 for a detailed presentation). CD spectroscopy has been applied widely for the investigation of both Cf. aurantiacus and Cb. tepidum chlorosomes (Olson, 1980; Brune et al., 1990; van Mourik et al., 1990; Otte et al., 1991; Griebenow et al., 1991; Lehmann et al., 1994; Niedermeier et al., 1992; Wang et al., 1995; Ma et al., 1996; Frese et al., 1997) and artificial BChl aggregates (Dudkowiak et al., 1995; Olson et al., 1985; Uehara et al., 1994; Balaban et al., 1995a; Ishii et al., 1998; Zhu et al., 1996). Surprisingly drastically different CD-spectra have been reported often for the same type of chlorosomes, but were obtained in independent preparations or by slightly different preparation procedures (see, for example, Olson, 1980; Griebenow et al., 1991; and publications discussed therein), or for different growth conditions (Ma et al., 1996). These changes often involved an apparent change in sign of the CD bands, while all the other optical spectra seemed to be the same, thus indicating the same structural arrangement. According to nomenclature introduced in Griebenow et al. (1991), the shape of the commonly observed CD-spectra of chlorosomes can be categorized into three types—type-I, where the sign of the CD-spectrum changes from positive at short wavelengths to negative at long wavelengths (+/−), the opposite behavior as type-II (−/+), and the so-called mixed-type (−/+/−) in which three maxima are present (for details, see Fig. 3 in Griebenow et al., 1991). The latter mixed-type of CD-spectra, with a varying type-I-to-type-II ratio, is typical for most chlorosome preparations, with some preference for a major type-II contribution. Note that the “pure” type-I CD-spectra actually were not observed in either Chloroflexus aurantiacus or Chlorobium tepidum chlorosomes with typical preparation. In Griebenow et al. (1991) it was also demonstrated that the mixed-type CD-spectrum can be phenomenological given as the sum of type-I and type-II spectra. Later this assumption was confirmed in Somsen et al. (1996). Such a decomposition of the mixed-type CD-spectrum (and its variation upon change in experimental conditions) was explained in that work by a variation of the transition dipole moment orientation of monomers with respect to the geometry of the rod aggregate. However, the structural variability for such aggregates is severely limited if the breaking of the important interactions, as, e.g., in the hydrogen bonds and the O-Mg-bonds, is to be avoided. Since the transition dipole moments are linked to the molecular frame of the monomers, they cannot be arbitrarily rotated with respect to the macroscopic symmetry axis without destroying the interactions that are decisive for yielding the spectral properties of such systems. This is the case, for example, in very recently published work of Psencik et al. (2003). To fit the experimental data, the authors chose a model of the rod aggregates for Cb. phaeobacteroides chlorosomes where the plane-to-plane distance between neighboring chlorins would be well below the van der Waals radii. Note that we present here the first exciton calculations on the chlorosome aggregates using an experimental structure (Balaban et al., 1995b; van Rossum et al., 2001). Due to the lack of detailed structural information, previous work was based only on assumed relative arrangement of the transition dipole moments of monomers without reference to actual chemical structure. This also applies to the work of Somsen et al. (1996). The authors claimed that small variations in the transition dipole moment directions of the monomers can drastically change the CD-shape. This conclusion was made by numerical calculations within a structural model in which the distance between chlorins in a stack was chosen to be 5 Å, and the angle between transition dipole moments of monomers (which is in plane of the chlorin ring) in respect to the macroscopic symmetry axes of rod-aggregate was 15°. Such an arrangement of chlorins is impossible from a chemical point of view since the distance between chlorin planes in that case is ≤1.3 Å (depending on orientation of transition dipole moment in respect to radius-vector of the rod-aggregate). Such models, chosen without taking into account the spatial and conformational limitations, are entirely arbitrary and would not be energetically stable in reality.

FIGURE 3.

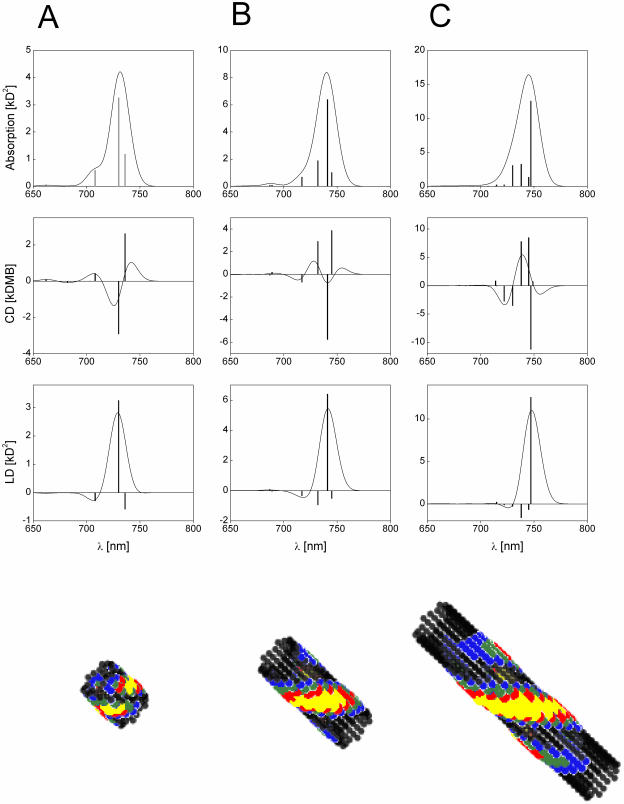
Calculated absorption-, CD-, and LD-spectra of aggregates from Cf. aurantiacus chlorosomes containing 10 (A), 20 (B), and 40 (C) molecules per stack. The stick-spectra are convoluted with a normalized Gaussian profile of FWHM = 350 cm⁻¹. Amplitude factor for the stick-components is 10⁻³. (Bottom) Distribution of occupied molecules in the lowest exciton state (frozen excitons).

In previous work (Prokhorenko et al., 2000a) we developed an exciton model for BChl-aggregates and chlorosomes, based on the spatial structure determined using the molecular modeling (Holzwarth and Schaffner, 1994). This exciton model suitably described the main features of their optical properties, including the influence of the superlattice organization of several adjacent rod aggregates in chlorosomes. However, the peculiar effects of mixed-type CD-spectra with varying ratios could not be explained by these calculations. Notably, the numerical calculations of the stick-spectra were performed in that work for relatively small aggregates (number of molecules per stack N_stack ∼7–10), and the calculated CD-spectra were essentially classified as type-II. (Note that CD-spectra published in that work were reversed in sign by mistake.)

We now extend this modeling to large aggregates of a length that is comparable to those present in native chlorosomes. We find an interesting and unexpected behavior of the CD of the larger aggregate length (Prokhorenko and Holzwarth, 2001, 2002). We call this the size effect of the CD-spectrum. Furthermore, we present a detailed exciton study for a new chlorosome structure based on solid-state NMR data and molecular modeling which applies also to the large diameter rods (∼10-nm diameter) of Cb. tepidum-type chlorosomes, the so-called double-tube structure (van Rossum et al., 1998b, 2001; Steensgaard et al., 2000). We also develop here a new approach allowing to visualize the exciton states and the movement of excitons, which provides an attractive possibility to get a “feeling” for the exciton dynamics in rod-aggregates and chlorosomes and which can be applied to the molecular aggregates in general.

METHODS

Theoretical approach

We will consider here the spectral properties of aggregates taking into account only interactions between transitions corresponding to the Q_y-absorption region of monomers. Since the Q_x absorption in the BChl c molecule has very small oscillator strength, and due to the large energy gap between transitions of the Soret band and the Q_y-transition, the mixing of higher transitions with Q_y-transition within excitonic-coupled ensemble of BChl c molecules is insignificant. This is also supported by the observed CD-spectra in the Q_y-band, which are essentially conservative. This means that the Q_y absorption band of aggregates can be modeled well within a two-level approximation for the monomers.

As in our previous work (Prokhorenko et al., 2000a), we will use the simplest approximation (Frenkel Hamiltonian) for calculating the excitonic states of an aggregate with N monomers, thus neglecting the interaction of the electronic transition with the phonons,

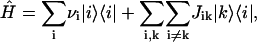(1)

where ν is the energy of the S₀→S₁ electronic transition of the i^th molecule whose excited state is described by the wave function 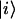, indices 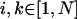, and J_i,k is the Coulomb interaction energy between the i^th and the k^th molecule for which we will use the point dipole-dipole approximation (Agranovich and Galanin, 1982):

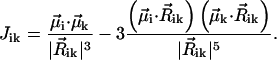(2)

.

Here the transition dipole moment of the i^th molecule is denoted by 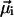, and the distance vector (defined with respect to the central magnesium atoms for BChls) is 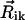. The validity of the dipole-dipole approximation for describing the interaction energy depends on the ratio between the dipole length (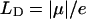, where e is the electron charge) and the intermolecular distance 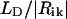, since this ratio is a series expansion parameter for the Coulomb interaction. The shortest distance between monomers in our structural model is 6.4 Å (within a stack, see below), and the dipole length for BChl c is 1.1 Å (calculated using a dipole strength of 30 D² as defined in Prokhorenko et al., 2000a) so that 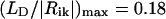, and thus the dipole-dipole approximation can be applied. (Note that authors often erroneously assume that the ratio between the molecule size and the intermolecular distance is the series expansion parameter, which indeed can be close to 1 in many cases. This question has been clarified, however, by Davydov, 1971.)

The usual way for solving the stationary Schrödinger equation,

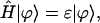(3)

is to expand the excitonic wave functions over an appropriate basis set (in this case, the set of the molecular monomer wave functions ):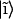

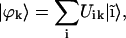(4)

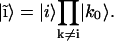(5)

The molecular wave function is a product of the ground-state wave functions of the N-1 nonexcited molecules and the excited-state wave function for the i^th excited molecule. The solution of Eq. 3 yields the excitonic transition energies and the amplitudes for the excitonic wave functions as

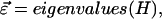(6.1)

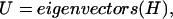(6.2)

where the interaction matrix H is

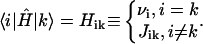(7)

The Hamiltonian Eq. 1 can also be rewritten using the one-exciton wave functions as

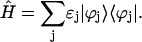(8)

For symmetrical structures (e.g., rod aggregates with infinite length) the Hamiltonian can be solved analytically using the second quantization and periodical boundary conditions (Didraga et al., 2002). However, such a solution is not always satisfying since it cannot be applied, for example, for analysis of the spectral properties of aggregates with finite length, for disordered systems, or for some higher order rod arrangement in chlorosomes. Thus we will use here a numerical diagonalization, which allows also for easy incorporation of both diagonal and off-diagonal disorder.

Spectra calculation

The absorption, CD, and linear dichroism (LD) stick-spectra can be calculated using the energies of the excitonic transitions and amplitudes of the stationary excitonic wave-functions, obtained after diagonalization of the Hamiltonian matrix, and the transition dipole moments of the monomers (Pearlstein, 1991), as

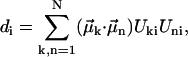(9.1)

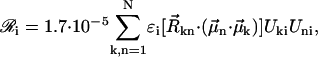(9.2)

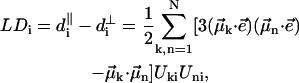(9.3)

where 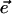is the unit vector in the direction of the macroscopically defined symmetry axis (usually the rotational symmetry axis of the rod aggregate). These expressions can also be written in matrix form, which largely speeds up the numerical calculations; and they are also more convenient for the analysis of the results. For that purpose we introduce the absorption (AM), the CD (CDM), and the LD (LDM) matrices,

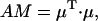(10.1)

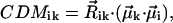(10.2)

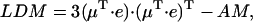(10.3)

where the superscript T stands for the transposed matrix (vector), and μ is the 3 × N matrix of the transition dipole moment vectors (the i^th column corresponds to the i^th molecule). Using these matrices, after simple algebraic manipulations the expressions (Eq. 9) for the stick-components of the corresponding spectra can be rewritten in straightforward manner as

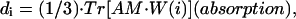(11.1)

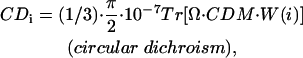(11.2)

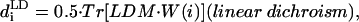(11.3)

(units: [μ] = Debye; [d] = Debye²; [R] = nm, [ɛ] = cm⁻¹; [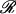] = Debye-Bohr magneton; and [CD] = Debye²) where the matrix 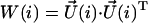is a product of the eigenvectors for the i^th excitonic transition, Tr denotes the trace of the matrix, and 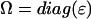is the diagonal matrix of the excitonic transition energies. The coefficient 1/3 in Eqs. 11.1 and 11.2 appears due to spatial averaging of the randomly distributed absorbers. For calculating the LD-spectra and for comparison with experimental data, it is important to take into account this space average. For better comparison of amplitudes for the CD- and absorption stick-components, the CD should be also given in Debye² units. For that in Eq. 11.2 a numerical pre-factor 1.7 · 10⁻⁵ is replaced by (π/2) · 10⁻⁷. For numerical calculations a value of the transition dipole moment of monomeric BChl c molecule of μ = 5.48 Debye was used (Prokhorenko et al., 2000a), and its direction is defined as a vector connecting the carbon of the C^13,1 keto group and the central Mg-atom. That direction is supported by semiempirical quantum-mechanical calculations performed for the BChl c molecule (data not shown). Any small deviations from that direction do not have any significant influence on the results presented here. These parameters result in an interaction energy of −541 cm⁻¹ in the model for Cf. aurantiacus aggregates between neighboring monomers in the same stack, whereas the interaction energies for monomers in different stacks range from +83 cm⁻¹ up to −291 cm⁻¹. The site energy (15390 cm⁻¹, close to the Q_y-transition of BChl c in methanol) is assumed to be equal for all monomers in an aggregate (for nondisorder calculations). Note that all structural parameters for the two types of chlorosome structures are compiled in Tables 1 and 2.

TABLE 1.

Structural parameters of the Cf. aurantiacus rod aggregates

Parameter	Value	Mean deviation
Radius (with respect to Mg-atoms - z-axis)	22.75 Å	±0.6 Å (along x-axis)
		±0.7 Å (along y-axis)
Distance between chlorins in stacks (Mg-Mg distance; along z-axis in a stack)	6.4 Å	±0.2 Å
Shift between neighbors stacks along z-axis	2.16 Å	±0.16 Å
Angle* between transition dipole moment vector and symmetry axis (α)	36.5°	±1.5°
Angle* between transition dipole moment vector and radius-vector connecting Mg-atom and z-axis (β)	280°	±4.3°
Number of stacks per rod aggregate	18	–

^*The angle definitions correspond to those in a spherical coordinate system which the z-axis coinciding with the symmetry axis of the aggregate (z-axis).

TABLE 2.

Structural parameters of the Cb. tepidum double-tube aggregates

Parameter	Value	Mean deviation
Inner tube
Radius (with respect to Mg-atoms - z-axis)	26.82 Å	±0.7 Å (along x-axis)
		±0.8 Å (along y-axis)
Distance between chlorins in stacks (Mg-Mg distance; along z-axis in a stack)	6.75 Å	±0.3 Å
Shift between neighbors stacks along z-axis	1.68 Å	±0.5 Å
Angle* between transition dipole moment vector and symmetry axis (α)	35.5°	±0.8°
Angle* between transition dipole moment vector and radius-vector connecting Mg-atom and z-axis (β)	274°	±2.8°
Number of stacks per tube	20	–
Outer tube
Radius (with respect to Mg-atoms - z-axis)	40.72 Å	±0.6 Å (along x-axis)
		±0.6 Å (along y-axis)
Distance between chlorins in stacks (Mg-Mg distance; along z-axis in a stack)	6.71 Å	±0.1 Å
Shift between neighbors stacks along z-axis	1.35 Å	±0.23 Å
Angle* between transition dipole moment vector and symmetry axis (α)	36°	±0.6°
Angle* between transition dipole moment vector and radius-vector connecting Mg-atom and z-axis (β)	265°	±2°
Number of stacks per tube	30	–

^*For the angle definition, see Table 1.

Disorder

The diagonal disorder can be directly incorporated into the interaction matrix H by randomizing the site transition energies of the molecules. Gaussian distributions of the site energies with FWHM of 430 cm⁻¹ or 210 cm⁻¹ were used for the aggregates (and unit cells) of the Cl. tepidum and Cf. aurantiacus chlorosomes, respectively, in accordance with the experimental photon echo data (Prokhorenko et al., 2000a). Inclusion of the off-diagonal disorder is not quite so straightforward and needs additional explanation. For excitonically coupled systems with a large number of molecules, the off-diagonal terms in the interaction matrix are not independent of each other. This can be understood easily by an estimation of the number of independent variables in the interaction matrix for N coupled molecules with an arbitrary geometry. 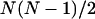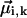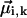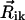Taking into account the diagonal symmetry of H, the total number of interaction terms is , whereas in the dipole-dipole approximation each off-diagonal element J_ik depends on six variables—the angle between the transition dipole moment vectors of the interacting molecules , their absolute magnitudes, and the angles between and , and 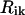. Thus, the interaction in a system containing N molecules is completely described by 6N variables, and from the equality—number of independent variables ≡ number of independent interaction terms (i.e., 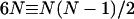)—it follows that for 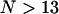the coupling energies become correlated, and the interaction matrix will be overdetermined. (This applies also to the excitonic wave functions. The matrix of amplitudes U will be also overdetermined—i.e., becomes correlated—for a system with number of molecules N > 13 independently of the aggregate structure. However, detailed analysis of such a correlation is beyond the aim of the present work.) Therefore the disordered interaction matrix was generated by randomizing the positions of the molecules and the directions of their dipole moment vectors around their symmetrical positions with FWHM values, as estimated from the deviations occurring in the molecular modeling calculations (see Tables 1 and 2; presented as error limits).

Visualization of exciton states

For better understanding the nature of the exciton states in aggregates it is helpful to visualize how the monomers, involved in an excitonic transition, are distributed over the aggregate body, and what their contributions to a particular excitonic wave function is. This can best be realized by a space plot of the probability of excitations (occupation) for the monomers. For this we take into account that the molecular basis functions are localized on the monomers, and since 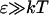, we can write for the probability that the i^th molecule will be occupied in the j^th exciton state that

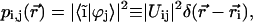(12)

where 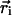is the center coordinate of the i^th molecule, and δ is the Kronecker delta-function ( 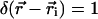if 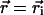and zero otherwise). Thus, the distribution of occupation of molecules in the j^th-exciton state is

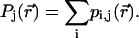(13)

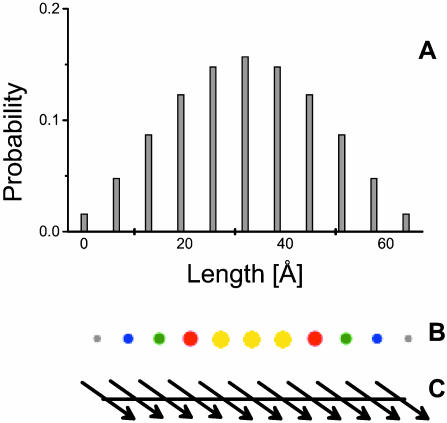
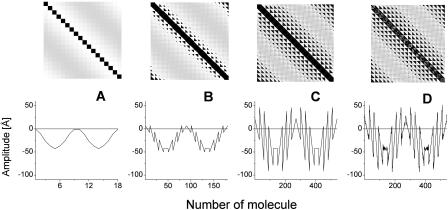
As an example, Fig. 1 a illustrates the plot of probability of excitation for the lowest exciton state in a simple aggregate containing 11 monomers arranged in a stack (Fig. 1 c). Such a graphical bar presentation is possible only for two-dimensional aggregates, however. For three-dimensional aggregates we can use a coloring scheme of molecules according to their probability of occupation, as illustrated in Fig. 1 b.

FIGURE 1.

(A) An x-y plot of distribution of occupation in the linear aggregate (stack of 11 molecules) for the lowest exciton state; (B) the same using coloring of the excited molecules. For clarity, the spatial arrangement of transition dipole moment vectors is also shown (C).

Visualization of excitons

When exciting an aggregate by a short light pulse, many exciton states with their individual transition energies within the spectral width of the pulse will be populated simultaneously and these states will thereupon evolve in time. Thus, for visualization of the exciton dynamics we need to plot the probability of the pigment occupancy not only in space, but also in time. The evolution of the excited states is described by the time-dependent total wave function 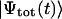satisfying the time-dependent Schrödinger equation,

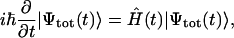(14)

where the time-dependent Hamiltonian includes in its general case the Hamiltonian of the system (Eq. 8), the system-bath interaction 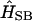, the Hamiltonian describing the bath 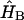, and the interaction of the system with the electrical field 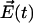given in the semiclassical approximation as

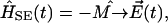(15)

where 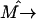is the transition dipole operator of the whole system. For the Frenkel excitons considered here, we neglect system-bath interaction, and the total wave function can be expressed over the basis set of the stationary exciton wave functions as

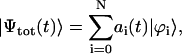(16)

where 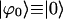is the ground state exciton wave function. The probability for the molecule labeled by index j to be excited (compare with Eq. 12) now is

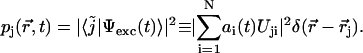(17)

After some algebraic manipulation, this expression gets the more compact and clearer form of

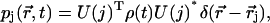(18)

where the asterisk (^*) denotes the complex conjugate, and 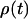is the density matrix of the system,

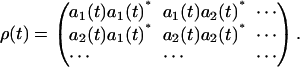(19)

According to Eq. 13 the time-dependent distribution of the probability of excitation (an exciton-snapshot) will be given as

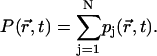(20)

For describing the time evolution of the density operator for the real system interacting with a bath, the Liouville equation should be applied (Blum, 1981; Prokhorenko and Holzwarth, 2000b). However, in the absence of the system-bath interaction, the time-dependent Schrödinger equation (Eq. 14) with Hamiltonian 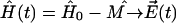can be solved directly,

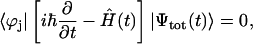(21)

thus allowing us to visualize the movement of the Frenkel excitons. The dipole moment operator, which describes the stimulated transitions, can be expressed in the excitonic picture in terms of the exciton wave functions and the transition dipole moment vectors of interacting molecules as (see, for example, Prokhorenko and Holzwarth, 2000b)

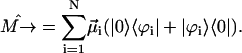(22)

Inserting this into Eq. 21 produces the system of N + 1 linear differential equations for the time-dependent coefficients a(t) as

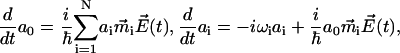(23)

where 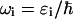is the frequency of the excitonic transition, and 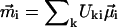is the corresponding transition dipole moment. This system can be easily solved at the initial conditions 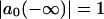, 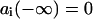(i.e., the nonexcited system in the ground state). For weak excitation (population of ground state close to 1) the amplitudes will not be coupled, and in the impulsive limit (the excitation pulse is assumed to be much shorter as compared to the characteristic beat frequencies between the exciton states), the solution simplifies to

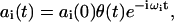(24)

where 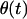is the Heavyside step function. The amplitude factor 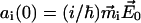depends on the spectral overlap of the excitation pulse with the particular excitonic transition, and the orientation of the transition dipole moment vector relative to the electrical field polarization.

RESULTS AND DISCUSSION

Analysis for Cf. aurantiacus chlorosomes

The arrangement of monomers in the stacks and the orientation of their transition dipole moments is illustrated in Fig. 2 a. All structural parameters for the BChl c aggregates, as determined from molecular modeling, are listed in Table 1. (The structural arrangement of BChls was improved as compared to previous work—Prokhorenko et al., 2000b—by averaging and symmetrizing of the molecular modeling data.) Fig. 3 shows the absorption, CD-, and LD-spectra for the Cf. aurantiacus rod aggregate and stack lengths of 10, 20, and 40 BChl c molecules per stack, calculated for a nondisordered system. As can be seen, at the aggregate length of ∼30 molecules the CD-spectrum radically changes its shape from a type-II to the so-called mixed-type. Further length increase does not affect the CD-shape, and for very large aggregates with length comparable to those in native chlorosomes (∼100 nm, corresponding to ∼150 BChl/stack) the CD-shape always corresponds to the mixed-type. Even taking into account disorder (for disorder parameters, see Table 1) the behavior of the CD-spectra is still the same, as can be seen in Fig. 4. Here the results of excitonic calculations for an aggregate with diagonal, off-diagonal, and both types of disorders are presented (stack length 40 BChls). For qualitative comparison, the measured spectra published in Griebenow et al. (1991), are also plotted. We see that the shape of the calculated CD-spectrum agrees well with the experimentally observed one. The ratio between maximal amplitudes of the CD- and absorption-spectra is CD(738)/Abs(747) = 2.1 · 10⁻³ (right panel on Fig. 4), and close to the experimentally observed. However, as it was mentioned in Griebenow et al. (1991), this ratio varies by a factor of ∼20 depending on sample preparation. The main deviation between the calculated and the measured absorption, CD- and LD-spectra shapes occurs in the blue spectral region, since we did not include any electron-phonon interaction which is very pronounced at room temperature. This is important especially for the LD-spectra, since the contribution of intense phonon wings from the low-lying transitions can be much higher than the contribution of the transitions (with negative sign), located on the blue edge of the spectrum, which are strongly broadened due to the ultrafast downhill energy transfer. However, presented numerical modeling shows that the LD-spectrum is substantially narrower than the absorption spectrum.

FIGURE 2.

Schematic presentation of the structures of aggregates from the Cf. aurantiacus (top) and Cb. tepidum chlorosomes (bottom), used in this work. Small arrows show the directions of the transition dipole moment vectors. For parameters, see Tables 1 and 2.

FIGURE 4.

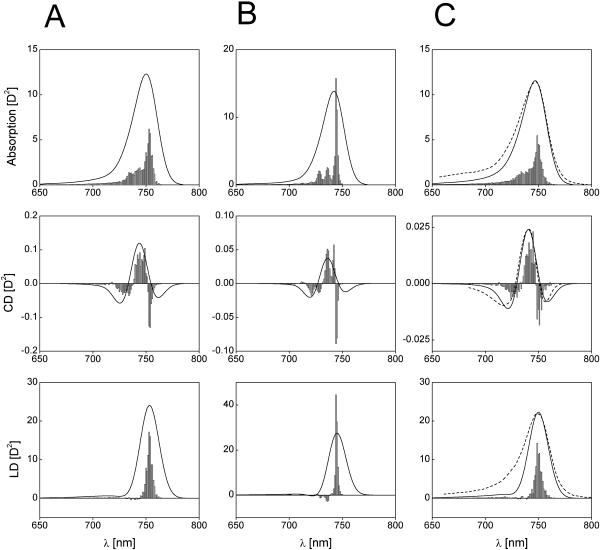
Calculated absorption-, CD-, and LD-spectra of aggregates consisting of 40 molecules per stack with diagonal disorder (A), off-diagonal disorder (B), and in the presence of both disorders (C) (an ensemble of 50 aggregates was calculated for the disorder-spectra). The stick-spectra are convoluted with a normalized Gaussian profile of FWHM = 350 cm⁻¹. Amplitude factor for the stick-components is 10⁻². For the disorder parameters, see Table 1. Dotted lines are measured spectra from Griebenow et al. (1991). For better comparison, their amplitudes are normalized to the calculated spectra, and are shifted by 7.5 nm to the red.

Let us now consider the dichroic ratio, defined as the ratio between the LD- and the isotropic absorption-spectrum, 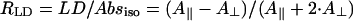(note that we consider here only the dichroic ratio at the maximum of the absorption band). This ratio depends substantially on the type and degree of disorder, and from degree of inhomogeneous broadening. For numerical calculations, we have chosen the FWHM of inhomogeneous broadening of 350 cm⁻¹ that is typical for the bacteriochlorophylls (and chlorophylls) in ether. By including only the diagonal disorder (Fig. 4 a), we get R_LD = 2.77; for an off-diagonally disordered ensemble, we get R_LD = 2.9 (Fig. 4 b), and for an ensemble of aggregates having both types of disorder (Fig. 4 c), R_LD = 2.6. Including the inhomogeneous broadening leads to further reduction of these ratios to 1.95, 2.0, and 1.93, respectively. The R_LD slightly depends on the aggregate length. For aggregates with a stack length of 30 molecules it is ∼1.87, whereas for longer aggregates (50 molecules/stack) the dichroic ratio reaches 2. Thus, diagonal disorder leads mainly to reduction of the dichroic ratio. From the exciton theory of circular aggregates, developed for nondisordered systems (Didraga et al., 2002), it follows that, for reasons of symmetry, the transition dipole vectors for all nonforbidden transitions are either directed along the z-axis or the perpendicular plane (this applies for aggregates without periodical shift between stacks). In the aggregates with finite lengths considered here, due to the stack shift, some dipole vectors of allowed exciton transitions are also oriented in other directions even for nondisordered aggregates, but their contribution to the overall absorbance is small. Thus, for the stick-components in the LD/absorption having the highest intensity, the dichroic ratio approaches 3 for long rods, entirely independent of the orientation of the transition dipole moment vectors of the monomer transition (see expressions 40, 41 in Didraga et al., 2002). Upon inclusion of disorder, many transition dipole moments will be disoriented from the z-axis direction, and dichroic ratio thus will be reduced significantly.

Calculated dichroic ratio cannot be directly compared with experimental values since the so-called compression factor n is usually close to 1 (in contrast to the calculated LD-spectra where n → ∞, i.e., aggregates are highly oriented). However, the equation for the experimentally measured dichroic ratio can be derived using the well-known expressions of Ganago et al. (1980) for rigid rod-shaped macromolecules (note that, in the original work, the expressions are obtained for the polarization ratio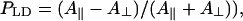

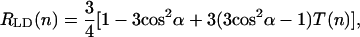(25)

where the orientation factor T(n) is defined by formula 17 in Ganago et al. (1980), and α is an angle between the transition dipole moment of the macromolecule and its symmetry axis. For infinitely high compression (i.e., a perfectly oriented sample) the orientation factor T(∞)→1, and Eq. 25 simplifies to

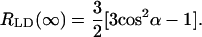(26)

As can be seen, for α = 0 (major transition stick-component in the absorption and LD-spectra of un-disordered aggregate) this ratio equals 3. The measured dichroic ratio depends strongly on the orientation factor. However, if the experimental conditions are known (n and R_LD(n)), the dichroic ratio for n→∞ can be also obtained and compared with that calculated using Eq. 25. For example, the measured R_LD = 0.75 published in Griebenow et al. (1991) with a compression factor of n = 1.56 gives, from the solution of Eq. 25, α = 15.5°. Using this angle as a parameter, for n→∞ (Eq. 26) we obtain R_LD(∞) = 2.68. The experimental data from Frese et al. (1997) (n = 1.19² ≡ 1.416, R_LD = 0.459, see Fig. 3 therein) delivers angle α = 26.5°, and for n→∞ we have R_LD(∞) = 2.1 which agrees with the calculated one for the case of both types of disorder and inhomogeneous broadening. Such deviation between these two experiments is mainly due to difference in width of Q_y-band in the linear dichroism spectra as compared to corresponding absorption spectra.

In numerous articles devoted to investigations of chlorosomes, the angle α which can be obtained from Eq. 25, has been interpreted to directly yield the angle between the direction of the monomer transition dipole moment and the rod axis of the chlorosome (see, for example, Griebenow et al., 1991; van Amerongen et al., 1988). We note, however, that this angle does not carry any direct information about the orientation of the transition dipole moment vector of the monomer or exciton state(s). Due to symmetry properties of rod-aggregates, for the main stick-components in the LD/absorption the dichroic ratio is always close to 3, independent of the monomer transition orientation. As it was mentioned above, due to disorder, homogeneous and inhomogeneous broadening of the excitonic transitions, in an ensemble of aggregates this ratio (taking at the maximum of absorption) will be reduced substantially. Thus the angle, obtained from Eq. 25 using the measured dichroic ratio and known compression factor, directly reflects more the inhomogeneity of the aggregates rather than the orientation angle. For example, the width of the Q_y-absorption band in Frese et al. (1997) is ∼35 nm and the corresponding dichroic ratio of R_LD(∞) = 2.1, whereas in Griebenow et al. (1991) the Q_y-band is substantially narrower (∼31 nm); and from the experimental data we find a higher value for the dichroic ratio of R_LD(∞) = 2.68. Our model calculations give clear evidence that the reduction of the dichroic ratio depends strongly on the degree of disorder.

The size effect on CD-spectra

Model calculations, performed for aggregates with different structures and for different lengths, show that the key structural parameter causing this peculiar behavior of the CD-spectra is the orientation of the transition dipole moment of the monomers with respect to the symmetry axis of the rod (z-axis). In our optimized structure 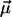deviates from the z-axis by an angle of α = 36.5° for Cf. aurantiacus chlorosomes (see Table 1). The pronounced length dependence of the CD-shape provides evidence that besides a microscopic chirality caused by the excitonic interaction of neighboring pigments, in the long rod aggregates a macroscopic chirality is also present. The appearance of such macroscopic chirality can be viewed by a plot of the CDM-matrix which describes the CD-spectrum (Eq. 10.2). Fig. 5 shows the CDM-matrices (note that the exact appearance of the matrix depends on how the pigments are numbered; in our calculation a sequential indexation is used—i.e., index i = s + n_st · p, where s is the number of the molecule in stack p, and n_st is the total number of stacks) for different aggregate lengths, starting from 1 pigment per stack (1 ring) up to 30 pigments per stack, and their diagonal cross-sections. For a single ring only chirality caused by interaction of the neighboring pigments appears as a low modulation of the CMD. The contribution of the macrochirality appears as a high-frequency modulation of the basic ring modulation whose relative amplitude grows when increasing the aggregate length. For a stack length of ≥30 pigments the amplitude of this modulation is comparable to the contribution of the microchirality to the CD, and consequently the CD-shape changes drastically. From the structure of the CDM-matrix it becomes clear why inclusion of disorder does not change the length dependence of the CD-spectra. Since the CDM-matrix depends only on the structural arrangement (see Eq. 10.2), diagonal disorder cannot affect its properties and the ratio between the amplitudes corresponding to the microscopic one and the macroscopic CD contributions remains the same, independent of the inclusion of diagonal disorder. For off-diagonally disordered systems both these contributions represent a kind of noise-contribution (Fig. 5 d), but their ratio does not change. The deeper physical origin of this macroscopic chirality can be understood if we look at the occupancy distribution of molecules in an aggregate. Using Eqs. 12 and 13, we can calculate and visualize this distribution, e.g., in the lowest exciton state. Fig. 3 (bottom) shows these “frozen” excitons for the tubular aggregates discussed above. We call this a frozen-exciton because the lowest exciton state is a terminal state to which all excitation relaxes (at least at low temperatures). In this case the excited molecules form a helical occupation pattern in a rod, extending along a direction matching exactly the projection of the dipole moment vector of the monomers on the z-axis. The switching point for the CD-shape, i.e., the length of the aggregate corresponding to equal contributions of the micro- and macroscopic chirality, occurs when the occupation pattern makes a full turn over the rod aggregate. A simple relationship following from geometrical considerations yields this condition,

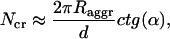(27)

where R_aggr is the radius of the aggregate, d is the distance between molecules along the stack, and N_cr is the number of molecules in a stack. As can be seen, for the aggregates from Cf. aurantiacus chlorosomes, the CD-spectrum changes its shape if the stack length is ∼30 pigments (see Table 1 for parameters). This size effect of the CD-spectra can, in particular, give an explanation for the results published in Ma et al. (1996), where different CD-spectral shapes were observed for Cf. aurantiacus chlorosomes isolated from cells grown under low and high light intensities. From our analysis it follows that at low growth intensities the aggregates in chlorosomes are presumably shorter or alternatively are broken up into small pieces, and the CD-shape would then correspond to type-II, whereas for chlorosomes grown at high light intensity the aggregates have a large length, and the CD-shape changes from type-II to the mixed-type.

FIGURE 5.

Plot of the CDM-matrices (top) and their diagonal cross-sections (bottom) for the aggregate lengths of 1 (A), 10 (B), and 30 (C) molecules. (D) CDM-matrix for off-diagonal disordered aggregate with 30 molecules per stack. Amplitudes are normalized to the dipole strength of BChl c molecule.

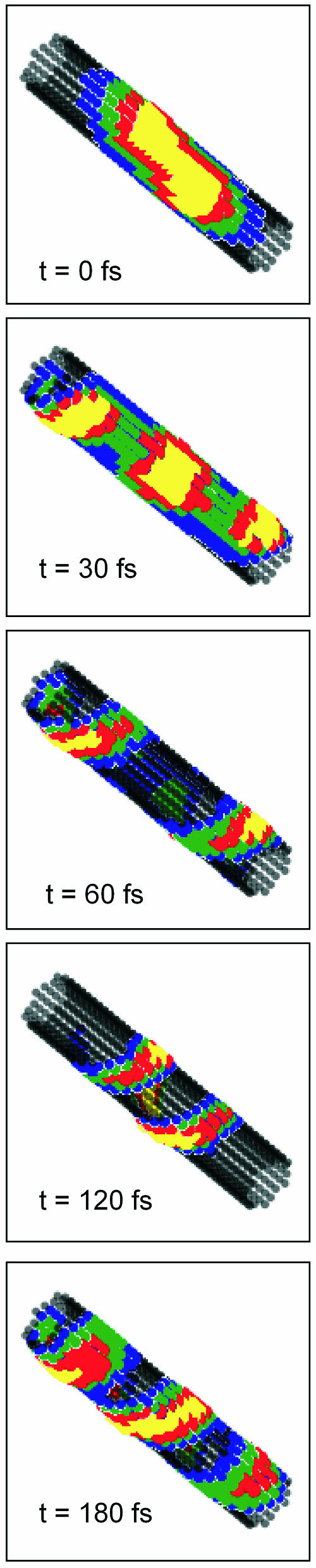
For more sophisticated considerations we should take into account all exciton states and also consider the dynamics of the excitons (we consider here only Frenkel excitons, for the sake of simplicity). This can be done by performing the exciton dynamics calculations using Eqs. 13, 18, 19, and 24. Fig. 6 shows the time-resolved images of the exciton movement, i.e., snapshots of the excitation pattern distributions of occupied pigments for different times starting from zero time after initial excitation with a very short light pulse, centered at ∼740 nm (i.e., close to the maximum of the absorption band). Since the amplitudes of the involved exciton states depend on the relative orientation of the corresponding transition dipole moment vectors and the electrical field vector (Eq. 24), for performing the calculations we assumed a depolarized excitation field. We see that after impulsive excitation the excitons move through the aggregate along helical trajectories, which reflects the macroscopic chirality (helicity) in the system. From these snapshots the degree of excitation delocalization, corresponding to the average number of excited molecules, can be also estimated. It is ∼40–50 for sufficiently long aggregates (>30 molecules/stack; note that this value depends on the aggregate length). For small aggregates having the length of 10 pigments/stack, as can be seen from Fig. 3, this number can estimated to be ∼20.

FIGURE 6.

Snapshots of the Frenkel exciton dynamics in aggregates from the Cf. aurantiacus chlorosomes. Corresponding elapsed time is indicated (see footnote on Supplementary Material). Excitation is assumed at 750 nm with a pulse duration of 20-fs FWHM.

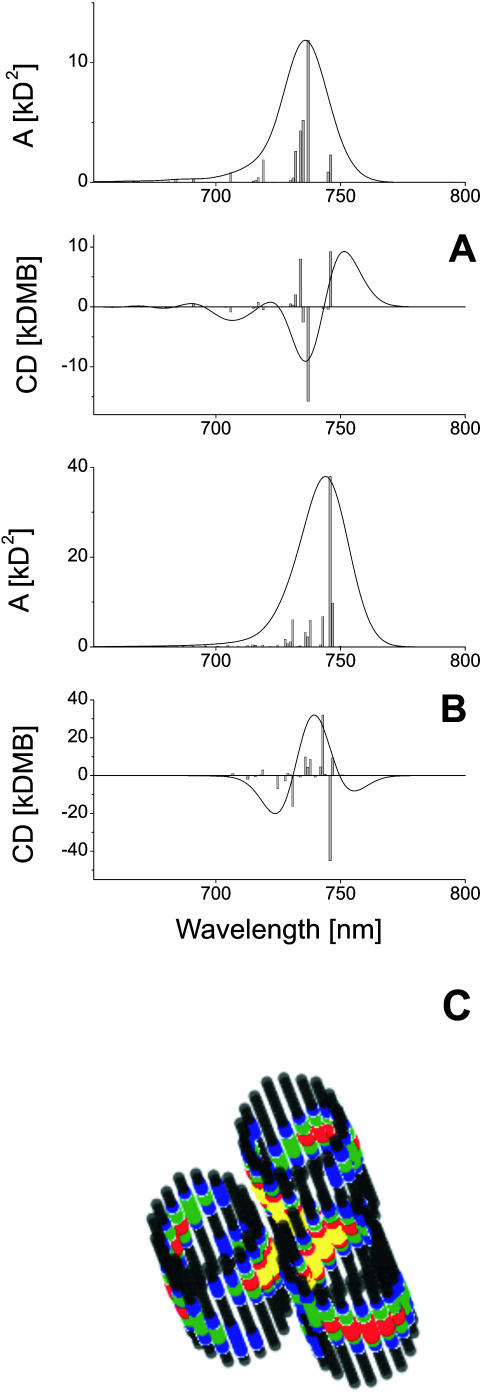
Influence of the rod-to-rod interaction in chlorosomes

In our previous work (Prokhorenko et al., 2000a) it was shown that the interaction between different rod aggregates in the chlorosomes plays an important role and should also be taken into account for modeling the optical properties of entire chlorosomes. The hexagonal packing of the rod aggregates in chlorosomes leads to a pronounced splitting of the first exciton band, and the spectra are changed substantially as compared to these of single rod aggregates. Thus we need to examine the length dependence of the CD-shape, for example, for the elementary unit of a chlorosome containing three hexagonally packed rods as discussed above. Fig. 7 shows the calculated steady-state spectra for an elementary unit containing rod aggregates with lengths of 20 (A) and 50 (B) monomers per stack, respectively. The center-to-center distance of rods is assumed to be 6 nm, in accordance with the electron microscopy data (Staehelin et al., 1978). It should be pointed out that, due to the excitonic interaction between the rods in chlorosomes, the CD-spectrum changes its shape if the rod length reaches ∼45 pigments. The excitonic interaction between rod-aggregates leads also to a redistribution of the excitation between rods. This can be seen from the frozen-exciton pictures, as calculated for the elementary unit (Fig. 7, bottom). We see that now the excitation is redistributed over many smaller spots, extending over different rods. These spots are oriented face-to-face in the unit cell of these rods. This coupling has interesting functional consequences. Note that introducing a small perturbation in the structure of the chlorosome like, for example, attaching the so-called base-plate which collects the excitation energy, can influences the exciton distribution significantly. Thus one can imagine that the proper placement of pigments of the base plate next to a chlorosome rod can substantially influence the exciton structure in the rods and can drain energy into the base plate as is required for its functioning in an efficient system. Investigating these effects in more detail by theoretical calculations will be an interesting future extension of this work.

FIGURE 7.

Calculated absorption and CD-spectra for an elementary unit of Cf. aurantiacus chlorosomes (three hexagonally packed rod aggregates) with stack length of 20 (A) and 50 (B) molecules. The stick-spectra are convoluted with a normalized Gaussian profile of FWHM = 350 cm⁻¹. Amplitude factor for the stick-components is 10⁻³. (C) Frozen-excitons in an elementary unit corresponding to A.

Summarizing this section, we conclude that the experimentally well-documented and, for a long time, highly puzzling drastic changes observed in the shape of the CD-spectra of otherwise seemingly identical chlorosomes, can now be understood straightforwardly from the theoretical side. It is particularly gratifying that it does not depend on any change in the interaction between rod aggregates in the chlorosome, nor on any other structural change in the relative arrangement of BChl monomers in the aggregates. Rather, it is controlled only by the effective length of the excitonically strongly coupled rods. Apparently green bacteria have a means to control this effective rod length (most likely indicated by the above-mentioned striations in the chlorosome rods), which thus can be significantly shorter than the physical rod length as given by the length of the entire chlorosome.

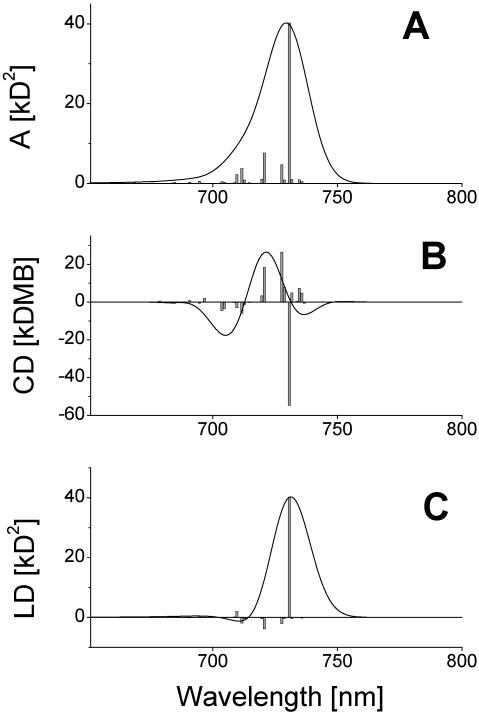
Cb. tepidum chlorosomes

In previous work, we proposed and analyzed a model for the type of chlorosome whose rod aggregates have an ∼10-nm diameter, simply by using the same stack geometry and the same dipole moment orientation as used for the Cf. aurantiacus chlorosomes (Prokhorenko et al., 2000a). The number of stacks was increased up to 36 to fit the rod diameter to that experimentally observed in electron microscopy for Cb. tepidum chlorosomes (Staehelin et al., 1980). However, recent studies of the supramolecular organization of Cb. tepidum chlorosomes using 3-D-MAS dipolar-correlation NMR spectroscopy (van Rossum et al., 2001) have considerably enhanced our structural knowledge about this type of chlorosome. These data show that the aggregate rods in Cb. tepidum chlorosomes are actually bilayered, i.e., they consist of double tubes. The two different tubes have different structures. When self-assembling BChl c/d molecules, several different aggregate structures can be realized, depending upon which diastereoisomers are involved in the aggregation (for example, all chlorosomes contain 3¹R- and 3¹S-BChls in different ratios; Olson, 1998). Using the same molecular mechanical and semiempirical quantum mechanical calculations, and including the NMR structure data, a detailed analysis of the supramolecular architecture of small BChl c aggregates was performed recently (D. B. Steensgaard, T. S. Balaban, K. Schaffner, and A. R. Holzwarth, unpublished data). Based on these results, the detailed structure of the double-tube model as suggested from the NMR data for the Cb. tepidum chlorosomes was developed. The relative arrangement of monomers in these double-tube aggregates differs significantly from the aggregates of Cf. aurantiacus chlorosomes due to the different size of rod elements and the different BChl side chains. This is schematically shown in Fig. 1 b. The corresponding structural parameters are listed in detail in Table 2. The inner tube consists of 20 stacks with the so-called syn- (3¹S) orientation of the axial ligation to the central magnesium atom relative to the farnesyl tails. The outer tube has 30 stacks with a anti- (3¹R) structure arrangement. (As anti-, we define here an isomer of a BChl c molecule in which the binding of the fifth ligand to magnesium is placed on the opposite side of the chlorin plane as compared to the farnesyl tail, and as syn-, the opposite ligation direction; for details, see D. B. Steensgaard, T. S. Balaban, K. Schaffner, and A. R. Holzwarth, unpublished results). As a consequence the farnesyl groups in the inner tube are directed toward the inside of the micelle, whereas in the outer tube they are directed to the outside, i.e., the same direction as for the single tubes of Cf. aurantiacus chlorosomes (van Rossum et al., 2001). Note, however, that for such an arrangement the density of BChls is just the same as for Cf. aurantiacus chlorosomes (0.5 monomer/nm³ vs. 0.52 monomer/nm³). Each stack in the inner tube is shifted along the z-axis with respect to its neighbors by one-quarter of the distance between monomers within a stack, whereas in the outer tube this shift is one-fifth. This difference in the stack shift originates from the difference in aggregation of syn- and anti- structures caused by the spatial properties of the stacked molecules, especially the different interactions of their 20-methyl groups and the 7, 8, and 12 side groups. As can be seen from Table 2, the difference in the self-assembly of these two different forms does not significantly affect the orientation of the transition dipole moments of the monomers with respect to the z-axis. However, in comparing the structural parameters given in Tables 1 and 2, one notes the remarkable difference in deviation of the transition dipole moments from the radius-vector of the rods for Cf. aurantiacus and Cb. tepidum chlorosomes. Nevertheless, this difference is of little effect for their exciton-spectra as indicated by the model calculations. The CD-spectrum changes its shape from type-II to the mixed-type at a stack length of 32 molecules for the inner tube and at 50 molecules for the outer tube (not shown) when calculated separately, which is in agreement with the estimated values using Eq. 27. Thus, we can expect that for the actual double-tube aggregate this switching point will be somewhere between these numbers. Numerical calculations indeed show that CD switching occurs for stacks having ∼40 molecules' length. Fig. 8 displays the absorption-, CD-, and LD-spectra of the double-tube aggregate (our current computing capabilities do not allow us to calculate the spectra for a unit cell consisting of double-tube aggregates with a stack length >∼20 pigments) for a stack length of 45 molecules. We see that the CD-spectrum corresponds already to the mixed-type. Further increasing the aggregate length does not change the CD-shape; only the local minimum at the red part of the spectrum will be more pronounced. It should be pointed out that the spectra for single-tube aggregates (from the Cf. aurantiacus chlorosomes, see Fig. 3) and for the double-tube aggregates considered here are very similar. This allows us to conclude that the presence of the inner tube in a rod of the Cb. tepidum chlorosomes does not interfere much with the exciton structure of the outer tube. For this reason also, steady-state optical spectroscopy is of little help in distinguishing between single- and double-tube structures.

FIGURE 8.

Absorption- (A), CD- (B), and LD- (C) spectra of double-tube aggregate from the Cb. tepidum chlorosomes. Both tubes have 45 molecules per stack. The stick-spectra are convoluted with a normalized Gaussian profile of FWHM = 350 cm⁻¹. Amplitude factor for the stick-components is 10⁻³.

CONCLUSIONS

We have calculated the spectra of the rod aggregates of Cf. aurantiacus and Cb. tepidum chlorosomes. For the Cf. aurantiacus aggregates we used a structural model, described previously (Holzwarth and Schaffner, 1994; Prokhorenko et al., 2000a), whereas for the Cb. tepidum rods we based our modeling on the new double-tube aggregate structure, taking into account the recent NMR structure data (van Rossum et al., 2001). Since the CD-spectrum reflects directly the excitonic properties of the supramolecular structures, we focused our attention on analysis of these CD features for aggregates having a finite length. Using the Frenkel exciton approach we can easily explain the size effect in the CD-spectra of these tubular aggregates. The origin of this effect is explained by two contributions to the CD: 1), the microscopic chirality caused by excitonic interaction of neighboring molecules; and 2), a macroscopic chirality appearing due to the specific distribution of the occupied excited pigments in the whole aggregate rod. The latter contribution grows with increasing the aggregate length, whereas the microscopic chirality remains constant and is independent of the size. For the long single rods and for the supramolecular rod units of chlorosomes with lengths approaching those in vivo, the shape of the CD-spectra thus corresponds to mixed-type.

The macroscopic chirality can be visualized nicely for each exciton state (compare to Fig. 3). Moreover, the calculations show that the excitation energy transport occurs along helical trajectories, which reflects the presence of the macroscopic chirality in the tubular aggregates. In this work we analyze only Frenkel excitons without taking into account their damping due to interactions with the surrounding bath. Nevertheless, we note here that the equations derived for the space- and time-resolved probability of pigment occupation (Eq. 19), expressed by the density matrix, allow straightforward incorporation of the damping rates for the exciton states—and thus the calculation of the actual dynamics of the excitons, which will be the subject of future work. The visualization technique for the excitons as implemented here can also be applied for the investigation of the energy transfer pathways in other photosynthetic antennae.

SUPPLEMENTARY MATERIAL

For supplemental material, please contact the author at prokh@nat.vu.nl or visit websites http://www.nat.vu.nl/∼prokh/movies.html, or http://www.mpi-muelheim.mpg.de/strneu/staff/holzwarth/BiophysJ_Supl/. This material includes movies showing the dynamics of the Frenkel exciton movement in rod aggregate, and also for unit cell of Cf. aurantiacus chlorosomes. These movies give a better picture of the exciton dynamics than could be provided here in the article, where only snapshots at certain times are given.