Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Nov;85(5):3187–3193. doi: 10.1016/S0006-3495(03)74736-5

Role of Backbone Hydration and Salt-Bridge Formation in Stability of α-Helix in Solution

Tuhin Ghosh *,†, Shekhar Garde †, Angel E García *
PMCID: PMC1303594  PMID: 14581218

Abstract

We test molecular level hypotheses for the high thermal stability of α-helical conformations of alanine-based peptides by performing detailed atomistic simulations of a 20-amino-acid peptide with explicit treatment of water. To assess the contribution of large side chains to α-helix stability through backbone desolvation and salt-bridge formation, we simulate the alanine-rich peptide, Ac-YAEAAKAAEAAKAAEAAKAF-Nme, referred to as the EK peptide, that has three pairs of “i, i + 3” glutamic acid(−) and lysine(+) substitutions. Efficient configurational sampling of the EK peptide over a wide temperature range enabled by the replica exchange molecular dynamics technique allows characterization of the stability of α-helix with respect to heat-induced unfolding. We find that near ambient temperatures, the EK peptide predominately samples α-helical configurations with 80% fractional helicity at 300 K. The helix melts over a broad range of temperatures with melting temperature, Tm, equal to 350 K, that is significantly higher than the Tm of a 21-residue polyalanine peptide, A21. Salt-bridges between oppositely charged Glu− and Lys+ side chains can, in principle, provide thermal stability to α-helical conformers. For the specific EK peptide sequence, we observe infrequent formation of Glu-Lys salt-bridges (with ∼10–20% probability) and therefore we conclude that salt-bridge formation does not contribute significantly to the EK peptide's helical stability. However, lysine side chains are found to shield specific “i, i + 4” backbone hydrogen bonds from water, indicating that large side-chain substituents can play an important role in stabilizing α-helical configurations of short peptides in aqueous solution through mediation of water access to backbone hydrogen bonds. These observations have implications on molecular engineering of peptides and biomolecules in the design of their thermostable variants where the shielding mechanism can act in concert with other factors such as salt-bridge formation, thereby increasing thermal stability considerably.

INTRODUCTION

The structure, stability, and function of biomolecules and biomolecular aggregates in aqueous media are governed by the properties of the solvent, namely water-water and solute-water interactions. Solvent-mediated interactions drive and stabilize biophysical assembly in solution. Understanding the role of water, therefore, has implications in a range of applications from engineering of the native state of biomacromolecules (Neidigh et al., 2002; Ventura et al., 2002) to the design of novel functional biomaterials (Ghirlanda et al., 2002; Nowak et al., 2002; Petka et al., 1998). The mesoscopic length- and time-scales characterizing self-assembly of macromolecules and aggregates, however, pose challenges for detailed molecular investigations. Therefore, for proteins, one effective approach involves the investigation of folding and stability of secondary structural elements such as the α-helix. Insights into thermodynamics and kinetics of these relatively smaller structural motifs can then be integrated to construct macroscopic mechanisms for globular proteins.

Numerous studies in the past have focused on thermal stability of α-helices (Scholtz and Baldwin, 1992) and helix nucleation/unfolding kinetics (Huang et al., 2002; Hummer et al., 2000, 2001; Williams et al., 1996). Extensive studies of de novo designed peptides by Baldwin and co-workers (Marqusee and Baldwin, 1987; Marqusee et al., 1989; Scholtz and Baldwin, 1992) have shown that isolated alanine-based peptides (∼16–17 residues long) with charged residues (Lys, Glu, or Arg) added for solubilization can form stable α-helices in aqueous solution. However, physical mechanisms underlying the high thermal stability of helices of alanine-based peptides are not entirely clear.

Thermal stability of isolated alanine-based helices in water has often been attributed to the intrinsic “high helix-forming potential” of alanine (Chakrabartty et al., 1994; Marqusee et al., 1989; Spek et al., 1999). The helical propensities of individual residues are often assigned by introducing natural amino acids as guests into a host matrix (Ingwall et al., 1968), or by fitting statistical-mechanical models of helix-coil transition, such as the Zimm-Bragg (Zimm and Bragg, 1959) or the Lifson-Roig model (Lifson and Roig, 1961), to the observed temperature dependence of helical content. Such an interpretation, however, does not incorporate the sequence context or the effect of tertiary interactions on the helix-forming tendency of a specific residue (Doig et al., 1994; Miller et al., 2002).

Other studies have postulated the stabilization of helical structure in alanine-based peptides resulting from interactions of charged side chains (such as Lys, Glu, or Arg) through formation of salt-bridges (Marqusee and Baldwin, 1987; Mayne et al., 1998), interactions of charged residues with the helix dipole (Huyghues-Despointes et al., 1993; Lockhart and Kim, 1993; Shoemaker et al., 1985), or the favorable free energy gained by hydration of charged residues (Vila et al., 1992; Williams et al., 1998). More recently, Vila et al. (2000) suggested that the high thermal stability of helices of alanine-based peptides containing large charged side-chain substituents results from the shielding of the hydrogen-bonding backbone amide (−N–H) and carbonyl (−C=O) groups from solvent water molecules by the side chains.

Evaluation of such inherently molecular mechanisms postulated to explain helical stability of peptides is difficult due to the lack of detailed experimental data at the molecular-level. On the other hand, trajectories from all-atom molecular dynamics (MD) simulations can shed light on relative contributions of intrinsic vis-a-vis context-dependent helix-stabilizing factors. Indeed, constant temperature MD simulation studies of short (5–7 AA) peptides have provided insights into helix formation and melting kinetics (Daura et al., 1999; Hummer et al., 2000, 2001). However, for longer peptides, the free energy landscape can become much more complex, with large barriers between different minima posing methodological difficulties for Boltzmann sampling of conformations. Free energy barriers between folded and unfolded conformations of a 16-residue β-hairpin-forming peptide were estimated to be 7–8 kBT at 300 K (García and Sanbonmatsu, 2001). As a result, a single constant temperature MD simulation trajectory frequently gets trapped in one of the local minima leading to biased configurational sampling.

Alanine-based peptides that are 16–20-AA long have been extensively studied experimentally (Marqusee and Baldwin, 1987; Scholtz and Baldwin, 1992). However, molecular simulations of these relatively long peptides in aqueous solution require novel sampling strategies. Simulation techniques developed over the past decade to study systems with rugged free-energy landscapes, e.g., spin-glasses (Marinari and Parisi, 1992), can be used to study 15–20-AA-long peptides in aqueous solution. For example, the replica-exchange molecular dynamics (REMD) technique formalized by Sugita and Okamoto (1999) employs MD simulations of several tens of noninteracting replicas performed over a wide range of temperatures with Metropolis Monte Carlo moves used to exchange temperatures of neighboring replicas. In addition to achieving broad and efficient sampling of configurational space, REMD allows characterization of thermodynamic quantities as a function of temperature.

REMD simulations were employed recently to study the helix-coil transitions of alanine-based peptides as a function of temperature (García and Sanbonmatsu, 2002). The two peptides studied were a pure alanine sequence (A21) and a peptide with three arginine substitutions (Fs or folded short peptide; Lockhart and Kim, 1993). The Fs peptide was shown to have significantly higher helical content than A21 at all temperatures, indicating a nontrivial helix-stabilizing role for the arginine side chains. Here we employ an identical simulation method to study an alanine-based peptide with substitutions by lysine and glutamic acid residues that can potentially form salt-bridges. The helical content and stability of this peptide (referred to hereafter as EK peptide) have been characterized in previous experimental investigations (Marqusee and Baldwin, 1987; Scholtz et al., 1995). Extensive REMD simulations of the EK peptide in aqueous solution, amounting to >200 ns of sampling, are used to study the thermodynamics of helix-coil transitions of the peptide and to probe intrinsic and extrinsic factors that stabilize helical configurations. In particular, comparisons of the EK peptide with A21 and Fs peptides (García and Sanbonmatsu, 2002) are used to evaluate contributions from salt-bridges, hydration of charged residues, and the shielding by large side chains toward stabilizing helices in alanine-based peptides.

MATERIALS AND METHODS

REMD simulations of the EK peptide (Ac-YAEAAKAAEAAKAAEAAKAF-NMe, with Ac = CH3CO – and NMe = – NHCH3) solvated in 3392 TIP3P (Jorgensen et al., 1983) water molecules were performed using AMBER 4.1 (Perlman et al., 1995) with suitable modifications to implement REMD with message passing between replicas. Lysine (K) and glutamic acid (E) residues were charged corresponding to neutral pH of the solution. Results from the REMD simulations of Ac-A21-NMe and of the Fs peptide (Ac-A5(AAARA)3-NMe; García and Sanbonmatsu, 2002) are also included here for comparison. The force field by Cornell et al. (1995) with modifications to peptide dihedral potentials (García and Sanbonmatsu, 2002) was used consistently in simulations of all three peptides.

Forty-four replicas of the EK peptide-water system were simulated at constant volume with temperatures spanning the range of 276–526 K. Details of the protocol used to decide the distribution of target temperatures for the replicas are outlined in a recent study (Sanbonmatsu and García, 2002). Initial configurations of the peptide-water system in each replica were obtained from a single simulation at 600 K after volume equilibration at 300 K and 1 atm. A time-step of 1.5 fs was used for MD sampling, and the production run for each replica spanned 5 ns, amounting to a total sampling time of 220 ns. Temperature exchanges between neighboring replicas were attempted every 250 integration steps, leading to an exchange rate of 10–15%.

Periodic boundary conditions were applied and electrostatic interactions were calculated using the generalized reaction field method (Hummer et al., 1994) with a cutoff distance of 8.0 Å. Bonds involving hydrogen atoms were constrained using the SHAKE (Ryckaert et al., 1977) algorithm with a relative geometric tolerance for coordinate resetting of 0.0005 Å. Berendsen's thermostat (Berendsen et al., 1984) was used to maintain constant temperature for each replica with the time constant for heat bath coupling for both the peptide and solvent set at 0.5 ps.

The helical content of the peptide was calculated using the Lifson-Roig model (Lifson and Roig, 1961), i.e., a residue i is marked helical if, and only if, its backbone dihedral angle pair (φi, ψi), as well as its adjacent residue angle pairs (φi–1,ψi–1) and (φi+1,ψi+1), lie in the helical region φ = −65 ± 35° and ψ = −37 ± 30°. Therefore, for the 20-residue EK peptide, the number of residues that can be labeled helical is ≤18. Melting profiles were obtained using the temperature-dependent helical content.

RESULTS AND DISCUSSION

Helix melting profile for A21, EK, and Fs peptides

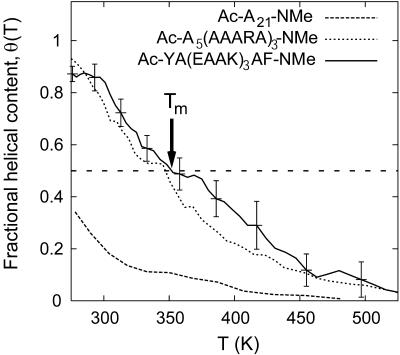
The fractional α-helical content in A21, EK, and Fs peptides is shown in Fig. 1 as a function of temperature of the solution. The helical content is higher near ambient temperatures and a melting transition occurs over a broad range of temperatures for these short peptides. In contrast, thermal melting transition for globular proteins containing a hydrophobic core is much sharper (Privalov, 1982). Nevertheless, the temperature at which the helical content equals 0.5, the so-called melting temperature (Tm), can be taken as a qualitative measure of the thermal stability of a helical peptide. For pure alanine peptide A21, at 276 K, the lowest temperature studied here, the helical content is only ∼40%, thus placing its Tm below 276 K. In contrast, both EK and Fs peptides display 80–90% helical content near ambient temperatures, with the melting temperature ∼350 K for both peptides. Experimental data on A21 are limited by its solubility in water, although results for melting of polyalanine chains flanked by solubilizing charged groups have been reported (Ingwall et al., 1968). The interpretation of helical content from circular dichroism measurements is often complicated by the model dependence of the results (Miller et al., 2002; Spek et al., 1999; Yang et al., 1998). Nevertheless, experimental data on EK (Marqusee and Baldwin, 1987; Scholtz et al., 1995) and Fs (Lockhart and Kim, 1993) peptides clearly indicate significant helical content at room temperature with a broad thermal transition with Tm values approximately equal to 320–340 K.

FIGURE 1.

FIGURE 1

Open in a new tab

Equilibrium fractional α-helical content, θ(T), for EK peptide as a function of temperature obtained from REMD simulations. Data for A21 and Fs (García and Sanbonmatsu, 2002) peptides is also shown for comparison. Arrow shows the helix melting temperature, Tm, for EK peptide.

The melting profiles and Tm values shown in Fig. 1 therefore imply near-equivalent thermal stability of helical configurations of EK and Fs peptides. More importantly, comparison of EK and Fs peptides with A21 highlights the remarkable thermal stability imparted to helical conformations of alanine-based peptides through a small number of simple substitutions of alanines by lysine (K) and glutamic acid (E) residues in EK peptide and by arginine (R) in Fs peptide. Below we investigate the molecular mechanisms that have been proposed to explain the increased thermal stability of helices through such amino-acid substitutions.

Investigation of the role of salt-bridges in the stability of EK peptide helix

Both E and K residues in the EK peptide are charged, leading to the possibility of formation of EK- or KE-type salt-bridges which could thereby stabilize the helical conformers. Indeed, previous experimental studies of alanine-based peptides containing oppositely charged residues have shown that both the locations and the spacing of substituents can influence peptide's helical content and stability (Marqusee and Baldwin, 1987). Since molecularly detailed configurations of the EK peptide are available from REMD simulation, we can monitor distances between atoms of salt-bridge-forming residues. We find that formation of the KE-type salt-bridges involves side-chain conformations with highly unfavorable side-chain torsion potentials. KE-type salt-bridges are therefore not observed throughout the course of the simulation.

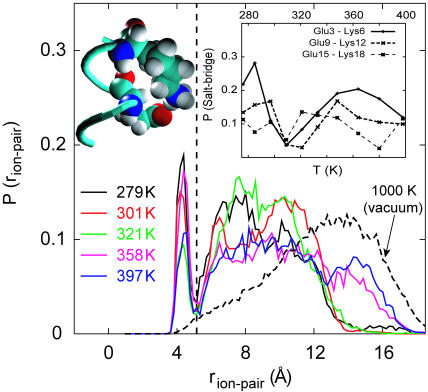
Fig. 2 shows the distribution of distances between the carboxylate carbon and amine nitrogen atoms of E− and K+ pairs averaged over the three pairs Glu3–Lys6, Glu9–Lys12, and Glu15–Lys18 at five different temperatures. At 279 K, the distribution of EK ion-pair separations shows two distinct regions—a well-defined narrow peak centered at ∼4.5 Å that is clearly separated from a region containing a broader sampling of larger separations. The sharply defined peak near 4.5 Å corresponds to contact configurations of EK residues (Fig. 2 b), whereas broader peaks near 7 and 10 Å correspond to one and two water-separated configurations. With increasing temperature, there is no systematic trend in the height of the contact peak at 4.5 Å; however, the population of water-separated conformations broadens further as shown in Fig. 2, indicating sampling of more extended conformations of peptide at higher temperature.

FIGURE 2.

FIGURE 2

Open in a new tab

Distribution of distances between the carboxylate carbon atom on Glu and amine nitrogen atom on Lys, averaged over the three “i, i + 3” (E,K) pairs in the EK peptide. Plots are shown for T = 279 K, 301 K, 321 K, 358 K, and 397 K obtained from REMD simulations and T = 1000 K obtained from an MD simulation of the uncharged peptide in vacuum. Snapshot of a typical Glu9-Lys12 contact/salt-bridge configuration at T = 279 K is also shown. Inset shows the probability of salt-bridge formation as a function of temperature obtained from REMD simulations of the EK peptide plotted separately for each of the three “i, i + 3” (E,K) pairs.

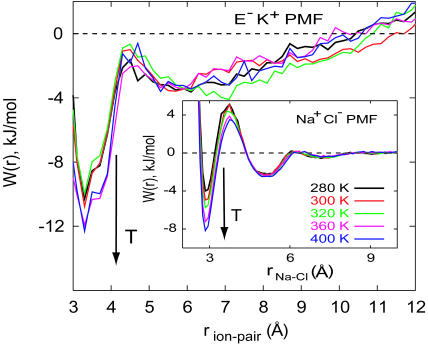
The chain entropy favors more extended configurations with increasing temperature. Sampling of salt-bridge populations shown in Fig. 2 results from different factors including electrostatic and solvation interactions as well as the chain entropy. It is, therefore, difficult to isolate the inherent stabilization, if at all, of salt-bridges with increasing temperature and their effect on helical stability. The probability of sampling a given ion-pair distance in Fig. 2 can be used to calculate the potential of mean force (PMF) for salt-bridge formation. Such a calculation requires normalization volumes for pair distances which were estimated from simulation of an isolated peptide at very high temperature (=1000 K). PMFs calculated in this manner are shown in Fig. 3 along with independent calculations of PMFs of sodium and chloride ions in water. Although the difficulty of calculating PMFs between groups that are covalently attached to a polypeptide backbone are apparent in this figure, especially at long distances, the contact minimum in the PMF appears to become more stable with increasing temperature. The magnitude of changes in PMF at the contact minimum are comparable to those calculated for a sodium chloride pair in water.

FIGURE 3.

FIGURE 3

Open in a new tab

Potential of mean force, 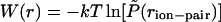Inline graphic, between the carboxylate carbon atom on Glu (E) and amine nitrogen atom on Lys (K), averaged over the three “i, i + 3” (E,K) pairs in the EK peptide at T = 279 K, 301 K, 321 K, 358 K, and 397 K (main panel). The normalized probability of ion-pair distances, 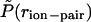Inline graphic, was obtained by dividing P(rion-pair) shown in Fig. 2 by the ion-pair distance distribution for the uncharged peptide in vacuum at T = 1000 K. Inset shows the PMF between Na+ and Cl− ions in dilute aqueous solution, W(rNa–Cl) = –kT ln[g(2)(rNa–Cl)], at temperatures similar to those shown for E,K pairs obtained from independent constant volume MD simulations of a 1 M NaCl solution (10 Na + 10 Cl + 560 TIP3P waters).

The probability of formation of a given salt-bridge in the EK peptide obtained from the area under the contact peak is shown in the inset of Fig. 2 as a function of temperature. At temperatures near 300 K, the probability is low ∼10–20% for all three E−,K+ pairs. Overall, the sampling of contact salt-bridge configurations is found to be relatively insensitive to temperatures up to 400 K. If formation of each salt-bridge is assumed to make an independent favorable contribution to helix stability, then the sum of such contributions again appears relatively insensitive to temperature, adding uniformly to the stability of helices over a broad range of temperatures. Low (∼10–20%) overall probability of individual salt-bridge formation and its relative temperature insensitivity indicate that the increased thermal stability of the EK peptide with respect to A21 peptide cannot be accounted for solely by salt-bridge formation. The thermally stable α-helical Fs peptide, studied recently by García and Sanbonmatsu (2002), has only Arg+ residues as charged substituents. Helicity of the Fs peptide cannot, however, be attributed to salt-bridge formation due to a complete lack of salt-bridges in this peptide. García and Sanbonmatsu attributed the high thermal stability of the Fs peptide helices to the desolvation of the backbone peptide bonds by the Arg+ substituents. A similar mechanism may be at work for the EK peptide as discussed below.

Solvent accessibility of the peptide backbone and shielding by the side chains

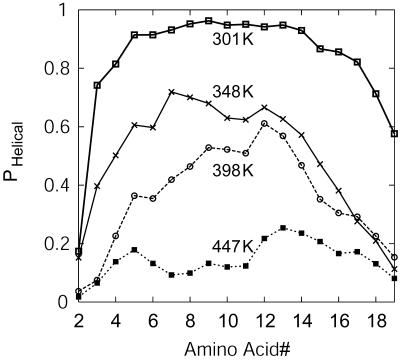
Several factors contribute to the free energy of helix-coil transition, including intrapeptide backbone hydrogen bonds, chain entropy, and solvation by water. A balance of these contributions leads to the observed temperature-dependent melting profile of the EK peptide. Fig. 4 shows the probability of each residue in the EK peptide sampling helical conformations at temperatures of 301, 348, 398, and 447 K. At 300 K, residue helicity (see definition in Methods section) is highest near the center of the peptide and decreases toward the termini. With increasing temperature, helix melts with increasing fraying observed near the ends, especially near the C-terminus. In the perfect helix, the access to solvent water molecules and hydration of −C=O and −N–H groups is only partial. Perturbations from helical state leading to more open structures would be highly unfavorable in vacuum or low dielectric medium. Water can stabilize such perturbations, however, by forming hydrogen bonds with peptide backbone in these open conformations. In light of this and the related shielding hypothesis of Scheraga and co-workers (Vila et al., 2000), the interactions of water with the peptide backbone as a function of temperature will provide insights into the role of water in helix stability.

FIGURE 4.

FIGURE 4

Open in a new tab

Average probability of each residue in the EK peptide sampling helical conformations at T = 301 K, 348 K, 398 K, and 447 K.

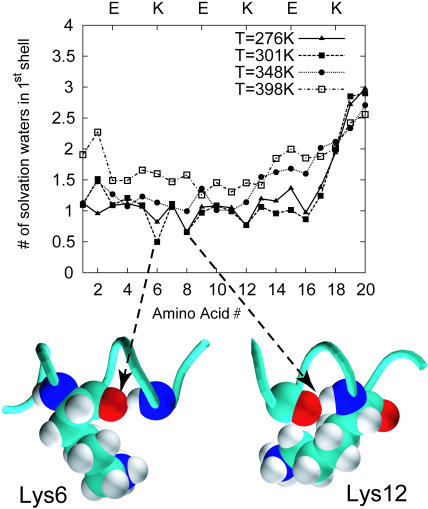
Coordinates of EK peptide and water obtained from REMD trajectories were used to investigate the hydration of backbone −C=O and −N–H groups as a function of temperature. Fig. 5 shows the average number of water oxygens in the first solvation shell (within 3.6 Å) of backbone carbonyl oxygens along the EK peptide. At high temperatures corresponding to well-hydrated unfolded configurations of the peptide backbone, we find an average of two water molecules coordinating each carbonyl oxygen; residues near the frayed C-terminus have even larger numbers of waters of hydration. With decreasing temperature, the average coordination number decreases corresponding to increasing fractional helical content. At 300 K, the EK peptide adopts predominately helical conformations and there is ∼1 water molecule in the solvation shell of the backbone carbonyl oxygens. The key feature in Fig. 5 is that at temperatures near 300 K, the average solvent coordination for three residues—Lys6, Ala8, and Lys12—is significantly lower than 1. A substantially lower solvent accessibility for specific residues was also reported for the Fs peptide, whereas a uniform hydration of the A21 backbone with water coordination number of 1 was seen at low temperatures (García and Sanbonmatsu, 2002). Thus, a distinct shielding of the backbone from water characterizes the hydration pattern of both EK and Fs peptides.

FIGURE 5.

FIGURE 5

Open in a new tab

Average number of water oxygens within the first hydration shell (i.e., within 3.6 Å) for the carbonyl oxygen of each residue in the EK peptide obtained from REMD simulations. Plots are shown for temperatures of 276 K, 301 K, 348 K, 398 K, and 447 K. Representative snapshots of conformations of EK peptide showing the shielding effect of Lys6 and Lys12 at T = 276 K are also shown.

An average water coordination number of 0.5–0.8 observed for Lys6, Ala8, and Lys12 at low temperatures (Fig. 5) implies a substantial population of configurations where the corresponding backbone hydrogen-bond-forming groups (−C=O and −N–H) are completely sequestered from water. As seen in the snapshots at T = 276 K obtained from REMD simulations (Fig. 5), the side chain of Lys6 shields its own carbonyl oxygen in ∼40% of the configurations sampled at 276 K, yielding an average water coordination of 0.6. The shielding is not always a local effect. For example, conformational sampling of the Lys12 side chain (see Fig. 5) leads to partial shielding of its own carbonyl oxygen as well as of the carbonyl oxygen of Ala8 four residues upstream. Snapshots from the REMD trajectories show that the carbonyl oxygen of Lys12 is also intermittently shielded by the glutamic acid residue at position 15, and by parts of the frayed C-terminus.

Our observations indicate that the shielding effect in EK peptide can be attributed to lysine side chains with little or no role for the glutamic acid residues. Lys6 and Lys12 are primarily involved in the shielding effect—the shielding provided by Lys12 is predominately nonlocal whereas that by Lys6 is local. Similar local and nonlocal shielding effects were observed in the arginine-substituted alanine-based Fs peptide (García and Sanbonmatsu, 2002). For the same force field used in REMD simulations, the melting temperature, Tm of both the EK and Fs peptides is significantly higher than that of A21 peptide for which no shielding was observed at low temperatures. This observation indicates the importance of shielding by large side chains in stabilizing helical conformers. Calculations by Scheraga (Vila et al., 2000) attribute the increased thermal stability to the strengthening of the shielded backbone hydrogen bonds in the lower dielectric shielded region. Indeed, we find that more open unfolded or partially unfolded conformations of the peptide that are generally stabilized by solvent water are less frequently sampled in the EK and Fs peptides compared to that in A21, consistent with the higher stability of these peptides.

CONCLUSIONS

The physicochemical interactions underlying thermal stability of helical conformers of short alanine-based peptides in water has been the focus of many investigations over the past several years (Scholtz and Baldwin, 1992). We used the replica-exchange molecular dynamics (REMD) technique to study the thermal stability of helical configurations in a 20-residue long alanine-based peptide with three pairs of charged glutamic acid(−) and lysine(+) substituents. REMD simulations of the peptide (referred to as EK) in explicit water show that the peptide forms stable helical configurations at low temperatures, with nearly 80% helical content at 300 K. The helix melting temperature was found to be ∼350 K, significantly higher than the melting temperature of a 21-residue polyalanine peptide, A21, studied recently using the same force field (García and Sanbonmatsu, 2002).

To understand the significantly higher thermal stability of the EK peptide, we investigated the potential stabilization of helical conformations due to salt-bridges. Potentials of mean force profiles show that formation of contact salt-bridges becomes more favorable with increasing temperature. The chain entropy contribution, in contrast, favors more extended chain conformations at higher temperatures. The spacing of E and K residues in EK peptide is such that the side-chain dihedral energies are somewhat unfavorable when a EK salt-bridge contact is formed. Therefore, the fraction of time that the three salt-bridge pairs actually spend in contact configurations is only near 10–20% over the entire temperature range. As a result, although salt-bridges have the potential to stabilize helical conformers, their contribution to the stability of EK helix is not a dominant one.

An alternative mechanism suggested by Scheraga and co-workers (Vila et al., 2000) involves stabilization of helical conformers through shielding of the backbone intrapeptide hydrogen bonds by large side-chain substituents. Indeed, the hydration pattern for the EK peptide backbone obtained from REMD simulations shows that lysine side chains sequester certain backbone H-bond-forming carbonyl (−C=O) and amide (−N–H) groups from water at low temperatures. A similar effect was reported recently for the Fs peptide that contains three positively charged arginines substituted in a polyalanine template (García and Sanbonmatsu, 2002). The increased thermal stability of EK and Fs peptides with respect to A21 observed in REMD simulations supports the hypothesis of Scheraga and co-workers (Vila et al., 2000). Availability of detailed snapshots of the peptide-water systems in REMD simulations provides further insights. For example, the shielding effect by the large side-chain substituent need not be a local effect; it depends on the sequence context as well as the relative positioning of the residues. In the specific EK peptide sequence studied here, positioning of the E and K residues was such that KE salt-bridges were never observed and the EK salt-bridge configurations were sparsely sampled. With proper placement of salt-bridge-forming residues along the sequence, it may be possible, to design highly thermostable helices in which stable salt-bridges are formed that simultaneously shield the backbone H-bonds from water.

A clearer understanding of factors imparting stability to helical conformers of short isolated peptides can provide valuable input to de novo design of helices. The importance of the shielding mechanism and other nonlocal tertiary effects is not limited to synthetic peptides and needs to be investigated through studies of peptides from naturally occurring proteins (Bystroff and Garde, 2003). The helical content and stability of such sequences are harder to quantify and characterize experimentally. Novel molecular simulation techniques such as REMD allow broad and efficient sampling of the configurational space of large systems that have rugged free energy landscapes and thus provide a powerful tool for studies of different peptides.

Acknowledgments

We thank Dr. K. Y. Sanbonmatsu for help with the REMD simulations and for insightful comments.

We gratefully acknowledge financial support from the National Science Foundation Career grant, CTS-0134023, and the American Chemical Society Petroleum Research Fund, PRF 37664-G7, for S.G; A.E.G. acknowledges financial support through Laboratory Directed Research and Development grant 2001013ER.

References

  1. Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  2. Bystroff, C., and S. Garde. 2003. Helix propensities of short peptides: molecular dynamics versus bioinformatics. Prot. Struct. Func. Gen. 50:552–562. [DOI] [PubMed] [Google Scholar]
  3. Chakrabartty, A., T. Kortemme, and R. L. Baldwin. 1994. Helix propensities of the amino acids measured in alanine-based peptides without helix-stabilizing side-chain interactions. Prot. Sci. 3:843–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cornell, W. D., P. Cieplak, C. I. Bayley, I. R. Gould, K. M. M. Jr., K. M. Ferguson, D. M. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A 2nd generation force-field for the simulation of proteins, nucleic acids, and organic-molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  5. Daura, X., W. F. van Gunsteren, and A. E. Mark. 1999. Folding-unfolding thermodynamics of a β-heptapeptide from equilibrium simulations. Prot. Struct. Func. Gen. 34:269–280. [DOI] [PubMed] [Google Scholar]
  6. Doig, A. J., A. Chakrabartty, T. M. Klinger, and R. L. Baldwin. 1994. Determination of free-energies of n-capping in α-helices by modification of the Lifson-Roig helix-coil theory to include n-capping and c–capping. Biochemistry. 33:3396–3403. [DOI] [PubMed] [Google Scholar]
  7. García, A. E., and K. Y. Sanbonmatsu. 2001. Exploring the energy landscape of a β-hairpin in explicit solvent. Prot. Struct. Func. Gen. 42:345–354. [DOI] [PubMed] [Google Scholar]
  8. García, A. E., and K. Y. Sanbonmatsu. 2002. Molecular evidence for alpha-helical stabilization by shielding the backbone hydrogen bonds by side-chain atoms. Proc. Natl. Acad. Sci. USA. 99:2782–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ghirlanda, G., J. D. Lear, N. L. Ogihara, D. Eisenberg, and W. F. DeGrado. 2002. A hierarchic approach to the design of hexameric helical barrels. J. Mol. Biol. 319:243–253. [DOI] [PubMed] [Google Scholar]
  10. Huang, C. Y., Z. Getahun, Y. J. Zhu, J. W. Klemke, W. F. DeGrado, and F. Gai. 2002. Helix formation via conformation diffusion search. Proc. Natl. Acad. Sci. USA. 99:2788–2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hummer, G., A. E. García, and S. Garde. 2000. Conformational diffusion and helix formation kinetics. Phys. Rev. Lett. 85:2637–2640. [DOI] [PubMed] [Google Scholar]
  12. Hummer, G., A. E. García, and S. Garde. 2001. Helix nucleation kinetics from molecular simulations in explicit solvent. Prot. Struct. Func. Gen. 42:77–84. [PubMed] [Google Scholar]
  13. Hummer, G., D. M. Soumpasis, and M. Neumann. 1994. Computer simulation of aqueous Na-Cl electrolytes. J. Phys. Cond. Matt. 6:A141–A144. [Google Scholar]
  14. Huyghues-Despointes, B. M. P., J. M. Scholtz, and R. L. Baldwin. 1993. Effect of a single aspartate on helix stability at different positions in a neutral alanine-based peptide. Prot. Sci. 2:1604–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ingwall, R. T., H. A. Scheraga, N. Lotan, A. Berger, and E. Katchalski. 1968. Conformational studies of poly-l-alanine in water. Biopolymers. 6:331–368. [DOI] [PubMed] [Google Scholar]
  16. Jorgensen, W. L., J. Chandrashekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple liquid potentials for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  17. Lifson, S., and A. Roig. 1961. On the theory of helix-coil transition in polypeptides. J. Chem. Phys. 34:1963–1974. [Google Scholar]
  18. Lockhart, D. J., and P. S. Kim. 1993. Electrostatic screening of charge and dipole interactions with the helix backbone. Science. 260:198–202. [DOI] [PubMed] [Google Scholar]
  19. Marinari, E., and G. Parisi. 1992. Simulated tempering: a new Monte Carlo scheme. Eur. Phys. Lett. 19:451–458. [Google Scholar]
  20. Marqusee, S., and R. L. Baldwin. 1987. Helix stabilization by Glu−-Lys+ salt-bridges in short peptides of de novo design. Proc. Natl. Acad. Sci. USA. 84:8898–8902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Marqusee, S., V. H. Robbins, and R. L. Baldwin. 1989. Unusually stable helix formation in short alanine-based peptides. Proc. Natl. Acad. Sci. USA. 86:5286–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mayne, L., S. W. Englander, R. Qiu, J. X. Yang, Y. X. Gong, E. J. Spek, and N. R. Kallenbach. 1998. Stabilizing effect of a multiple salt-bridge in a prenucleated peptide. J. Am. Chem. Soc. 120:10643–10645. [Google Scholar]
  23. Miller, J. S., R. J. Kennedy, and D. S. Kemp. 2002. Solubilized, spaced polyalanines: a context-free system for determining amino-acid α-helix propensities. J. Am. Chem. Soc. 124:945–962. [DOI] [PubMed] [Google Scholar]
  24. Neidigh, J. W., R. M. Fesinmeyer, and N. H. Andersen. 2002. Designing a 20-residue protein. Nat. Struct. Biol. 9:425–430. [DOI] [PubMed] [Google Scholar]
  25. Nowak, A. P., V. Breedveld, L. Pakstis, B. Ozbas, D. J. Pine, D. Pochan, and T. J. Deming. 2002. Rapidly recovering hydrogel scaffolds from self-assembling diblock copolypeptide amphiphiles. Nature. 417:424–428. [DOI] [PubMed] [Google Scholar]
  26. Perlman, D. A., D. A. Case, J. C. Caldwell, G. L. Seibel, U. C. Singh, P. Weiner, and P. A. Kollman. 1995. AMBER 4.1.
  27. Petka, W. A., J. L. Harden, K. P. McGrath, D. Wirtz, and D. Tirrell. 1998. Reversible hydrogels from self-assembling artificial proteins. Science. 281:389–392. [DOI] [PubMed] [Google Scholar]
  28. Privalov, P. L. 1982. Stability of proteins—proteins which do not present a single cooperative system. Adv. Prot. Chem. 35:1–104. [PubMed] [Google Scholar]
  29. Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
  30. Sanbonmatsu, K. Y., and A. E. García. 2002. Structure of met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Prot. Struct. Func. Gen. 46:225–234. [DOI] [PubMed] [Google Scholar]
  31. Scholtz, J. M., and R. L. Baldwin. 1992. The mechanism of α-helix formation by peptides. Annu. Rev. Biophys. Biomol. Struct. 21:95–118. [DOI] [PubMed] [Google Scholar]
  32. Scholtz, J. M., D. Barrick, E. J. York, J. M. Stewart, and R. L. Baldwin. 1995. Urea unfolding of peptide helices as a model for interpreting protein unfolding. Proc. Natl. Acad. Sci. USA. 92:185–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shoemaker, K. R., P. S. Kim, D. N. Brems, S. Marqusee, E. J. York, I. M. Chaiken, J. M. Stewart, and R. L. Baldwin. 1985. Nature of the charged-group effect on the stability of the c-peptide helix. Proc. Natl. Acad. Sci. USA. 82:2349–2353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Spek, E. J., C. A. Olson, Z. S. Shi, and N. R. Kallenbach. 1999. Alanine is an intrinsic α-helix stabilizing amino acid. J. Am. Chem. Soc. 121:5571–5572. [Google Scholar]
  35. Sugita, Y., and Y. Okamoto. 1999. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 314:141–151. [Google Scholar]
  36. Ventura, S., M. C. Vega, E. Lacroix, I. Angrand, L. Spagnolo, and L. Serrano. 2002. Conformational strain in the hydrophobic core and its implications for protein folding and design. Nat. Struct. Biol. 9:485–493. [DOI] [PubMed] [Google Scholar]
  37. Vila, J., D. R. Ripoll, and H. A. Scheraga. 2000. Physical reasons for the unusual α-helix stabilization afforded by charged or neutral polar residues in alanine-rich peptides. Proc. Natl. Acad. Sci. USA. 97:13075–13079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Vila, J., R. L. Williams, J. A. Grant, J. Wojcik, and H. A. Scheraga. 1992. The intrinsic helix-forming tendency of l-alanine. Proc. Natl. Acad. Sci. USA. 89:7821–7825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Williams, L., K. Kather, and D. S. Kemp. 1998. High helicities of lys-containing, ala-rich peptides are primarily attributable to a large, context-dependent lys stabilization. J. Am. Chem. Soc. 120:11033–11043. [Google Scholar]
  40. Williams, S., T. P. Causgrove, R. Gilmanshin, K. S. Fang, R. H. Callender, W. H. Woodruff, and R. B. Dyer. 1996. Fast events in protein folding: helix melting and formation in a small peptide. Biochemistry. 35:691–697. [DOI] [PubMed] [Google Scholar]
  41. Yang, J., K. Zhao, Y. Gong, A. Vologodskii, and N. R. Kallenbach. 1998. Alpha-helix nucleation constant in copolypeptides of alanine and ornithine or lysine. J. Am. Chem. Soc. 120:10646–10652. [Google Scholar]
  42. Zimm, B. H., and J. K. Bragg. 1959. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 31:476–485. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES